Electrochemical preparation and properties of a Mg–Li–Y alloy via co-reduction of Mg(II) and Y(III) in chloride melts

Abstract

Mg–Li based alloys have been widely used in various fields. However, the widespread use of Mg–Li based alloys were restricted by their poor properties. The addition of rare earth element in Mg–Li can significantly improve the properties of alloys. In the present work, different electrochemical methods were used to investigate the electrochemical behavior of Y(III) on the W electrode in LiCl–KCl melts and LiCl–KCl–MgCl₂ melts. In LiCl–KCl melts, typical cyclic voltammetry was used to study the electrochemical mechanism and thermodynamic parameters for the reduction of Y(III) to metallic Y. In LiCl–KCl–MgCl₂ melts, the formation mechanism of Mg–Y intermetallic compounds was investigated, and the results showed that only one kind of Mg–Y intermetallic compound was formed under our experimental conditions. Mg–Li–Y alloys were prepared via galvanostatic electrolysis, and XRD and SEM equipped with EDS analysis were used to analyze the samples. Because of the restrictions of EDS analysis, ICP-AES was used to analyze the Li content in Mg–Li–Y alloys. The microhardness and Young's modulus of the Mg–Li–Y alloys were then evaluated.

---

1. Introduction

Magnesium–lithium alloys are the lightest commercialized metallic structural material and have many advantages, such as high specific strength, high specific rigidity, and good casting capability. In the last few years, magnesium–lithium alloys have been widely used in various fields.^1,2 However, the widespread use of magnesium–lithium alloys has been restricted by their poor properties, including their low microhardness, low elastic modulus, and poor corrosion properties. In recent years, various methods have been used to improve the properties of magnesium–lithium alloys. Among these methods, the addition of a metallic element in magnesium–lithium alloys is one of the more effective means.^3–8 Because rare earth elements have a unique outer layer that is a 4f electronic layer structure, rare earth elements have only 5d and 6s electrons that can become free electrons. Therefore, rare earth elements have also been selected as the added metallic element in magnesium–lithium alloys to improve the properties of the alloys.

The traditional method for preparing magnesium–lithium alloys is mixing and fusing a metallic element, which has many shortcomings such as extremely expensive raw materials, high pollution and high-energy consumption. In recent years, aluminum, magnesium, and other metals alloys have been directly prepared via the electrochemical reduction method.^9–16 In comparison to the traditional method, an electrochemical reduction method that uses inorganic molten salts as electrolytes has many advantages of mass production, simple procedure and low-energy consume. In this work, Mg–Li-based alloys were directly prepared via electrochemical reduction using inorganic molten salts as electrolytes. Because the temperature of the molten salt system is evenly distributed, the electrolysis potential is easy to control in the electrolysis process, and the phase composition of specific intermetallic compounds can be controlled.^12,14 Furthermore, using electrochemical reduction with inorganic molten salts as electrolytes significantly reduces the reaction temperature, and this leads to lower energy consumption.^17,18 In the past few years, the information about the preparation and formation of Mg–Li and Mg–Li–RE alloys by molten salt electrolysis has been reported by many researchers. Yan et al. described the electrochemical behavior of Pr(III), Tm(III), Yb(III) in chloride melts, explored the formation mechanism of alloys, and successfully prepared the Mg–Li,¹⁹ Mg–Li–Pr,²⁰ Mg–Li–Tm²¹ and Mg–Li–Yb²² alloys by potentiostatic/galvanostatic electrolysis. In KCl–MgCl₂–PrCl₃ molten salts Mg–Pr intermetallic compounds were prepared by Sahoo et al.²³ XRD analysis illustrated that the phase conversion between MgPr, Mg₂Pr, Mg₃Pr and Mg₁₂Pr could be achieved by changing the concentration of MgCl₂ and PrCl₃. On an inert electrode, Zhang et al.^24–26 prepared Mg–Li-Gd, Mg–Li–La, Mg–Li–Er alloys in LiCl–KCl molten salt system. The effects of concentration, current density, experimental temperature and electrolysis time on the composition of the alloys were investigated. Based on above studies, the information about the preparation of Mg–Li–Y alloy by co-deposition of Mg(II) and Y(III) are rare.

The main purpose of this work is to prepare Mg–Li–Y alloys via electrochemical reduction using inorganic molten salts as electrolytes. Therefore, it is necessary to investigate the electrochemical behavior of Y(III) in inorganic molten salts. Over the past few years, many researchers have reported studies regarding the electrochemical behavior of RE(III) in molten salt.^27–37 The kinetic and thermodynamic parameters can be obtained via different electrochemical measurements. However, investigations regarding the electrochemical behavior of Y(III) in inorganic molten salts are rare in the literature.

Therefore, this research focuses on investigating the electrochemical behavior of Y(III) in LiCl–KCl molten salt using different electrochemical methods. Cyclic voltammetry and chronopotentiometry were used to determine the diffusion coefficient of Y(III) in LiCl–KCl melts. Cyclic voltammetry was also used to ascertain the apparent standard potential for the formation of metal Y. Cyclic voltammetry, square wave voltammetry, and chronopotentiometry were used to investigate the co-deposition mechanism of Mg(II) and Y(III) on the W electrode in LiCl–KCl melts. Mg–Li–Y alloys were then prepared via galvanostatic electrolysis, and XRD and SEM equipped with EDS analysis were used to analyze the deposits. The performance of the Mg–Li–Y alloy was tested using a Leitz microhardness tester and a tool for measuring the Young's modulus.

2. Experiment

Anhydrous LiCl and KCl were analytically pure and were obtained from Sinopharm Chemical Reagent Co., Ltd. YCl₃ (99.0%) and MgCl₂ (99.9%) were purchased from Aladdin Reagent Co., Ltd. All of the electrochemical measurements were carried out on in argon atmosphere. LiCl–KCl melts with a mass ratio of 1 : 1 were selected as the electrolyte. To measure the electrochemical behavior, the counter electrode that was used was a spectrally pure graphite rod (diameter of 6 mm). An Ag/AgCl electrode was used as the reference electrode, and all of the potentials were referenced to this Ag/AgCl couple. The working electrode was a tungsten electrode, and the electrode surface area was 0.322 cm².

All of electrochemical measurements were made using an Autolab potentiostat/galvanostat controlled with the Nova 1.11 software package. Electrochemical testing and preparation of the alloy were performed in a chamber electric furnace, and an electronic energy saving temperature controller was used to control the temperature. The Mg–Li–Y alloys were prepared via galvanostatic electrolysis on a W electrode with the assistance of MgCl₂. XRD (Rigaku D/max-TTR-III diffractometer) with Cu-Kα radiation at 40 kV and 150 mA was used to analyze the sample. Scanning electron microscopy (SEM) equipped with energy dispersive spectrometry (EDS) was used to investigate the microstructure and crystal structure of the sample. To determine the contents of Mg, Y, and Li in the sample, the sample was dissolved in aqua regia (a mixture of nitric acid and hydrochloric acid in a 1 : 3 molar ratio). The solution was diluted and analyzed using ICP-AES (Thermo Elemental, IRIS Intrepid II XSP). With testing conditions of a 50 N load force and 15 s of holding pressure time, a Leitzs microhardness tester was used to measure the microhardness of the alloy. Each group of experiments measured 20 points on the surface of the Mg–Li–Y alloy, and the final microhardness value was the average of the measurements. A 5077PR square wave pulser Receiver and Tektronix (DPO 3034) oscillograph was used to measure the Young's modulus of the Mg–Li–Y alloy.

3. Results and discussions

3.1 Electrochemical behavior of Y(III) on a W electrode in LiCl–KCl melts

In the following, the electrochemical behavior of Y(III) was first investigated using cyclic voltammetry. Fig. 1 shows typical cyclic voltammograms of LiCl–KCl melts before (black curve) and after (green curve) the addition of YCl₃ (2 wt%); the voltammograms were obtained on a W electrode at 823 K with a scan rate of 0.1 V s⁻¹. Before the addition of YCl₃ (2 wt%) in LiCl–KCl melts, one pair of redox signals (A/A′) and an oxidation signal (B′) are observed in the electrochemical window. At the beginning of the curve, the oxidation signal (B′) is related to the formation of Cl₂.^16,38,39 At the end of the curve, the reduction signal A is attributed to the formation of metal Li, and the other oxidation signal (A′) is related to the dissolution of metal Li. In the electrochemical window, the black curve that corresponds to purified blank salt shows no additional reaction signal. This indicates that purified LiCl–KCl melts are suitable for investigating the electrochemical behavior of Y(III).^27,39,40 After YCl₃ (2 wt%) was added to LiCl–KCl melts, redox signals (C/C′) are observed in the electrochemical window. The reduction signal C, which is at about −2.01 V vs. Ag/AgCl, corresponds to the formation of metal Y on the W electrode. Hua et al.³³ reported a similar reduction potential for NaCl–KCl melts. In the positive direction, the oxidation signal C′, which corresponds to the reduction signal C, is attributed to the dissolution of metal Y.

Fig. 1 Typical cyclic voltammogram of LiCl–KCl melts before (black curve) and after (green curve) the addition of YCl₃ (2 wt%) obtained on a W electrode (S = 0.322 cm²) at 823 K; Scan rate is 0.1 V s⁻¹.

Typical cyclic voltammograms were measured on the W electrode with different scan rates to further investigate the electrochemical mechanism and thermodynamic parameters for the formation of metal Y. Typical cyclic voltammograms with different scan rates at 823 K on the W electrode in LiCl–KCl–YCl₃ (2 wt%) melts are shown in Fig. 2a and c. The scan rate ranged from 10 mV s⁻¹ to 700 mV s⁻¹. For a soluble-insoluble reaction system, the ratio of the peak current density obtained from cyclic voltammetry is an inherent parameter. Therefore, this parameter is usually used to evaluate the reversibility of an electrode reaction.^30,41–43 Table 1 shows the values of the ratio of the peak current density that were obtained via cyclic voltammetry with different scan rates. When the scan rate is below 100 mV s⁻¹, the ratio of the peak current density is unity. However, the ratio of the peak current density deviated from unity when the scan rate ranged from 100 to 700 mV s⁻¹. These observations indicate that the redox of Y(III) on the W electrode was quasi-reversible. In other words, the redox process of Y(III) to metal Y is reversible when the scan rate is below 100 mV s⁻¹, and it is irreversible when the scan rate is greater than 100 mV s⁻¹. The relationship between E_p and ν^1/2 was then also plotted to illustrate the reversibility of the electrode reaction. Plots of peak potential versus the square root of the potential scan rate are shown in Fig. 2b and d. When the scan rate ranged from 10 to 100 mV s⁻¹, the peak potential did not change with respect to the scanning rate. When the scan rate is greater than 100 mV s⁻¹, the peak potentials change with an increasing in the scan rate. These results also illustrate that the redox process of Y(III) to metal Y is reversible at a low scan rate and irreversible at a high scan rate.

Fig. 2 Typical cyclic voltammogram of LiCl–KCl–YCl₃ (2 wt%) melts obtained on a W electrode (S = 0.322 cm²) with the different scan rate, (a): (10–50 mV s⁻¹) and (c): (100–700 mV s⁻¹) at 823 K; (b and d): peak potential versus the square root of the potential scan rate; (e and f): peak current versus the square root of the potential scan rate.

Table 1 Ratios of the anodic to cathodic peak current density

ν/mV s^−1	10	20	30	40	50	100	150	200	250	300	400	500	600	700
ipa/ipc	1.00	0.99	0.89	0.89	0.90	1.05	1.16	1.25	1.25	1.24	1.25	1.28	1.25	1.29

---

The relationship between peak current and the square root of the potential scan rate was used to investigate the control process of the electrode reaction. The relationship between peak current and the square root of the potential scan rate are shown in Fig. 2e and f. As seen in Fig. 2e and f, the peak current has an approximately linear relationship with the square root of the potential scan rate, and this indicates that the electrode reaction depends on the diffusion controlled.³⁴

For the reversible reaction at a low scanning rate, the diffusion coefficient for the reaction of Y(III) to metal Y on the W electrode can be calculated using the Berzins–Delahay equation.⁴⁴ The equation is as follows:

I_p = 0.611(nF)^3/2(RT)^−1/2SC₀D^1/2ϑ^1/2 (1)

where I_p corresponds to current intensity, n is the number of exchanged electrons, F is Faraday's constant, R is the gas constant, T is the absolute temperature, S is the effective electrode contact area, C₀ is the concentration of Y(III), D is the diffusion coefficient, and ν is the scan rate. According to previous work,³⁴ reduction of Y(III) to metal Y is a one-step process that involves the transfer of three electrons. Therefore, the diffusion coefficient of Y(III) on the W electrode is ultimately determined to be 8.3 × 10⁻⁵ cm² s⁻¹ at a low scanning rate.

For the irreversible reaction at a high scanning rate, the diffusion coefficient of Y(III) to metal Y on the W electrode can be calculated using the following equation:⁴⁵

I_p = −0.4958(F)^3/2(RT)^−1/2α^1/2SC₀D^1/2ϑ^1/2 (2)

The value of α can be obtained using the following equation:

where E_p is the cathode peak potential, E_p/2 is the half-peak potential of the cathode, and α is the charge transfer coefficient. At a high scanning rate, the diffusion coefficient of Y(III) on the W electrode is ultimately determined to be 1.07 × 10⁻⁴ cm² s⁻¹.

The apparent standard potential can be calculated from the cathodic peak potentials in a cyclic voltammogram. For the reversible soluble-insoluble system at a low scanning rate, the cathodic peak potential can be expressed as:

orwhere E_p is the cathodic peak potential, E_Y³⁺/Y⁰ is the standard potential, γ_Y³⁺ is the activity coefficient, and X_Y³⁺ is the mole fraction of Y³⁺ in the melts. The assumption is that the activity of the metal Y is unity. Therefore, the equation can be expressed as:where is the apparent standard potentials of Y³⁺/Y. Eqn (6) can be used to calculate the apparent standard potentials of Y³⁺/Y, which was ultimately calculated to be −2.01 V (vs. Ag/AgCl) at 823 K.

Chronopotentiometry was used to further investigate the electrochemical behavior of Y(III) and to calculate the diffusion coefficient of Y(III) in LiCl–KCl–YCl₃ (2 wt%) melts at different temperatures. Chronopotentiograms that were obtained on the W electrode in LiCl–KCl–YCl₃ (2 wt%) melts with different current intensity at 823 K are shown in Fig. 3a. As seen in Fig. 3a, a potential plateau (C) is observed at around −2.05 V; plateau C corresponds to the formation of metal Y. The obtained result is consistent with result observed in the cyclic voltammogram. The transition time (τ) can be acquired from the chronopotentiograms. Chronopotentiograms with different current intensities (−65 mA, −70 mA, −75 mA, and −80 mA) were measured at 823 K, 873 K, 923 K, and 973 K to calculate the diffusion coefficient of Y(III) in LiCl–KCl–YCl₃ (2 wt%) melts, and the different transition time (τ) were also obtained. Meanwhile, the dependence of I on the transition time τ was plotted. Fig. 3b exhibits a linear relationship of I versus τ^−1/2 for the chronopotentiometry at five different temperatures, and the straight line passes through the origin. In other words, a mass transport process mainly controls the reduction of Y(III) to metal Y. Thus, the Sand equation^13,28,46,47 can be used to calculate the diffusion coefficient of Y(III) in LiCl–KCl–YCl₃ melts on the W electrode. The Sand equation is as follows:

D = 4I²τ/n²F²πC²₀S² (7)

where τ corresponds to the transition time. The diffusion coefficients at different temperatures are listed in Table 2. As seen in Table 2, the experimental temperature can be used to control the diffusion coefficient. Along with an increasing in the experimental temperature, the diffusion coefficient is higher.

Fig. 3 (a): Chronopotentiograms obtained on the W electrode in LiCl–KCl–YCl₃ (2 wt%) melts with different current intensity at 823 K; (b): linear relationship of I versus τ^−1/2 for the chronopotentiometric at different temperatures.

Table 2 Diffusion coefficients of Y(III) ions on W electrode in LiCl–KCl–YCl₃ (2 wt%) melts at different temperatures

T(K)	823	873	923	973
D × 10^4/cm^2 s^−1	1.39	1.84	2.31	2.73

---

3.2 Electrochemical behavior of Y(III) and Mg(II) on a W electrode in LiCl–KCl melts

Cyclic voltammetry was used to investigate the electrochemical formation mechanism of Mg_xY_y intermetallic compounds. Fig. 4 shows a typical cyclic voltammogram of LiCl–KCl melts that have added MgCl₂ (1 wt%) and YCl₃ (2 wt%); the cyclic voltammograms were obtained on a W electrode (s = 0.322 cm²) at 823 K. Compared to the cyclic voltammogram of blank LiCl–KCl melts, the cyclic voltammogram of the sample with added MgCl₂ (1 wt%) showed a signal for F and a pair of redox signals for D/D′. The reduction signal D is related to the formation of metal Mg. The oxidation signal D′ corresponds to the reduction signal D and is attributed to the dissolution of metal Mg.^{20,21,48–50} The reduction signal F, which is near signal A, is associated with the formation of a Mg–Li intermetallic compound that is formed via underpotential deposition of Li(I) on Mg that was predeposited on the W electrode.⁴¹ After YCl₃ (2 wt%) was added to LiCl–KCl–MgCl₂ (1 wt%) melts, redox signals E and E′ are observed in addition to the redox signals A/A′, D/D′, and the reduction signal F. The reduction signal E, which is between signals D and F, are related to the formation of a Mg–Y intermetallic compound that is formed by underpotential deposition of Y(III) on the Mg that was predeposited on the W electrode. The oxidation signal E′ corresponds to the reduction signal E and is attributed to the subsequent dissolution of the Mg–Y intermetallic compound. According to the binary alloy phase diagram, there are three kinds of Mg–Y intermetallic compounds that should form on a W electrode. However, only one pair of electrochemical signals that correspond to the formation and dissolution of Mg–Y intermetallic compounds is detected. The absence of other Mg–Y intermetallic compounds may be because of the deposition potentials of signal E are similar and because the formation rate of other Mg–Y intermetallic compounds is very slow.^46,48,51

Fig. 4 Typical cyclic voltammogram of LiCl–KCl melts with the addition of MgCl₂ (1 wt%) and YCl₃ (2 wt%) obtained on a W electrode (S = 0.322 cm²) at 823 K; scan rate is 0.1 V s⁻¹.

To verify whether the Mg–Li and Mg–Y intermetallic compounds are formed via underpotential deposition of Li(I) and Y(III) on Mg that was predeposited on the W electrode, the semiempirical equation was used.^52–54 The equation is as follows:

ΔU = αΔφ (8)

where ΔU is the difference between the monolayer underpotential deposition voltage and the bulk deposition voltage, Δφis the difference between the work functions of the substrate and deposited metal, and α is a constant that has a value of 0.5 V eV⁻¹. ΔU values are calculated to be 0.38 (Mg–Li) and 0.08 (Mg–Y).⁵⁴ Thus, the underpotential deposition of Li(I) and Y(III) on the Mg that was predeposited on the W electrode was achieved under our experimental conditions.

An interesting phenomenon is found in Fig. 4. After YCl₃ (2 wt%) was added to LiCl–KCl–MgCl₂ (1 wt%) melts, the current density of the reduction signal D, which corresponds to the formation of Mg, is almost unchanged. However, the current density of the oxidation signal D′ significantly decreased; specifically, the current density decreased by 17.5%. This indicates that the mass of metal Mg that dissolved to Mg(II) decreases in the positive direction. This phenomenon may occur because the Mg that was pre-deposited on the W electrode is consumed in the reduction of Y(III) ions; the reaction equation is as follows:

3Mg + 2Y³⁺ → 2Y(in Mg–Y) + 3Mg²⁺ (9)

Square wave voltammetry is a more sensitive method than cyclic voltammetry. Therefore, we used square wave voltammetry to verify the results that were obtained via cyclic voltammetry. As seen in Fig. 5, three reduction signals (D, F, and G) were detected when MgCl₂ (1 wt%) was added to LiCl–KCl melts. The signal D is also related to the reduction of Mg(II) to metal Mg. Unlike the results obtained via cyclic voltammetry (Fig. 4), the second signal (G) corresponds to the formation of Mg–Li intermetallic compounds, and the signal F is not observed. However, the signal G was not observed in the cyclic voltammetry curves that were obtained for LiCl–KCl–MgCl₂ (1 wt%) melts. This phenomenon should be attributed to the reason that the reduction signal of Li(I) to metal Li is too large, and the reduction signal G overlapped with signal A. Therefore, the reduction signal G was not detected via cyclic voltammetry. When YCl₃ (2 wt%) was added to LiCl–KCl melts, signals A and C, which are attributed to the reduction of Li(I) and Y(III), respectively, were detected. When MgCl₂ (1 wt%) and YCl₃ (2 wt%) were both present in LiCl–KCl melts, three reduction signals (D, E, and A) are observed. The reduction signal E is related to the formation of the Mg–Y intermetallic compound. Interestingly, the same phenomenon occurs, that is, the current density of signal D significantly decreases when YCl₃ (2 wt%) was added to LiCl–KCl–MgCl₂ melts. The results from square wave voltammetry further verify the results that were obtained via cyclic voltammetry.

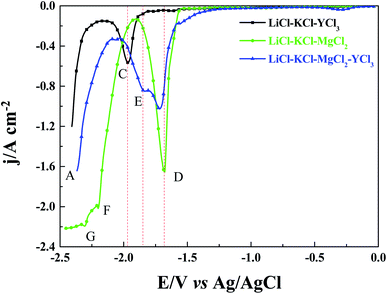Fig. 5 Square wave voltammogram of LiCl–KCl melts with the addition of MgCl₂ (1 wt%) and YCl₃ (2 wt%) obtained on a W electrode (S = 0.322 cm²) at 823 K.

The results that were obtained via cyclic voltammetry are not sufficient to explain the formation mechanism of intermetallic compounds. Hence, open circuit chronopotentiometry was used to investigate the formation mechanism of the Mg–Y intermetallic compound. The open-circuit potential transient curve of LiCl–KCl melts with added MgCl₂ (1 wt%) and YCl₃ (2 wt%) is shown in Fig. 6. When only MgCl₂ was present in LiCl–KCl melts, a potential platform (D), which corresponds to the reduction of Mg(II) to metal Mg is observed. The potential platform C, which is at around −1.92 V in the open-circuit potential transient curve that is obtained in LiCl–KCl melts with added YCl₃ (2 wt%), is related to the formation of metal Y. The result that is obtained via open circuit chronopotentiometry is in a good agreement with the result that is obtained via cyclic voltammetry. When MgCl₂ and YCl₃ are both present in molten salt systems, a new potential platform (I) is observed and can be interpreted as the formation of the Mg–Y intermetallic compound. According to the open circuit chronopotentiometry and XRD pattern in subsequent investigation, the electrochemical co-deposition of the Mg–Y intermetallic compound involves two consecutive steps, which can be described as follows:

24Mg²⁺ + 48e⁻ → 24Mg (10)

5Y³⁺ + 24Mg + 15e⁻ → Mg₂₄Y₅ (11)

Fig. 6 Open-circuit potential transient curve of LiCl–KCl melts with the addition of MgCl₂ (1 wt%) and YCl₃ (2 wt%) obtained on a W electrode (S = 0.322 cm²) at 823 K.

The overall reaction can be described as follows:

24Mg²⁺ + 5Y³⁺ + 63e⁻ → Mg₂₄Y₅ (12)

3.3 Electrochemical preparation and characterization of the Mg–Li–Y alloy

According to results from the different electrochemical method, one kind of Mg–Y intermetallic compound is formed under our experimental conditions. Preparation of Mg–Li–Y alloys via galvanostatic electrolysis was attempted with various concentrations of MgCl₂ at 823 K. However, it is difficult to produce large amounts of Mg–Li–Y alloys because of the undesirable coalescence (dendritic deposits), which occurs at low experimental temperature.³¹ Thus, we prepared Mg–Li–Y alloys at 973 K. The XRD pattern of Mg–Li–Y alloys that were obtained via galvanostatic electrolysis in LiCl–KCl–MgCl₂–YCl₃ melts on the W electrode at 973 K are shown in Fig. 7. The results show that the obtained alloy mainly contains Mg and Mg₂₄Y phases. SEM equipped with EDS mapping and quantitative analysis were used to further examine the microstructure and distribution of Mg and Y elements in Mg–Li–Y alloys. SEM images of the Mg–Li–Y alloy that was obtained on the W electrode at 973 K are shown in Fig. 8a and b. The Mg–Li–Y alloy can be clearly distinguished by the grey and bright zones (Fig. 8a and b), where the bright zones indicate the Mg–Y intermetallic compound and grey zones indicate the Mg substrate. Subsequently, we used EDS mapping and quantitative analysis to verify our conjecture. As seen in Fig. 8c and d, the EDS mapping analysis indicates that the Mg is mainly distributed in the grey zone, and the Y is mainly distributed in the bright zone. EDS quantitative analysis of the Mg–Li–Y alloy is shown in Fig. 8e and f. Point 1 is in the bright zone, and point 2 is in the grey zone. The EDS quantitative analysis further verified the results obtained via EDS mapping analysis. On the basis of the XRD, SEM, and EDS results, the electrochemical signal E, which is observed in different electrochemical curves, can be assigned to Mg₂₄Y₅.

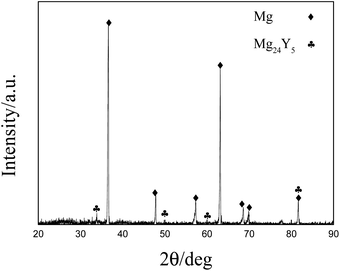Fig. 7 XRD pattern of Mg–Li–Y alloy obtained by galvanostatic electrolysis (−0.4 A) in MgCl₂ (8 wt%)–YCl₃ (2 wt%) melts on the W electrode (S = 0.322 cm²) at 973 K.

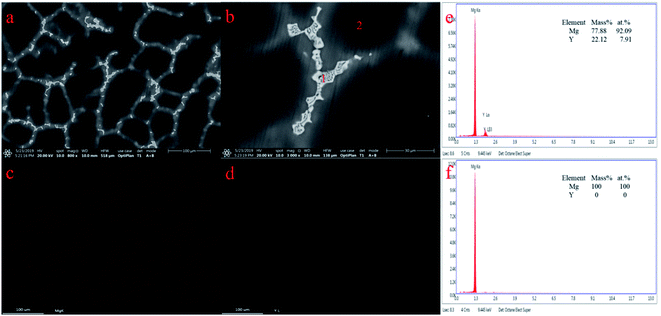Fig. 8 SEM (a and b), EDS mapping (c and d) and quantitative (e and f) analysis of Mg–Li–Y alloy obtained by galvanostatic electrolysis (−0.4 A) in LiCl–KCl–MgCl₂ (8 wt%)–YCl₃ (2 wt%) melts on the W electrode (S = 0.322 cm²) at 973 K.

It is well known that, the composition of an alloy could be adjusted by the concentrations of M_xCl_y (M = Al, Zn, and Mg).^13,40,46 Therefore, Mg–Li–Y alloys were prepared via galvanostatic electrolysis on the W electrode at 973 K using different concentrations of added MgCl₂. The EDS detectors cannot detect the presence of elements with atomic number less than 4, meaning that EDS cannot detect Li, thus the distribution of Li element is not shown in Fig. 8. Therefore, the ICP analysis were applied to analysis the content of Mg, Li and Y. Table 3 exhibits results of the ICP analysis of Mg–Li–Y alloys. As seen in Table 3, when the concentration of YCl₃ is constant, the concentration of MgCl₂ can be used to adjust the content of Y and Li in the Mg–Li–Y alloys.

Table 3 ICP analysis of Mg–Li–Y alloys obtained by galvanostatic electrolysis (−0.4 A) on W electrode (S = 0.322 cm²) in LiCl–KCl–YCl₃ (2 wt%) melts with the different concentrations of MgCl₂ at 973 K

Samples	MgCl2 concentration (wt%)	YCl3 concentration (wt%)	Y content (wt%)	Li content (wt%)	Mg content (wt%)
1	8.0	2	8.47	5.17	Bal.
2	10.0	2	6.65	4.36	Bal.
3	12.0	2	4.98	3.92	Bal.
4	14.0	2	3.03	2.77	Bal.

---

The main purpose of adding Y into the Mg–Li alloy is to strengthen the properties of the Mg–Li alloy. Therefore, the microhardness and Young's modulus of the Mg–Li–Y alloy were measured using a Leitzs microhardness tester and a tool for measuring Young's modulus. The Mg–Li and Mg–Li–Y alloys with nearly the same composition of Mg and Li were prepared under the same experiment condition. A diagram that compares the values of the microhardness and Young's modulus of the Mg–Li–Y alloy (column chart 1) and Mg–Li alloy (column chart 2) are shown in Fig. 9. Compared to the microhardness of the Mg–Li alloy, the microhardness of the Mg–Li–Y alloy was enhanced 14.26% (57.29 ± 0.5 GPa and 50.14 ± 0.4 GPa). In a work by Chapelon et al.⁵⁵ and our previous work,⁵³ the Young's modulus of the Mg–Li–Y alloy was measured using the tool for Young's modulus. As seen in Fig. 9, the Young's modulus of the Mg–Li–Y alloy is 55.97 ± 0.4 GPa, and that of the Mg–Li alloy is 47.65 ± 0.0.6 GPa. With the inclusion of Y, the Young's modulus of the Mg–Li based alloy increased 17.4%.

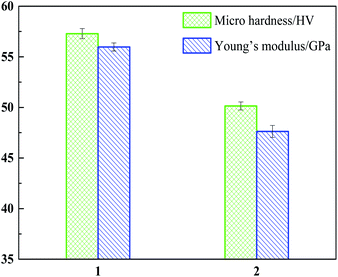Fig. 9 Comparison diagrams of micro hardness and Young's modulus of Mg–Li–Y (column 1) and Mg–Li (column 2) alloys.

4. Conclusions

Cyclic voltammetry and chronopotentiometry were used to determine the diffusion coefficient of Y(III) in LiCl–KCl melts on the W electrode. The calculated results from chronopotentiometry illustrate that the experimental temperature can be used to adjust the diffusion coefficient of Y(III) in LiCl–KCl melts. The results from the cyclic voltammetry show that the reduction process of Y(III) to metal Y is reversible when the scan rate is below 100 mV s⁻¹, and it is irreversible when the scan rate is greater than 100 mV s⁻¹. At a low scanning rate, the apparent standard potential of Y(III)/Y(0) was ultimately calculated to be −2.01 V at 823 K. The results obtained using different electrochemical methods show that only one kind of Mg–Y intermetallic compound was formed in LiCl–KCl–MgCl₂ melts under the experiment conditions. The Mg–Li–Y alloys were prepared via galvanostatic electrolysis, and the Mg₂₄Y₅ intermetallic compound was detected using XRD analysis. The ICP analysis of the Mg–Li–Y alloys illustrate that the concentration of MgCl₂ can be used to adjust the content of Y and Li in the Mg–Li–Y alloys. With the inclusion of Y, the microhardness and Young's modulus of the Mg–Li-based alloy increased 14.26% and 17.4%, respectively.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was financially supported by the National Natural Science Foundation of China (51574097 and 51774104), the China Postdoctoral Science Foundation (2017M621244), Postdoctoral Research Start-up Gold in Heilongjiang Province (16180019) and the Science Foundation of Northeast Petroleum University (15011030811, 1305021863 and 15041260347).

References

1. J. Song, T. Wen and J. Wang, Scr. Mater., 2007, 56, 529–532.
2. A. K. Sharma, R. U. Rain, H. Bhojaraj and H. Narayanamurthy, J. Appl. Electrochem., 1993, 23, 500–507.
3. D. Zdenvek, T. Zuzanka and K. Stanislav, J. Alloys Compd., 2004, 378, 192–195.
4. H. Takuda, S. Kikuchi, T. Tshukada, K. Kuboda and N. Hatta, J. Mater. Sci. Eng. A, 1999, 271, 251–256.
5. R. Wu, Z. Qu and M. Zhang, Rev. Adv. Mater. Sci., 2010, 24, 5–43.
6. Z. Chen and Z. Li, J. Mater. Sci. Eng. A, 2011, 528, 961–966.
7. T. Wang, M. Zhang, Z. Niu and B. Lin, J. Rare Earths, 2006, 24, 797–800.
8. R. Wu, Z. Qu and M. Zhang, J. Mater. Sci. Eng. A, 2009, 516, 96–99.
9. Y. Dong, T. Slade, J. S. Matthew, L. Li, N. G. Steven, L. Mai and S. Jin, Angew. Chem., Int. Ed., 2017, 56, 14453–14457.
10. G. Z. Chen, D. J. Fray and T. W. Farthing, Nature, 2000, 407, 361–364.
11. C. A. M. Abdelkader, K. T. Kilby, A. Cox and D. J. Fray, Chem. Rev., 2013, 113, 2863–2886.
12. D. Ji, Y. Yan, M. Zhang, X. Li, X. Jing, W. Han, Y. Xue, Z. Zhang and T. Hartmann, Electrochim. Acta, 2015, 165, 211–220.
13. Y. Yan, D. Ji, Y. Xue, M. Zhang, P. Wang, Y. Liu, T. Yin, P. Li, W. Han and J. Wang, J. Electrochem. Soc., 2017, 164, D429–D435.
14. S. Jiao, L. Zhang, H. Zhu and D. Fray, Electrochim. Acta, 2010, 55, 7016–7020.
15. Y. Liu, L. Yuan, K. Liu, L. Zhu, M. Zhang, Z. Chai and W. Shi, Electrochim. Acta, 2014, 147, 104–113.
16. T. Yin, K. Liu, Y. Liu, Y. Yan, G. Wang, Z. Chai and W. Shi, J. Electrochem. Soc., 2018, 165, D452–D460.
17. H. Yin, B. Chung and D. R. Sadoway, Nat. Commun., 2016, 7, 1–5.
18. A. Allanore, L. Yin and D. R. Sadoway, Nature, 2013, 497, 353–356.
19. Y. Yan, M. Zhang, W. Han, Y. Xue, D. Cao and Y. Yuan, Chem. Lett., 2008, 37, 212.
20. H. Tang, Y. Yan, M. Zhang, X. Li, W. Han, Y. Xue and H. He, Electrochim. Acta, 2013, 107, 209.
21. X. Li, Y. Yan, M. Zhang, H. Tang, D. Ji, W. Han and Z. Zhang, Electrochim. Acta, 2014, 135, 327.
22. X. Li, Y. Yan, M. Zhang, Y. Xue, D. Ji, H. Tang and Z. Zhang, J. Electrochem. Soc., 2014, 161, D704.
23. D. K. Sahoo, M. Anitha, D. K. Singh and V. Kain, Miner. Process. Extr. Metall., 2019, 12, 1.
24. S. Wei, M. Zhang, W. Han, Y. Yan, M. Zhang and B. Zhang, Transactions of Nonferrous Metals Society of China, 2011, 21, 825.
25. M. Zhang, P. Cao, W. Han, Y. Yan and L. Chen, Transactions of Nonferrous Metals Society of China, 2012, 22, 16.
26. P. Cao, M. Zhang, W. Han, Y. Yan, S. Wei and T. Zheng, J. Rare Earths, 2011, 29, 763.
27. H. Tang and B. Pesic, Electrochim. Acta, 2014, 119, 120–130.
28. T. Yin, Y. Liang, J. Qu, P. Li, R. An, Y. Xue, M. Zhang, W. Han, G. Wang and Y. Yan, J. Electrochem. Soc., 2017, 164, D835–D842.
29. P. Masset, J. Konings, R. Malmbeck, J. Serp and J. P. Glatz, J. Nucl. Mater., 2005, 344, 173–179.
30. P. Wang, D. Ji, D. Ji, J. Zheng, Y. Yan, M. Zhang, W. Han and H. Wu, J. Nucl. Mater., 2019, 517, 157–164.
31. Y. Gao, Y. Shi, X. Liu, C. Huang and B. Li, Electrochim. Acta, 2016, 190, 208–214.
32. K. Liu, Y. Liu, Z. Chai and W. Shi, J. Electrochem. Soc., 2017, 164, D169–D178.
33. H. Tang and B. Pesic, J. Nucl. Mater., 2015, 458, 37–44.
34. J. He, Z. Hua, H. Liu, L. Xu, S. He, Y. Yang and Z. Zhao, J. Electrochem. Soc., 2018, 165, E598–E603.
35. B. K. Kim and B. G. Park, Electrochim. Acta, 2019, 295, 270–277.
36. Y. Liu, L. Yuan, L. Zheng, L. Wang, B. Yao, Z. Chai and W. Shi, Electrochem. Commun., 2019, 103, 55–60.
37. M. Li, Y. Liu, Z. Sun, W. Han, M. Zhang, X. Yang and Y. Sun, Chem. Res. Chin. Univ., 2019, 35, 60–64.
38. T. Yin, K. Liu, Y. Liu, Y. Yan, G. Wang, Z. Chai and W. Shi, J. Electrochem. Soc., 2018, 165, D722–D730.
39. Y. Yan, H. Tang, M. Zhang, Y. Xue, W. Han, D. Cao and Z. Zhang, Electrochim. Acta, 2012, 59, 531–537.
40. D. Ji, T. Yin, Y. Yan, M. Zhang, P. Wang, Y. Liu, J. Zheng, Y. Xue, X. Jing and W. Han, RSC Adv., 2016, 6, 29353–29364.
41. W. Wu, S. Guo and J. Zhang, Int. J. Electrochem. Sci., 2008, 13, 225–234.
42. L. Massot, P. Chamelot, L. Cassayre and P. Taxil, Electrochim. Acta, 2009, 54, 6361–6366.
43. A. J. Bard and L. R. Faulkner, Electrochemical Methods: Principles and Applications, Wiley, New York, 2nd edn, 2001.
44. T. Berzins and P. Delahay, J. Am. Chem. Soc., 1953, 75, 555–559.
45. A. J. Bard and L. R. Faulkner, Electrochemical Methods Fundamentals and Applications, John Wiley & Sons, New York, 2nd edn, 2002.
46. Z. Hua, H. Liu, J. Wang, J. He, S. Xiao, Y. Xiao and Y. Yang, ACS Sustainable Chem. Eng., 2017, 5, 8089–8096.
47. H. Tang, Y. Ren, S. Wang, H. Deng, D. Cai, L. Shao, Y. Zhao, R. Gao, Y. Yan and M. Zhang, J. Electrochem. Soc., 2015, 162, 10–17.
48. Y. Xue, D. Ji, Y. Yan, M. Zhang, Y. Liu, P. Wang, T. Yin, P. Li, Y. Zhao and J. Wang, J. Electrochem. Soc., 164, D253–D262.
49. Y. Yan, M. Zhang, Y. Xue, W. Han, D. Cao and S. Wei, Electrochim. Acta, 2009, 54, 3387–3393.
50. M. Zhang, Y. Yan, W. Han, Y. Xue, X. Jing, X. Liu, S. Wang and X. Zhang, Electrochemistry, 2009, 8, 1–3.
51. Y. Castrillejo, P. Fernández, J. Medina, P. Hernández and E. Barrado, Electrochim. Acta, 2011, 56, 8638–8644.
52. H. A. Laitinen and W. S. Ferguson, Anal. Chem., 1957, 29, 4–9.
53. D. Ji, Y. Yan, M. Zhang, P. Wang, X. Yang, X. Jing, Y. Xue, W. Han and T. Hartmann, J. Electrochem. Soc., 2016, 163, D1–D8.
54. H. B. Michaelson, J. Appl. Phys., 1997, 48, 4729.
55. D. Ji, Y. Yan, M. Zhang, X. Li, X. Jing, X. Yang, X. Jing, W. Han, Y. Xue, Z. Zhang and T. Hartmann, RSC Adv., 2015, 5, 75863–75869.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra01349a

---