Abundant topological phases in hydrogenated group-IV binary alloy compounds

Abstract

Based on the widely studied two-dimensional layered materials, new materials with unique properties can be acquired by stacking the layered materials with different styles. By using density-functional calculations and symmetry analysis, we here present a route to produce abundant topologically nontrivial electronic states in three-dimensional compounds made of stacked monolayer hydrogenated group-IV binary alloys. Triply degenerate point (TDP) semimetals and Dirac semimetals are found in the hydrogenated SnPb compounds with different stacking configurations. The TDP semimetal is characterized by two sets of near-Dirac TDPs, stemming from the inversion of the s (p_z) and p_x,y bands from the Pb (and also Sn) atoms and protected by a C_3v double point group symmetry. Type-I and type-II states, and one essential Dirac semimetal state, coexist in a hydrogenated SnPb compound. Hourglass surface states are also observed in this case. For the hydrogenated GeSn and GePb compounds, normal insulators and weak topological insulators (and also Dirac semimetals) are obtained, respectively. The topological nature of the states is identified by calculations of topological indexes as well as surface states. With these extremely rich topological phases, the studied compounds offer an ideal material platform for realizing topological semimetals and insulators in experiments.

---

1. Introduction

Some of the most important discoveries in condensed matter physics over the last few decades have been about topological states of matter. Topological materials^1–4 feature an electronic band structure that exhibits a special band topology not determined by the Landau order parameter and the concept of symmetry breaking. The topologically protected electronic states are generally immune to environmental perturbations, making the topological materials promising for applications in low-dissipation and high-reliability microelectronic devices. Among the rich variety of topological materials, topological semimetals^2,5–9 have sparked intense research interest. Topological semimetals with zero-dimensional band crossings are characterized by discrete band degenerate points in the bulk spectra, in which these discrete points connect with open strings formed by topologically protected surface states on the boundaries, called Fermi arc states.⁸ Very exotic physical properties and further potential applications^2,9–11 can stem from the Fermi arc states. For example, the proximity-induced surface superconductivity found in the Dirac semimetal (DSM) Cd₃As₂ provides possibilities to manipulate superconducting quantum states,^12,13 which may be a building block for topological quantum computations. The spin-momentum-locking property of the Fermi arcs^14,15 is similar to the surface states of topological insulators, auspicious for current-induced spin polarization and realistic spintronic applications.

Currently, plenty of theoretical studies have been performed to produce topological semimetals.^{2,5–9,16–20} However, very little preliminary experimental progress has been achieved to date, such as in Na₃Bi,²¹ Cd₃As₂,²² and WC-type materials,^23,24 leaving many important physical effects not ready for practical applications. Some shortcomings or difficulties in utilizing the unique properties include: (i) the semimetal materials are generally difficult to fabricate and integrate in experiments.^5,25 (ii) The quasiparticle excitations around the discrete band degenerate points may be far away from the Fermi level (E_F).²⁴ Thus, the unique transport phenomena originating from the band degenerate points are difficult to observe. (iii) The band degenerate points may coexist with other unconcerned bands.^26–28 To further advance this field, we should go beyond the existing materials and find new topological semimetals without these drawbacks.

Van der Waals (vdW) layered systems represent a large family of materials with many tunable properties.^29–35 For instance, topological insulating states were previously found in the tetradymite-type Bi₂Te₃-class materials,³⁴ and Weyl semimetal states were observed in transition metal chalcogenides.³⁵ Currently, a new class of monolayer group-IV XPb (X = C, Si, Ge and Sn) alloys has been reported to be mechanically stable,³⁶ and their hydrogenated compounds can be topological insulators with large energy gaps.^37,38 Whether the topological properties of the hydrogenated XPb monolayers are similar to those of their three-dimensional (3D) crystals and the influences of vdW interactions on the electronic states remain to be explored. Particularly, two-dimensional (2D) Ge/Sn graphane-like alloys have been successfully synthesized via the topochemical deintercalation of CaGe_2−2xSn_2x in aqueous acidic conditions³⁹ and are suitable for fabrication into microelectronic devices. Thus, it is highly meaningful to explore the electronic states and possible topological behaviors of these 3D crystals built with pieces of these interesting and applicable 2D group-IV alloys.

In this work, we theoretically predict the existence of rich topological semimetal and insulating phases in hydrogenated group-IV binary alloy compounds. The hydrogenated SnPb (SnPbH₂) compounds can host the triply degenerate point (TDP) semimetal phase and the DSM phase, depending on the different stacking configurations. The TDP semimetal (TDPSM) is characterized by two sets of “near-Dirac” TDPs near the E_F, originating from the inversion of the s (p_z) and p_x,y bands of the Pb (and also Sn) atoms and protected by a C_3v double point group symmetry. The band inversion mechanism is explored by tuning the vdW interlayer space, which provides a clear physical picture of the band evolution from monolayers to 3D topological semimetals. The DSM features hourglass surface states, with two clean type-I Dirac points located exactly at the E_F, protected by a C_6v double point group symmetry. Two type-II points and a single essential Dirac point are also found coexisting near the E_F in the system. Normal insulators and weak topological insulators (and also DSMs) are achieved in the hydrogenated GeSn (GeSnH₂) and GePb (GePbH₂) systems, respectively. Our discoveries provide a new route to produce the interesting topological phases from 2D materials.

2. Models and methods

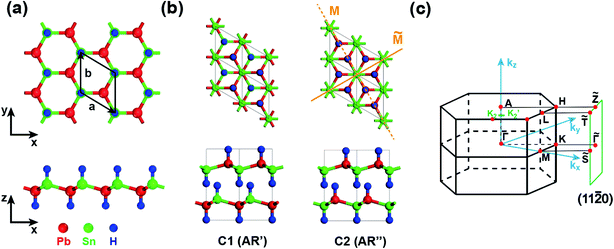
We now take SnPbH₂ as an example to analyze its topological electronic properties. The geometries of the SnPbH₂ monolayer are displayed in Fig. 1(a), in which the Sn and Pb atoms together form a buckled honeycomb structure with H atoms bonded to the Sn or Pb atoms on both sides of the plane in an alternating manner. The thermal and dynamical stability of the monolayer SnPbH₂ is illustrated in Fig. S1 of part A in the ESI.† The studied 3D SnPbH₂ crystals are built by stacking the pieces of the SnPbH₂ monolayers. In total, ten typical types of stacking configurations are considered, as shown in Table 1 and Fig. S2 in part B of the ESI.† The AR′ and AR′′ stacking configurations, renamed to C1 and C2, respectively, are displayed in Fig. 1(b). The first Brillouin zone (BZ) and the associated projected (112̄0) plane of the above two configurations are shown in Fig. 1(c).

Fig. 1 (a) Top and side views of the monolayer SnPbH₂. The black solid lines indicate the unit cell. (b) Top and side views of the 2 × 2 × 1 supercells of the two 3D SnPbH₂ crystals with the C1 (AR′) and C2 (AR′′) configurations, respectively. The yellow solid line and yellow dashed line in the top view of the C2 configuration indicate a glide mirror plane M̃ and a mirror plane M in the structure, respectively. (c) The first BZ of the 3D SnPbH₂ crystals with the C1 and C2 stacking configurations. Its projection onto the (112̄0) plane is also shown. The green line K₂–K₂′ is on the k_x–k_y plane with the k_z = 0.398 × 2π/c.

Table 1 Results for the built 3D SnPbH₂ crystals, including the symmetry, number (n) of the SnPbH₂ monolayer in the unit cell, lattice constants of a and c per layer (c/n), average total energy per layer (Δ), band gap, and average exfoliation energy per layer (ΔE_exf). The two most stable stacking configurations are marked in bold

	Symmetry	n	a (Å)	c/n (Å)	Δ (eV)	Band gap (meV)	ΔEexf (J m^−2)
AA	P3m1(156)	1	4.846	4.821	−6.284	0	0.214
AA′	P3̄m1(164)	2	4.843	4.830	−6.275	0	0.207
AR	P63mc(186)	2	4.863	4.571	−6.302	0 (DSM)	0.227
AR′ (C1)	P3m1(156)	2	4.866	4.548	−6.314	0 (TDPSM)	0.236
AR′′ (C2)	P63mc(186)	2	4.872	4.477	−6.324	0 (DSM)	0.243
AF	P6̄m2(187)	2	4.814	6.332	−6.117	383.1	0.084
AF′	P63mc (186)	2	4.810	6.448	−6.116	364.6	0.083
AX	P3m1(156)	2	4.879	5.065	−6.276	97.5	0.205
AX′	P3̄m1(164)	2	—	—	—	—	—
AX′′	P3̄m1(164)	2	4.889	5.117	−6.270	66.5	0.200

---

The electronic structures of the hydrogenated group-IV binary alloy compounds are calculated within the framework of density-functional theory (DFT), as implemented in the Vienna ab initio simulation package (VASP).^40,41 The Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE) is used to describe the exchange and correlation functional.⁴² The kinetic energy cutoff of the plane wave basis is set to be 500 eV. The convergence criterion for the total energy is set to 10⁻⁵ eV. The 15 × 15 × 15 and 15 × 15 × 7 Γ center Monkhorst–Pack grids are employed to perform the first BZ integral for the AA and the other nine configurations, respectively. All atoms in the unit cells are allowed to move until the Hellmann–Feynman force on each atom is smaller than 0.01 eV Å⁻¹. The lattice constants of the unit cell are simultaneously relaxed. The interlayer vdW interactions are taken into consideration by applying the optB86b-vdW correlation functional.^43,44 The topological properties are investigated by constructing the maximal localized Wannier functions using the WANNIER90 (ref. 45) package combined with the WANNIERTOOLS code.⁴⁶ To check the possible underestimation of band gaps in the PBE functional, hybrid-functional methods based on the HSE06 scheme⁴⁷ are adopted for the C1 and C2 SnPbH₂ crystals. The band structures obtained with the HSE06 functional are given in Fig. S3 and analyzed in the ESI.†

3. Results and discussion

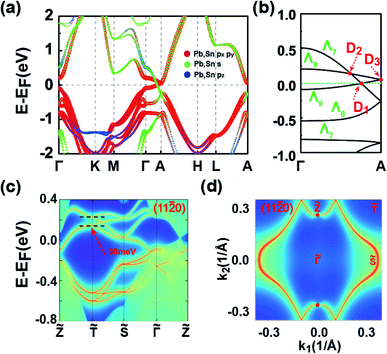
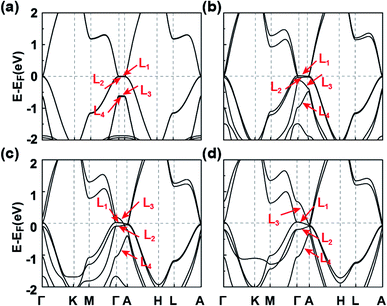
The symmetries, optimized lattice constants, and average total energy per layer obtained for the 3D SnPbH₂ crystals with different stacking configurations are given in Table 1. Except for the AX′ configuration, all the other configurations considered form stable vdW layered crystals. The in-plane lattice constants (a) of the nine stable crystals are very close to that (4.89 Å) of the monolayer SnPbH₂.³⁸ The average interlayer spaces between the two adjacent layers are, however, very diverse due to the different stacking configurations. As displayed in Table 1, the configurations of C1 and C2 have the two smallest lattice constants c per layer (c/n), corresponding to stronger interlayer interactions of these two stacking configurations. Thus, these two stacking configurations reasonably have the lowest total energies compared to those of the other seven stacking configurations. The exfoliation energies of the stable configurations are calculated through ΔE_exf = (E_iso − E_bulk/n)/A, where E_iso, E_bulk, n, and A represent the energy of the unit cell of an isolated monolayer SnPbH₂, the energy of the unit cell of the 3D SnPbH₂ crystal, the number of the SnPbH₂ layers in the unit cell, and the in-plane area of the 3D SnPbH₂ unit cell, respectively. The calculated exfoliation energies per layer⁴⁸ of the stable configurations range from 0.083 J m⁻² to 0.243 J m⁻², lower than that of graphene exfoliated from graphite (0.37 J m⁻²).⁴⁹ Thus, the vdW interactions between the two neighboring layers in the crystals are weak due to the H atoms saturating the p_z dangling bonds of the Sn and Pb atoms. In the following, we focus on the two most stable stacking configurations of C1 and C2 for the 3D vdW SnPbH₂ crystals. The dynamical stability of the above two configurations is confirmed by the calculations of the phonon spectra. As illustrated in Fig. S4 of the ESI,† no soft phonon mode appears for the two structures.

We now study the topological electronic structures of the C1 SnPbH₂, which owns a space group P3m1. Its orbital-resolved band structure is displayed in Fig. 2(a), where the spin–orbit coupling (SOC) is not considered. Obviously, the system shows gapless metallic behaviors around the E_F, with the bands contributed by the Pb (and also Sn) s and p orbitals. Along the Γ–A line, the point group symmetry is C_3v, with one 2D (Λ₃) and two one-dimensional (1D) (Λ₁, Λ₂) irreducible representations (IRs). Without SOC, the s (also p_z) orbitals and the p_x,y orbitals belong to the Λ₁ and Λ₃ IRs, respectively (Fig. 2(b)). Once the SOC is included, the crystal symmetry changes from the C_3v group symmetry to the C_3v double group symmetry. The C_3v double group contains one 2D (Λ₄) IR and two 1D (Λ₅, Λ₆) IRs. When the SOC is turned on, the Λ₁ band changes to the Λ₄ band and downshifts in energy, while the Λ₃ splits into the (Λ₄ + Λ₅ + Λ₆) bands, leading to two pairs of TDPs appearing near the E_F and at 105 meV above the E_F along the Γ–A line (marked by two red circles in Fig. 2(d)). The bands around the TDPs near the E_F are magnified in Fig. 2(e). The double degeneracy of the Λ₄ band comes from the existence of the σ_v mirror symmetry contained in the C_3v point group of the C1 configuration. If the σ_v mirror symmetry is broken, each TDP will split into two Weyl points with opposite chiralities. The dispersion around TDP1 in the k_x–k_y plane is highlighted in Fig. 2(f), which shows how the bands near the TDP1 disperse away from the Γ–A line. As displayed in Fig. 2(e), the energy splitting of the Λ₅ and Λ₆ bands is about 3 meV. With such small splitting, TDP1 and TDP2 can be regarded together as a near-Dirac semimetal.⁵⁰ The obtained results provide a promising venue for observing the DSMs and studying the related exotic properties.

Fig. 2 (a) Band structure of the C1 SnPbH₂ crystal without SOC. The sizes of the dots are proportional to the orbital contributions. (b) Amplified band structure of (a) along the high-symmetry line Γ–A. (c) and (d) are the same as (a) and (b), respectively, except with the SOC considered. Two pairs of TDPs in (d) are marked by red circles. (e) The amplified band structure of the TDPs closer to E_F in (d). The two TDPs in (e) are labeled TDP1 and TDP2, respectively. (f) Band structure in the k_x–k_y plane surrounding the TDP1. The K₂ and K₂′ points are displayed in Fig. 1(c).

To deeply comprehend the origination of TDP1 and TDP2, we analyze the evolution of energy bands near E_F with varying lattice constant in the absence of SOC, as illustrated in Fig. 3. When the interlayer space is large enough (c = 20 Å), the interaction between the two adjacent layers is negligible, leading to the weak band dispersion along the k_z axis (between Γ and A points) (Fig. 3(a)). At this stage, the L₁ and L₂ bands (primarily composed of the p_x,y orbitals), as well as the L₃ and L₄ bands (primarily composed of the s and p_z orbitals), are approximately degenerate. As the interlayer space decreases, the band dispersion increases gradually, especially for the L₃ and L₄ bands, due to the s and p_z orbitals being sensitive to interlayer interactions (Fig. 3(b) and (c)). When the interlayer space reaches the equilibrium space c = 9.096 Å, the L₃ band successively crosses the L₂ and L₁ bands along the Γ–A line, leading to the band inversion occurring at both the Γ and A points. Eventually, inclusion of the SOC interaction leads to the Λ₄ band intersecting with the Λ₅ and Λ₆ bands along the Γ–A line. Such intersection between singly and doubly degenerate bands results in the TDPs for the C1 SnPbH₂ crystal. Thus, the TDP1 and TDP2 appear due to band inversion of the s, p_z and p_x,y orbitals and protection by the C_3v double group symmetry.

Fig. 3 Band structures of the C1 SnPbH₂ crystal with the lattice constants c of (a) 20 Å, (b) 11 Å, (c) 10 Å, and (d) 9.096 Å, respectively. The distance between the two layers in the unit cell varies accordingly. The SOC is not considered.

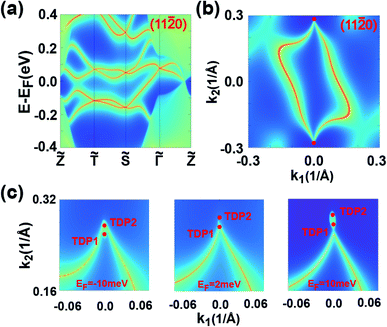
The topological behaviors of the C1 SnPbH₂ crystal are discussed based on the calculated surface states and the Fermi arcs (Fig. 4). Fig. 4(a) and (b) show the surface bands and the Fermi surface contour on the (112̄0) plane, respectively. On this plane, the Dirac cone state has its branches merging into the bulk states, and an arc-like Fermi surface is achieved. As shown in Fig. 4(b), two Fermi arcs touch each other at the plane projection of the two bulk Dirac points. The Fermi surface contours on the (112̄0) plane with tuned E_F are emphasized in Fig. 4(c), clearly illustrating the evolution of the Fermi arc states. These Fermi arcs are also protected by bulk Z₂ invariants, which are well defined in both k_z = 0 (Z₂ = 1) and k_z = π (Z₂ = 0) planes. Thus, a Kramers pair of surface states must exist on the k_z = 0 path for the side surfaces, ensuring the presence of a pair of surface Fermi arcs.

Fig. 4 (a) and (b) are the surface band structure and Fermi surface contour on the (112̄0) plane of the C1 SnPbH₂ crystal, respectively. (c) Fermi surfaces with different E_Fs for the (112̄0) plane of the 3D SnPbH₂ crystal. Two red dots in the magnified Fermi surfaces denote the surface projections of the two adjacent TDPs. k₁ and k₂ in (b) and (c) are the wave-vector units along the [capital Gamma, Greek, tilde]S̃ and [capital Gamma, Greek, tilde]Z̃ directions, respectively.

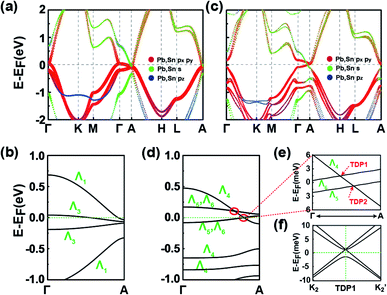
We now explore the topological electronic structures of the C2 SnPbH₂ crystal with space group P6₃mc. For the C2 configuration, the system has three important crystalline symmetries, including the mirror plane M (Fig. 1(b)), the glide-mirror plane M̃ (Fig. 1(b)), and the six-fold screw rotation S_6z. The orbital-resolved band structure of the C2 SnPbH₂ crystal in the presence of SOC is displayed in Fig. 5(a). Obviously, the system shows gapless semi-metallic behaviors around the E_F, with the bands contributed by the Pb (and also Sn) s and p orbitals. Two crossing points around the E_F along the high-symmetry line of Γ–A are labeled D₁ and D₂, as illustrated in Fig. 5(b). Because the crossing points are formed by two doubly degenerate bands, both D₁ and D₂ are gapless crossing points with quadruple degeneracy. By analyzing the orbital components, we find that the two crossing doubly degenerate bands are mainly composed of s and p_z orbitals, and p_x,y orbitals of the Pb (and also Sn) atoms, respectively. Symmetry analysis shows that these two doubly degenerate bands belong to the Λ₇ and Λ₉ IRs of the C_6v double group symmetry, respectively (Fig. 3(b)). Thus, two stable fourfold degenerate points (D₁ and D₂) arise from the band inversion between s, p_z orbitals and p_x,y orbitals of the Pb (and also Sn) atoms, protected by the different symmetric properties of the Λ₇ and Λ₉ bands. As displayed in Fig. 5(b), the slopes of the two crossing bands at D₁ have opposite signs, while the slopes of the two bands at D₂ have the same sign, leading to D₁ and D₂ being type-I and type-II Dirac points, respectively. The double degeneracy of all bands along the Γ–A line in Fig. 5(b) stems from the anticommutation relation {S_2z, M} = 0, where the S_2z is contained in the S_6z. If a uniaxial strain is applied to the system, the C_6v symmetry is broken, leading to the coupling of the s, p_z bands and the p_x,y bands. A strong topological insulating phase with indexes of (1; 000) can be obtained under this strain. In contrast to D₁ and D₂, D₃ appears at the high-symmetry point A on the BZ boundary. Due to four degenerate orthogonal states coexisting at A, D₃ is a degenerate quartet (see part C of the ESI†).

Fig. 5 (a) Band structure of the C2 SnPbH₂ crystal SOC. The projected Pb and Sn atomic orbitals are also displayed. The sizes of the dots are proportional to the orbital contributions. (b) Amplified band structure of (a) along the high-symmetry line Γ–A. The Dirac points in (b) are labeled D₁, D₂, and D₃, respectively. (c) and (d) are the surface band structure and Fermi surface contour on the (112̄0) plane for the C2 SnPbH₂ crystal, respectively. The dashed lines in (c) are used to guide the bandwidth of the hourglass cone. The red dots in (d) indicate the Dirac points. k₁ and k₂ in (d) are the wave-vector units along the [capital Gamma, Greek, tilde]S̃ and [capital Gamma, Greek, tilde]Z̃ directions, respectively.

We now take D₁ as an example to analyze its topological nature. The obtained Z₂ = 1 for the k_z = 0 plane and Z₂ = 0 for the k_z = π plane indicate the topological nontriviality of D₁. Fig. 5(c) and (d) show the surface bands and the Fermi surface contour for the (112̄0) plane of the C2 SnPbH₂ crystal, respectively. Different from the Dirac cone surface states,⁵ the (112̄0) plane possesses very exotic characteristics due to the unique geometrical symmetries of the plane. On the (112̄0) plane, the glide-mirror plane M̃ is preserved, giving rise to a surface fermion whose dispersion is shaped like an hourglass. The resultant hourglass surface state owns a relatively large bandwidth (about 80 meV) along the T̃S̃ directions, defined as the smaller energy window between the two twofold degenerate points at the same time reversal invariant k point (denoted by the dashed lines in Fig. 5(c)). This value is several times the bandwidths of previously reported hourglass fermions in KHgX⁵¹ and other 3D bulk materials.^52,53 The large bandwidth of the hourglass surface state favors detection using the standard angle-resolved photoemission spectroscopy (ARPES). The Fermi arc surface state of the C2 SnPbH₂ crystal is displayed in Fig. 5(d), where the large and clear Fermi arcs can also be easily measured or confirmed by ARPES or scanning tunneling microscopy.

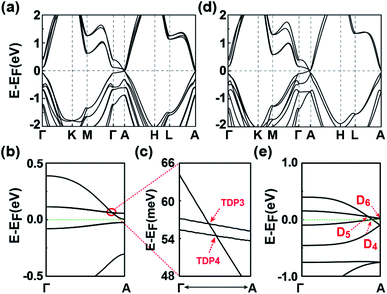
The electronic states and the topological properties of the 3D GeSnH₂ and GePbH₂ crystals are also investigated. The results are illustrated in part D of the ESI.† Among the ten typical stacking configurations, C1 and C2 are also found to be the two most stable configurations for both the 3D GeSnH₂ and GePbH₂ crystals. The electronic structures of the 3D GeSnH₂ and GePbH₂ crystals are somewhat different from those of the 3D SnPbH₂ crystals. For example, the C1 and C2 3D GeSnH₂ crystals are found to be normal insulators instead of the TDP or Dirac semimetals found in the SnPbH₂ crystals, which can be rationalized well by the stronger nonmetallic property of Ge atoms than that of Pb atoms. The C1 GePbH₂ crystal is found to be a weak topological insulator, with topological indexes of (0; 001) (Fig. 6(a) and (b)). The topologically nontrivial band gap at the E_F is about 28.6 meV (Fig. 6(b)). Similar to the C1 SnPbH₂ crystal, the two close TDPs (TDP3 and TDP4) form one “near-Dirac” point above the E_F (Fig. 6(b) and (c)). The C2 GePbH₂ crystal is a DSM with three Dirac points located around the E_F (Fig. 6(d) and (e)). Thus, very abundant topological phases, including TDPSMs, DSMs (with different types), and weak topological insulators, etc., are achieved in the hydrogenated group-IVA binary compounds. This covalently functionalized honeycomb lattice may be expanded to many other 2D materials with different lattices or functionalized chemical groups,^54–56 providing plenty of candidate materials for topologically nontrivial phases. The predicted multiple topological electronic states associated with multiple degrees of freedom of stacking configurations in the covalently functionalized honeycomb lattice pave a brand new way to develop novel quantum electronics with low power consumption and heat dissipation, and quantum computing free of decoherence.

Fig. 6 (a) Band structure of the C1 GePbH₂ crystal with SOC. (b) Amplified band structure of (a) along the high-symmetry line Γ–A. (c) The amplified TDPs in (b), labeled TDP3 and TDP4, respectively. (d) and (e) are the same as (a) and (b), respectively, but for the C2 GePbH₂ crystal. Three Dirac points in (e) are labeled D₄, D₅, and D₆, respectively.

4. Conclusions

In conclusion, using density-functional theory calculations and symmetry analysis, we predict a class of topological semimetal candidates in chemically modified group-IVA binary compounds. Topological semimetals are formed depending on the different stacking configurations. The C1 SnPbH₂ crystal is a TDPSM, characterized by two sets of “near-Dirac” TDPs and protected by a C_3v double point group symmetry. The origination of TDPs is understood by tuning the vdW interlayer space, which clearly demonstrates the band inversion between the s (p_z) and p_x,y bands from the Pb (and also Sn) atoms. By changing the stacking configuration, a DSM with hourglass surface states is obtained in the C2 SnPbH₂ crystal, featuring three kinds of Dirac points: one pair of clean type-I Dirac points located exactly at the E_F and one pair of type-II Dirac points, and a single essential Dirac point occurring near the E_F. The topological properties of the GeSnH₂ and GePbH₂ are also explored. The C1 and C2 GeSnH₂ crystals are found to be normal insulators, while the C1 GePbH₂ crystal turns out to be a weak topological insulator, and the C2 GePbH₂ crystal a DSM with hourglass surface states. Our work reveals a new class of novel 2D materials hosting rich topological phases triggered by various stacking configurations, which serve as good candidates for promising topotronics.

Author contributions

GG carried out the theoretical calculations with the assistance of HB, BZ, and HH. GG, BZ, and ZY analyzed the results. GG and ZY wrote the paper. ZY guided the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grants No. 11574051, No. 11604134, and No. 11874117. Most of the calculations were performed at the High Performance Computational Center (HPCC) of the Department of Physics at Fudan University.

References

1. M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045.
2. N. P. Armitage, E. J. Mele and A. Vishwanath, Rev. Mod. Phys., 2018, 90, 015001.
3. P. Liu, J. R. Williams and J. J. Cha, Nat. Rev. Mater., 2019, 4, 479.
4. X. L. Qi and S. C. Zhang, Rev. Mod. Phys., 2011, 83, 1057.
5. Z. Wang, Y. Sun, X.-Q. Chen, C. Franchini, G. Xu, H. Weng, X. Dai and Z. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195320.
6. B. Bradlyn, J. Cano, Z. Wang, M. G. Vergniory, C. Felser, R. J. Cava and B. A. Bernevig, Science, 2016, 353, aaf5037.
7. S. M. Young, S. Zaheer, J. C. Y. Teo, C. L. Kane, E. J. Mele and A. M. Rappe, Phys. Rev. Lett., 2012, 108, 140405.
8. X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205101.
9. A. Bernevig, H. Weng, Z. Fang and X. Dai, J. Phys. Soc. Jpn., 2018, 87, 041001.
10. S. A. Parameswaran, T. Grover, D. A. Abanin, D. A. Pesin and A. Vishwanath, Phys. Rev. X, 2014, 4, 031035.
11. A. A. Burkov and Y. B. Kim, Phys. Rev. Lett., 2016, 117, 136602.
12. A. Chen, D. I. Pikulin and M. Franz, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 174505.
13. C. Huang, B. T. Zhou, H. Zhang, B. Yang, R. Liu, H. Wang, Y. Wan, K. Huang, Z. Liao, E. Zhang, S. Liu, Q. Deng, Y. Chen, X. Han, J. Zou, X. Lin, Z. Han, Y. Wang, K. T. Law and F. Xiu, Nat. Commun., 2019, 10, 2217.
14. S.-Y. Xu, I. Belopolski, D. S. Sanchez, M. Neupane, G. Chang, K. Yaji, Z. Yuan, C. Zhang, K. Kuroda, G. Bian, C. Guo, H. Lu, T.-R. Chang, N. Alidoust, H. Zheng, C.-C. Lee, S.-M. Huang, C.-H. Hsu, H.-T. Jeng, A. Bansil, T. Neupert, F. Komori, T. Kondo, S. Shin, H. Lin, S. Jia and M. Z. Hasan, Phys. Rev. Lett., 2019, 116, 096801.
15. B. Q. Lv, S. Muff, T. Qian, Z. D. Song, S. M. Nie, N. Xu, P. Richard, C. E. Matt, N. C. Plumb, L. X. Zhao, G. F. Chen, Z. Fang, X. Dai, J. H. Dil, J. Mesot, M. Shi, H. M. Weng and H. Ding, Phys. Rev. Lett., 2015, 115, 217601.
16. A. A. Soluyanov, D. Gresch, Z. Wang, Q. Wu, M. Troyer, X. Dai and B. A. Bernevig, Nature, 2015, 527, 495.
17. Z. M. Zhu, G. W. Winkler, Q. S. Wu, J. Li and A. A. Soluyanov, Phys. Rev. X, 2016, 6, 31003.
18. H. Weng, C. Fang, Z. Fang and X. Dai, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 241202(R).
19. H. Huang, S. Zhou and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 121117(R).
20. G. Chang, S.-Y. Xu, S.-M. Huang, D. S. Sanchez, C.-H. Hsu, G. Bian, Z.-M. Yu, I. Belopolski, N. Alidoust, H. Zheng, T.-R. Chang, H.-T. Jeng, S. A. Yang, T. Neupert, H. Lin and M. Z. Hasan, Sci. Rep., 2017, 7, 1688.
21. Z. K. Liu, B. Zhou, Y. Zhang, Z. J. Wang, H. M. Weng, D. Prabhakaran, S. –K. Mo, Z. X. Shen, Z. Fang, X. Dai, Z. Hussain and Y. L. Chen, Science, 2014, 343, 864.
22. Z. K. Liu, J. Jiang, B. Zhou, Z. J. Wang, Y. Zhang, H. M. Weng, D. Prabhakaran, S.-K. Mo, H. Peng, P. Dudin, T. Kim, M. Hoesch, Z. Fang, X. Dai, Z. X. Shen, D. L. Feng, Z. Hussain and Y. L. Chen, Nat. Mater., 2014, 13, 677.
23. J.-Z. Ma, J.-B. He, Y.-F. Xu, B. Q. Lv, D. Chen, W.-L. Zhu, S. Zhang, L.-Y. Kong, X. Gao, L.-Y. Rong, Y.-B. Huang, P. Richard, C.-Y. Xi, E. S. Choi, Y. Shao, Y.-L. Wang, H.-J. Gao, X. Dai, C. Fang, H.-M. Weng, G.-F. Chen, T. Qian and H. Ding, Nat. Phys., 2018, 14, 349.
24. B. Q. Lv, Z.-L. Feng, Q.-N. Xu, X. Gao, J.-Z. Ma, L.-Y. Kong, P. Richard, Y.-B. Huang, V. N. Strocov, C. Fang, H.-M. Weng, Y.-G. Shi, T. Qian and H. Ding, Nature, 2017, 546, 627.
25. Z. Wang, H. Weng, Q. Wu, X. Dai and Z. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125427.
26. Q. D. Gibson, L. M. Schoop, L. Muechler, L. S. Xie, M. Hirschberger, N. P. Ong, R. Car and R. J. Cava, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205128.
27. W. Gao, X. Zhu, F. Zheng, M. Wu, J. Zhang, C. Xi, P. Zhang, Y. Zhang, N. Hao, W. Ning and M. Tian, Nat. Commun., 2018, 9, 3249.
28. Z. Wang, D. Gresch, A. A. Soluyanov, W. Xie, S. Kushwaha, X. Dai, M. Troyer, R. J. Cava and B. A. Bernevig, Phys. Rev. Lett., 2016, 117, 056805.
29. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419.
30. J. Zhang, B. Zhao, T. Zhou, Y. Xue, C. Ma and Z. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 085401.
31. X. Qian, J. Liu, L. Fu and J. Li, Science, 2014, 346, 1344.
32. M. M. Otrokov, I. P. Rusinov, M. Blanco-Rey, M. Hoffmann, A. Yu. Vyazovskaya, S. V. Eremeev, A. Ernst, P. M. Echenique, A. Arnau and E. V. Chulkov, Phys. Rev. Lett., 2019, 122, 107202.
33. J. Liu, H. Wang, C. Fang, L. Fu and X. Qian, Nano Lett., 2017, 17, 467.
34. H. Zhang, C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang and S.-C. Zhang, Nat. Phys., 2009, 5, 438.
35. L. Huang, T. M. McCormick, M. Ochi, Z. Y. Zhao, M. T. Suzuki, R. Arita, Y. Wu, D. X. Mou, H. B. Cao, J. Q. Yan, N. Trivedi and A. Kaminski, Nat. Mater., 2016, 15, 1155.
36. J. E. Padilha, R. B. Pontes, T. M. Schmidt, R. H. Miwa and A. Fazzio, Sci. Rep., 2016, 6, 26123.
37. L. Liu, H. Qin and J. Hu, Sci. Rep., 2017, 7, 42410.
38. S. J. Zhang, W. X. Ji, C. W. Zhang, S. S. Li, P. Li, M. J. Ren and P. J. Wang, RSC Adv., 2016, 6, 79452.
39. M. Q. Arguilla, S. Jiang, B. Chitara and J. E. Goldberger, Chem. Mater., 2014, 26, 6941.
40. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
41. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
43. J. Klimes, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
44. T. J. Björkman, J. Chem. Phys., 2014, 141, 074708.
45. A. A. Mostofi, J. R. Yates, G. Pizzi, Y. S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309.
46. Q. S. Wu, S. N. Zhang, H. F. Song, M. Troyer and A. A. Soluyanov, Comput. Phys. Commun., 2018, 224, 405.
47. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
48. J. H. Jung, C.-H. Park and J. Ihm, Nano Lett., 2018, 18, 2759.
49. R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406.
50. Z. Fang, H. Gao, J. W. F. Venderbos and A. M. Rappe, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 125202.
51. Z. Wang, A. Alexandradinata, R. J. Cava and B. A. Bernevig, Nature, 2016, 532, 189.
52. B. Singh, B. Ghosh, C. Su, H. Lin, A. Agarwal and A. Bansil, Phys. Rev. Lett., 2018, 121, 226401.
53. S.-S. Wang, Y. Liu, Z.-M. Yu, X.-L. Sheng and S. A. Yang, Nat. Commun., 2017, 8, 1844.
54. S. S. Li, W. X. Ji, S. J. Hu, C. W. Zhang and S. S. Yan, ACS Appl. Mater. Interfaces, 2017, 9, 41443.
55. Y. P. Wang, W. X. Ji, C. W. Zhang, P. Li, P. J. Wang, B. Kong, S. S. Li, S. S. Yan and K. Liang, Appl. Phys. Lett., 2017, 110, 233107.
56. M. H. Zhang, C. W. Zhang, P. J. Wang and S. S. Li, Nanoscale, 2018, 10, 20226.

---

Footnote

† Electronic supplementary information (ESI) available: The stability of monolayer SnPbH₂, various stacking configurations, the band structures based on the hybrid-functional methods for the C1 and C2 SnPbH₂, the phonon spectra for the C1 and C2 SnPbH₂, the symmetry analysis for the C2 SnPbH₂, and the geometric and electronic structures for the 3D GeSnH₂ and GePbH₂. See DOI: 10.1039/d1ra01136g

---