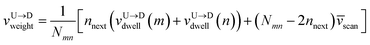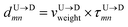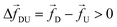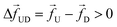DOI:
10.1039/D1RA00349F
(Paper)
RSC Adv., 2021,
11, 20781-20787
DNA barcode by flossing through a cylindrical nanopore†
Received
14th January 2021
, Accepted 21st May 2021
First published on 10th June 2021
Abstract
We report an accurate method to determine DNA barcodes from the dwell time measurement of protein tags (barcodes) along the DNA backbone using Brownian dynamics simulation of a model DNA and use a recursive theoretical scheme which improves the measurements to almost 100% accuracy. The heavier protein tags along the DNA backbone introduce a large speed variation in the chain that can be understood using the idea of non-equilibrium tension propagation theory. However, from an initial rough characterization of velocities into “fast” (nucleotides) and “slow” (protein tags) domains, we introduce a physically motivated interpolation scheme that enables us to determine the barcode velocities rather accurately. Our theoretical analysis of the motion of the DNA through a cylindrical nanopore opens up the possibility of its experimental realization and carries over to multi-nanopore devices used for barcoding.
1 Introduction
A DNA barcode consists of a short strand of DNA sequence taken from a targeted gene like COI or cox I (Cytochrome C Oxidase 1)1 present in the mitochondrial gene in animals. The unique combination of nucleotide bases in barcodes allows us to distinguish one species from another. Unlike relying on the traditional taxonomical identification methods, DNA barcoding provides an alternative and reliable framework to categorize a wide variety of specimens obtained from the natural environment. Though researchers relied on DNA sequencing techniques for the identification of unknown species for a long time, in 2003, Hebert et al.2 proposed the mitochondrial gene (COI) region barcoding to classify cryptic species3 from the entire animal population. Since then, several studies have shown the potential applications of barcoding in conserving biodiversity,4 estimating phyletic diversity, identifying disease vectors,5 authenticating herbal products,6 unambiguously labeling the food products,7,8 and protecting endangered species.4 Traditional sequencing methods based on chemical analysis are still been widely used in the biological community to determine the barcodes.
Since its discovery,9–12 last three decades have witnessed rapid progress in single nanopore based sequencing methods.13–16 Consequently, a variety of experimental protocols are being explored for a cost effective, high throughput, without the use of chemical reagents, and real time sequencing,17 sequence mapping,18 detection of duplex-DNA for genomic profiling,19 sorting of ultralong human genomic DNA,20 topological variations of DNA at the single molecule level,21 and barcode copying.22
Recently, the possibility of determining DNA barcodes has been demonstrated in a dual nanopore device, by scanning a captured dsDNA multiple times by applying a net periodic bias across the two pores.23–26 Theoretical and simulation studies have also been reported in the context of a double nanopore system.27–29 In this article, we investigate a similar strategy in silico in a cylindrical nanopore and demonstrate that a cylindrical nanopore can have a competitive advantage over a dual nanopore system. By studying a model dsDNA with barcodes using Brownian dynamics we establish an important result that it is due to the disparate dwell time and speed of the barcodes (“tags”) compared to the nucleotide segments (“monomers”) the current blockade time information only is not enough and will lead to an inevitable underestimation of the distance between the barcodes. Furthermore, using the ideas of the tension propagation theory,30,31 we demonstrate that information about the fast-moving nucleotides in between the barcodes, – not easily accessible experimentally, is a key element to resolve the underestimation. We suggest how to obtain this information experimentally and provide a physically motivated “two-step” interpolation scheme for an accurate determination of barcodes, even when the separation of the (unknown) tags has a broad distribution.
2 Methods
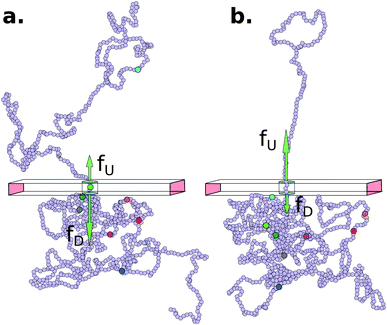
The Model System: Our in silico coarse-grained (CG) model of a dsDNA consist of 1024 monomers interspersed with 8 barcodes at different locations (shown in Fig. 1 and Table 1) is motivated by an experimental study by Zhang et al. on a 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 bp long dsDNA with 75 bp long protein tags at random locations along the chain24–26 using a dual nanopore device. Here we explore if a cylindrical nanopore with an applied bias force can resolve the barcodes with similar accuracy or better. We purposely choose positions of the 8 barcodes (Table 1) to study how the effect of disparate distances among the barcodes affects their measurements.
500 bp long dsDNA with 75 bp long protein tags at random locations along the chain24–26 using a dual nanopore device. Here we explore if a cylindrical nanopore with an applied bias force can resolve the barcodes with similar accuracy or better. We purposely choose positions of the 8 barcodes (Table 1) to study how the effect of disparate distances among the barcodes affects their measurements.
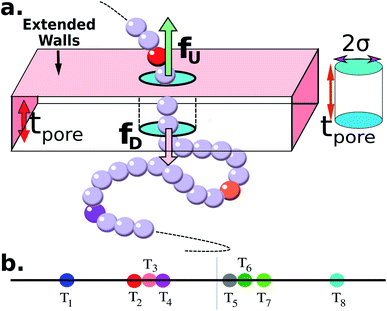 |
| | Fig. 1 (a) Schematics of a model dsDNA captured in cylindrical nanopore of diameter d = 2σ and thickness tpore, where σ is the diameter of each monomer (purple beads). Protein tags (barcodes) of the same diameter and of different colors (only three are shown in here) interspersed along the dsDNA backbone. Opposite but unequal forces 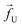 and and 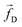 are applied in the nanopore to straighten the dsDNA as it translocates in the direction of the bias net force are applied in the nanopore to straighten the dsDNA as it translocates in the direction of the bias net force 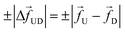 . (b) Positions of the protein tags along the contour length of the model dsDNA of length L = 1024σ which represents an actual dsDNA of 48 . (b) Positions of the protein tags along the contour length of the model dsDNA of length L = 1024σ which represents an actual dsDNA of 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 base pairs. The locations of the tags are listed in Table 1. 500 base pairs. The locations of the tags are listed in Table 1. | |
Table 1 Tag positions along the dsDNA
| Tag # |
T1 |
T2 |
T3 |
T4 |
T5 |
T6 |
T7 |
T8 |
| Position |
154 |
369 |
379 |
399 |
614 |
625 |
696 |
901 |
| Separation |
154 |
215 |
10 |
20 |
215 |
11 |
71 |
205 |
The tags T2, T3, T4 are closely spaced and form a group. Likewise, another group consisting of T5 and T6 are put in a closer proximity to T7. The tags T1 and T8 are further apart from the rest of the tags. The general scheme of the BD simulation strategy for a translocating homo-polymer under alternate force bias has been discussed in our recent publication27,28 and in the accompanying ESI.† In this article, tags are introduced by choosing the mass and friction coefficient to be different than the rest of the monomers present along the chain. This requires modification of the BD algorithm as discussed in the ESI-I.† The protein tags used in the experiments24–26 translate to about three monomers in the simulation. The heavier and extended tags introduce a larger viscous drag. Instead of explicitly putting side-chains at the tag locations, we made the mass and the friction coefficient of the tags 3 times larger. This we find enough to resolve the distance between the tags. Two forces 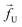 and at each end of the cylinder in opposite directions keep the DNA straight inside the channel and allows translocation in the direction of the net bias (please see Fig. 1 and 2).
and at each end of the cylinder in opposite directions keep the DNA straight inside the channel and allows translocation in the direction of the net bias (please see Fig. 1 and 2).
 |
| | Fig. 2 Demonstration of the epoch when the bias voltage is flipped. (a) Showing the last barcode is yet to translocate in the downward direction when the net bias 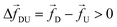 . (b) Shows the situation at a later time when all the barcodes crossed the cylindrical pore during downward translocation with a portion of the end segment still remaining inside the pore. At this point the bias is flipped with an upward bias . (b) Shows the situation at a later time when all the barcodes crossed the cylindrical pore during downward translocation with a portion of the end segment still remaining inside the pore. At this point the bias is flipped with an upward bias 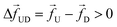 , translocation now occurs in the upward direction. In this way, the DNA remains captured all the time during repeated scans. , translocation now occurs in the upward direction. In this way, the DNA remains captured all the time during repeated scans. | |
3 Results and discussion
Barcodes from repeated scanning: As potentially could be done in a nanopore experiments, we switch the differential bias once the first tag or the last tag (T1, T8) translocates through the nanopore during up (U)/down (D) → D/U translocation yet having the end segments inside the pore (please see Fig. 2) so that the DNA remains captured in the cylindrical pore and the barcodes are scanned multiple times.
The question we ask: can we recover the actual barcode locations from these scanning measurements, so that the method can be applied to determine unknown barcodes ? We monitor two important quantities, – (i) the dwell time of each monomer and tag (ii) the time delay of arrival of any two tags at the pore as demonstrated in Fig. 3 and explained below. For each up/down-ward scan we measure the dwell time of a bead (either a monomer or a tag) with index m as follows:
| |
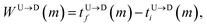 | (1a) |
| |
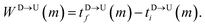 | (1b) |
Here,
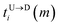
and
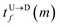
are the arrival and exit time of the
mth bead as further demonstrated in
Fig. 3(a). The corresponding dwell velocities
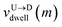
and
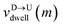
for the
mth bead along the nanopore channel axis (please see
Fig. 3(a)) can be obtained as follows,
| |
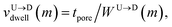 | (2a) |
| |
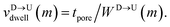 | (2b) |
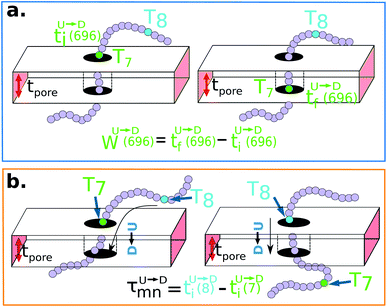 |
| | Fig. 3 (a) Demonstration of calculation of wait time for T7 which is of index m = 696. The dwell velocity is then calculated using eqn (2). (b) Demonstration of calculation of tag time delay 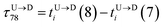 for tags T7 and T8 while they are moving downward. Please note that similar quantity for upward translocation for tags T7 and T8 while they are moving downward. Please note that similar quantity for upward translocation 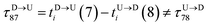 as there is no symmetry of the tag positions along the chain. as there is no symmetry of the tag positions along the chain. | |
In an actual experiment one measures the dwell velocities of the tags only which are equivalent to the current blockade durations.
Non uniformity of the dwell velocity: The presence of tags with heavier mass (mtag = 3mbulk) and larger solvent friction (γtag = 3γbulk) introduces a large variation in the dwell time and hence a large variation in the dwell velocities of the DNA beads and tags (see Fig. 4). In general, there is no up-down symmetry for the dwell time/velocity as tags are not located symmetrically along the chain backbone. Thus the physical quantities are averaged over U → D and D → U translocation data. The average dwell velocity 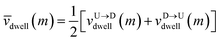 clearly shows two different velocity envelopes – the tags residing at the lower envelope. Fig. 4(b) shows that the dwell velocities of the tags (green circle
clearly shows two different velocity envelopes – the tags residing at the lower envelope. Fig. 4(b) shows that the dwell velocities of the tags (green circle  ) are significantly lower than the velocity of the nucleotides in between the tags, which will underestimate the barcode distances as explained later. We further notice that increasing the pore width resolves the barcodes better.
) are significantly lower than the velocity of the nucleotides in between the tags, which will underestimate the barcode distances as explained later. We further notice that increasing the pore width resolves the barcodes better.
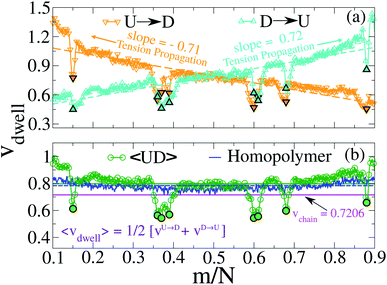 |
| | Fig. 4 (a) Dwell velocity of the monomers in a cylindrical nanopore system.  and and  represent downward and upward translocation directions respectively. (b) Dwell velocity averages of the both directions are represented in green circles ( represent downward and upward translocation directions respectively. (b) Dwell velocity averages of the both directions are represented in green circles ( ). Filled symbols correspond to the dwell velocities of the tags. The average velocity of both directions of a homo-polymer (tags are absent) is shown in the blue curve. The green and blue solid lines are the averages of the corresponding colored curves. The magenta solid line represents the average velocity of the entire chain obtained from eqn (6). ). Filled symbols correspond to the dwell velocities of the tags. The average velocity of both directions of a homo-polymer (tags are absent) is shown in the blue curve. The green and blue solid lines are the averages of the corresponding colored curves. The magenta solid line represents the average velocity of the entire chain obtained from eqn (6). | |
3.1 Barcode estimation using a cylindrical nanopore setup
If the dsDNA with barcodes were a rigid rod, then one could obtain the barcode distances 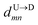 and
and 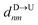 between tags Tm and Tn from the following equations (shown for downward translocation only):
between tags Tm and Tn from the following equations (shown for downward translocation only):| |
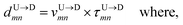 | (3a) |
| |
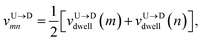 | (3b) |
| |
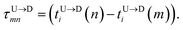 | (3c) |
Here 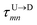 is the time delay of arrivals of Tm and Tn for downward translocation (please see Fig. 3(b) which explains the special case when m = 7 and n = 8). Similar equations can be obtained by flipping D and m with U and n respectively. In other words, eqn (3) gives the shortest distance and not necessarily the contour length (the actual distance) between the tags. However, this is the only data accessible through experiments and likely to provide an underestimation of the barcodes. Fig. 5(a) shows the data for 300 scans. The averages with error bars are shown in the 3rd column of Table 2. Excepting for T6 these measurements grossly underestimate the actual positions with large error bars.
is the time delay of arrivals of Tm and Tn for downward translocation (please see Fig. 3(b) which explains the special case when m = 7 and n = 8). Similar equations can be obtained by flipping D and m with U and n respectively. In other words, eqn (3) gives the shortest distance and not necessarily the contour length (the actual distance) between the tags. However, this is the only data accessible through experiments and likely to provide an underestimation of the barcodes. Fig. 5(a) shows the data for 300 scans. The averages with error bars are shown in the 3rd column of Table 2. Excepting for T6 these measurements grossly underestimate the actual positions with large error bars.
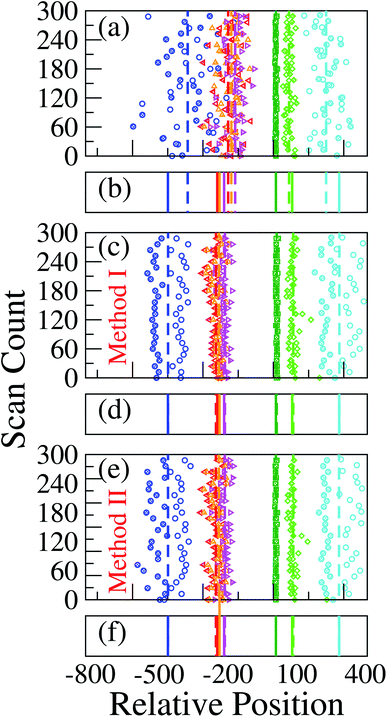 |
| | Fig. 5 (a) Barcodes are generated using different methods. In each graph, the colored symbols/lines refer to, from left to right the barcodes T1, T2, T3, T4, T6, T7, and T8 respectively. For better visibility every sixth data points are shown. The open and filled symbols represent barcodes for U → D and D → U translocation using (a) eqn (3); (c) using method 1, and (e) using method 2. In (b), (d) and (e) the solid lines refer to the actual location of the barcodes and the dashed lines correspond to the averages from (a), (c) and (e) respectively. The improved accuracy for the latter two methods are readily visible in (d) and (f) where the simulation and the actual data are almost indistinguishable. | |
Table 2 Barcode from various methods
| Tag label |
Relative distance w.r.t T5 |
Barcode |
| (Eqn (3)) |
(Method-I) |
(Method-II) |
| × |
✓ |
✓ |
| T1 |
460 |
373 ± 122 |
459 ± 59 |
460 ± 43 |
| T2 |
245 |
197 ± 67 |
250 ± 39 |
250 ± 32 |
| T3 |
235 |
183 ± 63 |
237 ± 38 |
237 ± 32 |
| T4 |
215 |
167 ± 54 |
211 ± 35 |
211 ± 30 |
| T5 |
0 |
0 |
0 |
0 |
| T6 |
11 |
11 ± 3 |
14 ± 4 |
11 ± 3 |
| T7 |
82 |
68 ± 23 |
86 ± 23 |
86 ± 21 |
| T8 |
287 |
230 ± 73 |
287 ± 65 |
287 ± 73 |
3.2 Tension propagation (TP) theory explains the source of discrepancy and provides solution
Unlike a rigid rod, tension propagation governs the semi-flexible chain's motion in the presence of an external bias. In TP theory and its implementation in Brownian dynamics, the motion of the subchain in the cis side decouples into two domains.30,31 In the vicinity of the pore, the tension front affects the motion directly while the second domain remains unperturbed, beyond the reach of the TP front. In our case, after the tag Tm translocates through the pore, following monomers are dragged into the pore quickly by the tension front, analogous to the uncoiling effect of a rope pulled from one end (please refer to the movie in the ESI†). The onset of this sudden faster motion continues to grow and reaches its maximum until the tension front hits the subsequent tag Tm±1, with larger inertia and viscous drag. At this time (called the tension propagation time32) the faster motion of the monomers (Fig. S2† in ESI) begins to taper down to the velocity of the tag Tm±1. This process continues from one segment to the other. These contour lengths of faster moving segments in between two barcodes are not accounted for in eqn (3). The experimental protocols are limited in extracting barcode information through eqn (3) (measuring current blockade time) and therefore, likely to underestimate the barcodes, unless the data is corrected to account for the faster moving monomers in between two tags.
How to determine the barcodes correctly? Fig. 1(b) and the 3rd column of Table 2 when looked closely provide clues to the solution of the underestimated tag distances. We note that locations of the isolated tags (such as, T1 and T8) far from T5 have larger error margins while T6 which is adjacent to T5 has the correct distance from eqn (3). It is simply because in the later case the contour length between T5 and T6 is almost equal to the shortest distance. Evidently, the error margins increase with increased separation.
To compare the barcodes obtained from eqn (3) with the actual contour length (see 2nd column of Table 2) between tag pairs, we invoke the Flory theory33 and describe the conformations of the translocating segments in terms of a dynamical effective exponent ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) which reveals the behavior of small and large segments between adjacent barcodes. The heatmap in Fig. 6 confirms that when the separation between the tag pairs is less compared to the DNA length, the connecting segment behaves like a rigid rod (
which reveals the behavior of small and large segments between adjacent barcodes. The heatmap in Fig. 6 confirms that when the separation between the tag pairs is less compared to the DNA length, the connecting segment behaves like a rigid rod (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) > 0.6). While for the isolated tags,
> 0.6). While for the isolated tags, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) < 0.6 suggests that barcodes are shorter than their respective contour lengths. This clarifies the reason behind the barcode underestimation for the tags which are spaced apart while yielding accurate barcodes for tags located in groups.
< 0.6 suggests that barcodes are shorter than their respective contour lengths. This clarifies the reason behind the barcode underestimation for the tags which are spaced apart while yielding accurate barcodes for tags located in groups.
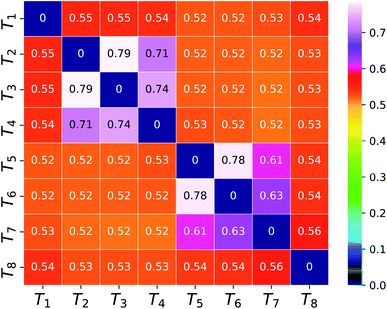 |
| | Fig. 6 The dynamical effective exponent (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) for the segment connecting a tag pair represented as a two dimensional heatmap array on the color scale ranging from blue to white. ) for the segment connecting a tag pair represented as a two dimensional heatmap array on the color scale ranging from blue to white. | |
Within the experimental set up we suggest the following two methods which will account for the larger velocities of the monomers.
Method 1 – Barcode from known end-to-end Tag distance: In order to measure the barcode distances accurately one thus needs the velocity of the entire chain. If the distance between (T1 and T8) d18 ≃ L, then the velocity of the segment d18 will approximately account for the average velocity of the entire chain vchain and correct the problem as demonstrated next. First we estimate the velocity of the chain
| |
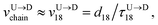 | (4) |
assuming we know
d18 and
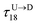
is the time delay of arrival at the pore between T
1 and T
8 for U → D translocation. We then estimate the barcode distance
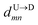
between tags T
m and T
n as
| |
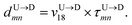 | (5) |
In the similar fashion one can calculate 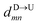 using
using 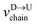 and
and 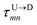 information respectively. How do we know d18? One can use d18 ≈ Lscan and vchain ≈
information respectively. How do we know d18? One can use d18 ≈ Lscan and vchain ≈ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) scan, from eqn (6) where
scan, from eqn (6) where ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) scan is the average velocity of the scanned length Lscan from repeated scanning as discussed in the next paragraph. This method is effective for estimating the long-spaced barcodes but it overestimates the barcode distance if multiple barcodes are close by as evident in Fig. 5(d) and the 4th column of Table 2. Thus, we know how to obtain barcode distances accurately when they are close by (from eqn (3)) and for large separation (eqn (5)). We now apply the physics behind these two schemes to derive an interpolation scheme that will work for all separations among the barcodes.
scan is the average velocity of the scanned length Lscan from repeated scanning as discussed in the next paragraph. This method is effective for estimating the long-spaced barcodes but it overestimates the barcode distance if multiple barcodes are close by as evident in Fig. 5(d) and the 4th column of Table 2. Thus, we know how to obtain barcode distances accurately when they are close by (from eqn (3)) and for large separation (eqn (5)). We now apply the physics behind these two schemes to derive an interpolation scheme that will work for all separations among the barcodes.
Method 2 – Barcode using two-step method: Average scan time ![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) scan for the entire chain (which can be measured experimentally) is a better way to estimate the average velocity of the chain. Lscan is the maximal length up to which the dsDNA segment remains captured inside the nanopore while getting scanned and denotes the theoretical maximum beyond which the dsDNA will escape from the nanopore, thus, L ≈ Lscan. For example, in our simulation, scanning length Lscan = 0.804L. We denote the average scan velocity as
scan for the entire chain (which can be measured experimentally) is a better way to estimate the average velocity of the chain. Lscan is the maximal length up to which the dsDNA segment remains captured inside the nanopore while getting scanned and denotes the theoretical maximum beyond which the dsDNA will escape from the nanopore, thus, L ≈ Lscan. For example, in our simulation, scanning length Lscan = 0.804L. We denote the average scan velocity as
| |
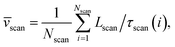 | (6) |
where
τscan(
i) is the scan time for the
ith event, and
Nscan = 300. To proceed further, we use our established results that the monomers of the dsDNA segments in between the tags move with velocity
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) scan
scan, while tags move with their respective dwell velocities
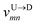
and
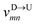
(
eqn (2)). We then calculate the segment velocity between two tags by taking the
weighted average of the velocities of tags and DNA segment in between as follows.
First, we estimate the approximate number of monomers 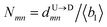 (〈bl〉 is the bond-length) by considering the tag velocities only using eqn (3). We then calculate the segment velocity accurately by incorporating weighted velocity contributions from both the tags and the monomers connecting the tags.
(〈bl〉 is the bond-length) by considering the tag velocities only using eqn (3). We then calculate the segment velocity accurately by incorporating weighted velocity contributions from both the tags and the monomers connecting the tags.
| |
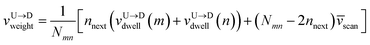 | (7) |
Here,
nnext are the number of neighboring monomers adjacent to the tags those share the same tag velocity. We checked that
nnext ≈ 1–3 does not make a noticeable difference in the final result. The barcodes are finally estimated by multiplying the calculated 2-step velocity in
eqn (7) above by the tag time delay as
| |
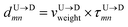 | (8) |
for U → D translocation and repeating the procedure for D → U translocation. This 2-step method accurately captures the distance between the barcodes when the two tags are in proximity or spaced apart from each other.
Table 2 and
Fig. 5 summarize our main results and claims.
4 Summary & future work
Motivated by the recent experiments we have designed barcode determination experiment in silico in a cylindrical nanopore using the Brownian dynamics scheme on a model dsDNA with known locations of the barcodes. We have carefully chosen the locations of the barcodes so that the separations among the barcodes span a broad distribution. We discover that if we only use the dwell time data for the tags from multiple scans of the dsDNA to calculate the velocity of the segments joining two tags then this method underscores the barcode distances for tags which are further apart. Our simulation guides us to conclude that the source of this underestimation lies in neglecting the information contained in the faster moving DNA segments in between any two tags. We use non-equilibrium tension propagation theory to explain the non-monotonic velocity of the chain segments where the barcodes lie at the lower bound of the velocity envelope as shown in Fig. 4(b). The emerging picture readily shows the way how to rectify this error by introducing an interpolation scheme that works well to determine barcodes spaced apart for all distances which we validate using simulation data. We suggest how to implement the scheme in an experimental setup. It is important to note that the interpolation scheme-based concept of the TP theory is quite general and we have ample evidence that this will work in a double nanopore system as well.
It is worth noting that our computational work has close similarity to a recent experimental study of sequence mapping using a plasmid DNA labeled with oligodeoxynucleotides at several locations.18 The velocity renormalization scheme is pretty much the same as ours – indicating the role of the velocity of the entire chain for an accurate determination of genomic distances. The origin of velocity fluctuation has also been discussed by Bo et al.34 for short chains. However, these papers studied and collected data from individual translocation events and did not scan the chain repeatedly.
We would like to conclude with some remarks about the limitations of the model and some refinements which we plan to accomplish in future. We carried out Brownian dynamics – thus we do not have hydrodynamics – any discussion of Zimm time as mentioned in some experiments is not relevant here. Also, typically, in such simulation protocols, the velocities are several orders of magnitude faster (this is a general rule of thumb in most of the CG simulations) and cannot be compared with experimental velocities directly. We also have the net force bias as a variable which would also make the velocity faster or slower. But there are other ways to compare with experiments by matching the simulation data with those obtained experimentally, such as distribution of wait time. This will require an adjustment of the external bias.
In a cylindrical nanopore the current blockade due to the tags is sequential once the DNA is captured in the pore,18 while in a double nanopore set up – once it is captured it is not known what fragment of the DNA is residing between the pores which may lead to ambiguity about identifying the tags. Thus it is worthwhile to explore the concept of flossing in a cylindrical nanopore set up. Finally, in this study we consider the electric field to be local, – strictly inside the pore, while the effect of the electric field is nonzero in the vicinity of the pore which will affect both the translocation speed and the dwell time distribution. Typically in experimental salt concentrations a dsDNA has a screened partial charge of 0.2–0.3 times the charge of an electron.34 With the electric field present beyond the pore, it will be worthwhile to study how the addition of a screened coulomb charge on the DNA monomer35,36 in our model will affect the flossing. We believe our results will promote new experimental and theoretical studies on nanopore translocation.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
The research has been supported by the grant number 1R21HG011236-01 from the National Human Genome Research Institute at the National Institute of Health. All computations were carried out using UCF's high performance computing cluster STOKES.
Notes and references
- P. D. N. Hebert, S. Ratnasingham and J. R. de Waard, Barcoding Animal Life: Cytochrome c Oxidase Subunit 1 Divergences among Closely Related Species, Proc. R. Soc. London, Ser. B, 2003, 270, 96 Search PubMed.
- P. D. N. Hebert, A. Cywinska, S. L. Ball and J. R. deWaard, Biological Identifications through DNA Barcodes, Proc. R. Soc. London, Ser. B, 2003, 270(1512), 313–321 CAS.
- P. D. N. Hebert, E. H. Penton, J. M. Burns, D. H. Janzen and W. Hallwachs, Ten Species in One: DNA Barcoding Reveals Cryptic Species in the Neotropical Skipper Butterfly Astraptes Fulgerator, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(41), 14812–14817 CrossRef CAS PubMed.
- R. Vernooy, E. Haribabu, M. R. Muller, J. H. Vogel, P. D. N. Hebert, D. E. Schindel, J. Shimura and G. A. C. Singer, Barcoding Life to Conserve Biological Diversity: Beyond the Taxonomic Imperative, PLoS Biol., 2010, 8(7), e1000417 CrossRef PubMed.
- N. J. Besansky, D. W. Severson and M. T. Ferdig, DNA Barcoding of Parasites and Invertebrate Disease Vectors: What You Don't Know Can Hurt You, Trends Parasitol., 2003, 19(12), 545–546 CrossRef CAS PubMed.
- N. Techen, I. Parveen, Z. Pan and I. A. Khan, DNA Barcoding of Medicinal Plant Material for Identification, Curr. Opin. Biotechnol., 2014, 25, 103–110 CrossRef CAS PubMed.
- X. Xiong, F. Yuan, M. Huang, L. Lu, X. Xiong and J. Wen, DNA Barcoding Revealed Mislabeling and Potential Health Concerns with Roasted Fish Products Sold across China, J. Food Prot., 2019, 82(7), 1200–1209 CrossRef CAS PubMed.
- E. H.-K. Wong and R. H. Hanner, DNA Barcoding Detects Market Substitution in North American Seafood, Food Res. Int., 2008, 41(8), 828–837 CrossRef CAS.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Characterization of Individual Polynucleotide Molecules Using a Membrane Channel, Proc. Natl. Acad. Sci. U. S. A., 1996, 93(24), 13770–13773 CrossRef CAS PubMed.
- M. Akeson, D. Branton, J. J. Kasianowicz, E. Brandin and D. W. Deamer, Microsecond Time-Scale Discrimination Among Polycytidylic Acid, Polyadenylic Acid, and Polyuridylic Acid as Homopolymers or as Segments Within Single RNA Molecules, Biophys. J., 1999, 77(6), 3227–3233 CrossRef CAS PubMed.
- A. Meller, L. Nivon, E. Brandin, J. Golovchenko and D. Branton, Rapid Nanopore Discrimination between Single Polynucleotide Molecules, Proc. Natl. Acad. Sci. U. S. A., 2000, 97(3), 1079–1084 CrossRef CAS PubMed.
- A. Meller, L. Nivon and D. Branton, Voltage-Driven DNA Translocations through a Nanopore, Phys. Rev. Lett., 2001, 86(15), 3435–3438 CrossRef CAS PubMed.
- M. Muthukumar, Polymer Translocation, Taylor & Francis, Boca Raton, 2011 Search PubMed.
- M. Wanunu, Nanopores: A Journey towards DNA Sequencing, Phys. Life Rev., 2012, 9(2), 125–158 CrossRef PubMed.
- V. V. Palyulin, T. Ala-Nissila and R. Metzler, Polymer Translocation: The First Two Decades and the Recent Diversification, Soft Matter, 2014, 10(45), 9016–9037 RSC.
- D. Deamer, M. Akeson and D. Branton, Three Decades of Nanopore Sequencing, Nat. Biotechnol., 2016, 34(5), 518–524 CrossRef CAS PubMed.
- N. Ashkenasy, J. Sánchez-Quesada, H. Bayley and M. R. Ghadiri, Recognizing a Single Base in an Individual DNA Strand: A Step Toward DNA Sequencing in Nanopores, Angew. Chem., 2005, 117(9), 1425–1428 CrossRef.
- K. Chen, F. Gularek, B. Liu, E. Weinhold and U. F. Keyser, Electrical DNA Sequence Mapping Using Oligodeoxynucleotide Labels and Nanopores, ACS Nano, 2021, 15(2), 2679–2685 CrossRef CAS PubMed.
- A. Singer, M. Wanunu, W. Morrison, H. Kuhn, M. Frank-Kamenetskii and A. Meller, Nanopore Based Sequence Specific Detection of Duplex DNA for Genomic Profiling, Nano Lett., 2010, 10(2), 738–742 CrossRef CAS PubMed.
- A. Zrehen, D. Huttner and A. Meller, On-Chip Stretching, Sorting, and Electro-Optical Nanopore Sensing of Ultralong Human Genomic DNA, ACS Nano, 2019, 13(12), 14388–14398 CrossRef CAS PubMed.
- K. Liu, C. Pan, A. Kuhn, A. P. Nievergelt, G. E. Fantner, O. Milenkovic and A. Radenovic, Detecting Topological Variations of DNA at Single-Molecule Level, Nat. Commun., 2019, 10(1), 1–9 CrossRef PubMed.
- F. Bošković, A. Ohmann, U. F. Keyser and K. Chen, DNA Structural Barcode Copying and Random Access, Small Structures, 2021, 2000144 CrossRef.
- S. Pud, S.-H. Chao, M. Belkin, D. Verschueren, T. Huijben, C. van Engelenburg, C. Dekker and A. Aksimentiev, Mechanical Trapping of DNA in a Double-Nanopore System, Nano Lett., 2016, 16(12), 8021–8028 CrossRef CAS PubMed.
- Y. Zhang, X. Liu, Y. Zhao, J.-K. Yu, W. Reisner and W. B. Dunbar, Single Molecule DNA Resensing Using a Two-Pore Device, Small, 2018, 14(47), 1801890 CrossRef PubMed.
- X. Liu, Y. Zhang, R. Nagel, W. Reisner and W. B. Dunbar, Controlling DNA Tug-of-War in a Dual Nanopore Device, Small, 2019, 15(30), 1901704 CrossRef PubMed.
- X. Liu, P. Zimny, Y. Zhang, A. Rana, R. Nagel, W. Reisner and W. B. Dunbar, Flossing DNA in a Dual Nanopore Device, Small, 2020, 16(3), 1905379 CrossRef CAS PubMed.
- A. Bhattacharya and S. Seth, Tug of War in a Double-Nanopore System, Phys. Rev. E, 2020, 101(5), 052407 CrossRef CAS PubMed.
- S. Seth and A. Bhattacharya, Polymer Escape through a Three Dimensional Double-Nanopore System, J. Chem. Phys., 2020, 153(10), 104901 CrossRef CAS PubMed.
- A. Choudhary, H. Joshi, H.-Y. Chou, K. Sarthak, J. Wilson, C. Maffeo and A. Aksimentiev, High-Fidelity Capture, Threading, and Infinite-Depth Sequencing of Single DNA Molecules with a Double-Nanopore System, ACS Nano, 2020, 14(11), 15566–15576 CrossRef PubMed.
- T. Sakaue, Nonequilibrium Dynamics of Polymer Translocation and Straightening, Phys. Rev. E, 2007, 76(2), 021803 CrossRef PubMed.
- T. Ikonen, A. Bhattacharya, T. Ala-Nissila and W. Sung, Influence of Non-Universal Effects on Dynamical Scaling in Driven Polymer Translocation, J. Chem. Phys., 2012, 137(8), 085101 CrossRef CAS PubMed.
- R. Adhikari and A. Bhattacharya, Driven Translocation of a Semi-Flexible Chain through a Nanopore: A Brownian Dynamics Simulation Study in Two Dimensions, J. Chem. Phys., 2013, 138(20), 204909 CrossRef PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, Oxford, 2003 Search PubMed.
- B. Lu, F. Albertorio, D. P. Hoogerheide and J. A. Golovchenko, Origins and Consequences of Velocity Fluctuations during DNA Passage through a Nanopore, Biophys. J., 2011, 101(1), 70–79 CrossRef CAS PubMed.
- L. Qiao and G. W. Slater, Capture of Rod-like Molecules by a Nanopore: Defining an “Orientational Capture Radius, J. Chem. Phys., 2020, 152(14), 144902 CrossRef CAS PubMed.
- L. Qiao, M. Ignacio and G. W. Slater, An Efficient Kinetic Monte Carlo to Study Analyte Capture by a Nanopore: Transients, Boundary Conditions and Time-Dependent Fields, Phys. Chem. Chem. Phys., 2021, 23(2), 1489–1499 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Information about the simulation setup, additional figure on tension propagation through the DNA backbone and the simulation movie. See DOI: 10.1039/d1ra00349f |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Aniket Bhattacharya
and
Aniket Bhattacharya *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 bp long dsDNA with 75 bp long protein tags at random locations along the chain24–26 using a dual nanopore device. Here we explore if a cylindrical nanopore with an applied bias force can resolve the barcodes with similar accuracy or better. We purposely choose positions of the 8 barcodes (Table 1) to study how the effect of disparate distances among the barcodes affects their measurements.
500 bp long dsDNA with 75 bp long protein tags at random locations along the chain24–26 using a dual nanopore device. Here we explore if a cylindrical nanopore with an applied bias force can resolve the barcodes with similar accuracy or better. We purposely choose positions of the 8 barcodes (Table 1) to study how the effect of disparate distances among the barcodes affects their measurements.

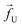 and
and 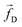 are applied in the nanopore to straighten the dsDNA as it translocates in the direction of the bias net force
are applied in the nanopore to straighten the dsDNA as it translocates in the direction of the bias net force 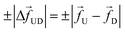 . (b) Positions of the protein tags along the contour length of the model dsDNA of length L = 1024σ which represents an actual dsDNA of 48
. (b) Positions of the protein tags along the contour length of the model dsDNA of length L = 1024σ which represents an actual dsDNA of 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 base pairs. The locations of the tags are listed in Table 1.
500 base pairs. The locations of the tags are listed in Table 1.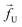 and at each end of the cylinder in opposite directions keep the DNA straight inside the channel and allows translocation in the direction of the net bias (please see Fig. 1 and 2).
and at each end of the cylinder in opposite directions keep the DNA straight inside the channel and allows translocation in the direction of the net bias (please see Fig. 1 and 2).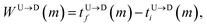
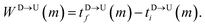
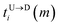 and
and 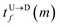 are the arrival and exit time of the mth bead as further demonstrated in Fig. 3(a). The corresponding dwell velocities
are the arrival and exit time of the mth bead as further demonstrated in Fig. 3(a). The corresponding dwell velocities 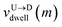 and
and 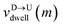 for the mth bead along the nanopore channel axis (please see Fig. 3(a)) can be obtained as follows,
for the mth bead along the nanopore channel axis (please see Fig. 3(a)) can be obtained as follows,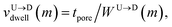
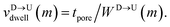

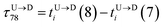 for tags T7 and T8 while they are moving downward. Please note that similar quantity for upward translocation
for tags T7 and T8 while they are moving downward. Please note that similar quantity for upward translocation 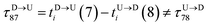 as there is no symmetry of the tag positions along the chain.
as there is no symmetry of the tag positions along the chain.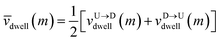 clearly shows two different velocity envelopes – the tags residing at the lower envelope. Fig. 4(b) shows that the dwell velocities of the tags (green circle
clearly shows two different velocity envelopes – the tags residing at the lower envelope. Fig. 4(b) shows that the dwell velocities of the tags (green circle  ) are significantly lower than the velocity of the nucleotides in between the tags, which will underestimate the barcode distances as explained later. We further notice that increasing the pore width resolves the barcodes better.
) are significantly lower than the velocity of the nucleotides in between the tags, which will underestimate the barcode distances as explained later. We further notice that increasing the pore width resolves the barcodes better.
 and
and  represent downward and upward translocation directions respectively. (b) Dwell velocity averages of the both directions are represented in green circles (
represent downward and upward translocation directions respectively. (b) Dwell velocity averages of the both directions are represented in green circles ( ). Filled symbols correspond to the dwell velocities of the tags. The average velocity of both directions of a homo-polymer (tags are absent) is shown in the blue curve. The green and blue solid lines are the averages of the corresponding colored curves. The magenta solid line represents the average velocity of the entire chain obtained from eqn (6).
). Filled symbols correspond to the dwell velocities of the tags. The average velocity of both directions of a homo-polymer (tags are absent) is shown in the blue curve. The green and blue solid lines are the averages of the corresponding colored curves. The magenta solid line represents the average velocity of the entire chain obtained from eqn (6).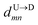 and
and 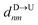 between tags Tm and Tn from the following equations (shown for downward translocation only):
between tags Tm and Tn from the following equations (shown for downward translocation only):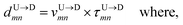
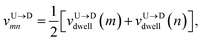
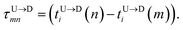
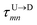 is the time delay of arrivals of Tm and Tn for downward translocation (please see Fig. 3(b) which explains the special case when m = 7 and n = 8). Similar equations can be obtained by flipping D and m with U and n respectively. In other words, eqn (3) gives the shortest distance and not necessarily the contour length (the actual distance) between the tags. However, this is the only data accessible through experiments and likely to provide an underestimation of the barcodes. Fig. 5(a) shows the data for 300 scans. The averages with error bars are shown in the 3rd column of Table 2. Excepting for T6 these measurements grossly underestimate the actual positions with large error bars.
is the time delay of arrivals of Tm and Tn for downward translocation (please see Fig. 3(b) which explains the special case when m = 7 and n = 8). Similar equations can be obtained by flipping D and m with U and n respectively. In other words, eqn (3) gives the shortest distance and not necessarily the contour length (the actual distance) between the tags. However, this is the only data accessible through experiments and likely to provide an underestimation of the barcodes. Fig. 5(a) shows the data for 300 scans. The averages with error bars are shown in the 3rd column of Table 2. Excepting for T6 these measurements grossly underestimate the actual positions with large error bars.

![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) which reveals the behavior of small and large segments between adjacent barcodes. The heatmap in Fig. 6 confirms that when the separation between the tag pairs is less compared to the DNA length, the connecting segment behaves like a rigid rod (
which reveals the behavior of small and large segments between adjacent barcodes. The heatmap in Fig. 6 confirms that when the separation between the tag pairs is less compared to the DNA length, the connecting segment behaves like a rigid rod (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) > 0.6). While for the isolated tags,
> 0.6). While for the isolated tags, ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) < 0.6 suggests that barcodes are shorter than their respective contour lengths. This clarifies the reason behind the barcode underestimation for the tags which are spaced apart while yielding accurate barcodes for tags located in groups.
< 0.6 suggests that barcodes are shorter than their respective contour lengths. This clarifies the reason behind the barcode underestimation for the tags which are spaced apart while yielding accurate barcodes for tags located in groups.
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) for the segment connecting a tag pair represented as a two dimensional heatmap array on the color scale ranging from blue to white.
) for the segment connecting a tag pair represented as a two dimensional heatmap array on the color scale ranging from blue to white.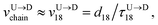
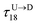 is the time delay of arrival at the pore between T1 and T8 for U → D translocation. We then estimate the barcode distance
is the time delay of arrival at the pore between T1 and T8 for U → D translocation. We then estimate the barcode distance 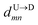 between tags Tm and Tn as
between tags Tm and Tn as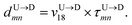
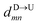 using
using 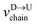 and
and 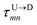 information respectively. How do we know d18? One can use d18 ≈ Lscan and vchain ≈
information respectively. How do we know d18? One can use d18 ≈ Lscan and vchain ≈ ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) scan, from eqn (6) where
scan, from eqn (6) where ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) scan is the average velocity of the scanned length Lscan from repeated scanning as discussed in the next paragraph. This method is effective for estimating the long-spaced barcodes but it overestimates the barcode distance if multiple barcodes are close by as evident in Fig. 5(d) and the 4th column of Table 2. Thus, we know how to obtain barcode distances accurately when they are close by (from eqn (3)) and for large separation (eqn (5)). We now apply the physics behind these two schemes to derive an interpolation scheme that will work for all separations among the barcodes.
scan is the average velocity of the scanned length Lscan from repeated scanning as discussed in the next paragraph. This method is effective for estimating the long-spaced barcodes but it overestimates the barcode distance if multiple barcodes are close by as evident in Fig. 5(d) and the 4th column of Table 2. Thus, we know how to obtain barcode distances accurately when they are close by (from eqn (3)) and for large separation (eqn (5)). We now apply the physics behind these two schemes to derive an interpolation scheme that will work for all separations among the barcodes.![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) scan for the entire chain (which can be measured experimentally) is a better way to estimate the average velocity of the chain. Lscan is the maximal length up to which the dsDNA segment remains captured inside the nanopore while getting scanned and denotes the theoretical maximum beyond which the dsDNA will escape from the nanopore, thus, L ≈ Lscan. For example, in our simulation, scanning length Lscan = 0.804L. We denote the average scan velocity as
scan for the entire chain (which can be measured experimentally) is a better way to estimate the average velocity of the chain. Lscan is the maximal length up to which the dsDNA segment remains captured inside the nanopore while getting scanned and denotes the theoretical maximum beyond which the dsDNA will escape from the nanopore, thus, L ≈ Lscan. For example, in our simulation, scanning length Lscan = 0.804L. We denote the average scan velocity as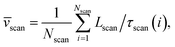
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) scan, while tags move with their respective dwell velocities
scan, while tags move with their respective dwell velocities 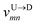 and
and 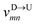 (eqn (2)). We then calculate the segment velocity between two tags by taking the weighted average of the velocities of tags and DNA segment in between as follows.
(eqn (2)). We then calculate the segment velocity between two tags by taking the weighted average of the velocities of tags and DNA segment in between as follows.
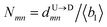 (〈bl〉 is the bond-length) by considering the tag velocities only using eqn (3). We then calculate the segment velocity accurately by incorporating weighted velocity contributions from both the tags and the monomers connecting the tags.
(〈bl〉 is the bond-length) by considering the tag velocities only using eqn (3). We then calculate the segment velocity accurately by incorporating weighted velocity contributions from both the tags and the monomers connecting the tags.