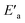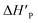Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reactions of aryl dimethylphosphinothioate esters with anionic oxygen nucleophiles: transition state structure in 70% water–30% ethanol†
Georgina I. Kalu a,
Collins I. Ubochi
a,
Collins I. Ubochi a and
Ikenna Onyido
a and
Ikenna Onyido *b
*b
aDepartment of Chemistry, Imo State University, Owerri, Nigeria
bDepartment of Pure and Industrial Chemistry, Nnamdi Azikiwe University, Awka, Nigeria. E-mail: ikennaonyido@yahoo.com; Tel: +234-806-268-5122
First published on 25th February 2021
Abstract
Aryl dimethylphosphinates, 2, react with anionic oxygen nucleophiles in water via a concerted (ANDN) mechanism. With EtO− in anhydrous ethanol, the mechanism is associative (AN + DN), with rate-limiting pentacoordinate intermediate formation. This change in mechanism with solvent change has been ascribed to changes in the nucleophile and leaving group basicities accompanying solvent change. This paper reports on a kinetic analysis of the reactions of the aryl dimethylphosphinothioates, 3a–g, with oxygen nucleophiles in 70% water–30% ethanol (v/v) solvent at 25 °C, reactions known to proceed by a concerted mechanism in water, to test the rationalization stated above, since the nucleophiles and LGs of interest are more basic in aqueous ethanol than in water. The change in solvent causes an ca. 14 to 320-fold decrease in rate. Hammett and Brønsted-type correlations characterize a concerted TS with less P–LG bonding in aqueous ethanol than in water. Two opposing consequences are associated with the solvent change: (a) increased basicity of nucleophiles and LGs, which lead to a modest tightening of the TS; and (b) better stabilization of the IS relative to the TS in aqueous ethanol, which results in a slower reaction with a more product-like TS. Hammond and anti-Hammond effects on the TS arising from better stabilization of the IS over the TS dominate over the effects of increased nucleophile and LG basicity in determining the looser TS structure in aqueous ethanol. An altered TS structure is consistent with an altered reaction potential energy surface, in this case caused by a change in solvent polarity.
Introduction
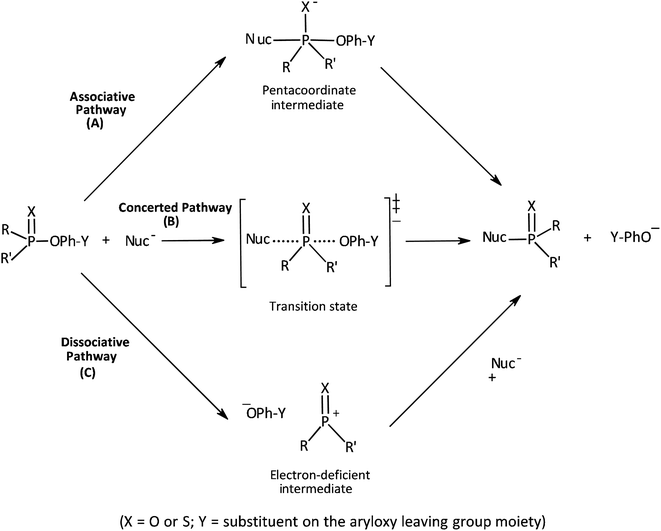
Our interest in the transfer of the (thio)phosphinoyl group1 between oxyanionic nucleophiles in hydroxylic solvents2–5 is based, in part, on the basic structural relationship of these substrates with (thio)phosphonate and (thio)phosphate esters frequently encountered in uncatalyzed and biological phosphoryl transfers.6 Even though phosphinate esters do not occur naturally, some phosphinic acids have found application as inhibitors of metalloproteases7 and as medicinal agents towards some diseases.8 The elucidation of the structure of the transition states of the reactions of phosphinate esters and other organophosphorus esters with a variety of nucleophiles in solution chemistry has contributed to the present status of understanding of the mechanistic details of phosphoryl transfer reactions.5,9–12 Of particular interest are the questions of whether biological phosphoryl transfers are concerted or stepwise mechanisms involving intermediates, and whether the TS in a chemical reaction is altered by a mediating enzyme in the analogous biochemical processes.13 It is also of interest to understand the factors that predispose reacting systems to the choices they make regarding their operational mechanisms and rate-limiting transition states under various reaction conditions.14,15The three possible mechanisms9 for the transfer of a phosphinoyl or thiophosphinoyl group1 between two nucleophiles are given in Scheme 1 in which X could be O or S, while Y represents one or more substituents on the aryloxy leaving group (LG) moiety. Pathways A, B and C in this scheme describe a stepwise associative (AN + DN) mechanism involving a pentacoordinate phosphorane-type intermediate whose formation or decomposition could be the rate-limiting step, a concerted (ANDN) mechanism involving the rate-limiting synchronous formation and breaking of bonds, and a stepwise dissociative (DN + AN) mechanism typically involving the rate-limiting ionization of the substrate to yield a metaphosphate-type intermediate, respectively. These mechanisms are also shown in the More O'Ferrall–Jencks diagram15,16 in Fig. 1 in which the intermediates formed in the associative and dissociative pathways are located at the top left corner and lower right corner of the diagram, respectively, while the diagonal from the lower left (reactant) corner to the upper right (product) corner defines the concerted pathway.
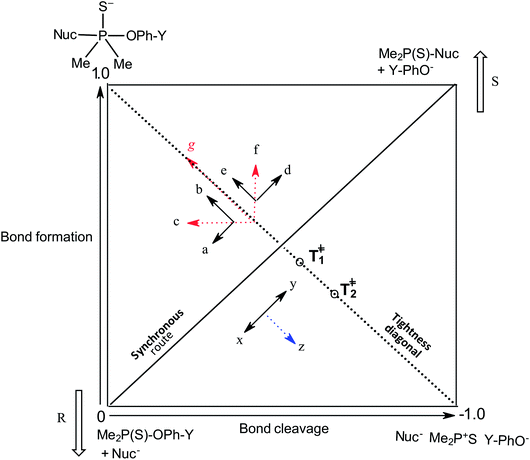 | ||
| Fig. 1 More O'Ferrall–Jencks diagram for the transfer of the thiophosphinoyl group between the nucleophile and an aryloxide LG. Extent of bond formation and bond fission is measured along the vertical and horizontal axes, respectively (see text). The TS in water, T‡1, is slightly displaced from the intersection of the synchronous route and tightness diagonal (see ref. 2). Change of solvent to ethanol moves the TS (resultant vector g) towards the associative corner (see text and ref. 4). Solvent change from water to 70% water–30% ethanol will slide T‡1 in the same direction but to a diminished extent due to basicity changes in nucleophile and LG. The reactant corner is stabilized by the aqueous ethanol solvent; this perturbation (lowering the reactant corner – bold arrow R – and raising the product corner – bold arrow S) would slide the TS along the reaction coordinate (x ↔ y motion) as the Hammond effect. The resultant movement perpendicular to the reaction coordinate, i.e. vector z = the anti-Hammond effect, would move the TS towards a looser TS, T‡2 (this work). | ||
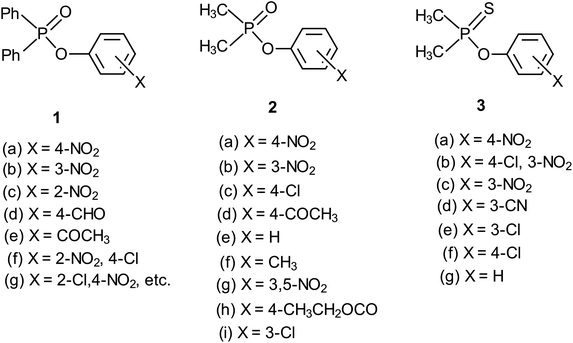
Rate data for the reactions of anionic oxygen nucleophiles (HO−, RO−, Y-PhO−) with aryl diphenylphosphinates (Ph2P(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–OPh-Y, 1) and aryl dimethylphosphinates (Me2P(
O)–OPh-Y, 1) and aryl dimethylphosphinates (Me2P(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–OPh-Y, 2) demonstrate an interesting mechanistic dichotomy in water and ethanol solvents. The alkaline hydrolysis of 1 in pure water17,18 and in a variety of water-containing binary solvent systems,17–21 as well as the ethanolysis of the same substrate series in pure ethanol,22 proceeds via the associative pathway, with rate-limiting formation of a pentacoordinate intermediate. The reaction of the same substrate series with the less basic phenoxide ion (PhO−) proceeds by a concerted mechanism in water.23 When the solvent is changed to ethanol, the mechanism for the reaction with PhO− as nucleophile becomes associative, with rate-limiting formation of the pentacoordinate intermediate.24
O)–OPh-Y, 2) demonstrate an interesting mechanistic dichotomy in water and ethanol solvents. The alkaline hydrolysis of 1 in pure water17,18 and in a variety of water-containing binary solvent systems,17–21 as well as the ethanolysis of the same substrate series in pure ethanol,22 proceeds via the associative pathway, with rate-limiting formation of a pentacoordinate intermediate. The reaction of the same substrate series with the less basic phenoxide ion (PhO−) proceeds by a concerted mechanism in water.23 When the solvent is changed to ethanol, the mechanism for the reaction with PhO− as nucleophile becomes associative, with rate-limiting formation of the pentacoordinate intermediate.24
The same mechanistic dichotomy outlined above for 1 is also encountered in the reactions of the Me2P(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–OPh-Y series of compounds, 2, with the anionic oxygen nucleophiles EtO− and HO−. Whereas the reaction of 2 with EtO− in pure ethanol occurs via a stepwise mechanism with rate-limiting formation of a pentacoordinate intermediate,4 its reaction with HO− in 90% water–10% dioxane occurs by a concerted SN2(P)-type mechanism, with Brønsted βnuc = 0.41.25 A value of βlg = −0.47 was calculated4 from the original data25 for this reaction from which the Leffler indices26 αbf = βnuc/βeq = 0.47 and αbr = βlg/βeq = −0.53 were obtained for bond formation and bond breaking,27 respectively, according to eqn (1), with βeq defined in eqn (2). These Leffler parameters locate the TS for the reactions of 2 with anionic oxygen nucleophiles in aqueous dioxane at T‡1 along the tightness diagonal, but slightly displaced from the intersection between the synchronous route and the tightness diagonal in Fig. 1.
O)–OPh-Y series of compounds, 2, with the anionic oxygen nucleophiles EtO− and HO−. Whereas the reaction of 2 with EtO− in pure ethanol occurs via a stepwise mechanism with rate-limiting formation of a pentacoordinate intermediate,4 its reaction with HO− in 90% water–10% dioxane occurs by a concerted SN2(P)-type mechanism, with Brønsted βnuc = 0.41.25 A value of βlg = −0.47 was calculated4 from the original data25 for this reaction from which the Leffler indices26 αbf = βnuc/βeq = 0.47 and αbr = βlg/βeq = −0.53 were obtained for bond formation and bond breaking,27 respectively, according to eqn (1), with βeq defined in eqn (2). These Leffler parameters locate the TS for the reactions of 2 with anionic oxygen nucleophiles in aqueous dioxane at T‡1 along the tightness diagonal, but slightly displaced from the intersection between the synchronous route and the tightness diagonal in Fig. 1.
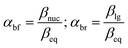 | (1) |
| βnuc − βlg = βeq | (2) |
The pKa values of the nucleophiles HO−, RO−, PhO− and other substituted phenoxides in water and ethanol are listed in Table 1 from which it is seen that the nucleophiles and leaving groups utilized in the studies cited above are more basic in ethanol than in water. It has been explained4 that in this reaction system, the change in nucleophile and LG basicity, ΔpKa ≥ 3 and ≥5, respectively, caused by changing the solvent from water to ethanol, induces the observed change of mechanism in ethanol, by moving the concerted TS toward more associative TS structures with greater bond formation and little or no bond cleavage. This explanation is amplified below using the More O'Ferrall–Jencks diagram in Fig. 1, in order to establish the rationale for the present study.
| Nucleophile | pKa (H2O)a | pKa (H2O–EtOH 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30)b,c 30)b,c |
pKa (EtOH) |
|---|---|---|---|
| a Values at 25 °C, taken from W. P. Jencks and J. Regenstein, in Handbook of Biochemistry, ed. H. A. Sober, The Chemical Rubber Co., Cleveland, 1970, 2nd edn, section J-187.b The aqueous ethanol solvent is 70% water–30% ethanol.c These pKa values were obtained as described in the Experimental section.d Values at 25 °C, taken from I.-H. Um, Y.-J. Hong and D.-S. Kwon, Tetrahedron, 1997, 53, 5073.e Values in 70% water–30% ethanol at 25 °C measured by A. C. Hengge and R. Hoff, personal communication of to be published results.f Value at 22 °C, given by G. Guanti, G. Cevasco, S. Thea, C. Dell'Erba and G. Petrillo, J. Chem. Soc., Perkin Trans. 2, 1981, 327. | |||
| EtO− | 16.0 | 16.81 | 19.18d |
| HO− | 15.74 | 16.60 | |
| CHCl2CH2O− | 12.89 | 13.53 (13.52)e | |
| CF3CH2O− | 12.43 | 12.96 (12.96)e | |
| CF3CF2CF2CH2O− | 11.40 | 12.06 | |
| 4-MeOPhO− | 10.20 | 10.83 | |
| PhO− | 9.95 | 10.54 (10.57)e | 15.76d |
| 4-ClPhO− | 9.38 | 10.02 (10.03)e | 14.90d (14.80)f |
| 3-ClPhO− | 9.02 | 9.58 | |
| 3-CNPhO− | 8.61 | 8.92 (8.89)e | |
| 4-CNPhO− | 7.95 | 8.30 (8.29)e | 13.04d |
| 2,5-Cl2PhO− | 7.51 | 7.82 | |
| 2,4,5-Cl3PhO− | 6.72 | 7.04 | |
| 2,3,5,6-F4PhO− | 5.53 | 5.86 (5.86)e | |
For the reaction of 2 with oxyanionic nucleophiles, the change in the basicity of the nucleophiles in going from water to ethanol is thought4 to lower the bottom corners in Fig. 1. This perturbation slides the concerted TS T‡1 parallel to the reaction coordinate toward the bottom left corner (arrow a), the so-called Hammond effect. The same perturbation would also slide T‡1 in a direction perpendicular to the reaction coordinate, toward the left top associative corner (arrow b), i.e. the anti-Hammond effect. The resultant vector (arrow c) makes βlg less negative, which is equivalent to a diminished separation of the leaving group in the TS in ethanol. The same argument has been advanced for the effect of solvent change, from water to ethanol, on the basicity of the aryloxide leaving groups in the substrate. Aryloxide ions are poorer leaving groups in ethanol, thus raising the energy of the right side of Fig. 1, compared to the left, a perturbation that moves T‡1 to the upper right as the Hammond effect (arrow d), while the anti-Hammond effect moves T‡1 to the upper left (arrow e), to produce the arrow f as the resultant vector. This movement results in a higher value of βnuc, i.e. greater bond formation between the nucleophile and the reaction site, with increased basicity of the leaving group. These responses of βlg and βnuc to enhanced basicity of the nucleophile and LG, respectively, which move the TS in the direction of the associative corner in Fig. 1 (with vector g as the resultant of vectors c and f), are a consequence of the positive cross interaction between the nucleophile and the LG in a concerted TS, quantified28 as the cross-interaction coefficient, pxy, defined in eqn (3).
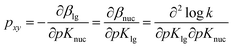 | (3) |
The above rationalization of the change in mechanism observed with solvent change from water to ethanol in these systems does not consider solvent polarity as an important variable that could affect reaction mechanisms and TS structures, even though the solvents of interest have significantly different polarities, as measured by their dielectric constants, D = 80.2 and 25.2 for water and ethanol, respectively, at 20 °C.29,30 Solvent and solvation effects are known to affect reactions in profound and, sometimes, complex ways.31 Bickelhaupt and coworkers32 have shown that the shapes of the potential energy surface of SN2-type processes are changed by solvation in ways that depend on solvent polarity and the way charges are distributed over the interacting entities, while the work of Carvalho et al.33 has highlighted the interplay between nucleophile charge and TS solvation in determining reactivities in the SN2(P) reactions of simple phosphoryl systems. In the reactions of phosphinate esters with anionic oxygen nucleophiles considered above, the polarities of water and ethanol in which the nucleophilic substitution reaction occurs through concerted and associative mechanisms, respectively, could be regarded as lying at two extremes. In the continuum of polarities between pure water and pure ethanol, the same reaction could conceivably occur with different transition states, such that a spectrum of transition states could occur in the progression from pure water, through water–ethanol mixtures of increasing ethanol content, to pure ethanol. The existence of a continuum of transition states in phosphoryl transfer reactions, in which bond formation and bond rupture are not necessarily synchronous, has been advanced.9
Three events are likely to occur in such a system as the ethanol content of the binary solvent increases from 0% in pure water to 100% in pure ethanol: (i) the strength of the nucleophile increases across the continuum of decreasing polarities due to increasing desolvation of the nucleophile; (ii) the strength of the P–LG bond becomes stronger as the LG becomes poorer (i.e. more basic) with decreasing polarity of the medium; and (iii) the reaction rate responds to decreasing polarity of the solvent, the specific response depending on the extent to which the initial state is stabilized or destabilized relative to the TS, with the consequential Hammond effects on the TS across the continuum of decreasing polarities. Such a study would be of interest because of the resulting information on the responses of the TS to changing solvent polarity and nucleophile/LG basicity, which could also shed some light on the factors that lead to changes in mechanism and/or TS structures in these reactions. These outcomes could be relevant in the discussion of mechanisms and transition states in uncatalyzed and biological phosphoryl transfer processes. Although studies of solvent effects on the reactions of phosphorus esters with a variety of nucleophiles have been reported34,35 the effects of solvent polarity on transition state structures of these reactions have not been specifically examined, to our knowledge.
We chose to study the effects of nucleophile/LG basicity and solvent polarity on the reactions of 3, thio analogues of 2, with the anionic oxygen nucleophiles HO−, alkoxides (RO−) and phenoxides (Y-PhO−) in 70% water–30% ethanol (v/v) with the specific objective of probing the TS structure using Hammett and Brønsted correlations. An earlier Brønsted and heavy atom kinetic isotope effect (KIE) study of the nucleophilic reaction of 3 with anionic oxygen nucleophiles in water showed2 unambiguously that the reaction proceeds via a concerted mechanism in which bond fission is slightly ahead of bond making in the TS (βnuc = 0.47, βlg = −0.53). Values of the Leffler indices αbf = 0.47 and αbr = −0.53 obtained from the Brønsted parameters for this concerted reaction locate its TS at T‡1 in Fig. 1, exactly the same TS structure for the reaction of its oxygen analogue, 2.4,25 The similarity in the TS structure for the reactions of 2 and 3 in water is entirely fortuitous since βnuc, βlg and βeq values for their reactions in this solvent are significantly dissimilar.4 As can be seen in Table 1, the pKa values of the nucleophiles and LGs employed in this and our earlier study2 are higher in 70% water–30% ethanol than in water. The results presented and discussed below with the aid of the More O'Ferrall–Jencks reaction map in Fig. 1 show that the concerted reaction TS is looser in the less polar solvent, in which case the change in solvent polarity has a dominant effect over solvent-induced changes in nucleophile and LG basicity in determining the TS structure in this solvent.
Results and discussion
The rates of the nucleophilic displacement reaction of oxyanions of the type HO−, RO− and X-PhO− (X = H and other substituents) with 4-nitrophenyl dimethylphosphinothioate ester, 3a, in 70% water–30% ethanol (v/v) were measured spectrophotometrically at 25 °C under pseudo-first-order conditions. The pseudo-first-order rate constants, kobs, calculated from linear plots of log(A∞ − At) versus time, are given as ESI.† Second-order rate constants, knuc, calculated from the linear plots of kobs versus nucleophile concentration for the different nucleophiles, are presented in Table 2, along with the pKa values of the nucleophiles in this solvent. These rate constants were used to obtain the Brønsted-type plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc versus pKa (nucleophile) shown in Fig. 2.
knuc versus pKa (nucleophile) shown in Fig. 2.
| Entry | Nucleophile | pKab | 104knucc/M−1 s−1 | de |
|---|---|---|---|---|
| a These rate constants were measured at ionic strength, I = 1.0 M (KCl).b Values of pKa were obtained as described in the Experimental section.c These knuc values were obtained from plots of kobs (given as ESI) versus nucleophile concentration, as described in the Experimental. Each kobs value is an average of duplicate runs with a deviation of ±3%; data for entries 10–12 were obtained by the initial rate method (see text) and are subject to an uncertainty of ±5%.d Values of knuc in water at 25 °C (kwaternuc) were taken from our previous work in ref. 2.e These (kaqEtOHnuc) are knuc values in 70% water–30% ethanol (this work). | ||||
| 1 | HO− | 16.60 | 830 | 79.9 |
| 2 | CHCl2CH2O− | 13.53 | 616 | 68.9 |
| 3 | CF3CH2O− | 12.96 | 427 | 89.2 |
| 4 | CF3CF2CF2CH2O− | 12.06 | 252 | 119.4 |
| 5 | 4-MeOPhO− | 10.83 | 14.1 | 158.2 |
| 6 | PhO− | 10.54 | 12.3 | 43.9 |
| 7 | 4-ClPhO− | 10.02 | 10.4 | 28.2 |
| 8 | 3-CNPhO− | 8.92 | 2.37 | 86.1 |
| 9 | 4-CNPhO− | 8.30 | 1.85 | 67.6 |
| 10 | 2,5-Cl2PhO− | 7.82 | 1.43 | 69.9 |
| 11 | 2,4,5-Cl3PhO− | 7.04 | 0.75 | 23.1 |
| 12 | 2,3,5,6-F4PhO− | 5.86 | 0.60 | 13.7 |
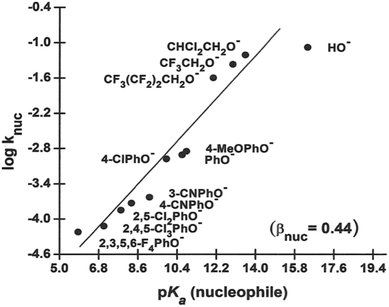 | ||
Fig. 2 Plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc vs. pKa (nucleophile) for the reaction of 3a with oxyanionic nucleophiles in 70% water–30% ethanol (v/v) solvent at 25 °C. The line is defined by eqn (4). The point for HO− shows a negative deviation and has been excluded in the calculation of βnuc according to eqn (4) (see text). knuc vs. pKa (nucleophile) for the reaction of 3a with oxyanionic nucleophiles in 70% water–30% ethanol (v/v) solvent at 25 °C. The line is defined by eqn (4). The point for HO− shows a negative deviation and has been excluded in the calculation of βnuc according to eqn (4) (see text). | ||
We have also measured polar substituent effects in the reactions of 3a–g with the nucleophiles HO− and PhO− at 25 °C in 70% water–30% ethanol. The pseudo-first-order rate constants, kobs, calculated from linear plots of log(A∞ − At) versus time, are also given as ESI.† The resulting knuc values are collected in Table 3. These knuc values were used to construct Hammett plots, using σ, σ0 and σ− constants from the literature;36,37 the plot with σ− constants is displayed in Fig. 3. The different ρ values obtained from Hammett plots using σ, σ0 and σ− constants, along with their corresponding R values, are assembled in Table 4. Brønsted-type plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc versus pKa (leaving group) for the reactions of 3a–g with HO− and PhO− were also constructed from the data in Table 3 and shown in Fig. 4.
knuc versus pKa (leaving group) for the reactions of 3a–g with HO− and PhO− were also constructed from the data in Table 3 and shown in Fig. 4.
| Entry | Leaving group | pKab | 104knucc/M−1 s−1 | d,e |
|---|---|---|---|---|
| a These rate constants were measured at ionic strength, I = 1.0 M (KCl).b Values of pKa were obtained as described in the Experimental section.c These knuc values were obtained from plots of kobs (given as ESI) versus nucleophile concentration, as described in the Experimental, in which each kobs value is the average of duplicate runs with a deviation of ±3%.d Values of knuc in water at 25 °C (kwaternuc) were taken from our previous work.2e These (kaqEtOHnuc) are knuc values in 70% water–30% ethanol (this work). | ||||
| (A) Nucleophile = HO− | ||||
| 1 | 4-NO2PhO− | 7.48 | 830 | 79.9 |
| 2 | 4-Cl, 3-NO2PhO− | 8.21 | 427 | 70.0 |
| 3 | 3-NO2PhO− | 8.84 | 175 | 94.9 |
| 4 | 3-CNPhO− | 8.92 | 118 | 105.9 |
| 5 | 3-ClPhO− | 9.58 | 83.6 | 57.4 |
| 6 | 4-ClPhO− | 10.02 | 40.1 | 109.7 |
| 7 | PhO− | 10.54 | 7.10 | 323.9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| (B) Nucleophile = PhO− | ||||
| 1 | 4-NO2PhO− | 7.48 | 12.3 | 13.5 |
| 2 | 4-Cl, 3-NO2PhO− | 8.21 | 4.11 | 88.8 |
| 3 | 3-NO2PhO− | 8.84 | 1.61 | 75.8 |
| 4 | 3-CNPhO− | 8.92 | 1.32 | 83.3 |
| 5 | 3-ClPhO− | 9.58 | 0.67 | |
| 6 | 4-ClPhO− | 10.02 | 0.37 | |
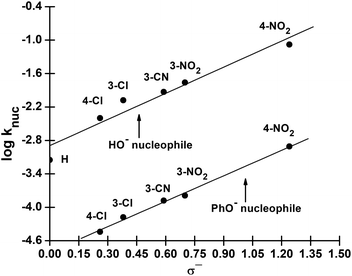 | ||
Fig. 3 Hammett (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc vs. σ−) plot for the reactions of 3a–g with HO− and PhO− in 70% water–30% ethanol (v/v) at 25 °C. knuc vs. σ−) plot for the reactions of 3a–g with HO− and PhO− in 70% water–30% ethanol (v/v) at 25 °C. | ||
| Substituent constanta | ρ value (R) | |
|---|---|---|
| HO− | PhO− | |
| a Values of these substituent constants were taken from C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165 and R. W. Taft, J. Phys. Chem., 1960, 64, 1805. | ||
| σ | 2.22 ± 0.24 (0.956) | 2.25 ± 0.25 (0.890) |
| σ0 | 2.21 ± 0.21 (0.967) | 2.33 ± 0.23 (0.920) |
| σ− | 1.57 ± 0.21 (0.968) | 1.52 ± 0.15 (0.998) |
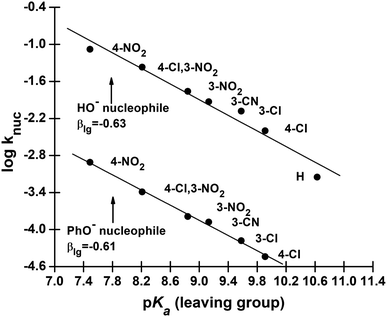 | ||
Fig. 4 Plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc vs. pKa (leaving group) for the reactions of HO− (upper plot) and PhO− (lower plot) with aryl dimethylphosphinothioate esters 3a–g in 70% water–30% ethanol (v/v) solvent at 25 °C. The lines for HO− and PhO− are defined by eqn (6) and (7), respectively. knuc vs. pKa (leaving group) for the reactions of HO− (upper plot) and PhO− (lower plot) with aryl dimethylphosphinothioate esters 3a–g in 70% water–30% ethanol (v/v) solvent at 25 °C. The lines for HO− and PhO− are defined by eqn (6) and (7), respectively. | ||
A variety of phosphinate and phosphinothioate esters have been shown2–4,14,15,17–25,38 to generally react with anionic oxygen nucleophiles in water, ethanol and water-containing binary solvents via nucleophilic attack at the substrate P centre, the only apparent exception to this general trend being the diphenyl phosphinate series of substrates, 1,17,25 whose nucleophilic reactions proceed by a general base-catalyzed pathway. For the specific case of the reaction of 3a with phenoxide and 4,4,4,3,3,2,2-heptafluorobutanol in water, the solvent isotope effect values of 1.00 ± 0.02 and 1.01 ± 0.05, respectively, reported2 for these nucleophiles are consistent with the behaviour of these bases as nucleophiles rather than as general bases. The fact that hydroxide ion (vide infra) and all the alkoxide nucleophiles employed in the present study define the same Brønsted plot as the phenoxides (see Fig. 2 and 3) indicates that the reactions involving these other nucleophiles also occur via nucleophilic attack at phosphorus. The reactions of these substrates in 70% water–30% ethanol herein reported are, as a consequence, discussed in terms of nucleophilic attack at the P centre to generate the reaction products.
Linear free energy relationship (LFER) correlations
The Brønsted plot in Fig. 2 is linear across the pKa range of 5.86–13.53 with phenoxides and alkoxides as nucleophiles; the regression line is defined by eqn (4), from which βnuc = 0.44 ± 0.03 (R = 0.967) is obtained. The fact that the linear plot in Fig. 1 spans the pKa range of 5.86–13.53, which bestrides the pKa of the leaving group (4-nitrophenol pKa in 70% water–30% ethanol (v/v) = 7.48 (ref. 41)), is good evidence that the reaction of 3a involving these nucleophiles proceeds by a concerted mechanism, via a single TS.23,25 Unlike the reaction in water, in which the strongly basic nucleophiles, hydroxide ion and alkoxides, follow a different linear correlation with a diminished slope relative to the slope described by the phenoxides,2 only the point for HO− (pKa = 16.60) shows a negative deviation in the aqueous ethanol solvent. Inclusion of the point for HO− in the plot in Fig. 1 gives a poorer correlation (R = 0.953) with βnuc = 0.37 ± 0.06. A possible explanation for the behaviour of HO− is that this oxyanion is sufficiently basic to be solvated in the aqueous ethanol solvent, which results in its decreased nucleophilic reactivity, a phenomenon known as solvational imbalance discussed by Jencks42,43 and Bernasconi.44 The idea that HO− in aqueous ethanol solvent is solvated by a combination of two or three ethanol and water molecules has long existed in the literature.45 Such solvational imbalances manifest as negative deviations of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc from the straight lines defined by less basic nucleophiles in Brønsted plots, according to eqn (5).42,43 The requirement for desolvating the nucleophile before a subsequent nucleophilic attack on the substrate is conveyed by Scheme 2, in which Kd is the equilibrium constant for the desolvation step. It is also possible for partial desolvation of the nucleophile and nucleophilic attack on the substrate to occur concurrently.44 Both models would result in decreased nucleophilicity of strongly basic nucleophiles in hydroxylic solvents, as observed for HO−.
knuc from the straight lines defined by less basic nucleophiles in Brønsted plots, according to eqn (5).42,43 The requirement for desolvating the nucleophile before a subsequent nucleophilic attack on the substrate is conveyed by Scheme 2, in which Kd is the equilibrium constant for the desolvation step. It is also possible for partial desolvation of the nucleophile and nucleophilic attack on the substrate to occur concurrently.44 Both models would result in decreased nucleophilicity of strongly basic nucleophiles in hydroxylic solvents, as observed for HO−.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc = (0.44 ± 0.03)pKa − (7.22 ± 0.33) knuc = (0.44 ± 0.03)pKa − (7.22 ± 0.33)
| (4) |
Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc = (1 − βnuc)log knuc = (1 − βnuc)log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd Kd
| (5) |
Rate data for the dependence of knuc on the basicity of the LG for the reactions of 3a–g with the nucleophiles HO− and PhO− given in Table 3 are plotted in Fig. 3. The straight lines in this figure are defined by eqn (6) and (7) for HO− and PhO− as nucleophiles, respectively, which give βlg = −0.63 ± 0.15 (R = 0.980) for HO− and −0.61 ± 0.04 (R = 0.998) for PhO−. Since βlg is similar for both nucleophiles, the average value of βlg = −0.62 is utilized in the following discussion. The similarity in βlg for the reactions of these two nucleophiles, as we argued previously,2 is a manifestation of the fact that nucleophilic attack by the weakly to moderately basic PhO− nucleophiles and the strongly basic RO− and HO− nucleophiles at the phosphorus centre reduces the effective charge on the departing aryloxy group in the TS to the same extent for both sets of nucleophiles. Stated alternatively, even though log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc for HO− deviates from the Brønsted correlation in Fig. 2 due to the stabilization of the ground state for its reaction by solvation, the amount of bonding in the TS is the same for this and other nucleophiles.
knuc for HO− deviates from the Brønsted correlation in Fig. 2 due to the stabilization of the ground state for its reaction by solvation, the amount of bonding in the TS is the same for this and other nucleophiles.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc = (−0.63 ± 0.15)pKa + (3.80 ± 0.26) knuc = (−0.63 ± 0.15)pKa + (3.80 ± 0.26)
| (6) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) knuc = (−0.61 ± 0.04)pKa + (1.68 ± 0.23) knuc = (−0.61 ± 0.04)pKa + (1.68 ± 0.23)
| (7) |
The Brønsted-type correlations undertaken above have produced Brønsted parameters βnuc = 0.44 and βlg = −0.62 for the reactions of 3a–g with anionic oxygen nucleophiles in 70% water–30% ethanol (v/v) solvent. Relative to their values in water (βnuc = 0.47, βlg = −0.53),2 these βnuc and βlg values point to very slightly reduced bond formation and increased bond breaking in the TS of the reaction in this solvent, i.e. a looser TS in aqueous ethanol. The values in aqueous ethanol may also be compared with βnuc = 0.41 and βlg = −0.47 obtained26 for the reactions of oxyanionic nucleophiles with aryl dimethylphosphinothioate esters, 2, the oxygen analogues of 3, in water.
Effective charge distribution and transition state structure
The methodology of Jencks28,46 and Williams37,47 is used here to map the effective charge, εTS, on the entering nucleophile and LG in the TS, to aid a discussion of the TS structure, using the values of βnuc (0.44) and βlg (−0.62) evaluated above for the reaction in aqueous ethanol. This exercise entails the estimation of βeq, on the conditions that (i) the values of βnuc and βlg are measured for reactions which are the microscopic reverse of each other, and (ii) both parameters are associated with the same rate-limiting step. The reaction under discussion satisfies these two conditions. The parameter βeq, already defined in eqn (2) and calculated as +1.06, measures the overall charge change on the nucleophile (or the leaving group) between the reactant and product states for the overall reaction.The effective charges on O of the attacking nucleophile and O of the departing nucleofuge in going from the ground state to the TS, Δε (GS → TS), are equal to βnuc (0.44) and βlg (−0.62), respectively, leaving a charge imbalance between the attacking and leaving group O of +0.18. This charge is probably offset by −0.18 charge unit from the thiophosphinoyl group in order to maintain overall charge neutrality. The quantity βnuc is related to the effective charge on the nucleophile in the TS according to eqn (8), where εR is the effective charge on the nucleophile in the ground state which, by definition, is −1. For the system under consideration, therefore, εTS = −0.56. The total charge of the nucleophile plus substrate in the ground state is −1, whilst the charges on the entering and departing groups in the TS sum up to −1.12, leaving a charge balance of −0.12, which is probably offset by +0.12 charge unit on the thiophosphinoyl group in order to maintain overall charge neutrality. The effective charges as evaluated above are shown in the TS, shown as structure 4 for the symmetrical identity reaction in Fig. 5a, in which nucleophile = leaving group = 4-nitrophenoxide. This charge distribution shows that the Me2P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S moiety carries significant positive charge in a TS that is trigonal bipyramidal, probably with lengthened axial distances to the entering and departing oxygens.23 The effective charges for the TS in water,2 5, are shown in Fig. 5b, for comparison. It is important to note that the Me2P
S moiety carries significant positive charge in a TS that is trigonal bipyramidal, probably with lengthened axial distances to the entering and departing oxygens.23 The effective charges for the TS in water,2 5, are shown in Fig. 5b, for comparison. It is important to note that the Me2P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S fragment in the TS carries double the amount of charge than it carries in pure water.
S fragment in the TS carries double the amount of charge than it carries in pure water.
| εTS = βnuc + εR | (8) |
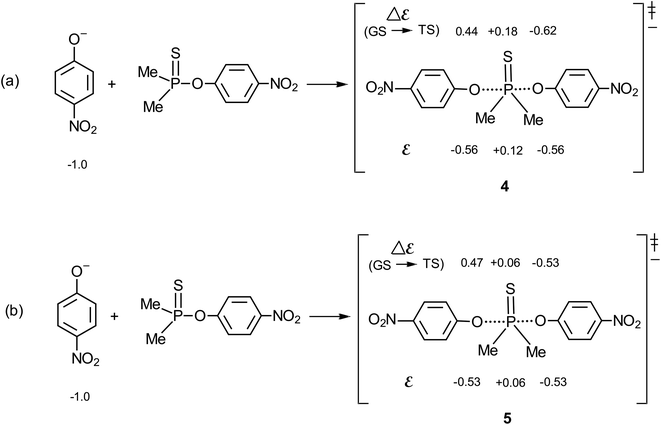 | ||
| Fig. 5 Effective charges in the TS of the identity reaction in which the nucleophile = leaving group = 4-nitrophenoxide: (a) this work, in 70% water–30% ethanol; and (b) in water, see ref. 2. | ||
The Leffler indices,26 which measure the extent of bond formation, αbf, and the extent of bond rupture, αbr, in the TS, already defined in eqn (1), are calculated by normalizing the Brønsted parameters βnuc and βlg with the βeq value. This procedure yields the values of 0.42 and −0.58 for αbf and αbr, respectively, which show that in 70% water–30% ethanol, bond fission is ahead of bond formation in a TS that is looser in this solvent than in water in which αbf = 0.47 and αbr = −0.53.2 The Leffler indices in aqueous ethanol locate the TS in this solvent at T‡2 further down along the tightness diagonal48 from T‡1, the TS in water. This outcome is explored further below by considering possible solvent/solvation effects on the reaction in the aqueous ethanol solvent, relative to water.
Solvent/solvation effects on rates and transition state structure
The Hughes–Ingold theory of solvent action49 generally predicts slower bimolecular nucleophilic substitution reactions of aliphatic substrates in polar solvents such as water than when they are conducted in less polar counterparts, if the nucleophile is negatively charged and the substrate is neutral, a charge-type 1 reaction. This is attributed to the stronger solvation of the initial state than the TS in polar solvents, hence rate accelerations occur when the solvent is changed to less polar solvents which destabilize the initial state by desolvating the ions, thus making the nucleophile more reactive. Since charge-type 1 reactions involve charge dispersal in the TS, the effect of a change, from a polar solvent to a less polar one or vice versa, is predicted to be relatively modest, as is usually observed experimentally.50The situation with the reaction of neutral phosphorus esters with charged nucleophiles is however different. Organic solvents decrease the rates of bimolecular reactions of phosphorus esters relative to their polar counterparts because the former group of solvents stabilize the initial states of the reactions by decreasing the activity coefficients of the neutral substrates. This inhibitory effect more than offsets the rate-enhancing IS destabilization (desolvation) of the anionic nucleophiles by organic co-solvents, leading to slower reactions.51 In some cases, the stabilization of the IS by the less polar solvent is partially offset by the stabilization of the TS.52 The hydrolysis of 4-nitrophenyl diphenylphosphate52 and a number of phosphinate esters51,53,54 have been shown to be faster in aqueous solvents than in binary aqueous organic solvents. The reactions of 3a–g with the different oxyanionic nucleophiles in 70% water–30% ethanol reported in this paper are all slower than the corresponding reactions in water,2 the ratio of the second-order rate constants of these reactions in water and aqueous ethanol solvent, 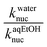 , ranging from 13.5 to 323.9 at 25 °C (see Tables 1 and 2), consistent with the effects of solvents on the reactions of phosphinate esters pointed out above. These rate differences translate to activation energy differences, ΔEa, in the range of 6.4–14.3 kJ mol−1, pointing to the significant effects which solvation factors could confer on these reactions. Water and 70% water–30% ethanol have dielectric constant (D) values of 80.2 and 64.0, respectively, at 20 °C,29,30 pointing to the difference in the polarities of these two solvents.
, ranging from 13.5 to 323.9 at 25 °C (see Tables 1 and 2), consistent with the effects of solvents on the reactions of phosphinate esters pointed out above. These rate differences translate to activation energy differences, ΔEa, in the range of 6.4–14.3 kJ mol−1, pointing to the significant effects which solvation factors could confer on these reactions. Water and 70% water–30% ethanol have dielectric constant (D) values of 80.2 and 64.0, respectively, at 20 °C,29,30 pointing to the difference in the polarities of these two solvents.
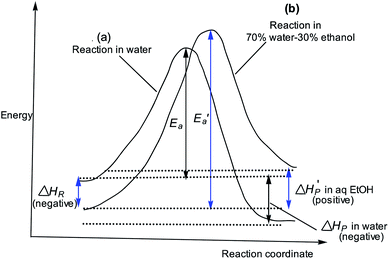
The slower reaction of 3a–g with oxyanionic nucleophiles in 70% water–30% ethanol are more endothermic (more positive or less negative 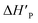 ) and, according to the Hammond postulate, should have a TS that is more product-like (i.e. later) than the TS in water. The effects of change in solvent polarity on the initial and final states of the reaction may be sketched as shown in the hypothetical reaction coordinate diagram in Fig. 6. The IS is stabilized by the less polar solvent by decreasing the activity coefficient of the neutral substrate, which more than offsets the destabilization of the negatively charged nucleophile,42 thereby decreasing the energy of the IS (i.e. ΔHR is negative). The slower reaction in the less polar solvent means that the more product-like TS benefits less than the IS from the stabilization that the solvent brings, the nett result being that the activation barrier in 70% water–30% ethanol,
) and, according to the Hammond postulate, should have a TS that is more product-like (i.e. later) than the TS in water. The effects of change in solvent polarity on the initial and final states of the reaction may be sketched as shown in the hypothetical reaction coordinate diagram in Fig. 6. The IS is stabilized by the less polar solvent by decreasing the activity coefficient of the neutral substrate, which more than offsets the destabilization of the negatively charged nucleophile,42 thereby decreasing the energy of the IS (i.e. ΔHR is negative). The slower reaction in the less polar solvent means that the more product-like TS benefits less than the IS from the stabilization that the solvent brings, the nett result being that the activation barrier in 70% water–30% ethanol, 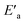 , becomes higher than it is in water, Ea. These considerations show that the change in solvent to one of lower polarity in this instance leads to a more product-like TS for the concerted reaction, which is in qualitative agreement with the direction of the Brønsted exponents calculated above for the reaction in 70% water–30% ethanol.
, becomes higher than it is in water, Ea. These considerations show that the change in solvent to one of lower polarity in this instance leads to a more product-like TS for the concerted reaction, which is in qualitative agreement with the direction of the Brønsted exponents calculated above for the reaction in 70% water–30% ethanol.
The change in the TS structure of this reaction in aqueous ethanol, relative to the TS in pure water (T‡1), can also be elucidated by means of the More O'Ferrall–Jencks diagram in Fig. 1. The stabilization of the IS by changing the solvent from water to the less polar 70% water–30% ethanol lowers the bottom left (reactant) corner of Fig. 1, represented by the bold arrow R. The Hammond effect of stabilizing the IS is to raise the upper right (products) corner of Fig. 1 as shown by the bold arrow S. These movements are equivalent to movement of the TS along the concerted reaction coordinate according to the arrow x ↔ y.55,56 The anti-Hammond effect is the movement of the TS in a direction perpendicular to the reaction coordinate as shown by vector z, thereby sliding the TS toward looser structures in this solvent than it is in pure water.
The outcome of this study, i.e. a looser TS for the reaction of 3 with oxygen anionic nucleophiles in 70% water–30% ethanol (βnuc = 0.44, βlg = −0.62) than in water (βnuc = 0.47, βlg = −0.53), is evidently the resultant of two opposing effects, namely: (i) the effect of the increase in the basicity of the nucleophiles and LGs in going from water to 70% water–30% ethanol which results in TS structures that are tighter in this solvent than in water, and (ii) solvent/solvation factors in the less polar solvent which result in a lowering of the energy of the IS of the reaction and, consequently, a slower reaction with a more product-like TS than measured in water. The fact that the nett movement of the TS is in the direction of looser TS shows that the effect due to solvent/solvation factors dominates over the effect of changes in nucleophile and LG basicity in determining TS structure in the less polar solvent. The solvent/solvation effect operational in the nucleophilic reactions of phosphinothioate esters with anionic oxygen nucleophiles in aqueous ethanol reported in this study has a different origin and manifestation from that reported in thiophosphoryl transfer from phosphorothioates to anionic oxygen nucleophiles in water,57 or in phosphoryl transfer from substituted phenyl phosphates and phosphorylated pyridine to amines and pyridines in water,58,59 or in acyl transfer between sulphur and oxygen nucleophiles in water,60 etc. In these literature examples, the observed solvation effect is due to the stabilization of the nucleophile in the IS by the solvent water which manifests in curved Brønsted correlations due to decreased rates, with little or no effect on the TS structure, whereas in the present study, stabilization of the neutral substrate in the IS in the presence of the organic co-solvent manifests in reduced reaction rates and altered TS structure due to Hammond and anti-Hammond movements of the TS.
The present data are insufficient to enable a determination of the cross-interaction coefficient, pxy (see eqn (3)), for this reaction, as a prelude to giving a quantitative expression to the effect of change of the basic strength of the nucleophiles and LGs on TS structure, which has been discussed qualitatively above. The value of this parameter is known for the nucleophilic reactions of some phosphorus esters. It has been shown23 that pxy = 0.072 for the identity reaction of 4-nitrophenoxide with 1a in water. Since steric factors present in the reaction of 1a with nucleophiles are absent in 3a, the value of pxy for the nucleophilic reactions of 1a may not serve as a reasonable model for this parameter in the reaction of the latter substrate. Values of pxy for phosphoryl transfer from phosphorylated pyridines to a variety of nucleophile types have been measured by Jencks and co-workers, to obtain smaller values of pxy = 0.013 for transfer to anionic oxygen nucleophiles,11c pxy = 0.014 for transfer to pyridines and primary amines,11b,59 and pxy ∼ 0.02 for transfer to a variety of amines.36,59 The reaction of phosphate esters with pyridine occurs with a value of pxy = 0.043.61 The charge type of these reacting systems are dissimilar to the present system which involves a reaction between a neutral substrate and an anionic nucleophile. Khan and Kirby62 obtained the values of pxy in the range of 0.058–0.069 for the attack of nucleophiles, including oxyanions, on neutral aryl phosphate triesters, while the pxy values measured for the hydrolysis of epimeric 2-(aryloxy)-2-oxydioxaphosphorinanes in aqueous dioxane by Rowell and Gorenstein63 lie in the range of 0.030–0.040. These observations suggest that pxy for the present system is likely to be modest, probably of the same order of magnitude as measured for the reactions of neutral substrates with anionic nucleophiles cited above. Since ΔpKa of the nucleophiles and LGs used in this study in going from water to 70% water–30% ethanol is narrow, it is evident that the magnitude of the changes in βnuc and βlg values, i.e. Δβnuc and Δβlg, caused by basicity changes in the nucleophiles and LGs is small in magnitude. In other words, the change in TS structure assignable to the effect of ΔpKa of nucleophiles and LGs, according to (i) above, is expected to be small. On this score, solvent and solvation factors arising from the change in solvent polarity in going from water to aqueous ethanol appear to be largely responsible for the changes in βnuc and βlg measured in this study, i.e. Δβnuc = 0.03 and Δβlg = −0.09. The nett outcome is a looser TS in the less polar solvent. It would be of mechanistic interest to explore how larger changes in nucleophile and LG basicity and further decreases in solvent polarity, both of which are realisable through increases in the ethanol content of the binary aqueous solvent, would further affect the TS structure of this concerted reaction. Such a mapping of the TS64 of the reaction, which may provide an insight into the spectrum of the reaction transition states that lie in the continuum of polarities between the extremes of the two solvents, water and ethanol, obtained by a systematic increase in the quantity of one component of the binary mixture at the expense of the other component, is under active consideration.
The significance of the present result, in which lowering the polarity of the reaction medium has given rise to a looser TS for a nucleophilic substitution at a phosphorus centre involving oxyanions, is that it highlights the need for caution in the extrapolation of results from uncatalyzed nucleophilic reactions of phosphorus substrates in water to analogous phosphoryl transfer reactions in biological systems. The microenvironment of the active site in which enzymatic reactions occur is known to be packed with macromolecules and other solutes.65,66 It is, by and large, a comparatively less polar medium than water and is known to promote specific interactions of ground states and transition states of reacting entities with endogenous amino acid residues and other solutes in the system.62,67 Such media are characteristically different from the dilute aqueous solutions in which the determination of transition states of the nucleophilic reactions of phosphorus ester substrates is mostly executed in analogous chemical reactions and may, therefore, affect mechanisms and TS structures in enzymatic reactions in ways that would not be predicted from analogous chemical reactions.
Experimental
Materials
Distilled and deionized water was degassed under vacuum. 1,4-Dioxane was purified by passing it through an alumina column in order to remove any adventitious peroxides. Anhydrous ethanol was first distilled before it was used to make the reaction medium, 70% water–30% ethanol (v/v), used in the kinetics experiments. The parent phenols and alcohols used to generate the nucleophiles were commercial products which were recrystallized before use. Analytical grade sodium hydroxide was standardized with phenolphthalein before use. The buffer materials CAPS, MOPS and Bis–Tris were all of analytical reagent grade. The syntheses of the substrates 3a–g have been described previously.2 The compounds were carefully stored in the refrigerator and were recrystallized to obtain melting points which agreed with literature values, before use. Additionally, experimental absorbances of the reaction solutions were measured at the end of each kinetic experiment (see below). In all cases the experimental absorbances at infinity agreed with the theoretical ones; these served as indirect checks on the integrity of the substrates.Determination of the pKa values of the nucleophiles in 70% water–30% ethanol
The pKa values of the hydroxide ion, alcoholates and phenolates utilized as nucleophiles and leaving groups in this study were obtained by the Yasuda–Shedlovsky extrapolation and interpolation procedure.68–70 The pKa values determined by this theoretical method are in perfect agreement with experimentally measured values (see pKa values in parenthesis and footnote e in Table 1), thereby reinforcing confidence in the extrapolation/interpolation procedure employed in determining the pKa values of the nucleophiles in the aqueous ethanol solvent used this study.Kinetic measurements
Kinetic measurements were made on a Yuefeng Model 752 spectrophotometer equipped with a Genlab WBH6/FL thermostatic water bath. Reactions with HO− as nucleophile were carried out in CAPS buffer solutions. For alcoholates and phenolates, except 2,4,5-Cl3PhO− and 2,3,5,6-F4PhO−, self-buffered nucleophile (Nuc−) solutions were obtained by partial neutralization of their conjugate acids (NucH) with NaOH, in a way that a NucH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nuc− ratio of 2
Nuc− ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was obtained. For 2,4,5-Cl3PhO− and 2,3,5,6-F4PhO−, appropriate amounts of the nucleophiles were generated by dissolving the parent phenols in MOPS and Bis–Tris buffer solutions, respectively. The details for preparing the nucleophile solutions from these two phenols have been given previously.2 All nucleophile solutions used in the kinetics experiments were maintained at ionic strength, I = 1 M (KCl). The procedures for the kinetic runs, including the precautions undertaken to ensure pseudo-first-order conditions, and the adjustments made to the experimental procedure to accord with (i) the reactivity of some of the phenolate nucleophiles and (ii) the charged or neutral state of the phenolic products in the reaction solution have been described earlier.2 The graphical procedures for reckoning the pseudo-first-order and second-order rate constants, kobs and knuc, respectively, have also been described.2 Each kobs value is an average of duplicate runs with a deviation of ±3%; kobs values for reactions involving the nucleophiles 2,5-Cl2PhO−, 2,4,5-Cl3PhO− and 2,3,5,6-F4PhO− are subject to an uncertainty of ±5%.
1 was obtained. For 2,4,5-Cl3PhO− and 2,3,5,6-F4PhO−, appropriate amounts of the nucleophiles were generated by dissolving the parent phenols in MOPS and Bis–Tris buffer solutions, respectively. The details for preparing the nucleophile solutions from these two phenols have been given previously.2 All nucleophile solutions used in the kinetics experiments were maintained at ionic strength, I = 1 M (KCl). The procedures for the kinetic runs, including the precautions undertaken to ensure pseudo-first-order conditions, and the adjustments made to the experimental procedure to accord with (i) the reactivity of some of the phenolate nucleophiles and (ii) the charged or neutral state of the phenolic products in the reaction solution have been described earlier.2 The graphical procedures for reckoning the pseudo-first-order and second-order rate constants, kobs and knuc, respectively, have also been described.2 Each kobs value is an average of duplicate runs with a deviation of ±3%; kobs values for reactions involving the nucleophiles 2,5-Cl2PhO−, 2,4,5-Cl3PhO− and 2,3,5,6-F4PhO− are subject to an uncertainty of ±5%.
Conclusions
Hammett ρ–σ− correlation for the reactions of 3a–g with PhO− in 70% water–30% ethanol solution yields a better linear correlation than ρ–σ or ρ–σ0 correlations, which shows that the rate-limiting step of the reaction involves LG separation. The Brønsted parameters βnuc = 0.44 and βlg = −0.62 obtained for the reaction of 4-nitrophenyl dimethylphosphinate with oxyanionic nucleophiles in aqueous ethanol are consistent with a single TS that is looser in the binary solvent than in water. The effects of changes in nucleophile/LG basicity and solvent polarity on the TS, analysed with the aid of the More O'Ferrall–Jencks reaction map, show that increased nucleophile and LG basicities in aqueous ethanol move the TS towards more associative structures. This effect is relatively moderate due to the modest pxy value for this reacting system and the small ΔpKa span of the nucleophiles and LGs utilized in the study. On the other hand, decreased solvent polarity stabilizes the IS better than the TS, giving rise to reduced rates and Hammond and anti-Hammond effects which move the TS towards more product-like structures. This latter effect is dominant over the effect of increased nucleophile and LG basicities, to yield a looser TS in the aqueous ethanol solvent. Thus a change in the polarity of the solvent water by the addition of ethanol has altered the potential energy surface of the reaction to yield a looser TS in the less polar solvent.Author contributions
Ikenna Onyido conceptualized this research, administered the project as the major supervisor, guided data analysis/interpretation and reviewed earlier drafts to produce the final version of the paper. Collins I. Ubochi supervised the experimental work, assisted in data interpretation and revised the first draft of the manuscript. Georgina I. Kalu performed all the experimental work, was involved in data interpretation, prepared the graphics and wrote the first draft of the paper.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This paper is dedicated to the memory of Professor Erwin Buncel, who mentored one of us (IO), for his inspiring mentorship and enduring friendship. We thank Professor Alvan C. Hengge for hospitality to one of us (IO) during visits to his laboratory for collaborative research, for access to yet to be published pKa values in the aqueous ethanol solvent, and for discussions with him which were helpful to the work presented in this paper.Notes and references
- The transfer of the phosphinyl group, RR′P(
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), the phosphonoyl group, RR′OP(
O), the phosphonoyl group, RR′OP(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), and the phosphoryl group, ROR′OP(
O), and the phosphoryl group, ROR′OP(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) is collectively termed phospho transfer. In the thio analogues of phosphinates, phosphonates and phosphates, the P(
O) is collectively termed phospho transfer. In the thio analogues of phosphinates, phosphonates and phosphates, the P(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) moiety is replaced with P(
O) moiety is replaced with P(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S).
S). - I. Onyido, K. Swierczek, J. Purcell and A. C. Hengge, J. Am. Chem. Soc., 2005, 127, 7703 CrossRef CAS.
- I. Onyido, K. Albright and E. Buncel, Org. Biomol. Chem., 2005, 3, 1468 RSC.
- E. Buncel, K. G. Albright and I. Onyido, Org. Biomol. Chem., 2004, 2, 601 RSC.
- A. C. Hengge and I. Onyido, Curr. Org. Chem., 2005, 9, 61 CrossRef CAS.
- C. Zeymer, N. D. Werbeck, S. Zimmermann, J. Reinstein and D. F. Hansen, Angew. Chem., Int. Ed., 2016, 55, 11533 CrossRef CAS.
- C. G. Caldwell, et al., Bioorg. Med. Chem. Lett., 1996, 6, 323 CrossRef CAS.
- M. M. Abdou, P. M. O'Neill, E. Amigues and M. Matziari, Drug Discovery Today, 2019, 24, 916 CrossRef CAS.
- J. K. Lassila, J. G. Zalatan and D. Herschlag, Annu. Rev. Biochem., 2011, 80, 669 CrossRef CAS , and references cited therein.
- (a) M. S. Pereira, B. Murta, T. C. F. Oliveira, A. M. Manfredi, F. Nome, A. C. Hengge and T. A. S. Brandão, J. Org. Chem., 2016, 81, 8663 CrossRef CAS; (b) A. C. Hengge, Chem. Rev., 2006, 106, 3252 CrossRef; (c) A. C. Hengge, Adv. Phys. Org. Chem., 2005, 40, 49 CrossRef CAS; (d) A. C. Hengge, Acc. Chem. Res., 2002, 35, 105 CrossRef CAS , and references cited therein.
- (a) D. Herschlag and W. P. Jencks, Biochemistry, 1990, 29, 5172 CrossRef CAS; (b) D. Herschlag and W. P. Jencks, J. Am. Chem. Soc., 1989, 111, 7579 CrossRef CAS; (c) D. Herschlag and W. P. Jencks, J. Am. Chem. Soc., 1989, 111, 7587 CrossRef CAS.
- (a) F. Duarte, J. Åqvist, N. H. Williams and S. C. L. Kamerlin, J. Am. Chem. Soc., 2015, 137, 1081 CrossRef CAS; (b) H. Korhonen, N. H. Williams and S. Mikkola, J. Phys. Org. Chem., 2013, 26, 182 CrossRef CAS; (c) A. Alkherraz, S. C. L. Kamerlin, G. Feng, Q. I. Sheikh, A. Warshel and N. H. Williams, Faraday Discuss., 2010, 145, 281 RSC.
- S. J. Admiraal and D. Herschlag, Chem. Biol., 1995, 2, 729 CrossRef CAS.
- (a) W. P. Jencks, Acc. Chem. Res., 1980, 13, 161 CrossRef CAS; (b) W. P. Jencks, Acc. Chem. Res., 1976, 9, 425 CrossRef CAS.
- W. P. Jencks, Chem. Rev., 1972, 72, 705 CrossRef CAS.
- R. A. More O'Ferrall, J. Chem. Soc. B, 1970, 274 RSC.
- R. D. Cook and L. Rahhal-Arabi, Tetrahedron Lett., 1985, 3147 CrossRef CAS.
- A. Williams and R. A. Naylor, J. Chem. Soc. B, 1971, 1967 RSC.
- P. Haake, D. R. McCoy, W. Okamura, S. R. Alpha, S.-Y. Wong, D. A. Tyson, J. P. McNeal and R. D. Cook, Tetrahedron Lett., 1968, 5243 CrossRef CAS.
- R. D. Cook, C. E. Diebert, W. Schwarz, P. C. Turley and P. Haake, J. Am. Chem. Soc., 1973, 95, 8088 CrossRef CAS.
- (a) B. I. Istomin, M. G. Voronkov, E. L. Zhdankovich and B. N. Bazhenov, Dokl. Akad. Nauk SSSR, 1981, 258, 659 Search PubMed ; Engl. Transl. p. 456; (b) B. I. Istomin, N. A. Sakhdrukova, A. V. Kalabina and Y. I. Sukhorkov, Zh. Obsch. Khim., 1982, 52, 2011 CAS ; Engl. Transl. p. 1787.
- (a) E. Buncel, E. J. Dunn, R. A. B. Bannard and J. G. Purdon, J. Chem. Soc., Chem. Commun., 1984, 162 RSC; (b) E. J. Dunn and E. Buncel, Can. J. Chem., 1989, 67, 1440 CrossRef CAS; (c) E. J. Dunn, R. Y. Moir and E. Buncel, Actual. Fis. Quim. Org., 1991, 110 Search PubMed.
- N. Bourne, E. Chrystiuk, A. M. Davis and A. Williams, J. Am. Chem. Soc., 1988, 110, 1890 CrossRef CAS.
- E. J. Dunn, R. Y. Moir, E. Buncel, J. G. Purdon and R. A. B. Bannard, Can. J. Chem., 1990, 68, 1837 CrossRef CAS.
- K. T. Douglas and A. Williams, J. Chem. Soc., Perkin Trans. 2, 1976, 515 RSC.
- (a) J. E. Leffler and E. Grunwald, Extra-thermodynamic Free Energy Relationships, in Rates and Equilibria of Organic Reactions, Wiley, New York, 1963, ch. 7 Search PubMed; (b) J. E. Leffler, Science, 1953, 117, 340 CrossRef CAS; (c) A. Williams, Acc. Chem. Res., 1984, 17, 425 CrossRef CAS; (d) A. Williams, Adv. Phys. Org. Chem., 1992, 27, 1 CrossRef CAS.
- Incidentally, the nucleophilic reactions of 3, the thio analogues of 2, yield the same values of αbf = 0.47 and αbr = −0.53 as reported for 2, even though βnuc and βlg values for the two reacting systems are dissimilar. This coincidence arises because of the different values of βeq used in the calculation of the Leffler indices for the two substrates series, 0.88 and 1.00 for 2 and 3, respectively.
- (a) W. P. Jencks, Chem. Rev., 1985, 85, 511 CrossRef CAS; (b) D. A. Jencks and W. P. Jencks, J. Am. Chem. Soc., 1977, 99, 7948 CrossRef CAS.
- L. G. Torres, A. Velasque and M. A. Brito-Arias, Adv. Biosci. Biotechnol., 2011, 2, 8 CrossRef CAS.
- N. Booth, Biochem. J., 1930, 1699 CrossRef CAS.
- E. Buncel, R. Stairs and H. Wilson, The Role of Solvents in Chemical Reactions, Oxford Chemistry Masters Series, Oxford University Press, Oxford, 2003 Search PubMed.
- T. A. Hamlin, B. van Beek, L. P. Wolters and F. M. Bickelhaupt, Chem.–Eur. J., 2018, 24, 5938 CrossRef.
- A. T. P. Carvalho, A. M. C. O'Donoghue, D. R. W. Hodgson and S. C. L. Kamerlin, Org. Biomol. Chem., 2015, 13, 5391 RSC.
- D. Xu, H. Guo, Y. Liu and D. M. York, J. Phys. Chem. B, 2005, 109, 13827 CrossRef CAS.
- (a) K. Sorensen-Stowell and A. C. Hengge, J. Org. Chem., 2006, 71, 7180 CrossRef CAS; (b) P. K. Gryska, P. G. Czyryca, J. Golightly, K. Small, P. Larsen, R. H. Hoff and A. C. Hengge, J. Org. Chem., 2002, 67, 1214 CrossRef; (c) I. E. Catrina and A. C. Hengge, J. Am. Chem. Soc., 1991, 121, 2156 CrossRef.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165 CrossRef CAS.
- R. W. Taft, J. Phys. Chem., 1960, 64, 1805 CrossRef CAS.
- M. J. Pregel, E. J. Dunn, R. Nagelkerke, G. R. J. Thatcher and E. Buncel, Chem. Soc. Rev., 1995, 24, 445 RSC.
- A. Williams, Free Energy Relationships in Organic and Bioorganic Chemistry, Royal Society of Chemistry, Cambridge, 2003 Search PubMed.
- I. Onyido, Catalysis, Structure and Reactivity in Chemistry and the Life Sciences, University Press Plc, Ibadan, Nigeria, 2018 Search PubMed.
- See the Experimental section where the procedure for obtaining this and other pKa values of the nucleophiles utilized in this study is described.
- W. P. Jencks, Effects of Solvation on Nucleophilic Reactivity in Hydroxylic Solvents, in Nucleophilicity, ed. J. M. Harris and S. P. McManus, American Chemical Society, Washington, DC, 1987, pp. 155–167 Search PubMed.
- W. P. Jencks, S. R. Brant, J. R. Gandler, G. Frendrich and C. Nakamura, J. Am. Chem. Soc., 1982, 104, 7045 CrossRef CAS.
- C. F. Bernasconi, Adv. Phys. Org. Chem., 1992, 27, 119 CrossRef CAS.
- C. A. Pollock and P. J. Cook, Can. J. Chem., 1971, 49, 3856 CrossRef CAS.
- D. Herschlag and W. P. Jencks, J. Am. Chem. Soc., 1990, 112, 1951 CrossRef CAS.
- (a) A. Williams, Adv. Phys. Org. Chem., 1992, 27, 1 CrossRef CAS; (b) A. Williams, Acc. Chem. Res., 1984, 17, 425 CrossRef CAS; (c) A. Williams, Chem. Soc. Rev., 1994, 23, 93 RSC.
- W. J. Albery and M. M. Kreevoy, Adv. Phys. Org. Chem., 1978, 16, 87 CrossRef CAS.
- C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell University Press, Ithaca, New York, 2nd edn, 1969, pp. 457–463; see also RSC; E. D. Hughes and C. K. Ingold, J. Chem. Soc., 1935, 244 RSC.
- A number of pertinent examples are given in A. J. Parker, Chem. Rev., 1969, 69, 1 CrossRef CAS.
- A. Blaskó, C. A. Bunton, Y. S. Hong, M. M. Mhala, J. R. Moffatt and S. Wright, J. Phys. Org. Chem., 1991, 4, 618 CrossRef.
- C. A. Bunton, N. D. Gillitt and A. Kumar, J. Phys. Org. Chem., 1996, 9, 145 CrossRef CAS.
- T. J. Broxton, J. R. Christie and R. P. T. Chang, J. Org. Chem., 1988, 53, 3081 CrossRef CAS.
- R. D. Cook, S. Farah, L. Ghawi, A. Itani and J. Rahil, Can. J. Chem., 1986, 64, 1630 CrossRef CAS.
- J. M. Harris, S. G. Shafer, J. R. Moffat and A. R. Becker, J. Am. Chem. Soc., 1979, 101, 3295 CrossRef CAS.
- D. Herschlag and W. P. Jencks, J. Am. Chem. Soc., 1987, 109, 4665 CrossRef CAS.
- J. E. Omakor, I. Onyido, G. W. vanLoon and E. Buncel, J. Chem. Soc., Perkin Trans. 2, 2001, 2, 324 RSC.
- W. P. Jencks, M. T. Haber, D. Herschlag and K. L. Nazaretian, J. Am. Chem. Soc., 1986, 108, 479 CrossRef CAS.
- M. T. Skoog and W. P. Jencks, J. Am. Chem. Soc., 1984, 106, 7597 CrossRef CAS.
- W. P. Jencks, S. R. Brant, J. R. Gandler, G. Fendrich and C. Nakamura, J. Am. Chem. Soc., 1982, 1084, 7045 CrossRef.
- A. J. Kirby and W. P. Jencks, J. Am. Chem. Soc., 1965, 87, 3209 CrossRef CAS.
- S. A. Khan and A. J. Kirby, J. Chem. Soc. B, 1970, 1172 RSC.
- R. Rowell and D. G. Gorenstein, J. Am. Chem. Soc., 1981, 103, 5894 CrossRef CAS.
- (a) N. Asaad, M. J. den Otter and J. B. F. N. Engberts, Org. Biomol. Chem., 2004, 2, 1404 RSC; (b) N. Asaad and J. B. F. N. Engberts, J. Am. Chem. Soc., 2003, 125, 6874 CrossRef CAS.
- S. Admiraal and D. Herschlag, Chem. Biol., 1995, 2, 729 CrossRef CAS.
- S. Cayley, B. A. Lewis, H. J. Guttman and M. T. Record Jr, J. Mol. Biol., 1991, 222, 281 CrossRef CAS.
- J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, W. H. Freeman and Company, New York, 7th edn, 2012, ch. 8 Search PubMed.
- Y. Altun and F. Koseoglu, J. Solution Chem., 2013, 42, 1691 CrossRef CAS.
- F. Kiani, A. Bahadori, S. Sharifi, F. Koohyar and M. Sharifirad, Eur. Online J. Nat. Soc. Sci., 2013, 2, 140 Search PubMed.
- S. Babic, A. J. M. Horvat, D. M. Pavlovic and M. Kastelan-Macan, Trends Anal. Chem., 2007, 25, 1043 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Pseudo-first-order rate constants for the reactions of aryl dimethylphosphinothioate esters with oxyanionic nucleophiles in 70% water–30% ethanol at 25 °C. See DOI: 10.1039/d0ra10759j |
| This journal is © The Royal Society of Chemistry 2021 |