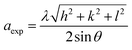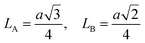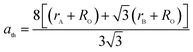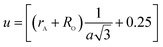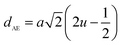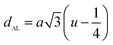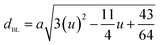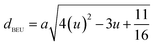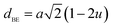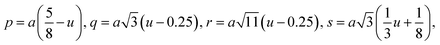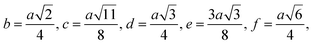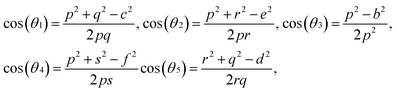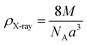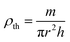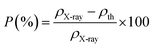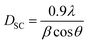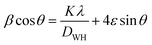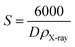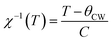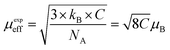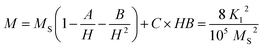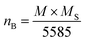Open Access Article
Open Access ArticleInfluence of neodymium substitution on structural, magnetic and spectroscopic properties of Ni–Zn–Al nano-ferrites
N. Amri *a,
J. Massoudi
*a,
J. Massoudi *a,
K. Nourib,
M. Trikic,
E. Dhahri
*a,
K. Nourib,
M. Trikic,
E. Dhahri a and
L. Bessaisb
a and
L. Bessaisb
aLaboratoire de Physique Appliquée, Faculté des Sciences de Sfax, Université de Sfax, B.P. 1171, 3000 Sfax, Tunisia. E-mail: amrinoura90@gmail.com; jalel.massoudi@gmail.com
bICMPE (UMR 7182), CNRS, UPEC, Université Paris Est, 94320 Thiais, France
cLaboratoire de Physique des Matériaux, Faculté des Sciences de Sfax, Université de Sfax, B. P 1171, 3000 Sfax, Tunisia. E-mail: mtriki_fss@yahoo.fr
First published on 8th April 2021
Abstract
Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 ferrite samples, with x = 0.00, 0.05, 0.075 and 0.1, were synthesized using the sol–gel method. The effects of Nd3+ doping on the structural, magnetic and spectroscopic properties were investigated. XRD Rietveld refinement carried out using the FULLPROF program shows that the Ni–Zn ferrite retains its pure single phase cubic structure with Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. An increase in lattice constant and porosity happens with increasing Nd3+ concentration. FTIR spectra present the two prominent absorption bands in the range of 400 to 600 cm−1 which are the fingerprint region of all ferrites. The change in Raman modes in the synthesized ferrite system were observed with Nd3+ substitution. The magnetization curves show a typical transition, at the Curie temperature TC, from a low temperature ferrimagnetic state to a high temperature paramagnetic state. The saturation magnetization, coercivity and remanence magnetization are found to be decreasing with increasing the Nd3+ concentration.
m space group. An increase in lattice constant and porosity happens with increasing Nd3+ concentration. FTIR spectra present the two prominent absorption bands in the range of 400 to 600 cm−1 which are the fingerprint region of all ferrites. The change in Raman modes in the synthesized ferrite system were observed with Nd3+ substitution. The magnetization curves show a typical transition, at the Curie temperature TC, from a low temperature ferrimagnetic state to a high temperature paramagnetic state. The saturation magnetization, coercivity and remanence magnetization are found to be decreasing with increasing the Nd3+ concentration.
Introduction
Spinel ferrites AB2O4 have a crystal structure belonging to Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group where the tetrahedral A site is occupied by divalent metals and the octahedral B site is occupied by trivalent cations. Particularly, Ni–Zn ferrites have enormous importance in technological and scientific applications such as electrical devices, microwave industries, chemical sensors, etc. due to their interesting physico-chemical properties. These materials are chosen for their high resistivity, high Curie temperature, low current losses etc.
m space group where the tetrahedral A site is occupied by divalent metals and the octahedral B site is occupied by trivalent cations. Particularly, Ni–Zn ferrites have enormous importance in technological and scientific applications such as electrical devices, microwave industries, chemical sensors, etc. due to their interesting physico-chemical properties. These materials are chosen for their high resistivity, high Curie temperature, low current losses etc.
Several studies were done with varying the doping cations (divalent or trivalent)1,2 and synthesizing the desired compounds with different methods such as sol–gel, thermal combustion, co-precipitation3–6 in order to ameliorate certain structural, magnetic or dielectric properties as required in scientific and technological domains.
The magnetic and dielectric properties of Ni–Zn ferrites are controlled by the substitution of iron sites by magnetic or non-magnetic ions. The neodymium Nd which is a magnetic ion with a greater ionic radius (0.99 Å) than iron (0.67 Å) has a capability to modify the characteristics of ferrites. The doping of neodymium (Nd3+) in spinel ferritesdecreases the saturation magnetization, and alsoincreases the density and resistivity of the spinel ferrite due to unpaired electrons in the 4f orbital of Nd3+ that give rise to ion with a nonmagnetic nature.7 Moreover, the larger ionic radii Nd3+ ions replace Fe ions at the octahedral site of the ferrites which results in improved magnetic and electrical properties of the ferrites for the high-frequency application.8–10
X. Wu et al.11 synthesized Ni0.5Zn0.5NdxFe2−xO4 (0.0 ≤ x ≤ 0.12) samples by calcining oxalates in air. They reported that magnetic properties were improved after doping with neodymium. P. Pranav et al.12 also announced an enhancement in saturation magnetization of Mn0.6Zn0.4Fe2−xNdxO4 (x = 0, 0.04, 0.06, 0.08, and 0.1) prepared using combustion method. Moreover, Luo et al.13 discussedthe impact of neodymium substitution on structural, dielectric and magnetic properties of polycrystalline Ni0.5Zn0.5NdxFe2−xO4 (0.002 ≤ x ≤![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.010) ferrites. They found that the mechanism of doping induced modulation on structural, dielectric and magnetic properties.
0.010) ferrites. They found that the mechanism of doping induced modulation on structural, dielectric and magnetic properties.
In this paper, we aim to investigate the effect of neodymium on the structural, morphological and magnetic properties of Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 synthesized using sol–gel route. Spectroscopic properties were discussed based on FTIR and Raman measurements.
Experimental procedure
Crystal nano-particles with chemical composition Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 with x = 0.00, 0.05, 0.075 and 0.1 were prepared via sol–gel method. The starting materials used to prepare our samples are NiCl2·6H2O, ZnO, Al2O3, Fe(NO3)3·9H2O and Nd2O3 (all used chemicals were of analytical grade with purity ≥99%). The required precursors NiCl2·6H2O and Fe(NO3)3·9H2O were taken in stoichiometric amounts and were dissolved in distilled water to obtain a mixed solution. The oxides powders ZnO, Al2O3 and Nd2O3 were dissolved in nitric acid thenjoinedto the solution drop by drop. Next, ethylene glycol (C2H6O2)was added to the mixture as a complexing agent in order to get transparent solution with homogenous distribution of metal ionsafter adding the citric acid (molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 of metal cation (Ni + Fe + Zn + Al + Nd) to citric acid). Using a hot plate magnetic stirrer, the mixture was stirred at 80 °C during 6 hours. After that, the viscous solution gets converted into a homogenous brown gel then to a powder. The burned gel was ground to get a fine ferrite powder by using an agate mortar. The powder were annealed at 500 °C for 6 hours in an electrical muffle furnace and cooled slowly in room temperature to decompose the organic matter. Finally, the obtained powder was pelletized and annealed at 900 °C during 6 hours.
1.5 of metal cation (Ni + Fe + Zn + Al + Nd) to citric acid). Using a hot plate magnetic stirrer, the mixture was stirred at 80 °C during 6 hours. After that, the viscous solution gets converted into a homogenous brown gel then to a powder. The burned gel was ground to get a fine ferrite powder by using an agate mortar. The powder were annealed at 500 °C for 6 hours in an electrical muffle furnace and cooled slowly in room temperature to decompose the organic matter. Finally, the obtained powder was pelletized and annealed at 900 °C during 6 hours.
Characterizations
In order to identify the crystal phase formation of our materials, we used the X-ray diffraction (XRD) patterns which were recorded on a Bruker D8 powder X-ray diffractometer using the Cu (Kα) radiation (λ = 1.5406 Å)with a step size of 0.015° for 13.5 s over a 2 h range from 15° to 80°. The morphological study was performed by Merlin Scanning Electron Microscopy (SEM) equipped with an energy-dispersive X-ray spectrometer (EDXS). Fourier transform infrared (FTIR) spectroscopy of synthesized samples was used to find the functional groups and vibrational structure on the surface, within Thermo Scientific Nicolet 6700 FTIR Spectrometer in the region 400–4000 cm−1 at room temperature with diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) technique. Raman scattering measurements were performed using a SENTERRA spectrometer (Bruker, Germany) with laser excitation of 532 nm at room temperature. Magnetic measurements of magnetization versus temperature for all ferrites samples were carried out using differential sample magnetometer MANICS in a field up to 16 kOe. Hysteresis loops of the present ferrites have been traced using a SQUID magnetometer under magnetic field up to 4 T, at room temperature.Results and discussion
Structural study
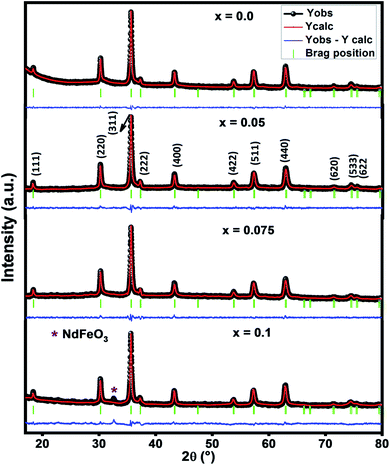
Fig. 1 presents the X-ray diffraction pattern of Ni–Zn–Al ferrite samples recorded in the 2θ range between 10° and 80°. The Rietveld refinements of these patterns show that all samples crystallize in the cubic structure with Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The essential reflection peaks were from the characteristic crystal planes of cubic single phase spinel structure (111), (220), (311), (222), (400), (422), (511), (440), (620) and (533).14–16 It can be observed from Fig. 1, the existence of extra peaks for x = 0.1 sample which refers to orthorhombic ferrite symmetry Pbnm as a second phase (NdFeO3) symbolized by (*). The orthorhombic ferrite phase has been also observed in the literature.17,18 However, the small amount of Nd3+ ions in Ni–Zn–Al ferrite can affect not only the phase composition but also the size of the spinel matrix, which is due to orthoferrite (NdFeO3) phase. Pawar et al.18 reported that the most important reason for the orthorhombic phase formation in the rare earth element substituted spinel ferrites is the electronic configuration, larger ionic radii of rare earth element and diffusion of rare earth ions at the grain boundaries. It is worth to mention here that, up to x = 0.075, Nd3+ is highly soluble in Ni–Zn–Al ferrite. This level of Nd3+ solubility is quite better as compared to previous reports related to rare earth doping.17,18
m space group. The essential reflection peaks were from the characteristic crystal planes of cubic single phase spinel structure (111), (220), (311), (222), (400), (422), (511), (440), (620) and (533).14–16 It can be observed from Fig. 1, the existence of extra peaks for x = 0.1 sample which refers to orthorhombic ferrite symmetry Pbnm as a second phase (NdFeO3) symbolized by (*). The orthorhombic ferrite phase has been also observed in the literature.17,18 However, the small amount of Nd3+ ions in Ni–Zn–Al ferrite can affect not only the phase composition but also the size of the spinel matrix, which is due to orthoferrite (NdFeO3) phase. Pawar et al.18 reported that the most important reason for the orthorhombic phase formation in the rare earth element substituted spinel ferrites is the electronic configuration, larger ionic radii of rare earth element and diffusion of rare earth ions at the grain boundaries. It is worth to mention here that, up to x = 0.075, Nd3+ is highly soluble in Ni–Zn–Al ferrite. This level of Nd3+ solubility is quite better as compared to previous reports related to rare earth doping.17,18
Rietveld refined parameters such as unweighted profile R-factor (Rp), weighted profile R-factor (Rw), expected R-factor (Re), goodness fit factor (χ2) and lattice parameter (ar) are given in Table 1. The values of χ2 inform us about the good refining and quality of the samples.
| Parameter | x = 0.0 | x = 0.05 | x = 0.075 | x = 0.1 |
|---|---|---|---|---|
| Space group | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
| ar (Å) | 8.347 | 8.351 | 8.350 | 8.354 |
| aexp (Å) | 8.325 | 8.331 | 8.335 | 8.339 |
| ath (Å) | 8.354 | 8.375 | 8.387 | 8.543 |
| V (Å3) | 577.1 | 582.4 | 582.3 | 583.1 |
| χ2 | 1.29 | 1.8 | 1.75 | 3.7 |
| Rp (%) | 24.9 | 23.1 | 18.6 | 35.5 |
| Rwp (%) | 11.1 | 11.9 | 10.6 | 17.1 |
| Re (%) | 9.71 | 8.84 | 8.03 | 8.89 |
| ρX-ray (g cm−3) | 5.124 | 5.176 | 5.227 | 5.277 |
| ρth (g cm−3) | 3.334 | 3.314 | 3.234 | 3.321 |
| P (%) | 34.93 | 35.97 | 38.12 | 37.06 |
| S (m2 g−1) | 39.56 | 37.88 | 39.17 | 39.34 |
| Dsc (nm) | 29.8 | 30.6 | 29.3 | 28.9 |
| Dwh (nm) | 62 | 70 | 65 | 59 |
| ε × 10−3 | 1.96 | 2.9 | 3.1 | 1.9 |
| Dsem (nm) | 37.62 | — | — | 35 |
The lattice parameter (aexp) of Ni–Zn–Al–Nd ferrite nanoparticles was determined from X-ray data analysis using the relation:19
It is clear from the Table 1 that both lattices parameter (ar and aexp) and the unit cell volume increase with the Nd3+ contents. This increase is due to the change in ionic radius from Fe3+ (0.67 Å) to larger ionic radius of Nd3+ (0.99 Å).20 Furthermore, although Nd3+ ions have a larger ionic radius in comparison to that of Fe3+ ions, a very thin insulating ultra-thin layer may be formed around the grains due to ions that have spread over the grain boundary. This phenomenon can cause the contraction of the spinel lattice.21
Cation distribution plays a vital role in governing the structural, electrical and magnetic properties of AB2O4 spinel ferrites. Thus, the understanding of the cation distribution is essential in understanding the intricate structural and physical property relationship. Massoudi et al.19 reported that the experimental intensities for the (220), (400) and (440) reflections are sensitive to cations on tetrahedral (A-) and octahedral (B-) site. In the present studies, the Bertaut method was adopted to compute the cation distribution estimated from XRD data.22 From the best-matched intensity ratio, the cation distribution was estimated and the values are:
| x = 0 (Zn0.4Al0.28Fe0.32) [Ni0.6Al0.22Fe1.18] |
| x = 0.05 (Zn0.4Al0.28Fe0.32) [Ni0.6Al0.22Nd0.05Fe1.13] |
| x = 0.075 (Zn0.4Al0.28Fe0.32) [Ni0.6Al0.22Nd0.075Fe1.105] |
| x = 0.1 (Zn0.4Al0.28Fe0.32) [Ni0.6Al0.22Nd0.1Fe1.08] |
For cubic spinel structures, the distance between magnetic ions (hopping length) in A site (tetrahedral) and B site (octahedral) (LA and LB) on A-site and B-site were calculated by using the following relations:23
It is obvious from the Table 2 that the value of hopping length of A-site (LA) is bigger than that of B site LB, which leads to deduce that the electron hopping between ions at B and B sites is more probable than that between A and B sites.
| Parameter | x = 0.0 | x = 0.05 | x = 0.075 | x = 0.1 |
|---|---|---|---|---|
| LA (Å) | 3.614 | 3.616 | 3.615 | 3.617 |
| LB (Å) | 2.951 | 2.952 | 2.952 | 2.953 |
| rA (Å) | 0.6492 | 0.6492 | 0.6492 | 0.6492 |
| rB (Å) | 0.6429 | 0.6525 | 0.6568 | 0.7152 |
| U (Å) | 0.3875 | 0.3874 | 0.3873 | 0.3872 |
| dAE (Å) | 3.247 | 3.237 | 3.236 | 3.236 |
| dBE (Å) | 2.639 | 2.653 | 2.656 | 2.660 |
| dAL (Å) | 1.998 | 1.982 | 1.982 | 1.981 |
| dBL (Å) | 1.979 | 1.984 | 1.986 | 1.988 |
| dBEU (Å) | 2.951 | 2.952 | 2.953 | 2.955 |
| p (Å) | 1.973 | 1.979 | 1.981 | 1.983 |
| q (Å) | 1.988 | 1.982 | 1.982 | 1.981 |
| r (Å) | 3.807 | 3.796 | 3.795 | 3.794 |
| s (Å) | 3.666 | 3.667 | 3.668 | 3.669 |
| b (Å) | 2.943 | 2.945 | 2.946 | 2.948 |
| c (Å) | 3.451 | 3.453 | 3.455 | 3457 |
| d (Å) | 3.604 | 3.607 | 3.609 | 3.610 |
| e (Å) | 5.407 | 5.411 | 5.413 | 5.416 |
| f (Å) | 5.098 | 5.101 | 5.104 | 5.106 |
| θ1 (°) | 121.16 | 121.32 | 121.34 | 121.40 |
| θ2 (°) | 136.18 | 136.71 | 136.85 | 137.00 |
| θ3 (°) | 127.72 | 127.39 | 127.28 | 127.23 |
| θ4 (°) | 126.68 | 126.61 | 126.63 | 126.60 |
| θ5 (°) | 68.87 | 69.26 | 69.34 | 69.40 |
The theoretical lattice parameter (ath) can be calculated using the following equation:19
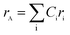 and
and 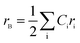 are the average ionic radii per molecule for the respective A and B-sites; here, Ci is the concentration of the element i with ionic radius ri on a particular site.
are the average ionic radii per molecule for the respective A and B-sites; here, Ci is the concentration of the element i with ionic radius ri on a particular site.
The increase of hopping length and radius of the ion with an increasing substitution of Nd3+ ions is related to the increase in lattice constant and to the difference in the ionic radii of Nd3+ ions and Fe3+ ions, which means that the magnetic ions move far from other ions (Table 1).
The oxygen positional parameter (u) can be determined using the relations:
As shown in Table 2, (u) decreased from 0.3879 Å to 0.3874 Å with the Nd substitution. According to many researchers, u would be expected to be 0.375 Å for the origin at tetrahedral sites and a centric crystal structure.24 According to XRD studies of some researchers, u > 0.375 Å for substituted ferrites.19,25 In the present study, u was determined to be higher than its expected “ideal” value of 0.375 Å.
The tetrahedral and octahedral bond lengths (dAE) and (dBE), tetrahedral edge (dAL), shared and unshared octahedral edge (dBL) and (dBEU) can be evaluated by:26
As shown in Table 2, dAE, dAL decrease while dBE, dBEU and dBL increase with an increase in Nd3+ content. These variations can be explained by the fact that as Nd3+ ions preferred to occupy the octahedral B sites where they have replaced the Fe3+ ions. Since the radius of Fe3+ ion is smaller than the radius of Nd3+ ions hence the increasing trend is then justified.
The bond lengths and bond angles between the cations are calculated by the following relations:19
Me–O distances
Me–Medistances
Bond angles
The X-ray density (ρX-ray) of the samples was calculated by considering that a basic unit cell of the cubic spinel structure contained eight ions using the following equation:27,28
The bulk density ρth was estimated using the following relation:29
The apparent porosity, P, for each sample was calculated using the following equation:29
The change in X-ray density and bulk density leads to an increase in porosity after adding the neodymium which is possibly originated from the vacancies created from the change of ionic radii.20
The average crystallite size of our samples was calculated from the full width at the half maximum (FWHM) of the most intense peak by using the Debye–Scherrer equation:30
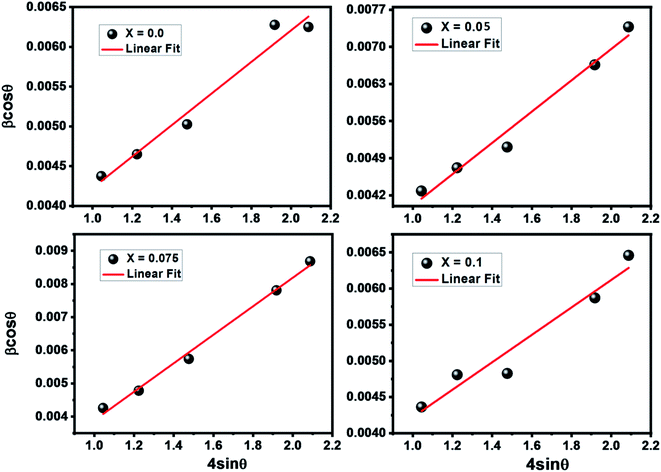
The Williamson–Hall (W–H) equation was also used to determine the average crystallite size and lattice strain in all the samples and can be expressed as followed:31
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus 4
θ versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ yields intercept as crystallite size and the slope as strain as shown in Fig. 2. The results are tabulated in Table 1. The observed positive slope in W–H plot confirmed the tensile strain experienced in smaller grain size.32 Moreover, the obtained values of lattice strain ε are in the range of 1.9 × 10−3 to 3.1 × 10−3 (Table 2). These values of lattice distortion are comparable with those previously reported for ferrite spinel.33,34
θ yields intercept as crystallite size and the slope as strain as shown in Fig. 2. The results are tabulated in Table 1. The observed positive slope in W–H plot confirmed the tensile strain experienced in smaller grain size.32 Moreover, the obtained values of lattice strain ε are in the range of 1.9 × 10−3 to 3.1 × 10−3 (Table 2). These values of lattice distortion are comparable with those previously reported for ferrite spinel.33,34
Assuming all the particles to be spherical, the specific surface area was calculated from the relation:35
Besides, the external morphology of Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 (x = 0.00 and 0.1) was visualized by SEM. The micrograph of the samples (indicated in Fig. 3a and b) shows clear indistinguishable grain boundaries and high surface energy. Both samples showed susceptibility towards clusters thanks to reciprocal magnetic interactions and electrostatic effects emerging among of ferrites. Having a closer look at the images, it can be observed that not regular spherical shaped and nano-size of the grains. These results are analogous to other researcher's work made previously such as P. P. Naik et al. who reported in their publication12 that “large agglomerates of many particles are formed”. Furthermore, the surface morphology exposes distribution of small grains at the grain boundaries, which is the unique mark of Ni–Zn ferrites. The obtained grain size results from SEM micrographs for x = 0.00 and x = 0.1 as shown in Fig. 3c and d (using the Image J software by fitting the particle size distribution with a Lorentz function) are 37.62 and 35 nm for x = 0.00 and x = 0.1, respectively. This reduction in grain size was also discovered by P. P. Naik et al.12 who have found that neodymium prefers to occupy octahedral sites which leads to strain on the grain boundaries causing an obstacle in grain growth and consequently the downturn of grain distribution with augmenting the Nd3+ doping level. By comparing the average size of the crystallites obtained from XRD and the particle size of the SEM analysis, we can deduce that every grain is almost monocrystalline, which confirms the nanometric size of our samples. It is well known that dispersive X-ray analysis (EDX) is a useful technique for chemical analysis and for estimating the atomic percentages of different constituents on surface layer of the solid investigated. Energy dispersive X-ray analysis was performed for prepared samples x = 0.00 and x = 0.1 and presented in Fig. 3e and f. The EDX spectrum confirm the presence of Fe, Ni, Zn, Al, Nd and O elements in the samples without any traceable impurities and confirms further the phase pure of Ni–Zn ferrite samples.
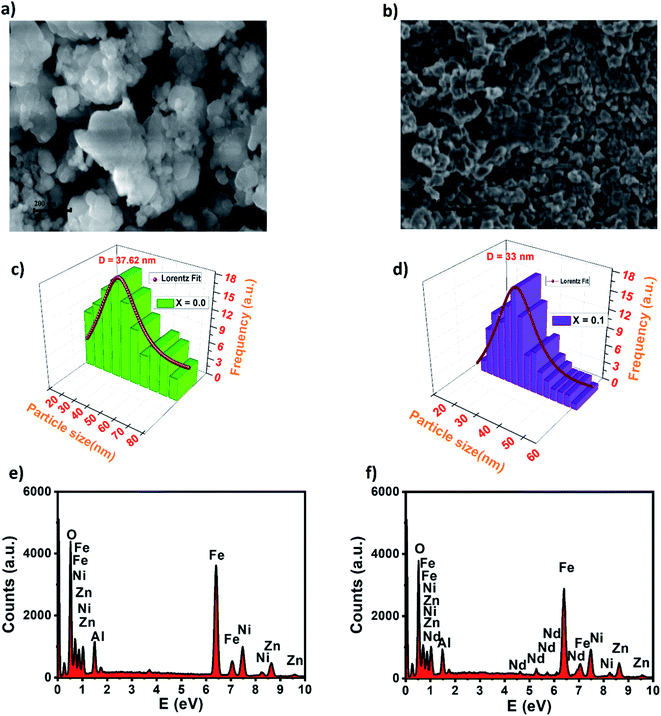 | ||
| Fig. 3 SEM micrograph of nickel–zinc ferrites for (a) x = 0.00, (b) x = 0.1, particle size distribution for (c) x = 0.00 and (d) x = 0.1 and EDX spectrum of (e) x = 0.00 and (f) x = 0.1. | ||
FTIR measurements
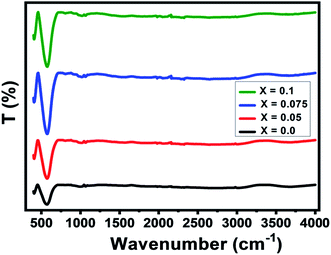
The Fourier-Transform Infrared (FTIR) spectra of Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 samples with x = 0.00; 0.05; 0.075 and 0.1 are studied in the range of 400–4000 cm−1 as illustrated in Fig. 4. As known for spinel ferrites, it exist two major metal–oxygen frequency bands υ1 and υ2 corresponding respectively to the metal ions stretching vibration in the tetrahedral site and that in the octahedral site.37–39 In our case, the higher frequency absorption band υ1 is assigned for Fe3+–O intrinsic vibration of tetrahedral group in the range of 570 cm−1 and the lower frequency absorption band υ2 is attributed to that of the octahedral group near 405 cm−1 which is the fingerprint of Zn–Ni ferrites.39,40 There are additional frequency band located near 1061 cm−1 corresponding to the O–H stretching vibrations.41It can be noted from the figure that the peaks intensity amplifies with raising the Nd3+ doping level. Such behavior can be justified by the changes in bond lengths of Fe3+–O tetrahedral and octahedral sites due to the insertion of doping ion Nd3+.37 Moreover, the vibration band (ν1) is widened and shifted towards the higher wavenumber region with an increased Nd3+ doping level (see Table 3). Same behavior was observed in Nd doped Mn0.6Zn0.4Fe2O4 reported by Naik et al.12 This shifting is also associated with the lattice constant variations. However, the presence of these absorption bands further confirms the formation of our spinel-structured Ni–Zn–Al ferrite.
| Parameter | x = 0.0 | x = 0.05 | x = 0.075 | x = 0.1 |
|---|---|---|---|---|
| ν1 (cm−1) | 571 | 572 | 573 | 576 |
| ν2 (cm−1) | 407 | 406 | 409 | 410 |
| νa (cm−1) | 489 | 489 | 491 | 493 |
| KT (N m−1) | 133.2 | 130.0 | 128.4 | 124.6 |
| KO (N m−1) | 177.1 | 184.4 | 188.7 | 192.8 |
| θD (K) | 703 | 703 | 706 | 708 |
The force constants (K) for the tetrahedral site (KT) and octahedral site (KO) can be calculated using the following relation:35
| KT,O = 4πC2ν1,22μ |
The calculated values of the force constants (KT) and (KO) are listed in Table 3. The force constants of the A and B sites increase with increasing the doping level x. This increase may be due to the motion of metallic ions between the A- and B-site, which changes the site radius, and variation in bond lengths, dA–O and dB–O.
The Debye temperature (θD) can be calculated using the equation given by Waldron:35
| θD = ℏCνa/kB = 1.438νa |
Raman spectroscopy
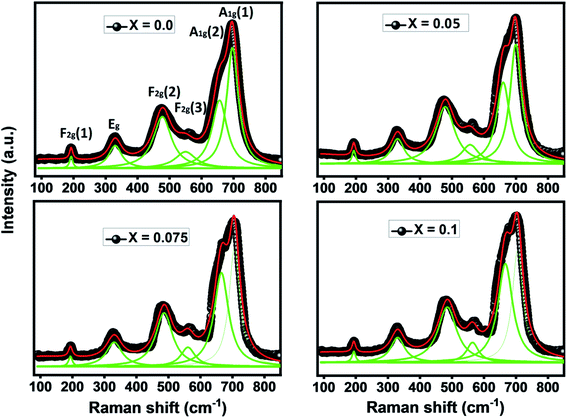
To shed more light on the vibrational study and confirm the formation of our compounds, we perform Raman scattering analysis at room temperature. Raman spectra in the region of 100 cm−1 to 850 cm−1 by using 540 nm laser excitation for Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 samples are presented in Fig. 5. It is well known that the spinel ferrite belong to Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group which gives rise to 39 normal vibrational modes, five of them are Raman active modes (A1g + Eg + 3T2g).43 In spinel ferrites, it exist two modes: the first is vibrations of the oxygen atoms in tetrahedral sites AO4 groups above 600 cm−1, and the second mode below this frequency is vibrations of the oxygen atoms in octahedral sublattice. The translation movement of the entire tetrahedral units MO4 is associated to T2g(1) phonon. The T2g(2) and T2g(3) Raman modes refer respectively to the symmetric and asymmetric bending of the oxygen atom in the metal–oxygen band at the octahedral site. Plus, the Eg Raman mode is correlated to the symmetric bending of the oxygen atom with respect to the metal ion at the octahedral site. Finally, the symmetric stretching of the oxygen atom in tetrahedral sites corresponds to A1g Raman mode.44 In order to better analyze the Raman results of our samples, Lorentzian function was used to fit the obtained Raman data. The Raman modes for all Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 samples (x = 0.00, x = 0.05 x = 0.075 and x = 0.1) are summarized in Table 4. These Raman band positions are in accord with previous researches about spinel ferrite.32,45 It is clear from the Table 4 that all modes of Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 are shifting to high frequency with increasing Nd3+ content. This shift in Raman modes is due to cation redistribution between octahedral and tetrahedral sites result from the incorporation of Nd3+ ions in spinel ferrite samples. Furthermore, the broad and shift of the Raman modes in the nano-particle can be also ascribed to phonon confinement and variations inphonon relaxation with the smaller particle size.35 From Fig. 5, we observe that no additional peak matching any other iron oxide phase is found for the compounds (monophasic composition), which confirms the results already found by the XRD analysis. In contrast with XRD analyze, it reveals that the absence of the orthoferrite phase NdFeO3 for x = 0.1 sample, which may be due to low percentage of this phase in the system. However, we conclude that all the Raman active bands of our samples are conforming to the theoretical vibrational modes of the spinel ferrites with cubic phase Fd
m space group which gives rise to 39 normal vibrational modes, five of them are Raman active modes (A1g + Eg + 3T2g).43 In spinel ferrites, it exist two modes: the first is vibrations of the oxygen atoms in tetrahedral sites AO4 groups above 600 cm−1, and the second mode below this frequency is vibrations of the oxygen atoms in octahedral sublattice. The translation movement of the entire tetrahedral units MO4 is associated to T2g(1) phonon. The T2g(2) and T2g(3) Raman modes refer respectively to the symmetric and asymmetric bending of the oxygen atom in the metal–oxygen band at the octahedral site. Plus, the Eg Raman mode is correlated to the symmetric bending of the oxygen atom with respect to the metal ion at the octahedral site. Finally, the symmetric stretching of the oxygen atom in tetrahedral sites corresponds to A1g Raman mode.44 In order to better analyze the Raman results of our samples, Lorentzian function was used to fit the obtained Raman data. The Raman modes for all Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 samples (x = 0.00, x = 0.05 x = 0.075 and x = 0.1) are summarized in Table 4. These Raman band positions are in accord with previous researches about spinel ferrite.32,45 It is clear from the Table 4 that all modes of Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 are shifting to high frequency with increasing Nd3+ content. This shift in Raman modes is due to cation redistribution between octahedral and tetrahedral sites result from the incorporation of Nd3+ ions in spinel ferrite samples. Furthermore, the broad and shift of the Raman modes in the nano-particle can be also ascribed to phonon confinement and variations inphonon relaxation with the smaller particle size.35 From Fig. 5, we observe that no additional peak matching any other iron oxide phase is found for the compounds (monophasic composition), which confirms the results already found by the XRD analysis. In contrast with XRD analyze, it reveals that the absence of the orthoferrite phase NdFeO3 for x = 0.1 sample, which may be due to low percentage of this phase in the system. However, we conclude that all the Raman active bands of our samples are conforming to the theoretical vibrational modes of the spinel ferrites with cubic phase Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, which also confirms the formation of Nd doped Ni–Zn–Al ferrite samples.
m space group, which also confirms the formation of Nd doped Ni–Zn–Al ferrite samples.
| Raman band position (cm−1) | x = 0.0 | x = 0.05 | x = 0.075 | x = 0.1 |
|---|---|---|---|---|
| A1g(1) | 691.5 | 697.2 | 701.3 | 702.4 |
| A1g(2) | 651.3 | 665 | 670.2 | 671.5 |
| F2g(3) | 493.5 | 497.9 | 559.1 | 563.4 |
| F2g(2) | 468.3 | 482.9 | 484.8 | 485.7 |
| Eg | 330.8 | 330.9 | 331.7 | 332.9 |
| F2g(1) | 191.3 | 193.1 | 193.3 | 193.6 |
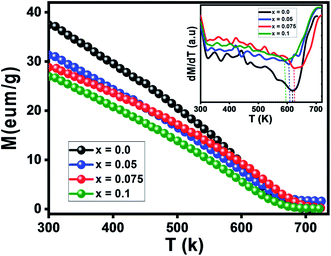
Magnetic study
The temperature versus magnetization curves for all studied samples were measured over a temperature range of 300–750 K under an external magnetic field of 1 kOe, as shown in Fig. 6. As clear in the figure, magnetization decreased continuously with temperature increasing till reaching a minimum value. This is probably caused by the thermal randomization of magnetic moments at various lattice sites.46 The TC values corresponding to the point of inflection in M(T) curves were determined from the first derivative of these curves (inset of Fig. 6). TC values are found to be decreasing approximately with increasing the Nd doping level x from 623 K for x = 0.00 to 591 K for x = 0.1 (see Table 5). This decrease in the value of Curie temperature with increasing Nd content may be due to a change in cation distribution between the tetrahedral and octahedral sites of the spinel lattice on the basis of strength of the exchange interactions. S. G. Kakade et al.45 reported that the Curie temperature decreases with Er substitution in CoFe2O4 due to decreasing the strength of A–B sublattice superexchange interactions. For the spinel oxides AB2O4, as reported by Néel about the two-sublattice model of ferrimagnetism,47 the magnetic properties are governed by competition among the magnetic interactions between ions occupying the A and B sub-lattices: the intrasite JAA and JBB(A–O–A and B–O–B) and the strongest and most dominant A–B sub-lattice exchange JAB. So, the replacement of iron by neodymium causes a weakening of the interaction JAB triggered by the presence of non-magnetic Nd3+ ions the crystallographic sites of the Ni–Zn–Al ferrite, and as a result of this, the Curie temperature decreases.48 As shown in Tables 1 and 2, the increase in lattice parameter, bond angles and bond lengths results in decreased A–B exchange interaction. As the exchange interaction is relatively strong, correspondingly higher thermal energy is required to disorient the moments,19 thereby resulting in lower TC values with increasing the Nd doping level x.| Parameter | x = 0.0 | x = 0.05 | x = 0.075 | x = 0.1 |
|---|---|---|---|---|
| TC (K) | 623 | 622 | 606 | 591 |
| θCW (K) | 668 | 601 | 669 | 655 |
| μeff (μB) | 3.13 | 1.13 | 0.37 | 0.25 |
| Ms (emu g−1) | 47 | 42 | 39.8 | 34 |
| Hc (Oe) | 34 | 25 | 20 | 15 |
| Mr (emu g−1) | 3.2 | 2 | 1.5 | 0.5 |
| Mr/Ms | 0.07 | 0.08 | 0.04 | 0.01 |
| K1 (J m−3) | 5.9 × 104 | 5 × 104 | 3.9 × 104 | 4.2 × 104 |
| nB (μB) | 1.87 | 1.7 | 1.63 | 1.41 |
| nth (μB) | 5.5 | 5.4 | 5.35 | 5.3 |
| Y–K angles (°) | 60.74 | 61.87 | 62.3 | 69.26 |
Fig. 7 depicts the inverse of susceptibilities versus temperature which ascend clearly when the ferrite nanoparticles change its magnetic state from ferrimagnetic to paramagnetic. In the temperature range, well above TC, the susceptibility follows the Curie–Weiss law:49
where NA is Avogadro number, kB is Boltzmann constant and μB is Bohr magneton. The obtained parameters θCW and μeff are listed in Table 5. As noticed from the table, the obtained values of θCW are slightly great comparable to TC. This difference may mostly caused by the presence of a magnetic inhomogeneity.50
Generally, the difference between TC and θCW is associated with the presence of short-range ordered slightly above TC. However, we mark a downturn in Curie temperature and θCW values which can be related to the weakening of A–B exchange interactions caused by the replacement of iron (Fe3+) by the neodymium (Nd3+). The decrease in the effective experimental paramagnetic moment with the increase in Nd3+ content may refer to the decrease in ferrimagnetic clusters present in the paramagnetic phase.51
The magnetic hysteresis loops obtained for the nanocrystalline undoped and neodymium-doped Ni–Zn–Al ferrite (Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4) Powdersat room temperature are shown in Fig. 8a. All the compositions exhibit typical soft ferrimagnetic nature. It could be observed from the hysteresis loop that all composition of nanoparticles shows negligible remanence and coercivity, which confirms the presence of super paramagnetic behavior in the samples. Moreover, the hysteresis loops are not well-saturated which may be related either to super paramagnetic state or to spin disorder at the surface of thin nanoparticles.19,52,53
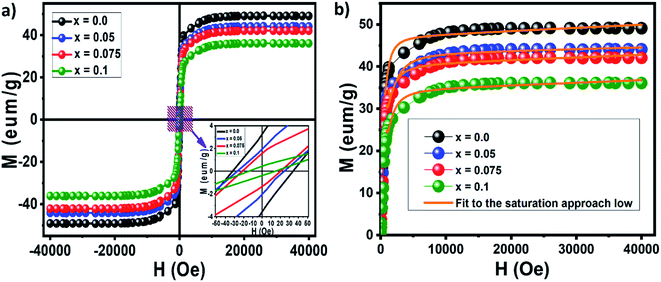 | ||
| Fig. 8 Magnetic hysteresis loops obtained for the nanocrystalline undoped and neodymium-doped Ni–Zn–Al ferrite (Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4) powders (a) and M–H variation curves (b). | ||
However, all samples exhibits a super paramagnetic behavior might be useful for biomedical applications such as hypothermia and contrast enhancement agents for magnetic resonance imaging (MRI).
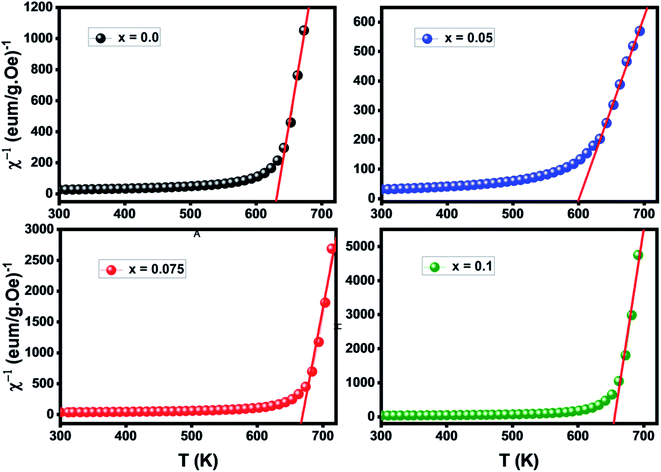
Magnetic parameters such as saturation magnetization (Ms), coercivity (Hc), remanent magnetization (Mr), magneto-crystalline anisotropy constant (K1) and reduced magnetization (Mr/Ms) were obtained from the hysteresis loop. The saturation magnetization (Ms) and magneto-crystalline anisotropy constant (K1) were obtained from the hysteresis loop by fitting the high field magnetization data (Fig. 8b) using the saturation approach low:
Moreover, the decrease in saturation magnetization of our ferrite samples can be explained on the basis of magnetic moment of metal ions in the samples. Magnetic moment of Nd3+ ion (3 μB)57 is smaller than that of Fe3+ ion (5 μB),58 when Fe3+ ions in nanoparticles spinel Ni0.6Zn0.4Al0.5Fe1.5O4 are partially doped by Nd3+ ions, the Nd3+ ions are preferentially occupied the octahedral sites (B-sites), which leads to the decrease in the net magnetic moment of octahedral sites in Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 with the rise of x. Similar saturation magnetization behavior has been reported for many rare earth doped spinel ferrites.59–62
The effective anisotropy constants K1 of Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 are showed in Table 5. K1 value decreases with the increase in Nd content.
The change in the magnetic parameters is due to the influence of cationic stoichiometry and occupancy at specific sites. In the present study, based on the cation distribution obtained from DRX, a deviation in the regular preferences of cations was observed. Ni2+ ions mainly occupy the octahedral sites whereas Zn2+ has strong preference for the tetrahedral sites, Al3+ and Fe3+ ions have a preference for both the available A and B sites and the Nd3+ ions are preferentially occupied the B sites. The corresponding magnetic moments of Ni2+, Nd3+, Zn2+, Al3+ and Fe3+ are 2 μB, 3 μB, 0 μB, 0 μB and 5 μB, respectively. By applying the collinear Néel two-sub-lattice model on the different assumed cation distribution configurations, the calculated magnetic moment value can be determined using the following formula:
| nth = MB − MA |
The dependence of the observed magnetic moment per formula unitin Bohr magneton (μB) with Nd3+ substitution in Ni–Zn–Al ferrite, is summarized in Table 5 after being calculated using the relation below:19
| nB = MB cos αY–K − MA |
The obtained values of Y–K angles are summerized in Table 5. It increases when Nd3+ concentration elevates, indicating increased contribution of non-collinear nature for magnetization variation. The non-zero Y–K angles support that the magnetization behavior can't be represented on the basic of Néel two sub-lattice model due to the presence of spin canting on the octahedral site (B site), which rises the B–B interaction, as a result the A–B interaction reduces.
Table 5 also shows that the coercivity (Hc) decreases from 35 Oe to 15 Oe as x is increased from x = 0.00 to x = 0.1. The decrease in coercivity is being attributed to the strong spin–orbit coupling of rare earth Nd3+ ions contribute to the anisotropy, when they are located in the B sites of ferrite. Another possible explanation is that the decrease in the size of the particles could cause a decrease in the coercivity. It is also found that the squareness ratio (Mr/Ms) decreases with increase Nd3+ substitution. The values of Mr/Ms for Nd-doped Ni–Zn–Al ferrites which vary from 0.08 to 0.01 are shown in Table 5. These values are less than the typical value of “0.5” expected for a single magnetic domain material.53 The low value of Mr/Ms could be attributed to the interactions between the grains which, in turn, area affected by the grain size distribution in the material.
To probe if our samples can be useful for high-frequency microwave applications, it is essential to have available materials with a high microwave frequency value.19,64 The microwave frequency (ωm) was calculated by the given equation:
| ωm = γ8π2Ms |
In general, a large magnetocaloric effect (ECM) value is observed near the transition temperature and is closely related to the order of the corresponding magnetic phase transition. The M(T) curves show a reversible character of the magnetization around the Curie temperature. Furthermore, the small area of the hysteresis cycle indicates low energy loss during a magnetization–demagnetization process. Therefore, the Nd doped Ni–Zn–Al ferrite can be considered as a candidate for magnetic refrigeration in a wide temperature range above room temperature and other various applications such as in biomedicine and in microwave devices.
Conclusion
The present study demonstrates the effect of Nd3+ substitution for Fe3+ in Ni–Zn ferrite nano-crystals morphology, structure and magnetic properties. Structural analysis of undoped and Nd3+ doped Ni0.6Zn0.4Al0.5Fe1.5−xNdxO4 with x = 0.00, 0.05, 0.075 and 0.1 showed a spinel cubic structure with Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Because of the large ionic radius of neodymium, the lattice parameter, cell volume and crystallite size were found to be increasing when the doping level is rising. Spectroscopic analysis demonstrates the change in the frequency intensities which affects the bond length in Fe3+–O tetrahedral and octahedral sites due to the insertion of doping ion Nd3+.Magnetic study proves a ferrimagnetic–paramagnetic transition at the Curie temperature. The cationic arrangement between the tetrahedral (A-) and octahedral (B-) of Ni–Zn–Al ferrite samples was estimated from the diffraction intensities of XRD data. Based on the cation arrangement, the estimated magnetic moment values, by adopting Néel's sublattice and Yafet–Kittel models, Ms variation with x is explained and found to reduce with the rise in Nd content. The magnetic hysteresis loops showed a soft ferrimagnetic nature and the presence of super paramagnetic behavior in this material, which can be considered as a good criterion for biomedical applications. Furthermore, high values of microwave frequency (ωm) in the range 7.5–10.6 GHz are also reported.
m space group. Because of the large ionic radius of neodymium, the lattice parameter, cell volume and crystallite size were found to be increasing when the doping level is rising. Spectroscopic analysis demonstrates the change in the frequency intensities which affects the bond length in Fe3+–O tetrahedral and octahedral sites due to the insertion of doping ion Nd3+.Magnetic study proves a ferrimagnetic–paramagnetic transition at the Curie temperature. The cationic arrangement between the tetrahedral (A-) and octahedral (B-) of Ni–Zn–Al ferrite samples was estimated from the diffraction intensities of XRD data. Based on the cation arrangement, the estimated magnetic moment values, by adopting Néel's sublattice and Yafet–Kittel models, Ms variation with x is explained and found to reduce with the rise in Nd content. The magnetic hysteresis loops showed a soft ferrimagnetic nature and the presence of super paramagnetic behavior in this material, which can be considered as a good criterion for biomedical applications. Furthermore, high values of microwave frequency (ωm) in the range 7.5–10.6 GHz are also reported.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Tunisian Ministere de l'Enseignement Superieur et de la Recherche Scientifique (PHCMaghreb 15 MAG07 program).References
- Y. K. Dasan, B. H. Guan, M. H. Zahari and L. K. Chuan, Influence of La3+ Substitution on Structure, Morphology and Magnetic Properties of Nanocrystalline Ni–Zn Ferrite, PLoS One, 2017, 12(1), e0170075 CrossRef CAS PubMed.
- L.-Z. Li, X.-X. Zhong, R. W. Wang, X.-Q. Tu, L. He and F.-H. Wang, J. Magn. Magn. Mater., 2019, 475, 1–4 CrossRef CAS.
- L. Andjelković, M. Šuljagić, M. Lakić, D. Jeremić, P. Vulić and A. S. Nikolić, A Study of the Structural and Morphological Properties of Ni–Ferrite, Zn–Ferrite and Ni–Zn–Ferrites Functionalized with Starch, Ceram. Int., 2018, 44(12), 14163–14168 CrossRef.
- M. Abbas, B. P. Rao and C. G. Kim, Mater. Chem. Phys., 2014, 1–9 Search PubMed.
- S. Kumar, P. Kumar, V. Singh, U. K. Mandal and R. K. Kotnala, J. Magn. Magn. Mater., 2015, 379, 50–57 CrossRef CAS.
- P. L. Leng, M. G. Naseri, E. Saion, A. H. Shaari and M. A. Kamaruddin, Adv. Nanopart., 2013, 2, 378–383 CrossRef.
- R. Rajesh Kanna, K. Sakthipandi, N. Lenin and E. James Jebaseelan Samuel, J. Mater. Sci.: Mater. Electron., 2019, 30, 4473–4486 CrossRef.
- Somnath, I. Sharma, R. K. Kotnala, M. Singh, A. Kumar, P. Dhiman, V. P. Singh, K. Verma and G. Kumar, J. Magn. Magn. Mater., 2017, 444, 77 CrossRef CAS.
- T. J. Shinde, A. B. Gadkari and P. N. Vasambekar, J. Alloys Compd., 2012, 513, 80 CrossRef CAS.
- R. S. Yadav, J. Havlica, J. Masilko, L. Kalina, J. Wasserbauer, M. Hajduchova, V. Enev, I. Kuritka and Z. Kozakova, J. Magn. Magn. Mater., 2016, 399, 109 CrossRef CAS.
- X. Wu, W. Chen, W. Wu, J. Wu and Q. Wang, Improvement of the magnetic moment of Ni–Zn ferrites induced by substitution of Nd3+ ions for Fe3+ ions, J. Magn. Magn. Mater., 2018, 453, 246–253 CrossRef CAS.
- P. P. Naik, R. B. Tangsali, S. S. Meena and S. M. Yusuf, Influence of Rare Earth (Nd3+) Doping on Structural and Magnetic Properties of Nanocrystalline Manganese–Zinc Ferrite, Mater. Chem. Phys., 2017, 191, 215–224 CrossRef CAS.
- G. S. Luo, W. P. Zhou and J. D. Li, et al., The influence of Nd3+ ions doping on structural, dielectric and magnetic properties of Ni–Zn ferrites, J. Mater. Sci.: Mater. Electron., 2017, 28, 7259–7263 CrossRef CAS.
- T. Şaşmaz Kuru, M. Kuru and S. Bağci, Structural, dielectric and humidity properties of Al–Ni–Zn ferrite prepared by co-precipitation method, J. Alloys Compd., 2018, 753, 483–490 CrossRef.
- A. Ahmad, H. Bae, I. Rhee and S. Hong, J. Magn. Magn. Mater., 2018, 447, 42–47 CrossRef CAS.
- N. Sharma, P. Aghamkar, S. Kumar, M. Bansal, Anju and R. P. Tondon, J. Magn. Magn. Mater., 2014, 369, 162–167 CrossRef CAS.
- Z. A. Gilania, M. F. Warsic, M. N. Anjum, I. Shakird, S. Naseeme, S. Riaze and M. A. Khana, J. Alloys Compd., 2015, 639(5), 268–273 CrossRef.
- R. A. Pawar, S. l. M. Patange and S. E. Shirsath, RSC Adv., 2016, 6, 76590 RSC.
- J. Massoudi, M. Smari, K. Nouri, E. Dhahri, K. Khirouni, S. Bertaina, L. Bessais and E. K. Hlil, RSC Adv., 2020, 10, 34556–34580 RSC.
- H. Javed, F. l. Iqbal, P. O. Agboola, M. A. Khan, M. F. Warsi and I. Shakir, Structural, electrical and magnetic parameters evaluation of nanocrystalline rare earth Nd3+ substituted nickel-zinc spinel ferrite particles, Ceram. Int., 2019, 45(8), 11125–11130 CrossRef CAS.
- H. S. Aziz, S. Rasheed, R. A. Khan, A. Rahim, J. Nisar, S. M. Shah, F. Iqbal and A. R. Khan, RSC Adv., 2016, 6, 6589 RSC.
- E. F. Bertaut, Structures des boroferrites, Acta Crystallogr., 1950, 3, 473–474 CrossRef.
- V. K. Lakhani, T. K. Pathak, N. H. Vasoya and K. B. Modi, Solid State Sci., 2011, 13, 539–547 CrossRef CAS.
- S. M. Patange, S. S. Desai, S. S. Meena, S. M. Yusuf and S. E. Shirsath, RSC Adv., 2015, 5(111), 91482–91492 RSC.
- L. Wang, B. K. Rai and S. R. Mishra, Structural and magnetic study of Al3+ doped Ni0.75Zn0.25Fe2xAlxO4 nanoferrites, Mater. Res. Bull., 2015, 65, 183–194 CrossRef CAS.
- J. Massoudi, D. Bouekkeze, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, Adv. Powder Technol., 2020, 31, 4714–4730 CrossRef CAS.
- S. Yadav, I. Kuritka, J. Vilcakova, P. Urbanek, M. Machovsky, M. Masar and M. Holek, J. Phys. Chem. Solids, 2017, 110, 87–99 CrossRef.
- R. Qindeel and N. H. Alonizan, Curr. Appl. Phys., 2018, 18, 519–525 CrossRef.
- Y. Gao, Z. Wang, J. Pei and H. Zhang, Structural, elastic, thermal and soft magnetic properties of Ni–Zn–Li ferrites, J. Alloys Compd., 2019, 774, 1233–1242 CrossRef CAS.
- N. Amri, M. Nasri, M. Triki and E. Dhahri, Synthesis and characterization of (1 − x)(La0.6Ca0.4MnO3)/x(Sb2O3) ceramic composites, Phase Transitions, 2018, 92, 52–64 CrossRef CAS.
- G. Kumar, R. K. Kotnal, J. Shah, V. Kumar, A. Kumar, P. Dhiman and M. Singh, Phys. Chem. Chem. Phys., 2017, 19, 16669 RSC.
- C. Murugesan and G. Chandrasekaran, RSC Adv., 2015, 5, 73714–73725 RSC.
- Somnath, I. Sharma, R. K. Kotnala, M. Singh, A. Kumar, P. Dhiman, V. P. Singh, K. Verma and G. Kumar, Structural, magnetic and Mössbauer studies of Nd-doped Mg–Mn ferrite nanoparticles, J. Magn. Magn. Mater., 2017, 444, 77–86 CrossRef CAS.
- S. I. Ahmad, S. A. Ansari and D. R. Kumar, Mater. Chem. Phys., 2018, 208, 248–257 CrossRef CAS.
- D. Bouokkeze, J. Massoudi, W. Hzez, M. Smari, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, RSC Adv., 2019, 9, 40940 RSC.
- E. R. Kumar, C. Srinivas, M. S. Seehra, M. Deepty, I. Pradeep, A. S. Kamzin, M. V. K. Mehar and N. K. Mohan, Sens. Actuators, A, 2018, 279, 10–16 CrossRef CAS.
- A. Javed, T. Szumiata, A. Sarwar and T. Fatima, Structure and Mössbauer spectroscopy studies of Ni0.5Zn0.5NdxFe2−xO4 (0.00 ≤ x ≤ 0.10) ferrites, Mater. Chem. Phys., 2018, 221, 99–107 CrossRef.
- R. S. Yadav, J. Havlica, J. Masilko, L. Kalina, J. Wasserbauer, M. Hajdúchová, V. Enev, I. Kuřitka and Z. Kožáková, J. Magn. Magn. Mater., 2016, 399, 109–117 CrossRef CAS.
- M. K. Kokare, N. A. Jadhav, Y. Kumar, K. M. Jadhav and S. M. Rathod, Effect of Nd3+ doping on structural and magnetic properties of Ni0.5Co0.5Fe2O4 nanocrystalline ferrites synthesized by sol–gel auto combustion method, J. Alloys Compd., 2018, 748, 1053–1061 CrossRef CAS.
- A. Bajorek, C. Berger, M. Dulski, P. Łopadczak, M. Zubko, K. Prusik, M. Wojtyniak, A. Chrobak, F. Grasset and N. Randrianantoandro, Microstructural and magnetic characterization of Ni0.5Zn0.5Fe2O4 ferrite nanoparticles, J. Phys. Chem. Solids, 2019, 129, 1–21 CrossRef CAS.
- M. M. Naik, H. S. B. Naik, G. Nagaraju, M. Vinuth, K. Vinu and S. K. Rashmi, J. Mater. Sci.: Mater. Electron., 2018, 29(23), 20395–20414 CrossRef CAS.
- S. A. Mazen, S. F. Mansour, E. Dhahri, H. M. Zaki and T. A. Elmosalami, J. Alloys Compd., 2009, 470, 294 CrossRef CAS.
- J. P. Singh, R. C. Srivastava, H. M. Agrawal and R. Kumar, J. Raman Spectrosc., 2011, 42, 1510 CrossRef CAS.
- M. Virumbrales-del Olmo, A. Delgado-Cabello, A. Andrada-Chacón, J. Sánchez-Benítez, E. Urones-Garrote, V. Blanco-Gutiérrez, M. J. Torralvo and R. Sáez-Puchea, Phys. Chem. Chem. Phys., 2017, 19, 8363–8837 RSC.
- S. G. Kakade, R. C. Kambale, C. V. Ramanna and Y. D. Kolekar, RSC Adv., 2016, 6, 33308–33317 RSC.
- M. A. Dar, K. Majid, M. H. Najar, R. K. Kotnala, J. Shah, S. K. Dhawan and M. Farukh, Phys. Chem. Chem. Phys., 2017, 9, 10629 RSC.
- L. Néel, C. R. Hebd. Seances Acad. Sci., 1950, 230, 375–377 Search PubMed.
- F. Saida, H. Harzali, A. Marzouki, A. Mgaidi, A. Megriche and J. Tun, Chem. Sci., 2017, 19, 26–31 Search PubMed.
- M. Jeddi, H. Gharsallah, M. Bejar, M. Bekri, E. Dhahri and E. K. Hlil, RSC Adv., 2018, 8, 943 Search PubMed.
- M. Nasri, M. Triki, E. Dhahri, M. Hussein, P. Lachkar and E. K. Hlil, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 408, 104 CrossRef CAS.
- B. Martinez, V. Laukhin, J. Fontcuberta, L. Pinsard and A. Revcolevschi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 054436 CrossRef.
- S. G. Gawas, S. S. Meena, P. Bhatt and V. M. S. Verenkar, Nanoscale-driven structural changes and associated superparamagnetism in magnetically diluted Ni–Zn ferrites, Mater. Chem. Front., 2018, 2(2), 300–312 RSC.
- F. Saffari, P. Kameli, M. Rahimi, H. Ahmadvand and H. Salamati, Ceram. Int., 2015, 41, 7352–7358 CrossRef CAS.
- Somnath, I. Sharma, R. K. Kotnala, M. Singh, A. Kumar, P. Dhiman, V. P. Singh, K. Verma and G. Kumar, J. Magn. Magn. Mater., 2017, 444, 77–86 CrossRef CAS.
- R. H. Kodama, A. E. Berkowitz, J. E. J. McNiff and S. Foner, Phys. Rev. Lett., 1996, 77, 394 CrossRef CAS PubMed.
- A. Munir, F. Ahmed, M. Saqib and M. Anis-ur-Rehman, J. Magn. Magn. Mater., 2016, 397, 188–197 CrossRef CAS.
- H. El Moussaoui, T. Mahfoud, M. Ben Ali, Z. Mahhouti, R. Masrour, M. Hamedoun, E. K. Hlil and A. Benyoussef, Mater. Lett., 2016, 171, 142–145 CrossRef CAS.
- R. S. Pandav, R. P. Patil, S. S. Chavan, I. S. Mulla and P. P. Hankare, J. Magn. Magn. Mater., 2016, 417, 407–412 CrossRef CAS.
- K. K. Bamzai, G. Kour, B. Kaur and S. D. Kulkarni, J. Magn. Magn. Mater., 2013, 327, 159–166 CrossRef CAS.
- S. I. Ahmad, S. A. Ansari and D. R. Kumar, Mater. Chem. Phys., 2018, 208, 248–257 CrossRef CAS.
- M. Maria, L. Sonia, S. Anand, V. M. Vinosel, M. A. Janifer, S. Pauline and A. Manikandan, J. Magn. Magn. Mater., 2018, 466, 238–251 CrossRef.
- S. Thankachan, B. P. Jacob, S. Xavier and E. M. Mohammed, Phys. Scr., 2013, 87(7), 025701 CrossRef CAS.
- J. Massoudi, M. Smari, K. Khirouni, E. Dhahri and L. Bessaisd, J. Magn. Magn. Mater., 2021, 528, 167806 CrossRef.
- M. N. Akhtar, M. Babar, S. Qamar, Z. ur-Rehman and M. A. Khan, Ceram. Int., 2019, 45, 10187–10195 CrossRef CAS.
- M. N. Akhtar, M. Saleem and M. A. Khan, J. Phys. Chem. Solids, 2018, 123, 260–265 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |