Open Access Article
Open Access ArticleElectrical conductivity and dielectric properties of Sr doped M-type barium hexaferrite BaFe12O19†
Y. Marouani *ab,
J. Massoudi
*ab,
J. Massoudi b,
M. Noumib,
A. Benaliabc,
E. Dhahri
b,
M. Noumib,
A. Benaliabc,
E. Dhahri b,
P. Sanguinod,
M. P. F. Graça
b,
P. Sanguinod,
M. P. F. Graça c,
M. A. Valentec and
B. F. O. Costaa
c,
M. A. Valentec and
B. F. O. Costaa
aUniversity of Coimbra, CFisUC, Physics Department, 3004-516 Coimbra, Portugal. E-mail: yosramarouani@gmail.com
bLaboratoire de Physique Appliquée, Faculté des Sciences, Université de Sfax, 3000, Tunisia
cI3N, PhysicsDepartment, Universityof Aveiro, 3810-193, Portugal
dUniversity of Coimbra, CEMMPRE, Mechanical Engineering Department, 3030-788 Coimbra, Portugal
First published on 5th January 2021
Abstract
The hexaferrite Ba1−xSrxFe12O19 compounds with x = 0, 0.5 and 1 were synthesized by the autocombustion method. X-ray diffraction (XRD), Raman spectroscopy and transmission electron microscopy (TEM) were used for structural and morphological studies.
The Raman results showed that the intensity of the resonance band remains unchanged in Ba1−xSrxFe12O19 compared to the undoped compound (x = 0) indicating that the polarizability did not change during the vibrations. The particle sizes, observed by TEM, are reduced from 228 nm to 176 nm with doping.
Electrical conductance measurements show that all samples present semiconductor-like behaviors. The Maxwell–Wagner model explains why the alternating electrical conductivity of the samples doped with Sr is lower compared to that of the undoped sample. The Correlated Barrier Hopping (CBH) model dominates the conduction process for the BaFe12O19 sample, whereas the No overlapping Small Polaron Tunneling (NSPT) model dominates the conduction process for the Ba0.5Sr0.5Fe12O19 sample. For SrFe12O19 the conduction is dominated by the NSPT model at temperatures below 240 K and by the CBH model above 240 K. The BaFe12O19 compound exhibits a giant dielectric constant (ε′) whose values reached 104 at low frequencies. This value is reduced to 150 in the Sr-doped hexaferrite.
1 Introduction
Ferrites are widely used in the magnet market due to their low price and reasonable magnetic performance.1 Hexagonal ferrites, also known as hexaferrites, are materials which have a much higher electrical resistivity than metallic ferromagnetic ceramics and which absorb the penetration of the electromagnetic field and reduce eddy current losses.2 All the hexaferrites have ferromagnetic properties which are primarily associated with crystal structure.3The hexaferrite family can be divided into six types, namely M type (BaFe12O19), Z type (Ba3Me2Fe24O41), Y type (Ba2Me2Fe12O22), W type (BaMe2Fe16O27), X Type (Ba2Me2Fe28O46) and U type (Ba4Me2Fe36O60), where “Me” can be inserted with the elements of Sr, Co, Ni or Zn.4 Inside type M, which has the general formula MFe12O19 (M = Ba, Sr, Pb), hexaferrite BaFe12O19 has the best physicochemical properties allowing it to be used in many applications.5 It can be used as filters for microwave devices,6 magnetic recording media,7 permanent magnet8 and high density magneto-optics.9 There are some requirements for the materials to be use in such applications, such as excellent chemical stability, high natural resonance frequency, good ability to absorb unwanted electromagnetic signals, high saturation magnetization and high magnetic anisotropy.
BaFe12O19 hexaferrite and the M-type ferrites, in general, have been intensively studied mainly because it can be used at a much higher frequency than other types of ferrites due to their higher intrinsic magnetocrystalline anisotropy.10,11 The influence of the synthesis technique in its properties has been analyzed. Therefore BaFe12O19 has been prepared by co-precipitation,12 citrate-precursor,13 microwave and hydrothermal,14,15 sol–gel,16–18 and others.19–24
These M-type hexaferrites, have been produced in nanosize to enlarge the specific surface area, improving the absorption capacity per unit mass, which induces their practical application in absorbent materials and microwave protection.10 Thus, by increasing the volume/area ratio the physical and chemical properties of nanosize materials greatly improves, differing strongly from the micron-size ones.25,26 The quality of the powder and the frequency strongly influence the dielectric properties of ferrites, therefore, the study of the dielectric properties and the electrical conductivity ac at different frequencies will give valuable information on the phenomenon of conduction in ferrites.27
Singh et al.28 synthesized Ba–Sr hexaferrite substituted by Co–Al and reported microwave absorption properties. Pereira et al.29 have shown that the values of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of the Ba0.45Sr0.55Fe12O19 compound decrease as a function of the frequency. The double substitution of Pr–Ni in the hexaferrite Sr0.5Ba1−xPrxFe12−yNiyO19, studied by Iqbal et al.30 shows high values of remanence and coercivity at low doping concentrations. The study of barium and strontium hexaferrite substituted by Nd–Ni31 shows that the ε′ and tan
δ of the Ba0.45Sr0.55Fe12O19 compound decrease as a function of the frequency. The double substitution of Pr–Ni in the hexaferrite Sr0.5Ba1−xPrxFe12−yNiyO19, studied by Iqbal et al.30 shows high values of remanence and coercivity at low doping concentrations. The study of barium and strontium hexaferrite substituted by Nd–Ni31 shows that the ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values have decreased up to the frequency value of 1 kHz and remain constant beyond 1 kHz.
δ values have decreased up to the frequency value of 1 kHz and remain constant beyond 1 kHz.
The increase in saturation magnetization and a decrease in coercivity are observed in of Ba–Sr hexaferrite substituted by Ni–Zr.32
In this paper, we have prepared nano-size Ba1−xSrxFe12O19 hexaferrites, study their dielectric properties dielectric constant (ε′), loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) and electrical conductivity (σac) and relate them to the structural properties.
δ) and electrical conductivity (σac) and relate them to the structural properties.
2 Experimental
2.1. Synthesis
The Ba1−xSrxFe12O19 (x = 0.0, 0.5, and 1) hexaferrites were synthesized by the autocombustion method33 according to the following reaction equation:| (1 − x)Ba(NO3)2 + xSr(NO3)2 + 12Fe(NO3)2·9H2O → Ba1−xSrxFe12O19 |
The reagents used in the reaction were of analytical grade. The oxidants are barium nitrate [Ba(NO3)2], strontium nitrate [Sr(NO3)2] and iron nitrate [Fe(NO3)3·9H2O] obtained from Sigma Aldrich, Germany. The fuel used to start the combustion process was glycine (G, C2H5NO2) obtained from SD Fine Chem. Ltd., Mumbai.
The amount of the fuel used was calculated fixing the glycine to nitrate ratio: G/N = 1.2, making the total composition with an excess of fuel greater than the stochiometric quantity required to complete the combustion process without heat exchange.
For all samples, the stochiometric quantities of nitrates and glycine were dissolved in 20 ml of distilled water and the solutions were heated to 80 °C under magnetic stirring until a homogenous and transparent solution was obtained. When the precursors are well mixed in a period of about 2 hours, the temperature is increased upto 180 °C and a viscous gel is formed.
Finally, and after letting the viscous solution stand for a period of 20 minutes, the gel was preheated to 350 °C, it boiled, swelled, releasing a large quantity of gas and then it ignites. An swollen black powders were obtained. The black powder was heat treated in a hot air oven at 700 °C, for 2 hours, to remove any organic product or unreacted glycine. The obtained powders were pressed into thin pellets of 8 mm in diameter and 1 mm in thickness and then sintered at different conditions: (i) 900 °C for 30 minutes; (ii) 1000 °C for 30 minutes; (iii) 1100 °C for 2 hours. In all treatments the temperature was slowly cooled to room temperature.
2.2. Characterization methods
The X-ray diffractograms of the samples were recorded using an X-ray diffractometer (D8 Advance, Bruker), equipped with a CuKα radiation source (λ = 1.5406 Å) in θ–2θ Bragg–Brentano geometry. XRD data were used to obtain the diffraction parameters by Rietveld analysis,34 using FullProf software.35The crystallite size (D) was calculated using the Scherrer relation:
 | (1) |
The X-ray density (DX) was calculated using:
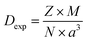 | (2) |
The surface morphology and elemental detection of the powders were examined with a Transmission Electron Microscope (TEM). TEM images were taken with an FEI Tecnai G2 with an acceleration voltage of 200 kV. For the analysis, the carbon grids were immersed in dilute suspensions of the powders. After the solvent evaporation the grids were placed in the microscope. Image J software was used to analyse the micrographs.
Raman spectroscopy was performed at room temperature under backscattering geometry, using a JobinYvon HR 800 system and an excitation wavelength of 473 nm. The Raman spectra were recorded with a modular double-grating excitation spectrofluorimeter with a TRIAX 320 emission monochromator (Fluorolog-3, Horiba Scientific) coupled to an HR 980 Hamamatsu photomultiplier, using a front face acquisition mode. As an excitation source, a 450 W X arc lamp was used.36
The dielectric measurements were performed using an Agilent 4294 network analyzer, operating between 100 Hz and 1 MHz in a Cp–Rp configuration (capacitance in parallel with resistance) was used for these measurements. To perform the measurements, each sample surface was painted with silver conductive paste and then placed in a sample holder and pressed between two parallel platinum plates, functioning as electrodes. The sample's impedance was measured in the temperature range from 160 K up to 400 K, in a nitrogen bath cryostat. To calculate the ac conductivity, the eqn (3) was used:
 | (3) |
Dielectric constant values were calculated by;
 | (4) |
For dielectric loss we used the relation:
 | (5) |
3 Results and discussion
3.1. XRD analysis
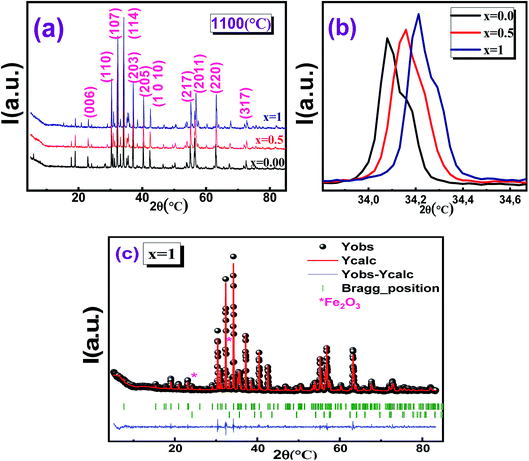
The XRD patterns of the sintered hexaferrite pellets Ba1−xSrxFe12O19 (x = 0.0, 0.5 and 1) are shown in Fig. 1(a–c). All the major peaks in the diffraction patterns could be indexed to various (hkl) planes of BaFe12O19 matching perfectly with the hexagonal structure (with the P63/mmc space group) of pure BaFe12O19 (JCPD card no. 00-051-1879). Fig. 1b shows an enlarged view of the major peak in the diffractograms of the three Ba1−xSrxFe12O19 samples indicating the shift of the XRD peak (114) towards upper angles, as the strontium content increases. This displacement of the peaks is due to the reduction in the lengths of the Fe–O bond, the angle of the Fe–O–Fe bond and the volume of the elementary cell. All samples showed well defined Bragg peaks, intense and sharp, indicating the highly crystalline nature of the samples. Minor impurity peaks were also present in the XRD patterns and the indexation done in X'PertHighScore showed that they correspond to the Fe2O3 phase. The presence of this impurity during the synthesis of hexaferrite was also unavoidable in similar works.37Table 1 shows the cell parameters, obtained by refinement with FullProf software, and it can be seen that the values of the parameter c have decreased with Sr doping, while there is no significant change in parameter a. Similar results have been reported by other authors.38–41 Thus, we deduce that the hexaferrites samples have a variable lattice parameter c, while the lattice constant a does not change.42
| Space group | Parameters | x = 0.00 | x = 0.5 | x = 1 |
|---|---|---|---|---|
| P63/mmc Ba1−xSrxFe12O19 | a (Å) | 5.892(8) | 5.885(5) | 5.880(6) |
| c (Å) | 23.231(9) | 23.156(8) | 23.071(9) | |
| V (Å3) | 698.649(6) | 694.664(7) | 690.972(6) | |
| % | 90.2 | 91.9 | 95.3 | |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c Fe2O3 c Fe2O3 |
A (Å) | 5.038(7) | 5.038(7) | 5.038(6) |
| c (Å) | 13.749(5) | 13.743(7) | 13.744(1) | |
| V (Å3) | 302.31(5) | 302.19(6) | 302.18(5) | |
| % | 9.8 | 8.1 | 4.7 | |
| χ2 | 1.85 | 1.32 | 1.37 |
The goodness of fit (χ2) affirms the correctness of fit and the high accuracy of refinement.
The value of the full-width at half-maximum of the strongest intensity diffraction peak was used to calculate the size of the crystallites (DSC), ranging from 44 nm to 56 nm, which is analogous to those obtained by Pereira et al.43
3.2. Morphological study
Fig. 2 shows the TEM micrographs of Ba1−xSrxFe12O19 hexaferrite samples. It can be seen that the particles, with a habit approximately spherical, are mostly agglomerated, as expected.38,39 The mean particle size of the BaFe12O19 sample is of the order of 228 nm. However, the mean particle size of Ba0.5Sr0.5Fe12O19 and SrFe12O19 compounds are on the order of 201 and 176 nm respectively, indicating that the grain size is reduced with the Sr doping. Similar results have been observed by other authors.38,39 The average grain size determined using TEM images is larger than the average size of the crystallites calculated by XRD, indicating that each grain is formed by several crystallites (Table 2). | ||
| Fig. 2 TEM images of Ba1−xSrxFe12O19 (a) −x = 0.0; (c) −x = 0.5; (e) −x = 1 and corresponding histograms of particle sizes (b) x = 0.0, (d) x = 0.5, (f) x = 1. | ||
| X | 0.0 | 0.5 | 1 |
| DSC (nm) | 56 | 48 | 44 |
| DTEM (nm) | 228 | 201 | 176 |
3.3. Raman analysis
The use of Raman spectroscopy in the study of oxides becomes especially useful for exploring local disorders.44 Indeed, Raman spectroscopy can efficiently probe the short-range disorder in oxygen octahedral induced by Jahn–Teller distortion and other interactions.45 All peaks in the spectra of Fig. 3 are related to the hexaferrite crystal structure and no additional vibrations, associated with secondary phase or impurities, were observed.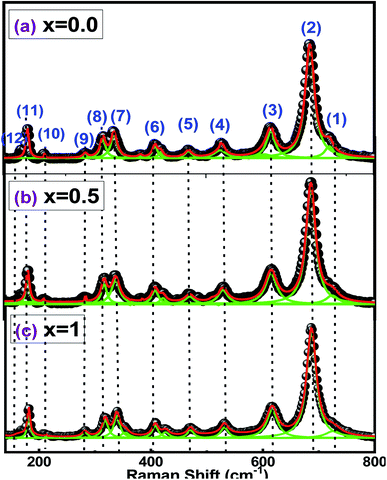 | ||
| Fig. 3 Raman spectra for barium hexaferrite with Sr substitution Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5 and (c) x = 1]. | ||
The peaks (1) and (2), at 720 and 685 cm−1, can be attributed to the A1g vibrations of the Fe–O bonds at the tetrahedral 4f1 and bipyramidal sites 2b, respectively. Furthermore, peaks (3), (5) and (8) at 616, 470 and 317 cm−1 are due to A1g vibrations of Fe–O bonds at octahedral sites 4f2, 2a and 12k, while peak (6) at 410 cm−1 is due to the vibration A1g at the 12k octahedral dominated site.
The peaks (4), (9) and (10) at 530, 284 and 212 cm−1 are due to the E1g vibrations, while peak (7) at 336 cm−1 is due to the E2g vibration. The peaks (11) and (12), at 180 and 168 cm−1, result from the E1g vibrations of the entire spinel block.
It must be noticed that Raman bands become broader with the increase of the value of x from 0 to 0.5 (Fig. 3). Changes in chemical composition, atomic radii, bond length and cell size can lead to the broadening of the Raman peaks.46 The attribution of the Raman spectra to the corresponding lattice symmetries is summarized in Table 3.
| Raman active modes | Number of peaks | Observed frequency (cm−1) | Assigned polyhedra |
|---|---|---|---|
| A1g | 1 | 720 | Tetrahedral 4f1 |
| 2 | 685 | Bipyramidal 2b | |
| 3 | 616 | Octahedral 4f2 | |
| 5 | 470 | Octahedral 2a | |
| 8 | 317 | Octahedral 12k | |
| 6 | 410 | Dominating octahedral 12k | |
| E1g | 4, 9, 10 | 530, 284, 212 | |
| 11, 12 | 180, 168 | Whole spinel block | |
| E2g | 7 | 336 | Octahedral 12k |
3.4 Electrical conductivity studies
AC conductivity (σac) was determined as a function of frequency at different temperatures, for all the samples, using the expression (3).Generally, the ac conductivity at a given temperature can be separated into two components, the dc and the ac, according to Almond–West expression (6):47
| σac = σdc(T) + Aωs(T) | (6) |
The first term of the conductivity, σdc, depends on the temperature and it is independent of the frequency. This is related to the drift mobility of free charge carriers and to the conduction band characteristics. The second term depends only on frequency, caused by the octahedral site hopping processes.
Fig. 4 shows the behavior of the conductivity with frequency, for all samples, measured at temperatures between 160 K to 400 K. Table 4 shows the values obtained from expression (6), of the σdc and s parameters.
 | ||
| Fig. 4 Conductivity spectra at various temperatures of Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5 and (c) x = 1]. | ||
| T (K) | s | σdc (S m−1) | ||||
|---|---|---|---|---|---|---|
| x = 0.00 | x = 0.5 | x = 1 | x = 0.00 | x = 0.5 | x = 1 | |
| 160 | 0.773 | 0.649 | 0.846 | 1723 × 10−7 | 6016 × 10−8 | 5846 × 10−9 |
| 180 | 0.730 | 0.689 | 0.874 | 4149 × 10−7 | 7052 × 10−8 | 1449 × 10−8 |
| 200 | 0.697 | 0.722 | 0.903 | 1146 × 10−6 | 1081 × 10−7 | 1824 × 10−8 |
| 220 | 0.649 | 0.750 | 0.940 | 2978 × 10−6 | 1684 × 10−7 | 1643 × 10−8 |
| 240 | 0.597 | 0.779 | 0.968 | 7669 × 10−6 | 2530 × 10−7 | 2804 × 10−8 |
| 260 | 0.568 | 0.813 | 0.928 | 1866 × 10−5 | 4259 × 10−7 | 3481 × 10−8 |
| 280 | 0.530 | 0.840 | 0.899 | 4372 × 10−5 | 7654 × 10−7 | 3717 × 10−8 |
| 300 | 0.497 | 0.873 | 0.865 | 9428 × 10−5 | 1416 × 10−6 | 4854 × 10−8 |
| 320 | 0.454 | 0.902 | 0.839 | 1978 × 10−4 | 2812 × 10−6 | 7466 × 10−8 |
| 340 | 0.420 | 0.932 | 0.813 | 4111 × 10−4 | 5552 × 10−6 | 1157 × 10−7 |
| 360 | 0.387 | 0.959 | 0.786 | 8530 × 10−4 | 1072 × 10−5 | 2104 × 10−7 |
| 380 | 0.354 | 0972 | 0.766 | 2030 × 10−3 | 2564 × 10−5 | 4501 × 10−7 |
| 400 | 0.320 | 0.986 | 0.740 | 3910 × 10−3 | 8678 × 10−5 | 1082 × 10−6 |
The conduction mechanism in hexaferrites is explained by the hop of charge carriers between Fe3+ ions at octahedral sites.49 In the high-frequency range, the conductivity increases with the rise of temperature. This is explained by the increased mobility of charge carriers but does not indicate an increase in the charge concentration.50 According to the Maxwell–Wagner model, the ac conductivity at low frequencies describes the contribution of the grain boundaries while at high frequencies, the dispersion can be attributed to grain conductivity and increased electron hopping between Fe3+ ions and Fe2+, promoting the increase of the conductivity. It is also observed that the conductivity decreases as the Sr content increases.
The conduction mechanism in the Ba1−xSrxFe12O19 compounds was determined by analyzing the temperature dependence of the “s” parameter. From Fig. 5a–c, the behavior of “s” changes with the Sr content and also as the temperature increases. A correlation between the conduction mechanism and s(T) behavior could suggest an appropriate model of this conduction mechanism.51
 | ||
| Fig. 5 Temperature evolution of “s” parameter and “1 − s” of the compounds. Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5, (c) and (d) for x = 1]. | ||
Based on the two distinct processes, the classical hopping over a potential barrier and the quantum-mechanical tunneling, or a combination of both, it has been differently assumed that the responsible charge carriers can be either electrons or ions.52 These different models have been defined according to the behavior of the “s” parameter. In fact, when the exponent “s” decreases with the increase in temperature, the Correlated Barrier Hopping (CBH) is the appropriate model.53 As the exponent “s” is practically constant (equal to 0.8) and independent of temperature or increases slightly with temperature, the most appropriate model is the Quantum Mechanical Tunneling (QMT).54,55 When the exponent depends on both temperature and frequency and decreases with increasing temperature to a minimum value, after increases as temperature increases, the model is Overlapping Large-Polaron Tunneling (OLPT).56 Finally, if the exponent “s” increases with the increase in temperature, the corresponding model is Small Polaron Tunneling without overlap (NSPT).54
To determine the appropriate mechanism of the conductivity, it is represented the variation of the exponent “s” as a function of the temperature in Fig. 5.
For x = 0.0, “s” gradually decreases as the temperature increases. This behavior is in good agreement with the Correlated Barrier Hopping (CBH) model.
The exponent “s” in this model can be expressed as follows:57
 | (7) |
If WM ≫ kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ωτ0) relation (7) can be simplified as:
ln(ωτ0) relation (7) can be simplified as:
 | (8) |
For x = 0.5, “s” increases progressively as a function of the temperature.
This behavior can be well adapted with the Small Polaron Tunneling without overlap model (NSPT)58,59 where the “s” exponent is given by:
 | (9) |
For large values of WM/kBT, “s” becomes:
 | (10) |
The energy WM can be determined from the slope of “s” and “1 − s” as a function of the temperature. Fig. 5a and b, shows this adjusts for the compounds x = 0 and x = 0.5, respectively.
The determined values of WM are 0.272 eV (x = 0) and 0.232 eV (x = 0.5).
It is observed that an increase in temperature causes a decrease in the binding energy of the charge carriers, making their hops between sites easier.
The sample with x = 1 (Fig. 5c and d), shows for the “s” parameter two different behaviors:
• For 150 K ≤ T ≤ 250 K, “s” increases with the rise of the temperature. This development can therefore be described by the Small Polaron Tunneling without overlap (NSPT).
This variation of “s” with temperature yields WM1 = 0.221 eV (Fig. 5c).
• From 250 to 400 K, “s” decreases with increasing temperature. There are several models, which can explain the ac-conduction mechanism in the disordered materials. For example, Mott variable range hopping conductivity,60 Efros-Shklosvkii conduction,61 ac-conduction mechanism with potential fluctuations.62 However, we believe that the Correlated Barrier Hopping (CBH) is the most suitable model to describe the conductivity in this temperature region.
In this range, where the plot of “1 − s” as a function of temperature is shown in Fig. 5d, the value of the average binding energy WM2 is estimated to be 0.369 eV.
This increase in hop polarization energy may be related to the increase in barrier height that charge carriers must overcome in order to hop from one site to another.
Fig. 6 shows the variation of ln(σdcT) against the inverse of the temperature for all samples. At high temperatures, the experimental data of the dc conductivity are well adjusted by the law of Mott and Davis which describes the small polaron hopping (SPH):63
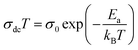 | (11) |
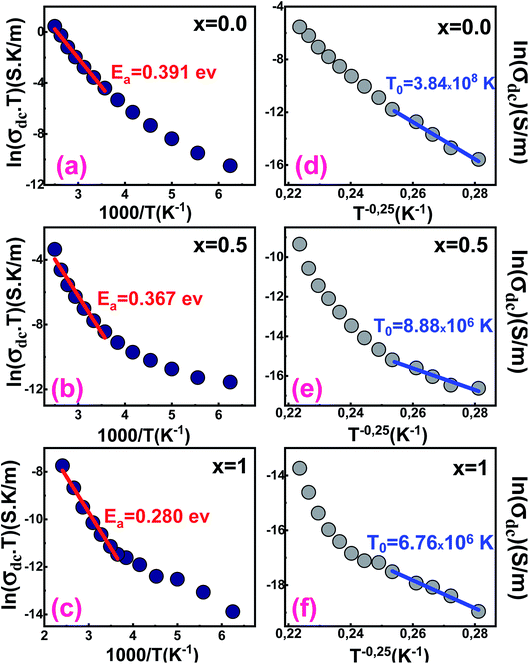 | ||
| Fig. 6 Variation of ln(σdcT) vs. (1000/T) of Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5 and (c) x = 1]. Variation of ln(σdc) vs. (T−0.25) of Ba1−xSrxFe12O19 [(d) x = 0.0, (e) x = 0.5 and (f) x = 1]. | ||
We notice that the Ea decreases from 0.391 eV to 0.280 eV when Ba is completely substituted by Sr (Fig. 6a–c and Table 4). The decrease may be related to the substitution of barium by strontium, which presents lower atomic radii that can cause a significant variation in bond lengths.
In the low-temperature range, σdc has been also analyzed by employing the variable range hopping model (VRH) for which dependence of the dc conductivity can be described by the relation (12):64
 | (12) |
According to Fig. 6d–f, the variation of ln(σdc) with T−0.25 obeys the variable range hopping conduction mechanism.
The temperature T0 decreases when the strontium content increases. Its values are respectively 3.84 × 108 K, 8.88 × 106 K and 6.76 × 106 K for samples x = 0.0, 0.5 and 1.
3.5. Dielectric analysis
Fig. 7 and 8 show the temperature and frequency dependence of the real (ε′) and imaginary (ε′′) parts of the dielectric permittivity for the Ba1−xSrxFe12O19 compounds. The ε′ and ε′′ values are high and both decreases when the strontium quantity increases. | ||
| Fig. 7 The dielectric constant as a function of frequency of Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5 and (c) x = 1]. | ||
 | ||
| Fig. 8 Imaginary part of the dielectric constant as a function of the frequency of. Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5 and (c) x = 1]. | ||
In particular, the giant dielectric constant values at low frequencies and at high temperatures were mainly related to the presence of different Schottky barriers at grain–grain boundaries, sample surface-bulk, and electrode-surface, whereas the low dielectric constant values at high frequencies were related to intrinsic effect (Fig. 7).65 The colossal static dielectric constant at low frequency obtained for BaFe12O19 sample is greater than those in Sr doped system, which makes it an interesting material for high-tech applications that require such type of characteristic.
Fig. 8 represents the variation of the imaginary part of the permittivity (ε′′) as a function of the frequency, at different temperatures for all the samples. It is noticed that (ε′′) decreases considerably with frequency and temperature. This could be explained by the strong interactions between dipoles at low frequencies, which weakens by increasing the frequency and lead to a remarkable reduction in dielectric loss.66 At high frequencies, the mechanisms of electronic and ionic polarization are dominant, while the polarization from the interfaces is dominant at low frequencies.67 The interfacial polarization, which is mainly due to grain boundary defects, which can be related to the Sr content, contributes to the increase of ε′ and ε′′.68,69 In these samples, the ε′′ strongly depends on the frequency. The nanometric size and the homogeneous and perfect structure of the Ba1−xSrxFe12O19 compounds lead to low values of dielectric losses (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ).
δ).
The variation of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ with frequency (Fig. 9) depends on the movement of the charge carriers. As the frequency increases, electrons rotate more frequently around their direction of motion, reducing the possibility of reaching grain boundaries. As a result, the polarization decreases, which results in a decrease in the tan
δ with frequency (Fig. 9) depends on the movement of the charge carriers. As the frequency increases, electrons rotate more frequently around their direction of motion, reducing the possibility of reaching grain boundaries. As a result, the polarization decreases, which results in a decrease in the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. This can be explained based on the Maxwell – Wagner Model.70,71
δ. This can be explained based on the Maxwell – Wagner Model.70,71
 | ||
| Fig. 9 Dielectric loss tangent as a function of the frequency of Ba1−xSrxFe12O19 [(a) x = 0.0, (b) x = 0.5 and (c) x = 1]. | ||
This model assumes that the dielectric structure is composed of conductive grains separated by grain boundaries. If the resistance of the grain boundaries is relatively high, the electrons which reach them by hop will accumulate and therefore producing a polarization.
For the sample with x = 0 and for temperatures above 280 K, the values of ε′ present an anomaly that is not visible for the Sr-doped samples (Fig. 9). This anomaly corresponds to a dielectric relaxation that can occur at lower frequencies for the Sr-doped samples. This indicates the existence of a phase transition at that temperature, or that the mobility of the charge carriers increases and allows them to flow to the grain boundaries where they can form electrical dipoles.
To use these materials in microwave devices like dielectric resonators, one has to find a balance between high dielectric constant and low loss.72 Generally, the structure of Ba1−xSrxFe12O19 leads to a large variation of the dielectric constant. We expect to find a situation of equilibrium with the maximum of the dielectric constant and a lower loss. This strongly suggests that Ba1−xSrxFe12O19 composites are good candidates for applications where high ε materials are sought with low loss in the radio frequency range.
4 Conclusions
The M-type barium hexaferrite BaxSr1–xFe12O19 (where0 < x < 1) alloys were prepared by autocombustion method. The X-ray pattern indexes well in the hexagonal magnetoplumbite (M-type) structure of space group P63/mmc, except for a very small amount of Fe2O3. The prepared samples were characterized by impedance spectroscopy, to establish the effects of temperature, frequency, and strontium substitution on both the transport and dielectric properties. We have found that the concentration of strontium significantly affects electrical conductivity and dielectric properties. The conduction mechanism in the Ba1−xSrxFe12O19 compounds was determined by analyzing the temperature dependence of the “s” parameter. The conduction process for the BaFe12O19 sample is dominated by the Correlated Barrier Hopping (CBH) model; whereas the No overlapping Small Polaron Tunneling (NSPT) model dominates the conduction process for Ba0.5Sr0.5Fe12O19 sample. For SrFe12O19 the conduction is dominated by the NSPT model at temperatures below 240 K and by the CBH model above 240 K. The variation of the dielectric constant as a function of temperature and frequency confirmed the contributions of different polarization mechanisms. In particular, the low dielectric constant ε′ values at high frequencies are mainly linked to intrinsic effects, on the other hand, the high values of ε′ at low frequencies and high temperatures are mainly linked to the presence of different Schottky barriers. The high values of the dielectric constant and the low losses of Ba1−xSrxFe12O19 compounds, strongly suggest that these materials may be good candidates for applications in the radio frequency range.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the support of the Tunisian Ministry of Higher Education and Scientific Research within the framework of the Tunisian-Portuguese cooperation in the field of scientific research and technology (Project of University of Sfax-University of Aveiro). CFisUC is supported by national funds from FCT – Fundação para a Ciência e a Tecnologia, I. P., within the project UID/04564/2020. Access to TAIL-University of Coimbra facility funded under QREN-Mais Centro Project No. ICT_2009_02_012_1890 is gratefully acknowledged.References
- F. Shaikh, M. Ubaidullah, R. S. Mane and A. M. Al-Enizi, Spinel Ferrite Nanostructures for Energy Storage Devices Micro and Nano Technologies, Types, Synthesis methods and applications of ferrites, 2020, ch. 4, pp. 51–82 Search PubMed.
- F. G. da Silva, J. Depeyrot, A. F. C. Campos, R. Aquino, D. Fiorani and D. Peddis, J. Nanosci. Nanotechnol., 2019, 19(8), 4888 CrossRef CAS.
- A. E. V. Arkel, et al., Rec. trav.chim., 1936, 55, 331 CrossRef.
- B. Jotania, R. B. Khomane, A. S. Deshpande, C. C. Chauhan and B. D. Kulkarni, J. Sci. Res., 2009, 1(1), 1 Search PubMed.
- R. C. Pullar, Prog. Mater. Sci., 2012, 57, 1191 CrossRef CAS.
- R. Nowosielski, R. Babilas, G. Dercz, L. Pająk and J. Wron, J. Achiev. Mater. Manuf. Eng., 2007, 28(12), 735 Search PubMed.
- T. L. Hylton, M. A. Parker, M. Ullah, K. R. Coffey and J. K. Howard, J. Appl. Phys., 1994, 75, 5960 CrossRef CAS.
- K. Chahal and K. S. Samra, J. Alloys Compd., 2018, 737, 387 CrossRef CAS.
- T. Shiratsu and H. Yao, Phys. Chem. Chem. Phys., 2018, 20, 4269 RSC.
- C. Chavan, S. E. Shirsath, M. L. Mane, R. H. Kadam and S. S. More, J. Magn. Magn. Mater., 2016, 398, 32 CrossRef.
- R. Dosoudil, M. Ušáková, A. Grusková and J. Sláma, J. Magn. Magn. Mater., 2008, 320, e849 CrossRef CAS.
- J. Iqbal, M. N. Ashiq, P. Hernandez-Gomez and J. M. Munoz, Scr. Mater., 2007, 57, 1093 CrossRef.
- K. Sankarnarayana and D. C. Khan, J. Magn. Magn. Mater., 1996, 153, 337 CrossRef.
- S. V. Trukhanov, A. V. Trukhanov, V. G. Kostishyn, L. V. Panina, A. V. Trukhanov, V. A. Turchenko, D. I. Tishkevich, E. L. Trukhanova, O. S. Yakovenko and L. Matzui, Dalton Trans., 2017, 46, 9010 RSC.
- V. Trukhanov, A. V. Trukhanov, V. G. Kostishyn, L. V. Panina, A. V. Trukhanov, V. A. Turchenko, D. I. Tishkevich, E. L. Trukhanova, O. S. Yakovenko, L. Y. Matzui, D. A. Vinnik and D. V. Karpinsky, J. Phys. Chem. Solids, 2017, 111, 142e152 CrossRef.
- Roohani, H. Arabi, R. Sarhaddi, S. Sudkhah and A. Shabani, Int. J. Mod. Phys. B, 2015, 29, 15501090 CrossRef.
- G. Patil, S. E. Shirsath, S. D. More, S. J. Shukla and K. M. Jadhav, J. Alloys Compd., 2009, 488, 199 CrossRef.
- K. Samikannu, J. Sinnappan, S. Mannarswamy, T. Cinnasamy and K. Thirunavukarasu, Mater. Sci. Appl., 2011, 2(6), 638 CAS.
- X. Liu, J. Wang, L. M. Gan, S. C. Ng and J. Ding, J. Magn. Magn. Mater., 1998, 184, 344 CrossRef CAS.
- P. Shepherd, K. K. Mallick and R. J. Green, J. Magn. Magn. Mater., 2007, 311, 683 CrossRef CAS.
- V. Trukhanov, K. A. Astapovich, M. A. Almessiere, V. A. Turchenko, E. L. Trukhanova, V. V. Korovushkin, A. A. Amirov, M. A. Darwish, D. V. Karpinsky, D. A. Vinnik, D. S. Klygach, M. G. Vakhitov, M. V. Zdorovets, A. L. Kozlovskiy and S. V. Trukhanov, J. Alloys Compd., 2020, 822, 153575 CrossRef.
- T. H. Ting and K. H. Wu, J. Magn. Magn. Mater., 2010, 322, 2160 CrossRef CAS.
- I. Bsoul and S. H. Mahmood, J. Alloys Compd., 2010, 489, 110 CrossRef CAS.
- X. Liu, J. Wang, L. M. Gan and S. C. Ng, J. Magn. Magn. Mater., 1999, 195, 452 CrossRef CAS.
- Tiwari,A. K. Mishra, H. Kobayashi and A. P. F. Turner, Intelligent Wiley-Scrivener Publishing, 2012, DOI:10.1002/9781118311974.
- G. Kumar, R. Rani, V. Singh, S. Sharma, K. M. Batoo and M. Singh, Adv. Mater. Lett., 2013, 4, 682 CrossRef CAS.
- Kumar, S. Sharma, R. K. Kotnala, J. Shah, S. E. Shirsath, K. M. Batoo and M. Singh, J. Mol. Struct., 2013, 1051, 336 CrossRef CAS.
- J. Singh, C. Singh, D. Kaur, S. B. Narang, R. Joshi, S. Mishra, R. Jotania, M. Ghimire and C. C. Chauhan, Mater. Des., 2016, 110, 749–761 CrossRef CAS.
- F. M. M. Pereira, M. R. P. Santos, R. S. T. M. Sohn, J. S. Almeida, A. M. L. Medeiros, M. M. Costa and A. S. B. Sombra, J. Mater. Sci.: Mater. Electron., 2009, 20, 408–417 CrossRef CAS.
- M. J. Iqbal and S. Farooq, J. Alloys Compd., 2010, 505, 560–567 CrossRef CAS.
- M. J. Iqbal and S. Farooq, Mater. Res. Bull., 2011, 46, 662–667 CrossRef CAS.
- S. Kanagesan, S. Jesurani, R. Velmurugan, S. Parbu and T. Kalaivani, Mater. Res. Bull., 2012, 47, 188–192 CrossRef CAS.
- R. Shariff, H. K. Choudhary, V. Khopkar, A. Yadav, R. Madhusudhana and B. Sahoo, Ceram. Int., 2020 DOI:10.1016/j.ceramint.2020.07.034.
- A. Young, TheRietveld Method, Oxford University Press, New York, 1993 Search PubMed.
- Roisnel, J. Rodriguez-Carvajal, Computer Program FULLPROF,LLB-LCSIM, 2003 Search PubMed.
- A. Benali, M. Bejar, E. Dhahri, M. Sajieddine, M. P. F. Graça and M. A. Valente, Mater. Chem. Phys., 2015, 149–150, 467 CrossRef CAS.
- R. C. Pullar, Prog. Mater. Sci., 2012, 57, 1191 CrossRef CAS.
- M. J. Iqbal and S. Farooq, J. Alloys Compd., 2010, 505, 560 CrossRef CAS.
- J. Iqbal and S. Farooq, Mater. Res. Bull., 2011, 46, 662 CrossRef.
- S. Kanagesan, S. Jesurani, R. Velmurugan, S. Parbu and T. Kalaivani, Mater. Res. Bull., 2012, 47, 188 CrossRef CAS.
- J. Singh, C. Singh, D. Kaur, S. B. Narang, R. Joshi, S. Mishra, R. Jotania, M. Ghimire and C. C. Chauhan, Mater. Des., 2016, 110, 749 CrossRef CAS.
- H. Kojima, in Fundamental Properties of Hexagonal Ferrites with Magnetoplumbite Structure, E. P. Wohlfarth, vol. 3, 1982, p.305 Search PubMed.
- M. Pereira, C. A. R. Junior, M. R. P. Santos, R. S. T. M. Sohn, F. N. A. Freire, J. M. Sasaki, J. A. C. de Paiva and A. S. B. Sombra, J. Mater. Sci.: Mater. Electron., 2008, 19, 627 CrossRef.
- A. Ahlawat and V. G. Sathe, J. Raman Spectrosc., 2011, 42, 1087 CrossRef CAS.
- A. Dubey, V. G. Sathe and R. Rawat, J. Appl. Phys., 2008, 104, 113530 CrossRef.
- J. Kreisel, G. Lucazeau and H. Vincent, J. Raman Spectrosc., 1999, 30, 115 CrossRef CAS.
- MujasamBatoo, Physica B, 2011, 406, 382 CrossRef.
- D. P. Almond, A. R. West and R. J. Grant, Solid State Commun., 1982, 44, 1277 CrossRef CAS.
- S. R. Elliott, Solid State Ionics, 1994, 70, 27 CrossRef.
- S. M. El-Sayed, T. M. Meaz, M. A. Amer and H. A. El Shersaby, Physica B, 2013, 426, 137 CrossRef CAS.
- S. R. Elliot, Adv. Phys., 1987, 36, 135 CrossRef.
- M. B. Bechir, K. Karoui, M. Tabellout, K. Guidara and A. B. Rhaiem, J. Alloys Compd., 2014, 588, 551 CrossRef.
- S. Mollah, K. K. Som, K. Bose and B. K. Chaudhuri, J. Appl. Phys., 1993, 74, 931 CrossRef CAS.
- A. Ghosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1479 CrossRef CAS.
- M. Pollak, Philos. Mag., 1971, 23, 519 CrossRef CAS.
- M. Megdiche, C. Perrin–Pellegrino and M. Gargouri, J. Alloys Compd., 2014, 584, 209 CrossRef CAS.
- I. Mohamed, J. Phys. Chem. Solids, 2000, 61, 1357 CrossRef.
- A. Kahouli, A. Sylvestre, F. Jomni, B. Yangui and J. Legrand, J. Phys. Chem. A, 2012, 116, 1051 CrossRef CAS.
- N. Bhowmik, Ceram. Int., 2012, 38, 5069 CrossRef.
- Y. Moualhi, R. M'nassri, H. Rahmouni, M. Gassoumi and K. Khirouni, RSC Adv., 2020, 10, 33868 RSC.
- S. M. Wasim, L. Essaleh, G. Marín, C. Rincón, S. Amhil and J. Galibert, Superlattices Microstruct., 2017, 107, 285 CrossRef CAS.
- S. Abdalla, M. Dongol and M. M. Ibrahim, J. Non-Cryst. Solids, 1989, 113(2–3), 221 CrossRef CAS.
- H. Rahmouni, B. Cherif, K. Khirouni, M. Baazaoui and S. Zemni, J. Phys. Chem. Solids, 2016, 88, 40 CrossRef.
- P. Ma, Q. Geng, X. Gao, S. Yang and G. Liu, RSC Adv., 2016, 6, 32947 RSC.
- W. Hzez, A. Benali, H. Rahmouni, E. Dhahri, K. Khirouni and B. F. O. Costa, J. Phys. Chem. Solids, 2018, 117, 112 CrossRef.
- M. Afandiyeva, İ. Dökme, Ş. Altındal and A. Tataroğlu, Microelectron. Eng., 2008, 85, 247 CrossRef.
- D. Değerve and H. K. Ulutaş, Vacuum, 2004, 72, 307 CrossRef.
- Z. Haijun, L. Zhichao, M. Chenliang, Y. Xi, Z. Liangying and W. Mingzhong, Mater. Chem. Phys., 2003, 80, 129 CrossRef.
- A. Stergiou, I. Manolakis, T. V. Yioultsis and G. Litsardakis, J. Magn. Magn. Mater., 2010, 322, 1532 CrossRef.
- K. W. Wagner, Ann. Phys., 1913, 40, 817 CrossRef.
- J. C. Maxwell, Electricity and Magnetism, Oxford University Press, London, 1973 Search PubMed.
- F. M. M. Pereira, M. R. P. Santos, R. S. T. M. Sohn, J. S. Almeida, A. M. L. Medeiros, M. M. Costa and A. S. B. Sombra, J. Mater. Sci.: Mater. Electron., 2009, 20, 417 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra09465j |
| This journal is © The Royal Society of Chemistry 2021 |