Dispersion forces drive water oxidation in molecular ruthenium catalysts

Abstract

Rational design of artificial water-splitting catalysts is central for developing new sustainable energy technology. However, the catalytic efficiency of the natural light-driven water-splitting enzyme, photosystem II, has been remarkably difficult to achieve artificially. Here we study the molecular mechanism of ruthenium-based molecular catalysts by integrating quantum chemical calculations with inorganic synthesis and functional studies. By employing correlated ab initio calculations, we show that the thermodynamic driving force for the catalysis is obtained by modulation of π-stacking dispersion interactions within the catalytically active dimer core, supporting recently suggested mechanistic principles of Ru-based water-splitting catalysts. The dioxygen bond forms in a semi-concerted radical coupling mechanism, similar to the suggested water-splitting mechanism in photosystem II. By rationally tuning the dispersion effects, we design a new catalyst with a low activation barrier for the water-splitting. The catalytic principles are probed by synthesis, structural, and electrochemical characterization of the new catalyst, supporting enhanced water-splitting activity under the examined conditions. Our combined findings show that modulation of dispersive interactions provides a rational catalyst design principle for controlling challenging chemistries.

---

Introduction

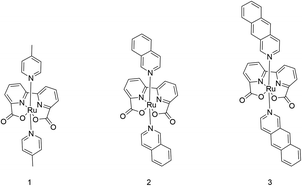
The molecular design of catalysts with the ability to lower the activation barrier of the chemically challenging water oxidation reaction is central in the production of solar fuels and sustainable energy technology.^1–4 The natural photosystem II (PSII) has been considered a holy grail of water oxidation catalysts (WOCs), as it efficiently drives light-driven water splitting at ambient temperatures, without releasing harmful side-products.⁵ Although light-activated catalysts resembling the natural oxo-manganese-calcium (Mn₄O₅Ca) centre of PSII have not been achieved,^6–10 electrochemical and photocatalytic water-splitting rates of recent catalysts^11–20 have tremendously improved upon the initial “blue dimer” WOC by Meyer and co-workers²¹ from the early 1980s.

Sun, Llobet and co-workers²⁰ synthesized a new molecular Ru catalyst with a turnover frequency (TOF) for electrochemical water-splitting of ca. 300 s⁻¹ (Scheme 1, catalyst 2). This represented an important milestone in the development of artificial water-splitting catalysts, by providing the first manmade catalyst with an activity comparable to the light-driven turnover rate of PSII. Although the exact underlying mechanism of the catalysts still remains unclear, both experimental^21–25 and computational studies have been central in understanding their mechanistic principles.^26–33 Here we employ large-scale quantum chemical calculations to elucidate the mechanism of Ru-based WOCs, and by combining inorganic synthesis, structural studies, and electrochemical characterization, we design a new catalyst with improved reaction energetics based on understanding the quantum chemical interactions.

Scheme 1 Structures of catalysts Ru-BdaPic₂ (1), Ru-BdaIsoq₂ (2), and Ru-BdaBenz₂ (3).

Methods

Quantum chemical calculations

The geometries of ruthenium-2,2′-bipyridine-6,6′-dicarboxylic-acid-dibenz[g]isoquinoline, Ru-BdaBenz₂ (3), ruthenium-2,2′-bipyridine-6,6′-dicarboxylic-acid-diisoquinoline, Ru-BdaIsoq₂ (2), and ruthenium-2,2′-bipyridine-6,6′-dicarboxylic-acid-di-4-picoline, Ru-BdaPic₂ (1) were optimized in Ru^IV and Ru^V states, with oxo- and dioxygen ligands, at density functional theory (DFT) level, using the TPSSh-D3(BJ) hybrid functional corrected for dispersion interactions,^34–37 in combination with the def2-TZVPD basis set for the Ru=O unit, and def2-SVP for the other atoms.^38,39 Final electronic energies were computed using the def2-QZVPP basis sets, with added diffuse functions (def2-QZVPPD) on the Ru=O unit. Solvation effects were treated using the conductor-like screening model (COSMO)⁴⁰ with a dielectric constant of 78, mimicking the dielectric response of an aqueous environment. The dimeric models, comprising 108–144 atoms, are shown in Fig. 1. Reaction paths for the O–O bond formation process were studied using a multi-dimensional reaction path optimization approach,⁴¹ related to the zero-temperature string method.⁴² Based on the optimized reaction paths, transition state optimizations for the central models were performed. Particular care was taken to ensure that the located transition states are true transition states and not saddle points on the rather shallow free energy surfaces of these complexes. All transitions states were validated with frequency calculations (see ESI-Table 1†). For comparison, the electronic energies of selected points along the reaction path were computed with the random phase approximation (RPA) using TPSSh orbitals.^43–46 The RPA correlation energy was extrapolated towards the complete basis set (CBS) limit using the two-point formula by Halkier et al.⁴⁷ in connection with the def2-TZVPP(D) and def2-QZVPP(D) basis sets, with diffuse functions on the heavy atoms of the axial ligands and the Ru=O unit, in order to properly account for dispersion effects. Entropic and enthalpic effects were evaluated using the harmonic oscillator approximation, with possible low-frequency modes below 50 cm⁻¹ set to 50 cm⁻¹. The full molecular Hessian was computed using numerical second derivatives. Non-covalent interaction (NCI) analyses were performed with NCIplot version^48,49 and visualized with VMD.⁵⁰ Energy decomposition analyses were performed within the Su–Li scheme.⁵¹ All quantum chemical calculations were performed using TURBOMOLE.^52,53 See the ESI† for further simulation details.

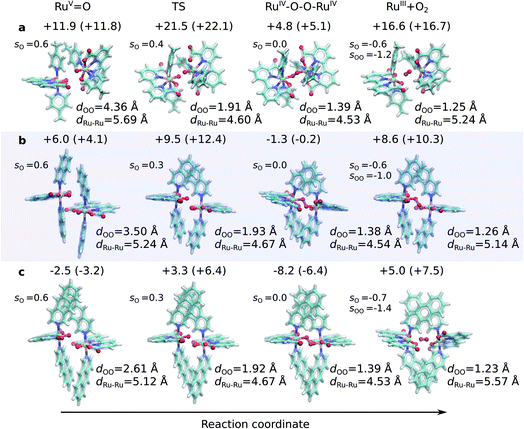Fig. 1 Structures along the optimized open-shell singlet reaction pathway for (a) 1, (b) 2, and (c) 3. See ESI-Fig. 1† for triplet state structures. The modelled catalytic reaction starts after oxidation of Ru^II–H₂O that yields the Ru^V=O species. Energetics are reported at TPSSh-D3(BJ)/def2-QZVPP(d)/ε = 78 level. See also ESI-Fig. 3.†

Synthesis of Ru catalysts

Ru(DMSO)₄Cl₂ (200.0 mg, 0.4 mmol), 2,2′-bipyridine-6,6′-dicarboxylic acid (H₂bda) (100.8 mg, 0.4 mmol) and NEt₃ (0.84 mL, 6 mmol) were mixed in 60 mL of methanol. The solution was sparged with Ar for 15 min and stirred at 70 °C for 2 h. Upon heating the solution became dark red. Benz[g]isoquinoline (740 mg, 4 mmol) was added and the reaction was stirred overnight. The solvent was removed and the crude product was purified by column chromatography on silica using a DCM : MeOH gradient (100 : 1, 25 : 1, 25 : 2). The red brown solid obtained after solvent removal was washed with water and ether. Afterwards, the dark red solid was dissolved in DCM, filtered and the solvent was removed. After recrystallization from MeOH, 50 mg of 3 (0.07 mmol, 17%) were obtained as a dark red solid. Single crystals suitable for X-ray diffraction were obtained by slow diffusion of pentane into a solution of 3 in DCM. See the ESI† for further experimental details.

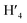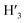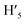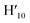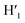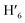R_f value (25 : 1) = 0.13 UV/Vis λ_max (DCM)/nm 493, 402, 381, 351, 331 and 301 (ε/M⁻¹ × 10³ cm⁻¹ 11.1, 9.0, 9.5, 11.5, 8.4, 22.9); ¹H-NMR (400 MHz, CD₂Cl₂): δ [ppm] 8.81 (s, 2H, H₄, ), 8.75 (d, J = 7.95 Hz, 2H, H₃, ), 8.57 (s, 2H, H5, ), 8.45 (s, 2H, H₁₀, ), 8.08 (m, 6H, H₁, , H₆, , H₉, 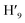), 7.98 (t, J = 7.86 Hz, 2H, H₂, 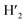), 7.73 (d, J = 6.90 Hz, 2H, H₁₂, 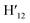), 7.63 (m, 6H, H₇, 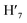, H₈, 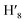, H₁₁, ) LRMS (ESI^†) m/z = 703.12 [M + H]⁺.

Results

Dispersion drives catalysis in molecular ruthenium catalysts

To probe the origin of the higher TOF of Ru-BdaIsoq₂ (2) relative to Ru-BdaPic₂ (1),²⁰ we employed multi-dimensional reaction pathway optimizations, within the quantum chemical density functional theory (DFT) framework. Our modelled reaction pathways start from the monomeric Ru^V=O states, obtained by oxidation of Ru^II–H₂O with an external electron acceptor (not modelled here), and proceed toward the O₂ product states, shown in Fig. 1. In the catalytic process, the mononuclear Ru^V=O centres associate, and form a dimeric core complex along open-shell singlet (S_dimer = 0) and triplet (S_dimer = 1) pathways, with key energetic differences (Fig. 2, see below).

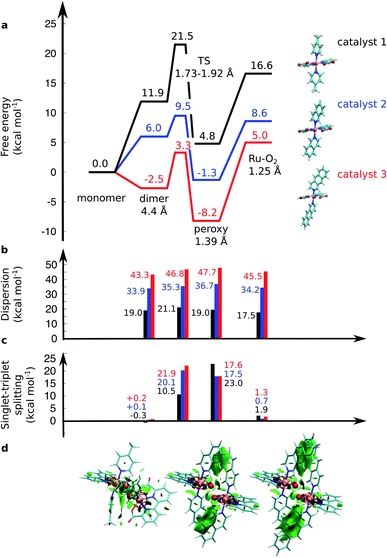Fig. 2 (a) Computed free energy profile (kcal mol⁻¹) along the water-splitting reaction path for catalyst 1 (in black), 2 (in blue), and 3 (in red). The magnitude of (b) the dispersion interaction and (c) the singlet–triplet (S–T) splitting is marked with bars. Positive S–T splitting energies indicate energetically preferred singlet states. (d) Non-covalent interaction plots⁴³ of catalysts 1, 2, and 3 in the TS. Green areas depict dispersion interactions within the molecular systems. Energetics are reported at TPSSh-D3(BJ)/def2-QZVPP(d)/ε = 78 level.

The O–O distance (d_OO) in the initial dimeric complex is ca. 4.4 Å and 3.5 Å, for 1 and 2, respectively (Fig. 1a and b), from which the reaction proceeds towards the transition state (TS), where the O–O bond is formed. Along the open-shell singlet pathway, d_OO at the TS is ca. 1.9 Å, while only ca. 1.7 Å in the triplet TS (ESI-Fig. 1†). The transition states have significant imaginary frequencies in the −200 to −500 cm⁻¹ range (see ESI-Table S1†). Further shortening leads to the elongation of the Ru–O bonds, and a symmetric Ru–O–O–Ru bridge, with an O–O bond length around 1.4 Å, resembling a peroxy compound. The peroxy-intermediate continues over a vanishingly small reaction barrier, where the closed shell singlet turns to open shell, to form a superoxide complex (ESI-Fig. 2†), characterized by an O–O bond of ca. 1.25 Å and one net unpaired electron on the resulting O₂ unit (Fig. 1, ESI-Fig. 3†). In subsequent steps, one of the Ru–O bonds breaks, whereas the other Ru–O bond elongates, leading to a hatching state, with a fully formed O₂ species, loosely bound to its parent complex.

The energetics along the reaction pathway are strikingly different for catalysts 1 and 2 (Fig. 2, ESI-Table 1†), an effect that results mainly from differences in π-stacking dispersion energy within the reaction complexes. The dispersion interaction is 19 kcal mol⁻¹ for catalyst 1, and 34 kcal mol⁻¹ for catalyst 2, that correlates with differences in d_OO distances in the initial core complex. However, despite the strong π-stacking, the complexes are rather loosely bound, with overall complexation free energies of ca. +12 and +6 kcal mol⁻¹ for 1 and 2, respectively (Fig. 2a).

To further validate the dispersion interactions beyond empirical corrections in DFT (DFT-D3),³⁷ we employed the ab initio random phase approximation (RPA), which model these electron correlation effects in a parameter-free form^43–46,54 (ESI-Table S2†). The singlet transition state of catalyst 2 has a free energy barrier of 12.4 kcal mol⁻¹ at the RPA level (9.5 kcal mol⁻¹ at DFT-D3), whereas an experimental barrier of ca. 14.6 kcal mol⁻¹ can be extrapolated based on transition state theory using a standard pre-exponential factor. The small difference between the RPA and experimental estimates could result from basis set or dynamic effects, including explicit solvent interactions, that are neglected in the current QM cluster models. For the less efficient catalyst 1, the RPA energies of +22.5 kcal mol⁻¹ also compare well to DFT-D3 barriers of +21.5 kcal mol⁻¹, and with an extrapolated experimental barrier of ca. 20 kcal mol⁻¹.²⁰ A similar free energy barrier of 19.8 kcal mol⁻¹ for the pyridine analogue of catalyst 1 was recently determined by Xie et al.,⁵⁵ but cf.²⁷

The transition states along the singlet pathways have a ΔG^‡ of +21.5 kcal mol⁻¹ and +9.5 kcal mol⁻¹ for 1 and 2, respectively, and are reached via a further 1–2 kcal mol⁻¹ increase in the π-stacking interaction between the aromatic ring systems. The transition states relax to closed-shell singlet peroxide intermediates, with ΔG increase in non-covalent of +4.8 kcal mol⁻¹ (1) and −1.3 kcal mol⁻¹ (2), from which the O₂ species forms with an overall endergonicity of +16.6 kcal mol⁻¹ (1) and +8.6 kcal mol⁻¹ (2), but achieved via entropic stabilization, driving the release of the O₂ product to the monomeric catalyst form. Considerably higher barriers of 18.5 kcal mol⁻¹ (1) and 9.3 kcal mol⁻¹ (2) are obtained along the triplet state pathways for both catalysts and later TS at a d_OO of 1.74 Å. Interestingly, the triplet pathways lack stable potential energy minima for the peroxide intermediate that is strongly stabilized along the singlet pathway (ESI-Fig. 1†). The near degeneracy of the spin states in the monomeric and Ru–O₂ forms thus suggests that spin crossing may be involved in the final steps of the water-splitting process with an interesting connection to the Mn₄O₅Ca of PSII, which also has near degenerate high and low spin states in key steps of its reaction cycle.^56–60 Moreover, similar to PSII, the O₂ species is likely to form via a radical coupling mechanism,^59,61,62 as indicated by a unit spin density on the oxygenous-ligand along the O–O bond formation process (Fig. 1, ESI-Fig. 3, ESI-Table 1†).

Our findings thus suggest that the energy gained from the dispersion interactions is employed for lowering the activation barrier for the water oxidation process. Switching off dispersion interactions in the employed DFT models prevents the formation of the initial dimer catalyst complexes, as their free energy increases by 20–30 kcal mol⁻¹ relative to the separated monomers (Fig. 2b, ESI-Table 3†). Catalyst 2 is stabilized by ca. 4 kcal mol⁻¹ stronger dispersive interaction per aromatic unit relative to 1, as the extended axial ligands enable 2 to embrace the opposite monomer with both isoq units, whereas the less extended aromatic system of 1 allows only for π-stacking of one of the Pic units in the transition state (Fig. 1a and b).

Design of an improved water-splitting catalyst

Having established the importance of dispersion interactions on the activation energy, we next proceeded to further strengthen the dispersion forces upon formation of the transition state. To further strengthen dispersion forces at the transition state, we computationally designed a putative catalyst by extending the aromatic system of the axial ligands by using the benzo[g]isoq molecules (Ru-BdaBenz₂, catalyst 3 in Scheme 1) with three aromatic rings. The free energy profiles for 3 show that increased intermolecular interactions stabilize the initial dimeric complex by almost 9 kcal mol⁻¹ relative to 2.

In contrast to 1 and 2, the dimeric complex of 3 becomes more stable relative to the free monomers that facilitate the initial complex formation (Fig. 1a). The complexation free energy is <3 kcal mol⁻¹ that allows the complexes to dissociate after product formation. The increased π-stacking interaction also affects the geometric properties by shortening the d_OO for the dimeric pre-complex of 3 to ca. 2.6 Å from 3.5 Å for catalyst 2 Å and 4.4 Å for catalyst 1 (Fig. 1c). The transition state of 3 at 1.9 Å has a free energy barrier of only 3.3 kcal mol⁻¹ in the open-shell singlet state with respect to the free monomers, and the activation free energy is <6 kcal mol⁻¹ as compared to the initial dimeric complex (Fig. 1a). The formation of the O₂ in catalyst 3 takes place via a peroxy-state with a relative free energy of −8.2 kcal mol⁻¹ that is stabilized relative to the catalysts 1 and 2. The hatching Ru–O₂ state has a free energy barrier of 5 kcal mol⁻¹ above the monomeric state, suggesting that 3 has overall improved catalytic properties over 1 and 2. Interestingly, the lowering of the catalytic barriers correlates with increased dispersion interactions between the axial ligands of 3 as compared to 2 (Fig. 1b, ESI-Table 1†), as reflected by gradual increase in non-covalent interactions from 1 to 3 (Fig. 1d). Energy decomposition analysis⁵¹ further supports that in addition to dispersion, electrostatic interactions also stabilize the catalytic dimer (ESI-Table 3†). Although the lowered chemical barrier for 3 is expected to overall favour the catalyst turnover, we note that the stabilized peroxy state could also kinetically trap the catalyst in this transient state by preventing efficient release of the O₂ product in the bulk solvent.

Synthesis and experimental characterization

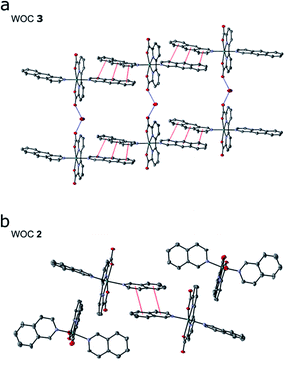
Encouraged by our computational findings, we next synthesized 3, verified its structure by NMR spectroscopy and mass spectrometry, and resolved its molecular structure by X-ray crystallography (see ESI†). We also synthesized and crystallized 2, as the molecular structure of the Ru^II-BdaIsoq₂ was unknown. In our resolved X-ray structures of 2 and 3 (Fig. 3), the Ru centre is six-coordinate and adopts a distorted pentagonal bipyramidal structure, similar to that of 1¹⁹ (ESI-Table 4†). The equatorial Bda ligand enforces a large O1–Ru–O3 angle of ca. 120° (ESI-Table 4†), which allows for binding of a seventh ligand.¹⁹ While the geometry of all three Ru complexes is similar, differences in intermolecular interactions are apparent among the crystal structures. Notably, π-stacking is not observed for 1,¹⁹ whereas two individual Ru complexes of 2 form π-stacks involving one isoq ligand from each complex (Fig. 3b). The structure of 3 exhibits significantly enhanced π-interactions that involve both Benz ligands (Fig. 3a), and it forms unique chain structures that are stabilized via hydrogen-bonding between water molecules and the Bda ligand (Fig. 3a). This hydrogen-bonding network is not observed in the structure of 2, nor is it present in other Ru–Bda complexes.^63,64 The extended aromatic system of the Benz ligand thus leads to significant changes in intermolecular interactions, validating our computational data.

Fig. 3 Crystal structures of (a) WOCs 3 and (b) 2; 50% ellipsoids; hydrogen atoms and solvent molecules, other than water, omitted for clarity. Red dashed lines indicate π-stacking interactions; blue dashed lines represent hydrogen bonding interactions.

As further predicted by the computational data, the augmented π-system affects the solubility of catalyst 3. The catalyst is soluble in organic solvents such as DCM, MeOH, or TFE, but insoluble in pure water, in contrast to 2, which is slightly water soluble. The absorption spectra for 3 in TFE exhibit a series of transitions in the visible region that originate from the Bda and Benz ligands (ESI-Fig. 7 and ESI-Fig. 8†). pH dependent changes also are observed for 3 (ESI-Fig. 8†), consistent with the behavior of 2, for which a dynamic equilibrium between various coordination modes were established.⁶⁵

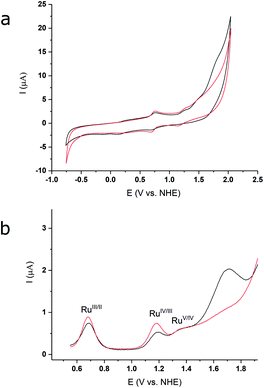
The redox properties and electrocatalytic behaviour of complex 3 were further assessed by electrochemical studies. Cyclic and differential pulse voltammetry (CV and DPV) of 3, in a 2 : 1 TFE/pH 1_aq solution (Fig. 4a), exhibit three oxidative events at 0.69 V, 1.19 V, and 1.37 V (vs. NHE), which are assigned to the Ru^III/II, Ru^IV/III, and Ru^V/IV couples, respectively. The DPV measurement illustrates a significant current increase at ∼1.43 V (Fig. 4b, black lines), indicating that catalysis occurs after formation of the putative Ru^V species. The redox potentials for the oxidative couples of 2 in 2 : 1, TFE/pH 1_aq are identical to those of 3 (Fig. 4a, red lines), but only a modest current increase is observed after the Ru^V/IV couple for 2. Thus, under our experimental conditions based on optimized solubility (see Methods, and ESI†), the designed catalyst 3 shows an enhanced WOC activity relative to 2. The relative activities of the two compounds can be estimated from the relative i_cat/i_p values from the CV data (see ESI†), based on which, 3 shows an approximately three-fold higher activity compared to 2.

Fig. 4 (a) CV of 2 (red) and 3 (black) in 2 : 1, TFE/pH 1_aq media; glassy carbon electrode, 10 mV s⁻¹. (b) DPV measurement for 2 (red) and 3 (black) in 2 : 1, TFE/pH 1_aq media; glassy carbon electrode, pulse height = 50 mV, pulse width = 2.5 s, step height = 4 mV, step time = 5 s, sampling time = 500 ms.

Discussion

Our models suggest that part of the catalytic power in the studied Ru-catalysts arises from maintaining some molecular flexibility that allows for an extended tuning of dispersion interactions during the reaction pathway. Similar effects that rely on formation of multiple weak interactions are commonly employed in enzymes to lower chemical transformation barriers. For example, in the Mn₄O₅Ca centre of PSII, the water-splitting site is dynamically flexible, and it samples both open/closed conformational and high/low-spin states^56–62 before funnelling into the structurally and electronically more uniform S₃ state,⁶⁶ which initiates the O–O bond formation process. Recent studies support that reorganizing the water structure within the catalytic core contributes to the unique catalytic properties.^59,67–70 Although PSII is structurally very different from the studied molecular WOCs, both systems might employ a radical coupling mechanism in the O–O bond formation process,^5,59,61 although acid–base coupling mechanisms have also been suggested cf. ref. 5 and references therein.

The dynamic flexibility allowing for the small structural perturbations required to switch between different charge and spin states suggest that the studied Ru-catalysts have a low reorganization energy and over-potential. In natural photosynthesis, these effects could minimize loss of free energy transduced from the light-capturing process, a future target also for the artificial WOC.

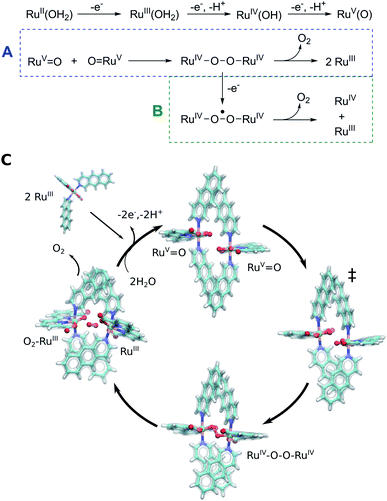
The Ru-catalysts studied here are suggested to bind a water ligand in their reduced Ru^II or Ru^III form, followed by stepwise oxidation and deprotonation to the highly oxidizing Ru^V=O state that triggers O₂ formation (Fig. 5A–C). Our combined data suggest that the Ru^V=O species associate by forming a dimeric core complex that is stabilized by dispersion forces, an effect that is thermodynamically gradually favoured from catalyst 1 to 3. The O₂ formation chemistry involves rotation of the aromatic ring systems with respect to each other, that in turn enhances the dispersive interactions (Fig. 1, ESI-Fig. 1,† 5C). A gradual improvement in the TS stabilization can also here be observed for our new catalyst 3. The O–O bond formation takes place according to our reaction pathway optimizations via a Ru^IV–O–O–Ru^IV peroxy intermediate (d_OO = 1.39 Å) that follows a transition state at d_OO = 1.91 Å (Fig. 5C). Also here, catalyst 3 showed improved energetics relative to 1 and 2. We note, however, that in addition to the peroxy intermediate, competing side pathways might dominate under different experimental conditions.⁷¹ For example, oxidation of the Ru^IV–O–O–Ru^IV intermediate under highly oxidizing conditions could trigger O₂ release via a Ru^IV–O–O˙–Ru^IV intermediate (Fig. 5, pathway B).²⁰ The peroxy state is followed by a hatching Ru–O₂ state that dissociates to the monomeric catalyst form. The balance between solvation effects, which could be enhanced by polar substitution in the aromatic ring system, and dispersive stacking interaction, which modulate the energetics of intermediate steps, could further provide rational ways to fine tune the catalytic properties of the molecular Ru catalysts.

Fig. 5 Putative reaction mechanism of catalyst 3. Oxidation of Ru^II–H₂O yields the Ru^V=O species from which the catalysis starts. Catalyst 3 forms a dimeric core complex, and via radical coupling and peroxo Ru^IV–O–O–Ru^IV intermediate yields O₂ (pathway A). Under highly oxidizing conditions, the Ru^IV–O–O–Ru^IV intermediate could be further oxidized to yield O₂ and a mixed valence Ru^IV/Ru^III product state (pathway B). (C) Structure of computed intermediates within putative reaction cycle of catalyst 3.

Conclusions

In summary, using mechanistic insight gained from quantum chemical calculations, we designed here a new molecular Ru catalyst (3) with enhanced π-stacking dispersion interactions that lower the catalytic water oxidation barrier. Experimentally, we observed a three-fold higher activity for the water oxidation reaction, relative to the previously known WOC (2) under the conditions examined. The resolved crystal structures confirm that the catalytic core forms stronger dispersive interactions relative to previous WOCs 1 and 2, thus further validating our computational design principles. Despite structural differences, the catalytic reaction shows an interesting resemblance in terms of radical coupling and spin energetics with PSII.^5,67,69 Our integrated computational and experimental approach provides a powerful approach to rational design of new light-driven, biomimetic water-splitting catalysts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was supported by the Jane and Aatos Erkko Foundation (V. R. I. K.), by the Academy of Finland (grants 289179 and 319453, M. P. J.), and Waldemar von Frenckells stiftelse (M. P. J.). CSC – The Finnish IT Center for Science, the Finnish Grid and Cloud Infrastructure (urn:nbn:fi:research-infras-2016072533), provided computational resources.

References

1. S. Berardi, S. Drouet, L. Francàs, C. Gimbert-Suriñach, M. Guttentag, C. Richmond, T. Stoll and A. Llobet, Chem. Soc. Rev., 2014, 43, 7501–7519.
2. R. Matheu, M. Z. Ertem, C. Gimbert-Suriñach, X. Sala and A. Llobet, Chem. Rev., 2019, 119, 3453–3471.
3. D. G. Nocera, Acc. Chem. Res., 2017, 50, 616–619.
4. R. Matheu, P. Garrido-Barros, M. Gil-Sepulcre, M. Z. Ertem, X. Sala, C. Gimbert-Suriñach and A. Llobet, Nat. Rev. Chem., 2019, 3, 331–341.
5. N. Cox, D. A. Pantazis, F. Neese and W. Lubitz, Acc. Chem. Res., 2013, 46, 1588–1596.
6. J. S. Kanady, E. Y. Tsui, M. W. Day and T. Agapie, Science, 2011, 333, 733–736.
7. J. S. Kanady, P.-H. Lin, K. M. Carsch, R. J. Nielsen, M. K. Takase, W. A. Goddard and T. Agapie, J. Am. Chem. Soc., 2014, 136, 14373–14376.
8. C. Zhang, C. Chen, H. Dong, J.-R. Shen, H. Dau and J. Zhao, Science, 2015, 348, 690–693.
9. S. Paul, N. Cox and D. A. Pantazis, Inorg. Chem., 2017, 56, 3875–3888.
10. H. B. Lee, D. A. Marchiori, R. Chatterjee, P. H. Oyala, J. Yano, R. D. Britt and T. Agapie, J. Am. Chem. Soc., 2020, 142, 3753–3761.
11. J. M. Thomsen, D. L. Huang, R. H. Crabtree and G. W. Brudvig, Dalton Trans., 2015, 44, 12452–12472.
12. T. Liu, B. Zhang and L. Sun, Chem.–Asian J., 2019, 14, 31–43.
13. L. D. Wickramasinghe, R. Zhou, R. Zong, P. Vo, K. J. Gagnon and R. P. Thummel, J. Am. Chem. Soc., 2015, 137, 13260–13263.
14. M. M. Najafpour, G. Renger, M. Hołyńska, A. N. Moghaddam, E.-M. Aro, R. Carpentier, H. Nishihara, J. J. Eaton-Rye, J.-R. Shen and S. I. Allakhverdiev, Chem. Rev., 2016, 116, 2886–2936.
15. S. Paul, F. Neese and D. A. Pantazis, Green Chem., 2017, 19, 2309–2325.
16. J. M. Thomsen, D. L. Huang, R. H. Crabtree and G. W. Brudvig, Dalton Trans., 2015, 44, 12452–12472.
17. L. D. Wickramasinghe, R. Zhou, R. Zong, P. Vo, K. J. Gagnon and R. P. Thummel, J. Am. Chem. Soc., 2015, 137, 13260–13263.
18. M. M. Najafpour, G. Renger, M. Hołyńska, A. N. Moghaddam, E.-M. Aro, R. Carpentier, H. Nishihara, J. J. Eaton-Rye, J.-R. Shen and S. I. Allakhverdiev, Chem. Rev., 2016, 116, 2886–2936.
19. L. Duan, A. Fischer, Y. Xu and L. Sun, J. Am. Chem. Soc., 2009, 131, 10397–10399.
20. L. Duan, F. Bozoglian, S. Mandal, B. Stewart, T. Privalov, A. Llobet and L. Sun, Nat. Chem., 2012, 4, 418–423.
21. S. W. Gersten, G. J. Samuels and T. J. Meyer, J. Am. Chem. Soc., 1982, 104, 4029–4030.
22. D. Lebedev, Y. Pineda-Galvan, Y. Tokimaru, A. Fedorov, N. Kaeffer, C. Copéret and Y. Pushkar, J. Am. Chem. Soc., 2018, 140, 451–458.
23. J. J. Concepcion, D. K. Zhong, D. J. Szalda, J. T. Muckerman and E. Fujita, Chem. Commun., 2015, 51, 4105–4108.
24. Y. Tsubonouchi, S. Lin, A. R. Parent, G. W. Brudvig and K. Sakai, Chem. Commun., 2016, 52, 8018–8021.
25. Q. Q. Yang, X. Jiang, B. Yang, Y. Wang, C. H. Tung and L. Z. Wu, iScience, 2020, 23, 100969.
26. Q. Daniel, P. Huang, T. Fan, Y. Wang, L. Duan, L. Wang, F. Li, Z. Rinkevicius, F. Mamedov, M. S. G. Ahlquist, S. Styring and L. Sun, Coord. Chem. Rev., 2017, 346, 206–215.
27. J. Nyhlen, L. Duan, B. Akermark, L. Sun and T. Privalov, Angew. Chem., Int. Ed., 2010, 49, 1773–1777.
28. L. Tong, L. Duan, Y. Xu, T. Privalov and L. Sun, Angew. Chem., Int. Ed., 2011, 50, 445–449.
29. L. Wang, L. Duan, B. Stewart, M. Pu, J. Liu, T. Privalov and L. Sun, J. Am. Chem. Soc., 2012, 134, 18868–18880.
30. L. Duan, C. M. Araujo, M. S. G. Ahlquist and L. Sun, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15584–15588.
31. T. Fan, S. Zhan and M. S. G. Ahlquist, ACS Catal., 2016, 6, 8308–8312.
32. S. Zhan, D. Martensson, M. Purg, S. C. L. Kamerlin and M. S. G. Ahlquist, Angew. Chem., Int. Ed., 2017, 56, 6962–6965.
33. S. Zhan and M. S. G. Ahlquist, J. Am. Chem. Soc., 2018, 140, 7498–7503.
34. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
35. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
36. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
37. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
38. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
39. D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105.
40. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 5, 799–805.
41. P. Plessow, J. Chem. Theory Comput., 2013, 9, 1305–1310.
42. E. Weinan, W. Ren and E. Vanden-Eijnden, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 052301.
43. F. Furche, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195120.
44. H. Eshuis, J. E. Bates and F. Furche, Theor. Chem. Acc., 2012, 131, 1084.
45. G. P. Chen, V. K. Voora, M. M. Agee, S. G. Balasubramani and F. Furche, Annu. Rev. Phys. Chem., 2017, 68, 421–445.
46. H. Eshuis and F. Furche, J. Phys. Chem. Lett., 2011, 2, 983–989.
47. A. Halkier, R. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
48. E. R. Johnson, S. Keinan and P. Mori-Sánchez, J. Am. Chem. Soc., 2010, 132, 6498–6506.
49. J. Contreras-García, E. R. Johnson, E. S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and D. W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
50. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
51. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
52. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
53. Turbomole V7.1-7.3, 2016-2018, A Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from, http://www.turbomole.com.
54. G. P. Chen, C. K. Voora, M. M. Agee, S. G. Balasubramani and F. Furche, Annu. Rev. Phys. Chem., 2017, 68, 421–445.
55. Y. Xie, D. W. Shaffer and J. J. Concepcion, Inorg. Chem., 2018, 57, 10533–10542.
56. D. A. Pantazis, W. Ames, N. Cox, W. Lubitz and F. Neese, Angew. Chem., Int. Ed., 2012, 51, 9935–9940.
57. D. Bovi, D. Narzi and L. Guidoni, Angew. Chem., Int. Ed., 2013, 52, 11744–11749.
58. H. Isobe, M. Shoji, S. Yamanaka, H. Mino, Y. Umena, K. Kawakami, N. Kamiya, J.-R. Shen and K. Yamaguchi, Phys. Chem. Chem. Phys., 2014, 16, 11911–11923.
59. I. Ugur, A. W. Rutherford and V. R. I. Kaila, Biochim. Biophys. Acta, Bioenerg., 2016, 1857, 740–748.
60. A. Boussac, I. Ugur, A. Marion, M. Sugiura, V. R. I. Kaila and A. W. Rutherford, Biochim. Biophys. Acta, Bioenerg., 2018, 1859, 342–356.
61. P. E. M. Siegbahn, Chem.–Eur. J., 2006, 12, 9217–9227.
62. V. Krewald, F. Neese and D. A. Pantazis, J. Inorg. Biochem., 2019, 199, 110797.
63. D. W. Shaffer, Y. Xie, D. J. Szalda and J. J. Concepcion, Inorg. Chem., 2016, 55, 12024–12035.
64. C. J. Richmond, R. Matheu, A. Poater, L. Falivene, J. Benet-Buchholz, X. Sala, L. Cavallo and A. Llobet, Chem.–Eur. J., 2014, 20, 17282–17286.
65. R. Matheu, M. Z. Ertem, C. Gimbert-Suriñach, X. Sala and A. Llobet, Chem. Rev., 2019, 119, 3453–3471.
66. N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808.
67. M. Suga, F. Akita, M. Sugahara, M. Kubo, Y. Nakajima, T. Nakane, K. Yamashita, Y. Umena, M. Nakabayashi and T. Yamane, et al., Nature, 2017, 543, 131–135.
68. C. J. Kim and R. J. Debus, Biochemistry, 2017, 56, 2558–2570.
69. J. Kern, R. Chatterjee, I. D. Young, F. D. Fuller, L. Lassalle, M. Ibrahim, S. Gul, T. Fransson, A. S. Brewster and R. Alonso-Mori, et al., Nature, 2018, 563, 421–425.
70. M. Ibrahim, et al., Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12624–12635.
71. D. W. Shaffer, Y. Xie and J. Concepcion, Chem. Soc. Rev., 2017, 46, 6170–6193.

---

Footnotes

† Electronic supplementary information (ESI) available: Simulation and experimental details. CCDC 1950904 and 1950905. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra09004b

‡ Contributed equally to this work.

---