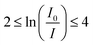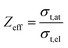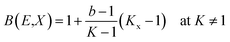Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gamma radiation shielding characteristics of various spinel ferrite nanocrystals: a combined experimental and theoretical investigation
Rajkumar M. Lokhande*a,
Vithal Vinayakb,
Sachin V. Mukhamalec and
Pankaj P. Khirade *d
*d
aDepartment of Physics, Shirish Madhukarrao Chaudhari College, Jalgaon, MS 425001, India. E-mail: rajml@gmail.com
bDepartment of Chemistry, Shri Chhatrapati Shivaji College, Omerga, Osmanabad, MS 413606, India
cDepartment of Physics, Shri Pundlik Maharaj Mahavidyalaya, Nandura Rly, MS 443404, India
dDepartment of Physics, Shri Shivaji Science College, Amravati, MS 444603, India. E-mail: pankajkhirade@gmail.com
First published on 19th February 2021
Abstract
This work presents the facile synthesis of Ni, Mn, Zn, Cu and Co spinel ferrite nanocrystals via sol–gel auto-ignition and the investigation of their structural and gamma ray shielding characteristics. Experimentally, gamma ray shielding parameters are determined with different gamma ray sources and NaI(Tl) scintillation detector and theoretically via Monte-Carlo simulation (Geant4) as well as NIST-XCOM database. X-ray diffractograms elucidate the cubic spinel structure without any contaminating phases for all synthesized nano-ferrites. TEM results evidence the formation of ultrafine crystallites in nano-regime dimensions. Nanocrystalline spinel ferrites in pellet form have been exposed to gamma radiation from diverse sources by changing the radiation dose intensity. The comparative study of the linear attenuation coefficient, mass attenuation coefficient, total atomic cross section, total electronic cross section, effective atomic number, effective electron density and half value layer for manufactured spinel ferrites is carried out using NIST-XCOM and Geant4 at 122–1330 keV. Gamma ray energy absorption buildup factor (EABF) is investigated for five selected ferrites at 100 keV to 1500 keV incident photon energy and penetration depth from 1 to 40 mfp using geometric progression (G-P) fitting technique. EABF is found to be maximum at an intermediate region, mainly attributed to the Compton scattering process. Zinc ferrite exhibits a higher value of EABF among other ferrites, which mainly depends on the chemical composition of the material and crystallite size effect. The EABF is investigated as a function of penetration depth and is found to be maximum for a penetration depth of 40 mfp. Experimental and theoretical simulation results are found to be in good agreement. The Monte-Carlo simulation of radiation interaction with materials has evidenced to be an excellent approximation tool in exploring spinel ferrite performance in radiation atmosphere.
1. Introduction
Nanotechnology is one of the fastest growing scientific fields with applications in many diverse areas, including electronics. The term nanoelectronics refers to the use of nanotechnology in electronic components with critical dimensions and size ranging between 1 nm and 100 nm.1 All electronics devices manufactured by humans are continuously exposed to diverse types of radiation from natural sources as well as man-made sources. The miniaturization of electronic devices and growing integration of electronic components may have an undesirable impact on the component sensitivity towards ionizing radiations.2Currently, spinel ferrites of nano-dimensions are technologically trending materials due to their distinct electromagnetic characteristics.3–5 Spinel ferrites (M–Fe2O4) have several applications such as in transformers, inductors, capacitors, isolators, circulators, gyrators, phase shifters, reconfigurable antennas, spintronics memory devices, wireless mobile communication, and biomedical instrumentation.6–10
Gamma rays are a kind of electromagnetic radiation, and are the packets of energy called photons (hv) emitted by the nucleus of some radionuclides resulting in radioactive decay. Gamma rays are most energetic photons in the electromagnetic spectrum having energies beyond 100 keV.11 Gamma radiation interacts with matter through ionization through three phenomena: photoelectric effect, Compton scattering and pair production. The enormously high energy of gamma rays permits them to enter just about everything.12 They can even pass-through skin, teeth, and bones and destroy living cells, produce gene mutations which cause cancer. This makes gamma rays extremely hazardous.13 Gamma radiation is powerful and can affect most electrical components. Simple equipment including motors, switches, incandescent lights, wiring, and solenoid are fairly radiation resistant and might never show any radiation impacts, even after exposure to large radiation. However, diodes and computer chips are much more sensitive to gamma radiation. Diodes and computer chips will show very slight functional damage up to about 50 to 100 Sv.14,15
The effect of gamma radiation on electronic memory devices has been investigated by I. Fetahović et al.16 The impact of direct ionizing radiation on semiconductor memory performance has been scrutinized by using Monte-Carlo simulation technique. The internal crystalline structure of the materials of electronic components is disrupted on interaction with gamma radiation. The functioning of electronic components breaks down and then fails when they are exposed to significant gamma radiation.
Ionizing radiation creates hole–electron couples in the electronic components, changes the transistor parameters and eventually destroys them. It can also cause leakage currents among circuits. As radiation particles voyage through a material they transfer part of their energies to the electrons and the nucleus of the material and rupture the chemical bonds, producing ionization and atomic displacement.17 For example, proton damage to a transistor consists of ionization and results in damage.18
In order to protect the electronic devices from gamma radiation several approaches are being established. Likewise, some electronics can be toughened so that they are not influenced as much by larger gamma radiation doses by providing shielding or by coating with radiation-resistant materials.19 Most nuclear reactors and electronic sectors can only maintain their functionality in radioactive environments with tungsten or lead shielding.20 It is heavy and bulky, and its design, installation and replacement are complex and expensive processes. The mass attenuation coefficient, total atomic cross section, total electronic cross section, energy absorption buildup factor (EABF) and exposer buildup factor (EBF) are the basic parameters for measuring the interaction of radiation with matter, which can be applied for the shielding purposes.21
In the literature, the comparison of the experimental results on nanomaterials, soils, glass materials, composite materials, different detector materials, rocks and concrete, polymer, and biomaterials with the NIST-XCOM (photon cross sections database) and Monte-Carlo simulations is available.22,23
R. H. Kadam et al. have determined the mass attenuation coefficient of magnesium ferrite produced via ceramic method.24 The Hubbel's mixture rule is utilized to find the mass absorption coefficient and related parameters for the prepared MgFe2O4.25 S. D. Raut et al. have investigated the gamma ray energy absorption and exposure buildup aspects of Co/Zn/Ni/Mg spinel ferrites utilizing G-P fitting method in the energy range of 0.015–15.00 MeV up to the penetration depth of 40 mfp.26
However, there are no noteworthy literature available on the shielding characteristics of spinel ferrite electronic materials. Monte-Carlo simulation is found to be the most effective tool to determine the radiation interaction parameters in diverse kinds of materials, compounds and composites for shielding properties. Demonstrating the photon attenuation properties of materials via computer software offers superior accuracy and flexibility of use than the experimental procedure. There are many Monte-Carlo simulation codes available for the study of radiation transport, particle physics, medical physics, cosmo-physics, radiotherapy, and radiation biology, namely, MCNP, GEANT4 and FLUKA.27–29 Geant4 is a Monte-Carlo simulation code based on C++, an object-oriented programming method, and is freely available. Geant4 code is applicable for measurement of approximation of photon mass attenuation coefficients for different types of most common scintillation crystal detectors at different energies.30
The aim of this research work is to fabricate single-phase nanocrystalline spinel ferrite materials via the ecofriendly sol–gel technique and to inspect the performance of these materials when exposed to gamma radiation in order to establish their functionality in a radiation atmosphere. The experimental procedure has been used to test the radiation attenuation parameters of spinel ferrites. Diverse kinds of spinel ferrites viz. nickel ferrite (NiFe2O4), manganese ferrite (MnFe2O4), zinc ferrite (ZnFe2O4), copper ferrite (CuFe2O4) and cobalt ferrite (CoFe2O4) have been exposed to ionizing gamma radiation by varying the radiation dose intensity. The impact of direct ionizing radiation on spinel ferrite materials' shielding characteristics has been explored by using Monte-Carlo simulation (Geant4) and NIST-XCOM database. Also, a theoretical study has been undertaken to get information on the energy absorption buildup factor of five ferrite materials using G-P fitting method at incident photon energy of 100 keV to 1500 keV up to penetration depths of 40 mfp. The obtained radiological data can be very much useful for elucidating the gamma ray shielding characteristics of spinel ferrite electronic materials.
2. Experimental and calculation method
2.1 Synthesis of nanocrystalline spinel ferrite
2.2 Synthesis and characterizations
Nanocrystalline spinel ferrite materials viz. nickel ferrite (NiFe2O4), manganese ferrite (MnFe2O4), zinc ferrite (ZnFe2O4), copper ferrite (CuFe2O4) and cobalt ferrite (CoFe2O4), were efficiently produced via the sol–gel auto-ignition technique and L-ascorbic acid as a combustion agent. The AR grade nitrates of Ni, Mn, Zn, Cu, Co and L-ascorbic acid were liquified in distilled water distinctly to accomplish a homogenous solution. The precursor metal nitrates were dissolved together with the least amount of distilled water essential to achieve a clear solution. The reaction procedure was done in an air atmosphere deprived of the shield of inert gases. The metal nitrates to combustion agent (L-ascorbic acid) ratio was preserved as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Liquified ammonia was added dropwise to maintain the pH at the neutral value 7. The auto-ignition reaction was carried out for few hours with continuous thermal treatment at 100 °C to produce the required product. The as-prepared powders were sintered at 750 °C for 6 h and utilized for further examinations. The sintered powder samples were assorted with polyvinyl alcohol (PVA) mediator as a binder and hard-pressed into compact cylindrical pellets with dimensions of 10 mm diameter and less than 3 mm thickness by the isostatic pressing method under a pressure of 550 kg cm−2. The pellets were heat-treated in a furnace at 430 °C for 2 h for the exclusion of PVA and then used for radiation exposure.
3. Liquified ammonia was added dropwise to maintain the pH at the neutral value 7. The auto-ignition reaction was carried out for few hours with continuous thermal treatment at 100 °C to produce the required product. The as-prepared powders were sintered at 750 °C for 6 h and utilized for further examinations. The sintered powder samples were assorted with polyvinyl alcohol (PVA) mediator as a binder and hard-pressed into compact cylindrical pellets with dimensions of 10 mm diameter and less than 3 mm thickness by the isostatic pressing method under a pressure of 550 kg cm−2. The pellets were heat-treated in a furnace at 430 °C for 2 h for the exclusion of PVA and then used for radiation exposure.
Xray diffraction (XRD) analysis was conducted on a PANalytical X'pert pro-diffractometer. The wavelength of the X-ray was 1.542 Å (Cu-Kα radiation, 40 kV and 100 mA), in the 2θ scale of 20°–80° and at the scanning rate of 0.02°. The bright-field surface topography of the samples and particle size distribution were obtained by transmission electron microscopy (TEM, CM-200 FEG PHILIPS).
2.3 Experimental procedures
The synthesized nanocrystalline spinel ferrites in pellet form were irradiated with gamma rays generated by the radioactive sources, 57Co, 133Ba, 22Na, 137Cs, 54Mn and 60Co, via the narrow beam geometry setup NaI (Tl) scintillation detector. All these radioactive sources acquired from Bhabha Atomic Research Centre (BARC), Mumbai, India producing different energies viz. 57Co (122 keV), 133Ba (356 keV), 22Na (511 and 1275 keV), 137Cs (662 keV), 54Mn (835 keV) and 60Co (1173 and 1332 keV) were collimated. The angle between a radioactive source and the pellet materials was kept as 90° for narrow beam analysis. The NaI scintillation detector with narrow beam geometry was utilized as the gamma ray spectroscopic system. The analysis of the amplified signals by selecting a spectrometry system included a (2′′ × 2′′) NaI (Tl) crystal with an energy resolution of 8.2% at 662 keV from the gamma decay of 137Cs. The peak measurement energy versus count depends on full width at half maxima (FWHM) and the 8 K multichannel analyzer. The diameters of the pellets played an important role in the narrow beam system (source–sample–detector) and were determined using a traveling microscope for more accuracy. The samples were put in a lead-shielded narrow beam geometry set up (source–sample–detector). The sample thickness was selected in order to satisfy the following ideal condition.31There are two steps in determining the attenuation coefficient by experiment; first to calculate with the source and without the sample and then with the source and with the sample. The present experiments were carried out in an air-conditioned room to avoid possible shifts of the photo-peaks. The room temperature was maintained at 20 ± 1 °C throughout the experiment.
I = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−μmt) exp(−μmt)
| (1) |
| μm = ∑iwi(μm)i | (2) |
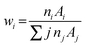 | (3) |
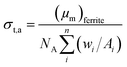 | (4) |
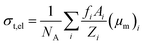 | (5) |
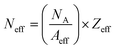 | (7) |
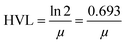 | (8) |
Here, μ is the linear attenuation coefficient. The μ measured experimentally from the narrow beam geometry setup of NaI(Tl) detector results from the energy and counts observed on the monitor of the system.
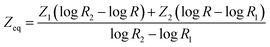 | (9) |
The G-P fitting method is provided by the American National Standards (ANSI/ANS-6.4.3-1991).38 Using the interpolation formula, five G-P fitting parameters (a, b, c, d and Xk) for the selected samples were computed at different incident photon energies (100–1500 keV) using equivalent atomic number (Zeq) up to the penetration depth of 40 mfp. The interpolated values were obtained by using the following equation:39
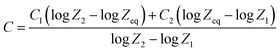 | (10) |
The calculation of the energy absorption buildup factor with the assistance of the G-P fitting formula depends on the shielding thickness as given by following equations:
| B(E,X) = 1 + (b − 1) at K = 1 |
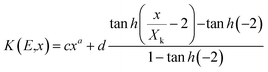 | (11) |
3. Results and discussion
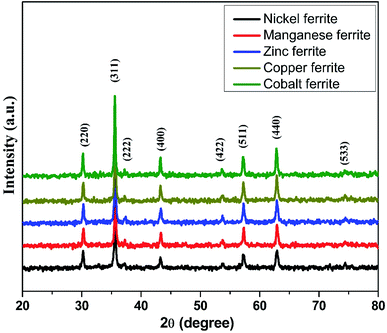
The room-temperature X-ray diffraction (XRD) outlines of spinel ferrites synthesized via the sol–gel auto-ignition technique are presented in Fig. 1. The occurrence of a single intense peak at 2θ ∼ 35° is usually related to the most intense (311) diffraction plane characteristics of cubic symmetry. All the reflections observed could be attributed to a cubic spinel lattice, without evidence of additional impurities, showing their single-phase structure. From the XRD profile, the average crystallite sizes of the samples were calculated by the Debye–Scherrer formula based on the diffraction peak of the highly intense (311) plane.40 The average crystallite size was found to be in the range of 32–52 nm for all the ferrite samples. The lattice parameter (a) obtained by using XRD data was found to lie in the range of 8.3619–8.4742 Å for different spinel ferrites. The structural parameters are shown in Table 1.| Sample | Space group | Average crystallite size (nm) from XRD | Crystallite size (nm) from TEM | Lattice parameter (Å) |
|---|---|---|---|---|
| NiFe2O4 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
36.25 | 34.02 | 8.3619 |
| MnFe2O4 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
33.87 | 35.46 | 8.4742 |
| ZnFe2O4 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
32.31 | 37.62 | 8.4516 |
| CuFe2O4 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
39.75 | 42.54 | 8.3839 |
| CoFe2O4 | Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
52.45 | 56.02 | 8.3891 |
The microstructural characteristics of the ferrite nanocrystals were exposed by employing transmission electron microscopy (TEM) as shown in Fig. 2(a–f). Fig. 2(a), (c) and (e) depicts the bright field TEM pictures of the representative nickel ferrite, zinc ferrite and cobalt ferrite nanocrystalline samples, respectively, while the adjacent plots, Fig. 2(b), (d) and (f), demonstrate the crystallite size distribution obtained using the statistical method (Gaussian fitting) from the TEM pictures. Also, the derived mean crystallite sizes are listed in Table 1. The TEM micrographs depict that the surface is composed of homogeneously distributed single and partially polycrystalline facetted grains of varying sizes in nano dimension scale.
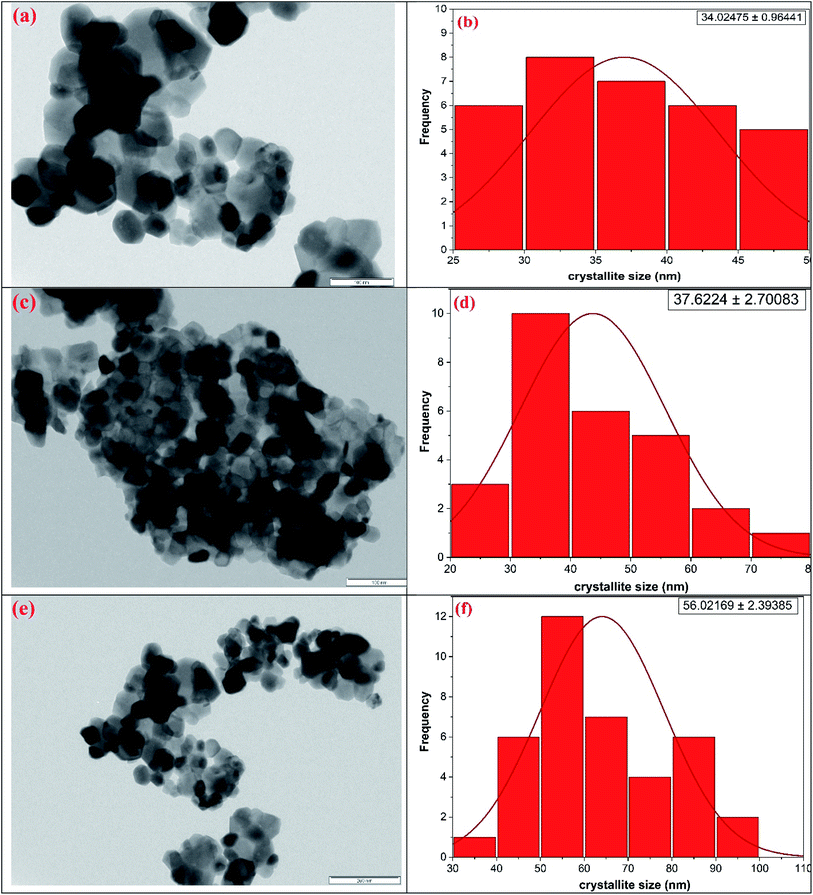 | ||
| Fig. 2 TEM micrographs along with particle size distribution for the representative (a and b) nickel ferrite (c and d) zinc ferrite and (e and f) cobalt ferrite nanocrystals. | ||
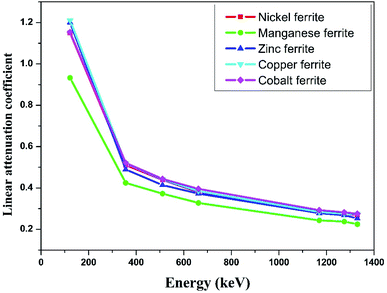
We successfully carried out the narrow beam geometry experimental investigations on the manufactured nano-ferrites in pellet form using different gamma ray sources such as 57Co (122 keV), 133Ba (356 keV), 22Na (511 and 1275 keV), 137Cs (662 keV), 54Mn (835 keV) and 60Co (1173 and 1332 keV) and NaI(Tl) detector. The linear attenuation coefficient (μ) for the synthesized nickel, manganese, zinc, copper and cobalt nano-ferrites was measured at room temperature for the evaluation of the shielding characteristics with respect to incident photon energy in the range of 122 keV to 1330 keV.
The linear attenuation coefficient (μ) with respect to photon energy of all the selected nano-ferrites is graphically represented in Fig. 3. It can be observed that as the photon energy increases the linear attenuation coefficient decreases exponentially for all the synthesized nano-ferrites. Zinc and cobalt nano-ferrites exhibit high values of μ; however, manganese nano-ferrite displays the lowest value. Also, zinc ferrite with more discrepancy rapidly decreases in the energy range of 122 to 356 keV and then linearly declines with energy compared to the other spinel ferrites. The linear attenuation coefficient is an imperative parameter for the measurement of the shielding characteristics of materials.41
The mass attenuation coefficient (μm) was determined using eqn (1). The theoretical mass attenuation coefficient was simulated by the Monte-Carlo simulation (Geant4) method as well as X-Com (NIST) database as shown in Table 2. The experimental, theoretical and simulated values of the mass attenuation coefficient fairly match with each other for all the synthesized nano-ferrites. Fig. 4 depicts the mass attenuation coefficient (μm) versus incident photon energy (keV) plot of the representative zinc ferrite sample determined using experimental and theoretical (viz. Monto-Carlo simulation and XCOM) techniques, which exhibits the analogous nature. The same trend was observed for all the fabricated nano-ferrites. The value of the mass attenuation coefficient primarily depends on the incident photon energy, and it suddenly decreases with energy (E < 400 keV) as photoelectric effect is dominant here; at the moderate energy region the curve remains continual due to Compton scattering phenomenon as reported by Medhat et al.42 It reflects that Monte-Carlo simulation, experimental and theoretical outcomes are in good agreement with each other. The Monte-Carlo simulation results were more effective than the NIST-XCOM data.
| Energy (keV) | Nickel ferrite | Manganese ferrite | Zinc ferrite | Copper ferrite | Cobalt ferrite | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | |
| 122 | 0.2185 | 0.2409 | 0.2142 | 0.2043 | 0.2249 | 0.2023 | 0.2270 | 0.2502 | 0.2308 | 0.2210 | 0.2437 | 0.2241 | 0.2119 | 0.2335 | 0.2086 |
| 356 | 0.0980 | 0.1010 | 0.0951 | 0.0966 | 0.0993 | 0.0921 | 0.0976 | 0.1006 | 0.0942 | 0.0973 | 0.1001 | 0.0961 | 0.0970 | 0.0998 | 0.0943 |
| 511 | 0.0839 | 0.0848 | 0.0818 | 0.0828 | 0.0836 | 0.0809 | 0.0832 | 0.0842 | 0.0796 | 0.0830 | 0.0840 | 0.0818 | 0.0830 | 0.0839 | 0.0802 |
| 662 | 0.0747 | 0.0751 | 0.0708 | 0.0739 | 0.0741 | 0.0711 | 0.0741 | 0.0744 | 0.0717 | 0.0740 | 0.0742 | 0.0712 | 0.0740 | 0.0743 | 0.0715 |
| 1170 | 0.0568 | 0.0567 | 0.0564 | 0.0562 | 0.0560 | 0.0528 | 0.0563 | 0.0561 | 0.0535 | 0.0562 | 0.0561 | 0.0526 | 0.0562 | 0.0561 | 0.0529 |
| 1275 | 0.0544 | 0.0543 | 0.0519 | 0.0538 | 0.0536 | 0.0516 | 0.0538 | 0.0537 | 0.0516 | 0.0538 | 0.0537 | 0.0511 | 0.0538 | 0.0537 | 0.0510 |
| 1330 | 0.0532 | 0.0531 | 0.0499 | 0.0526 | 0.0525 | 0.0488 | 0.0527 | 0.0526 | 0.0486 | 0.0526 | 0.0525 | 0.0507 | 0.0527 | 0.0526 | 0.0498 |
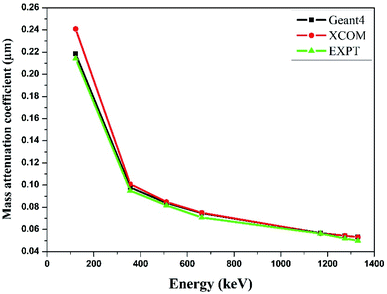 | ||
| Fig. 4 Comparison of experimental and theoretical mass attenuation coefficient against incident photon energy for zinc ferrite. | ||
Nano-magnesium ferrite has greater linear and mass attenuation coefficients compared to that of bulk magnesium ferrite synthesized via the standard ceramic technique reported in the literature.24 This could be accredited to the homogenous distribution of nano-crystallites with high electron density, which results in higher interaction probability between incident photons and nanocrystals compared to that with bulk ferrite.
Likewise, A. M. El-Khatib et al. investigated the gamma attenuation coefficients of micro-sized and nano-sized cadmium oxide (CdO) particles mixed with high-density polyethylene (HDPE) prepared by the compression molding technique.43 They observed superior gamma ray shielding characteristics in nano-dimension cadmium oxide compared with that in micro-dimension cadmium oxide.
The effect of particle size on the gamma radiation shielding property of gadolinium oxide dispersed epoxy resin matrix composite was studied by Ran Li et al.44 They concluded that the produced nano-Gd2O3 reinforced epoxy composite shows both good shielding and mechanical properties as compared to micro-fillers and suggested this material as a promising novel shielding material for radiation protection purpose.
Similarly, we obtained the total atomic cross section (σt,at) and total electronic cross section (σt,el) parameters of the nano-ferrites with the help of eqn (4) and (5), respectively. The experimental and theoretical values of σt,at and σt,el for all the synthesized nano-ferrites are tabulated in Tables 3 and 4, respectively. The graphical representation of the total atomic cross section (σt,at) and total electronic cross section (σt,el) of the representative zinc ferrite sample are revealed in Fig. 5 and Fig. 6, respectively. Fig. 5 and 6 show that the experimental results are in good agreement with the Geant4 and XCOM outcomes. Also, they reflect that both σt,at and σt,el decrease with increasing incident photon energy.
| Energy (keV) | Nickel ferrite | Manganese ferrite | Zinc ferrite | Copper ferrite | Cobalt ferrite | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | |
| 122 | 85.0012 | 93.7153 | 83.3284 | 78.2055 | 86.0911 | 77.4399 | 90.8285 | 100.1114 | 92.3490 | 87.7528 | 96.7663 | 88.9837 | 82.5181 | 90.9295 | 81.2330 |
| 356 | 38.1241 | 39.2912 | 36.9959 | 36.9782 | 37.9926 | 35.2556 | 39.0522 | 40.2526 | 37.6918 | 38.6351 | 39.7469 | 38.1586 | 37.7737 | 38.8524 | 36.7223 |
| 511 | 32.6389 | 33.0046 | 31.8220 | 31.6956 | 32.0172 | 30.9683 | 33.2904 | 33.6906 | 31.8500 | 32.9569 | 33.3461 | 32.4804 | 32.3218 | 32.6684 | 31.2315 |
| 662 | 29.0599 | 29.1961 | 27.5427 | 28.2887 | 28.3576 | 27.2169 | 29.6493 | 29.7693 | 28.6890 | 29.3833 | 29.4786 | 28.2715 | 28.8171 | 28.9144 | 27.8435 |
| 1170 | 22.0964 | 22.0497 | 21.9408 | 21.5132 | 21.4443 | 20.2117 | 22.5271 | 22.4590 | 21.4067 | 22.3154 | 22.2559 | 20.8860 | 21.8854 | 21.8465 | 20.6003 |
| 1275 | 21.1628 | 21.1083 | 20.1902 | 20.5945 | 20.5256 | 19.7523 | 21.5268 | 21.4987 | 20.6465 | 21.3624 | 21.3029 | 20.2904 | 20.9508 | 20.9118 | 19.8604 |
| 1330 | 20.6959 | 20.6609 | 19.4122 | 20.1351 | 20.0892 | 18.6805 | 21.0866 | 21.0426 | 19.4461 | 20.8860 | 20.8502 | 20.1315 | 20.5224 | 20.4679 | 19.3931 |
| Energy (keV) | Nickel ferrite | Manganese ferrite | Zinc ferrite | Copper ferrite | Cobalt ferrite | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | |
| 122 | 5.2665 | 5.8064 | 5.1629 | 4.8038 | 5.2882 | 4.7567 | 4.7804 | 5.2690 | 4.8605 | 5.5365 | 6.1051 | 5.6141 | 4.8540 | 5.3488 | 4.7784 |
| 356 | 2.3621 | 2.4344 | 2.2922 | 2.2714 | 2.3337 | 2.1656 | 2.0554 | 2.1186 | 1.9838 | 2.4375 | 2.5077 | 2.4075 | 2.2220 | 2.2854 | 2.1601 |
| 511 | 2.0222 | 2.0449 | 1.9716 | 1.9469 | 1.9667 | 1.9022 | 1.7521 | 1.7732 | 1.6763 | 2.0793 | 2.1039 | 2.0492 | 1.9013 | 1.9217 | 1.8371 |
| 662 | 1.8005 | 1.8089 | 1.7065 | 1.7376 | 1.7419 | 1.6718 | 1.5605 | 1.5668 | 1.5099 | 1.8538 | 1.8598 | 1.7837 | 1.6951 | 1.7008 | 1.6379 |
| 1170 | 1.3690 | 1.3662 | 1.3594 | 1.3215 | 1.3172 | 1.2415 | 1.1856 | 1.1821 | 1.1267 | 1.4079 | 1.4042 | 1.3177 | 1.2874 | 1.2851 | 1.2118 |
| 1275 | 1.3112 | 1.3078 | 1.2509 | 1.2650 | 1.2608 | 1.2133 | 1.1330 | 1.1315 | 1.0867 | 1.3478 | 1.3440 | 1.2801 | 1.2324 | 1.2301 | 1.1683 |
| 1330 | 1.2823 | 1.2801 | 1.2027 | 1.2368 | 1.2340 | 1.1475 | 1.1098 | 1.1075 | 1.0235 | 1.3177 | 1.3155 | 1.2701 | 1.2072 | 1.2040 | 1.1408 |
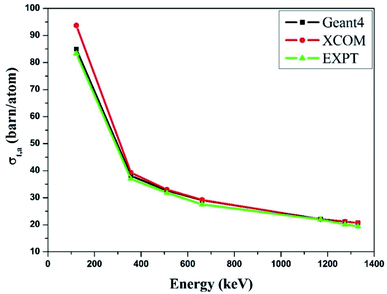 | ||
| Fig. 5 Comparative study of the total atomic cross-section (σt,a) verses incident photon energy for zinc ferrite. | ||
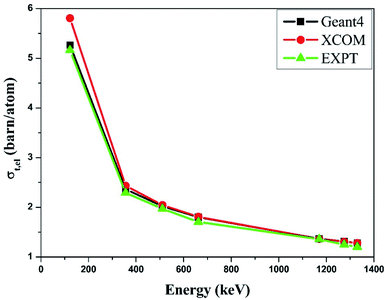 | ||
| Fig. 6 Comparative study of the total electronic cross-section (σt,el) versus incident photon energy of zinc ferrite. | ||
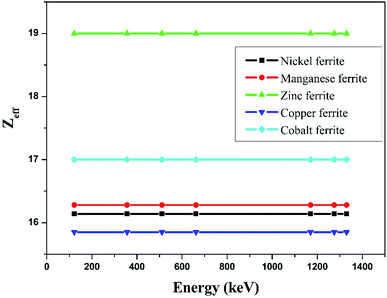
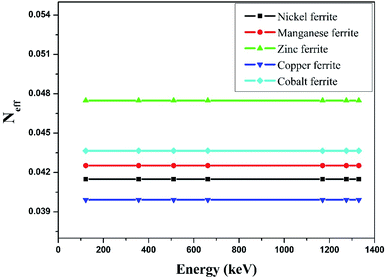
The effective atomic number (Zeff) was estimated by using eqn (6). The value of Zeff is graphically represented in Fig. 7 for all the synthesized nano-ferrites against photon energy. It can be observed in Fig. 7 that the value of Zeff is declining with rise in photon energy (122–1330 keV). The decreasing behavior of Zeff with increasing energy is mainly because the photons live longer due to the photoelectric effect, Compton effect and pair production phenomenon.45 The nano-ferrites absorb more photons at higher energy and absorb minimum at lower energy. It reflects that at higher energy the Compton process is dominant, therefore, Zeff has a lower value due to the recoiling of the photons (∼1330 keV). Zinc ferrite has the highest Zeff value compared with the other synthesized nano-ferrites, and manganese ferrite exhibits the lowest Zeff value. Fig. 8 demonstrates the dependence of effective electron density (Neff) on incident photon energy. Neff shows the same behavior as Zeff in the incident photon energy range of 122–1330 keV.
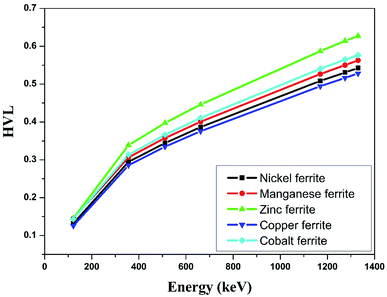
The half value layer (HVL), mean free path (mfp) and tenth value layer (TVL) are also vital parameters in predicting the gamma radiation shielding characteristics of the materials. In the present study, we have estimated the half value layer value utilizing relation (8).
Table 5 shows the half value layer parameter evaluated using Monte-Carlo simulation, XCOM and experimental data for the synthesized nano-ferrites. Fig. 9 shows the plots of HVL against incident photon energy for all the nano-ferrites. As the incident photon energy increases the half value layer value improves significantly. The zinc ferrite sample exhibits superior HVL values as compared to the other fabricated nano-ferrites. The high HVL value of the synthesized nano-ferrites reflects the gamma ray shielding characteristics.
| Energy (keV) | Nickel ferrite | Manganese ferrite | Zinc ferrite | Copper ferrite | Cobalt ferrite | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | Geant4 | NIST | EXPT | |
| 122 | 0.1322 | 0.1314 | 0.1348 | 0.1449 | 0.1441 | 0.1463 | 0.1456 | 0.1450 | 0.1432 | 0.1257 | 0.1250 | 0.1240 | 0.1434 | 0.1426 | 0.1457 |
| 356 | 0.2947 | 0.2938 | 0.3036 | 0.3064 | 0.3060 | 0.3214 | 0.3386 | 0.3382 | 0.3508 | 0.2855 | 0.2853 | 0.2891 | 0.3132 | 0.3128 | 0.3222 |
| 511 | 0.3442 | 0.3458 | 0.3530 | 0.3575 | 0.3592 | 0.3659 | 0.3972 | 0.3992 | 0.4152 | 0.3347 | 0.3363 | 0.3396 | 0.3661 | 0.3678 | 0.3788 |
| 662 | 0.3866 | 0.3886 | 0.4079 | 0.4005 | 0.4036 | 0.4163 | 0.4460 | 0.4493 | 0.4609 | 0.3754 | 0.3784 | 0.3902 | 0.4106 | 0.4136 | 0.4249 |
| 1170 | 0.5084 | 0.5120 | 0.5490 | 0.5267 | 0.5307 | 0.5606 | 0.5870 | 0.5917 | 0.6178 | 0.4943 | 0.4981 | 0.5282 | 0.5406 | 0.5440 | 0.5744 |
| 1275 | 0.5308 | 0.5347 | 0.5564 | 0.5502 | 0.5541 | 0.5736 | 0.6143 | 0.6178 | 0.6405 | 0.5164 | 0.5200 | 0.5437 | 0.5648 | 0.5680 | 0.5958 |
| 1330 | 0.5428 | 0.5459 | 0.5787 | 0.5627 | 0.5660 | 0.6066 | 0.6271 | 0.6310 | 0.6800 | 0.5282 | 0.5311 | 0.5480 | 0.5765 | 0.5802 | 0.6101 |
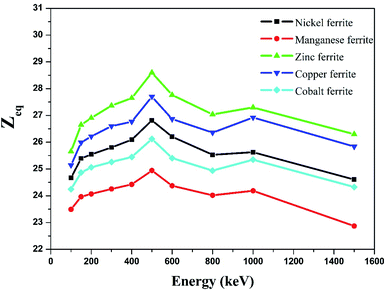
The equivalence atomic number (Zeq) of nano-ferrites at different photon energies was estimated using eqn (9) and is graphically presented in Fig. 10. The Zeq value strongly relies on the incident photon energy. The higher values of Zeq at the middle energy range are attributed to the Compton phenomenon, after that the lower or decreasing values of Zeq are attributed to the photoelectric process. The Zeq is highest for zinc ferrite and lowest for manganese ferrite.
The variation in the energy absorption buildup factor (EABF) at an incident photon energy of 100–1500 keV up to the penetration depth 1 mfp, 10 mfp, 20 mfp, 40 mfp was estimated using the G-P fitting method. The geometric progression parameter a, b, c, d and Xk of spinel ferrites were determined by using ANSI/ANS-6.4.3-1991 data sheet and the interpolation formula developed by Harima.46,47 With the help of Harima's interpolation formulae and ANSI 6.4.3 we also measured the EABF for all the nano-ferrites. Here, b is the buildup factor of nano-ferrites and k is a multiplication factor for dose at different penetration depths (when k ≠ 1). Fig. 11(a–d) shows the variation in the EABF at different penetration depths viz. 1 mfp, 10 mfp, 20 mfp and 40 mfp for all the produced spinel ferrite samples. All the spinel ferrites show unique behavior at different energy ranges. The curves of Fig. 11(a–d) reflect that, initially at the low energy region, the EABF increases with increasing photon energy, which is attributed to the dominance of the photoelectric effect, as the photoelectric process is directly proportional to the square of the atomic number and inversely to the cube of its energy.48
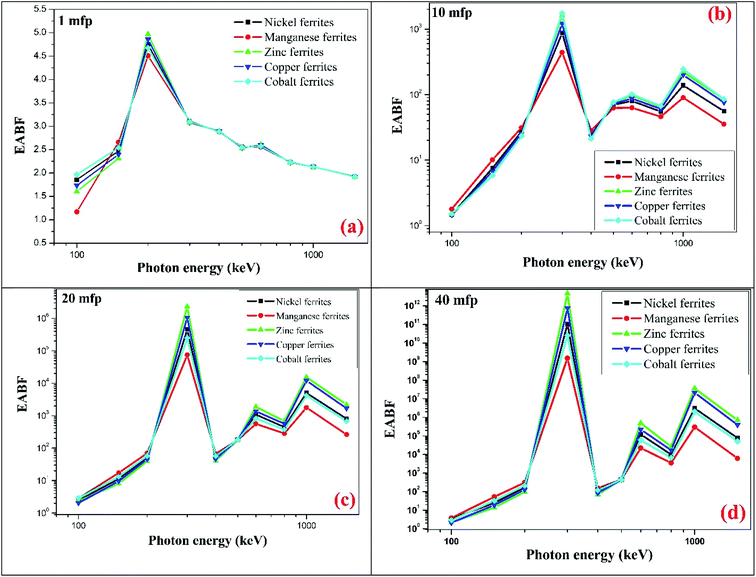 | ||
| Fig. 11 Theoretical EABF values against incident photon energy up to penetration depth (a) 1 mfp (b) 10 mfp (c) 20 mfp and (d) 40 mfp of the synthesized ferrites at photon energy of 100 to 1500 keV. | ||
The EABF enhances significantly in the intermediate region of frequency which can be attributed to Compton process mainly because of multiple scattering of photons. Also, it is observed that the buildup factor value abruptly upsurges in the intermediate region for all penetration depths because of the generation of secondary gamma photons, which demonstrates multiple scattering.49 In the third region, as photon energy increases the EABF factor exhibits a simultaneous decreasing and increasing trend, ∼1000 keV, which can be mainly accredited to the pair production phenomenon.
Fig. 11(a–d) clearly depicts that the energy absorption buildup factor increases with increase in penetration depth from 1 mfp to 40 mfp. Zinc ferrite exhibits the highest EABF value and manganese ferrite has the lowest EABF value at the penetration depth of 1 mfp to 40 mfp with photon energy of 100–1500 keV. In earlier reports, B. Singh et al. have examined the EABF value of low Zeq shielding materials and have observed that the materials with low Zeq exhibit a high EABF value.50 However, our result shows a greater value of the EABF with higher value of Zeq. Zinc nano-ferrite exhibits a higher EABF compared with the other spinel ferrite materials.
The observed values of Zeq and EABF reflect that the EABF is dependent on the chemical composition of the materials. For better elucidation of the energy absorption buildup factor with different penetration depths of 1 mfp, 5 mfp, 10 mfp, 20 mfp, 30 mfp and 40 mfp at various photon energies, the EABF as a function of incident photon energy at 122 keV, 356 keV, 662 keV, and 1530 keV is portrayed in Fig. 12(a–d). All the ferrite materials show the same trend, the EABF increases with increasing photon energy. The energy absorption buildup factor is the lowest at 122 keV energy and highest at 356 keV.
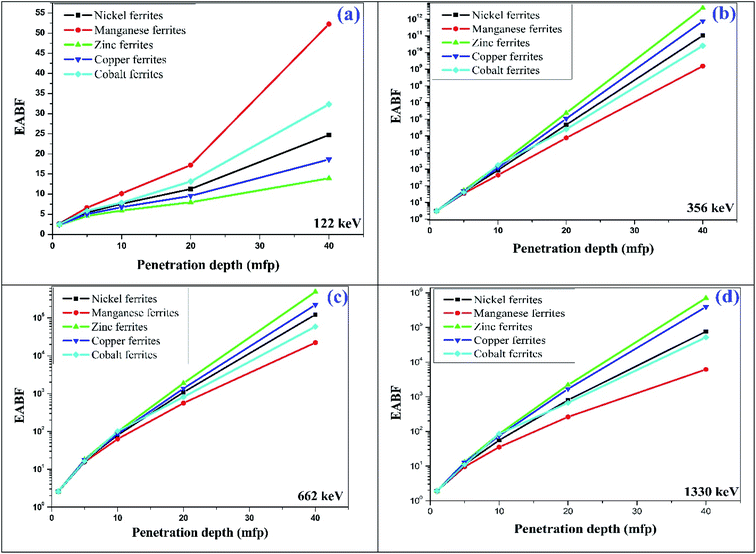 | ||
| Fig. 12 Typical plot of penetration depth against EABF at (a) 122 keV, (b) 356 keV, (c) 662 keV and (d) 1330 keV photon energy for the synthesized spinel ferrites. | ||
Therefore, it can be concluded that nano-spinel ferrite materials are promising highly efficient shielding materials that can be used to reduce radiation dose. The EABF is an important parameter for the measurement of the radiation shielding properties of materials. The obtained EABF values of the present nano-ferrite samples were compared with those of the existing materials utilized for gamma radiation shielding, such as oxide glasses, bismuth borate glasses and marble (for typical 10 MFP). The current samples under investigation show nearly the same order of EABF values at lower photon energy. However, at higher incident photon energy the spinel ferrite nanocrystals show superior values compared with oxide glasses, bismuth borate glasses and marble materials.51–53
Also, zinc ferrite displays higher shieling parameter (such as linear attenuation coefficient, effective atomic number, and EABF) values as compared to the other spinel ferrites. This can be understood on the basis of the crystallite size effect; zinc ferrite possesses a lower crystallite size (∼32.31 nm) compared to nickel ferrite (∼36.25 nm), manganese ferrite (∼33.87) copper ferrite (∼39.75 nm) and cobalt ferrite (∼52.45 nm). The obtained spinel ferrites in nano-dimensions are efficient in attenuating radiation since nanomaterials are more uniform and have less agglomeration in the matrix. Also, it is due to the fact that the cross section of photon interaction with material depends on the surface to volume ratio of nanoparticles. Hence, these materials can enhance the shielding ability of the electronic device.
This study reflects the high values of the energy absorption buildup factor for the fabricated spinel ferrite nanomaterials, which can be used for gamma ray shielding purposes, and the performance of electronic components based on spinel ferrite materials in gamma radiation atmosphere.
4. Conclusions
In summary, spinel ferrite nanocrystals with high purity were effectively produced by the sol–gel auto-ignition route. Single-phase spinel ferrite nanocrystals of the cubic spinel (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) phase were confirmed through X-ray analysis. The TEM outcomes showed the finely distributed uniform crystals in nano-dimensions. The mass attenuation coefficient of the ferrites was estimated at distinct incident photon energy in the range of 122–1330 keV. The mass attenuation coefficient, total atomic cross section, total electronic cross section and half value layer determined using Monto-Carlo simulation using Geant4, XCOM (NIST) and experimental procedure were in good agreement. The energy absorption buildup factor was measured at incident photon energy of 100–1500 keV at penetration depths from 1 to 40 mfp via the geometric progression (G-P) fitting method. The EABF values were mainly dependent on the chemical composition and Zeq of the material. Zinc ferrite displayed a higher EABF value and manganese ferrite had the lowest EABF value. Monte-Carlo simulation via Geant4 was found to be the most effective tool for theoretical parameter determination. Zinc ferrite displayed higher shieling parameters as compared to the other spinel ferrites. This can be understood on the basis of the crystallite size effect; zinc ferrite possesses a lower crystallite size (∼32.31 nm) compared to the other produced ferrites. This can be attributed to the homogenous distribution of nano-crystallites with high electron density, which results in higher interaction probability between incident photons and nanocrystals. This experimental and theoretical investigation suggests a new approach towards spinel ferrite nanomaterial at different penetration depths and different energy atmospheres. This gives vital information about the physico-chemical characteristics of spinel ferrites and their shielding properties upon interaction with gamma radiation, which can be applicable in the biomedical field, radiation protection for shielding purposes and performance of electronic appliances in radiation atmosphere.
m) phase were confirmed through X-ray analysis. The TEM outcomes showed the finely distributed uniform crystals in nano-dimensions. The mass attenuation coefficient of the ferrites was estimated at distinct incident photon energy in the range of 122–1330 keV. The mass attenuation coefficient, total atomic cross section, total electronic cross section and half value layer determined using Monto-Carlo simulation using Geant4, XCOM (NIST) and experimental procedure were in good agreement. The energy absorption buildup factor was measured at incident photon energy of 100–1500 keV at penetration depths from 1 to 40 mfp via the geometric progression (G-P) fitting method. The EABF values were mainly dependent on the chemical composition and Zeq of the material. Zinc ferrite displayed a higher EABF value and manganese ferrite had the lowest EABF value. Monte-Carlo simulation via Geant4 was found to be the most effective tool for theoretical parameter determination. Zinc ferrite displayed higher shieling parameters as compared to the other spinel ferrites. This can be understood on the basis of the crystallite size effect; zinc ferrite possesses a lower crystallite size (∼32.31 nm) compared to the other produced ferrites. This can be attributed to the homogenous distribution of nano-crystallites with high electron density, which results in higher interaction probability between incident photons and nanocrystals. This experimental and theoretical investigation suggests a new approach towards spinel ferrite nanomaterial at different penetration depths and different energy atmospheres. This gives vital information about the physico-chemical characteristics of spinel ferrites and their shielding properties upon interaction with gamma radiation, which can be applicable in the biomedical field, radiation protection for shielding purposes and performance of electronic appliances in radiation atmosphere.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are very much indebted to Department of Physics, IIT Mumbai for XRD facility, Sophisticated Analytical Instrument Facility (SAIF), IIT Bombay, Mumbai for TEM characterization, and Department of Physics, Dr Babasaheb Ambedkar Marathwada University for radiation measurements.References
- B. Bhushan, Springer handbook of nanotechnology, Springer, 2017 Search PubMed.
- J. Lee, A. Yadav, M. Antia, V. Zaffino, E. Flitsiyan, L. Chernyak, J. Salzman, B. Meyler, S. Ahn and F. Ren, Low dose 60Co gamma-irradiation effects on electronic carrier transport and DC characteristics of AlGaN/GaN high-electron-mobility transistors, Radiat. Eff. Defects Solids, 2017, 172, 250–256 CrossRef CAS.
- V. Vinayak, P. P. Khirade, S. D. Birajdar, R. Alange and K. Jadhav, Electrical and dielectrical properties of low-temperature-synthesized nanocrystalline Mg 2+-substituted cobalt spinel ferrite, J. Supercond. Novel Magn., 2015, 28, 3351–3356 CrossRef CAS.
- M. Han and L. Deng, Doping effect of multiwall carbon nanotubes on the microwave electromagnetic properties of NiCoZn spinel ferrites, Appl. Phys. Lett., 2007, 90, 011108 CrossRef.
- A. R. Chavan, S. B. Somvanshi, P. P. Khirade and K. Jadhav, Influence of trivalent Cr ion substitution on the physicochemical, optical, electrical, and dielectric properties of sprayed NiFe2O4 spinel-magnetic thin films, RSC Adv., 2020, 10, 25143–25154 RSC.
- M. Pardavi-Horvath, Microwave applications of soft ferrites, J. Magn. Magn. Mater., 2000, 215, 171–183 CrossRef.
- R. Valenzuela, Novel applications of ferrites, Phys. Res. Int., 2012, 2012 Search PubMed.
- J.-J. Lee, Y.-K. Hong, S. Bae, J.-H. Park, J. Jalli, G. S. Abo, R. Syslo, B.-C. Choi and G. W. Donohoe, High-quality factor Ni–Zn ferrite planar inductor, IEEE Trans. Magn., 2010, 46, 2417–2420 CAS.
- S. B. Somvanshi, S. R. Patade, D. D. Andhare, S. A. Jadhav, M. V. Khedkar, P. B. Kharat, P. P. Khirade and K. Jadhav, Hyperthermic evaluation of oleic acid coated nano-spinel magnesium ferrite: enhancement via hydrophobic-to-hydrophilic surface transformation, J. Alloys Compd., 2020, 835, 155422 CrossRef CAS.
- P. P. Khirade, Structural, microstructural and magnetic properties of sol–gel-synthesized novel BaZrO3–CoFe2O4 nanocomposite, J. Nanostruct. Chem., 2019, 9, 163–173 CrossRef CAS.
- G. J. Hine and G. L. Brownell, Radiation dosimetry, Elsevier, 2013 Search PubMed.
- K. Siegbahn, Alpha-, beta-and gamma-ray spectroscopy, Elsevier, 2012 Search PubMed.
- E. B. Podgoršak, Radiation physics for medical physicists, Springer, 2006 Search PubMed.
- H. Lischka, H. Henschel, O. Kohn, W. Lennartz and H. Schmidt, Radiation effects in light emitting diodes, laser diodes, photodiodes, and optocouplers, in RADECS 93. Second European Conference on Radiation and its Effects on Components and Systems (Cat. No. 93TH0616-3), IEEE, 1993, pp. 226–231 Search PubMed.
- E. H. Lee, A. Indluru, D. R. Allee, L. T. Clark, K. E. Holbert and T. L. Alford, Effects of gamma irradiation and electrical stress on a-Si: H thin-film transistors for flexible electronics and displays, J. Disp. Technol., 2011, 7, 325–329 CAS.
- I. Fetahović, M. Pejović and M. Vujisić, Radiation damage in electronic memory devices, Int. J. Photoenergy, 2013, 2013 Search PubMed.
- H. Nikjoo, S. Uehara and D. Emfietzoglou, Interaction of radiation with matter, CRC press, 2012 Search PubMed.
- X. Li, C. Liu and J. Yang, Synergistic effect of ionization and displacement damage in NPN transistors caused by protons with various energies, IEEE Trans. Nucl. Sci., 2015, 62, 1375–1382 CAS.
- (a) M. Rand and P. Schmidt, Radiation resistant coatings for semiconductor devices, US Pat. 3,765,935, Washington, DC, 1973 Search PubMed; (b) S. J. Zinkle and L. L. Snead, Designing radiation resistance in materials for fusion energy, Annu. Rev. Mater. Res., 2014, 44, 241–267 CrossRef CAS.
- E. Little, Development of radiation resistant materials for advanced nuclear power plant, Mater. Sci. Technol., 2006, 22, 491–518 CrossRef CAS.
- S. S. Obaid, M. Sayyed, D. Gaikwad and P. P. Pawar, Attenuation coefficients and exposure buildup factor of some rocks for gamma ray shielding applications, Radiat. Phys. Chem., 2018, 148, 86–94 CrossRef CAS.
- R. M. Lokhande, C. V. More, B. S. Surung and P. P. Pawar, Determination of attenuation parameters and energy absorption build-up factor of amine group materials, Radiat. Phys. Chem., 2017, 141, 292–299 CrossRef CAS.
- A. H. Taqi and H. J. Khalil, An investigation on gamma attenuation of soil and oil–soil samples, J. Radiat. Res. Appl. Sci., 2017, 10, 252–261 CrossRef CAS.
- R. Kadam, S. Alone, G. Bichile and K. Jadhav, Measurement of atomic number and mass attenuation coefficient in magnesium ferrite, Pramana, 2007, 68, 869–874 CrossRef CAS.
- D. Creagh and J. Hubbell, Problems associated with the measurement of X-ray attenuation coefficients. I. Silicon. Report of the International Union of Crystallography X-ray Attenuation Project, Acta Crystallogr., Sect. A: Found. Crystallogr., 1987, 43, 102–112 CrossRef.
- S. Raut, V. Awasarmol, S. Shaikh, B. Ghule, S. Ekar, R. Mane and P. Pawar, Study of gamma ray energy absorption and exposure buildup factors for ferrites by geometric progression fitting method, Radiat. Eff. Defects Solids, 2018, 173, 329–338 CrossRef CAS.
- S. Agostinelli, J. Allison, K. a. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, D. Axen, S. Banerjee and G. Barrand, GEANT4—a simulation toolkit, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 506, 250–303 CrossRef CAS.
- T. Böhlen, F. Cerutti, M. Chin, A. Fassò, A. Ferrari, P. G. Ortega, A. Mairani, P. R. Sala, G. Smirnov and V. Vlachoudis, The FLUKA code: developments and challenges for high energy and medical applications, Nucl. Data Sheets, 2014, 120, 211–214 CrossRef.
- S. A. Pozzi, E. Padovani and M. Marseguerra, MCNP-PoliMi: a Monte-Carlo code for correlation measurements, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 513, 550–558 CrossRef CAS.
- J. Allison, K. Amako, J. Apostolakis, P. Arce, M. Asai, T. Aso, E. Bagli, A. Bagulya, S. Banerjee and G. Barrand, Recent developments in Geant4, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 835, 186–225 CrossRef CAS.
- D. K. Gaikwad, P. P. Pawar and T. P. Selvam, Mass attenuation coefficients and effective atomic numbers of biological compounds for gamma ray interactions, Radiat. Phys. Chem., 2017, 138, 75–80 CrossRef CAS.
- P. Limkitjaroenporn, J. Kaewkhao, P. Limsuwan and W. Chewpraditkul, Physical, optical, structural and gamma-ray shielding properties of lead sodium borate glasses, J. Phys. Chem. Solids, 2011, 72, 245–251 CrossRef CAS.
- K. Singh, H. Singh, V. Sharma, R. Nathuram, A. Khanna, R. Kumar, S. S. Bhatti and H. S. Sahota, Gamma-ray attenuation coefficients in bismuth borate glasses, Nucl. Instrum. Methods Phys. Res., Sect. B, 2002, 194, 1–6 CrossRef CAS.
- N. Singh, K. J. Singh, K. Singh and H. Singh, Gamma-ray attenuation studies of PbO–BaO–B2O3 glass system, Radiat. Meas., 2006, 41, 84–88 CrossRef CAS.
- M. Sayyed, M. AlZaatreh, M. Dong, M. Zaid, K. Matori and H. Tekin, A comprehensive study of the energy absorption and exposure buildup factors of different bricks for gamma-rays shielding, Results Phys., 2017, 7, 2528–2533 CrossRef.
- Y. Harima, Y. Sakamoto, S. Tanaka and M. Kawai, Validity of the geometric-progression formula in approximating gamma-ray buildup factors, Nucl. Sci. Eng., 1986, 94, 24–35 CrossRef CAS.
- H. Saleh, J. Sharaf, S. Alkhateeb and M. Hamideen, Studies on equivalent atomic number and photon buildup factors for some tissues and phantom materials, Radiat. Phys. Chem., 2019, 165, 108388 CrossRef CAS.
- H. Manjunatha and B. Rudraswamy, Computation of exposure build-up factors in teeth, Radiat. Phys. Chem., 2011, 80, 14–21 CrossRef CAS.
- D. Sardari and M. Kurudirek, A semi-empirical approach to the geometric progression (GP) fitting approximation in estimating photon buildup factor in soft tissue, water, and dosimetric materials, Int. J. Phys. Sci., 2012, 7, 5852–5860 CAS.
- A. Raut, P. Khirade, A. Humbe, S. Jadhav and D. Shengule, Structural, electrical, dielectric and magnetic properties of Al3+ substituted Ni–Zn ferrite, J. Supercond. Novel Magn., 2016, 29, 1331–1337 CrossRef CAS.
- K. Mahmoud, O. Tashlykov, A. El Wakil and I. El Aassy, Aggregates grain size and press rate dependence of the shielding parameters for some concretes, Prog. Nucl. Energy, 2020, 118, 103092 CrossRef CAS.
- M. Medhat, N. Demir, U. Akar Tarim and O. Gurler, Calculation of gamma-ray mass attenuation coefficients of some Egyptian soil samples using Monte Carlo methods, Radiat. Eff. Defects Solids, 2014, 169, 706–714 CrossRef CAS.
- A. M. El-Khatib, M. I. Abbas, M. Abd Elzaher, M. S. Badawi, M. T. Alabsy, G. A. Alharshan and D. A. Aloraini, Gamma attenuation coefficients of nano cadmium oxide/high density polyethylene composites, Sci. Rep., 2019, 9, 1–11 CrossRef CAS.
- R. Li, Y. Gu, Y. Wang, Z. Yang, M. Li and Z. Zhang, Effect of particle size on gamma radiation shielding property of gadolinium oxide dispersed epoxy resin matrix composite, Mater. Res. Express, 2017, 4, 035035 CrossRef.
- S. S. Obaid, D. K. Gaikwad and P. P. Pawar, Determination of gamma ray shielding parameters of rocks and concrete, Radiat. Phys. Chem., 2018, 144, 356–360 CrossRef CAS.
- J. Ryman, F. Alpan, L. Durani, K. Eckerman, R. Faw, L. Ruggieri and C. Sanders, Revision of ANSI/ANS-6.4. 3, Transactions, 2008, 99, 613–614 Search PubMed.
- Y. Yoshida, Development of fitting methods using geometric progression formulae of gamma-ray buildup factors, J. Nucl. Sci. Technol., 2006, 43, 1446–1457 CrossRef CAS.
- S. Schön, Nuclear/Radioactive Properties, in Handbook of Petroleum Exploration and Production, Elsevier, 2011, pp. 107–148 Search PubMed.
- M. Halimah, A. Azuraida, M. Ishak and L. Hasnimulyati, Influence of bismuth oxide on gamma radiation shielding properties of boro-tellurite glass, J. Non-Cryst. Solids, 2019, 512, 140–147 CrossRef CAS.
- T. Singh, N. Kumar and P. S. Singh, Chemical composition dependence of exposure buildup factors for some polymers, Ann. Nucl. Energy, 2009, 36, 114–120 CrossRef CAS.
- S. Gupta and G. S. Sidhu, Energy absorption buildup factor for some oxide glasses: penetration depth, photon energy and effective atomic number dependence, Int. J. Sci. Res., 2012, 2, 1–7 Search PubMed.
- M. S. Al-Buriahi and B. T. Tonguc, Study on gamma-ray buildup factors of bismuth borate glasses, Appl. Phys. A, 2019, 125, 1–7 Search PubMed.
- M. Büyükyıldız, A. Kılıç and D. Yılmaz, White and some colored marbles as alternative radiation shielding materials for applications, Radiat. Eff. Defects Solids, 2020, 175, 657–671 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |