Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unlocking the potential of furan-based poly(ester amide)s: an investigation of crystallization, molecular dynamics and degradation kinetics of novel poly(ester amide)s based on renewable poly(propylene furanoate)†
Lazaros
Papadopoulos
 a,
Panagiotis A.
Klonos
a,
Panagiotis A.
Klonos
 b,
Marcel
Kluge
b,
Marcel
Kluge
 c,
Alexandra
Zamboulis
c,
Alexandra
Zamboulis
 a,
Zoi
Terzopoulou
a,
Zoi
Terzopoulou
 a,
Dimitra
Kourtidou
a,
Dimitra
Kourtidou
 d,
Andreas
Magaziotis
a,
Konstantinos
Chrissafis
d,
Apostolos
Kyritsis
d,
Andreas
Magaziotis
a,
Konstantinos
Chrissafis
d,
Apostolos
Kyritsis
 b,
Dimitrios N.
Bikiaris
b,
Dimitrios N.
Bikiaris
 a and
Tobias
Robert
a and
Tobias
Robert
 *c
*c
aDepartment of Chemistry, Laboratory of Polymer Chemistry and Technology, Aristotle University of Thessaloniki, GR-541 24, Thessaloniki, Greece. E-mail: tobias.robert@wki.fraunhofer.de
bDepartment of Physics, National Technical University of Athens, Zografou Campus, GR-15780, Athens, Greece
cFraunhofer Institute for Wood Research – Wilhelm-Klauditz-Institut WKI, Bienroder Weg 54E, 38108 Braunschweig, Germany
dLaboratory of X-ray, Optical Characterization and Thermal Analysis, Physics Department, Aristotle University of Thessaloniki, GR-541 24, Thessaloniki, Greece
First published on 8th September 2021
Abstract
In this work, novel polyester amides (PEAs) based on renewable poly(propylene furanoate) (PPF) were prepared via traditional melt polycondensation utilizing a preformed symmetric amido diol (AD) containing two internal amide bonds. Owing to this innovative synthetic strategy, enhanced crystallization, both in terms of quantity and rate, was observed compared to neat PPF, which is characterized by slow crystallization kinetics. Moreover, the intramolecular hydrogen bonding usually observed in furan dicarboxylic acid (FDCA)-based polyamides, that results in the formation of low-molecular weight materials, was circumvented and copolymers of random structure and higher molecular weight were obtained. Due to the AD unit and the ensuing suppression of intramolecular hydrogen bonds, chain mobility (diffusion) is improved, leading in turn to enhanced crystallization. The crystallinity and crystal structure of PEAs were assessed via the combination of differential scanning calorimetry (DSC), X-ray diffraction (XRD) and polarized optical microscopy (POM). Furthermore, thermal degradation of the furan-based PEAs was thoroughly investigated for the first time, employing thermogravimetric analysis (TGA) kinetic modeling and Pyrolysis-Gas Chromatography–Mass Spectroscopy (Py-GC/MS). Finally, the complex molecular dynamics of PEAs was studied employing broadband dielectric spectroscopy (BDS). This study shows that PEAs have the potential to further enlarge the properties and applications of polyesters derived from FDCA.
1. Introduction
Over the last decades, rising concentrations of greenhouse gases and over-exploitation of finite resources made it apparent that our linear economy based on petrochemicals needs to be replaced in the medium term with a circular bioeconomy relying on renewable resources.1–3 As a result, alternative routes have been examined for the valorization of biomass streams, to produce fuels,4 chemicals,5 and polymeric materials.6 Among the various bioderived monomers, the furan family, especially 5-hydroxymethylfurfural, holds a prominent position as a chemical platform accessible from cellulose,7 which can be utilized for many different applications – from the synthesis of alkaloids,8 to the production of liquid hydrocarbon fuels and fuel additives derived from hydrogenated hydroxymethylfurfural (HMF) structures.9 However, one of the most studied applications for furan derivatives is the production of thermoplastic polyesters as an alternative to polyesters from aromatic dicarboxylic acids.10–13 Due to the heteroatom present in the structure of the furan ring, these polyesters present excellent gas barrier properties and are considered a possible replacement of terephthalic acid based polyesters that currently dominate the food packaging market.12,14,15In order to expand the possible applications of furan-based polymers though, the exploration of other polymeric classes, besides polyesters, is of high interest. In this respect, polyamides (PA)s and poly(ester amide)s (PEA)s are promising classes of polymers suitable for applications where superior thermal and mechanical properties are required.16 Those properties originate from the intermolecular hydrogen bonds that increase the interactions between the polymer chains. However, producing semi aromatic PAs or PEAs from 2,5-furandicarboxylic acid (FDCA) is by no means straightforward. Elevated temperatures are required for conventional polymerization, that generally involves a “prepolymer” synthesis via salt formation, followed by solid-state polymerization (SSP) to increase the molecular weight. Under such conditions, however, side reactions like decarboxylation and N-methylation of FDCA occur, leading to low molecular weight polymers and materials that are either amorphous or have low degrees of crystallinity.17–22 The reason behind the latter was examined by Wilsens et al.,23 who concluded that intramolecular hydrogen bonds are formed between the amide protons and the oxygen atom of the furan ring, and those impede the formation of intermolecular hydrogen bonds that are the main crystallization force in PAs.
Another synthetic strategy that has been employed for the production of furan-based PAs is enzymatic polymerization.24 Starting from dimethyl furandicarboxylate (DMFD), an immobilized form of Candida Antarctica lipase b catalyzes the polycondensation between DMFD and aliphatic diamines in mild reaction conditions, producing PAs from long or short chain diamines,16,25,26 heteroatom containing diamines27 and most recently PEAs.28 With this technique, problems referred to above like the decarboxylation of FDCA and N-methylation can be overcome while also employing nontoxic biocatalysts. However, despite these advantageous features, optimizations concerning the low yields and the enzyme activity in different conditions are still needed for this technique to be viable on an industrial scale.28 Furthermore, the materials prepared with this strategy are either amorphous,27 or cannot crystallize from the melt in bulk conditions due to slow crystallization25,26 unless treated with solvents. This is an important factor that could affect their processability for future applications.
We have recently demonstrated that long chain PEAs containing furan moieties can be obtained through traditional melt polycondensation.29 Indeed, semicrystalline materials/polymers, that crystallized from the molten state, were produced starting from a preformed symmetric amido diol, 1,10-decanediol and DMFD. The introduction of the amide moieties increased the crystallinity of the materials, while also enhancing their thermal and mechanical properties.29 The above mentioned side reactions occurring in traditional melt polycondensations were suppressed, while in parallel the use of solvents that are mandatory for enzymatic polymerization was completely avoided, granting a greener approach to the synthesis of furan-based PEAs.
Inspired by those results, we were intrigued to determine if similar results can be obtained when other diols are being used in these FDCA-based PEAs. To this end, the polymer selected for the synthesis of novel PEAs is poly(propylene furanoate) (PPF), that exhibits slow crystallization due to the odd number of methylene groups in propane diol, whereas at the same time, is screened as a potential replacement of fossil-based analogs in many applications.30,31 Along with PEF, they are the most credible alter egos for PET, due to their outstanding gas barrier properties.12,32,33 Moreover, different aspects of the PEAs in question, such as the thermal degradation kinetics and decomposition mechanism, thermal transitions with emphasis on crystallization and semicrystalline morphology, as well as molecular mobility/dynamics, are studied in depth and reported for the first time. For the scope of this project, we have employed a series of complementary techniques, namely, X-ray diffraction (XRD), differential scanning calorimetry (DSC), polarized light microscopy (POM), thermogravimetric analysis (TGA) kinetic modeling and broadband dielectric spectroscopy (BDS), in addition to the usual structural techniques, Fourier Transform Infra-Red (FTIR) and Nuclear Magnetic Resonance (NMR) spectroscopies and intrinsic viscosity measurements.
2. Materials and methods
2.1 Materials
Dimethyl 2,5-furandicarboxylate (DMFD, 99%) was obtained from Global Chemie, Mumbai, India. Titanium(IV) isopropoxide (TIS, 97%), 1,3-propanediol (PDO, 99%), and trifluoroacetic acid-d1 (99.5% D) were bought from Sigma-Aldrich Chemie, Steinheim, Germany. Phenol (99+%) and 1,1,2,2-tetrachloroethane (98+%) were bought from Alfa Aesar, Kandel, Germany. The chemicals were used without further purification. N,N′-(butane 1,4-diyl)bis(6-hydroxyhexanamide) (amido diol, AD) was synthesized as previously reported.29,342.2 Synthesis of polyesters
For the synthesis of the materials, a three-step melt polycondensation method was used. To give an example, the synthesis of PEA 50–50 is described. For the preparation of 10 g of polymer, 1.27 g of DMFD and 1.05 g of PDO (diol/ester ratio of 1/2), along with 400 ppm TIS based on DMFD, were placed in a round bottom flask equipped with a mechanical stirrer, a condenser, and a nitrogen inlet. Three vacuum/nitrogen cycles were conducted and then the flask was placed in a salt bath at 160 °C for 1.5 h, at 170 °C for another 1.5 h and at 180 °C for 1 h, under a nitrogen stream to facilitate methanol removal. The flask was then allowed to cool at room temperature under a N2 atmosphere overnight. Afterwards, 4.35 g of AD, 3.8 g of DMFD and a second portion of the catalyst were added to the flask for a final diol/diester ratio of 1/1. For the second step the temperature-time program of the first step was repeated, followed by the slow evacuation of the flask over a 30 minutes period (0.05 mbar). The reaction was continued under vacuum for 2 hours at 180 °C and for another 3 h at 190 °C. Then, the mixture was left to cool overnight and the polymers were easily removed from the flask, milled, and characterized without further purification.2.3 Characterization methods
FTIR spectra were recorded by applying the ATR technique in the transmission mode (32 scans, resolution of 4 cm−1) using a Thermo Scientific Nicolet iS5 FTIR instrument (Thermo Fisher Scientific, Waltham, MA, USA).NMR spectra were recorded on an Agilent 500 spectrometer (Agilent Technologies, Santa Clara, CA, USA), at room temperature. Polymers were dissolved in deuterated trifluoroacetic acid (TFA-d1) and spectra were recorded in the presence of a DMSO-d6 probe. Spectra were calibrated using the residual solvent peaks.
Intrinsic viscosities [η] were measured with a Ubbelohde viscosimeter at 25 °C, using a 60/40 w/w mixture of phenol and 1,1,2,2-tetrachloroethane as solvent. The samples were dissolved at 90 °C, cooled at room temperature and filtered through a disposable membrane filter made from Teflon. The intrinsic viscosity of each sample was calculated using the Solomon – Ciuta equation of a single point measurement:
DSC measurements were conducted by means of a TA Q200 series DSC instrument (TA, USA), calibrated with indium for temperature and enthalpy and sapphire for heat capacity. Samples of ∼8 mg in mass closed in TA TZero aluminium pans and studied in nitrogen atmosphere and in the temperature range from −25 to 200 °C. Upon erasing the thermal history (scan 1), two main thermal protocols were employed. (Scan 2) standard cooling from the melt at 10 K min−1 and (scan 3) faster cooling from the melt at ∼100 K min−1. Final heating scans were performed from −25 up to 200 °C at the fixed rate of 10 K min−1.
XRD was performed on thin films prepared with a thermopress. For the first set of measurements, the materials were melted at 190 °C and left to cool to room temperature. For the second set, the same films were annealed at 120 °C for one hour and then cooled down at room temperature. A MiniFlex II XRD system (Rigaku Corporation, Tokyo, Japan) with Cu Kα radiation (λ = 1.5406 Å) in a 2θ scan range of 5–50° (steps of 0.05°, 1° min−1) was used to record the spectra.
The POM technique was employed to assess the semicrystalline morphology (i.e. the number, size, and distributions of materials’ spherulites). POM images were first recorded during cooling from the melt (190 °C) at a rate of 10 °C min−1. Then, for a second set of measurements, quenched materials were heated at a rate of 10 °C min−1 up to 120 °C. For that, a Nikon Optiphot-1 polarizing microscope equipped with a Linkam THMS 600 heated stage, a Linkam TP91 control unit and a Jenoptic ProgRes C10Plus camera were employed.
BDS measurements35 were performed to investigate molecular mobility (dynamics), by means of Novocontrol BDS setup (Novocontrol GmbH, Germany). The samples were melted between finely polished brass plates, employing thin (∼50 μm) silica spacers, forming a sandwich-like capacitor of 20 mm in diameter. Upon application of alternating voltage, the complex dielectric permittivity, ε* = ε′–i·ε′′, was recorded (response of the sample) isothermally as a function of frequency in the range from 10−1 to 106 Hz and in the temperature range between −140 and 120 °C, upon heating at steps of 5 and 10 K, depending on the followed process.
Thermogravimetric analysis (TGA) of PPF and PEA copolymers was performed on a TGA/DSC 1 (Mettler-Toledo, Greifensee, Switzerland). The samples (10 ± 0.1 mg) were heated from 25 to 800 °C in a 35 mL min−1 flow of N2 at heating rates of 5, 10, 15 and 20 °C min−1. Continuous recording of the sample temperature and sample weight was carried out at any case. Thermal degradation kinetic analysis of PPF, PEA 50–50 and PEA 0–100 was performed using NETZSCH Kinetics Neo software (NETZSCH, Selb, Germany).
For Pyrolysis-Gas Chromatography–Mass Spectroscopy (Py-GC/MS) analysis of polyesters a very small amount of each material is “dropped” initially into the “Double-Shot” EGA/PY-3030D Pyrolyzer (Frontier Laboratories Ltd, Fukushima Japan) using a CGS-1050Ex (Kyoto, Japan) carrier gas selector. For pyrolysis analysis (flash pyrolysis) each sample was placed into the sample cup which afterwards fell free into the Pyrolyzer furnace. The pre-selected pyrolysis temperatures were 370 and 450 °C and the GC oven temperature was heated from 50 to 300 °C at 20 °C min−1. Those two temperatures were selected based on the EGA pyrogram and represent the sample prior and after thermal decomposition. Sample vapors generated in the furnace were split (at a ratio of 1/50), a portion moved to the column at a flow rate of 1 mL min−1, pressure 53.6 kPa and the remaining portion exited the system via the vent. The pyrolyzates were separated using temperature programmed capillary column of a Shimadzu QP-2010 Ultra Plus (Kyoto, Japan) gas chromatograph and analyzed by a Shimadzu MS-QP2010SE mass spectrometer at 70 eV. Ultra ALLOY® metal capillary column from Frontier Laboratories Ltd (Fukushima, Japan) was used containing 5% diphenyl and 95% dimethylpolysiloxane stationary phase, column length 30 m and column ID 0.25 mm. For the mass spectrometer the following conditions were used: Ion source heater 200 °C, interface temperature 300 °C, vacuum 10–4–100 Pa, m/z range 10–500 amu and scan speed 10.000. The chromatograph and spectra retrieved by each experiment were subjected to further interpretation through Shimadzu and Frontier post-run software (Kyoto, Japan).
3. Results and discussion
3.1 Polymer synthesis
The synthesis of the amido diol was previously described.34,36 In brief, it involves the ring-opening of ε-caprolactone by 1,4-diaminobutane. In the ESI,† details about the synthesis of this monomer can be found.To obtain the series of PEAs, a modified three-step melt polycondensation method was applied (Scheme 1). This method was adopted by our group to produce homopolymers with long chain diols, that cannot be removed by distillation in traditional two-step polycondensation processes, due to high boiling points. To circumvent this limitation, bis(hydroxy propylene)-2,5-furan dicarboxylate oligomers are first prepared from PDO and DMFD, and are then reacted with a second DMFD portion, together with the preformed amido diol. This way, instead of the long chain diol, the removable byproduct is the more volatile methanol. Furthermore, moderate temperatures (up to 190 °C) are used, resulting in limited coloration of the final materials and satisfactory molecular weight as indicated by the values of intrinsic viscosity (Table 1).
| Sample | Molar composition | Microstructureb | [η] | |||
|---|---|---|---|---|---|---|
| (PDO-AD) | Feed | Founda | L PF | L ADF | R | dL g−1 |
| a Calculated by 1H spectroscopy. b Calculated by 13C spectroscopy. | ||||||
| PEA 0–100 | 0.38 | |||||
| PEA 25–75 | 25–75 | 17–83 | 1.5 | 6.5 | 0.82 | 0.43 |
| PEA 50–50 | 50–50 | 42–58 | 1.9 | 2.6 | 0.92 | 0.41 |
| PEA 60–40 | 60–40 | 52–48 | 2.1 | 1.9 | 1.00 | 0.44 |
| PEA 65–35 | 65–35 | 57–43 | 2.4 | 1.8 | 0.98 | 0.44 |
| PEA 70–30 | 70–30 | 64–36 | 2.8 | 1.6 | 0.98 | 0.45 |
| PEA 75–25 | 75–25 | 70–30 | 3.4 | 1.4 | 1.00 | 0.38 |
| PPF | 0.49 | |||||
3.2 Structural characterization
The ATR-FTIR spectra of PPF and the prepared poly(ester amide)s are shown in Fig. 1. The spectra of PPF shows all the characteristic peaks described in literature,31,37 in particular the peaks of the ester bonds appearing at 1718 and 1122 cm−1 (Fig. 1, b and e), for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–O–C stretching vibrations, respectively. For the copolymers, new signals derived from the incorporation of the amido diol can be seen around 3295, 1630 and 1534 cm−1 (Fig. 1, a, c and d), corresponding to the stretching vibrations of the hydrogen-bonded N–H groups, C
O and C–O–C stretching vibrations, respectively. For the copolymers, new signals derived from the incorporation of the amido diol can be seen around 3295, 1630 and 1534 cm−1 (Fig. 1, a, c and d), corresponding to the stretching vibrations of the hydrogen-bonded N–H groups, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Amide I) stretching, and N–H (Amide II) bending vibrations. As discussed in the introduction, it is very important to avoid intramolecular H bonding, as it impedes the crystallization of the final polymers. Those intramolecular H bonds can be detected by ATR spectrometry. In a recent study on furan polyamides, two separate vibration bands related to nonbonded and hydrogen bonded N–H groups were reported.19 Moreover, in the study of Wilsens et al.23 the intramolecular hydrogen bonds between the oxygen atom of the furan ring and the hydrogens of the amide bonds were recorded after melt crystallization at 3373 cm−1. In our case, only a single peak corresponding to the intermolecular hydrogen bonded N–H groups was found at 3295 cm−1 for all the produced materials. In combination with our recent work,29 where a similar behavior was observed, these results suggest that introducing an aliphatic “spacer” between the furan ring and the amide bonds suppresses the intramolecular hydrogen bonding. This allows for to the desired intermolecular interactions between the polymer chains, vital for semi-crystalline PEAs.
O (Amide I) stretching, and N–H (Amide II) bending vibrations. As discussed in the introduction, it is very important to avoid intramolecular H bonding, as it impedes the crystallization of the final polymers. Those intramolecular H bonds can be detected by ATR spectrometry. In a recent study on furan polyamides, two separate vibration bands related to nonbonded and hydrogen bonded N–H groups were reported.19 Moreover, in the study of Wilsens et al.23 the intramolecular hydrogen bonds between the oxygen atom of the furan ring and the hydrogens of the amide bonds were recorded after melt crystallization at 3373 cm−1. In our case, only a single peak corresponding to the intermolecular hydrogen bonded N–H groups was found at 3295 cm−1 for all the produced materials. In combination with our recent work,29 where a similar behavior was observed, these results suggest that introducing an aliphatic “spacer” between the furan ring and the amide bonds suppresses the intramolecular hydrogen bonding. This allows for to the desired intermolecular interactions between the polymer chains, vital for semi-crystalline PEAs.
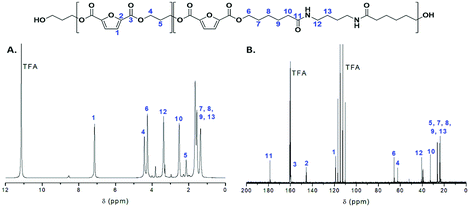
All copolymers were also characterized by NMR spectroscopy (Fig. S1 and S2†). The 1H NMR spectrum of the PEA 50–50 copolymer is displayed on Fig. 2A. Typical resonances of propanediol furanoate units are observed at 2.2, 4.5 and 7.2 ppm, while signals corresponding to the amido diol furanoate segments are also clearly visible.29 The composition of the polymer regarding the two diols can be easily calculated based on the resonances at circa 4.3 and 4.5 ppm which correspond to the methylene groups adjacent to the ester moieties for AD and PD respectively. As we can observe in Table 1, the PDO percentage in the final copolymers is slightly lower than in the feed. This can be correlated to the lower boiling point of PDO which may cause some loss of monomer during polymerization, while the AD cannot be distilled under the conditions applied at any step of the synthetic procedure.
The structure of the polymers was further confirmed by 13C NMR spectroscopy. The complete assignment of the peaks for a typical copolymer is presented in Fig. 2B. 13C spectroscopy also allowed us to get some insights in the microstructure of the prepared copolymers. Indeed, the quaternary aromatic carbon atoms of the furanic ring are sensitive to the diol forming the ester bond: the signals splits into four peaks between 145.5 and 145.8 ppm, Fig. S3A,† corresponding to the diester and diester amide sequences present in the poly(ester amide). Therefore, three different triads can be defined in the poly(ester amide) structure as illustrated in Fig. S3B.† Assuming similar relaxation times for the same carbon in the different ester groups and that substitution on one side of the triad does not influence substitution on the other side, the number average sequence lengths (LPF and LADF for propylene-furanoate and amido diol-furanoate units) and the degree of randomness, R, were estimated by integrating the triad-associated peaks and applying eqn (A)–(C), where I is the integration of the different peaks as defined in Fig. S3.† The obtained results are listed in Table 1. As expected, with increasing propanediol content LPF increases and LADF decreases. For all copolymers, the degrees of randomness are close to 1 indicating random arrangement of the monomers. The copolymers with increased amido diol content exhibit lower R values than the other copolymers, indicating a less random microstructure and suggesting that it is more difficult for the AD–F–AD segments to undergo transesterification compared to the P–F–P segments.38
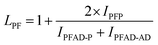 | (A) |
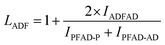 | (B) |
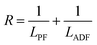 | (C) |
3.3 Thermal transitions and crystallinity assessment
The thermal transitions of the materials were studied by DSC, with different programs (as detailed in the Experimental section), involving slow and faster cooling rates, in order to influence crystallization. The raw DSC results can be seen in Fig. 3 and 4. The data have been evaluated in terms of characteristic temperatures and enthalpies of all thermal transitions and are given below in Table 2. | ||
| Fig. 3 DSC curves of scan 2 showing the thermal transitions of all compositions during (a) cooling at 10 K min−1, (b) heating at 10 K min−1. The heat flow has been normalized to the sample mass. | ||
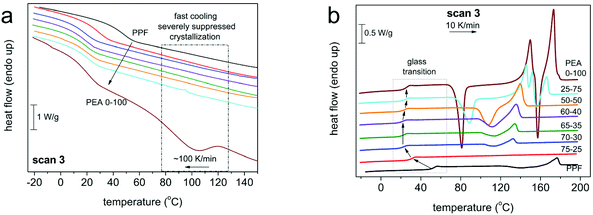 | ||
| Fig. 4 Thermal transitions of DSC scan 3 for all compositions during (a) cooling at 100 K min−1, (b) heating at 10 K min−1. The heat flow has been normalized to the sample mass. | ||
| Scan | Sample | T c (°C) | ΔHc (J g−1) | T g (°C) | Δcp (J gK−1) | T cc (°C) | ΔHcc (J g−1) | T m1 (°C) | T m2 (°C) | ΔHm (J g−1) |
|---|---|---|---|---|---|---|---|---|---|---|
| a Total value equaling to the sum of multiple events of the same type. b Main (stronger) crystallization at 127 °C accompanied by weaker events at 82 and 48 °C. | ||||||||||
| Scan 2 (cooling at 10 K min−1) | PPF neat | — | 0 | 51 | 0.40 | 141 | 9 | 177 | — | 9 |
| PEA 75–25 | — | 0 | 29 | 0.48 | — | 0 | 133 | — | 0.2 | |
| PEA 70–30 | — | 0 | 21 | 0.44 | 113 | 6 | 132 | — | 7 | |
| PEA 65–35 | — | 0 | 21 | 0.45 | 113 | 10 | 134 | — | 11 | |
| PEA 60–40 | — | 0 | 20 | 0.45 | 111 | 21 | 136 | — | 22 | |
| PEA 50–50 | 101 | 2 | 22 | 0.44 | 106 | 37 | 140 | — | 41 | |
| PEA 25–75 | 116 | 58 | 21 | 0.17 | — | 0 | 148 | 167 | 55 | |
| PEA 0–100 | 128 | 61 | 22 | 0.19 | 80 | 1 | 152 | 173 | 98a | |
| AD neat | 127b | 200a | — | 0 | — | 0 | 82 | 141 | 206a | |
| Scan 3 (cooling at ∼100 K min−1) | PPF neat | — | 0 | 52 | 0.42 | 141 | 9.2 | 177 | — | 9 |
| PEA 75–25 | — | 0 | 30 | 0.50 | — | 0 | 133 | — | 0.2 | |
| PEA 70–30 | — | 0 | 22 | 0.47 | 114 | 4 | 132 | — | 5 | |
| PEA 65–35 | — | 0 | 22 | 0.47 | 114 | 8 | 134 | — | 9 | |
| PEA 60–40 | — | 0 | 21 | 0.48 | 111 | 18 | 136 | — | 19 | |
| PEA 50–50 | — | 0 | 23 | 0.45 | 108 | 35 | 140 | — | 38 | |
| PEA 25–75 | — | 0 | 24 | 0.46 | 89 | 52 | 146/152 | 167 | 61a | |
| PEA 0–100 | 101 | 7.3 | 25 | 0.40 | 81 | 42 | 150 | 173 | 78a | |
For all polymers, a single glass transition step was recorded, supporting the findings of 1H NMR concerning the randomness of the copolymers. However, the evolution of the glass transition temperature, Tg, (Fig. 5, estimated by the half change of heat capacity) of the materials against their composition cannot be described by known prediction models like the ones described by the equations of Fox39 or Gordon-Taylor.40 This is a most probably a result of the intermolecular forces that form between the macromolecular chains, introduced by the amide bonds. Instead, as depicted in Fig. 5, the Tg of initial PPF that equals 51 °C decreases until an AD content of 30%, and above that the Tg values stabilize around 25 °C. Considering that furan polyesters from long chain diols present significantly lower glass transitions {e.g. poly(dodecylene furanoate) reported Tg is −22 °C41}, this is a direct indication of the strong interchain interactions, developed due to the incorporation of the amido diol, that affect the mobility of the polymeric chains. The data on Tg are almost identical between scans 2 (10 K min−1) and 3 (100 K min−1). Moreover, the trend in supported by the dielectric glass transition values calculated by BDS (included in Fig. 5, Tg,diel).
As expected, those same interactions significantly affect the crystallization and melting of the copolymers as well. Neat PPF is amorphous, presenting limited ability to crystallize regardless of the cooling rate applied – 10 K min−1vs. 100 K min−1 result in almost identical crystallization phenomena in the subsequent heating, Fig. 3 and 4. Its redundant crystallization is a well-documented phenomenon that is not derived from hindered diffusion of the polymeric chains, but from its limited ability to nucleate,42,43 due to the odd number of methylene units in the diol segment.30 This behavior is altered by the introduction of AD, as the hydrogen bonds between the amide segments greatly facilitate nucleation.29 Already from 30% ester amide content a cold crystallization is recorded; moreover, it is enhanced in rate (Fig. 6a) and amount/enthalpy (Fig. 6b). The increase in rate (acceleration) is demonstrated by the shifting of Tc and Tcc to higher and lower temperatures, respectively, as the ester amide content increases (Fig. 6). This suggests an increased population of nuclei forming during the supercooling and possibly alterations in their structure. In addition to that and taking into account the lowering of Tg, the accelerated crystallization should be helped also by the easier diffusion of the chains, this being expected since larger ΔH are recorded. The latter is also expected to lead to gradually larger crystallites in the presence of more amide segments, this being confirmed by POM measurements (vide infra).
 | ||
| Fig. 6 Evaluation of DSC results for crystallization in terms of (a) temperatures, Tc and Tcc, and (b) enthalpies, ΔHc and ΔHcc, versus composition. | ||
The effect of the ester amide segments gets more pronounced at a content above 50%, as these materials are able to crystallize from the melt. Here the intermolecular interactions are so strong that crystallization of neat PEA could not be suppressed even at the highest cooling rate (100 K min−1). Overall, the results obtained reveal that for this series of copolymers, the AD is the main crystallization force, a direct result of the internal amide bonds in its structure. With small contents of PDO, the materials retain their ability to crystallize from the melt, while for compositions between 30 and 50% AD, only cold crystallization is recorded. The temperatures of the thermal transitions and their respective enthalpies indicate that nuclei are formed from the ester amide segments and increasing PDO content results in alternations in semicrystalline morphology. The ester segments were not able to form a crystalline phase under the conditions applied, even at content as high as 75%, which is relatively expected given the odd number of methylene groups and the inherent inability of PPF to crystallize. It is interesting to report that, recently, we have recorded qualitatively similar effects in PEAs consisting of the same AD and a different polymer, poly(propylene succinate).44
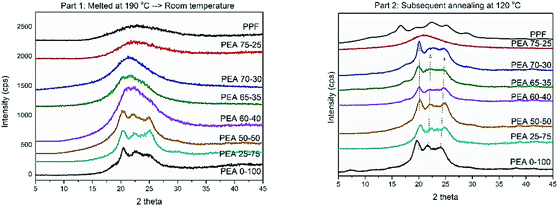
DSC measurements were complemented by XRD recordings. Two different protocols were followed, in an effort to imitate the thermal processing that the materials were subjected to. First the materials were melted and left to cool at ambient temperature and subsequently annealed at 120 °C. After applying the first protocol, only materials with high contents (above 50%) of amido diol were able to crystallize. They present reflections derived from the neat PEA at ∼20°, ∼22° and ∼24° respectively, with small displacements and changes in intensity. The patterns recorded suggest that the ester amide segments are those that induce crystallization and some alterations of crystal characteristics (lamellae thickness) are to be expected (Fig. 7a). The rest of the material follow the pattern of neat PPF, which is not able to crystallize under the applied conditions. Therefore, a broad amorphous halo around 21° is observed in their diffractograms.
In Fig. 7b, the diffractograms of the materials subjected to the second thermal protocol are presented. Polymers containing more than 30% of amido diol are found able to organize in crystalline domains, confirming DSC findings. The large supercooling that precedes the second measurement favors nucleation, and the thermal annealing that followed increased the diffusivity of the polymer chains. The reflections obtained, even at lower intensities compared to the pristine material, again follow the pattern of PEA 0–100, further promoting the concept that crystallization is induced from the intermolecular interactions occurring in the ester amide segments. Finally, pristine PPF presents the typical pattern with four main signals at 17.5°, 24°, 28° and 30°. There are no indications that the ester segments are able to organize into crystalline domains, as the reflections of PPF are absent from the rest of the materials. These results are constant with the findings of other studies on PEAs based on poly(decylene furanoate),29 poly(ethylene succinate)34 and poly(propylene succinate).45
3.4 POM results
POM was employed to directly observe the polymer crystals during the stages of crystallization. Performing the measurements during the cooling of the materials allowed us to record the differences in size, population and distribution of the formed crystals (Fig. 8). While monitoring the ability of the material to crystallize from the melt, it is clear that the introduction of 25% and then 50% of PDO into their structure significantly alters crystallization, resulting in crystals significantly smaller in size and also lesser in number, especially comparing PEA 25–75 with PEA 50–50. Nevertheless, the resemblance in the morphology of the crystals is clear, proving the claim made based on XRD and DSC results, that the ester amide segments are the driving force of nucleation and the formed crystals do not include any ester segments. A second set of measurements involved the same three materials and PPF, in an effort to evaluate the crystals formed after isothermal annealing at 120 °C. However, this thermal processing leads to a number of tiny spherulites (Fig. S3†) that are very difficult to evaluate and therefore the findings of the second XRD measurements could not be clearly depicted. | ||
| Fig. 8 Photographs obtained from POM measurements. For PEA neat and PEA 25–75 the scale bar in the upper row is 100 μm and in the bottom row 200 μm. For PEA 50–50 the scale bar is 50μm. | ||
3.5 Molecular dynamics
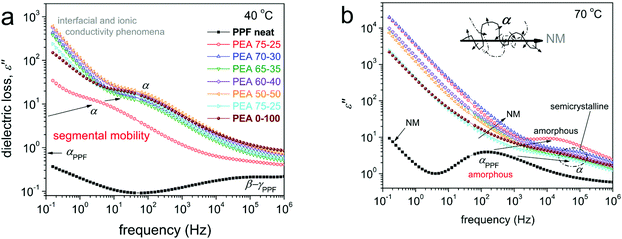
Dielectric spectroscopy is a special technique known to produce in depth information at the nanoscale regarding polymer mobility of the local and segmental type.35,46,47 The results obtained by BDS are shown here in the form of the frequency dependence of the imaginary part of dielectric permittivity, ε′′, which representative of dielectric loss. At lower temperatures, below Tg, a variety of relaxation processes, observed as peaks of ε′′, are recorded. Representative data can be seen in Fig. S6.† These processes correspond to the most localized molecular motions of the polymers.43,44The discussion will focus on the recordings obtained at temperatures above Tg, with the main focus on the segmental α relaxation, being considered the dielectric analogue of glass transition. α relaxation is believed to monitor the dipolar motion perpendicular to the chain backbone. The α relaxation can be seen in Fig. 9 at 40 and 70 °C, comparatively for all compositions.
The results of Fig. 9 have been analyzed in terms of known models (e.g. Havriliak-Negami,35 not shown) in order to distinguish the multiple contributions to the dielectric signal and evaluate the relaxation processes in terms of accurate time scale. During this analysis processes, for all samples, including neat PPF, an additional relaxation slower than α was revealed. With the naked eye, this additional process can be observed as a shoulder of the uprising signal (ionic conductivity) at lower frequency side. The additional process is quite narrow, however, with a strength in the same order with that of α. As shown in previous work on PPF of relatively low molecular weight43 (such as in our case) this process most probably originates in the Normal Mode (NM) relaxation.48 NM is the dielectric process that monitors the relaxation of the chain end-to-end dipole (vector, inset scheme to Fig. 9b), thus, is related to the glass transition and is favorably recorded for short polymer chains, such as the studied PEAs.
The overall results on the relaxations time scale can be seen in the dielectric map of Fig. 10, in the overall temperature range (Fig. 10a) and with focus on segmental dynamics (Fig. 10b).
For the sake of simplicity, we present in Fig. 10a the full temperature molecular dynamics, which is quite rich and seems rather complex, especially in the lower temperatures range. Within this range, the more localized molecular relaxations are shown (β, γ and δ processes). The origins of these local relaxations can be found in previous works.42–44,49–51 Prior to that, it should be marked that for such or similar aromatic polyesters there has been reported a coupling-like behavior between local (sub-glass transition) dynamics and segmental α.52–55 A similar relationship is recorded also here. Since the main interest here is on segmental dynamics, we will not further comment on local relaxations.
Coming to the glass transition dynamics, for a fixed temperature in Fig. 10b and with the increase of AD, α relaxation migrates toward higher frequencies. This suggests the acceleration of segmental dynamics, or in terms of glass transition, a lowering of the dielectric Tg. Please compare with Fig. 5, for the quantitative resemblance between the calorimetric and dielectric Tgs. This resemblance is not always the case between DSC and BDS, as the two methods follow in principle different modes regarding chains mobility. A weak exception to the said quantitative resemblance here seems to be the case of PEA 50–50 in Fig. 5. In that case, there seems to be a decoupling between the α relaxation (dipole moments perpendicular to the chain backbone) and the thermal cooperative diffusion of the chains. The difference for this composition is discussed below also in the light of the evaluation of the fragility index for α relaxation.
We should note, from a methodological point of view, that the BDS data shown can be directly compared with the DSC data obtained by scan 3, where a faster cooling from the melt is involved. Also, based on DSC, neat PPF and PEA 75–25, are amorphous, whereas for further AD addition the PEAs are either amorphous (at 40 °C) or exhibit cold crystallization (e.g. at 70 °C, semicrystalline). Cold crystallization is recorded as a disturbance in the normal temperature evolution of ε′′(f), please follow the corresponding disturbances in the time scale in Fig. 10b. By fitting the results on the time-scale of α, we may evaluate the fragility index, m, which may well represent the degree of cooperativity.35,44 The results are shown in Fig. 10b, wherein m of α drops with the addition of AD, namely from 120 in neat PPF to 109 in PEA 0–100. The absolute values regarding the poly(alkylene furanoate) are in accordance with previous findings from the literature.43,49 The fragility drop is, interestingly, not monotonic, as minimum values are recorded for the intermediate AD contents (30–50%). These results may seem strange at first glance; however, the trend fits qualitatively to the non-monotonic drop of Tg recorded in Fig. 5. Thus, taking these results into account, in combination with the negligible change in [η] (chain length), we conclude that the strong suppression in cooperativity should be due to the involved interchain associations (hydrogen bonds), as discussed in Section 3.3. As expected, the NM process follows the changes of α relaxation. Therefore, it is possible that for the said composition, there a decoupling between the calorimetric and the dielectric data is revealed. Such differences are recorded in the case of polymers of special states/structures, namely, different from the bulky state.47,56
3.6 Thermal degradation kinetics
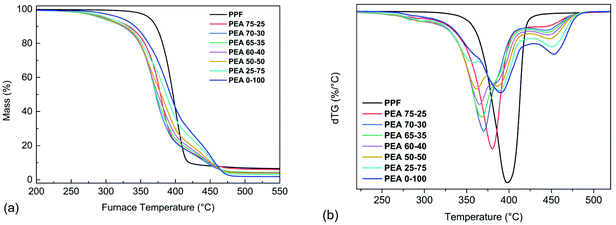
A preliminary evaluation of the decomposition of the materials was performed using TGA. The samples were initially heated with a heating rate of 10 °C min−1 under nitrogen atmosphere, to obtain information regarding the steps and the start of the degradation process. The mass loss and the derivative mass loss (dTG) curves of PPF, PEA 0–100 and the copolymers are presented in Fig. 11. It can be seen from the dTG curves (Fig. 11b) that the degradation of PPF is carried out in a single step where the maximum decomposition rate is achieved at 400 °C, while no significant mass loss has occurred until 300 °C. In the case of the amide containing materials, the observed initial mass loss (≈2–6%) that takes place in the range of 200–300 °C, could be attributed to the decomposition of oligomers present in the as received samples. Regarding the PEA 0–100 degradation process, two main steps are observed; the first step which takes place between 320–430 °C and corresponds to a mass loss of 75% caused by the degradation of polyester segments, and the second step which occurs between 430–500 °C with a mass loss of 24% and corresponds to the degradations of the amide segments. In the case of the copolymers, as the amido diol content increases, three main degradation steps appear. As observed in Fig. 11b, the first step of the copolymers’ degradation occurs at 320–380 °C and is attributed to the degradation of PPF's chain segments while at the same time the corresponding dTGpeak becomes less intense as the PPF content decreases. In the second degradation step, the amido diol polyester segments decompose at 365–420 °C while the dTGpeak is more intense for the copolymers with a higher amido diol content. The final degradation step of the copolymers is observed in the range of 420–500 °C and corresponds to the thermal degradation of the amide segments.The temperatures corresponding to 5 and 10% mass loss of are presented in Table 3. The incorporation of the amido diol into the copolymers led to a lower thermal stability compared to the neat materials, however this could also be associated to their lower molecular weight. To better understand the degradation mechanism of the prepared materials, kinetic analysis of the thermal degradation process was carried out on three materials, neat PPF, neat poly(ester amide) and the 50–50 copolymer, according to ICTAC.57 Thus, measurements under the heating rate of 5, 10, 15 and 20 °C min−1 were conducted in order to evaluate the kinetic parameters of the reactions, such as the activation energy E, the pre-exponential factor A and the conversion function f(a).
| Sample | T 5% (°C) | T 10% (°C) | Residual mass % |
|---|---|---|---|
| PPF | 355 | 372 | 5.8 |
| PEA 75–25 | 300 | 333 | 5.3 |
| PEA 70–30 | 293 | 324 | 3.8 |
| PEA 65–35 | 294 | 324 | 3.9 |
| PEA 60–40 | 296 | 325 | 3.6 |
| PEA 50–50 | 297 | 327 | 3.4 |
| PEA 25–75 | 302 | 331 | 2.8 |
| PEA 0–100 | 320 | 342 | 1.7 |
 | (D) |
It is widely accepted that every isoconversional method carries different errors at a given value of a. For this reason, two isoconversional methods were applied in this work, the differential method of Friedman and the integral method of Ozawa–Flynn–Wall (OFW).
The differential Friedman's method60 is based on the following equation:
 | (E) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [βi(da/dT)] against (1/T) for a constant a value.
[βi(da/dT)] against (1/T) for a constant a value.
The integral method of Ozawa, Flynn and Wall (OFW)61–63 was also used to evaluate the activation energy E as a function of the degree of conversion which is described by the following equation:
 | (F) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs. 1/T.
β vs. 1/T.
The dependence of the activation energy E on the degree of conversion a, according to both methods, is shown in Fig. 12. The values of E derived from Friedman's method, are higher compared to the corresponding ones obtained from the OFW approach, due to the systematical error which is introduced as a result of improper integration.64,65 The method of Friedman is very sensitive to experimental noise since the instantaneous rate values are employed. In the OFW method, the activation energy is assumed to be constant which leads to the introduction of a systematic error in the estimation of E when the activation energy varies with a. This error can be estimated by comparison with the Friedman results.66 Nevertheless, the calculated activation energy values, using both methods, follow relatively similar behavior for all the studied materials.
 | ||
| Fig. 12 Dependence of the activation energy E on the degree of conversion a according to (a) Friedman's and (b) Ozawa-Flynn-Wall's (OFW) isoconversional methods. | ||
As seen in Fig. 12, the E values of neat PPF present a minor increase with increasing degree of conversion a. The mean values of PPF's activation energy are 195 and 185 kJ mol−1 using Friedman and OFW methods respectively, which are in agreement with the findings of our previous work.67
The activation energy of neat poly(ester amide) presents a rather complex behavior and can be divided into three regions. More specifically, the E values slightly increase with increasing degree of conversion until a is equal to 0.6 but remain lower than the activation energy values of PPF. When the conversion a is between 0.6 and 0.85, the activation energy increases rapidly and takes higher values than the corresponding E of PPF, possibly due to the degradation of amide segments, while for higher values of a it remains relatively constant. The mean values of the activation energy are 187.9 and 177.2 kJ mol−1 for the Friedman and OFW methods respectively, lower than those of PPF. However this is expected with the increased number of methylene groups in the aliphatic chain, as was demonstrated for furan polyesters with long chain diols.68
In the case of the PEA 50–50 copolymer, the activation energy steadily increases until a takes the value of 0.15 and then presents a minor decrease until the degree of conversion is equal to 0.35. For values of a between 0.4 and 0.7, E increases with increasing conversion and presents lower values compared to the corresponding ones of neat PEA 0–100 and PPF, confirming the lower thermal stability of the copolymer which was previously mentioned. When the degree of conversion is between 0.7 and 0.8, the augmentation of E is rapid, even though, the values of the activation energy remain lower than the ones of PEA 0–100 but higher than the corresponding E values of PPF. This behavior could be explained by the lower content of amide segments compared to PEA 0–100. For higher values of a, the activation energy remains relatively constant. The mean values of the activation energy are 175.5 and 165.9 kJ mol−1 using Friedman and OFW methods respectively.
These observed variations of the activation energy on the degree of conversion for the three polymers are an indication of complex reactions that occur during the degradation process, which can probably be described by two and/or more different mechanisms.
 | ||
| Fig. 13 Mass loss and fitting curves of (a) PPF using the Cn–Cn model, (b) PEA 0–100 using the Cn–Cn–Cn model and (c) PEA 50–50 copolymer using the Fn–Cn–Cn model. | ||
Considering the results derived from the isoconversional analysis, the assumption that more than a single-step reaction mechanism occurs during the degradation of all the samples was made. The kinetic models which fitted best the experimental data, as well as the corresponding parameters of the thermal degradation process are summarized in Table S1.†
The reaction model which fitted the best the experimental data of PPF is presented in Fig. 13a and consists of two consecutive mechanisms which are the n-th order with autocatalysis in both steps (Cn–Cn). The corresponding parameters obtained by the tested models are summarized in Table S1.† The activation energy and contribution of the first reaction mechanism are 175.1 kJ mol−1 and 0.332 respectively suggesting that this step takes place in the initial stages of the degradation. The E values and contribution for the second step are 196.3 kJ mol−1 and 0.668 indicating that it occurs in the middle and final stages of the process. These results are consistent with the isoconversional analysis since the activation energy presents a steady augmentation during the degradation process, as was earlier suggested.
The thermal degradation of PEA 0–100 is a more complex process due to the multiple decomposition steps that occur. A reaction model consisting of three reaction mechanisms, best fitted the experimental results and is presented in Fig. 13b. The first two steps correspond to two consecutive reaction mechanisms which are the n-th order with autocatalysis in both steps (Cn–Cn). The activation energies and contributions are 135.1 kJ mol−1 and 0.307 for the first step, and 182.8 kJ mol−1 and 0.43 for the second step respectively. Taking into consideration the E and contribution values, these reaction steps could be attributed to the thermal degradation of polyester segments which takes place in the initial and middle stages of the process. The third step of the degradation corresponds to an independent reaction and the mechanism which resulted in the best fit of the experimental curve was the n-th order with autocatalysis (Cn). The activation energy and contribution of this step is 238.5 kJ mol−1 and 0.263 respectively, suggesting that it takes place during the final stages of the process. This reaction could be ascribed to the degradation of the amide segments which presents a higher activation energy value, as it has already been suggested by the isoconversional analysis.
The reaction model for the copolymer PEA 50–50 is presented in Fig. 13c and consists of two consecutive mechanisms followed by an independent reaction step. The first two mechanisms correspond to the n-th order and the n-th order with autocatalysis reaction models (Fn–Cn), with activation energy and contribution values of 128.6 kJ mol−1 and 0.091 for the first step, and 151.1 kJ mol−1 and 0.727 for the second step respectively. The n-th order with autocatalysis reaction model is ascribed to the third independent step of the degradation. The corresponding activation energy and contribution values are 231.7 kJ mol−1 and 0.182 suggesting that this step occurs in the final stages of the process. This reaction could be attributed to the degradation of the amide segments of the copolymer. The activation energy value of PEA 0–100 corresponding to the third independent reaction of the degradation is higher compared to the one of PEA 50–50 copolymer. This could be attributed to the lower content of amide segments in the macromolecular chains, as was earlier suggested by the isoconversional analysis.
The model fitting kinetics of the thermal degradation resulted in activation energies that follow the same trend with the ones obtained from the isoconversional analysis in all cases. This is an indication that the models that best describe the degradation process of these materials are the ones presented above.
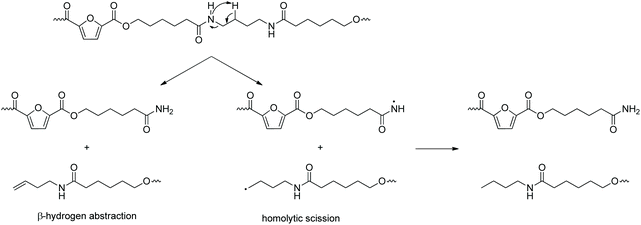
Total ion chromatographs of the two homopolymers as well as all the copolymers after pyrolysis at 370 °C are presented in Fig. S5.† Possible compounds of the pyrolysis of the two materials at 370 °C and 450 °C are presented in Table S2.† A number of vinyl-terminated compounds have been identified, either as a result of β-hydrogen scissions (occurring in β positions to both ester and amide bonds, Scheme 2) and consequent rearrangements, or as a result of dehydration processes. Intramolecular cyclizations accompanied by water loss were also observed, similar to the study of the commercial PEA of poly(butylene adipate-co-caproamide), that has been reported to pyrolyze into caprolactam and typical products of the pyrolysis of poly(butylene adipate).73 Additionally, carboxylic acids and alcohols, and amides (Scheme 2), possibly formed by homolytic scissions of the ester and amide linkages, respectively, as well as nitriles were identified. The latter are more likely to occur at higher degradation temperatures, in accordance with the activation energies that were recorded in the TGA measurements. In other words, the relative intensity of these signals in the chromatographs obtained at 450 °C (e.g. retention times 14.56 and 21.17 min) is higher compared to the corresponding signals from the pyrolysis at 370 °C, suggesting that the formation of those products’ formation is favored at higher temperatures. This is in accordance with the study by Guo et al.,74 where the thermal degradation of an aromatic poly(ester amide) was studied, and the degradation of the ester backbone was reported at lower temperatures compared to the amide linkages. Regarding the copolymer's pyrolysis, most of the products formed are due to either pure PPF or PEA 0–100 segments, however some products formed by mixed units were observed as well. Generally speaking, homolytic scissions were reported followed by secondary reactions (rearrangements, protonations, dehydrations) yielding alcohols, amines, nitriles, shorter amides, isocyanates, etc. Heterolytic and homolytic mechanisms can be in competition depending on the temperature. Most identified products result from the initial cleavage of the furanoate ester bonds. This observation is in agreement with the TGA results, according to which a two-step degradation is observed, the first step being related to ester thermal degradation and the second one to amide degradation.
4. Conclusions
In this work, novel semicrystalline poly(ester amide)s (PEAs) based on bio-derived polypropylene furanoate (PPF) were prepared. Intramolecular H-bonding between the amide group and the furan ring, which usually is the reason for amorphous behavior of FDCA-derived polyamides and PEAs, can be suppressed by incorporating a preformed amido diol (AD) into the PPF. The amido diol installs a spacer in between the amide group and the furan ring, resulting in intermolecular H-bonding. Structural characterization showed that random copolymers were prepared. The crystallinity of the materials was thoroughly investigated, to determine whether the AD addition could enhance the low crystallization ability of PPF. From an AD content of 30% and above the materials presented cold crystallization, while above 50% the materials were able to crystallize from the melt. XRD showed that the ester amide segments were the ones inducing crystallization, while with increasing AD content, the crystals formed were larger in size and population, as observed with POM. The key role of AD-induced inter-chain interactions (H-bonds) on nucleating crystallization is revealed, in accordance with previous findings with different starting polyesters. At the same origins were found the sudden drops of static and dynamic Tg of PPF, as well as the degree of cooperativity, with the addition of AD. BDS enabled the construction of the full molecular mobility/relaxation mapping. The thermal degradation of the materials was also studied in depth and the evolution of the activation energy depending on the composition was recorded. Amide segments decomposed after the ester segments, and the products of thermal degradation were identified by Py GC-MS. Overall, several parameters of furan-based PEAs were studied in depth, with molecular dynamics and thermal degradation kinetics and degradation products being reported for the first time. The results show once more that with our synthetic strategy it is indeed possible to obtain PEAs from FDCA that do not suffer from intramolecular H-bonding. The thorough study of the structure-properties relationship shows that altering the composition allows for the manipulation of the final properties of the PEAs. This is easy to control and will help to further enlarge the material variety of bio-based polymers from FDCA as potential alternatives to materials from petrochemical resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication is based upon work from COST Action FUR4Sustain, CA18220, supported by COST (European Cooperation in Science and Technology).References
- Y. Zhu, C. Romain and C. K. Williams, Nature, 2016, 540, 354–362 CrossRef CAS PubMed.
- R. M. O'Dea, J. A. Willie and T. H. Epps, ACS Macro Lett., 2020, 476–493 CrossRef.
- T. P. Haider, C. Völker, J. Kramm, K. Landfester and F. R. Wurm, Angew. Chem., Int. Ed., 2019, 58, 50–62 CrossRef CAS PubMed.
- S. Shylesh, A. A. Gokhale, C. R. Ho and A. T. Bell, Acc. Chem. Res., 2017, 50, 2589–2597 CrossRef CAS PubMed.
- R. A. Sheldon, Green Chem., 2014, 16, 950–963 RSC.
- M. A. Hillmyer, Science, 2017, 358, 868–870 CrossRef CAS PubMed.
- J. J. Bozell and G. R. Petersen, Green Chem., 2010, 12, 539 RSC.
- D. Kalaitzakis, A. Bosveli, K. Sfakianaki, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2021, 60, 4335–4341 CrossRef CAS PubMed.
- M. J. Climent, A. Corma and S. Iborra, Green Chem., 2014, 16, 516 RSC.
- G. Papamokos, T. Dimitriadis, D. N. Bikiaris, G. Z. Papageorgiou and G. Floudas, Macromolecules, 2019, 52, 6533–6546 CrossRef CAS.
- K. Loos, R. Zhang, I. Pereira, B. Agostinho, H. Hu, D. Maniar, N. Sbirrazzuoli, A. J. D. Silvestre, N. Guigo and A. F. Sousa, Front. Chem., 2020, 8, 1–18 CrossRef PubMed.
- G. Guidotti, M. Soccio, M. C. García-Gutiérrez, T. Ezquerra, V. Siracusa, E. Gutiérrez-Fernández, A. Munari and N. Lotti, ACS Sustainable Chem. Eng., 2020, 8, 9558–9568 CrossRef CAS PubMed.
- X. Fei, J. Wang, J. Zhu, X. Wang and X. Liu, ACS Sustainable Chem. Eng., 2020, 8, 8471–8485 CrossRef CAS.
- S. K. Burgess, J. E. Leisen, B. E. Kraftschik, C. R. Mubarak, R. M. Kriegel and W. J. Koros, Macromolecules, 2014, 47, 1383–1391 CrossRef CAS.
- S. K. Burgess, G. B. Wenz, R. M. Kriegel and W. J. Koros, Polym., 2016, 98, 305–310 CrossRef CAS.
- W. Huang, X. Hu, J. Zhai, N. Zhu and K. Guo, Mater. Today Sustain., 2020, 10, 100049 CrossRef.
- Y. K. Endah, S. H. Han, J. H. Kim, N.-K. Kim, W. N. Kim, H.-S. Lee and H. Lee, J. Appl. Polym. Sci., 2016, 133, 43391 CrossRef.
- T. Cousin, J. Galy, A. Rousseau and J. Dupuy, J. Appl. Polym. Sci., 2018, 135, 7–9 CrossRef.
- K. Luo, Y. Wang, J. Yu, J. Zhu and Z. Hu, RSC Adv., 2016, 6, 87013–87020 RSC.
- H. Hopff and A. Krieger, Helv. Chim. Acta, 1961, 44, 1058–1063 CrossRef CAS.
- V. H. Hopff and A. Krieger, Die Makromol. Chemie, 1961, 47, 93–113 CrossRef.
- P. M. Heertjes and G. J. Kok, Delft Prog. Rep., Ser. A, 1974, 1, 59–63 CAS.
- C. H. R. M. Wilsens, Y. S. Deshmukh, B. A. J. Noordover and S. Rastogi, Macromolecules, 2014, 47, 6196–6206 CrossRef CAS.
- F. Silvianti, D. Maniar, L. Boetje and K. Loos, in ACS Symposium Series, American Chemical Society, 2020, vol. 1373, pp. 3–29 Search PubMed.
- Y. Jiang, D. Maniar, A. J. J. Woortman, G. O. R. Alberda van Ekenstein and K. Loos, Biomacromolecules, 2015, 16, 3674–3685 CrossRef CAS PubMed.
- Y. Jiang, D. Maniar, A. J. J. Woortman and K. Loos, RSC Adv., 2016, 6, 67941–67953 RSC.
- D. Maniar, K. F. Hohmann, Y. Jiang, A. J. J. Woortman, J. Van Dijken and K. Loos, ACS Omega, 2018, 3, 7077–7085 CrossRef CAS PubMed.
- D. Maniar, F. Silvianti, V. M. Ospina, A. J. J. Woortman, J. van Dijken and K. Loos, Polymer, 2020, 205, 122662 CrossRef CAS.
- M. Kluge, L. Papadopoulos, A. Magaziotis, D. Tzetzis, A. Zamboulis, D. N. Bikiaris and T. Robert, ACS Sustainable Chem. Eng., 2020, 8 DOI:10.1021/acssuschemeng.0c02730.
- G. Z. Papageorgiou, D. G. Papageorgiou, V. Tsanaktsis and D. N. Bikiaris, Polym., 2015, 62, 28–38 CrossRef CAS.
- L. Papadopoulos, Z. Terzopoulou, D. Bikiaris, D. Patsiaoura, K. Chrissafis, D. Papageorgiou and G. Papageorgiou, Polymers, 2018, 10, 937 CrossRef PubMed.
- G. Guidotti, M. Soccio, N. Lotti, M. Gazzano, V. Siracusa and A. Munari, Polymers, 2018, 10(7), 785 CrossRef PubMed.
- G. Guidotti, L. Genovese, M. Soccio, M. Gigli, A. Munari, V. Siracusa and N. Lotti, Int. J. Mol. Sci., 2019, 20, 1–15 Search PubMed.
- M. Kluge, H. Rennhofer, H. C. Lichtenegger, F. W. Liebner and T. Robert, Eur. Polym. J., 2020, 129, 109622 CrossRef CAS.
- F. Kremer and A. Schönhals, Broadband Dielectric Spectroscopy, Springer Berlin Heidelberg, Berlin, Heidelberg, 2003 Search PubMed.
- H. R. Stapert, P. J. Dijkstra and J. Feijen, Macromol. Symp., 1998, 130, 91–102 CrossRef CAS.
- M. Soccio, N. Lotti, A. Munari, E. Rebollar and D. E. Martínez-Tong, Polymer, 2020, 202, 122666 CrossRef CAS.
- N. Kasmi, N. M. Ainali, E. Agapiou, L. Papadopoulos, G. Z. Papageorgiou and D. N. Bikiaris, Polym. Degrad. Stab., 2019, 169, 108983 CrossRef.
- T. G. Fox, Bull. Am. Phs. Soc., 1952, 1, 123 Search PubMed.
- M. Gordon and J. S. Taylor, J. Appl. Chem., 1952, 2, 493–500 CrossRef CAS.
- V. Tsanaktsis, G. Z. Papageorgiou and D. N. Bikiaris, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 2617–2632 CrossRef CAS.
- L. Papadopoulos, P. A. Klonos, D. Tzetzis, G. Z. Papageorgiou, A. Kyritsis and D. N. Bikiaris, Polymer, 2020, 189, 122172 CrossRef CAS.
- P. A. Klonos, L. Papadopoulos, G. Z. Papageorgiou, A. Kyritsis, P. Pissis and D. N. Bikiaris, J. Phys. Chem. C, 2020, 124, 10220–10234 CrossRef CAS.
- P. A. Klonos, M. Kluge, T. Robert, A. Kyritsis and D. N. Bikiaris, Polymer, 2020, 186, 122056 CrossRef CAS.
- M. Kluge, D. N. Bikiaris and T. Robert, Eur. Polym. J., 2019, 120, 109195 CrossRef CAS.
- M. Füllbrandt, P. J. Purohit and A. Schönhals, Macromolecules, 2013, 46, 4626–4632 CrossRef.
- P. A. Klonos, N. Patelis, E. Glynos, G. Sakellariou and A. Kyritsis, Macromolecules, 2019, 52, 9334–9340 CrossRef CAS.
- J. Ren, O. Urakawa and K. Adachi, Polymer, 2002, 44, 847–855 CrossRef.
- M. Soccio, D. E. Martínez-Tong, G. Guidotti, B. Robles-Hernández, A. Munari, N. Lotti and A. Alegria, Polymers, 2020, 12, 1–16 CrossRef PubMed.
- M. Soccio, D. E. Martínez-Tong, A. Alegría, A. Munari and N. Lotti, Polymer, 2017, 128, 24–30 CrossRef CAS.
- L. Genovese, M. Soccio, N. Lotti, A. Munari, A. Szymczyk, S. Paszkiewicz, A. Linares, A. Nogales and T. A. Ezquerra, Phys. Chem. Chem. Phys., 2018, 20, 15696–15706 RSC.
- A. Sanz, A. Nogales, T. A. Ezquerra, N. Lotti and L. Finelli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 21502 CrossRef PubMed.
- M. Soccio, A. Nogales, N. Lotti, A. Munari and T. A. Ezquerra, Polymer, 2007, 48, 4742–4750 CrossRef CAS.
- M. Soccio, A. Nogales, M. C. García-Gutierrez, N. Lotti, A. Munari and T. A. Ezquerra, Macromolecules, 2008, 41, 2651–2655 CrossRef CAS.
- A. Sanz, A. Nogales, N. Lotti, A. Munari and T. A. Ezquerra, J. Non-Cryst. Solids, 2007, 353, 3989–3995 CrossRef CAS.
- C. Zhang, V. M. Boucher, D. Cangialosi and R. D. Priestley, Polymer, 2013, 54, 230–235 CrossRef CAS.
- S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19 CrossRef CAS.
- K. Chrissafis, J. Therm. Anal. Calorim., 2009, 95, 273–283 CrossRef CAS.
- N. Sbirrazzuoli, Thermochim. Acta, 2013, 564, 59–69 CrossRef CAS.
- H. L. Friedman, J. Polym. Sci., Part C: Polym. Symp., 2007, 6, 183–195 CrossRef.
- J. H. Flynn and L. A. Wall, J. Polym. Sci., Part B: Polym. Lett., 1966, 4, 323–328 CrossRef CAS.
- S. Vyazovkin, J. Therm. Anal. Calorim., 2006, 83, 45–51 CrossRef CAS.
- T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38, 1881–1886 CrossRef CAS.
- N. Sbirrazzuoli, Macromol. Chem. Phys., 2007, 208, 1592–1597 CrossRef CAS.
- M. J. Starink, Thermochim. Acta, 2003, 404, 163–176 CrossRef CAS.
- S. Vyazovkin, J. Comput. Chem., 2001, 22, 178–183 CrossRef CAS.
- Z. Terzopoulou, E. Tarani, N. Kasmi, L. Papadopoulos, K. Chrissafis, D. G. Papageorgiou, G. Z. Papageorgiou and D. N. Bikiaris, Molecules, 2019, 24, 1717 CrossRef PubMed.
- Z. Terzopoulou, V. Tsanaktsis, M. Nerantzaki, D. S. Achilias, T. Vaimakis, G. Z. Papageorgiou and D. N. Bikiaris, J. Anal. Appl. Pyrolysis, 2016, 117, 162–175 CrossRef CAS.
- V. Tsanaktsis, E. Vouvoudi, G. Z. Papageorgiou, D. G. Papageorgiou, K. Chrissafis and D. N. Bikiaris, J. Anal. Appl. Pyrolysis, 2015, 112, 369–378 CrossRef CAS.
- P. Kusch, in Characterization and Analysis of Microplastics, ed. T. A. P. Rocha-Santos and A. C. B. T.-C. A. C. Duarte, Elsevier, 2017, vol. 75, pp. 169–207 Search PubMed.
- S. V. Levchik, L. Costa and G. Camino, Polym. Degrad. Stab., 1994, 43, 43–54 CrossRef CAS.
- S. Orsini, J. La Nasa, F. Modugno and M. P. Colombini, J. Anal. Appl. Pyrolysis, 2013, 104, 218–225 CrossRef CAS.
- C. Eldsäter, A.-C. Albertsson and S. Karlsson, Int. J. Polym. Anal. Charact., 2000, 5, 415–435 CrossRef.
- W. Guo, W.-T. Leu, S.-H. Hsiao and G.-S. Liou, Polym. Degrad. Stab., 2006, 91, 21–30 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1py00713k |
| This journal is © The Royal Society of Chemistry 2021 |