Spin-crossover complexes in nanoscale devices: main ingredients of the molecule–substrate interactions

Abstract

Spin-crossover complexes embedded in nanodevices experience effects that are absent in the bulk that can modulate, quench and even suppress the spin-transition. In this work we explore, by means of state-of-the-art quantum chemistry calculations, different aspects of the integration of SCO molecules on active nanodevices, such as the geometry and energetics of the interaction with the substrate, extension of the charge transfer between the substrate and SCO molecule, impact of the applied external electric field on the spin-transition, and sensitivity of the transport properties on the local conditions of the substrate. We focus on the recently reported encapsulation of Fe(II) spin-crossover complexes in single-walled carbon nanotubes, with new measurements that support the theoretical findings. Even so our results could be useful to many other systems where SCO phenomena take place at the nanoscale, the spin-state switching is probed by an external electric field or current, or the substrate is responsible for the quenching of the SCO mechanism.

---

1. Introduction

Spin crossover molecules are bistable compounds, most of them based on Fe(II) d⁶, that under an external stimulus such as temperature or light reversibly switch between a low-spin state (LS) and high-spin state (HS). This spin-state switching goes along with changes in the optical, mechanical, electrical and magnetic properties of the material.^1,2–4 Their properties, well-known in the bulk and macroscopic samples, are mainly triggered by the ligands coordinated to the metal centre, that modulate the metal ligand field strength, and the cooperative effects resulting from the intermolecular interactions in the lattice, responsible for the thermal hysteresis cycle.

Investigated for a long-time, there exists a renewed interest in these materials due to their potential for applications in molecular electronics, spintronics, data storage and sensing,^2,3,5,6 although the integration of SCO complexes into nanodevices faces different challenges. To realize SCO-based applications it is crucial to downscale to thin films or even to single or assemblies of few molecules in contact with a suitable substrate.^2,5,7 Most of the SCO complexes have negligible electrical conductivity,⁸ and different strategies have been developed to overcome this intrinsic limitation for integration into nanoelectronic devices, such as the embedding of the SCO molecules in conducting matrices such as electroactive polymers,⁹ or the deposition of hybrid SCO materials in the form of adsorbed nanoparticles¹⁰ or molecules on graphene.¹¹

The size reduction and the interaction with the substrate can lead to a significant modulation of the SCO properties,^12–14 modifying the transition temperature,^15,16 the completeness of the transition^17–19 and the hysteresis width,⁵ even completely suppressing the spin-transition.²⁰ Additionally, the contact with the electrodes can also modify their magnetic and SCO properties,^21,22 as well as the organization and positioning of the SCO between the device electrodes.^5,23

In fact, at the nanoscale the SCO molecules are subject to strong electric fields, experience surface/interface effects absent in the bulk and local irregularities of the substrate such as impurities, defects, doping, polymorphism, etc. that can modulate the electrostatic environment of the SCO molecule and have an impact on their properties.⁵ This explains the significant diversity of the available experimental data regarding SCO-based devices and the difficulties found to rationalize the different reported behaviours.

The aim of this work is to explore in depth, with the help of state-of-the-art quantum chemistry calculations, the different aspects of the integration of SCO molecules on active nanodevices. While the relative stability of the LS and HS states of Fe(II) and Fe(III) SCO complexes have been extensively evaluated in the gas-phase,^24–34 works devoted to the theoretical study of SCO complexes on the surface are rather scarce,^35–41 even though they can provide valuable information on the molecular scale, difficult or impossible to measure, such as details of bonding on surfaces, or the impact of strong electric fields. For this study, we take benefit from a recent work where two Fe(II) SCO complexes are encapsulated within single-walled carbon nanotubes (SWCNT) (Fig. 1a and b).⁴² Conductance through the host nanotube showed a distinct bistability associated with the spin state of the guest SCO molecules. A conductance hysteresis not present in the magnetism of macroscopic crystals was reported as a consequence of the particular conditions that molecules experience at the nanoscale (Fig. 1c). We use this particular system as a model with different ingredients modulating the SCO properties under extreme conditions such as the confinement imposed by the nanotube and the strong electrical fields.

Fig. 1 (a) SCO1 [Fe(H₂Bpz₂)₂(phen)] and SCO2 [Fe(H₂Bpz₂)₂(bipy)] complexes. (b) Scanning electron microscopy (SEM) image of a nanoscale transistor device containing an individual SCO2@SWCNT trapped by dielectrophoresis. (c) Current I measured at a fixed bias V = 1 V as a function of the temperature across a SCO2@SWCNT hybrid; i.e. SCO₂ molecules encapsulated in SWCNTs. Adapted from ref. 42. The insets are schematics showing the SCO2@SWCNT hybrid complexes and changes in them with the spin state.

In particular, we study by means of density functional theory (DFT)-based calculations the interaction of the SCO complex with the SWCNT and evidence how this interaction impacts the LS → HS transition energy. We analyze the effect that small variations in the SCO ligands produce on the stable geometries at the nanoscale (Fig. 1a). We address some additional aspects of the molecule–nanotube interaction such as the potential spin-dependent charge transfer between both fragments and the impact of confinement on the geometry of the HS and LS SCO molecules. Besides, we study the influence that differences in the local environment, like p-doping of the SWCNT, may have on the relative conductance of HS and LS states by means of simulation of the current vs. temperature curves. We also reconsider the impact of an external electric field on the relative energies of the HS and LS molecules and the spin transition energies and examine how this external electric field modifies the Fe ligand field. We provide new measurements that support our theoretical findings, a set of samples with a rather different behaviour to that previously reported under the same conditions, the LS state being less conductive than the HS one, resulting in “inverted” hysteresis loops with temperature.

Although we focus on the particular case of the SCO complexes encapsulated within SWCNT, our results could be useful to many other systems where the SCO phenomena take place at the nanoscale, the spin-state switching is studied by an external electric field or current, or the substrate is responsible for the quenching of the SCO mechanism.

2. Description of the systems

Recently we have reported for the first time the encapsulation of Fe(II) spin-crossover complexes in single-walled carbon nanotubes.⁴² Two Fe(II) SCO complexes with the formula [Fe(H₂Bpz₂)₂(L)] were studied, with H₂Bpz₂ = dihydrobis(pyrazolyl)borate and L = 1,10-phenanthroline (phen, SCO1) or 2,2′-bipyridine (bipy, SCO2) (Fig. 1a). These complexes as powder samples show abrupt thermally induced spin-transitions at 167 K and 160 K for SCO1 and SCO2, respectively, from the high spin (HS, S = 2) to low spin (LS, S = 0) state. Both complexes can be sublimed and their SCO properties are known to be retained when deposited on different surfaces.^21,43,44 Commercially available chemical vapour deposition-grown SWCNTs were used, with diameters ranging from 1.6 to 2.2 nm. Details regarding the encapsulation process and verification measurements can be found in ref. 42.

The electron transport across individual SCO@SWCNT hybrids was studied in a solid-state field-effect transistor configuration (Fig. 1b). The electrical conductivity of the nanotube was modulated by the spin-state of the Fe(II) SCO complex, while the encapsulated complex retained the SCO properties. Upon cooling from room temperature down to 90 K the current switched to a high-conductance state at temperatures (T_HC) close to the transition temperature of the SCO complexes (Fig. 1c, blue curve). Upon heating back to room temperature, the current remains in the high-conductance state (Fig. 1c, red curve) at temperatures higher than the transition temperature, where it drops back to the low-conductance state (T_LC). In this hysteresis cycle, switching induces a reversible change in the conductivity of the SWCNT, the high-conductance state has been assigned to the LS complex, while the low-conductance regime is related to the HS state of the complex. Most of the considered samples showed an overall similar shape of the I vs. T curves, although some particularities have been observed regarding the position and amplitude of the jumps (large/small jumps) between the low-conductance and high-conductance curves.

In this work we focus on a new set of current vs. temperature measurements (Fig. 7), obtained under the same conditions, but with a radically different behaviour that can be related to differences in the local environment of the SWCNT, as suggested by our DFT-based calculations. The relevance of this study resides in the fact that could help explain the variety of experimental results reported in the literature for nanoscale devices.

3. Computational details

3.1 Periodic calculations

The crystallographic data reported by Real et al.⁴⁵ were used as the starting point to build the models of SCO1 and SCO₂ complexes. The geometry of each complex has been fully optimized once encapsulated in the SWCNT. In all calculations the SWCNT is a (16,8) nanotube with a diameter of 1.65 nm and a unit cell of 224 carbon atoms. This chirality corresponds to a semiconductor, in agreement with the transport measurements of the bare SWCNT,⁴² while the relatively reduced size of the unit cell enables the complete optimization of both the SCO complex and the nanotube.

The encapsulation has been studied in the frame of periodic DFT using the generalized gradient approximation (GGA) with the revised Perdew–Burke–Ernzerhof functional (rPBE)⁴⁶ and projector-augmented wave (PAW) potentials.^47,48 All the calculations have been performed using the VASP (Vienna ab initio simulation package) code.^49–52 rPBE functional has been proven to provide a good LS–HS balance (much better than other GGA functionals such as PBE) for well-known SCO complexes containing Fe(II) and Fe(III),²⁵ and has been previously employed to describe the deposition of SCO complexes on different substrates.^36,37,53 Valence electrons are described using a plane-wave basis set with a cutoff of 500 eV and the Γ-point of the Brillouin zone is used.⁵⁴ The optimized lattice parameters for the nanotube are a = b = 16.75 Å and c = 11.35 Å. Hence, the diameter of the nanotube once optimized is 1.675 nm.

To study the encapsulation, we have used a 1 × 1 × 2 supercell (54 Å × 54 Å × 22.7 Å) containing 448 carbon atoms and a single Fe SCO complex, with 37 Å of vacuum between nanotubes. Electronic relaxation has been performed until the change in the total energy between two consecutive steps was smaller than 10⁻⁶ eV and the ionic relaxation has been performed until the Hellmann–Feynman forces were lower than 0.025 eV Å⁻¹.

The NUPDOWN option of the VASP code is used to converge different magnetic solutions. This forces the difference between the number of electrons in up and down spin channels, N_α–N_β, to be equal to 0 (LS) or 4 (HS). Several starting geometries for geometry optimizations were tested (Fig. 2), as described in the next section, and the interaction energies between the encapsulated SCO complex and the nanotube, E_int, were calculated as E_int = E_SCO@SWCNT − (E_SWCNT + E_SCO). A negative E_int value indicates that the encapsulated molecule is more stable than the free molecule.

Fig. 2 The three explored orientations of the SCO complex inside the nanotube. The figures correspond to the SCO2 complex, similar to the SCO1 one.

3.2 Molecule–nanotube charge transfer

The charge transfer between the SCO complex and the SWCNT is explored by means of plots of the charge density difference, Δρ, evaluated as:

Δρ = ρ_SCO@SWCNT − ρ_SCO − ρ_SWCNT

where SCO@SWCNT corresponds to the encapsulated complex, SCO and SWCNT are the isolated complex and nanotube, each with the same geometry as in SCO@SWCNT. A positive value (yellow surfaces) gives regions where the SCO@SWCNT system gains electrons with respect to the fragments. The negative values correspond to the cyan surfaces. The dependence of Δρ on the nature and spin state of the complex and geometry adopted inside the nanotube has been studied.

3.3 Transport properties

The temperature dependent conductivity σ of the SCO@SWCNT system, in terms of relaxation time τ, was computed employing the BoltzTrap2 code,⁵⁵ based on the semi-classical Boltzmann transport theory. In this method, the transport coefficients are calculated on the frame of the rigid-band approximation (RBA), which assumes that changing the temperature (T), or the Fermi energy of the system (μ), does not change the band structure. The electrical conductivity is computed using the following expression:
where q is the electron charge, f(0) is the Fermi distribution function and σ*(ε, T) is the transport distribution function, computed by means of a linearized version of the Boltzmann transport equation, under constant relaxation time approximation.⁵⁶ The code uses as the starting point the information provided by the previous VASP calculations for each magnetic solution, namely the density of states and eigenvalues stored in the corresponding OUTCAR, EIGENVAL and POSCAR files generated by the VASP code.

The electrical conductivity has been evaluated for the SCO2@SWCNT system considering that the SCO2 molecule is encapsulated in a pristine nanotube or a p-doped nanotube, since carbon-based materials like SWCNT and graphene are typically p-doped.⁵⁷ The p-doping is defined as the difference between the intrinsic electronic density, D_int, and the density once a certain fraction of electrons, δe, has been removed, D_n.

The explored p-doping is around the value resulting from the extraction of one complete electron, corresponding to p-doping = 1.51 × 10¹⁹ cm⁻³. In this regime, the conductivity of the SWCNT presents different trends depending on the spin state of the encapsulated SCO complex, and it is possible to explain the hysteresis loop observed experimentally.

3.4 Electric field effects

The impact of an external electric field on the relative stability of the HS and LS states of the SCO1 complex has been explored by means of a set of single-point density-functional theory based calculations of the most stable geometry adopted by the complex inside the nanotube. The hybrid TPSSh^58,59 exchange–correlation functional has been employed, with basis sets of quality def2-TZVPP⁶⁰ for all atoms of the complex. The choice of the exchange–correlation functional and basis sets is based on previous benchmark calculations on SCO complexes containing Fe(II) and Fe(III) centres.^24,25 Electric fields of increasing strength were imposed along the x, y, and z axis. The molecule is oriented in such a way that the Fe atom occupies the centre of the coordinate system and the phen ligand occupies the yz plane. All the calculations have been performed using the Gaussian 09 code.⁶¹

3.5 Ligand field parameters

The ligand field parameters of the SCO1 complex on the geometry adopted inside the nanotube (geo2) have been extracted by means of the ab initio ligand field theory (AILFT) approach implemented in the ORCA program package.⁶² Basis sets of quality def2-TZVPP⁶⁰ have been chosen for all atoms, except for Fe for which the basis of quality def2-QZVPP was chosen.⁶⁰ The scalar relativistic effects are included by means of ZORA approximation.⁶³ State-average CASSCF (6,5) calculations with six electrons occupying the five 3d orbitals were carried out for each multiplicity (S = 0, 1, 2) with equally weighted roots on each multiplicity (50 singlets, 45 triplets and 5 quintets).

4. Results and discussion

4.1 Interaction with the nanotube

The stability of the encapsulated SCO1 (SCO2) complexes inside the SWCNT has been evaluated for three different orientations of the phen (bipy) ligand with respect to the nanotube walls. As the starting point for geometry optimization, the complex was centred on the nanotube cavity, with the Fe ion placed on the nanotube axis (z axis). The complex was oriented in such a way that the phen (bipy) ligand is placed on the yz, xz or xy plane, (geo1, geo2 and geo3, respectively, Fig. 2). Both the nanotube and the complex were fully optimized for the low- and high-spin states. The xyz coordinates of the most stable orientation of encapsulated SCO1 and SCO2 complexes are provided in the ESI.†

For the SCO1 complex, the most stable geometry among the explored ones is geo2 for both spin states, with the phen ligand on the xz plane (Table 1). This orientation is just 90 meV more stable than geo1, with the phen group on the yz plane. For the optimized geo2 the molecule rests on the centre of the cavity, establishing short contacts with the nanotube wall through the C–H bonds of the pyrazole ligands (distances of about 3.1–3.3 Å). For the two other orientations, the molecule slightly moves toward the nanotube wall, with the phen ligand a bit more distant to the wall than the pyrazole ones. Both ligands participate in the short C–H⋯ nanotube contacts, being in general shorter for geo3 than geo1, as shown in Fig. S1.†

Table 1 Relative energies and interaction energies of SCO–nanotube for encapsulated SCO1 and SCO2 complexes with different orientations with respect to the nanotube main axis. All values are in eV. In gray, the most stable orientation for each encapsulated complex. In parenthesis, the increase of the LS → HS transition energy of the encapsulated complex with respect to the isolated one

Complex	Orientation	E LS	E HS	E HS − ELS	E int LS	E int HS
SCO1 (phen)	geo1	0.090	0.575	0.485	−0.024	0.035
	geo2	0.000	0.445	0.445 (4.5%)	−0.114	−0.095
	geo3	0.240	0.821	0.581	0.126	0.281
	Isolated complex			0.426
SCO2 (bipy)	geo1	0.000	0.487	0.487 (10.6%)	−0.127	−0.080
	geo2	0.046	0.519	0.473	−0.081	−0.049
	geo3	0.123	0.654	0.530	−0.003	0.086
	isolated complex			0.440

---

In the case of the SCO2 complex, geo1 and geo2 are very close in energy, geo1 being slightly more stable than geo2 (just 46 meV). In both orientations, the closest contacts between the molecule and the nanotube are established through the H atoms of the pyrazole ligand. As it occurs for SCO1, in geo3 also the bipy ligand participates in these short contacts with the nanotube (Fig. S1†). Two additional sets of calculations were performed, with the molecule oriented as in geo1, but shifted toward the wall. These arrangements showed a large energy penalty with respect to the orientations where the molecule is centred on the cavity.⁴² Thus, small variations in the SCO ligands do not significantly alter the accommodation of the SCO molecules within the SWCNT.

In both complexes, the energy difference between the LS and HS states, E_HS − E_LS, significantly increases for the encapsulated complex (∼5–14% for SCO1, ∼10–20% for SCO2). This enhancement could be related to the structural changes induced by the encapsulation, as well as to the electronic effects due to the molecule–nanotube interaction. The Fe–N distances of the FeN₆ core are reported in Table 2, both for the free and encapsulated molecules in the LS and HS states. In general, the HS complex presents greater changes on the FeN₆ core than the LS ones once encapsulated. The complexes expand along the Fe–N bonds corresponding to the L ligands (bipy and phen), while slightly compress for the Fe–N bonds related to the pyrazolyl groups.

Table 2 Mean Fe–N distances of SCO1 and SCO2 complexes for the free and encapsulated optimized geometries

Complex	Mean distances (Å)	Free		Encapsulated
		LS	HS	LS	HS
SCO1 (phen)	Fe–N1 (phen)	1.974	2.219	1.981	2.242
	Fe–N2	2.043	2.255	2.039	2.223
	Fe–N3	2.040	2.182	2.039	2.179
SCO2 (bipy)	Fe–N1 (bipy)	1.966	2.221	1.970	2.232
	Fe–N2	2.049	2.266	2.038	2.255
	Fe–N3	2.043	2.192	2.042	2.178

---

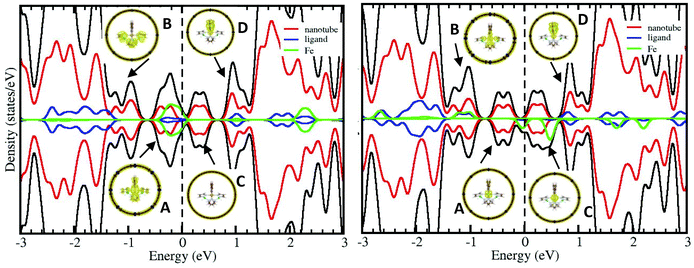
The interaction energies between the encapsulated molecule and the nanotube are reported in Table 1. Negative interaction energies correspond to those situations where the encapsulated molecule is more stable than the free one. For the optimal geometry, the SCO molecule is placed on the centre of the cavity and both the HS and LS complex are estabilized inside the nanotube. In all cases, the interaction energy is significantly smaller than 1 eV, considered as the threshold value that distinguishes chemisorption (E_int > 1 eV) and physisorption (E_int < 1 eV).⁶⁴ The interaction is larger for the LS than the HS complexes, regardless of the L ligand. The same trends have been reported for the deposition of similar Fe SCO complexes on metallic substrates.^35,36,40,53 This can be related to the spin-dependent degree of mixing of the molecules and nanotube states. Fig. 3 shows the density of states (DOS) and projected DOS on the Fe, nanotube and complex ligands for SCO2@SWCNT. Similar plots are obtained for SCO1@SWCNT (Fig. S2†). The hybridization between the nanotube and complex states is larger for the LS complex, in particular for those occupying states close to the Fermi level as shown in inset A. This represents the electronic density isosurface for the states placed between the Fermi level E_F and E_F − 1 V. The electronic density is equally distributed among the nanotube and the complex, with relevant participation of the complex ligands that favours the interaction with the nanotube. For the HS complex, however, the complex ligands have almost no effect on these bands, and the electronic density is mainly placed on Fe and the nanotube.

Fig. 3 Density of states (black) and projected density of states on Fe (green), ligands (blue) and carbon nanotube (red) for the SCO2@SWCNT system, LS (left) and HS (right) states. The insets represent the electronic density (yellow surfaces, isosurface level = 0.002 e per bohr³) for occupied bands in ranges of [E_F − 1 V, E_F] (A) and [E_F − 1.5 V, E_F − 1] (B) and empty bands in ranges of [E_F, E_F + 0.6 V] (C) and [E_F + 0.6 V, E_F + 1 V] (D), with E_F being the Fermi level.

The larger participation of the ligands on the LS state correlates to the strength of the Fe ligand field, which is about two times stronger for the LS complex than the HS one (Fig. 4). The stronger the field, the higher the participation of the complex ligands in the t_2g-like and e_g-like orbitals. In the case of the HS complex, the t_2g-like orbitals are almost localized on the Fe centre (Fig. 4), and only the 3d e_g-like orbitals present a non-negligible contribution of the ligands, in agreement with the projected DOS of empty bands (inset D in Fig. 3 for the HS complex). The larger interaction energy for LS between the molecule and SWCNT may be the reason behind the shift of the LS to HS transition to higher temperatures and therefore the opening of hysteresis observed in several experimental reports.^42,65,66

Fig. 4 Ligand field parameters and orbitals for SCO1 from AILFT calculations with the geometry adopted inside the nanotube LS (left) and HS (right) states.

Comparing the behaviour of the two Fe complexes, the interaction between SCO1 and the nanotube is weaker than the interaction with SCO2 for the most stable coordination (Table 1). In fact, half of the explored states for the encapsulated SCO1 complex are not stable with respect to the free complex. At the same time, the enhancement of the LS → HS transition energy is higher for the confined SCO2 than SCO1 complex. This seems to be in agreement with the slightly higher LS–>HS transition temperature obtained for SCO2@SWCNT when compared to SCO1@SWCNT in most measured samples. A larger statistical set of experimental measurements would be needed to establish a conclusion.

4.2 Molecule–nanotube charge transfer

Raman measurements at room temperature of the SCO1@SWCNT and SCO2@SWCNT hybrids showed blue shifted peaks both for the complexes and the nanotube (Fig. S6†).⁴² Different factors could be invoked to explain these shifts such as changes in the environment of the molecules, a small charge transfer between the SCO molecule and SWCNT, strain or aggregation effects. Fig. 5 shows the charge density difference plots for the SCO1@SWCNT and SCO2@SWCNT hybrids, in geo1 and geo2 geometries. All the plots refer to an isodensity value of 10⁻⁴ e per bohr³, higher values are shown in Fig. S3.† These plots give information about the net charge transfer between the molecule and nanotube. Hence, the yellow surfaces correspond to positive charge differences, i.e., they represent charge accumulation, while the blue surfaces correspond to charge depletion. The charge density difference plots indicate a certain complex-to-nanotube charge transfer of different extensions depending on the geometry adopted by the complex inside the nanotube. In the case of geo1, a certain net charge transfer from the molecule to the nanotube is observed (Fig. 5d), mainly between the bipy ligand and the closest carbon atoms. However, for geo2 both depletion and accumulation regions are observed on the nanotube, although a small net molecule-to-nanotube charge transfer can be inferred, since the molecule mainly concentrates in the depletion regions (Fig. 5a–c). The behaviour is similar for both complexes in this orientation (Fig. 5b and c). The charge transfer is found to be spin-dependent, slightly enhanced for the HS state (compare Fig. 5d and e for SCO2@SWCNT and Fig. S3a and S3b† for SCO1@SWCNT). The existence of a net charge transfer between both components, even if rather small, is an indication of the presence of SWCNT and SCO states of similar energy, that make the charge transfer possible. For slightly p-doped nanotubes, with empty levels in the valence band,⁶⁷ it is then reasonable to expect the enhancement of the molecule-to-nanotube charge transfer, which could explain in part the blueshift observed in the SWCNT Raman bands of both SCO@SWCNT hybrids (Fig. S6†). The slightly different charge transfer predicted for SCO1@SWCNT and SCO2@SWCNT is too subtle to be detected in the Raman spectra. The SWCNT Raman bands of both SCO1@SWCNT and SCO2@SWCNT show a similar blueshift, slightly larger for the 2D band in the SCO1@SWCNT and slightly larger for the G band in SCO2@SWCNT (Fig. S6†). Besides, temperature-dependent Raman spectroscopy of SCO1@SWCNT shows a small monotonous blueshift as the temperature is decreased. This tendency with temperature, however, does not significantly differ from that of the empty carbon nanotubes (Fig. S7†). It seems therefore that the slightly different charge transfer predicted for HS and LS states is rather small in comparison with extrinsic factors like aggregation or strain. It also implies that molecule-to-nanotube charge transfer is not responsible for a change in the oxidation state of Fe ion that could explain the distinct conductance of HS and LS states.

Fig. 5 Charge density difference plots of the SCO@SWCNT system. Yellow (positive difference) and cyan (negative difference) surfaces represent charge accumulation and depletion, respectively. (a and b) side and axial views of LS SCO2@SWCNT on geo2, (c) LS SCO1@SWCNT on geo2, and (d and e) LS and HS SCO2@SWCNT on geo1. Isodensity value of 10⁻⁴ e per bohr³.

4.3 Impact of the external electric field

The conductance of the SCO@SWCNT hybrid system was measured at a fixed bias voltage of 1 V. During these measurements, the molecule inside the nanotube is subjected to the electric field imposed by the applied bias. To explore the impact on the SCO properties, we perform a set of calculations where we impose an external electric field to the molecule using the most stable geometry adopted inside the nanotube (geo2 for SCO1, and geo1 for SCO2). The molecule is placed at the coordination axis centre, in such a way that the dipole, mainly oriented from the Fe atom to the aromatic ring (phen and bipy ligands for SCO1 and SCO2, respectively), points to the positive z axis. The external electric field strongly impacts the LS and HS energies specially when applied along the z axis (red lines in Fig. 6; blue (x axis) and green (y axis) lines in Fig. S4†). For SCO1 HS complex, there are two electronic states close in energy, separated by about 300 cm⁻¹ in the absence of the electric field. They are represented by the dotted and dashed lines in Fig. 6a. The electric dipole moment is larger for the HS states than the LS one, then the interaction with the electric field along the z axis is stronger for the HS states. Therefore, a large impact is observed on the HS–LS transition energy when the field is applied along the z axis. The transition energy is significantly reduced when the dipole moment and field are parallel (field points in the positive z axis) and enhanced for the antiparallel orientation (field points in the negative z axis). Additionally, the relative energy of the two accessible HS states is reversed for z-fields ≥7 × 10⁻³ au, the HS–LS energy separation is additionally reduced for fields stronger than this threshold value. In fact, the external electric field modifies the energy of the three orbitals with the z component (d_xz, d_yz, and d_z²) and changes the relative distribution of two of the t_2g-like 3d orbitals (red and green lines in Fig. S5†), although it does not significantly affect the strength of the Fe ligand field (Fig. S5†).

Fig. 6 (left) Total energy (in eV) of the LS and HS states of SCO1 in the presence of an external electric field (in au) along the z axis. Solid lines correspond to the LS state, while dashed and dotted lines represent two thermally accessible HS states. (right) Impact of the applied electric field along the z axis on the HS–LS transition energy (eV). The solid (dashed) lines correspond to the energy difference between the LS state and the lowest (excited) HS state in the absence of field. The inset represents the optimal orientation of the encapsulated SCO1 complex, the black arrow is the electric dipole moment, and the blue, green and red arrows represent the electric fields along x, y and z axis, respectively.

These results provide evidence for the potential effect of an external field on the SCO properties, although the field required for observing a significant change in the energies is significantly higher than the field nominally experienced by the encapsulated SCO complex in our system (about 10 kV cm⁻¹ ∼ 2 × 10⁻⁶ au). For this discrepancy it is important to first point the intrinsic limitations of these evaluations. In fact, the HS–LS transition energy is overestimated in the absence of an external field, fixed geometries are employed to the calculations in the presence of the electric field, the nanotube is not included, nor the charge transfer between nanotube and molecule, that could also alter the electric dipole of the SCO molecule and the interaction with the external field. Moreover, our results are obtained in the frame of a particular quantum chemistry approach, and dependencies on the chosen approach cannot be discarded. Then it could be possible that the applied external fields are overestimated in our calculations. On the other hand, it is important to note that the effective electric field experienced by the molecule inside the nanotube can be enhanced due to electrostatic interactions induced by doping, defects in the nanotube and impurities. Among others, these factors reduce the effective gap between the electrodes, enhancing the field. Despite the limitations, our results could be relevant in single-molecule experiments where the experimental electrical field can be orders of magnitude higher, like systems where the spin switching is promoted by an applied voltage through a STM tip. This is the case of the hairclip Ni-porphyrin deposited on Ag(111), where the spin transition is individually promoted by a voltage of 2.1–2.7 V (ref. 68) (electric field ∼0.005 au), or in single molecule–graphene junctions²² (electric field ∼0.001 au). It is significant that for an electric field of about ±0.005 au, the modulation of the HS–LS transition energy is about 8%, similar to the effect of the interaction with the nanotube.

4.4 Simulation of I -vs.- T curves

Regarding the thermal dependence of the current measured at a fixed bias V = 1 V, it has been observed in most of the samples that by cooling from room temperature down to 90 K the current switches to a high-conductance state at around 175 K, close to the transition temperature of the SCO complex. By heating the current remains in the high-conductance states, at about 225 K, where it drops back to the low-conductance state. In this hysteresis loop, the high-conductance state has been assigned to the LS complex, while the low-conductance regime is related to the HS state (Fig. 1c). When we simulate the transport properties of the SCO2@SWCNT device using the semi-classical Boltzmann transport theory we find that the conductivity is larger for the HS complex than the LS one for all temperatures (Fig. 7a), in discrepancy with most of the registered I vs. T curves (Fig. 1c). Note, however, that our simulations correspond to a single SCO molecule encapsulated inside a pristine nanotube. Interestingly, it is well-known that the SWCNTs, as well as any other carbon-based substrates like graphene, are typically p-doped systems.⁵⁷ We introduce this effect in our simulations by reducing the electronic density of the system as explained in section 3. We explore p-doping values of around 1.51 × 10¹⁹ cm⁻³, which corresponds to extract one complete electron from the system (central column in Fig. 7). A similar effect can be obtained by tuning the position of the Fermi level in our simulations (left column in Fig. 7), since the impact of p-doping on the relative current of the LS and HS states can be related, among other factors, to the shift of the Fermi level to more negative values. Interestingly, the fitting of the simulated LS and HS curves to the Arrhenius law for thermally activated electron transport provides values for the activation energy (around 2 × 10³ K, Table S1†) in the same order of magnitude as those resulting from the experimental curves (ranging from 1–4 × 10³ K).⁴²

Fig. 7 (a–k) Electron transport across SCO2@SWCNT, theoretical predictions vs. experimental I vs. T curves. Simulated conductivity vs. temperature curves for the SCO2@SWCNT device for (top) the pristine nanotube, (middle column) the nanotube with increasing p-doping, (left column) when the Fermi level of the system is shifted to more negative values. (Right column) Experimental I vs. T curves in correspondence with the theoretical predictions. The curves were measured for (d and g) SCO1@SWCNT and (i and k) SCO2@SWCNT under identical conditions (V = 1 V and ΔT = 5 K min⁻¹).

The conductivity is extremely sensitive to doping, and it changes to different extents depending on the spin state of the encapsulated complex. For p-doping of 1.30 × 10¹⁹ cm⁻³ the LS and HS curves approach themselves, although still HS is more conducting than the LS complex (Fig. 7c). A similar behaviour is found when the Fermi level is shifted to −0.135 eV (Fig. 7b). For a p-doping of about 1.47 × 10¹⁹ cm⁻³, both states present almost the same conductivity (Fig. 7f), the same trend is observed when the Fermi level is shifted to −0.150 eV (Fig. 7e). For a slightly larger p-doping of 1.50 × 10¹⁹ cm⁻³ the curves cross, the LS complex presents higher conductivity than the HS one at high temperatures (Fig. 7 h). Shifting the Fermi level to −0.164 eV, the LS complex is more conductive than the HS one (Fig. 7j). This last case reproduces most of the experimental I vs. T curves (Fig. 1c and 7k) and suggests that most of the nanotubes employed in the measurements are p-doped as expected. Interestingly, a minor number of experimental I vs. T curves can be identified by the DFT predictions for lower p doping. The right column on Fig. 7 shows these experimental curves next to the corresponding predictions. In a broad perspective, our predictions bring out the wild variety of experimental I vs. T curves that can be potentially obtained for the same SCO molecule depending on the specific local conditions, like doping, met in nanoscale devices, as has been reported in the literature.^22,69–72

5. Conclusions

The effective incorporation of spin-crossover molecules as active components of nanodevices rests on the possibility of controlling the spin-dependent modulation of physical properties such as electrical conductance. The large variety of behaviours reported up to now, although clearly demonstrate the preservation of the spin-transition once the molecule is embedded in the device, makes difficult the rationalization and much more the prediction. In this work, we have explored by means of state-of-the-art quantum chemistry calculations, the different factors governing the spin-transition at the nanoscale. We observe that the HS–LS energy gap is enhanced once the complex is encapsulated in the nanotube, the interaction with the substrate being larger for the LS than the HS state. This is not a particular feature of the molecule–SWCNT interaction, but it has been also observed for the deposition of Fe(II) SCO complexes on different substrates.^35,36,40,53 These results are in line with the opening of a hysteresis observed in our I vs. T measurements⁴² as well as many others measurements in the literature.^65,66 The differential stabilization of the LS state of the confined molecule is driven by the Fe ligand field, which is higher for the LS than the HS state. The strength of the metal–ligand field determines the degree of participation of the ligand states on the bands close to the Fermi level, the higher the field, the larger the participation. The ligand orbitals spatially extended more than the metal one allowing for a stronger interaction with the substrate. It is then expected that the stronger interaction of the LS state with the substrate will be a general trend of the SCO molecule–substrate interaction.

We have checked the impact of the L ligand (bipy, phen) on both the accommodation of the molecule inside the nanotube and the energetics of the interaction. We found that the SCO molecule experiences a spin-dependent distortion after encapsulation and there are two orientations in competition, although very close in energy, in particular for the SCO2 complex. Then, in our case, small variations in the SCO ligands do not significantly alter the accommodation of the SCO molecules within the SWCNT, but it is important to keep in mind the strong similarities of bipy and phen ligands.

The rather small charge transfer between the pristine nanotube and the SCO molecule predicted by our calculations rules out the possibility of change of the Fe oxidation state to be responsible for the different conductance registered for LS and HS states. The blueshift observed in the SWCNT Raman bands for both SCO@SWCNT hybrids⁴² could be related to extrinsic factors and only in part to the small molecule-to-nanotube charge transfer.

The strong electric field experienced by the SCO molecule on the nanodevice can modulate the spin transition to different extents depending on the relative orientation of the molecule with the respect to the imposed field. The field also modifies the relative energy of the Fe 3d orbitals, which could also promote the switching between different orientations inside the nanotube, and could drive changes on the coordination sphere of the FeN₆ core. The non-negligible impact of the external electric field on the HS–LS transition energy could be the origin, for instance, of the reported telegraph-like switch between two states of different conductance below the transition temperature for SCO-based nanodevices.^22,73

Finally, our simulations provide evidence for how the specific local conditions of the substrate dramatically affect the I vs. T curves of the SCO@SWCNT system, and could help explain the large diversity of reported I vs. T behaviours for nanoscale devices, such as HS being more conductive than LS,^71,74–76 indistinguishable HS–LS conductance,⁴⁴ crossing HS–LS curves and, the most common case in this study, LS being more conductive than the HS state.^23,42,72

Author contributions

C.J.C. and E.B. designed and supervised the theoretical calculations and experiments, respectively. R.SdA., N.M-P. and C.J.C. realized the DFT and wave-function based calculations. A.D. fabricated the nanodevices and performed the electron transport measurements. All the authors contributed to the discussion of the results. C.J.C. wrote the manuscript with input from all the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support provided by the Ministerio de Ciencia e Innovación − Agencia Estatal de Investigación (Spain) and FEDER funds through Project PGC2018-101689-B-I00 (MCI/AEI/FEDER,UE), RTI2018-096075-A-C22 and RYC2019-028429-I is acknowledged. N.M-P. thanks the financial support of ANID (CHILE) under Project “Postdoctorado FONDECYT 2021 No. 3210181”. The authors acknowledge Julia Villalva, Jose Sánchez Costa and Emilio M. Pérez for the initial preparation of the samples. The technical support of the Supercomputing Team of the Centro Informático Científico de Andalucía (CICA) and the access to the computational facilities of the “Centro de Servicios de Informática y Redes de Comunicaciones” (CSIRC, Universidad de Granada, Spain) are also acknowledged.

References

1. P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed. Engl., 1994, 33, 2024–2054.
2. K. S. Kumar and M. Ruben, Angew. Chem., Int. Ed, 2021, 60, 7502–7521.
3. A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335.
4. L. Kipgen, M. Bernien, F. Tuczek and W. Kuch, Adv. Mater., 2021, 33, 2008141.
5. G. Molnar, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Adv. Mater., 2018, 30, 17003862.
6. K. S. Kumar and M. Ruben, Coord. Chem. Rev., 2017, 346, 176–205.
7. M. Gruber and R. Berndt, Magnetochemistry, 2020, 6, 35.
8. A. Rotaru, I. A. Gural'skiy, G. Molnar, L. Salmon, P. Demont and A. Bousseksou, Chem. Commun., 2012, 48, 4163–4165.
9. Y. S. Koo and J. R. Galan-Mascaros, Adv. Mater., 2014, 26, 6785–6789.
10. D. Qiu, D. H. Ren, L. Gu, X. L. Sun, T. T. Qu, Z. G. Gu and Z. J. Li, RSC Adv., 2014, 4, 31323–31327.
11. K. S. Kumar, I. Salitros, Z. Boubegtiten-Fezoua, S. Moldovan, P. Hellwig and M. Ruben, Dalton Trans., 2018, 47, 35–40.
12. A. Bousseksou, G. Molnar, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313–3335.
13. T. Forestier, A. Kaiba, S. Pechev, D. Denux, P. Guionneau, C. Etrillard, N. Daro, E. Freysz and J. Letard, Chem. – Eur. J., 2009, 15, 6122–6130.
14. F. Volatron, L. Catala, E. Riviere, A. Gloter, O. Stephan and T. Mallah, Inorg. Chem., 2008, 47, 6584–6586.
15. L. Kipgen, M. Bernien, S. Ossinger, F. Nickel, A. J. Britton, L. M. Arruda, H. Naggert, C. Luo, C. Lotze, H. Ryll, F. Radu, E. Schierle, E. Weschke, F. Tuczek and W. Kuch, Nat. Commun., 2018, 9, 2984.
16. S. Shi, G. Schmerber, J. Arabski, J.-B. Beaufrand, D. J. Kim, S. Boukari, M. Bowen, N. T. Kemp, N. Viart, G. Rogez, E. Beaurepaire, H. Aubriet, J. Petersen, C. Becker and D. Ruch, Appl. Phys. Lett., 2009, 95, 043303.
17. M. Gruber, V. Davesne, M. Bowen, S. Boukari, E. Beaurepaire, W. Wulfhekel and T. Miyamachi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195415.
18. K. Bairagi, O. Iasco, A. Bellec, A. Kartsev, D. Li, J. Lagoute, C. Chacon, Y. Girard, S. Rousset, F. Miserque, Y. J. Dappe, A. Smogunov, C. Barreteau, M.-L. Boillot, T. Mallah and V. Repain, Nat. Commun., 2016, 7, 12212.
19. H. Naggert, J. Rudnik, L. Kipgen, M. Bernien, F. Nickel, L. M. Arruda, W. Kuch, C. Näther and F. Tuczek, J. Mater. Chem. C, 2015, 3, 7870–7877.
20. A. Pronschinske, Y. Chen, G. F. Lewis, D. A. Shultz, A. Calzolari, M. B. Nardelli and D. B. Dougherty, Nano Lett., 2013, 13, 1429–1434.
21. B. Warner, J. C. Oberg, T. G. Gill, F. El Hallak, C. F. Hirjibehedin, M. Serri, S. Heutz, M.-A. Arrio, P. Sainctavit, M. Mannini, G. Poneti, R. Sessoli and P. Rosa, J. Phys. Chem. Lett., 2013, 4, 1546–1552.
22. E. Burzurí, A. García-Fuente, V. García-Suárez, K. S. Kumar, M. Ruben, J. Ferrer and H. S. J. van der Zant, Nanoscale, 2018, 10, 7905–7911.
23. A. Rotaru, J. Dugay, R. P. Tan, I. A. Gural'skiy, L. Salmon, P. Demont, J. Carrey, G. Molnar, M. Respaud and A. Bousseksou, Adv. Mater., 2013, 25, 1745–1749.
24. K. P. Kepp, Inorg. Chem., 2016, 55, 2717–2727.
25. O. S. Siig and K. P. Kepp, J. Phys. Chem. A, 2018, 122, 4208–4217.
26. S. Vela, M. Fumanal, J. Ribas-Arino and V. Robert, Phys. Chem. Chem. Phys., 2015, 17, 16306–16314.
27. S. Vela, M. Fumanal, J. Ribas-Ariño and V. Robert, J. Comput. Chem., 2016, 37, 947–953.
28. J. Cirera and E. Ruiz, J. Mater. Chem. C, 2015, 3, 7954–7961.
29. N. Suaud, M.-L. Bonnet, C. Boilleau, P. Labèguerie and N. Guihéry, J. Am. Chem. Soc., 2009, 131, 715–722.
30. B. Ordejón, C. de Graaf and C. Sousa, J. Am. Chem. Soc., 2008, 130, 13961–13968.
31. M. Kepenekian, B. Le Guennic and V. Robert, J. Am. Chem. Soc., 2009, 131, 11498–11502.
32. J. Cirera and E. Ruiz, Comments Inorg. Chem., 2019, 39, 216–241.
33. S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772–774.
34. J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105.
35. M. Gruber, T. Miyamachi, V. Davesne, M. Bowen, S. Boukari, W. Wulfhekel, M. Alouani and E. Beaurepaire, J. Chem. Phys., 2017, 146, 092312.
36. N. Montenegro-Pohlhammer, R. Sánchez-de-Armas and C. J. Calzado, Chem. – Eur. J., 2021, 27, 712–723.
37. N. Montenegro-Pohlhammer, R. Sánchez-de-Armas, C. J. Calzado, M. Borges-Martínez and G. Cárdenas-Jirón, Dalton Trans., 2021, 50, 6578–6587.
38. S. Lebègue, S. Pillet and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 024433.
39. T. Bučko, J. Hafner, S. Lebègue and J. G. Ángyán, Phys. Chem. Chem. Phys., 2012, 14, 5389–5396.
40. S. Gueddida and M. Alouani, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 144413.
41. S. Gueddida, M. Gruber, T. Miyamachi, E. Beaurepaire, W. Wulfhekel and M. Alouani, J. Phys. Chem. Lett., 2016, 7, 900–904.
42. J. Villalva, A. Develioglu, N. Montenegro-Pohlhammer, R. Sánchez-de-Armas, A. Gamonal, E. Rial, M. García-Hernández, L. Ruiz-Gonzalez, J. S. Costa, C. J. Calzado, E. M. Pérez and E. Burzurí, Nat. Commun., 2021, 12, 1578.
43. M. Bernien, H. Naggert, L. M. Arruda, L. Kipgen, F. Nickel, J. Miguel, C. F. Hermanns, A. Krüger, D. Krüger, E. Schierle, E. Weschke, F. Tuczek and W. Kuch, ACS Nano, 2015, 9, 8960–8966.
44. C. Lefter, S. Rat, J. S. Costa, M. D. Manrique-Juarez, C. M. Quintero, L. Salmon, I. Seguy, T. Leichle, L. Nicu, P. Demont, A. Rotaru, G. Molnar and A. Bousseksou, Adv. Mater., 2016, 28, 7508–7514.
45. J. A. Real, M. C. Muñoz, J. Faus and X. Solans, Inorg. Chem., 1997, 36, 3008–3013.
46. B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
47. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
48. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4.
50. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
51. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50.
52. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
53. C. M. Palomino, R. Sánchez-de-Armas and C. J. Calzado, J. Chem. Phys., 2021, 154, 034701.
54. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
55. G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145.
56. J. P. Jesson, S. Trofimenko and D. R. Eaton, J. Am. Chem. Soc., 1967, 89, 3148–3158.
57. B. Nieto-Ortega, J. Villalva, M. Vera-Hidalgo, L. Ruiz-González, E. Burzurí and E. M. Pérez, Angew. Chem., Int. Ed., 2017, 56, 12240–12244.
58. J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
59. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129.
60. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
61. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
62. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
63. E. V. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
64. J. P. Muscat and D. M. Newns, Prog. Surf. Sci., 1978, 9, 1–43.
65. X. Jiang, G. Hao, X. Wang, A. Mosey, X. Zhang, L. Yu, A. J. Yost, A. D. DiChiara, A. T. N'Diaye, X. Cheng, J. Zhang, R. Cheng, X. Xu and P. A. Dowben, J. Phys.: Condens. Matter, 2019, 31, 315401.
66. H. Peng, S. Tricard, G. Félix, G. Molnár, W. Nicolazzi, L. Salmon and A. Bousseksou, Angew. Chem., Int. Ed., 2014, 53, 10894–10898.
67. R. L. McSweeney, T. W. Chamberlain, M. Baldoni, M. A. Lebedeva, E. S. Davies, E. Besley and A. N. Khlobystov, Chem. – Eur. J., 2016, 22, 13540–13549.
68. A. Köbke, F. Gutzeit, F. Röhricht, A. Schlimm, J. Grunwald, F. Tuczek, M. Studniarek, D. Longo, F. Choueikani, E. Otero, P. Ohresser, S. Rohlf, S. Johannsen, F. Diekmann, K. Rossnagel, A. Weismann, T. Jasper-Toennies, C. Näther, R. Herges, R. Berndt and M. Gruber, Nat. Nanotechnol., 2020, 15, 18–21.
69. D. Tanaka, N. Aketa, H. Tanaka, S. Horike, M. Fukumori, T. Tamaki, T. Inose, T. Akai, H. Toyama, O. Sakata, H. Tajiri and T. Ogawa, Dalton Trans., 2019, 48, 7074–7079.
70. J. Dugay, M. Aarts, M. Giménez-Marqués, T. Kozlova, H. W. Zandbergen, E. Coronado and H. S. J. van der Zant, Nano Lett., 2017, 17, 186–193.
71. T. G. Gopakumar, F. Matino, H. Naggert, A. Bannwarth, F. Tuczek and R. Berndt, Angew. Chem., Int. Ed., 2012, 51, 6262–6266.
72. J. Dugay, M. Giménez-Marqués, T. Kozlova, H. W. Zandbergen, E. Coronado and H. S. J. van der Zant, Adv. Mater., 2015, 27, 1288–1293.
73. T. Jasper-Toennies, M. Gruber, S. Karan, H. Jacob, F. Tuczek and R. Berndt, Nano Lett., 2017, 17, 6613–6619.
74. R. Frisenda, G. D. Harzmann, J. A. Celis Gil, J. M. Thijssen, M. Mayor and H. S. J. van der Zant, Nano Lett., 2016, 16, 4733–4737.
75. T. Miyamachi, M. Gruber, V. Davesne, M. Bowen, S. Boukari, L. Joly, F. Scheurer, G. Rogez, T. K. Yamada, P. Ohresser, E. Beaurepaire and W. Wulfhekel, Nat. Commun., 2012, 3, 938.
76. F. Prins, M. Monrabal-Capilla, E. A. Osorio, E. Coronado and H. S. J. van der Zant, Adv. Mater., 2011, 23, 1545–1549.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr04577f

---