Open Access Article
Open Access ArticleDynamic Kerr and Pockels electro-optics of liquid crystals in nanopores for active photonic metamaterials
Andriy V.
Kityk
 *a,
Marcjan
Nowak
a,
Manuela
Reben
b,
Piotr
Pawlik
c,
Monika
Lelonek
d,
Anatoliy
Andrushchak
e,
Yaroslav
Shchur
f,
Nazariy
Andrushchak
gh and
Patrick
Huber
*a,
Marcjan
Nowak
a,
Manuela
Reben
b,
Piotr
Pawlik
c,
Monika
Lelonek
d,
Anatoliy
Andrushchak
e,
Yaroslav
Shchur
f,
Nazariy
Andrushchak
gh and
Patrick
Huber
 *ijk
*ijk
aFaculty of Electrical Engineering, Czestochowa University of Technology, Al. Armii Krajowej 17, 42-200 Czestochowa, Poland. E-mail: andriy.kityk@univie.ac.at
bFaculty of Materials Science and Ceramics, AGH-University of Science and Technology, al. Mickiewicza 30, 30-059 Cracow, Poland
cFaculty of Production Engineering and Materials Science, Czestochowa University of Technology, Al. Armii Krajowej 19, 42-200 Czestochowa, Poland
dSmartMembranes GmbH, Heinrich-Damerow-Str. 4, 06120 Halle(Saale), Germany
eDepartment of Applied Physics and Nanomaterials Science, Lviv Polytechnic National University, 12 Bandery Str., Lviv 79013, Ukraine
fInstitute for Condensed Matter Physics, 1 Svientsitskii str., 79011 Lviv, Ukraine
gDepartment of Computer-Aided Design Systems, Lviv Polytechnic National University, 12 Bandery Str., Lviv 79013, Ukraine
hPrivate Enterprise SoftPartners, 97 Konovalca str., 79057 Lviv, Ukraine
iHamburg University of Technology, Institute for Materials and X-Ray Physics, 21073 Hamburg, Germany. E-mail: patrick.huber@tuhh.de
jDeutsches Elektronen-Synchrotron DESY, Centre for X-Ray and Nano Science CXNS, 22607 Hamburg, Germany
kHamburg University, Centre for Hybrid Nanostructures CHyN, 22607 Hamburg, Germany
First published on 5th November 2021
Abstract
Photonic metamaterials with properties unattainable in base materials are already beginning to revolutionize optical component design. However, their exceptional characteristics are often static, as artificially engineered into the material during the fabrication process. This limits their application for in-operando adjustable optical devices and active optics in general. Here, for a hybrid material consisting of a liquid crystal-infused nanoporous solid, we demonstrate active and dynamic control of its meta-optics by applying alternating electric fields parallel to the long axes of its cylindrical pores. First-harmonic Pockels and second-harmonic Kerr birefringence responses, strongly depending on the excitation frequency and temperature, are observed in a frequency range from 50 Hz to 50 kHz. This peculiar behavior is quantitatively traced by a Landau–De Gennes free energy analysis to an order–disorder orientational transition of the rod-like mesogens and intimately related changes in the molecular mobilities and polar anchoring at the solid walls on the single-pore, meta-atomic scale. Thus, our study provides evidence that liquid crystal-infused nanopores exhibit integrated multi-physical couplings and reversible phase changes that make them particularly promising for the design of photonic metamaterials with thermo-electrically tunable birefringence in the emerging field of space–time metamaterials aiming at full spatio-temporal control of light.
1 Introduction
2-D and 3-D metamaterials offer exciting opportunities for the manipulation of light propagation and light–matter interaction.1–3 Although metamaterials have proven to be a versatile platform for passive optics, active controlling of their optical properties is still a challenging task. Here phase-change materials that employ inorganic, hard matter with an amorphous to crystalline transition open up many opportunities for implementing externally tunable metamaterials as the reversible transition is accompanied by a considerable change of the refractive index.4–6 Also embedding liquid crystals (LCs) in nanoporous solids allows one to combine self-assembly and phase transition behavior of organic, soft matter with a scaffold structure that provides mechanical robustness. Thereby it is possible to fabricate soft–hard hybrids with tunable multi-physical couplings in terms of self-organization, mechanical, electrical and optical properties.7–11 For example, LC-functionalized porous media were recently employed to fabricate smart windows materials with voltage-switchable scattering properties.12,13If the pore size is below the visible light wavelength the single pores act as meta-atoms. The effective optics is then determined by the pore shape, size and orientation. Moreover, the pore filling allows one to adjust the light–matter interaction on the meta-atomic scale.9,11,14,15 Effective optical properties not achievable in base materials are possible,2,11,14,16–22 specifically adjustable birefringence.9 However, the resulting optics here is also often static as dictated by the fabrication process and cannot easily be dynamically adapted, as it is required for the emerging field of active and space–time photonic metamaterials.3,6,23,24 Dynamic 2-D photonic meta-surfaces will allow for dynamic holographic techniques with applications in 3D displays, optical storage, optical encryption, and optical information processing25 or the active control of the angular momentum of light.26
Here, we follow the strategy to overcome the static behavior by applying external electric fields to liquid crystals confined in anodic aluminum oxide nanopores.
Hereby, we have to consider that in many previous experimental and theoretical studies27–42 it has been shown that the self-assembly behavior and molecular mobility can be substantially modified in spatially confined geometries. More importantly, the impacts of these confinement effects on the electro-optics have been barely explored so far. Therefore, we will also study the phase behavior of the confined liquid crystal and its impact on thermo-optical and electro-optical couplings in nanoconfinement.
In the following we provide a brief introduction to electro-optic effects and then present our experimental study aimed at integrating these functionalities in a nanoporous composite. The electro-optic effect was first reported by John Kerr in 1875.43 While examining optically isotropic media he noticed electric field-induced optical birefringence (anisotropy), the magnitude of which increased quadratically with the electric field strength. Eight years later, Röntgen and Kundt independently reported electro-optic effects in quartz and tourmaline, i.e., in anisotropic piezoelectric crystalline materials.44 In contrast to the Kerr effect, the electrically induced birefringence changed linearly with the applied electric field. In a number of later experiments it was demonstrated that the linear electro-optic effect is observable only in non-centrosymmetric crystals and it was appropriately described by Pockels in 1893 within a phenomenological theory based on crystal symmetry and tensor analysis.44
Thus, in crystalline materials both linear and quadratic electro-optic effects are essentially related to anisotropic effective optical properties. The corresponding tensor analysis shows that inversion symmetry implies that a linear response is forbidden. For this reason the Pockels effect is in particular observable in piezoelectric crystals with broken inversion symmetry. Moreover, it may be found in poled glasses or ceramics45 and likewise in other noncrystalline polar materials, as well as chiral LC materials, for example in tilted chiral smectics (ferroelectric LCs).41,46–48
The Kerr effect, in contrast, is also observable in centrosymmetric media, including isotropic liquids. Both linear Pockels and quadratic Kerr effects are caused by the rotational diffusion of molecules, the dipoles of which are able to follow the applied electric field. Liquids consisting of small polar molecules are characterized by fast electro-optic response times, usually in the range of nanoseconds or even below.49,50 By contrast the dynamics slows down for large molecules.51,52
From the application point of view both electro-optic effects provide means for refractive index modulation driven by an applied electric field. This offers an elegant possibility to integrate the modulation of phase retardation or light intensity into a material.44
Here we report a dynamic electro-optical study (electro-optical response time) on the rod-like nematic LC 7CB embedded into cylindrical nanopores of anodic alumina oxide (AAO) membranes. Linear and quadratic electro-optical effects are explored via first and second harmonic response, respectively, measured by a lock-in technique in a frequency window from 50 Hz to 50 kHz and a broad temperature range encompassing paranematic and confined nematic states. These electro-optic measurements are complemented by simultaneous polarimetric measurements of the optical retardation (birefringence). The latter reveal the temperature evolution of the static orientational order in the region of the paranematic-to-nematic transition. The obtained results are analyzed within a phenomenological Landau–De Gennes model accounting for the interaction of the nematic order parameter and the applied electric field.
2 Experimental
2.1 Materials and sample preparation
Nematic liquid crystal 7CB (4-heptyl-40-cyano biphenyl, see Fig. 2d) was purchased from Merck AG. A characteristic feature of 7CB is a simple phase diagram in the bulk state. It exhibits only a single first order phase transition during cooling from the isotropic (I) to the nematic (N) phase at TIN = 315.5 K (ref. 53) before solidification. The AAO (membrane thickness h = 130 μm) was synthesized by means of a double-stage electrochemical etching process of pure aluminum in an oxalic acid (30%) electrolyte. The resulting mesoporous AAO matrices consist of a hexagonally arranged, parallel array of slightly conical channels (mean pore diameter 65 nm), see Fig. 2a. The conicity of the pores results from the unidirectional etching process.54 The as-fabricated oxidic pore walls are polar, hydrophilic.37 No surface treatment was employed before embedding the liquid crystals.The nematic 7CB melt was embedded into the cylindrical nanopores by capillarity-driven spontaneous imbibition.55 To build an electro-optical cell for the dynamic electro-optic and the polarimetric measurements the AAO:7CB composite membrane was clamped between two transparent ITO glass electrodes, see Fig. 2a, b and c, respectively. The electro-optic cell was placed into a temperature cell operated by a temperature controller (Lakeshore-340) with a control accuracy of 0.01 K.
2.2 Electro-optic setup
In Fig. 1b the laboratory setup for simultaneous optical retardation and electro-optic measurements is shown. It combines a photo-elastic modulation polarimeter and lock-in amplifier technique for a reference registration of the first (1Ω) and second (2Ω) harmonics of the electro-optic response. Since the AAO membrane consists of an array of parallel tubular nanopores, both the empty AAO matrices as well as the LC nanocomposites effectively exhibit uniaxial optical anisotropy with one optical axis parallel to the long pore axis.30–32 The anisotropy is described by an optical indicatrix with rotational symmetry (n1 = n2 = no, n3 = ne). Temperature changes, likewise the electric field applied along the channel axis, result in a deformation of the optical indicatrix only, not in a rotation. Moreover, the prolate indicatrix shape is conserved. Accordingly, the optical birefringence can be explored only in the tilted sample geometry. Following Berek's equation the optical retardation R(Θ) is expressed in this case as , where d is the sample thickness, λ is the light wavelength, and Θ is the incident angle.56 Electro-optically induced changes of the optical retardation ΔR(Θ), likewise R(Θ), increase with Θ starting from a zero response at Θ = 0. The larger the incident angle the larger the measured R or ΔR. At considerably large incident angles (Δ > ∼50 deg) light reflection considerably increases. This complicates the polarimetry measurements. In addition, the range of incident angles is limited also by the sample aperture. Therefore, incident angles in the range of 35–40 deg are considered to be the most appropriate. Here, we tilted the sample with respect to the normal incidence of the laser beam by ∼40 degrees along the incident laser beam direction, see Fig. 1a and b. Measurements of the thermotropic or electro-induced retardation as a function of this tilt angle do not give any new insight into the phenomena discussed. Having measured R or ΔR just for one specific angle Θ < > 0, one can easily and precisely determine both quantities for any other incident angle Θ by Berek's equation.
, where d is the sample thickness, λ is the light wavelength, and Θ is the incident angle.56 Electro-optically induced changes of the optical retardation ΔR(Θ), likewise R(Θ), increase with Θ starting from a zero response at Θ = 0. The larger the incident angle the larger the measured R or ΔR. At considerably large incident angles (Δ > ∼50 deg) light reflection considerably increases. This complicates the polarimetry measurements. In addition, the range of incident angles is limited also by the sample aperture. Therefore, incident angles in the range of 35–40 deg are considered to be the most appropriate. Here, we tilted the sample with respect to the normal incidence of the laser beam by ∼40 degrees along the incident laser beam direction, see Fig. 1a and b. Measurements of the thermotropic or electro-induced retardation as a function of this tilt angle do not give any new insight into the phenomena discussed. Having measured R or ΔR just for one specific angle Θ < > 0, one can easily and precisely determine both quantities for any other incident angle Θ by Berek's equation.
The measuring process switched between two detection modes, the polarimetry and the electro-optic response mode, respectively. The polarimetry mode is active when the photo-elastic modulator (PEM, f = 50 kHz, PEM-90 Hind Instruments) was turned on. The optical retardation, Δ, is defined as ΔnL, where Δn is the effective birefringence in the direction of light propagation and L is the length of the pathway of light traveling through the anisotropic medium. In this mode a simultaneous reference detection of the first (r1f) and second (r2f) harmonics of modulated light (hereafter termed PEM harmonics) by means of the lock-in amplifier (Stanford Research, SR-830) yielded the value of the optical retardation Δ = arctan(kr1f/r2f). Here the factor k, which is defined by a ratio of Bessel functions J2(A0)/J1(A0) at the retardation PEM amplitude (A0 = 0.383λ) and the photodetector (PD) frequency response characteristic, was determined within a calibration procedure, for additional details see ref. 9, 30, 41, 47, 56 and 57.
2.3 Dynamic electro-optic analysis
In the electro-optic response mode the PEM was turned off. An alternating electric field E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Ωt) (E0 ∼ 3000 V cm−1) was applied parallel to the nanopore axis by applying electric potentials between the transparent ITO electrodes. This induces an electro-optic retardation. In the low frequency limit (Ωτ ≪ 1) the linear electro-optic effect implies that the electro-induced retardation Δe ∝ E0
sin(Ωt) (E0 ∼ 3000 V cm−1) was applied parallel to the nanopore axis by applying electric potentials between the transparent ITO electrodes. This induces an electro-optic retardation. In the low frequency limit (Ωτ ≪ 1) the linear electro-optic effect implies that the electro-induced retardation Δe ∝ E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Ωt), i.e., its phase modulation has the same frequency as the exciting electrical field, Ω. For the quadratic electro-optic effect, in contrast, Δe ∝ E02
sin(Ωt), i.e., its phase modulation has the same frequency as the exciting electrical field, Ω. For the quadratic electro-optic effect, in contrast, Δe ∝ E02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(Ωt) = E02(1 − cos(2Ωt))/2 = E02/2 + (E02/2)sin(2Ωt + π/2) the electric field-induced retardation is characterized by the static component (∝E02) and a dynamic component of doubled frequency, 2Ω that is phase shifted by π/2 and ∝E02. At higher frequencies relaxation processes emerge (Ωτ ∼ 1) leading to a phase shift φ in the electro-optic response. In the polarizer–analyzer system the electric field-induced dynamic retardation is converted into a modulated light intensity, which is detected by the photodetector PD and subsequently analyzed by the lock-in amplifier SR-830 with respect to the applied reference voltage, extracting thus the amplitude (ρΩi) and phase (φi) of its first (1Ω) and second (2Ω) harmonic components of the complex electro-optic responses, i.e.
sin2(Ωt) = E02(1 − cos(2Ωt))/2 = E02/2 + (E02/2)sin(2Ωt + π/2) the electric field-induced retardation is characterized by the static component (∝E02) and a dynamic component of doubled frequency, 2Ω that is phase shifted by π/2 and ∝E02. At higher frequencies relaxation processes emerge (Ωτ ∼ 1) leading to a phase shift φ in the electro-optic response. In the polarizer–analyzer system the electric field-induced dynamic retardation is converted into a modulated light intensity, which is detected by the photodetector PD and subsequently analyzed by the lock-in amplifier SR-830 with respect to the applied reference voltage, extracting thus the amplitude (ρΩi) and phase (φi) of its first (1Ω) and second (2Ω) harmonic components of the complex electro-optic responses, i.e. = ρ1Ω
= ρ1Ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iφ1) and
exp(iφ1) and  = ρ2Ω
= ρ2Ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(i(φ2 + π/2)) = iρ2Ω
exp(i(φ2 + π/2)) = iρ2Ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iφ2), respectively.
exp(iφ2), respectively.
Please note that a retardation-to-intensity conversion function in the system with crossed polarizer P and analyzer A is defined as ∝I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2(Δ/2) = I0(1 − cos
sin2(Δ/2) = I0(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ)/2, see Fig. 2e. Here, I0 is the incident light intensity of the coherent He–Ne laser light (λ = 633 nm). The total retardation Δ, in general, represents a superposition of the static retardation, Δ0, induced by the sample (S) and the Babinet compensator (BC), as well as the dynamic electro-optic component, Δi(E0)sin(Ωit + φi). Accordingly, the dynamic retardation is converted to the modulated light intensity in an undistorted way (linear conversion) if the static retardation Δ0 = (2n ± 1/2)π (n = 0, 1, 2, …) whereas Δi(E0) ≪ π. Taking into account that the sample birefringence changes with temperature the BC serves here to precisely adjust the static phase shift to the conditions mentioned above. The corresponding manual adjustment, which corresponds to the condition that the first PEM harmonic r1f reaches a maximum (i.e. r2f = 0), was made in the polarimetry mode at each temperature set point prior to the electro-optic response measurements.
Δ)/2, see Fig. 2e. Here, I0 is the incident light intensity of the coherent He–Ne laser light (λ = 633 nm). The total retardation Δ, in general, represents a superposition of the static retardation, Δ0, induced by the sample (S) and the Babinet compensator (BC), as well as the dynamic electro-optic component, Δi(E0)sin(Ωit + φi). Accordingly, the dynamic retardation is converted to the modulated light intensity in an undistorted way (linear conversion) if the static retardation Δ0 = (2n ± 1/2)π (n = 0, 1, 2, …) whereas Δi(E0) ≪ π. Taking into account that the sample birefringence changes with temperature the BC serves here to precisely adjust the static phase shift to the conditions mentioned above. The corresponding manual adjustment, which corresponds to the condition that the first PEM harmonic r1f reaches a maximum (i.e. r2f = 0), was made in the polarimetry mode at each temperature set point prior to the electro-optic response measurements.
The magnitude of the first PEM harmonic, r1f(A0 = 0.383λ), which is proportional to the incident light intensity I0, has also been used as the reference value for the normalization of the electro-optic response amplitudes ρ1Ω and ρ2Ω. The electro-optic retardation amplitude Δi(E0), on the other hand, did not exceed our experimental value of one angular minute. Note that the amplitudes ρ1Ω and ρ2Ω are normalized by a value of 10–6r1ω(0.383λ) as reference magnitude, that is extracted in the polarimetry mode for a PEM retardation amplitude set to 0.383λ.
3 Results and discussion
3.1 Temperature-dependent static collective orientational order and dynamic electro-optics
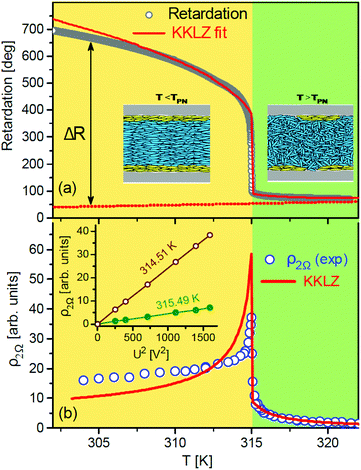
It has been established that for cylindrical pores distinct liquid-crystalline configurations exist. These encompass five untwisted stable configurations of the nematic director field depending on the anchoring conditions: uniform axial, planar radial, planar polar, escaped radial, and escaped radial with point defects.58–61 Since we employ native, oxidic AAO pore walls with planar anchoring, we expect uniform axial arrangements of the 7CB molecules with a positive optical anisotropy upon entering the nematic phase, also based on the results from previous experiments.32Indeed, the optical retardation, R(T) that characterizes the evolution of the static orientational ordering inside the nanochannels (R ∝ S, where S is the nematic order parameter), indicates the formation of an axial arranged state as a function of cooling, see Fig. 3. In the paranematic phase (T > TPN) R(T) is small indicating an almost isotropic confined LC. However, the R(T)-dependence exhibits a characteristic pretransitional tail typical of nematic precursor ordering in the interfacial region of tubular nanochannels.30 A near step-like increase at TPN indicates a discontinuous evolution of the paranematic-to-nematic ordering caused by an abrupt appearance of axial nematic molecular arrangement in the core region of the pore filling, see Fig. 3.30
How is this thermotropic orientational order connected with the electro-optic response to an alternating external electric field  , see Fig. 1. In Fig. 4 we show the amplitudes of the first [ρ1Ω] and second [ρ2Ω] harmonics of the electro-optic response vs. temperature T at a fixed driving frequency of 420 Hz and a voltage amplitude of 40 V. Whereas the observation of a finite quadratic Kerr amplitude is expected as a response of the confined LC, we also observe a linear Pockels effect. At first glance it is symmetry forbidden, since a non-centrosymmetric structure of the nanocomposite is not apparent. The existence of both distinct electro-optic effects is unambiguously corroborated by the voltage dependencies of the amplitudes of the first and second harmonic amplitude, ρ1Ω(U) and ρ2Ω(U2). As expected they scale linearly and quadratically on the amplitude of the applied voltage and thus to the applied external electric field, respectively.
, see Fig. 1. In Fig. 4 we show the amplitudes of the first [ρ1Ω] and second [ρ2Ω] harmonics of the electro-optic response vs. temperature T at a fixed driving frequency of 420 Hz and a voltage amplitude of 40 V. Whereas the observation of a finite quadratic Kerr amplitude is expected as a response of the confined LC, we also observe a linear Pockels effect. At first glance it is symmetry forbidden, since a non-centrosymmetric structure of the nanocomposite is not apparent. The existence of both distinct electro-optic effects is unambiguously corroborated by the voltage dependencies of the amplitudes of the first and second harmonic amplitude, ρ1Ω(U) and ρ2Ω(U2). As expected they scale linearly and quadratically on the amplitude of the applied voltage and thus to the applied external electric field, respectively.
We trace the linear electro-optic response of the confined mesogens to a preferential unipolar interfacial ordering that breaks the macroscopic centrosymmetry of the bulk isotropic or nematic ordering. However, given the cylindrical pore wall geometry this would still result in centrosymmetric structures. Thus we suggest that the conicity of the channels, as dictated by the fabrication process,54 results in macroscopic non-centrosymmetric polarizability along the channel axis and thus causes the Pockels effect. It is interesting to mention that a similar impact of conicity on second harmonic generation has recently been reported for chromophores embedded in conical silica nanochannels.15
In Fig. 5 we show the frequency dispersion of the real and imaginary parts of the first ( = ρ1Ω
= ρ1Ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iφ1), left) and second (
exp(iφ1), left) and second ( = −ρ2Ω
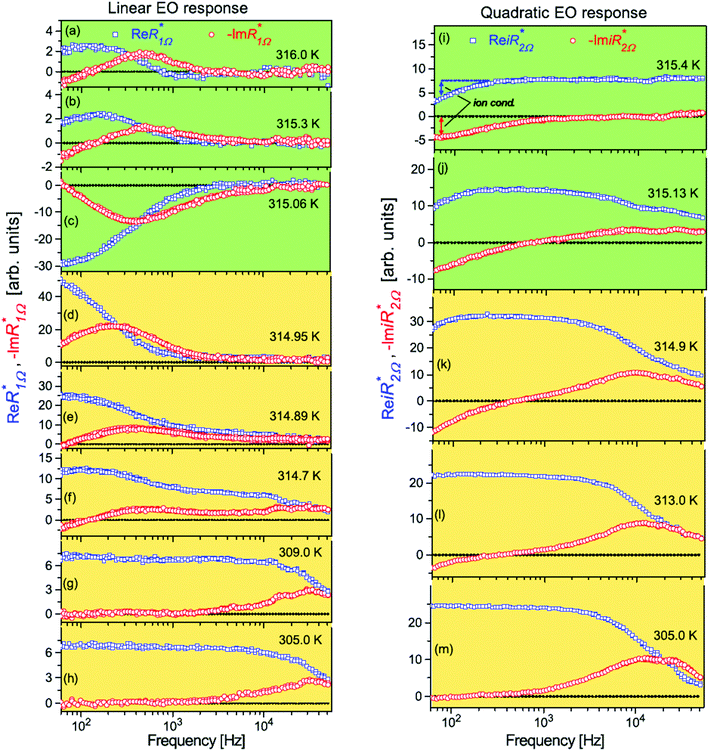
= −ρ2Ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iφ2), right) harmonics of the electro-optic response measured at different temperatures. The dynamic electro-optic measurements are limited in our experiments to a frequency window of 0.05–50 kHz. Whereas its upper frequency limit is given by the instrumental constraints of the lock-in technique, the lower one originates from ionic conductivity rising strongly at lower frequencies. It results in additional phase shifts and losses in the low frequency electro-optic responses below ∼200 Hz, especially at higher temperatures, see the mark in Fig. 5. The ionic conductivity influences both the linear and quadratic electro-optic responses. At driving frequencies above 400 Hz, however, the ionic conductivity is considerably suppressed. Therefore, we usually omit the frequency region below 400 Hz in our discussion.
exp(iφ2), right) harmonics of the electro-optic response measured at different temperatures. The dynamic electro-optic measurements are limited in our experiments to a frequency window of 0.05–50 kHz. Whereas its upper frequency limit is given by the instrumental constraints of the lock-in technique, the lower one originates from ionic conductivity rising strongly at lower frequencies. It results in additional phase shifts and losses in the low frequency electro-optic responses below ∼200 Hz, especially at higher temperatures, see the mark in Fig. 5. The ionic conductivity influences both the linear and quadratic electro-optic responses. At driving frequencies above 400 Hz, however, the ionic conductivity is considerably suppressed. Therefore, we usually omit the frequency region below 400 Hz in our discussion.
In the paranematic phase T > TPN linear and quadratic electro-optic responses indicate quite different frequency dispersions, compare panels (a) and (i) in Fig. 5. The linear response, symmetry forbidden in the bulk, exhibits a slow Debye-like relaxation observed in the frequency dispersions of its real  and imaginary
and imaginary  parts, see panels (a) and (b) in Fig. 5. A characteristic relaxation maximum in the
parts, see panels (a) and (b) in Fig. 5. A characteristic relaxation maximum in the  curve appears at a frequency fr = 2π/ωr of about 0.5 kHz.
curve appears at a frequency fr = 2π/ωr of about 0.5 kHz.
The quadratic electro-optic response, by contrast, remains practically constant in the paranematic phase in the frequency range of up to 50 kHz indicating thus a much faster relaxation with characteristic frequencies beyond the f-window of the electro-optic measurements.
These distinct electro-optical dynamics originates in the heterogeneous molecular dynamics of molecular matter confined in nanopores. It has been demonstrated in a series of experimental studies that molecules show a slow molecular dynamics near the pore wall and a fast relaxation in the core region of the pore filling.62–66
Thus the fast quadratic Kerr electro-optic response is dominated by the molecular dynamics originating from the isotropic (centrosymmetric) core region, whereas the linear Pockels effect owes its slow dynamics to the slow interfacial dipolar relaxations.
Cooperative molecular ordering in LCs, which accompanies phase transformations, may lead to an additional slowing down of the relaxation dynamics or even its anomalous behavior in the region of phase transformations.41,48 Therefore, a peculiar behavior can be found for bulk liquid-crystalline materials. In the isotropic phase far above the clearing point nematic LCs (with dipolar mesogens) behave like dipolar liquids with a quadratic electro-optic response that diverges upon approaching the transition temperature to the nematic phase. According to the Landau–de Gennes free energy model for LC phase transitions67,68 the magnitude of the Kerr effect, as quantified by the Kerr constant, grows as (T − T*)−γ where T* denotes the second-order pretransitional temperature (supercooling limit of the isotropic phase) and γ is a critical exponent equal to 1 in mean-field approximation.69–72
Also here for the confined L–C state both the Pockels and the Kerr effect exhibit an anomalous behavior in the vicinity of the paranematic-to-nematic phase transition, see Fig. 3 and 4.
In the confined nematic phase, immediately below the transition temperature TPN, the relaxation dynamics of the quadratic electro-optic response experiences a strong slowing down apparently caused by nematic ordering of the entire core region. The corresponding broad relaxation band in the dispersion curve  appears in the frequency region of 10–20 kHz, see Fig. 5(k–m). Interestingly, the slow relaxation of the linear electro-optic response, which is still dominated in the close vicinity of TPN disappears at lower temperatures, see Fig. 5(c–e). It is replaced by a considerably faster response dynamics with characteristic relaxation rates in the frequency range of 30–40 kHz as evidenced in panels (g) and (h) in Fig. 5.
appears in the frequency region of 10–20 kHz, see Fig. 5(k–m). Interestingly, the slow relaxation of the linear electro-optic response, which is still dominated in the close vicinity of TPN disappears at lower temperatures, see Fig. 5(c–e). It is replaced by a considerably faster response dynamics with characteristic relaxation rates in the frequency range of 30–40 kHz as evidenced in panels (g) and (h) in Fig. 5.
The origin of this peculiarity deserves a more detailed discussion. According to dielectric studies62,64,65,73 slow relaxations of confined LCs suggest that the mobility of molecules in the surface layers is strongly affected by the boundary conditions. Near-interfacial layers are characterized by a considerably larger effective viscosity compared to the bulk one which solely slows down the dipolar relaxation. It thus cannot explain an abrupt change in the response dynamics. We suggest that rather a mechanism based on interphase boundary dynamics in an alternating electric field is responsible for the peculiar dynamics.
The left sections of the sketch in Fig. 6 show the orientational ordering of the rod-like LC molecules inside a cylindrical channel in the paranematic state (T > TPN), in the close vicinity of the phase transition (T ≈ TPN) and in the confined nematic state (T < TPN), respectively. The right section sketches the corresponding phase boundary (“domain wall”) separating the symmetry broken (non-centrosymmetric) interfacial polar regions and the centrosymmetric core region. An alternating electric field, applied along the pore axis, results in an oscillating radial shift of the phase boundary thereby causing an alternating optical birefringence, i.e., the dynamic electro-optic effect.
Note that similar domain-like or soliton approaches have been successful in the explanation of anomalous behavior of dielectric and elastic properties in a number of ferroelectric and ferroelastic materials, see e.g. in ref. 74–76. The corresponding domain wall dynamics is due to its collective slow character compared to the dynamics of individual molecules. This feature is evidently presented in the frequency dispersions of the imaginary part of the linear electro-optic response, 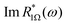 , recorded in the paranematic phase: A characteristic relaxation band appears in the frequency range of several hundred Hertz, see Fig. 5(a–d). The electro-optic contribution due to the alternating phase boundary dynamics is expected to be substantial whenever the birefringence of neighboring phase regions, i.e., the interfacial birefringence, Δni, and the core birefringence, Δnc, substantially differ from each other, see Fig. 6.
, recorded in the paranematic phase: A characteristic relaxation band appears in the frequency range of several hundred Hertz, see Fig. 5(a–d). The electro-optic contribution due to the alternating phase boundary dynamics is expected to be substantial whenever the birefringence of neighboring phase regions, i.e., the interfacial birefringence, Δni, and the core birefringence, Δnc, substantially differ from each other, see Fig. 6.
Analytically, an effective linear electro-optic coefficient r ∝ Δ(Δn)/ΔE ∝ (Δni − Δnc)·(Δx/ΔE) results, where Δx is the radial shift of the phase boundary (domain wall) induced by the applied electric field ΔE. In the paranematic phase, Δni ≫ Δnc = 0 thus the domain wall contribution with slow relaxation dynamics is evidently presented here, see panels (a) and (b) in Fig. 5. Far above TPN the interfacial polar regions form just rare local islands. Their number grows, however, as the temperature decreases, transforming them into closed surface layers upon approaching the paranematic-to-nematic transition temperature TPN. This behavior is characterized by a pretransitional tail, i.e., a slowly increasing retardation, evidently seen in the temperature dependence of the optical retardation above TPN, see Fig. 4.
Note that in the close vicinity of TPN the core region is still isotropic (Δnc = 0). Thus due to the large interphase area the linear electro-optic response is anomalous, see Fig. 5(c, d) and 4(a, b). An abrupt almost step-like increase in the optical retardation right below TPN indicates a complete nematic ordering in the core region.
Considerably below TPN, Δni ≈ Δnc thus the domain like contribution, which is ∝(Δni − Δnc), becomes evidently suspended, see Fig. 5(g and h). The remaining linear electro-optic response is fast and originates from the orientational dynamics of individual molecular dipoles in an alternating electric field. The surface induced polarity in the interfacial molecular layer may be transferred via intermolecular interactions towards the nematic core region of the pore filling. Accordingly, a larger number of molecular dipoles may contribute to the linear electro-optic response. This explains its larger magnitude in the confined nematic phase compared to the paranematic one.
3.2 Landau–De Gennes free energy analysis of confined liquid-crystalline order and Kerr electro-optics
Although the description of the linear electro-optic response has qualitative character, the Kerr effect in the AAO:7CB nanocomposite and the quadratic electro-optic response may be described phenomenologically by employing the Kutnjak–Kralj–Lahajnar–Zumer (KKLZ)-model.29,77 The orientational order inside the nanochannels results in excess optical retardation ΔR ∝ S, see Fig. 3a, where is the scalar order parameter, φ is the angle between the characteristic axis of the molecules and a direction of preferred local molecular orientation (the so-called director
is the scalar order parameter, φ is the angle between the characteristic axis of the molecules and a direction of preferred local molecular orientation (the so-called director  ).
).
The KKLZ model extends phenomenological the Landau–de Gennes approach towards spatially confined nematic phases by introducing a so-called nematic ordering field σ which couples bilinearly with the nematic order parameter.29,77 For the untreated host AAO matrix the channel walls enforce planar anchoring, whereas their elongated cylindrical geometry induces preferential ordering of guest rod-like molecules parallel to the long channel axes. The ordering field σ is proportional to the anchoring strength and inversely proportional to the pore diameter, i.e. it is defined by host–guest interactions at the channel wall interface and its geometrical constraints. The KKLZ free energy is expressed in terms of the dimensionless scaled order parameter q = S/S0, where S0 = S(TIN) stands for the nematic order parameter value at the isotropic-to-nematic transition temperature of the bulk system, TIN. The dimensionless free energy of the spatially confined nematic LC is then represented as follows:
| f = f(q) + f(q,σ) + f(q,κ) + f(q,E), | (1) |
| f(q) = tq2 − 2q3 + q4, | (1a) |
| f(q,σ) = −qσ, | (1b) |
| f(q,κ) = κq2, | (1c) |
| f(q,E) = −a1qE2 − a2q2E2. | (1d) |
For symmetry reasons the electric field couples quadratically with the order parameter, i.e. two terms qE2 and q2E2 are presented in the Landau–de Gennes free energy.78 The quenched disorder (κ-therm) results in a downward shift of the effective transition temperature tn, whereas all other coupling terms increase their value as tn = 1 + σ − κ + a1E2 + a2E2. Here we assume that the electric coupling constants a1 and a2 are positive, i.e., an application of the electric field lowers the free energy of the axial nematic state making it energetically preferable. Moreover, the bilinear coupling term qσ, likewise qE2-term, induces a nematic ordering also above tn. The geometrical constraint results in a precursor behavior with characteristic paranematic tails observed in the temperature dependence of the nematic order parameter. In the vicinity of the paranematic-to-nematic transition the order parameter is characterized by a discontinuous subcritical (σ < 1/2) or a continuous overcritical (σ > 1/2) evolution29–32,77,79 depending on the pore diameter.
Minimization of the free energy expansion (eqn (1)) with respect to the order parameter q at E = 0 gives its equilibrium value qe. It scales linearly with the measured excess retardation, ΔR. A transfer from a reduced dimensionless temperature scale to the normal allows one to calibrate the model parameter ΔT* = TIN − T* to 3.4 K, as derived in previous polarimetric studies.32 The best fit in the region of the nematic-to-isotropic (paranematic) phase transition yields σ = 0.18 and κ = 0.15. Both values agree well with ref. 32 as extrapolations of σ- and κ-values obtained in a series of AAO:7CB nanocomposites with host matrices with smaller pore diameters.
The solid line in Fig. 4a represents the best fit of the experimental data points obtained within the KKLZ model. The dotted line traces the thermo-optic contribution (base line) obtained by the same fitting procedure. Overall, the KKLZ model describes remarkably well the behavior of the optical retardation in the paranematic state, as well as in a broad temperature region of the paranematic-to-nematic phase transition. Deviations far below TPN can be attributed to a saturation of the nematic ordering in the core region of pore filling that originates from the limitation to fourth-order terms.31
The amplitude of the quadratic electro-optic response, measured at an applied field E = U/h (U is the applied voltage), scales linearly with the difference ΔR(E) − ΔR(0). ΔR(E) may be derived similarly to ΔR(0) as described above, i.e., by the minimization of the free energy expansion (eqn (1)) with respect to the order parameter q taking into account the electrical coupling terms of the free energy defined by eqn (1c). The quadratic electro-optic response derived in such a way, ρ2Ω = k[ΔR(E) − ΔR(0)] ∝ [qe(E) − qe(0)] (k is the scaling parameter), is shown in Fig. 4b. The measured quadratic electro-optic response is presented for comparison. Here the coupling constants a1 = 1.0 × 10–13 cm2 V−2 and a2 = 1.3 × 10–12 cm2 V−2 have been chosen in a way that provides the values of field induced optical retardation close to those observed in the experiment.
The presented phenomenological model well reproduces basic features of the anomalous electro-optic behavior, particularly the asymmetric peak of the quadratic electro-optic response. A discrepancy between the theory and experiment, evidently seen in the confined nematic state, may have several reasons. Our phenomenological approach considers the static electro-optic response (ω = 0), whereas the experiments explore the quasi-static electro-optic response (ω/2π = 420 Hz). The chosen frequency can be considered as a compromise, providing, on the one hand, a reduced influence of the ionic conductivity, and on the other hand, still insignificant dipolar relaxation losses. However, at least a weak influence of the ionic conductivity on the measured electro-optic response, which is considerably temperature-dependent, is indeed presented. Also spatial inhomogeneities of the channel diameters (up to 10% radius variation) can result in gradient field effects and likewise field depolarization at channel interfaces.
4 Conclusion
We presented a study on the electro-optical dynamics of the rod-like liquid crystal 7CB embedded into parallel arrays of cylindrical nanopores in anodic aluminum oxide. Linear and quadratic electro-optical effects are explored via first- and second-harmonic polarimetry responses that are measured by a lock-in technique in a frequency window from 0.05–50 kHz and a broad temperature range comprising a phase transition between a confined paranematic and nematic state.We find that a linear electro-optic response, symmetry forbidden in bulk nematics, occurs in both states due to polar ordering at the nanopore walls. The dynamics of the quadratic electro-optic response reveals anomalous dynamical behavior during the paranematic-to-nematic phase transformation that can be quantitatively described by a Landau–De Gennes free energy model. The linear and quadratic electro-optical effects are characterized by substantially different molecular relaxation rates caused apparently by a slow and fast mesogen reorientation in the proximity of the pore wall and in the pore center, respectively.
One can envision that the observed integrated electro-optic effects that sensitively depend on multiphyiscal couplings are particularly interesting to induce lateral phase shift gradients for electromagnetic waves in solid supports or surfaces at will by the external electric field and temperature gradients. Such active photonic metamaterials are demanded for the design of in-operando adjustable optical components.23,80–84
Thus, similarly, as it has been demonstrated for liquid-infused porous structures with electrochemical actuation85 and wetting changes,86 as well as versatile multifunctional material behavior in general,87 our study indicates that liquid crystal-infused nanoporous solids allow for quite simple fabrication of electro-active functional nanomaterials. The functionalization approach by capillarity-driven spontaneous imbibition of the liquid-crystalline melt in combination with tailorability of anodic aluminum oxide41,88–90 and the availability of other self-organized, optically transparent mesoporous media10,66,91,92 demonstrate also the versatile character of the presented material fabrication process.
Finally, our study is a fine example of how the combination of soft and hard matter opens up the possibility of using multi-scale self-assembly and phase transitions to transport peculiar multi-physical couplings in geometrical confinement from the nano- via the meso- to the macroscale to design robust hybrid materials with integrated functionality, similar to that found in many biological composites.93,94
Author contributions
A. V. K., A. A., M. R., N. A., and P. H. conceived and designed the electro-optic experiments. A. V. K, M. L., and P. P. fabricated the nanocomposites. A. V. K. and M. N. performed the optical experiments. A. V. K. and Y. S. analyzed the data. A. V. K., Y. S., and P. H. interpreted the experiments. A. V. K. and P. H. wrote the manuscript. All authors proofread and edited the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The presented results are part of a project that has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 778156. Support from resources for science in the years 2018–2022 granted for the realization of the international co-financed project no. W13/H2020/2018 (Dec. MNiSW 3871/H2020/2018/2) is also acknowledged. We also benefited from support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the Collaborative Reserach Center SFB 986 “Tailor-Made Multi-Scale Materials Systems”, project number (192346071).References
- N. Yu and F. Capasso, Nat. Mater., 2014, 13, 139–150 CrossRef CAS PubMed.
- M. Kadic, G. W. Milton, M. van Hecke and M. Wegener, Nat. Rev. Phys., 2019, 1, 198–210 CrossRef.
- C. Caloz and Z.-L. Deck-Leger, IEEE Trans. Antennas Propag., 2020, 68, 1569–1582 Search PubMed.
- S. Lepeshov and A. Krasnok, Nat. Nanotechnol., 2021, 16, 615–616 CrossRef CAS PubMed.
- Y. Zhang, C. Fowler, J. Liang, B. Azhar, M. Y. Shalaginov, S. Deckoff-Jones, S. An, J. B. Chou, C. M. Roberts, V. Liberman, M. Kang, C. Ríos, K. A. Richardson, C. Rivero-Baleine, T. Gu, H. Zhang and J. Hu, Nat. Nanotechnol., 2021, 16, 661–666 CrossRef CAS PubMed.
- Y. Wang, P. Landreman, D. Schoen, K. Okabe, A. Marshall, U. Celano, H.-S. P. Wong, J. Park and M. L. Brongersma, Nat. Nanotechnol., 2021, 16, 667–672 CrossRef CAS PubMed.
- A. Ruiz-Clavijo, O. Caballero-Calero and M. Martín-González, Nanoscale, 2021, 13, 2227–2265 RSC.
- S. H. Ryu and D. K. Yoon, ACS Appl. Mater. Interfaces, 2017, 9, 25057–25061 CrossRef CAS PubMed.
- K. Sentker, A. Yildirim, M. Lippmann, A. W. Zantop, F. Bertram, T. Hofmann, O. H. Seeck, A. V. Kityk, M. G. Mazza, A. Schönhals and P. Huber, Nanoscale, 2019, 11, 23304–23317 RSC.
- M. Spengler, R. Y. Dong, C. A. Michal, W. Y. Hamad, M. J. MacLachlan and M. Giese, Adv. Funct. Mater., 2018, 28, 1800207 CrossRef.
- J. Xu, R. Yang, Y. Fan, Q. Fu and F. Zhang, Front. Phys., 2021, 9, 1–14 CAS.
- L. M. Pappu, R. Martin-Palma, B. Martín-Adrados and I. Abdulhalim, J. Mol. Liq., 2019, 281, 108–116 CrossRef CAS.
- P. L. Madhuri, S. Shuddhodana, Z. M. A. Judeh and I. Abdulhalim, Part. Part. Syst. Charact., 2020, 37, 2000067 CrossRef CAS.
- J. Sautter, I. Staude, M. Decker, E. Rusak, D. N. Neshev, I. Brener and Y. S. Kivshar, ACS Nano, 2015, 9, 4308–4315 CrossRef CAS PubMed.
- K. Waszkowska, P. Josse, C. C. Cabanetos, P. Blanchard, B. Sahraoui, D. Guichaoua, I. Syvorotka, O. Kityk, R. Wielgosz, P. Huber and A. V. Kityk, Opt. Lett., 2021, 46, 845–848 CrossRef PubMed.
- Q. Liu, Y. Cui, D. Gardner, X. Li, S. He and I. I. Smalyukh, Nano Lett., 2010, 10, 1347–1353 CrossRef CAS PubMed.
- N. Yu, P. Genevet, M. A. Kats, F. Aieta, J.-P. P. Tetienne, F. Capasso and Z. Gaburro, Science, 2011, 334, 333–337 CrossRef CAS PubMed.
- N. I. Zheludev and Y. S. Kivshar, Nat. Mater., 2012, 11, 917 CrossRef CAS PubMed.
- D. Jalas, L.-H. Shao, R. Canchi, T. Okuma, S. Lang, A. Petrov, J. Weissmüller and M. Eich, Sci. Rep., 2017, 7, 44139 CrossRef CAS PubMed.
- X. Guo, H. Hu, X. Zhu, X. Yang and Q. Dai, Nanoscale, 2017, 9, 14998–15004 RSC.
- A. Lininger, A. Y. Zhu, J.-S. S. Park, G. Palermo, S. Chatterjee, J. Boyd, F. Capasso and G. Strangi, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 20390–20396 CrossRef CAS PubMed.
- N. Maccaferri, I. Zubritskaya, I. Razdolski, I.-A. Chioar, V. Belotelov, V. Kapaklis, P. M. Oppeneer and A. Dmitriev, J. Appl. Phys., 2020, 127, 080903 CrossRef CAS.
- A. M. Shaltout, V. M. Shalaev and M. L. Brongersma, Science, 2019, 364, eaat3100 CrossRef CAS PubMed.
- N. Engheta, Nanophotonics, 2021, 10, 639–642 Search PubMed.
- H. Gao, X. Fan, W. Xiong and M. Hong, Opto-Electron. Adv., 2021, 210030 Search PubMed.
- F. Zhang, X. Xie, M. Pu, Y. Guo, X. Ma, X. Li, J. Luo, Q. He, H. Yu and X. Luo, Adv. Mater., 2020, 32, 1908194 CrossRef CAS PubMed.
- G. P. Crawford, R. J. Ondris-Crawford and J. W. Doane, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3647–3661 CrossRef CAS PubMed.
- D. Wallacher, R. Ackermann, P. Huber, M. Enderle and K. Knorr, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184203 CrossRef.
- Z. Kutnjak, S. Kralj, G. Lahajnar and S. Zumer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021705 CrossRef PubMed.
- A. V. Kityk, M. Wolff, K. Knorr, D. Morineau, R. Lefort and P. Huber, Phys. Rev. Lett., 2008, 101, 187801 CrossRef PubMed.
- S. Calus, D. Rau, P. Huber and A. V. Kityk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 21701 CrossRef PubMed.
- S. Całus, B. Jabłońska, M. Busch, D. Rau, P. Huber and A. V. Kityk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062501 CrossRef PubMed.
- J. Kopitzke, J. H. Wendorff and B. Glusen, Liq. Cryst., 2000, 27, 643–648 CrossRef CAS.
- C. V. Cerclier, M. Ndao, R. Busselez, R. Lefort, E. Grelet, P. Huber, A. V. Kityk, L. Noirez, A. Schoenhals and D. Morineau, J. Phys. Chem. C, 2012, 116, 18990–18998 CrossRef CAS.
- A. V. Kityk, M. Busch, D. Rau, S. Calus, C. V. Cerclier, R. Lefort, D. Morineau, E. Grelet, C. Krause, A. Schoenhals, B. Frick and P. Huber, Soft Matter, 2014, 10, 4522–4534 RSC.
- K. Sentker, A. W. Zantop, M. Lippmann, T. Hofmann, O. H. Seeck, A. V. Kityk, A. Yildirim, A. Schönhals, M. G. Mazza and P. Huber, Phys. Rev. Lett., 2018, 120, 067801 CrossRef CAS PubMed.
- A. Yildirim, K. Sentker, G. J. Smales, B. R. Pauw, P. Huber and A. Schönhals, Nanoscale Adv., 2019, 1, 1104–1116 RSC.
- G. Chahine, A. V. Kityk, N. Demarest, F. Jean, K. Knorr, P. Huber, R. Lefort, J.-M. Zanotti and D. Morineau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 011706 CrossRef PubMed.
- C. Grigoriadis, H. Duran, M. Steinhart, M. Kappl, H. J. Butt and G. Floudas, ACS Nano, 2011, 5, 9208–9215 CrossRef CAS PubMed.
- A. V. Kityk and P. Huber, Appl. Phys. Lett., 2010, 97, 153124 CrossRef.
- M. Busch, A. V. Kityk, W. Piecek, T. Hofmann, D. Wallacher, S. Całus, P. P. Kula, M. Steinhart, M. Eich, P. Huber, S. Calus, P. P. Kula, M. Steinhart, M. Eich and P. Huber, Nanoscale, 2017, 9, 19086–19099 RSC.
- R. Wittmann, L. B. G. Cortes, H. Löwen and D. G. A. L. Aarts, Nat. Commun., 2021, 12, 623 CrossRef CAS PubMed.
- J. Kerr, London, Edinburgh Dublin Philos. Mag. J. Sci., 1875, 50, 337–348 CrossRef.
- T. S. Narasimhamurti, Photoelastic and Electro-Optic Properties of Crystals, Plenum, New York, 1981 Search PubMed.
- K. Yamaoka, Y. Takahashi, Y. Yamazaki, N. Terakado, T. Miyazaki and T. Fujiwara, Sci. Rep., 2015, 5, 12176 CrossRef CAS PubMed.
- M. Skarabot, I. Musevic and R. Blinc, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6725–6731 CrossRef CAS.
- M. Skarabot, M. Cepic, B. Zeks, R. Blinc, G. Heppke, A. V. Kityk and I. Musevic, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 575–584 CrossRef CAS.
- M. Skarabot, S. Kralj, R. Blinc and I. Musevic, Liq. Cryst., 1999, 26, 723–729 CrossRef CAS.
- R. Righini, Science, 1993, 262, 1386–1390 CrossRef CAS PubMed.
- J. M. Halbout and C. L. Tang, Appl. Phys. Lett., 1982, 40, 765–767 CrossRef CAS.
- V. Bermudez, N. Capron, T. Gase, F. G. Gatti, F. Kajzar, D. A. Leigh, F. Zerbetto and S. W. Zhang, Nature, 2000, 406, 608–611 CrossRef CAS PubMed.
- J. Niziol, M. Prato, C. Soombar, E. Vazquez, E. Gondek, I. Rau and F. Kajzar, Mol. Cryst. Liq. Cryst., 2010, 522, 491–502 Search PubMed.
- I. Chirtoc, M. Chirtoc, C. Glorieux and J. Thoen, Liq. Cryst., 2004, 31, 229–240 CrossRef CAS.
- L. G. Cencha, P. Huber, M. Kappl, G. Floudas, M. Steinhart, C. L. A. Berli and R. Urteaga, Appl. Phys. Lett., 2019, 115, 113701 CrossRef.
- S. Gruener and P. Huber, J. Phys.: Condens. Matter, 2011, 23, 184109 CrossRef PubMed.
- K. Sentker, Ph.D. thesis, Hamburg University of Technology, 2019.
- S. Calus, M. Busch, A. V. Kityk, W. Piecek, P. Huber, S. Całus, M. Busch, A. V. Kityk, W. Piecek and P. Huber, J. Phys. Chem. C, 2016, 120, 11727–11738 CrossRef CAS.
- P. Cladis and M. Kléman, J. Phys., 1972, 33, 591–598 CrossRef CAS.
- R. B. Meyer and P. S. Pershan, Solid State Commun., 1973, 13, 989–992 CrossRef.
- G. P. Crawford, D. W. Allender and J. W. Doane, Phys. Rev. A, 1992, 45, 8693–8708 CrossRef CAS PubMed.
- S. Mor, V. Torres-Costa, R. J. Martín-Palma and I. Abdulhalim, Appl. Phys. Lett., 2010, 97, 113106 CrossRef.
- F. M. Aliev, M. R. Bengoechea, C. Y. Gao, H. D. Cochran and S. Dai, J. Non-Cryst. Solids, 2005, 351, 2690–2693 CrossRef CAS.
- F. M. Aliev, E. F. Arroyo and V. Dolidze, J. Non-Cryst. Solids, 2010, 356, 657–660 CrossRef CAS.
- S. Calus, A. V. Kityk, M. Eich and P. Huber, Soft Matter, 2015, 11, 3176–3187 RSC.
- S. Całus, L. Borowik, A. V. Kityk, M. Eich, M. Busch and P. Huber, Phys. Chem. Chem. Phys., 2015, 17, 22115–22124 RSC.
- P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102 CrossRef PubMed.
- P. G. de Gennes, Phys. Lett. A, 1969, 30, 454–455 CrossRef.
- P. G. de Gennes, Mol. Cryst. Liq. Cryst., 1971, 12, 193–214 CrossRef CAS.
- V. N. Tsvetkov and E. I. Ryumtsev, Sov. Phys. Crystallogr., USSR, 1968, 13, 225 Search PubMed.
- J. Philip and T. A. P. Rao, Phys. Rev. A, 1992, 46, 2163–2165 CrossRef CAS PubMed.
- H. Khoshsima, H. Tajalli, A. G. Gilani and R. Dabrowski, J. Phys. D: Appl. Phys., 2006, 39, 1495–1499 CrossRef CAS.
- M. C. Schlick, N. Kapernaum, M. M. Neidhardt, T. Woehrle, Y. Stoeckl, S. Laschat and F. Giesselmann, ChemPhysChem, 2018, 19, 2305–2312 CrossRef CAS PubMed.
- M. R. Bengoechea and F. M. Aliev, J. Non-Cryst. Solids, 2005, 351, 2685–2689 CrossRef CAS.
- A. V. Kityk, V. P. Soprunyuk, A. Fuith, W. Schranz and H. Warhanek, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 6337–6344 CrossRef CAS PubMed.
- P. Sondergeld, W. Schranz, A. Troster, M. A. Carpenter, E. Libowitzky and A. V. Kityk, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6143–6147 CrossRef CAS.
- W. Schranz, P. Sondergeld, A. V. Kityk and E. K. H. Salje, Phase Transitions, 1999, 69, 61–76 CrossRef CAS.
- Z. Kutnjak, S. Kralj, G. Lahajnar and S. Zumer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051703 CrossRef PubMed.
- E. I. Rjumtsev, M. A. Osipov, T. A. Rotinyan and N. P. Yevlampieva, Liq. Cryst., 1995, 18, 87–95 CrossRef CAS.
- P. Huber, K. Sentker, M. Busch and A. V. Kityk, Liquid Crystals Confined in Nanoporous Solids: From Fundamentals to Functionalities, in Soft Matter And Biomaterials On The Nanoscale: The WSPC Reference On Functional Nanomaterials-Part I (In 4 Volumes), World Scientific Publishing, Singapore, 2020 Search PubMed.
- N. Yu, P. Genevet, M. A. Kats, F. Aieta, J.-P. Tetienne, F. Capasso and Z. Gaburro, Science, 2011, 334, 333–337 CrossRef CAS PubMed.
- J. B. Pendry, A. Aubry, D. R. Smith and S. A. Maier, Science, 2012, 337, 549–552 CrossRef CAS PubMed.
- O. Buchnev, N. Podoliak, M. Kaczmarek, N. I. Zheludev and V. A. Fedotov, Adv. Opt. Mater., 2015, 3, 674–679 CrossRef CAS.
- A. Nemati, Q. Wang, M. Hong and J. Teng, Opto-Electron. Adv., 2018, 1, 18000901–18000925 Search PubMed.
- M. Zhang, M. Pu, F. Zhang, Y. Guo, Q. He, X. Ma, Y. Huang, X. Li, H. Yu and X. Luo, Adv. Sci., 2018, 5, 1800835 CrossRef PubMed.
- M. Brinker, G. Dittrich, C. Richert, P. Lakner, T. Krekeler, T. F. Keller, N. Huber and P. Huber, Sci. Adv., 2020, 6, eaba1483 CrossRef CAS PubMed.
- Y. Xue, J. Markmann, H. Duan, J. Weissmüller and P. Huber, Nat. Commun., 2014, 5, 4237 CrossRef CAS PubMed.
- R. W. Style, R. Tutika, J. Y. Kim and M. D. Bartlett, Adv. Funct. Mater., 2021, 31, 2005804 CrossRef CAS.
- W. Lee and S.-J. Park, Chem. Rev., 2014, 114, 7487–7556 CrossRef CAS PubMed.
- Y. Chen, A. Santos, Y. Wang, T. Kumeria, C. Wang, J. Li and D. Losic, Nanoscale, 2015, 7, 7770–7779 RSC.
- S. Sukarno, C. S. Law and A. Santos, Nanoscale, 2017, 9, 7541–7550 RSC.
- F. Gallego-Gómez, A. Blanco, V. Canalejas-Tejero and C. López, Small, 2011, 7, 1838–1845 CrossRef PubMed.
- C. T. Sousa, D. C. Leitao, M. P. Proenca, J. Ventura, A. M. Pereira and J. P. Araujo, Appl. Phys. Rev., 2014, 1, 31102–31122 Search PubMed.
- M. Eder, S. Amini and P. Fratzl, Science, 2018, 362, 543–547 CrossRef CAS PubMed.
- O. Gang, P. Huber, A. Karim, I. Zvonkina, S.-W. Lee, J.-W. Kim, D. K. Roper and W. J. Li, Soft Matter and Biomaterials on the Nanoscale, World Scientific, 2020, vol. 1 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |