Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nanocapsule designs for antimicrobial resistance†
Irene
Marzuoli
a,
Carlos H. B.
Cruz‡
a,
Christian D.
Lorenz
 b and
Franca
Fraternali
b and
Franca
Fraternali
 *a
*a
aRandall Centre for Cell and Molecular Biology, King's College London, London, UK. E-mail: franca.fraternali@kcl.ac.uk
bDepartment of Physics, King's College London, London, WC2R 2LS, UK
First published on 5th April 2021
Abstract
The pressing need of new antimicrobial products is growing stronger, particularly because of widespread antimicrobial resistance, endangering our ability to treat common infections. The recent coronavirus pandemic has dramatically highlighted the necessity of effective antibacterial and antiviral protection. This work explores at the molecular level the mechanism of action of antibacterial nanocapsules assembled in virus-like particles, their stability and their interaction with mammal and antimicrobial model membranes. We use Molecular Dynamics with force-fields of different granularity and protein design strategies to study the stability, self-assembly and membrane poration properties of these nanocapsules.
Introduction
In the past decades the constant threat of antimicrobial resistance encouraged the development of novel antimicrobial strategies.1 Antimicrobial peptides (AMPs) are highly versatile biomolecules able to disrupt bacterial activity in a plethora of different ways,2,3 mostly leading to perturbation and/or poration of the bacterial membrane.2,4,5 These biologics qualify as a novel weapon against drug-resistant bacteria because their spectrum of action is substantially different from that of small molecule drugs: this not only opens new therapeutic possibilities, but the characteristics of their broad range action suggest a slower development of resistance once they are employed against common pathogens.6,7Several effective synthetic AMPs have been developed in the past, exploiting information from the naturally occurring ones. In a straightforward approach, natural sequences can be used as templates to generate more powerful or selective peptides via iterative single-point mutations.8–11 More generally, virtual screenings of thousands of AMPs have highlighted recurring patterns connected with their activity,12–15 and the physico-chemical properties inducing their function started to be elucidated by biophysical studies in vitro but also in silico, e.g. employing Molecular Dynamics simulations.10,16,17
Combining this available knowledge with protein engineering techniques, it is possible to design AMPs that perform additionally desired functions, such as self-assembly into organised objects:18–21 this can boost the antimicrobial activity of the peptide by enhancing its local concentration, generating premises for effective drug or gene delivery. The success of such a design strategy depends on an accurate knowledge of the molecular-level interactions the peptide has with its copies and with the bacterial membrane. Even for systems with proven antimicrobial activity, a deep understanding of these details is beneficial to set in place design strategies for activity enhancement.
Molecular Dynamics (MD) simulations have been extensively used in the past to elucidate the mechanisms of action of AMPs, where experiments were insufficient to fully uncover their details.22–32 Ongoing advances in computing power are continuously increasing the potential of MD simulations,33,34 which have contributed to clarify how peptides translocate through membranes,25,26 how they oligomerise before translocation,27 and to identify the role of specific amino acids and secondary structures in interacting with bacterial membranes.28,29
The development of models for bacterial membranes plays a crucial role in the success of such investigations. The simplest ones are bilayers composed of a few phospholipids species with an overall negative charge,31,35,36 to capture both the hydrophobic environment and the characteristic electrostatic interaction that AMPs have to overcome to penetrate into the bacterial cytoplasm. These bilayers can also be experimentally assembled and their interactions with AMPs measured with precision,18,37,38 which makes the comparison with MD simulations possible, as exploited in this work.
A more faithful representation of bacterial membranes requires the parametrisation of a greater variety of such phospholipids (e.g. phosphocholines, phosphoetilamine, phosphoglycerols),39–43 together with peptidoglycans (PG)44,45 and lipopolyaccharides (LPS).46–48 The combination of these molecules allows to represent the Gram positive bacteria cell membrane (a double layer of phospholipids coated with long PG chains),49 and the double membrane of Gram negative ones (an inner membrane of phospholipids, and an outer one formed by phospholipids at the interior and LPSs externally, with the two interspaced by a layer of PGs).49 LPSs are therefore of particular interest as the first molecules approached by external agents, such as AMPs, when attacking Gram negative bacteria.
As the translocation of AMPs and other membrane-penetrating nanoparticles requires long simulation time, the introduction of an electric field across the two sides of the membrane is a useful procedure not only to model the transmembrane potential, but also to accelerate penetration.41,50–54 This external perturbation causes the membrane itself to be more prone to disruption,51 and pushes positively charged nanoparticles/peptides toward the membrane.52–54 The effect of an electric field can also be assessed experimentally and compared with the simulations data,55 but the intensity of the field should be kept within physiological values.
Several penetration mechanisms are known, in presence or absence of electric field, and their understanding is crucial for the design of new AMPs. For example, short helical AMPs insert vertically in the membrane and gather together to form a water channel;2,56–58 nanoparticles strongly attach to the membrane enhancing its curvature until disruption;48,59 additionally Arginine rich peptides exploit the local defects of the membrane to pass through it despite their high charge, as proven by MD simulations.28 Finally, transmembrane proteins on the outer Gram negative membrane can facilitate the penetration of some AMPs. Nevertheless models of these systems are computationally expensive and require large scale simulations.60–62
A peptide with established assembly and antimicrobial activity is capzip,18,63 which self-assembles into hollow capsules with a predominant size range of 20–200 nm, and derives its antimicrobial activity from a short six amino acid sequence of the antimicrobial portion64–66 of bovine Lactoferrin (PDB code: 1LFC), mutated to favour self-assembly (Fig. 1). Molecular Dynamics simulations have helped identifying the assembled structure and how it approaches the membrane,63 but further investigation is necessary to identify the determinants of its selectivity between mammalian and bacterial membranes, and to quantify the perturbations imposed on the latter. A characteristic of the capzip peptide is its branched sequence, constituted by a central scaffold and three short arms without any secondary structure. The arms both favour the pairing with other copies of the molecule by antiparallel β-sheet formation, and bear the positive charge known to perturb the bacterial membrane.2,5,67
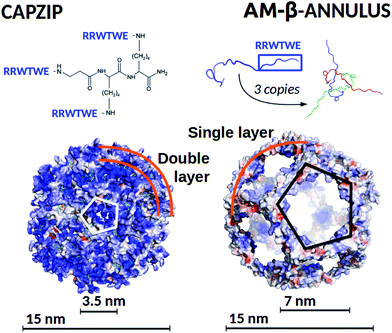 | ||
| Fig. 1 (Top) Capzip peptide (which constitutes the capsule building block), and AM-β-annulus peptide, with the respective capsule building block, constituted by three AM-β-annulus peptides. (Bottom) Modelled antimicrobial capsules, capzip on the left and AM-β-annulus on the right. Capsules are shown in surface representation, colour coded by surface charge with blue positive, white neutral, and red negative charge (pyMol software89). The diameter of the modelled antimicrobial capsules and of the holes on their surfaces are indicated. | ||
The design of self-assembling peptides is an established field which has successfully led to the design of multi-purpose materials.68–72 The interesting results we obtained for the capzip system by the use of combined simulations and experimental investigations encouraged the in silico design of a new antimicrobial capsule obtained by grafting the same six amino acid antimicrobial motif composed from the capzip peptide onto a new scaffold, the β-annulus construct from the C chain of the Tomato Bush Stunt virus protomer (TBSV, PDB code 2TBV73). This is a peptide of 24 amino acids sequence which, in the original viral structure (hosting several other proteins), assembles with two other copies of itself to provide a triangular block with three extended arms, similar to the capzip peptide.
The 24-mer alone was shown in previous work to self-assemble into hollow capsules both in its native state74 and when functionalised with additional chemical entities, such as gold or zinc nanoparticles,75,76 short DNA strands77 or peptides.78,79 In our design, the RRWTWE antimicrobial sequence was transplanted onto the extended arms of the β-annulus to ensure antimicrobial activity. It should be noted that the resulting AM-β-annulus capsule has a different ratio between the antimicrobial portion and the non functional moiety joining the arms with respect to the capzip capsule.
In this context, the present work establishes a pipeline of molecular modelling and multi-scale Molecular Dynamics simulations (from atomistic to coarse-grained) to study the stability of the capzip and AM-β-annulus capsules in water, and their interaction with model membranes. Our computational approach can be used as a framework to test novel antimicrobial self-assembling compounds and their mode of action.
Methods
Capzip modelling and simulations
Following up from previous work,63 we performed atomistic and coarse-grained simulations of a capzip capsule in solution and on model membranes, using the atomistic GROMOS 54a8 force field,80,81 and the coarse-grained description provided by MARTINI82,83 and SIRAH.84,85 All simulations were performed with the GROMACS software, version 5.5 and 2016.86–88Table 1 reports all the simulations performed.| Systema | Force field | Time (ns) |
|---|---|---|
In the System field the following abbreviations are used: bact. m. for bacterial membrane DLPC/DLPG 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (except for b where it is POPC/POPS 3 1, (except for b where it is POPC/POPS 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); LPS m. for bacterial outer membrane LPS (top leaflet) and POPE/POPG/CDL 85 1); LPS m. for bacterial outer membrane LPS (top leaflet) and POPE/POPG/CDL 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (bottom leaflet); mamm. m. for mammal membrane (DLPC). The notation (P) for the MARTINI force field indicates the Polar water model. 10 (bottom leaflet); mamm. m. for mammal membrane (DLPC). The notation (P) for the MARTINI force field indicates the Polar water model. |
||
| Capzip bilayer capsule | GROMOS | 100 |
| Capzip bilayer capsule | MARTINI | 1000 |
| Capzip bilayer capsule | SIRAH | 1000 |
| Capzip monolayer capsule | MARTINI | 1000 |
| Capzip monolayer capsule | SIRAH | 1000 |
| AM-β-annulus capsule | SIRAH | 1000 |
| Capzip pentagonal unit on: | ||
| Small bact. m. | GROMOS | 500 |
| Large bact. m. | GROMOS | 500 |
| Small bact. m., increasing E | GROMOS | (Total) 2000 |
| Small bact. m., 130 mV nm−1 | GROMOS | 500 |
| Large bact. m., 130 mV nm−1 | GROMOS | 500 |
| Bact. m., 130 or 140 mV nm−1 | GROMOS | 500 |
| Capzip bilayer capsule on: | ||
| Bact. m. | MARTINI | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Bact. m., 20 mV nm−1 | MARTINI (P) | 500 |
| Bact. m., 40 mV nm−1 | MARTINI (P) | 500 |
| LPS m.a | MARTINI (P) | 1000 |
| Mamm. m. | MARTINI | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Mamm. m., 20 mV nm−1 | MARTINI (P) | 500 |
| Mamm. m., 40 mV nm−1 | MARTINI (P) | 500 |
| Bact. m.,a 4 mV nm−1 | SIRAH | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Bact. m., 20 or 40 mV nm−1 | SIRAH (P) | 500 |
| Mamm. m., 20 or 40 mV nm−1 | SIRAH (P) | 500 |
| AM-β-annulus monolayer capsule on: | ||
| Bact. m.,b 4 mV nm−1 | SIRAH | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 bilayer was selected to model bacterial membranes, consistent with previous in vitro experiments performed on Supported Lipid Bilayers with the capzip peptide:18 the negative charge of DLPG captures one of the main characteristics that distinguishes bacterial from mammal membranes,49,91–93 and mimics the inner Gram negative membrane. The atomistic coordinates for the membrane were built with the PACKMOL software.94 Two patches were built, hosting 512 and 740 lipids respectively. The expected area per lipid was reached during a 400 ns equilibration (see simulations details below), the final configuration of which was used for simulations with the peptide. To simulate the action of the capzip peptide on the membranes, a pentagonal unit of the double-layered truncated icosahedron (10 molecules overall) was taken as representative of the full capsule, to allow a faster sampling, and simulated in proximity of the membrane plane. For the bacterial membrane model, additional simulations were run with an external electric field pointing from the side hosting the capsid peptides to the opposite side, to mimic the transmembrane potential.
1 bilayer was selected to model bacterial membranes, consistent with previous in vitro experiments performed on Supported Lipid Bilayers with the capzip peptide:18 the negative charge of DLPG captures one of the main characteristics that distinguishes bacterial from mammal membranes,49,91–93 and mimics the inner Gram negative membrane. The atomistic coordinates for the membrane were built with the PACKMOL software.94 Two patches were built, hosting 512 and 740 lipids respectively. The expected area per lipid was reached during a 400 ns equilibration (see simulations details below), the final configuration of which was used for simulations with the peptide. To simulate the action of the capzip peptide on the membranes, a pentagonal unit of the double-layered truncated icosahedron (10 molecules overall) was taken as representative of the full capsule, to allow a faster sampling, and simulated in proximity of the membrane plane. For the bacterial membrane model, additional simulations were run with an external electric field pointing from the side hosting the capsid peptides to the opposite side, to mimic the transmembrane potential.
For all atomistic simulations, the systems were solvated with single point charge (SPC) water;95 Na+ and Cl− ions were added to balance the charge and to reach a salt concentration of 150 mM, matching the experimental conditions. The capzip peptide parametrisation was built by comparison with tabulated data for peptidic bonds and amino acid moieties. Lipid parameters were taken from ref. 39 for DLPC, while for DLPG they were built from the POPG ones available in ref. 43. Temperature was maintained by independently coupling protein, membrane, and solvent (plus ions) to three external temperature baths using a velocity rescaling thermostat96 with coupling constant τT of 0.1 ps. Pressure was kept at 1 bar by Berendsen97 or Parrinello–Rahman barostats98 (for equilibration and production, respectively) using an isotropic or semi-isotropic coupling (simulations without and with membrane), with isothermal compressibility of 4.5 × 10–5 bar−1 and coupling constant τP of 1 ps. Electrostatic interactions were treated using the smooth Particle Mesh Ewald algorithm99 with a Fourier grid spacing of 0.12 nm, and a short-range cutoff of 1.2 nm; van der Waals interactions were calculated with a 1.2 nm cutoff. All atomistic runs were performed using a 2 fs time step.
Simulations of the capzip capsule in solution were run for 100 ns, in three replicas. In order to stabilise the structure, an equilibration was run where the initial distances between the paired arms of different capzip peptides (i.e. laying on the same edge of the truncated icosahedron) were restrained with a harmonic potential of 1000 kJ (mol nm2)−1 force constant, and progressively released over 150 ns. All the assembled membrane bilayers were first equilibrated for 50 ps at 50 K, then the temperature was gradually increased to 300 over 500 ps, and finally a 400 ns production run was performed (using the NPT ensemble). A similar equilibration procedure was followed for peptide–membrane systems. Exploratory simulations on the membranes with an external electric field were run for the bacterial model with 512 lipids as follows: starting from 20 mV nm−1, the field was increased by 20 mV nm−1 every 200 ns, up to electroporation value of the membrane in presence of the peptide. Three replicas were run at the electroporation value to confirm the results, and an additional one on the larger membrane hosting 740 lipids. A similar procedure was performed for the membrane alone. ESI Table 2 and ESI Fig. 4 and 5† reports information on the simulations of the membrane without capzip.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The capzip capsule was initially placed at a minimum distance of 1 nm from the membrane surface. Simulations were performed with the standard MARTINI water model and Cl− counter ions. The same configuration was simulated with an external electric field (20 or 40 mV nm−1, one replica each) with MARTINI polar water103 and solution of sodium chloride in concentration 0.15 mM. The effect of the field was tested on pure membranes as a control. Furthermore, a model Gram negative outer membrane was built with CHARMM-GUI:104 it hosts in the upper layer 567 LPS molecules, and in the bottom layer a mixture of POPE, POPG and cardiolipin in proportion 85
1). The capzip capsule was initially placed at a minimum distance of 1 nm from the membrane surface. Simulations were performed with the standard MARTINI water model and Cl− counter ions. The same configuration was simulated with an external electric field (20 or 40 mV nm−1, one replica each) with MARTINI polar water103 and solution of sodium chloride in concentration 0.15 mM. The effect of the field was tested on pure membranes as a control. Furthermore, a model Gram negative outer membrane was built with CHARMM-GUI:104 it hosts in the upper layer 567 LPS molecules, and in the bottom layer a mixture of POPE, POPG and cardiolipin in proportion 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, for a total of 1512 molecules.34 Calcium ions were added to balance the LPS charges, the remaining ones were neutralised with sodium ions, finally sodium chloride ions in concentration 0.15 mM were added to the solvent. After the initial equilibration, the membrane was simulated together with the capzip capsule at the initial distance of 1 nm.
10, for a total of 1512 molecules.34 Calcium ions were added to balance the LPS charges, the remaining ones were neutralised with sodium ions, finally sodium chloride ions in concentration 0.15 mM were added to the solvent. After the initial equilibration, the membrane was simulated together with the capzip capsule at the initial distance of 1 nm.
To quantify the different binding propensity of capzip capsule for bacterial versus mammal membrane, we computed the Potential of Mean Force (PMF) by applying an external force to impose penetration, pulling the capzip capsule it across the DLPC/DLPG lipid bilayer (chosen versus the LPS membrane for its minor complexity). We then performed umbrella sampling simulations, with a coarse-grained Polar MARTINI description.
For simulations with the standard water model (DLPC/LDPG and DLPC membranes without electric field), temperature coupling was performed with a velocity rescaling thermostat96 with a coupling constant τT of 1 ps. A semi-isotropic pressure coupling was applied at 1 bar pressure, with 4.6 × 10–5 bar−1 isothermal compressibility, using a Berendsen97 or Parrinello–Rahman barostat98 (equilibration and production phase respectively) with τP of 2 ps or 12 ps. Coulomb interactions were treated with a Reaction Field scheme105 and cut off radius of 1.1 nm, van der Waals interactions with a cut off scheme and the same cut off radius. The relative dielectric constant was set to 15. Simulations performed with the polar water model (DLPG/DLPC and DLPC with electric field; LPS membrane) were run with the parameters above, except the relative dielectric constant set to 2.5, and the choice of a Particle Mesh Ewald scheme for long-range Coulomb interactions (1.2 nm cut off radius), in agreement with the setup suggested in ref. 103.
Simulations of the capsule in solution were run for 1 μs, in three replicas with initial constraints over the arms as performed for the atomistic simulation. The membrane models were equilibrated for 1 μs with standard water (DLPC/DLPG and DLPC) or following the standard CHARMM-GUI protocol104 (LPS membrane), and the final configuration was used to build peptide–membrane systems, together with the capsule structure (obtained after a 1 μs equilibration run). The full systems were energy minimised, equilibrated for 500 ps and production was followed for 10 μs for capzip capsule – DLPC/DLPG or DLPC systems with standard water, 500 ns when they are run with polar water (due to the faster binding of the capsule and the speed-up induced by the electric field); and 1 μs for the capsule – LPSs system. For the simulation with a 40 mV nm−1 electric field, after pore formation, the pressure coupling was switched to isotropic and the simulation prolonged for 100 ns. Control simulations with electric field of the magnitudes used were performed on the membranes alone (ESI Table 2†).
For umbrella sampling simulations, we first performed a steered simulation pulling the capsule through each membrane. A force of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ (mol nm2)−1 was applied between the center of mass (COM) of the capsule and the COM of the lipids falling in a circle of radius 12 nm centred on the projection of the capsule COM on xy plane of the membrane. The pulling rate was 10–4 nm ps−1. From these trajectories, 100 frames were extracted, with the z position of the capsule center of mass roughly 0.2 nm apart. Each frame was simulated for 15 ns restraining the capsule center of mass in its original position with a force constant of 500 kJ (mol nm2)−1.
000 kJ (mol nm2)−1 was applied between the center of mass (COM) of the capsule and the COM of the lipids falling in a circle of radius 12 nm centred on the projection of the capsule COM on xy plane of the membrane. The pulling rate was 10–4 nm ps−1. From these trajectories, 100 frames were extracted, with the z position of the capsule center of mass roughly 0.2 nm apart. Each frame was simulated for 15 ns restraining the capsule center of mass in its original position with a force constant of 500 kJ (mol nm2)−1.
All MARTINI simulations were run with a 20 fs time step.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were selected among the SIRAH available lipids, as POPC is zwitterionic and POPS is negatively charged, reflecting the characteristics of DLPC and DLPG, respectively.
1) were selected among the SIRAH available lipids, as POPC is zwitterionic and POPS is negatively charged, reflecting the characteristics of DLPC and DLPG, respectively.
The SIRAH parameters and coarse-grained coordinates were assigned to the protein molecules through the cgconv script, distributed with the force field. The mapping of the central branched residue of capzip from atomistic to coarse-grained beads was performed manually, matching when possible similar building blocks of amino acid side chains. The studied capsules were solvated in aqueous solution of sodium chloride in physiologic concentration (0.15 mM), ensuring the systems’ neutrality. After energy minimisation, the systems were heated from 0 to 300 K over 10 ns at constant volume (10 fs time step), with protein coordinates constrained to their initial position. Like for the other force fields, initial distances between the paired arms of different capzip peptides were restrained with a harmonic potential of 1000 kJ mol−1 nm−2, and progressively released over 80 ns (20 fs time step), then the system was simulated for 1 μ (three replicas). The pressure and temperature were kept constant at 1 bar and 300 K, controlled respectively using a V-rescale thermostat and a Berendsen barostat with 2 ns collision-frequency and 8 ps pressure-coupling time. Short-interactions were treated with a 1.2 nm cut-off radius, whereas the long-range interactions using Particle Mesh Ewald (PME) method.
The POPC/POPS 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 model bacterial membrane (3488 lipids) was built using the CHARMM-GUI membrane builder,104 and converted to coarse-grained through the cgconv script. Subsequently it was simulated placing the initially equilibrated antimicrobial capsule at 2 nm distance from the membrane. The system was solvated as above. The membrane was equilibrated over 0.5 μs (20 fs time step) at constant temperature and pressure of 300 K and 1 bar (now maintained with a semi-isotropic Parrinello–Rahman coupling), with the capsule coordinates constrained to their initial positions (1000 kJ mol−1 nm−2 constraints force constant). The constraints were then released gradually in four steps, and the simulation was continued for 1 μs, until the capsule was stably attached to the membrane. Subsequently, a 4 mV nm−1 electric field was applied along the z-axis to simulate the transmembrane potential, and the simulation carried on for 1.5 μs.
1 model bacterial membrane (3488 lipids) was built using the CHARMM-GUI membrane builder,104 and converted to coarse-grained through the cgconv script. Subsequently it was simulated placing the initially equilibrated antimicrobial capsule at 2 nm distance from the membrane. The system was solvated as above. The membrane was equilibrated over 0.5 μs (20 fs time step) at constant temperature and pressure of 300 K and 1 bar (now maintained with a semi-isotropic Parrinello–Rahman coupling), with the capsule coordinates constrained to their initial positions (1000 kJ mol−1 nm−2 constraints force constant). The constraints were then released gradually in four steps, and the simulation was continued for 1 μs, until the capsule was stably attached to the membrane. Subsequently, a 4 mV nm−1 electric field was applied along the z-axis to simulate the transmembrane potential, and the simulation carried on for 1.5 μs.
β-Annulus functional design and simulations
Previous investigations on β-annulus (sequence ITHVGGVGGSIMAPVAVSRQLVGS) decorated with gold nanoparticles suggested a geometry compatible with a dodecahedral architecture, consistently with the complete TBSV capsid geometry.75 In this light we modelled the assembly according to the same geometry.The triskelion structure formed by three β-annulus chains (Fig. 1) was extracted from the Tomato Bushy Stunt Virus (TBSV, PDB code: 2TBV73). Twenty triskelion copies were then assembled into a dodecahedral capsule with the C-terminal fragments joined through anti-parallel β-sheets using the Chimera program.106 This resulted in a capsule of 15 nm diameter (Fig. 2a, and ESI Table 1†). Next, the antimicrobial sequence RRWTWE was aligned to the β-annulus sequence and threaded onto the structure via AlignedThread.107 It resulted structurally aligned with the RQLVS stretch at the C-terminal (ESI Fig. 1†), thus forming antiparallel β-sheets with another triskelion copy (Fig. 2b).
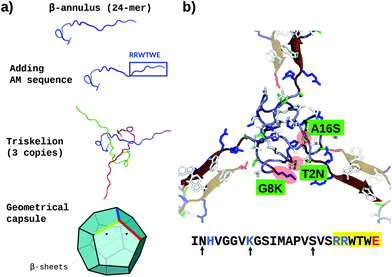 | ||
| Fig. 2 (a) Schematic of the AM-β-annulus capsule building strategy. (b) Representation of three AM-β-annulus sequences forming a vertex of the AM-β-annulus capsule, with matching arms coming from other vertices (faded). Maroon cartoon shows the RRWTWE antimicrobial sequences. The three residues mutated to improve the solubility are highlighted in red blobs and green panels. Charged amino acid side chains are blue (positive) and red (negative). The sequence of each AM-β-annulus chain is shown at the bottom: antimicrobial sequence highlighted in yellow, mutations indicated by arrows, positive and negative residues in blue and red respectively [VMD software108]. | ||
It has to be noticed that the β-annulus triskelion within the virus structure is co-assembling with other viral proteins and therefore once extracted from its original environment hydrophobic residues are exposed on the surface. To improve the stability and solubility of this β-annulus triskelion, mutagenic assays based on Position-Specific Score Matrix (PSSM) were performed, leaving the antimicrobial sequence as is (Fig. 2b). Twenty Monte Carlo cycles with 3 PSSM-based design rounds with multiples energy minimizations steps each were performed, evaluating the energy within the full capsule assembly, with ROSETTA scripts.107,109 Of them, only mutations with negative mutational energy (T2N, G8 K and A16S) were accepted (see Fig. 2b and ESI Fig. 1†). The characteristics of the resulting capsule are shown in Fig. 1 and ESI Table 1.†
The resulting structure (AM-β-annulus capsule) was simulated with the SIRAH force field in aqueous environment for 1 μs and the antimicrobial activity was explored against a POPC/POPS 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 membrane (see details in paragraph on SIRAH simulations of capzip capsule). For the latter, the equilibrated AM-β-annulus capsule was initially placed at 2 nm of distance from the membrane surface. After binding to the membrane (at 500 ns), the simulation was continued for 1 μs. In this case, only a small electric field (4 mV nm−1) was necessary to initiate poration. All equilibration procedures are the same as described for the SIRAH simulations of the capzip capsule.
1 membrane (see details in paragraph on SIRAH simulations of capzip capsule). For the latter, the equilibrated AM-β-annulus capsule was initially placed at 2 nm of distance from the membrane surface. After binding to the membrane (at 500 ns), the simulation was continued for 1 μs. In this case, only a small electric field (4 mV nm−1) was necessary to initiate poration. All equilibration procedures are the same as described for the SIRAH simulations of the capzip capsule.
Analysis
Root Mean Square Deviations (RMSD, with respect to the initial configuration shown in Fig. 1) and radius of gyration (Rg) are computed on the positions of the Cα or coarse-grained backbone beads. The thickness of the capsule wall was computed by fitting a Gaussian on the radial distribution from the centre of the capsule. Hydrogen bonds and Solvent Accessible Surface Area are computed with the native GROMACS tools. The number of conserved arm–arm contacts (which relates loosely to the number of conserved β-sheets), were computed taking the center of mass (COM) of each antimicrobial arm and counting the contact pairs at less than 1.2 nm of distance. This holds for both atomistic and coarse-grained representation.For simulations involving membranes, the area per lipid was obtained from the lateral dimensions of the box. The curvature of the lipid patches was minimal so that this type of computation was accurate within the methods error. The lateral diffusion coefficient D of lipids was obtained for each leaflet from a linear fit of the Mean Square Displacement of the phosphorus atoms (or corresponding coarse-grained bead) as a function of time, according to Einstein equation in two dimensions:110 〈r2〉 = 4Dt. The fit was performed in the regions which showed a linear dependence, and the coefficients from the two leaflets were averaged. The COM movement of each leaflet was removed beforehand for control simulations involving only the membrane. The COM movement of the peptide assembly was instead removed when the capzip capsule or pentagonal unit was present and bound to the lipids. For atomistic simulations in presence of capzip pentagonal unit, the diffusion constant was also computed selectively on the lipids which, at the initial time, were within 1 nm, 2 nm or 3 nm from the protein, or in a region at distances larger than 3 nm. Moreover, we monitored hydrogen bonds between capzip molecules and lipids.
For the umbrella sampling simulations of the capzip capsule penetrating the membrane, we derived the free energy profiles using the Weighted Histogram Analysis Method (WHAM) as implemented in GROMACS.111 The errors on the profiles were obtained through Bayesian bootstrapping, using 100 iterations.
Results
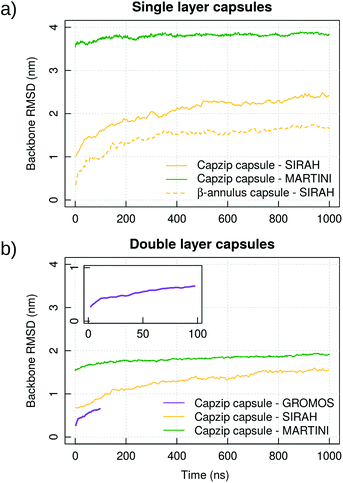
Capzip in solution
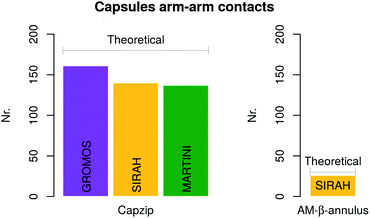
Atomistic simulations of the capzip capsule in solution show a structure going towards an equilibrated configuration within the force field applied, with a final arrangement slightly less regular than the initially imposed one. The atomistic RMSD (in purple in Fig. 3b) starts plateauing around 0.7 nm and the structure remains hollow. The system shrinks with respect to its initial configuration, as the gap between the two layers of the capsule tightens (final size 5.45 nm, initial one 7 nm), with an estimated wall thickness of 2.2 nm. A similar trend is observed for MARTINI and SIRAH simulations, with RMSD of 1 nm and 1.5 nm (Fig. 3a), final size of 5.05 nm and 6.6 nm and wall thickness of 1.9 nm and 2.9 nm, respectively. The SIRAH force field suggests more mobility of the arms and thus a larger rearrangement of the peptides, but the capsule still maintains a regular and hollow structure.For the atomistic description, intermolecular contacts are mediated by hydrogen bonds (Fig. 4). In particular, the Tryptophan engages in H-bonds with its backbone polar atoms, enforcing the β-sheet pairing hypothesised for the capzip antimicrobial arms.63 Arginine side chains engage with many other side chains as donors, and especially with glutamic acid, as expected from the juxtaposed positions they occupy in the β-sheet arrangement, and their opposite charges. This arrangement is reflected also in the coarse-grained descriptions by the proximity of the corresponding beads, attracted by electrostatic (not shown). Moreover, on average, 161 of the 180 β-sheets keeping the capzip peptides together in the capsule are maintained throughout the GROMOS 54A8 atomistic simulations, 140 in the MARTINI and 137 in the SIRAH forcefield (Fig. 5).
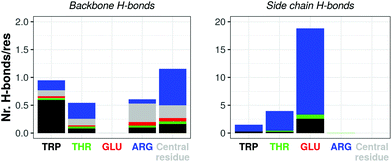 | ||
| Fig. 4 Atomistic simulation of capzip capsule (replica 1): average number of hydrogen bonds per residue occurring between amino acids backbone (left) and side chains (right) in the last 50 ns of simulation (central residue refers to the moiety linking the antimicrobial arms – see Fig. 1). For each bar, the residue on the x-axis is the acceptor, and the bar is split by the identity of the donors. Corresponding plots for hydrogen bonds between side chain and backbone atoms are shown in ESI Fig. 3.† | ||
To prove that the bilayer is essential to prevent disassembly or deformation of the structure, we performed simulations of a monolayer capsule at the coarse-grained levels (specifically taking the external layer of the capsule already simulated). The structure collapses toward its centre for both the MARTINI and SIRAH description, yielding a much higher RMSD than in the double layer case (3.8 nm versus 1.9 nm for MARTINI and 2.4 nm versus 1.4 nm for SIRAH, Fig. 3). Based on this, we concluded that the capzip capsules observed experimentally must have a non-monolayer structure to provide enough structural stability to the proposed geometrical assembly. This is consistent with cryo-EM images of capzip capsules which show a mutilayer structure.63
Capzip–membrane interaction: atomistic simulations
Comparing simulations of a bacterial model membrane (DLPC/DLPG 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, large patch of 740 lipids) with or without the capzip pentagonal unit in contact with it, no significant change is observed in the area per lipid ApL (0.569(4) nm2). Similarly, a 20 mV nm−1 electric field (magnitude compatible with the transmembrane potential) does not affect the ApL in either configuration. The lateral diffusion varies between the replicas (between 0.3 and 0.5 μm2 s−1) and for both lipids, but especially DLPG, the diffusion coefficient increases with the distance from the peptide (Fig. 6). This is due to the hydrogen bonds between both lipid species and the peptide, and net electrostatic interactions between positive arginines and negative DLPG lipids. We computed the former, for each amino acid type, and filtered for the ones present more than 50% of the simulation time (persistent bonds). When no field is applied, arginine residues promote 32 persistent bonds, 12 of which are with DLPG, although this lipid constitutes only 25% of the membrane. In a simulation with a 20 mV nm−1 electric field, they increase to 34, 16 of which are with DLGP. Tryptophan and threonine residues promote fewer persisting bonds (10 and 8 for the simulation without field, and 9 and 11 for the one with electric field), with no particular preference for DLPG, and glutamate residues do not engage in any hydrogen bond. The central residue joining the arms does not form persistent hydrogen bonds with the lipids.
1, large patch of 740 lipids) with or without the capzip pentagonal unit in contact with it, no significant change is observed in the area per lipid ApL (0.569(4) nm2). Similarly, a 20 mV nm−1 electric field (magnitude compatible with the transmembrane potential) does not affect the ApL in either configuration. The lateral diffusion varies between the replicas (between 0.3 and 0.5 μm2 s−1) and for both lipids, but especially DLPG, the diffusion coefficient increases with the distance from the peptide (Fig. 6). This is due to the hydrogen bonds between both lipid species and the peptide, and net electrostatic interactions between positive arginines and negative DLPG lipids. We computed the former, for each amino acid type, and filtered for the ones present more than 50% of the simulation time (persistent bonds). When no field is applied, arginine residues promote 32 persistent bonds, 12 of which are with DLPG, although this lipid constitutes only 25% of the membrane. In a simulation with a 20 mV nm−1 electric field, they increase to 34, 16 of which are with DLGP. Tryptophan and threonine residues promote fewer persisting bonds (10 and 8 for the simulation without field, and 9 and 11 for the one with electric field), with no particular preference for DLPG, and glutamate residues do not engage in any hydrogen bond. The central residue joining the arms does not form persistent hydrogen bonds with the lipids.
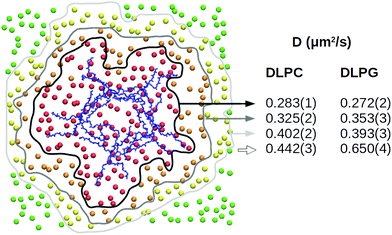 | ||
| Fig. 6 Atomistic simulation of capzip pentagonal unit on model bacterial membrane (512 lipids): local lateral diffusion computed along 500 ns for DLPC and DLPG lipids which, at the initial time, are at a distance smaller than 1 nm (red), 2 nm (orange) or 3 nm (yellow) from the peptide or larger than 3 nm (green), centring the trajectory around the Protein COM (blue) [VMD software108]. | ||
To observe the penetration of capzip through the membrane within the available simulation time, we performed atomistic electroporation simulations, by applying an increasing electric field on a 512 lipids patch (Fig. 7). Poration happened at the value of 130 mV nm−1 in presence of the peptide. This is confirmed by three replicas on both the 512 and 740 lipid patches, where the 130 mV nm−1 field was applied directly and poration happens within 20 to 75 ns of simulation in all the cases. Control simulations on a 512 lipid bacterial membrane without capzip show no poration at 130 mV nm−1 (600 ns simulations, 3 replicas). It was instead observed with a 140 mV nm−1 electric field after 150 ns and 154 ns, while a third replica presented a curved but still intact membrane after 200 ns.
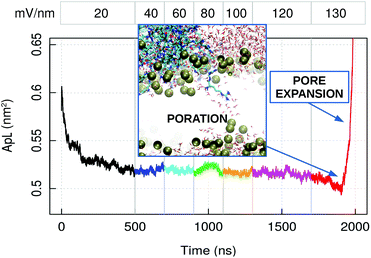 | ||
| Fig. 7 Atomistic simulation of capzip pentagonal unit on model bacterial membrane (512 lipids) with increasing applied external electric field: average area per lipid (ApL). The numbers at the top indicate the magnitude of the field in mV nm−1. The inset shows the poration event: Lipid boundaries in surface representation, peptides and water molecules in bond representation [VMD software108]. The increase in ApL after pore formation is due to the pore expansion. | ||
The application of an electric field to the system of capzip capsule–bacterial membrane accelerates the bilayer disruption process, as reported previously.112 This is due to perturbations caused to the membraneous arrangement by the inserting peptide through charged and hydrogen bond interactions mentioned before. These promote charged arginine residue insertion and initiate water penetration in the hydrophobic core of the membrane. Similar initiation processes have been observed for arginine rich cell penetrating peptides in experiments113,114 and MD simulations.114,115
Capzip–membrane interactions: coarse-grained simulations
Coarse-grained simulations allow to model the full capsule interacting with the membrane. Simulations with MARTINI (standard water model) proved the binding of capzip capsule to the bacterial model membrane, but not to the mammal (in the 10 μs simulated). In both runs, the peptide gets in contact with the bacterial membrane after about 2 μs and remains membrane-bound, diffusing laterally and producing an increasingly high curvature on the bilayer (Fig. 8, top). No poration is observed, probably because longer time scales are needed to simulate it.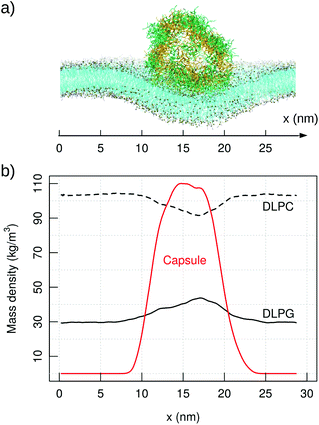 | ||
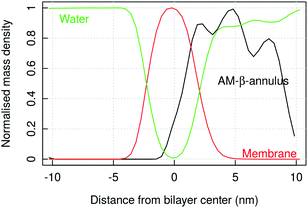
| Fig. 8 MARTINI simulation of capzip capsule on bacterial model membrane (10 μs): (a) snapshot of the final configuration (capsule in stick representation, outer and inner layer in green and yellow respectively; lipids in line representation and phosphate beads in golden van der Waals – VMD software108); (b) corresponding mass density of capzip, DLPC and DLPG along the x-axis, averaged on the last μs of simulation. | ||
The binding is driven by charge–charge interactions, and the presence of the capsule impacts strongly on the diffusion and distribution of the lipids. The lateral diffusion coefficient drops from 74.28(1) to 70.51(1) μm2 s−1 for DLPC, and from 73.34(2) to 62.59(2) μm2 s−1 for DLPG. The larger effect on DLPG is due to its negative net charge and a strong attraction to the positively charged peptide. This is confirmed by the RDF of the capzip amino acids around different lipids moieties, as the strongest signal comes from the Arg residue around the DLPG phosphate groups, and is less so from the DLPC phosphate moieties (ESI Fig. 6†). As a consequence, DLPG lipids are enriched nearby the capsule (Fig. 8), at the expense of DLPC molecules. This enrichment can be observed at the coarse-grained level only, as the lipid patch is large enough, and the time simulated sufficient, to allow a collective rearrangement of the membrane components.
The adoption of Polar water103 alone (without applied electric field) sped up considerably the binding of the capsule to the membrane (within the first 50 ns, as opposed to 2 μs of the standard water simulation). Then, in a 500 ns simulation under the action of a 20 mV nm−1 electric field, the curvature of the membrane rapidly increased, and after switching to a 40 mV nm−1 field the membrane porated within 200 ns. Analogous simulations on the membrane alone did not trigger poration in 500 ns (40 mV nm−1). Continuing the simulation of the porated membrane (40 mV nm−1), we observe the capsule penetrating within 10 ns. The lipids do not seal around the capsule, allowing the passage of water and ions, which is consistent with our findings for the atomistic simulations. During the membrane penetration process, the capsule deforms and partially opens. Longer simulations might lead to poration with a lower field strength, as the initiation of a pore is a stochastic event. Nevertheless, the simulations set an important comparison with the model mammalian membrane, as for the latter no binding was observed even with an applied electric field.
Simulations of the phospholipid mixture DLPC/DLPG elucidates why the capzip capsule is active on in vitro model lipid bilayers and reproduces the experimental conditions with which capzip was developed.18,63 One could enquire how this activity can be tested with models of the Gram negative outer membrane. We performed two simulations of the capzip capsule on the LPS membrane, for a total of 2 μs. Starting with the capsule at 1 nm distance from the LPS membrane, the capsule attaches to it after 270 ns, attracted by the negative charge of the LPS molecules. The membrane is thicker and thus less flexible than the previous DLPC/DLPG model: while in that case the charge–charge interaction forced the membrane to curve and partially wrap the capsule, on LPS this effect is smaller. On the contrary the capsule quickly opens to increase the interactions with the LPS molecules after the attachment, rearranging itself in the following 300 ns, after which the configuration is kept stable (ESI Fig. 10†). The peptide residues lying on the surface penetrate down to the region of calcium ions, but do not cross it in the simulation time. Arginine residues are also in this case the ones penetrating deeper. This is confirmed by the simulation starting with the capsule in contact with the membrane.
As penetration events are slow, longer simulations might indicate further rearrangement of the peptides. Additionally, the properties of the membrane at the interface are significantly influenced by the presence of high concentration of calcium ions116 and therefore the mechanism of adhesion and penetration of the capsule maybe severely altered with respect to the DLPC/DLPG membrane. More accurate studies varying calcium concentration and fine tuning the interactions with the highly charged capsule and lipids are necessary to elucidate this. Of note, the capsule simulated has a size of 15 nm, while the experiments detect capsules of bigger sizes as well,18,63 and a larger localised concentration of capzip molecules would be more effective in perturbing the membrane.
To further clarify the difference in the mechanisms of interaction of the capzip peptide between the bacterial and mammal model membrane, and to speed up the process of capzip capsule membrane passage, we pulled the capsule through the DLPC/DLPG and the DLPC model membranes. We reverted back to the simpler bacterial model membrane (mimicking the inner membrane) as a simpler and more easily interpretable system. The PMF profile was computed using an umbrella sampling procedure (Fig. 9). In the mammalian model, the membrane constitutes a high energy barrier to the approach and penetration of the capsule, and the PMF rises consistently while the capsule–membrane distance is decreasing. To be noticed that the distance reported in Fig. 9 is measured as the z position of the centre of mass of the capsule minus the z position of the centre of mass of an outer disc of lipids, i.e. lipids which are not within a 12 nm radius from the z-projection of the capsule COM on the membrane. Poration happens at distance larger than 0 nm due to the size of the capsule. After the disruption, the membrane quickly rearranges around the capsule. As umbrella sampling should be performed in near to equilibrium conditions for each window, we did not evaluate the PMF after the poration event.
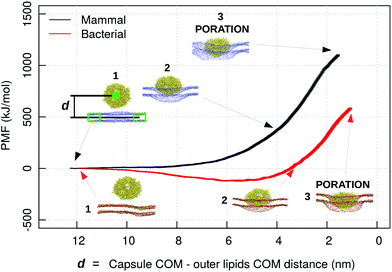 | ||
| Fig. 9 PMF profile of a capzip capsule penetrating a mammal (black) and bacterial (red) model membrane (MARTINI simulations), in function of the distance d between capzip capsule centre of mass and the centre of mass of the outer ring of lipids not involved in the pulling groups (lipids which are not within a 12 nm radius from the z-projection of the capsule COM on the membrane), which represent the unperturbed membrane. The snapshots show different stages of the penetration process; peptide and phosphate beads of lipids in van der Waals representation (blue for DLPC in the mammal membrane; red and green for DLPC and DLPG in the bacterial one) [VMD software108]. | ||
Nevertheless the simulation brings some useful insight. Contrary to the mammal case, for the bacterial membrane the PMF decreases during the capsule approach (of about 100 kJ mol−1), and increases only afterwards. The first effect is promoted by the negatively charged lipids which attract the positive capsule. This proves once more that the bacterial membrane has a stronger affinity for the capzip capsule and therefore their poration and disruption action is more pronounced for these systems, and consequently the antimicrobial function is more effectively exerted.
As stated in the methods, while the combination of atomistic and MARTINI force fields was selected for the exploratory analysis, the SIRAH force field, of intermediate granularity between the two, is suitable to pursue further investigation on the β-annulus interaction with the membrane. Moreover, the β-annulus has a well defined secondary structure in its core and the SIRAH set up allows to simulate the molecule without recurring to constraints to maintain its secondary structure like in MARTINI's approach. To confirm the suitability of the force field we repeated the simulations of capzip capsule on the bacterial membrane with the SIRAH parameters. The capsule attaches to the membrane within the first 100 ns and deforms it but no poration is observed in the 10 μs simulated, consistent with the MARTINI simulations. The diffusion of the charged lipids (POPS in this case) is similar to the one of the zwitterionic POPC, being respectively 16.2. and 16.6 μm2 s−1 and no enrichment of POPS nearby the capsule is observed. In the MARTINI simulations, the negatively charged lipid was recruited within the same amount of simulation time: the difference with the SIRAH force field is likely due to the different parametrisations.
Functionalised β-annulus simulations
Simulations of the AM-β-annulus capsule in solution show that the capsule equilibrates (with RMSD of 1.7 nm) with a radius of gyration of 4.5 nm (Fig. 3 and ESI Fig. 1†). Similarly to the capzip capsule, it shrinks during the simulation to achieve its equilibrium size. Out of the 30 pre-imposed arm–arm pairs, 26 are maintained during the simulation, proving that the initial geometry is well conserved.Simulations of the AM-β-annulus capsule on the bacterial membrane show attachment to the lipids within 1 μs of the simulation without electric field. This is compatible with what observed for capzip, however with the introduction of a small electric field (4 mV nm−1), a small pore is forming within 1.5 μs, contrary to capzip, for which poration is not observed in the 10 μs simulated (Fig. 10). Some portions of the capsule reach the core of the membrane (Fig. 11). The presence of the AM-β-annulus capsule on the membrane does not affect the lateral diffusion of lipids, which remains 14.2 μm2 s−1 for POPC and 15.9 μm2 s−1 for POPS, nor induces any recruitment of the negatively charged POPS.
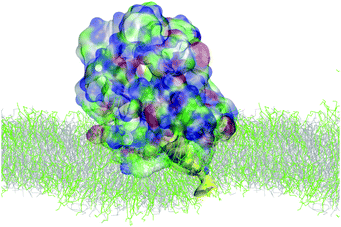 | ||
| Fig. 10 SIRAH simulation of AM-β-annulus capsule on bacterial model membrane: snapshot of poration due to the combined action of the capsule and a 4 mV nm−1 electric field. Capsule in surface representation, color coded by amino acid type (blue positive, red negative, green polar, white hydrophobic). Pore highlighted in yellow surface. Lipids in grey (POPC) and green (POPS) lines [VMD software108]. | ||
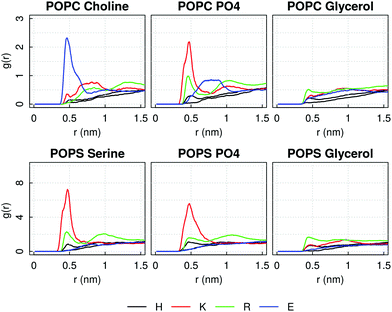
In investigating the reasons for the pore formation, we computed the Radial Distribution Function of any of the amino acid type forming the AM-β-annulus sequence around typical moieties of the lipids heads, in order to identify key peptide–lipid interactions. It emerges a strong interaction of the positive POPC choline head group with the negative glutamic acid residue, and of the negative phosphate groups with lysine and arginine residues. Additionally, lysine interacts with the L-serine POPS head group (Fig. 12, similar plots for all the other residues are shown in ESI Fig. 8 and 9†). In the case of the capzip capsule, the tryptophan interacts very weakly with the DLPC glycerol and slightly more with the DLPG one (ESI Fig. 6 and 7†). For the AM-β-annulus capsule instead the hydrophobic residues are interacting with the lipids.
This is compatible with the values of Surface Accessible Solvent Area (QSASA, normalised by the nominal experimental value) computed for positive, negative, polar and hydrophobic amino acids on the atomistic structures of capzip and AM-β-annulus capsules (ESI Table 1†). The positive amino acids QSASA is higher for the capzip capsule (more exposed positive residues), and the hydrophobic one is lower (less exposed), leading to a faster attachment of the capzip capsule to the membrane (100 ns versus 500 ns) driven by a charge recognition mechanism. On the contrary, in the AM-β-annulus capsule, the more exposed hydrophobic residues facilitate the insertion process, with their propensity to segregate from water.
The difference in hydrophobic residues exposition is due to the double layer structure of the capzip capsule, but also on the higher content of hydrophobic residues in the AM-β-annulus. Thus features from the core of this construct are contributing to the antimicrobial activity together with the RRWTWE sequence itself.
Conclusions
The investigations performed proved the power of the use of combined protein design and molecular simulations with force fields of different granularity to elucidate details of nanoscale systems with antimicrobial activity. We explored potential arrangements in pre-assembled nanocapsule systems of a specific antimicrobial sequence from Lactoferrin and studied their stability and their interaction with model membranes. The two systems reported here were selected for different reasons: for the capzip system we had a number of supporting experiments suggesting that our design in a double layered capsule is correct; we wanted to explore in detail the interaction with mammals vs. non mammals model membranes to clarify the efficacy of the capzip system. For the AM-β-annulus system we have proposed a designed nanocapsule with self assembling elements: (a) a peptide element that is experimentally proven to self-assemble in a triskelion geometry suitable for a nanocapsule;74–79 and (b) the antimicrobial sequence used for the capzip system as antimicrobial moiety.18,63 This original design has been investigated for its stability in solution and interaction with a model membrane in silico.When investigating the assembly process of capzip peptides, the use of atomistic simulations gave insights into the role of specific amino acids in the pairing and assembly of the many copies of the molecule, the role of the ‘arms’ and the precise indentation of the residues forming the β-sheet elements necessary to hold the scaffold of the capsule.
Coarse-grained simulations proved extremely useful in the evaluation of the stability of the pre-assembled structures on the long time scale. Additionally, we showed here that simplified models were sufficient to evaluate processes like the absorption on different types of membranes. Overall, we were able to conclude that the ability of capzip to form capsules lays not only in the scheme of opposite charges that it hosts along its arms, but also in the presence of many hydrophobic residues, which favour the assembly with attractive hydrophobic forces. Thus, the proposed structure contains a bilayer arrangement of the molecules, which is demonstrated to be more stable than a monolayer one, and is consistent with the more recent experimental findings showing multilayer capsules.63
Coarse-grained simulations were also able to clarify the interaction of capzip with the membrane. Capzip has a propensity to bind to negatively charged membranes, which are a simplified model for the bacterial inner membrane, but not to zwitterionic lipids, which model a mammalian membrane. Moreover, on the bacterial membrane, the buckyball recruits negatively charged lipids in its proximity, reducing their diffusion. Atomistic simulations complemented these findings showing the details of such interaction: on a bacterial membrane, capzip interacts with the lipids forming many hydrogen bonds and inserting the Arginine side chains deep in the phosphate region of the lipids. Consequently, the lipids around the peptide are slowed down in their diffusion on the measured time scale of atomistic simulations.
Finally, simulations with an external electric field applied (within physiological ranges) to the system showed that the peptide bound to the bacterial membrane promotes poration at values of the field which would not cause electroporation on the membrane alone.
The above results integrate the ones from pulling experiments, which show a favourable attraction between capzip and a model bacterial membrane, and a lower energy barrier for poration in the bacterial versus the mammal membrane case. This gives a more complete picture on the characteristics of this capzip, in agreement with the experimentally proven selectivity but non-toxicity of the peptide.18,63
The results on the AM-β-annulus system prove the possibility of designing AM nanocapsules with self-assembling elements that can impose a specific geometry to the capsule. We hope that the proposed design will stimulate experimental studies on the stability and organisation of the assembly in monolayer capsules and on their antimicrobial activity.
The outcome of the research presented here can be leveraged for future design strategies as it highlights the crucial and necessary components for the assembly, as well as the ones where there is scope for improvement or modification. Future investigations will tackle this problem, unifying again the experimental and computational settings to help a fast screening of newly generated compounds.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I. M. acknowledges funding by the Engineering and Physical Sciences Research Council (EPSRC) through the Centre for Doctoral Training “Cross Disciplinary Approaches to Non-Equilibrium Systems” (CANES, Grant No. EP/L015854/1). C. H. B. C. acknowledges funding from CAPES – Proc. n 88881.197985/2018-01. This project made use of the following resources: computer time on ARCHER granted via the UK High-End Computing Consortium for Biomolecular Simulation, HECBioSim (http://hecbiosim.ac.uk), supported by EPSRC (grant no. EP/R029407/1); resources provided by the Cambridge Service for Data Driven Discovery (CSD3) operated by the University of Cambridge Research Computing Service (http://www.csd3.cam.ac.uk/), provided by Dell EMC and Intel using Tier-2 funding from the Engineering and Physical Sciences Research Council (capital grant EP/P020259/1), and DiRAC funding from the Science and Technology Facilities Council (http://www.dirac.ac.uk).References
- P. Mantravadi, K. Kalesh, R. Dobson, A. Hudson and A. Parthasarathy, Antibiotics, 2019, 8, 8 CrossRef CAS PubMed.
- L. T. Nguyen, E. F. Haney and H. J. Vogel, Trends Biotechnol., 2011, 29, 464–472 CrossRef CAS PubMed.
- A. Ebbensgaard, H. Mordhorst, M. T. Overgaard, C. G. Nielsen, F. M. Aarestrup and E. B. Hansen, PLoS One, 2015, 10, e0144611 CrossRef PubMed.
- T. Ebenhan, O. Gheysens, H. G. Kruger, J. R. Zeevaart and M. M. Sathekge, BioMed Res. Int., 2014, 867381 Search PubMed.
- M. Mahlapuu, J. Håkansson, L. Ringstad and C. Björn, Front. Cell. Infect. Microbiol., 2016, 6, 194 CrossRef PubMed.
- A. Peschel and H.-G. Sahl, Nat. Rev. Microbiol., 2006, 4, 529–536 CrossRef CAS PubMed.
- A. Lewies, L. H. Du Plessis and J. F. Wentzel, Probiotics Antimicrob. Proteins, 2019, 11, 370–381 CrossRef CAS PubMed.
- K. Hilpert, R. Volkmer-Engert, T. Walter and R. E. W. Hancock, Nat. Biotechnol., 2005, 23, 1008–1012 CrossRef CAS PubMed.
- D. Migoń, M. Jaśkiewicz, D. Neubauer, M. Bauer, E. Sikorska, E. Kamysz and W. Kamysz, Probiotics Antimicrob. Proteins, 2018, 1–13 Search PubMed.
- S. Liu, J. Bao, X. Lao and H. Zheng, Sci. Rep., 2018, 8, 11189 CrossRef PubMed.
- Z. Jiang, A. I. Vasil, L. Gera, M. L. Vasil and R. S. Hodges, Chem. Biol. Drug Des., 2011, 77, 225–240 CrossRef CAS PubMed.
- C. D. Fjell, J. A. Hiss, R. E. W. Hancock and G. Schneider, Nat. Rev. Drug Discovery, 2011, 11, 37 CrossRef PubMed.
- V. V. Kleandrova, J. M. Ruso, A. Speck-Planche and M. N. Dias Soeiro Cordeiro, ACS Comb. Sci., 2016, 18, 490–498 CrossRef CAS PubMed.
- D. Veltri, U. Kamath and A. Shehu, Bioinformatics, 2018, 34, 2740–2747 CrossRef CAS PubMed.
- F. Cipcigan, A. P. Carrieri, E. O. Pyzer-Knapp, R. Krishna, Y.-W. Hsiao, M. Winn, M. G. Ryadnov, C. Edge, G. Martyna and J. Crain, J. Chem. Phys., 2018, 148, 241744 CrossRef PubMed.
- H. Khandelia and Y. N. Kaznessis, Peptides, 2005, 26, 2037–2049 CrossRef CAS PubMed.
- A. Farrotti, P. Conflitti, S. Srivastava, J. Ghosh, A. Palleschi, L. Stella, G. Bocchinfuso, A. Farrotti, P. Conflitti, S. Srivastava, J. K. Ghosh, A. Palleschi, L. Stella and G. Bocchinfuso, Molecules, 2017, 22, 1235 CrossRef PubMed.
- V. Castelletto, E. de Santis, H. Alkassem, B. Lamarre, J. E. Noble, S. Ray, A. Bella, J. R. Burns, B. W. Hoogenboom, M. G. Ryadnov, J. Vandesompele and C. T. Wittwer, Chem. Sci., 2016, 7, 1707–1711 RSC.
- H. Sun, Y. Hong, Y. Xi, Y. Zou, J. Gao and J. Du, Biomacromolecules, 2018, 19, 1701–1720 CrossRef CAS PubMed.
- F. Cao, L. Mei, G. Zhu, M. Song and X. Zhang, RSC Adv., 2019, 9, 30803–30808 RSC.
- C. Morris, S. J. Glennie, H. S. Lam, H. E. Baum, D. Kandage, N. A. Williams, D. J. Morgan, D. N. Woolfson and A. D. Davidson, Adv. Funct. Mater., 2019, 29, 1807357 CrossRef PubMed.
- G. Manzo, P. M. Ferguson, C. K. Hind, M. Clifford, V. B. Gustilo, H. Ali, S. S. Bansal, T. T. Bui, A. F. Drake, R. A. Atkinson, J. M. Sutton, C. D. Lorenz, D. A. Phoenix and A. J. Mason, Sci. Rep., 2019, 9, 10934 CrossRef PubMed.
- G. Manzo, P. M. Ferguson, V. B. Gustilo, C. K. Hind, M. Clifford, T. T. Bui, A. F. Drake, R. A. Atkinson, J. M. Sutton, G. Batoni, C. D. Lorenz, D. A. Phoenix and A. J. Mason, Sci. Rep., 2019, 9, 1385 CrossRef PubMed.
- S. B. T. Amos, L. S. Vermeer, P. M. Ferguson, J. Kozlowska, M. Davy, T. T. Bui, A. F. Drake, C. D. Lorenz and A. J. Mason, Sci. Rep., 2016, 6, 1–13 CrossRef PubMed.
- H. Leontiadou, A. E. Mark and S.-J. Marrink, J. Am. Chem. Soc., 2006, 128, 12156–12161 CrossRef CAS PubMed.
- J. P. Ulmschneider, Biophys. J., 2017, 113, 73–81 CrossRef CAS PubMed.
- Y. Wang, C. H. Chen, D. Hu, M. B. Ulmschneider and J. P. Ulmschneider, Nat. Commun., 2016, 7, 13535 CrossRef CAS PubMed.
- D. Sun, J. Forsman and C. E. Woodward, J. Phys. Chem. B, 2015, 119, 14413–14420 CrossRef CAS PubMed.
- L. Zhao, Z. Cao, Y. Bian, G. Hu, J. Wang and Y. Zhou, Int. J. Mol. Sci., 2018, 19, 1186 CrossRef PubMed.
- Y. Wang, D. E. Schlamadinger, J. E. Kim and J. A. McCammon, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 1402–1409 CrossRef CAS PubMed.
- R. Lipkin, A. Pino-Angeles and T. Lazaridis, J. Phys. Chem. B, 2017, 121, 9126–9140 CrossRef CAS PubMed.
- G. E. Balatti, E. E. Ambroggio, G. D. Fidelio, M. F. Martini and M. Pickholz, Molecules, 2017, 22(10), 1775–1792 CrossRef PubMed.
- D. Tieleman, Biophys. J., 2017, 113, 1–3 CrossRef CAS PubMed.
- D. Jefferies and S. Khalid, J. Mol. Biol., 2020, 432, 1251–1264 CrossRef CAS PubMed.
- C. Chen, C. G. Starr, E. P. Troendle, G. Wiedman, W. C. Wimley, J. P. Ulmschneider and M. B. Ulmschneider, J. Am. Chem. Soc., 2019, 141, 4839–4848 CrossRef CAS PubMed.
- Y. Zhao, W. Yang, D. Wang, J. Wang, Z. Li, X. Hu, S. King, S. Rogers, J. R. Lu and H. Xu, Small, 2018, 14, 1703216 CrossRef PubMed.
- E. Glukhov, M. Stark, L. L. Burrows and C. M. Deber, J. Biol. Chem., 2005, 280, 33960–33967 CrossRef CAS PubMed.
- M. Tang and M. Hong, Mol. BioSyst., 2009, 5, 317 RSC.
- D. Poger, W. F. Van Gunsteren and A. E. Mark, J. Comput. Chem., 2010, 31, 1117–1125 CrossRef CAS PubMed.
- S.-W. Chiu, M. Clark, V. Balaji, S. Subramaniam, H. L. Scott and E. Jakobsson, Biophys. J., 1995, 69, 1230–1245 CrossRef CAS PubMed.
- T. J. Piggot, D. A. Holdbrook and S. Khalid, J. Phys. Chem. B, 2011, 115, 13381–13388 CrossRef CAS PubMed.
- I. Marzuoli, C. Margreitter and F. Fraternali, J. Chem. Theory Comput., 2019, 15, 5175–5193 CrossRef CAS PubMed.
- A. Kukol, J. Chem. Theory Comput., 2009, 5, 615–626 CrossRef CAS PubMed.
- J. C. Gumbart, M. Beeby, G. J. Jensen and B. Roux, PLoS Comput. Biol., 2014, 10, 1–10 CrossRef.
- M. L. Ortiz-Suarez, F. Samsudin, T. J. Piggot, P. J. Bond and S. Khalid, Biophys. J., 2016, 111, 1692–1702 CrossRef CAS.
- K. N. Kirschner, R. D. Lins, A. Maass and T. A. Soares, J. Chem. Theory Comput., 2012, 8, 4719–4731 CrossRef CAS PubMed.
- T. J. Piggot, D. A. Holdbrook and S. Khalid, Biochim. Biophys. Acta, Biomembr., 2013, 1828, 284–293 CrossRef CAS.
- P.-C. Hsu, D. Jefferies and S. Khalid, J. Phys. Chem. B, 2016, 120, 11170–11179 CrossRef CAS PubMed.
- T. J. Silhavy, D. Kahne and S. Walker, Cold Spring Harbor Perspect. Biol., 2010, 2, a000414–a000414 Search PubMed.
- D. P. Tieleman, BMC Biochem., 2004, 5, 10 CrossRef PubMed.
- R. A. Böckmann, B. L. de Groot, S. Kakorin, E. Neumann and H. Grubmüller, Biophys. J., 2008, 95, 1837–1850 CrossRef PubMed.
- J. Lin and A. Alexander-Katz, ACS Nano, 2013, 7, 10799–10808 CrossRef CAS PubMed.
- K. Shimizu, H. Nakamura and S. Watano, Nanoscale, 2016, 8, 11897–11906 RSC.
- H. Nakamura, K. Sezawa, M. Hata, S. Ohsaki and S. Watano, Phys. Chem. Chem. Phys., 2019, 21, 18830–18838 RSC.
- J. T. Sengel and M. I. Wallace, Philos. Trans. R. Soc., B, 2017, 372, 20160227 CrossRef PubMed.
- L. Yang, T. A. Harroun, T. M. Weiss, L. Ding and H. W. Huang, Biophys. J., 2001, 81, 1475–1485 CrossRef CAS PubMed.
- K. J. Hallock, D.-K. Lee and A. Ramamoorthy, Biophys. J., 2003, 84, 3052–3060 CrossRef CAS PubMed.
- A. Spaar, C. Münster and T. Salditt, Biophys. J., 2004, 87, 396–407 CrossRef CAS PubMed.
- J. T. Wiemann, Z. Shen, H. Ye, Y. Li and Y. Yu, Nanoscale, 2020, 12, 20326–20336 RSC.
- F. Samsudin and S. Khalid, J. Phys. Chem. B, 2019, 123, 2824–2832 CrossRef CAS PubMed.
- A. T. Asmar and J.-F. Collet, FEMS Microbiol. Lett., 2018, 365, fny199 CrossRef CAS PubMed.
- S. Khalid, T. J. Piggot and F. Samsudin, Acc. Chem. Res., 2019, 52, 180–188 CrossRef CAS PubMed.
- I. E. Kepiro, I. Marzuoli, K. Hammond, X. Ba, H. Lewis, M. Shaw, S. B. Gunnoo, E. De Santis, U. Łapińska, S. Pagliara, M. A. Holmes, C. D. Lorenz, B. W. Hoogenboom, F. Fraternali and M. G. Ryadnov, ACS Nano, 2019, 14, 1609–1622 CrossRef PubMed.
- P. M. Hwang, N. Zhou, X. Shan, C. H. Arrowsmith and H. J. Vogel, Biochemistry, 1998, 37, 4288–4298 CrossRef CAS PubMed.
- D. J. Schibli, P. M. Hwang and H. J. Vogel, FEBS Lett., 1999, 446, 213–217 CrossRef CAS PubMed.
- A. G. Cochran, N. J. Skelton and M. A. Starovasnik, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 5578–5583 CrossRef CAS PubMed.
- M. Ashrafuzzaman, C. Y. Tseng and J. A. Tuszynski, J. Mol. Graphics Modell., 2020, 95, 107502 CrossRef CAS PubMed.
- W. Wu, S. C. Hsiao, Z. M. Carrico and M. B. Francis, Angew. Chem., Int. Ed., 2009, 48, 9493–9497 CrossRef CAS PubMed.
- L. Schoonen and J. C. M. van Hest, Nanoscale, 2014, 6, 7124–7141 RSC.
- R. F. Silva, D. R. Araújo, E. R. Silva, R. A. Ando and W. A. Alves, Langmuir, 2013, 29, 10205–10212 CrossRef CAS PubMed.
- T. O. Yeates, Nature, 2019, 569, 340–342 CrossRef CAS PubMed.
- A. D. Malay, N. Miyazaki, A. Biela, S. Chakraborti, K. Majsterkiewicz, I. Stupka, C. S. Kaplan, A. Kowalczyk, B. M. A. G. Piette, G. K. A. Hochberg, D. Wu, T. P. Wrobel, A. Fineberg, M. S. Kushwah, M. Kelemen, P. Vavpetič, P. Pelicon, P. Kukura, J. L. P. Benesch, K. Iwasaki and J. G. Heddle, Nature, 2019, 569, 438–442 CrossRef CAS PubMed.
- P. Hopper, S. C. Harrison and R. T. Sauer, J. Mol. Biol., 1984, 177, 701–713 CrossRef CAS PubMed.
- K. Matsuura, K. Watanabe, T. Matsuzaki, K. Sakurai and N. Kimizuka, Angew. Chem., Int. Ed., 2010, 49, 9662–9665 CrossRef CAS PubMed.
- S. Fujita and K. Matsuura, Nanomaterials, 2014, 4, 778–791 CrossRef PubMed.
- K. Matsuura, G. Ueno and S. Fujita, Polym. J., 2015, 47, 146–151 CrossRef CAS.
- Y. Nakamura, S. Yamada, S. Nishikawa and K. Matsuura, J. Pept. Sci., 2017, 23, 636–643 CrossRef CAS PubMed.
- K. Matsuura, Y. Mizuguchi and N. Kimizuka, Biopolymers, 2016, 106, 470–475 CrossRef CAS PubMed.
- K. Matsuura, T. Nakamura, K. Watanabe, T. Noguchi, K. Minamihata, N. Kamiya and N. Kimizuka, Org. Biomol. Chem., 2016, 14, 7869–7874 RSC.
- C. Oostenbrink, T. A. Soares, N. F. A. van der Vegt and W. F. van Gunsteren, Eur. Biophys. J., 2005, 34, 273–284 CrossRef CAS PubMed.
- M. M. Reif, M. Winger and C. Oostenbrink, J. Chem. Theory Comput., 2013, 9, 1247–1264 CrossRef CAS PubMed.
- S.-J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834 CrossRef CAS PubMed.
- M. R. Machado, E. E. B. Guisasola, F. Klein, M. Sóñora, S. Silva and S. Pantano, J. Chem. Theory Comput., 2019, 15, 2719–2733 CrossRef CAS PubMed.
- E. E. Barrera, M. R. Machado and S. Pantano, J. Chem. Theory Comput., 2019, 15, 5674–5688 CrossRef CAS PubMed.
- H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- M. J. Abraham, D. van der Spoel, E. Lindahl, B. Hess and the GROMACS development team, GROMACS User Manual version 2016, 2018 Search PubMed.
- Schroedinger, LLC, The PyMOL Molecular Graphics System, Version 1.2r3pre Search PubMed.
- Chemical Computing Group ULC, Molecular Operating Environment (MOE), 2013.08, 2018, 1010 Sherbooke St. West, Suite 910, Montreal, QC, Canada, H3A 2R7 Search PubMed.
- T.-Y. Lin and D. B. Weibel, Appl. Microbiol. Biotechnol., 2016, 100, 4255–4267 CrossRef CAS PubMed.
- A. A. Spector and M. A. Yorek, J. Lipid Res., 1985, 26, 1015–1035 CrossRef CAS.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- H. Berendsen, J. Postma, W. Van Gunsteren and J. Hermans, Intermolecular Forces, D. Reidel Publishing Company, Dordrecht, 1981, pp. 331–342 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef CAS PubMed.
- J. A. Graham, J. W. Essex and S. Khalid, J. Chem. Inf. Model., 2017, 57, 650–656 CrossRef CAS.
- T. A. Wassenaar, H. I. Ingólfsson, R. A. Böckmann, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 2144–2155 CrossRef CAS PubMed.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S.-J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810 CrossRef PubMed.
- S. Jo, T. Kim and W. Im, PLoS One, 2007, 2, 1–9 CrossRef.
- I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459 CrossRef CAS.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- A. Leaver-Fay, M. Tyka, S. M. Lewis, O. F. Lange, J. Thompson, R. Jacak, K. Kaufman, P. D. Renfrew, C. A. Smith, W. Sheffler, I. W. Davis, S. Cooper, A. Treuille, D. J. Mandell, F. Richter, Y.-E. A. Ban, S. J. Fleishman, J. E. Corn, D. E. Kim, S. Lyskov, M. Berrondo, S. Mentzer, Z. Popović, J. J. Havranek, J. Karanicolas, R. Das, J. Meiler, T. Kortemme, J. J. Gray, B. Kuhlman, D. Baker and P. Bradley, Methods Enzymol., 2011, 487, 545–574 CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- A. Goldenzweig, M. Goldsmith, S. E. Hill, O. Gertman, P. Laurino, Y. Ashani, O. Dym, T. Unger, S. Albeck, J. Prilusky, R. L. Lieberman, A. Aharoni, I. Silman, J. L. Sussman, D. S. Tawfik and S. J. Fleishman, Mol. Cell, 2016, 63, 337–346 CrossRef CAS PubMed.
- A. Einstein and R. Fürt, Investigations on the theory of Brownian movement, Dover Publications, 1956, p. 119 Search PubMed.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- B. Wang, J. Zhang, Y. Zhang, Z. Mao, N. Lu and Q. H. Liu, RSC Adv., 2018, 8, 41517–41525 RSC.
- M. Tang, A. J. Waring and M. Hong, J. Am. Chem. Soc., 2007, 129, 11438–11446 CrossRef CAS PubMed.
- M.-L. Jobin, L. Vamparys, R. Deniau, A. Grélard, C. Mackereth, P. Fuchs and I. Alves, Int. J. Mol. Sci., 2019, 20, 4441 CrossRef CAS PubMed.
- H. Herce, A. Garcia, J. Litt, R. Kane, P. Martin, N. Enrique, A. Rebolledo and V. Milesi, Biophys. J., 2009, 97, 1917–1925 CrossRef CAS PubMed.
- A. Melcrová, S. Pokorna, S. Pullanchery, M. Kohagen, P. Jurkiewicz, M. Hof, P. Jungwirth, P. S. Cremer and L. Cwiklik, Sci. Rep., 2016, 6, 1–12 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional information on the capsules; alignment of Wild Type and modified β-annulus; radius of gyration of the capsules simulated; area per lipid, component density and lipidtail order of membrane simulations (no capsules); side chains/backbone hydrogen bonds for atomistic simulation of capzip capsule; radial distribution function of capzip and β-annulus capsules amino acids around bacterial membrane lipid moieties. See DOI: 10.1039/D0NR08146A |
| ‡ Present address: Instituto de Tecnologia Química e Biológica António Xavier, Universidade Nova de Lisboa, Oeiras, Portugal. |
| This journal is © The Royal Society of Chemistry 2021 |