Enhanced photoluminescence of silicon quantum dots in the presence of both energy transfer enhancement and emission enhancement mechanisms assisted by the double plasmon modes of gold nanorods

Abstract

We propose a scheme utilizing the double plasmon modes of gold nanorods (GNRs) to efficiently increase the Förster resonant energy transfer (FRET) efficiency and enhance the photoluminescence (PL) of Si quantum dots (Si QDs) nearby. Detailed PL and decay dynamics studies are performed for the hybrid nanostructures composed of metallic nanoparticles (MNPs) coated with a Si QD-absorbed silica shell. Plasmon enhanced FRET between Si QDs has been observed and proposed as the third enhancement mechanism for the plasmon-enhanced photoluminescence in addition to excitation enhancement and emission enhancement mechanisms. A maximum FRET efficiency of 46.3% is obtained, which is enhanced by a factor of 8.7 compared to that of samples without MNPs. The dependence of the energy transfer efficiency and the enhancement of the acceptor emission on the surface plasmon resonance (SPR) wavelength, metal-QD distance and QD ratio is examined. The FRET enhancement mechanism dominates when the coupling of plasmon-donor is much stronger than that of plasmon-acceptor with a high acceptor/donor ratio.

---

1 Introduction

With the continuous improvement of integration, microelectronic chips are facing problems such as signal delay, power consumption and electromagnetic interference. Therefore, optical interconnection¹ has gradually become a frontier research hotspot. Silicon quantum dots represent one of the key luminescent materials for the research of silicon-based light sources in optical interconnections, which has the advantages of easy modification, adjustable emission wavelength, good biocompatibility, and high compatibility with semiconductor manufacturing processes. Si QDs have been widely used in biophotonics² and optoelectronics,³ such as color tuning or white-light-emitting structures, solar cells, and sensors.^4–6 Nevertheless, the research on silicon quantum dot devices still has the following limitations: (1) compared with II–VI and IV–VI QDs,⁷ Si QDs exhibit smaller absorption cross sections and lower quantum efficiency due to the indirect nature of the energy band. (2) There is certain difficulty in the research on inter-QD interactions, such as the overlapping of wave functions and long-range dipole–dipole interactions called Förster resonance energy transfer (FRET),^8–12 due to the shortcomings of the large size of Si QDs and surface-functionalized long alkyl chains. (3) The PL properties of organic functionalized Si QDs are often degraded by the formation of assemblies.

The emergence of surface plasmon materials has provided a solution for the limitations of Si QDs, which breaks through the optical diffraction limit of traditional optics and provides the possibility to realize the regulation of light on a sub-wavelength scale. Noble metal nanoparticles have received extensive attention due to their unique surface plasmon effect. Surface plasmon resonance in metal nanoparticles is a collective oscillation of free electrons, resulting in the nanoscale confinement of electromagnetic fields near the metal surface.^13–16 It has a series of novel optical properties, which have been widely employed to study the interactions between plasmons and illuminants, such as fluorescence enhancement,^17–23 realization of a nanolaser^24–26 and FRET regulation.^27–30 The energy transfer efficiency between silicon quantum dots is relatively low because of their shortcomings mentioned above. In order to circumvent the problems, silver nanoparticles with a single broad resonance peak were introduced in our previous work.³³ LSP enhanced energy transfer between Si QDs has been observed, which exhibits reduced emission of donors (D) and increased emission of the acceptors (A). The FRET efficiency and characteristic distance are also significantly improved.

In principle, for the plasmon-enhanced luminescence of single QDs, there are two types of enhancement mechanisms:^17,31,32 excitation enhancement and emission enhancement, which requires that the SPR peaks match the excitation wavelength or the emission wavelength of the QDs, respectively. The situation is more complicated in a mixed quantum dot assemble due to inter-QD interactions, mainly FRET. When FRET efficiency is significantly improved as MNPs are introduced, the impact of the FRET mechanism can't be neglected. From another perspective, this is also an enhancement mechanism for acceptor quantum dots. LSP-coupled FRET is a complex mechanism with many parameters that can be tuned. The FRET mechanism between the donor and acceptor competes with other decay mechanisms. Therefore, the various dependences need to be fully investigated and well understood to develop systems that can take advantage of plasmon controlled FRET for light emission, light harvesting, or sensing applications.

Here we present a scheme to further increase the FRET efficiency and PL intensity of acceptors. We prepared core–shell structures, in which gold nanospheres (GNSs) or gold nanorods (GNRs) with double SPR wavelengths, transversal and longitudinal surface plasmon resonance (TSPR and LSPR, respectively) modes, were coated with a uniform silica shell. Si QDs absorbed on the surface of the shell were close-packed. Different from the single resonance peak of gold and silver nanoparticles, the double resonance peaks of GNRs can be adjusted separately to overlap with the spectra overlap region and emission spectra of the donor or acceptor, respectively, so that optimum FRET efficiency and emission enhancement can be achieved. The dependence of the energy transfer efficiency and the enhancement of the acceptor emission on the SPR wavelength, metal-QD distance and QD ratio is examined by precisely controlling the size and aspect ratio of MNPs and the thickness of the SiO₂ shell. From the analysis of PL intensity and decay rates of Si QDs in the hybrid nanostructures with different structural parameters, the competition between the FRET enhancement mechanism and the emission mechanism is discussed in combination with theoretical modeling.

2 Experimental section

GNRs were prepared via a modified seed growth method³⁴ and dissolved in a CTAB solution with an appropriate concentration. After standing at room temperature for more than 2 hours, the pH of the solution was adjusted to 10–11. Then, tetraethylorthosilicate (TEOS) was added to the solution. GNRs will be coated with silica in 12 hours and redispersed into toluene. Then, the silica surface was activated by the addition of 3-aminopropyl triethoxysilane (APTES). After stirring for 12 hours, the solution was centrifuged twice and dissolved in 2 mL of THF. Finally, aliphatic amine modified QD solution was added dropwise with vigorous stirring for an additional 12 hours.

In the following, we refer the samples as X-Y-Z, where X is the type of metal nanoparticle (GNS or GNR), Y is the thickness of the silica shell, and Z is the type of Si QD (D or A). Samples composed of Si QDs with two different diameters are referred to as X-Y-(D + A)_N1/N2, where N1 and N2 are the number ratios of two different sized QDs. The default value of Y and N1/N2 is 10 nm and 1 : 1, respectively. The default value is not displayed below.

The core–shell structure of the samples was measured by transmission electron microscopy (TEM, Tecnai F30G2). The absorption spectra were recorded by using a UV-vis-NIR spectrophotometer (U4100, Hitachi) with an optical path of 2 mm over the range of 200–1100 nm. Photoluminescence and time-resolved photoluminescence were characterized by using a multichannel photon counting system (F920, Edinburgh Instruments).

3 Results and discussion

The hybrid nanostructures are characterized by high resolution transmission electron microscopy, as shown in Fig. 1a. It can be clearly seen from the inset that the quantum dots are adsorbed on the surface of the SiO₂ shell with a high density. The GNRs in the core are 40 ± 3 nm in length and 21 ± 2 nm in diameter, and the silica shell has a uniform thickness of 10 ± 1.3 nm. The lattice fringes of Si quantum dots on the SiO₂ surface are clearly visible, which corresponds to the {111} planes of crystalline Si.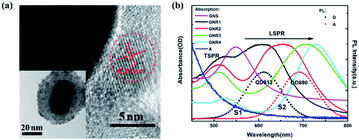

Fig. 1 (a) TEM (inset) and HRTEM images of the hybrid nanostructures. (b) PL spectra of the donor (D) and acceptor (A) Si QDs given with absorption spectra of GNSs, GNRs and A.

Spectral overlap plays an important role in the energy transfer process between silicon quantum dots. First, we chose silicon quantum dots of different sizes as donors (3.1 ± 0.5 nm) and acceptors (4.9 ± 0.7 nm). Fig. 1b shows the emission spectra of D and A given with the absorption spectrum of A. S1 represents the spectral overlap region of the emission spectrum of the donor with the absorption spectrum of the acceptor, and S2 represents the spectral overlap region of the emission spectra of D and A. In order to explore the influence of the SPR wavelength on silicon quantum dot fundamental optical processes, three types of metallic nanoparticles were selected as follows: (1) GNSs, which had a single SPR wavelength (548 nm) that was matched with the spectral overlap region S1 and far away from the emission peak of acceptors; (2) GNR1 and GNR3, whose TSPR wavelengths were matched with S1, and LSPR wavelengths (610 and 703 nm, respectively) were matched with the emission spectra of donors and acceptors, respectively; (3) GNR2 and GNR4 with different LSPR wavelengths centered at 656 nm and 727 nm, as shown in Fig. 1b.

Fig. 2a shows the PL spectra of GNR1-10-D (black line), GNR1-10-A (red line) and GNR1-10-(D + A) (blue line). Due to the slight deviation in the number of quantum dots adsorbed on the surface of different core–shell nanostructures, we have prepared sufficient samples with the same parameters and verified the repeatability of the experimental results, and the spectra were normalized after considering the concentration, size of GNRs and quantum dot ratio. The deconvolution of the emission spectrum of GNR1-10-(D + A) into peak 1 and peak 2 is also displayed. It is clearly seen that the photoluminescence intensity of peak 1 is smaller than that of GNR1-10-D, while the photoluminescence intensity of peak 2 is larger compared to that of GNR1-10-A, which is an indication of energy transfer. Interestingly, there is a slight red shift of the deconvolution peak compared with the PL peak of GNR1-10-D and GNR1-10-A. We speculate that this is due to the uneven size distribution of quantum dots. When GNRs are introduced, energy transfer occurs between adjacent donors (acceptors) in a locally amplified electromagnetic field. Förster resonance energy transfer between Si quantum dots was confirmed by conducting time-resolved experiments with a TCSPC system. Fig. 2b shows the time-resolved PL decay curves of donors in different samples, which are fit with a multiexponential decay model and averaged lifetimes are calculated. The amplitude averaged photoluminescence lifetimes τ of donors in SiO₂-D, GNR1-10-D and GNR1-10-(D + A) are 9.2 μs, 6.1 μs and 3.6 μs, respectively. After the introduction of GNRs, the shorter lifetime of donors in GNR1-10-D indicates that the emission rate of donors at the LSPR wavelength is greatly enhanced, which is physically caused by both the increased local densities of optical states and radiative recombination rate of excitons resulting from the plasmon-QD coupling. The donor PL intensity in GNR1-10-(D + A) decays much faster than that in GNR1-10-D as acceptor quantum dots are introduced, which provides further evidence of the occurrence of the FRET process. It should be noted that the PL lifetimes discussed in this work are in the range of 1–10 μs, which is many orders of magnitude longer than the characteristic time of Auger recombination in Si QD assemblies.³⁵ FRET is a donor deexcitation mechanism with rate k_T that competes with the radiative and nonradiative decay mechanisms of the excited donor state. The efficiency of energy transfer (E)³⁶ is the fraction of photons absorbed by the donor which are transferred to the acceptor. This fraction is given by:

where τ_D is the amplitude averaged lifetime of the donor in the absence of the acceptor, and the rate of energy transfer from a donor to an acceptor k_T(r) is given by:where Q_D is the quantum yield of the donor in the absence of the acceptor, n is the refractive index of the medium, N is Avogadro's number, r is the distance between the donor and acceptor, F_D(λ) is the corrected fluorescence intensity of the donor and ε_A(λ) is the extinction coefficient of the acceptor at λ. The term κ² is a factor describing the relative orientation of the transition dipoles which is usually assumed to be equal to 2/3 for dynamic random averaging of the donor and acceptor.^12,37 The distance at which FRET is 50% efficient is called the Förster distance (R₀).

Fig. 2 (a) PL spectra of GNR1-10-D, GNR1-10-A and GNR1-10-(D + A). (b) Time-resolved PL decay curves of donor Si QDs in different samples as noted. (c) Dependence of energy transfer efficiency on the SPR wavelength.

For comparison, we prepared silica spheres with the same ratio of quantum dots adsorbed on the surface as a reference sample, the Förster distance R₀ and energy transfer efficiency E of which equal 5.0 nm and 5.3%. In order to explore the impact of the introduction of GNRs on the energy transfer process, the energy transfer rate can be obtained from the donor lifetimes. When GNRs are introduced, the energy transfer rate due to coupling with the GNRs (k_m) has to be considered:³⁸

FRET efficiency and lifetime are available from experiments, and thus k_T and k_m can be calculated from eqn (1) and (3). The rate of energy transfer, k_T, was estimated to be 6.1 × 10³ s⁻¹ for SiO₂-(D + A). Similarly, the rate of transfer in GNR1-10-(D + A), k_m, was estimated to be 1.1 × 10⁵ s⁻¹, which is close to the decay rate of D and ∼18 times greater than the energy transfer rate k_T in SiO₂-(D + A). It demonstrates the important role of GNRs in FRET between donor and acceptor Si QDs. By comparing the donor lifetime in the presence of the acceptors τ_DA,MNP = (τ_D,MNP⁻¹ + k_T)⁻¹ to the donor lifetime τ_D,MNP, the experimentally obtained energy transfer efficiencies given by E = 1 − τ_DA,MNP/τ_D,MNP are summarized in Fig. 2c. One can clearly see that GNR1, which has double SPRs matched with both the spectral overlap region S1 and the emission band of donors, has the largest energy transfer efficiency (∼41.0%). The introduction of MNPs contributes to the strong confinement of light and generates SP dipole fields, which is in resonance with the emitting and absorbing transition dipoles. Thus, the interaction between the modified exciton dipoles is enhanced. Eqn (1) and (2) show that the quantum yield and the decay rate of the donors are important factors affecting the FRET efficiency. Compared with GNSs, GNR1 with two resonance peaks not only overlaps with S1, but also matches the emission wavelength of D. Thus, GNR1 has stronger plasmon-D coupling and higher energy transfer efficiency is achieved. As the central wavelength of the LSPR peak shifted to the red (GNR2, GNR3 and GNR4) with respect to the spectral overlap region S1 and the emission wavelength of donors, a weaker interaction with donors is expected and the plasmon-coupled FRET efficiency is gradually reduced.

Since the luminescence can be quenched when QDs are located very close to MNPs,³⁹ a spacer layer is needed to change the metal-QD distance and adjust the coupling strength of the LSP and the excitons. Silica is an appropriate material which is transparent to visible light and facilitates the surface modification, so that the quantum dots can be adsorbed on the surface and the PL intensity of quantum dots will not be reduced. Here, the silica shell was prepared with a uniform thickness of 6.0 ± 0.8 nm, 10 ± 1.0 nm, 14 ± 1.3 nm and 20 ± 2.1 nm, respectively, to demonstrate the dependence of the FRET process on the metal-QD distance, as shown in Fig. 3a. After the introduction of metals, there are two competing mechanisms. On the one hand, the coupling of LSP and quantum dots induces exciton dipoles efficiently through a locally amplified electromagnetic field near the metals. It provides extra radiative pathways that increase the decay rate and the emission of Si QDs is enhanced. On the other hand, the introduction of MNPs also generates energy dissipation due to the nonradiative energy transfer from the QDs to MNP and thermal effects. As the distance increases, the plasmon-QD coupling declines and energy dissipation is reduced as well. The position dependence of the energy transfer efficiency qualitatively reflects the vertically evanescent nature of the SP dipole fields. At first, the energy dissipation is relatively large and dominant with a small distance, resulting in that the energy transfer efficiency in GNR1-10-(D + A) is larger than that in GNR1-6-(D + A). When the thickness of SiO₂ is large enough in GNR1-14-(D + A) and GNR1-20-(D + A), the energy dissipation is relatively small, and the coupling effect is dominant. Thus, the energy transfer efficiency decreases with a further increased distance. In other words, the key reason for the existence of the optimal distance is that the metal-exciton coupling and energy dissipation have different decreasing trends with the distance. A similar distance correlation can be obtained in other metal nanostructures in which the optimum distance ranges from 8–16 nm. The optimum distance depends upon the extent of spectral overlap, the distribution of the electromagnetic field around the metal, surrounding dielectric environment, and the luminous properties of quantum dots. It should be noted that the plasmon resonance wavelength of GNR@SiO₂ has a slight red shift compared with that of GNRs since the SiO₂ layer has a larger refractive index than the solvent. Generally, as the thickness increases, the red shift increases. In this work, the LSPR wavelength shifts from 610 nm to 627 nm as the thickness of SiO₂ increases from 6 nm to 20 nm. Fig. 2c shows that in this resonance wavelength range, the plasmon-QD coupling decreases as the resonance wavelength increases, which means a weaker electromagnetic field intensity and reduced energy dissipation at the same distance. Nevertheless, compared to the exponential correlation between the local electromagnetic field intensity and distance, the slight red shift of the resonance wavelength caused by the coated silica has a much weaker effect on the PL and FRET processes.

Fig. 3 Dependence of energy transfer efficiency on the metal-QD distance (a) and QD ratio (b).

Furthermore, we studied the effect of the number ratio of acceptors and donors on energy transfer, as shown in Fig. 3b. It can be seen that the FRET efficiency is gradually increased to ∼46.3% as the ratio was regulated from 1 : 2 to 2 : 1. Increasing the A : D ratio means more acceptors and fewer donors, which is conducive to the enhancement of FRET as more acceptors per donor are available. The reason is that the probability of energy transfer for each donor is increased. In the bilayer structure, taking account of the exclusion zone,⁴⁰ Förster resonance energy transfer efficiency can be deduced:

Eqn (4) shows that the energy transfer efficiency is positively correlated with the concentration of acceptor quantum dots, which is consistent with our conclusion.

In principle, for the plasmon-enhanced luminescence, there are two kinds of enhancement mechanisms: excitation enhancement and emission enhancement. We have explored the regulation of FRET by GNRs above. One of the indications of energy transfer is that the donor luminescence intensity decreases while the acceptor luminescence intensity increases (Fig. 2a), which is proposed as the third enhancement mechanism for acceptors named the FRET enhancement mechanism in this work. To verify the idea of utilizing the double SPR modes of GNRs to realize the FRET enhancement and emission enhancement mechanisms simultaneously, the calculated PL enhancement factors with different structural parameters are summarized in Fig. 4, where the columns and the broken line represent the PL enhancement factor of Si QDs in MNP-SiO₂-D (or A) and acceptors in MNP-SiO₂-(D + A), respectively. Fig. 4a shows that the largest PL enhancement factors with only D or A are achieved in GNR1-10-D and GNR3-10-A respectively, which is a clear indication of the emission enhancement. When both D and A are present, plasmon-coupled FRET occurs. It should be mentioned that excitation enhancement is not discussed here, since the SPR wavelengths of GNRs and GNSs are not matched with the excitation wavelength (325 nm). Interestingly, the PL enhancement factor of A reaches its maximum at a LSPR wavelength of ∼656 nm in GNR2-10-(D + A), where both the plasmon-A coupling and the energy transfer efficiency are not optimum. One of the key issues is that FRET enhancement is not only related to the overlap of the TSPR peak and S1, but also related to the plasmon-D coupling. As the LSPR peak gradually approaches the PL peak of A, the plasmon-A coupling and emission of A are enhanced, while the PL intensity of D and FRET efficiency decrease. In other words, the optimum PL enhancement factor in GNR2 is the consequence of the competition between the FRET enhancement mechanism and emission enhancement mechanism.

Fig. 4 Correlation of PL enhancement factors with the SPR wavelength (a), metal-QD distance (b) and QD ratio (c).

To further explore the optimum structural parameters of the hybrid nanostructures, the dependance of PL intensity on the metal-QD distance and QD ratio is studied. Comparing Fig. 3a and 4b, it is easy to draw conclusions that the PL enhancement in GNR1-10-(D + A) is most obvious, because the FRET efficiency of the sample is largest, and the emission enhancement for acceptors is strongest. However, the comparison of Fig. 3b and 4c shows that even though the FRET efficiency and PL intensity continue to increase, the acceptor emission still drops at an A : D ratio of 2 : 1. We speculate that the FRET enhancement mechanism is dominant rather than the emission enhancement mechanism in a specific quantum dot ratio range, since GNR1, which has the strongest coupling effect with D, is selected as the core. The average number of the nearest neighbor acceptors per donor is proportional to the A : D ratio. Although the FRET efficiency is high, the effect of the energy transfer at high A : D ratios on the overall emission of A becomes comparatively small resulting from the sufficiently low number of D. A similar effect has been reported by Manuela Lunz et al.,⁴¹ who investigated energy transfer in a mixed CdTe QD monolayer. They also found that the acceptors were sufficiently separated at low A : D ratios, and energy is not only transferred from nearest neighbors but donors at larger distances also contribute. It should be mentioned that this conclusion is not necessarily applicable to our work, since the FRET efficiency of silicon quantum dots is much lower than that of CdTe QDs (over 90%) at the same distance, due to the smaller oscillator strength of the indirect transitions and functionalized long alkyl chains on the surface.

Different structural parameters regulate the luminescence performance of Si QDs by influencing the competition between the three enhancement mechanisms. By systematically studying the effects of different factors on energy transfer and photoluminescence, our experimental results demonstrate the feasibility of utilizing the double SPRs of GNRs for simultaneous FRET enhancement and emission enhancement. Nevertheless, a finer structure and more complete theoretical simulations are needed for future research on a single D–A pair of silicon quantum dots.

4 Conclusions

In summary, we have proposed and demonstrated an effective scheme to achieve FRET enhancement and photoluminescence enhancement utilizing the double SPR modes of GNRs. By experimentally using the GNR-SiO₂ core–shell structure with Si quantum dots adsorbed on the surface of silica, the optimum FRET efficiency is obtained when the TSPR wavelength of GNRs is well matched with S1, the spectral overlap region of the emission spectrum of the donor with the absorption spectrum of the acceptor, and LSPR wavelengths are matched with the emission band of donors, respectively. The maximum photoluminescence enhancement factor is obtained when the TSPR and LSPR wavelengths of GNRs are well matched with S1 and S2, the spectral overlap region of the emission spectra of D and A, respectively. It is also demonstrated that the FRET and PL processes can be controlled by the metal-QD distance and the acceptor/donor number ratio. When the FRET enhancement mechanism is dominant, another important factor that cannot be ignored is the luminescence properties of the donor quantum dots. Particularly, the effect of the energy transfer on the overall emission of acceptors at high A : D ratios becomes comparatively small resulting from the sufficiently low number of donors. Considering the existence of multiple D–A pairs, the experimentally obtained ration between the PL enhancement factor and the acceptor/donor ratio is well explained by FRET theory. Our scheme has provided a new way for enhancing the FRET efficiency and photoluminescence intensity by fully utilizing the multiple SPRs of plasmonic nanostructures and provides an idea for the development of nanophotonic devices and sensors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors appreciate the financial support from the National Key R&D Program of China (2018YFB2200102) and the National Natural Science Foundation of China (No. 61874095 and 61721005).

Notes and references

1. R. A. Soref and J. P. Lorenzo, Electron. Lett., 1985, 21(21), 953–954.
2. F. Erogbogbo, K. Yong, I. Roy, G. Xu, N. P. Prasad and T. M. Swihart, ACS Nano, 2008, 2, 873–878.
3. F. Priolo, T. Gregorkiewicz, M. Galli and T. F. Krauss, Nat. Nanotechnol., 2014, 9, 19–32.
4. V. I. Yusupov and V. N. Bagratashvili, Langmuir, 2018, 34, 12794–12801.
5. W. Gu, X. K. Liu, X. D. Pi, X. L. Dai, S. X. Zhao, L. Yao, D. S. Li, Y. Z. Jin, M. S. Xu and D. R. Yang, IEEE Photonics J., 2017, 9, 1.
6. Z. Y. Ni, L. L. Ma, S. C. Du, Y. Xu, M. Yuan, H. H. Fang, Z. Wang, M. S. Xu, D. S. Li, J. Y. Yang, W. D. Hu, X. D. Pi and D. R. Yang, ACS Nano, 2017, 11, 9854–9862.
7. D. V. Talapin, J.-S. Lee, M. V. Kovalenko and E. V. Shevchenko, Chem. Rev., 2010, 110(1), 389–458.
8. C. Kagan, C. Murray, M. Nirmal and M. Bawendi, Phys. Rev. Lett., 1996, 76, 1517–1520.
9. C. R. Kagan, C. B. Murray and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 8633–8643.
10. O. I. Micic, K. M. Jones, A. Cahill and A. J. Nozik, J. Phys. Chem. B, 1998, 102, 9791–9796.
11. S. A. Crooker, J. A. Hollingsworth, S. Tretiak and V. I. Klimov, Phys. Rev. Lett., 2002, 89, 186802.
12. K. Chou and A. Dennis, Sensors, 2015, 15, 13288–13325.
13. O. J. F. Martin, C. Girard and A. Dereux, Phys. Rev. Lett., 1995, 74(4), 526–529.
14. U. Hohenester, H. Ditlbacher and J. R. Krenn, Phys. Rev. Lett., 2009, 103, 106801.
15. B. J. Wiley, S. H. Im, Z. Y. Li, J. McLellan, A. Siekkinen and Y. N. Xia, J. Phys. Chem. B, 2006, 110(32), 15666–15675.
16. M. Hu, J. Y. Chen, Z. Y. Li, L. Au, G. V. Hartland, X. D. Li, M. Marquez and Y. N. Xia, Chem. Soc. Rev., 2006, 35(11), 1084–1094.
17. T. Ming, L. Zhao, Z. Yang, H. J. Chen, L. D. Sun, J. F. Wan and C. H. Yan, Nano Lett., 2009, 9(11), 3896–3903.
18. N. Zhou, M. Yuan, Y. H. Gao, D. S. Li and D. R. Yang, ACS Nano, 2016, 104, 4154–4163.
19. N. Zhou, T. Liu, D. S. Li and D. R. Yang, Nanomater. Nanotechnol., 2016, 6, 16.
20. T. Y. Zhang, G. W. Lu, W. Q. Li, J. Liu, L. Hou, P. Perriat, M. Martini, O. Tillement and Q. H. Gong, J. Phys. Chem. C, 2012, 116(15), 8804–8812.
21. F. Tam, G. P. Goodrich, B. R. Johnson and N. J. Halas, Nano Lett., 2007, 7(2), 496–501.
22. R. Bardhan, N. K. Grady, J. R. Cole, A. Joshi and N. J. Halas, ACS Nano, 2009, 3(3), 744–752.
23. J. A. Schuller, E. S. Barnard, W. S. Cai, Y. C. Jun, J. S. White and M. L. Brongersma, Nat. Mater., 2010, 9(3), 193–204.
24. R. F. Oulton, V. J. Sorger, T. Zentgraf, R. M. Ma, C. Gladden, L. Dai, G. Bartal and X. Zhang, Nature, 2009, 461(7264), 629–632.
25. P. Berini and I. De Leon, Nat. Photonics, 2012, 6(1), 16–24.
26. M. A. Noginov, G. Zhu, A. M. Belgrave, R. Bakker, V. M. Shalaev, E. E. Narimanov, S. Stout, E. Herz, T. Suteewong and U. Wiesner, Nature, 2009, 460(7259), 1110–1112.
27. A. O. Govorov, J. Lee and N. A. Kotov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125308.
28. F. Reil, U. Hohenester, J. R. Krenn and A. Leitner, Nano Lett., 2008, 8(12), 4128–4133.
29. M. L. Viger, M. Rioux, L. Rainville and D. Boudreau, Nano Lett., 2009, 9(8), 3067.
30. X. Zhang, C. A. Marocico, M. Lunz, V. A. Gerard, Y. K. Gun’ko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, ACS Nano, 2014, 8(2), 1273–1283.
31. H. J. Chen, T. A. Ming, L. Zhao, F. Wang, L. D. Sun, J. F. Wang and C. H. Yan, Nano Today, 2010, 5(5), 494–505.
32. X. Li, F. J. Kao, C. C. Chuang and S. L. He, Opt. Express, 2010, 18(11), 11335–11346.
33. J. H. Cao, H. J. Zhang, X. K. Liu, N. Zhou, X. D. Pi, D. S. Li and D. R. Yang, J. Phys. Chem. C, 2019, 123, 23604–23609.
34. X. Ye, C. Zheng, J. Chen, Y. Gao and C. B. Murray, Nano Lett., 2013, 13(2), 765–771.
35. M. Kořínek, F. Trojánek, D. Hiller, S. Gutsch, M. Zacharias, C. Kübel and P. Malý, Appl. Surf. Sci., 2016, 377, 238–243.
36. J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, 2006.
37. A. J. Mork, M. C. Weidman, F. Prins and W. A. Tisdale, J. Phys. Chem. C, 2014, 118, 13920–13928.
38. J. R. Lakowicz, Anal. Biochem., 2005, 337, 171.
39. X. Li, J. Qian, L. Jiang and S. L. He, Appl. Phys. Lett., 2009, 94(6), 063111.
40. M. Lunz and A. L. Bradley, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115423.
41. M. Lunz and A. L. Bradley, J. Phys. Chem. C, 2009, 113, 3084–3088.

---