Open Access Article
Open Access ArticleRole of Ce concentration on the structural and magnetic properties of functional magnetic oxide particles
Jyoti
Saini
a,
Monika
Sharma
ab and
Bijoy Kumar
Kuanr
 *a
*a
aSpecial Centre for Nanoscience, Jawaharlal Nehru University, New Delhi, 110067, India. E-mail: bkkuanr@gmail.com
bDepartment of Physics, Deshbandhu College, University of Delhi, New Delhi, 110019, India
First published on 25th August 2021
Abstract
Functional magnetic oxide particles offer exceptional GHz frequency capabilities, which can significantly enhance the utility of communication and signal processing devices. In the present work, we have investigated the structural and magnetic properties of rational multifunctional oxide Y2.9−xCexBi0.1Fe5O12 particles – a full series with x = 0.0, 0.2, 0.4, 0.6, 0.8 and 1 via a conventional solid-state route. The X-ray diffraction pattern validated the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d cubic garnet phase in all samples. From Rietveld refinement, it is observed that the ceric oxide (CeO2) impurity increases with an increase of Ce concentration, evincing a partial substitution of cerium (Ce) element into the garnet structure. The magnetic oxide particles with Ce concentration x = 0.4 showed a better crystallite size, dodecahedral site occupancy and solubility of cerium in the garnet phase. The morphological visualization of random shaped grains in the micrometer range was performed using the scanning electron microscopy (SEM) technique. The static magnetic properties showed that the saturation magnetization (Ms) decreases up to 43% and coercivity increases up to 59% with the increase of Ce concentration. The dynamic investigation on these oxide particles exhibits various intriguing and novel properties. Various intrinsic material parameters such as saturation magnetization (Ms), gyromagnetic ratio (γ), Gilbert damping constant (α) and extrinsic contribution (ΔHo) to linewidth were determined from the fitting of resonance field (Hr) and field linewidth (ΔHr) data. We ascertained that the damping constant increases with the increase of Ce concentration, which can be explained in terms of two magnon scattering and local defects caused by CeO2 inhomogeneity. The proposed doped garnets can be a potential candidate for high frequency microwave applications and spin-transfer-torque devices.
d cubic garnet phase in all samples. From Rietveld refinement, it is observed that the ceric oxide (CeO2) impurity increases with an increase of Ce concentration, evincing a partial substitution of cerium (Ce) element into the garnet structure. The magnetic oxide particles with Ce concentration x = 0.4 showed a better crystallite size, dodecahedral site occupancy and solubility of cerium in the garnet phase. The morphological visualization of random shaped grains in the micrometer range was performed using the scanning electron microscopy (SEM) technique. The static magnetic properties showed that the saturation magnetization (Ms) decreases up to 43% and coercivity increases up to 59% with the increase of Ce concentration. The dynamic investigation on these oxide particles exhibits various intriguing and novel properties. Various intrinsic material parameters such as saturation magnetization (Ms), gyromagnetic ratio (γ), Gilbert damping constant (α) and extrinsic contribution (ΔHo) to linewidth were determined from the fitting of resonance field (Hr) and field linewidth (ΔHr) data. We ascertained that the damping constant increases with the increase of Ce concentration, which can be explained in terms of two magnon scattering and local defects caused by CeO2 inhomogeneity. The proposed doped garnets can be a potential candidate for high frequency microwave applications and spin-transfer-torque devices.
I. Introduction
Multiferroics is a well known subject of next generation multifunctional materials, which amalgamates simultaneously magnetic, electric and elastic properties.1–10 Multifunctional materials have attracted a lot of interest due to their fascinating electric, magnetic and optical properties.11–20 This has led to a variety of technological applications such as microwave devices, spintronics, sensors, transducers, energy harvesting, random access multi-state memories, data storage recording technologies and communication systems.21–41 Since the last three to four decades, yttrium iron oxide (YIG) has been established as one of the promising multifunctional materials due to its potential electromagnetic properties such as high saturation magnetization, low damping constant (order of 10−5), longer spin-wave propagation length, high resistivity (∼1013 Ω cm), moderate thermal expansion coefficient, low ohmic losses and high Faraday rotation, which are very important for magnetic, spintronic, magnonic and high frequency microwave devices.42–53In recent years, doping of rare earth (RE) and transition metals in YIG has attracted tremendous interest due to their modified magnetic, optical and electrical properties suitable for new applications such as 5G telecommunication and drug delivery systems.54–60 The performance of rare earth substituted garnets (RE:YIG) relies upon the dopant type, amount of dopant and preparation technique.61–65 Specifically, the study of bismuth and cerium substituted YIG has attracted a lot of interest due to their high Faraday rotation and strong magneto-optical activity at near infrared telecommunication wavelengths.52,53,56,65 Cerium (Ce) element has amazing quality as it can be effortlessly exchangeable between the 4+ valence state and 3+ valence state.66 Also, cerium substituted yttrium iron oxide has attracted much attention due to its remarkable multiferroic (MF) properties such as magneto-dielectric (MD) and strong magneto-optical (MO) effects.67–69 Soumah Lucile, et al. demonstrated that bismuth substituted yttrium iron oxide (Bi:YIG) leads to extremely low Gilbert damping together with perpendicular magnetic anisotropy (PMA).70 Goto Taichi, et al. reported that enhanced magneto-optical properties with very low optical losses can be accomplished with the cerium substitution in YIG.71 Higuchi and the co-workers have achieved Ce:YIG thin films for magnetic sensor application.72 Fu Chen et al. reported the enhanced magneto-dielectric response with increase of cerium content.69 A. Ikesue et al. showed that the Faraday rotation increases from 144 deg. cm−1 for 1 at% of Ce to 990 deg. cm−1 for 8 at% of Ce substitution in YIG.73 They also reported that Faraday rotation for Ce doped garnet was around 5 times higher than that of 1 at% of Bi substitution. Elhamali et al. investigated the influence of erbium (Er) on the structural, magnetic and optical properties of Ce:YIG films.74 M. R. Khalifeh reported recently the effect of Dy3+ incorporation on the structural and magnetic properties of Y2.8−xDyxCe0.1Bi0.1Fe5O12 garnet.75 In spite of the fact that cerium strongly manipulates the magnetic, dielectric, thermal and optical properties of YIG,67–69,71–73 its solubility inside the garnet phase is still a challenging task.
The only magnetic ion in yttrium iron oxide (YIG) is Fe3+. In each molecular formula unit, Y3+ ions occupy dodecahedral sites surrounded with eight oxygen ions, namely the “c” site, whereas three out of five Fe3+ ions occupy the tetrahedral “d” site surrounded with four oxygen ions and the rest of the two Fe3+ ions are present at the octahedral “a” site surrounded with six oxygen ions. The controlling super-exchange interaction renders the magnetic moments of the “a” and “d” site positions antiparallel.76
In the present investigation, engineered and custom-modified garnet based multifunctional oxides having the representative formula Y2.9−xCexBi0.1Fe5O12 (or CexBi0.1:YIG with x = 0.0, 0.2, 0.4, 0.6, 0.8 and 1) have been synthesized by a conventional solid-state reaction method. We systematically investigated the phase identification with crystal structure analysis and cerium solubility inside the garnet structure. Also, we studied elemental analysis, morphological/microstructural analysis, and static and dynamic magnetic properties. Mao Tze-Chern, et al. reported the maximum solubility of cerium in YIG for 2% cerium content.77 However, in the present investigation we successfully observed that the solubility of cerium element in the garnet phase can be achievable up to 4% cerium concentration and decreases with a further increase. It is also confirmed by the maximum value of dodecahedral site occupancy for the x = 0.4 sample. The magnetic squareness increases with Ce increment. From the ferromagnetic resonance (FMR) measurements we have observed the magnetic damping constant to increase with Ce-content. It has to be mentioned here that the increased damping ameliorate for spin-transfer-torque devices.
II. Experimental details
The investigated garnet based oxides were synthesized by the conventional solid state reaction method from the oxide powders of Y2O3 (yttrium(III) oxide), Bi2O3 (bismuth(III) oxide), CeO2 (cerium(IV) oxide), and Fe2O3 (iron(III) oxide) from Sigma Aldrich with purity >99%. The fine oxide powders were mixed at a stoichiometric proportion with an accuracy of 1 mg and mixed well by grinding in a pestle-mortar with the addition of ethanol for 12 hours at room temperature. This synthesis method is advantageous as it is cost-effective, reduces pollution, requires less synthesis steps, simple in handling and gives a homogeneous product for commercial purpose. The benefit of using this method is to obtain a large particle size so that the number of grain boundaries and corresponding losses can be minimized.78 After that, the completely dried mixture was annealed at 1250 °C for 10 hours under an air atmosphere.79 Thereafter, uniform pellets were formed with 0.3 g of sintered oxide powders and 5 wt% polyvinyl alcohol (PVA) aqueous solution as a binder under 450 MPa pressure. The size of the obtained pellets was about 10 mm in diameter and 1 mm in thickness. Pressed pellets were sintered at 1350 °C for 6 hours under an air atmosphere.79Fig. 1 shows the schematic representation of the synthesis process. The studied samples with compositions Y2.9−xCexBi0.1Fe5O12 (x = 0.0, 0.2, 0.4, 0.6, 0.8 and 1) were labelled as S1, S2, S3, S4, S5 and S6 respectively.The X-ray diffraction (XRD) technique was used to examine the phases and crystal structure of the synthesized samples. Room temperature XRD analysis of powdered samples was carried out with a Miniflex 600 X-ray diffractometer from Rigaku with an X-ray radiation source CuKα (λ = 1.54181 Å) at 40 kV and 15 mA in the diffraction angle (2θ) range of 20°–80°, with a step size of 0.02° and a scanning speed of 5° min−1. All the observed XRD profiles were fitted with the pseudo-Voigt peak profile function using Rietveld analysis on FullProf Suite software. The Raman spectra were recorded using an Enspectr Raman spectrometer in the range 150–800 cm−1 using a green laser source with a power of 300 mW and a wavelength of 532 nm. The rigorous analysis of Raman spectra has been performed using the Gaussian peak profile function for multiple peak fitting. Scanning electron microscopy (SEM) (ZEISS EVO40 electron microscope) was used to visualize the surface morphology and analyze the grain size distribution of gold coated sintered pellets. The grain size statistical distribution was obtained from Gaussian fitting of histograms (for approximately 150 grains) showing different grain sizes present in the respective samples. In order to analyze more accurately the grain size distribution, the histogram has been plotted with three to four SEM images of each sample. EDX measurements were also used to identify the desired proportion of elemental compositions. High resolution transmission electron microscopy (HRTEM) was performed at 200 kV using a JEOL 2100F transmission electron microscope (TEM) and sample preparation was done by drop-casting the ethanol dispersed powdered samples on carbon grid mesh. Room temperature magnetic hysteresis loops of the powder samples were measured using VSM (Cryogenics, UK.) by the application of DC magnetic field up to 10 kOe. The coercivity (Hc) was calculated precisely from the M–H curve. Moreover, the saturation magnetization (Ms) and first order magneto-crystalline anisotropy constant K1 were calculated from linear fitting of the law of approach to saturation or LAS (i.e. M vs. 1/H2 plot) using saturated data points of the first quadrant of the M–H loop. Room temperature dynamic magnetic properties of the studied samples have been studied using the conventional ferromagnetic resonance (FMR) technique in field sweep mode using a flip-chip geometry. FMR is a magnificent dynamic technique to study the microwave absorption (MA) properties of the magnetic materials.54,80,81 A vector network analyzer (VNA) was used to generate microwave energy, whereas a coplanar waveguide (CPW) was used as a device for propagation of EM-waves. The samples were placed on a CPW in flip-chip geometry. In this technique, microwave energy interacts with the magnetic oxide samples before being dissipated as heat to the lattice. In the FMR technique, the external magnetic field leads to the precession of magnetic moments in the ferromagnetic material and was applied at right angle to the radio frequency (RF) magnetic field of the signal line which satisfies the FMR condition. In the field sweep mode, frequency (f) was kept fixed, whereas external DC magnetic field was swept from 0 to 12 kOe range in a step of 20 Oe. The measurements were performed for a broad range of frequencies from 6 GHz to 22 GHz. The S21 parameters (scattering matrix transmission parameters) were recorded for each DC magnetic field using computer controlled software. The S21 data show a resonance dip at FMR and the precise resonance field (Hr) and field linewidth (ΔHr) were obtained from Lorentzian fitting to the FMR data. Also, the various intrinsic and extrinsic contributions to field and linewidth were determined from the fitting of resonance field (Hr) and field linewidth (ΔHr) plots.
III. Results and discussion
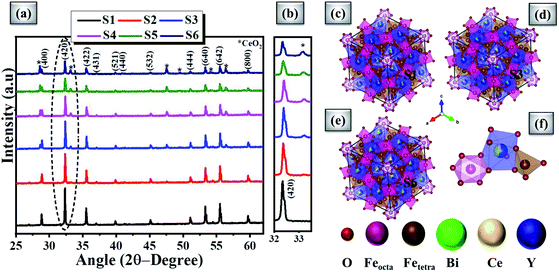
A. XRD results
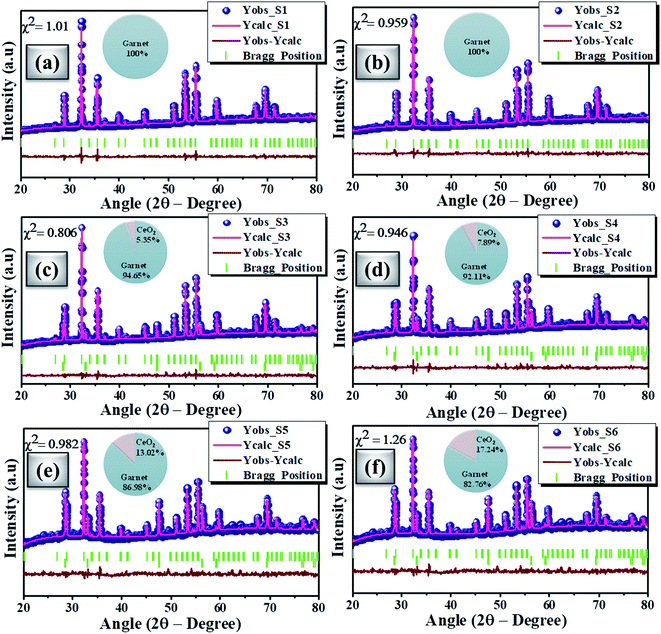
Fig. 2(a) shows the powdered XRD patterns of the investigated multifunctional magnetic oxides. The XRD pattern confirms the formation of Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d cubic symmetry of the yttrium iron oxide (YIG) phase (JCPDS data no. 43-0507). Also, additional secondary phase of CeO2 (JCPDS card no. 81-0792) is observed in doped YIG samples as denoted by the symbol *. The existence of CeO2 impurities reveals the partial substitution of cerium element into the garnet structure.77 Rietveld refinement of the crystal structure from the experimental XRD profile is performed in a two phase model using FullProf Suite software and the goodness of fit parameter (χ2) is refined to the acceptable limit. The refinement of XRD data is performed by minimizing the difference between observed and calculated diffraction peaks of substituted YIG samples. The crystal structure is drawn using VESTA software after refinement of XRD profiles as shown in Fig. 2 (b–e). Also, the experimental and refined diffraction patterns of all the oxide samples are shown in Fig. 3(a–f). All the refined parameters using FullProf Suite software are tabulated in Tables 1–4. It is observed from the results (Table 1) that the lattice constant depends upon ionic radii of doped elements (i.e. Ce3+ and Bi3+). Also, lattice constant is inversely related to the dodecahedral site occupancy and directly related to the ionic radii. From the refined results, we observed that the density increases with Ce-content in investigated oxide samples. Further, the value of dodecahedral site occupancy (Table 2) is found to be maximum for the x = 0.4 sample which interprets the better solubility of cerium element in the garnet phase and decreases further. The improvement of cerium solubility in the garnet structure is better as compared to previous reports.77Table 3 presents the refined bond lengths of R–O*, R–O** (R–Y, Bi, and Ce), Fe(T)–O and Fe(O)–O in all the samples. In yttrium iron oxide, the Y3+ ion is bonded to the Fe3+ ion by oxygen, resulting in a creation of two different length R–O* and R–O** bonds. Consequently, two different angles are formed for each Fe3+ ion located in the tetrahedral and octahedral sublattices corresponding to two oxygen bond lengths.82–84
d cubic symmetry of the yttrium iron oxide (YIG) phase (JCPDS data no. 43-0507). Also, additional secondary phase of CeO2 (JCPDS card no. 81-0792) is observed in doped YIG samples as denoted by the symbol *. The existence of CeO2 impurities reveals the partial substitution of cerium element into the garnet structure.77 Rietveld refinement of the crystal structure from the experimental XRD profile is performed in a two phase model using FullProf Suite software and the goodness of fit parameter (χ2) is refined to the acceptable limit. The refinement of XRD data is performed by minimizing the difference between observed and calculated diffraction peaks of substituted YIG samples. The crystal structure is drawn using VESTA software after refinement of XRD profiles as shown in Fig. 2 (b–e). Also, the experimental and refined diffraction patterns of all the oxide samples are shown in Fig. 3(a–f). All the refined parameters using FullProf Suite software are tabulated in Tables 1–4. It is observed from the results (Table 1) that the lattice constant depends upon ionic radii of doped elements (i.e. Ce3+ and Bi3+). Also, lattice constant is inversely related to the dodecahedral site occupancy and directly related to the ionic radii. From the refined results, we observed that the density increases with Ce-content in investigated oxide samples. Further, the value of dodecahedral site occupancy (Table 2) is found to be maximum for the x = 0.4 sample which interprets the better solubility of cerium element in the garnet phase and decreases further. The improvement of cerium solubility in the garnet structure is better as compared to previous reports.77Table 3 presents the refined bond lengths of R–O*, R–O** (R–Y, Bi, and Ce), Fe(T)–O and Fe(O)–O in all the samples. In yttrium iron oxide, the Y3+ ion is bonded to the Fe3+ ion by oxygen, resulting in a creation of two different length R–O* and R–O** bonds. Consequently, two different angles are formed for each Fe3+ ion located in the tetrahedral and octahedral sublattices corresponding to two oxygen bond lengths.82–84
| Sample name | Lattice constant (Å) | Volume (Å3) | X-ray density (g cm−3) |
|---|---|---|---|
| S1 | 12.3835 | 1899.03 | 4.988 ± 0.01 |
| S2 | 12.3945 | 1904.07 | 4.999 ± 0.01 |
| S3 | 12.3918 | 1902.87 | 5.244 ± 0.01 |
| S4 | 12.3924 | 1903.12 | 5.199 ± 0.01 |
| S5 | 12.3929 | 1903.33 | 5.255 ± 0.01 |
| S6 | 12.3884 | 1901.29 | 5.415 ± 0.01 |
| Sample name | Site occupancy (R = Y, Bi, Ce) | |||
|---|---|---|---|---|
| O | R | Fe(T) | Fe(O) | |
| S1 | 1 | 0.924 | 0.908 | 0.965 |
| S2 | 1 | 0.909 | 0.904 | 0.967 |
| S3 | 1 | 0.948 | 0.962 | 0.991 |
| S4 | 1 | 0.910 | 0.935 | 0.983 |
| S5 | 1 | 0.896 | 0.933 | 0.977 |
| S6 | 1 | 0.931 | 0.973 | 0.973 |
| Sample name | Bond length (Å) (R = Y, Bi, Ce) | |||
|---|---|---|---|---|
| R–O* | R–O** | Fe(T)–O | Fe(O)–O | |
| S1 | 2.38353 | 2.39364 | 1.9083 | 2.00031 |
| S2 | 2.35747 | 2.41445 | 1.88898 | 2.02289 |
| S3 | 2.36407 | 2.42665 | 1.87094 | 2.02619 |
| S4 | 2.40746 | 2.40195 | 1.9074 | 1.98647 |
| S5 | 2.35796 | 2.44368 | 1.84448 | 2.04432 |
| S6 | 2.34886 | 2.42924 | 1.87056 | 2.03048 |
| Sample name | Bond angle (deg.) (R = Y, Bi, Ce) | |||||
|---|---|---|---|---|---|---|
| R–O–R | Fe(T)–O– Fe(O) | R–O*–Fe(T) | R–O**–Fe(T) | R–O*–Fe(O) | R–O**–Fe(O) | |
| S1 | 105.066 | 124.623 | 91.648 | 123.224 | 103.946 | 103.588 |
| S2 | 105.357 | 124.616 | 93.061 | 123.272 | 104.276 | 102.295 |
| S3 | 104.737 | 125.390 | 93.293 | 123.465 | 103.907 | 101.751 |
| S4 | 104.175 | 125.621 | 91.025 | 122.995 | 103.642 | 103.838 |
| S5 | 104.405 | 125.856 | 94.199 | 123.876 | 103.554 | 100.658 |
| S6 | 105.083 | 125.102 | 93.757 | 123.287 | 104.263 | 101.495 |
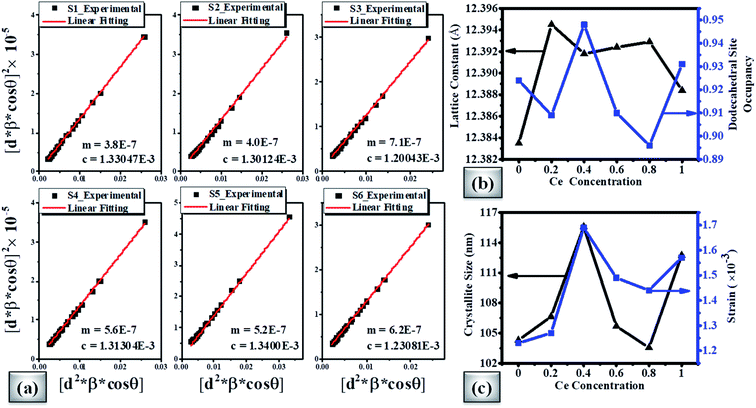
Fig. 4(a) shows the average crystallite size (D) and lattice strain (ε) of doped magnetic oxides which are calculated using the size–strain plot (SSP) from eqn (1);85
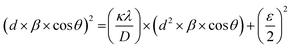 | (1) |
Here, d is the interplanar spacing which is calculated using Bragg's law (2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = nλ), β is the full-width at half-maximum (FWHM), θ is the Bragg angle, κ is the shape factor (∼0.9), and λ is the X-ray wavelength (Cu Kα ∼1.54181 Å). The results showed that with the increase of Ce concentration in CexBi0.1:YIG magnetic oxides, the lattice strain increases up to x = 0.4 Ce concentration. The positive sign of lattice strain signifies the tensile nature, which is perhaps due to larger ionic radii of Ce3+ and Bi3+ ions as compared to the Y3+ ion [i.e. Y3+ (1.02 Å), Ce3+ (1.14 Å) and Bi3+ (1.17 Å)].86 The crystallite size in all the samples is in accordance with the value of strain. Fig. 4(b) shows the variation of lattice constant and dodecahedral site occupancy with cerium concentration and Fig. 4(c) shows the behaviour of crystallite size and strain with cerium concentration. The calculated values of crystallite size and lattice strain from the size–strain plot are tabulated in Table 5.85 One of the major findings from the XRD confirms that cerium element solubility increases inside the garnet structure up to x = 0.4 at. wt%.
θ = nλ), β is the full-width at half-maximum (FWHM), θ is the Bragg angle, κ is the shape factor (∼0.9), and λ is the X-ray wavelength (Cu Kα ∼1.54181 Å). The results showed that with the increase of Ce concentration in CexBi0.1:YIG magnetic oxides, the lattice strain increases up to x = 0.4 Ce concentration. The positive sign of lattice strain signifies the tensile nature, which is perhaps due to larger ionic radii of Ce3+ and Bi3+ ions as compared to the Y3+ ion [i.e. Y3+ (1.02 Å), Ce3+ (1.14 Å) and Bi3+ (1.17 Å)].86 The crystallite size in all the samples is in accordance with the value of strain. Fig. 4(b) shows the variation of lattice constant and dodecahedral site occupancy with cerium concentration and Fig. 4(c) shows the behaviour of crystallite size and strain with cerium concentration. The calculated values of crystallite size and lattice strain from the size–strain plot are tabulated in Table 5.85 One of the major findings from the XRD confirms that cerium element solubility increases inside the garnet structure up to x = 0.4 at. wt%.
B. Raman spectroscopy
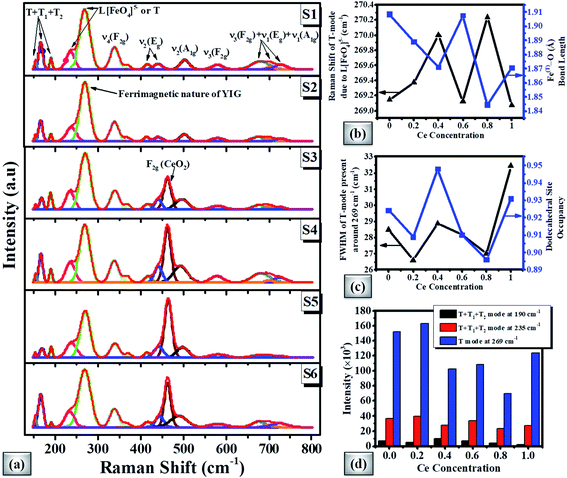
Fig. 5(a) shows the Raman spectra of magnetic oxide pellets. According to the group theory, the cubic symmetry of the garnet based crystal structure represents 25 Raman modes (3 A1g+ 8 Eg + 14 F2g).87,88 The Raman spectra of the doped YIG pellet demonstrate peaks around 154, 168, 190, 235, 269, 338, 368, 415, 441, 502, 580, 675, 700, and 727 cm−1 respectively. The ferrimagnetic nature can be linked with the most intense peak at 269 cm−1. The partial substitution of Ce element in the garnet phase can be depicted by CeO2 degenerated vibrational mode near 462 cm−1 for higher Ce-content samples. The Raman spectra of CexBi0.1:YIG (x = 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0) garnets clearly show peak shifting due to induced lattice strain. It is observed that the Raman shift of the most intense T mode (or translational mode) around 269 cm−1 depends upon the Fe(T)–O bond length of doped YIG crystal as shown in Fig. 5(b).54 In addition, the full width at half maximum (FWHM) can be directly related to the doping at the dodecahedral site as shown in Fig. 5(c). The intensity variation of T + T1 + T2 and T modes present at 190, 235 and 269 cm−1 with Ce concentration is presented in Fig. 5(d), where T1, T2 and T translation refer to Feocta3+, R3+ and [FetetraO4]5− respectively. These results confirmed good crystalline nature for x = 0.4 Ce concentration and generation of lattice strain due to cerium doping.C. Microstructural/morphological study
Morphological visualization and statistics of grain size distribution were studied by scanning electron microscopy (SEM). The SEM images of investigated samples S1, S3 and S6 are presented in Fig. 6(a–c). The SEM snapshots unveiled the random shaped grains. The grain size distribution study has been performed using Gaussian fitting of histograms as shown in the inset of Fig. 6(a–c). Digimizer software was used to analyse the grain size distribution. From Gaussian fitting, the average grain size is observed in the micrometer range and that is comparatively bigger than that from previous studies.75,89–91 It is clear from the SEM micrographs that, for higher cerium concentration the primary particle order gets densified along with lattice diffusion which can be correlated with the ionic radii of the doped elements (i.e. Ce3+ and Bi3+).92 As observed that the density increases with Ce concentration there are chances of grain boundary diffusion causing enhanced grain size. SEM images reveal that the grain size increases from 5 μm to 12 μm for samples S1 to S6. Also, the agglomeration increases because of different compositions and their presence may depend upon magnetic interaction and the chemical reaction during the sintering process at a particular temperature which shows better alignment between the grains.92Fig. 6(d–f) shows the EDX analysis which discloses the presence of elemental compositions. We interpreted from the morphological analysis that the oxide particles show a large grain size for the x = 0.4 Ce sample like a monocrystalline phase.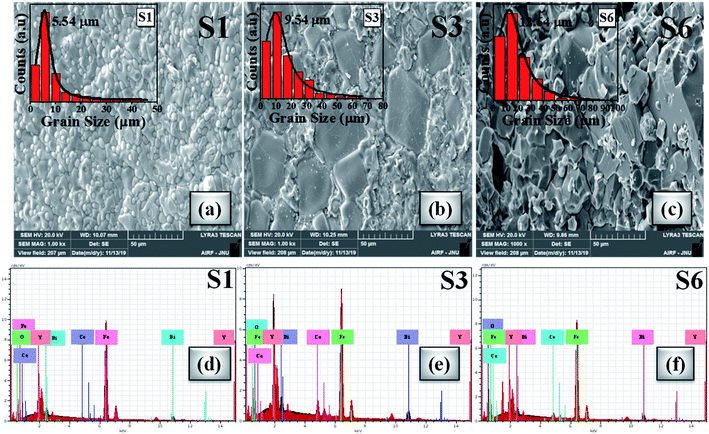 | ||
| Fig. 6 (a–c) SEM micrographs of S1, S3 and S6 oxide samples (inset: Gaussian distribution of grain sizes). (d–f) EDX spectra of S1, S3 and S6 samples. | ||
Fig. 7(a–c) shows the HRTEM images of S1, S3 and S6 samples. It can be seen that samples S1 and S3 show clear fringes, which reflects good crystallinity, and for sample S6, blurred fringes are observed on account of accentuated ceric oxide impurity. The d-spacing of HRTEM micrographs is calculated by inverse finite Fourier transform (FFT) method and is in accordance with the planes indexed in the XRD pattern. The maximum portion in each HRTEM image corresponds to the (400) crystal plane, confirming the mono-crystalline behaviour which is also confirmed by the SAED pattern as shown in Fig. 7(d–f). The SAED patterns are indexed by calculating d-values using the distance between the central spot and investigated spot. The calculated d-values of the SAED pattern are very well matched with the d-values calculated using Bragg's law and support most of the planes indexed in the XRD pattern. It is observed from the SAED pattern that S1 and S3 show good monocrystalline nature of studied garnet structures. With a further increase of Ce concentration (>S3 sample), due to the increase of CeO2, distortion increases, resulting in polycrystalline nature as shown in Fig. 7(f).
 | ||
| Fig. 7 (a–c) HRTEM images of S1, S3 and S6 oxide samples (inset: inverse FFT of the selected region). (d–f) SAED pattern of S1, S3 and S6 samples. | ||
D. Static and dynamic magnetization study
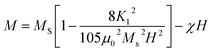 | (2) |
| Mnet = |M(3Fetetra3+) − M(2Feocta3+)| − M(RE3+) = M(Fetetra3+) − M(RE3+) | (3) |
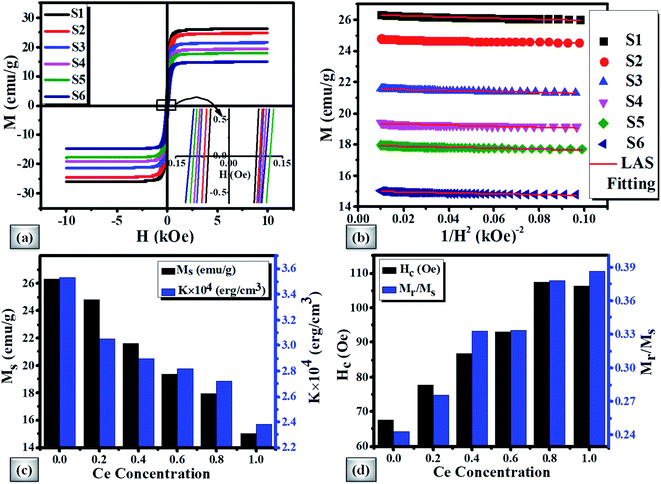
The Ms decreases in view of the fact that Ce3+ paramagnetic ions have a magnetic moment of 1 μB and there is no contribution either from Y3+ or Bi3+ diamagnetic ions (each having a magnetic moment of 0 μB).97 The saturation magnetization also decreases with the increase of non-magnetic CeO2 phase which results in oxygen reduction leading to the conversion of Fe3+ ions to Fe2+ ions. The variation of saturation magnetization (Ms) and first order magneto-crystalline anisotropy constant K1 at different Ce concentrations is shown in Fig. 8(c). The magneto-crystalline anisotropy results from the interaction of the electron orbitals with the potentials of the lattice. So, it is directly affected by lattice distortion due to the increase of Ce content.98 It is observed that the coercive force (Hc) increases up to 59% with the increase of Ce-content which may be attributed to lattice strain and ceric oxide inhomogeneity.
The magnetic squareness (Mr/Ms) is also showing similar behaviour with a Ce content from 0.243 to 0.386 respectively. This increase in squareness can be related to the transformation of the magnetic oxide phase to monocrystalline nature and inclined orientation towards the magnetic easy axis. The variation of Hc and Mr/Ms with Ce-content is demonstrated in Fig. 8(d). The observed magnetic parameters are tabulated in Table 6.
| Sample | Static magnetic parameters | Dynamic magnetic parameters | α | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M s (emu g−1) | H c (Oe) | M r/Ms | K 1 × 104 (erg cm−3) | M s (kOe) | γ′ (GHz kOe−1) | H ani (kOe) | ΔHo (Oe) | ||
| S1 | 26.316 | 67.656 | 0.243 | 3.53 | 1.648 | 2.78 | 0.191 | 378 | 1.3 × 10−3 |
| S2 | 24.783 | 77.631 | 0.275 | 3.05 | 1.556 | 2.86 | 0.187 | 450 | 1.4 × 10−3 |
| S3 | 21.570 | 86.657 | 0.332 | 2.90 | 1.42 | 2.9 | 0.186 | 535 | 1.9 × 10−3 |
| S4 | 19.355 | 92.946 | 0.333 | 2.82 | 1.263 | 2.93 | 0.224 | 615 | 2.0 × 10−3 |
| S5 | 17.940 | 107.346 | 0.378 | 2.72 | 1.184 | 2.97 | 0.229 | 668 | 2.5 × 10−3 |
| S6 | 14.999 | 106.392 | 0.386 | 2.38 | 1.02 | 2.86 | 0.231 | 562 | 1.9 × 10−3 |
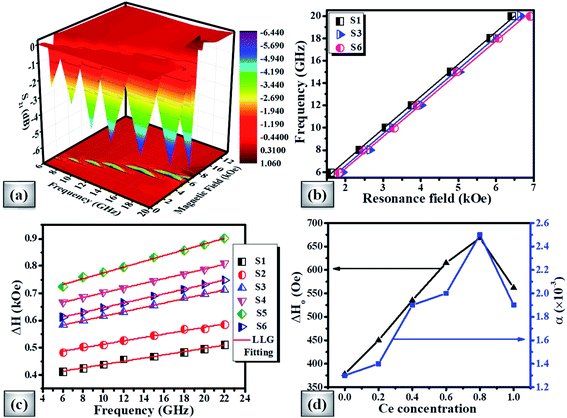
From the FMR spectra, we determined the resonance field (Hr) and field linewidth (ΔH) as a function of frequency for all the samples using Lorentzian fitting. Fig. 9(b) shows the operational frequency as a function of resonance field for samples S1, S3 and S6 respectively. For spherical nanoparticles, we can use the Kittel expression as given in eqn (4) for determining the intrinsic material parameters;99,100
| f = γ′(Hr + Heff) | (4) |
| Heff = HD + Hani + Hint | (5) |
The derived FMR linewidth (ΔH) is a combination of the intrinsic and extrinsic contribution. The intrinsic contribution arises due to material properties and extrinsic contribution is due to defects and inhomogeneous broadening. It is observed that ΔH increases with the increase of Ce-content up to sample S5 and further addition decreases ΔH for sample S6. This can be explained as the lattice distortion and dodecahedral site occupancy increase up to S5 (as shown in Fig. 4(b)) and decrease further for sample S6. Fig. 9(c) shows the FMR linewidth (ΔH) as a function of applied operating frequency (f) for all the magnetic oxide samples. The observed data were fitted to a line by considering the Landau–Lifshitz–Gilbert (LLG) model represented by eqn (6);101,102
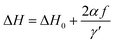 | (6) |
The deteriorating values of ΔH0 and α for x = 1.0 cerium concentration can be decoded by the increase in dodecahedral site occupancy value as shown in Fig. 4(b). The studied properties of the present investigation have been compared with other literature works in Table 7.
| Parameters | Bi0.1:YIG104–106 | Cex:YIG54,77,92,107,108 | CexBi0.1:YIG (present work) |
|---|---|---|---|
| Cerium solubility | — | 0.2 at. wt% | 0.4 at. wt% |
| Crystallite size (nm) | 65 | 93 | 104–115 |
| Grain size (μm) | — | 0.3 | 5.5–12.6 |
| M s (emu g−1) | 21.81 | 25.12–20 | 26.32–15.0 |
| H c (Oe) | 17.72 | 12 | 67.66–107.35 |
| M r/Ms | 0.063 | 0.0–0.05 | 0.24–0.39 |
| α | 2.0 × 10−3 | 2.8 × 10−3 | 1.3 × 10−3 |
From the ensemble of Table 7, we like to emphasize that the observed parameters like cerium solubility, crystallite size, grain size, saturation magnetization, coercivity, squareness ratio and magnetic damping are better than the earlier reported data. Hence, the present investigated series, especially x = 0.4 cerium concentration composition, can be a good candidate for spin-transfer torque MRAM (STT-MRAM) devices and magnetic sensor applications.
IV. Conclusion
Succinctly, a meticulous study for the fabrication of doped magnetic oxides has been successfully carried out using a solid state reaction method. The detailed analysis of the phase and crystal structure was performed using Rietveld refinement of XRD data. We demonstrated that with the increase of Ce concentration lattice distortion increases due to lattice strain and CeO2 impurities. SSP results showed the tensile nature of strain together with large crystallite sizes (>100 nm). The SEM micrographs asserted the existence of very large grain size in the micrometer range (5–12 μm). Saturation magnetization decreased up to 43% due to Ce3+ paramagnetic ions and coercivity increased up to 59%. The generation of strain-induced anisotropy was clearly evident from the dc magnetic measurements, whereas the magnetization dynamic study clearly showed that the microwave absorption decreases with the increase of Ce content. It was also observed that the Gilbert damping parameter (α) and extrinsic contribution (ΔH0) increase with Ce concentration. In conclusion, we demonstrated that the cerium substitution maneuvers the saturation magnetization, anisotropy field and Gilbert damping together with large crystallite and grain sizes. Such observed properties will be good for new generation microwave devices, spin-transfer-torque devices such as spin-transfer torque MRAM (STT-MRAM), and magnetic sensors with multi-functional features.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the MHRD-IMPRINT grant, DST-SERB, DST-AMT grant of Govt. of India. One of the authors (Jyoti Saini) is thankful to the Ministry of Human Resource Development, Govt. of India, for providing Prime Minister's Research Fellowship.References
- J. Wu, Z. Fan, D. Xiao, J. Zhu and J. Wang, Multiferroic bismuth ferrite-based materials for multifunctional applications: ceramic bulks, thin films and nanostructures, Prog. Mater. Sci., 2016, 84, 335–402 CrossRef CAS.
- M. Bibes and A. Barthélémy, Towards a magnetoelectric memory, Nat. Mater., 2008, 7(6), 425–426 CrossRef CAS PubMed.
- C. A. Vaz, J. Hoffman, C. H. Ahn and R. Ramesh, Magnetoelectric coupling effects in multiferroic complex oxide composite structures, Adv. Mater., 2010, 22(26–27), 2900–2918 CrossRef CAS PubMed.
- M. M. Vopson, Fundamentals of multiferroic materials and their possible applications, Crit. Rev. Solid State Mater. Sci., 2015, 40(4), 223–250 CrossRef CAS.
- N. Ortega, A. Kumar, J. F. Scott and R. S. Katiyar, Multifunctional magnetoelectric materials for device applications, J. Phys.: Condens. Matter, 2015, 27(50), 504002 CrossRef CAS PubMed.
- K. Ramam, B. S. Diwakar, K. Varaprasad, V. Swaminadham and V. Reddy, Magnetic properties of nano-multiferroic materials, J. Magn. Magn. Mater., 2017, 442, 453–459 CrossRef CAS.
- G. S. Lotey and N. K. Verma, Multiferroic properties of Tb-doped BiFeO 3 nanowires, J. Nanopart. Res., 2013, 15(4), 1–14 CrossRef.
- S. Ravi and C. Senthilkumar, Multiferroism in new Bi2FeMoO6 material, Mater. Express, 2015, 5(1), 68–72 CrossRef CAS.
- R. Liu, Y. Zhao, R. Huang, Y. Zhao and H. Zhou, Multiferroic ferrite/perovskite oxide core/shell nanostructures, J. Mater. Chem., 2010, 20(47), 10665–10670 RSC.
- C. Lu, W. Hu, Y. Tian and T. Wu, Multiferroic oxide thin films and heterostructures, Appl. Phys. Rev., 2015, 2(2), 021304 Search PubMed.
- G. Subramanyam, M. W. Cole, N. X. Sun, T. S. Kalkur, N. M. Sbrockey, G. S. Tompa, X. Guo, C. Chen, S. P. Alpay, G. A. Rossetti Jr and K. Dayal, Challenges and opportunities for multi-functional oxide thin films for voltage tunable radio frequency/microwave components, J. Appl. Phys., 2013, 114(19), 13 CrossRef.
- C. Wang, H. Xu, C. Liang, Y. Liu, Z. Li, G. Yang, L. Cheng, Y. Li and Z. Liu, Iron oxide@polypyrrole nanoparticles as a multifunctional drug carrier for remotely controlled cancer therapy with synergistic antitumor effect, ACS Nano, 2013, 7(8), 6782–6795 CrossRef CAS PubMed.
- S. H. Baek and C. B. Eom, Epitaxial integration of perovskite-based multifunctional oxides on silicon, Acta Mater., 2013, 61(8), 2734–2750 CrossRef CAS.
- N. Izyumskaya, Y. Alivov and H. Morkoc, Oxides, oxides, and more oxides: high-κ oxides, ferroelectrics, ferromagnetics, and multiferroics, Crit. Rev. Solid State Mater. Sci., 2009, 34(3–4), 89–179 CrossRef CAS.
- Tsymbal, E. Y., Dagotto, E. R., Eom, C. B. and Ramesh, R., Multifunctional Oxide Heterostructures, Oxford University Press, 2012 Search PubMed.
- Y. Xue, H. Chen, D. Yu, S. Wang, M. Yardeni, Q. Dai, M. Guo, Y. Liu, F. Lu, J. Qu and L. Dai, Oxidizing metal ions with graphene oxide: the in situ formation of magnetic nanoparticles on self-reduced graphene sheets for multifunctional applications, Chem. Commun., 2011, 47(42), 11689–11691 RSC.
- K. J. Jin, H. B. Lu, K. Zhao, C. Ge, M. He and G. Z. Yang, Novel multifunctional properties induced by interface effects in perovskite oxide heterostructures, Adv. Mater., 2009, 21(45), 4636–4640 CrossRef CAS.
- X. Chen, Z. Tang, P. Liu, H. Gao, Y. Chang and G. Wang, Smart utilization of multifunctional metal oxides in phase change materials, Matter, 2020, 3(3), 708–741 CrossRef.
- Y. M. Huh, Y. W. Jun, H. T. Song, S. Kim, J. S. Choi, J. H. Lee, S. Yoon, K. S. Kim, J. S. Shin, J. S. Suh and J. Cheon, In vivo magnetic resonance detection of cancer by using multifunctional magnetic nanocrystals, J. Am. Chem. Soc., 2005, 127(35), 12387–12391 CrossRef CAS PubMed.
- S. R. Singamaneni, J. T. Prater and J. Narayan, Multifunctional epitaxial systems on silicon substrates, Appl. Phys. Rev., 2016, 3(3), 031301 Search PubMed.
- M. M. Vopson, Fundamentals of multiferroic materials and their possible applications, Crit. Rev. Solid State Mater. Sci., 2015, 40(4), 223–250 CrossRef CAS.
- M. Bibes and A. Barthelemy, Oxide spintronics, IEEE Trans. Electron Devices, 2007, 54(5), 1003–1023 CAS.
- J. Huang, H. Wang, X. Sun, X. Zhang and H. Wang, Multifunctional La0. 67Sr0.33MnO3 (LSMO) thin films integrated on mica substrates toward flexible spintronics and electronics, ACS Appl. Mater. Interfaces, 2018, 10(49), 42698–42705 CrossRef CAS PubMed.
- G. Pacchioni, Two-dimensional oxides: Multifunctional materials for advanced technologies, Chem.–Eur. J., 2012, 18(33), 10144–10158 CrossRef CAS PubMed.
- W. Chen, X. Hou, X. Shi and H. Pan, Two-dimensional Janus transition metal oxides and chalcogenides: multifunctional properties for photocatalysts, electronics, and energy conversion, ACS Appl. Mater. Interfaces, 2018, 10(41), 35289–35295 CrossRef CAS PubMed.
- Pawade, V.B., Salame, P.H. and Bhanvase, B.A., Multifunctional Nanostructured Metal Oxides for Energy Harvesting and Storage Devices. CRC Press, 2020 Search PubMed.
- Guo, Z., Chen, Y. and Lu, N. L., Multifunctional Nanocomposites for Energy and Environmental Applications, John Wiley & Sons, 2018 Search PubMed.
- G. Pacchioni, Two-dimensional oxides: Multifunctional materials for advanced technologies, Chem.–Eur. J., 2012, 18(33), 10144–10158 CrossRef CAS PubMed.
- F. A. Blyakhman, N. A. Buznikov, T. F. Sklyar, A. P. Safronov, E. V. Golubeva, A. V. Svalov, S. Y. Sokolov, G. Y. Melnikov, I. Orue and G. V. Kurlyandskaya, Mechanical, electrical and magnetic properties of ferrogels with embedded iron oxide nanoparticles obtained by laser target evaporation: Focus on multifunctional biosensor applications, Sensors, 2018, 18(3), 872 CrossRef PubMed.
- L. Zhang, W. F. Dong and H. B. Sun, Multifunctional superparamagnetic iron oxide nanoparticles: design, synthesis and biomedical photonic applications, Nanoscale, 2013, 5(17), 7664–7684 RSC.
- M. Opel, S. Geprägs, E. P. Menzel, A. Nielsen, D. Reisinger, K. W. Nielsen, A. Brandlmaier, F. D. Czeschka, M. Althammer, M. Weiler and S. T. Goennenwein, Novel multifunctional materials based on oxide thin films and artificial heteroepitaxial multilayers, Phys. Status Solidi A, 2011, 208(2), 232–251 CrossRef CAS.
- G. Subramanyam, M. W. Cole, N. X. Sun, T. S. Kalkur, N. M. Sbrockey, G. S. Tompa, X. Guo, C. Chen, S. P. Alpay, G. A. Rossetti Jr. and K. Dayal, Challenges and opportunities for multi-functional oxide thin films for voltage tunable radio frequency/microwave components, J. Appl. Phys., 2013, 114(19), 191301 CrossRef.
- H. Liu, Recent progress in atomic layer deposition of multifunctional oxides and two-dimensional transition metal dichalcogenides, J. Mol. Eng. Mater., 2016, 4(04), 1640010 CrossRef CAS.
- N. Izyumskaya, Y. Alivov and H. Morkoc, Oxides, oxides, and more oxides: high-κ oxides, ferroelectrics, ferromagnetics, and multiferroics, Crit. Rev. Solid State Mater. Sci., 2009, 34(3–4), 89–179 CrossRef CAS.
- H. Wang, X. Liang, J. Wang, S. Jiao and D. Xue, Multifunctional inorganic nanomaterials for energy applications, Nanoscale, 2020, 12(1), 14–42 RSC.
- M. Mohapatra and S. Anand, Synthesis and applications of nano-structured iron oxides/hydroxides–a review, Int. J. Eng. Sci. Technol., 2010, 2(8), 127–146 Search PubMed.
- K. Salonitis, J. Pandremenos, J. Paralikas and G. Chryssolouris, Multifunctional materials: engineering applications and processing challenges, Int. J. Adv. Manuf. Technol., 2010, 49(5–8), 803–826 CrossRef.
- G. Subramanyam, M. W. Cole, N. X. Sun, T. S. Kalkur, N. M. Sbrockey, G. S. Tompa, X. Guo, C. Chen, S. P. Alpay, G. A. Rossetti Jr and K. Dayal, Challenges and opportunities for multi-functional oxide thin films for voltage tunable radio frequency/microwave components, J. Appl. Phys., 2013, 114(19), 13 CrossRef.
- M. M. El-Hammadi and J. L. Arias, Iron oxide-based multifunctional nanoparticulate systems for biomedical applications: a patent review (2008–present), Expert Opin. Ther. Pat., 2015, 25(6), 691–709 CrossRef CAS PubMed.
- R. Hao, R. Xing, Z. Xu, Y. Hou, S. Gao and S. Sun, Synthesis, functionalization, and biomedical applications of multifunctional magnetic nanoparticles, Adv. Mater., 2010, 22(25), 2729–2742 CrossRef CAS PubMed.
- A. B. Ustinov, A. V. Drozdovskii and B. A. Kalinikos, Multifunctional nonlinear magnonic devices for microwave signal processing, Appl. Phys. Lett., 2010, 96(14), 142513 CrossRef.
- L. Soumah, N. Beaulieu, L. Qassym, C. Carrétéro, E. Jacquet, R. Lebourgeois, J. B. Youssef, P. Bortolotti, V. Cros and A. Anane, Ultra-low damping insulating magnetic thin films get perpendicular, Nat. Commun., 2018, 9(1), 1–6 CrossRef CAS PubMed.
- M. Collet, O. Gladii, M. Evelt, V. Bessonov, L. Soumah, P. Bortolotti, S. O. Demokritov, Y. Henry, V. Cros, M. Bailleul and V. E. Demidov, Spin-wave propagation in ultra-thin YIG based waveguides, Appl. Phys. Lett., 2017, 110(9), 092408 CrossRef.
- J. R. Eshbach, Spin-wave propagation and the magnetoelastic interaction in yttrium iron garnet, J. Appl. Phys., 1963, 34(4), 1298–1304 CrossRef CAS.
- G. P. Gauthier, A. Courtay and G. M. Rebeiz, Microstrip antennas on synthesized low dielectric-constant substrates, IEEE Trans. Antennas Propag., 1997, 45(8), 1310–1314 CrossRef.
- Y. S. Chen, J. G. Lin, S. Y. Huang and C. L. Chien, Incoherent spin pumping from YIG single crystals, Phys. Rev. B, 2019, 99(22), 220402 CrossRef CAS.
- D. C. Bullock and D. J. Epstein, Negative Resistance, Conductive Switching, and Memory Effect in Silicon-Doped Yttrium-Iron Garnet Crystals, Appl. Phys. Lett., 1970, 17(5), 199–201 CrossRef CAS.
- R. W. Cooper, W. A. Crossley, J. L. Page and R. F. Pearson, Faraday rotation in YIG and TbIG, J. Appl. Phys., 1968, 39(2), 565–567 CrossRef CAS.
- M. Wu and A. Hoffmann, Recent Advances in Magnetic Insulators-From Spintronics to Microwave Applications, 2013 Search PubMed.
- A. A. Serga, A. V. Chumak and B. Hillebrands, YIG magnonics, J. Phys. D: Appl. Phys., 2010, 43(26), 264002 CrossRef.
- S. A. Nikitov, D. V. Kalyabin, I. V. Lisenkov, A. Slavin, Y. N. Barabanenkov, S. A. Osokin, A. V. Sadovnikov, E. N. Beginin, M. A. Morozova, Y. A. Filimonov and Y. V. Khivintsev, Magnonics: a new research area in spintronics and spin wave electronics, Phys.-Usp., 2015, 58(10), 1002 CrossRef CAS.
- M. Gomi, K. Satoh and M. Abe, Giant Faraday rotation of Ce-substituted YIG films epitaxially grown by RF sputtering, Jpn. J. Appl. Phys., 1988, 27(8A), L1536 CrossRef CAS.
- H. Uchida, Y. Masuda, R. Fujikawa, A. V. Baryshev and M. Inoue, Large enhancement of Faraday rotation by localized surface plasmon resonance in Au nanoparticles embedded in Bi:YIG film, J. Magn. Magn. Mater., 2009, 321(7), 843–845 CrossRef CAS.
- V. Sharma and B. K. Kuanr, Magnetic and crystallographic properties of rare-earth substituted yttrium-iron garnet, J. Alloys Compd., 2018, 748, 591–600 CrossRef CAS.
- M. Yousaf, A. Noor, S. Xu, M. N. Akhtar and B. Wang, Magnetic characteristics and optical band alignments of rare earth (Sm+ 3, Nd+ 3) doped garnet ferrite nanoparticles (NPs), Ceram. Int., 2020, 46(10), 16524–16532 CrossRef CAS.
- M. Huang and S. Y. Zhang, Growth and characterization of cerium-substituted yttrium iron garnet single crystals for magneto-optical applications, Appl. Phys. A: Solids Surf., 2002, 74(2), 177–180 CrossRef CAS.
- J. F. Dillon Jr, Ferrimagnetic resonance in rare-earth-doped yttrium iron garnet. III. Linewidth, Phys. Rev., 1962, 127(5), 1495 CrossRef.
- G. J. Chen and L. F. Wang, Design of magnetic nanoparticles-assisted drug delivery system, Curr. Pharm. Des., 2011, 17(22), 2331–2351 CrossRef CAS PubMed.
- M. T. I. S. Munaweera, Nanoparticles and Nanofiber Composites for Drug Delivery, Cancer Chemoradiotherapy and Other Biological Applications, The University of Texas at Dallas, 2015 Search PubMed.
- A. R. Bhalekar and L. N. Singh, Structural and Magnetic Studies of Aluminum Substituted YIG Nanoparticles Prepared by a Sol-Gel Route, Braz. J. Phys., 2019, 49(5), 636–645 CrossRef CAS.
- Z. Xia and A. Meijerink, Ce 3+-Doped garnet phosphors: composition modification, luminescence properties and applications, Chem. Soc. Rev., 2017, 46(1), 275–299 RSC.
- A. Jain, P. Sengar and G. A. Hirata, Rare-earth-doped Y3Al5O12 (YAG) nanophosphors: synthesis, surface functionalization, and applications in thermoluminescence dosimetry and nanomedicine, J. Phys. D: Appl. Phys., 2018, 51(30), 303002 CrossRef.
- A. Sunny, V. Viswanath, K. P. Surendran and M. T. Sebastian, The effect of Ga3+ addition on the sinterability and microwave dielectric properties of RE3Al5O12 (Tb3+, Y3+, Er3+ and Yb3+) garnet ceramics, Ceram. Int., 2014, 40(3), 4311–4317 CrossRef CAS.
- R. K. Singh, N. Jain, P. Singh, R. Kumar, J. Singh, S. Dutta, T. M. Chen, S. Som and H. C. Swart. Development in the innovation of lead halide-based perovskite quantum dots from rare earth-doped garnet-based phosphors for light-emitting diodes, in Spectroscopy of Lanthanide Doped Oxide Materials, Woodhead Publishing, 2020, pp. 21–56 Search PubMed.
- G. B. Scott and D. Lacklison, Magneto-optic properties and applications of bismuth substituted iron garnets, IEEE Trans. Magn., 1976, 12(4), 292–311 CrossRef.
- H. B. Vasili, B. Casals, R. Cichelero, F. Macià, J. Geshev, P. Gargiani, M. Valvidares, J. Herrero-Martin, E. Pellegrin, J. Fontcuberta and G. Herranz, Direct observation of multivalent states and 4 f → 3 d charge transfer in Ce-doped yttrium iron garnet thin films, Phys. Rev. B, 2017, 96(1), 014433 CrossRef.
- M. C. Onbasli, L. Beran, M. Zahradník, M. Kučera, R. Antoš, J. Mistrík, G. F. Dionne, M. Veis and C. A. Ross, Optical and magneto-optical behavior of Cerium Yttrium Iron Garnet thin films at wavelengths of 200–1770 nm, Sci. Rep., 2016, 6(1), 1–10 CrossRef PubMed.
- S. Higuchi, Y. Furukawa, S. Takekawa, O. Kamada, K. Kitamura and K. Uyeda, Magneto-optical properties of cerium-substituted yttrium iron garnet single crystals for magnetic-field sensor, Sens. Actuators, A, 2003, 105(3), 293–296 CrossRef CAS.
- F. Chen, X. Wang, Y. Nie, Q. Li, J. Ouyang, Z. Feng, Y. Chen and V. G. Harris, Ferromagnetic resonance induced large microwave magnetodielectric effect in cerium doped Y3Fe5O12 ferrites, Sci. Rep., 2016, 6(1), 1–8 CrossRef CAS.
- L. Soumah, N. Beaulieu, L. Qassym, C. Carrétéro, E. Jacquet, R. Lebourgeois, J. B. Youssef, P. Bortolotti, V. Cros and A. Anane, Ultra-low damping insulating magnetic thin films get perpendicular, Nat. Commun., 2018, 9(1), 1–6 CrossRef CAS PubMed.
- T. Goto, M. C. Onbaşlı and C. A. Ross, Magneto-optical properties of cerium substituted yttrium iron garnet films with reduced thermal budget for monolithic photonic integrated circuits, Opt. Express, 2012, 20(27), 28507–28517 CrossRef CAS PubMed.
- S. Higuchi, K. Ueda, F. Yahiro, Y. Nakata, H. Uetsuhara, T. Okada and M. Maeda, Fabrications of cerium-substituted YIG thin films for magnetic field sensor by pulsed-laser deposition, IEEE Trans. Magn., 2001, 37(4), 2451–2453 CrossRef CAS.
- A. Ikesue, Y. L. Aung, R. Yasuhara and Y. Iwamoto, Giant Faraday rotation in heavily ce-doped YIG bulk ceramics, J. Eur. Ceram. Soc., 2020, 40(15), 6073–6078 CrossRef CAS.
- S. M. Elhamali, N. B. Ibrahim and S. Radiman, Influence of erbium on the structural, optical and magnetic properties of sol–gel Ce: YIG films, J. Sol-Gel Sci. Technol., 2018, 85(3), 693–702 CrossRef CAS.
- M. R. Khalifeh, H. Shokrollahi, F. S. Nogorani and M. Basavad, Improving Dy, Ce, Bi: YIG phase formation and magnetic features via heat treatment and chemical composition, Appl. Phys. A: Solids Surf., 2020, 126(9), 1–16 CrossRef.
- M. Golkari, H. Shokrollahi and H. Yang, The influence of Eu cations on improving the magnetic properties and promoting the Ce solubility in the Eu, Ce-substituted garnet synthesized by the solid state route, Ceram. Int., 2020, 46(7), 8553–8560 CrossRef CAS.
- T. C. Mao and J. C. Chen, Influence of the addition of CeO2 on the microstructure and the magnetic properties of yttrium iron garnet ceramic, J. Magn. Magn. Mater., 2006, 302(1), 74–81 CrossRef CAS.
- P. Pahuja, C. Prakash and R. P. Tandon, Comparative study of magnetoelectric composite system Ba0. 95Sr0.05TiO3–Ni0.8Co0.2Fe2O4 with ferrite prepared by different methods, Ceram. Int., 2014, 40(4), 5731–5743 CrossRef CAS.
- G. Gurjar, V. Sharma, S. Patnaik and B. K. Kuanr, Structural and magnetic properties of high quality single crystalline YIG thin film: A comparison with the bulk YIG, AIP Conf. Proc., 2019, 2115(No. 1), 030323 CrossRef.
- B. Bhoi, N. Venkataramani, R. P. R. C. Aiyar and S. Prasad, FMR and magnetic studies on polycrystalline YIG thin films deposited using pulsed laser, IEEE Trans. Magn., 2013, 49(3), 990–994 CAS.
- V. Sharma, J. Saha, S. Patnaik and B. K. Kuanr, YIG based broad band microwave absorber: A perspective on synthesis methods, J. Magn. Magn. Mater., 2017, 439, 277–286 CrossRef CAS.
- S. Geller and M. A. Gilleo, The crystal structure and ferrimagnetism of yttrium-iron garnet, Y3Fe2 (FeO4)3, J. Phys. Chem. Solids, 1957, 3(1–2), 30–36 CrossRef CAS.
- M. Basavad, H. Shokrollahi and M. Golkari, Effect of thermal cycle and Bi/Eu doping on the solubility of Ce in YIG, Ceram. Int., 2020, 46(12), 20144–20154 CrossRef CAS.
- S. Tan, W. Zhang, L. Yang, J. Chen and Z. Wang, Intrinsic defects in yttrium iron garnet: A first-principles study, J. Appl. Phys., 2020, 128(18), 183904 CrossRef CAS.
- D. Nath, F. Singh and R. Das, X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles-a comparative study, Mater. Chem. Phys., 2020, 239, 122021 CrossRef CAS.
- J. Saini, D. Yadav, V. Sharma, M. Sharma and B. K. Kuanr, Effect of Aliovalent Substitution in Y 2.9 Bi 0.1 Fe5O12: Magnetization Dynamic Study, IEEE Trans. Magn., 2020, 57(2), 1–5 Search PubMed.
- J. J. Song, P. B. Klein, R. L. Wadsack, M. Selders, S. Mroczkowski and R. K. Chang, Raman-active phonons in aluminum, gallium, and iron garnets, J. Opt. Soc. Am., 1973, 63(9), 1135–1140 CrossRef CAS.
- E. J. J. Mallmann, A. S. B. Sombra, J. C. Goes and P. B. A. Fechine, Yttrium iron garnet: properties and applications review, Solid State Phenom., 2013, 202, 65–96 Search PubMed.
- R. Nazlan, I. Ismail, Z. Abbas, I. R. Ibrahim, F. M. Idris, F. N. Shafiee, A. S. Aripin and N. A. N. Busra, Dependence of magnetic and microwave loss on evolving microstructure in yttrium iron garnet, J. Mater. Sci.: Mater. Electron., 2018, 29(10), 8688–8700 CrossRef CAS.
- O. Opuchovic, M. Andrulevicius, S. Tamulevicius, J. L. Rehspringer, A. Beganskiene, R. Skaudzius, K. Ishikawa and A. Kareiva, Cerium doping and cerium aluminium co-doping effects on the sol-gel processing of Y3Fe5O12 (YIG): Bulk and thin films, Solid State Sci., 2020, 99, 106065 CrossRef CAS.
- M. N. Akhtar, A. B. Sulong, M. A. Khan, M. Ahmad, G. Murtaza, M. R. Raza, R. Raza, M. Saleem and M. Kashif, Structural and magnetic properties of yttrium iron garnet (YIG) and yttrium aluminum iron garnet (YAIG) nanoferrites prepared by microemulsion method, J. Magn. Magn. Mater., 2016, 401, 425–431 CrossRef CAS.
- R. B. Borade, S. E. Shirsath, G. Vats, A. S. Gaikwad, S. M. Patange, S. B. Kadam, R. H. Kadam and A. B. Kadam, Polycrystalline to preferred-(100) single crystal texture phase transformation of yttrium iron garnet nanoparticles, Nanoscale Adv., 2019, 1(1), 403–413 RSC.
- M. Niyaifar and H. Mohammadpour, Study on magnetic role of Bi3+ ion by random cation distribution model in Bi–YIG system, J. Magn. Magn. Mater., 2015, 396, 65–70 CrossRef CAS.
- M. Niyaifar and H. Mohammadpour, Study on magnetic role of Bi3+ ion by random cation distribution model in Bi–YIG system, J. Magn. Magn. Mater., 2015, 396, 65–70 CrossRef CAS.
- Z. Cheng, Y. Cui, H. Yang and Y. Chen, Effect of lanthanum ions on magnetic properties of Y 3 Fe 5 O 12 nanoparticles, J. Nanopart. Res., 2009, 11(5), 1185–1192 CrossRef CAS.
- Z. Cheng, H. Yang, L. Yu and W. Xu, Saturation magnetic properties of Y3−x RexFe5O12 (Re: Gd, Dy, Nd, Sm and La) nanoparticles grown by a sol–gel method, J. Mater. Sci.: Mater. Electron., 2008, 19(5), 442–447 CrossRef CAS.
- G. F. Dionne, Magnetic Oxides, New York, Springer, 2009, vol. 14, p. 15 Search PubMed.
- H. Kirchmayr, Magnetic Anisotropy, 2001 Search PubMed.
- D. Polder, VIII. On the theory of ferromagnetic resonance, London Edinburgh Philos. Mag. J. Sci., 1949, 40(300), 99–115 CrossRef CAS.
- J. H. Van Vleck, Concerning the theory of ferromagnetic resonance absorption, Phys. Rev., 1950, 78(3), 266 CrossRef.
- K. Seemann, H. Leiste and C. Klever, Determination of intrinsic FMR line broadening in ferromagnetic (Fe44Co56) 77Hf12N11 nanocomposite films, J. Magn. Magn. Mater., 2010, 322(20), 2979–2983 CrossRef CAS.
- L. Qiao, X. Han, B. Gao, J. Wang, F. Wen and F. Li, Microwave absorption properties of the hierarchically branched Ni nanowire composites, J. Appl. Phys., 2009, 105(5), 053911 CrossRef.
- B. Heinrich, J. F. Cochran and R. Hasegawa, FMR line broadening in metals due to two-magnon scattering, J. Appl. Phys., 1985, 57(8), 3690–3692 CrossRef CAS.
- Y. P. Fu, C. W. Cheng, D. S. Hung and Y. D. Yao, Formation enthalpy and magnetic properties of Bi-YIG powders, Ceram. Int., 2009, 35(4), 1509–1512 CrossRef CAS.
- Y. J. Siao, X. Qi, C. R. Lin and J. C. A. Huang, Dielectric relaxation and magnetic behavior of bismuth-substituted yttrium iron garnet, J. Appl. Phys., 2011, 109(7), 07A508 CrossRef.
- H. Xu, H. Yang, W. Xu and L. Yu, Magnetic properties of Bi-doped Y3Fe5O12 nanoparticles, Curr. Appl. Phys., 2008, 8(1), 1–5 CrossRef.
- M. Golkari, H. Shokrollahi and H. Yang, The influence of Eu cations on improving the magnetic properties and promoting the Ce solubility in the Eu, Ce-substituted garnet synthesized by the solid state route, Ceram. Int., 2020, 46(7), 8553–8560 CrossRef CAS.
- E. Baños-López, C. A. Cortés-Escobedo, F. Sánchez-De Jesús, A. Barba-Pingarrón and A. M. Bolarín-Miró, Crystal structure and magnetic properties of cerium-doped YIG: Effect of doping concentration and annealing temperature, J. Alloys Compd., 2018, 730, 127–134 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |