Open Access Article
Open Access ArticleLattice-distorted lithiation behavior of a square phase Janus MoSSe monolayer for electrode applications†
Xin
Tang
a,
Han
Ye
 *a,
Wenjun
Liu
*a,
Wenjun
Liu
 a,
Yumin
Liu
a,
Yumin
Liu
 a,
Zhenlin
Guo
b and
Mingchao
Wang
a,
Zhenlin
Guo
b and
Mingchao
Wang
 *cd
*cd
aState Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications, Beijing 100876, China. E-mail: Han_ye@bupt.edu.cn
bMechanics Division, Beijing Computational Science Research Center, Beijing 100193, China
cDepartment of Materials Science and Engineering, Monash University, Clayton, VIC 3800, Australia. E-mail: mingchao.wang@monash.edu
dCentre for Theoretical and Computational Molecular Science, Australian Institute for Bioengineering and Nanotechnology, The University of Queensland, St Lucia, QLD 4072, Australia
First published on 17th March 2021
Abstract
Janus transition metal dichalcogenides with unique physical properties have recently attracted increasing research interest for their energy and catalytic applications. In this paper, we investigate the lithiation behavior of a square phase Janus MoSSe monolayer (1S-MoSSe) using first-principles calculations. Computational results show that a single Li atom energetically prefers to adsorb on the central site of the octagonal ring (O site) and on the S-layer side of 1S-MoSSe. The predicted energy barriers for Li diffusion are surface dependent and in the range of 0.33 to 0.51 eV, indicating the acceptable Li migration kinetics on 1S-MoSSe in comparison with other 2D TMD materials. Further thermodynamic analysis demonstrates that Li adsorption on 1S-MoSSe is energetically stable up to a Li concentration of x = 1.0, above which the lithiation process becomes unstable with a negative charging potential. Phonon calculations also confirm that Li adsorption (0.25 ≤ x ≤ 0.75) results in the lattice distortion of 1S-MoSSe in order to suppress the structural instability of the lithiated monolayer 1S-LixMoSSe with imaginary phonon frequencies. The less symmetric nature of 1S-MoSSe is believed to destabilize Li adsorption at much smaller x than 1H-MoSSe does, regardless of the higher dipole moment of 1S-MoSSe. This computational study provides a fundamental understanding of the electrochemical performance of 1S-MoSSe, as well as useful insight into the material design of Janus TMD anodes for Li-ion batteries.
1. Introduction
Layer-structured materials with two-dimensional (2D) layer components have attracted wide research interest for their energy applications in alkali metal batteries owing to their unique physical properties (i.e. large surface area and fast ion transport).1–3 Among various 2D-based materials, graphene and transition metal dichalcogenide (TMD) based materials have been widely studied as potential electrodes for Li-ion batteries (LIBs).3–5 For example, graphite has been used as a commercial anode in LIBs due to its excellent electrical conductivity and good stability.6,7 However, the graphite anode suffers from a low capacity of 372 mA h g−1, which hardly satisfies the current energy demand for electrified vehicles and grid energy storage.8,9 As for TMD-based materials, although certain TMD candidates such as MoS2 exhibit excellent specific capacity as high as 554 mA h g−1,10 they still suffer from low electrical conductivities, as well as sluggish ion diffusion within the interlayer spacings.4,5,11 It is therefore urgently necessary to enhance the battery performance of layered material electrodes with excellent thermodynamic and kinetic stabilities.Recently, various material design strategies have been proposed for improving the electrochemical properties of 2D-based electrodes for LIBs. For instance, layered materials with heterostructures (i.e. graphene/MoS2 (ref. 12 and 13)) or expanded interlayer spacings14–16 enable the acceleration of Li intercalation kinetics, while it is compensated with capacity fading and cycling stability due to the weakened interaction between the layer structures and Li ions. In the extreme case of interlayer expansion, some 2D materials, including graphene and MoS2, become thermodynamically unstable upon Li adsorption, resulting in the irreversible formation of Li metal clusters.17–19 To overcome such a limitation, surface defects in 2D layers have been demonstrated as an effective way to enhance the thermodynamic stability of both graphene and TMD monolayers, contributed by increased charge transfer.20–23 Unfortunately, such a defect engineering method is highly limited by its uncontrollable synthesis procedure and undesired mechanical failure upon lithiation.
In addition to defect engineering, synthesizing novel phases of regular graphene and TMD structures serves as an alternative way to improve their electrochemical performance for LIBs. For example, some allotropes of graphene, such as phagraphene (defected graphene with 5- to 7-membered rings)24,25 and graphdiyne,17,26,27 exhibit both excellent ion mobility and high specific capacity as promising anodes for LIBs. A square phase allotrope of MoS2 is also observed near the grain boundary of H-phase MoS2,28–30 and is predicted to possess a theoretical capacity of 670 mA h g−1.31 Compared with regular TMDs, recent experiments have successfully fabricated a new class of TMD structures called Janus TMDs (i.e. MoSSe), with controlled sulfurization of their one-side atoms.32–34 The intrinsic dipole moment of H-phase (H-) Janus MoSSe promotes Li adsorption, leading to an improved thermodynamic stability.35 Different from square phase TMDs, there is lack of intensive investigation on the electrochemical behavior of square phase Janus TMDs, regardless of recent theoretical studies of their catalytic applications.36–38
With the above in mind, we carry out a systematic study of the Li adsorption behavior of a square phase Janus MoSSe monolayer (1S-MoSSe) as a LIB anode using first-principles calculations. Structural, energetic and electrochemical properties of 1S-MoSSe upon lithiation are predicted respectively. It is found that 1S-MoSSe has more energetically stable binding sites than some other TMD-based monolayers. Different Li migration pathways and kinetics are analyzed as well. Finally, we estimate the thermodynamic stability, as well as open cell voltage and Li storage capacity, of lithiated 1S-MoSSe at the Li concentration of x, denoted as 1S-LixMoSSe. Phonon calculations demonstrate that Li adsorption results in the structural instability of LixMoSSe, and is further suppressed by local lattice distortion. In addition, 1S-MoSSe has a maximum Li concentration of x = 1.0 (129.47 mA h g−1), above which Li adsorption becomes unstable associated with a negative charging voltage.
2. Computational methods
All density functional theory (DFT) calculations are conducted using the Vienna ab initio simulation package (VASP) code.39 The electron core-valence and exchange–correlation interactions are described by projector augmented plane wave (PAW) pseudopotentials40 and the Perdew–Burke–Ernzerhof (PBE) functional,41 respectively. We select a plane-wave based kinetic energy cutoff of 600 eV, and the 5 × 5 × 1 Monkhorst–Pack42k-point mesh for sampling the Brillouin zones of Janus structures. The thickness of vacuum spacing is set as 18 Å to avoid the interaction between the Janus monolayer and its images. Atomic structures are optimized until the force and energy of each atom are smaller than 0.02 eV Å−1 and 10−6 eV, respectively. Grimme's energy correction method (DFT-D3) is employed to correctly account for long-range dispersion interactions.43 Dipole correction is also considered here along the z axis to eliminate any spurious interaction between Janus monolayers.The Bader charge analysis44,45 is conducted to analyze the charge transfer between Li ions and the MoSSe monolayer. The minimum energy paths of Li ion migration are identified through the climbing image nudged elastic band (CI-NEB) method.46 In order to assess the dynamic stability of Janus monolayers upon Li adsorption, their vibrational properties are obtained from phonon dispersion calculations based on density functional perturbation theory. The force constant matrix is constructed from the 3 × 3 × 1 supercell in the PHONOPY package.47 The adsorption energy per Li atom (Eatomads) is defined as:
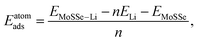 | (1) |
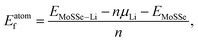 | (2) |
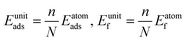 | (3) |
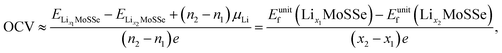 | (4) |
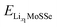 and
and 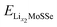 are the total energies of the lithiated structures LixMoSSe, and Eunitf(Lix1MoSSe) and Eunitf(Lix2MoSSe) are the formation energies per MoSSe unit cell, at adjacent Li concentrations of x1 and x2.
are the total energies of the lithiated structures LixMoSSe, and Eunitf(Lix1MoSSe) and Eunitf(Lix2MoSSe) are the formation energies per MoSSe unit cell, at adjacent Li concentrations of x1 and x2.
3. Results and discussion
3.1 Structural and electronic properties of 1S-MoSSe
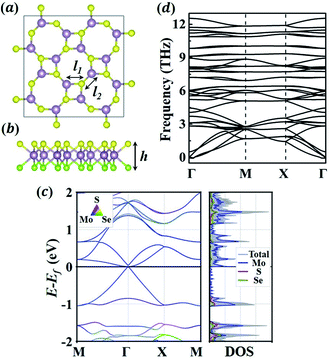
We first evaluate the fundamental properties of the 1S-MoSSe monolayer. Fig. 1(a and b) exhibits the relaxed 2 × 2 supercell of 1S-MoSSe consisting of alternating square and octagonal rings. The lattice constant of the primitive cell is 6.421 Å, with a thickness of 3.243 Å. As shown in Table 1, the nearest Mo–S (2.449 Å) and Mo–Se (2.587 Å) bonds in the square ring are both longer than those in the octagonal ring (2.393 Å and 2.484 Å, respectively), which is well consistent with previous computational results.36,37 1S-MoSSe has a lattice constant and thickness that are between those of the 1S-MoS2 and 1S-MoSe2 monolayers, while the trend of Mo–S and Mo–Se bond lengths among these 3 monolayers is unobvious. Owing to the structural asymmetry, 1S-MoSSe has a dipole moment of 2.99 Debye along its thickness direction, which is larger than that of the 1H-MoSSe monolayer (1.61 Debye). The effect of dipole moment on its Li adsorption behavior will be discussed later.Fig. 1(c) characterization of the electronic properties of 1S-MoSSe. Different from 1H-MoS2 and 1H-MoSe2,49 1S-MoSSe behaves as a semi-metal with the valence band maximum and conduction band minimum crossing each other at the Fermi-level, which has also been observed in other square-phase TMD monolayers.31,50 In addition, the phonon dispersion curves (see Fig. 1(d)) of 1S-MoSSe are predicted to determine its intrinsic structural stability. The absence of imaginary frequencies around the Γ point in the reciprocal space confirms that 1S-MoSSe is dynamically stable. As a result, the robustness of 1S-MoSSe guarantees it as an anode candidate for LIBs.
3.2 Energetic and electronic properties of Li adsorption on 1S-MoSSe
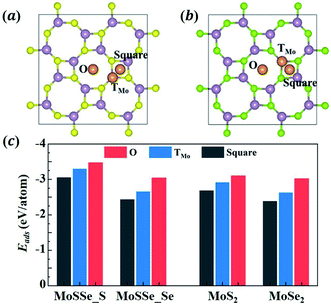
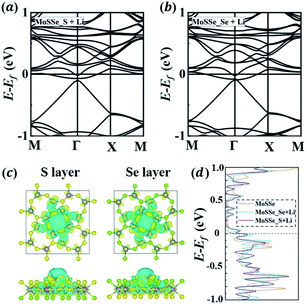
To understand the lithiation behavior of 1S-MoSSe, we then explore its potential binding sites for isolated Li atom adsorption. The 2 × 2 supercell of 1S-MoSSe is adopted here. To identify the most stable site for Li adsorption, three possible sites on each side of 1S-MoSSe are considered, including the O site: the central site of the octagonal ring; the TMo site: the top site of Mo; and the square site: the central site of the square ring, as presented in Fig. 2(a and b). According to the definition of adsorption energy per Li atom (Eatomads) in eqn (1), the more negative value of Eatomads the system possesses, the more energetically favorable the binding site is. Fig. 2(c) demonstrates that the O site on both sides of 1S-MoSSe has the lowest value of Eatomads, indicating it as the most energetically favorable site for Li adsorption followed by TMo and square sites. Fig. 2(c) also shows that these binding sites on the S-layer side have a lower Eatomads than those on the Se-layer side, which can result in asymmetric Li adsorption. In addition, all 3 binding sites on 1S-MoSSe are more energetically stable than those on 1S-MoS2 and 1S-MoSe2. Such a higher binding strength of 1S-MoSSe can be attributed to the existence of its dipole moment, which facilitates Li adsorption by an intrinsic electric field.35To further understand the asymmetric Li adsorption behavior of 1S-MoSSe, we calculate the electronic properties of 1S-MoSSe with a single Li atom adsorbed on the O sites of both sides, labeled as 1S-MoSSe_S + Li and 1S-MoSSe_Se + Li, respectively. Fig. 3(a and b) show that both adsorption systems are still semi-metallic with zero band gap at the Fermi level. The corresponding charge transfer is analyzed on the basis of charge density difference (see Fig. 3(c)). It is shown that charge accumulation occurs in 1S-MoSSe, whereas charge depletion occurs on the Li atom. Bader charge calculations confirm that more electrons (0.87 e) transfer from the Li atom to the S-layer side than to the Se-layer side (0.84 e), which supports the ionic nature of Li adsorption. The electronic DOS curves of 1S-MoSSe before and after Li adsorption are given in Fig. 3(d). Different from the pristine 1S-MoSSe, 1S-MoSSe_S + Li and 1S-MoSSe_Se + Li systems exhibit narrower DOS peaks near the Fermi level, and the DOS peaks of 1S-MoSSe_S + Li are slightly closer to the Fermi level compared to those of 1S-MoSSe_Se + Li. This also represents the higher adsorption strength of 1S-MoSSe_S + Li than that of 1S-MoSSe_Se + Li. Based on this consideration, Li adsorption should start from the S-layer side, accompanied by the gradual adsorption of more Li on both sides upon lithiation. The electronic band structure and DOS of the system with Li adsorbed on TMo and square sites are illustrated in Fig. S1 in the ESI.†
3.3 Kinetics of Li migration on 1S-MoSSe
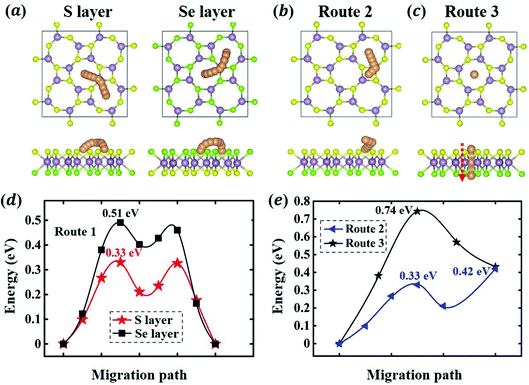
In addition to the energetics of Li adsorption, here, we study the kinetics of Li migration on 1S-MoSSe. To determine the optimal migration path and the corresponding energy barrier, we consider three Li diffusion pathways on 1S-MoSSe (see Fig. 4(a–c)): (1) a Li atom diffuses between two nearest O sites; (2) a Li atom diffuses from an O site to the nearest square site; (3) a Li atom diffuses from an O site on the S-layer side to the neighboring O site on the Se-layer side. The minimum energy paths (MEPs) and corresponding diffusion barriers are presented in Fig. 4(d and e). For route 1 on both sides of 1S-MoSSe, the corresponding MEPs form zigzag shaped curves which span across another energy minimum site between 2 nearest O sites. Owing to the asymmetry of 1S-MoSSe, such an energy minimum site is different from the TMo site (see Fig. 2(a and b)), which results in the asymmetric shape of MEPs. Between the different sides of 1S-MoSSe for route 1, the calculated energy barrier on the Se-layer side is 0.51 eV higher than that on the S-layer side of 0.33 eV, which is interestingly in contrast to the difference between their adsorption energies on different binding sites.Since the S-layer side has a much lower energy barrier for route 1, routes 2 and 3 are only considered on the S-layer side. The diffusion barrier for route 2 is 0.42 eV, and the TMo site is thermodynamically unstable and will migrate to a nearby energy minimum site under certain perturbations. The higher diffusion barrier for route 2 (0.42 eV) than that for route 1 (0.33 eV) results from the thermodynamical instability of square site. As for route 3, however, it requires much higher energy (0.74 eV) to migrate across the Janus monolayer. The energy barriers for surface migration routes on 1S-MoSSe (0.33–0.51 eV) are a little bit higher than those on 1H-MoSSe (0.24–0.29 eV)35 as well as 1H-MoS2 (0.21 eV) and 1H-MoSe2 (0.225 eV).18 As a result, 1S-MoSSe may have slower but comparable Li migration kinetics according to the Arrhenius relationship.
3.4 Electrochemical properties of 1S-MoSSe upon lithiation
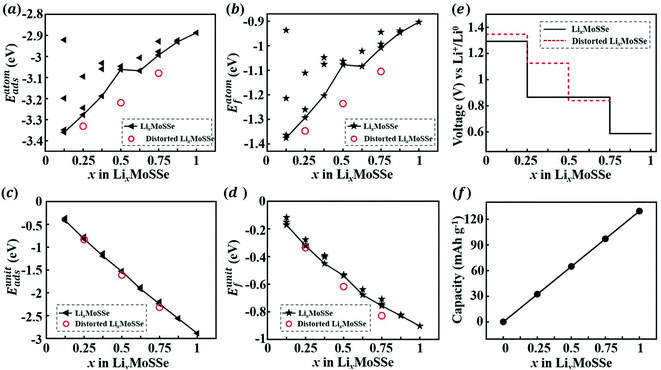
Finally, we calculate the thermodynamic properties of the lithiated Janus MoSSe monolayer (1S-LixMoSSe) at a Li concentration of x = 0.125–1.0 with an increment of Δx = 0.125. As discussed in the previous section, Li prefers to adsorb on the S-layer side rather than the Se-layer side. In order to determine the most energetically stable configurations at different values of x, Li atoms are placed preferentially on the O sites of the S-layer side when x ≤ 0.5. As for 0.5 < x ≤ 1, the subsequent Li ions are randomly adsorbed on the O sites of the Se-layer side. Different adsorption configurations with the same Li concentration are considered. Fig. 5(a) and (c) show the adsorption energy per atom and per unit of different 1S-LixMoSSe configurations. All the negative adsorption energies imply that the process of Li adsorption on 1S-MoSSe is thermodynamically stable, but such a lithiation process gradually becomes more difficult, associated with the increase of Eatomads (Fig. 5(a)). It should also be noted that Eatomads is much lower than the cohesive energy of the Li bcc crystal (−1.99 eV per atom) up to x = 1.0, indicating that Li adsorption on 1S-MoSSe is more energetically favorable than Li clustering. This is also consistent with all the negative values of formation energy in Fig. 5(b) and (d), and the charging/discharging process in such a concentration range is thermodynamically reversible without Li plating.In addition to the thermodynamic analysis of 1S-LixMoSSe, we further perform phonon dispersion calculations to check the structural stability of 1S-LixMoSSe. As shown in Fig. 6(a–c), large negative frequencies occur at M and X points in the reciprocal space within the concentration range of 0 < x < 1. These imaginary frequencies normally represent a dynamically unstable configuration (see Fig. 7(a–c)). After checking the corresponding eigenvectors of imaginary frequencies, minor structural distortion is introduced into 1S-LixMoSSe to find their stable configurations after relaxation. Fig. 7(d–f) shows that lattice distortion further stabilizes 1S-LixMoSSe with lower adsorption energy. Meanwhile, the phonon dispersion curves of distorted configurations in Fig. 6(d–f) also confirm the improvement of their structural stability. The updated high symmetric points for distorted configurations are shown in Fig. S2 (see the ESI†). With the increase of x, adsorbing more Li atoms can stabilize 1S-LixMoSSe at x = 1.0 (Fig. 6(g)) without imaginary frequencies at M and X points. It should be noted that the very small imaginary frequencies observed in Fig. 6(d–g) may result from numerical errors in phonon calculations.51 Similar structural instability (imaginary frequencies) has also been found in other TMDs.52–55 Different from the lattice distortion of 1S-LixMoSSe, the remarkable H to T phase transition of these TMDs suppresses their structural instability upon ion adsorption. Such a significant structural change induced by phase transition may trigger the structural failure of these layered anodes, causing the degradation of battery performance.
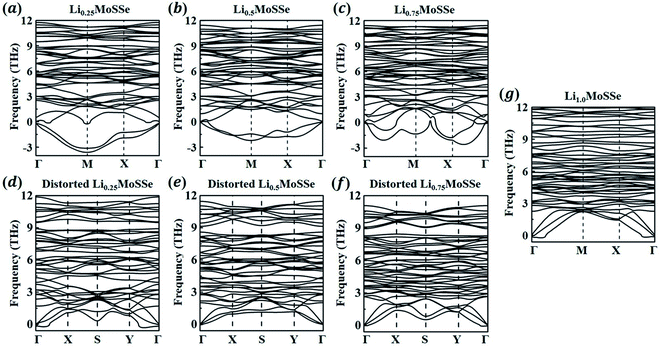 | ||
| Fig. 6 Phonon dispersion curves of 1S-LixMoSSe without (a–c and g) and with (d–f) lattice distortion perturbation at a Li concentration of x = 0.25–1.0. | ||
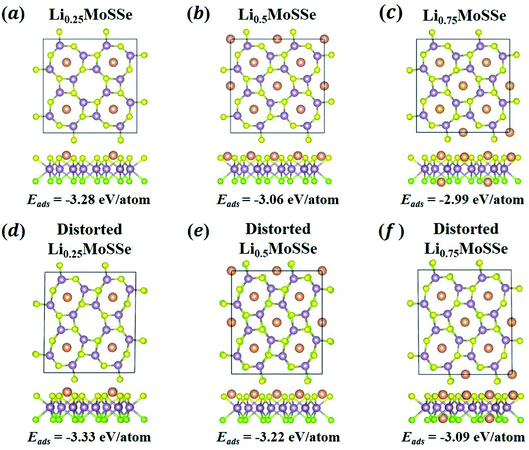 | ||
| Fig. 7 The atomic configurations and adsorption energies of 1S-LixMoSSe without (a–c) and with (d–f) lattice distortion perturbation at a Li concentration of x = 0.25, 0.5 and 0.75. | ||
Based on the calculated formation energies of 1S-LixMoSSe, we predict the open cell voltage (OCV) profile as a function of Li concentration. Fig. 5(e) shows that lattice distortion increases the initial OCV to ∼1.35 V and then drops gradually to 0.59 V with the increase of Li adsorption. When x is larger than 1.0, Eunitf gets increased, and the evaluated negative charge potential according to eqn (4) indicates the initiation of an unstable charging process. Therefore, 1S-MoSSe has a maximum Li concentration of x ∼ 1.0, while some TMD monolayers fail to stably adsorb Li atoms at extremely low x owing to the higher adsorption energy than the cohesive energy of the Li bcc crystal.18 However, such a maximum concentration as well as the corresponding specific capacity (Fig. 5(f)) is still lower than those of 1S-MoS2 (ref. 31) and 1H-MoSSe.35 Such a capacity difference may be due to the fact that the less symmetric structure of 1S-MoSSe causes the unstable charging process at lower Li concentration. In addition, electronic DOS calculations (see Fig. S3 in the ESI†) show that 1S-LixMoSSe remains metallic and still has good electronic conductivity upon Li adsorption.
4. Conclusions
In summary, we conduct DFT calculations to investigate the structural, thermodynamic and electrochemical behaviors of a square phase Janus MoSSe monolayer (1S-MoSSe) for LIB anode applications. Computational results show that Li adsorption is most energetically stable at O sites on both sides of 1S-MoSSe, followed by the TMo site and square site. The analysis of Li diffusion kinetics demonstrates that 1S-MoSSe possesses an acceptable surface Li mobility with an energy barrier in the range of 0.33 to 0.51 eV. Such Li migration behavior is also surface dependent and has faster diffusion kinetics on the S-layer side than on the Se-layer side. Energetic calculations of the charging (lithiation) process reveal that Li adsorption on 1S-MoSSe is thermodynamically stable and free of irreversible Li plating up to a Li concentration of x = 1.0, above which the lithiation process becomes unstable with a negative charging potential. Phonon calculations also exhibit that more Li adsorption (0.25 ≤ x ≤ 0.75) can trigger the structural instability of the lithiated monolayer, 1S-LixMoSSe, and be further suppressed by the lattice distortion of ring structures. Overall, 1S-MoSSe exhibits much better lithiation stability and capacitive behavior than other 2D TMD monolayers (i.e. 1H-MoS2 and 1H-MoSe2). However, the less symmetric nature of 1S-MoSSe is believed to destabilize Li adsorption at much smaller x than 1H-MoSSe does. This comprehensive study can provide fundamental insight into not only the electrochemical performance of other Janus TMD monolayers, but also the optimal design of high-performance TMD-based anodes for LIBs.Author contributions
XT – methodology, formal analysis, writing – original draft; HY – conceptualization, supervision, funding acquisition; WL – writing – review and editing; YL – supervision, writing – review and editing; ZG – writing – review and editing; MW – conceptualization, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11974003).References
- L. Peng, Y. Zhu, D. Chen, R. S. Ruoff and G. Yu, Two-Dimensional Materials for Beyond-Lithium-Ion Batteries, Adv. Energy Mater., 2016, 6, 1600025 CrossRef.
- Y. Xue, Q. Zhang, W. Wang, H. Cao, Q. Yang and L. Fu, Opening Two-Dimensional Materials for Energy Conversion and Storage: A Concept, Adv. Energy Mater., 2017, 7, 1602684 CrossRef.
- L. Ma, J. Wu, G. Zhu, Y. H. Lv, Y. Zhang and H. Pang, Recent Advances in Two-Dimensional Materials for Alkali Metal Anodes, J. Mater. Chem. A, 2021, 9, 5232–5257 RSC.
- B. Chen, D. Chao, E. Liu, M. Jaroniec, N. Zhao and S.-Z. Qiao, Transition Metal Dichalcogenides for Alkali Metal Ion Batteries: Engineering Strategies at the Atomic Level, Energy Environ. Sci., 2020, 13, 1096–1131 RSC.
- Q. Yun, L. Li, Z. Hu, Q. Lu, B. Chen and H. Zhang, Layered Transition Metal Dichalcogenide-Based Nanomaterials for Electrochemical Energy Storage, Adv. Mater., 2020, 32, 1903826 CrossRef CAS PubMed.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, Lithium Diffusion in Graphitic Carbon, J. Phys. Chem. Lett., 2010, 1, 1176–1180 CrossRef CAS.
- J. Billaud, F. Bouville, T. Magrini, C. Villevieille and A. R. Studart, Magnetically Aligned Graphite Electrodes for High-Rate Performance Li-Ion Batteries, Nat. Energy, 2016, 1, 16097 CrossRef CAS.
- M. Winter, J. O. Besenhard, M. E. Spahr and P. Novák, Insertion Electrode Materials for Rechargeable Lithium Batteries, Adv. Mater., 1998, 10, 725–763 CrossRef CAS.
- S. W. Lee, N. Yabuuchi, B. M. Gallant, S. Chen, B.-S. Kim, P. T. Hammond and Y. Shao-Horn, High-Power Lithium Batteries from Functionalized Carbon-Nanotube Electrodes, Nat. Nanotechnol., 2010, 5, 531–537 CrossRef CAS.
- L. Wang, Y. Ma, M. Yang and Y. Qi, Hierarchical Hollow MoS2 Nanospheres with Enhanced Electrochemical Properties Used as An Electrode in Supercapacitor, Electrochim. Acta, 2015, 186, 391–396 CrossRef CAS.
- X. Sun, P. Bonnick and L. F. Nazar, Layered TiS2 Positive Electrode for Mg Batteries, ACS Energy Lett., 2016, 1, 297–301 CrossRef CAS.
- K. Chang and W. Chen, L-Cysteine-Assisted Synthesis of Layered MoS2/Graphene Composites with Excellent Electrochemical Performances for Lithium Ion Batteries, ACS Nano, 2011, 5, 4720–4728 CrossRef CAS PubMed.
- K. Xu, N. Liao, M. Zhang and W. Xue, Atomic-Scale Investigation of Enhanced Lithium, Sodium and Magnesium Storage Performance from Defects in MoS2/Graphene Heterostructures, Nanoscale, 2020, 12, 7098–7108 RSC.
- J. Shuai, H. D. Yoo, Y. Liang, Y. Li, Y. Yao and L. C. Grabow, Density Functional Theory Study of Li, Na, and Mg Intercalation and Diffusion in MoS2 with Controlled Interlayer Spacing, Mater. Res. Express, 2016, 3, 064001 CrossRef.
- Y. Meng, Y. Zhao, D. Wang, D. Yang, Y. Gao, R. Lian, G. Chen and Y. Wei, Fast Li+ Diffusion in Interlayer-Expanded Vanadium Disulfide Nanosheets for Li+/Mg2+ Hybrid-Ion Batteries, J. Mater. Chem. A, 2018, 6, 5782–5788 RSC.
- Y. Li, Y. Lu, P. Adelhelm, M.-M. Titirici and Y.-S. Hu, Intercalation Chemistry of Graphite: Alkali Metal Ions and Beyond, Chem. Soc. Rev., 2019, 48, 4655–4687 RSC.
- C. Sun and D. J. Searles, Lithium Storage on Graphdiyne Predicted by DFT Calculations, J. Phys. Chem. C, 2012, 116, 26222–26226 CrossRef CAS.
- D. Wang, L.-M. Liu, S.-J. Zhao, Z.-Y. Hu and H. Liu, Potential Application of Metal Dichalcogenides Double-Layered Heterostructures as Anode Materials for Li-Ion Batteries, J. Phys. Chem. C, 2016, 120, 4779–4788 CrossRef CAS.
- J. Hao, J. Zheng, F. Ling, Y. Chen, H. Jing, T. Zhou, L. Fang and M. Zhou, Strain-Engineered Two-Dimensional MoS2 as Anode Material for Performance Enhancement of Li/Na-ion Batteries, Sci. Rep., 2018, 8, 2079 CrossRef PubMed.
- D. Datta, J. Li, N. Koratkar and V. B. Shenoy, Enhanced Lithiation in Defective Graphene, Carbon, 2014, 80, 305–310 CrossRef CAS.
- D. Datta, J. Li and V. B. Shenoy, Defective Graphene as a High-Capacity Anode Material for Na- and Ca-Ion Batteries, ACS Appl. Mater. Interfaces, 2014, 6, 1788–1795 CrossRef CAS PubMed.
- X. Sun, Z. Wang and Y. Q. Fu, Defect-Mediated Lithium Adsorption and Diffusion on Monolayer Molybdenum Disulfide, Sci. Rep., 2015, 5, 18712 CrossRef CAS PubMed.
- K. Yao, Z. Xu, J. Huang, M. Ma, L. Fu, X. Shen, J. Li and M. Fu, Bundled Defect-Rich MoS2 for a High-Rate and Long-Life Sodium-Ion Battery: Achieving 3D Diffusion of Sodium Ion by Vacancies to Improve Kinetics, Small, 2019, 15, 1805405 CrossRef PubMed.
- D. Ferguson, D. J. Searles and M. Hankel, Biphenylene and Phagraphene as Lithium Ion Battery Anode Materials, ACS Appl. Mater. Interfaces, 2017, 9, 20577–20584 CrossRef CAS PubMed.
- Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Phagraphene: A Low-Energy Graphene Allotrope Composed of 5–6–7 Carbon Rings with Distorted Dirac Cones, Nano Lett., 2015, 15, 6182–6186 CrossRef CAS PubMed.
- B. Jang, J. Koo, M. Park, H. Lee, J. Nam, Y. Kwon and H. Lee, Graphdiyne as A High-Capacity Lithium Ion Battery Anode Material, Appl. Phys. Lett., 2013, 103, 263904 CrossRef.
- H. Shang, Z. Zuo, L. Yu, F. Wang, F. He and Y. Li, Low-Temperature Growth of All-Carbon Graphdiyne on a Silicon Anode for High-Performance Lithium-Ion Batteries, Adv. Mater., 2018, 30, 1801459 CrossRef PubMed.
- S. Najmaei, Z. Liu, W. Zhou, X. Zou, G. Shi, S. Lei, B. I. Yakobson, J.-C. Idrobo, P. M. Ajayan and J. Lou, Vapour Phase Growth and Grain Boundary Structure of Molybdenum Disulphide Atomic Layers, Nat. Mater., 2013, 12, 754–759 CrossRef CAS PubMed.
- A. M. van der Zande, P. Y. Huang, D. A. Chenet, T. C. Berkelbach, Y. You, G.-H. Lee, T. F. Heinz, D. R. Reichman, D. A. Muller and J. C. Hone, Grains and Grain Boundaries in Highly Crystalline Monolayer Molybdenum Disulphide, Nat. Mater., 2013, 12, 554–561 CrossRef CAS PubMed.
- Z. Zhang, X. Zou, V. H. Crespi and B. I. Yakobson, Intrinsic Magnetism of Grain Boundaries in Two-Dimensional Metal Dichalcogenides, ACS Nano, 2013, 7, 10475–10481 CrossRef CAS PubMed.
- G. Barik and S. Pal, 2D Square Octagonal Molybdenum Disulfide: An Effective Anode Material for LIB/SIB Applications, Adv. Theory Simul., 2020, 3, 2000157 CrossRef CAS.
- Y. C. Cheng, Z. Y. Zhu, M. Tahir and U. Schwingenschlögl, Spin-Orbit–Induced Spin Splittings in Polar Transition Metal Dichalcogenide Monolayers, Europhys. Lett., 2013, 102, 57001 CrossRef.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, Janus Monolayer Transition-Metal Dichalcogenides, ACS Nano, 2017, 11, 8192–8198 CrossRef CAS PubMed.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Janus Monolayers of Transition Metal Dichalcogenides, Nat. Nanotechnol., 2017, 12, 744–749 CrossRef CAS PubMed.
- C. Shang, X. Lei, B. Hou, M. Wu, B. Xu, G. Liu and C. Ouyang, Theoretical Prediction of Janus MoSSe as a Potential Anode Material for Lithium-Ion Batteries, J. Phys. Chem. C, 2018, 122, 23899–23909 CrossRef CAS.
- Y. Zhang, H. Ye, Z. Yu, Y. Liu and Y. Li, First-Principles Study of Square Phase MX2 and Janus MXY (M = Mo, W; X, Y = S, Se, Te) Transition Metal Dichalcogenide Monolayers under Biaxial Strain, Phys. E, 2019, 110, 134–139 CrossRef CAS.
- X. Lai, Y. Zhang, Y. Zheng, X. Xiang, H. Ye, W. Liu and Y. Liu, Catalytic Activity for Hydrogen Evolution Reaction in Square Phase Janus MoSSe Monolayer: A First-Principles Study, Phys. E, 2021, 126, 114485 CrossRef CAS.
- Z. Wang, 2H → 1T′ Phase Transformation in Janus Monolayer MoSSe and MoSTe: An Efficient Hole Injection Contact for 2H-MoS2, J. Mater. Chem. C, 2018, 6, 13000–13005 RSC.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using A Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- D. L. Cooper, J. Gerratt and M. Raimondi, Applications of Spin-Coupled Valence Bond Theory, Chem. Rev., 1991, 91, 929–964 CrossRef CAS.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- D. Alfè, PHON: A Program to Calculate Phonons Using the Small Displacement Method, Comput. Phys. Commun., 2009, 180, 2622–2633 CrossRef.
- M. K. Aydinol, A. F. Kohan, G. Ceder, K. Cho and J. Joannopoulos, Ab Initio Study of Lithium Intercalation in Metal Oxides and Metal Dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1354–1365 CrossRef CAS.
- C. Ataca, H. Şahin and S. Ciraci, Stable, Single-Layer MX2 Transition-Metal Oxides and Dichalcogenides in a Honeycomb-Like Structure, J. Phys. Chem. C, 2012, 116, 8983–8999 CrossRef CAS.
- Y. Ma, L. Kou, X. Li, Y. Dai, S. C. Smith and T. Heine, Quantum Spin Hall Effect and Topological Phase Transition in Two-Dimensional Square Transition-Metal Dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085427 CrossRef.
- Z. Wang and G. Shao, High-Capacity Cathodes for Magnesium Lithium Chlorine Tri-Ion Batteries through Chloride Intercalation in Layered MoS2: A Computational Study, J. Mater. Chem. A, 2018, 6, 6830–6839 RSC.
- Z. Li, X. Mu, Z. Zhao-Karger, T. Diemant, R. J. Behm, C. Kübel and M. Fichtner, Fast Kinetics of Multivalent Intercalation Chemistry Enabled by Solvated Magnesium-Ions into Self-Established Metallic Layered Materials, Nat. Commun., 2018, 9, 5115 CrossRef PubMed.
- Y. Cheng, A. Nie, Q. Zhang, L.-Y. Gan, R. Shahbazian-Yassar and U. Schwingenschlogl, Origin of the Phase Transition in Lithiated Molybdenum Disulfide, ACS Nano, 2014, 8, 11447–11453 CrossRef CAS.
- M. Mortazavi, C. Wang, J. Deng, V. B. Shenoy and N. V. Medhekar, Ab Initio Characterization of Layered MoS2 as Anode for Sodium-Ion Batteries, J. Power Sources, 2014, 268, 279–286 CrossRef CAS.
- Q. Huang, X. Li, M. Sun, L. Zhang, C. Song, L. Zhu, P. Chen, Z. Xu, W. Wang and X. Bai, The Mechanistic Insights into the 2H-1T Phase Transition of MoS2 upon Alkali Metal Intercalation: From the Study of Dynamic Sodiation Processes of MoS2 Nanosheets, Adv. Mater. Interfaces, 2017, 4, 1700171 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Figures. See DOI: 10.1039/d1na00112d |
| This journal is © The Royal Society of Chemistry 2021 |