Open Access Article
Open Access ArticleDynamics in hydrated inorganic nanotubes studied by neutron scattering: towards nanoreactors in water†
Sophie
Le Caër
 *a,
Marie-Claire
Pignié
a,
Quentin
Berrod
*a,
Marie-Claire
Pignié
a,
Quentin
Berrod
 b,
Veronika
Grzimek
c,
Margarita
Russina
b,
Veronika
Grzimek
c,
Margarita
Russina
 c,
Cédric
Carteret
d,
Antoine
Thill
c,
Cédric
Carteret
d,
Antoine
Thill
 a,
Jean-Marc
Zanotti
a,
Jean-Marc
Zanotti
 e and
José
Teixeira
e and
José
Teixeira
 e
e
aNIMBE, UMR 3685 CEA, CNRS, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France. E-mail: sophie.le-caer@cea.fr
bCNRS, CEA, Université Grenoble Alpes SyMMES, 38000 Grenoble, France
cHelmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, 14109 Berlin, Germany
dUniversité de Lorraine, CNRS, LCPME, 54000 Nancy, France
eLaboratoire Léon Brillouin, CEA-CNRS (UMR-12), CEA Saclay, Université Paris-Saclay, 91191 Gif-sur-Yvette Cedex, France
First published on 21st December 2020
Abstract
Water dynamics in inorganic nanotubes is studied by neutron scattering technique. Two types of aluminosilicate nanotubes are investigated: one is completely hydrophilic on the external and internal surfaces (IMO-OH) while the second possesses an internal cavity which is hydrophobic due to the replacement of Si–OH bonds by Si–CH3 ones (IMO-CH3), the external surface being still hydrophilic. The samples have internal radii equal to 7.5 and 9.8 Å, respectively. By working under well-defined relative humidity (RH) values, water dynamics in IMO-OH was revealed by quasi-elastic spectra as a function of the filling of the interior of the tubes. When one water monolayer is present on the inner surface of the tube, water molecules can jump between neighboring Si–OH sites on the circumference by 2.7 Å. A self-diffusion is then measured with a value (D = 1.4 × 10−5 cm2 s−1) around half of that in bulk water. When water molecules start filling also the interior of the tubes, a strong confinement effect is observed, with a confinement diameter (6 Å) of the same order of magnitude as the radius of the nanotube (7.5 Å). When IMO-OH is filled with water, the H-bond network is very rigid, and water molecules are immobile on the timescale of the experiment. For IMO-OH and IMO-CH3, motions of the hydroxyl groups are also evidenced. The associated relaxation time is of the order of 0.5 ps and is due to hindered rotations of these groups. In the case of IMO-CH3, quasi-elastic spectra and elastic scans are dominated by the motions of methyl groups, making the effect of the water content on the evolution of the signals negligible. It was however possible to describe torsions of methyl groups, with a corresponding rotational relaxation time of 2.6 ps. The understanding of the peculiar behavior of water inside inorganic nanotubes has implications in research areas such as nanoreactors. In particular, the locking of motions inside IMO-OH when it is filled with water prevents its use under these conditions as a nanoreactor, while the interior of the IMO-CH3 cavity is certainly a favorable place for confined chemical reactions to take place.
1 Introduction
Reconciling human development and the preservation of environment is one of the most difficult tasks researchers will have to face in the coming years. This will be all the more difficult with the need to reduce the use of fossil fuels, find alternatives for rare elements and manage resources in a more sustainable way. In chemistry, this requires the development of functional catalytic materials made with abundant elements. In addition, these new materials will have to be more selective and consume less energy. Among the active research directions, the use of nano-confined chemical reactions is promising.1–4 Indeed, when confined in a nanoreactor, structurally controlled interactions between the substrate and the guest molecules can modify chemical reactions. The goal is thus to have nanoreactors made from abundant materials, which would advantageously replace catalytic materials based on rare elements.Nanotubes appear as very promising to exploit those confinement effects.5,6 Indeed, they have huge specific surface areas with two distinct curved surfaces (internal and external). If reachable by reactants, the inside of nanotubes offers a well-defined limited space in which all (or most) guest molecules are influenced by local interactions. Finally, in order to act as an efficient and sustainable nanoreactor, a nanotube should be usable in water and reconcile confinement and accessibility, while its reactivity should be tunable.
Among the many nanotubes (NTs), natural or synthesized, imogolites match well these requirements. Chemically, they are aluminosilicates with the chemical formula (OH)3Al2O3Si(OH). They are therefore only composed of the most abundant elements on earth. They form very small open nanocylinders with a monodisperse diameter of about 2–3 nm, which is a highly confining environment, while remaining potentially accessible to molecules. The versatility of imogolites results from the possibility of modifying the chemical groups on the surface of the tubes without modifying their well-defined tubular geometry.7,8 In its standard form (IMO-OH), the tube wall consists of a single sheet of gibbsite (Al(OH)3) type, which is linked to isolated silanol groups on the inner surface. In this form, hydroxyl groups pave both internal and external surfaces. It is also possible to synthesize a hybrid form (IMO-CH3), whose chemical formula is (OH)3Al2O3Si(CH3). Hydrophobic –CH3 groups cover only the internal surface of the nanotubes, while the external surface remains hydrophilic. Noteworthy, the external surface (Al2-μOH groups) remains hydrophilic in both imogolites.
IMO-OH is very hygroscopic since –OH groups naturally form hydrogen bonds with the lone pairs of water molecules. However, the volume accessible to water within the tubes (especially along the radius) is too small to allow the formation of the tetrahedral network of hydrogen bonds, which is at the origin of the unique properties of the liquid. On the contrary, the local arrangement of water molecules and of their hydrogen bonds are largely imposed by the local density of the –OH groups or by the hydrophobicity of the methyl groups sitting on the internal surface of the NTs in the case of IMO-CH3. As a result, the properties of water inside the tubes are expected to be very different both from a normal liquid and from bulk water. This holds also for water present in the very small interstices between the tubes. IMO-OH could thus play an interesting role as nanoreactor for chemical reactions involving water only (water splitting, radiolysis…). To our knowledge, the accessibility of the internal cavity of IMO-OH for other molecules or ions in presence of water has not been described yet. IMO-CH3 has a hydrophobic internal cavity, accessible to small molecules.9,10 Moreover, water does almost not penetrate in IMO-CH3, even when the NTs are dispersed in water. As both imogolites can be dispersed in water, it is thus important to understand the structural and dynamical properties of confined water in these low-dimensional nanoreactors.
The first question deals with the water behavior in imogolites as a function of the water chemical potential. Previous studies by infrared spectroscopy11,12 of the water sorption revealed thus substantial differences between the number and strength of hydrogen bonds formed between water and OH groups on the surface of nanotubes, depending on the level of hydration. Noteworthy, different types of pores are found outside the NTs, according to their packing.11,12 When the NTs are closely packed in a 2D hexagonal phase, micropores are formed between the NTs assembled in bundles. Between the bundles, mesopores of various sizes are formed. While bonds formed by water outside the nanotubes do not depend on the nature of the internal surface (water fills gradually the external porosities of increasing size, as the relative humidity (RH) increases), there are substantial differences between water filling hydrophilic nanotubes and water that hardly penetrate the hydrophobic tube of the hybrid form of imogolite. In the latter case, water, present in tiny amount and not forming bonds with the internal surface, may generate enhanced 1-dimensional diffusion along the axis.12 In contrast, water adsorption in the IMO-OH NTs powder occurs since the lowest relative humidity (RH < 10%). From the measurements of the O–H stretching band, it was possible to describe different stages of the filling process of the interior of IMO-OH tubes:12 (i) formation, at first, of a strong H-bond network (RH < 3%), with 2D water patches initially formed on the walls of the NTs; (ii) water plugs filling gradually the center of the tubes (3% < RH < 46%); (iii) overall strengthening of the O–H bond network (RH > 46%). When the last water molecules fill the interior of the tubes, the H-bond network is more rigid than at the lowest RH values. Bearing this in mind, the purpose of the present work is to gain insight into the dynamics of water molecules in this confining geometry. To reach this goal, we have chosen to work with 3 RH values of interest, according to our previous infrared results:12 3, 11 and 43% and to compare IMO-OH and IMO-CH3 samples.
While the nature of the bonds formed by water molecules with other water molecules or with the walls of the NTs is well described by infrared or neutron spectroscopies, water dynamics, which is very important for confined chemical reactions, has to be obtained by other experimental techniques. Among them, femtosecond infrared spectroscopy,13–15 Field cycling NMR dispersion technique16 and inelastic neutron scattering techniques17 provide valuable data on the behavior of water, and on the specificities of confined vs. bulk water. Here, we have chosen to use incoherent quasi-elastic (QENS) and inelastic neutron scattering (INS) techniques to probe water dynamics at the molecular scale.
Incoherent neutron scattering probes directly individual motions of hydrogen atoms. It provides the ensemble average of the time correlation function of hydrogen atom positions, 〈ri(0)ri(t)〉, where ri(t) represents the position of atom i at time t and 〈…〉 denotes the ensemble average over all hydrogen atoms of the sample. The experiments measure the scattered intensity, I(θ,ω), as a function of the scattering angle, θ, and of the energy exchange, ω, between incident neutrons and hydrogen atoms. For each θ, there is a relation between momentum exchange, Q = ℏ(ki − kf) and ω, which allows the evaluation of the isotropic incoherent dynamic scattering function Sinc(Q,ω) ∝ (kf/ki)I(Q,ω), where ki and kf are the wave vectors of incident and scattered neutrons, respectively. Depending on the analyzed dynamic range and on instrumental energy resolution, different measurements can be performed:
(1) Quasi-elastic scattering (QENS) evaluates Sinc(Q,ω) around elastic scattering (ω = 0) in function of both Q and ω. The analysis assumes a convenient model of the motions of hydrogen atoms, which includes molecular dynamics. In the case of dense molecular liquids, it is common to use the jump diffusion model, which gives information about self-diffusion, D, and molecular residence time, τres, of diffusing molecules. With increasing Q, i.e. going from large to local length scales, measured relaxation times decrease from the hydrodynamic limit (Fick's law), 1/(DQ2) to τres.
(2) Inelastic scattering (INS) measures transitions between ground and excited states, the vibrational density of states, essentially in the intermolecular domain, corresponding to the far infra-red absorption spectroscopy. In contrast with the latter that depends on electromagnetic interaction with the electronic cloud, it is a direct measurement of the energy exchange with atomic nuclei.
(3) Elastic scans measure the temperature dependence of the scattering in a domain of energy narrower than the energy resolution of the instrument. Since no exchange of energy can be recorded in this energy range, no correlation time can be recovered. Nevertheless, from the exponential fall-off of the elastic intensity vs. Q2, one can derive an estimate of the spatial extent, the mean square displacement (MSD), of the atomic/molecular motions, which includes the amplitude 〈u2〉 of the Debye–Waller factor. MSD provides qualitative information about transitions, such as the onset of dynamic processes or phase transitions.
The combination of IR experiments and of water adsorption isotherms together with the present dynamic study will provide fundamental knowledge required to understand the reactivity within IMO-OH and IMO-CH3 nanoreactors.
2 Methods
2.1 Sample preparation
Natural imogolite (IMO-OH) was synthesized following methods inspired by Farmer et al.18,19 AlCl3 was dissolved in MilliQ water at a concentration of 2 mM together with tetraethoxysilane (TEOS) at a molar ratio Si/Al of 0.55. A slightly higher ratio than the stoichiometric Si/Al ratio (0.5) was used to prevent the formation of undesired hydroxyaluminum (gibbsite). Under continuous stirring, NaOH was slowly introduced in the solution at a rate of 0.5 mM min−1 until a molar ratio OH/Al of 2.0 was reached. The dispersion was stirred for 1 h after NaOH injection until the solution was completely clear. The suspension was then placed in an oven for 5 days at a temperature of 90 °C. After heating, the dispersion was concentrated by tangential ultrafiltration using 8 kDa membranes. The concentrated suspension was then dialyzed against Milli-Q water.Hybrid imogolite (IMO-CH3) was prepared using a protocol inspired by Bottero et al.7 Aluminum-tri-sec-butoxide (ASB) was added to 800 mL of an HClaq solution (40 mM) with an HCl/Al molar ratio of 0.5 and stirred for 1 h. Trimethoxymethylsilane was slowly added to obtain a Si/Al molar ratio of 0.6. As for IMO-OH, this molar ratio is higher than the stoichiometric ratio of 0.5 to minimize the production of hydroxyaluminum by-products.20 The dispersion was then heated in an oven for 5 days at 90 °C. Lastly, the dispersion was dialyzed against Milli-Q water using a 8 kDa membrane.
In order to obtain powders, both types of imogolite dispersions were freeze-dried at −57 °C under vacuum (0.035 mbar) using a Christ BETA 1–8 LDplus freeze-dryer. Samples were frozen in a freezer overnight. A drying treatment was first applied in order to have the same starting state for all samples. The imogolite powder was heated at 220 °C for IMO-OH and at 110 °C for IMO-CH3 for 12 h. Desiccators containing saturated salt solutions, were then used in order to impose the relative humidity (RH) value (silica gel: 3%, LiCl saturated solution: 11%, K2CO3 saturated solution: 43%). The powders were then stored until the equilibrium was reached. Sample weight stability during at least 3 weeks attested the equilibrium state in the desiccators. The samples were then transferred into the cells in aluminum specially designed for the neutron experiments. During this procedure, we worked in a glove box under argon (for samples equilibrated at 3% RH) or in a cold room (for samples equilibrated at the other RH values) in order to prevent any change in the hydration state of the powder. Nevertheless, this is difficult for the dry powder (RH = 0%) which, consequently, could not be studied.
Both imogolites were then characterized by Small Angle X-ray Scattering (SAXS) performed at a wavelength of 1.542 Å (Cu Kα) under vacuum with a Xeuss 2.0 apparatus (Xenocs).11,12 Briefly, IMO-CH3 presents clear oscillations in the large angle region characteristic of a well-defined cylindrical shape. The angular position of these oscillations is consistent with an internal radius of 9.8 Å and a wall thickness of 5.5 Å. The curves measured for IMO-OH reveal an internal radius of 7.5 Å and a wall thickness of 5.5 Å.
Complete water vapor adsorption–desorption isotherms at 25 °C were obtained using a MicrotracBEL Belsorp-Max volumetric adsorption analyzer equipped with three pressure sensors (133 kPa, 1.33 kPa and 13.3 Pa). In the case of the water vapor isotherm, a long acquisition time (7 days per isotherm) was required because of the slow equilibrium kinetics. Isotherms were acquired for IMO-OH and IMO-CH3. Samples were initially outgassed at 100 °C under vacuum (∼3 × 10−6 Pa) during 20 hours.
2.2 Instruments NEAT and IN6-SHARP
Incoherent quasielastic and inelastic data were collected at the spectrometer IN6-SHARP at ILL, Grenoble, France (run by the Laboratoire Léon Brillouin). Elastic scans were performed at the spectrometer NEAT of the Helmholtz Zentrum Berlin, Germany.21,22 Both IN6 and NEAT are time-of-flight spectrometers using cold neutrons and monochromatic incident beams.In our experiments, the resolution of IN6 was 70 μeV (full width at half maximum, FWHM), at the wavelength 5.1 Å. The elastic momentum transfer covered the range 0.38 to 2.01 Å−1.
Elastic scans were recorded at NEAT. We used the wavelength 8 Å corresponding to the resolution 28 μeV (FWHM). The covered momentum transfer extended from 0.15 to 1.55 Å−1. Each sample was cooled continuously from room temperature down to 20 K at a rate of 40 K h−1. Along this regular cooling, data were accumulated for periods of 20 minutes, representing 18 experimental points. After, the sample was heated gradually from 20 K until room temperature at 65 K h−1 stopping for one hour at intermediate stages, 20, 50, 120, 200 and 230 K. The precision on the temperatures was better than 1 K.
For all experiments, samples in the form of powders filling rectangular aluminum cells (3 × 4 cm2) were adapted to the size of the incident neutron beam. The global thickness of the powders was in average 1.5 mm. The mass of all samples was of the order of 1 g. Samples were then introduced by a can inside a cryostat. The cells were placed in a position forming 135° with the incident neutron beam, corresponding to a reduction of the intensity at intermediate angles.
3 Results and discussion
3.1 Behavior of imogolite nanotubes with water
The water uptake in natural and hybrid imogolites was described in a previous work using thin films.11,12,23 In the present study, the water sorption isotherms are measured on freeze-dried powders, which have been manually ground before complete drying (Fig. 1). For IMO-CH3, the interior of the tubes remains globally free from water molecules. This is even true for IMO-CH3 NTs fully immersed in water.24 Water adsorption mainly occurs at the outer surface of the tubes where Al2-μOH groups are present. Water progressively fills the porosities of increasing size when RH increases as shown by the progressive mass uptake (Fig. 1). In contrast, water adsorption in the IMO-OH NTs powder is steeper and occurs at the lowest RHs (<10%). This part is mainly explained by the filling of the internal cavity12 whereas the pores between the tubes or the bundles are progressively filled when RH increases as in the case of IMO-CH3. However, the different slopes for IMO-OH and IMO-CH3 of mass uptake at elevated RHs reveal a different powder texture (Fig. 1).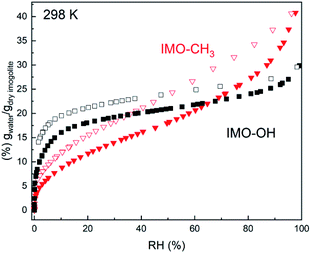 | ||
| Fig. 1 Water vapor adsorption (full symbols)/desorption (empty symbols) isotherms of IMO-OH (black squares) and of IMO-CH3 (red triangles). | ||
With an internal radius of roughly 0.6 nm, the internal microporous volume would be 0.12 cm3 g−1. Upon desorption, a significant amount of water 0.13 g g−1 remains adsorbed in IMO-OH, even at RH = 0%. This is in good agreement with the amount of internal water and confirms the known result that drastic drying conditions are required to remove internal water.25,26
The water content inside and outside the nanotubes is easily obtained for IMO-CH3 as it is known that the vast majority of the water is adsorbed outside the nanotubes. So the external water content is directly obtained from the adsorption curve. In the case of IMO-OH, it is more difficult to discriminate between the internal and external water content as a function of RH. This distinction has to rely on hypothesis or modeling of the adsorption isotherm.
The slope of the water sorption isotherm in the intermediate RH between 10 and 80% is mainly controlled by the size distribution of the mesopores and their progressive filling with capillary condensation. The modelling of this phenomenon is generally performed using a DFT approach. In such approach, adsorption kernels describing the adsorption and capillary condensation inside mesopores of various sizes is used to determine the pore size distribution.27 Such kernels have to be adapted for each pore geometry, material and gas type. In absence of such a kernel for the complex case of water adsorption inside and outside flexible inorganic nanotubes bundles, we have used a simpler approach based on a modified version of the Or and Tuller model.28 The details of the model are presented in the ESI.† From this model, an estimate of the proportion of water present inside or outside the NTs can be obtained.
3.2 Hydrogen populations in the studied samples
Because the incoherent cross section of hydrogen atoms is very large, the total scattered intensity is almost exclusively due to individual hydrogen motions and is independent of the scattering angle, thus of the momentum transfer Q, except for the Debye–Waller factor. In our samples, besides mobile hydration water molecules, both IMO-OH and IMO-CH3 samples contain a large number of hydrogen atoms. Therefore, the contributions to the scattered intensity come not only from the variable amount of hydration water but also from the –OH and –CH3 groups. More precisely, a distinction must be made between the OH groups located outside or inside the nanotubes in IMO-OH. Both types can form hydrogen bonds with water molecules. From water adsorption isotherms recorded for IMO-OH and IMO-CH3 (Fig. 1) and from the modelling of these isotherms (ESI with details of the modeling and Fig. S1–S3†), the relative amount of each family of hydrogen atoms can be calculated at each relative humidity for IMO-OH and IMO-CH3, respectively (Tables 1 and 2). TEM images of dried suspensions of imogolites are provided in Fig. S4 in the ESI.† From Fig. S2 in the ESI,† the proportion of water outside and inside the tubes in IMO-OH can also be estimated (Table 1). From Table 1 and Fig. S2 in the ESI,† it is clear that we mainly study the behavior of water confined inside the nanotubes in the case of IMO-OH. Note, as evidenced by the IMO-OH isotherms that the samples equilibrated at 11% and 43% RH are quite similar (Table 1). In the case of IMO-CH3, water is only located outside the tubes. As for all situations of confinement, the mobility of water molecules depends of course on their interaction with the walls of the nanotubes, in particular on the formation of hydrogen bonds with hydroxyl groups.| Hydration (RH%) | % H from H2O molecules (internal and external water) | % H from OH groups (1/4 inside, 3/4 outside the nanotubes) |
|---|---|---|
| Dry sample | 0 | 100 |
| 3% | 41.2 (72%) | 58.8 |
| 11% | 51.7 (76%) | 48.3 |
| 43% | 58.5 (61%) | 41.5 |
| Hydration (RH%) | % H from H2O molecules (external water) | % H from OH groups (outside the tubes) | % H from CH3 groups (inside the tubes) |
|---|---|---|---|
| Dry sample | 0 | 50 | 50 |
| 3% | 17.2 | 41.4 | 41.4 |
| 11% | 26.4 | 36.8 | 36.8 |
| 43% | 42.0 | 29.0 | 29.0 |
3.3 Vibrational density of states
The energy distribution of the scattered intensity, f(ω), can be written:| f(ω) ∝ exp(−〈u2〉Q2/3)(ω/Q2)χ′′(ω) | (1) |
| χ′′(ω) = Sinc(Q,−ω)/n(ω) |
| n(ω) = [exp(ω/kBT) − 1]−1 |
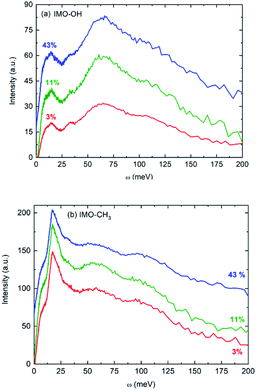
Fig. 2 presents f(ω) for all the samples. In first approximation, they represent the vibrational density of states of hydrogen atoms. Noteworthy, for one given sample, all vibrational density of states look very similar, whatever the RH value is.
The main features in IMO-OH (Fig. 2a) are located around 14, 32, 64 with also a contribution around 107 meV, while they are found at 6 (shoulder), 17, 55 and 97 meV in IMO-CH3 (Fig. 2b). In IMO-OH (Fig. 2a), the band centered at 32 meV can be speculatively assigned to hydrogen-bond stretching modes parallel to the line formed by the hydrogen bond,29,30 while the broad band around 64 meV is attributed to the librational band of water.31 The position of the latter band is consistent with that in germanium-based imogolite nanotubes which was reported to be about 70 meV.32
The contribution around 107 meV can be understood as hydrogen motions arising from vibrations of the SiO4 network. Indeed, Raman spectroscopy evidences a corresponding band at 860 cm−1 described as a symmetric stretching mode of the SiO4 tetrahedra.33 In IMO-CH3, we assign tentatively the band observed at 55 meV to libration motions of the –OH groups and of water present outside the nanotubes. In IMO-OH samples, this band merges the very intense librational band of water. Note that, as in IMO-OH, a weak contribution may be present around 31 meV whose assignment is the same as described above. In IMO-CH3, the shoulder detected around 6 meV is assigned to transverse collective modes due to intermolecular OOO bending.30,34,35 An extreme confinement limits the amplitude of this motion, thus the intensity of this spectral line. Indeed, as pointed out by the water adsorption simulations (Fig. S2 and S3 in the ESI†), water is strongly confined in the 3–43% RH range in both imogolites. In IMO-OH samples and due to the filling of the nanotube with water, the shoulder at 6 meV merges with the component at 14 meV, which we will discuss later. The band detected at 17 meV in IMO-CH3 is due to torsional modes of the methyl group. Indeed, this mode was for instance already reported around 23 meV in glassy polyisoprene36 and around 18 meV in N-methylacetamide (τ(N-CH3) mode).37 Lastly, the 97 meV can be assigned, based on infrared spectroscopy, to the coupling between the Si–C stretching mode and the methyl rocking mode for the Si–CH3 group.38 The component at 14 meV is detected in IMO-OH and not in IMO-CH3. Note that a peak was detected at a similar frequency (15 meV) in the case of germanium-imogolite (IMO-GeOH).32 This peak was explained as being due to a stretching-like translational mode of water molecules bonded to internal –OH groups.32 The same attribution can be proposed here.
Noteworthy, the spectra measured for both imogolite samples are clearly different. One distinct feature lies in the 6 meV component, which is clearly detected in the spectra of IMO-CH3 samples only. This is expected because, for a given RH value, there are more bonds formed between water molecules in IMO-CH3 samples as compared to IMO-OH than bonds between water and the –OH groups. It was indeed calculated that inside IMO-OH nanotubes, water molecules interact stronger with surface hydroxyl groups than with other adsorbed water molecules, whereas it is the opposite outside the nanotubes.39 This can also be linked to the fact that the SiOH groups are more hydrophilic than the Al2-μOH groups, leading to stronger H-bond in the first case and thus to a low mobility of the water molecules along the circumference of the tube.39
3.4 Elastic scans
Elastic scans performed as a function of temperature provide information about the Debye–Waller factor and about the amount of hydrogen atoms for which the slow dynamics falls inside the instrumental resolution. Fig. 3 represents this scattered intensity summed over all scattering angles. It includes the elastic component due to immobile atoms, the small contribution of coherent scattering and a small part of the quasi-elastic intensity. At very low temperature, only vibrational motion, described by the Debye–Waller factor, is activated and contributes to the temperature dependence of the scattered intensity; 〈u2〉 is proportional to temperature. With increasing temperature, one observes the onset of different motions in addition to vibrations that lead to more or less sharp decrease of the intensity of elastic scans plotted as a function of temperature. As in the case of Fig. 2, the evolution of the normalized elastic intensity looks very similar for each sample, at the various RH values studied, but is clearly different in IMO-OH as compared to IMO-CH3.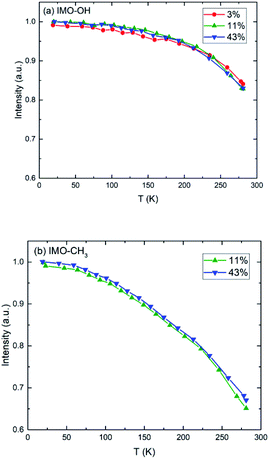 | ||
| Fig. 3 Normalized elastic intensity plotted versus temperature for (a) IMO-OH samples; (b) IMO-CH3 samples. The RH values at which the samples are equilibrated, are indicated. | ||
As expected, we observe, at increasing temperatures, a regular decrease of the elastic intensity due to thermal activation of vibration modes that make the delocalization of protons more prominent. The onset of rotational motions of water molecules followed by self-diffusion is marking a transition observed around 200 K. The relative decrease of intensity between 0 and 300 K is smaller for IMO-OH samples (18%) than for IMO-CH3 samples (35%). This is due to the dynamics of methyl groups, which are active since the lowest temperatures.
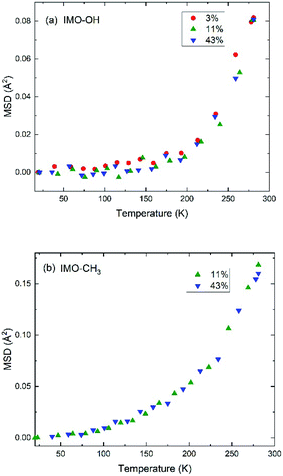
It is however more significant to analyze the temperature dependence of the mean square displacement (MSD), which includes the delocalization described by the Debye–Waller factor and slow motions seen as elastic (Fig. 4). It is obtained from logarithmic plots of the intensity scattered elastically in function of the square of the momentum transfer. In these plots, deviations from the straight line that corresponds to the Debye–Waller component are due to motions that become active with increasing temperature. In practice, the plots are done in function of the scattering angle.
Within the accuracy of the data, for the IMO-OH samples, we observe a gradual small increase of the MSD up to 150–200 K, followed by a sharp increase that corresponds to the onset of the mobility of water molecules, both local motions and self-diffusion. This result is also shown in Fig. S5 in ESI† where the quasi-elastic intensity integrated near the elastic line ([0.025![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.075] meV) drastically increases from 200 K in the case of IMO-OH. This observation is consistent with many situations where water is confined. Indeed, it was previously shown in the case of one water layer adsorbed on the surface of a Vycor (porous silica) glass that, starting from an amorphous state of water at low temperature, different phenomena take place starting from 160 K: formation of low density patches of 4 hydrogen-bonded water molecules, then percolation and total invasion of the surface by them.40
0.075] meV) drastically increases from 200 K in the case of IMO-OH. This observation is consistent with many situations where water is confined. Indeed, it was previously shown in the case of one water layer adsorbed on the surface of a Vycor (porous silica) glass that, starting from an amorphous state of water at low temperature, different phenomena take place starting from 160 K: formation of low density patches of 4 hydrogen-bonded water molecules, then percolation and total invasion of the surface by them.40
In the case of IMO-CH3 samples, the increase of MSD with increasing temperature starts at low temperature (50 K) due to rotations of methyl groups and is consistent with similar observations performed in polymer systems at about the same temperature.36,41 The relatively small amount of water molecules (see Fig. 1) makes it impossible to observe the changes in this curve due to the dynamics of confined water. The temperature dependence of the MSD is dominated by the contribution of methyl groups, visible since the lowest temperatures.
In all cases, the largest contribution to the elastic scans is due to vibrations of the –OH or –CH3 groups and to part of the water molecules, which include large amplitudes vibrational motions. This accounts for the fact that all curves look very similar.
3.5 Quasi-elastic spectra
Quasi-elastic spectra of all samples were measured at room temperature at 14 different angles. The analysis was performed by the fitting program QENSH42 in the energy exchange domain −2.0 < ω < 1.0 meV.As pointed out above, the scattered intensity is almost exclusively due to hydrogen atoms of water and of hydroxyl groups. In the case of IMO-CH3 samples, it is mainly due to methyl groups. A more detailed balance should discriminate between OH groups on the internal and on the external surface of the nanotubes. To each group correspond a different motion and different relaxation times but it is impossible to establish a global model, which would include a too large number of parameters. Because our main purpose is the analysis of the differences between samples with different RH, we assume average motions of hydrogen atoms other than those of water. For each population i of hydrogen atoms, we can thus write:
| Siinc(Q,ω) = Ai(Q)δ(ω) + [1 − Ai(Q)]Li(Q,ω) | (2) |
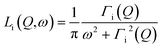 | (3) |
It includes an elastic component and a Lorentzian, Li(Q,ω), with half-width at half maximum (HWHM) equal to Γi(Q). In the cases i refers to hydroxyl or methyl groups, the intensity of the elastic component, Ai(Q), is the Elastic Incoherent Structure Factor (EISF) of the motions of hydrogens in OH or CH3 groups, respectively. In the case of hydrogen atoms of water molecules, Awater(Q)δ(ω) takes into account water molecules with dynamics falling under the instrumental resolution seen, consequently, like immobile molecules.
In the case of IMO-OH samples, Sinc(Q,ω) includes the contributions of OH groups and of water:
| Sinc(Q,ω) ∝ [NOHAOH(Q) + NwaterAwater(Q)]δ(ω) + NOH[1 − AOH(Q)]LOH(Q,ω) + Nwater[1 − Awater(Q)]Lwater(Q,ω) | (4) |
| Sinc(Q,ω) × R(Q,ω) ∝ [A(Q)δ(ω) + B(Q)LOH(Q,ω) + C(Q)Lwater(Q,ω)] × R(Q,ω) | (5) |
Lorentzian functions are associated to relaxation times τi = ℏ/Γi. In the case of diffusive motions, τi = 1/(DQ2) yields the self-diffusion D at scale 1/Q.
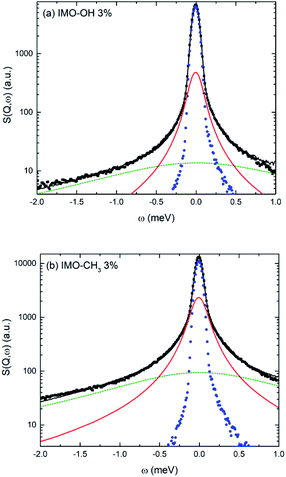
Fig. 5 shows an example of data fitting for both IMO-OH and IMO-CH3 equilibrated at 3% RH, for Q = 1.75 Å−1. The three components are well-separated enabling the extraction of two relaxation times without ambiguity. Because of localized motions of hydrogen atoms in hydroxyl or methyl groups, the elastic components are very intense.
Fig. 6 depicts, for each IMO-OH sample, the fitted linewidth of the narrowest Lorentzian, Γwater, as a function of the square of the momentum transfer, Q2. In order to better visualize the differences between the samples, all the data are also represented on the same figure in Fig. S6 in ESI.†
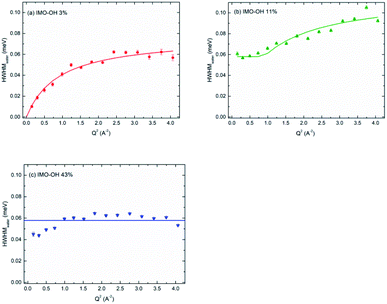 | ||
| Fig. 6 HWHM of the narrow Lorentzian component plotted versus Q2, for the IMO-OH samples equilibrated at: (a) 3%; (b) 11% and (c) 43% RH value. | ||
In the case of the less hydrated sample (IMO-OH equilibrated at 3% RH) for which a water monolayer is formed on the inner surface of imogolite,12 the Q dependence of Γwater is well described by a classical model of translational diffusion (Fig. 6a). It reproduces conveniently the diffusive axial motions of water inside the nanotubes (see the discussion related to Fig. 2), likely on the surface of the internal walls, given the small amount of water present outside the nanotubes and that is neglected here.
The slope at origin of Γwater(Q2) gives a value of the self-diffusion coefficient D = 1.4 × 10−5 cm2 s−1. Its value is roughly one-half the value of self-diffusion in bulk water at 298 K (2.3 × 10−5 cm2 s−1)43–45 and is comparable to the value measured in bulk water at 280 K.45 This slowdown is partly due to excluded volume effects and to a strengthening of the H-bond network. At 300 K, this coefficient has for instance been reported to be equal to a few 10−6 cm2 s−1 in hydrated zeolites46 or in hydrated synthetic clay minerals, which are typical 2D confining systems.47 It is however similar to that of water in highly ordered porous silica (MCM-41).48 The value we measure here is four times higher than the value calculated in simulations, for a similar water content.49 However, simulations consider ideal nanotubes. This may account for the discrepancy observed here with our real systems.
At large values of Q, Γwater deviates from the linear dependence on Q2, which characterizes the Fick's law for self-diffusion. The simplest model of translational diffusion at the molecular length scale assumes the molecule trapped in a cage formed by neighboring molecules during a residence time τres, then jumping a distance L in a very short time.50 The resulting Q dependence of Γwater is:
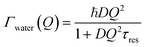 | (6) |
Fig. 6a shows that, in the case of IMO-OH equilibrated at 3% RH, the asymptotic value at large Q is τres = 9 ps, from which, we can derive the average length of a jump equal to 2.7 Å. For the purpose of comparison, at room temperature, the residence time in water is equal to 1.25 ps while the average jump length is 1.3 Å.51 However, it may be more pertinent to compare the dynamics of confined water at room temperature to that of bulk water at −10 °C, for which τres = 7 ps.52
The observed τres is even larger certainly because of the surface character of the diffusion and because of the relatively large distance between hydrophilic sites on the surface of the NTs. Indeed, in IMO-OH nanotubes, there are two characteristic distances between two SiOH groups on the internal wall. The short one (O⋯O distance) is perpendicular to the axis of the tube and is of the order of 3.3 Å.49 The large one (O⋯O distance) makes an angle of about 30° with the axis of the tube and is equal to 4.6 Å.49 Noteworthy, H⋯H distances have to be considered for water jumps. Nevertheless, at least the 3.3 Å value is compatible with the calculated water jump between two adjacent SiOH groups. Indeed, due to libration, the internal HOH angle is flexible and it can fluctuate. For instance, in bulk water, the jump distance at room temperature is 1.3 Å (ref. 51) to be compared to the distance between two adjacent hydrogen atoms, which is equal to 1.6 Å.53 From the composition, at 3% RH value, the available water molecules inside the nanotube form hydrogen bonds with about 1/2–1/3 of available OH sites. Therefore, the measured quasi-elastic spectrum shows that water molecules can jump between neighboring sites on the circumference of the tube, which corresponds to the measured self-diffusion due to molecular jumps, contrary to rotational jumps observed in bulk water. Contrary to other findings, the dynamical measurements evidence that water is not immobile at this low RH value.32
At 11% RH value (Fig. 6b), water plugs fill gradually the center of the tubes12 and the H-bond network is stronger, making diffusion difficult over long distances. Indeed, in this case, the linewidth Γwater goes to a plateau at low values of Q. This situation is typical of strong confinement. It is well-described by the model of F. Volino and A. J. Dianoux.54 The fit gives a local diffusion of the order of Dloc = 2.0 × 10−5 cm2 s−1 and a radius a of the equivalent sphere of confinement that can be obtained from the expression Γplateau = Γwater(Q = 0) = 4.333 ℏDloc/a2, where Γplateau = 0.058 meV. We obtain a value 2a of the order of 6 Å, compatible with the radius of the tube (7.5 Å), although slightly smaller. Noteworthy, the local diffusion Dloc corresponds to water diffusion in absence of confinement. The same model was applied in totally hydrated Vycor glass,55 and similar values as ours were reported.55
For the IMO-OH sample equilibrated at 43% RH (Fig. 6c), the width of the narrow Lorentzian is almost Q independent, meaning that only local motions are possible. A precise description of the motions is not possible because it should take into account the formation of hydrogen bonds between water molecules. We can only deduce a relaxation time of the order of 11 ps that could correspond to tumbling motions. This implies that in the most hydrated sample, water is immobile on the time scale of the experiments. This apparently surprising result is due to the fact that, at this RH value, the interior of the tube is full of water molecules. Therefore the corresponding H-bond network is rigid and locks the motions, preventing its use as a nanoreactor at this RH value.12 However, it can be envisioned at low RH values for reactions involving only water (water splitting, radiolysis…).
In the case of IMO-CH3 samples, Sinc(Q,ω) can be written as:
| Sinc(Q,ω) × R(Q,ω) ∝ [A(Q)δ(ω) + B(Q)LOH(Q,ω) + C(Q)Lwater(Q,ω) + D(Q)LCH3(Q,ω)] × R(Q,ω) | (7) |
Data analysis cannot discriminate more than two quasi-elastic components. In all samples, the narrow component of the fit (Fig. 5b) is almost constant for Q > 1 Å−1, whatever the equilibration state of the sample is (see Fig. 7 with the example of the sample equilibrated at 43% RH). Therefore, we attribute it to rotational motions of hydrogen atoms of methyl groups. Certainly, it includes a contribution of water molecules outside the NTs that cannot be discriminated. Indeed, the fact that the narrow component of the fit decreases slightly when Q decreases from 1 to 0 Å−1 (Fig. 7, and for all RH values) is consistent with the presence of diffusing water molecules. Moreover, the behavior of these water molecules is not sensitive to RH. This is consistent with the fact that the outer surfaces can almost be considered as hydrophobic ones. Therefore, water molecules will mainly interact between themselves and will not be very sensitive to RH value. The half width at half maximum (HWHM) of this narrow component is ΓCH3 = 2ℏDrot = 85 μeV that corresponds to a rotational relaxation time τrot = 1/(6Drot) = 2.6 ps. Following the analysis of B. Frick and L. J. Fetters,36 we can combine this result with the inelastic peak observed in the vibrational density of states at Γ0 = 17 meV (Fig. 2b) to describe the torsion of –CH3. Writing the relation ΓCH3 = Γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT), with Γn = 0.085 meV measured at 300 K, we obtain the activation energy Ea = 13.2 kJ mol−1, which is a reasonable value for this motion.36 Therefore, this calculation provides a model of the torsion of methyl groups.
exp(−Ea/kBT), with Γn = 0.085 meV measured at 300 K, we obtain the activation energy Ea = 13.2 kJ mol−1, which is a reasonable value for this motion.36 Therefore, this calculation provides a model of the torsion of methyl groups.
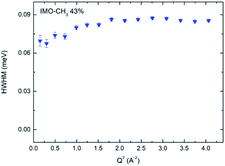 | ||
| Fig. 7 HWHM of the narrow component plotted versus Q2, for the IMO-CH3 sample equilibrated at 43% RH. | ||
As shown in Fig. 5b, a broad Lorentzian is necessary to fit the large energy exchange part of the spectra of both IMO-OH and IMO-CH3 samples, which we ascribe to motions of hydroxyl groups present in both sets of samples. In all cases, we obtain linewidths ΓOH of these broad components that are independent of Q, therefore corresponding to local motions. In the case of IMO-OH samples, ΓOH = 1.3 meV for the samples equilibrated at 3 and 11% RH and 1.1 meV for IMO-OH equilibrated at 43% RH. In the case of IMO-CH3, ΓOH = 1.1 meV at all RH values studied. Because of the similarity of these values, common to all samples, we associate the broad components to motions of the hydroxyl groups. A similar calculation to that performed for methyl groups can be made, associating the broad components of the quasi-elastic spectra to the inelastic component at 55 meV. The resulting activation energy is 9.6 kJ mol−1, a plausible value. This is however only a putative interpretation of the data. The associated relaxation times are of the order of 0.5 ps that can be interpreted as due to hindered rotations of these groups present on the surface of the walls of the nanotubes (only on external walls in IMO-CH3).
The fitted intensities of each component of Sinc(Q,ω), A(Q), B(Q) and C(Q), are related to relative weight of hydrogen atoms of each species and to EISF which depends on Q (eqn (5) and (7)). The complexity of the samples and the variety of hydrogen populations is hardly compatible with a precise analysis of their Q dependence. However, in all cases, we find a Q dependence of 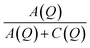 , i.e. EISF decreases with increasing Q in the domain analyzed by the experiments (see the example of IMO-OH equilibrated at 11% RH in Fig. S7 of ESI†). This is compatible with the expected value of the square of the zeroth order spherical Bessel function [sin(Qa)/(Qa)]2 where a represent the radius of the domain where the localized motions take place. In the case of OH and CH3 groups, a must be compared to the interatomic distances O–H and C–H, respectively. In both cases the expected value a = 1 Å describes well the Q dependence of EISF. It is interesting to note that, in the case of the sample IMO-OH with RH = 3%, for which self-diffusion of water is observed, the intensity of the Lorentzian Lwater(Q,ω), given by C(Q) = Nwater[1 − Awater(Q)], does not depend on Q, meaning that all water molecules participate to diffusion along the walls of the nanotubes. For other RH values, C(Q) depends on Q but a complete analysis would imply a discrimination between different species of water molecules, more or less mobile, what is not possible in our complex samples.
, i.e. EISF decreases with increasing Q in the domain analyzed by the experiments (see the example of IMO-OH equilibrated at 11% RH in Fig. S7 of ESI†). This is compatible with the expected value of the square of the zeroth order spherical Bessel function [sin(Qa)/(Qa)]2 where a represent the radius of the domain where the localized motions take place. In the case of OH and CH3 groups, a must be compared to the interatomic distances O–H and C–H, respectively. In both cases the expected value a = 1 Å describes well the Q dependence of EISF. It is interesting to note that, in the case of the sample IMO-OH with RH = 3%, for which self-diffusion of water is observed, the intensity of the Lorentzian Lwater(Q,ω), given by C(Q) = Nwater[1 − Awater(Q)], does not depend on Q, meaning that all water molecules participate to diffusion along the walls of the nanotubes. For other RH values, C(Q) depends on Q but a complete analysis would imply a discrimination between different species of water molecules, more or less mobile, what is not possible in our complex samples.
The interior of the IMO-CH3 tube is accessible at all RH values and the onset of the methyl motions occurs at very low temperature (50 K). This creates a favorable environment for confined reactions even in liquid water.
4 Conclusions
In fully hydrophilic IMO-OH, the very small radius of nanotubes can accommodate a very small number of molecules across their diameter generating very important steric effects. At low hydration levels (RH 3%), water molecules cover the internal surface of the nanotubes and show a 2D diffusion with jumps between neighboring Si–OH sites that cover the surface on the circumference of the tubes. With increasing RH, steric effects become dominant and diffusion is limited to restricted volumes, well described by models of molecular diffusion inside small volumes. Further increase of water concentration blocks diffusive motions of water at the time scale probed by the experiment, i.e. at least up to tens of ps. In all cases, elastic scans show that water molecules (which include hydrogen bond dynamics) are active above 150–200 K, in agreement with many studies of water under confinement.We analyzed the motions of OH groups that form hydrogen bonds with water molecules. At room temperature, the associated relaxation time is very short, of the order of 0.5 ps, which is compatible with the small interatomic O–H length. We associate these motions to the energy of the first excited state of libration at 55 meV observed in the vibrational density of states because it corresponds to expected activation energies of the order of 10 kJ mol−1.
Dynamics of CH3 groups in hybrid imogolites dominate the scattered intensity. They are active since the lowest temperature. Comparing our data for rotational motions of hydrogen atoms at room temperature to the energy of excited states of libration, we deduce an activation energy around 13 kJ mol−1. From the observation of the MSD determined from elastic scans, we observe that the transition from librational motions to free rotation takes place around 50 K at all studied RH values.
We conclude that dynamics of both hydroxyl and methyl groups are well described by local hindered rotations at room temperature and do not depend on water content. Instead, as often, dynamics of water molecules is extremely dependent on geometrical constrains. In hydrophilic imogolites, the complete filling of the very narrow nanotubes totally blocks self-diffusion, thus preventing its use as a nanoreactor. However, it can be envisioned at low RH values for reactions involving only water. On the contrary, the interior of IMO-CH3 was shown to be a favorable place for nanoconfined chemical reactions to take place. This study paves the way to the peculiar behavior of the dynamics of confined water inside inorganic nanochannels, which has strong implications in nanoreactors, but also in nanofluidics research fields.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Helmholtz Zentrum Berlin is gratefully acknowledged for financial support. We thank LLB for beamtime allocation at ILL on IN6-SHARP (DOI: 10.5291/ILL-DATA.CRG-2679). Maïté Paternostre is acknowledged for the access to the mini electron microscopy platform “TEM-team” (I2BC, Institute for Integrative Biology of the Cell (I2BC/Institut Joliot)). Dr Frédéric Gobeaux is gratefully acknowledged for the TEM images.Notes and references
- D. M. Vriezema, M. C. Aragonèes, J. A. A. W. Elemans, J. J. L. M. Cornelissen, A. E. Rowan and R. J. M. Nolte, Chem. Rev., 2005, 105, 1445–1490 CrossRef CAS.
- T. S. Koblenz, J. Wassenaar and J. N. H. Reek, Chem. Soc. Rev., 2008, 37, 247–262 RSC.
- K. Renggli, P. Baumann, K. Langowska, O. Onaca, N. Bruns and W. Meier, Adv. Funct. Mater., 2011, 21, 1241–1259 CrossRef CAS.
- S. H. Petrosko, R. Johnson, H. White and C. A. Mirkin, J. Am. Chem. Soc., 2016, 138, 7443–7445 CrossRef CAS.
- D. G. Shchukin, G. B. Sukhorukov, R. R. Price and Y. M. Lvov, Small, 2005, 1, 510–513 CrossRef CAS.
- S. A. Miners, G. A. Rance and A. N. Khlobystov, Chem. Soc. Rev., 2016, 45, 4727–4746 RSC.
- I. Bottero, B. Bonelli, S. E. Ashbrook, P. A. Wright, W. Zhou, M. Tagliabue, M. Armandi and E. Garrone, Phys. Chem. Chem. Phys., 2011, 13, 744–750 RSC.
- P. Picot, F. Gobeaux, T. Coradin and A. Thill, Appl. Clay Sci., 2019, 178, 105133 CrossRef CAS.
- M.-S. Amara, E. Paineau, S. Rouziere, B. Guiose, M.-E. M. Krapf, O. Taché, P. Launois and A. Thill, Chem. Mater., 2015, 27, 1488–1494 CrossRef CAS.
- P. Picot, O. Tache, F. Malloggi, T. Coradin and A. Thill, Faraday Discuss., 2016, 191, 391–406 RSC.
- Y. Liao, P. Picot, J.-B. Brubach, P. Roy, S. Le Caër and A. Thill, Appl. Clay Sci., 2018, 164, 58–67 CrossRef CAS.
- Y. Liao, P. Picot, M. Lainé, J.-B. Brubach, P. Roy, A. Thill and S. Le Caër, Nano Res., 2018, 11, 4759–4773 CrossRef CAS.
- H. J. Bakker and H.-K. Nienhuys, Science, 2002, 297, 587–590 CrossRef CAS.
- S. Le Caër, D. J. Palmer, M. Lima, J. P. Renault, G. Vigneron, R. Righini and S. Pommeret, J. Am. Chem. Soc., 2007, 129, 11720–11729 CrossRef.
- R. Musat, J. P. Renault, M. Candelaresi, D. J. Palmer, S. Le Caër, R. Righini and S. Pommeret, Angew. Chem., Int. Ed., 2008, 47, 8033–8035 CrossRef CAS.
- P. Levitz, M. Zinsmeister, P. Davidson, D. Constantin and O. Poncelet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 030102 CrossRef CAS.
- M. C. Bellissent-Funel, Eur. Phys. J. E, 2003, 12, 83–92 CrossRef CAS.
- V. C. Farmer, A. R. Fraser and J. M. Tait, J. Chem. Soc., Chem. Commun., 1977, 13, 462–463 RSC.
- V. C. Farmer, M. J. Adams, A. R. Fraser and F. Palmieri, Clay Miner., 1983, 18, 459–472 CrossRef CAS.
- P. Picot, Y. Y. Liao, E. Barruet, F. Gobeaux, T. Coradin and A. Thill, Langmuir, 2018, 34, 13225–13234 CrossRef.
- G. Günther and M. Russina, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 828, 250–261 CrossRef.
- M. Russina, G. Guenther, V. Grzimek, R. Gainov, M.-C. Schlegel, L. Drescher, T. Kaulich, W. Graf, B. Urban, A. Daske, K. Grotjahn, R. Hellhammer, G. Buchert, H. Kutz, L. Rossa, O.-P. Sauer, M. Fromme, D. Wallacher and K. Rolfs, Phys. B, 2018, 551, 506–511 CrossRef CAS.
- Y. Y. Liao, P. Picot, J. B. Brubach, P. Roy, A. Thill and S. Le Caer, J. Phys. Chem. C, 2019, 123, 19768–19777 CrossRef CAS.
- M. Boyer, E. Paineau, M. Bacia-Verloop and A. Thill, Appl. Clay Sci., 2014, 96, 45–49 CrossRef CAS.
- W. C. Ackerman, D. W. Hua, Y. W. Kim, J. C. Huling and D. M. Smith, Adsorption Studies of Pure and Modified Imogolite as a Potential Pore-Size Standard, Elsevier Science Publ B. V., Amsterdam, 1994, vol. 87, pp. 735–744 Search PubMed.
- D.-Y. Kang, J. Zang, E. R. Wright, A. L. McCanna, C. W. Jones and S. Nair, ACS Nano, 2010, 4, 4897–4907 CrossRef CAS.
- J. P. Olivier, W. B. Conklin and M. v. Szombathely, Stud. Surf. Sci. Catal., 1994, 87, 81–89 CrossRef CAS.
- D. Or and M. Tuller, Water Resour. Res., 1999, 35, 3591–3605 CrossRef CAS.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS.
- K. Amann-Winkel, M. C. Bellissent-Funel, L. E. Bove, T. Loerting, A. Nilsson, A. Paciaroni, D. Schlesinger and L. Skinner, Chem. Rev., 2016, 116, 7570–7589 CrossRef CAS.
- J. T. Cabral, A. Luzar, J. Teixeira and M. C. Bellissent-Funel, J. Chem. Phys., 2000, 113, 8736–8745 CrossRef CAS.
- G. Monet, E. Paineau, Z. Chai, M. S. Amara, A. Orecchini, M. Jimenez-Ruiz, A. Ruiz-Caridad, M. Fine, S. Rouzière, L.-M. Liu, G. Teobaldi, S. Rols and P. Launois, Nanoscale Adv., 2020, 2, 1869–1877 RSC.
- B. Creton, D. Bougeard, K. S. Smirnov, J. Guilment and O. Poncelet, J. Phys. Chem. C, 2008, 112, 10013–10020 CrossRef CAS.
- S. Krishnamurthy, R. Bansil and J. Wiafe-Akenten, J. Chem. Phys., 1983, 79, 5863–5870 CrossRef CAS.
- M. Russina, G. Günther, V. Grzimek, M.-C. Schlegel, C. M. Veziri, G. N. Karanikoos, T. M. Yamada and F. Mezei, J. Phys. Chem. Lett., 2019, 10, 6339–6344 CrossRef CAS.
- B. Frick and L. J. Fetters, Macromolecules, 1994, 27, 974–980 CrossRef CAS.
- M. Barthes, H. N. Bordallo, J. Eckert, O. Maurus, G. de Nunzio and J. Léon, J. Phys. Chem. B, 1998, 102, 6177–6183 CrossRef CAS.
- N. B. Colthup, L. H. Daly and S. E. Wiberley, Introduction to Infrared and Raman Spectroscopy, Academic Press, San Diego, Third edn, 1990 Search PubMed.
- B. Creton, D. Bougeard, K. S. Smirnov, J. Guilment and O. Poncelet, Phys. Chem. Chem. Phys., 2008, 10, 4879–4888 RSC.
- J.-M. Zanotti, P. Judeinstein, S. Dalla-Bernardina, G. Creff, J.-B. Brubach, P. Roy, M. Bonetti, J. Ollivier, D. Sakellariou and M.-C. Bellissent-Funel, Sci. Rep., 2016, 6, 25938 CrossRef CAS.
- J. Colmenero, A. J. Moreno and A. Alegria, Prog. Polym. Sci., 2005, 30, 1147–1184 CrossRef CAS.
- http://iramis.cea.fr/llb/Phocea/Page/index.php?id=21 .
- K. T. Gillen, D. C. Douglass and M. J. R. Hoch, J. Chem. Phys., 1972, 57, 5117–5119 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685–688 CAS.
- W. S. Price, H. Ide and Y. Arata, J. Phys. Chem. A, 1999, 103, 448–450 CrossRef CAS.
- W. A. Kamitakahara and N. Wada, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041503 CrossRef.
- N. C. Malikova, A. Cadène, E. Dubois, V. Marry, S. Durand-Vidal, P. Turq, J. Breu, S. Longeville and J.-M. Zanotti, J. Phys. Chem. C, 2007, 111, 17603–17611 CrossRef CAS.
- I. M. Briman, D. Rébiscoul, O. Diat, J.-M. Zanotti, P. Jollivet, P. Barboux and S. Gin, J. Phys. Chem. C, 2012, 116, 7021–7028 CrossRef CAS.
- L. Scalfi, G. Fraux, A. Boutin and F.-X. Coudert, Langmuir, 2018, 34, 6748–6756 CrossRef CAS.
- K. S. Singwi and A. Sjölander, Phys. Rev., 1960, 119, 863–871 CrossRef CAS.
- J. Teixeira, M. C. Bellissent-Funel, S. H. Chen and A. J. Dianoux, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1913–1917 CrossRef CAS.
- J. Teixeira, J.-M. Zanotti, M. C. Bellissent-Funel and S.-H. Chen, Phys. B, 1997, 234–236, 370–374 CrossRef CAS.
- A. K. Soper, J. Phys.: Condens. Matter, 2007, 19, 335206 CrossRef CAS.
- F. Volino and A. J. Dianoux, Mol. Phys., 1980, 41, 271–279 CrossRef CAS.
- M. C. Bellissent-Funel, S. H. Chen and J.-M. Zanotti, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4558–4569 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: modeling of water adsorption isotherms (Fig. S1–S3), quasi-elastic intensity integrated near the elastic line for IMO-OH and IMO-CH3 (both 11% RH) versus temperature (Fig. S4), QENS data on one figure (Fig. S5) and EISF of IMO-OH 11% (Fig. S6). See DOI: 10.1039/d0na00765j |
| This journal is © The Royal Society of Chemistry 2021 |