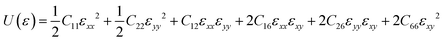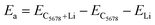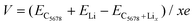Open Access Article
Open Access ArticleTwo-dimensional C5678: a promising carbon-based high-performance lithium-ion battery anode†
Da
Li

State Key Lab of Superhard Materials, College of Physics, Jilin University, Changchun, 130012, P. R. China. E-mail: dali@jlu.edu.cn
First published on 9th December 2020
Abstract
The non-hexagonal carbon rings significantly affect the electrode application of two-dimensional carbon allotropes. Many studies have been devoted to exploring novel two-dimensional carbon allotropes. However, two-dimensional carbon allotropes with a high degree of the local carbon-ring disorder are still nonexistent. Here, we design a new metallic two-dimensional planar carbon allotrope C5678 by using first-principles calculations. C5678 is composed of pentagonal, hexagonal, heptagonal, and octagonal carbon rings with a higher degree of local carbon-ring disorder. It has good dynamic, thermal, and mechanical stability. The local carbon-ring disorder results in many local electron-deficient regions and local strain regions on the basal plane of C5678 that can accommodate more electrons from lithium atoms and increase the adsorption sites, respectively, thus further enhancing the lithium storage capacity. It has a one-sided maximum theoretical capacity of 697 mA h g−1, a lower Li diffusion barrier (<0.44 eV), and a lower average open-circuit voltage (0.33 V). These results not only propose a candidate electrode material for a lithium-ion battery but also offer insights for understanding the effect of non-hexagonal carbon rings on lithium adsorption and storage.
1. Introduction
Graphene, a flagship two-dimensional (2D) material with a zero bandgap and a highly stable planar honeycomb lattice, has attracted much attention due to its fascinating physical and chemical properties which are much different from those of its bulk counterpart diamond/graphite. Graphene is a promising material for lithium-ion batteries (LIBs) because its ultraflat honeycomb lattice results in a high capacity of lithium atom storage. But still there is some debate on the application of graphene as an electrode material. Some studies indicate that graphene nanosheets have a higher specific capacity of 460 mA h g−1.1,2 While others argue that under a higher lithium concentration, lithium atoms on the surface of pristine graphene tend to form clusters instead of adsorbing on the unoccupied hollow sites of graphene.3–5Recent studies indicate that introducing defects into pristine graphene is a good strategy to suppress the formation of lithium clusters on the surface of graphene.4,6,7 Although the presence of structural defects such as vacancy and Stone–Wales defects destroys the perfect symmetry of graphene; it also produces many local electron-deficient regions around the defects8–10 and many effective adsorption positions for lithium atoms on the surface of graphene. This results in a significant increase in the lithium storage capacity of graphene nanomaterials.4,11,12 Recently, Tsai et al. theoretically confirmed that increasing the degree of local carbon-ring disorder could effectively enhance the lithium storage capacity of graphene. The local carbon-ring disorder introduces more electron-deficient regions on the basal plane of graphene. In experiments, structural defects always appear during the process of graphene growth and production. These structural defects will change the local properties of graphene around the structural defects.13–15 For example, the bond rotation induced Stone–Wales defect16 can covert hexagonal carbon rings into non-hexagonal carbon rings (pentagons and heptagons). These non-hexagonal carbon rings create local strains on the basal plane of graphene. Recently, Li et al. proposed that applying strain on the pristine graphene can further enhance the lithium adsorption ability of graphene.17 Therefore, we could expect that the 2D carbon allotropes composed of complete or partial non-hexagonal carbon rings should have much potential to be used as electrode materials in LIBs. Recently, many 2D carbon allotropes with ordered and symmetrized non-hexagonal carbon-ring arrangements such as penta-graphene, ψ-graphene, phagraphene, biphenylene, Θ-graphene, and net-τ graphene, have been proposed by first-principles calculations. They have better lithium storage capacities, lower diffusion energy barriers, and lower open-circuit voltages.4,18–25 However, the 2D carbon allotropes with a high degree of local carbon-ring disorder are still missing.
In this work, we predicted a new 2D carbon allotrope C5678 which is composed of pentagon, hexagon, heptagon, and octagon. C5678 is an energetically metastable carbon allotrope with respect to graphene. It has better dynamic stability. C5678 possesses metallicity and shows a good electrochemical performance for use in LIBs. The higher degree of the local carbon-ring disorder of C5678 results in a high theoretical lithium storage capacity of 697 mA h g−1 (the maximum Li concentration LiC3.2), which is larger than those of local carbon-ring ordered penta-graphene and ψ-graphene, is little smaller than that of Θ-graphene. Furthermore, the lower Li diffusion barrier (<0.44 eV) and average open-circuit voltage (0.33 V) are beneficial for practical applications of C5678 as a good electrode material for LIBs.
2. Methods
The calculations are performed within the density functional theory (DFT) framework, carried out within the Vienna ab initio simulation package (VASP) using the projector augmented wave method.26,27 The 2s22p2 electrons of carbon atoms are treated as valence electrons. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof functional for the exchange correlation was employed.28 The tested plane-wave cutoff energy was taken as 500 eV. The k-points with a grid spacing of 2π × 0.03 Å−1 for the integration of the electronic Brillouin zone (BZ) were used. The Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional is used to calculate the accurate electronic band structure.29 An 18 Å vacuum space in the simulation cell is adopted to avoid the image interaction between neighboring layers. The weak van der Waals (vdW) interactions are omitted in current calculations because the effect of vdW is less significant for the monolayer systems.6 The geometries are fully optimized until the residual Hellmann–Feynman forces are less than 0.01 eV Å−1. The diffusion barriers of Li atoms on the surface of C5678 are calculated by using the climbing-image nudged elastic band (CI-NEB) method. Theoretical phonon spectra are calculated using the supercell approach as implemented in the PHONOPY package.30Ab initio molecular dynamics (AIMD) simulations under the canonical (NVT) ensemble were used to study the thermal stability of C5678 at high temperatures. The particle-swarm optimization (PSO) algorithm performed on the Crystal structure Analysis by Particle Swarm Optimization (CALYPSO) code was used to obtain reasonable absorption configurations for LiCx with various concentrations.31–33 A 2 × 1 supercell of C5678 was chosen as the initial substrate. Various lithium concentrations (1, 2, 4, 6, 8, and 10 lithium atoms on the basal plane) were considered. The adsorption structure search was performed for 30 generations at each concentration. Approximately 1500 candidate adsorption structures were calculated at each concentration in the global search.3. Results and discussion
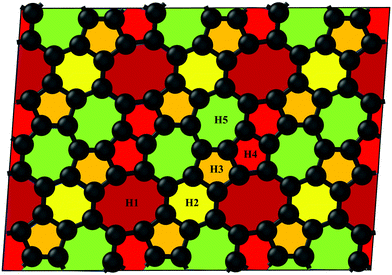
3.1 Structure and structural stability
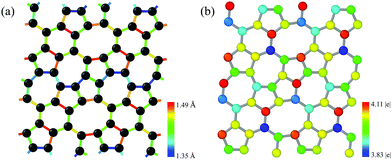
The pentagon–heptagon carbon ring alignment has good ability and is a basic structural unit of many 2D carbon allotropes such as xgraphene, ψ-graphene, and PAI-graphene.13,21,34 Therefore, it is a good strategy to design a novel 2D carbon allotrope by using similar pentagon–heptagon alignments. Here, the double inversed pentagon–heptagon alignments (Fig. S1, ESI†) are chosen as basic units to design a novel 2D carbon allotrope. A novel 2D carbon allotrope C5678 which is composed of 5-6-7-8 carbon rings, is predicted as depicted in Fig. 1. The five inequivalent carbon rings are highlighted in different colors. C5678 is ultraflat and one-atom-thick with 16 carbon atoms in its unit cell. It has p1 plane symmetry with the optimized equilibrium lattice constants of a = 6.41 Å and b = 6.9 Å (Table S1, ESI†). Three types of non-hexagonal carbon rings pentagon, heptagon, and octagon are arranged in local disorder. The neighboring hexagons are separated by non-hexagonal carbon rings. Meanwhile, the neighboring pentagon alignments and heptagon alignments are also separated by other carbon rings. Therefore, C5678 has a high degree of local carbon-ring disorder that destroys the hexagonal symmetry of pristine graphene. The shortest bond length of neighboring carbon atoms in C5678 is 1.35 Å, as highlighted in red in Fig. 2a. The longest bond length of neighboring carbon atoms is 1.49 Å, as highlighted in blue. Other bond lengths of carbon–carbon bonds in C5678 are in the range of 1.35 Å to 1.49 Å, indicating that the bond lengths in C5678 show high local disorder. Furthermore, the charge distribution of C5678 also shows high local disorder. The electron charges of carbon atoms in C5678 are in the range of 3.83 |e| to 4.11 |e|. The disorder of local carbon rings, bond lengths, and atomic charges indicate that C5678 has good potential to adsorb more Li atoms on its surface.To confirm the thermodynamic stability, we compare the total energy of C5678 to that of recently proposed carbon-based electrode materials including penta-graphene, h567, Θ-graphene, ψ-graphene, and phagraphene. C5678 has a lower total energy of −8.88 eV per atom, which is lower than those of famous penta-graphene (−8.32 eV per atom)20 and C568 (8.83 eV per atom),35 much close to those of net-τ (−8.89 eV per atom),4 Θ-graphene (−8.98 eV per atom),25 and h567 (−8.99 eV per atom),36 and a little higher than those of phagraphene, ψ-graphene, and graphene (−9.03 eV per atom, −9.07 eV per atom, and −9.23 eV per atom).21,37 These indicate that similar to penta-graphene, C568, net-τ, Θ-graphene, etc., C5678 is a metastable carbon allotrope.
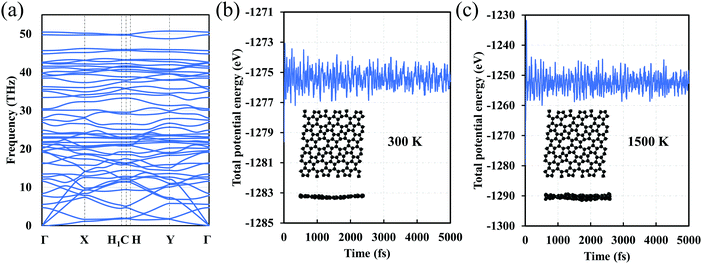
We also investigate the dynamic stability of C5678. The phonon dispersion of C5768 shows that there are no imaginary phonon modes that imply kinetic stability of C5678 (Fig. 3a). To finally confirm the dynamic stability, AIMD simulations for C5678 was performed (Fig. 3b and c). A (3 × 3) supercell of C5678 is used in our AIMD simulation. Two temperatures (300 K and 1500 K) are used to check the stability of C5678. It is found that the geometry of C5678 is preserved very well at temperatures of 300 and 1500 K during the AIMD simulations. Furthermore, the total potential energies of the C5678 supercell only fluctuate around a constant value. These calculations further confirm the dynamic stability of C5678.
To guarantee the mechanical stability of C5678, the corresponding elastic constants of C5678 are calculated by using the following formula:
For the oblique structure, six independent elastic constants C11, C22, C12, C16, C26, and C66 of C5678 must satisfy the Born–Huang criteria:38C11 > 0, C11C22 > C122, and det(Cij) > 0. The calculated elastic constants C11, C22, C12, C16, C26, and C66 are 291.51, 291.60, 82.02, 7.39, 5.47, and 29.07 N m−1, respectively. They satisfy the Born–Huang criteria indicating C5678 is a mechanically stable carbon allotrope. The calculated in-plane Young's modulus of C5678 is 268.4 N m−1 which is smaller than that of graphene (342.2 N m−1), and much close to those of penta-graphene (263.8 N m−1) and h-BN monolayer (275.8 N m−1), suggesting that C5678 has good mechanical properties. Furthermore, C5678 is an anisotropic two-dimensional material because its two-dimensional elastic anisotropy index (0.68) is larger than that of graphene (0) and much close to that of black phosphorene (0.65).39
3.2 Electronic properties
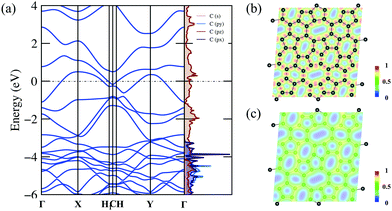
The detailed electronic structure is much important for understanding the fundamental properties of C5678. Therefore, we calculate the electronic band structure and projected density of states (DOS) of C5678 as shown in Fig. 4a. The DFT results with PBE (Fig. 4a) and HSE06 (Fig. S2, ESI†) functionals indicate that C5678 is a metallic material because two bands cross the Fermi level. As shown in Fig. 4a, significant overlaps between 2s, 2px, and 2py orbitals can be found that underlie strong sp2 hybridization of carbon atoms in C5678. The projected DOS also indicates that the pz orbitals occupy the bonding and antibonding states simultaneously and this results in the formation of π bonds between neighboring carbon atoms and the conductivity of C5678. To analyze the bonding features of C5678, the electron localization function (ELF) of C5678 was calculated. It is well known that the values of ELF are between 0 and 1, which corresponds to perfect localization and delocalization of electrons in a material. The ELF value of 0.5 corresponds to the state of the electron–gas-like pair. The ELF slice presented in Fig. 4b shows that the electrons localize in the middle of two neighboring carbon atoms, signaling the strong σ bonding states of the nearest neighboring carbon atoms. When the slice is moved 1 Å up from the plane of the structure (Fig. 4c), the ELF value remains nearly constant (approximately 0.5), indicating there is a delocalized electron state induced by the pz orbitals of carbon atoms, which results in the metallicity of C5678. The strong structural stability and the presence of delocalized pz orbitals are beneficial for the application of C5678 as an electrode material of LIBs.3.3 Potential application as an anode material for LIBs
Next, we calculate the adsorption energy of a single Li atom on the surface of a 2 × 2 supercell of C5678 to check the possibility of electrode application of C5678. According to previous studies, the lithium atoms preferably absorb on the hollow sites of 2D carbon allotropes. Therefore, considering the structural features of C5678, five possible hollow adsorption sites H1–H5 are chosen in our adsorption calculations, as shown in Fig. 1. The adsorption energy of lithium atoms is described as:where Ea is the adsorption energy, EC5678+Li and EC5678 are the total energies of the system with and without lithium adsorption, respectively. ELi is the lithium atom energy in bulk Li metal. The calculated adsorption energies of lithium atoms on H1, H2, H3, H4, and H5 sites are −0.52, −0.45, −0.50, −0.47, and −0.42 eV, respectively, comparable to that of recently predicted 2D carbon allotrope net-τ (−0.37 to −0.60 eV).4 The negative adsorption energies also indicate that lithium atoms tend to adsorb on the surface of C5678 and will not form lithium clusters. Furthermore, Bader charge analysis shows that the charge transfer from Li to the C5678 is ∼0.89 |e| for the H1 site, indicating that C5678 has the potential to accommodate more electrons from lithium atoms.
Lithium mobility is an important factor that determines the rate performance of LIBs. To investigate the lithium mobility on the surface of C5678, the six possible migration pathways from the H1 site to the neighbor H1 site along various directions are chosen to calculate the migration barrier (Fig. 5a). The transition states of six migration pathways are presented in Fig. 5b. It is found that the diffusion barrier along the nearest neighboring path 1 is 0.33 eV, which is close to that of graphene (0.31 eV) and ψ-graphene (0.313 eV).21,40 The diffusion barrier along path 2 is 0.29 eV which is smaller than that of graphene. We see that the diffusion barriers of both path 3 and path 4 are 0.364 eV, while for paths 5 and 6 the diffusion barriers are 0.44 and 0.42 eV, respectively. Although the maximum diffusion barrier of C5678 (0.44 eV) is larger than that of graphene, it still smaller than those of Θ-graphene (0.48 eV),25 xgraphene (0.49 eV),34 and popgraphene (0.55 eV).24 The average migration barrier of the Li atom on the surface of C5678 is 0.37 eV. Such a lower barrier results in a higher Li-ion mobility ability, indicating a good charge–discharge rate of C5678 as an anode for LIBs.
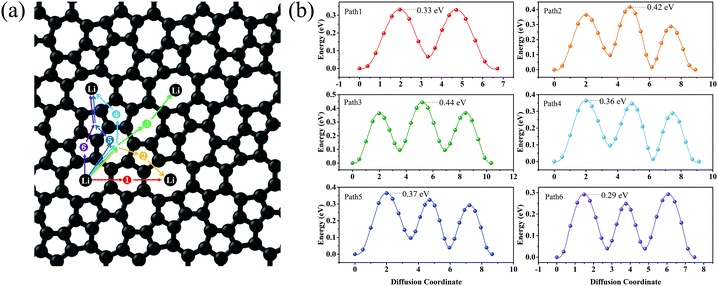 | ||
| Fig. 5 Six possible Li-ion migration pathways (a) and their corresponding diffusion barrier for Li on the surface of C5678. | ||
In addition to the diffusion barrier, the lithium storage capacity is also an important factor for the performance of electrode materials. Therefore, the candidate adsorption configurations of lithium under various lithium concentrations are fully explored by the PSO method performed in the CALYPSO code. One side mode was used in our adsorption configuration prediction. The most stable structural configurations under various lithium atom concentrations are given in Fig. S3 (ESI†). The maximum lithium atom number is ten in Li10C32. The corresponding specific capacity can reach 697 mA h g−1 that is larger than those of graphite and pristine graphene. Meanwhile, corresponding adsorption energy of lithium atom is −0.07 eV in Li10C32, which is equal to that of xgraphene (−0.07 eV). The open-circuit voltage (OCV) is another important factor for the application of a 2D carbon electrode. We use the following equation to estimate the OCV of C5678 with different lithium concentrations LiCx:41
The calculated V is 0.78 V for the stoichiometry of LiC32. When the lithium concentration increases to LiC3.2, V decreases to 0.07 V. The calculated average OCV is 0.33 V, which is larger than that of graphite (0.11 V),42 much close to that of popgraphene (0.3 V),24 and much lower than that of ψ-graphene (0.64 V).21 Thus, the lower average OCV shows the feasibility of C5678 to be a desirable electrode material in LIBs.
4. Conclusions
In summary, we predicted a novel metallic 2D carbon allotrope C5678 by using first-principles calculation and the CALYPSO method. C5678 is composed of 5-6-7-8 carbon rings with highly locally disordered carbon rings. Due to the delocalized pz orbitals of carbon atoms in C5678, C5678 exhibits intrinsic metallization that results in good mobility of lithium on the surface of C5678. The local carbon-ring disorder of C5678 produces many electron-deficiency regions which make C5678 have a better ability to accommodate more electrons of lithium atoms. These make C5678 have a high specific capacity (697 mA h g−1) and a lower diffusion energy barrier for Li-ions (<0.44 eV). It is expected that C5678 can be used as an electrode material for LIBs. The current study will encourage further studies on the application of 2D carbon allotropes as electrode materials.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 91745203 and 11404134). Supported by High Performance Computing Center of Jilin University, China.References
- G. Wang, X. Shen, J. Yao and J. Park, Carbon, 2009, 47, 2049–2053 CrossRef CAS.
- X.-Y. Shan, G. Zhou, L.-C. Yin, W.-J. Yu, F. Li and H.-M. Cheng, J. Mater. Chem. A, 2014, 2, 17808–17814 RSC.
- S. Yu, Y.-C. Rao, S.-F. Li and X.-M. Duan, Appl. Phys. Lett., 2018, 112, 053903 CrossRef.
- X. Wang, Z. Feng, J. Rong, Y. Zhang, Y. Zhong, J. Feng, X. Yu and Z. Zhan, Carbon, 2019, 142, 438–444 CrossRef CAS.
- M. Liu, A. Kutana, Y. Liu and B. I. Yakobson, J. Phys. Chem. Lett., 2014, 5, 1225–1229 CrossRef CAS PubMed.
- H. Yildirim, A. Kinaci, Z.-J. Zhao, M. K. Y. Chan and J. P. Greeley, ACS Appl. Mater. Interfaces, 2014, 6, 21141–21150 CrossRef CAS PubMed.
- E. Lee and K. A. Persson, Nano Lett., 2012, 12, 4624–4628 CrossRef CAS PubMed.
- Y.-J. Tsai and C.-L. Kuo, ACS Appl. Mater. Interfaces, 2020, 12, 22917–22929 CrossRef CAS PubMed.
- S. Chen, P. Bao, L. Xiao and G. Wang, Carbon, 2013, 64, 158–169 CrossRef CAS.
- T. Morresi, A. Pedrielli, S. A. Beccara, R. Gabbrielli, N. M. Pugno and S. Taioli, Carbon, 2020, 159, 512–526 CrossRef CAS.
- A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873 CrossRef CAS PubMed.
- D. Datta, J. Li, N. Koratkar and V. B. Shenoy, Carbon, 2014, 80, 305–310 CrossRef CAS.
- X. Chen, A. Bouhon, L. Li, F. M. Peeters and B. Sanyal, Carbon, 2020, 170, 477–486 CrossRef CAS.
- B. Ram and H. Mizuseki, Carbon, 2018, 137, 266–273 CrossRef CAS.
- S. W. Cranford, Carbon, 2016, 96, 421–428 CrossRef CAS.
- A. J. Stone and D. J. Wales, Chem. Phys. Lett., 1986, 128, 501–503 CrossRef CAS.
- P. Li, Z. Li and J. Yang, J. Phys. Chem. Lett., 2018, 9, 4852–4856 CrossRef CAS PubMed.
- A. Rajkamal and R. Thapa, Adv. Mater. Technol., 2019, 4, 1900307 CrossRef CAS.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 CrossRef CAS PubMed.
- B. Xiao, Y.-c. Li, X.-f. Yu and J.-b. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 35342–35352 CrossRef CAS PubMed.
- X. Li, Q. Wang and P. Jena, J. Phys. Chem. Lett., 2017, 8, 3234–3241 CrossRef CAS PubMed.
- S. Thomas, E. B. Nam and S. U. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 36240–36248 CrossRef CAS PubMed.
- D. Ferguson, D. J. Searles and M. Hankel, ACS Appl. Mater. Interfaces, 2017, 9, 20577–20584 CrossRef CAS PubMed.
- S. Wang, B. Yang, H. Chen and E. Ruckenstein, J. Mater. Chem. A, 2018, 6, 6815–6821 RSC.
- S. Wang, B. Yang, H. Chen and E. Ruckenstein, Energy Storage Mater., 2019, 16, 619–624 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- Y. Wang, M. Miao, J. Lv, L. Zhu, K. Yin, H. Liu and Y. Ma, J. Chem. Phys., 2012, 137, 224108 CrossRef PubMed.
- S. Wang, Y. Si, B. Yang, E. Ruckenstein and H. Chen, J. Phys. Chem. Lett., 2019, 3269–3275, DOI:10.1021/acs.jpclett.9b00905,.
- B. Ram and H. Mizuseki, Carbon, 2020, 158, 827–835 CrossRef CAS.
- S. Thomas, H. Jung, S. Kim, B. Jun, C. H. Lee and S. U. Lee, Carbon, 2019, 148, 344–353 CrossRef CAS.
- Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182–6186 CrossRef CAS PubMed.
- V. Wang, N. Xu, J. C. Liu, G. Tang and W.-T. Geng, 2020, arXiv:1908.08269 [cond-mat].
- R. Li, Q. Shao, E. Gao and Z. Liu, Extreme Mech. Lett., 2020, 34, 100615 CrossRef.
- G.-C. Guo, D. Wang, X.-L. Wei, Q. Zhang, H. Liu, W.-M. Lau and L.-M. Liu, J. Phys. Chem. Lett., 2015, 6, 5002–5008 CrossRef CAS PubMed.
- K. Kang, H.-S. Lee, D.-W. Han, G.-S. Kim, D. Lee, G. Lee, Y.-M. Kang and M.-H. Jo, Appl. Phys. Lett., 2010, 96, 053110 CrossRef.
- Y. Jing, Z. Zhou, C. R. Cabrera and Z. Chen, J. Phys. Chem. C, 2013, 117, 25409–25413 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Data supporting this publication are provided as ESI; further data will be made available through an online repository. See DOI: 10.1039/d0ma00858c |
| This journal is © The Royal Society of Chemistry 2021 |