Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Development of an in-line magnetometer for flow chemistry and its demonstration for magnetic nanoparticle synthesis†
Maximilian O.
Besenhard
 *a,
Dai
Jiang
*a,
Dai
Jiang
 b,
Quentin A.
Pankhurst
b,
Quentin A.
Pankhurst
 c,
Paul
Southern
c,
Paul
Southern
 c,
Spyridon
Damilos
c,
Spyridon
Damilos
 a,
Liudmyla
Storozhuk
a,
Liudmyla
Storozhuk
 c,
Andreas
Demosthenous
c,
Andreas
Demosthenous
 b,
Nguyen T. K.
Thanh
b,
Nguyen T. K.
Thanh
 cde,
Peter
Dobson
cde,
Peter
Dobson
 f and
Asterios
Gavriilidis
f and
Asterios
Gavriilidis
 a
a
aDepartment of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK. E-mail: m.besenhard@ucl.ac.uk
bDepartment of Electronic and Electrical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK
cUCL Healthcare Biomagnetics Laboratory, University College London, 21 Albemarle Street, London W1S 4BS, UK
dUCL Nanomaterials Laboratory, University College London, 21 Albemarle Street, London W1S 4BS, UK
eBiophysics Group, Department of Physics and Astronomy, University College London, Gower Street, London, WC1E 6BT, UK
fThe Queen's College, University of Oxford, Oxford OX1 4AW, UK
First published on 18th August 2021
Abstract
Despite the wide usage of magnetic nanoparticles, it remains challenging to synthesise particles with properties that exploit each application's full potential. Time consuming experimental procedures and particle analysis hinder process development, which is commonly constrained to a handful of experiments without considering particle formation kinetics, reproducibility and scalability. Flow reactors are known for their potential of large-scale production and high-throughput screening of process parameters. These advantages, however, have not been utilised for magnetic nanoparticle synthesis where particle characterisation is performed, with a few exceptions, post-synthesis. To overcome this bottleneck, we developed a highly sensitive magnetometer for flow reactors to characterise magnetic nanoparticles in solution in-line and in real-time using alternating current susceptometry. This flow magnetometer enriches the flow-chemistry toolbox by facilitating continuous quality control and high-throughput screening of magnetic nanoparticle syntheses. The sensitivity required to monitor magnetic nanoparticle syntheses at the typically low concentrations (<100 mM of Fe) was achieved by comparing the signals induced in the sample and reference cell, each of which contained near-identical pairs of induction and pick-up coils. The reference cell was filled only with air, whereas the sample cell was a flow cell allowing sample solution to pass through. Balancing the flow and reference cell impedance with a newly developed electronic circuit was pivotal for the magnetometer's sensitivity. To showcase its potential, the flow magnetometer was used to monitor two iron oxide nanoparticle syntheses with well-known particle formation kinetics, i.e., co-precipitation syntheses with sodium carbonate and sodium hydroxide as base, which have been previously studied via synchrotron X-ray diffraction. The flow magnetometer facilitated batch (on-line) and flow (in-line) synthesis monitoring, providing new insights into the particle formation kinetics as well as, effect of temperature and pH. The compact lab-scale flow device presented here, opens up new possibilities for magnetic nanoparticle synthesis and manufacturing, including 1) early stage reaction characterisation 2) process monitoring and control and 3) high-throughput screening in combination with flow reactors.
Introduction
Magnetic nanoparticles (MNPs) containing iron, cobalt or nickel, form a class of materials whose properties are of great interest to the fields of electronics, separation and purification, catalysis, and especially biomedicine.1–6 The applications utilising MNPs have in common the need for distinct particle characteristics in terms of size, magnetic moment, surface chemistry, colloidal stability, etc. Therefore, for an application to reach market maturity it requires a reproducible and scalable synthetic procedure, optimised to synthesise MNPs with desired features.Flow reactors have been successfully used not only for large scale production, but also for high-throughput screening platforms for nanomaterial synthesis.7–12 These platforms are capable of covering a wide range of parameters, yielding not only optimised synthetic conditions, but also deeper understanding of particle formation mechanisms, hence, providing the ability to tune nanomaterial properties. These platforms enable the combination of autonomous optimisation algorithms and in situ nanomaterial analysis. So far, the latter has been restricted to spectral characterisation, mostly by UV-vis and photo luminescence spectroscopy.13 Therefore, these platforms are restricted to nanomaterials with a clear correlation between the optical properties and the NP characteristics, such as plasmonic NPs and quantum dots, which excludes important nanomaterials such as MNPs.
Although larger MNPs (>100 nm) or magnetic beads are commonly used in flow chemistry for separation and sorting,14–17 as well as biosensors,18 and flow reactors are well known for their benefits for their synthesis,19–22 efforts towards in-line MNP characterisation are rare. The in-line characterisation of MNPs with respect to their size and molecular structure is challenging and requires elaborate techniques. Recent examples utilised flow cells for small angle X-ray scattering (SAXS) and X-ray diffraction (XRD), mostly using synchrotron set-ups.23–27 The in-line monitoring of the MNPs' magnetic properties during synthesis, however, has been reported with techniques not requiring special facilities.28–31
Milosevic et al. monitored the evolution of magnetic properties during a co-precipitation synthesis of iron oxide nano particles (IONPs) via the MIAtek® technology.28 The sample passes through a coil generating a magnetic field which is excited by two different frequencies. A second coil (inside the field generation coil) around the sample measures the induced signal which is intermodulated depending on the sample's magnetic properties. Ström et al. used an adapted alternating current (AC) susceptometer to measure the susceptibility of a 1 ml sample vial in which IONP co-precipitation occurred in real-time.29 In this vial, the solutions formed after mixing the (ferric and ferrous) iron precursor with the base solution to induce co-precipitation, were collected to study changes of the magnetic properties for different mixing conditions and base concentrations. In a similar study, Fernández-García et al. studied the influence of mixing for an IONP co-precipitation batch synthesis using a custom made AC susceptometer set-up. The precursor and base solution was mixed in a sample vial placed inside one of two (sample and reference) identical sensing coils in the centre of Helmholtz coils.30,31
Recently more compact susceptometers were designed for in vivo monitoring of MNPs,32–36 and lateral flow assays based on MNP quantification.37–39 These studies demonstrate the possibility of characterising MNPs in real-time. To fully exploit this potential, for example for high-throughput screening of MNP synthetic conditions, we developed a highly sensitive AC susceptometer for flow reactors, which we refer as “flow magnetometer”. Special care was taken to perfectly balance the impedance of the sample flow cell and the reference cell. This facilitated a sensitivity sufficient to monitor common MNP syntheses with concentrations of Fe below 100 mM. The flow magnetometer was used to monitor several IONP co-precipitation syntheses of which insights into the particle formation are available from in situ XRD and SAXS analysis.23,27 Our inexpensive, compact and easy to use device confirmed known kinetics and provided new information on the temperature and pH dependence of the magnetic iron oxide phase formation.
Development of flow magnetometer
Measurement concept
The magnetisation over time (t) induced by an alternating magnetic field with an amplitude H0 and a frequency of ω/2π is given by| M(t) = χ·H0·sin(ω·t) | (1) |
| B(t) = μ0·(H(t) + M(t)) | (2) |
| H = n·I/l | (3) |
 | (4) |
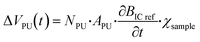 | (5) |
Flow magnetometer design
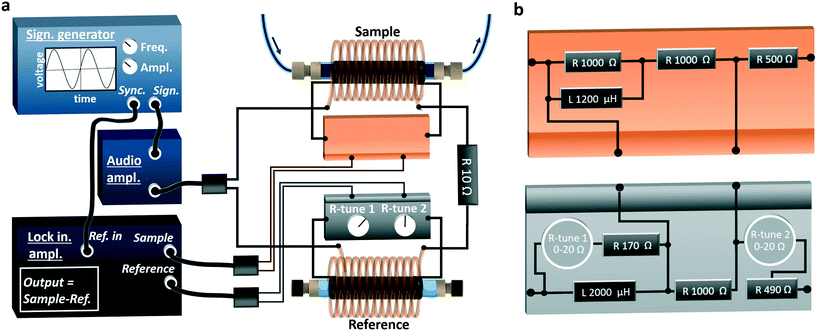
Following the concept described above, measurements of ΔVPU can be implemented using an identical sample and reference pick-up coils, and two identical induction coils generating the magnetic fields in the pick-up coils. Also necessary are electronics to supply sufficient current through the induction coils and to accurately record the difference of voltages induced in the pick-up coils.To facilitate the monitoring of MNP properties in solution via a flow cell, the sample pick-up coil was made using 1/4′′ (= 6.35 mm) PTFE plastic tubing (inner diameter 4 mm). Three layers of insulated copper wire (0.15 mm core) were wound around this tubing with a total of ∼500 turns covering a distance of 4 cm. The 1/4′′ tubing was connected with standard reducing units (Upchurch Scientific) to 1/16′′ (= 1.59 mm) to the flow cell inlet and outlet tubing. The 1/4′′ tubing was preferred for the flow cell, as the larger cross section increased the sensitivity (see eqn (5)). The reference pick-up coil was generated likewise, but both ends of the 1/4′′ tubing were plugged, i.e., the reference material was air. The induction coils were made likewise. Insulated copper wire (0.5 mm core) was wound over 8 cm in 5 layers around 2.2 cm diameter PVC plastic tubing comprising ∼400 turns. The pick-up coils were then fixed in the centre of the induction coils by plastic frames clamping the coils on both sides. Further details of the pick-up and induction coil construction are provided in ESI† section S3.1.
To shield the sample and reference cell (comprising one pick-up and induction coil each) from external electromagnetic fields, they were placed inside Faraday cages made of 3 mm thick perforated aluminium sheets. The resultant flow magnetometer, with the sample induction and pick-up coil is shown in Fig. 1.
To induce a sufficient field strength, the induction coils were powered by a TTi-TG2511 signal generator operating at 12 kHz feeding a CleverLittleBox-CIE.CA9.2 12 W power amplifier. With the settings used, a magnetic field strength amplitude of H0 = 1.6 kA m−1 (= 20 Oe) was estimated as described in ESI† section S3.2. A Jupiter Microsystems-LA9060 digital lock-in amplifier was used to accurately record the difference in voltage induced in the reference and sample pick-up coils ΔVPU(t). The lock-in amplifier output (= magnetometer signal):
| R = ((VPU sample·cos(θ))2 − (VPU ref·cos(θ))2)1/2 | (6) |
Details of all the components used as well as an overview of the magnetometer set-up is provided in Table S3 and Fig. S2.† A schematic of the set-up is shown in Fig. 2a.
Although the inductances of the pick-up (232.0 and 231.9 μH) and induction coils (984 and 994 μH) were comparable, they were not identical. These small deviations, in addition to differences in impedance due to the wiring, gave rise to a substantial ΔVPU signal that potentially overwhelms the magnetic sample signal. To address this, a balancing circuit was developed (see Fig. 2b) to match the inherent amplitude and phase of VPU ref(t) and VPU sample(t). This electronic circuit made it possible to accurately adapt the VPU ref(t) amplitude and phase with two high-precision tuneable resistors (R-tune 1 and R-tune 2). All components, such as resistors, potentiometers, inductors, were selected based on power ratings and temperature coefficient of resistance to minimise any temperature induced fluctuations. The NI Multisim (v 14.02) circuit simulation file of the balancing circuit is available for download in the ESI.†
Monitoring of IONP synthesis
Among the various synthetic routes for the production of IONPs, the most common one is aqueous co-precipitation. This method uses inexpensive and non-toxic chemicals and the particles are formed after an increase in pH of the ferrous and ferric iron precursor solution, commonly by mixing with a base solution. Below, we show how the flow magnetometer was used to monitor co-precipitation syntheses using sodium carbonate and sodium hydroxide base solutions.Chemicals and characterisation
Iron(III) chloride hexahydrate (≥99%), iron(II) chloride tetrahydrate (≥99.0%), sodium carbonate decahydrate (99.0%), and sodium hydroxide (2 M, ≥99.0%) were used as received. Details of the chemicals used are provided in Table S2.† Deionised water (15 MΩ) was used for all solutions. For all syntheses the precursor solution was a 0.1 M Fe ion solution prepared by dissolving the ferrous and ferric chlorides in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio. The base solution was either a 0.34 M sodium carbonate solution or a sodium hydroxide solution (different molarities used).
2 molar ratio. The base solution was either a 0.34 M sodium carbonate solution or a sodium hydroxide solution (different molarities used).
XRD patterns were collected from 2θ = 20° to 100° using an X'Pert Pro (PanAlytical) X-ray diffractometer using CoKα radiation (λ = 0.179 nm) source. For XRD, the IONP solutions were washed and dried before depositing on a zero-background silicon wafer.
Co-precipitation with sodium carbonate in batch
The well-studied IONP co-precipitation synthesis using sodium carbonate (Na2CO3) was chosen as a first model system. For this synthesis it has been shown that formation of the most magnetic phases, i.e., magnetite (Fe3O4) and maghemite (γ-Fe2O3), depends strongly on the temperature.40 When performed at 60 °C, magnetite/maghemite forms over a period of several minutes from the initially precipitated non (or poorly) magnetic intermediate phases, as shown via synchrotron XRD.23 In the following, “magnetite” is used to refer to an unknown mixture or solid solution of magnetite and/or maghemite, since a differentiation based on XRD pattern is not possible due to the line broadening induced by the small particle sizes.The batch co-precipitation synthesis was monitored using an on-line set-up, recycling the solution containing the precipitates through the magnetometer flow cell via a peristaltic pump. Interference due to the peristaltic pump induced fluctuations was not expected, as its frequency (<10 Hz) was several orders of magnitude below the magnetic field frequency of 12 kHz. The precursor and base solution were preheated to the reaction temperature before mixing (30 ml each of precursor and sodium carbonate base solution were placed in vials immersed in a heated water bath). Initially, only the precursor solution was recycled through the magnetometer flow cell, and the amplitude and phase imbalances between sample and reference cell signal were corrected. The synthesis was then initiated by rapidly adding the sodium carbonate base solution to the precursor solution under vigorous stirring, which was maintained throughout the synthesis. The volume of the tubing and flow cell was approximately 4 ml, i.e., ∼6% of the total solution volume, and the recirculation time was ∼20 s. A schematic of the set-up is shown in Fig. 3 and a photograph in Fig. S4.†
 | ||
| Fig. 3 Schematic of set-up used for on-line monitoring of Na2CO3 co-precipitation synthesis of IONPs at 30–90 °C. | ||
At all temperatures, particle formation occurred as soon as synthesis was initiated, i.e., after adding the base solution, and the mixture turned into an opaque solution. Despite this rapid particle formation, the magnetometer signal increased only marginally over the first minutes when co-precipitation occurred at 60 °C, confirming that the initially formed particles are poorly magnetic. This changed ∼6 min after synthesis initiation, when the magnetometer signal started to increase drastically indicating the onset of magnetite formation. After ∼7 min, the magnetometer signal reached a level at which the lock-in amplifier sensitivity had to be changed to avoid overload (R > 10 V). The magnetometer signal up to this change in sensitivity, the subsequent recording while cleaning the flow cell with HCl, and after the switch back to the initial sensitivity (showing that the magnetometer signal drops to the initial value) is shown in Fig. S5.†
The magnetometer signal increase after 6 min is in good agreement with the reported time scales of approximately 5 min till the onset of magnetite formation, studied by synchrotron XRD.23 These XRD measurements had a time resolution of 1–2 min (due to sampling and 1 min exposure time) and could therefore not reveal the transition period, i.e., the time it takes until most intermediate phases had transformed to magnetite after the onset of magnetite formation (at 6 min). The flow magnetometer provides the unique insight that this transition period is relatively short (∼1 min, starting at 6 min) at 60 °C. In addition, the flow magnetometer simplified synthesis monitoring significantly making repetitions easy, hence, simplifying reproducibility studies. The five repetitions performed (see Fig. 4a) show that the magnetite formation onset time varies from 5 to 7 min. This indicates a stochastic behaviour of magnetite formation, which can be expected for the discussed phase transitions of this synthesis at 60 °C.23
To study the effect of reaction temperature for the sodium carbonate co-precipitation synthesis, the procedure was repeated at 90 °C and 30 °C (see Fig. 4b). For the synthesis at 90 °C, the lock-in amplifier got overloaded as soon as the mixed solution passed the magnetometer flow, i.e., ∼10 s after initiating the synthesis, demonstrating the rapid formation of the most magnetic phases at this temperature. For the synthesis at 30 °C, however, there was no indication of magnetite formation for the first 30 min after synthesis initiation, i.e., the magnetometer signal remained constant (and below the noise level of R < 0.3 V). Subsequently, the temperature of the water bath where the vial was placed, was increased to 60 °C to initiate the magnetite formation (Fig. S6† shows the magnetometer signal during the entire experiment). When reaching 40 °C, the magnetometer signal increased slightly, but a significant increase was observed when the vial reached 45 °C. The observed transition period of ∼3 min (see Fig. S6†) was much longer compared to the ∼30 s at 60 °C and the rapid (<10 s) magnetite formation at 90 °C.
These on-line studies of the magnetic properties during the sodium carbonate co-precipitation synthesis show that i) temperatures above 30 °C are required to initiate the magnetite formation (within 30 min); ii) the onset of magnetite formation is earlier for higher temperatures; iii) this formation proceeds slower at lower temperatures.
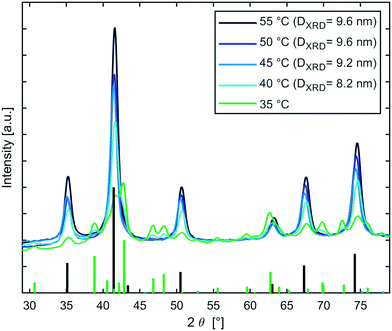
The influence of the temperature for the magnetite transition was studied further, since timescales for nanoparticle synthesis correlate frequently with nanoparticle properties such as size. Therefore, a semi-batch set-up (continuous mixing in T-mixer, collection in aging vial) as described in ESI† section S4.2, was used to initiate sodium carbonate co-precipitation syntheses at 30 °C and subsequently age the solution for 20 min at 30–55 °C. XRD patterns (see Fig. 5) showed that all samples comprised of the inverse spinel structure of magnetite/maghemite, except the sample aged at 30 °C which could not be prepared for XRD analysis via magnetic decantation. Samples synthesised at reaction temperatures ≥45 °C showed no other phase besides magnetite, whereas the samples aged at 35 °C and 40 °C showed also goethite. The MNP diameters calculated from the peak broadening using the Scherrer equation (DXRD) were around 9 nm. Samples processed at 35 °C and 40 °C showed slightly smaller diameters, which could be assigned to incomplete growth of magnetite, as other oxide phases were still present. The XRD analysis confirmed the results obtained via the in-line magnetometer that is: i) the presence of magnetite; ii) the sensitivity of the onset of magnetite formation to the temperature in the range of 30–45 °C (Fig. S8† shows the IONP solutions beside a magnet); and revealed that the final MNP size does not correlate with the period of time required for the transition to magnetite.
Co-precipitation with sodium hydroxide in flow
For the IONP co-precipitation synthesis using sodium hydroxide, we have shown in previous work that magnetite forms rapidly (between 0.5 and 5 s after mixing the precursor and a 0.57 M NaOH solution).27,41 These initial reaction stages were characterised by means of “freezing” transient reaction states by connecting the outlet of the T-mixer to an XRD flow cell placed in a synchrotron beamline. Here, we used a similar set-up, combining a flow reactor and the flow magnetometer to study the effect of pH on the early stages of this synthesis. The flow reactor comprising a preheating and mixing stage (T-mixer) has been described previously.23,27 The T-mixer outlet was connected to the magnetometer flow cell with a short tubing to characterise the magnetic properties just after mixing (after ∼3 s when operating the flow reactor at a total flow rate of 10 ml min−1). A schematic of the set-up is shown in Fig. 6 and a photograph in Fig. S9.† | ||
| Fig. 6 Schematic of set-up used for in-line monitoring of the magnetic properties during continuous NaOH co-precipitation synthesis of IONPs. | ||
To identify the pH required for magnetite formation just after mixing the precursor and base solution, the precursor solution flow rate was fixed to 5 ml min−1 while increasing the flowrate of a 0.57 M NaOH base from 0–5 ml min−1 (5–10 ml min−1 in total), i.e., 0–100%, hence, the mixed solution entered the flow cell after 6–3 s respectively. The flow reactor temperature was set to 25 °C and the amplitude and phase of the sample and reference cell signal were balanced before feeding NaOH solution.
The magnetometer signal during this NaOH feed rate increase is shown in Fig. 7. The first presence of magnetite is indicated after the NaOH solution flow rate exceeded 2.5 ml min−1 (50%, Fe/OH = 0.35). With higher NaOH feed rates, the magnetometer signal increased, which suggests a more rapid magnetite formation at higher pH values. When the NaOH feed rate reached 5 ml min−1 (= 100%), the magnetometer signal temporarily stopped its rapid increase, but then continued (non-monotonously). This continuous increase after the maximum NaOH concentration was reached, was assigned to accumulation of magnetic sample in the flow cell due to sedimentation. This was expected as the NaOH co-precipitation synthesis, especially at high pH, is known to yield highly agglomerated structures that sediment easily if not stabilised.27
 | ||
| Fig. 7 Magnetometer signal of precursor solution (5 ml min−1) alone and mixed (6–3 s before the measurement) with 0.57 M sodium hydroxide solution at 0.5–5 ml min−1, i.e., 10–100%. | ||
To minimise IONP accumulation, the total flow rate was increased by pumping both solutions at 5 ml min−1 (= 10 ml min−1 in total for all NaOH concentrations tested) and the NaOH concentration was reduced by diluting the 0.57 M NaOH solution (100%). All tubing of the flow reactor was filled initially with water that was displaced by the precursor and sodium hydroxide solution before the flow reactor reached steady state. Therefore, water passed through the magnetometer flow cell after initiating feeding (for ∼2 min), followed by a water/precursor/base solution mixture till the steady state was reached, i.e., solutions entering the magnetometer flow cell were precipitated at the precursor and sodium hydroxide solution concentration. The magnetometer signals of the five experiments using four different NaOH concentrations are shown in Fig. 8.
Again, the magnetometer signal was higher for more concentrated NaOH solutions, i.e., when co-precipitation occurred at higher pH values. For the 0.29 M (50%, Fe/OH = 0.35) and the 0.57 M (100%, Fe/OH = 0.18) NaOH base solution, the magnetometer signal clearly shows the immediate formation of magnetite after mixing.
As the magnetometer signal is expected to start plateauing as the steady state is reached, the continuous increase for the 100% NaOH solution was assigned to sedimentation of magnetic samples at this high pH as described before (see Fig. 7). It should be noted that sedimentation is an exception when synthesising MNP and can be avoided as discussed below. When the pumps were stopped after ∼7 min, the magnetometer signal kept increasing, which was attributed to the continuation of magnetite formation (in the stagnant solution) through post-nucleation MNP growth. The signal increase slowed down before the recording stopped 1.5 min later, which agrees with previous studies for this NaOH concentration (100%) showing that growth is completed within 1–3 min (yielding particles with a magnetisation of ∼60 Am2 kg−1 of washed and dried IONPs determined by SQUID magnetometry).27
For the lowest NaOH concentration (30%, 0.17 M), there was no indication of immediate magnetite formation after mixing the precursors solution with the base solution. Even when stopping the pumps, causing the solution to stay in the magnetometer flow cell where the reaction had time to proceed, the magnetometer signal did not increase. Also, for the 40% sodium hydroxide solution (0.23 M) there was no indication of immediate magnetite formation. The magnetometer signal increased, however, once the pumps stopped, showing that magnetite formed >3 s after mixing. This was confirmed by adding 4.25 m of tubing (inner diameter 1 mm) to increase the time after which the reactor effluent entered the magnetometer flow cell by 20 s, i.e., 23 s in total. This added tubing was in the form of a coiled flow inverter (CFI, see Fig. S10†) to reduce the width of the residence time distribution.42,43 The magnetometer signal was considerably higher when the CFI was used, as shown by the dashed line in Fig. 8. This confirmed the presence of magnetite 20 + 3 s after mixing the 40% NaOH with the precursor solution (Fe/OH = 0.44), demonstrating magnetite formation over this period.
This combination of a flow reactor with in-line analysis of the magnetic properties showed that: i) the time scales for magnetite formation are strongly pH dependent and higher NaOH concentrations resulted in shorter times; ii) an NaOH > 0.29 M (Fe/OH = 0.35) was required to form magnetite within the first 3 s after mixing; iii) even for the NaOH solution of the highest concentration tested (0.57 M, Fe/OH = 0.18) magnetite formation is completed within minutes and not seconds.
The in-line studies also showed that, unsurprisingly, MNP accumulation in the flow cell can bias the magnetometer signal. MNP sedimentation is an exception and happens only due to a lack of stabilisation. It must be avoided, however, in particular when synthesising magnetic materials of larger dimensions. Strategies to avoid sedimentation include periodic cleaning cycles (e.g., with an HCl solution for IONP syntheses), higher shear rates (via higher flow rates, smaller flow cell diameter, or oscillatory flow),44,45 ultra-sonication,46 or simply a vertical flow cell assembly. Another alternative is multiphase flow such as gas–liquid,47 or liquid–liquid segmented flow as commonly used for nanomaterial synthesis48,49 (and especially the high-throughput screening platforms) including IONPs.50–53 As neither air, other gases or the solvents for liquid–liquid segmented flow are magnetic, they would not interfere with the magnetometer measurements. For the flow cell described (made of PTFE tubing), a non-polar solvent would preferably wet the flow cell, hence become the hydrophobic carrier phase for an aqueous dispersed phase (here the IONP solution) that is prevented from wall contact.
Conclusion
The complexity of magnetic nanoparticle syntheses demands detailed experimental studies during process development. Here, we have presented an important step towards automated process development, i.e., on-line and in-line (facilitating in situ) magnetic characterisation of nanoparticle solutions in real-time using a flow magnetometer. The magnetometer (which is strictly speaking a susceptometer) developed primarily for flow reactors comprised a sample flow cell, made of a pick-up coil through which solution passed, placed in the centre of an induction coil (for the magnetic field generation) and a replicated reference cell filled with air. The difference in voltage induced in the sample and reference pick-up coil enabled continuous monitoring of the magnetic properties of the passing solutions.Comparator electronics improved the sensitivity of the instrument, allowing use of a high gain lock-in amplifier and the detection of marginal differences in the signals induced by the sample and reference. The high sensitivity of the flow magnetometer made it possible to monitor nanoparticle syntheses at concentrations relevant for production processes, i.e., ≤100 mM of Fe (which was demonstrated), Ni, or Co, rather than just a proof concept study using unusually high metal concentrations. This was demonstrated by monitoring two well documented syntheses of iron oxide nanoparticles, i.e., co-precipitation synthesis with sodium carbonate and sodium hydroxide as bases. With the aid of the newly developed flow magnetometer it was possible to confirm known (from previous synchrotron XRD studies) particle formation kinetics for both syntheses, but also to provide new insights. For example, for the sodium carbonate co-precipitation synthesis studied it was established that: i) the required temperature for magnetite to form is above 35 °C; ii) higher temperature accelerates magnetite formation; and iii) the onset of magnetite formation is likely to be of a stochastic nature. For the sodium hydroxide co-precipitation synthesis studied it was established that: i) magnetite forms just after synthesis initiation when the sodium hydroxide concentration is sufficiently high (>0.29 M, Fe/OH = 0.35); ii) with a ∼20 s delay at 0.23 M (Fe/OH = 0.44); and iii) not at all at lower concentrations.
The flow magnetometer developed was shown to be sensitive, robust and versatile. We anticipate that this and similar instruments open up new possibilities for magnetic nanoparticle synthesis and manufacturing, as it facilitates early stage reaction characterisation, process monitoring and control, and in particular, high-throughput screening using flow chemistry.
Associated content
Further details on the flow magnetometer fundamentals on AC susceptometry for flow chemistry such as calculations, photographs, and set-up overviews are provided in the ESI.† The NI Multisim circuit simulation file of the circuit used to balance the amplitude and phase shift are also provided online.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank the EPSRC UK for financial support (EP/M015157/1) through the Manufacturing Advanced Functional Materials (MAFuMa) scheme. We would also like to thank Albert Corredera (UCL, Department of Chemical Engineering) for his great support during the initial development and Coilcraft Inc. for providing high-quality tuneable inductances, which were essential components of the first prototype.References
- L. Gloag, M. Mehdipour, D. Chen, R. D. Tilley and J. J. Gooding, Adv. Mater., 2019, 31, 1904385 CrossRef CAS.
- K. Zhu, Y. Ju, J. Xu, Z. Yang, S. Gao and Y. Hou, Acc. Chem. Res., 2018, 51, 404–413 CrossRef CAS PubMed.
- N. T. K. Thanh, Clinical Applications of Magnetic Nanoparticles: Design to Diagnosis Manufacturing to Medicine, CRC Press Taylor & Francis Group, London, 2018 Search PubMed.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS PubMed.
- V. F. Cardoso, A. Francesko, C. Ribeiro, M. Bañobre-López, P. Martins and S. Lanceros-Mendez, Adv. Healthcare Mater., 2018, 7 Search PubMed.
- L. Wu, A. Mendoza-Garcia, Q. Li and S. Sun, Chem. Rev., 2016, 116, 10473–10512 CrossRef CAS PubMed.
- R. W. Epps, K. C. Felton, C. W. Coley and M. Abolhasani, Lab Chip, 2017, 17, 4040–4047 RSC.
- K. Abdel-Latif, R. W. Epps, C. B. Kerr, C. M. Papa, F. N. Castellano and M. Abolhasani, Adv. Funct. Mater., 2019, 29, 1970157 CrossRef.
- L. J. Pan, J. W. Tu, H. T. Ma, Y. J. Yang, Z. Q. Tian, D. W. Pang and Z. L. Zhang, Lab Chip, 2017, 18, 41–56 RSC.
- B. Pinho and L. Torrente-Murciano, React. Chem. Eng., 2020, 5, 342–355 RSC.
- R. W. Epps, M. S. Bowen, A. A. Volk, K. Abdel-Latif, S. Han, K. G. Reyes, A. Amassian and M. Abolhasani, Adv. Mater., 2020, 32, 2001626 CrossRef CAS PubMed.
- L. Bezinge, R. M. Maceiczyk, I. Lignos, M. V. Kovalenko and A. J. Demello, ACS Appl. Mater. Interfaces, 2018, 10, 18869–18878 CrossRef CAS.
- A. A. Volk, R. W. Epps and M. Abolhasani, Adv. Mater., 2021, 33, 2004495 CrossRef CAS PubMed.
- S. A. Peyman, A. Iles and N. Pamme, Chem. Commun., 2008, 1220–1222 RSC.
- A. Q. Alorabi, M. D. Tarn, J. Gómez-Pastora, E. Bringas, I. Ortiz, V. N. Paunov and N. Pamme, Lab Chip, 2017, 17, 3785–3795 RSC.
- Q. Cao, X. Han and L. Li, Lab Chip, 2014, 14, 2762–2777 RSC.
- Q. Zhang, T. Yin, R. Xu, W. Gao, H. Zhao, J. G. Shapter, K. Wang, Y. Shen, P. Huang, G. Gao, Y. Wu and D. Cui, Nanoscale, 2017, 9, 13592–13599 RSC.
- G. Lin, D. Makarov and O. G. Schmidt, Lab Chip, 2017, 17, 1884–1912 RSC.
- J. Mahin and L. Torrente-Murciano, Chem. Eng. J., 2020, 396, 125299 CrossRef CAS.
- M. Besenhard, A. LaGrow, S. Famiani, M. Pucciarelli, P. Lettieri, N. T. K. Thanh and A. Gavriilidis, React. Chem. Eng., 2020, 5, 1474 RSC.
- R. Bleul, A. Baki, C. Freese, H. Paysen, O. Kosch and F. Wiekhorst, Nanoscale Adv., 2020, 2, 4510–4521 RSC.
- M. James, R. A. Revia, Z. Stephen and M. Zhang, Nanomaterials, 2020, 10, 1–19 CrossRef PubMed.
- A. P. LaGrow, M. O. Besenhard, A. Hodzic, A. Sergides, L. K. Bogart, A. Gavriilidis and N. T. K. Thanh, Nanoscale, 2019, 11, 6620–6628 RSC.
- A. Lassenberger, T. A. Grünewald, P. D. J. van Oostrum, H. Rennhofer, H. Amenitsch, R. Zirbs, H. C. Lichtenegger and E. Reimhult, Chem. Mater., 2017, 29, 4511–4522 CrossRef CAS PubMed.
- A. Kabelitz, A. Guilherme, M. Joester, U. Reinholz, M. Radtke, R. Bienert, K. Schulz, R. Schmack, R. Kraehnert, F. Emmerling and J. Polte, CrystEngComm, 2015, 17, 8463–8470 RSC.
- Z. Schnepp, A. E. Danks, M. J. Hollamby, B. R. Pauw, C. A. Murray and C. C. Tang, Chem. Mater., 2015, 27, 5094–5099 CrossRef CAS.
- M. O. Besenhard, A. P. LaGrow, A. Hodzic, M. Kriechbaum, L. Panariello, G. Bais, K. Loizou, S. Damilos, M. Margarida Cruz, N. T. K. Thanh and A. Gavriilidis, Chem. Eng. J., 2020, 399, 125740 CrossRef CAS.
- I. Milosevic, F. Warmont, Y. Lalatonne and L. Motte, RSC Adv., 2014, 4, 49086–49089 RSC.
- V. Ström, R. T. Olsson and K. V. Rao, J. Mater. Chem., 2010, 20, 4168 RSC.
- M. P. Fernández-García, J. M. Teixeira, P. Machado, M. R. F. F. Oliveira, J. M. Maia, C. Pereira, A. M. Pereira, C. Freire and J. P. Araujo, Rev. Sci. Instrum., 2015, 86, 043904 CrossRef PubMed.
- M. P. Fernández-García, J. M. Teixeira, P. Machado, M. Enis Leblebici, J. C. B. Lopes, C. Freire and J. P. Araujo, Chem. Eng. Sci., 2015, 138, 600–606 CrossRef.
- I. Pérez, J. Á. H. Cuevas and J. T. E. Galindo, Eur. J. Phys., 2018, 39, 035203 CrossRef.
- A. G. Próspero, C. C. Quini, A. F. Bakuzis, P. Fidelis-de-Oliveira, G. M. Moretto, F. P. F. Mello, M. F. F. Calabresi, R. V. R. Matos, E. A. Zandoná, N. Zufelato, R. B. Oliveira and J. R. A. Miranda, J. Nanobiotechnol., 2017, 15, 22 CrossRef PubMed.
- E. R. Price, A. L. Khoury, L. J. Esserman, B. N. Joe and M. D. Alvarado, Am. J. Roentgenol., 2018, 210, 913–917 CrossRef PubMed.
- M. M. van de Loosdrecht, S. Waanders, H. J. G. Krooshoop and B. ten Haken, J. Magn. Magn. Mater., 2019, 475, 563–569 CrossRef CAS.
- M. P. Nikitin, A. V. Orlov, I. L. Sokolov, A. A. Minakov, P. I. Nikitin, J. Ding, S. D. Bader, E. A. Rozhkova and V. Novosad, Nanoscale, 2018, 10, 11642–11650 RSC.
- N. V. Guteneva, S. L. Znoyko, A. V. Orlov, M. P. Nikitin and P. I. Nikitin, Microchim. Acta, 2019, 186, 1–9 CrossRef CAS PubMed.
- S. L. Znoyko, A. V. Orlov, V. A. Bragina, M. P. Nikitin and P. I. Nikitin, Talanta, 2020, 216, 120961 CrossRef CAS PubMed.
- M. J. Jacinto, J. R. C. Trabuco, B. V. Vu, G. Garvey, M. Khodadady, A. M. Azevedo, M. R. Aires-Barros, L. Chang, K. Kourentzi, D. Litvinov and R. C. Willson, PLoS One, 2018, 13, 1–14 CrossRef PubMed.
- C. Blanco-Andujar, D. Ortega, Q. A. Pankhurst and N. T. K. Thanh, J. Mater. Chem., 2012, 22, 12498 RSC.
- M. O. Besenhard, L. Panariello, C. Kiefer, A. P. LaGrow, L. Storozhuk, F. Perton, S. Begin, D. Mertz, N. T. K. Thanh and A. Gavriilidis, Nanoscale, 2021, 13, 8795–8805 RSC.
- M. Schmalenberg, W. Krieger and N. Kockmann, Chem. Ing. Tech., 2019, 91, 567–575 CrossRef CAS.
- D. Rossi, L. Gargiulo, G. Valitov, A. Gavriilidis and L. Mazzei, Chem. Eng. Res. Des., 2017, 120, 159–170 CrossRef CAS.
- P. Bianchi, J. D. Williams and C. O. Kappe, J. Flow Chem., 2020, 10, 475–490 CrossRef CAS.
- B. J. Doyle, B. Gutmann, M. Bittel, T. Hubler, A. Macchi and D. M. Roberge, Ind. Eng. Chem. Res., 2020, 59, 4007–4019 CrossRef CAS.
- Z. Dong, C. Delacour, K. Mc Carogher, A. P. Udepurkar and S. Kuhn, Materials, 2020, 13, 344 CrossRef CAS PubMed.
- M. O. Besenhard, P. Neugebauer, O. Scheibelhofer and J. G. Khinast, Cryst. Growth Des., 2017, 17, 6432–6444 CrossRef CAS PubMed.
- Y. He, K.-J. Kim and C. Chang, Nanomaterials, 2020, 10, 1421 CrossRef CAS PubMed.
- V. Sebastian Cabeza, S. Kuhn, A. A. Kulkarni and K. F. Jensen, Langmuir, 2012, 28, 7007–7013 CrossRef CAS PubMed.
- L. Panariello, G. Wu, M. O. Besenhard, K. Loizou, L. Storozhuk, N. T. K. Thanh and A. Gavriilidis, Materials, 2020, 13, 1019 CrossRef CAS PubMed.
- L. Frenz, A. El Harrak, M. Pauly, S. Bégin-Colin, A. D. Griffiths and J.-C. Baret, Angew. Chem., Int. Ed., 2008, 47, 6817–6820 CrossRef CAS PubMed.
- K. Kumar, A. M. Nightingale, S. H. Krishnadasan, N. Kamaly, M. Wylenzinska-Arridge, K. Zeissler, W. R. Branford, E. Ware, A. J. deMello and J. C. deMello, J. Mater. Chem., 2012, 22, 4704 RSC.
- A. Larrea, V. Sebastian, A. Ibarra, M. Arruebo and J. Santamaria, Chem. Mater., 2015, 27, 4254–4260 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1lc00425e |
| This journal is © The Royal Society of Chemistry 2021 |