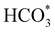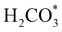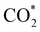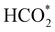Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of surface oxidation and Fe–Ni synergy in Fe–Ni–S catalysts for CO2 hydrogenation†‡
Claire E.
Mitchell
 a,
David
Santos-Carballal
a,
David
Santos-Carballal
 b,
Andrew M.
Beale
b,
Andrew M.
Beale
 cd,
Wilm
Jones
cd,
Wilm
Jones
 cd,
David J.
Morgan
cd,
David J.
Morgan
 a,
Meenakshisundaram
Sankar
a,
Meenakshisundaram
Sankar
 *a and
Nora H.
de Leeuw
*a and
Nora H.
de Leeuw
 *abe
*abe
aCardiff Catalysis Institute, School of Chemistry, Cardiff University, Cardiff, CF10 3AT, UK. E-mail: Sankar@cardiff.ac.uk
bSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK. E-mail: n.h.deleeuw@leeds.ac.uk
cDepartment of Chemistry, University College London, London, WC1H 0AJ, UK
dResearch Complex at Harwell, Rutherford Appleton Laboratory, Harwell Science & Innovation Campus, Harwell, Didcot, OX11 0FA, UK
eDepartment of Earth Sciences, Utrecht University, Princetonlaan 8a, 3584 CB Utrecht, The Netherlands
First published on 20th January 2021
Abstract
Increasing carbon dioxide (CO2) emissions, resulting in climate change, have driven the motivation to achieve the effective and sustainable conversion of CO2 into useful chemicals and fuels. Taking inspiration from biological processes, synthetic iron–nickel-sulfides have been proposed as suitable catalysts for the hydrogenation of CO2. In order to experimentally validate this hypothesis, here we report violarite (Fe,Ni)3S4 as a cheap and economically viable catalyst for the hydrogenation of CO2 into formate under mild, alkaline conditions at 125 °C and 20 bar (CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1
H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Calcination of violarite at 200 °C resulted in excellent catalytic activity, far superior to that of Fe-only and Ni-only sulfides. We further report first principles simulations of the CO2 conversion on the partially oxidised (001) and (111) surfaces of stoichiometric violarite (FeNi2S4) and polydymite (Ni3S4) to rationalise the experimentally observed trends. We have obtained the thermodynamic and kinetic profiles for the reaction of carbon dioxide (CO2) and water (H2O) on the catalyst surfaces via substitution and dissociation mechanisms. We report that the partially oxidised (111) surface of FeNi2S4 is the best catalyst in the series and that the dissociation mechanism is the most favourable. Our study reveals that the partial oxidation of the FeNi2S4 surface, as well as the synergy of the Fe and Ni ions, are important in the catalytic activity of the material for the effective hydrogenation of CO2 to formate.
1). Calcination of violarite at 200 °C resulted in excellent catalytic activity, far superior to that of Fe-only and Ni-only sulfides. We further report first principles simulations of the CO2 conversion on the partially oxidised (001) and (111) surfaces of stoichiometric violarite (FeNi2S4) and polydymite (Ni3S4) to rationalise the experimentally observed trends. We have obtained the thermodynamic and kinetic profiles for the reaction of carbon dioxide (CO2) and water (H2O) on the catalyst surfaces via substitution and dissociation mechanisms. We report that the partially oxidised (111) surface of FeNi2S4 is the best catalyst in the series and that the dissociation mechanism is the most favourable. Our study reveals that the partial oxidation of the FeNi2S4 surface, as well as the synergy of the Fe and Ni ions, are important in the catalytic activity of the material for the effective hydrogenation of CO2 to formate.
Introduction
Although CO2 acts as a pollutant, contributing to climate change and global warming, it can also be considered as a cheap and abundant C-1 building block for the production of simple carbon-based chemicals.1,2 A barrier to this prospective beneficial use is the requirement to overcome the initial thermodynamically unfavourable CO2 reduction step.3 In contrast to synthetic catalysts,4–6 nature has developed a sophisticated reaction pathway utilising mixed Fe–Ni clusters for efficient CO2 reduction.7 In prokaryotes, the core enzyme within the acetyl-CoA pathway, carbon monoxide dehydrogenase (CODH), is coupled with acetyl-CoA synthase (ACS). In a dual active site reaction, the reduction of CO2 to CO is thought to occur with the help of electrons at the asymmetric [Ni–4Fe–5S] clusters.8,9 The structures of these metal clusters within CODH–ACS are very similar to mineral forms of (Fe,Ni)S, leading to the intriguing theory that these minerals participated as catalysts in the early onset of life.8–12 The electronic interaction between Fe and Ni has been well established to enhance catalytic performance.13,14 The flexibility in coordination and charge transfer of Ni enables an important role in biological catalysis, which can also be relayed to chemical catalysis.15 The synergy between Fe and Ni has been reported to lead to excellent catalytic performance for the reduction of CO2 into methane16 and CO,17 and the reduction of HCO3− to formic acid;18 the bimetallic materials outperform their analogous monometallic counterparts, which can be attributed to intermediate bond strengthening.17,18 In 2019, Piontek et al.11 synthesised and developed the pentlandite mineral, Fe4.5Ni4.5S8, to mimic [NiFe] hydrogenase, which successfully performed in the electrocatalytic carbon dioxide reduction reaction (CO2RR). Using aprotic solvents, CO2RR was favoured over the hydrogen evolution reaction, with the main products of CO and methane. Despite the relatively unremarkable products, Piontek has shown the potential of these materials. The electrocatalytic abilities of the iron sulphide mineral greigite, Fe3S4, have also achieved success in the hydrogenation of CO2,19 albeit with low yields. Recently, we have reported the pyrrhotite material Fe1−xS as an effective catalyst for the hydrogenation of CO2via a HCO3− intermediate.20,21 Calcination of the pyrrhotite catalyst increased the activity of the material, as a result of the formation of a unique O–Fe–S active site. The iron–nickel sulfide violarite, (Fe,Ni)3S4, is isostructural with greigite, and introducing Ni into this structure may therefore produce an even more successful catalyst as a result of the discussed enhanced electronic interaction. The Fe and Ni within violarite are distributed over tetrahedral and octahedral sites in a cubic close packed (ccp) array of S atoms.22 Within the inverse thiospinel structure, half of the Ni cations occupy the tetrahedral sites, with the other Ni cations and the Fe atoms located in the octahedral positions.23,24 The interaction of CO2 with violarite has been compared to that with greigite (Fe3S4) in a computational study,24 where replacing an Fe atom by Ni exhibited a strengthening effect on the binding of the CO2 molecule, although not enough to activate it. Iron, nickel and sulphur are cheap, non-toxic, and readily available elements and catalysts made from them are therefore ideal for large-scale use, particularly if the reactions can occur under moderate reaction conditions.In general, the low-Miller index surfaces are the most stable in spinel structured materials, expressed in both the computational25 and experimental crystal morphologies of natural26 and synthetic samples.27 The octahedral crystal habits of spinels are typically enclosed by (111) surfaces, where the corners may be truncated by (001) planes.25,27 For example, the (001) and (111) surfaces have been prominent in high resolution transmission electron microscopy (HRTEM) images of polydymite (Ni3S4).28,29 Moreover, density functional theory (DFT) simulations have also suggested that the low-Miller index planes of violarite (FeNi2S4) have the lowest surface energies.30 The (001) and (111) facets of FeNi2S4 have been the subject of a number of studies, where their adsorption and catalytic properties towards H2O30 and CO2 (ref. 31) have been assessed.
Building upon the foundation of previous work, here we report for the first time the facile synthesis, characterisation and catalytic application of violarite for the hydrogenation of CO2. In tandem, we have employed DFT techniques to calculate the CO2 conversion into formate in the presence of H2O on the partially oxidised low-Miller index (001) and (111) surfaces of FeNi2S4 and Ni3S4. We have simulated the co-adsorption of the reactants on the partially oxidised sulfide surfaces, alongside the mechanistic pathways leading to the formation of formate, to examine their change of activity upon oxidation. Through investigation of the proposed synergy between Fe and Ni in the partially oxidised surfaces, violarite is revealed to be an excellent candidate to catalyse CO2 hydrogenation into formate.
Materials and methods
Catalyst preparation
The (Fe,Ni)S synthesis was adapted21 from the procedure reported by Beal et al.32 using the following chemicals: iron(II) acetylacetonate Fe(acac)2 (99.9%) (Molekula), nickel(II) acetylacetonate Ni(acac)2 (Sigma Aldrich), sulfur (sublimed) (99.5%) (Alfa Aesar) and oleylamine (OAm) (70%) (Sigma Aldrich). The synthesis was carried out in a three-necked flask equipped with a condenser, temperature probe and magnetic stirrer bar. OAm was initially degassed by bubbling nitrogen rapidly for 30 minutes, and the synthesis was done under a nitrogen atmosphere. Fe(acac)2 and/or Ni(acac)2 (4.5 mmol, precursor molar ratios listed in Table 1) and sulfur (0.147 g, 4.5 mmol) were placed in a flask, and flushed with nitrogen. The degassed OAm (60 cm3) was added and stirred to produce a dark red suspension. While constantly bubbling nitrogen through the reaction mixture, the suspension was rapidly heated to 310 °C and held for 12 hours before being cooled to room temperature. To remove the OAm, acetone was added (40 cm3), followed by centrifugation and the removal of the organic brown supernatant layer. To wash the black (Fe,Ni)S nanocrystals, the solid was then resuspended in toluene (Sigma Aldrich, 99.8%), followed by centrifugation. This step was repeated until the supernatant was clear and colourless. The sample was then left in a vacuum oven at room temperature overnight and stored as a powder in a sealed vial flushed with N2.| Sample number | Fe(acac)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni(acac)2 Ni(acac)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sulfur (molar ratio) sulfur (molar ratio) |
Dominant structure(s) | |
|---|---|---|---|
| Fresh | Calcined | ||
| 1 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Fe1−xS | Amorphous |
| 2 | 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.25 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Fe1−xS/Ni3S2/(Fe,Ni)3S4 | (Fe,Ni)3S4 |
| 3 | 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
(Fe,Ni)3S4 | (Fe,Ni)3S4 |
| 4 | 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.75 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Ni3S2 | (Fe,Ni)3S4/NiS* |
| 5 | 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Ni3S4/Ni3S2 | Ni3S4* |
Calcination of the powder was performed in a furnace with air flowing at a specific temperature, typically 200 °C, with a ramp rate of 5 °C min−1, and the temperature was maintained for 4 hours. The material was then cooled to room temperature before being stored in a sealed vial flushed with N2.
Catalytic CO2 hydrogenation and product analyses
The hydrogenation of CO2 to formate was carried out in a high-pressure stainless steel 10 mL autoclave reactor. In a typical reaction, 20 mg of the catalyst was charged in a glass liner containing 4 mL of 1 M NaOH and a stirrer bar; the glass liner was placed inside the autoclave reactor before the reactor was closed airtight. The reactor and its contents were first purged with N2 (3 times) and then with CO2 (3 times) to remove traces of air or oxygen from the system and then finally charged with 30 bar CO2. The CO2 was left to dissolve for 20 minutes at room temperature before the pressure was reduced to 10 bar, and then H2 (10 bar) was added. Next, the reactor was heated to the reaction temperature (125 °C) while stirring at 1450 rpm. After 3 days of reaction, the reactor was cooled using an ice bath, the liquid sample was collected, and the solid catalyst was removed via centrifugation followed by filtration using a syringe filter fitted with a 45 μL filter tip. The identity of the product (HCOOH) was confirmed and quantified using proton nuclear magnetic resonance (1H-NMR) analysis (Bruker 500 MHz spectrometer), where 0.7 mL of the reaction solution was mixed with 0.1 mL D2O (for lock) and a sealed glass tube insert containing 1% tetramethylsilane (TMS) in CDCl3 as an internal standard. A series of known standard solutions of formic acid were calibrated against the TMS insert, generating a calibration curve and response factors which were used for quantitative analyses of the reaction mixtures.Catalyst characterisation
Computational details
The Vienna Ab initio Simulation Package (VASP) code was used to carry out spin-polarized simulations of all structures and energies within the usual Kohn–Sham implementation of density functional theory (DFT).33–36 The meta-generalized gradient approximation (meta-GGA) was employed with the strongly constrained and appropriately normed (SCAN) semi-local density functional.37Meta-GGA functionals include the electron density as well as its first and second derivatives, the electron gradient and the non-interacting kinetic energy density terms, respectively, making them more accurate than their parent GGA approximations, which only have the first two types of contributions.38–40 In particular, only the SCAN functional satisfies all 17 known exact constraints within the meta-GGA approach.37 The inner electrons, comprising the levels [Ar] for Ni and Fe, [Ne] for S and [He] for O and C, the kinetic energy of the core states and the interaction with the valence states were described by the projector augmented wave (PAW) method,41,42 whereas the electron of the H atom was treated as a valence electron. The non-spherical contributions to the gradient of the density were also included within the PAW spheres, which is essential for an appropriate simulation of the Ni and Fe d electrons when using meta-GGA functionals. Long-range dispersion interactions were applied using the D2 semi-empirical method of Grimme,43 which is needed to describe properly the bulk and surface properties of different materials.31,44–52 The Kohn–Sham valence states were expanded in a periodic plane-wave basis set with a cut-off fixed at 400 eV for the kinetic energy. The optimisation of the electronic density was considered converged when the energy difference between two consecutive self-consistent loop steps was below 10−5 eV. We have used the Hubbard approximation53 in the form of the scheme by Dudarev et al.54 to improve the description of localized d states in the transition metal atoms. The values for the on-site Coulomb interaction term in this study were Ueff = 1.7 eV for Fe and 2.0 eV for Ni, which were developed by fitting the simulated lattice parameters of the pure greigite (Fe3S4) and Ni3S4 to their experimental values. The geometries were relaxed using an efficient conjugate-gradients technique based on the Newton line optimizer,55,56 which was stopped when the Hellmann–Feynman forces on all atoms were smaller than 0.01 eV Å−1. The saddle points and minimum energy paths (MEPs) between initial and final states were simulated using the climbing image nudged elastic band (cNEB) approach.57,58 We used five images to model the MEP, which were optimised globally by means of the limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) method.55,59 The saddle points were characterised by single imaginary frequencies along the reaction coordinate, which were determined using the central finite differences method. These criteria allowed convergence of the total electronic energy to within 1 meV per atom.The electronic integrations of the (001) and (111) surfaces of the thiospinels were calculated in reciprocal space using a Γ-centred Monkhorst–Pack (MP) sampling grid60 containing 3 × 3 × 1 k-points, which ensured a minimum spacing of 0.14 Å−1 between k-points. However, the projection operators were evaluated in real space. The electronic partial occupancies were determined using the Gaussian smearing method with a smearing width of 0.05 eV. The tetrahedron method with Blöchl corrections61 was used to obtain very accurate total energies. The isolated molecules were modelled in a cell with broken symmetry of 10.0 × 10.5 × 11.0 Å3, considering only the Γ point of the Brillouin zone.
The simulation cell of the thiospinel surfaces contained 56 atoms, distributed as 4 repeat formula unit (f.u.) layers stacked along the direction perpendicular to the surface. The two bottom-most repeat f.u. layers were kept frozen at their relaxed bulk positions, while the remaining layers were allowed to relax. A vacuum of 10 Å was added between the periodic images of the slab in the direction perpendicular to the surface. The ferrimagnetic configuration was considered for the thiospinels in our simulations, where the initial magnetic moments of the tetrahedral and octahedral sublattices were set antiparallel, with the ions in the high-spin state.25,31,47,62–67 Dipole corrections perpendicular to the surface were applied in our simulations to account for any dipole created by the adsorbates.
The adsorption energies (Eads) were defined as the difference between the energy of the surface slab containing the adsorbates and the sum of the energies of the isolated adsorbates and surface slab. The activation energy (Eai) was calculated as the difference between the energy of the saddle point and the energy of the reactants, where the index i refers to each of the four elemental steps that we simulated. The energy of the elemental step (ΔEi) was obtained as the difference between the energy of the products and the energy of the reactants.
Results and discussion
Catalytic testing and optimisation
(Fe,Ni)S catalysts were tested for the hydrogenation of CO2 under hydrothermal conditions, using 1 M NaOH solvent, applying 20 bar pressure (at 25 °C CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2, 1
H2, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) before heating to a reaction temperature of 125 °C. Dissolution of CO2 in alkaline aqueous media forms bicarbonate,5 the desired intermediate for this reaction owing to the improved adsorption properties of HCO3− in comparison to CO2.18 To initiate this study, the catalyst synthesis procedure was first optimised. Iron nickel sulfide materials were synthesised by altering the Fe(acac)2
1) before heating to a reaction temperature of 125 °C. Dissolution of CO2 in alkaline aqueous media forms bicarbonate,5 the desired intermediate for this reaction owing to the improved adsorption properties of HCO3− in comparison to CO2.18 To initiate this study, the catalyst synthesis procedure was first optimised. Iron nickel sulfide materials were synthesised by altering the Fe(acac)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni(acac)2 precursor molar ratios, as presented in Table 1. All 5 samples were also calcined in flowing air at 200 °C to provide a series of 5 fresh and 5 calcined catalysts, which were tested for CO2 hydrogenation. As presented in Fig. 1a, the freshly prepared FexNiySz catalysts showed good performance for CO2 hydrogenation in comparison to the monometallic iron and nickel sulfides. Sample 3, prepared with a 1
Ni(acac)2 precursor molar ratios, as presented in Table 1. All 5 samples were also calcined in flowing air at 200 °C to provide a series of 5 fresh and 5 calcined catalysts, which were tested for CO2 hydrogenation. As presented in Fig. 1a, the freshly prepared FexNiySz catalysts showed good performance for CO2 hydrogenation in comparison to the monometallic iron and nickel sulfides. Sample 3, prepared with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Fe
1 Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni precursor ratio, outperformed all other catalysts, producing 1.8 μmol of formate, in comparison to iron and nickel sulfides which produced 0.3 μmol and 1.2 μmol of formate, respectively. Calcining the samples improved the catalytic activity of all samples, with sample 3 again providing the best catalytic performance, producing 4.9 μmol of formate.
Ni precursor ratio, outperformed all other catalysts, producing 1.8 μmol of formate, in comparison to iron and nickel sulfides which produced 0.3 μmol and 1.2 μmol of formate, respectively. Calcining the samples improved the catalytic activity of all samples, with sample 3 again providing the best catalytic performance, producing 4.9 μmol of formate.
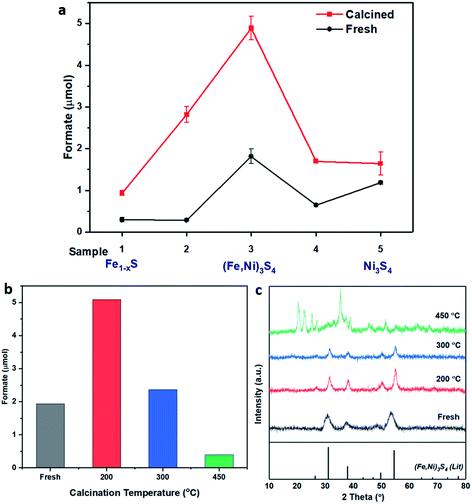 | ||
Fig. 1 (a) Catalyst comparison of fresh (black) and calcined (red) iron nickel sulfides with altering Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni ratio during synthesis. Sample preparation and labelling described in Table 1. Comparison of (b) formate productivity and (c) XRD of sample 3, (Fe,Ni)3S4: fresh (grey), calcined at 200 °C (red), 300 °C (blue) and 450 °C (green). Compared to violarite reference file (JCPDS 00-002-0779 PDF file). Reaction conditions: (Fe,Ni)S catalyst: 20 mg; 1 M NaOH solution: 4 mL; p(CO2): 10 bar (at 25 °C); p(H2): 10 bar (at 25 °C); reaction temperature: 125 °C; reaction time: 3 days. Ni ratio during synthesis. Sample preparation and labelling described in Table 1. Comparison of (b) formate productivity and (c) XRD of sample 3, (Fe,Ni)3S4: fresh (grey), calcined at 200 °C (red), 300 °C (blue) and 450 °C (green). Compared to violarite reference file (JCPDS 00-002-0779 PDF file). Reaction conditions: (Fe,Ni)S catalyst: 20 mg; 1 M NaOH solution: 4 mL; p(CO2): 10 bar (at 25 °C); p(H2): 10 bar (at 25 °C); reaction temperature: 125 °C; reaction time: 3 days. | ||
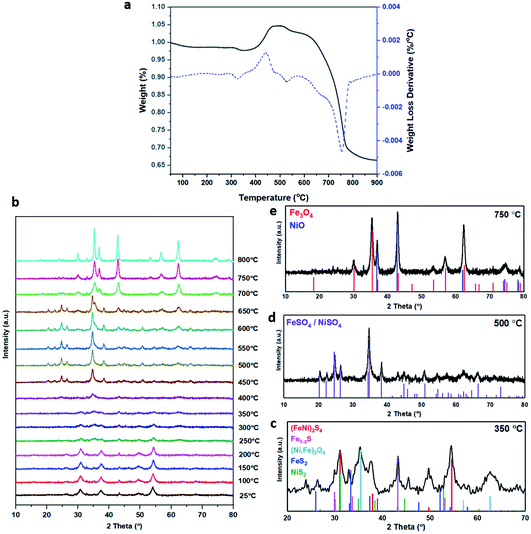
The XRD pattern of the most active material, sample 3, presented in Fig. 1c, exhibits four major reflections, observed at 2θ values of approximately 31°, 38°, 50° and 55°, corresponding to the iron–nickel sulfide mineral violarite (Ni,Fe)3S4. The Fe-only sulfide, sample 1, corresponds to the pyrrhotite structure, Fe1−xS, while the Ni-only sulfide, sample 5, predominantly consists of a polydymite (Ni3S4) structure; these structures are determined by the XRD diffraction patterns, presented in Fig. S1.† Samples 2 and 4 presented a mixture of Fe1−xS, NiS, Ni3S2 and (Fe,Ni)3S4 structures, also observed in the XRD patterns. All XRD profiles are displayed and compared in Fig. S1.† A calcination pre-treatment at 200 °C enhanced violarite formation, observed as an increase in XRD peak intensity (Fig. 1c), and improved the catalytic activities for all 5 samples (Fig. 1a). This enhanced activity was previously discovered in pyrrhotite.21 The results show that Fe1−xS and Ni3S4 have lower activity compared to (Fe,Ni)3S4, suggesting a synergy effect between Fe and Ni atoms. Increasing the calcination pre-treatment temperature to 300 °C and 450 °C lowers formate production to 2.4 and 0.4 μmol, respectively (see Fig. 1b). Calcination at 300 °C decreases the violarite crystallinity, as displayed in Fig. 1c, and at 450 °C iron and nickel sulfates and oxides begin to form, as discussed below. Commercial sources of Fe3O4, NiSO4 and FeSO4 were found to produce formate at a much lower quantity than all FexNiySz samples synthesised here (see Table S1†), ruling out iron oxides or nickel sulfate as active species for CO2 hydrogenation under these reaction conditions.
Calcination study and material characterisation
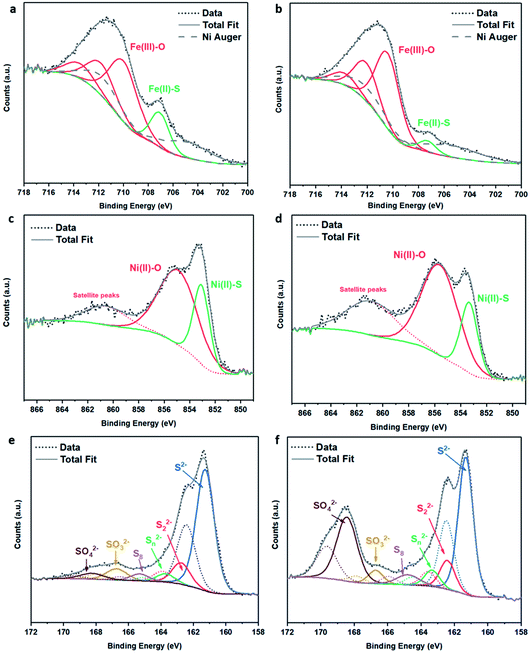 | ||
| Fig. 3 XPS spectra of (Fe,Ni)3S4: (a) Fe 2p fresh, (b) Fe 2p calcined at 200 °C, (c) Ni 2p fresh, (d) Ni 2p calcined at 200 °C, (e) S 2p fresh, (f) S 2p calcined at 200 °C. | ||
The S 2p spectra are fitted with a doublet representing the spin–orbit splitting into S 2p3/2 and S 2p1/2 lines (Fig. 3e and f) and show the presence of many sulfur species, which we ascribe to monosulfide (161.3 eV), disulfide (162.6 eV), polysulfide (163.2 eV) and elemental sulfur (165.1 eV), together with sulfites SO32− (166.8 eV) and sulfates SO42− (168.5 eV). These binding energies are in excellent agreement with Buckley et al.72 and Pratt et al.73 Upon exposure to air, the migration of Fe and Ni towards the surface to combine with oxygen causes metal–sulfur bond cleavage and leaves metal vacancies within the structure, which forces the formation of S–S disulfide and polysulfide bonds. The formation of disulfides and polysulfides requires the oxidation of some sulfide (S2−), which explains the presence of elemental sulfur,73 as discussed in detail in our recent paper.21 The S 2p XPS spectra reveal that the intensity of the Fe–S monosulfide peak at 161.3 eV significantly decreases, owing to the formation of SOx species, which leaves Fe vacancies, thereby forcing the remaining Fe(II)–S to form disulfide bonds, as evident from Table S2.† The Fe 2p and Ni 2p spectra of fresh (Ni,Fe)3S4 can be compared to those of synthesised Fe1−xS and Ni3S4 samples (see Fig. S2 and Table S3†). The XPS spectra of (Fe,Ni)3S4 calcined at 300 °C (as shown in Fig. S3 and Table S4†) can be compared to those of the optimised sample calcined at 200 °C, providing further understanding of the active sites, and why increased thermal oxidation causes a drop in activity. The Fe 2p spectra (see Fig. S3a†) show a further drop in Fe(II)–S content, with the binding energy of Fe–S exhibiting a +0.8 eV shift in binding energy to 708.1 eV. In this range, Fe–S is becoming more oxidised, forming more Fe(III)–S character.74 The Ni 2p spectrum loses Ni(II)–S character and exhibits new peaks at 855.6 eV and 858.8 eV, corresponding to the formation of NiSO4, correlating with the work of Legrand.75 The S 2p spectrum reveals a drop in monosulfide content and an increase in disulfide content as more metal–sulfide bonds are cleaved in favour of metal oxides. The evidence for Fe(III)–S and NiSO4 shows that the enhanced interaction between Fe and Ni is lost. The atomic Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ni
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S
S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratios in fresh and calcined (Fe,Ni)3S4 samples were calculated as approximately 12
O ratios in fresh and calcined (Fe,Ni)3S4 samples were calculated as approximately 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 and 10
42 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, respectively, corresponding to a highly oxidised surface, although surface sulfur was still present after calcination. The crucial role of surface oxygen and sulfur is discussed in detail in the computational findings below.
60, respectively, corresponding to a highly oxidised surface, although surface sulfur was still present after calcination. The crucial role of surface oxygen and sulfur is discussed in detail in the computational findings below.
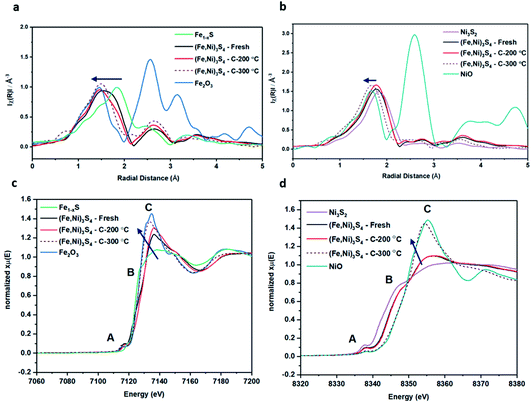
XANES analysis provides the opportunity to study the iron K-edge and nickel K-edge, presented in Fig. 4c and d, respectively. First to note is a characteristic pre-edge (feature A) from the contribution of the Fe/Ni 1s to Fe/Ni 3d transition.65,81 There is a shoulder to the edge (B), indicating the coordination between Fe/Ni and S and representing the normally forbidden Fe/Ni 1s to Fe/Ni 4s transition. There is also white line intensity (C), corresponding to the first allowed Fe/Ni 1s to Fe/Ni 4p transition.65,81 Fe/Ni oxide can be characterised by a sharp white line intensity (C), while Fe/Ni sulfide displays a broad XANES edge. Within the Fe XANES K-edge, there is an intense peak at feature C for the fresh violarite sample and the sample calcined at 200 °C, compared to Fe1−xS, which confirms the presence of an Fe oxide-like character within the violarite material. The Ni XANES edge at region C is broad and without oxide character below 200 °C calcination temperature. Calcining the material at 300 °C causes an increase in intensity at C for both Fe and Ni, as Fe–S and Ni–S character is lost, forming Fe3O4, FeSO4 and NiSO4 structures, as indicated by XRD and illustrated in Fig. 2c. In the Ni XANES spectrum (see Fig. 4d), the shoulder at B indicates the coordination between Ni and S as seen for Ni3S2. Ni in Ni3S2 adopts tetrahedral coordination, exhibiting lower energy, while in NiO it adopts octahedral coordination, exhibiting higher energy. Violarite presents a shoulder at feature B, with higher energy than Ni3S2 and lower energy than NiO, indicating that Ni–S contributes mixed tetrahedral and octahedral sites. Feature A is also consistent with the expected tetrahedral/octahedral Ni environments of violarite, namely the feature is higher energy for tetrahedral Ni environments (Ni3S2) due to lack of inversion symmetry around the metal ion. Thus, at feature A violarite exhibits a lower energy than the Ni3S2 tetrahedral environment and a higher energy than the NiO octahedral environment due to its mixed Ni geometry. Calcination at 200 °C appears to have little effect on the coordination of nickel, but increasing the calcination temperature to 300 °C causes a shift to higher energy at feature B and lower energy at feature A, indicating dominant Ni–O character and octahedral coordination. The Fe XANES spectrum in Fig. 4c also reveals coordination information. Still focusing on shoulder edge B, violarite lies at a higher energy than Fe1−xS and Fe2O3. In Fe1−xS and Fe2O3, iron adopts Fe(III) high-spin state octahedral coordination, although tetrahedral Fe coordination would possess lower energy, while the higher energy of the iron in violarite is the result of octahedral coordination in the Fe(II) low-spin state.80 Upon calcination at 200 °C, Fe shifts only marginally to a higher energy at feature B as Fe replaces sulfur with oxygen ligands whilst maintaining the Fe(II) low-spin state, whereas calcination at 300 °C causes a large shift to lower energy, caused by the transformation into iron oxide, with the Fe(III) high-spin state and octahedral coordination. It may be deduced that Fe–O species are forming, while Ni remains stable as coordinated Ni–S within the bulk. Fe–O formation within iron sulfide structures has previously resulted in enhanced catalytic capabilities, which is discussed in detail in previous work.21 We should remember that the metal oxidation states are Fe2+Ni23+S4 in bulk violarite. Fe(III) has a high redox potential situated at +0.77 eV, and is thus easily reduced. Using supporting evidence from XPS and XAFS, we can conclude that Ni(III) in violarite is capable of maintaining Fe(II) in the lower oxidation state. This is vital for stabilising these important S–Fe–O active sites, resulting in improved catalytic activity compared to the pyrrhotite structure, where nickel is absent.21
Calculated reaction profiles
Our initial experimental findings, discussed above, have shown that surface-oxidised violarite is a superior catalyst for the hydrogenation of CO2 compared to its Fe-only and Ni-only counterparts. We aim to aid the rationalisation of the catalytic trends observed in the experiments for our thiospinels through calculations based on density functional theory (DFT), where we apply and complement the knowledge gained from the materials characterisation. As such, we have studied the catalytic properties of the partially oxidised (001) and (111) surfaces of FeNi2S4 and Ni3S4 by simulating the co-adsorption and conversion of CO2 and H2O into formate and surface hydroxyls. We have decided to use the FeNi2S4 composition, which we identified in previous work to be dominant, with a very exothermic minimum, in the thermodynamic mixing between greigite and polydymite.82We have used the most stable non-polar terminations to simulate the (001) and (111) surfaces, which were created from the bulk FeNi2S4 (ref. 83) and Ni3S4 (ref. 83) thiospinels using METADISE.84 The most stable terminations of both the (001) and (111) facets were reconstructed Tasker type 3 surfaces, where half of the cations were shifted from the exposed layer of the relaxed side to the unrelaxed side of the slab to remove the unrealistic dipole perpendicular to the surface.85 The simulations of the (001) surfaces were performed using a slab terminated in the bulk plane, comprising S atoms and octahedral cations and decorated by 0.5 monolayer (ML) of tetrahedral ions arranged in 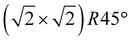 symmetry. The calculations of the (111) surface were carried out using a cell terminated by the face-centred cubic (fcc) close-packed plane of S atoms, decorated by 0.5 ML of both tetrahedral and octahedral ions, forming an incomplete hexagonal honeycomb arrangement. The partially oxidised surfaces were obtained by replacing 75% of the S atoms by O in the topmost layer of the surfaces, in as close agreement as possible with the XPS findings. We tested different scenarios and found that the substitution of the most coordinated S atoms led to the ground state configurations of the partially oxidised slabs, which are defined as o-FeNi2S4 and o-Ni3S4.
symmetry. The calculations of the (111) surface were carried out using a cell terminated by the face-centred cubic (fcc) close-packed plane of S atoms, decorated by 0.5 ML of both tetrahedral and octahedral ions, forming an incomplete hexagonal honeycomb arrangement. The partially oxidised surfaces were obtained by replacing 75% of the S atoms by O in the topmost layer of the surfaces, in as close agreement as possible with the XPS findings. We tested different scenarios and found that the substitution of the most coordinated S atoms led to the ground state configurations of the partially oxidised slabs, which are defined as o-FeNi2S4 and o-Ni3S4.
The reduction of CO2 by H2 to produce HCOO− under alkaline conditions takes place according to the equation:
| CO2(g) + H2(g) + OH−(aq) = HCOO−(aq) + H2O(l). | (1) |
In order to simplify the computational simulation of eqn (1), we have considered that CO2, once dissolved, reacts with OH−(aq), producing bicarbonate [HCO3−(aq)] as
| CO2(g) + OH−(aq) = HCO3−(aq). | (2) |
We have also assumed that H2 adsorbs dissociatively on the spinel sulfides, as we have seen this behaviour on greigite:86
| H2(g) = 2H*, | (3) |
The combination of eqn (1)–(3) leads to the simplified chemical reaction simulated in this work for the conversion of CO2 into HCOO−:
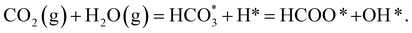 | (4) |
Note that we have not represented the solubility of gaseous CO2 and H2 in water or the vapour pressure of H2O in equilibrium with its condensed phase, as these processes occur in the liquid phase before any interaction of these species with the surface of the catalysts. The gaseous species are treated as isolated molecules in our calculations.
We have intentionally not considered the desorption of the final products HCOO* and OH*, since that would entail modelling isolated charged species. In the context of our simulations, the surface supercell of the Fe–Ni sulfides is wide enough to act as a source or sink of electrons, ensuring that the final adsorbed products are negatively charged, similar to the way that spin-forbidden reactions are allowed in heterogeneous catalysis.87,88
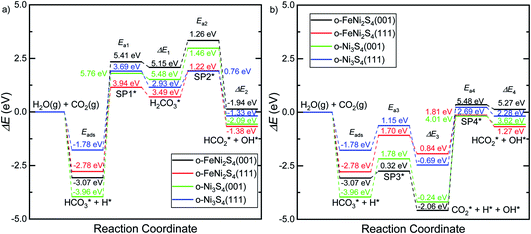
Fig. 5 displays the minimum energy pathways (MEPs) for CO2 reduction by H2O on the (001) and (111) surfaces of the o-FeNi2S4 and o-Ni3S4 thiospinels. We first modelled the co-adsorption of CO2 and H2O, which provides the elements needed to produce HCOO*. The co-adsorption of the reactants as 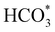 and H* on the (001) surfaces of o-FeNi2S4 and o-Ni3S4 releases the largest binding energy Eads = −3.07 and −3.96 eV, respectively, which could lead to catalyst poisoning. Our calculations suggest that the least exothermic co-adsorption process takes place on the o-Ni3S4(111) surface, which is 1 eV less favourable than co-adsorption on the same facet of the o-FeNi2S4 counterpart. For CO2 reduction into HCOO* on the thiospinel surfaces, we have proposed two alternative pathways via (i) substitution and (ii) dissociation mechanisms, shown in Fig. 5a and b, respectively, and in line with previous reports.89,90 Elemental step 1 of the substitution mechanism leads to the formation of the
and H* on the (001) surfaces of o-FeNi2S4 and o-Ni3S4 releases the largest binding energy Eads = −3.07 and −3.96 eV, respectively, which could lead to catalyst poisoning. Our calculations suggest that the least exothermic co-adsorption process takes place on the o-Ni3S4(111) surface, which is 1 eV less favourable than co-adsorption on the same facet of the o-FeNi2S4 counterpart. For CO2 reduction into HCOO* on the thiospinel surfaces, we have proposed two alternative pathways via (i) substitution and (ii) dissociation mechanisms, shown in Fig. 5a and b, respectively, and in line with previous reports.89,90 Elemental step 1 of the substitution mechanism leads to the formation of the 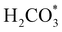 intermediate, which is an endothermic process on any catalyst surface. Our calculations indicate that the most favourable elemental step 1 is promoted by the o-Ni3S4(111) surface, requiring 2.93 eV of energy, but the
intermediate, which is an endothermic process on any catalyst surface. Our calculations indicate that the most favourable elemental step 1 is promoted by the o-Ni3S4(111) surface, requiring 2.93 eV of energy, but the 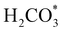 intermediate is still approximately 0.5 eV less stable than on the o-FeNi2S4(111) surface. The formation of the adduct
intermediate is still approximately 0.5 eV less stable than on the o-FeNi2S4(111) surface. The formation of the adduct 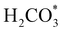 on the o-Ni3S4(111) and o-FeNi2S4(111) surfaces has to overcome relatively large energy barriers Ea1 = 3.69 and 3.94 eV, respectively. However, the activation energies and energy differences for elemental step 1 are more than 5 eV for the (001) surfaces of the two thiospinels, suggesting that these facets are not catalytically active for this process. Elemental step 2, where the adduct dissociates into
on the o-Ni3S4(111) and o-FeNi2S4(111) surfaces has to overcome relatively large energy barriers Ea1 = 3.69 and 3.94 eV, respectively. However, the activation energies and energy differences for elemental step 1 are more than 5 eV for the (001) surfaces of the two thiospinels, suggesting that these facets are not catalytically active for this process. Elemental step 2, where the adduct dissociates into 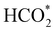 and OH*, is exothermic over all catalysts, releasing the largest energies on the two (001) surfaces. However, the o-FeNi2S4(001) surface also leads to products that are less stable than the initial isolated molecules and surface slab, further indicating the unsuitability of this catalytic system. The most stable final products were formed on the o-Ni3S4(001) and o-FeNi2S4(111) surfaces, while the most stable saddle points were calculated for the two (111) facets, which lie very close in our energy diagrams. Interestingly, activation energy 2 is ∼0.5 eV lower on the o-Ni3S4(111) surface than on the o-FeNi2S4(111) surface, while the energy difference for elemental step 2 is ∼0.70 eV lower for the o-Ni3S4(001) facet than for the o-FeNi2S4(111) facet.
and OH*, is exothermic over all catalysts, releasing the largest energies on the two (001) surfaces. However, the o-FeNi2S4(001) surface also leads to products that are less stable than the initial isolated molecules and surface slab, further indicating the unsuitability of this catalytic system. The most stable final products were formed on the o-Ni3S4(001) and o-FeNi2S4(111) surfaces, while the most stable saddle points were calculated for the two (111) facets, which lie very close in our energy diagrams. Interestingly, activation energy 2 is ∼0.5 eV lower on the o-Ni3S4(111) surface than on the o-FeNi2S4(111) surface, while the energy difference for elemental step 2 is ∼0.70 eV lower for the o-Ni3S4(001) facet than for the o-FeNi2S4(111) facet.
Elemental step 3 of the dissociation mechanism is exothermic on all surfaces, apart from the o-FeNi2S4(111) surface where it requires ΔE3 = 0.84 eV (see Fig. 5b). However, the dissociation products 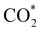 , H* and OH* as well as saddle point 3 are more stable than the isolated CO2, H2O and surface slab, especially on the (001) facets. All the activation energies for elemental step 3 are below 1.80 eV, suggesting that they are feasible under our experimental conditions. Elemental step 4, where the H* atom attacks the activated
, H* and OH* as well as saddle point 3 are more stable than the isolated CO2, H2O and surface slab, especially on the (001) facets. All the activation energies for elemental step 3 are below 1.80 eV, suggesting that they are feasible under our experimental conditions. Elemental step 4, where the H* atom attacks the activated 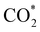 molecule, is an endothermic reaction. We obtained the lowest energy of ΔE4 = 1.27 eV for elemental step 4 on the o-FeNi2S4(111) surface, with the remaining systems requiring more than 2.2 eV. The activation energies of saddle point 4 show a similar trend to the energies of elemental step 4, supporting the good catalytic performance of the o-FeNi2S4(111) surface.
molecule, is an endothermic reaction. We obtained the lowest energy of ΔE4 = 1.27 eV for elemental step 4 on the o-FeNi2S4(111) surface, with the remaining systems requiring more than 2.2 eV. The activation energies of saddle point 4 show a similar trend to the energies of elemental step 4, supporting the good catalytic performance of the o-FeNi2S4(111) surface.
In summary, our simulations show that the reaction of CO2 with H2O is thermodynamically spontaneous on the two surfaces of o-Ni3S4 and on the o-FeNi2S4(111) surface. The energy diagram of the substitution pathway also shows that all intermediates and transition states lie above the isolated H2O and CO2 molecules and surface slab, which are defined as the energy reference in our study. The least unstable intermediates and saddle points of the substitution mechanism are found on the o-FeNi2S4 and o-Ni3S4(111) surfaces. However, for the dissociation mechanism, all intermediates and saddle points on the o-FeNi2S4(111) and o-Ni3S4(001) surfaces are more stable than the initial isolated reactants. The lowest activation energies for the dissociation pathway were calculated for the o-FeNi2S4(111) surface. Thus, according to both thermodynamic and kinetic arguments, the best catalytic activity is achieved on the o-FeNi2S4(111) surface for CO2 reduction via a dissociation mechanism. Irrespective of their oxidation state, our results allow us to generalise that spinel-structured sulfides are catalytically active for the conversion of CO2via dissociation of the 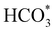 surface species.89
surface species.89
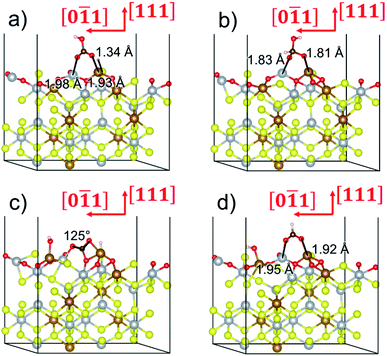
To gain further insight into the mechanisms, we now analyse the geometries of the reactants and intermediates adsorbed on the most catalytically active o-FeNi2S4(111) surface. Fig. 6a shows that 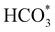 exhibits bidentate coordination to the surface Fe and Ni atoms, at 1.93 and 1.98 Å, respectively, while an H atom sits on a nearby S atom at a distance of 1.34 Å. Following the formation of the
exhibits bidentate coordination to the surface Fe and Ni atoms, at 1.93 and 1.98 Å, respectively, while an H atom sits on a nearby S atom at a distance of 1.34 Å. Following the formation of the 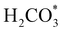 intermediate, the Fe–O and Ni–O distances become shorter and are very similar, with an average value of 1.82 Å (see Fig. 6b). We found that the
intermediate, the Fe–O and Ni–O distances become shorter and are very similar, with an average value of 1.82 Å (see Fig. 6b). We found that the 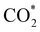 intermediate in the alternative dissociation mechanism remains in an activated configuration, since the bent apex angle is 125°, as shown in Fig. 6c. The larger stability of the
intermediate in the alternative dissociation mechanism remains in an activated configuration, since the bent apex angle is 125°, as shown in Fig. 6c. The larger stability of the 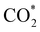 intermediate with respect to
intermediate with respect to 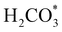 can be rationalised in terms of its carbonate-like geometry, since it forms an additional bond to the surface O lying between the coordinated Fe and Ni atoms. Finally, the
can be rationalised in terms of its carbonate-like geometry, since it forms an additional bond to the surface O lying between the coordinated Fe and Ni atoms. Finally, the 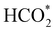 product exhibits a bidentate adsorption configuration similar to the one calculated for
product exhibits a bidentate adsorption configuration similar to the one calculated for 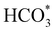 , where the Fe–O and Ni–O bond distances become elongated to 1.92 and 1.95 Å, respectively (see Fig. 6d).
, where the Fe–O and Ni–O bond distances become elongated to 1.92 and 1.95 Å, respectively (see Fig. 6d).
Conclusions
With the demand to produce a catalyst that is environmentally friendly, Earth-abundant, highly stable and produced via an economically viable synthesis, iron–nickel sulfides are promising candidates. In this work, violarite (Fe,Ni)3S4 has been synthesised within a shorter period of time (12 h) than any of the alternative methods reported in the literature.91–93 Further investigation revealed that calcination at 200 °C favours violarite formation and improves the catalytic activity towards CO2 hydrogenation. CO2 and H2 conversion into formate was achieved in alkaline media under mild hydrothermal conditions of 20 bar (CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2) and 125 °C. Violarite achieved superior results compared to Fe-only and Ni-only sulfides, i.e. Fe1−xS and Ni3S4, which implies that an enhanced synergistic interaction between Fe and Ni resulted in improved catalytic efficacy. A calcination study using in situ XRD and TGA displayed the many metal sulfide/sulfate/oxide structures that are formed and transformed during calcination at up to 800 °C, ending with fully oxidised Fe2O3 and NiO structures. XPS showed that the freshly synthesised violarite material possessed enhanced Ni–Fe interaction and electron transfer, whereas calcination at 200 °C formed a dominant metal oxide/sulfoxide surface. XAFS helped in analysing the bulk structural characteristics and oxidative effects of nickel and iron within the structure. Violarite possesses an inverse spinel structure, where Fe fills the octahedral holes and Ni has mixed tetrahedral and octahedral coordination, with little change in coordination and oxidation state observed upon calcination at 200 °C. FT-EXAFS of the Fe k-edge shows that iron possesses a mixture of Fe–O and Fe–S character and XANES reveals an Fe(II) low-spin octahedral state, suggesting O–Fe–S species. The enhanced crystallinity of partially oxidised violarite after calcination, as confirmed by XRD, indicates that the oxygen incorporated within the structure does not disrupt the crystal lattice. The bulk metal atoms have Fe(II) and Ni(III) oxidation states, where Ni(III) can facilitate charge transfer, which is essential to maintain the Fe(II) oxidation state.
H2) and 125 °C. Violarite achieved superior results compared to Fe-only and Ni-only sulfides, i.e. Fe1−xS and Ni3S4, which implies that an enhanced synergistic interaction between Fe and Ni resulted in improved catalytic efficacy. A calcination study using in situ XRD and TGA displayed the many metal sulfide/sulfate/oxide structures that are formed and transformed during calcination at up to 800 °C, ending with fully oxidised Fe2O3 and NiO structures. XPS showed that the freshly synthesised violarite material possessed enhanced Ni–Fe interaction and electron transfer, whereas calcination at 200 °C formed a dominant metal oxide/sulfoxide surface. XAFS helped in analysing the bulk structural characteristics and oxidative effects of nickel and iron within the structure. Violarite possesses an inverse spinel structure, where Fe fills the octahedral holes and Ni has mixed tetrahedral and octahedral coordination, with little change in coordination and oxidation state observed upon calcination at 200 °C. FT-EXAFS of the Fe k-edge shows that iron possesses a mixture of Fe–O and Fe–S character and XANES reveals an Fe(II) low-spin octahedral state, suggesting O–Fe–S species. The enhanced crystallinity of partially oxidised violarite after calcination, as confirmed by XRD, indicates that the oxygen incorporated within the structure does not disrupt the crystal lattice. The bulk metal atoms have Fe(II) and Ni(III) oxidation states, where Ni(III) can facilitate charge transfer, which is essential to maintain the Fe(II) oxidation state.
We have also employed DFT+U-D2 calculations to investigate CO2 conversion into formate on the partially oxidised low-Miller index (001) and (111) surfaces of FeNi2S4 and Ni3S4. We have simulated the co-adsorption of 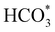 and H* and found that these are thermodynamically feasible processes, leading to particularly stable configurations on both (001) surfaces, which could, however, poison the catalyst. The minimum energy pathway via the substitution mechanism involves unstable intermediates, while the saddle points have large activation energies. We identified that the carbonate-like intermediate is a key species, which means that the dissociation mechanism is the most likely to occur and that the partially oxidised FeNi2S4(111) surface is the most active catalyst. Experiments and computer simulations together have revealed that both the synergistic presence of Ni and Fe in the composition of the thiospinel violarite and the partial oxidation of its surface, expressed in the form of S–Fe–O moieties, are key for the enhanced catalytic performance of the material. Our work shows that violarite may play an essential role in future CO2 utilisation technologies for the production of sustainable fuels and chemicals.
and H* and found that these are thermodynamically feasible processes, leading to particularly stable configurations on both (001) surfaces, which could, however, poison the catalyst. The minimum energy pathway via the substitution mechanism involves unstable intermediates, while the saddle points have large activation energies. We identified that the carbonate-like intermediate is a key species, which means that the dissociation mechanism is the most likely to occur and that the partially oxidised FeNi2S4(111) surface is the most active catalyst. Experiments and computer simulations together have revealed that both the synergistic presence of Ni and Fe in the composition of the thiospinel violarite and the partial oxidation of its surface, expressed in the form of S–Fe–O moieties, are key for the enhanced catalytic performance of the material. Our work shows that violarite may play an essential role in future CO2 utilisation technologies for the production of sustainable fuels and chemicals.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Engineering and Physical Sciences Research Council (EPSRC grant EP/K009567) for funding. Via our membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, and EP/R029431), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). This research was undertaken using the Supercomputing Facilities at Cardiff University operated by the Advanced Research Computing @ Cardiff (ARCCA) Division on behalf of the Supercomputing Wales (SCW) project, which is part-funded by the European Regional Development Fund (ERDF) via the Welsh Government. Further work was undertaken on ARC4, part of the High-Performance Computing facilities at the University of Leeds, United Kingdom.References
- G. Centi, E. A. Quadrelli and S. Perathoner, Energy Environ. Sci., 2013, 6, 1711 Search PubMed.
- P. Styring, D. Jansen, H. de Coninck, H. Reith and K. Armstrong, Carbon Capture and Utilisation in the green economy, 2011 Search PubMed.
- A. Álvarez, M. Borges, J. J. Corral-Pérez, J. G. Olcina, L. Hu, D. Cornu, R. Huang, D. Stoian and A. Urakawa, ChemPhysChem, 2017, 18, 3135–3141 Search PubMed.
- M. D. Porosoff, B. Yan and J. G. Chen, Energy Environ. Sci., 2016, 9, 62–73 Search PubMed.
- C. Mitchell, U. Terranova, I. AlShibane, D. J. Morgan, T. Davies, Q. He, J. Hargreaves, M. Sankar and N. H. De Leeuw, New J. Chem., 2019, 43, 13985–13997 Search PubMed.
- H. Yang, C. Zhang, P. Gao, H. Wang, X. Li, L. Zhong, W. Weiab and Y. Sun, Catal. Sci. Technol., 2017, 7, 4580–4598 Search PubMed.
- H. Dobbek, Science, 2001, 293, 1281–1285 Search PubMed.
- M. J. Russell and W. Martin, Trends Biochem. Sci., 2004, 29, 358–363 Search PubMed.
- R. Vasiliadou, N. Dimov, N. Szita, S. F. Jordan and N. Lane, Interface Focus, 2019, 9, 20190073 Search PubMed.
- A. Yamaguchi, M. Yamamoto, K. Takai, T. Ishii, K. Hashimoto and R. Nakamura, Electrochim. Acta, 2014, 141, 311–318 Search PubMed.
- S. Piontek, K. junge Puring, D. Siegmund, M. Smialkowski, I. Sinev, D. Tetzlaff, B. Roldan Cuenya and U.-P. Apfel, Chem. Sci., 2019, 10, 1075–1081 Search PubMed.
- B. Konkena, K. junge Puring, I. Sinev, S. Piontek, O. Khavryuchenko, J. P. Dürholt, R. Schmid, H. Tüysüz, M. Muhler, W. Schuhmann and U.-P. Apfel, Nat. Commun., 2016, 7, 12269 Search PubMed.
- L. Wang, D. Li, M. Koike, S. Koso, Y. Nakagawa, Y. Xu and K. Tomishige, Appl. Catal., A, 2011, 392, 248–255 Search PubMed.
- T. Zhang, Z. Liu, Y. A. Zhu, Z. Liu, Z. Sui, K. Zhu and X. Zhou, Appl. Catal., B, 2020, 264, 118497 Search PubMed.
- J. Jiang, S. Lu, H. Gao, X. Zhang and H. Q. Yu, Nano Energy, 2016, 27, 526–534 Search PubMed.
- D. Pandey and G. Deo, J. Mol. Catal. A: Chem., 2014, 382, 23–30 Search PubMed.
- L. R. Winter, E. Gomez, B. Yan, S. Yao and J. G. Chen, Appl. Catal., B, 2018, 224, 442–450 Search PubMed.
- L. Gong, J. J. Chen and Y. Mu, Phys. Chem. Chem. Phys., 2017, 19, 28344–28353 Search PubMed.
- A. Roldan, N. Hollingsworth, A. Roffey, H.-U. Islam, J. B. M. Goodall, C. R. A. Catlow, J. A. Darr, W. Bras, G. Sankar, K. B. Holt, G. Hogarth and N. H. de Leeuw, Chem. Commun., 2015, 51, 7501–7504 Search PubMed.
- U. Terranova, C. Mitchell, M. Sankar, D. Morgan and N. H. De Leeuw, J. Phys. Chem. C, 2018, 122, 12810–12818 Search PubMed.
- C. E. Mitchell, U. Terranova, A. M. Beale, W. Jones, D. J. Morgan, M. Sankar and N. H. de Leeuw, Catal. Sci. Technol., 2021, 11, 779–784 Search PubMed.
- D. J. Vaughan and J. R. Craig, Am. Mineral., 1985, 70, 1036–1043 Search PubMed.
- C. Tenailleau, B. Etschmann, R. M. Ibberson and A. Pring, Am. Mineral., 2006, 91, 1442–1447 Search PubMed.
- S. Posada-Pérez, D. Santos-Carballal, U. Terranova, A. Roldan, F. Illas and N. H. De Leeuw, Phys. Chem. Chem. Phys., 2018, 20, 20439–20446 Search PubMed.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097 Search PubMed.
- D. Schüler, J. Mol. Microbiol. Biotechnol., 1999, 1, 79–86 Search PubMed.
- L. Zhao, H. Zhang, Y. Xing, S. Song, S. Yu, W. Shi, X. Guo, J. Yang, Y. Lei and F. Cao, Chem. Mater., 2008, 20, 198–204 Search PubMed.
- H. Wang, M. Liang, D. Duan, W. Shi, Y. Song and Z. Sun, Chem. Eng. J., 2018, 350, 523–533 Search PubMed.
- Q. Liu, A. Díaz, A. Prosvirin, Z. Luo and J. D. Batteas, Nanoscale, 2014, 6, 8935–8942 Search PubMed.
- S. Haider, A. Roldan and N. H. De Leeuw, J. Phys. Chem. C, 2014, 118, 1958–1967 Search PubMed.
- S. Posada-Pérez, D. Santos-Carballal, U. Terranova, A. Roldan, F. Illas and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2018, 20, 20439–20446 Search PubMed.
- J. H. L. Beal, P. G. Etchegoin and R. D. Tilley, J. Solid State Chem., 2012, 189, 57–62 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 Search PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 Search PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 Search PubMed.
- J. Sun, A. Ruzsinszky and J. Perdew, Phys. Rev. Lett., 2015, 115, 1–6 Search PubMed.
- D. Mejía-Rodríguez and S. B. Trickey, Phys. Rev. B, 2020, 102, 1–4 Search PubMed.
- J. H. Yang, D. A. Kitchaev and G. Ceder, Phys. Rev. B, 2019, 100, 1–10 Search PubMed.
- Y. Zhang, J. Sun, J. P. Perdew and X. Wu, Phys. Rev. B, 2017, 96, 1–16 Search PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 Search PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 Search PubMed.
- B. Farkaš, D. Santos-Carballal, A. Cadi-Essadek and N. H. de Leeuw, Materialia, 2019, 7, 100381 Search PubMed.
- M. J. Ungerer, D. Santos-Carballal, A. Cadi-Essadek, C. G. C. E. van Sittert and N. H. de Leeuw, J. Phys. Chem. C, 2019, 123, 27465–27476 Search PubMed.
- L. M. Botha, D. Santos-Carballal, U. Terranova, M. G. Quesne, M. J. Ungerer, C. G. C. E. van Sittert and N. H. de Leeuw, RSC Adv., 2019, 9, 16948–16954 Search PubMed.
- D. Santos-Carballal, P. E. Ngoepe and N. H. de Leeuw, Phys. Rev. B, 2018, 97, 085126 Search PubMed.
- V. Postica, A. Vahl, J. Strobel, D. Santos-Carballal, O. Lupan, A. Cadi-Essadek, N. H. De Leeuw, F. Schütt, O. Polonskyi, T. Strunskus, M. Baum, L. Kienle, R. Adelung and F. Faupel, J. Mater. Chem. A, 2018, 6, 23669–23682 Search PubMed.
- V. Postica, A. Vahl, D. Santos-Carballal, T. Dankwort, L. Kienle, M. Hoppe, A. Cadi-Essadek, N. H. de Leeuw, M.-I. Terasa, R. Adelung, F. Faupel and O. Lupan, ACS Appl. Mater. Interfaces, 2019, 11, 31452–31466 Search PubMed.
- L. Reguera, N. L. López, J. Rodríguez-Hernández, M. González, C. E. Hernandez-Tamargo, D. Santos-Carballal, N. H. de Leeuw and E. Reguera, Eur. J. Inorg. Chem., 2017, 2017, 2980–2989 Search PubMed.
- B. Ramogayana, D. Santos-Carballal, P. A. Aparicio, M. G. Quesne, K. P. Maenetja, P. E. Ngoepe and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2020, 22, 6763–6771 Search PubMed.
- A. Vahl, O. Lupan, D. Santos-Carballal, V. Postica, S. Hansen, H. Cavers, N. Wolff, M.-I. Terasa, M. Hoppe, A. Cadi-Essadek, T. Dankwort, L. Kienle, N. H. de Leeuw, R. Adelung and F. Faupel, J. Mater. Chem. A, 2020, 8, 16246–16264 Search PubMed.
- V. I. I. Anisimov, M. A. A. Korotin, J. Zaanen and O. K. K. Andersen, Phys. Rev. Lett., 1992, 68, 345–348 Search PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 Search PubMed.
- D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106 Search PubMed.
- M. R. Hestenes and E. Stiefel, J. Res. Natl. Bur. Stand., 1952, 49, 409 Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 Search PubMed.
- J. Nocedal, Math. Comput., 1980, 35, 773 Search PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 Search PubMed.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 Search PubMed.
- A. Roldan, D. Santos-Carballal and N. H. de Leeuw, J. Chem. Phys., 2013, 138, 204712 Search PubMed.
- D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195106 Search PubMed.
- D. Santos-Carballal, A. Roldan and N. H. de Leeuw, J. Phys. Chem. C, 2016, 120, 8616–8629 Search PubMed.
- S. N. A. Zakaria, N. Hollingsworth, H. U. Islam, A. Roffey, D. Santos-Carballal, A. Roldan, W. Bras, G. Sankar, G. Hogarth, K. B. Holt and N. H. de Leeuw, ACS Appl. Mater. Interfaces, 2018, 10, 32078–32085 Search PubMed.
- D. Santos-Carballal, A. Roldan, N. Y. Dzade and N. H. de Leeuw, Philos. Trans. R. Soc., A, 2018, 376, 20170065 Search PubMed.
- D. Santos-Carballal, A. Roldan and N. H. De Leeuw, Faraday Discuss. 10.1039/C9FD00141G.
- J. G. Dunn and V. L. Howes, Thermochim. Acta, 1996, 282–283, 305–316 Search PubMed.
- C. Zhao, C. Zhang, S. Bhoyate, P. K. Kahol, N. Kostoglou, C. Mitterer, S. Hinder, M. Baker, G. Constantinides, K. Polychronopoulou, C. Rebholz and R. K. Gupta, Catalysts, 2019, 9, 597 Search PubMed.
- R. Karthikeyan, D. Thangaraju, N. Prakash and Y. Hayakawa, CrystEngComm, 2015, 17, 5431–5439 Search PubMed.
- N. S. McIntyre, D. G. Zetaruk and D. Owen, Appl. Surf. Sci., 1978, 2, 55–73 Search PubMed.
- A. N. Buckley and R. Woods, Appl. Surf. Sci., 1985, 20, 472–480 Search PubMed.
- A. R. Pratt, I. J. Muir and H. W. Nesbitt, Geochim. Cosmochim. Acta, 1994, 58, 827–841 Search PubMed.
- J. R. Mycroft, H. W. Nesbitt and A. R. Pratt, Geochim. Cosmochim. Acta, 1995, 59, 721–733 Search PubMed.
- D. L. Legrand, H. Wayne Nesbitt and G. M. Bancroft, Am. Mineral., 1998, 83, 1256–1265 Search PubMed.
- J. Charnock, C. D. Garner, R. A. D. Pattrick and D. J. Vaughan, Am. Mineral., 1990, 75, 247–255 Search PubMed.
- R. T. Wilkin and D. G. Beak, Chem. Geol., 2017, 462, 15–29 Search PubMed.
- I. Bezverkhyy, P. Afanasiev and M. Danot, J. Phys. Chem. B, 2004, 108, 7709–7715 Search PubMed.
- S. Liu, Y. Li, Y. Ju, J. Liu, J. Liu and Y. Shi, Geochim. Cosmochim. Acta, 2018, 222, 1–16 Search PubMed.
- D. J. Vaughan, R. G. Burns and V. M. Burns, Geochim. Cosmochim. Acta, 1971, 35, 365–381 Search PubMed.
- Y. Mikhlin, Y. Tomashevich, S. Vorobyev, S. Saikova, A. Romanchenko and R. Félix, Appl. Surf. Sci., 2016, 387, 796–804 Search PubMed.
- S. Haider, R. Grau-Crespo, A. J. Devey and N. H. de Leeuw, Geochim. Cosmochim. Acta, 2012, 88, 275–282 Search PubMed.
- Y. Kesler, S. Smirnov, K. Pokholok and B. Viting, Inorg. Mater., 1991, 27, 977–980 Search PubMed.
- G. W. Watson, E. T. Kelsey, N. H. de Leeuw, D. J. Harris and S. C. Parker, J. Chem. Soc., Faraday Trans., 1996, 92, 433–438 Search PubMed.
- P. W. Tasker, J. Phys. Chem. C, 1979, 12, 4977–4984 Search PubMed.
- A. Roldan and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2019, 21, 2426–2433 Search PubMed.
- K. Reuter and M. Scheffler, Phys. Rev. Lett., 2003, 90, 4 Search PubMed.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–11 Search PubMed.
- A. Roldan, N. Hollingsworth, A. Roffey, H.-U. U. Islam, J. B. M. M. Goodall, C. R. A. A. Catlow, J. A. Darr, W. Bras, G. Sankar, K. B. Holt, G. Hogarth and N. H. De Leeuw, Chem. Commun., 2015, 51, 7501–7504 Search PubMed.
- C. S. He, L. Gong, J. Zhang, P. P. He and Y. Mu, J. CO2 Util., 2017, 19, 157–164 Search PubMed.
- J. R. Craig, Am. Mineral., 1971, 56, 1303–1311 Search PubMed.
- F. Xia, J. Zhou, J. Brugger, Y. Ngothai, B. O’Neill, G. Chen and A. Pring, Chem. Mater., 2008, 20, 2809–2817 Search PubMed.
- W. H. Jørgensen, H. Toftlund and T. E. Warner, Hydrometallurgy, 2012, 115–116, 98–103 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0fd00137f |
| ‡ All data obtained during this research are provided in full in the results section of this paper and data sets are openly available from the Cardiff University Research Portal at DOI: 10.17035/d.2020.0122176413. |
| This journal is © The Royal Society of Chemistry 2021 |