Nonstationary stochastic simulation method for the risk assessment of water allocation

Abstract

Due to climate change and human activities, the assumption of the stationarity of hydrological variables no longer hold, and increases the risk of water resources management. To analyze the risk of water allocation schemes under nonstationary conditions, a nonstationary stochastic simulation-based risk assessment method is proposed. This objective was achieved via the following five steps: probability distribution analysis, hydrological scenario setting, inflow stochastic simulation, allocation model optimization, and mathematical statistical analysis. This is the first time that the hydrological nonstationary has been considered in water allocation risk assessment. The methodology was applied to the Zhanghe Irrigation District to assess the risk of water allocation to the municipality, industry, hydropower, and agriculture. The Zhanghe reservoir annual inflow, which is the main hydrological variable in the district, was found to be nonstationary. The results showed that the risks of water allocation schemes are larger than 0.60, except for in the very low scenario. Moreover, through comparing with the results under the assumption of the stationarity, it is necessary to consider the nonstationarity of the Zhanghe reservoir annual inflow in the process of risk assessment.

---

Water impact

The study proposes a nonstationary stochastic simulation-based risk assessment method to analyze the risk of water allocation plan, which provides the possibility to correctly understand the risk of water resources allocation under nonstationary conditions. The research provides a basis for further mitigating the risk and has important benefits for improving the efficient use of water resources.

1. Introduction

Due to the rapid development of society and the economy, the contradiction between increased water demand and limited water resources is more and more evident in many countries and regions, especially in areas of water scarcity.¹ The resulting water shortage seriously restricts the progress of industry, agriculture, and the sustainable development of human life.² Therefore, there is an urgent need to develop sound management plans to utilize water resources reasonably and effectively.³ Many different deterministic optimization models have been proposed to optimize water resources allocation.⁴ Such optimization techniques have been employed for irrigation management,^5–8 crop cultivation pattern,^9–12 groundwater management,^13–16 reservoir operation,^17–22 and the conjunctive use of surface–groundwater.^23–26 Without considering uncertainties, the application of linear programming,^27,28 nonlinear programming,^29–31 and dynamic programming^32–34 optimization models are widely applied. However, there are many uncertainties existing in water resources allocation, such as the available water, water demand, and corresponding costs and benefits of the water supply, and so on. Among all the uncertainties, the main uncertainty is the randomness of hydrological variables, such as the streamflow and rainfall. To deal with the stochastic uncertainties in water resources allocation, many uncertain optimization models have also been developed, such as stochastic dynamic programming,^35–37 two-stage/multi-stage stochastic programming,^38–41 and chance constraint programming.^42–45

Due to the stochastic uncertainties of hydrological variables, there are risks in water allocation schemes obtained by both deterministic methods and uncertain methods. To provide a reliable decision aid for water managers, it is necessary to analyze the risks of the water allocation schemes. In order to reduce the risks in water allocation schemes obtained by uncertain methods, the conditional value-at-risk has been integrated into some stochastic optimization models.^46–48 In addition, a lot of studies have been done to assess the risk of water allocation schemes obtained by deterministic methods.^49–51 However, the impact of nonstationarity in hydrology on the risk has rarely been taken into consideration in the above studies. Due to climate change and human activities, the hydrological variables may be nonstationary in most parts of the world.⁵² For example, hydrological features, such as rainfall and streamflow, have been found to be nonstationary in China,⁵³ Canada,⁵⁴ America,⁵⁵ Western Europe,⁵⁶ Australia,⁵⁷ and India.⁵⁸ Thus, it is necessary to consider the nonstationarity when assessing the risk of water allocation schemes.

In this study, a nonstationary stochastic simulation-based risk assessment method was developed to analyze the risk of water allocation under nonstationary conditions. The method consisted of five core contents: 1) probability distribution analysis: the generalized additive model is chosen to analyze the probability distribution of the hydrological historical series under both stationary and nonstationary conditions; 2) scenarios setting: here, the continuous hydrological variable is divided into several hydrological scenarios according to the fitted probability distribution obtained under the stationary assumption; 3) stochastic simulation: a stochastic sample with several simulated values of the hydrological variable is generated by the Monte Carlo method according to the fitted probability distribution obtained under the nonstationary condition; 4) model optimization: a water management model is developed to optimize the water allocation under each hydrological scenario or simulated value; 5) statistical analysis: the risk of the water allocation scheme is obtained by statistical analysis. The method was applied to the Zhanghe Irrigation District to analyze the risk of water allocation to the municipality, industry, hydropower, and agriculture under the nonstationarity of the Zhanghe reservoir annual inflow.

2. Research methodology

In practice, the main hydrological variable in water allocation is the system water inflow. Water allocation schemes are commonly obtained under several typical hydrological scenarios of the inflow. However, due to the stochastic uncertainty of the inflow, there exist risks in water allocation schemes obtained only under several scenarios. In addition, the inflow may be nonstationary due to climate change, which increases the risks. In this study, a nonstationary stochastic simulation-based risk assessment (NSSRA) method was developed to analyze the risks of water allocation schemes under nonstationary conditions. The flow diagram of NSSRA method is shown in Fig. 1. There are several key steps: probability distribution analysis, hydrological scenario setting, inflow stochastic simulation, allocation model optimization, and mathematical statistical analysis, which are described in detail in the following sections.

Fig. 1 Flow diagram of the nonstationary stochastic simulation-based risk assessment method.

2.1. Probability distribution analysis

In fitting a suitable probability distribution to a stationary hydrological series, the parameters are usually assumed to remain constant over the years. For nonstationary hydrological series, the parameters are expected to change with time and can be expressed as a function of some explanatory variables with time. Among all the fitting models, the generalized additive model (GAMLSS) provides a very flexible framework for modeling probability distributions that are applicable to both stationary and nonstationary series.⁵⁹ It is flexible and capable of modeling parameters of a probability distribution as linear and/or nonlinear, highly skewed and/or kurtotic, parametric and/or additive non-parametric.⁶⁰ In addition to a lot of built-in probability distributions, others can also be generated. So, the GAMLSS was chosen to fit the probability distribution of the inflow in this study.

For GAMLSS modeling, the probability distribution type should be decided first. Given that the Pearson type three (P-III) distribution is one of the most suitable distributions for hydrologic variables, such as rainfall and streamflow in China,⁶¹ it was also chosen to fit the inflow series in this study. The descriptions of the P-III distribution are as follows:

where μ, σ, and ν are three parameters named the location parameter, scale parameter, and shape parameter, respectively.

Then, the types of GAMLSS pattern should be decided. In this study, the following seven patterns were considered: pattern 1, the three parameters are all stationary; pattern 2, the location parameter is time-varying and modeled by a linear function, while the scale parameter and shape parameter are stationary; pattern 3, the location parameter and scale parameter are time-varying and modeled by linear functions, while the shape parameter is stationary; pattern 4, the three parameters are all time-varying and modeled by linear functions; pattern 5, the location parameter is time-varying and modeled by a nonlinear function, while the scale parameter and shape parameter are stationary; pattern 6, the location parameter and scale parameter are time-varying and modeled by nonlinear functions, while the shape parameter is stationary; pattern 7, the three parameters are all time-varying and modeled by nonlinear functions. The nonlinear function used was a cubic polynomial just like Tan and Gan used.⁶²

The selection of the optimal pattern was based on the values of Akaike information criterion (AIC) and likelihood ratio test (LRT). First, the pattern with the minimum AIC value was selected as the latent pattern. Then, the LRT was applied to test whether the latent pattern was significantly better than the other simpler patterns. If the p-value obtained by LRT was less than the confidence level, the latent pattern was considered a significantly better fit than the simpler model and was chosen as the best pattern; otherwise, the simpler model was chosen as the best pattern. In this study, the confidence level was set as 0.05, just as Jiang and Xiong did.⁶³

If pattern 1 is selected as the best pattern, the hydrological series is stationary; otherwise, the hydrological series is nonstationary. Based on the fitting results by the best pattern, functions describing the change of three parameters over time can be determined and the proper probability distribution of inflow in the planning year can be obtained.

2.2. Hydrological scenario setting

In practice, water allocation schemes are commonly obtained under several typical hydrological scenarios without considering the nonstationarity. Therefore, the probability distribution of the inflow obtained by the GAMLSS model with three stationary parameters is used for hydrological scenario setting. The water inflow can be divided into several scenarios by selected percentiles according to the fitted probability distribution. Just as Xu et al. did,⁶⁴ four percentiles (12.5th, 37.5th, 62.5th, and 87.5th) were used to divide the water inflow into five scenarios: very low, low, medium, high, and very high. The P-III distribution with three parameters of 2, 10, and 100 is taken as an example to show the principle of scenario division (see Fig. 2).

Fig. 2 Demonstration of the scenario division of a hydrological random variable based on its probability distribution function.

Under each scenario, the expected inflow can be calculated as follows:

where WI_k is the expected inflow under scenario k (m³); f(ξ) is the probability density function of the water inflow; and are the upper border and lower border of the water inflow under scenario k (m³); P_k and is the probability of the occurrence of scenario k. Under each scenario, the water allocation model can be solved and the expected benefit can be obtained based on the expected inflow as input.

2.3. Inflow stochastic simulation

After fitting the actual probability distribution of inflow by the method presented in section 2.1, a stochastic sample with several simulated inflows can be generated by a Monte Carlo (MC) simulation, just as Chen et al. did.⁶⁵ First, a lot of samples with many simulated inflows in each sample are stochastically generated according to the fitted probability distribution. Then, the P-III distribution is also used to fit the series in each sample. Last, the sample whose parameters are closest to that of the fitted probability distribution is selected as the optimized stochastic sample. Under each simulated inflow, the water allocation model can be solved and the actual benefit (M_j) can be obtained.

2.4. Mathematical statistical analysis

Let N_s represents the number of simulated inflows in the optimized stochastic sample. The risk of the water allocation scheme (R_k) under scenario k can be calculated as follow:where M_j represents the actual benefit obtained under the simulated inflow j; and represents the expected benefit obtained under scenario k.

3. Case study

3.1. Problem description

The selected study area was the Zhanghe Irrigation District (ZID), which is in the Yangtze River basin of China. It features a subtropical monsoon climate and humid climatic conditions, with an average annual rainfall of 884.5 mm from 1963 to 2016. Zhanghe reservoir is the largest reservoir in the ZID with an average annual inflow of 801.7 million m³ (1963–2016). According to the administrative divisions, the ZID is divided into several sub-districts, in which there are also some small and medium reservoirs used for irrigation (Fig. 3).

Fig. 3 Schematic map of the Zhanghe Irrigation District. DB represents Dongbao District; DD represents Duodao District; DY represents Dangyang District; JZ represents Jingzhou District; SY represents Shayang District; ZH represents Zhanghe District; ZX represents Zhongxiang District.

There are three non-agricultural water users (municipal, industrial, hydropower) in the ZID and three main crops (semi-late rice, winter rape, cotton) in each sub-district. The Zhanghe Project Management Bureau is responsible for optimally allocating the available water from Zhanghe reservoir to non-agricultural and agricultural water users. Also, the water allocation schemes are usually achieved under several typical hydrological scenarios. However, the Zhanghe reservoir annual inflow (ZRAI) is a random variable. Moreover, ZRAI has found to decline during the past 50 years due to climate change and human activity. Thus, there exists risks in obtained water allocation schemes and it is necessary to carry out a risk assessment.

3.2. Problem solution

In this study, the NSSRA method was applied to analyze the risk of water allocation schemes in the planning year. Considering that the hydrological data were from 1963 to 2016, 2017 was set as the planning year. The resolution process is described below.

(1) Probability distribution analysis. After fitting the ZRAI series by seven patterns, the goodness-of-fit of all the patterns was first assessed by AIC values, which are shown in Table 1. The minimum AIC value was obtained by pattern 6. Then the LRT was applied to test whether pattern 6 was significantly better than other simpler models. The p-values are also shown in Table 1. From Table 1, all the p-values were less than 0.05 (confidence level), which indicated that pattern 6 was the best pattern in this case. Therefore, the best pattern for the ZRAI series was a P-III distribution with location and scale parameters based on the nonlinear function of time, which indicated that the ZRAI was nonstationary.

Table 1 AIC values obtained when modeling the ZRAI series by different patterns and the p-values obtained when comparing the minimum AIC value model with simpler models

Pattern	Type of GAMLSS model	AIC value	p-value
a Represents the pattern with the minimum AIC value. b Represents that the pattern is more complex than the minimum AIC value model.
1	Stationary	1307.6	<0.001
2	Linear model of only location parameter	1301.2	<0.001
3	Linear model of location and scale parameters	1299.2	<0.001
4	Linear model of location, scale, and shape parameters	1296.8	<0.001
5	Nonlinear model of only location parameter	1294.8	0.004
6	Nonlinear model of location and scale parameters	1289.6
7	Nonlinear model of location, scale, and shape parameters	1293.3

---

(2) Hydrological scenario setting. According to the modeling results of the ZRAI series by the GAMLSS model with three stationary parameters (pattern 1), the probability density function of ZRAI without considering the nonstationarity is a P-III distribution with a μ of −803.5, σ of 13 496.2, and ν of 6.01. According to the method presented in section 2.2, the inflow ranges under the five hydrological scenarios can be obtained by the four selected percentiles (12.5th, 37.5th, 62.5th, and 87.5th). After that, the expected inflow under each scenario can be calculated by eqn (2), with the results shown in Table 2.

Table 2 Expected inflow under each hydrological scenario without considering the nonstationary of the ZRAI series

Hydrological scenario	Probability	Inflow range (10^4 m^3)	Expected inflow (10^4 m^3)
Very low	0.125	Less than 44 640.8	34 985.5
Low	0.25	[44 640.8, 66 028.0)	55 916.9
Medium	0.25	[66 028.0, 86 423.6)	75 921.0
High	0.25	[86 423.6, 118 721.3)	10 0419.6
Very high	0.125	More than 118 721.3	14 0272.4

---

(3) Inflow stochastic simulation. According to the modeling results of the ZRAI series by the GAMLSS model with the best pattern, the nonlinear functions of the location parameter and scale parameter over time could be obtained. Based on the functions, the actual probability density function of ZRAI at any stage could also be obtained. In the planning year, the actual probability density function was a P-III distribution with a μ of −975.4, σ of 8246.4, and ν of 6.23. Then, a sample with 5000 simulated inflows was generated by the method presented in section 2.3. After that, the stochastic sample was divided into five subsamples according to the inflow range in Table 2: very low subsample, low subsample, medium subsample, high subsample, and very high subsample, respectively. The numbers of simulated inflows within the above subsamples were 1974, 1917, 796, 274, and 39, respectively.

(4) Allocation model optimization. Considering that the maximum agricultural irrigation water demand varies under different hydrological scenarios, the irrigable area target is taken as the decision variable for an agricultural water user. In addition, the small- and medium-sized reservoirs can be used for irrigation in each sub-district. Therefore, the suitable model optimally allocating available water from Zhanghe reservoir is given as follows:where M represents the net system benefit (yuan), yuan is the legal currency of China; r represents the index of a non-agricultural water user; T_NAr represents the water allocation target for a non-agricultural water user r (m³); B_NAr represents the net benefit of a non-agricultural water user r (yuan per m³); s represents the index for a sub-district; t represents the index for a crop; T_Ast represents the irrigable area target of crop t in sub-district s (ha); B_Ast represents the net benefit of crop t in sub-district s (yuan per ha); WA represents the available water from Zhanghe reservoir (m³); I_s represents the irrigation water allocated for sub-district s (m³); Q_t represents the irrigation quota of crop t (m³ ha⁻¹); q_s represents the available irrigation water from the small- and medium-sized reservoirs in sub-district s (m³); η_s is the overall project efficiency in sub-district s; ηr_s represents the conveyance efficiency of the canal between the Zhanghe reservoir and sub-district s. T^max_NAr represents the maximum water demand of non-agricultural water user r (m³); and T^max_Ast represents the maximum irrigation area requirement of crop t in sub-district s (ha).

There are many parameters that should be determined to run the optimization model. Table 3 shows the maximum demands and benefits for non-agricultural users and agricultural users. The above maximum demands of the municipality, industry, and agriculture are approximated from the statistical analysis of the historical demands, while the water required for the maximum power generation of the power station is selected as the maximum water demand of hydropower. The benefits are approximated from some socio-economic parameters, like water consumption for ten thousand industrial outputs and the crop price. Crop irrigation quota and the available irrigation water from small- and medium-sized reservoirs under each hydrological scenario are shown in Table 4. In addition, the available water from Zhanghe reservoir was calculated by annual inflow minus water loss.

Table 3 Maximum water demand and water supply benefit of each water user

Water user		Maximum demand (ha or 10^4 m^3)	Benefit (yuan per ha or yuan per m^3)
a Represents agricultural users. The units of the maximum demand are ha and 10^4 m^3 for agricultural users and non-agricultural users, respectively. The units of the benefit are yuan per ha and yuan per m^3 for agricultural users and non-agricultural users, respectively.
Dongbao^a	Semi-late rice	7793.3	4144.5
	Winter rape	7500.8	1561.2
	Cotton	733.3	1431.1
Duodao^a	Semi-late rice	17 906.5	3933.7
	Winter rape	17 240.6	1481.8
	Cotton	1693.3	1358.3
Dangyang^a	Semi-late rice	12 013.6	4214.7
	Winter rape	11 846.7	1587.7
	Cotton	2280.0	1455.3
Jingzhou^a	Semi-late rice	12 020.4	3652.8
	Winter rape	12 286.7	1376.0
	Cotton	1206.7	1261.3
Shayang^a	Semi-late rice	75 766.7	3512.3
	Winter rape	73 460.0	1323.0
	Cotton	7200.0	1212.8
Zhanghe^a	Semi-late rice	5160.0	4566.0
	Winter rape	4966.7	1719.9
	Cotton	486.6	1576.6
Zhongxiang^a	Semi-late rice	17 479.9	3723.0
	Winter rape	16 813.3	1402.4
	Cotton	1653.4	1285.5
Non-agricultural user	Municipality	5068.0	32.5
	Industry	2072.0	6.3
	Hydropower	75 340.8	0.031

---

Table 4 Irrigation quota for each crop and available irrigation water from the small- and medium-sized reservoirs in each sub-district under each hydrological scenario

Type	Very low	Low	Medium	High	Very high
Available irrigation water from small and medium-sized reservoir (10^4 m^3)
Dongbao	674.7	952.4	1632.6	2207.1	3027.7
Duodao	478.5	739.8	1379.6	1920.2	2692.2
Dangyang	157.0	258.8	508.2	718.8	1019.7
Jingzhou	67.2	192.1	498.0	756.3	1125.3
Shayang	87.3	489.3	1473.7	2305.3	3493.0
Zhenghe	298.2	425.0	735.4	997.7	1372.3
Zhongxiang	960.0	1368.6	2369.0	3214.1	4421.2
Irrigation quota (m^3 ha^−1)
Semi-late rice	4019.3	3451.4	2597.6	1757.4	1359.6
Winter rape	436.5	383.8	322.1	186.3	53.8
Cotton	449.9	376.5	214.4	67.6	0

---

Under each hydrological scenario, all the parameters needed for the optimization model can be determined and the model can be solved to obtain the water allocation scheme and its expected benefit. Here, we assumed that the crop irrigation quota and the available irrigation water from small- and medium-sized reservoirs were the same under different simulated inflows within the same subsample, and they were the same with that under corresponding hydrological scenario. For example, the irrigation quota and the available irrigation water from small- and medium-sized reservoirs under a simulated inflow within the very low subsample were the same as under the very low scenario. Thus, under each simulated inflow, all the parameters needed for the optimization model could also be determined and the model could be solved to obtain the actual benefit.

After solving the model under all the hydrological scenarios and simulated inflows, the method presented in section 2.4 was used to calculate the risk of water allocation schemes in the planning year.

3.3. Results analysis

(1) Modeling results under simulated inflows. Under each simulated inflow, the optimization water allocation model was solved to obtain the actual benefit (f_j). Within the threshold, the obtained actual benefit increases with the simulated inflow. If the simulated inflow is larger than the threshold, the actual benefit will no longer increases. Through statistical analysis of the optimized results in each subsample, the frequency of each actual benefit was calculated and is shown in Fig. 4. In the very high subsample, the actual benefits were the same under all the simulated inflows. Therefore, Fig. 4 only shows the frequency distributions of the other four subsamples.

Fig. 4 Frequency of the actual benefits calculated under the simulated inflows within the very low subsample, low subsample, medium subsample, and high subsample.

From the figure, the range of actual benefit varied across the four subsamples. The actual benefits were the smallest in the very low subsample, while they were the largest in the high subsample. That's because the simulated inflows were the smallest in the very low subsample among the four subsamples. In addition, the range was also different. The range was the largest in the very low subsample, while it was the smallest in the high subsample. One explanation is that the number of simulated inflows was the most in the very low subsample. In addition, although the actual benefit increases with the simulated inflow, the marginal benefit may decrease.

Fig. 4 also demonstrates that the frequency distributions of the actual benefits were different in the four subsamples. In the very low subsample, the frequency increased with the actual benefit slowly at first and then decreased quickly. Except for the first and last, the frequency remained basically unchanged in the low subsample. However, the frequency increased to the maximum quickly and decreased with the actual benefit slowly in the medium subsample and high subsample.

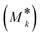(2) Risks of allocation schemes under different scenarios. Under each hydrological scenario, the optimization water allocation model was solved to obtain the expected benefit based on the expected inflow as input. According to the expected benefit under each hydrological scenario and the actual benefit under each simulated inflow, the risks of the water allocation schemes under the five scenarios were calculated by eqn (3) and the results are shown in Fig. 5.

Fig. 5 Risks of water allocation schemes obtained under the nonstationary simulation condition of the Zhanghe reservoir annual inflow.

From Fig. 5, the risk of water allocation obtained under the very low scenario was the lowest, while it was the largest under the very high scenario. Except for the very low scenario, the risks of the water allocation schemes obtained under the other four scenarios were larger than 0.60. These results indicated that if the water allocation schemes were obtained under these four scenarios, the probability of the actual benefit being less than the expected benefit was very large. Thus, the water allocation schemes obtained under the very low scenarios should be applied to reduce the risks under nonstationary conditions.

4. Discussion

In order to demonstrate the impact of nonstationarity on the risk of water allocation schemes, the risk was also analyzed under the condition of not considering nonstationarity of the ZRAI in the step of inflow stochastic simulation (called the stationary simulation condition). Under the stationary simulation condition, the stochastic sample was generated based on the probability distribution obtained under the stationary assumption, which was the same with that used in the step of the hydrological scenario setting. Through the stochastic simulation, the numbers of simulated inflows within the five subsamples were 630, 1212, 1282, 1279, and 597 respectively, which were very different from those under the nonstationary simulation condition. The numbers of simulated inflows in the very low subsample and low subsample were less than that under the nonstationary simulation condition, while the numbers of simulated inflows in the medium subsample, high subsample, and very high subsample were more than that under the nonstationary simulation condition. That is because the expected value of the stochastic sample series under the stationary simulation condition was larger than that under the nonstationary simulation condition.

Through model optimization and statistical analysis, the risks of the water allocation schemes under the stationary simulation condition are shown in Fig. 6. The above results were very different from those under the nonstationary simulation condition. From Fig. 6, the risks of the water allocation schemes under the five scenarios under the stationary simulation condition were much smaller than those under the nonstationary simulation condition. The above results indicated that the risks of the water allocation schemes in the planning year will be underestimated if the nonstationarity of the ZRAI is not considered in the step of the inflow stochastic simulation. Thus, it is necessary to consider the nonstationarity of the hydrological variable in the process of water allocation risk assessment, especially in basins that are greatly affected by climate change and human activities.

Fig. 6 Risks of water allocation schemes obtained under the assumption of the stationarity of the Zhanghe reservoir annual inflow.

5. Conclusions

This study proposes a nonstationary stochastic simulation-based risk assessment (NSSRA) method to analyze the risk of the water allocation scheme under nonstationary conditions. The method consists of five core contents: probability distribution analysis, hydrological scenario setting, inflow stochastic simulation, allocation model optimization, and mathematical statistical analysis. First, the GAMLSS model is chosen to analyze the probability distribution of inflow historical series under both stationary assumption and nonstationary conditions. Then, the inflow is divided into several hydrological scenarios under the stationary assumption. After that, a stochastic sample with several simulated inflows is generated under the nonstationary condition. Then, a water allocation model is developed and optimized under each hydrological scenario or simulated inflow. Finally, the risk of the water allocation scheme is obtained by statistical analysis.

The methodology was applied to the Zhanghe Irrigation District to analyze the risk of water allocation to agricultural and non-agricultural users under the nonstationarity of the ZRAI. The appropriate water allocation schemes and the corresponding risks in the planning year under nonstationary conditions could be obtained through the NSSRA method. The results showed that the risks of water allocation schemes were larger than 0.60 under four scenarios (low, medium, high, and very high scenarios), while the risk was only 0.21 under the very low scenario. The above results can provide a foundation to water managers for developing a water allocation scheme in the ZID under the nonstationary condition. Through comparing with the results under the stationary simulation condition, the nonstationarity of the hydrological variable was found to be necessary to take into consideration in the process of water allocation risk assessment, especially in basins that are greatly affected by climate change and human activities.

Funding

The study was financially supported by the State Key Research and Development Plan of China (No. 2017YFC0405302, 2016YFC0502201), the Fundamental Research Funds for Central Public Welfare Research Institutes (Grant No. CKSF2019173, CKSF2019478 and CKSF2019490), and National Natural Science Foundation of China (No. 51779013).

Conflicts of interest

There is no conflict of interest.

References

1. K. D. W. Nandalal and S. P. Simonovic, Water Resour. Res., 2003, 39, 1–11.
2. A. Bronstert, A. Jaeger, A. Guntner, M. Hauschild, P. Döll and M. Krol, Physics and Chemistry of the Earth, Part B: Hydrology, Oceans and Atmosphere, 2010, 25, 227–232.
3. H. S. Wheater and P. Gober, Water Resour. Res., 2015, 51, 5406–5424.
4. A. Singh, J. Hydrol., 2012, 466, 167–182.
5. L. S. Pereira, T. Oweis and A. Zairi, Agric. Water Manag., 2002, 57, 175–206.
6. A. V. Ines, K. Honda, A. D. Gupta, P. Droogers and R. S. Clemente, Agric. Water Manag., 2006, 83, 221–232.
7. M. García-Vila and E. Fereres, Eur. J. Agron., 2012, 36, 21–31.
8. F. Li, D. Yu and Y. Zhao, Water Resour. Manag., 2019, 33, 39–55.
9. D. K. Singh, C. S. Jaiswal, K. S. Reddy, R. M. Singh and D. M. Bhandarkar, Agric. Water Manag., 2001, 50, 1–8.
10. L. N. Sethi, S. N. Panda and M. K. Nayak, Agric. Water Manag., 2006, 83, 209–220.
11. J. Zhang, J. Sun, A. Duan, J. Wang, X. Shen and X. Liu, Agric. Water Manag., 2007, 92, 41–47.
12. A. Daghighi, A. Nahvi and U. Kim, Agriculture, 2017, 7, 73,  DOI:10.3390/agriculture7090073.
13. E. H. Keating, J. Doherty, J. A. Vrugt and Q. Kang, Water Resour. Res., 2010, 46, W10517,  DOI:10.1029/2009WR008584.
14. S. Gaur, B. R. Chahar and D. Graillot, J. Hydrol., 2011, 402, 217–227.
15. A. Sedki and D. Ouazar, Water Resour. Manag., 2011, 25, 2855–2875.
16. S. Ghadimi and H. Ketabchi, J. Hydrol., 2019, 578, 124094,  DOI:10.1016/j.jhydrol.2019.124094.
17. M. F. Allawi, O. Jaafar, M. Ehteram, F. M. Hamzah and A. El-Shade, Water Resour. Manag., 2018, 32, 1–17.
18. M. F. Allawi, O. Jaafar, F. M. Hamzah and A. El-Shafie, J. Cleaner Prod., 2019, 206, 928–943.
19. S. Vedula and D. N. Kumar, Water Resour. Res., 1996, 32, 1101–1108.
20. A. Ahmad, A. El-Shafie, S. F. M. Razali and Z. S. Mohamad, Water Resour. Manag., 2014, 28, 3391–3405.
21. K. Jafarzadegan, A. Abed-Elmdoust and R. Kerachian, Stochastic Environ. Res. Risk Assess., 2014, 28, 1343–1358.
22. A. Zarei, S. F. Mousavi, M. E. Gordji and H. Karami, Water Resour. Manag., 2019, 33, 3071–3093.
23. M. Pulido-Velázquez, J. Andreu and A. Sahuquillo, J. Water Resour. Plan. Manag., 2006, 132, 454–467.
24. H. R. Safavi and M. Esmikhani, Water Resour. Manag., 2013, 27, 2623–2644.
25. X. Wu, Y. Zheng, B. Wu, Y. Tian, F. Han and C. Zheng, Agric. Water Manag., 2016, 163, 380–392.
26. R. Sepahvand, H. R. Safavi and F. Rezaei, Water Resour. Manag., 2019, 33, 2123–2137.
27. H. Noory, A. M. Liaghat, M. Parsinejad and O. B. Haddad, Journal of Irrigation and Drainage Engineering, 2012, 138, 437–444.
28. B. Das, A. Singh, S. N. Panda and H. Yasuda, Land use policy, 2015, 42, 527–537.
29. S. K. Sadati, S. Speelman, M. Sabouhi, M. Gitizadeh and B. Ghahraman, Water, 2014, 6, 3068–3084.
30. D. A. An-Vo, S. Mushtaq, T. Nguyen-Ky, J. Bundschuh, T. Tran-Cong, T. N. Maraseni and K. Reardon-Smith, Water Resources Management, 2015, 29, 2153–2170.
31. A. A. Aljanabi, L. W. Mays and P. Fox, Water, 2018, 10, 1291,  DOI:10.3390/w10101291.
32. R. Q. Grafton, H. L. Chu, M. Stewardson and T. Kompas, Water Resour. Res., 2011, 47, W00G08,  DOI:10.1029/2010WR009786.
33. T. Zhao, X. Cai, X. Lei and H. Wang, J. Water Resour. Plan Manag., 2012, 138, 590–596.
34. R. Lalehzari, S. Boroomand Nasab, H. Moazed and A. Haghighi, Journal of Irrigation and Drainage Engineering, 2016, 142, 05015008,  DOI:10.1061/(ASCE)IR.1943-4774.0000933.
35. W. S. Butcher, J. Am. Water Resour. Assoc., 1971, 7, 115–123.
36. C. Cervellera, V. C. Chen and A. Wen, Eur. J. Oper. Res., 2006, 171, 1139–1151.
37. C. Davidsen, S. J. Pereira-Cardenal, S. Liu, X. Mo, R. Dan and P. Bauer-Gottwein, J. Water Resour. Plan Manag., 2015, 141, 08214001,  DOI:10.1061/(ASCE)WR.1943-5452.0000482.
38. S. Wang and G. Huang, J. Environ. Manage., 2011, 92, 1986–1995.
39. J. Nematian, J. Environ. Inform., 2016, 27, 72–84.
40. Y. Zhou, G. Huang, S. Wang, Y. Zhai and X. Xin, Stochastic Environ. Res. Risk Assess., 2016, 30, 795–811.
41. S. Guo, F. Zhang, C. Zhang, Y. Wang and P. Guo, J. Cleaner Prod., 2019, 234, 85–199.
42. A. K. Takyi and B. J. Lence, Water Resour. Res., 1999, 35, 1657–1670.
43. Y. Liu, H. Guo, F. Zhou, X. Qin, K. Huang and Y. Yu, J. Water Resour. Plan Manag., 2008, 134, 347–356.
44. J. M. Grosso, C. Ocampo-Martínez, V. Puig and B. Joseph, J. Process Control, 2014, 24, 504–516.
45. S. Kaviani, A. M. Hassanli and M. Homayounfar, Water Resour. Manag., 2015, 29, 1003–1018.
46. L. Shao, X. Qin and Y. Xu, Water Resour. Manag., 2011, 25, 2125–2145.
47. G. J. Syme, Stochastic Environ. Res. Risk Assess., 2014, 28, 113–121.
48. X. Zhuang, Y. Li, G. Huang and X. Zeng, Stochastic Environ. Res. Risk Assess., 2015, 29, 1287–1301.
49. K. E. Haynes and T. D. Georgianna, Comput. Environ. Urban Syst., 1989, 13, 75–94.
50. J. Stewart, Desalination, 2006, 188, 61–67.
51. M. Lambourne and K. H. Bowmer, Mar. Freshw. Res., 2013, 64, 761–773.
52. J. M. Cunderlik and D. H. Burn, J. Hydrol., 2003, 276, 210–223.
53. H. Li, D. Wang, V. P. Singh, Y. Wang, J. Wu, J. Wu, J. Liu, R. He, J. Zhang and Y. Zou, J. Hydrol., 2019, 571, 114–131.
54. A. N. Thiombiano, S. El-Adlouni, A. St-Hilaire, T. B. Ouarda and N. El-Jabi, Theor. Appl. Climatol., 2017, 129, 413–426.
55. S. Sadri, J. Kam and J. Sheffield, Hydrol. Earth Syst. Sci., 2016, 20, 1–38.
56. E. S. Steirou, L. Gerlitz, H. Apel, X. Sun and B. Merz, Hydrol. Earth Syst. Sci., 2019, 23, 1305–1322.
57. M. M. Rashid and S. Beecham, Sci. Total Environ., 2019, 657, 882–892.
58. L. K. Ray and N. K. Goel, J. Hydrol. Eng., 2019, 24, 05019018,  DOI:10.1061/(ASCE)HE.1943-5584.0001808.
59. S. Chen, D. Shao, X. Tan, W. Gu and C. Lei, Agric. Water Manag., 2017, 191, 98–112.
60. R. A. Rigby and D. M. Stasinopoulos, J. R. Stat. Soc. Ser. C Appl. Stat., 2005, 54, 507–554.
61. T. Li, S. Guo, L. Chen and J. Guo, J. Hydrol. Eng., 2013, 18, 1018–1030.
62. X. Tan and T. Y. Gan, J. Clim., 2015, 28, 1788–1805.
63. C. Jiang and L. Xiong, Acta Geogr. Sin., 2012, 67, 1505–1514.
64. Y. Xu, S. Zhu, W. Zhang and L. Zhou, Journal of Yangtze River Scientific Research Institute, 2018, 35, 19–23.
65. S. Chen, D. Shao, X. Tan, W. Gu and C. Lei, J. Water Resour. Plan. Manag., 2019, 145, 04018102,  DOI:10.1061/(ASCE)WR.1943-5452.0001042.

---