Effect of rhamnolipid biosurfactant on transport and retention of iron oxide nanoparticles in water-saturated quartz sand†
Shuchi
Liao
 a,
Anushree
Ghosh
bc,
Matthew D.
Becker
d,
Linda M.
Abriola
d,
Natalie L.
Cápiro
a,
Anushree
Ghosh
bc,
Matthew D.
Becker
d,
Linda M.
Abriola
d,
Natalie L.
Cápiro
 e,
John D.
Fortner
c and
Kurt D.
Pennell
e,
John D.
Fortner
c and
Kurt D.
Pennell
 *a
*a
aSchool of Engineering, Brown University, Providence, Rhode Island 02912, USA. E-mail: kurt_pennell@brown.edu
bDepartment of Energy, Environmental, and Chemical Engineering, Washington University in St. Louis, St. Louis, MO 63130, USA
cDepartment of Chemical and Environmental Engineering, Yale University, New Haven, CT 06520, USA
dDepartment of Civil and Environmental Engineering, Tufts University, Medford, Massachusetts 02155, USA
eDepartment of Civil and Environmental Engineering, Auburn University, Auburn, Alabama 36849, USA
First published on 18th December 2020
Abstract
Although prior studies have investigated the effects of solution constituents, including dissolved organic matter and synthetic polymers, on nanoparticle mobility in porous media, far less attention has been directed toward evaluating the impacts of biosurfactants secreted by microorganisms on the transport and retention behavior of nanomaterials. The objective of this study was to explore the influence of rhamnolipid, a biosurfactant associated with biofilms, on the transport and retention of iron oxide nanoparticles (IONPs) in a water-saturated quartz sand. Column experiments were conducted using aerobic medium (ionic strength = 50.4 mM) or 10 mM NaCl as background electrolyte at a pore velocity of 0.43 m per day and pH 6.8 ± 0.2. In aerobic medium columns, nearly all introduced nanoparticles were retained when IONPs were injected alone, whereas the presence of 10 mg L−1 or 50 mg L−1 rhamnolipid resulted in ∼25% and ∼50% breakthrough of the injected IONP mass, respectively. Moreover, preflushing media with 50 mg L−1 rhamnolipid further increased IONP mass breakthrough by ∼30%. Similar enhancement of nanoparticle mobility by 50 mg L−1 rhamnolipid was also measured in lower ionic strength (10 mM NaCl) columns. Mathematical models that incorporated nanoparticle filter ripening and biosurfactant competitive adsorption successfully reproduced experimental observations. Modeling results predicted an order-of-magnitude decrease in IONP filter ripening rate coefficient and a three-fold drop in average IONP retention capacity in the presence of rhamnolipid, consistent with a stabilizing effect and competition for surface sites. These findings demonstrate that rhamnolipid biosurfactant can potentially enhance nanomaterial stability and mobility in subsurface environments and that these effects should be considered when evaluating the impact of biological process on nanoparticle fate and transport in porous media.
Environmental significanceThe mobility and fate of engineered nanoparticles (ENPs) in the subsurface can be strongly influenced by biological process, including the presence of biosurfactants in the aqueous phase and adsorbed on solid surfaces. In this work, a combination of column transport experiments and mathematical modeling was undertaken to assess the impacts of a representative biosurfactant, rhamnolipid, on the transport behavior of oleic-acid coated iron oxide nanoparticles (IONPs) in water-saturated quartz sand. Co-injection of rhamnolipid increased IONP transport by up to 50%, while preflushing rhamnolipid further increased IONP transport by an additional 30%, demonstrating that both aqueous and adsorbed phase rhamnolipid contribute to enhanced IONP mobility. A multi-constituent mathematical model that accounts for competition at surface sites and filter ripening was able to accurately capture the measured IONP effluent breakthrough curves and retention profiles, and revealed that rhamnolipid can decrease the rate of filter ripening by up to an order of magnitude and decrease IONP attachment by 3-fold. These findings demonstrate that in contrast to biofilms, biologically generated surfactants have the potential to dramatically enhance ENP mobility in water-saturated porous media and should be accounted for when describing ENP transport behavior in biologically active systems. |
1. Introduction
In response to public and scientific community concerns related to engineered nanoparticle (ENP) toxicity and fate in the environment,1,2 substantial research efforts have been made to improve our understanding of the transport, transformation and retention of ENPs in porous media.3–5 Due to their ability to effectively retain particles, surface soils and other natural porous media systems (e.g., aquifers) will likely serve as important sinks, and may ultimately entrap most ENPs entering the environment6 from unintentional releases (e.g., landfill leachate) and intentional applications (e.g., subsurface characterization and enhanced oil recovery). The transport behaviour of natural and synthetic micro-size particles, such as bacteria and viruses,7–12 clay minerals,13,14 latex particles,15–17 and silica microspheres,18,19 and various nanoparticles1,20,21 in porous media has been extensively studied for more than 30 years.22,23 Previous experimental studies of particle transport and retention in packed columns have demonstrated that particle attachment can vary spatially and temporally, leading to non-exponential particle retention distributions.24–26 For example, Wang et al. reported nearly constant retention of nanoscale fullerene aggregates (nC60, mean diameter = 95 nm) along the length of water-saturated columns packed with 40–50 mesh Ottawa sand (d50 = 0.36 mm), indicating a limiting or maximum retention capacity.27 Liang et al. co-injected 10 mg L−1 stabilized silver nanoparticle with a mixture of 10 mg L−1 and 30 mg L−1 polyoxyethylene glycerol trioleate and polyoxyethylene (20) sorbitan monolaurate (Tween 20), respectively, and observed retention that was lowest near the column inlet and increased to a maximum at the column midpoint.28 Similarly, several studies by Johnson et al. have demonstrated non-exponential retention, including hyper-exponential and nonmonotonic profiles, of microspheres and colloids (from 0.1 to 6.8 μm) under unfavourable (energy barrier) deposition conditions.26,29–33These studies demonstrated that transport and retention of colloids and ENP in porous media is complex and can involve a number of processes (aggregation, attachment, detachment, physical straining, filter ripening and particle near-surface retention/mobilization32,34,35) that are strongly influenced by interactions between particles and the porous media. Such interactions are not only influenced by the physicochemical conditions36 of the transport system, such as ionic strength (IS) and pH, but can also be impacted by nanoscale surface heterogeneity33,35and co-constituents present in the aqueous phase and/or adsorbed on solid phases. In regard to co-constituents, the effects of natural organic matter (NOM)37–40 and polymer/surfactant stabilizers41–46 on particle transport have received considerable attention. The majority of these studies observed enhancements in nanoparticle mobility in the presence of NOM/polymers under environmentally relevant conditions. Increased effective transport, and the corresponding reduction in attachment, has been attributed to greater electrostatic repulsion and/or steric hindrance between nanoparticles and the solid phase due to surface adsorption or coating by NOM/polymers.36,47–49 Additionally, several studies have demonstrated that competition between ENP and NOM/polymers for attachment sites can also limit nanoparticle deposition.28,50,51 For example, Wang et al.44 reported reduced retention of quantum dots (QDs) near the column inlet and an increasing solid-phase QD concentration with distance, observations that contradict classical colloid filtration theory. This behaviour was attributed to the presence of residual polymer coatings in the QD suspension, which preferentially adsorbed and competed for attachment sites.
Similarly, extracellular biological constituents, such as biofilms and biosurfactants, have the potential to impact interactions between nanoparticles and porous media surfaces.52 A number of studies have demonstrated that biofilms enhance nanoparticle retention53–55 in porous media through reduced repulsive force(s), hydrogen bonding, hydrophobic or hydrophilic bridging interactions,56,57 and strengthened filtration and physical straining processes due to biofilm induced roughness58 and smaller pore size.59–61 In contrast, far less attention has been directed to the potential impact of biosurfactants such as rhamnolipids, which are produced by some species of Pseudomonas (e.g., Pseudomonas aeruginosa), on nanoparticle mobility. Rhamnolipids are anionic surfactants that consist of rhamnose linked to one or two molecules of β-hydroxydecanoic acid.62 Due to their surface activity, rhamnolipids have been considered as potential replacements for synthetic surfactants and have been shown to exhibit similar levels of detergency compared to sodium dodecyl sulfate (SDS), a widely used anionic surfactant.63 Basnet and coworkers investigated the effects of rhamnolipid biosurfactant on the aggregation and transport behavior of palladium-doped zerovalent iron nanoparticles (Pd-NVZI) in a water-saturated quartz sand64 and a loamy sand.65 Rhamnolipid-coated Pd-NVZI exhibited good colloidal stability and enhanced transport in both porous media even at the highest IS considered (300 mM NaHCO3), suggesting that rhamnolipid acted to stabilize the Pd-NZVI suspension. They also found that deposition rate of rhamnolipid coated Pd-NZVI increased with time (exhibiting ripening-type behavior), distinctive from the decreasing or constant deposition rate observed for carboxymethyl cellulose coated and soybean flour coated nanoparticles.65 However, in these studies, rhamnolipid was only used as a nanoparticle surface modifier and the potential effects of rhamnolipid in the aqueous and solid phases on nanoparticle mobility were not considered.
Mathematical models are valuable tools for analyzing nanoparticle transport behavior in porous media and for identifying associated attachment parameters. Several studies have demonstrated that simultaneous model fitting to both nanoparticle effluent concentration data and retention profiles can provide important insight into retention processes. For example, Li et al.24 employed a mathematical model, based upon a modification of classical colloid filtration theory, to fit experimental observations of fullerene (C60) breakthrough and retention in packed columns. This simultaneous fitting process revealed that nanoparticle attachment on mineral surfaces exhibited a maximum capacity (Smax) that was far smaller than monolayer coverage, and that the attachment rate coefficient and Smax were dependent upon flow velocity and grain size. This work was extended by Becker et al.25 who developed a multi-constituent site blocking (MCB) model based upon column observations of nanoparticle transport in the presence of free polymer. In that study, residual polymer present in quantum dot suspensions was shown to compete with nanoparticles for attachment sites, resulting in nanoparticle retention that increased with distance from the column inlet, counter to predictions from classical colloid filtration theory. In a subsequent study, the developed modeling framework was implemented in a multi-dimensional simulator to successfully predict the transport of polymer-coated magnetite nanoparticles in a heterogeneous flow cell.66
Building on this prior work, the goal of this research was to investigate the effects of aqueous phase and adsorbed rhamnolipid biosurfactant on the transport and retention behaviour of ENPs in a water-saturated porous medium through a combination of experimental and mathematical modelling studies. We hypothesize that rhamnolipid adsorbed on the solid phase will inhibit nanoparticle attachment, while rhamnolipid present in the aqueous phase will act to stabilize nanoparticles as well as compete for attachment sites, and that the combined effects of these processes will result in enhanced nanoparticle mobility compared to rhamnolipid-free control experiments. Oleic acid coated iron oxide nanoparticles (IONPs) were chosen as model ENPs due to their stability, low toxicity, broad range of applications, and reproducibility.67–71 Batch studies were conducted to determine the effect of rhamnolipid, as a function of concentration, on the aggregation kinetics and zeta potential of IONP. A series of column experiments was then performed to investigate the impacts of rhamnolipid on IONP mobility and deposition. Aqueous and solid phase concentrations of IONP were measured to construct IONP breakthrough curves (BTCs), retention profiles, and to calculate mass balance. Based on these experimental data, a two-site, multi-constituent transport model, was developed that incorporates both filter ripening (particle–particle interactions) and competitive adsorption effects on attachment. This model, an extension of the MCB model,25 was then used to estimate nanoparticle attachment rate and capacity parameters in the presence and absence of rhamnolipid.
2. Materials and methods
2.1 Materials
Iron oxide nanoparticles (magnetite, 8 nm core diameter) were synthesized using the method described by Li et al.70 Briefly, 0.178 g FeO(OH) fine powder, 2.26 g oleic acid and 5.0 g 1-octadecene were mixed in a three-neck flask equipped with a heating mantle and a temperature controller. The system was maintained at 120 °C for 1 h to remove residual water and then heated to 320 °C for 1 h under constant argon environment. The resulting brown-black colloid was purified using acetone and hexane with 4–5 washes by centrifugation (Sorvall WX Ultra 80, Thermo Scientific, MA) at 8000 rpm for 10 min to remove unreacted iron salts. After the final wash, nanoparticles in the hexane phase were transferred to water by adding a second layer of oleic acid (as a stabilizer) using a probe sonicator.67 After sonication, the suspension was stirred for 24 h to evaporate residual hexane. The aqueous phase was collected and washed with Milli-Q water (18.2 MΩ cm) 5–6 times to separate out the nanoparticles. Under the conditions and time frames considered in this study, the oleic acid coating is stable and not considered to be a sensitive variable.72Rhamnolipid biosurfactant (90% purity) was purchased from AGAE Technologies (Corvallis, OR). According to the manufacturer, the ratio of mono-rhamnolipid to di-rhamnolipid is approximately 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, which yields an average molecular weight of 563 g mol−1 with a reported critical micelle concentration (CMC) of approximately 100 mg L−1.73 Aerobic medium and 10 mM NaCl solution were prepared to represent biotic and environmental-relevant background electrolytes, respectively. Aerobic medium was prepared with 1.50 g L−1 KH2PO4, 1.00 g L−1 (NH4)2SO4, 0.10 g L−1 MgSO4·7H2O, 0.05 g L−1 CaCl2·2H2O and 5.00 g L−1 glycerol (IS = 50.4 mM).74 The aerobic medium was sterilized using an autoclave (Amsco Century Medium Steam Sterilizer; Steris, OH) with a liquid cycle maintaining at 120 °C for at least 60 minutes. Prior to use, a sterilized NaOH solution was added to adjust the pH of aerobic medium and 10 mM NaCl solution to 6.8 ± 0.2. All chemicals used as background electrolytes were purchased from Fisher Scientific (Fair Lawn, NJ). Ottawa sand (80–100 mesh) with a mean diameter (d50) of 165 μm was obtained from US Silica (Ottawa, IL) as F65 and separated using a programmable sieve shaker (Tyler Ro-Tap, W.S. Tyler Industrial Group, OH). Prior to use, the 80–100 mesh size fraction was cleaned using a sequential acid wash, water rinse, ultrasonication, and oven-drying procedure.27
2, which yields an average molecular weight of 563 g mol−1 with a reported critical micelle concentration (CMC) of approximately 100 mg L−1.73 Aerobic medium and 10 mM NaCl solution were prepared to represent biotic and environmental-relevant background electrolytes, respectively. Aerobic medium was prepared with 1.50 g L−1 KH2PO4, 1.00 g L−1 (NH4)2SO4, 0.10 g L−1 MgSO4·7H2O, 0.05 g L−1 CaCl2·2H2O and 5.00 g L−1 glycerol (IS = 50.4 mM).74 The aerobic medium was sterilized using an autoclave (Amsco Century Medium Steam Sterilizer; Steris, OH) with a liquid cycle maintaining at 120 °C for at least 60 minutes. Prior to use, a sterilized NaOH solution was added to adjust the pH of aerobic medium and 10 mM NaCl solution to 6.8 ± 0.2. All chemicals used as background electrolytes were purchased from Fisher Scientific (Fair Lawn, NJ). Ottawa sand (80–100 mesh) with a mean diameter (d50) of 165 μm was obtained from US Silica (Ottawa, IL) as F65 and separated using a programmable sieve shaker (Tyler Ro-Tap, W.S. Tyler Industrial Group, OH). Prior to use, the 80–100 mesh size fraction was cleaned using a sequential acid wash, water rinse, ultrasonication, and oven-drying procedure.27
2.2 Column experiments
To minimize potential microbial contamination, column equipment and materials were sterilized using either an autoclave or disinfectant (70% ethanol) prior to use. A total of 15 columns were packed with quartz sand and completely saturated with water following procedures described previously.44 Briefly, borosilicate glass columns (5 cm diameter × 15 cm length) were packed with washed 80–100 mesh Ottawa sand in 1 cm increments under gentle vibration. The column endplates were fitted with two 40 mesh nylon screens and a 40 μm nylon filter to support the solid phase and promote uniform flow. The packed columns were then flushed with CO2 gas for at least 60 min to facilitate subsequent dissolution of entrapped gas during the water imbibition process. To fully saturate the columns, at least 10 pore volumes (PVs) of background solution were introduced into the column in an up-flow mode using a high-performance liquid chromatography (HPLC) pump (ChromTech, MN). After water saturation, a non-reactive tracer test was conducted using sterilized NaBr solution (50 mM or 10 mM) to characterize water flow and hydrodynamic dispersion. The effluent bromide ion concentrations were measured using ion-selective electrode(Cole-Parmer, IL) and fit to a one-dimensional form of the advective–dispersive–reactive (ADR) transport equation using CXTFIT ver. 2.1 (ref. 75) to obtain the hydrodynamic dispersion coefficient (DH) and the retardation factor (RF).Five sets of column experiments were performed to evaluate the effects of rhamnolipid on nanoparticle transport and retention in water-saturated 80–100 mesh Ottawa sand. The initial set of column experiments was conducted to obtain baseline IONP transport and retention behaviour in water-saturated porous medium in the absence of rhamnolipid. Here, 3 PVs of approximately 5 mg L−1 IONP (as iron) either in aerobic medium or 10 mM NaCl were injected to the saturated columns, followed by 3 PVs of IONP-free background electrolytes to displace unattached nanoparticles from the column. To characterize the transport of rhamnolipid alone, a second set of column experiments was conducted by injecting solutions containing only rhamnolipid. Here, 5 PVs of 10 mg L−1 or 50 mg L−1 rhamnolipid in aerobic medium or 10 mM NaCl were introduced to water-saturated columns, followed by 3 PVs rhamnolipid-free background solution. The third set of column experiments was performed to explore the influence of rhamnolipid pre-treatment on IONP transport. Here, the water-saturated column was first pre-flushed with approximately 5 PVs 10 mg L−1 or 50 mg L−1 rhamnolipid solution, followed by 3 PVs of background electrolyte solution to remove any free rhamnolipid from the column. A 3 PV pulse of approximately 5 mg L−1 IONP solution (as iron) was then introduced into the column, followed by 3 PVs IONP-free background solution. In the fourth set of column experiments, IONP transport and retention behaviours were evaluated in the presence of free rhamnolipid (i.e., co-injection). Here, 3 PVs aerobic medium solution containing 5 mg L−1 IONP (as iron) and either 10 mg L−1 or 50 mg L−1 rhamnolipid or 3PVs 10 mM NaCl solution containing 5 mg L−1 IONP (as iron) and 50 mg L−1 rhamnolipid were introduced to the water saturated columns, followed by 3PVs background electrolyte solution (aerobic medium or 10 mM NaCl solution). In the fifth and final set of column experiments, IONP transport was evaluated under the more realistic condition where rhamnolipid was present in both solid and aqueous phases (i.e., pre-treatment + co-injection). Here, the water-saturated columns were first flushed with 5 PVs of 10 mg L−1 or 50 mg L−1 rhamnolipid solution and 3 PVs rhamnolipid-free background solution (aerobic medium or 10 mM NaCl), followed by the injection of 3 PVs of suspension containing 10 mg L−1 or 50 mg L−1 rhamnolipid and approximately 5 mg L−1 IONP (as iron), and finally, 3 PVs background electrolyte solution.
All the column experiments described above were conducted at a constant flow rate of 0.06 ± 0.001 mL min−1 corresponding to a pore-water velocity of approximately 0.43 m per day. All influent solutions were prepared by co-injecting the stock nanoparticle solution (∼150 mg L−1) and background solution (with or without rhamnolipid) at a flow rate of 0.002 mL min−1 and 0.058 mL min−1, respectively, and the two solutions were mixed immediately before introduction to the column (Fig. S2†). The nanoparticle size was monitored at the start and end of the injection and no significant changes were observed. Effluent samples from the columns were collected continuously using a fraction collector (CF-2, Spectrum Laboratories, CA). To construct IONP BTCs, effluent concentrations expressed as the relative concentration (C/C0), where C0 is the applied influent concentration, were plotted versus the number of dimensionless PVs of solution delivered. To obtain IONP retention profiles at the conclusion of each experiment, the columns were sectioned into ten increments and the solid-phase concentrations were measured and plotted versus the distance from the column inlet. Duplicate experiments were conducted for 50% of the columns to confirm reproducibility. Experimental conditions for IONP column studies are summarized in Table 1, while the rhamnolipid only column results are provided in Table S2.†
| Experimental parameters | Mathematically fitted parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Column identifiera | C 0 (mg L−1) | PWc (PV) | BTd (%) | MBe (%) | k att (h−1) | S p 1, max (μg g−1) | k rip (h−1) | k ads (h−1) | α | R 2 |
| a “AE”: aerobic medium as background electrolyte, “NaCl”: 10 mM NaCl as background electrolyte, “R10”: 10 mg L−1 rhamnolipid solution, “R50”: 50 mg L−1 rhamnolipid solution, “_”: preflood, “&”: co-injection, e.g. “AE-R10&IONP”: IONP and 10 mg L−1 rhamnolipid were co-injected into the column using aerobic medium as background electrolyte; “AE-R50_IONP”: column preflushed with 50 mg L−1 rhamnolipid solution and then IONPs were injected using aerobic medium as background electrolyte. “NaCl-R50_R50&IONP”: column preflushed with 50 mg L−1 rhamnolipid and then IONP with 50 mg L−1 rhamnolipid were injected using 10 mM NaCl as background electrolyte. “-1” and “-2” indicate duplicate experiments. b Input IONP concentration (as iron). c Pulse width. d Percent of IONP breakthrough mass to total applied mass. e Mass balance. f IONP attachment rate coefficient. g Maximum retention capacity of porous media surface (type 1 site capacity for two-site model). h IONP filter ripening attachment rate coefficient. i Rhamnolipid adsorption rate coefficient. The 95% confidence limits of fitted parameters are also presented after fitted parameters in parenthesis. The relatively large 95% confidence intervals (CI) for Spmax and kads in the columns “AE-R50&IONP” and “AE-R50_R50&IONP” indicate that the model predictions are not sensitive to maximum retention capacity and first order adsorption rate under the experimental conditions. Additionally, zero-truncation for the lower bound of CI was used, given that Spmax and kads are positive values. Analysis of the CI obtained for these column experiments are documented in the ESI.† j Collision efficiency factor. Collision efficiency factors were estimated by classical filtration theory97 and empirical correlation equations developed by Tufenkji and Elimelech.98 The sum of attachment rate and ripening attachment rate coefficient was used in the calculation. | ||||||||||
| AE-IONP-1 | 5.0 | 3.0 | 3.2 | 94.8 | 0.52 (0.39, 0.65) | 5.60 (1.38, 9.82) | 0.64 (0.23, 1.05) | NA | 0.051 | 0.99 |
| AE-IONP-2 | 5.6 | 3.0 | 1.1 | 96.1 | 0.49 (0.37, 0.61) | 6.11 (1.21, 11.01) | 0.57 (0.20, 0.94) | NA | 0.046 | 0.99 |
| AE-R10_IONP | 4.9 | 3.1 | 1.0 | 93.9 | 0.55 (0.43, 0.67) | 4.03 (1.44, 6.62) | 0.49 (0.22, 0.76) | NA | 0.046 | 0.99 |
| AE-R50_IONP | 4.6 | 3.2 | 12.9 | 105.1 | 0.19 (0.16, 0.22) | 2.24 (0.81, 3.67) | 0.21 (0.10, 0.31) | NA | 0.017 | 0.97 |
| AE-R10&IONP | 5.1 | 3.1 | 24.9 | 107.4 | 0.32 (0.25, 0.39) | 6.85 (5.72, 7.98) | 0.06 (0.05, 0.07) | 2.73 (1.75, 3.71) | 0.017 | 0.96 |
| AE-R50&IONP-1 | 5.0 | 3.1 | 56.6 | 106.6 | 0.43 (0.05, 0.81) | 5.98 (0, 41.78) | NA | 0.08 (0, 0.87) | 0.021 | 0.92 |
| AE-R50&IONP-2 | 4.8 | 3.0 | 43.2 | 99.7 | 0.38 (0.26, 0.50) | 7.67 (0, 42.54) | NA | 0.09 (0, 0.74) | 0.027 | 0.87 |
| AE-R10_R10&IONP | 4.9 | 3.1 | 28.4 | 97.9 | 0.25 (0.23, 0.27) | 6.74 (5.89, 7.59) | 0.07 (0.06, 0.08) | 1.70 (1.19, 2.21) | 0.014 | 0.92 |
| AE-R50_R50&IONP-1 | 5.4 | 3.1 | 78.7 | 99.0 | 0.09 (0.06, 0.12) | 2.64 (0, 53.55) | NA | 0.03 (0, 0.96) | 0.007 | 0.95 |
| AE-R50_R50&IONP-2 | 4.8 | 3.0 | 83.0 | 97.6 | 0.16 (0.07, 0.25) | 1.94 (0, 34.86) | NA | 0.05 (0, 1.34) | 0.010 | 0.95 |
| NaCl-IONP-1 | 5.3 | 3.0 | 14.9 | 104.5 | 0.70 (0.55, 0.85) | 3.75 (3.57, 3.93) | NA | NA | 0.030 | 0.97 |
| NaCl-IONP-2 | 5.1 | 3.0 | 12.3 | 102.9 | 0.55 (0.44, 0.66) | 4.04 (3.74, 4.34) | NA | NA | 0.024 | 0.96 |
| NaCl-R50&IONP-1 | 5.8 | 3.0 | 67.3 | 92.2 | 0.84 (0.60, 1.08) | 8.56 (7.95, 9.17) | NA | 2.01 (0.68, 3.34) | 0.037 | 0.98 |
| NaCl-R50&IONP-2 | 5.2 | 3.0 | 66.9 | 99.7 | 0.58 (0.46, 0.70) | 9.08 (8.50, 9.68) | NA | 1.68 (0.77, 2.59) | 0.025 | 0.99 |
| NaCl-R50_R50&IONP | 5.8 | 3.0 | 95.3 | 100.4 | 0.18 (0.09, 0.27) | 2.37 (1.36, 3.36) | NA | 183.8 (161.5, 206.1) | 0.008 | 0.99 |
2.3 Analytical method
The hydrodynamic diameter and electrophoretic mobility of IONP in suspension were characterized with a Malvern ZetaSizer Nano ZS (Malvern, Cambridge, United Kingdom) using dynamic light scattering (DLS) and laser Doppler velocimetry, respectively. These measurements were conducted at room temperature (i.e., approximately 22 °C) and a scattering angle of 90 degrees. The Smoluchowski approximation was used to relate electrophoretic mobility to zeta potential. An ultra-high-resolution field emitter scanning electron microscope (SEM) (Zeiss LEO 1530 VP, MN) equipped with an energy dispersive spectrometer (EDS) was used to image sand grains and to characterize surface chemistry. Prior to SEM imaging and EDS analysis, all samples were secured on carbon conductive tape and coated with a layer of gold and palladium. IONP core size and morphology were characterized by transmission electron microscopy (TEM, FEI Tecnai G2 Spirit, OR) operated at 120 kV (Fig. S1a†). TEM sample was prepared by placing a small drop (10 μL) of diluted IONP suspension on a carbon coated copper grid (Electron Microscopy Sciences, PA) and left to dry at room temperature (22 ± 0.5 °C). The IONP core size distribution was obtained by counting more than 500 randomly chosen nanoparticles from the TEM images using ImageJ software (National Institutes of Health, MD), as shown in Fig. S1b.†Quantification of rhamnolipid concentrations in aerobic medium was performed with a Jasco V-730 UV-vis spectrophotometer (Easton, MD) using a modified anionic surfactant-methylene blue method.76,77 In solutions containing 10 mM NaCl as the background electrolyte, rhamnolipid concentrations were determined using a total organic carbon analyzer model TOC-L series with Autosampler ASI-L (Shimadzu Scientific Instruments, Columbia, MD). For both methods, seven-point calibration curves were constructed using rhamnolipid solutions (0–100 mg L−1), which yielded linear fits with regression coefficients (R2) greater than 0.98.
Iron concentrations in aqueous and solid samples were determined using a Jasco V-730 UV-vis spectrophotometer based on a modified ferrozine method.78 The method detection limit for total iron was 10.7 μg L−1, obtained using the method of Armbruster and Pry.79 Prior to UV-vis measurement, the IONPs in aqueous and solid samples were digested by 10% hydrochloric acid (HCl) under sonication (ultrasonic batch, Fisher Scientific, MA) for 2 h at room temperature. The average background iron concentration of the cleaned 80–100 mesh Ottawa sand was 4.7 ± 0.3 μg Fe per g sand for this digestion method. Accuracy of the UV-vis method was confirmed using an Optima 7300 DV inductively coupled plasma optical emission spectrometer (ICP-OES) (PerkinElmer, Waltham, MA).
2.4 Mathematical modelling
A multi-constituent nanoparticle transport model developed in prior work25 serves as the foundation for the mathematical model employed herein. Consistent with the experimental observations described below, two types of sites were modelled. The first type of site (type 1 site) accounts for nanoparticle attachment and biosurfactant adsorption on porous media surfaces, assuming a Langmuir-type limiting or maximum surface capacity. The second type of site (type 2 site) accounts for filter ripening, where previously deposited nanoparticles provide additional sites for nanoparticle deposition. A coupled system of one-dimensional aqueous phase transport equations is used to describe constituent transport and retention in a homogeneously packed column: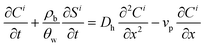 | (1) |
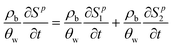 | (2) |
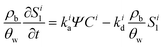 | (3) |
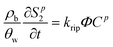 | (4) |
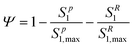 | (5) |
The deposition of nanoparticles on type 2 sites is related to type 1 site attachment through use of a ripening evaluation function Φ (M M−1), which increases proportionally with the total deposition of nanoparticles(Sp):80,81
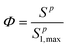 | (6) |
In addition to the two-site multi-constituent model described above, a two-site single constituent model (TSC), which only accounts for filter ripening (no competition for type 1 sites), was used to model experimental results of IONP transport in columns where there was no secondary constituent. For NaCl columns, a modified filtration theory model (MFT)24 was employed in conjunction with a one-site multi-constituent model (MCB)25 to simulate experimental data when there was no indication of filter ripening. Governing equations and comparisons of these models to other commonly used mathematical models (e.g. clean-bed filtration model) are summarized in the ESI.†
The mathematical expressions were implemented using a central-in-space and fully implicit-in-time finite difference scheme in MATLAB R2020a (The MathWorks, Natick, MA), and the transport and solid-phase interaction equations for each constituent were solved sequentially. Model parameters, including attachment/adsorption rate coefficients, filter ripening rate coefficient and maximum retention capacity of the porous medium surface, were estimated by fitting the models to experimental breakthrough curves and corresponding retention profiles using a least-squares optimization procedure based on the following objective function:
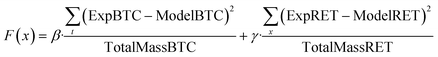 | (7) |
3. Results and discussion
3.1 IONP transport in aerobic medium
To simulate conditions conducive to microbial growth that would likely yield relatively large quantities of rhamnolipid, ten column experiments were conducted with aerobic growth medium (IS = 50.4 mM, pH = 6.8 ± 0.2), as described above, as the background electrolyte. The transport and retention of oleic acid coated IONPs was evaluated in the absence of rhamnolipid, with rhamnolipid pre-treatment, co-injection, and pre-treatment plus co-injection at two rhamnolipid concentrations (10 and 50 mg L−1). The experimental conditions for these IONP column experiments are summarized in Table 1. The nanoparticle transport models were fit to the measured effluent breakthrough curves and retention profiles to obtain the following parameters: IONP attachment rate coefficient (katt), surface (type 1 site if two-site model) retention capacities for IONP (Sp1,max) and if applicable, IONP filter ripening rate coefficient (krip), rhamnolipid retention capacity (SR1,max), as well as rhamnolipid adsorption rate coefficient (kads), (Table 1). All R2 values obtained by model fitting were greater than 0.87, indicating that the mathematical models were able to capture both the transport and retention characteristics of nanoparticles in water-saturated 80–100 mesh Ottawa sand. Experimental breakthrough curves and retention profiles, and the mathematical simulation results are shown in Fig. 1 and 3.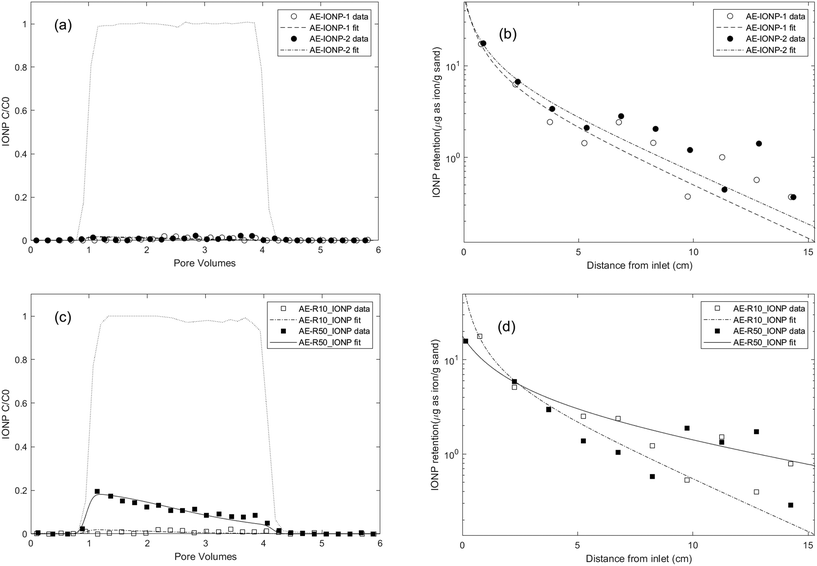 | ||
| Fig. 1 Experimental and fitted effluent breakthrough curves and retention profiles for IONP transport experiments conducted in water-saturated columns packed with 80–100 mesh Ottawa sand with aerobic medium as background electrolyte at a pore-water velocity of 0.43 m per day using different injection procedures and with different rhamnolipid concentrations. Symbols represent experimental data from each IONP column experiment shown in Table 1. (a) and (b): IONP transport alone column results. (c) and (d): 10 mg L−1 and 50 mg L−1 rhamnolipid preflood column results. | ||
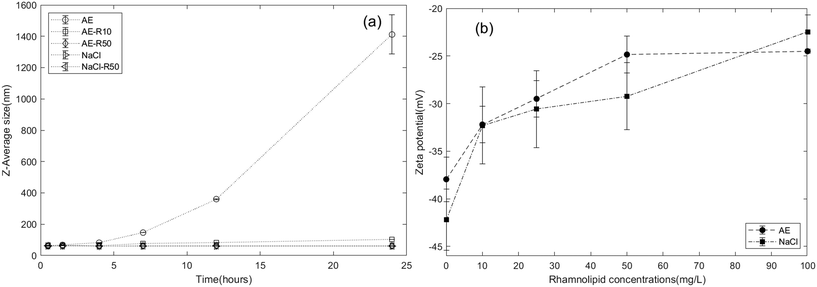
Energy profile calculations based on Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory (Fig. S5a†) revealed a secondary minimum and a small energy barrier (less than 1 kT) between IONPs in the aerobic medium, in agreement with DLS results that IONPs tended to agglomerate in the aerobic medium. The interaction energy between IONPs and the quartz sand surface was also calculated using DLVO theory (Fig. S6†) and resulted in an energy barrier of 4.8 kT. This suggests that IONP attachment might be more favourable to the surface of other IONPs than to that of quartz sands. Thus, we attribute the observed hyper-exponential retention profiles to physical straining induced by a filter ripening process,100i.e., we assume that IONPs preferentially deposit onto previously attached nanoparticles, creating increasing layers of retained nanoparticles over time near the column inlet96 and induces straining process.101 This ripening/straining phenomenon has been observed previously for other ENPs (e.g., gold nanoparticles,96 TiO2 (ref. 102 and 103)). For example, Chen et al.103 observed TiO2 breakthrough curves that displayed a transition from blocking to filter ripening with increasing ionic strength, and hyper-exponential retention profiles occurring at high ionic strength condition. They concluded that net attractive nanoparticle–nanoparticle interactions were responsible for the ripening and subsequent physical straining processes. Mathematical simulations of the experimental data also showed that the two-site mathematical model incorporating a filter ripening process more accurately captured the hyper-exponential decay feature of retention profiles compared to one-site models (Fig. S9†). The fitted filter ripening rate coefficients (krip) were 1.16 and 1.23 times greater than the nanoparticle attachment rate coefficient for the replicate columns, respectively (Table 1). These results imply that filter ripening played a more important role than nanoparticle attachment in the IONP retention process for IONP transport within an aerobic medium background solution. This is also consistent with DLVO calculations, which show that nanoparticle–nanoparticle interactions experience a slightly smaller energy barrier than nanoparticle–sand interactions.
To further understand the effect of the rhamnolipid preflood on IONP mobility, additional batch studies and column experiments were performed, using only rhamnolipid as the solute, to obtain baseline data of rhamnolipid sorption and transport (Fig. S7 and S8†) in 80–100 mesh Ottawa sand. As shown in Fig. S8,† the Langmuir model provided a good fit to the batch adsorption data, yielding a maximum adsorption capacity of 15.38 and 16.36 μg rhamnolipid per g sand in aerobic medium (R2 = 0.895) and 10 mM NaCl (R2 = 0.963), respectively. These data support the use of a Langmuir-type limiting capacity or maximum surface coverage for type 1 sites in the model. In column experiments, when 10 mg L−1 and 50 mg L−1 rhamnolipid were injected alone in 80–100 mesh Ottawa sand with aerobic medium as the background electrolyte, 12.9% and 17.9% of the injected mass was retained, corresponding to approximately 1.9 μg and approximately 8.0 μg rhamnolipid retention per gram sand, respectively. Using a rate limited sorption model with a desorption term (with the same mathematical form as given by eqn (1) and (3)), the fitted adsorption capacities were determined to be 3.31 ± 2.51 μg g−1 and 11.84 ± 5.11 μg g−1 for rhamnolipid at concentrations of 10 mg L−1 and 50 mg L−1 (Table S2†), respectively, which were also consistent with batch adsorption results at these concentrations (4 μg g−1 and 15 μg g−1). The fitted rhamnolipid adsorption rate coefficient was at least 10 times larger than desorption rate coefficient, which suggested that rhamnolipid desorption from the quartz sand was negligible compared to the adsorption process. Using the fitted parameters, rhamnolipid retention profiles were also simulated (Fig. S7b†), which indicated that the absorbed rhamnolipid was distributed uniformly over the column length, consistent with the limiting sorption capacity assumption of the mathematical model.
The results from rhamnolipid-only batch and column studies suggested that the observed increase in IONP mobility following a 50 mg L−1 rhamnolipid preflood was due to blocking of attachment sites on mineral surfaces, thereby reducing nanoparticle deposition.39,50,105 However, when the rhamnolipid concentration was lowered (i.e., preflood with 10 mg L−1 rhamnolipid), a sufficient number of attachment sites were still available to retain the applied IONP mass. Similar observations of increased nanoparticle mobility after pretreatment with surfactants105/polymers25/NOMs39 have been reported. For example, Kmetz et al.105 pretreated a sand column with 1000 mg L−1 HEC-10, followed by the introduction of 2500 mg L−1 magnetite nanoparticles, which resulted in 93% mass recovery of the injected nanoparticles. More recently, Xu et al.39 preflushed soil columns with dissolved organic matter (DOM) and observed a 2- to 5-fold increase in the mobility of hydroxyapatite nanoparticles (nHAP) compared to untreated soil columns with increasing preflood DOM concentrations. The authors concluded that DOM was adsorbed on favourable attachment sites and decreased soil surface potentials by 2–5 mV, as well as provided steric hindrance to nHAP deposition.
The two-site model, which incorporated filter ripening, was able to reproduce the declining plateau of the BTC and the hyper-exponentially decreased retention profiles. Compared to modelling results obtained for the IONP baseline experiment, the fitted type 1 site maximum capacity decreased to 4.03 and 2.24 μg as Fe per g sand, after a preflood of 10 mg L−1 and 50 mg L−1 rhamnolipid solution, respectively, corresponding to a reduction in the number of attachment sites. Additionally, the fitted attachment rate coefficient after a preflood with 50 mg L−1 rhamnolipid was approximately 2.5 times smaller (0.19 h−1) than those obtained from the baseline column experiment (0.49 h−1 and 0.52 h−1), suggesting that adsorption of rhamnolipid on sand surface altered interactions between nanoparticles and the porous medium.
Fig. 3a and b showed the effect of co-injecting rhamnolipid with IONPs on the IONP breakthrough curves and retention profiles in 80–100 mesh Ottawa sand, respectively. Compared to the minimal breakthrough measured when IONPs were injected alone (Fig. 1), considerably more breakthrough of IONP was measured in the presence of 10 or 50 mg L−1 rhamnolipid. Specifically, addition of 10 mg L−1 rhamnolipid resulted in 24.9% of the applied mass recovered in the column effluent, while co-injection with 50 mg L−1 rhamnolipid yielded 43.2% and 56.6% IONP breakthrough for duplicate columns. In contrast to IONP baseline columns where near column inlet a large amount of nanoparticle aggregates were observed due to filter ripening, the deposited nanoparticles in IONP and rhamnolipid co-injection columns sparsely distributed and remained monodisperse on the sand surface, as shown in Fig. 4c (nanoparticles are highlighted in red circles). These data indicated that the observed increases in nanoparticle mobility in the presence of rhamnolipid are due to the combined effects of nanoparticle stabilization and the site blocking mechanisms.
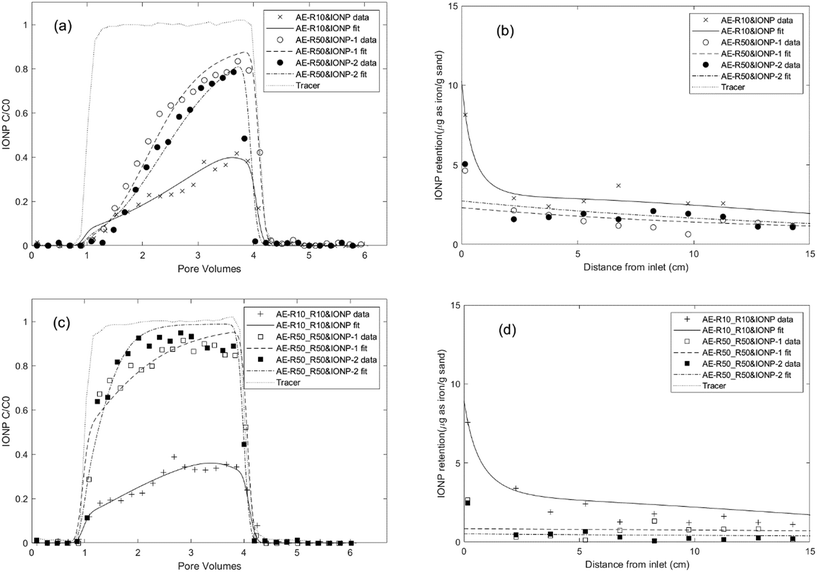 | ||
| Fig. 3 Experimental and fitted effluent breakthrough curves and retention profiles for IONP transport experiments conducted in water-saturated columns packed with 80–100 mesh Ottawa sand with aerobic medium as background electrolyte at a pore-water velocity of 0.43 m per day using different injection procedures and with different rhamnolipid concentrations. Symbols represent experimental data from each IONP column experiment shown in Table 1. (a) and (b): IONP and rhamnolipid co-injection column results. (c) and (d): rhamnolipid preflood and co-injection with IONP column results. | ||
All IONP breakthrough curves obtained for the co-injection columns exhibited asymmetrical shapes with the relative concentration (C/C0) in the column effluent gradually increasing to a maximum and then rapidly declining to 0 after nanoparticle injection ceased (Fig. 3a), consistent with a maximum retention capacity (Smax) and irreversible attachment (kdet = 0). The retention profiles obtained for IONP on the solid phase displayed a monotonically decreasing trend with the highest IONP deposition at the column inlet (Fig. 3b). For the column co-injected with 10 mg L−1 rhamnolipid, IONP retention near the column inlet may be slightly impacted by filter ripening, as the fitted ripening rate (krip) decreased to 0.06 h−1, only one fifth of attachment rate (0.32 h−1). For 50 mg L−1 rhamnolipid co-injection columns, model fitting of the data indicated that rhamnolipid adsorption rates were approximately 4–5 times smaller than the IONP attachment rates (e.g., 0.09 h−1vs. 0.38 h−1), suggesting that IONP exhibited more favourable deposition than rhamnolipid. This meant that the IONPs were able to effectively occupy more attachment sites near the column inlet compared to the rhamnolipid. As IONP mass in the aqueous phase was depleted with travel distance, rhamnolipid adsorption then became more dominant. As a consequence, the IONP retention profile decreased monotonically, with greatest retention near the column inlet. These results were in contrast to prior studies which showed that a residual coating polymer rapidly adsorbed near the column inlet, resulting in attachment site blocking and an increasing QD retention profile with distance from the inlet.25,44 The multi-constituent model yielded better fit to the experimental data compared to a single-constituent model (Fig. S10†), demonstrating the importance of accounting for competitive attachment to accurately simulate IONP transport and retention behaviour in this complex system. Additionally, the fitted type 1 site retention capacities (Table 1) were similar (approximately 5.98–7.67 μg g−1 sand) for co-injection columns at approximately 5 mg L−1 IONP (as iron) co-injected with 10 mg L−1 rhamnolipid (AE-R10&IONP) and with 50 mg L−1 rhamnolipid (AE-R50&IONP, duplicates), further demonstrating the robustness of the (two-site) multi-constituent mathematical model.
3.2 IONP transport in 10 mM NaCl
A second set of column experiments was performed using 10 mM NaCl as the background electrolyte to assess the effect of rhamnolipid on IONP transport and retention under a lower ionic strength condition. Baseline transport and retention data for IONP or rhamnolipid alone in 10 mM NaCl were first obtained, followed by IONP co-injection with 50 mg L−1 rhamnolipid, and finally preflood and co-injection of IONP with 50 mg L−1 rhamnolipid. The resulting IONP BTCs and retention profiles are shown in Fig. 5. For the duplicate IONP-alone column experiments, breakthrough of IONP represented 12.3% and 14.9% of the applied mass, which were higher than the minimal breakthrough obtained for IONP baseline experiments with aerobic medium as the background solution. This finding is consistent with aggregation kinetic results (Fig. 2a) and DLVO calculations (Fig. S5b†) demonstrating that IONPs exhibit greater stability in 10 mM NaCl compared to the aerobic medium. The improved transport of IONP in 10 mM NaCl is also consistent with prior nanoparticle transport experiments in which mobility increased and retention decreased in lower ionic strength monovalent cation solutions.103,107,108 In contrast to the hyper-exponentially declining retention profiles observed with aerobic medium (Fig. 1), the retained IONPs in these two columns exhibited a relatively uniform distribution over the length of the columns, consistent with a limiting retention capacity and indicating the absence of filter ripening or straining processes (Fig. 5b). Therefore, a modified filtration theory model24 that incorporates the maximum nanoparticle attachment capacity (Smax) was employed to simulate these column data, yielding IONP attachment rate coefficients of 0.5–0.7 h−1 and a maximum retention capacity of approximately 4 μg as iron per g sand. The attachment rates of IONP baseline columns in 10 mM NaCl were similar to the values obtained when using aerobic medium as background, while the retention capacities were slightly smaller than those obtained in the aerobic medium columns, consistent with other nanoparticle transport studies showing that higher IS results in higher retentions.103,107,109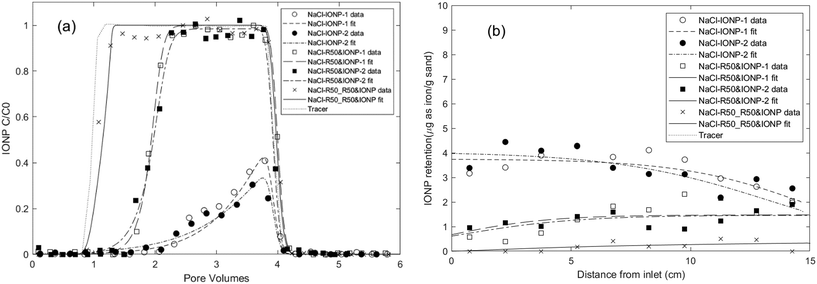 | ||
| Fig. 5 Experimental and fitted (a) effluent breakthrough curves and (b) retention profiles for IONP column experiments using 10 mM NaCl solution as background electrolyte. First, IONPs were injected alone in duplicate columns (NaCl-IONP-1 and -2), then IONPs were co-injected with 50 mg L−1 rhamnolipid in duplicate columns (NaCl-R50&IONP-1 and -2), and finally the column was pre-flushed and IONPs were co-injected with 50 mg L−1 rhamnolipid (NaCl_R50_R50&IONP). Symbols represent experimental results from IONP column experiments in Table 1. | ||
When IONPs were co-injected with 50 mg L−1 rhamnolipid in duplicate columns, enhanced breakthrough of nanoparticle was measured (66.9% and 67.3% of the applied mass, Table 1). Additionally, the IONP retention profiles displayed a monotonically increasing trend, with the smallest deposition near the column inlet. These results suggest that the enhanced IONP mobility was related to the competitive effect of adsorbed rhamnolipid which reduced the number of IONP attachment sites. A one-site multi-constituent model developed in our previous work25 successfully captured the delayed IONP effluent breakthrough and the reduction in solid phase IONP concentrations near the column inlet. The resulting rhamnolipid adsorption rate coefficients were nearly 3-times greater than the nanoparticle attachment rates, which supported the assumption that rhamnolipid outcompeted IONPs for attachment sites. Notably, the fitted maximum retention capacities (Sp1,max) for IONP were approximately 2-times greater than those obtained without rhamnolipid (4.04 μg g−1vs. 8.56 μg g−1, respectively), indicating that more sites were available for IONP attachment in the absence of rhamnolipid.
When the column was preflushed and co-injected with 50 mg L−1 rhamnolipid, even greater breakthrough of IONPs was measured (95.3% of injected mass), yielding a BTC that nearly coincided with that measured for non-reactive tracer (Fig. 5a). The corresponding retention profile exhibited a gradual decrease in concentration with distance, with minimal IONP deposition near column inlet, indicating competitive attachment between rhamnolipid and nanoparticles. The fitted maximum nanoparticle attachment capacity following the rhamnolipid preflood was determined to be 2.43 μg g−1 using one-site multi-constituent model, which represents a 2- and 4-fold reduction compared to the values obtained from the baseline (no rhamnolipid) and co-injection columns respectively, further demonstrating that adsorbed rhamnolipid enhances nanoparticle mobility by competing for attachment sites.
Conclusions
The effects of rhamnolipid biosurfactant on the transport and retention behaviour of IONP in 80–100 mesh Ottawa sands were investigated using coupled experimental and mathematical modelling studies. When using aerobic medium (IS = 50.4 mM) as the background electrolyte, IONPs were almost completely retained within the column due to the instability of nanoparticles and filter ripening. A preflood with either 10 mg L−1 or 50 mg L−1 rhamnolipid resulted in incremental increases in IONP mobility, which were attributed to rhamnolipid adsorption that blocked potential nanoparticle attachment sites. When nanoparticles were co-injected with 10 mg L−1 or 50 mg L−1 rhamnolipid, greater breakthrough of IONP was observed, which was attributed to a combination of improved suspension stability and the site blocking mechanism. The greatest IONP mobility was observed when the columns were preflushed and co-injected with 50 mg L−1 rhamnolipid. These findings were confirmed under a low ionic strength condition (10 mM NaCl), where IONP mobility was considerably greater and the competitive effect of rhamnolipid adsorption on IONP attachment was more apparent. Simulations of the experimental BTCs and retention profiles using mathematical models that accounted for nanoparticle filter ripening processes and/or competitive adsorption were able to capture experimental measurements and provided attachment rate parameters and maximum retention capacities that supported the interpretation of rhamnolipid effects on IONP transport and retention behaviour. These findings demonstrate that biosurfactants can have a substantial effect on the mobility and retention of nanoparticles in porous media and should be taken into account when evaluating the environmental fate of both natural and engineered nanoparticles in the subsurface.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support for this research was provided by the National Science Foundation (NSF), award number CBET-170536 and the U.S. Department of Agriculture (NIFA 2018-67021-28319). The work has not been subject to NSF or USDA review, and therefore, does not necessarily reflect the views of the organization and no official endorsement should be inferred. Special thanks to the Institute for Molecular and Nanoscale Innovation (IMNI) at Brown University for use of their SEM imaging facility.Notes and references
- X. Meng and D. Yang, Critical Review of Stabilized Nanoparticle Transport in Porous Media, J. Energy Resour. Technol., 2019, 141, 070801 CrossRef CAS.
- J. R. Lead, G. E. Batley, P. J. J. Alvarez, M. N. Croteau, R. D. Handy, M. J. McLaughlin, J. D. Judy and K. Schirmer, Nanomaterials in the environment: Behavior, fate, bioavailability, and effects-An updated review, Environ. Toxicol. Chem., 2018, 37, 2029–2063 CrossRef CAS.
- G. Cornelis, K. Hund-Rinke, T. Kuhlbusch, N. van den Brink and C. Nickel, Fate and Bioavailability of Engineered Nanoparticles in Soils: A Review, Crit. Rev. Environ. Sci. Technol., 2014, 44, 2720–2764 CrossRef CAS.
- F. Gottschalk, T. Sun and B. Nowack, Environmental concentrations of engineered nanomaterials: review of modeling and analytical studies, Environ. Pollut., 2013, 181, 287–300 CrossRef CAS.
- S. J. Klaine, P. J. Alvarez, G. E. Batley, T. F. Fernandes, R. D. Handy, D. Y. Lyon, S. Mahendra, M. J. McLaughlin and J. R. Lead, Nanomaterials in the environment: behavior, fate, bioavailability, and effects, Environ. Toxicol. Chem., 2008, 27, 1825–1851 CrossRef CAS.
- H. H. Liu and Y. Cohen, Multimedia environmental distribution of engineered nanomaterials, Environ. Sci. Technol., 2014, 48, 3281–3292 CrossRef CAS.
- R. W. Harvey and S. P. Garabedian, Use of Colloid Filtration Theory in Modeling Movement of Bacteria through a Contaminated Sandy Aquifer, Environ. Sci. Technol., 1991, 25, 178–185 CrossRef CAS.
- Y. Tan, J. Gannon, P. Baveye and M. Alexander, Transport of bacteria in an aquifer sand: Experiments and model simulations, Water Resour. Res., 1994, 30, 3243–3252 CrossRef.
- T. A. Camesano, K. M. Unice and B. E. Logan, Blocking and ripening of colloids in porous media and their implications for bacterial transport, Colloids Surf., A, 1999, 160, 291–308 CrossRef CAS.
- K. Shellenberger and B. E. Logan, Effect of molecular scale roughness of glass beads on colloidal and bacterial deposition, Environ. Sci. Technol., 2002, 36, 184–189 CrossRef CAS.
- G. Gargiulo, S. A. Bradford, J. Simunek, P. Ustohal, H. Vereecken and E. Klumpp, Bacteria Transport and Deposition under Unsaturated Flow Conditions: The Role of Water Content and Bacteria Surface Hydrophobicity, Vadose Zone J., 2008, 7, 406–419 CrossRef.
- N. Weisbrod, H. Meron, S. Walker and V. Gitis, Virus transport in a discrete fracture, Water Res., 2013, 47, 1888–1898 CrossRef CAS.
- P. Grindrod, The Impact of Colloids on the Migration and Dispersal of Radionuclides within Fractured Rock, J. Contam. Hydrol., 1993, 13, 167–181 CrossRef CAS.
- C. V. Chrysikopoulos and V. I. Syngouna, Effect of gravity on colloid transport through water-saturated columns packed with glass beads: modeling and experiments, Environ. Sci. Technol., 2014, 48, 6805–6813 CrossRef CAS.
- S. B. Roy and D. A. Dzombak, Colloid release and transport processes in natural and model porous media, Colloids Surf., A, 1996, 107, 245–262 CrossRef CAS.
- S. A. Bradford, S. R. Yates, M. Bettahar and J. Simunek, Physical factors affecting the transport and fate of colloids in saturated porous media, Water Resour. Res., 2002, 38, 63 CrossRef.
- C. Shen, Y. Huang, B. Li and Y. Jin, Effects of solution chemistry on straining of colloids in porous media under unfavorable conditions, Water Resour. Res., 2008, 44, W05419 CrossRef.
- M. Elimelech, M. Nagai, C. H. Ko and J. N. Ryan, Relative insignificance of mineral grain zeta potential to colloid transport in geochemically heterogeneous porous media, Environ. Sci. Technol., 2000, 34, 2143–2148 CrossRef CAS.
- Y. Fujita and M. Kobayashi, Transport of colloidal silica in unsaturated sand: Effect of charging properties of sand and silica particles, Chemosphere, 2016, 154, 179–186 CrossRef CAS.
- I. L. Molnar, E. Pensini, M. A. Asad, C. A. Mitchell, L. C. Nitsche, L. J. Pyrak-Nolte, G. L. Miño and M. M. Krol, Colloid Transport in Porous Media: A Review of Classical Mechanisms and Emerging Topics, Transp. Porous Media, 2019, 130, 129–156 CrossRef.
- G. Liu, H. Zhong, Z. Ahmad, X. Yang and L. Huo, Transport of engineered nanoparticles in porous media and its enhancement for remediation of contaminated groundwater, Crit. Rev. Environ. Sci. Technol., 2019, 50, 2301–2378 CrossRef.
- T. Kanti Sen and K. C. Khilar, Review on subsurface colloids and colloid-associated contaminant transport in saturated porous media, Adv. Colloid Interface Sci., 2006, 119, 71–96 CrossRef CAS.
- S. A. Bradford and S. Torkzaban, Colloid transport and retention in unsaturated porous media: A review of interface-, collector-, and pore-scale processes and models, Vadose Zone J., 2008, 7, 667–681 CrossRef.
- Y. Li, Y. Wang, K. D. Pennell and L. M. Abriola, Investigation of the transport and deposition of fullerene (C60) nanoparticles in quartz sands under varying flow conditions, Environ. Sci. Technol., 2008, 42, 7174–7180 CrossRef CAS.
- M. D. Becker, Y. Wang, K. D. Pennell and L. M. Abriola, A multi-constituent site blocking model for nanoparticle and stabilizing agent transport in porous media, Environ. Sci.: Nano, 2015, 2, 155–166 RSC.
- X. Li, T. D. Scheibe and W. P. Johnson, Apparent decreases in colloid deposition rate coefficients with distance of transport under unfavorable deposition conditions: a general phenomenon, Environ. Sci. Technol., 2004, 38, 5616–5625 CrossRef CAS.
- Y. Wang, Y. Li, J. D. Fortner, J. B. Hughes, L. M. Abriola and K. D. Pennell, Transport and retention of nanoscale C60 aggregates in water-saturated porous media, Environ. Sci. Technol., 2008, 42, 3588–3594 CrossRef CAS.
- Y. Liang, S. A. Bradford, J. Simunek, H. Vereecken and E. Klumpp, Sensitivity of the transport and retention of stabilized silver nanoparticles to physicochemical factors, Water Res., 2013, 47, 2572–2582 CrossRef CAS.
- X. Li and W. P. Johnson, Nonmonotonic variations in deposition rate coefficients of microspheres in porous media under unfavorable deposition conditions, Environ. Sci. Technol., 2005, 39, 1658–1665 CrossRef CAS.
- W. P. Johnson, X. Li and S. Assemi, Deposition and re-entrainment dynamics of microbes and non-biological colloids during non-perturbed transport in porous media in the presence of an energy barrier to deposition, Adv. Water Resour., 2007, 30, 1432–1454 CrossRef.
- E. Pazmino, J. Trauscht, B. Dame and W. P. Johnson, Power law size-distributed heterogeneity explains colloid retention on soda lime glass in the presence of energy barriers, Langmuir, 2014, 30, 5412–5421 CrossRef CAS.
- W. P. Johnson, A. Rasmuson, E. Pazmino and M. Hilpert, Why Variant Colloid Transport Behaviors Emerge among Identical Individuals in Porous Media When Colloid-Surface Repulsion Exists, Environ. Sci. Technol., 2018, 52, 7230–7239 CrossRef CAS.
- C. A. Ron, K. VanNess, A. Rasmuson and W. P. Johnson, How nanoscale surface heterogeneity impacts transport of nano- to micro-particles on surfaces under unfavorable attachment conditions, Environ. Sci.: Nano, 2019, 6, 1921–1931 RSC.
- P. Babakhani, J. Bridge, R. A. Doong and T. Phenrat, Continuum-based models and concepts for the transport of nanoparticles in saturated porous media: A state-of-the-science review, Adv. Colloid Interface Sci., 2017, 246, 75–104 CrossRef CAS.
- W. P. Johnson, Quantitative Linking of Nanoscale Interactions to Continuum-Scale Nanoparticle and Microplastic Transport in Environmental Granular Media, Environ. Sci. Technol., 2020, 54, 8032–8042 CrossRef CAS.
- Y. Wang, B. Gao, V. L. Morales, Y. Tian, L. Wu, J. Gao, W. Bai and L. Yang, Transport of titanium dioxide nanoparticles in saturated porous media under various solution chemistry conditions, J. Nanopart. Res., 2012, 14, 1095 CrossRef.
- W. Yang, S. A. Bradford, Y. Wang, P. Sharma, J. Shang and B. Li, Transport of biochar colloids in saturated porous media in the presence of humic substances or proteins, Environ. Pollut., 2019, 246, 855–863 CrossRef CAS.
- K. Dibyanshu and T. Raychoudhury, Co-transport behavior of nano-ZnO particles in the presence of metal-nanoparticles through saturated porous media, J. Environ. Chem. Eng., 2019, 7, 103103 CrossRef.
- S. Xu, X. Chen and J. Zhuang, Opposite influences of mineral-associated and dissolved organic matter on the transport of hydroxyapatite nanoparticles through soil and aggregates, Environ. Res., 2019, 171, 153–160 CrossRef CAS.
- T. Ben-Moshe, I. Dror and B. Berkowitz, Transport of metal oxide nanoparticles in saturated porous media, Chemosphere, 2010, 81, 387–393 CrossRef CAS.
- M. Zhang, S. A. Bradford, J. Simunek, H. Vereecken and E. Klumpp, Co-transport of multi-walled carbon nanotubes and sodium dodecylbenzenesulfonate in chemically heterogeneous porous media, Environ. Pollut., 2019, 247, 907–916 CrossRef CAS.
- X. Yin, Y. Jiang, Y. Tan, X. Meng, H. Sun and N. Wang, Co-transport of graphene oxide and heavy metal ions in surface-modified porous media, Chemosphere, 2019, 218, 1–13 CrossRef CAS.
- J. Englehart, B. A. Lyon, M. D. Becker, Y. Wang, L. M. Abriola and K. D. Pennell, Influence of a polymer sunscreen additive on the transport and retention of titanium dioxide nanoparticles in water-saturated porous media, Environ. Sci.: Nano, 2016, 3, 157–168 RSC.
- Y. Wang, M. D. Becker, V. L. Colvin, L. M. Abriola and K. D. Pennell, Influence of residual polymer on nanoparticle deposition in porous media, Environ. Sci. Technol., 2014, 48, 10664–10671 CrossRef CAS.
- I. G. Godinez, C. J. Darnault, A. P. Khodadoust and D. Bogdan, Deposition and release kinetics of nano-TiO2 in saturated porous media: effects of solution ionic strength and surfactants, Environ. Pollut., 2013, 174, 106–113 CrossRef CAS.
- A. Tiraferri and R. Sethi, Enhanced transport of zerovalent iron nanoparticles in saturated porous media by guar gum, J. Nanopart. Res., 2008, 11, 635–645 CrossRef.
- M. Chen, D. Wang, F. Yang, X. Xu, N. Xu and X. Cao, Transport and retention of biochar nanoparticles in a paddy soil under environmentally-relevant solution chemistry conditions, Environ. Pollut., 2017, 230, 540–549 CrossRef CAS.
- P. Han, X. Wang, L. Cai, M. Tong and H. Kim, Transport and retention behaviors of titanium dioxide nanoparticles in iron oxide-coated quartz sand: Effects of pH, ionic strength, and humic acid, Colloids Surf., A, 2014, 454, 119–127 CrossRef CAS.
- G. Chen, X. Liu and C. Su, Distinct effects of humic acid on transport and retention of TiO2 rutile nanoparticles in saturated sand columns, Environ. Sci. Technol., 2012, 46, 7142–7150 CrossRef CAS.
- Y. Wang, Y. Li, J. Costanza, L. M. Abriola and K. D. Pennell, Enhanced mobility of fullerene (C60) nanoparticles in the presence of stabilizing agents, Environ. Sci. Technol., 2012, 46, 11761–11769 CrossRef CAS.
- D. Wang, C. Su, C. Liu and D. Zhou, Transport of fluorescently labeled hydroxyapatite nanoparticles in saturated granular media at environmentally relevant concentrations of surfactants, Colloids Surf., A, 2014, 457, 58–66 CrossRef CAS.
- J. Kumari, N. Chandrasekaran, R. Nagarajan and A. Mukherjee, Individual, co-transport and deposition of TiO 2 and ZnO nanoparticles over quartz sand coated with consortium biofilm, J. Environ. Chem. Eng., 2016, 4, 3954–3960 CrossRef CAS.
- S. Tripathi, D. Champagne and N. Tufenkji, Transport behavior of selected nanoparticles with different surface coatings in granular porous media coated with Pseudomonas aeruginosa biofilm, Environ. Sci. Technol., 2012, 46, 6942–6949 CrossRef CAS.
- R. N. Lerner, Q. Lu, H. Zeng and Y. Liu, The effects of biofilm on the transport of stabilized zerovalent iron nanoparticles in saturated porous media, Water Res., 2012, 46, 975–985 CrossRef CAS.
- M. Tong, J. Ding, Y. Shen and P. Zhu, Influence of biofilm on the transport of fullerene (C60) nanoparticles in porous media, Water Res., 2010, 44, 1094–1103 CrossRef CAS.
- X. Wang, B. Liu, X. Pan and G. M. Gadd, Transport and retention of biogenic selenium nanoparticles in biofilm-coated quartz sand porous media and consequence for elemental mercury immobilization, Sci. Total Environ., 2019, 692, 1116–1124 CrossRef CAS.
- M. R. Mitzel, S. Sand, J. K. Whalen and N. Tufenkji, Hydrophobicity of biofilm coatings influences the transport dynamics of polystyrene nanoparticles in biofilm-coated sand, Water Res., 2016, 92, 113–120 CrossRef CAS.
- Y. Han, G. Hwang, D. Kim, S. A. Bradford, B. Lee, I. Eom, P. J. Kim, S. Q. Choi and H. Kim, Transport, retention, and long-term release behavior of ZnO nanoparticle aggregates in saturated quartz sand: Role of solution pH and biofilm coating, Water Res., 2016, 90, 247–257 CrossRef CAS.
- J. Z. He, D. J. Wang, H. Fang, Q. L. Fu and D. M. Zhou, Inhibited transport of graphene oxide nanoparticles in granular quartz sand coated with Bacillus subtilis and Pseudomonas putida biofilms, Chemosphere, 2017, 169, 1–8 CrossRef CAS.
- Z. Li, A. Aly Hassan, E. Sahle-Demessie and G. A. Sorial, Transport of nanoparticles with dispersant through biofilm coated drinking water sand filters, Water Res., 2013, 47, 6457–6466 CrossRef CAS.
- X. Jiang, X. Wang, M. Tong and H. Kim, Initial transport and retention behaviors of ZnO nanoparticles in quartz sand porous media coated with Escherichia coli biofilm, Environ. Pollut., 2013, 174, 38–49 CrossRef CAS.
- M. L. Chen, J. Penfold, R. K. Thomas, T. J. Smyth, A. Perfumo, R. Marchant, I. M. Banat, P. Stevenson, A. Parry, I. Tucker and I. Grillo, Mixing behavior of the biosurfactant, rhamnolipid, with a conventional anionic surfactant, sodium dodecyl benzene sulfonate, Langmuir, 2010, 26, 17958–17968 CrossRef CAS.
- A. K. Mukherjee, Potential application of cyclic lipopeptide biosurfactants produced by Bacillus subtilis strains in laundry detergent formulations, Lett. Appl. Microbiol., 2007, 45, 330–335 CrossRef CAS.
- M. Basnet, S. Ghoshal and N. Tufenkji, Rhamnolipid biosurfactant and soy protein act as effective stabilizers in the aggregation and transport of palladium-doped zerovalent iron nanoparticles in saturated porous media, Environ. Sci. Technol., 2013, 47, 13355–13364 CrossRef CAS.
- M. Basnet, C. Di Tommaso, S. Ghoshal and N. Tufenkji, Reduced transport potential of a palladium-doped zero valent iron nanoparticle in a water saturated loamy sand, Water Res., 2015, 68, 354–363 CrossRef CAS.
- B. A. Lyon-Marion, M. D. Becker, A. A. Kmetz, E. Foster, K. P. Johnston, L. M. Abriola and K. D. Pennell, Simulation of magnetite nanoparticle mobility in a heterogeneous flow cell, Environ. Sci.: Nano, 2017, 4, 1512–1524 RSC.
- W. Li, C. H. Hinton, S. S. Lee, J. Wu and J. D. Fortner, Surface engineering superparamagnetic nanoparticles for aqueous applications: design and characterization of tailored organic bilayers, Environ. Sci.: Nano, 2016, 3, 85–93 RSC.
- S. S. Lee, W. Li, C. Kim, M. Cho, B. J. Lafferty and J. D. Fortner, Surface functionalized manganese ferrite nanocrystals for enhanced uranium sorption and separation in water, J. Mater. Chem. A, 2015, 3, 21930–21939 RSC.
- W. Li, J. T. Mayo, D. N. Benoit, L. D. Troyer, Z. A. Lewicka, B. J. Lafferty, J. G. Catalano, S. S. Lee, V. L. Colvin and J. D. Fortner, Engineered superparamagnetic iron oxide nanoparticles for ultra-enhanced uranium separation and sensing, J. Mater. Chem. A, 2016, 4, 15022–15029 RSC.
- W. Li, S. S. Lee, J. Wu, C. H. Hinton and J. D. Fortner, Shape and size controlled synthesis of uniform iron oxide nanocrystals through new non-hydrolytic routes, Nanotechnology, 2016, 27, 324002 CrossRef.
- A. H. Lu, E. E. L. Salabas and F. Schüth, Magnetic nanoparticles: synthesis, protection, functionalization, and application, Angew. Chem., Int. Ed., 2007, 46, 1222–1244 CrossRef CAS.
- W. Li, S. S. Lee, A. M. Mittelman, D. Liu, J. Wu, C. H. Hinton, L. M. Abriola, K. D. Pennell and J. D. Fortner, Aqueous Aggregation Behavior of Engineered Superparamagnetic Iron Oxide Nanoparticles: Effects of Oxidative Surface Aging, Environ. Sci. Technol., 2016, 50, 12789–12798 CrossRef CAS.
- I. O. Olasanmi and R. W. Thring, Evaluating rhamnolipid-enhanced washing as a first step in remediation of drill cuttings and petroleum-contaminated soils, J. Adv. Res., 2020, 21, 79–90 CrossRef CAS.
- J. Spizizen, Transformation of biochemically deficient strains of Bacillus subtilis by deoxyribonucleate, Proc. Natl. Acad. Sci. U. S. A., 1958, 44, 1072 CrossRef CAS.
- N. Toride, F. Leij and M. T. Van Genuchten, The CXTFIT code for estimating transport parameters from laboratory or field tracer experiments, Version 2.1, Research Report No. 137, Agricultural Research Service, US Department of Agriculture, Riverside, California, 1995 Search PubMed.
- E. Jurado, M. Fernandez-Serrano, J. Nunez-Olea, G. Luzon and M. Lechuga, Simplified spectrophotometric method using methylene blue for determining anionic surfactants: applications to the study of primary biodegradation in aerobic screening tests, Chemosphere, 2006, 65, 278–285 CrossRef CAS.
- N. M. Pinzon and L. K. Ju, Analysis of rhamnolipid biosurfactants by methylene blue complexation, Appl. Microbiol. Biotechnol., 2009, 82, 975–981 CrossRef CAS.
- E. Viollier, P. W. Inglett, K. Hunter, A. N. Roychoudhury and P. Van Cappellen, The ferrozine method revisited: Fe (II)/Fe (III) determination in natural waters, Appl. Geochem., 2000, 15, 785–790 CrossRef CAS.
- D. A. Armbruster and T. Pry, Limit of blank, limit of detection and limit of quantitation, Clin. Biochem. Rev., 2008, 29(Suppl 1), S49–S52 Search PubMed.
- J. L. Darby, R. E. Attanasio and D. F. Lawler, Filtration of Heterodisperse Suspensions - Modeling of Particle Removal and Head Loss, Water Res., 1992, 26, 711–726 CrossRef CAS.
- M. D. Becker, On the Influence of Co-Constituents on Nanoparticle Transport in Heterogeneous Porous Media, PhD, Tufts University, 2015 Search PubMed.
- M. Tong, T. A. Camesano and W. P. Johnson, Spatial variation in deposition rate coefficients of an adhesion-deficient bacterial strain in quartz sand, Environ. Sci. Technol., 2005, 39, 3679–3687 CrossRef CAS.
- G. Gargiulo, S. Bradford, J. Simunek, P. Ustohal, H. Vereecken and E. Klumpp, Bacteria transport and deposition under unsaturated conditions: the role of the matrix grain size and the bacteria surface protein, J. Contam. Hydrol., 2007, 92, 255–273 CrossRef CAS.
- D. Wang, L. Ge, J. He, W. Zhang, D. P. Jaisi and D. Zhou, Hyperexponential and nonmonotonic retention of polyvinylpyrrolidone-coated silver nanoparticles in an Ultisol, J. Contam. Hydrol., 2014, 164, 35–48 CrossRef CAS.
- T. Lu, T. Xia, Y. Qi, C. Zhang and W. Chen, Effects of clay minerals on transport of graphene oxide in saturated porous media, Environ. Toxicol. Chem., 2017, 36, 655–660 CrossRef CAS.
- Y. Wang, J. H. Kim, J. B. Baek, G. W. Miller and K. D. Pennell, Transport behavior of functionalized multi-wall carbon nanotubes in water-saturated quartz sand as a function of tube length, Water Res., 2012, 46, 4521–4531 CrossRef CAS.
- L. Cai, J. Zhu, Y. Hou, M. Tong and H. Kim, Influence of gravity on transport and retention of representative engineered nanoparticles in quartz sand, J. Contam. Hydrol., 2015, 181, 153–160 CrossRef CAS.
- Y. Su, B. Gao and L. Mao, Concurrent agglomeration and straining govern the transport of (14) C-labeled few-layer graphene in saturated porous media, Water Res., 2017, 115, 84–93 CrossRef CAS.
- P. Sun, A. Shijirbaatar, J. Fang, G. Owens, D. Lin and K. Zhang, Distinguishable transport behavior of zinc oxide nanoparticles in silica sand and soil columns, Sci. Total Environ., 2015, 505, 189–198 CrossRef CAS.
- T. Raychoudhury, N. Tufenkji and S. Ghoshal, Straining of polyelectrolyte-stabilized nanoscale zero valent iron particles during transport through granular porous media, Water Res., 2014, 50, 80–89 CrossRef CAS.
- A. R. Esfahani, A. F. Firouzi, G. Sayyad and A. R. Kiasat, Transport and retention of polymer-stabilized zero-valent iron nanoparticles in saturated porous media: Effects of initial particle concentration and ionic strength, J. Ind. Eng. Chem., 2014, 20, 2671–2679 CrossRef CAS.
- S. A. Bradford, J. Simunek, M. Bettahar, M. T. van Genuchten and S. R. Yates, Significance of straining in colloid deposition: Evidence and implications, Water Resour. Res., 2006, 42, W12S15 Search PubMed.
- M. Tong and W. P. Johnson, Colloid population heterogeneity drives hyperexponential deviation from classic filtration theory, Environ. Sci. Technol., 2007, 41, 493–499 CrossRef CAS.
- S. A. Bradford and S. Torkzaban, Colloid interaction energies for physically and chemically heterogeneous porous media, Langmuir, 2013, 29, 3668–3676 CrossRef CAS.
- S. A. Bradford, S. Torkzaban and J. Simunek, Modeling colloid transport and retention in saturated porous media under unfavorable attachment conditions, Water Resour. Res., 2011, 47 Search PubMed.
- M. Y. Chan and P. J. Vikesland, Porous media-induced aggregation of protein-stabilized gold nanoparticles, Environ. Sci. Technol., 2014, 48, 1532–1540 CrossRef CAS.
- K.-M. Yao, M. T. Habibian and C. R. O'Melia, Water and waste water filtration. Concepts and applications, Environ. Sci. Technol., 1971, 5, 1105–1112 CrossRef CAS.
- N. Tufenkji and M. Elimelech, Correlation equation for predicting single-collector efficiency in physicochemical filtration in saturated porous media, Environ. Sci. Technol., 2004, 38, 529–536 CrossRef CAS.
- A. Braun, E. Klumpp, R. Azzam and C. Neukum, Transport and deposition of stabilized engineered silver nanoparticles in water saturated loamy sand and silty loam, Sci. Total Environ., 2015, 535, 102–112 CrossRef CAS.
- A. G. Nascimento, M. R. Totola, C. S. Souza, M. T. Borges and A. C. Borges, Temporal and spatial dynamics of blocking and ripening effects on bacterial transport through a porous system: a possible explanation for CFT deviation, Colloids Surf., B, 2006, 53, 241–244 CrossRef CAS.
- G. Liu, H. Zhong, Z. Ahmad, X. Yang and L. Huo, Transport of engineered nanoparticles in porous media and its enhancement for remediation of contaminated groundwater, Crit. Rev. Environ. Sci. Technol., 2019, 1–78 Search PubMed.
- N. Solovitch, J. Labille, J. Rose, P. Chaurand, D. Borschneck, M. R. Wiesner and J. Y. Bottero, Concurrent aggregation and deposition of TiO2 nanoparticles in a sandy porous media, Environ. Sci. Technol., 2010, 44, 4897–4902 CrossRef CAS.
- G. Chen, X. Liu and C. Su, Transport and retention of TiO2 rutile nanoparticles in saturated porous media under low-ionic-strength conditions: measurements and mechanisms, Langmuir, 2011, 27, 5393–5402 CrossRef CAS.
- C. Ma, X. Huangfu, Q. He, J. Ma and R. Huang, Deposition of engineered nanoparticles (ENPs) on surfaces in aquatic systems: a review of interaction forces, experimental approaches, and influencing factors, Environ. Sci. Pollut. Res., 2018, 25, 33056–33081 CrossRef CAS.
- A. A. Kmetz, M. D. Becker, B. A. Lyon, E. Foster, Z. Xue, K. P. Johnston, L. M. Abriola and K. D. Pennell, Improved Mobility of Magnetite Nanoparticles at High Salinity with Polymers and Surfactants, Energy Fuels, 2016, 30, 1915–1926 CrossRef CAS.
- G. Fritz, V. Schädler, N. Willenbacher and N. J. Wagner, Electrosteric stabilization of colloidal dispersions, Langmuir, 2002, 18, 6381–6390 CrossRef CAS.
- A. Esfandyari Bayat, R. Junin, M. N. Derahman and A. A. Samad, TiO (2) nanoparticle transport and retention through saturated limestone porous media under various ionic strength conditions, Chemosphere, 2015, 134, 7–15 CrossRef CAS.
- S. Kamrani, M. Rezaei, M. Kord and M. Baalousha, Transport and retention of carbon dots (CDs) in saturated and unsaturated porous media: Role of ionic strength, pH, and collector grain size, Water Res., 2018, 133, 338–347 CrossRef CAS.
- C. Chen, T. Waller and S. L. Walker, Visualization of transport and fate of nano and micro-scale particles in porous media: modeling coupled effects of ionic strength and size, Environ. Sci.: Nano, 2017, 4, 1025–1036 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Further details of experimental setup, IONP characterizations, rhamnolipid isothermal sorption data and rhamnolipid transport alone column experimental/modelling results. Additional details on DLVO calculation and mathematical model comparison and selection. See DOI: 10.1039/d0en01033b |
| This journal is © The Royal Society of Chemistry 2021 |