DOI:
10.1039/D1EE01313K
(Analysis)
Energy Environ. Sci., 2021,
14, 6074-6098
Determinants of lithium-ion battery technology cost decline†
Received
30th April 2021
, Accepted 16th August 2021
First published on 22nd November 2021
Abstract
Prices of lithium-ion battery technologies have fallen rapidly and substantially, by about 97%, since their commercialization three decades ago. Many efforts have contributed to the cost reduction underlying the observed price decline, but the contributions of these efforts and their relative importance remain unclear. Here we address this gap by developing a set of cost change models to disentangle these efforts and estimate their individual contributions to the cost decline of lithium-ion cells. We collect data on lithium-ion cell components and their prices, develop a cost equation and cost change equations for these cells, and estimate the contributions of different low-level mechanisms of cost reduction, such as the impacts of changes in energy capacity characteristics, reductions in material prices, and changes in non-material costs. We find that between the late 1990s and early 2010s, about 38% of the observed cost decline resulted from efforts to increase cell charge density. Meanwhile, reductions in cathode materials prices contributed 18% of the cost reduction, and changes in non-material costs accounted for 14% of the cost decline. We also consider the contributions of high-level mechanisms, including research and development (R&D), learning-by-doing, and economies of scale. We find that the largest share of cost change was driven by public and private research and development, which we estimate contributed a majority of the observed cost reduction, with a lower contribution from economies of scale. Moreover, we find that the majority of the R&D contribution can be attributed to advancements in chemistry and materials science. Looking to the future, these results suggest that the nature of electrochemical battery technology, which often allows for many different combinations of electrode materials and electrolyte chemistries, presents further opportunities for new approaches and cost decline in batteries. However, public policy may be needed to help avoid premature lock-in, which can result from market forces favoring incumbent technologies.
Broader context
Electrochemical energy storage technologies can help reduce greenhouse gas emissions. Already, lithium-ion batteries are helping enable the electrification of cars and buses, and are beginning to support the integration of renewable energy resources into the electricity grid. While the costs of lithium-ion technologies have fallen rapidly and substantially since their commercialization, the growth in their deployment will depend in part on their costs as well as on trends in other battery technologies. To understand past improvement and inform strategies to further improve electrochemical storage technologies, we elucidate the mechanisms of the cost decline observed for lithium-ion technologies. We disentangle and quantify the contributions to cost change from various factors, including changes in cell charge density, material prices, and plant production capacities. We also estimate the contributions of higher-level mechanisms typically associated with policy and business strategies, including research and development (R&D), learning-by-doing, and economies of scale. We demonstrate that R&D, especially in chemistry and materials science, played an outsized role in the cost decline of lithium-ion technologies. Our results indicate that the chemical diversity accessible to lithium-ion technologies might help explain their rapid improvement. Moreover, our results suggest that, given appropriate policies and investments, this diversity might present opportunities to further improve and reduce the costs of electrochemical storage technologies.
|
Introduction
In an effort to reduce greenhouse gas emissions, electrochemical energy storage technologies (i.e. batteries) are being deployed to electrify transportation systems, and increasingly integrate intermittent renewable energy resources into the broader electricity grid.1–4 However, the deployment of these technologies remains limited, in part because without significant incentives they likely require considerable improvement to meet cost-competitiveness targets, particularly for grid applications.5–10 Of the range of battery varieties, lithium-ion technologies are considered especially promising due to their historic cost decline and relatively high energy densities, as well as their growth in production.2,11–18 Since their commercialization in 1991, the real price of lithium-ion cells, in USD kW−1 h−1, has fallen nearly 97% (Fig. 1).18 However, uncertainty remains as to which strategies or incentives could help further reduce the costs of lithium-ion technologies and, more generally, enable energy storage technologies to reach cost-competitiveness. Should companies and policymakers provide more funding for research and development (R&D)? If so, which research and development objectives should be prioritized? Should this support be balanced with market incentives that encourage large-scale deployment?
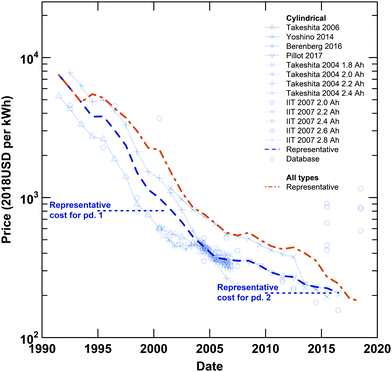 |
| | Fig. 1 Lithium-ion cell prices for cylindrical cells (blue) and all types of cells (orange). Time series (lines with symbols) and single-year records (symbols) are plotted for cylindrical cell prices, along with representative time series of prices for cylindrical cells (blue, bolded, dashed line) and all types of cells (orange, bolded, dashed line). The representative cell-level costs estimated in this work for the late 1990s and early 2010s are also plotted (blue, horizontal, dotted lines). Since their introduction in 1991, the prices of both all types of cells and cylindrical cells, the focus of this analysis, have declined approximately 97%. Details on the data included and the development of the representative price series were reported previously.18 | |
Many energy and environmentally relevant technologies have faced similar questions,19 and new insight has been emerging in recent research. In the case of lithium-ion technologies, detailed bottom-up battery design and production models have been developed to help understand and project cost reduction opportunities from electrode material and design changes as well as production improvements.20–34 These models tend to be static, focusing on a single point in time or future year. These efforts sometimes include detailed models of cell characteristics, costs, and performance, though generally they do not clearly delineate the relationships between changes in technology characteristics and changes in cost and performance that exist while many non-additive characteristics change simultaneously. As a result, these models are not typically well-suited to the investigation of the mechanisms through which technologies have improved in the past, and the quantitative roles of various drivers of technological change, both historically and going forward.35 Meanwhile, top-down performance curve models have been employed to measure and project overall cost or price decline at the cell, pack, and system levels.15,18,36–43 These analyses tend to assume that cost reduction is related to various high-level drivers, such as production and research and development efforts, and infer the influence these drivers have based on correlation. For lithium-ion technologies, many of these analyses examine the observed relationship between battery price and cumulative production to infer how additional deployment might reduce costs. Related analyses examine how costs decline with time. These performance curve models are typically dynamic—they consider how the technologies change over time—and they can be useful for informing forecasts when combined with appropriate error models.44 But they are not suited to examining the underlying mechanisms of change. They treat technologies as “black boxes” and are thus unable to identify which design changes, research efforts, or incentives led to observed cost changes and have the potential to enable further cost reduction.45,46 Even when two-factor performance curve models47 are used, for example to investigate the roles of research and development efforts and scales of production in an effort to separate these drivers’ impacts on costs,36,40 the insights into the underlying mechanisms remain limited. Moreover, these two-factor models can be prone to overfitting given data limitations.44
Recently, a new conceptual framework and dynamic, detailed quantitative models have been applied to study the cost changes observed for notable energy technologies.35,48 These models start from a cost equation that computes a technology's overall cost scaled by its service (e.g. typically USD W−1 for power generating technologies, USD W−1 h−1 for energy storage technologies, etc.) at a given point in time. These cost equations comprise variables that represent specific cost determinants, while balancing model fidelity and data availability. From a given cost equation, cost change equations are derived that estimate each variable's contribution to the overall cost change between two points in time. In this fashion, these models can separate the impacts that individual material, design, and production changes have on overall cost, even when many of these variables change simultaneously. Changes in these variables constitute low-level causes, or “mechanisms”, of cost change; and they represent measurable, often tangible, changes to the technology. In the case of lithium-ion technologies, low-level mechanisms might include an increase in cathode specific capacity or decrease in separator thickness. Contributions of low-level mechanisms can be aggregated to reveal the influence of changes in various technology or production characteristics that encompass multiple low-level mechanisms, such as increasing cell charge density. These low-level mechanisms can also be categorized and summed to estimate the impact of high-level cost change mechanisms that reflect the objectives of industry-scale processes and government policies often associated with technological improvement, such as research and development and learning-by-doing (LBD), as well as emergent phenomena such as economies of scale (EOS).19,49–51 Using this approach, we can identify those mechanisms that have driven historical technological change and could continue to do so going forward.
In this work, we apply these methods to lithium-ion cells to investigate why their cost declined. We focus this analysis on changes in the cost to manufacture lithium-ion cells, as opposed to the price to purchase them, and we scale this cost by cell-level energy capacity. The cost of energy storage capacity, in units of USD W−1 h−1, helps determine the adoption of battery technologies for a range of applications. In the case of lithium-ion battery technologies, this characteristic continues to influence their adoption for battery electric vehicles and stationary storage roles. As such, this metric has received substantial attention; and further cost reduction, for both lithium-ion battery and other energy storage technologies, remains the focus of considerable research, business, and policy efforts. Considering the diversity of applications to which lithium-ion technologies have been adapted and applied, we focus on comparing cylindrical cells with high energy density, and we examine changes in cell chemistry, electrode structure, material prices, and non-material costs. As lithium-ion technologies are relatively new, we examine the technology's status at two times; we compare representative cylindrical cells produced in the late 1990s to those manufactured in the early 2010s. We relate detailed cell chemistry and design changes to technology-specific characteristics and high-level cost change mechanisms. Through this work, we distill lessons for researchers, firms, non-governmental organizations, and governments. We elucidate and estimate the impact of factors that led to the observed cost decline in an effort to inform research directions, investment decisions, and public policies that aim to further reduce costs. We also identify those features of lithium-ion batteries that can help explain their substantial historical cost decline and could help enable additional performance improvement and cost reduction for electrochemical energy storage technologies more generally.
Methods
General computational methods
Currency conversion, inflation adjustment, database parsing, and plotting of composition and component cost and price data were performed using R (v 4.0.4).52 String manipulation and comparison were implemented using stringi.53 Data were stored in Microsoft Excel files (xlsx format) and read and modified in R with the help of the readxl54 and openxlsx55 packages. Implementation of the cost change methodology35 and plotting of cost change results were performed using MATLAB (v. R2021a).56
Currency conversions
Historical foreign exchange rates for the conversion of Japanese Yen to US Dollars (USD) were obtained from the Board of Governors of the Federal Reserve System.57 The Yen to USD dataset included yearly, monthly, and daily rates, all released on 2020-06-01.
Inflation adjustment
Unless otherwise noted, all currency values in US Dollars are adjusted for inflation by converting them to real 2018 US Dollars (i.e. 2018USD) using the Implicit Price Deflator for Gross Domestic Product (Table 1.1.9) published by the US Department of Commerce's Bureau of Economic Analysis.58 The data were revised on 2020-05-28 and contained series with both yearly and quarterly resolution.
Limitations
While we strove to collect data from a wide variety of physical and digital sources, searching for and scanning of references was primarily conducted in English. When potentially useful resources were encountered in other languages, translation generally relied on various online translation tools (e.g. Google Translate).
Additional details
Additional details describing the methods and a flowchart (Fig. S1, ESI†) summarizing the data collection and analysis process are available in the ESI.†
Data collection and analysis
Data on lithium-ion cell composition, performance, overall cost, material prices, and component costs were collected from academic, government, and industry literature published between 1990 and the present. Data collection focused on commercial cylindrical cells containing liquid electrolyte, but data from prismatic and pouch cells were also included and used to corroborate values that are likely consistent across cell types (e.g. foil and separator thicknesses, specific capacities, etc.). To avoid double-counting, we focused on tracing values back to their original sources when possible and using those data directly. Data on lithium-ion cell production and plants’ production capacities were similarly collected from the same types of sources, as well as newspaper articles, press releases, and annual reports. Data on specific capacities of cathode and anode materials were also collected, primarily from academic articles, books, and material suppliers. Overall, the datasets consist of 1057 records (i.e. rows) that, in total, contain over 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 quantitative (e.g. masses, prices, plant capacity estimates, etc.) and qualitative (e.g. cell shape, commercial availability, etc.) data points. These data were obtained from approximately 280 references. Portions of this analysis also rely on the previously described lithium-ion technology database, which contains 1716 records from nearly 600 sources.18
000 quantitative (e.g. masses, prices, plant capacity estimates, etc.) and qualitative (e.g. cell shape, commercial availability, etc.) data points. These data were obtained from approximately 280 references. Portions of this analysis also rely on the previously described lithium-ion technology database, which contains 1716 records from nearly 600 sources.18
When collecting data on cell components, we primarily relied on values obtained from academic, government, and industry reports that describe the components of commercially available cells. These reports often describe the opening of cells and the extraction, separation, and characterization of their contents. Occasionally, similar metrics were obtained from studies that examined cells using various imaging techniques (e.g. X-ray computed tomography). In a few cases, metrics from prototype cells were also included in our dataset, especially when a report indicated that the researchers were working at or collaborating with companies that manufactured cells or specifically designed their prototypes to mimic characteristics observed in commercially available cells. When a single report included replicate measurements, the relevant measures were averaged, and the average was employed in this work. When reports provided ranges without specifying a most probable, average, median, or other “central” value, the average of the lower and upper values was used in this work.
When collecting cost and price data, as well as production and plant production capacity estimates, we excluded projected values, as are sometimes employed in various cost models and industrial reports and presentations. When series were provided that appeared to combine historical and present-day estimates with projections and the division between estimates and projections was not specified, the data preceding the publication or presentation date were assumed to be estimates while the remaining values were assumed to be projections.
Data were binned by year. In the case of academic publications whose submission and publication dates are in different years, the submission year was used to date the values collected in this work.
Estimates of representative values
Sets of values were estimated to represent the designs, materials, material prices, yields, and other cost-influencing variables for lithium-ion cells manufactured during two time periods: 1995–2000 (period 1) and 2010–2015 (period 2). Periods comprising multiple years were used as opposed to individual years as a result of limited data availability. In addition, while more recent data were available for a few cell components and costs, these were insufficient to reliably extend the analysis past 2015.
As lithium-ion technologies diversified to suit an expanding variety of applications,18,59,60 the sets of values developed herein were specifically designed to represent 18650-sized, cylindrical cells with high energy density. This narrowing of scope enables a fairer comparison of cost change between the two periods by limiting the “service” these cells provide to “storing as much energy as possible in a given volume.” This approach strives to minimize the cost and cost change influences of other material, design, and production changes that were instituted to alter other performance features of lithium-ion cells, such as those observed in cells designed for power tools or electric vehicles. In period 1, all commercially available cells were classified as “high energy density” cells. In period 2, representative values for cell and material characteristics that appeared to depend strongly on energy density were primarily estimated from data relevant to cells with energy densities greater than or equal to 550 W h L−1. In a few cases, other characteristics (e.g. charge capacity for a given cell size) were used to identify values relevant to high energy density cells.
Generally, these representative values were determined by collecting relevant data (e.g. specific capacity values, electrode material quantity required per cell, electrode material prices, plant production capacities, etc.) for the given period, categorizing as appropriate (e.g. grouping data by material, application, or cell type), rejecting non-applicable or low reliability data, and averaging the remaining results. For example, specific capacities and prices of various cathode active materials are presented in Fig. 2 and 3, respectively. The focus on cells designed for high energy density sometimes required excluding materials or component specifications relevant to cells designed for other applications, for example excluding LiFePO4 prices from the estimation of a representative cathode active material price for period 2 (see Fig. 3 and ESI,† Section S4). In a few cases, representative values determined for one or more variable(s) were used in combination with previously reported data to estimate values for other variables or cost components.
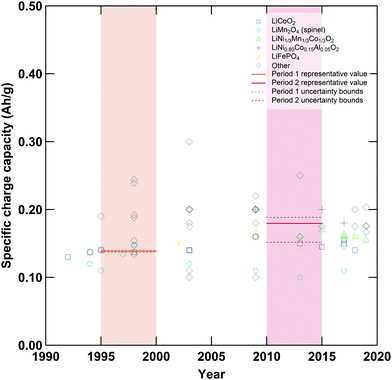 |
| | Fig. 2 Specific charge capacities of various cathode active materials employed in lithium-ion cells. Shaded regions denote the first (orange) and second (red) periods compared in this analysis, while symbols denote various cathode materials. Unbroken horizontal lines within each shaded region are the representative values while dashed lines represent the upper and lower bounds employed in the data-informed sensitivity analysis. Additional plots displaying data for other variables are available in the ESI.† | |
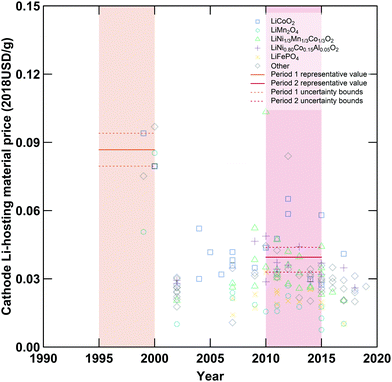 |
| | Fig. 3 Specific prices of various cathode active materials employed in lithium-ion cells. Shaded regions denote the first (orange) and second (red) periods compared in this analysis, while symbols denote various cathode materials. Unbroken horizontal lines within each shaded region are the representative values while dashed lines represent the upper and lower bounds employed in the data-informed sensitivity analysis. Additional plots displaying data for other variables are available in the ESI.† | |
Upper and lower bounds for each representative value were also developed to enable a data-informed sensitivity analysis of our results (see ESI,† Section S9.2). In some cases, the diversification of cell materials and designs led to an increase in the uncertainty range between period 1 and period 2, as demonstrated by the proliferation of different cathode active materials (Fig. 2). In other cases, improved data availability or coalescence around certain design choices led to decreases in the uncertainty ranges.
The representative values for each variable, their symbols, and their units are presented in Tables 1–3, and the values with their uncertainty ranges are provided in Tables S7–S9 (ESI†). Additional details regarding the assumptions used when analyzing previously reported cell component data and the development of specific representative values can be found in the ESI.† Plots of the data, representative values, and uncertainty ranges are also provided in the ESI.†
Table 1 Data employed to calculate mass-related cell cost components
| Variable |
Symbol |
Units |
Period 1 1995–2000 |
Period 2 2010–2015 |
| Cathode active material mass fraction |
w
act,ca
|
Unitless (fraction out of 1) |
0.905 |
0.960 |
| Cathode active material price |
p
act,ca
|
USD g−1 |
0.087 |
0.040 |
| Cathode binder mass fraction |
w
bin,ca
|
Unitless (fraction out of 1) |
0.028 |
0.022 |
| Cathode binder price |
p
bin,ca
|
USD g−1 |
0.014 |
0.017 |
| Cathode conductor mass fraction |
w
con,ca
|
Unitless (fraction out of 1) |
0.067 |
0.018 |
| Cathode conductor price |
p
con,ca
|
USD g−1 |
0.009 |
0.008 |
| Cathode active material specific charge capacity |
q
ca
|
Ampere hour per gram |
0.139 |
0.180 |
| Cathode material yield |
y
ca
|
Unitless (fraction out of 1) |
0.889 |
0.922 |
| N/P ratio |
(N/P)Q |
Unitless (ratio of capacities) |
1.403 |
1.068 |
| Anode active material mass fraction |
w
act,an
|
Unitless (fraction out of 1) |
0.901 |
0.941 |
| Anode active material price |
p
act,an
|
USD g−1 |
0.044 |
0.019 |
| Anode binder mass fraction |
w
bin,an
|
Unitless (fraction out of 1) |
0.079 |
0.046 |
| Anode binder price |
p
bin,an
|
USD g−1 |
0.014 |
0.011 |
| Anode conductor mass fraction |
w
con,an
|
Unitless (fraction out of 1) |
0.020 |
0.013 |
| Anode conductor price |
p
con,an
|
USD g−1 |
0.009 |
0.008 |
| Anode active material specific charge capacity |
q
an
|
Ampere hour per gram |
0.334 |
0.361 |
| Anode material yield |
y
an
|
Unitless (fraction out of 1) |
0.880 |
0.922 |
| Electrolyte solution mass to cathode charge capacity ratio |
D
el
|
g A−1 h−1 |
3.003 |
1.464 |
| Electrolyte solution price |
p
el
|
USD g−1 |
0.074 |
0.019 |
| Electrolyte solution yield |
y
el
|
Unitless (fraction out of 1) |
0.875 |
0.940 |
Table 2 Data employed to calculate area-related cell cost components
| Variable |
Symbol |
Units |
Period 1 1995–2000 |
Period 2 2010–2015 |
| Cathode foil area |
a
Al
|
Meters2 |
0.030 |
0.039 |
| Cathode foil thickness |
t
Al
|
Meters |
24 × 10−6 |
19 × 10−6 |
| Cathode foil price |
p
Al
|
USD g−1 |
0.028 |
0.015 |
| Cathode foil yield |
y
Al
|
Unitless (fraction out of 1) |
0.889 |
0.902 |
| Anode foil to cathode foil area ratio |
(an/ca)A |
Unitless (ratio of areas) |
1.075 |
1.028 |
| Anode foil thickness |
t
Cu
|
Meters |
18 × 10−6 |
14 × 10−6 |
| Anode foil price |
p
Cu
|
USD g−1 |
0.021 |
0.020 |
| Anode foil yield |
y
Cu
|
Unitless (fraction out of 1) |
0.880 |
0.902 |
| Separator to cathode foil area ratio |
(se/ca)A |
Unitless (ratio of areas) |
2.422 |
2.299 |
| Separator thickness |
t
se
|
Meters |
25 × 10−6 |
18 × 10−6 |
| Separator price |
p
V,se
|
USD meters−3 |
0.200 × 106 |
0.077 × 106 |
| Separator yield |
y
se
|
Unitless (fraction out of 1) |
0.995 |
0.980 |
Table 3 Data employed to calculate other cell cost components and cell-level characteristics
| Variable |
Symbol |
Units |
Period 1 1995–2000 |
Period 2 2010–2015 |
|
Cell-level characteristics
|
| Charge capacity utilization |
η
util
|
Unitless (fraction out of 1) |
0.836 |
0.952 |
| Cathode charge capacity for a fixed volume |
Q
ca
|
Ampere hour per cell |
1.726 |
3.129 |
| Cell voltage |
V
|
volts |
3.642 |
3.659 |
| Cell-level yield |
y
cell
|
Unitless (fraction out of 1) |
0.990 |
0.992 |
|
Hardware cost component
|
| Other hardware price |
p
can
|
USD per cell |
0.559 |
0.469 |
| Other hardware yield |
y
can
|
Unitless (fraction out of 1) |
1.00 |
1.00 |
|
Plant size–dependent characteristics
|
| Material cost fraction |
θ
|
Unitless (fraction out of 1) |
0.753 |
0.796 |
| Plant size |
K
|
cells per year |
27 × 106 |
120 × 106 |
| Scaling factor |
b
|
Unitless |
0.30 |
0.30 |
Cost model
Cost decomposition strategy
We develop a cost model for lithium-ion technologies that includes major cost contributors and their relationships to total cell-level cost. We employ an approach similar to that previously reported in a study of photovoltaic (PV) modules,35 where the total cost of a cell is equal to the sum of cost components (Ci) that are typically the products of usage ratios (ϕ) and input prices (p), divided by relevant yields (y),61 as in:| | 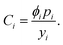 | (1) |
Note that these cost components can comprise both physical “hardware” costs, such as materials, and also non-hardware “soft” costs, such as labor, engineering design, and administration.48,62 As such, these components can reflect changes in cell materials and designs as well as manufacturing processes, equipment, and overhead. Also note that in this analysis “input prices” refer to the prices a technology manufacturer pays to purchase materials that they use in their manufacturing process. When materials are made by the manufacturer itself (e.g. cell components, such as mixtures of electrode materials, or the completed cell itself), their monetary values are referred to as “costs.” This definition reflects our choice of boundary for this analysis: the cell manufacturing plant. The various materials required are treated as though they are “purchased” by the plant operator, and the plant operator then uses these goods to manufacture lithium-ion cells. Mechanisms that influence the cost of producing these materials, such as a shift to using less-expensive metals in cathode materials, are reflected as changes in their input prices.
As considerably more data describing the materials that compose lithium-ion cells were available than data describing their production processes, the initial cost equation splits the total cost of a cell (Ccell) into the sum of the cell's electrochemical components, other hardware, and plant size–dependent costs (eqn (2)). The electrochemical components of a lithium-ion cell can be further separated into those whose cost contribution generally scales with their mass (Cmass) (e.g. metal oxide cathode material, graphitic anode material) or their area (Carea) (e.g. the separator and current collectors foils). The other hardware cost component (Ccan) comprises hardware, such as the can, terminals, and safety components, that are typically required on a one-piece-per-cell basis (e.g. one can per cell). The plant size–dependent component (CK) comprises costs incurred throughout the manufacturing process that are expected to scale with production capacity, such as electricity consumption, operations and maintenance, labor, and equipment. In addition, a coefficient scales the cost per cell by the energy capacity per cell (CapE), which in turn is estimated by the product of charge capacity for an 18650-sized cell (CapQ) and the average cell voltage (V) (i.e. CapE ≈ CapQV). Note that CapQ is constrained volumetrically as a result of limiting this analysis to cells with the same volume, specifically 18650-sized cells. This initial coefficient also incorporates a cell-level yield (ycell) to account for not all cells passing through the cell formation, aging, and associated quality control steps. The resulting equation gives cost in units of USD W−1 h−1 and can be expressed as:
| | 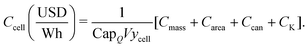 | (2) |
While this cost equation is designed to detail costs for lithium-ion cells, the division between mass- and area-related components could also be employed in the development of cost equations for energy storage technologies in which these components are linked to more easily separable energy capacity and power capacity characteristics, respectively, such as pumped hydroelectric storage systems, redox flow batteries, and fuel cells.
6,63–66 Separating the cost contributions of energy capacity– and power capacity–related components could ease comparison of cost change mechanisms across energy storage technologies.
Mass-related cost components
The mass-related cost component (Cmass) can be expanded to separate cost contributions from the cathode (ca), anode (an), and electrolyte solution (el). (Note that names, symbols, and units of variables employed in the cost equation are listed in Tables 1–3.) For each, the cost can be expressed as the product of the mass (m) of material in the final cell (in grams) and the specific price (p) of the material (in USD gram−1) divided by the yield (y) of the material through the manufacturing processes up to the cell formation step (as a fraction out of 1). The mass-related cost component can thus be expressed as:| | 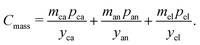 | (3) |
The cathode and anode materials are themselves mixtures and these cost components can be further separated to reflect their compositions. Generally, the primary component of cathode and anode materials is a lithium-hosting, or “active”, material. In the case of the cathode, the active material is typically a mid-to-late first-row transition metal oxide (e.g. LiCoO2, LiNi1/3Mn1/3Co1/3O2, LiFePO4) or a mixture of these transition metal oxides. In the case of the anode, the active material is typically a carbonaceous material (e.g. graphite, or an amorphous (hard or soft) carbon) or less commonly an early-transition metal oxide (e.g. Li4Ti5O12). In the cathode, the active material is often mixed with a binder (e.g. poly(vinylidene fluoride) (PVDF)) and a conductor (e.g. carbon black, acetylene black, graphite). In the anode, the active material is also typically mixed with binder (e.g. PVDF, carboxymethylcellulose with styrene-butadiene rubber, etc.) and sometimes an additional conductor. For both the cathode and anode materials, their cost compositions can be represented by expanding the overall price into the sum of the component materials prices weighted by their mass fractions (w). For the cathode, this decomposition takes the form of:| |  | (4) |
where wact,ca, wbin,ca, and wcon,ca are the mass fractions of the cathode's active, binder, and conductor materials, respectively, while the pact,ca, pbin,ca, and pcon,ca are these materials’ prices. The anode material's overall cost can be similarly represented as:| | 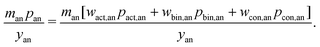 | (5) |
We assume that the materials that compose either the cathode or anode have the same yield in the manufacturing process.
Substituting masses with charge capacities
While these sums can adequately represent the costs of cathode and anode material mixtures, the technical variables do not necessarily represent characteristics that were the direct focus of research and development activities, such as the specific capacities of cathode and anode materials. More informative variables could be the cell charge capacity for a given volume and the specific capacities of the cathode and anode active materials. To investigate the role these values played in the cost change of lithium-ion technologies, the cathode and anode material masses can be replaced by the quotient of the cathode or anode charge capacity (Q, in A h) and its respective specific capacity (q, in A h g−1), as in:| | 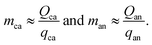 | (6) |
However, these specific capacities must also be adjusted to reflect the mass fraction of the active material in the total electrode material mixture, yielding| | 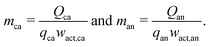 | (7) |
Like the cell charge capacity (CapQ) introduced earlier, in this analysis both the cathode and anode charge capacities (Qca and Qan) are for the fixed volume of an 18650-sized cell. In addition, we assume for simplicity that the surface-electrolyte interphase (SEI) layer does not substantially alter the masses, charge capacities, or specific capacities of the electrode materials.
Relating cathode and anode charge capacities
In commercially available cells, the cathode and anode material masses are typically related to each other, or “balanced”,67 to nearly equalize their charge capacities, with some deviation to ensure safety and a reasonable cycle life. To incorporate this ratio and how it has changed into the model, we define the ratio between the electrode charge capacities (the N/P ratio, (N/P)Q) and use it to define the anode charge capacity as the product of the cathode charge capacity and the N/P ratio:
Determining electrolyte solution mass
Three options were examined for incorporating electrolyte solution mass. The first option is to directly use empirical measures or estimates of electrolyte solution mass from relevant cells. The second involves calculating electrolyte solution volume based on materials’ post-calendering volumes and porosities and the interior volume of the cell and converting from volume to mass using the density of the electrolyte solution. The third entails estimating the electrolyte solution mass per cathode charge capacity (Del) to investigate how this characteristic influenced cost change, and then multiplying this value by the cathode charge capacity of the cell (Qca). The resulting product can then substitute for electrolyte solution mass (mel). Considering the historical data available and their uncertainties, this third approach was employed, giving a cost component of:| | 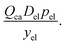 | (9) |
While electrolyte solutions for lithium-ion cells comprise various salts, solvents, and additives, insufficient data were available to further breakdown electrolyte solution cost into a sum of the costs of these constituents.
Mass-related cost components equation
Given the expansions and substitutions described above, the mass-related cost components can be decomposed as shown here:| |  | (10) |
Area-related cost components
The area-related cost component (Carea) can be expanded to separate cost contributions from the cathode foil, denoted with Al as it is typically aluminum; anode foil, denoted with Cu as it is typically copper; and the separator (se). The cost of each of these materials can be expressed as the product of the area (a) of the material in the final cell (in m2) and the price (pa) of the material (in USD m−2) divided by the yield (y) of the material through the manufacturing processes up to the cell formation step (as a fraction out of 1). The area-related cost component can be expressed as:| | 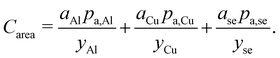 | (11) |
Incorporating thicknesses into current collector foil cost components
Foil thicknesses are another key characteristic of current collector foils that available data suggest changed over time. These can be explicitly incorporated into the cost equation by changing foil prices to units of USD gram−1 (denoted p as opposed to pa) and introducing thicknesses (t, in units of meters) and metal densities (ρ, in units of grams meter−3) into the numerators, giving:| | 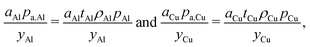 | (12) |
for the cathode and anode foils respectively.
Incorporating thickness into the separator cost component
As with foils, separator thickness has also changed over time. Separator thickness can similarly be explicitly incorporated into the cost equation by changing foil prices to units of USD gram−1 (denoted p as opposed to pa) and introducing thickness (t, in units of meters) and separator density (ρ, in units of grams meter−3) into the numerator. However, most separator prices were given in units of USD m−2, and there is considerable uncertainty regarding estimates of separator densities (in units of grams meter−3), which would be required to use prices in units of USD gram−1. There is less uncertainty in estimates of separator thicknesses, required to convert prices per area to prices per volume. To reduce the impact of uncertainties in separator densities, we employ price densities, in units of USD meter−3 and denoted pV. As a result, the separator term is expanded to give:| | 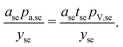 | (13) |
Note that the separator area, thickness, and volume measurements refer to apparent, exterior dimensions.
Relating current collector and separator areas
The areas of current collector foils and separators can also be related by a ratio (e.g. (an/ca)A) that describes areal “oversizing”. This areal oversizing can be employed to improve cell safety or cycle life, or specifically in the case of the separator, to wrap the outermost layer of the “jelly roll”. The anode area can be defined in terms of the cathode area with:while the separator area can be defined analogously in terms of the cathode area with:Of the commercial cell designs encountered in our data collection, most exhibited cathode and anode current collectors that were coated on both sizes. As a result, the separator is often significantly larger than the cathode and anode current collector foils.
Area-related cost components equation
Give the expansions and substitutions described for area-related cost components, the equation for this set of components is:| | 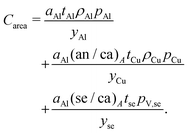 | (16) |
Hardware cost components
We assume per-cell hardware and safety components, including the can, terminals, header, and tabs, are all purchased by the cell manufacturer. Given the data limitations, especially regarding historical prices, the sum of the hardware and safety-related cost components is treated as a single cost component, abbreviated pcan, which represents the total price (in USD per cell) the cell manufacturer pays for these components. This price is also adjusted by the yield (ycan) of the sum of these materials. Additional details on the component prices that compose this price for the periods available are included in the ESI.† The cost of the hardware cost component is expressed as:| | 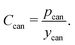 | (17) |
Plant size–dependent costs
A variety of costs are expected to scale with the size of the plant producing lithium-ion cells. Notably, these include capital costs of constructing new plants. These also include consumable inputs, such as electricity, as well as recyclable inputs, such as solvent. Similarly, labor, maintenance, overhead, and other “soft” costs are expected to experience economies of scale. Drawing on the methodology developed for PV modules,35 we represent these costs using a power law model:| | 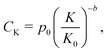 | (18) |
where p0 represents the sum of these costs, in units of USD per cell, for a plant of reference production capacity, or “size”, K0. Both this reference plant and the examined plant size (K) are measured by the number of cells that can be produced per year, and in this work K0 is chosen to be the representative plant size in period 1. The exponent b is a scaling factor.
The scaling factor b was estimated using the BatPaC cost model and varied in the sensitivity analyses.33 BatPaC was employed to estimate the non-material costs of manufacturing cells with a variety of different cell chemistries and performance characteristics in plants of different sizes. To estimate b, a power law was fit to the data describing the relationship between non-material costs of these various cells and plant size (see Fig. S67, ESI†). Then, for each period, p0 was estimated using the aforementioned representative material costs, plant sizes, and scaling factor along with representative values for ratios of material, and thus also non-material, costs to overall cell costs. A representative material cost fraction (θ) for each period was developed from estimates of material and non-material cell costs collected from literature reports (see ESI,† Section S6.3). For each period, the material costs per cell (i.e. mass-related, area-related, and hardware costs per cell) were summed, and this sum was used along with the material cost fraction to estimate the total non-material costs per cell, in units of USD per cell. This estimate of non-material costs per cell was then divided by (K/K0)−b to provide an estimate of p0. Additional details on the estimation of b and p0 and the development of representative values for K are available in the ESI† (see Section S6).
Scaling by energy capacity and cell-level yield
The sum of the aforementioned cost components gives the cost for a single lithium-ion cell. However, costs and prices of lithium-ion cells are typically scaled by energy capacity, as described earlier. We also need to correct for cell-level yield (ycell) as described earlier. Both of these factors can be included in the denominator of a coefficient, expressed as:| | 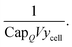 | (19) |
Relating cathode charge capacity to overall charge capacity
In cells where (N/P)Q > 1, the charge capacity is “cathode-limited” while in cells where (N/P)Q < 1, the capacity is “anode-limited”. This work examines cathode-limited cells—those that have slightly more anode charge capacity than cathode charge capacity—which reduces the risk of lithium metal plating. (Additional details are available in the ESI.†) Ostensibly, this restriction allows for the cell charge capacity (CapQ) to be set equal to the cathode charge capacity (Qca). However, other factors limit how much of the available cathode charge capacity is used, including charging and discharging voltage limits. As such, the cell capacity is defined as the product of the cathode cell capacity for a fixed volume and a utilization parameter (ηutil), which represents the fraction of the cathode charge capacity that is utilized during cell discharge:
Final cost equation
The final cost equation combines the various cell-level cost components.| | 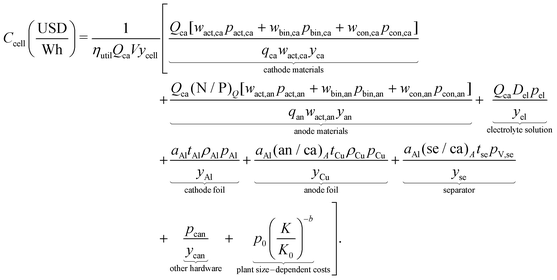 | (21) |
This cost equation can be separated into twelve cost components:| | 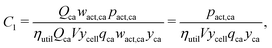 | (22) |
| |  | (23) |
| | 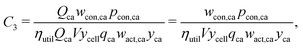 | (24) |
| | 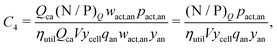 | (25) |
| | 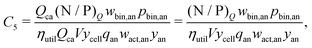 | (26) |
| |  | (27) |
| | 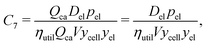 | (28) |
| | 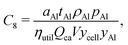 | (29) |
| | 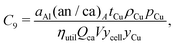 | (30) |
| | 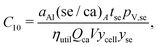 | (31) |
| | 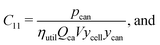 | (32) |
| | 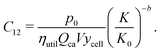 | (33) |
Rewriting the cost equation as the sum of its separable cost components can demonstrate relationships in the cost structure of lithium-ion cells. For example, the presence of cell energy capacity, as the product ηutilQcaV, in the denominator of components C8 through C12 (eqn (29)–(33)) highlights how increasing cell energy capacity for a fixed volume can lower the cost contributions of cell components not directly involved in charge storage, such as the hardware and the non-material costs. Similarly, the presence of voltage (V) in the denominator of components C1 through C7 (eqn (22)–(28)) shows why increasing cell voltage can reduce the contribution of mass-related costs to cost per energy capacity even as charge capacity remains unchanged.
Developing cost models requires balancing a desire to reflect all impactful contributors to cost change and the limitations on data availability. Data reliably detailing the components of lithium-ion cells, component prices, manufacturing processes, and especially soft costs, were often sparse. This final cost equation contains variables chosen to reflect important design characteristics and costs that were the focus of academic, industrial, and government-supported improvement efforts, while minimizing the impacts of data uncertainty. These variables were also chosen to allow for their reasonable assignment to various high-level mechanisms of cost change. Some of these variables could be further separated into other variables, yielding additional model detail and intricacy. A notable example is cathode charge capacity. Cathode charge capacity of a cell with a given volume can be estimated from a variety of other variables, including specific charge values of cathode and anode materials; materials’ post-calendering densities, volumes, and porosities; can and header volumes; etc. However, the data to accurately disentangle and separately model these factors both for historical and modern cells were not available. As a result of these simplifications in our model, other variables’ cost and cost change contributions could be slightly under- or overestimated. For example, increases in specific capacities of cathode and anode active materials enabled increases in cathode charge capacity for an 18650-sized cell. As the relationship between these variables is not explicitly modeled, i.e. as we do not replace Qca with a function of qca, qan, and other relevant variables, we could underestimate the impact of improvements in the specific capacities of electrode materials. Similarly, our data collection efforts did not yield sufficient details to decompose historical plant size–dependent costs in a fashion similar to that pursued in other models that examine more recent and prospective cell manufacturing,25,31 necessitating the use of a simpler power law model. In both cases, however, the model's separation of factors is sufficient to allow reasonable assignment of the low-level mechanisms to high-level mechanisms of cost change.
Cost change equations
Between the late 1990s and early 2010s, many of the variables that compose the cost equation changed and contributed to change in overall cell-level cost (Ccell). We use the term “low-level mechanisms” to refer to changes in these variables. While determining the dependence of overall cost change on a given variable is simple when only that one variable changes, a model is needed to disentangle the contributions of individual low-level mechanisms when multiple, non-additive variables changed concurrently. We employ a general method described previously35 to decompose the overall cost change observed between the two times into contributions from individual low-level mechanisms. The approach is summarized here.
Let us define a generic cost equation C(r1, r2,…), where individual variables r can be material properties, prices, dimensions, yields, labor rates, and other low-level technology characteristics that influence cost. These variables compose the vector r. We decompose this cost equation into a sum of cost components (Ci) that are functions of r, giving:
| | 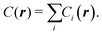 | (34) |
noting that a given cost component (
Ci) might not depend on every variable in
r. For example, in this work the first cost component is:
| | 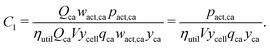 | (35) |
If we could observe changes in
r continuously, the cost change contribution of a given variable
rz between times
t1 and
t2 could be given by:
| | 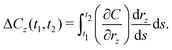 | (36) |
However, data in our cost change studies are sampled at discrete times, requiring us to develop an approximation. In our studies of other technologies and in this work (vide supra), we have found that the cost components are often products of functions of the variables in r and for a given cost component Ci can be represented as
| | 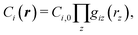 | (37) |
where
Ci,0 is a constant and
giz(·) is the function that gives the dependence of cost component
Ci on variable
rz. The cost equation we developed (
eqn (21)) is a sum of such products.
Given that our cost components are of this form, we find the integral (eqn (36)) can be approximated by:
| | 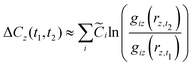 | (38) |
where
rz,t1 and
rz,t2 are the values of variable
rz at times
t1 and
t2, respectively; and
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i
i is a constant that is a representative value of cost component
Ci during the period between
t1 and
t2. Previous work has demonstrated that a good approximation of
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i
i is the logarithmic mean:
| | 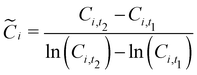 | (39) |
where
Ci,t1 and
Ci,t2 are the cost components at
t1 and
t2. For example, the cost change attributable to the change in cathode charge capacity
Qca, is estimated by:
| | 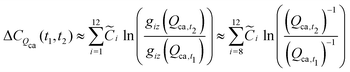 | (40) |
where the constant
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i
i can be computed as given in
eqn (39). Note that the sum for this variable is limited to cost components 8 through 12 as the variable cancels out in components 1 through 7.
Sensitivity analyses
Sensitivity analyses were performed to estimate and bound the uncertainty associated with our results. These analyses examined sensitivity of: (1) the model to its constituent variables (ESI,† Section S9.1), (2) our low-level mechanism results to data uncertainty (ESI,† Section S9.2), (3) our high-level mechanism results to alternative assignments (ESI,† Section S10), and (4) the cost change attributable to chemistry and materials science R&D to alternative assignments (ESI,† Section S11).
The first two of these sensitivity analyses were conducted by varying the input data for each variable and calculating the results for every combination of values for the given variable for the times being compared. In this work, we examined low and high estimates in addition to the representative values and investigated cost change between two times. As a result, for each variable we performed nine calculations, which include results from employing the representative values. The one exception was b, which is constant across both times and thus only required three calculations. The minimum and maximum cost change contributions of the low-level mechanisms are then determined and presented as error bars that bound the uncertainty that results from varying the given variable. This process is repeated, varying input data for each variable in the cost equation (i.e. Fig. S75–S115 and S117–S157, ESI†). We also determined the minimum and maximum cost change contributions observed across variations of all variables (i.e. Fig. S116, S158, and S159, ESI†). Additional details are available in the ESI† (Sections S9.1 and S9.2).
The second two sensitivity analyses were performed by developing alternative assignments of the low-level mechanisms or disaggregations of the high-level mechanisms. We then calculate the cost change contributions that result from each combination of the primary and alternative assignments. For example, providing three alternative assignments for cathode active material price yields four scenarios including the primary assignment. Providing three alternative assignments each for cathode and anode active material price and two for can price yields 48 scenarios. The results of these analyses are presented directly or the minimum and maximum contributions observed across all scenarios are included as error bars. Additional details are available in the ESI† (Sections S10 and S11).
Results and discussion
Cost components within each period
Populating eqn (21) with representative values for each variable for period 1 (1995–2000) and period 2 (2010–2015) (Tables 1–3) provides the contributions of cost components to total cost within each period, as depicted in Fig. 4. In period 1, the total cost is estimated to be approximately 810 USD kW−1 h−1. Cathode material is the largest cost contributor (29%), followed by non-material costs (25%) and other hardware costs (13%). Meanwhile, the costs of anode material, electrolyte solution, and separator components are similar (ca. 9–10%) The large influence of cathode material and non-material costs is consistent with cell-level cost component estimates reported between 1995 and 2000.20,68 In period 2, costs fell to about 210 USD kW−1 h−1, and our results indicate that cathode material remains the primary cost component (34%). The cost contribution from non-material costs fell (to 20%) while the contribution from other hardware increased (to 21%). The substantial influence, observed in both periods, of cathode materials on overall materials costs and cell-level costs is similar to that reported by more recent cost breakdowns.31,32,69
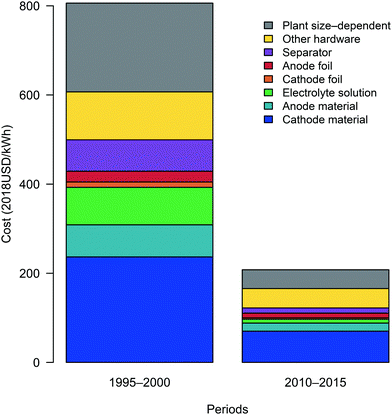 |
| | Fig. 4 Component costs of cylindrical lithium-ion battery cells during period 1 and period 2. Costs are grouped according to the categories presented using underbraces in eqn (21), with the coefficient multiplied through all cost components. | |
In both periods examined, estimated cell-level costs (in USD kW−1 h−1) are below representative prices reported previously for cylindrical cells (see Fig. 1).18 The differences between the costs estimated using the bottom-up approach described herein and the top-down prices reported previously provide a sense of the “residual” change in cell-level prices not explained by this analysis. This residual could result both from differences between cost and price (e.g. profit) as well as limitations of the data available and our model. For the late 1990s, there is a substantial difference between the average price (2140 USD kW−1 h−1 for 1995 through 2000, inclusive) and estimated cost (810 USD kW−1 h−1). However, this gap between cost and price should be interpreted with caution as data describing cell components in the late 1990s were limited, and input data were especially sparse and tended to be dated closer to 2000 than to 1995 (see Fig. S43–S58 and S64, ESI†). As such, the representative cost estimated for the first period might be weighted toward 2000, when the average cell-level price is approximately 990 USD kW−1 h−1. Moreover, the percent difference between cost and price in the year 2000 is similar to that observed for the early 2010s. Between 2010 and 2015, inclusive, the average price is approximately 260 USD kW−1 h−1 and the representative cost is 210 USD kW−1 h−1. Overall, the decrease in price from the year 2000 through the early 2010s is approximately 74%, which mirrors the cost change estimated between the late 1990s and early 2010s. As the costs and prices are estimated using different methods and datasets, the magnitude and similarity of the percent differences between cost and price in the two periods provide reasonable confidence that our analysis captures a substantial portion of the cost change that occurred between the late 1990s and early 2010s.
Low-level cost change mechanisms
Developing the cost change equations and populating them with data enables us to separate the total cost change between the late 1990s and early 2010s into the cost changes attributable to changes in each variable (Fig. 5). These changes in variables are referred to as low-level cost change mechanisms. The increase in cathode charge capacity for a fixed volume, from 1.7 to 3.1 Ah for an 18650-sized cell, is the primary low-level mechanism, responsible for 23% of the observed cost decline between the two periods. This near doubling is the consequence of many improvements, including increases in both the reversible specific charge and charge density capabilities of electrode active materials, which have been a significant focus of research and development efforts.13,30,68–81 The collected data suggest that specific charge increased nearly 30% for the cathode active material and 8% for the anode active material. The improvement in cathode charge capacity also results from an increase in the total amount of electrode material fit into a given cell. The data indicate that high energy density, 18650-sized cells manufactured in period 2 have 40% more cathode active material, by mass, than those manufactured in period 1, and 28% more anode active material (see Fig. S68 and S69, ESI†). These increases are ostensibly the result of a variety of chemistry and design changes in high energy density cells, including increased mass fractions of cathode active material (see Fig. S7–S9, ESI†), decreasing foil and separator thicknesses (see Fig. S36–S38, ESI†), and increasing electrode material thicknesses (see Fig. S70 and S71, ESI†).32,69,82–86 These increases also likely result from production improvements, for example in the calendering processes.32,82,87,88 Meanwhile, cathode specific charge and anode specific charge are also separate variables that contribute 6% and 0.5% of cost change, respectively, which are likely underestimates of their cost change impacts as portions of their contributions are encompassed in the increase in the cathode charge capacity for a fixed-volume cell.
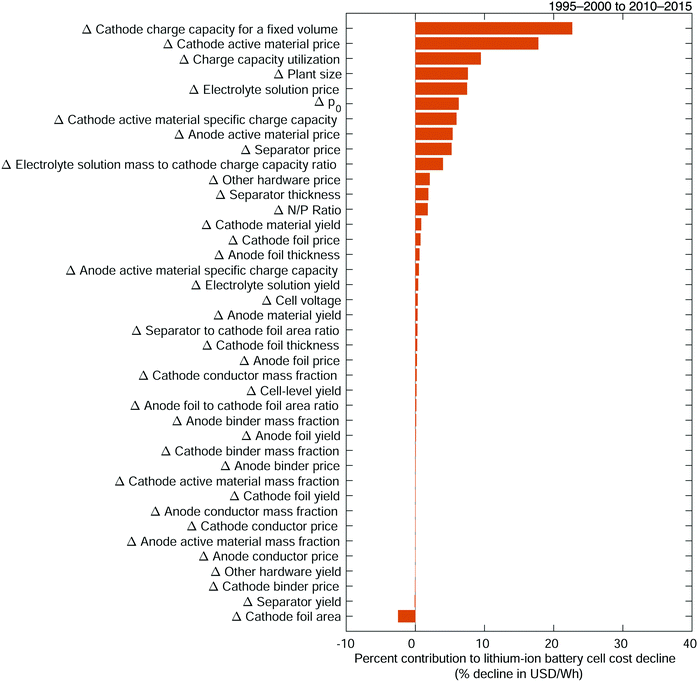 |
| | Fig. 5 Contributions of low-level mechanisms to the cost decline of 18650-sized lithium-ion battery cells between the late 1990s and early 2010s. The total change in cost is measured in units of USD W−1 h−1, as per the cost equation (eqn (21)), while cost change contributions are expressed as percentages of this total cost change. Mechanisms are listed in order of decreasing contribution to cost reduction. | |
Considering the intertwined nature of these and other variables, we sum the cost change contributions of variables that impact reasonably separable technological characteristics (Fig. 6), while combining material prices by cell component. The result is a set of aggregated low-level cost change mechanisms. Aggregation assignments are provided in Table 4. Here, the cost changes associated with increasing the amount of cathode and anode active material in a cell and increasing the charge capacity of these materials are aggregated into the “cell charge density” mechanism. In addition, for each electrode, the contributions from changing prices of active materials, binders, and conductors are similarly summed. Meanwhile, cost reductions that result from improved yields are aggregated into “materials and manufacturing yields,” and cost improvements resulting from changes in plant size and p0 are similarly combined. While some detail is lost when aggregating the variables’ contributions, this approach limits underestimating the influence of important characteristics and technological changes.
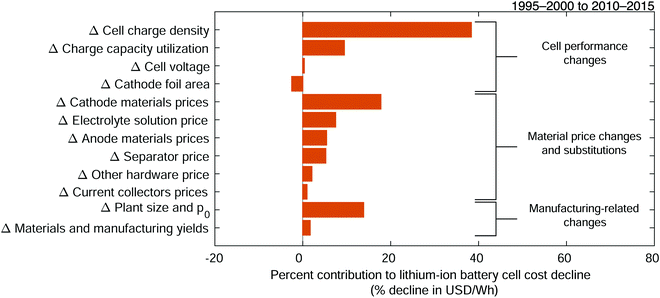 |
| | Fig. 6 Contributions of aggregated low-level mechanisms to the cost decline of 18650-sized lithium-ion battery cells between the late 1990s and early 2010s. The low-level mechanisms are aggregated into reasonably separable technology characteristics and cost components. The detailed aggregation assignments are given in Table 4. The total change in cost is measured in units of USD W−1 h−1 while cost change contributions are expressed as percentages of this total cost change. Mechanisms are listed in order of decreasing contribution to cost reduction across and within each group of mechanisms. | |
Table 4 Aggregation of low-level cost change mechanisms
| Aggregated low-level mechanism |
Constituent low-level mechanisms |
|
Cell performance changes
|
| Cell charge density |
Cathode charge capacity for a fixed volume (Qca), Cathode and anode specific charge values (qca, qan), Cathode and anode material mass fractions (wact,ca, wbin,ca, wcon,ca, wact,an, wbin,an, wcon,an), N/P ratio ((N/P)Q), Electrolyte solution mass to cathode charge capacity ratio (Del), Current collector and separator thicknesses (tAl, tCu, tse), and Anode and separator to cathode foil ratios ((an/ca)A, (se/ca)A) |
| Charge capacity utilization |
Charge capacity utilization (ηutil) |
| Cell voltage |
Cell voltage (V) |
| Cathode foil area |
Cathode foil area (aAl) |
|
Material price changes and substitutions
|
| Cathode materials prices |
Cathode active material, binder, and conductor prices (pact,ca, pbin,ca, pcon,ca) |
| Anode materials prices |
Anode active material, binder, and conductor prices (pact,an, pbin,an, pcon,an) |
| Electrolyte solution price |
Electrolyte solution price (pel) |
| Current collectors prices |
Cathode and anode foil prices (pAl, pCu) |
| Separator price |
Separator price (pV,se) |
| Other hardware price |
Other hardware price (pcan) |
|
Manufacturing-related changes
|
| Materials and manufacturing yields |
Cell-level (ycell), cathode material (yca), anode material (yan), electrolyte solution (yel), cathode foil (yAl), anode foil (yCu), separator (yse), and other hardware (ycan) yields |
| Plant size and p0 |
Plant size (K) and p0 |
Among the aggregated low-level cost change mechanisms, the increase in cell charge density dominates the estimated cost change, contributing 38% of cost decline observed between period 1 and period 2. This mechanism reflects concurrent contributions from changes in many variables, including the aforementioned improvements in reversible specific charge and charge density capacities of active materials and the increased mass of these active materials fit into 18650-sized cells. An increase in the utilization of this charge capacity also provided considerable cost reduction, approximately 9.5% of that observed. This parameter is estimated from the ratios of the reported, typically nameplate, overall charge capacities of cells to the measured or estimated charge capacities of the cathode active materials for the same cells. The collected data indicate that for cylindrical, 18650-sized cells designed for high energy capacity, charge capacity utilization increased from approximately 84% to 95% from period 1 to period 2. This change could result in part from expansion of the operating voltage window range of lithium-ion cells and improved electrode and cell manufacturing processes that allow more of the active electrode material to be used effectively.32,71,82,87,88 As the utilization fraction also reflects nameplate charge capacity estimates, it is possible that some of this increase results from other improvements that allowed cell manufacturers to minimize capacity fade, improve quality control, or otherwise ensure higher usable charge capacity, which in turn would allow them to increase cells’ capacity ratings. Meanwhile, between the late 1990s and early 2010s, the increase in cell operating voltage was small (see Fig. S42, ESI†) and consequently contributed little to cost reduction.
These results allow us to quantitatively estimate how improving energy density reduced costs. Previously, researchers have noted an intrinsic relationship between cell costs and energy density, specifically that increasing energy density can distribute material and manufacturing costs over a higher energy capacity, thereby reducing costs scaled by energy capacity.89 Taking the sum of the cost change contributions of mechanisms that also increased usable energy density (i.e. cell charge density, charge capacity utilization, and cell voltage) provides an estimate of the relationship between cell-level costs and energy density. Our results indicate that between the late 1990s and early 2010s the combined efforts to increase energy density reduced cell-level costs by approximately 48% for energy dense 18650-sized cells. However, as discussed in previous work, allowing battery cells to be less energy dense could enable more rapid cost reduction for certain applications.18
The second most influential aggregated low-level mechanism was the reduction in cathode materials prices, which provided 18% of the estimated cost decline. Nearly all of this contribution results from a decrease in the price of cathode active material, which in this work is assumed to be purchased by the cell manufacturer to allow for a simpler comparison between periods because purchasing active materials was reported to be a common practice during period 1.20,90 In a sensitivity analysis (vide infra), the representative price of cathode active materials for the early 2010s is varied over a range of more than 10%, which approximately also accounts for markups associated with purchasing, as opposed to manufacturing, this material.26,91 Changes in binder and conductor prices were trivial in comparison. The price reduction of cathode active material is likely a consequence of many factors, including raw material prices (e.g. see Fig. S72, ESI†), processing improvements, increased production scales, and a transition to cathode materials composed of less expensive metals.20,21,25,31,60,73,76,81,91–98 For example, the partial substitution of nickel, manganese, and aluminum for cobalt in LiCoO2 allowed less expensive metals to be used while improving performance for certain applications. Meanwhile, over the same two decades, changes in prices of anode materials, electrolyte solution, and separators each contributed approximately 5–7% of the cost reduction; and changes in other hardware and current collectors prices each contributed 1–2%. Overall, reductions in materials’ prices impacted multiple cost components and collectively contributed 39% of cell-level cost decline.
Plant size–dependent costs had the third largest influence on cost change, composing 14% of cost reduction. The change in the prefactor p0 is estimated to have decreased costs about 6.3% while the increase in plant size decreased costs 7.6%. The variable p0 estimates the sum of per-cell plant size–dependent costs for a plant with a fixed size (K0) which is taken to be the plant size in the first period. These costs include electricity, solvent, labor, maintenance, depreciation, and other overhead; the sum of which was estimated from reported ratios of material to non-material costs. This cost change is consistent with improvements in automated, high-speed production processes, which have been reported to enable cost reductions.69,76 Similarly, increasing plant output capacity, from representative estimates of 27 to 120 million cells per year per plant, enabled scale economies that have also reduced non-material production costs.69,76 However, different accounting scopes as well as the dearth of clearly defined, comparable non-material cost estimates and studies of scaling exponents introduce some uncertainty into our estimates of the contributions from plant size–dependent costs and their interpretation. We address this in the sensitivity analysis (see ESI†, Section S9.2).
Production processes also improved between the two periods, and various changes in materials and manufacturing yields contributed 2% of cost decline. However, the paucity of manufacturing yield estimates and their wide variation both within and across cell types introduce considerable ambiguity into estimates of their cost change contribution, limiting insight into the impact of these mechanisms (see ESI† for additional details, and Fig. S52–S58 as well as Fig. S124, S133, S136, S140, S144, S148, S152, and S154).20,99
While most changes resulted in cost declines, the increase in cathode foil area, which in turn increased anode foil and separator areas, increased costs by approximately 2.5%. This cost change results from the representative cathode current collector foil area increasing approximately 31%, which could reflect both increases in charging and discharging power capabilities as well as increasing cell charge capacities given a constraint on the maximum achievable electrode thickness.20,25,100
We also examined the sensitivity of our results to data uncertainty. For this “data-informed” sensitivity analysis, we developed low and high values for each variable based on the uncertainty in the data we collected and used to estimate the representative values. We then estimated cost change contributions for each low-level mechanism for all combinations of representative, low, and high values for each variable. The low-level cost change contributions were aggregated as previously described, and we found the minimum and maximum cost change contributions for each aggregated mechanism across all combinations of variables (see Fig. S159, ESI†). These minima and maxima provide a sense of the uncertainty in the estimated cost change contributions of the aggregated low-level mechanisms. Overall, we find that the reported contributions of the aggregated low-level mechanisms to cost decline are relatively robust to uncertainty in the underlying data. For example, the cost change contribution of the increase in cell charge density is bounded by a minimum of 34% and a maximum of 43%, around a central value of 38%. Similarly, the contribution of decreases in cathode materials prices has a minimum of 14% and maximum of 22%, with a central value of 18%. However, the cost change contribution of plant size and p0 combined is considerably more uncertain, ranging from 1.0 to 26%, around a central estimate of 14%. Ranges for all other low-level and aggregated low-level mechanisms, as well as additional details are available in the ESI† (see Section S9.2). Across all of the combinations examined, the increase in cell charge density remains the largest contributor to cost change while the reduction in cathode materials prices is nearly always the second largest cost contributor.
High-level cost change mechanisms
Low-level mechanisms can be assigned to high-level mechanisms often associated with the development of public policy and business strategies to drive technological change, notably research and development and learning-by-doing, and with the emergence of economies of scale (Fig. 7). The assignment process resembles the method to estimate cost change contributions from separable technological characteristics; we categorize the low-level mechanisms and sum their cost contributions within each category. However, this categorization focuses on determining which high-level mechanisms likely led to the low-level mechanisms. The assignment strategy employed in this work follows the general approach described previously for solar photovoltaic modules.35 Assignment details are available in the ESI† (Tables S4–S6) and are summarized here.
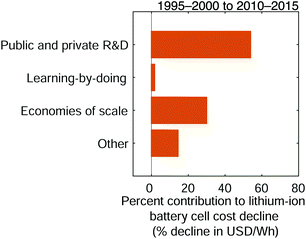 |
| | Fig. 7 The contributions of high-level mechanisms to the cost decline of 18650-sized lithium-ion battery cells between the late 1990s and early 2010s. The total change in cost is measured in units of USD W−1 h−1 while cost change contributions are expressed as percentages of this total cost change. Public and private R&D comprises changes that require laboratory settings or non-routine production activities (e.g. pilot-scale manufacturing), while learning-by-doing includes improvements that result from repeated manufacturing activity at commercial scale. Economies of scale comprises cost changes that result from increasing plant sizes and purchasing volumes. | |
Research and development is defined broadly in this study and comprises changes that require experimental settings, such as laboratories studying fundamental properties; designing or testing experimental cells; or establishing and operating pilot-scale production lines.101 This research and development includes work conducted in both the public and private sectors. Learning-by-doing meanwhile encompasses changes informed by routine manufacturing activity at commercial scale, including incremental process refinements. Finally, economies of scale comprises cost changes that result from increasing scales of manufacturing plant production and production capacity, as well as price reductions of input materials for volume purchases. The definitions employed here are similar to those used in a previous study of photovoltaic modules.35
For lithium-ion cells, the variables representing quantities and characteristics of materials (e.g. cathode charge capacity for a fixed volume, specific capacities, cathode foil area), their ratios, and their utilization (e.g. charge capacity utilization, cell voltage) are assigned to R&D. Development of higher capacity, higher voltage materials has been pursued in academic, government, and corporate laboratories.13,71,72,74,102–106 Similarly, in an effort to improve overall cell charge and power capacities, research and development at the laboratory and pilot scale also informed changes to electrode compositions and cell designs, including electrode material ratios and foil and separator dimensions.32,82,83,87,107,108 Changes to electrode density, particle sizes, foil dimensions, electrolyte solution wettability, and filling processes influence the total void space filled with electrolyte solution;109–114 and, as a result, the change in the ratio of electrolyte solution mass to cathode charge capacity is also assigned to R&D. Little reliable information was available concerning electrolyte additives in commercial cells, consistent with reports of their formulations being proprietary and closely held.89 However, their influences on cell capacity are attributed to R&D via a variety of variables, including those representing cathode charge capacity for a fixed volume and charge capacity utilization as well as cathode and anode specific capacities.
Meanwhile, yields likely improved as a result of learning-by-doing, reflecting changes made at commercial (or “industrial”) scales with the aim of maximizing material throughput. Research and development employing pilot scale lines might have also led to some improvement in yields but the considerable differences between pilot and commercial scale production lines32 suggest that most yield changes can be attributed to LBD.
Increasing plant size resulted in economies of scale, which we assume influenced all non-material costs. Plant sizes, as measured in the number of cells that can be produced per year, increased between the late 1990s and early 2010s (see Fig. S60–S63, ESI†) to meet increasing demand for lithium-ion cells for a range of applications.18 This scaling likely allowed for the use of physically larger and/or faster equipment and expanded automation,25,32 as well as the distribution of capital, labor, maintenance, overhead and similar costs over more cells, reducing non-material costs per cell.
Volume manufacturing and purchasing of materials can also result from economies of scale. However, between the 1990s and 2010s, changes in material prices were potentially driven by a range of factors, complicating their assignment to high-level mechanisms. Notably, prices of cathode active materials could have been influenced by changes in constituent metals’ prices (e.g. see Fig. S72–S74, ESI†), shifts to metal oxide compositions using less cobalt, improved processing methods, and, possibly, increases in production scales.25,91 Metal prices themselves can depend on a variety of factors, especially for cobalt, which over the time periods considered was primarily produced as a byproduct of copper and nickel mining.115–117 Changes to metal prices could thus be considered exogenous and assigned to an ‘other’ high-level mechanism category. Meanwhile, the shift to metal oxides containing less cobalt could be attributed to R&D efforts. Finally, manufacturing costs remain important contributors to cathode active material costs and prices,60,91,118 indicating that some cost change could be attributed to LBD and EOS. As a result of these intertwined effects, we attribute the change in cathode active material price to a combination of high-level mechanisms. Considering the limited definition of learning-by-doing employed herein, the change in cathode active material price is assigned equally to R&D, EOS, and ‘other’ and then these assignments are varied in the sensitivity analysis to arrive at conclusions that are robust to assignment uncertainty (Fig. 8). Anode active materials’ prices can similarly be influenced by a variety of factors and are assigned to high-level mechanisms in the same fashion.
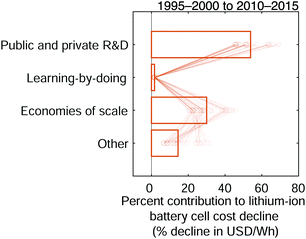 |
| | Fig. 8 The contributions of high-level mechanisms to lithium-ion battery cell cost decline between the late 1990s and early 2010s, including both the base case as well as combinations of other assignments. The primary assignment results are presented as bars. The results of all combinations of alternative assignments of the prices of cathode and anode active materials and other hardware are plotted as lines with markers ( ). ). | |
When comparing the representative, high energy density cells examined, most other materials have not undergone major changes in composition. For example, the predominant cathode binder material appeared to be PVDF throughout both periods. Similarly, for cells whose breakdown information could be obtained, the electrolyte solution was almost always reported to be approximately 1 M lithium hexafluorophosphate (LiPF6) dissolved in organic carbonates, a combination that has persisted over the time periods considered.13,69,109,111,119,120 In the cases where a component's composition did not appear to change considerably, price changes were assumed to result from volume manufacturing and purchasing and were assigned to economies of scale. However, considering that current collector foils’ prices were potentially also impacted by market influences on their respective metal prices, their changes are split between the economies of scale and ‘other’ categories. In the case of anode binder material, where the representative material changed from PVDF to carboxymethylcellulose, its price change was split equally between R&D and EOS. Finally, as can materials and header components in high energy density cells have likely improved in part through research and development, the hardware component price change was also split, with 25% of its change attributed to R&D and 75% to EOS. Finally, we assign p0 to the ‘other’ category as it encapsulates a range of costs that can be influenced by many high-level mechanisms. Data were not available to disentangle these influences, precluding more detailed assignments.
Given these assignments, we sum the cost changes attributed to high-level mechanisms to estimate the contribution of these mechanisms to cell-level cost decline (Fig. 7). Our estimates indicate that R&D had a substantial impact on cost reduction between the late 1990s and early 2010s, driving about 54% of cost decline. Meanwhile, economies of scale had a smaller but still considerable impact on cost decline, contributing nearly 30%. Learning-by-doing had a much smaller impact (2%) and ‘other’ influences, including those that were not easily disentangled in this analysis, had a moderate impact (14%).
In a sensitivity analysis, we explore alternative scenarios to evaluate the impact on our results of our assignments of low-level mechanisms to high-level mechanisms (Fig. 8, and Section S10 in the ESI†). In this analysis, we posit extreme (100%) assignments of cathode and anode active material prices to R&D, EOS, or the ‘other’ category and of hardware costs to either EOS or ‘other’. Examining the contributions that result from the combinations of these extreme assignments allows us to evaluate how robust to underlying uncertainties our ranking of high-level mechanisms is. This analysis demonstrates that the relative importance of the different high-level mechanisms is robust to alternative assignments of low-level mechanisms. R&D is nearly always the primary contributor to cost decline while EOS is relatively consistently the secondary contributor.
The relative contributions of high-level mechanisms to cell-level cost decline are similar to those estimated for the cost decline of terrestrial photovoltaic modules between 1980 and 2001.35 For both technologies, R&D contributed the most to cost reduction, followed by EOS. These examples both provide quantitative evidence that technological development can proceed through a phase early in development, but after commercialization, during which cost reduction is dominated by R&D while EOS remains secondary. For both technologies, LBD contributed considerably less cost reduction, which could result from the reliance on automation in the manufacturing processes for both technologies and the narrow definition of LBD that was shared by these two studies and drawn from the definition used in economics research.35,101 However, the studies of PV and lithium-ion technologies are only two examples; additional mechanistic modeling of the cost change of other technologies is required to determine how general these patterns are. Moreover, it remains to be seen whether lithium-ion technologies will follow the trajectory observed for PV modules and enter a phase in which EOS becomes the primary contributor to cost decline.
Linking the effects of high-level mechanisms of the cost decline of lithium-ion technologies to government and corporate policies is challenging. The basic science research that underpins lithium-ion technologies extends back years before their commercial introduction in the early 1990s.120,121 Considerable public and private applied research and development efforts enabled the commercialization of lithium-ion technologies and their continued improvement for portable electronics applications.13,80,120,122,123 Moreover, since the early 1990s, governments have directly funded research and development efforts to advance lithium-ion technologies for both electric vehicle and load-leveling applications, often in conjunction with private companies, including battery and car manufacturers.124–128 Governments have also implemented policies to promote adoption of electric vehicles,129–131 which have indirectly stimulated the market for lithium-ion technologies and very likely encouraged a combination of private R&D as well as LBD and EOS. During the time range studied, additional incentives were also introduced for stationary energy storage applications, likely similarly contributing to a combination of high-level mechanisms.132
Many developments and improvements in lithium-ion technologies have been anecdotally attributed to advancements in chemistry and materials science.81,89,133,134 The analysis presented herein allows us to begin to quantitatively evaluate this assertion, at least with respect to the cost reduction observed for lithium-ion cells between the late 1990s and early 2010s. We can disaggregate the contribution of R&D to cost decline into those advancements that resulted from chemistry and materials science, including material synthesis, characterization, and processing, and those that resulted from design changes, such as making current collector foils thinner. Assignments of the low-level mechanisms to each of these categories are given in Tables S10–S12 (ESI†). The increase in cathode charge capacity for a fixed volume, which can be attributed to both advancements in chemistry and materials science and design and other changes, is split between the two categories 90%:10%. (For details, see Section S11 in the ESI.†) The uncertainty in these assignments is bounded by the same extreme cases examined in the aforementioned sensitivity analysis for the assignment of high-level mechanisms as well as cases where the split in cathode charge capacity for a fixed volume is varied between 85%:15% and 95%:5%.
The results of this disaggregation reveal that advancements in chemistry and materials science do indeed compose the majority of cost change attributed to research and development (Fig. 9), over 90% in the base case. Moreover, these advancements contributed approximately half of all cost reduction observed between the late 1990s and early 2010s. However, these advancements were driven not only by a need to reduce costs but also by a desire to improve a range of performance characteristics, including energy density, cycle-life, and safety.13,18,68,70,89,124,134–142 As different combinations of these performance characteristics are expected to be relevant for various applications of lithium-ion and related energy storage technologies, chemistry and materials science R&D is expected by some to continue to contribute substantially to performance improvement and cost decline.134 The results presented here show just how much R&D in chemistry and materials science contributed to past cost reduction for lithium-ion technologies and suggest that similar efforts might substantially contribute to cost reduction and performance improvement for nascent electrochemical energy storage technologies for a range of applications.
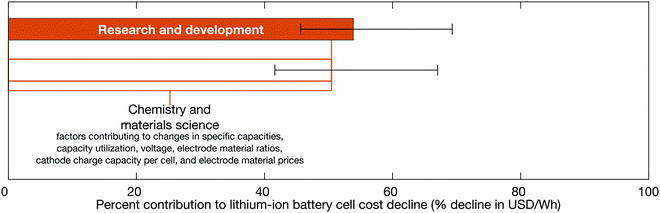 |
| | Fig. 9 Contributions of public and private research and development to cell-level cost decline between the late 1990s and early 2010s. The top bar depicts the contribution of multiple types of R&D while the bottom bar depicts the contribution of R&D factors that were heavily influenced by chemistry and materials science research, including both materials synthesis and processing. Uncertainties are estimated as described in the text and the ESI† (Section S11), and the minimum and maximum values from our sensitivity analyses are presented as error bars. | |
Conclusions and implications
The costs and prices of lithium-ion technologies have fallen dramatically since their commercialization in the early 1990s.18 Meanwhile, lithium-ion technologies have diversified to satisfy an expanded array of applications, including in mobile electronics, power tools, electric vehicles, and recently, stationary storage, all favoring different cell-level characteristics.59,60,143 To elucidate the mechanisms that led to cost decline amidst this diversification, we developed cost and cost change equations and employed them to compare cylindrical, 18650-sized cells with similar characteristics, specifically high energy density and specific energy.
We collected data describing how various materials, prices, designs, and other contributors to the cost of lithium-ion technologies changed between the late 1990s and early 2010s; and, with cost change equations, we estimate the contributions of these factors to the observed cost decline. By aggregating the contributions of changes in individual components and prices, we are able to examine the impact that changes in core technological characteristics had on reducing costs. Our estimates indicate that between the late 1990s and early 2010s, cell-level cost reduction primarily resulted from efforts to increase cell charge density and reduce cathode materials prices, contributing 38% and 18% of cost decline, respectively. Reductions in non-material costs (14% contribution) and an increase in charge capacity utilization (9.5% contribution) were also important contributors to cost decline. Decreases in the prices of other materials reduced costs to a lesser extent, while an increase in cathode foil area increased costs slightly.
Notably, our analysis enables us to also disentangle and estimate the effects of various high-level mechanisms, whose intertwined nature often complicates studies of their impacts on technological improvement.144–146 Of the high-level mechanisms considered, research and development contributed the majority of cost reduction (54%) while economies of scale also contributed considerably (30%). Meanwhile, learning-by-doing only contributed 2% of cost reduction over the two decades examined. This small contribution in part reflects the traditional definition of LBD employed herein, which includes changes from repeated manufacturing at commercial or industrial scales of production, which are routine in the sense that they do not require an experimental manufacturing line or pause in full-scale operations.35,101 This definition is also sensible in context. Japanese companies were responsible for much of the initial production of lithium-ion cells, and associated norms; and this expansive definition of R&D is consistent with earlier descriptions of Japanese firms closely integrating R&D and production.147 Moreover, the use of pilot-scale production lines, whose improvements are considered part of R&D, and a high degree of process automation in the manufacturing of lithium-ion cells likely further limit the cost reduction attributable to learning-by-doing. More generally, this and previous work highlights the importance of specifying definitions of qualitative terms describing high-level mechanisms, whatever those definitions may be, in order to enable a quantitative examination of their effects.35
The primacy of R&D's contribution to cost decline is robust to a variety of alternative assignments of low-level mechanisms to high-level mechanisms of cost change. Meanwhile, EOS was consistently the next most important contributor to cost decline. Our sensitivity analysis bounds these estimates; it proposes extreme alternative assignments for impactful low-level mechanisms with uncertain influences (e.g. attributing 100% of a low-level mechanism to R&D, EOS, or ‘other’) and determines the results of all possible combinations of such assignments. In historical studies that attempt to disentangle cost change contributions and assign them to high-level mechanisms, such an examination of extremes helps estimate the uncertainty when identifying the multiple processes influencing a given low-level cost change mechanism. Consistency of results across many alternative assignments can increase confidence in observed trends.
Our finding that both R&D and EOS made substantial contributions to observed cost decline supports the efficacy of policy proposals that have encouraged both additional innovation and deployment in an effort to further reduce costs.40,148 Market-stimulating policies are often an important complement to public R&D investments, especially in circumstances where markets would not grow without these additional incentives, as they can encourage private R&D along with EOS and LBD. The extent to which lithium-ion cell and pack technologies for battery electric vehicles (BEVs) advanced specifically in response to BEV market growth, as supported by market-expansion policies, is a topic deserving additional investigation, as is the role that such policies can play in further advancing BEV batteries. In the case of stationary storage applications, market expansion policies will likely play an important role in shaping both the growth in markets and storage technology improvement.
Advancements in chemistry and materials science accounted for most of the R&D contribution to cost reduction, and their contributions to many impactful low-level mechanisms highlight an important feature of lithium-ion technologies that might help explain their rapid improvement: the chemical diversity they can access. For example, in the case of prominent metal oxide cathode materials, partial substitution of other elements for cobalt in LiCoO2 creates a diverse chemical space and many opportunities for performance improvement and cost reduction. While different cathode chemistries were being explored, various forms of carbon and other materials were also being investigated to improve anode capabilities. In turn, combinations of different cathode and anode materials further add to the options available to lithium-ion cell designers to improve performance. Meanwhile, we anticipate that another factor supporting these improvements, in addition to the chemical diversity itself, may have been that these electrode active materials can typically be integrated into existing designs without requiring entirely new cell materials, architectures, and manufacturing processes. That is, these active materials might be considered drop-in technologies75 in a modular design, i.e. a design with low “design complexity.”149 Similarly, the separator material, electrolyte solution, and various manufacturing processes could be improved without requiring drastic changes in electrode material composition and other components.
The degree to which lithium-ion technologies have a low design complexity (or high modularity) requires further study to estimate, by examining the dependencies between cells' components as well as between the components and cell manufacturing processes. The number of dependencies between cost components of a technology has been proposed to be inversely related to the rate of technological improvement.149 In this case, the limited number of component dependencies might have enabled the rapid improvement of lithium-ion technologies. In addition, the ability to improve components separately can allow the benefits of certain improvements to be shared by different technology variants.150 For lithium-ion technologies, the limited number of dependencies may have enabled the introduction of new materials that lowered costs and enabled more diverse applications while allowing experience and scale economies to be applied across cell types. These effects can be formally investigated in future research.
Our results provide quantitative, mechanistic evidence that technologies can proceed through a phase early in their development, but after their commercial introduction, during which cost reduction remains dominated by public and private R&D. A recent analysis of the cost change observed for photovoltaic modules provides similar evidence, and suggests that EOS then grows in effect.35 These results are consistent with studies that emphasize the important role of fundamental research and development in the early phases of technological improvement, as well as evidence that “science and technology–push” can precede “demand-pull” processes.19,147,151–155 The mechanistic insights presented here, however, further suggest that technology-push policies may remain important for longer periods for certain technologies even as demand-pull processes take off. Specifically, these results suggest that sustaining public R&D investments over longer periods of time may be particularly essential for improving technologies, such as electrochemical batteries, for which a diversity of material choices and design options could afford improvement, especially if this diversity might not be explored by the private sector alone. Additional mechanistic modeling that compares how a variety of technologies change could further elucidate how certain features of technologies might influence how their improvement responds to different policies at various stages of their development. Such future studies could provide additional insight on how to tailor the balance of policies for different technologies in order to enhance cost reduction and other performance improvement.
The rapid cost reduction of lithium-ion technologies has also underpinned concerns of technological lock-in.156–158 Recently, some studies have outlined scenarios in which lithium-ion technologies become the dominant energy storage technology for many, or even nearly all, stationary energy storage applications.17,159–162 Through its application to both transportation and stationary storage roles, lithium-ion technologies could be deployed widely and benefit from increasing returns to adoption that further reduce its cost via additional private R&D, learning-by-doing, and economies of scale. If such a process occurs quickly enough, lithium-ion technologies could outcompete other technologies before they have the opportunity to advance sufficiently, precluding the development of potentially more cost-effective, environmentally beneficial, or resilient storage technologies. These concerns have focused attention on efforts to reduce the chance of premature lock-in by encouraging technological diversity.160,163–166 Others have focused instead on lithium-ion–adjacent technologies (e.g. lithium–air, lithium–sulfur), which could benefit from continued improvements in lithium-ion technologies while introducing diversity that could reduce costs for other energy storage applications.134,162,167
The chemical diversity available to electrochemical energy storage may provide an opportunity to limit lock-in. The sheer number of options accessible to electrochemical storage technologies increases the probability that lithium-ion technologies are not the optimal option for every application. This diversity also yields many different combinations of electrode materials and electrolytes that can compose potentially useful electrochemical storage technologies.75,168–176 Moreover, like lithium-ion cells, many proposed electrochemical technologies can allow for concurrent improvements in cathode and anode materials and can decouple some materials choices from manufacturing processes. Just as lithium-ion technologies have benefited from a diversity of chemical options, this feature could similarly benefit other electrochemical technologies.134 However, these other options will not necessarily be explored without sufficient support for research and development.
Using the history of lithium-ion technologies as a model for the future, investments that encourage the exploration of diverse chemistries and materials that can be combined in a modular design might enable other electrochemical storage technologies to improve in performance and come down in cost. Moreover, a balance of support for research and development and market-stimulating policies has enabled the cost decline of other technologies35 and could do the same for nascent options for stationary energy storage. Meanwhile, ensuring that investments in energy storage research appreciate the potential of this diversity, and are not just applied to those technologies with the lowest costs today, could help avoid premature lock-in. By encouraging investigation of a diverse chemical space, we can reduce the risk of exhausting the improvement opportunities available to lithium-ion and other electrochemical energy storage technologies before climate-relevant performance and cost targets are reached.10
This analysis was limited by the sparse data available for commercially produced lithium-ion cells, especially for those manufactured in the 1990s, leading to uncertainties in our results. Limited data availability also precluded extending the cost change analysis beyond 2015. However, despite this limitation, the cost change mechanisms we identify in this study remain descriptive of the overall cost decline, even considering changes since 2015. This is because the cost decline covered by this analysis, from 810 to 210 USD kW−1 h−1 from the late 1990s through the early 2010s, is substantially larger than the cost change that has occurred since 2015 as implied by the price decline observed since then. For example, the prices for all-types of lithium-ion cells, which tend to be higher than those for cylindrical cells, fell from approximately 270 USD kW−1 h−1 in 2015 to 180 USD kW−1 h−1 in 2018.18 Assuming that the costs for cylindrical cells fell comparably, the additional cost change included by extending this analysis past 2015 would remain small compared to that observed between the late 1990s and early 2010s. As a result, the major drivers of cost change that we identify by examining technological change through 2015 would remain dominant even if the study were extended through the late 2010s. Yet, we still expect that as more data on cell components and manufacturing costs become publicly available, the modeling approach we describe can be employed to study further cost reduction and elucidate any changes in the relative effects of the drivers of cost change. We also expect that given additional data, the model could be used to compare cost changes associated with modifying lithium-ion cells for different applications and to examine other performance metrics beyond USD W−1 h−1.18 In addition, given appropriate estimates, the model, and the data collected, can help inform prospective evaluation of the impacts of possible material improvements or cost reductions for lithium-ion and related technologies. Similarly, the estimates of which technological characteristics and high-level mechanisms contributed to cost reduction can guide research and development efforts and business and government decisions that aim to enable further cost reduction and other performance improvement for a range of energy storage technologies.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
We thank the Alfred P. Sloan Foundation for funding this research. We also acknowledge the Environmental Defense Fund for partial funding of this research. In addition, M. S. Z. was supported in part by a Research to Policy Engagement Initiative Fellowship from the MIT Technology and Policy Program. We also thank Dr James McNerney, Dr Gökşin Kavlak, and Dr Gonçalo D. Pereira for valuable input.
References
- DOE Global Energy Storage Database; Sandia National Laboratories and DOE Office of Electricity, US Department of Energy, 2019.
-
P. Ralon, M. Taylor, A. Ilas, H. Diaz-Bone and K.-P. Kairies, Electricity Storage and Renewables: Costs and Markets to 2030, International Renewable Energy Agency, Abu Dhabi, 2017 Search PubMed.
- U.S. Battery Storage Market Trends, U.S. Energy Information Administration, Washington, DC, 2018.
- Battery Storage in the United States: An Update on Market Trends, U.S. Energy Information Administration, Washington, D.C., 2020.
- Batteries: 2018 Annual Progress Report; DOE/EE-1831, Vehicle Technologies Office, Office of Energy Efficiency and Renewable Energy, 2019.
- W. A. Braff, J. M. Mueller and J. E. Trancik, Value of Storage Technologies for Wind and Solar Energy, Nat. Clim. Change, 2016, 6, 964–969 CrossRef.
- Duration Addition to electricity Storage (DAYS) Overview, 2018.
- M. Miotti, G. J. Supran, E. J. Kim and J. E. Trancik, Personal Vehicles Evaluated against Climate Change Mitigation Targets, Environ. Sci. Technol., 2016, 50, 10795–10804 CrossRef CAS PubMed.
-
K. Mongird, V. Fotedar, V. Viswanathan, V. Koritarov, P. Balducci, B. Hadjerioua and J. Alam, Energy Storage Technology and Cost Characterization Report, PNNL-28866, Pacific Northwest National Laboratory, Argonne National Laboratory, Oak Ridge National Laboratory, 2019.
- M. S. Ziegler, J. M. Mueller, G. D. Pereira, J. Song, M. Ferrara, Y.-M. Chiang and J. E. Trancik, Storage Requirements and Costs of Shaping Renewable Energy Toward Grid Decarbonization, Joule, 2019, 3, 2134–2153 CrossRef.
- G. Crabtree, E. Kócs and L. Trahey, The Energy-Storage Frontier: Lithium-Ion Batteries and Beyond, MRS Bull., 2015, 40, 1067–1078 CrossRef CAS.
- B. R. Sutherland, Charging up Stationary Energy Storage, Joule, 2019, 3, 1–3 CrossRef.
-
A. Yoshino, in Lithium-Ion Batteries, ed. Pistoia, G., Elsevier, Amsterdam, 2014, pp. 1–20 Search PubMed.
-
H. Takeshita, The current status and future of the battery industry, 2006.
- O. Schmidt, A. Hawkes, A. Gambhir and I. Staffell, The Future Cost of Electrical Energy Storage Based on Experience Rates, Nat. Energy, 2017, 2, 17110 CrossRef.
-
S. Michaelis, E. Rahimzei, A. Kampker, H. Heimes, C. Lienemann, C. Offermanns, M. Kehrer, A. Thielmann, T. Hettesheimer, C. Neef, A. Kwade, W. Haselrieder, S. Rahlfs, R. Uerlich and N. Bognar, Roadmap: Battery Production Equipment: 2030, VDMA Battery Production, Frankfurt, Germany, 2018 Search PubMed.
- O. Schmidt, S. Melchior, A. Hawkes and I. Staffell, Projecting the Future Levelized Cost of Electricity Storage Technologies, Joule, 2019, 3, 81–100 CrossRef.
- M. S. Ziegler and J. E. Trancik, Re-Examining Rates of Lithium-Ion Battery Technology Improvement and Cost Decline, Energy Environ. Sci., 2021, 14, 1635–1651 RSC.
-
C.-O. Wene, Experience Curves for Energy Technology Policy, OECD/IEA, Paris, France, 2000.
-
L. Gaines and R. Cuenca, Costs of Lithium-Ion Batteries for Vehicles; ANL/ESD-42, Argonne National Laboratory, Argonne, Illinois, 2000, p. 73 Search PubMed.
-
G. L. Henriksen, K. Amine, J. Liu and P. A. Nelson, Materials Cost Evaluation Report for High-Power Li-Ion HEV Batteries, ANL-03/5, Argonne National Laboratory, Argonne, Illinois, 2002, p. 70.
-
B. Barnett, PHEV Battery Cost Assessment, 2009 DOE Merit Review, 2009.
-
A. Dinger, R. Martin, X. Mosquet, M. Rabl, D. Rizoulis, M. Russo and G. Sticher, Batteries for Electric Cars: Challenges, Opportunities, and the Outlook to 2020, The Boston Consulting Group, Inc., 2010.
-
S. Rajagopalan, H. Kamath and F. Kalhammer, Large-Format Lithium-Ion Battery Costs Analysis; Technical Results 1019923, Electric Power Research Institute, Palo Alto, CA, 2010, p. 40 Search PubMed.
-
P. A. Nelson, K. G. Gallagher, I. D. Bloom and D. W. Dees, Modeling the Performance and Cost of Lithium-Ion Batteries for Electric-Drive Vehicles, Technical Report ANL-12/55, Argonne National Lab, Argonne, IL, 2011.
- Technology & Market Drivers for Stationary and Automotive Battery Systems, Batteries 2012 Nice, France, 2012.
- A. Sakti, J. J. Michalek, E. R. H. Fuchs and J. F. Whitacre, A Techno-Economic Analysis and Optimization of Li-Ion Batteries for Light-Duty Passenger Vehicle Electrification, J. Power Sources, 2015, 273, 966–980 CrossRef CAS.
- G. Patry, A. Romagny, S. Martinet and D. Froelich, Cost Modeling of Lithium-Ion Battery Cells for Automotive Applications, Energy Sci. Eng., 2015, 3, 71–82 CrossRef.
- R. Petri, T. Giebel, B. Zhang, J.-H. Schünemann and C. Herrmann, Material Cost Model for Innovative Li-Ion Battery Cells in Electric Vehicle Applications, Int. J. Precis. Eng. Manuf.-Green Tech., 2015, 2, 263–268 CrossRef.
- D. L. Wood, J. Li and C. Daniel, Prospects for Reducing the Processing Cost of Lithium Ion Batteries, J. Power Sources, 2015, 275, 234–242 CrossRef CAS.
- R. E. Ciez and J. F. Whitacre, Comparison between Cylindrical and Prismatic Lithium-Ion Cell Costs Using a Process Based Cost Model, J. Power Sources, 2017, 340, 273–281 CrossRef CAS.
- A. Kwade, W. Haselrieder, R. Leithoff, A. Modlinger, F. Dietrich and K. Droeder, Current Status and Challenges for Automotive Battery Production Technologies, Nat. Energy, 2018, 3, 290–300 CrossRef.
- BatPaC., version 4.0, Argonne National Laboratory, Argonne, Illinois, 2020.
- BattModels/BatteryCost., Viswanathan Group, Carnegie Mellon University, 2021.
- G. Kavlak, J. McNerney and J. E. Trancik, Evaluating the Causes of Cost Reduction in Photovoltaic Modules, Energy Policy, 2018, 123, 700–710 CrossRef.
- T. Mayer, D. Kreyenberg, J. Wind and F. Braun, Feasibility Study of 2020 Target Costs for PEM Fuel Cells and Lithium-Ion Batteries: A Two-Factor Experience Curve Approach, Int. J. Hydrogen Energy, 2012, 37, 14463–14474 CrossRef CAS.
- S. Matteson and E. Williams, Learning Dependent Subsidies for Lithium-Ion Electric Vehicle Batteries, Technol. Forecase. Soc., 2015, 92, 322–331 CrossRef.
- B. Nykvist and M. Nilsson, Rapidly Falling Costs of Battery Packs for Electric Vehicles, Nat. Clim. Change, 2015, 5, 329–332 CrossRef.
-
D. Feldman, R. Margolis, P. Denholm and J. Stekli, Exploring the Potential Competitiveness of Utility-Scale Photovoltaics plus Batteries with Concentrating Solar Power, 2015–2030, NREL/TP-6A20-66592, National Renewable Energy Lab. (NREL), Golden, CO (United States), 2016.
- N. Kittner, F. Lill and D. M. Kammen, Energy Storage Deployment and Innovation for the Clean Energy Transition, Nat. Energy, 2017, 2, 17125 CrossRef.
- I.-Y. L. Hsieh, M. S. Pan, Y.-M. Chiang and W. H. Green, Learning Only Buys You So Much: Practical Limits on Battery Price Reduction, Appl. Energy, 2019, 239, 218–224 CrossRef.
-
W. Cole and A. W. Frazier, Cost Projections for Utility-Scale Battery Storage, Technical Report NREL/TP-6A20-73222, National Renewable Energy Laboratory, Golden, CO, 2019.
-
N. Kittner, O. Schmidt, I. Staffell and D. M. Kammen, in Technological Learning in the Transition to a Low-Carbon Energy System, ed. M. Junginger and A. Louwen, Academic Press, 2020, pp. 119–143 Search PubMed.
- B. Nagy, J. D. Farmer, Q. M. Bui and J. E. Trancik, Statistical Basis for Predicting Technological Progress, PLoS One, 2013, 8, e52669 CrossRef CAS PubMed.
-
N. Rosenberg, Inside the Black Box: Technology and Economics, Cambridge University Press, Cambridge, 1983 Search PubMed.
-
J. E. Trancik, Understanding and Predicting Technological Innovation: New Data and Theory, MIT Professional Education, Massachusetts Institute of Technology, 2018 Search PubMed.
- S. Kahouli-Brahmi, Technological Learning in Energy–Environment–Economy Modelling: A Survey, Energy Policy, 2008, 36, 138–162 CrossRef.
- P. Eash-Gates, M. M. Klemun, G. Kavlak, J. McNerney, J. Buongiorno and J. E. Trancik, Sources of Cost Overrun in Nuclear Power Plant Construction Call for a New Approach to Engineering Design, Joule, 2020, 4, 2348–2373 CrossRef.
- R. R. Nelson, The Simple Economics of Basic Scientific Research, J. Political Econ., 1959, 67, 297–306 CrossRef.
- K. J. Arrow, The Economic Implications of Learning by Doing, Rev. Econ. Stud., 1962, 29, 155–173 CrossRef.
- A. Silberston, Economies of Scale in Theory and Practice, Econ. J., 1972, 82, 369–391 CrossRef.
- R Core Team R: A Language and Environment for Statistical Computing., version 4.0.4, R Foundation for Statistical Computing, Vienna, Austria, 2021.
-
M. Gagolewski, Stringi: Character String Processing Facilities., in collab. with Tartanus, B.; IBM; Unicode, Inc., version 1.5.3, 2020.
-
H. Wickham and J. Bryan, Readxl: Read Excel Files., in collab. with RStudio; Kalicinski, M.; Valery, K.; Leitienne, C.; Colbert, B.; Hoerl, D.; Miller, E., version 1.3.1, 2019.
-
P. Schauberger, A. Walker and L. Braglia, Openxlsx: Read, Write and Edit Xlsx Files., version 4.2.3, 2020.
- MATLAB., version R2021a, MathWorks, 2021.
- Foreign Exchange Rates - H.10, Board of Governors of the Federal Reserve System, https://www.federalreserve.gov/releases/H10/default.htm (accessed 06/19/2020).
- Interactive Data Tables | National Data | National Income and Product Accounts. Bureau of Economic Analysis, U.S. Department of Commerce, https://apps.bea.gov/iTable/iTable.cfm?reqid=19&step=3&isuri=1&categories=survey&nipa_table_list=13 (accessed 06/12/2020).
-
H. Takeshita, Worldwide Battery Market Status & Forecast., Power 2001, 2001.
-
C. Pillot, The Rechargeable Battery Market and Main Trends 2016-2025, 33rd International Battery Seminar & Exhibit, Fort Lauderdale, FL, 2017.
-
R. Kirchain and F. R. Field III, in Encyclopedia of Materials Science & Engineering, Elsevier Science Pubs, 2001, vol. 2, pp 1718–1727 Search PubMed.
-
M. M. Klemun, G. Kavlak, J. McNerney and J. E. Trancik, Solar Energy Cost Trends Reveal Mechanisms of Hardware and Soft Technology Evolution, 2021, in review.
- B. Dunn, H. Kamath and J.-M. Tarascon, Electrical Energy Storage for the Grid: A Battery of Choices, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- R. M. Darling, K. G. Gallagher, J. A. Kowalski, S. Ha and F. R. Brushett, Pathways to Low-Cost Electrochemical Energy Storage: A Comparison of Aqueous and Nonaqueous Flow Batteries, Energy Environ. Sci., 2014, 7, 3459–3477 RSC.
-
K. Ardani, E. O’Shaughnessy, R. Fu, C. McClurg, J. Huneycutt and R. Margolis, Installed Cost Benchmarks and Deployment Barriers for Residential Solar Photovoltaics with Energy Storage: Q1 2016, NREL/TP-7A40-67474, National Renewable Energy Laboratory, 2017.
- E. Hittinger and R. E. Ciez, Modeling Costs and Benefits of Energy Storage Systems, Annu. Rev. Environ. Resour., 2020, 45, 445–469 CrossRef.
- J. Kasnatscheew, T. Placke, B. Streipert, S. Rothermel, R. Wagner, P. Meister, I. C. Laskovic and M. Winter, A Tutorial into Practical Capacity and Mass Balancing of Lithium Ion Batteries, J. Electrochem. Soc., 2017, 164, A2479–A2486 CrossRef CAS.
-
M. W. Juzkow and S. T. Mayer, The Twelfth Annual Battery Conference on Applications and Advances, The Twelfth Annual Battery Conference on Applications and Advances, Long Beach, CA, USA, 1997, pp. 181–188 Search PubMed.
- R. Schmuch, R. Wagner, G. Hörpel, T. Placke and M. Winter, Performance and Cost of Materials for Lithium-Based Rechargeable Automotive Batteries, Nat. Energy, 2018, 3, 267–278 CrossRef CAS.
-
L. Xie, D. Fouchard and S. Megahed, MRS Proceedings, Symposium W – Materials for Electrochemical Energy Storage and Conversion, Cambridge University Press, 1995, vol. 393, pp. 285–304 Search PubMed.
-
J. B. Goodenough, in Lithium Ion Batteries: Fundamentals and Performance, ed. E. M. Wakihara and O. Yamamoto, Wiley-VCH Verlag GmbH, 1998, pp. 1–25 Search PubMed.
-
Y. Nishi, in Lithium Ion Batteries: Fundamentals and Performance, ed. M. Wakihara and O. Yamamoto, Wiley-VCH Verlag GmbH, 1998, pp. 181–198 Search PubMed.
- Y. Nishi, Lithium Ion Secondary Batteries; Past 10 Years and the Future, J. Power Sources, 2001, 100, 101–106 CrossRef CAS.
-
R. J. Brodd, in Battery Technology and Fuel Cell Technology: A Retrospective, 201st ECS Meeting, The Electrochemical Society, Philadelphia, PA, 2002, vol. 2002-1 Search PubMed.
- M. S. Whittingham, Lithium Batteries and Cathode Materials, Chem. Rev., 2004, 104, 4271–4302 CrossRef CAS PubMed.
-
R. J. Brodd, in Lithium-Ion Batteries, Springer, New York, NY, 2009, pp. 1–7 Search PubMed.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Positive Electrode Materials for Li-Ion and Li-Batteries, Chem. Mater., 2010, 22, 691–714 CrossRef CAS.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Li-Ion Battery Materials: Present and Future, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- C. Liu, Z. G. Neale and G. Cao, Understanding Electrochemical Potentials of Cathode Materials in Rechargeable Batteries, Mater. Today, 2016, 19, 109–123 CrossRef CAS.
- Y. Nishi, The Dawn of Lithium-Ion Batteries, Electrochem. Soc. Interface, 2016, 25, 71–74 CrossRef.
- A. Manthiram, A Reflection on Lithium-Ion Battery Cathode Chemistry, Nat. Commun., 2020, 11, 1–9 Search PubMed.
-
R. J. Brodd and K. Tagawa, in Advances in Lithium-Ion Batteries, Springer, Boston, MA, 2002, pp. 267–288 Search PubMed.
-
Handbook of Battery Materials, ed. C. Daniel and J. O. Besenhard, Wiley-VCH, Weinheim, Germany, 2nd edn, 2011, p. 1007 Search PubMed.
- H. Lee, M. Yanilmaz, O. Toprakci, K. Fu and X. Zhang, A Review of Recent Developments in Membrane Separators for Rechargeable Lithium-Ion Batteries, Energy Environ. Sci., 2014, 7, 3857–3886 RSC.
- C. Daniel, Lithium Ion Batteries and Their Manufacturing Challenges, Bridge, 2015, 45, 21–24 Search PubMed.
- Z. Du, D. L. Wood, C. Daniel, S. Kalnaus and J. Li, Understanding Limiting Factors in Thick Electrode Performance as Applied to High Energy Density Li-Ion Batteries, J. Appl. Electrochem., 2017, 47, 405–415 CrossRef CAS.
- T. Marks, S. Trussler, A. J. Smith, D. Xiong and J. R. Dahn, A Guide to Li-Ion Coin-Cell Electrode Making for Academic Researchers, J. Electrochem. Soc., 2010, 158, A51–A57 CrossRef.
-
Y. Wu, Lithium-Ion Batteries: Fundamentals and Applications, ed. Y. Wu, CRC Press/Taylor and Francis, Boca Raton, FL, 2015 Search PubMed.
- M. Li, J. Lu, Z. Chen and K. Amine, 30 Years of Lithium-Ion Batteries, Adv. Mater., 2018, 30, 1800561 CrossRef PubMed.
-
F. R. Kalhammer, Batteries for Electric and Hybrid Vehicles: Recent Development Progress, State of California Air Resources Board, Sacramento, California, 1999 Search PubMed.
- S. Ahmed, P. A. Nelson, K. G. Gallagher, N. Susarla and D. W. Dees, Cost and Energy Demand of Producing Nickel Manganese Cobalt Cathode Material for Lithium Ion Batteries, J. Power Sources, 2017, 342, 733–740 CrossRef CAS.
-
F. K. Shokoohi, J. M. Tarascon and D. Guyomard, Rechargeable LiMn2O4/Carbon Lithium Ion Batteries, in Progress in Batteries and Battery Materials, ed. R. J. Brodd, 1995, vol. 14, pp. 199–217 Search PubMed.
-
R. J. Brodd, J. L. Morris, W. Guindy and R. J. Horning, Thirteenth Annual Battery Conference on Applications and Advances. Proceedings of the Conference, Thirteenth Annual Battery Conference on Applications and Advances, IEEE: Long Beach, CA, USA, 1998, pp. 205–209.
- A. G. Ritchie, Recent Developments and Likely Advances in Lithium Rechargeable Batteries, J. Power Sources, 2004, 136, 285–289 CrossRef CAS.
-
M. Yoshio and H. Noguchi, in Lithium–Ion Batteries, ed. M. Yoshio, R. J. Brodd and A. Kozawa, Springer, New York, NY, 2009, pp. 9–48 Search PubMed.
- J. Li, C. Daniel and D. Wood, Materials Processing for Lithium-Ion Batteries, J. Power Sources, 2011, 196, 2452–2460 CrossRef CAS.
- R. E. Ciez and J. F. Whitacre, The Cost of Lithium Is Unlikely to Upend the Price of Li-Ion Storage Systems, J. Power Sources, 2016, 320, 310–313 CrossRef CAS.
- Cutting Cobalt, Nat. Energy, 2020, 5, 825 CrossRef.
- A. Sakti, I. M. L. Azevedo, E. R. H. Fuchs, J. J. Michalek, K. G. Gallagher and J. F. Whitacre, Consistency and Robustness of Forecasting for Emerging Technologies: The Case of Li-Ion Batteries for Electric Vehicles, Energy Policy, 2017, 106, 415–426 CrossRef.
- K. G. Gallagher, P. A. Nelson and D. W. Dees, Simplified Calculation of the Area Specific Impedance for Battery Design, J. Power Sources, 2011, 196, 2289–2297 CrossRef CAS.
- G. P. Pisano, Learning-before-Doing in the Development of New Process Technology, Res. Policy, 1996, 25, 1097–1119 CrossRef.
- R. Koksbang, J. Barker, H. Shi and M. Y. Saïdi, Cathode Materials for Lithium Rocking Chair Batteries, Solid State Ionics, 1996, 84, 1–21 CrossRef CAS.
-
N. Imanishi, Y. Takeda and O. Yamamoto, in Lithium Ion Batteries: Fundamentals and Performance, ed. M. Wakihara and O. Yamamoto, Wiley-VCH Verlag GmbH, 1998, pp. 98–126 Search PubMed.
-
J. B. Goodenough, in Advances in Lithium-Ion Batteries, Springer, Boston, MA, 2002, pp. 135–154 Search PubMed.
-
Z. Ogumi and M. Inaba, in Advances in Lithium-Ion Batteries, Springer, Boston, MA, 2002, pp. 79–101 Search PubMed.
-
K. Matsuki and K. Ozawa, in Lithium Ion Rechargeable Batteries, ed. K. Ozawa, Wiley-VCH Verlag GmbH & Co. KgaA, 2009, pp. 1–9 Search PubMed.
-
J. Flynn and C. Marsh, Thirteenth Annual Battery Conference on Applications and Advances. Proceedings of the Conference, Thirteenth Annual Battery Conference on Applications and Advances, 1998, pp. 81–84.
-
K.-Y. Lee, LG Chem's Lithium Ion Battery Development Status, 1998 Symposium on Battery Technology, Seoul, Korea.
- K. Xu, Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- S. S. Zhang, A Review on Electrolyte Additives for Lithium-Ion Batteries, J. Power Sources, 2006, 162, 1379–1394 CrossRef CAS.
- K. Xu, Electrolytes and Interphases in Li-Ion Batteries and Beyond, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- A. Davoodabadi, J. Li, H. Zhou, D. L. Wood, T. J. Singler and C. Jin, Effect of Calendering and Temperature on Electrolyte Wetting in Lithium-Ion Battery Electrodes, J. Energy Storage, 2019, 26, 101034 CrossRef.
- F. J. Günter, C. Burgstaller, F. Konwitschny and G. Reinhart, Influence of the Electrolyte Quantity on Lithium-Ion Cells, J. Electrochem. Soc., 2019, 166, A1709–A1714 CrossRef.
- M. Li, C. Wang, Z. Chen, K. Xu and J. Lu, New Concepts in Electrolytes, Chem. Rev., 2020, 120, 6783–6819 CrossRef CAS PubMed.
-
J. D. Donaldson and D. Beyersmann, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2000 Search PubMed.
- K. B. Shedd, E. A. McCullough and D. I. Bleiwas, Global Trends Affecting the Supply Security of Cobalt, Min. Eng., 2017, 69, 37–42 Search PubMed.
- G. A. Campbell, The Cobalt Market Revisited, Miner. Econ., 2020, 33, 21–28 CrossRef.
-
W. Bernhart, in Lithium-Ion Batteries, ed. G. Pistoia, Elsevier, Amsterdam, 2014, pp. 553–565 Search PubMed.
- J. Kalhoff, G. G. Eshetu, D. Bresser and S. Passerini, Safer Electrolytes for Lithium-Ion Batteries: State of the Art and Perspectives, ChemSusChem, 2015, 8, 2154–2175 CrossRef CAS PubMed.
- M. Winter, B. Barnett and K. Xu, Before Li Ion Batteries, Chem. Rev., 2018, 118, 11433–11456 CrossRef CAS PubMed.
- C. A. Vincent, Lithium Batteries: A 50-Year Perspective, 1959–2009, Solid State Ionics, 2000, 134, 159–167 CrossRef CAS.
- M. S. Whittingham, Introduction: Batteries, Chem. Rev., 2014, 114, 11413 CrossRef CAS PubMed.
-
D. Chung, E. Elgqvist and S. Santhanagopalan, Automotive Lithium-Ion Cell Manufacturing: Regional Cost Structures and Supply Chain Considerations, Technical Report NREL/TP-6A20-66086, Clean Energy Manufacturing Analysis Center, Golden, CO, 2016 Search PubMed.
-
B. Andersson, B. Hallgren, A. Johansson and P. Selånger, Lithium Batteries for Electric Road Vehicle Applications, Swedish National Board for Industrial and Technical Development, Stockholm, Sweden, 1995 Search PubMed.
-
R. J. Brodd, Factors Affecting U.S. Production Decisions: Why Are There No Volume Lithium-Ion Battery Manufacturers in the United States?, Working Paper 05–01, Economic Assessment Office, Advanced Technology Program, National Institute of Standards and Technology, 2005, p. 92 Search PubMed.
-
M. Lowe, S. Tokuoka, T. Trigg and G. Gereffi, Lithium-Ion Batteries for Electric Vehicles: The U.S. Value Chain, Center on Globalization, Governance & Competitiveness, Duke University, 2010 Search PubMed.
-
C. Cluzel and C. Douglas, Cost and Performance of EV Batteries: Final Report for The Committee on Climate Change, Element Energy Limited, Cambridge, UK, 2012 Search PubMed.
-
Quadrennial Technology Review 2015, Department of Energy, Washington, DC, 2015 Search PubMed.
- T. Lieven, Policy Measures to Promote Electric Mobility – A Global Perspective, Transp. Res. Part A: Policy Pract., 2015, 82, 78–93 CrossRef.
-
S. Bennett, A. Blasi, M. Waldron, Y. Nobuoka and A. Toril, World Energy Investment 2018, Paris, France, 2018.
- Global EV Outlook 2020: Entering the Decade of Electric Drive? International Energy Agency, Paris, France, 2020.
-
R. Kempener and E. Borden, Battery Storage for Renewables: Market Status and Technology Outlook, International Renewable Energy Agency, Abu Dhabi, 2015 Search PubMed.
- M. Armand and J.-M. Tarascon, Building Better Batteries, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- L. Trahey,
et al., Energy Storage Emerging: A Perspective from the Joint Center for Energy Storage Research, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12550–12557 CrossRef CAS PubMed.
- T. Nagaura and K. Tozawa, Lithium Ion Rechargeable Battery, Prog. Batteries Sol. Cells, 1990, 9, 209–217 CAS.
- S. Megahed and B. Scrosati, Lithium-Ion Rechargeable Batteries, J. Power Sources, 1994, 51, 79–104 CrossRef CAS.
-
D. Friel, Understanding Lithium Battery Tradeoffs In Mobile Devices, Electronic Design, 2013 Search PubMed.
- T. Hazama, M. Miyabayashi, H. Andoh, R. Ishikawa, S. Furuta, H. Ishihara and J. Shonaka, Lithium Secondary Batteries in Japan, J. Power Sources, 1995, 54, 306–309 CrossRef CAS.
- S. C. Levy, Safety and Reliability Considerations for Lithium Batteries, J. Power Sources, 1997, 68, 75–77 CrossRef CAS.
-
Y. Nishi, Past, Present and Future of Lithium-Ion Batteries: Can New Technologies Open up New Horizons? in Lithium-Ion Batteries, ed. G. Pistoia, Elsevier, Amsterdam, 2014, pp. 21–39 Search PubMed.
- B. B. Owens and T. Osaka, Panel Discussion Future Prospects of Lithium Batteries, J. Power Sources, 1997, 68, 173–186 CrossRef.
- H. Koh and C. L. Magee, A Functional Approach for Studying Technological Progress: Extension to Energy Technology, Technol. Forecase. Soc., 2008, 75, 735–758 CrossRef.
- J. B. Goodenough and A. Manthiram, A Perspective on Electrical Energy Storage, MRS Commun., 2014, 4, 135–142 CrossRef CAS.
- C. Goddard, Debunking the Learning Curve, IEEE Trans. Compon., Hybrids, Manuf. Technol., 1982, 5, 328–335 CrossRef.
- L. Argote and D. Epple, Learning Curves in Manufacturing, Science, 1990, 247, 920–924 CrossRef CAS PubMed.
- F. Ferioli, K. Schoots and B. C. C. van der Zwaan, Use and Limitations of Learning Curves for Energy Technology Policy: A Component-Learning Hypothesis, Energy Policy, 2009, 37, 2525–2535 CrossRef.
- C. Freeman, The Economics of Technical Change, Cambridge J. Econ., 1994, 18, 463–514 CrossRef.
-
J. E. Trancik, P. Brown, J. Jean, G. Kavlak, M. M. Klemun, M. R. Edwards, J. McNerney, M. Miotti, J. M. Mueller and Z. A. Needel, Technology improvement and emissions reductions as mutually reinforcing efforts: Observations from the global development of solar and wind energy, Massachusetts Institute of Technology, Cambridge, MA, 2015 Search PubMed.
- J. McNerney, J. D. Farmer, S. Redner and J. E. Trancik, Role of Design Complexity in Technology Improvement, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9008–9013 CrossRef CAS PubMed.
- R. Rothwell and P. Gardiner, Re-innovation and Robust Designs: Producer and User Benefits, J. Mark. Manage., 1988, 3, 372–387 CrossRef.
-
V. Bush, Science: The Endless Frontier, United States Government Printing Office, Washington, DC, 1945, p. 241 Search PubMed.
- Report to the President on Federal Energy Research and Development for the Challenges of the Twenty-First Century; President's Committee of Advisors on Science and Technology: Panel on Energy Research And Development, 1997.
- A. Grübler, N. Nakićenović and D. G. Victor, Dynamics of Energy Technologies and Global Change, Energy Policy, 1999, 27, 247–280 CrossRef.
-
Accelerating Energy Innovation, ed. R. M. Henderson and R. G. Newell, University of Chicago, Chicago, IL, 2011 Search PubMed.
- L. M. A. Bettencourt, J. E. Trancik and J. Kaur, Determinants of the Pace of Global Innovation in Energy Technologies, PLoS One, 2013, 8, e67864 CrossRef CAS PubMed.
- P. A. David, Clio and the Economics of QWERTY, Am. Econ. Rev., 1985, 75, 332–337 Search PubMed.
- W. B. Arthur, Competing Technologies, Increasing Returns, and Lock-In by Historical Events, Econ. J., 1989, 99, 116–131 CrossRef.
- G. C. Unruh, Understanding Carbon Lock-In, Energy Policy, 2000, 28, 817–830 CrossRef.
-
D. M. Hart, W. B. Bonvillian and N. Austin, Energy Storage for the Grid: Policy Options for Sustaining Innovation, 2018.
- V. Sivaram, J. O. Dabiri and D. M. Hart, The Need for Continued Innovation in Solar, Wind, and Energy Storage, Joule, 2018, 2, 1639–1642 CrossRef.
- L. Haelg, M. Waelchli and T. S. Schmidt, Supporting Energy Technology Deployment While Avoiding Unintended Technological Lock-in: A Policy Design Perspective, Environ. Res. Lett., 2018, 13, 104011 CrossRef.
- M. Beuse, B. Steffen and T. S. Schmidt, Projecting the Competition between Energy-Storage Technologies in the Electricity Sector, Joule, 2020, 4, 2162–2184 CrossRef CAS.
- T. S. Schmidt, B. Battke, D. Grosspietsch and V. H. Hoffmann, Do Deployment Policies Pick Technologies by (Not) Picking Applications?—A Simulation of Investment Decisions in Technologies with Multiple Applications, Res. Policy, 2016, 45, 1965–1983 CrossRef.
- J. E. Trancik, Scale and Innovation in the Energy Sector: A Focus on Photovoltaics and Nuclear Fission, Environ. Res. Lett., 2006, 1, 014009 CrossRef.
- J. C. J. M. Van den Bergh, Optimal Diversity: Increasing Returns versus Recombinant Innovation, J. Econ. Behav. Org., 2008, 68, 565–580 CrossRef.
- F. C. Krysiak, Environmental Regulation, Technological Diversity, and the Dynamics of Technological Change, J. Econ. Dyn. Control, 2011, 35, 528–544 CrossRef.
- S. Dörfler, H. Althues, P. Härtel, T. Abendroth, B. Schumm and S. Kaskel, Challenges and Key Parameters of Lithium-Sulfur Batteries on Pouch Cell Level, Joule, 2020, 4, 539–554 CrossRef.
- C.-X. Zu and H. Li, Thermodynamic Analysis on Energy Densities of Batteries, Energy Environ. Sci., 2011, 4, 2614–2624 RSC.
- C. Wadia, P. Albertus and V. Srinivasan, Resource Constraints on the Battery Energy Storage Potential for Grid and Transportation Applications, J. Power Sources, 2011, 196, 1593–1598 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation, APL Mater., 2013, 1, 011002 CrossRef.
- X. Qu, A. Jain, N. Nidhi Rajput, L. Cheng, Y. Zhang, S. Ping Ong, M. Brafman, E. Maginn, L. A. Curtiss and K. A. Persson, The Electrolyte Genome Project: A Big Data Approach in Battery Materials Discovery, Comput. Mater. Sci., 2015, 103, 56–67 CrossRef CAS.
- L. Ghadbeigi, J. K. Harada, B. R. Lettiere and T. D. Sparks, Performance and Resource Considerations of Li-Ion Battery Electrode Materials, Energy Environ. Sci., 2015, 8, 1640–1650 RSC.
- G. L. Soloveichik, Flow Batteries: Current Status and Trends, Chem. Rev., 2015, 115, 11533–11558 CrossRef CAS PubMed.
- Y. Zhao, Y. Ding, Y. Li, L. Peng, H. R. Byon, J. B. Goodenough and G. Yu, A Chemistry and Material Perspective on Lithium Redox Flow Batteries towards High-Density Electrical Energy Storage, Chem. Soc. Rev., 2015, 44, 7968–7996 RSC.
- Z. Li, M. S. Pan, L. Su, P.-C. Tsai, A. F. Badel, J. M. Valle, S. L. Eiler, K. Xiang, F. R. Brushett and Y.-M. Chiang, Air-Breathing Aqueous Sulfur Flow Battery for Ultralow-Cost Long-Duration Electrical Storage, Joule, 2017, 1, 306–327 CrossRef CAS.
- X. Ji, A Paradigm of Storage Batteries, Energy Environ. Sci., 2019, 12, 3203–3224 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01313k |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Juhyun
Song
a,
Juhyun
Song
 a and
Jessika E.
Trancik
a and
Jessika E.
Trancik
 *ab
*ab

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 quantitative (e.g. masses, prices, plant capacity estimates, etc.) and qualitative (e.g. cell shape, commercial availability, etc.) data points. These data were obtained from approximately 280 references. Portions of this analysis also rely on the previously described lithium-ion technology database, which contains 1716 records from nearly 600 sources.18
000 quantitative (e.g. masses, prices, plant capacity estimates, etc.) and qualitative (e.g. cell shape, commercial availability, etc.) data points. These data were obtained from approximately 280 references. Portions of this analysis also rely on the previously described lithium-ion technology database, which contains 1716 records from nearly 600 sources.18


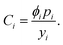
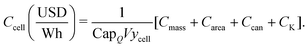
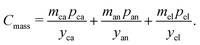

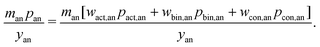
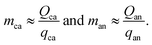
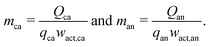
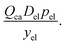

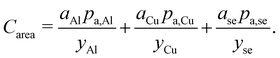
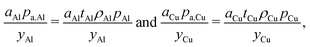
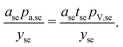
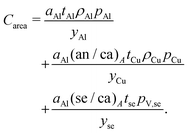
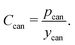
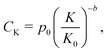
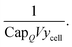

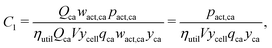

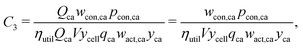
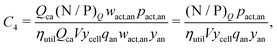
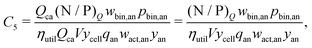

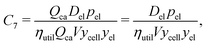
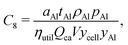
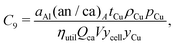
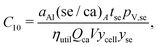
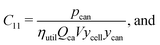
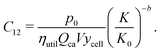
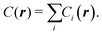
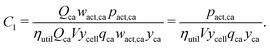
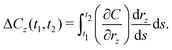
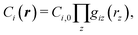
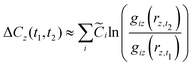
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i is a constant that is a representative value of cost component Ci during the period between t1 and t2. Previous work has demonstrated that a good approximation of
i is a constant that is a representative value of cost component Ci during the period between t1 and t2. Previous work has demonstrated that a good approximation of ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i is the logarithmic mean:
i is the logarithmic mean: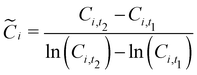
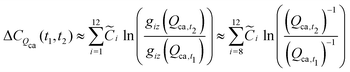
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) i can be computed as given in eqn (39). Note that the sum for this variable is limited to cost components 8 through 12 as the variable cancels out in components 1 through 7.
i can be computed as given in eqn (39). Note that the sum for this variable is limited to cost components 8 through 12 as the variable cancels out in components 1 through 7.







