Open Access Article
Open Access ArticleCharting lattice thermal conductivity for inorganic crystals and discovering rare earth chalcogenides for thermoelectrics†
Taishan
Zhu‡
a,
Ran
He‡
b,
Sheng
Gong‡
 a,
Tian
Xie
a,
Prashun
Gorai
a,
Tian
Xie
a,
Prashun
Gorai
 c,
Kornelius
Nielsch
b and
Jeffrey C.
Grossman
c,
Kornelius
Nielsch
b and
Jeffrey C.
Grossman
 *a
*a
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: jcg@mit.edu
bLeibniz Institute for Solid State and Materials Research, Dresden, 01069, Germany
cDepartment of Metallurgical and Materials Engineering, Colorado School of Mines, Golden, CO 80401, USA
First published on 16th April 2021
Abstract
Thermoelectric power generation represents a promising approach to utilize waste heat. The most effective thermoelectric materials exhibit low thermal conductivity κ. However, less than 5% out of about 105 synthesized inorganic materials are documented with their κ values, while for the remaining 95% κ values are missing and challenging to predict. In this work, by combining graph neural networks and random forest approaches, we predict the thermal conductivity of all known inorganic materials in the Inorganic Crystal Structure Database, and chart the structural chemistry of κ into extended van-Arkel triangles. Together with the newly developed κ map and our theoretical tool, we identify rare-earth chalcogenides as promising candidates, of which we measured ZT exceeding 1.0. We note that the κ chart can be further explored, and our computational and analytical tools are applicable generally for materials informatics.
Broader contextMade possible by high-throughput calculations and recent machine-learning techniques, this work frames the structural chemistry of lattice thermal conductivity into generalized von-Arkel triangles, and charts the lattice thermal conductivity of 105 inorganic materials for fast materials screening. Immediate applications include thermal management and thermoelectrics. For instance, the rare-earth chalcogenides (REX) family stands out as promising thermoelectric materials, exhibiting zT higher than 1.0 and stable at temperatures higher than 1000 K. The REX family can still be explored further. While more material systems could be identified for thermal-related applications using this conductivity map, the developed computational framework can be extended for materials informatics generally, including electronic and optical predictions. |
Introduction
Entropic consideration favors low thermal conductivity for thermoelectric efficiency to approach the Carnot limit.1,2 The discovery of the Seebeck and Peltier effects has enabled driving charge flows by heat and vice versa,3,4 which has been employed in a range of applications, from powering the Explorer in the deep space to cooling medicine at pharmaceutical sites.5,6 Such thermoelectric mechanisms have attracted considerable interest and research efforts for more than a century, with recent excitement and attention given their potential use in green energy generation.1 However, the barrier for large-scale technical translation of thermoelectrics remains their low efficiencies (e.g., <5% for most thermoelectric materials on the market3,7). A critical factor that leads to low efficiency is unstoppable heat flow, which gives rises to irreversibility and is governed by thermal conductivity, which must be low for high efficiency.8In fact, solids with both low and high extreme thermal conductivity have been pursued fundamentally and practically for decades.9–16 Currently the records are held by diamond (∼2000 W m−1 K−1)17 in the upper limit and aerogels (∼0.01 W m−1 K−1) on the lower end,18 although it remains unclear whether these are hard limits. Regardless, the search for alternative materials that lie at or beyond these extremes is also of practical importance, particularly when multiple constraints are imposed, such as specific mechanical properties for thermal coatings19 and (opto-) electronic properties for applications in energy conversion.3,20 Beyond thermoelectrics, diverse applications range from thermal management in electronics and avionics,21 to high-temperature coatings in turbines19 and human healthcare,22 to name only a few examples.
However, knowledge of the governing physics of lattice thermal conductivity (κ) remains incomplete at the atomic scale.23,24 Current understanding derives largely from kinetic theory and relates to unit cell properties (e.g., average atomic mass, density, symmetry).15 This understanding has been historically encapsulated into analytical models, such as the Debye–Callaway (D–C) model25 and its variants.23 Similarly, analytical models for κ of solid-solution alloys, such as the Klemens model,26 are based on unit cell properties and scattering parameters. These models are explicit, but have parameters either numerically fitted or computed from first principles. For instance, Miller et al. developed a modified D–C model with speed of sound and Grüneisen parameter, which are derived from bulk modulus and average coordination number.27
An emerging approach has been driven by learning from the existing data of κ, benefited from the developments in high-throughput screening and machine learning methods.4,28–31 Through high-throughput calculations, databases are growing in size via approaches for computing κ based on the Green–Kubo formalism32,33 and Boltzmann theory.15,34 However, relying on dynamical and/or large-scale first-principles calculations, these methods are often computationally expensive, and most high-throughput studies are limited within certain material families.30 Alternatively, the above semi-empirical models have also been successfully implemented for high-throughput predictions.35 Experimental data is even less available. To date, only some hundreds of the total ∼105 synthesized materials documented in the Inorganic Crystal Structure Database (ICSD) have κ values measured.36 Thus, while machine learning techniques have shown initial success,24,37–41 both more data and novel approaches are needed in order to explore the vast materials space.
Towards this end, general guidelines for navigating and sampling the materials space for κ will be valuable. Predicting/understanding κ has posed a catch-22 situation. On the one hand, descriptor-based methods assume a priori knowledge of the physics of κ, so that appropriate features can be populated for materials.37 However, since the structural chemistry of κ is largely unknown, the choice of atomic features is currently somewhat arbitrary.37 On the other hand, techniques based on graph neural networks assume little pre-knowledge of κ, and can predict material properties directly from structure.43 However, these methods are “black-boxes”,44 and the challenge of interpreting the structure-κ relation remains.
In this work, we predict κ for all ordered and stoichiometric materials in ICSD (92919 entries), and then reveal the structural chemistry of κ. Two complementary approaches, neural networks and random forest, are thus combined. While the former predicts κ directly from structures with little need for featurization, the latter extracts the hidden chemistry in the dataset. With resolved important atomic and structural features that govern κ, we are able to chart the structural chemistry of κ using generalized van-Arkel triangles. Aiming at learning and predicting κ measured by experiments, we build an experimental dataset (κexp) collected from the literature, and extend our earlier graph neural networks model43 with transfer learning (TL-CGCNN, details in ESI†). Based on the charts, we identify a set of rare-earth chalcogenides, as a new class of promising thermoelectric materials, of which the figure of merit shows 1.1 at 800 K.
Predicting κ for all known inorganic crystals
We start by learning from our recently prepared high-throughput κC dataset,35 before moving to the broader ICSD and the underlying structural chemistry. The κC dataset contains computed κ of 2668 ordered and stoichiometric inorganic structures from the ICSD. The predicted κ is fairly accurate, with an average factor difference of 1.5 from experimentally measured values, over a range of κ values that span 4 orders of magnitude.27 In this section, we will show both the transferability and limitation of this dataset, and in the next section we will show its implicit physics. Note that these two purposes suit two separate but complementary machine learning models: crystal graph convolutional neural network (CGCNN),43 and interpretable random forest. These models are illustrated in Fig. 1(a), with further details available in the ESI.† For our high-throughput dataset, we randomly reserve 20% of the entries as the test set, as plotted in Fig. 1(b). Both CGCNN and random forest models could predict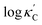 with MAE < 0.15 and R2 > 0.85.
with MAE < 0.15 and R2 > 0.85.
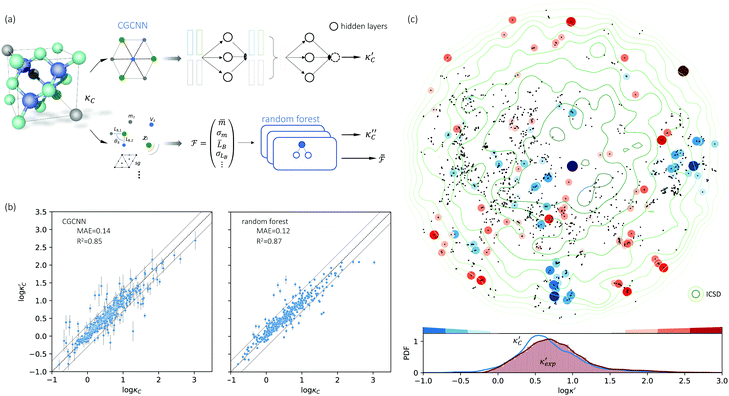 | ||
Fig. 1 (a) Schematic of two complementary models: CGCNN and random forest. (b) Predicted 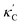 from these two models. The dashed band denotes a factor of 2. (c) High-throughput from these two models. The dashed band denotes a factor of 2. (c) High-throughput 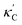 for all ordered ICSD structures, full data available online.42 The contour denotes the distribution of ICSD materials in the feature space reduced to 2D via PCA/t-SNE, along with the training set denoted by the dots. The histograms are the distribution of predicted for all ordered ICSD structures, full data available online.42 The contour denotes the distribution of ICSD materials in the feature space reduced to 2D via PCA/t-SNE, along with the training set denoted by the dots. The histograms are the distribution of predicted 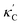 and and 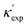 . See text for the prediction of . See text for the prediction of 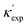 . . | ||
Moreover, different from CGCNN, random forest requires featurization for crystal structures before running through decision trees, which is largely physics-based and in many cases ad hoc. Guided by lattice dynamical theory, we choose configurational features from elemental to atomic packing and bonding nature, which are constructed through Matminer,45 Magpie,46 and in-house codes. Since κ is sensitive to both absolute values and variations of atomic properties, our feature engineering leads to a 154-dimensional descriptor, including the statistics (mean ![[. with combining macron]](https://www.rsc.org/images/entities/char_002e_0304.gif) , standard deviation σ, range {.} and mode) of atomic number, covalent radius (ra), atomic mass (m), periodic table group and row number, Mendeleev number, volume per atom from ground state (VGS), Pauling electronegativity (χa), melting point (Tm), number (NV) and unfilled (NU) valence electrons in the s, p, d, and f shells of constituting elements, as well as structural features at the cell scale (space group, volume per atom Va, packing fraction ϕ, density ρ, bond length LB, bond angle θB, and coordination number CN).
, standard deviation σ, range {.} and mode) of atomic number, covalent radius (ra), atomic mass (m), periodic table group and row number, Mendeleev number, volume per atom from ground state (VGS), Pauling electronegativity (χa), melting point (Tm), number (NV) and unfilled (NU) valence electrons in the s, p, d, and f shells of constituting elements, as well as structural features at the cell scale (space group, volume per atom Va, packing fraction ϕ, density ρ, bond length LB, bond angle θB, and coordination number CN).
To visualize the feature space, we project it onto two dimensions, as shown in Fig. 1(c) (see also methods in ESI†). Materials from our high-throughput dataset and the ICSD dataset are considered together, denoted by the scattered points and contour respectively. Note that the x and y axes are abstract linear combinations of all structural features. On this projected materials-feature space, the contour lines show the distribution of all inorganic materials. Deeper color indicates more materials existing in ICSD (we have removed the contour levels though to stress that the magnitude is relative). The contour shows that most materials are populated in the central area, and the distribution varies smoothly, thus amenable to machine learning algorithms. Our high-throughput entries (scattered points) with the highest and lowest κ values highlighted, sample the reduced feature space quite satisfactorily in terms of uniformity, suggesting the potential transferability of our high-throughput dataset to ICSD. We did so using both CGCNN and random forest models, and we have made the data of 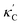 available online.42 From the histogram in 1(c), the distribution of predicted
available online.42 From the histogram in 1(c), the distribution of predicted 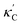 follows approximately a normal distribution, with mean log
follows approximately a normal distribution, with mean log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ ∼ 0.8 (
κ ∼ 0.8 (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ∼ 6 W m−1 K−1) and standard deviation σlog
∼ 6 W m−1 K−1) and standard deviation σlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ ∼ 0.5.
κ ∼ 0.5.
As a first validation, we compare our predictions with experimental values. As shown in Fig. S3 (ESI†), 63(88) and 66(86) of 132 measured values align with our predictions within a factor of 2(3), for random forest and CGCNN, respectively. More detailed accuracy analysis, compared to different approaches, is presented in Table S1 (ESI†). We note that the accuracy is lower than the existing models (e.g. high-throughput27), but our models predict κ directly from atomic structures, without the need of expensive calculations for bulk modulus and Grüneisen parameter. Instead, if we introduce bulk modulus into our random-forest model, the MAE reduces to 0.04, which suggests the accuracy of our machine learning models could be at par with density functional theory (DFT) predictions.
To further validate our machine-learning predictions, we compare them to experimental measurements, and/or to first-principles calculations49 (see details of experimental and computational methods in ESI†). In addition to the measurements in the literature, we also chose 12 materials from different structures/compositions/families, and measured their κ. The comparisons are presented in Table 1 for several low- and high-κ materials. Overall, our machine learning models can unanimously screen the lowest from the highest, which might be already sufficient for many materials selection/design scenarios, such as for thermoelectrics and thermal management, where either the lowest or the highest κ values are sought. For instance, in Table 1, we have identified rare-earth chalcogenides (REX) as promising thermoelectric materials, which are interesting for future exploration (see below). The other reason that we test our machine-learning models with these extremes is to show their reliability for extrapolation (transferability), which is often more challenging numerically than interpolation.
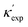 is from a random forest model for the low regime of κ, and TL-CGCNN for high values. The entries without references are measured/calculated in this work
is from a random forest model for the low regime of κ, and TL-CGCNN for high values. The entries without references are measured/calculated in this work
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κexp κexp |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κDFT κDFT |
|||
|---|---|---|---|---|
| a New four-phonon plus SCPH calculations give −0.5. | ||||
| Cu2HfTe3 | −0.016 | 0.016 | 0.022 | |
| Cu3VTe4 | 0.19 | 0.26 | 0.28 | |
| TaCoTe2 | −0.21 | −0.32 | 0.052 | |
| AgAlTe2 | −0.21 | −0.36 | 0.042 | |
| FeIn2S4 | 0.16 | 0.58 | 0.46 | |
| NbTe4 | 0.28 | 0.30 | 0.36 | |
| TiFeCoGa | 0.69 | 0.86 | 1.09 | |
| Er2Se3 | 0.15 | 0.21 | 0.071 | |
| Er2Te3 | 0.19 | 0.18 | 0.32 | |
| Tb2Te3 | −0.027 | 0.15 | 0.21 | |
| Dy2Te3 | 0.0056 | 0.18 | 0.22 | |
| Ho2Te3 | 0.16 | 0.20 | 0.32 | |
| Cs2BiAgCl6 | −1.2 | −0.1 | −0.3 | |
| CsTlF3 | −1.0 | 0.2 | −0.1 | |
| CsTlI3 | −1.3 | −0.1 | −0.3 | |
| CsPbI3 | −0.447 | −1.020 | −0.2 | −0.2 |
| Tl3VSe4 | −0.59 | −0.89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−0.2 | −0.3 |
| Be2C | 2.06 | 2.9 | 2.6 | |
| C3N4 | 2.4 | 2.5 | 2.6 | |
| BP | 2.6048 | 2.8215 | 2.4 | 2.6 |
| BAs | 3.0812–14 | 3.5015 | 2.0 | 2.2 |
| BN | 3.2011 | 3.3315 | 2.6 | 2.9 |
| Diamond | 3.3617 | 3.5415 | 3.1 | 3.4 |
More quantitatively, the error of our machine learning models is comparable to first-principles calculations based on DFT (κDFT). For instance, in the case of diamond, the extrapolated values, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) κ = 3.1 and 3.4, are close to the experimental value 3.36, comparing to 3.54 from DFT calculations. Such level of error applies to nearly all examined entries, except several outlying cases, such as BAs, for which the accuracy is less satisfactory. Other possible outliers are also observed when experimental values are missing and a substantial difference can be seen between DFT and machine learning, such as CsTlF3 in Table 1. However, such possible outliers should be further examined due to the possible underestimation from DFT calculations. In some cases, a difference of 50–100% between DFT and experimental values can arise from the relaxation-time approximation up to 3-phonon interactions, which might be resolved by more sophisticated calculations, such as four-phonon and temperature-dependent dispersion.9,50,51 In many other cases, our machine learning prediction can be even more accurate than DFT, such as the iodide perovskite CsPbI3 and the recently studied Tl3VSe4 (see Table 1). Moreover, note that our above error analyses is based on extrapolation. Even for the highest and lowest values, the machine learning models show satisfactory stability and prediction accuracy.
κ = 3.1 and 3.4, are close to the experimental value 3.36, comparing to 3.54 from DFT calculations. Such level of error applies to nearly all examined entries, except several outlying cases, such as BAs, for which the accuracy is less satisfactory. Other possible outliers are also observed when experimental values are missing and a substantial difference can be seen between DFT and machine learning, such as CsTlF3 in Table 1. However, such possible outliers should be further examined due to the possible underestimation from DFT calculations. In some cases, a difference of 50–100% between DFT and experimental values can arise from the relaxation-time approximation up to 3-phonon interactions, which might be resolved by more sophisticated calculations, such as four-phonon and temperature-dependent dispersion.9,50,51 In many other cases, our machine learning prediction can be even more accurate than DFT, such as the iodide perovskite CsPbI3 and the recently studied Tl3VSe4 (see Table 1). Moreover, note that our above error analyses is based on extrapolation. Even for the highest and lowest values, the machine learning models show satisfactory stability and prediction accuracy.
Nevertheless, our machine learning model is still limited by the quality and finiteness of our dataset. Since the training set used is the largest reliable dataset available, this limitation will be translated to guidelines for future high-throughput calculations. This is discussed further as we extend CGCNN with transfer learning (TL-CGCNN) to predicting experimental values 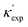 (Section S1 in ESI†). The top 50 lowest-κ and highest-κ values are uniformly scattered, suggesting little knowledge content. However, as we present in Fig. 2(a), these top 100 points are clustered when we plot without ICSD. This is another indication of the limited transferability to ICSD, but also demonstrates the knowledge content in our known dataset.
(Section S1 in ESI†). The top 50 lowest-κ and highest-κ values are uniformly scattered, suggesting little knowledge content. However, as we present in Fig. 2(a), these top 100 points are clustered when we plot without ICSD. This is another indication of the limited transferability to ICSD, but also demonstrates the knowledge content in our known dataset.
 | ||
| Fig. 2 (a) Clustering of the high-throughput database using PCA and tSNE, low-κ and high-κ entries are highlighted. (b) Top 20 important features and their F scores. (c) Dimension reduction by random-forest-ranked feature selection lead to even lower than PCA, and MAE approaches to CGCNN around 10 atomic features. Low-κ and high-κ materials can be divided by important features, (d) is an example of using ϕ − Va. (e and f) Chemical space illustrated by van-Arkel triangles, examples of structural (VGS) and bonding (χa) information. Similar triangles are available in Fig. S5 (ESI†). | ||
Structural chemistry of κ
Such knowledge content can be extracted in the form of ranked features (details in ESI†). In Fig. 2(b), the top 20 features are ranked in decreasing order. These features include the elemental type (VGS, NV, NU, m) and structural type, the latter consisting of bonding properties (LB, θB, CN), and packing properties (Va, Dim, ϕ, SG, ρ). The learning of important features is different from a simple correlation relation (see Fig. S4, ESI†). Fig. 2(c) shows the MAE as a function of increasing number of features, picking from the most important features, from PCA and random forest respectively. As the number of features increases, MAE reduces quickly and reaches our CGCNN accuracy with less than 10 features, and both are lower than PCA. The latter is usually chosen when little pre-knowledge is assumed, and our case shows that the accuracy of such purely data-driven techniques (e.g. PCA for dimensional reduction) could be surpassed by physics-informed approaches. Another interesting application of these important features is to physically categorize/cluster all the training materials. An example is shown in Fig. 2(d), where high-κ and low-κ values could be separated by the dashed line.Further, phonon transport is sensitive to chemical variations, more than corresponding mean fields. Examples are mass and bond strength: the mean values define mean-field harmonic properties (e.g., group velocity), while the differences determine both harmonic (e.g., phononic bandgap) and anharmonic properties (e.g., higher-order force constants). This is also suggested in Fig. 2(b), where both mean values and variances are ranked most important, such as LB, θB, CN, and NV. Note that our machine learning models start from a different feature list from that of our D–C model. For instance, none of the crucial variances enters the D–C model. This is also true for the past predictions of harmonic properties, such as Debye temperature and vibrational entropy.36,52,53 Despite the partial overlap between our important feature list and those for harmonic-property predictions, which is expected because κ is determined by both harmonic and more challenging anharmonic properties, the newly revealed variance and how the mean-variance information together impacts κ is unknown. More importantly, other than widely-applied correlograms, an anaytlical tool to study this is still missing.
Inspired by various forms of van-Arkel-type triangles, we use mean and standard deviation to construct extended triangles and generalize extensively to other atomic features (see ESI†). Invented originally for binary inorganic compounds, van-Arkel-type triangles were constructed to characterize bonding nature, using the average and difference of the two elements' electronegativity χa. In our case, we have multi-component compounds and more dominant quantities than χa. Therefore, we extend the original van-Arkel triangle to include more components with mean and standard deviation, and to more physical descriptors important for κ. For instance, the VGS- and χa-triangles shown in Fig. 2(e–f) characterize packing and bonding information, respectively. More such charts are shown in Fig. S5 (ESI†). Although the extension is straightforward, it helps to chart the structural chemistry of κ. For instance, each of these triangles illustrates a projected materials space, within which all materials should be confined. While the coverage is essential for validating our dataset, it is also interesting to note that many of the chosen features are effective divisors (e.g. VGS, χa, LB, θB, ra, NV, m). In other words, given the mean and deviation of any of these features for a unit cell, the relative magnitude of κ can already be estimated.
Note that our work confirms and also enhances our existing understanding of trends in κ. For instance, it is commonly established that low-κ materials often have (i) high average atomic mass ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Fig. S5(g), ESI†), and (ii) weak interatomic bonding, so that group velocity can be low, and (iii) high anharmonicity in order to have short relaxation time (e.g. more scattering channels resulting from complex crystal structures). However, bonding strength and anharmonicity are computationally expensive quantities. Meanwhile, predicting κ directly from atomic structures was at best qualitative in the literature. With our analysis based on Fig. 2 and Fig. S5 (ESI†), we now have proxies for bond strength and even κ, such as VGS, LB, and ra. On the other hand, our analysis also shows that χa and CN are more complicated than their reported influences. For instance, a strong correlation has been identified between CN and κ.54 However, Fig. S5(c) (ESI†) exhibits a rather mixed trend. This mixed trend for CN can be understood by its competing impacts between bond strength and anharmonicity due to bonding-environment complexity: (i) higher CN suggests larger anharmonicity due to more complexity in the bonding environment, (ii) higher CN means weaker bond strength, as stated by Pauling's second rule, due to electrostatic repulsion; (iii) a large CN also suggests a stiff lattice, thus large sound speed. Therefore, the classic χa and CN may be sub-optimal features. Moreover, our identified structural features have only partial overlap with previous works on learning vibrational properties.36,52,53 In particular, comparing to the learning of harmonic properties, these mean-variance pairs which inspired the extension of van-Arkel triangles also suggest the importance of structural variance and complexity in anharmoncity.
(Fig. S5(g), ESI†), and (ii) weak interatomic bonding, so that group velocity can be low, and (iii) high anharmonicity in order to have short relaxation time (e.g. more scattering channels resulting from complex crystal structures). However, bonding strength and anharmonicity are computationally expensive quantities. Meanwhile, predicting κ directly from atomic structures was at best qualitative in the literature. With our analysis based on Fig. 2 and Fig. S5 (ESI†), we now have proxies for bond strength and even κ, such as VGS, LB, and ra. On the other hand, our analysis also shows that χa and CN are more complicated than their reported influences. For instance, a strong correlation has been identified between CN and κ.54 However, Fig. S5(c) (ESI†) exhibits a rather mixed trend. This mixed trend for CN can be understood by its competing impacts between bond strength and anharmonicity due to bonding-environment complexity: (i) higher CN suggests larger anharmonicity due to more complexity in the bonding environment, (ii) higher CN means weaker bond strength, as stated by Pauling's second rule, due to electrostatic repulsion; (iii) a large CN also suggests a stiff lattice, thus large sound speed. Therefore, the classic χa and CN may be sub-optimal features. Moreover, our identified structural features have only partial overlap with previous works on learning vibrational properties.36,52,53 In particular, comparing to the learning of harmonic properties, these mean-variance pairs which inspired the extension of van-Arkel triangles also suggest the importance of structural variance and complexity in anharmoncity.
Exploring the non-existing and experimental confirmation of REX for thermoelectrics
The structural chemistry of κ can be used to extend the predictions from machine learning. For instance, in the upper limit, machine learning predicts the κ values for BN and diamond to be 764 W m−1 K−1 and 2225 W m−1 K−1, which are close to experimental values. As shown in Fig. 3(a), from the van-Arkel triangle of χa, we notice two candidate materials between BN and diamond: C3N4 and B4C3. The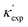 of C3N4 ranked in the top 1% in our machine learning predictions over ICSD. In contrast, B4C3 is absent from ICSD, and is obtained by reading the van-Arkel triangle. One can also use this approach to search for low-κ materials. Guided by the triangles, we adapt the corner of thalium, and iodine, considering their atomic weight and electronegativity. As shown in Fig. 3(b), binary and ternary compounds (e.g. TlI, CsTlF3, CsPbI3) are predicted from machine learning. Based on these, we could hypothesize that CsTlI3 would have a low κ, which is also absent from the ICSD and confirmed by our DFT calculations (Table 1).
of C3N4 ranked in the top 1% in our machine learning predictions over ICSD. In contrast, B4C3 is absent from ICSD, and is obtained by reading the van-Arkel triangle. One can also use this approach to search for low-κ materials. Guided by the triangles, we adapt the corner of thalium, and iodine, considering their atomic weight and electronegativity. As shown in Fig. 3(b), binary and ternary compounds (e.g. TlI, CsTlF3, CsPbI3) are predicted from machine learning. Based on these, we could hypothesize that CsTlI3 would have a low κ, which is also absent from the ICSD and confirmed by our DFT calculations (Table 1).
 | ||
| Fig. 3 Proposed searching directions of (a) high- and (b) low-κ materials. While C3N4 exists in ICSD and is recommended by TL-CGCNN, van-Arkel analysis suggests B4C3 (absent in ICSD) to have high κ as well. (b) is part of periodic table that m and χa are both large, based on which binary/ternary compounds are recommended (TlI, CsTlF3, CsPbI3) and hypothesized (CsTlI3). (c) The proposed REX system, and the temperature-dependent thermal conductivity of 6 chosen REX materials. The materials marked empty are chosen for further thermoelectric measurements. (d) Temperature-dependent thermal conductivity, electrical resistivity, and Seebeck coefficient of compound series Er2Te3−xBix and Y2Te3−yBiy with x = 0, 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6, and y = 0, 0.2, 0.3 and 0.4. (e) Temperature-dependent zT of REX, compared to Yb14MnSb11 (Zintl phase55), ZrNiSn (Half-Heusler56), SiGe alloy (bulk alloy57), and La3Te4 (REX58). | ||
Another group of the least thermally conducting materials are the REX family. As mentioned above, the REX materials rank the lowest 5% in the κ chart. To further confirm their transport properties, we show in Fig. 3(c) the temperature-dependent thermal conductivity of six compounds (Er2Se3, Er2Te3, Tb2Te3, Dy2Te3, Ho2Te3, and Y2Te3) that belong to the REX family. Note that the electronic contribution to the thermal conductivity is negligible since these materials are insulators. We obtain fairly low κ for these compounds with minimum values of 0.5 to 0.6 W m−1 K−1 at 973 K for several compounds such as Er2Te3, Tb2Te3, and Dy2Te3. The κ values of REX are comparable with Zintl phase Yb14MnSb11,55 and lower than SiGe bulk alloy57 and half-Heusler ZrNiSn.56 The low κ suggests the potential of these materials for thermoelectric applications. Advanced thermoelectric materials require decent electronic transport performance, which can be enabled by aliovalent doping to modify the Fermi level.
Among the REX compounds with charted thermal conductivity, we select Er2Te3 and Y2Te3 for case studies to investigate their full-thermoelectric properties through partial substitution of Bi at the Te sites. Fig. 3(d) shows the temperature-dependent thermal conductivity, which increases with the content of Bi, especially at elevated temperature. Such a thermal-conductivity increase has an electronic origin due to reduced electrical resistivity, which is also shown in Fig. 3(d) for compound series Er2Te3−xBix and Y2Te3−yBiy with x = 0.2, 0.3, 0.4, 0.5 and 0.6, and y = 0.3 and 0.4, whereas the resistivities of the compounds with x = 0, 0.1, and y = 0, 0.2 are not shown since they are too high to measure. Generally, the substitution of Bi yields reduced electrical resistivity for both series, which is accompanied by the reduced Seebeck coefficient (S). The combination of S2ρ, termed as the power factor, exhibits a maximum of 1.15 mW m−1 K−2 for compounds with x = 0.3 at 973 K, which is comparable to some advanced TE materials such as Cu2Se59 and SnSe.60 The combination of power factor and thermal conductivity yields the thermoelectric figure-of-merit, zT, which shows a peak exceeding 1.0 at 973 K for Er2Te2.7Bi0.3 with an increasing trend, thus suggesting even higher zT is possible at higher temperature. The obtained zT for Er2Te2.7Bi0.3 is comparable to other high-zT TE materials, such as Zintl phase (Yb14MnSb1155), Half-Heusler (ZrNiSn56), bulk alloy (SiGe57), and another REX (La3Te458). Our reported zT has higher value at either high temperature or the whole temperature range. Er2Te3 and Y2Te3 are two examples of the REX system, which merits further exploration for high-temperature thermoelectrics.
Conclusion
In summary, we studied the structural chemistry of lattice thermal conductivity κ for inorganic crystals, and predicted κ for a large set of inorganic compounds, directly from their atomic structures. We extended our graph neural network model to include transfer learning, and using as input our recently prepared database of κ. Combining the neural networks model and interpretable random forest, we extract atomic features that dominate the physics of κ, including elemental (χa, VGS, ra) and packing (LB, Va). Other features, such as CN, are shown to be also important but more complicated than conventionally assumed. With these identified features, we extended van-Arkel triangles as two-dimensional projected materials space. This analytical tool allows the projection and visualization of materials spaces for κ, and could be applied to other materials informatics studies. We also identified rare-earth chalcogenides (REX), which exhibit a ZT exceeding 1.0 and could be a promising material system for thermoelectrics. A limitation of the current models is to fully predict the six tensor components of κ (our current values are polar averages of these tensor components), thus the possible anisotropy. This will be technically possible with increasing database for anisotropic κ.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by various computational resources: (i) Comet at the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562, through allocation TG-DMR090027, and (ii) the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This work is supported by Toyota Research Institute, and also by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001205.References
- D. M. Rowe, Thermoelectrics handbook: macro to nano, CRC press, 2018 Search PubMed.
- G. S. Nolas, J. Sharp and J. Goldsmid, Thermoelectrics: basic principles and new materials developments, Springer Science & Business Media, vol. 45, 2013 Search PubMed.
- J. He and T. M. Tritt, Science, 2017, 357, 1369 CAS.
- P. Gorai, V. Stevanović and E. S. Toberer, Nat. Rev. Mater., 2017, 2, 1 Search PubMed.
- F. J. DiSalvo, Science, 1999, 285, 703 CrossRef CAS PubMed.
- J. Mao, G. Chen and Z. Ren, Nat. Mater., 2020, 1, 454 Search PubMed.
- G. J. Snyder and T. S. Ursell, Phys. Rev. Lett., 2003, 91, 148301 CrossRef PubMed.
- G. J. Snyder and E. S. Toberer, Materials for sustainable energy: a collection of peer-reviewed research and review articles from Nature Publishing Group, World Scientific, 2011, pp. 101–110 Search PubMed.
- S. Mukhopadhyay, D. S. Parker, B. C. Sales, A. A. Puretzky, M. A. McGuire and L. Lindsay, Science, 2018, 360, 1455 CrossRef CAS PubMed.
- C. Chiritescu, D. G. Cahill, N. Nguyen, D. Johnson, A. Bodapati, P. Keblinski and P. Zschack, Science, 2007, 315, 351 CrossRef CAS PubMed.
- K. Chen, B. Song, N. K. Ravichandran, Q. Zheng, X. Chen, H. Lee, H. Sun, S. Li, G. A. Gamage and F. Tian, et al. , Science, 2020, 367, 555 CrossRef CAS PubMed.
- S. Li, Q. Zheng, Y. Lv, X. Liu, X. Wang, P. Y. Huang, D. G. Cahill and B. Lv, Science, 2018, 361, 579 CrossRef CAS PubMed.
- F. Tian, B. Song, X. Chen, N. K. Ravichandran, Y. Lv, K. Chen, S. Sullivan, J. Kim, Y. Zhou and T.-H. Liu, et al. , Science, 2018, 361, 582 CrossRef CAS PubMed.
- J. S. Kang, M. Li, H. Wu, H. Nguyen and Y. Hu, Science, 2018, 361, 575 CrossRef CAS PubMed.
- L. Lindsay, D. Broido and T. Reinecke, Phys. Rev. Lett., 2013, 111, 025901 CrossRef CAS PubMed.
- D. G. Cahill, W. K. Ford, K. E. Goodson, G. D. Mahan, A. Majumdar, H. J. Maris, R. Merlin and S. R. Phillpot, J. Appl. Phys., 2003, 93, 793 CrossRef CAS.
- L. Wei, P. Kuo, R. Thomas, T. Anthony and W. Banholzer, Phys. Rev. Lett., 1993, 70, 3764 CrossRef CAS PubMed.
- X. Lu, M. Arduini-Schuster, J. Kuhn, O. Nilsson, J. Fricke and R. Pekala, Science, 1992, 255, 971 CrossRef CAS PubMed.
- D. R. Clarke and S. R. Phillpot, Mater. Today, 2005, 8, 22 CrossRef CAS.
- T. Zhu and E. Ertekin, Energy Environ. Sci., 2019, 12, 216 RSC.
- P. K. Schelling, L. Shi and K. E. Goodson, Mater. Today, 2005, 8, 30 CrossRef CAS.
- Y. Peng and Y. Cui, Joule, 2020, 4, 724 CrossRef CAS.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843 RSC.
- A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput and I. Tanaka, Phys. Rev. Lett., 2015, 115, 205901 CrossRef PubMed.
- D. T. Morelli and G. A. Slack, High Thermal Conductivity Materials, Springer, 2006, p. 37 Search PubMed.
- R. Gurunathan, R. Hanus and G. J. Snyder, Mater. Horiz., 2020, 7, 1452 RSC.
- S. A. Miller, P. Gorai, B. R. Ortiz, A. Goyal, D. Gao, S. A. Barnett, T. O. Mason, G. J. Snyder, Q. Lv, V. Stevanovic and E. S. Toberer, Chem. Mater., 2017, 29, 2494 CrossRef CAS.
- C. Toher, J. J. Plata, O. Levy, M. de Jong, M. Asta, M. B. Nardelli and S. Curtarolo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 174107 CrossRef.
- J. Carrete, W. Li, N. Mingo, S. Wang and S. Curtarolo, Phys. Rev. X, 2014, 4, 011019 CAS.
- A. van Roekeghem, J. Carrete, C. Oses, S. Curtarolo and N. Mingo, Phys. Rev. X, 2016, 6, 041061 Search PubMed.
- S. Wang, Z. Wang, W. Setyawan, N. Mingo and S. Curtarolo, Phys. Rev. X, 2011, 1, 021012 Search PubMed.
- A. J. McGaughey and M. Kaviany, Adv. Heat Transfer, 2006, 39, 169 CAS.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144306 CrossRef.
- A. J. McGaughey, A. Jain, H.-Y. Kim and B. Fu, J. Appl. Phys., 2019, 125, 011101 CrossRef.
- P. Gorai, D. Gao, B. Ortiz, S. Miller, S. Barnett, T. Mason, Q. Lv, V. Stevanović and E. S. Toberer, Comput. Mater. Sci., 2016, 112, 368 CrossRef.
- M. W. Gaultois, T. D. Sparks, C. K. H. Borg, R. Seshadri, W. D. Bonificio and D. R. Clarke, Chem. Mater., 2013, 25, 2911 CrossRef CAS.
- H. Wei, S. Zhao, Q. Rong and H. Bao, Int. J. Heat Mass Transfer, 2018, 127, 908 CrossRef.
- S. Ju, T. Shiga, L. Feng, Z. Hou, K. Tsuda and J. Shiomi, Phys. Rev. X, 2017, 7, 021024 Search PubMed.
- L. Chen, H. Tran, R. Batra, C. Kim and R. Ramprasad, Comput. Mater. Sci., 2019, 170, 109155 CrossRef CAS.
- E. J. Kautz, A. R. Hagen, J. M. Johns and D. E. Burkes, Comput. Mater. Sci., 2019, 161, 107 CrossRef CAS.
- H. Zhou, G. Zhang and Y.-W. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 16165 RSC.
- T. Zhu, “Github link to data,” https://github.com/taishanG2e/kappa_ML.git.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. Rudin, Nature Machine Intelligence, 2019, 1, 206 CrossRef.
- L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom and M. Dylla, et al. , Comput. Mater. Sci., 2018, 152, 60 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- W. Lee, H. Li, A. B. Wong, D. Zhang, M. Lai, Y. Yu, Q. Kong, E. Lin, J. J. Urban and J. C. Grossman, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8693 CrossRef CAS PubMed.
- Y. Kumashiro, T. Mitsuhashi, S. Okaya, F. Muta, T. Koshiro, Y. Takahashi and M. Mirabayashi, J. Appl. Phys., 1989, 65, 2147 CrossRef CAS.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- L. Lindsay, A. Katre, A. Cepellotti and N. Mingo, J. Appl. Phys., 2019, 126, 050902 CrossRef.
- Y. Xia, K. Pal, J. He, V. Ozolinš and C. Wolverton, Phys. Rev. Lett., 2020, 124, 065901 CrossRef CAS PubMed.
- M. De Jong, W. Chen, R. Notestine, K. Persson, G. Ceder, A. Jain, M. Asta and A. Gamst, Sci. Rep., 2016, 6, 34256 CrossRef CAS PubMed.
- F. Legrain, J. Carrete, A. van Roekeghem, S. Curtarolo and N. Mingo, Chem. Mater., 2017, 29, 6220 CrossRef CAS.
- E. B. Isaacs, G. M. Lu and C. Wolverton, arXiv preprint arXiv:2004.01579 (2020).
- S. R. Brown, S. M. Kauzlarich, F. Gascoin and G. J. Snyder, Chem. Mater., 2006, 18, 1873 CrossRef CAS.
- S. Chen, K. C. Lukas, W. Liu, C. P. Opeil, G. Chen and Z. Ren, Adv. Energy Mater., 2013, 3, 1210 CrossRef CAS.
- C. B. Vining, CRC Handbook of Thermoelectrics, ed. D. M. Rowe, CRC Press, 1995 Search PubMed.
- A. F. May, J.-P. Fleurial and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125205 CrossRef.
- D. Yang, X. Su, J. Li, H. Bai, S. Wang, Z. Li, H. Tang, K. Tang, T. Luo and Y. Yan, et al. , Adv. Mater., 2020, 32, 2003730 CrossRef CAS PubMed.
- C. Chang, M. Wu, D. He, Y. Pei, C.-F. Wu, X. Wu, H. Yu, F. Zhu, K. Wang and Y. Chen, et al. , Science, 2018, 360, 778 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee00442e |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |