Open Access Article
Open Access ArticleA combined experimental and computational study to decipher complexity in the asymmetric hydrogenation of imines with Ru catalysts bearing atropisomerizable ligands†
Félix
León‡
a,
Aleix
Comas-Vives
 b,
Eleuterio
Álvarez
b,
Eleuterio
Álvarez
 a and
Antonio
Pizzano
a and
Antonio
Pizzano
 *a
*a
aInstituto de Investigaciones Químicas and Centro de Innovación en Química Avanzada (ORFEO-CINQA), CSIC and Universidad de Sevilla, Avda Américo Vespucio 49, 41092 Sevilla, Spain. E-mail: pizzano@iiq.csic.es
bDepartment of Chemistry, Universitat Autònoma de Barcelona, 08193 Cerdanyola del Vallès, Catalonia, Spain
First published on 21st January 2021
Abstract
RuCl2(P–OP)(N–N) complexes (1) containing an atropisomerizable phosphine–phosphite (P–OP) and a chiral C2 symmetric diamine (N–N) are readily prepared as trans isomers by successive addition of P–OP and N–N ligands to RuCl2(PPh3)3. For these complexes, fast atropisomerization of the biaryl fragment at room temperature has been observed. Compound trans-1a cleanly isomerizes into a mixture of cis isomers in EtOH upon heating. DFT calculations reproduce accurately the ratio of isomers observed as well as the greater thermodynamic stability of the cis isomers of 1a. Complexes 1 are efficient catalyst precursors for the asymmetric hydrogenation of N-aryl imines 5 in toluene under very mild conditions using KOtBu as a base (4 bar H2, room temperature, 5/1/KOtBu = 500/1/10). Among the catalyst precursors, 1f provides good enantioselectivities in the hydrogenation of a wide range of N-aryl imines (84–96% ee, 16 examples). From DFT calculations, a mechanism consisting in stepwise transfer of a hydride and a proton from the dihydride to the imine has been proposed, with the most favourable paths for R and S products involving cis-dihydrides d1R and d3S, respectively. Among several hydrogen activation pathways examined in the pro-R route, the most favorable one consists of hydrogen coordination to a Ru–amido/amine adduct, followed by amine assisted activation of dihydrogen.
Introduction
Chiral Ru complexes bearing P- and N-ligands constitute a group of catalysts of paramount importance in the area of asymmetric hydrogenation.1 Fueled by the seminal discovery by Noyori and coworkers about the outstanding performance of complexes containing BINAP and DPEN or DAIPEN ligands in the asymmetric hydrogenation of ketones,2 the field has grown impressively and a vast diversity of catalysts comprising different combinations of ligands can be found in the literature.3 Moreover, these types of catalysts have displayed a broad substrate scope for catalytic hydrogenation beyond ketones, which includes imines, esters, and amides, among others.4The study of the mechanism of the prototypical asymmetric hydrogenation of ketones with the aforementioned catalysts has deserved considerable attention as well.5 From this background, it is concluded that the ketone is reduced by an octahedral dihydride, generated in the reaction medium from a dihalo or a halo-hydride complex by the action of a base and hydrogen,5a–c by an outer sphere pathway. In this regard, computational studies by Dub and Gordon have shown the prevalence of a stepwise mechanism over a concerted one.6 Another key mechanistic aspect regards the stereochemistry of the reducing dihydride. Due to their octahedral geometry, several isomers are possible depending on the nature of the ancillary ligands. It is worthy to note that cis isomers possess an additional source of chirality due to a stereogenic center located at the metal.7 In this context, a detailed study by Morris and coworkers on the Ru(H)2(PPh3)2((R,R)-dach) complex (A, Fig. 1) has shown that the trans,cis isomer is the active catalyst in the hydrogenation of acetophenone, while the cis,cis isomers (two isomers differing in metal configuration; only the Λ isomer is shown) are precursors of the active one.5c Aligned with these observations, mechanistic studies on Ru(H)2((S)-BINAP)((S,S)-DPEN) (B) have considered the trans isomer as the competent catalyst.5h It is pertinent to note that Ohkuma and coworkers have otherwise proposed a cis dihydride catalyst in the asymmetric hydrogenation of imines catalyzed by cis-Ru(Br)2((S,S)-Xyl-skewphos)((S,S)-DPEN) (C).8 In connection with this, it should also be noticed that cis dichloro complexes based on diphosphine and amino-pyridine ligands are also effective in the asymmetric transfer hydrogenation of ketones.9
 | ||
| Fig. 1 Structures of cis and trans dihydride isomers relevant in the catalytic hydrogenation of ketones and imines. | ||
Following our interest in the application of chiral phosphine–phosphites (P–OP) in hydrogenation reactions, we preliminarily described the application of Ru(Cl)2(P–OP)(DPEN) complexes (Fig. 2) in the enantioselective hydrogenation of N-aryl imines.10a Compared to ubiquitous diphosphine catalysts, the presence of a phosphite fragment in these complexes may have a profound influence in the catalytic system due to its π-acidity. Comparison between structures of the Ru(Cl)2(P–OP)(DPEN) complexes showed that both cis and trans isomers can be formed depending on the structure of the P–OP ligand. Moreover, a remarkable feature of this catalytic system is that high levels of enantioselectivity were achieved with P–OP ligands bearing atropisomerizable phosphite fragments.10a This is an intriguing observation considering the complexity of the system, as the combination of two different phosphorus functionalities, the access to both cis and trans isomers and the atropisomerizable phosphite fragment can lead up to ten dihydrides with potential catalytic reactivity. In this contribution, we present a combined experimental and computational study on this catalytic system which explains the high levels of observed enantioselectivity. In addition, catalyst screening covering diverse combinations of P–OP and diamine ligands has detected a practical and versatile catalyst with the DPEN diamine as the sole chiral ligand, capable of reducing a variety of N-aryl imines under very mild conditions with good levels of activity and enantioselectivity.
Results and discussion
Synthesis and structural features of Ru(Cl)2(P–OP)(N–N) complexes
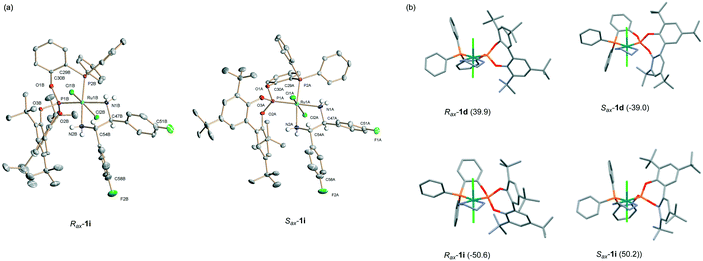
Ru(Cl)2(P–OP)(N–N) complexes (1a–1k, Scheme 1) were prepared in a one-pot reaction by successive addition of phosphine–phosphite and diamine ligands to RuCl2(PPh3)3. Monitoring the reactions by 31P{1H} NMR showed the formation of one set of signals, enabling the isolation of compounds 1 with moderate to high yields (56–76%). This procedure thus constitutes a substantial improvement over the reaction of Ru(2-Me-C3H4)2(P–OP) with HCl and diamine used by us before,10 which led to complexes 1 as diastereomeric mixtures with rather low yields (ca. 10–40%). In the case of complexes 1a–1c, characterized by an oxamethylene backbone, the undesired formation of Ru(Cl)2(P–OP)2 was observed. Latter complexes are characterized by triplets in the phosphine and phosphite regions in the 31P{1H} NMR spectra (e.g. centred at 133.0 and 4.5 ppm, 2JPP = 37 Hz, in the synthesis of 1c). These by-products result from the reaction of RuCl2(P–OP)(PPh3) with P–OP and better yields of 1a–1c were obtained in more diluted reactions. The procedure in Scheme 1 is rather versatile and allowed us to introduce several chiral 1,2-diaryl-1,2-ethanediamines (3a–3d) or a 1,2-diisopropyl derivative (4) as well as P–OP ligands differing in their backbone structure. In the search for chirally-economic catalysts,9b an atropisomerizable biaryl fragment in the P–OP ligand has been maintained as a common element11 in the library of catalysts. The exploitation of such an element is a rather powerful strategy in the design of chiral catalysts as it generates a stereogenic axis from an achiral ligand upon coordination, with its configuration being potentially controlled by a chiral ancillary ligand.12 For instance, this approach has been applied successfully in Ru hydrogenation catalysts by the combination of chiral diamines (e.g. DPEN) and atropisomerizable diphosphines.12a,b,eThe structure of some representative complexes 1 was then examined by X-ray crystallography. It should be recalled that the preliminary structure determination of complex 1d displayed the presence of two diastereomeric structures with a trans stereochemistry, differing in the configuration of the biaryl fragment.10a,13 Analysis of complex 1i showed an analogous pattern (Fig. 3a), as well as 1a and 1c (see the ESI†). This stereochemistry seems associated with the synthetic route in Scheme 1 and can reasonably be assumed for the rest of complexes 1. To avoid redundancy, an explicit mention of the trans stereochemistry of 1 will only be made in selected cases for the sake of clarity. The change in the configuration of the stereogenic axis is accompanied by an extensive conformational change of the P–OP ligand backbone and of the arrangement of the phenylphosphine substituents, in such a way that both structures would be mirror images if the diamine backbone were not considered.13b Another common feature of these structures is that the axial hydrogens of amino groups display a hydrogen bond with an adjacent chloro ligand,14 as the corresponding distances range between 2.7 and 2.8 Å, while the sum of van der Waals radii lies between 2.9 and 3.0 Å.15 Moreover, these axial hydrogens exhibit a syn periplanar orientation with chloro ligands, with torsion angles ranging between ca. 13 and 22 degrees. Finally, an interesting difference between structures of complexes 1d and 1i regards the different orientation of the phenylene backbone fragment with regard to the phosphite biaryl moiety as shown by the opposite signs of the values of the PO–Ru–PC–CAr dihedral angle (Fig. 3b) in the Rax and Sax diastereomers.
According to the presence of two diastereomers of complexes 1 in the crystal lattice, the observation of one set of signals in 31P{1H} NMR at room temperature agrees with the fast atropisomerization of the biaryl moiety.16 Confirmation of the existence of a dynamic process comes from variable temperature 31P{1H} NMR spectroscopy of 1b (Fig. 4), which shows the existence of two species in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio at −90 °C, characterized by doublets in the phosphine and phosphite regions (major: 174.5, 69.5 ppm; minor: 175.4, 67.6 ppm) with a coincident value of 2JPP coupling constants (47 Hz). Coalescence of signals was observed at around −70 °C, while over −50 °C, two sharp doublets were observed. For this dynamic process, a free activation energy of 9.2 kcal mol−1 was determined at the coalescence temperature by lineshape analysis, while an analogous analysis for 1d gave a value of 10.2 kcal mol−1 (coalescence temperature −65 °C, see the ESI† for details).
1 ratio at −90 °C, characterized by doublets in the phosphine and phosphite regions (major: 174.5, 69.5 ppm; minor: 175.4, 67.6 ppm) with a coincident value of 2JPP coupling constants (47 Hz). Coalescence of signals was observed at around −70 °C, while over −50 °C, two sharp doublets were observed. For this dynamic process, a free activation energy of 9.2 kcal mol−1 was determined at the coalescence temperature by lineshape analysis, while an analogous analysis for 1d gave a value of 10.2 kcal mol−1 (coalescence temperature −65 °C, see the ESI† for details).
Pertinent to note in this context, Ohkuma and coworkers have observed that a mixture of cis and trans isomers of Ru(Br)2((S,S)-Xyl-skewphos)((S,S)-DPEN) can be converted into the cis isomer by treatment with a iPrOH/CH2Cl2 mixture. The aforementioned allyl route led to a mixture of isomers of Ru(Cl)2(2a)(3a) composed of trans complex 1a and additional isomers. From this mixture, a cis isomer could be characterized by X-ray diffraction (cis-1a; cis-1 type structure, Rax configuration; see Fig. 5a in the Computational studies section).10b According to this finding, we have examined the isomerization of trans complex 1a in alcoholic solvents. Interestingly, heating a solution of this complex in EtOH for 16 h at 60 °C leads to a mixture of two new species in a 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with almost complete conversion (95%). These compounds are characterized by very similar NMR data and among them, an upfield shift of resonances of NH signals with respect to those of the starting trans complex can be remarked, attributable to the proximity of the biaryl phosphite moiety to the amino fragments and hence indicative of a cis structure. From the mixture, it was possible to crystallize the major isomer which was identified as cis-1a by X-ray analysis (minor cis isomer will be denoted as cis-1a′). In contrast, 1d is rather unreactive under these reaction conditions and only a conversion of 10% could be observed after 3 days at 70 °C in an EtOH–1,2-dichloroethane (1
1 ratio with almost complete conversion (95%). These compounds are characterized by very similar NMR data and among them, an upfield shift of resonances of NH signals with respect to those of the starting trans complex can be remarked, attributable to the proximity of the biaryl phosphite moiety to the amino fragments and hence indicative of a cis structure. From the mixture, it was possible to crystallize the major isomer which was identified as cis-1a by X-ray analysis (minor cis isomer will be denoted as cis-1a′). In contrast, 1d is rather unreactive under these reaction conditions and only a conversion of 10% could be observed after 3 days at 70 °C in an EtOH–1,2-dichloroethane (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture, exhibiting two new species in a ca. 3
1) mixture, exhibiting two new species in a ca. 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio by 31P{1H} NMR.
1 ratio by 31P{1H} NMR.
Catalytic studies
In our preliminary study of the hydrogenation of imine 5a with Ru(Cl)2(P–OP)(N–N) complexes (Scheme 2), we screened several reaction conditions.10a Among them, the best results were obtained under very mild conditions in toluene with Ru(Cl)2(2f)(3a) (4 bar H2, RT, S/C/KOtBu = 500/1/10, full conversion in 24 h; 93% ee). Examination of the performance of the series of catalyst precursors 1 under these reaction conditions (Table 1) showed near complete reactions with the only exception of 1c (86%, entry 3) and particularly 1k, for which a poor value was observed (27%, entry 10). Moreover, good values of enantioselectivity were obtained (89–95% ee), with 1a and 1f surpassing the p-tolyl catalyst (entries 1 and 5, respectively). The uniformly high levels of enantioselectivity with complexes 1 also demonstrate that the atropisomerizable phosphite fragment is a valuable element for the design of chirally economic catalysts. It is worth noting that no influence of the electronic properties of DPEN substituents was observed with catalyst precursors 1i and 1j (entries 8 and 9). For the couple of diastereomeric complexes 1g and 1h, little matching/mismatching effects were observed, with a small difference of enantioselectivity between them and the configuration of the product determined by that of DPEN (entries 6 and 7). This is general and for catalyst precursors bearing (S,S)-diamines, the R product is formed (and conversely the S product from (R,R)-diamines). Among the complexes examined, 1f showed the best performance with a complete conversion and 95% ee. From this satisfactory result, we next screened the application of this complex in the hydrogenation of a set of N-aryl imines derived from aryl alkyl ketones (5b–5o). For these substrates, full conversion and enantioselectivities between 84 and 96% ee were observed (Table 2). It is worth noting that the set includes demanding ortho substituted imines (entries 8 and 9), naphthyl imines (entries 13 and 14) and a thienyl example (entry 12). In contrast, no conversion was observed in the hydrogenation of challenging isopropyl methyl imine 5p.| Entry | Cat | Conv (%) | ee (%; config) |
|---|---|---|---|
| a Reactions performed under 4 bar H2 in toluene at room temperature for 24 h with KOtBu as a base; S/C/B = 500/1/10; conversion was determined by 1H NMR. % ee determined by HPLC. Configuration was determined by comparison with literature data.17 | |||
| 1 | 1a | 100 | 94 (R) |
| 2 | 1b | 100 | 94 (S) |
| 3 | 1c | 86 | 90 (S) |
| 4 | 1e | 100 | 92 (S) |
| 5 | 1f | 100 | 95 (S) |
| 6 | 1g | 100 | 89 (R) |
| 7 | 1h | 100 | 93 (S) |
| 8 | 1i | 100 | 90 (R) |
| 9 | 1j | 95 | 90 (S) |
| 10 | 1k | 27 | nd |
| Entry | Imine | % ee (conf) |
|---|---|---|
| a Reactions performed under 4 bar H2 in toluene at room temperature for 24 h with KOtBu as a base; S/C/B = 500/1/10; full conversion (1H NMR) was observed in all reactions. % ee determined by HPLC. See the ESI† for determination of configuration. | ||
| 1 | 5b | 94 (S) |
| 2 | 5c | 94 (S) |
| 3 | 5d | 87 (S) |
| 4 | 5e | 94 (S) |
| 5 | 5f | 91 (S) |
| 6 | 5g | 96 (S) |
| 7 | 5h | 95 (S) |
| 8 | 5i | 93 (S) |
| 9 | 5j | 95 (S) |
| 10 | 5k | 94 (S) |
| 11 | 5l | 91 (S) |
| 12 | 5m | 95 (S) |
| 13 | 5n | 84 (S) |
| 14 | 5ñ | 92 (S) |
| 15 | 5o | 96 (S) |
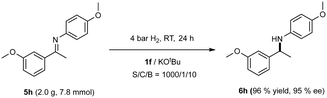
To examine the practical character of 1f, we have also prepared for the gram scale hydrogenation of 5h (Scheme 3), as the resulting product has attracted interest in the synthesis of the NPS R-568 calcimimetic.18 We were pleased to note that a reaction using 2.0 g of 5h at S/C/B = 1000/1/10 led to full conversion in 24 h, yielding amine 6h with 96% isolated yield and 95% ee.
Detailed mechanistic studies by the group of Noyori have shown that hydride–borohydride complexes Ru(H)(BH4)(tol-BINAP)(1,2-diamine) (1,2-diamine = DPEN, en, DAIPEN) are suitable catalyst precursors for the hydrogenation of ketones in isopropanol without the need of an additional base,19,20 while no catalytic activity was observed in toluene.5b Based on this background, we have prepared Ru(H)(BH4)(2c)(3b) (7) by treating 1e with an excess of NaBH4 in a toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH (1
EtOH (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture (Scheme 4).21 An analysis by NMR of the product showed the existence of two isomers of 7 in a 7
1) mixture (Scheme 4).21 An analysis by NMR of the product showed the existence of two isomers of 7 in a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. A 2D NOESY experiment with the mixture indicates that the major isomer possesses a trans stereochemistry, while the minor one, attending to the similarity between the spectroscopic data of both species, can be assigned as the alternative trans isomer. We have next analysed the performance of 7 in the hydrogenation of 5a in the absence of a base. First, no reaction was observed in toluene, in accord with the literature precedent mentioned above. On the other hand, a reaction performed under 20 bar H2 in iPrOH and 60 °C with an S/C = 100 showed a complete conversion and 84% ee after 24 h. For comparison, a reaction prepared with 1e under the same reaction conditions but with addition of a small amount of KOtBu to guarantee catalyst activation (S/C/B = 100/1/5) provided 91% conversion and 83% ee. These results point to a common enantiodetermining step starting from 1e and KOtBu or 7 in isopropanol. These observations are analogous to those reported for the BINAP/DPEN system in the asymmetric hydrogenation of acetophenone.5b
3 ratio. A 2D NOESY experiment with the mixture indicates that the major isomer possesses a trans stereochemistry, while the minor one, attending to the similarity between the spectroscopic data of both species, can be assigned as the alternative trans isomer. We have next analysed the performance of 7 in the hydrogenation of 5a in the absence of a base. First, no reaction was observed in toluene, in accord with the literature precedent mentioned above. On the other hand, a reaction performed under 20 bar H2 in iPrOH and 60 °C with an S/C = 100 showed a complete conversion and 84% ee after 24 h. For comparison, a reaction prepared with 1e under the same reaction conditions but with addition of a small amount of KOtBu to guarantee catalyst activation (S/C/B = 100/1/5) provided 91% conversion and 83% ee. These results point to a common enantiodetermining step starting from 1e and KOtBu or 7 in isopropanol. These observations are analogous to those reported for the BINAP/DPEN system in the asymmetric hydrogenation of acetophenone.5b
In addition, we have examined the hydrogenation of 5g under our standard conditions with trans complex 1a, with the mixture of cis-1a and cis-1a′ isomers (resulting from isomerization of 1a) and with cis-1a (obtained by crystallization of the latter mixture). Full conversion and coincident enantioselectivities (94.2, 94.2 and 94.6% ee, respectively) were observed in the three reactions, pointing to the same catalyst formed independently of the stereochemistry of the catalyst precursor.
It is worth noting in this context that Bäckvall and coworkers reported the racemization of some enantiopure amines 6 in toluene at 110 °C using the Shvo catalyst and 0.5 equivalents of 2,4-dimethyl-3-pentanol, with the racemization rate being significantly reduced when the reaction temperature was lowered.22a Moreover, in the presence of a hydrogen acceptor, imines 5 could be obtained.22b Based on this background, it seems highly interesting to examine if the formation of amines 6 is irreversible in the present catalytic system. To this aim, the hydrogenation of 5g using 1a under standard reaction conditions was stopped at 25% conversion. This reaction showed a 93.4% ee, which is very close to the value obtained at full conversion (94.2% ee). In addition, a sample of rac-6g was exposed to catalytic reaction conditions for 24 h and neither a variation of the enantiomeric ratio nor imine were observed. To discard the idea that any impurity could inactivate the catalyst generated from 1a in the latter experiment, a complementary one using a mixture of 5g and rac-6g (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.4) was examined under the same reaction conditions. After 24 h, complete reduction of the imine was observed and determination of the enantioselectivity of 6g gave a value of 20.8% ee. For this experiment, a theoretical value of 21.2% ee can be estimated if the imine were hydrogenated with a 93% ee. These results therefore indicate that no reversibility of the reduction step should occur under the mild catalytic conditions used.
3.4) was examined under the same reaction conditions. After 24 h, complete reduction of the imine was observed and determination of the enantioselectivity of 6g gave a value of 20.8% ee. For this experiment, a theoretical value of 21.2% ee can be estimated if the imine were hydrogenated with a 93% ee. These results therefore indicate that no reversibility of the reduction step should occur under the mild catalytic conditions used.
Computational studies
We subsequently did computational studies to complement the experimental results via DFT-based methods.23 These comprise the structural and stereochemical features of complex 1a as well as the study of the mechanism of a representative imine hydrogenation reaction, with the aim of understanding the role of the atropisomerizable phosphite fragment and the high enantioselectivities observed. In addition, some studies regarding 1d and the corresponding dihydride will be included for comparative purposes. As mentioned, outer sphere reduction by Ru(H)2(diphosphine)(diamine) is a well-established step in the asymmetric hydrogenation of ketones in both protic and aprotic solvents.5 Moreover, due to the similarity between the Ru catalyzed hydrogenation of imines and ketones,1b some catalysts have been proposed to reduce imines enantioselectively following an outer sphere mechanism,4a,b,8 although no detailed computational study has been provided. In this regard, results of reactions performed with 1a and 7 in isopropanol point to an outer sphere reduction of 5a by Ru(H)2(2a)(3a) as the enantioselective step. Although the nature of the resting catalyst state in toluene and isopropanol should be different,5b it is reasonable to assume that this reduction mode should also operate in toluene.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 calculated ratio, which is in good agreement with the ratio of cis-1a and cis-1a′ species observed after the isomerization. Finally, c1R shows the same stereochemistry as that of the predominant cis isomer in solution (cis-1a), while the minor one (cis-1a′) should have the structure shown by c3S.
1 calculated ratio, which is in good agreement with the ratio of cis-1a and cis-1a′ species observed after the isomerization. Finally, c1R shows the same stereochemistry as that of the predominant cis isomer in solution (cis-1a), while the minor one (cis-1a′) should have the structure shown by c3S.
A remarkable result regards differences in energy between cis structures differing in the configuration of the phosphite stereogenic axis. Thus, low to negligible differences are observed between atropisomers of types cis-2 and cis-4, which contain the phosphite fragment coordinated in a cis position to one NH2 group. In contrast, there are considerable energy differences between atropisomers of types cis-1 and cis-3, characterized by a phosphite cis to both NH2 groups in an arrangement which favors the interaction between the biaryl phosphite and the diamine backbone. Most interestingly, the preferred biaryl configuration depends on that of the metal, with c1R and c3S being appreciably more stable than their respective atropisomers c1S and c3R, with free energy differences of 8.1 and 5.9 kcal mol−1, respectively.
Moreover, we have examined selected structures for complex 1d. Initially, examination of trans structures with the backbone orientation shown by X-ray analysis leads to a couple of diastereomers (ctR′ and ctS′) structurally very close to the experimental structures, with a minimal free energy difference between them (0.4 kcal mol−1). In addition, structures with a backbone orientation shown by 1i were also investigated. Notably, the corresponding trans diastereomers (ctR′′ and ctS′′) were appreciably more stable than ctR′ and ctS′, with free energy differences of 4.5 and 5.6 kcal mol−1, respectively. Among the four isomers, ctS′′ is the more stable one, with the ctR′′ isomer being 1.5 kcal mol−1 higher in free energy than the former species. Presumably, easy interconversion between the four conformers should occur in solution, while the observation of less stable conformers of 1d by X-ray crystallography should be caused by a better packing in the crystal lattice. On the other hand, a comparison between cis-1-R and cis-3-S type structures for 1d (c1R′ and c3S′, respectively) shows a higher stability for the former species (1.6 kcal mol−1 in free energy). However, these cis structures are slightly less stable than ctS′′, with free energy differences of 0.4 and 2.0 kcal mol−1, respectively. Therefore, the comparison of energies of isomers 1a and 1d indicates that the cis/trans preference in dichloro complexes is rather sensitive to the precise structure of the phosphine–phosphite ligand.
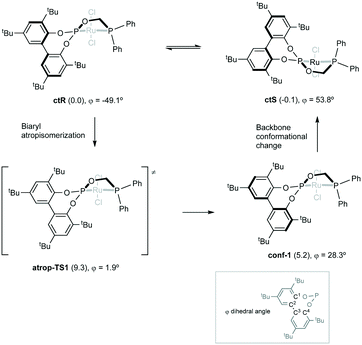
In addition, the atropisomerization of 1a has also been studied (Fig. 6). As mentioned, this dynamic process involves a conformational change not only in the biaryl moiety, but also in the backbone and in the position of the phosphine substituents. Starting from ctR, which is characterized by a biaryl dihedral angle (φ) of −49.1°, a scan of the reduction of this parameter allowed us to locate a transition state (atrop-TS1, φ = 1.9°) lying 9.3 kcal mol−1 in free energy above ctR. This transition state leads to an alternative conformer (conf-1, ΔG = 5.2 kcal mol−1) characterized by a value of 28.3° for φ, and thus displaying the Sax configuration. To complete the dynamic process to reach ctS, a pathway involving two additional transition states and two conformers has been found (see the ESI† for further details). Notably, the highest point along the whole atropisomerization pathway corresponds to atrop-TS1, in good agreement with the experimental value obtained by VT-NMR for the energy barrier of the fluxional process shown by 1a.
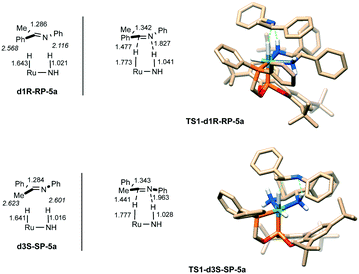
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N fragment to the corresponding Ru(H)–NH2 moiety. As mentioned above, the Ru–H distances in the computed structures indicate an appreciably longer distance for the hydride trans to the phosphite in comparison with that trans to the amino ligand in d1R (1.670 vs. 1.604 Å) and d3S (1.666 vs. 1.604 Å). Based on these considerations, we have reasonably assumed an easier transference of the hydride trans to the phosphite from either d1R or d3S to 5a, compared with that trans to the amine.
N fragment to the corresponding Ru(H)–NH2 moiety. As mentioned above, the Ru–H distances in the computed structures indicate an appreciably longer distance for the hydride trans to the phosphite in comparison with that trans to the amino ligand in d1R (1.670 vs. 1.604 Å) and d3S (1.666 vs. 1.604 Å). Based on these considerations, we have reasonably assumed an easier transference of the hydride trans to the phosphite from either d1R or d3S to 5a, compared with that trans to the amine.
Considering the presence of two NH2 groups in d1R (trans to phosphine or to hydride) and two prochiral faces of 5a, four different approaches of the imine can be considered (Fig. 8c), as well as in the case of d3S. It is worth noting that the approximation of the substrate to the dihydride leads to the formation of loose precomplexes. Among the eight precomplexes, significant stabilization over their components is observed in the cases of d1R-RP-5a and d3S-SP-5a, with ΔG values of −7.1 and −7.0 kcal mol−1, respectively. This stabilization can be ascribed to diverse substrate–ligand non-covalent interactions (NCI).26 For instance, in the case of d1R-RP-5a, C–H/aryl interactions,27 a high number of C–H/C–H dispersion interactions,28 and a N⋯H–N interaction between the imine nitrogen and a NH fragment of the diamine ligand have been detected (Fig. 9). This NCI driven stabilization is a remarkable aspect for an outer-sphere mechanism, as these weak interactions enable structural preorganization29 of the substrate–catalyst complex favoring the reduction.
 | ||
| Fig. 9 d1R-RP-5a (a). Plot of non-covalent interactions for the latter precomplex (b, color ranges from strong attractive interactions in blue to strong repulsive ones in red; distances between interacting atoms or centroids of aryl rings in Å).30 | ||
From imine–dihydride precomplexes, the hydride transfer step to give monohydride–amide ionic pair species was next investigated. This class of transition states will be referred in the following as TS1. Among the TS1 transition states for d1R and d3S (Fig. 10), the most favorable one corresponds to pro-R precomplex d1R-RP-5a (TS1-d1R-RP-5a, ΔΔG‡ = 0.0 kcal mol−1; in the following, this transition state will be used as the reference to compare energies of TS1 transition states). The most favorable TS1 for the S enantiomer (TS1-d3S-SP-5a) involves d3S dihydride and has a ΔΔG‡ value equal to 1.6 kcal mol−1 (see the ESI† for data on TS1 energies for the rest of the dihydride precomplexes). This is, moreover, the lowest TS1 transition state for d3S dihydride, followed by a pro-R one with ΔΔG‡ = 4.9 kcal mol−1. Despite TS1-d1R-RP-5a and TS1-d3S-SP-5a lying 6.2 and 7.8 kcal mol−1 in free energy above the corresponding dihydride imine precomplexes, they are very close in free energy to the starting dihydrides and free imine (−0.88 and 0.76 kcal mol−1 for TS1-d1R-RP-5a and TS1-d3S-SP-5a compared with d1R and free 5a, respectively), due to the stabilization associated with the formation of the dihydride imine precomplexes.
 | ||
| Fig. 10 General scheme for the reduction of imine 5a (ΔG relative to d1R + 5a in kcal mol−1 in brackets). | ||
Based on the literature precedents on the higher reactivity of trans dihydrides over cis ones5 and considering that trans-dihydrides have the longest Ru–H bond distances in the series of Ru(H)2(2a)(3a) dihydrides, it seems pertinent to study the barrier for the hydride transfer step for dtR and dtS. An inspection of these structures indicates that one of the hydride ligands is protected by a P–Ph and a tBu group from the approach of the imine (views for dtR collected in Fig. 11); therefore, participation of this hydride should only be possible after atropisomerization of the P–OP ligand (i.e. conversion of dtR in dtS and vice versa). Accordingly, only the transference of the less encumbered hydride needs to be examined for these dihydrides. As mentioned above for d1R and d3S, there are four possible imine approaches for both dtR and dtS, leading to eight precomplexes and corresponding TS1 transition states. For those leading to the R product, the ΔΔG‡ values range between 3.9 and 18.2 kcal mol−1, while for the pro-S ones, we found ΔΔG‡ values that range between 8.7 and 18.6 kcal mol−1. Presumably, steric effects associated with the bulky phosphite fragment in the equatorial plane should be responsible for the higher barriers observed for the trans-dihydrides. Likewise, an examination of the structures of dihydrides of types cis-2 and cis-4 indicates a substantial steric encumbrance around the hydride located in the trans coordination position to the phosphine ligand (i.e. that characterized by a longer Ru–H bond) because of the orientation of the biaryl phosphite, with the exception of d2S. For this dihydride, the corresponding set of four precomplexes was calculated, with d2S-RP-5a and d2S-RH-5a being already higher in free energy than TS1-d1R-RP-5a by 3.4 and 5.5 kcal mol−1, respectively. On the other hand, d2S-SH-5a is 2.8 kcal mol−1 over TS1-d3S-SP-5a, while d2S-SP-5a is only 0.8 kcal mol−1 more stable in free energy than the latter transition state, with TS1-d2S-SP-5a being 11.8 kcal mol−1 higher in free energy than TS1-d3S-SP-5a. Considering that TS1 possess the highest free energy in the reduction pathway of 5a by d1R and d3S (Fig. 10), the values of transition states of type TS1 for d2S, dtR and dtS point to cis-dihydrides d1R and d3S as the actual catalysts in the present system.
A remarkable feature of precomplexes d1R-RP-5a and d3S-SP-5a is that they show the substrate appropriately arranged for the hydride transfer step and a minimal structural variation from the precomplexes to the corresponding TS1 is required (Fig. 12). Moreover, TS1-d1R-RP-5a and TS1-d3S-SP-5a are stabilized by a hydrogen bond between the imine nitrogen and a N–H of the diamine, with N⋯H distances of 1.827 and 1.963 Å, respectively.31 On the other hand, the distances between the hydride and the iminic carbon have values of 1.477 and 1.441 Å, respectively. In addition, expected elongations of the Ru–H and the C–N imine bonds are observed from the imine adducts to TS1 structures. In both transition states, the substrate displays a similar orientation, with the iminic nitrogen interacting with the amino ligand located in a trans coordination position to the phosphine, while the pseudoaxial Ph phosphine and the C–Ph imine substituents point to opposite directions.
The hydride transfer step from TS1-d1R-RP-5a and TS1-d3S-SP-5a next leads to ion pairs ip-pro-R and ip-pro-S, respectively.32 These species are stabilized by a hydrogen bond, with N⋯H distances of 1.788 Å and 1.821 Å for ip-pro-R and ip-pro-S, respectively, as well as by an agostic interaction provided by the new C–H bond, with Ru–H distances of 2.031 Å and 2.033 Å, respectively. From the respective ion pair intermediates, a very easy proton transfer (TS2) viaTS2-pro-R and TS2-pro-S can take place, lying 1.3 and 0.4 kcal mol−1 above the corresponding ion-pairs, respectively. The proton transfer step leads to adducts formed by an amido complex and enantiomers of amine 6a (a1R-R-6a and a3S-S-6a, respectively). It is worth noting that this step also displays the completion of the hydride transfer step, as shown by a shortening of the corresponding C–H distance (e.g. from 1.201 Å in ip-pro-R to 1.119 Å in a1R-R-6a) with a concomitant lengthening of the C–N bond of the product (e.g. from 1.394 to 1.462 Å in the pro-R route). Complexes a1R-R-6a and a3S-S-6a are stabilized as well by a hydrogen bond between the amido ligand and 6a with N⋯H distances of 2.011 Å and 1.969 Å for a1R-R-6a and a3S-S-6a, respectively. The proton transfer step raises an important difference with the hydrogenation of acetophenone, as the deprotonation of the DPEN ligand by N-(phenyl)-1-phenylethylamide should be easier than that by 1-phenylethoxide, due to the higher basicity of the former. In addition, amido–amino complexes are significantly more stable than the parent ion pair species, with respective gains of free energy equal to 6.0 and 9.1 kcal mol−1 for a1R-R-6a and a3S-S-6a, respectively. It is worth noting in this context that the evolution of ionic pair species to the corresponding amido (or alkoxo complexes in ketone hydrogenation) is typically a very thermodynamically favorable step.5h,33 In the present case, amido complex N1R is 4.2 kcal mol−1 lower in free energy than ip-pro-R, although the magnitude of the stabilization is not as pronounced as reported for an N-(phenyl)phenylmethylamide compound.33 Thus, a1R-R-6a is 1.8 kcal mol−1 more stable than N1R in free energy.34
Hydrogen interaction with a1R-R-6a started with a sequence of steps for H2 coordination (Fig. 13). Approach of the H2 molecule to the amido complex shows a first transition state (TS3a) with Ru–H distances of 2.812 and 2.662 Å, while the H–H distance in the complex is 0.749 Å, indicating a minimal interaction with the metal center (0.744 Å computed for free hydrogen). From TS3a, the reaction sequence first produces a loose dihydrogen complex h1R-R-6a-l (d(Ru–H) = 2.106, 2.160 Å, d(H–H) = 0.779 Å) and then a tight one h1R-R-6a-t characterized by shorter Ru–H distances of 1.779 and 1.746 Å and a H–H distance of 0.839 Å, as well as the corresponding transition state between them (TS3b). It is worthy to note that both dihydrogen complexes as well as transition states along the pathway are stabilized by a hydrogen bond to (R)-6a. TS4a connects the tight H2 bound complex with a hydrogen bonded adduct between d1R and (R)-6a (d1R-R-6a). However, TS4a mainly shows proton transfer from (R)-6a to the complex to generate an ionic-pair type species along with incipient activation of the coordinated H2, assisted by deprotonated (R)-6a. Further activation of the coordinated H2 is easy and IRC analysis from TS4a leads to d1R-R-6a in the product direction. It is worthy to note that the free energy of TS4a is only 1.8 kcal mol−1 above that of h1R-R-6a-t, indicating that ionization induced by the proton transfer step enables very easy hydrogen activation. Notwithstanding that, this is the step with the highest barrier in the coordination-activation of H2 by a1R-R-6a.
 | ||
| Fig. 13 Hydrogen activation by a1R-R-6a (ΔG and ΔE values in kcal mol−1 referenced to a1R + (R)-6a + H2, bond distances in Å). | ||
Analysis of H2 coordination to ip-pro-R led to a high energy transition state (TS3c, ΔG‡ = 16.4 kcal mol−1, Fig. 14). It seems that separation in toluene of the tightly bonded ionic components of the pair due to the uncompleted hydride transfer and the agostic interaction has a considerable energetic cost. TS3c shows a dissimilar interaction between Ru and both atoms of the H2 molecule, with Ru–H distances of 2.161 and 2.548 Å, while the H–H distance (0.761 Å) indicates the scarce activation of dihydrogen. In addition, the N–H distances reflect the ionic-pair character of TS3c. Based on the comments made above, one might expect that H2 is quite ready to be activated from TS3c and indeed, an IRC analysis from this transition state directly leads in the product direction to a hydrogen bonded adduct between (R)-6a and d1R, which differs from d1R-R-6a in the orientation of the amine.
 | ||
| Fig. 14 General scheme for the hydrogen activation pathways. ΔG values in brackets in kcal mol−1 referred to a1R + (R)-6a + H2. | ||
A third possible H2 activation pathway corresponds to non-assisted activation by amido complex a1R. Examination of the coordination of the hydrogen molecule to the a1R complex displayed an analogous pathway to that described for a1R-R-6a, with loose and tight H2 complexes and corresponding transition states (see the ESI† for further details). Activation of the coordinated hydrogen in the tight complex h1R-t leads to TS4b (ΔG‡ = 16.6 kcal mol−1) and then to d1R. It is worthy to note that most of the energetic cost of the hydrogen activation process corresponds to the coordination of the H2 molecule, since reaching the h1R-t species has an energetic cost of 12.1 kcal mol−1 with respect to a1R and H2, while the subsequent step (TS4b) has a low relative ΔG‡ value (4.5 kcal mol−1) with respect to h1R-t. The comparison between the activation schemes by a1R-R-6a and a1R indicates hydrogen bond stabilization from (R)-6a along the pathway in the first case, leading to a more favorable hydrogen activation route. Moreover, loose interaction between a1R and (R)-6a in a1R-R-6a compared with ionic fragments in ip-pro-R enables easier H2 coordination. Finally, an analysis of the reaction profile using the energetic span model35 indicates that the turnover determining intermediate (TDI) is a1R-R-6a, while the turnover determining transition state (TDTS) is TS4a, with an energetic span (δE) of 17.5 kcal mol−1, which is an affordable free energy barrier at room temperature.
Although the results described above point to hydrogen activation as the turnover-limiting step, it should be noticed that the determination of the lowest hydrogen activation route in the present system is an exceedingly difficult task. For instance, a1R-R-6a should easily exchange amine with its S enantiomer. In addition, hydrogen bond interaction between 6a and the amido complex generates a stereogenic center at nitrogen for which two configurations are possible resulting from easy nitrogen inversion in 6a. In addition, proton transfer between amido and amino fragments of the DPEN ligand assisted by 6a should also be a feasible step. As already mentioned, easy atropisomerization of the biaryl fragment in pentacoordinate amido complexes is an additional variable to consider. Recalling, finally, the fluxional nature described for RuH(NHCMe2CMe2NH2)(PPh3)25a and considering the existence of several amido–hydride complexes in a narrow interval of energy (Fig. 7), isomerization of a1R may be an additional factor to consider.
There is extensive information in the literature about fluxionality and isomerization of ruthenium dihydrides.37 Particularly relevant in this context, Morris has studied in detail the behavior of complex A, observing the isomerization between trans,cis and cis,cis isomers (with the latter being more stable),5c pointing to a non-dissociative trigonal twist mechanism for the exchange.38 Due to the complexity introduced by the atropisomerization of the phosphine–phosphite ligand, we have not investigated the exchange between d1R and d3S, but considering that coincident enantioselectivities were obtained independent of the stereochemistry of Ru(Cl)2(2a)(3a), such an exchange may also be operative in the present system. Following this assumption, the value of ΔΔG‡ of 1.6 kcal mol−1 between TS1-d1R-RP-5a and TS1-d3S-SP-5a gives an estimation of 88% ee for the enantioselectivity, while the value of ΔΔE‡ of 1.9 kcal mol−1 corresponds to 92% ee. Using a more extended basis set (def2QZVP for Ru and 6-311++g(2d,p) for main group atoms), a value of ΔΔE‡ equal to 1.9 kcal mol−1 was obtained (91% ee). These values therefore show a good agreement with the experimental value of 94% ee. A remarkable difference between these transition states regards metal configuration.39 Thus, in the case of d1R, there is a matched combination of diamine and metal configurations which enables a better fitting of the substrate in the pocket generated by the dihydride, therefore allowing a shorter N(imine)⋯HN hydrogen bond40 in TS1-d1R-RP-5a than in TS1-d3S-SP-5a.
Despite the different backbones in dihydrides Ru(H)2(2a)(3a) and Ru(H)2(2c)(3a), a comparison between isomers of each type (i.e.d1R, d3S, dtR and dtS with d1R′, d1S′, dtR′′ and dtS′′, respectively) shows rather coincident structures. In addition, from the Ru–H distances of the Ru(H)2(2c)(3a) complexes, a comparable reactivity between cis and trans dihydrides can be expected. Based on these considerations, a pathway involving cis-dihydrides seems also plausible for catalysts with a phenylene backbone. However, as the stabilization of imine–dihydride precomplexes and corresponding TS1 depend on a precise substrate–complex recognition, this possibility cannot be ascertained without a detailed analysis of all possible pathways, which is further complicated by the conformational properties of the phosphine–phosphite ligand.
Conclusions
Complexes 1 have selectively been obtained as trans isomers by subsequent treatment of RuCl2(PPh3)3 with P–OP and N–N ligands. In the case of 1a, a clean trans to cis isomerization has been observed by heating in EtOH. DFT calculations performed with Ru(Cl)2(2a)(3a) reproduce the higher stability of the cis isomers over the trans isomers as well as the low energy difference between atropisomers of trans-1a observed experimentally. Moreover, a strong bias on biaryl configuration caused by metal and diamine chirality is observed in cis-1 and cis-3 type isomers. Complexes 1 are effective catalyst precursors for the enantioselective hydrogenation of N-aryl imines 5 under very mild conditions with satisfactory enantioselectivities (84–96% ee, 16 examples). The catalyst performance is also suitable for multigram hydrogenation as shown in the case of the synthesis of 6h. Complex Ru(H)(BH4)(2c)(3b) hydrogenates 5a in iPrOH without the need of an additional base, giving nearly coincident enantioselectivity with 1e in iPrOH using 5 equiv. of base, pointing to a common enantiodetermining step in both reactions. Likewise, the enantioselectivity in the hydrogenation of 5g under standard conditions did not depend on the stereochemistry of starting Ru(Cl)2(2a)(3a), while additional experiments pointed to the irreversible reduction of this substrate.In addition, the mechanism of the reduction of 5a by Ru(H)2(2a)(3a) has been calculated by DFT methods. Results obtained from the latter are in accord with a stepwise reduction of the imine,41 with the hydride transfer being enantiodetermining, while the pro-R and the pro-S routes are generated by d1R and d3S dihydrides, respectively. Calculations rationalize the configuration of the preferred product enantiomer and show a good agreement with experimental enantioselectivity. From the examination of several hydrogen activation pathways, the most favourable one is initiated by hydrogen coordination to hydrogen bonded adduct a1R-R-6a, followed by activation of the η2-H2 assisted by the amine. In the latter, proton transference from the amine to the amido ligand, leading to an ion pair species, has been observed before an easy hydrogen activation step.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Spanish Ministry of Science and Innovation (projects CTQ2016-75193-P; AEI/FEDER, UE, RED2018-102387-T, PID2019-110856GA-I00 and PGC2018-100818-A-I00). The Mass Spectrometry Service of the Universidad de Sevilla (CITIUS) is acknowledged for technical assistance as well as the Supercomputing Center of Galicia (CESGA) for the access to computing facilities. Dr. Joaquín López-Serrano is also gratefully acknowledged for providing valuable comments. A. C.-V. also thanks the Spanish MEC and the European Social Fund (Ramón y Cajal Fellowship: RyC-2016-19930). We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI). This work is dedicated to Prof. Antonio Otero on the occasion of his retirement.Notes and references
- For reviews on this topic, see: (a) R. Noyori and T. Ohkuma, Angew. Chem., Int. Ed., 2001, 40, 40 CrossRef CAS; (b) S. E. Clapham, A. Hadzovic and R. H. Morris, Coord. Chem. Rev., 2004, 248, 2201 CrossRef CAS; (c) M. Ito and T. Ikariya, Chem. Commun., 2007, 5134 RSC.
- (a) T. Ohkuma, H. Ooka, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1995, 117, 10417 CrossRef CAS; (b) T. Ohkuma, H. Ooka, S. Hashiguchi, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1995, 117, 2675 CrossRef CAS; (c) H. Doucet, T. Ohkuma, K. Murata, T. Yokozawa, M. Kozawa, E. Katayama, A. F. England, T. Ikariya and R. Noyori, Angew. Chem., Int. Ed., 1998, 37, 1703 CrossRef CAS; (d) T. Ohkuma, M. Koizumi, H. Doucet, T. Pham, M. Kozawa, K. Murata, E. Katayama, T. Yokozawa, T. Ikariya and R. Noyori, J. Am. Chem. Soc., 1998, 120, 13529 CrossRef CAS; (e) T. Ohkuma, D. Ishii, H. Takeno and R. Noyori, J. Am. Chem. Soc., 2000, 122, 6510 CrossRef CAS; (f) T. Ohkuma, C. A. Sandoval, R. Srinivasan, Q. Lin, Y. Wei, K. Muñiz and R. Noyori, J. Am. Chem. Soc., 2005, 127, 8288 CrossRef CAS.
- (a) V. F. Kuznetsov, G. P. A. Yap and H. Alper, Organometallics, 2001, 20, 1300 CrossRef CAS; (b) Y. Xu, N. W. Alcock, G. J. Clarkson, G. Docherty, G. Woodward and M. Wills, Org. Lett., 2004, 6, 4105 CrossRef CAS; (c) R. Guo, C. Elpelt, X. Chen, D. Song and R. H. Morris, Chem. Commun., 2005, 3050 RSC; (d) Q. Jing, X. Zhang, J. Sun and K. Ding, Adv. Synth. Catal., 2005, 347, 1193 CrossRef CAS; (e) W. Li, X. Sun, L. Zhou and G. Hou, J. Org. Chem., 2009, 74, 1397 CrossRef CAS; (f) Y. Li, K. Ding and C. A. Sandoval, Org. Lett., 2009, 11, 907 CrossRef CAS; (g) B. Stegink, L. van Boxtel, L. Lefort, A. J. Minnaard, B. L. Feringa and J. G. de Vries, Adv. Synth. Catal., 2010, 352, 2621 CrossRef CAS; (h) Q. Zhu, D. Shi, C. Xia and H. Huang, Chem. – Eur. J., 2011, 17, 7760 CrossRef CAS; (i) K. Matsumura, N. Arai, K. Hori, T. Saito, N. Sayo and T. Ohkuma, J. Am. Chem. Soc., 2011, 133, 10696 CrossRef CAS.
- (a) K. Abdur-Rashid, A. J. Lough and R. H. Morris, Organometallics, 2000, 19, 2655 CrossRef CAS; (b) C. J. Cobley and J. P. Henschke, Adv. Synth. Catal., 2003, 345, 195 CrossRef CAS; (c) K. Abdur-Rashid, R. Guo, A. J. Lough, R. H. Morris and D. Song, Adv. Synth. Catal., 2005, 347, 571 CrossRef CAS; (d) J.-H. Xie, Z.-T. Zhou, W.-L. Kong and Q.-L. Zhou, J. Am. Chem. Soc., 2007, 129, 1868 CrossRef CAS; (e) T. Li, I. Bergner, F. N. Haque, M. Z. De Iuliis, D. Song and R. H. Morris, Organometallics, 2007, 26, 5940 CrossRef CAS; (f) J. M. John and S. H. Bergens, Angew. Chem., Int. Ed., 2011, 50, 10377 CrossRef CAS.
- (a) K. Abdur-Rashid, S. E. Clapham, A. Hadzovic, J. N. Harvey, A. J. Lough and R. H. Morris, J. Am. Chem. Soc., 2002, 124, 15104 CrossRef CAS; (b) C. A. Sandoval, T. Ohkuma, K. Muñiz and R. Noyori, J. Am. Chem. Soc., 2003, 125, 13490 CrossRef CAS; (c) R. Abbel, K. Abdur-Rashid, M. Faatz, A. Hadzovic, A. J. Lough and R. H. Morris, J. Am. Chem. Soc., 2005, 127, 1870 CrossRef CAS; (d) A. Hadzovic, D. Song, C. M. MacLaughlin and R. H. Morris, Organometallics, 2007, 26, 5987 CrossRef CAS; (e) M. Z.-D. Iuliis and R. H. Morris, J. Am. Chem. Soc., 2009, 131, 11263 CrossRef; (f) A. Comas-Vives, G. Ujaque and A. Lledós, Inner- and Outer-Sphere Hydrogenation Mechanisms: A Computational Perspective, Elsevier Masson SAS, 2010, vol. 62 Search PubMed; (g) F. Hasanayn and R. H. Morris, Inorg. Chem., 2012, 51, 10808 CrossRef CAS; (h) P. A. Dub, N. J. Henson, R. L. Martin and J. C. Gordon, J. Am. Chem. Soc., 2014, 136, 3505 CrossRef CAS; (i) P. A. Dub and J. C. Gordon, Dalton Trans., 2016, 45, 6756 RSC.
- P. A. Dub and J. C. Gordon, ACS Catal., 2017, 7, 6635 CrossRef CAS.
- (a) D. S. Zerla, I. Rimoldi, E. Cesarotti, G. Facchetti, M. Pellizzoni and M. Fusè, J. Organomet. Chem., 2014, 771, 2 CrossRef CAS; (b) T. Cruchter and V. A. Larionov, Coord. Chem. Rev., 2018, 376, 95 CrossRef CAS.
- N. Arai, N. Utsumi, Y. Matsumoto, K. Murata, K. Tsutsumi and T. Ohkuma, Adv. Synth. Catal., 2012, 354, 2089 CrossRef CAS.
- (a) W. Baratta, G. Chelucci, E. Herdtweck, S. Magnolia, K. Siega and P. Rigo, Angew. Chem., Int. Ed., 2007, 46, 7651 CrossRef CAS; (b) F. Chen, D. He, L. Chen, X. Chang, D. Z. Wang, C. Xu and X. Xing, ACS Catal., 2019, 9, 5562 CrossRef CAS.
- (a) M. Vaquero, A. Suárez, S. Vargas, G. Bottari, E. Álvarez and A. Pizzano, Chem. – Eur. J., 2012, 18, 15586 CrossRef CAS; (b) P. Kleman, M. Vaquero, I. Arribas, A. Suárez, E. Álvarez and A. Pizzano, Tetrahedron: Asymmetry, 2014, 25, 744 CrossRef CAS.
- For examples of catalysts containing atropisomerizable phosphites, see: (a) G. J. H. Buisman, M. E. Martin, E. J. Vos, A. Klootwijk, P. C. J. Kamer and P. W. N. M. van Leeuwen, Tetrahedron: Asymmetry, 1995, 6, 719 CrossRef CAS; (b) S. Deerenberg, H. S. Schrekker, G. P. F. Van Strijdonck, P. C. J. Kamer, P. W. N. M. Van Leeuwen, J. Fraanje and K. Goubitz, J. Org. Chem., 2000, 65, 4810 CrossRef CAS; (c) S. Deerenberg, O. Pàmies, M. Diéguez, C. Claver, P. C. J. Kamer and P. W. N. M. Van Leeuwen, J. Org. Chem., 2001, 66, 7626 CrossRef CAS; (d) J. Mazuela, J. J. Verendel, M. Coll, B. Schäffner, A. Börner, P. G. Andersson, O. Pàmies and M. Diéguez, J. Am. Chem. Soc., 2009, 131, 12344 CrossRef CAS.
- (a) K. Mikami, T. Korenaga, M. Terada, T. Ohkuma, T. Pham and R. Noyori, Angew. Chem., Int. Ed., 1999, 38, 495 CrossRef CAS; (b) K. Aikawa and K. Mikami, Angew. Chem., Int. Ed., 2003, 42, 5455 CrossRef CAS; (c) K. Akiyama, K. Wakabayashi and K. Mikami, Adv. Synth. Catal., 2005, 347, 1569 CrossRef CAS; (d) K. Mikami, H. Kakuno and K. Aikawa, Angew. Chem., Int. Ed., 2005, 44, 7257 CrossRef CAS; (e) K. Mikami, K. Wakabayashi and K. Aikawa, Org. Lett., 2006, 8, 1517 CrossRef CAS; (f) K. Mikami, K. Wakabayashi, Y. Yusa and K. Aikawa, Chem. Commun., 2006, 2365 RSC; (g) K. Wakabayashi, K. Aikawa, S. Kawauchi and K. Mikami, J. Am. Chem. Soc., 2008, 130, 5012 CrossRef CAS.
- For other examples of Ru complexes crystallized as mixture of diastereomers, see: (a) H. Brunner, M. Weber, M. Zabel and T. Zwack, Angew. Chem., Int. Ed., 2003, 42, 1859 CrossRef CAS; (b) H. Brunner, T. Tsuno, M. Bodensteiner, S. Gärtner, C. Miyahara, S. Ito, T. Kurosawa and K. Koyama, Eur. J. Inorg. Chem., 2016, 2016, 5405 CrossRef CAS.
- For other examples, see: (a) M. D. Fryzuk, C. D. Montgomery and S. J. Rettig, Organometallics, 1991, 10, 467 CrossRef CAS; (b) P. Crochet, J. Gimeno, S. García-Granda and J. Borge, Organometallics, 2001, 20, 4369 CrossRef CAS.
- (a) R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384 CrossRef CAS; (b) J. Reedijk, Chem. Soc. Rev., 2013, 42, 1776 RSC.
- For other examples of phosphite complexes exhibiting fast atropisomerization, see: (a) G. J. H. Buisman, L. A. van der Veen, A. Klootwijk, W. G. J. de Lange, P. C. J. Kamer, P. W. N. M. van Leeuwen and D. Vogt, Organometallics, 1997, 16, 2929 CrossRef CAS; (b) S. Deerenberg, P. C. J. Kamer and P. W. N. M. Van Leeuwen, Organometallics, 2000, 19, 2065 CrossRef CAS; (c) A. Suarez, A. Pizzano, I. Fernandez and N. Khiar, Tetrahedron: Asymmetry, 2001, 12, 633 CrossRef CAS; (d) M. Rubio, A. Suarez, D. D. Río, A. Galindo, E. Álvarez and A. Pizzano, Organometallics, 2009, 28, 547 CrossRef CAS; (e) M. Jouffroy, D. Sémeril, D. Armspach and D. Matt, Eur. J. Org. Chem., 2013, 6069 CrossRef CAS.
- E. de Julián, E. Menéndez-Pedregal, M. Claros, M. Vaquero, J. Díez, E. Lastra, P. Gamasa and A. Pizzano, Org. Chem. Front., 2018, 5, 841 RSC.
- A. Chelouan, R. Recio, L. G. Borrego, E. Álvarez, N. Khiar and I. Fernández, Org. Lett., 2016, 18, 3258 CrossRef CAS.
- (a) T. Ohkuma, M. Koizumi, K. Muñiz, G. Hilt, C. Kabuto and R. Noyori, J. Am. Chem. Soc., 2002, 124, 6508 CrossRef CAS; (b) C. A. Sandoval, Y. Yamaguchi, T. Ohkuma, K. Kato and R. Noyori, Magn. Reson. Chem., 2006, 44, 66 CrossRef CAS.
- For other hydride–borohydride ruthenium complexes, see: (a) R. Guo, R. H. Morris and D. Song, J. Am. Chem. Soc., 2004, 127, 516 CrossRef; (b) R. Guo, X. Chen, C. Elpelt, D. Song and R. H. Morris, Org. Lett., 2005, 7, 1757 CrossRef CAS.
- The synthesis of dihydrides of formula RuH2(2)(3a) was attempted using procedures described in the literature for the synthesis of ruthenium hydrides (e.g. treatment with H2 in the presence of a base or reaction with hydride reagents), obtaining complex reaction mixtures in all cases. Moreover, attempts to access chlorohydrides RuH(Cl)(2)(3a) failed as well due to phosphite decomposition under reaction conditions in the reaction of RuH(Cl)(PPh3)3 (ref. 3c) with phosphine–phosphite ligands.
- (a) O. Pàmies, A. H. Éll, J. S. M. Samec, N. Hermanns and J. E. Bäckvall, Tetrahedron Lett., 2002, 43, 4699 CrossRef; (b) A. H. Ell, J. S. M. Samec, C. Brasse and J.-E. Backvall, Chem. Commun., 2002, 1144 RSC.
- Calculations were performed with the Gaussian 09 program, using the B3PW91 functional, with the SDD basis set for Ru and 6-31g(d,p) for main group atoms, including D3 dispersion corrections and the use of the SMD continuum solvent model. For the latter, toluene was used for all calculations as it is the solvent used in the catalytic reactions (see the ESI† for further details).
- It should be recalled that two different mechanistic pathways have been proposed to explain the dependence of the concentration of base in the asymmetric hydrogenation of ketones (ref. 5h). In reactions prepared without an added base or with a low concentration of base, ketone reduction by Ru(H)2(diphosphine)(diamine) is proposed. In contrast, under high base concentration, alkaline dihydride–amidate complexes resulting from deprotonation of the diamine ligand are proposed as the key reductive species. Considering the low amount of base used in the present reactions, we have assumed that the neutral dihydride Ru(H)2(2a)(3a) should be the reducing species in reactions performed with 1a in toluene.
- (a) T. G. Appleton, H. C. Clark and L. E. Manzer, Coord. Chem. Rev., 1973, 10, 335 CrossRef CAS; (b) B. J. Coe and S. J. Glenwright, Coord. Chem. Rev., 2000, 203, 5 CrossRef CAS.
- For studies considering non-covalent interactions in Noyori type catalysts, see: (a) C. A. Sandoval, Q. Shi, S. Liu and R. Noyori, Chem. – Asian J., 2009, 4, 1221 CrossRef CAS; (b) R. Feng, A. Xiao, X. Zhang, Y. Tang and M. Lei, Dalton Trans., 2013, 42, 2130 RSC.
- A. J. Neel, M. J. Hilton, M. S. Sigman and F. D. Toste, Nature, 2017, 543, 637 CrossRef CAS.
- For studies illustrating the importance of dispersion interactions in metal catalyzed reactions, see: (a) E. Lyngvi, I. A. Sanhueza and F. Schoenebeck, Organometallics, 2015, 34, 805 CrossRef CAS; (b) A. A. Thomas, K. Speck, I. Kevlishvili, Z. Lu, P. Liu and S. L. Buchwald, J. Am. Chem. Soc., 2018, 140, 13976 CrossRef CAS; (c) F. H. Zhang, F. J. Zhang, M. L. Li, J. H. Xie and Q. L. Zhou, Nat. Catal., 2020, 3, 621 CrossRef CAS.
- P. Dydio and J. N. H. Reek, Chem. Sci., 2014, 5, 2135 RSC.
- Graphical representation of NCI interactions performed with Multiwfn software: T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS.
- In this context, it should be mentioned that a key element in the catalytic transfer hydrogenation of imines by the Shvo catalyst is substrate activation by hydrogen bonding: (a) J. S. M. Samec, A. H. Ell and J. E. Backvall, Chem. Commun., 2004, 2748 RSC; (b) C. P. Casey, G. A. Bikzhanova, Q. Cui and I. A. Guzei, J. Am. Chem. Soc., 2005, 127, 14062 CrossRef CAS; (c) J. B. Aberg, J. S. M. Samec and J. E. Backvall, Chem. Commun., 2006, 2771 RSC; (d) C. P. Casey, T. B. Clark and I. A. Guzei, J. Am. Chem. Soc., 2007, 129, 11821 CrossRef CAS; (e) A. Comas-Vives, G. Ujaque and A. Lledós, Organometallics, 2007, 26, 4135 CrossRef CAS; (f) A. Comas-Vives, G. Ujaque and A. Lledós, Organometallics, 2008, 27, 4854 CrossRef CAS.
- A detailed analysis of the hydride transfer step shows the participation of intermediate ion pair species ag-pro-R and ag-pro-S, respectively, with Ru–H distances of 1.903 and 1.899 Å, respectively, while the C–H ones amount to 1.228 and 1.223 Å, respectively, displaying an uncompleted hydride transfer (see the ESI† for details).
- M. Hernández-Juárez, J. López-Serrano, P. Lara, J. P. Morales-Cerón, M. Vaquero, E. Álvarez, V. Salazar and A. Suárez, Chem. – Eur. J., 2015, 21, 7540 CrossRef.
- A considerable effort has been dedicated to find TS connecting ip-pro-R and N1R without success. From data obtained from reaction scan, a barrier of ΔE‡ = 6.4 kcal mol-1 and ΔG‡ = 4.0 kcal mol-1 over ip-pro-R could be estimated (see the ESI† for details).
- (a) S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101 CrossRef CAS; (b) A. Uhe, S. Kozuch and S. Shaik, J. Comput. Chem., 2011, 32, 978 CrossRef CAS.
- For examples of reactions in which the enantiodetermining step is followed by a turnover determining one, see: (a) J. T. Issenhuth, F. P. Notter, S. Dagorne, A. Dedieu and S. Bellemin-Laponnaz, Eur. J. Inorg. Chem., 2010, 529 CrossRef CAS; (b) J. S. Bandar, M. T. Pirnot and S. L. Buchwald, J. Am. Chem. Soc., 2015, 137, 14812 CrossRef CAS.
- (a) D. H. Gerlach, W. G. Peet and E. L. Muetterties, J. Am. Chem. Soc., 1972, 94, 4545 CrossRef CAS; (b) P. Meakin, E. L. Muetterties and J. P. Jesson, J. Am. Chem. Soc., 1973, 95, 75 CrossRef CAS; (c) D. G. Gusev and H. Berke, Chem. Ber., 1996, 129, 1143 CrossRef CAS; (d) J. A. Ayllón, C. Gervaux, S. Sabo-Etienne and B. Chaudret, Organometallics, 1997, 16, 2000 CrossRef; (e) C. Soubra, Y. Oishi, T. A. Albright and H. Fujimoto, Inorg. Chem., 2001, 40, 620 CrossRef CAS; (f) D. Schott, C. J. Sleigh, J. P. Lowe, S. B. Duckett, R. J. Mawby and M. G. Partridge, Inorg. Chem., 2002, 41, 2960 CrossRef CAS.
- (a) A. Rodger and B. F. G. Johnson, Inorg. Chem., 1988, 27, 3061 CrossRef CAS; (b) S. Li and M. B. Hall, Organometallics, 1999, 18, 5682 CrossRef CAS.
- An analogous reaction scheme with cis dihydrides differing in metal configuration leading to opposite product enantiomers has been previously proposed by Morris5c to explain low enantioselectivities observed in the stoichiometric hydrogenation of acetophenone with a mixture of Δ-cis,cis and Λ-cis,cis-A dihydrides.
- For other examples of transition states in bifunctional catalysis stabilized by hydrogen bonds, see: (a) J. F. Sonnenberg, K. Y. Wan, P. E. Sues and R. H. Morris, ACS Catal., 2017, 7, 316 CrossRef CAS; (b) C. S. G. Seo, T. Tannoux, S. A. M. Smith, A. J. Lough and R. H. Morris, J. Org. Chem., 2019, 84, 12040 CrossRef CAS.
- For concerted imine reduction pathways, see: (a) M. Yamakawa, H. Ito and R. Noyori, J. Am. Chem. Soc., 2000, 122, 1466 CrossRef CAS; (b) Ref. 4e.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details of the synthesis and characterization of Ru complexes and procedures for asymmetric hydrogenation reactions. X-ray crystallographic data for 1a, 1c, 1i and cis-1a and computational details. CCDC 2045798 (1a), 2045799 (1c), 2045800 (1i), 2045801 and 2045802 (cis-1a). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0cy02390f |
| ‡ Present address: Nanyang Technological University, Singapore. |
| This journal is © The Royal Society of Chemistry 2021 |