Open Access Article
Open Access ArticleRevealing the electronic properties of the B–B bond: the bis-catecholato diboron molecule†
D.
Toffoli
 a,
C.
Grazioli
a,
C.
Grazioli
 b,
M.
Monti
b,
M.
Monti
 a,
M.
Stener
a,
M.
Stener
 a,
R.
Totani
a,
R.
Totani
 c,
R.
Richter
c,
R.
Richter
 d,
L.
Schio
d,
L.
Schio
 b,
G.
Fronzoni
b,
G.
Fronzoni
 *a and
A.
Cossaro
*a and
A.
Cossaro
 *ab
*ab
aDepartment of Chemical and Pharmaceutical Sciences, University of Trieste, 34127 Trieste, Italy. E-mail: fronzoni@units.it; acossaro@units.it
bIOM-CNR, Istituto Officina dei Materiali-CNR, S.S.14, Km 163.5, 34149 Trieste, Italy
cISM-CNR, Istituto di Struttura della Materia, LD2 Unit, 34149 Trieste, Italy
dElettra-Sincrotrone Trieste, 34149 Basovizza, Trieste, Italy
First published on 28th September 2021
Abstract
The electronic properties of a diboron molecule, namely bis(catecholato)diboron (2-(1,3,2-benzodioxaborol-2-yl)-1,3,2-benzodioxaborole) (B2Cat2), have been studied by comparing the results of photoemission (XPS) and near edge X-ray absorption spectroscopy (NEXAFS) experiments with the outcome of DFT calculations. The B 1s, C 1s and O 1s K-edges have been investigated for both the isolated gas phase molecule and the adsorbed one on the Au(111) surface. The main features of the polarized NEXAFS spectra at each of the three edges considered are not significantly affected by the presence of the substrate, with respect to the isolated molecule, indicating that the molecule–gold interaction is weak. Moreover, the comparison between the observed dichroism in the NEXAFS spectra of the adsorbed B2Cat2 and that in the NEXAFS spectra of the isolated molecule has confirmed the orbital symmetry assigned in the gas phase absorption spectra. The transitions to π(B–B) bonding and π*(B–B) anti-bonding final states represent the most relevant probe of the chemistry of the B2Cat2 molecule. We show that their theoretical description requires that the treatment of the relaxation changes among different excited state configurations, which we successfully implemented by using ΔSCF-DFT (ΔSCF) calculations.
Introduction
Since the last two decades organo-boron chemistry has been playing an emerging role in the development of novel green and sustainable organic-based technologies.1–3 This promotes the research of convenient synthetic routes for the production of boron compounds. Among the investigated strategies, both metal-catalyzed and metal-free synthetic processes involving diboron(4) compounds as the reactants represent the most promising tool for the synthesis of molecules containing B–C bonds.4 The properties of the B–B bond of these molecules is the key factor in the synthesis reactions. While being thermodynamically stable,5 its Lewis acid character favors its activation upon interaction with bases.4,6 The resulting adducts are precursors of the B–B bond cleavage for the formation of boron compounds.7–11 Besides its employment in synthesis processes, due to this strong affinity with bases, diboron(4) compounds may be of potential interest as building blocks in the 2D supramolecular assembly on surfaces as well. The introduction of functionalities on surfaces allows tailoring of intermolecular recognition processes and design of specific interaction schemes.12–14 To our knowledge, and quite surprisingly, the use of diboron molecules to this aim and, in general, the study of the chemistry of the B–B bond on surfaces is mostly unexplored yet. We have recently reported on the on-surface synthesis of a 2D covalent framework supported by the Au(111) surface, formed by a network of B–B bonded boroxine groups,15 which exhibits delocalized electronic states in the valence band, likely due to hybridization of the outer electronic states of the framework with the substrate. A proper description of the electronic properties of diboron systems on surfaces is mandatory for both exploring their use in synthesis processes catalyzed by the surface and describing the functionalities of 2D architectures they may be part of bis(catecholato)diboron (2-(1,3,2-benzodioxaborol-2-yl)-1,3,2-benzodioxaborole, B2Cat2 in the following) (see Fig. 1) is, together with bis(pinacolato)diboron, among the most frequently adopted diboron precursors in the synthesis of boronic compounds. It is a relatively simple molecule we selected as a prototype of diboron species and we present here a combined theoretical and experimental study of its electronic properties by comparing photoemission (XPS) and near edge X-ray absorption spectroscopy (NEXAFS) with DFT calculations. Experiments have been performed both for the isolated molecule in the gas phase and on a poorly reactive surface like Au(111) to evidence dichroic effects in the absorption. Dichroic effects on the Au(111) surface have been studied by measuring NEXAFS spectra in p-polarization (p-pol), i.e. with the light electric field plane perpendicular to the metal surface, and in s-polarization (s-pol), i.e. with the light electric field plane parallel to the metal surface.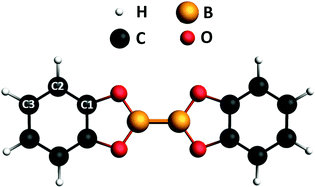 | ||
| Fig. 1 Chemical structure of B2Cat2. The labels indicate the nonequivalent carbon atoms. The molecular plane corresponds to the xy plane, with the direction of the B–B bond along the x axis. | ||
From a general perspective, the theoretical description of B 1s core excitations of boronic- and B–B containing systems is a challenging task, as static correlation effects between different excited states need to be taken into account.16 This can be done using wave function based approaches, which becomes however prohibitively expensive when the size of the system increases, as in the case of the B2Cat2 molecule. Therefore, it is necessary to search for an alternative, less expensive method to calculate the B 1s core excited states. In the ΔSCF-DFT (ΔSCF) method, based on the energy difference between two self-consistent-field (SCF) calculations, the core excited state is found by promoting an electron from the core orbital to one of the unoccupied orbitals in the ground state. The MOs are then re-optimized for each excited electron configuration and a different set of MOs for each excited state is obtained. Relaxation changes among different excited-state configurations relative to the same core hole are therefore taken into account at the ΔSCF level, while they are not considered at the DFT level employing transition potential (TP) approximation17,18 (DFT-TP), which employs the same fixed set of orbitals obtained from a single TP calculation to describe the entire excited state manifold.
We show here how the ΔSCF calculations better reproduce the B K-edge NEXAFS experimental spectrum with respect to both DFT-TP and time-dependent DFT (TDDFT). We give a detailed description of the transitions corresponding to the peaks of the NEXAFS O, B and C K-edges and to the geometry of the related molecular orbitals.
Theoretical methods and computational details
The ground-state equilibrium geometry of B2Cat2 was computed at the density functional theory (DFT)19 level, employing the hybrid B3LYP xc functional and a basis set of Slater-type orbitals (STO) of triple-zeta quality (TZP) for all atoms. Calculations were performed by using the Amsterdam Density Functional (ADF) quantum chemistry code.20 The geometrical parameters (bond lengths and bond angles) of the optimized geometry are presented in Fig. S1 and Table S1 of the ESI† and show a close agreement with the experimental data derived from the crystallographic structure.21 The molecule is planar (D2h point group symmetry) and the molecular plane corresponds to the xy plane in the molecular frame, with the B–B bond along the x direction (see Fig. 1).The XPS and NEXAFS spectra at the B 1s, C 1s and O 1s edges were computed at the DFT level employing the PW86xPerdew (PW86) generalized gradient approximation (GGA) for the xc functional22,23 as implemented in the ADF program.20,24
In order to accurately describe higher excitations close to the ionization threshold, an even tempered Quadruple-Zeta basis set with three polarization and three diffuse functions (designated as ET-QZ3P-3DIFFUSE in the ADF database) has been employed for the core-excited atom (B, C or O, respectively), while a TZP (Triple Zeta + polarization) basis set was used for the remaining atoms. In particular, a frozen core TZP.1s basis set has been employed for the B, C and O non-excited atoms, to ensure the correct localization of the half core hole.
For the XP spectrum simulation, the B 1s, O 1s and C 1s core Ionization Potentials (IPs) have been calculated at the ΔSCF Kohn–Sham level allowing a full relaxation of the ionized core hole. The energy of each 1s−1 ionic state has been obtained through a SCF unrestricted calculation. The relative intensity among different primary lines is simply assumed to be proportional to the number of equivalent atoms of the same type. This is a good approximation since the XPS spectra were measured with a photon energy well above the considered ionization thresholds.
The B, O and C K-edge NEXAFS spectra at each non-equivalent atomic center have been computed with the DFT-TP method in which half an electron is removed from the initial core orbital and all the orbitals are relaxed until self-consistency is obtained. Relaxation effects upon the core-hole formation are usually adequately included in the DFT-TP approach.25 The performance of the hybrid B3LYP potential26–28 has also been tested considering the B 1s core excitation spectrum (see Fig. S5 of the ESI†). No significant differences emerged from the comparison between the PW86 and B3LYP calculated spectra.
For each of the three non-equivalent C sites of the B2Cat2 molecule (see Fig. 1), a separate computation of the C 1s excitation spectrum has been performed and the total spectrum has been obtained by summing up the partial contributions weighted for the number of equivalent atoms.
Within the DFT-TP scheme, the excitation energies correspond to the differences between the eigenvalues of the virtual orbitals and the 1s core orbitals referred to the TP configuration:
| ΔEi→f = εTPf − εTPi, | (1) |
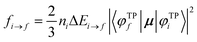 | (2) |
Due to the discrepancies between experiments and the theoretical DFT-TP results of the B 1s NEXAFS spectrum, the B 1s core excitations of the gas-phase B2Cat2 have been also computed at the TDDFT level, which formally includes the coupling between the single excited configurations, employing different xc functionals with the ground state electron configuration. The TDDFT computational details and the results are reported in Section S4 of the ESI,† which show that no improvement is obtained at the TDDFT level compared to the simpler DFT-TP scheme.
To better describe electronic relaxation effects, the B 1s core excitations and oscillator strengths have been also calculated at the ΔSCF level employing the procedure described in the following. In the ΔSCF method, the initial (Ψi) and final (Ψf) N-electron wave functions entering the dipole matrix element (computed in the length gauge of the dipole operator),
μi→f = 〈Ψf|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Ψi〉, |Ψi〉, | (3) |
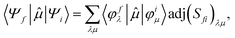 | (4) |
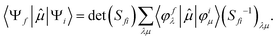 | (5) |
In order to compare the theoretical results with the NEXAFS experimental measurements recorded for the B2Cat2 molecule adsorbed on the Au(111) surface (in s- and p-polarization), we have considered the molecule fixed in space and have calculated the NEXAFS p- and s-pol intensities employing the following formula for the oscillator strength:
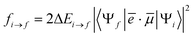 | (6) |
The ΔSCF B 1s, C 1s and O 1s IPs are presented in the figure of the corresponding NEXAFS spectrum and mark a separation of the whole spectral region into two sub-regions with different physical meanings. Only transitions that occur below the ionization threshold IP can be accurately described by the employed computational protocol. Above the IP only qualitative information can be extracted since the electronic continuum wave function cannot be properly described with standard basis sets of quantum chemistry programs.
Results and discussion
In the first part of the discussion the experimental XPS and NEXAFS spectra at the B 1s, O 1s and C 1s edges of the gas phase B2Cat2 will be compared with the theoretical results in order to achieve an assignment of the spectral features. In the second part, the polarization dependent NEXAFS measurements of the B2Cat2 adsorbed on the Au(111) surface will be analysed with the support of the theoretical results obtained for the fixed-in-space molecule. The experimental data have been acquired at the Gas Phase beamline32 and at the ANCHOR-SUNDYN endstation33 at the Elettra Synchrotron. Experimental details are reported in the ESI.†Gas phase results
The C 1s photoelectron spectrum of B2Cat2 is presented in Fig. S3 of the ESI† together with the calculated ΔSCF IPs of the three nonequivalent carbon atoms of the molecule (C1, C2 and C3, see Fig. 1). The two experimental peaks are assigned to the C2, C3 sites (first peak at 290.49 eV) and to the C1 site (second peak, at 291.94 eV); their energy splitting (1.45 eV) is a consequence of the reduced shielding of the C1 site, which is adjacent to the O atom, with respect to C2 and C3 sites. Calculations provide a chemical shift of 131 meV between the C2 and C3 sites with the lower binding energy associated to C3. The experimental line shape shows a pronounced asymmetry, detected also in catecholborane34 and attributed to vibrational effects. The spectrum was fitted with a function of three skew gaussians and the extracted peak positions are 291.95, 290.58 and 290.38 eV in accordance with the calculated IPs.
The O 1s photoelectron spectrum of B2Cat2 is shown in Fig. S4 of the ESI.† The peak at 539.03 eV represents the IP of the four equivalent oxygen atoms, as also indicated by the calculated ΔSCF IP line. The second intense peak around 541 eV is due to the O 1s signal of CO2 that we dosed together with B2Cat2 in order to have a known feature in the spectra to properly calibrate the photon energy scale. Details about the calibration references we used are reported in the ESI.†
The origin of the incorrect intensity distribution calculated at the DFT-TP level for the B 1s transitions has been already discussed in previous studies on boronic acid derivatives.16,35 We demonstrated that to correctly reproduce the B 1s NEXAFS spectrum one needs to include static correlation effects beyond those described by the coupling of singly-excited configurations, as in the TDDFT approach. In ref. 16 this was achieved by performing ab initio Multi-Configuration Self-Consistent-Field (MCSCF) calculations. We are led to assume that the inclusion of residual static correlation effects plays an important role in the description of the B 1s photoexcitation of B2Cat2, as also evidenced by the shake-up structures of the XPS B 1s spectrum in Fig. S2 (ESI;† see the “B 1s, C 1s and O 1s photoelectron spectra” section).
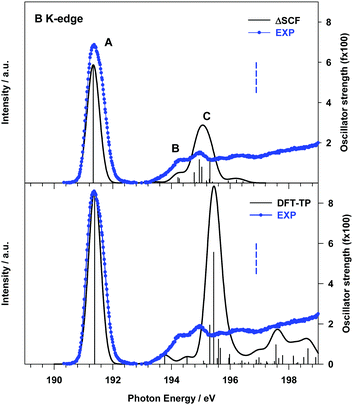
The effect of a more accurate treatment of relaxation, which is the dominant electron correlation effect at play in core excitation processes, is apparent from the comparison between the B 1s experimental NEXAFS spectrum and the ΔSCF results, presented in the upper panel of Fig. 2.
A significant improvement of the description of the experimental spectrum is obtained compared to DFT-TP results, in particular as concerns the intensity distribution among the spectral features. The ΔSCF spectrum has been obtained by calculating, for each dipole-allowed final symmetry, the first six excitation energies and transition dipole moments. This choice has been supported by the analysis of the DFT-TP results, which allows the identification of the final MOs involved in the description of the main spectral features below the edge. The ΔSCF B 1s core excitation energies and oscillator strengths are presented in Table 1, together with the attribution of the spectral features and the experimental data. The first calculated peak A arises from the B 1s transition to the LUMO orbital (7b1) which has a predominant π(B–B) bonding character (out of plane (oop) B 2p atomic components) with minor π*(B–O) antibonding contributions (the 3D plot of the 7b1 final MO is presented in Fig. S7 of the ESI†).
| Peak | ΔSCF transitiona | E (eV) | f × 100c | Assignment, main character of the final MO |
|---|---|---|---|---|
| a When the core hole is localized on the B site the molecular symmetry lowers from D2h to C2v and the molecular plane is yz with the B–B bond along the z axis. b Calculated excitation energies shifted by 0.45 eV to match the first experimental peak. c Only calculated transitions with f × 100 ≥ 0.20 are reported. | ||||
| A | B 1s → 7b1 | 191.33 | 5.87 | πout![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) plane(B–B) + π*(B–O) plane(B–B) + π*(B–O) |
| B | B 1s → 29a1 | 194.22 | 0.27 | Rydberg (in plane AO components) |
| B 1s → 9b1 | 194.27 | 0.21 | π*(C–C) | |
| C | B 1s → 23b2 | 194.78 | 0.52 | Mixed valence πin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) plane(B–B)/Rydberg plane(B–B)/Rydberg |
| B 1s → 10b1 | 194.95 | 1.15 | Mixed valence π*out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) plane (B–B)/Rydberg plane (B–B)/Rydberg |
|
| B 1s → 24b2 | 195.03 | 0.79 | Mixed valence πin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) plane(B–B)/Rydberg plane(B–B)/Rydberg |
|
| B 1s → 11b1 | 195.31 | 1.25 | Mixed valence π*out![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) of of![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) plane (B–B)/Rydberg plane (B–B)/Rydberg |
|
The two main transitions of feature C (at 194.95 and 195.31 eV) involve final MOs with mainly valence π*(B–B) (out of plane) antibonding character mixed with diffuse atomic components, while MOs with π(B–B) (in plane) bonding character, mixed with diffuse components, characterize the other two transitions at 194.78 and 195.03 eV (see Fig. S7 of the ESI†). The lower energy tail of C, labelled B in Fig. 2, arises from two low intensity transitions, one of diffuse nature (at 194.22 eV) and the other of mainly π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) antibonding character (at 194.27 eV).
C) antibonding character (at 194.27 eV).
The analysis of the contributions to the transition dipole moment (see eqn (4) and (5)) for the ΔSCF 9a1 (B 1s−1) → 7b1 transition reveals that the intensity is mainly contributed by the 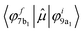 dipole matrix element between the initial 9a1 MO of the GS and the 7b1 MO of the ΔSCF excited state. The value of the cofactor, which multiplies the dipole integral, is close to 1 (0.918), and thus it does not influence the calculated intensity of this transition. On this ground, the relatively large oscillator strength computed for the ΔSCF 9a1 → 7b1 transition can be related to the composition of the 7b1 final MO, notably the significant participation of the B 2p atomic components, which carries most of the dipole transition moment. Considering the transitions of peak C, this kind of analysis still points out that the intensity of each transition is dominated by the contribution of the dipole matrix element between the initial 9a1 MO (B 1s−1) of the GS and the final MO of the ΔSCF transition considered.
dipole matrix element between the initial 9a1 MO of the GS and the 7b1 MO of the ΔSCF excited state. The value of the cofactor, which multiplies the dipole integral, is close to 1 (0.918), and thus it does not influence the calculated intensity of this transition. On this ground, the relatively large oscillator strength computed for the ΔSCF 9a1 → 7b1 transition can be related to the composition of the 7b1 final MO, notably the significant participation of the B 2p atomic components, which carries most of the dipole transition moment. Considering the transitions of peak C, this kind of analysis still points out that the intensity of each transition is dominated by the contribution of the dipole matrix element between the initial 9a1 MO (B 1s−1) of the GS and the final MO of the ΔSCF transition considered.
Also the relative intensity of these transitions, compared to the first peak, can be correlated to the atomic composition of the final MO, in particular the B 2p/np atomic contributions, which turn out to be reduced with respect to the final 7b1 MO of the first transition.
The significant decrease of the oscillator strength obtained at the ΔSCF level compared to the DFT-TP ones for the transitions of peak C can be mainly ascribed to the decreased value of the dipole integral of the corresponding transitions and therefore to the relaxation changes among different excited state configurations neglected in the DFT-TP approach, which treats the relaxation effects in an average way. We underline that the value of the cofactor multiplying the dominant dipole integral of the transitions of peak C is lower (around 0.8) than the one corresponding to the 9a1 (B 1s−1) → 7b1 transition and the calculated intensity is further reduced compared to the DFT-TP results.
The intensity distribution as well as the energy separation between the π(B–B) bonding and the π*(B–B) anti-bonding final states we described here represents a sensitive monitor of the chemistry the molecule is involved in, recalling what we discussed in the introduction. The Lewis acid character of the molecule is expected to be related to these orbitals, as they are localized on the B atoms.
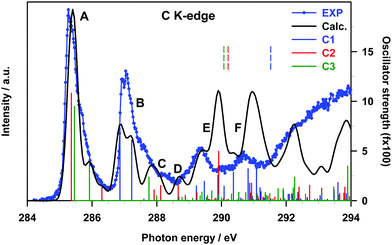
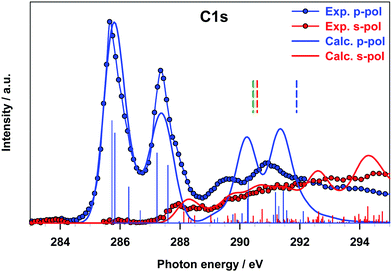
The gas phase experimental C K-edge NEXAFS spectrum of B2Cat2 is shown in Fig. 3 together with the theoretical DFT-TP results. The calculated excitation energies and oscillator strengths are presented in Table 2, along with their assignment to single-particle transitions. Two main experimental peaks characterize the low energy region (around 285 and 287 eV, respectively), while several less intense and broader structures are present in going towards the ionization threshold. The spectrum resembles the one measured for catecholborane,34 as expected due to the same chemical configuration for the carbon atoms in the two cases.
| Peak | E (eV) | f | Site | Assignment |
|---|---|---|---|---|
| a Calculated excitation energies shifted by −0.37 eV to match the first experimental peak. b Only the main transitions contributing to the theoretical features are presented. | ||||
| A | 285.36 | 10.81 | C2 | π*(C–C) + π(B–B) (LUMO) |
| 285.46 | 9.49 | C3 | π*(C–C) + π(B–B) (LUMO) | |
| 285.92 | 3.79 | C3 | π*(C–C) + π(B–B) (LUMO+1) | |
| 286.30 | 1.30 | C2 | ||
| B | 286.86 | 7.38 | C1 | π*(C–C) + π(B–B) (LUMO) |
| 287.22 | 6.08 | C1 | π*(C–C) + π(B–B) (LUMO+1) | |
| C | 287.76 | 2.38 | C3 | Rydberg (in plane components) |
| 288.12 | 1.51 | C2 | ||
| D | 288.66 | 1.60 | C2 | |
| E | 289.23 | 1.47 | C1 | |
| 289.47 | 1.94 | C1 | ||
| 289.89 | 2.57 | C3 | Mixed π*(C–C)/Rydberg | |
| 289.91 | 4.95 | C2 | ||
| 290.08 | 1.45 | C1 | Rydberg (in plane components) | |
| 290.37 | 2.85 | C1 | Mixed π(B–B)/Rydberg (in plane components) | |
| F | 290.82 | 3.21 | C1 | Mixed valence π*(C–C)/Rydberg |
| 291.08 | 3.33 | C1 | ||
The comparison with the theory points out a good agreement for the groups of excited states which contribute to the first structures (A, B and C, with C describing the higher energy tail of the second experimental band). Conversely, a poorer agreement is observed at a higher energy, in particular in the energy region around 290 eV with an overestimation of the intensity provided by the calculations. Indeed, the close proximity of the ionization region, above which the discretization of the non-resonant continuum affects the calculations, can explain the only qualitative description of the intensity distribution around and above 290 eV. Nonetheless, the attribution of the experimental features, which we will present in the following, can still be considered with confidence.
Band A arises from transitions from the C2 and C3 sites of the phenyl rings, namely the two C 1s → LUMO transitions, which contribute to the main peak, and the two C 1s → LUMO+1 transitions, which contribute to the higher energy tail of peak A (see Table 2). The same transitions from the C1 site, which is bonded to the O atom of the catechol moieties, are shifted to higher energies and give rise to peak B. The energy separation between the LUMO transitions of peaks A and B (about 1.4 eV) reflects the shift of IPs between C2/C3 and C1 sites (1.37 eV), denoting a predominance of initial state effects on these excitation energies. Both LUMO and LUMO+1 final orbitals are localized on the phenyl ring and present a π*(C–C) antibonding character with a minor contribution from the π(B–B) bond between the B atoms connecting the two catechol moieties (a plot of the LUMO orbital with the core hole localized on the C2 site is presented in Fig. S8 of the ESI†).
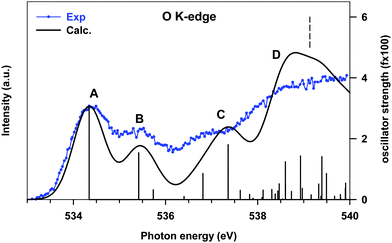
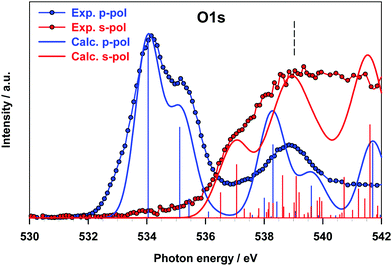
The higher energy tail of peak B (denoted as C in Fig. 3) as well as feature D and the lower energy shoulder (around 289.5 eV) of peak E are contributed by several low intensity transitions towards final MOs of diffuse nature (see Table 2). In the energy region of 289.5–291 eV the agreement between the theory and experiment deteriorates, as previously commented: the calculations provide two more intense peaks (E and F) around the C 1s thresholds, while two broad features, slightly shifted to lower energies, are present in the experiment. The high intensity of E and F theoretical peaks mainly arises from transitions towards final MOs with a π*(C–C) antibonding character mixed with some diffuse components starting from all the C sites (peak E) and from the C1 site (peak F). The O K-edge NEXAFS experimental spectrum of gas phase B2Cat2 is compared with the DFT-TP theoretical spectrum in Fig. 4. The assignment of the main peaks in terms of the calculated excitation energies and oscillator strengths is presented in Table 3. The experimental spectrum shows two main features in the energy range up to 536 eV, followed by a quite smooth signal of increasing intensity towards the ionization threshold. The good agreement between the calculated and measured spectra confirms the adequacy of the DFT-TP scheme to describe the core excitations of the O 1s channel in the B2Cat2 molecule.
| Peak | E (eV) | f × 100b | Assignments |
|---|---|---|---|
| a Calculated excitation energies shifted by 0.10 eV to match the first experimental peak. b Only the main transitions contributing to the theoretical features are reported. | |||
| A | 534.34 | 3.06 | πoop(B–B) + π*(B–O) |
| B | 535.42 | 1.54 | π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) + π*(C C) + π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
| C | 536.81 | 0.85 | Rydberg (in plane components) |
| 537.36 | 1.80 | ||
| D | 538.60 | 1.24 | Mixed valence π*(B–B) + π*(B–O)/Rydberg |
| 538.93 | 1.43 | Rydberg (in plane components) | |
The stronger calculated transition at 534.34 eV gives rise to peak A and involves the LUMO orbital which presents mainly a π(B–B, out of plane) bonding character with a minor π*(B–O) antibonding contribution (see Fig. S9 of the ESI†), similarly to the LUMO orbital obtained from the DFT-TP calculation with the core-hole localized on the B site.
Peak B mainly arises from the O 1s → LUMO+1 transition. The LUMO+1 MO is strongly localized on the phenyl ring (π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) character) with only a weak conjugation with the O 2pz components, consistent with the low intensity calculated for this transition. Features C and D are characterized by several low intensity transitions toward MOs of mainly diffuse nature.
C) character) with only a weak conjugation with the O 2pz components, consistent with the low intensity calculated for this transition. Features C and D are characterized by several low intensity transitions toward MOs of mainly diffuse nature.
It is worth noting that the transition at 538.60 eV (peak D) involves a final orbital which is the antibonding counterpart of the LUMO although several diffuse components are also present. The energy separation between the transitions towards the π(B–B) bonding and antibonding orbitals is about 4 eV, a value very close to that found for the corresponding transitions in the B 1s NEXAFS spectrum.
We underline the relatively low oscillator strengths provided by the DFT-TP calculations for the O 1s transitions, which stem from the small O 2p atomic contribution to the virtual orbitals compared to the C and B atomic contributions. This is a sign of the polarization of the C–O and B–O bonds and of the large involvement of O 2p atomic components in the occupied MOs.
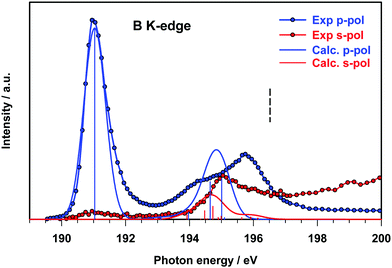
The B 1s experimental and calculated p- and s-pol spectra are presented in Fig. 5, in the energy region below the threshold. The intensity contribution from the p-pol component is prevalent in all the spectral region below the edge. The most remarkable dichroic effects are present in the region of the first experimental peak (around 191 eV) and are correctly reproduced by the calculations. This behavior reflects the π symmetry of the final orbital (7b1, LUMO) involved in the transition responsible for this peak. In the energy region above 194 eV both p- and s-pol components are present. In particular, the s-pol component gives a significant contribution around 195 eV, which appears slightly underestimated by the theory and corresponds to the transitions encompassed by peak C in the gas phase spectrum, assigned to the excitations to the in-plane π(B–B) MOs.
In this energy region the p-pol experimental component is still stronger than the s-pol one, with a large feature with a maximum around 196 eV, while the theory provides one p-pol peak mainly derived from the two out of plane π*(B–B) antibonding transitions.
Fig. 6 presents the C 1s experimental polarized spectra and their comparison with the calculated ones for the fixed in space B2Cat2 molecule. The p-pol component dominates in all the energy range below the threshold and the theory correctly describes the strong dichroic effects associated with the π out of plane nature of most final MOs. In particular, the first two peaks correspond to the A and B peaks of the gas-phase spectrum (Fig. 3) associated to π*(C–C) antibonding transitions.
Around 288 eV the s-pol component starts to acquire some intensity with a feature corresponding to peak C of the gas phase spectrum due to the transitions towards diffuse MOs with in plane atomic components. Transitions of similar nature contribute to the experimental s-pol broad signal present in the energy range of 289–292 eV. The p-pol component contributes to this energy range with two broad features whose theoretical counterparts appear still overestimated and slightly shifted at a higher energy and correspond to the E and F peaks of the gas phase spectrum. This analysis of the p- and s-pol components of the C K-edge spectrum confirms the attribution of the spectral features proposed for the gas-phase experimental spectrum despite some discrepancies provided by the theory in the energy range around C 1s thresholds.
The results for the O K-edge p-pol and s-pol spectra are shown in Fig. 7. The dichroic effects are still relevant at a lower energy, while both components provide significant contributions to the features above 536 eV. The agreement between the experiment and theory is good for both components, and the strong dichroic effects present in the lower energy region are consistent with the π nature of the transitions relative to the A and B peaks of the gas phase spectrum.
The intensity of the s-pol component mainly arises from transitions of diffuse nature (peak C of the gas phase spectrum), while the intensity distribution between the s- and p-pol components near the threshold reflects the character of the transitions contributing to peak D of the gas phase spectrum (see Table 3). The good agreement found between theoretical calculations on the oriented molecule and experimental results for B2Cat2 adsorbed on Au(111) proves that the Au surface does not perturb the transitions of any of the B 1s, C 1s and O 1s channels confirming the weak interaction of the molecule with the surface.
Conclusions
DFT calculations have been used to assign the features observed in the B, C and O K-shell XPS and NEXAFS spectra of the B2Cat2 molecule, with the aim of obtaining detailed information on the B2Cat2 electronic structure. The assignment of the absorption peaks observed in the gas-phase NEXAFS spectra has been validated by a study of the corresponding NEXAFS spectra for the molecule adsorbed on the poorly reactive Au(111) surface, which allowed confirmation of the nature of the virtual electronic states involved in the core-excitation process. This represents a valuable reference to explore the surface chemistry of diboron compounds with other molecular species or with reactive metallic substrates. In particular the energy position and intensity of the B 1s core to the π(B–B) bonding and anti-bonding orbitals represent a sensitive probe of the chemistry of the molecule. In this regard, for example, we outline that, in the B 1s edge spectra, a quite different position of the first transition (∼191 eV) is found with respect to the case of the covalent framework of boroxine groups based on the B–B bond (∼194 eV).15 We suggest therefore that in the latter case a stronger interaction with the substrate was established and that the B–B centers were involved in a charge transfer process with a consequent change in their chemical environment.Finally, our results point out that the ΔSCF method is required to describe the B 1s core excited states in order to reach a good agreement with the experimental data, with respect to both DFT-TP and linear response TDDFT approaches. This indicates the importance of explicitly treating the relaxation changes among different excited-state configurations relative to the B 1s core hole, unlike the C and O K-edges which can be conveniently described at the DFT-TP level with the relaxation effects included in an average way. This behavior can be traced to the less pronounced relaxation following the formation of the shallower B 1s core hole compared to the heavier first row atoms, such as C and O.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computational research was supported by Finanziamento per ricerca di ateneo, FRA 2018–2020 of the Università degli Studi di Trieste. The authors are grateful to the Stiftung Beneficentia for a generous grant employed to set up a computational server.Notes and references
- A. L. Korich and P. M. Iovine, Boroxine chemistry and applications: A perspective, Dalton Trans., 2010, 39, 1423–1431 Search PubMed.
- E. Dimitrijević and M. S. Taylor, Organoboron Acids and Their Derivatives as Catalysts for Organic Synthesis, ACS Catal., 2013, 3, 945–962 Search PubMed.
- G. Duret, R. Quinlan, P. Bisseret, N. Blanchard, A. R. Martin, J.-J. Vasseur and M. Smietana, Boron chemistry in a new light, Chem. Sci., 2013, 42, 5684–5713 Search PubMed.
- E. C. Neeve, S. J. Geier, I. A. I. Mkhalid, S. A. Westcott and T. B. Marder, Diboron(4) Compounds: From Structural Curiosity to Synthetic Workhorse, Chem. Rev., 2016, 116, 9091–9161 Search PubMed.
- J. Wang, W. Zheng and Y. Zheng, Theoretical study on homolytic B-B cleavages of diboron(4) compounds, RSC Adv., 2017, 7, 49251–49272 Search PubMed.
- M. Eck, S. Würtemberger-Pietsch, A. Eichhorn, J. H. J. Berthel, R. Bertermann, U. S. D. Paul, H. Schneider, A. Friedrich, C. Kleeberg, U. Radius and T. B. Marder, B-B bond activation and NHC ring-expansion reactions of diboron(4) compounds, and accurate molecular structures of B2(NMe2)4, B2eg2, B2neop2 and B2pin2, Dalton Trans., 2017, 46, 3661–3680 Search PubMed.
- A. F. Eichhorn, L. Kuehn, T. B. Marder and U. Radius, Facile insertion of a cyclic alkyl(amino) carbene carbon into the B-B bond of diboron(4) reagents, Chem. Commun., 2017, 53, 11694–11696 Search PubMed.
- Y. Katsuma, H. Asakawa and M. Yamashita, Reactivity of highly Lewis acidic diborane(4) towards pyridine and isocyanide: Formation of boraalkene-pyridine complex and: Ortho -functionalized pyridine derivatives, Chem. Sci., 2018, 9, 1301–1310 Search PubMed.
- A. F. Pécharman, N. A. Rajabi, M. S. Hill, C. L. McMullin and M. F. Mahon, Diborane heterolysis and P(v) reduction by Ph3P
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O coordination to magnesium, Chem. Commun., 2019, 55, 9035–9038 Search PubMed.
O coordination to magnesium, Chem. Commun., 2019, 55, 9035–9038 Search PubMed. - S. Pietsch, U. Paul, I. A. Cade, M. J. Ingleson, U. Radius and T. B. Marder, Room Temperature Ring Expansion of N-Heterocyclic Carbenes and B-B Bond Cleavage of Diboron(4) Compounds, Chem. – Eur. J., 2015, 21, 9018–9021 Search PubMed.
- T. Ishiyama, K. Ishida and N. Miyaura, Synthesis of pinacol arylboronates via cross-coupling reaction of bis(pinacolato)diboron with chloroarenes catalyzed by palladium(0)-tricyclohexylphosphine complexes, Tetrahedron, 2001, 57, 9813–9816 Search PubMed.
- A. Cossaro, M. Puppin, D. Cvetko, G. Kladnik, A. Verdini, M. Coreno, M. De Simone, L. Floreano and A. Morgante, Tailoring SAM-on-SAM formation, J. Phys. Chem. Lett., 2011, 2, 3124–3129 Search PubMed.
- Z. Feng, G. Kladnik, G. Comelli, C. Dri and A. Cossaro, Growth of regular nanometric molecular arrays on a functional 2D template based on a chemical guest–host approach, Nanoscale, 2018, 10, 2067–2072 Search PubMed.
- J. V. Barth, Molecular architectonic on metal surfaces, Annu. Rev. Phys. Chem., 2007, 58, 375–407 Search PubMed.
- M. Stredansky, A. Sala, T. Fontanot, R. Costantini, C. Africh, G. Comelli, L. Floreano, A. Morgante and A. Cossaro, On-surface synthesis of a 2D boroxine framework: a route to a novel 2D material?, Chem. Commun., 2018, 54, 3971–3973 Search PubMed.
- D. Toffoli, A. Ponzi, E. Bernes, M. De Simone, C. Grazioli, M. Coreno, M. Stredansky, A. Cossaro and G. Fronzoni, Correlation effects in B 1s core-excited states of boronic-acid derivatives: An experimental and computational study, J. Chem. Phys., 2019, 151, 134306 Search PubMed.
- J. C. Slater, in Advances in Quantum Chemistry, ed. P.-O. Löwdin, Academic Press, 1972, vol. 6, pp. 1–92 Search PubMed.
- L. Triguero, L. G. M. Pettersson and H. Ågren, Calculations of near-edge X-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8097–8110 Search PubMed.
- W. Parr and R. G. Yang, Density-functional theory of atoms and molecules, Oxford University Press, New York, 1989 Search PubMed.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Towards an order-N DFT method, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- W. Clegg, M. R. J. Elsegood, F. J. Lawlor, N. C. Norman, N. L. Pickett, E. G. Robins, A. J. Scott, P. Nguyen, N. J. Taylor and T. B. Marder, Structural Studies of Bis-Catecholate, Bis-Dithiocatecholate, and Tetraalkoxy Diborane(4) Compounds, Inorg. Chem., 1998, 37, 5289–5293 Search PubMed.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 Search PubMed.
- J. P. Perdew, Erratum: Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 Search PubMed.
- E. J. Baerends, D. E. Ellis and P. Ros, Self-consistent molecular Hartree–Fock–Slater calculations I. The computational procedure, Chem. Phys., 1973, 2, 41–51 Search PubMed.
- P. Norman and A. Dreuw, Simulating X-ray Spectroscopies and Calculating Core-Excited States of Molecules, Chem. Rev., 2018, 118, 7208–7248 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 Search PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627 Search PubMed.
- T. Ziegler, A. Rauk and E. J. Baerends, On the calculation of multiplet energies by the Hartree-Fock-slater method, Theor. Chim. Acta, 1977, 43, 261–271 Search PubMed.
- P.-O. Löwdin, Quantum Theory of Many-Particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction, Phys. Rev., 1955, 97, 1474–1489 Search PubMed.
- S. Bourne Worster, O. Feighan and F. R. Manby, Reliable transition properties from excited-state mean-field calculations, J. Chem. Phys., 2021, 154, 124106 Search PubMed.
- K. C. Prince, R. R. Blyth, R. Delaunay, M. Zitnik, J. Krempasky, J. Slezak, R. Camilloni, L. Avaldi, M. Coreno, G. Stefani, C. Furlani, M. De Simone and S. Stranges, The gas-phase photoemission beamline at Elettra, J. Synchrotron Radiat., 1998, 5, 565–568 Search PubMed.
- R. Costantini, M. Stredansky, D. Cvetko, G. Kladnik, A. Verdini, P. Sigalotti, F. Cilento, F. Salvador, A. De Luisa, D. Benedetti, L. Floreano, A. Morgante, A. Cossaro and M. Dell’Angela, ANCHOR-SUNDYN: A novel endstation for time resolved spectroscopy at the ALOISA beamline, J. Electron Spectrosc. Relat. Phenom., 2018, 229, 7–12 Search PubMed.
- I. Ljubić, M. T. Cvitaš, C. Grazioli, M. Coreno, S. Kazazić and I. Novak, Vibrationally resolved valence and core photoionization and photoexcitation spectra of an electron-deficient trivalent boron compound: The case of catecholborane, Phys. Chem. Chem. Phys., 2020, 22, 25396–25407 Search PubMed.
- D. Toffoli, M. Stredansky, Z. Feng, G. Balducci, S. Furlan, M. Stener, H. Ustunel, D. Cvetko, G. Kladnik, A. Morgante, A. Verdini, C. Dri, G. Comelli, G. Fronzoni and A. Cossaro, Electronic properties of the boroxine–gold interface: evidence of ultra-fast charge delocalization, Chem. Sci., 2017, 8, 3789–3798 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03428f |
| This journal is © the Owner Societies 2021 |