Shock wave and modelling study of the unimolecular dissociation of Si(CH3)2F2: an access to spectroscopic and kinetic properties of SiF2†
Received
19th July 2021
, Accepted 22nd September 2021
First published on 23rd September 2021
Abstract
The thermal dissociation of Si(CH3)2F2 was studied in shock waves between 1400 and 1900 K. UV absorption-time profiles of its dissociation products SiF2 and CH3 were monitored. The reaction proceeds as a unimolecular process not far from the high-pressure limit. Comparing modelled and experimental results, an asymmetric representation of the falloff curves was shown to be most realistic. Modelled limiting high-pressure rate constants agreed well with the experimental data. The UV absorption spectrum of SiF2 was shown to be quasi-continuous, with a maximum near 222 nm and a wavelength-integrated absorption cross section of 4.3 (±1) × 10−23 cm3 (between 195 and 255 nm, base e), the latter being consistent with radiative lifetimes from the literature. Experiments over the range 1900–3200 K showed that SiF2 was not consumed by a simple bond fission SiF2 →SiF + F, but by a bimolecular reaction SiF2 + SiF2 → SiF + SiF3 (rate constant in the range 1011–1012 cm3 mol−1 s−1), followed by the unimolecular dissociation SiF3 → SiF2 + F such that the reaction becomes catalyzed by the reactant SiF2. The analogy to a pathway CF2 + CF2 → CF + CF3, followed by CF3 → CF2 + F, in high-temperature fluorocarbon chemistry is stressed. Besides the high-temperature absorption cross sections of SiF2, analogous data for SiF are also reported.
Introduction
The role of SiF2 in the etching of silicon by fluorine atoms continues to be under debate (see, for example, the review in ref. 1). Part of the problem lies in the scarcity of quantitative information on the properties of this intermediate in chemical or plasma-assisted etching processes employing fluorine-containing compounds. A limited amount of kinetic data is available for room temperature conditions (e.g., ref. 2–6), while less is known for elevated temperatures. The present article intends to improve this situation by investigating kinetic properties of SiF2 under high-temperature conditions in shock waves.
First, a suitable source for SiF2 had to be selected. It has been shown that the thermal dissociation of Si2F6, in a process Si2F6 → SiF2 + SiF4 and with a rate constant 1012.41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−193.5 kJ mol−1/RT) s−1, directly produces SiF2.7,8 The thermal dissociation of SiF4, on the other hand, in a sequence SiF4 → SiF3 → SiF2 also leads to SiF2, but, because of the large thermal stability of SiF4, requires considerably higher temperatures than the dissociation of Si2F6. In the present work, instead of Si2F6 or SiF4, it appeared more suitable to use Si(CH3)2F2 as the precursor for SiF2. This compound is easy to handle in shock wave experiments and, at comparably low temperatures, it forms SiF2 in a sequence of the two steps
exp(−193.5 kJ mol−1/RT) s−1, directly produces SiF2.7,8 The thermal dissociation of SiF4, on the other hand, in a sequence SiF4 → SiF3 → SiF2 also leads to SiF2, but, because of the large thermal stability of SiF4, requires considerably higher temperatures than the dissociation of Si2F6. In the present work, instead of Si2F6 or SiF4, it appeared more suitable to use Si(CH3)2F2 as the precursor for SiF2. This compound is easy to handle in shock wave experiments and, at comparably low temperatures, it forms SiF2 in a sequence of the two steps
| |  | (1) |
| |  | (2) |
(the given reaction enthalpies at 0 K,

, were determined by quantum-chemical calculations as described in the ESI
†).
Next, a detection method for SiF2 had to be chosen. As the UV absorption of CF2 has been found useful to study high-temperature fluorocarbon chemistry,9–11 one may try to employ the analogous spectrum of SiF2 to investigate reactions of the latter. At room temperature, SiF2 has a band spectrum which is similarly structured and intense as that of CF2.13 One may expect that this spectrum at high temperatures becomes similarly quasi-continuous as that of CF2. One of the goals of the present work, therefore, was the characterization of the UV absorption spectrum of SiF2 at elevated temperatures and to determine its absorption cross section as a function of temperature and wavelength in comparison to quantum-chemical calculations of its oscillator strength (as described in the ESI†).
There are more aspects of the present work. Monitoring SiF2 formation in reactions (1) and (2) enables one to follow the unimolecular dissociation reaction of Si(CH3)2F2. This molecule is sufficiently large to dissociate (under typical shock wave conditions) not far from the high-pressure limit of the unimolecular reaction. Therefore, a study of the pressure dependence of the dissociation rate constant k appears suitable to analyze its approach to the high-pressure rate constant k∞. This is an issue in standard unimolecular rate theory. The various versions of the latter propose different approaches of k to k∞.14,15 By comparing experimental and modelled rate constants, the present study provides an opportunity to address this problem in particular detail. In addition, in high-temperature fluorocarbon chemistry an autocatalytic pathway for CF2 decomposition of the type CF2 + CF2 → CF + CF3, followed by CF3 → CF2 + F, was observed.11 It appears of interest to search for an analogous pathway SiF2 + SiF2 → SiF + SiF3, followed by SiF3 → SiF2 + F, in high-temperature fluorosilicon chemistry. In both cases, the very endothermic direct dissociation of CF2 or SiF2, respectively, then can be circumvented by a faster mechanism which also leads to dissociation.
Experimental technique and results
The present experiments have been performed by heating mixtures of Si(CH3)2F2 and Ar in shock waves. Si(CH3)2F2 (from abcr with a purity of 99%) could be used without further purification, because it was highly diluted (down to about 30 ppm) in the bath gas Ar (from Air Liquide with a purity of 99.9999%). The shock tube, as well as the UV lamp – quartz monochromator – photomultiplier – data aquisition equipment for recording absorption-time profiles, have, e.g., been detailed in ref. 11 and 16 such that no further description is given here. In the first part of the present experiments, absorption-time profiles of shock-heated mixtures of about 100 ppm of Si(CH3)2F2 in Ar were recorded at the wavelength of 222 nm, i.e. near to the maximum of the room-temperature absorption of SiF2.12Fig. 1 shows an example for a temperature of 1660 K behind the reflected shock wave. Directly behind the Schlieren peaks of the incident and reflected shock waves, no absorption signal is observed. This indicates that the absorption continuum of the parent molecule Si(CH3)2F2 (having a room-temperature maximum near 155 nm17) with increasing temperature does not broaden to such an extent that it would influence absorption measurements at 222 nm. The absorption signal of Fig. 1 then can directly be related to the formation of SiF2 (as reaction (1) is by far more endothermic than reaction (2), Si(CH3)F2 should rapidly dissociate to CH3 + SiF2). One may also look for an absorption signal from CH3. It is known that there is an absorption band of CH3 not far from that of SiF2. However, its maximum is located at shorter wavelengths (near to 215 nm) and its maximum absorption cross section is much smaller than that of SiF2.18 Because the absorption cross section of SiF2 decreases with decreasing wavelength, a signal from CH3 could, nevertheless, be detected together with that from SiF2. Fig. 2 shows a signal recorded at 200 nm and employing larger reactant concentrations than in Fig. 1. Its magnitude corresponds to the marked decrease of the SiF2 absorption cross section with decreasing wavelength as analyzed below and to the absorption cross section of CH3 as reported in ref. 18. Fig. 2 indicates that [SiF2] and [CH3] have different time dependences. While [CH3] first increases and then decreases, [SiF2] like in Fig. 1 reaches a stationary final level. The decay of the CH3 signal corresponds to the dimerization 2CH3 → C2H6, whose rate, under the present conditions, is known.18 In contrast to [CH3], [SiF2] finally remains constant such as shown in Fig. 1. Apparently, the reverse of reactions (1) and (2) do not play a role, such that the signal of Fig. 1 can be attributed to the slower of reactions (1) and (2), in this case, obviously to reaction (1).
 |
| | Fig. 1 Absorption-time profile at 222 nm of SiF2 forming by unimolecular dissociation of Si(CH3)2F2 behind reflected shock wave (T = 1660 K, [Ar] = 8.6 × 10−5 mol cm−3, 100 ppm of Si(CH3)2F2 in Ar; OD = σl [SiF2] with l = 9.4 cm). | |
 |
| | Fig. 2 As Fig. 1, but at 200 nm; superimposed absorptions of SiF2 and CH3 (T = 1720 K, [Ar] = 8.2 × 10−5 mol cm−3, 210 ppm of Si(CH3)2F2 in Ar). | |
Absorption cross sections of SiF2
Systematically inspecting final absorption levels of signals like Fig. 1 and 2, high-temperature absorption cross sections of SiF2 were derived. Varying the temperature between 1500 and 1900 K (where the reaction was complete within the available observation time of about 1 ms), a major influence of temperature on the final absorption level could not be detected. On the one hand, this proved that the dissociation of Si(CH3)2F2 was complete and no back-reaction took place. The final absorption level was found to be proportional to the reactant concentration which confirmed this conclusion. On the other hand, a temperature dependence of the absorption cross section of SiF2 over this temperature range was only small. Slightly varying the wavelength (between 220 and 225 nm) indicated that the room-temperature band structure12 was absent at the present elevated temperatures and that the SiF2 spectrum now indeed was quasi-continuous. Assuming that each decomposing Si(CH3)2F2 produces one SiF2, a maximum absorption cross section σ(SiF2, 222 nm) = (2.45 ± 0.5) × 10−17 cm2 (base e) was derived for temperatures near 1600 K. Fig. 3 shows the results for the wavelength dependence of σ(SiF2, λ) near 1600 and 3000 K (Table S1 of the ESI† shows experimental values of σ(SiF2, λ)). Analogous to the observations for CF2 from ref. 9, σ(SiF2, λ) has a Gaussian shape. The wavelength-integrated absorption cross section  (SiF2, λ) dλ (between 195 and 255 nm) is equal to 4.3 (±1) × 10−23 cm3, being close to the value 5.2 × 10−23 cm3 derived in ref. 12 from the experimental radiative lifetimes of SiF2 from ref. 19.
(SiF2, λ) dλ (between 195 and 255 nm) is equal to 4.3 (±1) × 10−23 cm3, being close to the value 5.2 × 10−23 cm3 derived in ref. 12 from the experimental radiative lifetimes of SiF2 from ref. 19.
 |
| | Fig. 3 Absorption cross sections σ of SiF2 (experimental points from the present work, T near 1600 K, ●, and 3000 K, ○; representation of σ(T) by eqn (3) for T = 1600 K, solid line, and 3000 K, dashed line). | |
A representation of the complete wavelength and temperature dependence of σ in Sulzer–Wieland form20
| | σ(ν, T) ≈ σmax[tanh(θ0/2T)]1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{−tanh(θ0/2T) [(ν − ν0)/Δν0]2} exp{−tanh(θ0/2T) [(ν − ν0)/Δν0]2} | (3) |
(with
ν = 1/
λ) requires information on the four parameters
σmax,
θ0,
ν0, and
ν0. Fitting the data of
Fig. 3 to
eqn (3) leads to the parameters
σmax ≈ 2.87 × 10
−17 cm
2,
ν0 ≈ 45
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
045 cm
−1, and Δ
ν0 ≈ 1785 cm
−1. The determination of the parameter
θ0 requires experiments over larger temperature ranges. In the present case, experiments were extended up to temperatures of 3200 K where Si(CH
3)
2F
2 decomposes in less than a μs.
Fig. 4 shows an example for 3060 K. Instead of staying constant as in
Fig. 1, the signal here decreases by secondary reactions which will be analyzed later. Nevertheless, the absorption cross section of SiF
2 can be determined before this decay becomes a problem (
e.g., after 10 μs in
Fig. 4). Selected results are included in
Fig. 3 and compared with a Sulzer–Wieland plot using
θ0 ≈ 3000 K. This value of
θ0 is relatively uncertain. It is mainly based on measurements at 222 nm and it is definitely larger than the corresponding value
9 for the spectrum of CF
2 (it should be mentioned that the present results are consistent with values derived from the thermal dissociation of SiF
4 which will be reported separately, thus supporting the described analysis). It should also be mentioned that absorption-time signals at wavelengths larger than 240 nm increasingly deviate from
Fig. 1. Apparently, absorptions from other species here are superimposed on the absorptions from SiF
2, such as analyzed below.
 |
| | Fig. 4 As Fig. 1, but at higher temperatures (210 ppm of Si(CH3)2F2 in Ar; T = 1470 K and [Ar] = 1.6 × 10−5 mol cm−3 behind incident shock wave; T = 3060 K and [Ar] = 8.1 × 10−5 mol cm−3 behind reflected shock wave; time scale behind incident shock wave compressed by a factor of 3.3). | |
Unimolecular dissociation of Si(CH3)2F2
In the second part of our experiments, the kinetics of Si(CH3)2F2 dissociation was explored. The time dependence of the absorption-time profile of Fig. 1 corresponds to a first-order process, i.e. [SiF2](t) = [Si(CH3)2F2](t = 0) {1 − exp(−kt)} with k = 8.3 × 103 s−1. In cases where [SiF2](t) did not approach the final level [SiF2](t = ∞) sufficiently well within the available observation time, i.e. at temperatures below about 1500 K, the initial rate of absorption increase could also be evaluated to derive k. This required the use of absorption cross sections σ from eqn (3). Then, dOD(t)/dt = σl [SiF2](t = ∞)k (with the optical density OD = σl [SiF2] and the optical path length l = 9.4 cm of our arrangement) also led to rate constants k. This evaluation was necessary in particular for measurements behind incident shock waves. Fig. 4 shows an example. As our modelling (see the ESI†) predicted an only weak dependence of k on [Ar], only the comparison of measurements behind incident and reflected shock waves provided a sufficiently large variation of bath gas concentrations to draw meaningful conclusions on the shape of falloff curves k([Ar]) (the accessible range was from [Ar] ≈ 10−5 mol cm−3 in incident waves to 10−4 mol cm−3 in reflected waves). Fig. 5 compares two alternative representations of k([Ar]) with experimental results from incident and reflected shock waves (a doubly-reduced representation of k/k∞vs. k0/k∞ was chosen in order to include results from different temperatures; the used k0 and k∞ are from the modelled expressions given below). A more complete representation of experimental data is provided by the Arrhenius plots of Fig. 6 (for constant [Ar]; small mismatches of the experimental [Ar] from the given values were accounted for by the [Ar]-dependences of Fig. 5; the scatter of about ±20% of the points in Fig. 5 and 6 is larger than the systematic uncertainty of the measurements). Within the scatter, measured and modelled rate constants agree. As the reaction was studied not far from the high-pressure limit, the agreement mostly confirms the quality of the quantum-chemistry based calculation of k∞ (see the ESI†). Because of the uncertainty of the used collisional energy transfer parameters (see the ESI†), the modelling of the low-pressure rate constants k0 is less certain. Its influence on the derived high-pressure constants k∞, however, is only weak. In conclusion, the experimental data are remarkably consistent with the high-pressure rate constants such as modelled in the ESI.† These can be expressed by| | k∞ = 1.24 × 1019 (T/2000 K)−6.63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−58 exp(−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 K/T) s−1 400 K/T) s−1 | (4) |
Low-pressure rate constants were modelled as| | k0 ≈ [Ar] 2.94 × 1025 (T/2000 K)−25.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−61 exp(−61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 K/T) cm3 mol−1 s−1 980 K/T) cm3 mol−1 s−1 | (5) |
The representation of the falloff curves of Fig. 5 has employed expressions of the form| | | k([Ar])/k∞ = [x/(1 + x)]F(x) | (6) |
with x = k0/k∞ and “broadening factors” F(x). Either “symmetric broadening factors” F(x) (i.e., F(x) = F(1/x)) of the form proposed in ref. 21,| | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F(x) ≈ log F(x) ≈ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fcent/[1 + (log Fcent/[1 + (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x/N)2] x/N)2] | (7) |
(with N ≈ 0.75–1.27 log Fcent and system-specific “center broadening factors” Fcent22), or “asymmetric broadening factors” F(x) (i.e. F(x) ≠ F(1/x)) were used, the latter being of the form proposed in ref. 14 and 15| | | F(x) ≈ (1 + x/x0)/[1 + (x/x0)n]1/n | (8) |
(with n = [ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/ln(2/Fcent)] [1 – b + b(x/x0)q], q = (Fcent − 1)/ln(Fcent/10), and the parameters x0 and b close to x0 = 1(±0.1) and b = 0.2(±0.05)). The comparison of the two alternative expressions for falloff curves with the experimental data in Fig. 5 suggests that the asymmetric form of F(x), i.e.Eqn (8), near to the high-pressure limit performs much better than the symmetric form of F(x), i.e.Eqn (7).
2/ln(2/Fcent)] [1 – b + b(x/x0)q], q = (Fcent − 1)/ln(Fcent/10), and the parameters x0 and b close to x0 = 1(±0.1) and b = 0.2(±0.05)). The comparison of the two alternative expressions for falloff curves with the experimental data in Fig. 5 suggests that the asymmetric form of F(x), i.e.Eqn (8), near to the high-pressure limit performs much better than the symmetric form of F(x), i.e.Eqn (7).
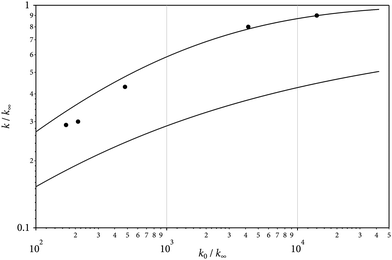 |
| | Fig. 5 Doubly-reduced representation of falloff curves k([Ar]) for the unimolecular dissociation of Si(CH3)2F2 (representation of k([Ar])/k∞ as a function of k0/k∞with k0 from eqn (5) and k∞ from eqn (4); upper solid line: modelling with eqn (8), lower solid line: modelling with eqn (7); experimental points from left to right: T/K = 1400, 1500, 1600, 1700, 1800, respectively). | |
 |
| | Fig. 6 Arrhenius plots of rate constants k(T) for the unimolecular dissociation of Si(CH3)2F2 at [Ar] ≈ 10−5 (○) and 10−4 (●) mol cm−3, between T = 1370 and 1890 K (modelled lines: representation of falloff curves by eqn (8), from bottom to top for [Ar] = 10−5 mol cm−3, [Ar] = 10−4 mol cm−3, and k∞, see the ESI†). | |
Kinetics of SiF2 reactions
The experiments described so far, which characterize the formation of SiF2 (and CH3) in the unimolecular dissociation of Si(CH3)2F2, finally were extended to higher temperatures where the primary dissociation is so rapidly complete that it cannot be resolved any longer. Fig. 4 gives an example for the reflected shock wave. If only reactions (1) and (2) would take place, the absorption signal behind the reflected shock wave then would remain constant. Instead, one observes a decrease to a new steady level. The decrease of the signal is much faster than expected for the thermal dissociation of SiF2, i.e.| |  | (9) |
(for this reaction, a rate constant of k9,0 = [Ar] 2 × 1016 (T/1000 K)−1.34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−72
exp(−72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 K/T) cm3 mol−1 s−1 has been modelled analogous to the calculations described in the present ESI,† such that SiF2 would have a half-life of about 7 s; likewise, the final absorption level of Fig. 4 cannot correspond to a dissociation equilibrium SiF2 ↔ SiF + F). An unambiguous interpretation of the signal, instead, is provided by measurements at wavelengths where an absorption from SiF2 can be neglected. Fig. 3 indicates that, even at the temperature of Fig. 4, an absorption signal from SiF2 should be negligible at wavelengths larger than about 250 nm. Fig. 7 gives an example for a wavelength of 265 nm and nearly the same temperature as in Fig. 4. The initial decay of the SiF2 signal from Fig. 4 now is mirrored by an absorption increase in Fig. 7. The rate of the initial decay of SiF2 in Fig. 4 and the formation of a reaction product in Fig. 7 both were found to increase proportional to [SiF2](t = 0), i.e. the observation corresponds to a bimolecular process. In addition, the rate constant for this process was found to have an only small positive temperature coefficient. These observations suggest that SiF2 is consumed by a reaction
910 K/T) cm3 mol−1 s−1 has been modelled analogous to the calculations described in the present ESI,† such that SiF2 would have a half-life of about 7 s; likewise, the final absorption level of Fig. 4 cannot correspond to a dissociation equilibrium SiF2 ↔ SiF + F). An unambiguous interpretation of the signal, instead, is provided by measurements at wavelengths where an absorption from SiF2 can be neglected. Fig. 3 indicates that, even at the temperature of Fig. 4, an absorption signal from SiF2 should be negligible at wavelengths larger than about 250 nm. Fig. 7 gives an example for a wavelength of 265 nm and nearly the same temperature as in Fig. 4. The initial decay of the SiF2 signal from Fig. 4 now is mirrored by an absorption increase in Fig. 7. The rate of the initial decay of SiF2 in Fig. 4 and the formation of a reaction product in Fig. 7 both were found to increase proportional to [SiF2](t = 0), i.e. the observation corresponds to a bimolecular process. In addition, the rate constant for this process was found to have an only small positive temperature coefficient. These observations suggest that SiF2 is consumed by a reaction| |  | (10) |
A modelling of the rate constant for unimolecular dissociation of SiF3 analogous to that described in the present ESI,† on the other hand, indicates that SiF3 under the conditions of Fig. 4 and 7 should rapidly dissociate by| |  | (11) |
The sequence of reactions (10) and (11), i.e.| |  | (12) |
then corresponds to a process which is catalyzed by the reactant SiF2 and which is much faster than the slow thermal dissociation of SiF2 by reaction (9). We found no evidence against the assumption that reaction (12) proceeds until SiF2 is completely consumed and converted to SiF + F. In this case, the final absorption levels of Fig. 4 and 7 can be attributed exclusively to SiF and high-temperature absorption cross sections of SiF can also be derived. Values of σ/10−17 cm2 = 1.0, 2.2, 1.3, 0.9, 0.5, 0.3, 0.4, 0.5, 0.8, 0.6, and 0.2 were determined near 3000 K for wavelengths of 200, 210, 220, 230, 240, 250, 260, 270, 280, 290, and 300 nm, respectively. It is known that SiF has numerous band systems from the vacuum-UV to the red (see a summary in ref. 23). At high temperatures, hot bands from these systems overlap into a broad quasi-continuum, extending beyond that from SiF2, but intense enough to be observed. The oscillator strengths of the band systems of SiF and SiF2 in the ESI† were modelled to be of similar magnitude, which appears consistent with the present observations.
 |
| | Fig. 7 As Fig. 1, but at 265 nm, showing the formation of SiF in the consumption of SiF2 by reaction (12) (reflected shock wave with T = 3080 K, [Ar] = 3.8 × 10−5 mol cm−3, 210 ppm of Si(CH3)2F2 in Ar). | |
Evaluating SiF2 consumption and SiF formation from experiments like Fig. 7, led to rate constants k10 in the range 1011–1012 cm3 mol−1 s−1 between T = 1900 and 3500 K, respectively. Experiments with varying reactant concentrations led to similar values which supported the proposed interpretation. One may finally ask for the fate of the F atoms from the net reaction (12). This question could not be answered here. It may be that leftover C2H6 and CH3 from the precursor act as a sink for these atoms. Evidence for an interference with the described mechanism of reactions (10) and (11) was not found. It should finally be mentioned that absorption signals like Fig. 7 at higher temperatures and higher reactant concentration show a decrease with time, before another increase sets in. These observations are similar as those found in the fluorocarbon system.11 An analogous interpretation by secondary reactions like SiF + SiF → Si2F + F, followed by Si2F → Si2 + F, would appear possible, but cannot be confirmed at this stage. More details of the suggested autocatalytic reaction sequence of reactions (10) and (11) clearly have to be explored.
Conclusions
The present work illustrated that the thermal dissociation of Si(CH3)2F2 is a suitable source for generating SiF2 under high-temperature conditions such as studied in shock waves. On the one hand, this allowed to record and calibrate the temperature- and wavelength-dependence of UV absorption cross sections of SiF2. The wavelength-integrated absorption cross section here was found to be consistent with the value derived from the radiative lifetime of the species at room temperature.12 In future work on high-temperature reactions of SiF2, the absorption cross sections from eqn (3) will serve for quantitative determinations of SiF2 concentrations.
In addition to the study of the UV spectrum of SiF2, the thermal dissociation of Si(CH3)2F2 could be studied under conditions where the reaction is unimolecular. The reaction was found to be not far from its high-pressure limit. A quantum-chemistry based modelling of the rate constant gave results in close agreement with the experiments, which confirmed the reliability of the modelling approach. The falloff curves of the unimolecular reaction could best be represented with asymmetric broadening factors in the form suggested in ref. 14 and 15.
It was finally suggested that the consumption of SiF2 under the applied conditions did not proceed by thermal unimolecular dissociation, but by an autocatalytic process, i.e. via a sequence of the steps SiF2 + SiF2 → SiF + SiF3, followed by SiF3 → SiF2 + F. An analogy to the reaction sequence CF2 + CF2 → CF + CF3, followed by CF3 → CF + F, as observed in high-temperature fluorocarbon chemistry appears obvious.
Conflicts of interest
There are no conflicts of interest to report.
Acknowledgements
Discussions of this work with Klaus Hintzer and Arne Thaler as well as financial support by the Deutsche Forschungsgemeinschaft (Project TR69/20-1) are gratefully acknowledged. Open Access funding provided by the Max Planck Society.
References
- V. M. Donnelly, Review article: Reactions of fluorine atoms with silicon, revisited, again, J. Vac. Sci. Technol., A, 2017, 35, 05C202 CrossRef.
- A. C. Stanton, A. Freedman, J. Worthoudt and P. P. Gaspar, Gas phase reactions of SiF2 with F2 and Cl2, Chem. Phys. Lett., 1985, 122, 190–195 CrossRef CAS.
- D. R. Harding and D. Husain, Kinetics of SiF(X 2Πr) by time-resolved molecular resonance absorption spectroscopy following the reaction of Si(3 3PJ, 3 1D2, 3 1S0), generated by pulse irradiation, with fluorinated compounds, J. Chem. Soc., Faraday Trans. 2, 1986, 937–952 RSC.
- H. F. Winters and I. C. Plumb, Etching reactions for silicon with F atoms: Product distributions and ion enhancement mechanisms, J. Vac. Sci. Technol., B, 1991, 9, 197–207 CrossRef CAS.
- S. Vanhaelemeersch, J. Van Hoeymissen, D. Vermeylen and J. Peeters, SiF2 as a primary desorption product of Si etching by F atoms: Interpretation of laser-induced fluorescence spectra; rate constant of the gas phase SiF2 + F reaction, J. Appl. Phys., 1991, 70, 3892–3898 CrossRef CAS.
- N. S. J. Braithwaite, J. P. Booth and G. Cunge, A novel electrostatic probe method for ion flux measurements, Plasma Sources Sci. Technol., 1996, 5, 677–684 CrossRef CAS.
- S. Konieczny, P. P. Gaspar and J. Wormhoudt, Flow pyrolysis of hexafluorodisilane as a source of highly reactive difluorosilylene, J. Organomet. Chem., 1986, 307, 151–155 CrossRef CAS.
- S. C. Bains, P. N. Noble and R. Walsh, Kinetics and mechanism of the gas-phase pyrolysis of hexafluorodisilane in the presence of iodine and some reactions of silicon difluoride, J. Chem. Soc., Faraday Trans. 2, 1986, 837–847 RSC.
- C. J. Cobos, A. E. Croce, K. Luther, L. Sölter, E. Tellbach and J. Troe, Experimental and modeling study of the reaction C2F4 (+M) → CF2 + CF2 (+M), J. Phys. Chem. A, 2013, 117, 11420–11429 CrossRef CAS PubMed.
- C. J. Cobos, G. Knight, L. Sölter, E. Tellbach and J. Troe, Kinetic and spectroscopic studies of the reaction of CF2 with H2 in shock waves, J. Phys. Chem. A, 2017, 121, 7827–7834 CrossRef CAS PubMed.
- C. J. Cobos, K. Hintzer, L. Sölter, E. Tellbach, A. Thaler and J. Troe, High-temperature fluorocarbon chemistry revisited, J. Phys. Chem. A, 2021, 125, 5626–5632 CrossRef CAS PubMed.
- M. Kogelschatz, G. Cunge and N. Sadeghi, Identification of halogen containing radicals in silicon etching plasmas and density measurement by UV broad band absorption spectroscopy, J. Phys. D: Appl. Phys., 2004, 37, 1954–1964 CrossRef CAS.
- S. Sharpe, B. Hartnett, H. S. Sethi and D. S. J. Sethi, Absorption cross sections of CF2 in the A 1B1 →X 1A1 transition at 0.5 nm intervals and absolute rate constant for 2 CF2 →C2F4 at 298 K ± 3 K, J. Photochem., 1987, 38, 1–13 CrossRef CAS.
- J. Troe and V. G. Ushakov, Revisiting falloff curves of thermal unimolecular reactions, J. Chem. Phys., 2011, 135, 054304 CrossRef CAS PubMed.
- J. Troe and V. G. Ushakov, Representation of “broad “ falloff curves for dissociation and recombination reactions, Z. Phys. Chem., 2014, 228, 1–10 CrossRef CAS.
- C. J. Cobos, K. Hintzer, L. Sölter, E. Tellbach, A. Thaler and J. Troe, Shock wave and modelling study of the UV spectra of perfluorocarbon iodides and perfluorocarbon radicals, Combust. Flame, 2021, 224, 177–182 CrossRef CAS.
- R. Roberge, C. Sandorfy, J. I. Matthews and O. P. Strausz, The far ultraviolet and HeI photoelectron spectra of alkyl and fluorine substituted silane derivatives, J. Chem. Phys., 1978, 69, 5105–5112 CrossRef CAS.
- K. Glänzer, M. Quack and J. Troe, High temperature UV absorption and recombination of methyl radicals in shock waves, Proc. Combust. Inst., 1977, 16, 949–960 CrossRef.
- J. P. Booth, G. Cunge, F. Neuilly and N. Sadeghi, Absolute radical
densities in etching plasmas determined by broad-band UV absorption spectroscopy, Plasma Sources Sci. Technol., 1998, 7, 423–430 CrossRef CAS.
- P. Sulzer and K. Wieland, Intensitätsverteilung eines kontinuierlichen Absorptionsspektrums in Abhängigkeit von Temperatur und Wellenzahl, Helv. Phys. Acta, 1952, 25, 653–676 CAS.
- J. Troe, Predictive possibilities of unimolecular rate theory, J. Phys. Chem., 1979, 83, 114–126 CrossRef CAS.
- J. Troe, Theory of thermal unimolecular reactions in the falloff range. I. Strong collision rate constants, Ber. Bunsenges. Phys. Chem., 1983, 87, 161–169 CrossRef CAS.
-
R. W. B. Pearse and A. G. Gaydon, The Identification of Molecular Spectra, 3rd edn, Chapman and Hall, London, 1963 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03298d |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
L.
Sölter
a,
L.
Sölter
 bc,
E.
Tellbach
bc,
E.
Tellbach
 bc and
J.
Troe
bc and
J.
Troe
 *bc
*bc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−193.5 kJ mol−1/RT) s−1, directly produces SiF2.7,8 The thermal dissociation of SiF4, on the other hand, in a sequence SiF4 → SiF3 → SiF2 also leads to SiF2, but, because of the large thermal stability of SiF4, requires considerably higher temperatures than the dissociation of Si2F6. In the present work, instead of Si2F6 or SiF4, it appeared more suitable to use Si(CH3)2F2 as the precursor for SiF2. This compound is easy to handle in shock wave experiments and, at comparably low temperatures, it forms SiF2 in a sequence of the two steps
exp(−193.5 kJ mol−1/RT) s−1, directly produces SiF2.7,8 The thermal dissociation of SiF4, on the other hand, in a sequence SiF4 → SiF3 → SiF2 also leads to SiF2, but, because of the large thermal stability of SiF4, requires considerably higher temperatures than the dissociation of Si2F6. In the present work, instead of Si2F6 or SiF4, it appeared more suitable to use Si(CH3)2F2 as the precursor for SiF2. This compound is easy to handle in shock wave experiments and, at comparably low temperatures, it forms SiF2 in a sequence of the two steps

 , were determined by quantum-chemical calculations as described in the ESI†).
, were determined by quantum-chemical calculations as described in the ESI†).

 (SiF2, λ) dλ (between 195 and 255 nm) is equal to 4.3 (±1) × 10−23 cm3, being close to the value 5.2 × 10−23 cm3 derived in ref. 12 from the experimental radiative lifetimes of SiF2 from ref. 19.
(SiF2, λ) dλ (between 195 and 255 nm) is equal to 4.3 (±1) × 10−23 cm3, being close to the value 5.2 × 10−23 cm3 derived in ref. 12 from the experimental radiative lifetimes of SiF2 from ref. 19.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{−tanh(θ0/2T) [(ν − ν0)/Δν0]2}
exp{−tanh(θ0/2T) [(ν − ν0)/Δν0]2}![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 cm−1, and Δν0 ≈ 1785 cm−1. The determination of the parameter θ0 requires experiments over larger temperature ranges. In the present case, experiments were extended up to temperatures of 3200 K where Si(CH3)2F2 decomposes in less than a μs. Fig. 4 shows an example for 3060 K. Instead of staying constant as in Fig. 1, the signal here decreases by secondary reactions which will be analyzed later. Nevertheless, the absorption cross section of SiF2 can be determined before this decay becomes a problem (e.g., after 10 μs in Fig. 4). Selected results are included in Fig. 3 and compared with a Sulzer–Wieland plot using θ0 ≈ 3000 K. This value of θ0 is relatively uncertain. It is mainly based on measurements at 222 nm and it is definitely larger than the corresponding value9 for the spectrum of CF2 (it should be mentioned that the present results are consistent with values derived from the thermal dissociation of SiF4 which will be reported separately, thus supporting the described analysis). It should also be mentioned that absorption-time signals at wavelengths larger than 240 nm increasingly deviate from Fig. 1. Apparently, absorptions from other species here are superimposed on the absorptions from SiF2, such as analyzed below.
045 cm−1, and Δν0 ≈ 1785 cm−1. The determination of the parameter θ0 requires experiments over larger temperature ranges. In the present case, experiments were extended up to temperatures of 3200 K where Si(CH3)2F2 decomposes in less than a μs. Fig. 4 shows an example for 3060 K. Instead of staying constant as in Fig. 1, the signal here decreases by secondary reactions which will be analyzed later. Nevertheless, the absorption cross section of SiF2 can be determined before this decay becomes a problem (e.g., after 10 μs in Fig. 4). Selected results are included in Fig. 3 and compared with a Sulzer–Wieland plot using θ0 ≈ 3000 K. This value of θ0 is relatively uncertain. It is mainly based on measurements at 222 nm and it is definitely larger than the corresponding value9 for the spectrum of CF2 (it should be mentioned that the present results are consistent with values derived from the thermal dissociation of SiF4 which will be reported separately, thus supporting the described analysis). It should also be mentioned that absorption-time signals at wavelengths larger than 240 nm increasingly deviate from Fig. 1. Apparently, absorptions from other species here are superimposed on the absorptions from SiF2, such as analyzed below.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−58
exp(−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 K/T) s−1
400 K/T) s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−61
exp(−61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 980 K/T) cm3 mol−1 s−1
980 K/T) cm3 mol−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F(x) ≈ log
F(x) ≈ log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fcent/[1 + (log
Fcent/[1 + (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x/N)2]
x/N)2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2/ln(2/Fcent)] [1 – b + b(x/x0)q], q = (Fcent − 1)/ln(Fcent/10), and the parameters x0 and b close to x0 = 1(±0.1) and b = 0.2(±0.05)). The comparison of the two alternative expressions for falloff curves with the experimental data in Fig. 5 suggests that the asymmetric form of F(x), i.e.Eqn (8), near to the high-pressure limit performs much better than the symmetric form of F(x), i.e.Eqn (7).
2/ln(2/Fcent)] [1 – b + b(x/x0)q], q = (Fcent − 1)/ln(Fcent/10), and the parameters x0 and b close to x0 = 1(±0.1) and b = 0.2(±0.05)). The comparison of the two alternative expressions for falloff curves with the experimental data in Fig. 5 suggests that the asymmetric form of F(x), i.e.Eqn (8), near to the high-pressure limit performs much better than the symmetric form of F(x), i.e.Eqn (7).



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−72
exp(−72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 K/T) cm3 mol−1 s−1 has been modelled analogous to the calculations described in the present ESI,† such that SiF2 would have a half-life of about 7 s; likewise, the final absorption level of Fig. 4 cannot correspond to a dissociation equilibrium SiF2 ↔ SiF + F). An unambiguous interpretation of the signal, instead, is provided by measurements at wavelengths where an absorption from SiF2 can be neglected. Fig. 3 indicates that, even at the temperature of Fig. 4, an absorption signal from SiF2 should be negligible at wavelengths larger than about 250 nm. Fig. 7 gives an example for a wavelength of 265 nm and nearly the same temperature as in Fig. 4. The initial decay of the SiF2 signal from Fig. 4 now is mirrored by an absorption increase in Fig. 7. The rate of the initial decay of SiF2 in Fig. 4 and the formation of a reaction product in Fig. 7 both were found to increase proportional to [SiF2](t = 0), i.e. the observation corresponds to a bimolecular process. In addition, the rate constant for this process was found to have an only small positive temperature coefficient. These observations suggest that SiF2 is consumed by a reaction
910 K/T) cm3 mol−1 s−1 has been modelled analogous to the calculations described in the present ESI,† such that SiF2 would have a half-life of about 7 s; likewise, the final absorption level of Fig. 4 cannot correspond to a dissociation equilibrium SiF2 ↔ SiF + F). An unambiguous interpretation of the signal, instead, is provided by measurements at wavelengths where an absorption from SiF2 can be neglected. Fig. 3 indicates that, even at the temperature of Fig. 4, an absorption signal from SiF2 should be negligible at wavelengths larger than about 250 nm. Fig. 7 gives an example for a wavelength of 265 nm and nearly the same temperature as in Fig. 4. The initial decay of the SiF2 signal from Fig. 4 now is mirrored by an absorption increase in Fig. 7. The rate of the initial decay of SiF2 in Fig. 4 and the formation of a reaction product in Fig. 7 both were found to increase proportional to [SiF2](t = 0), i.e. the observation corresponds to a bimolecular process. In addition, the rate constant for this process was found to have an only small positive temperature coefficient. These observations suggest that SiF2 is consumed by a reaction




