Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
What can we learn from transition path time distributions for protein folding and unfolding?
Rajesh
Dutta
 and
Eli
Pollak
and
Eli
Pollak
 *
*
Chemical and Biological Physics Department, Weizmann Institute of Science, 76100 Rehovot, Israel. E-mail: eli.pollak@weizmann.ac.il
First published on 7th October 2021
Abstract
Recent advances in experimental measurements of transition path time distributions have raised intriguing theoretical questions. The present interpretation of the experimental data indicates a small value of the fitted transition path barrier height as compared to the barrier height of the unfolded to folded transition. Secondly, as shown in this paper, it is essential to analyse the experimental data using absorbing boundary conditions at the end points used to determine the transition paths. Such an analysis reveals long time tails that have thus far eluded quantitative theoretical interpretation. Is this due to uncertainty in the experimental data or does it call for a rethinking of the theoretical interpretation? A detailed study of the transition path time distribution using a diffusive model leads to the following conclusions. a. The present experimental data is not accurate enough to discern between functional forms of bell shaped free energy barriers. b. Long time tails indicate the possible existence of a “trap” in the transition path region. c. The “trap” may be considered as a well in the free energy surface. d. The long time tail is quite sensitive to the form of the trap so that future measurements of the long time tail as a function of the location of the end points of the transition path may make it possible to not only determine the well depth but also to distinguish between different functional forms for the free energy surface. e. Introduction of a well along the transition path leads to good fits with the experimental data provided that the transition path barrier height is ∼3kBT, substantially higher than the estimates of ∼1kBT based on bell shaped functions. The results presented here negate the need of introducing multi-dimensional effects, free energy barrier asymmetry, sub-diffusive memory kernels or systematic ruggedness to explain the experimentally measured data.
1 Introduction
Understanding the folding and unfolding dynamics of biomolecules of proteins and nucleic acids from the perspective of both theory1–5 and experiment6–15 has been an important aim in recent years, especially in view of the experimental results. The folding and unfolding dynamics is generally understood in terms of a transition in a multidimensional free energy landscape. In a simplified approach, one describes the transition as one-dimensional diffusion in a free energy landscape with two minima separated by a barrier whose height is much larger than the thermal energy. As a result, the biomolecules predominantly spend the time near one of the minima; the top of the barrier is rarely visited. Transition paths are the relatively rare traversals of the molecule as it leaves one minimum, moves across the barrier to end up in the other minimum. In principle, transition paths contain microscopic information on the folding and unfolding dynamics. However, as transition paths are short-lived as compared to the dwell times in the respective wells, it is experimentally challenging to observe the transition event. It is thus remarkable that recent advances in temporal resolution of single molecule experiments have made it possible to observe the transition and measure not only the mean transition path time8,9 but also the detailed transition path time distribution.The first such measurements of the detailed transition path time distribution11 were explained in terms of a one dimensional diffusion equation in which the shape of the barrier was assumed to be parabolic. Fitting the experimental results to such a theory leads to two parameters. One is a frictional time scale, the other a reduced (in terms of the thermal energy) transition path barrier height (Utp/kBT). The results were intriguing. Foremost, the resulting barrier height was found to be an order of magnitude lower than that of the known barrier heights of the thermal transition obtained from the residence times in each well. Secondly, one should understand why a Smoluchowski equation description is at all a valid tool for describing the dynamics. Thirdly, as considered in some detail in this paper, the theory as employed thus far is not able to account correctly for the long time tail of the distribution, which typically is much longer than predicted by the parabolic barrier diffusion model (with absorbing boundary conditions). Fourthly, isn't the one dimensional parabolic barrier model too simplistic? What is the role of added dimensions? Finally, the diffusion equation assumes a Markovian process, why is this justified? Shouldn't memory play a role?
These challenges have led to a flurry of theoretical activity. As suggested in ref. 17 it is now well understood that the transition path barrier height (Utp) should be smaller than the true barrier height (U) since the experiment measures the transition path time distribution for two points located on either side of the barrier but still distant from the wells. Indeed, it was suggested already in ref. 17 that by changing the initial and final points of measurement, one should be able to extract information about the shape of the free energy surface.
The justification for the use of a Smoluchowski equation to describe the transition path time distribution is based on a coarse grained picture of the barrier crossing dynamics. The accepted picture is that the transition is in reality a series of uncorrelated transitions between the many microstates that exist along the reaction path. The hops between the microstates are random, therefore as a reasonable zero-th order approximation the motion is diffusive hopping between nearest neighbor sites, without memory. van Kampen16 showed that when taking this picture to the continuum limit, the discrete master equation which describes the hopping transitions between nearest neighbor microstates of the protein reduces to the Smoluchowski equation. The “friction coefficient” within this picture is related to the mean time spent in the microstates before escaping them. This mean time is long, as compared to the time scale of vibrational motion, and assumed to be dominated by the entropic barriers separating the microstates. The free energy barrier heights themselves cannot be too large, as the overall barrier height measured for the folding–unfolding transition is ∼10kBT.
The question of memory effects has received much attention.17–22 Using the normal mode transformation23–25 as applied to dissipative dynamics,26 it was possible to derive analytic expressions for the transition path time distribution in the presence of a parabolic barrier and memory friction.17 Subsequently, the effects of the inertial term in a generalized Langevin equation description of the dynamics as well as memory effects were studied at length by many researchers in the field.22,27 Makarov and co-workers incorporated memory by implementing models that are based on the fractional Fokker–Planck equation and fractional Brownian motion.18,19 They also explored the effect of memory on the time duration of transition paths using the generalized Langevin equation with an exponential memory kernel.21 Carlon and coworkers extended the study by invoking a power-law-type memory kernel.20 The inclusion of such a memory kernel broadens the distribution when the motion is sub-diffusive, leading to a longer time tail, but not sufficiently long to agree with the experimental observations.
The effect of the shape of the barrier-whether parabolic, symmetric, or asymmetric, was studied by Carlon and co-workers.28 They showed that asymmetry could lead to a broadening of the transition path time distribution. Metzler et. al.,29 using a simplistic model, investigated the role of ruggedness30 of the free energy profile on the transition path time distribution. Yet, the upshot of all this work was that the experimentally measured distributions on the one hand could not affirm whether memory was important, nor could one derive from them a characteristic memory time. The long time tails were not accounted for, and the experimental data was not sufficient for determining how anharmonic or asymmetric the free energy surface is.
In principle, it should be possible to extract the shape of the free energy barrier from the experimentally determined time distribution.31 Unfortunately, although possible in principle, experimental inaccuracies and complications associated with the coupling of the molecules to the tethers make this inversion as of now, indefinitive. As noted by Covino et. al.,31 “even exponentially small inaccuracies in the observed committor lead to large errors in the barrier height of the reconstructed molecular free energy profile.”
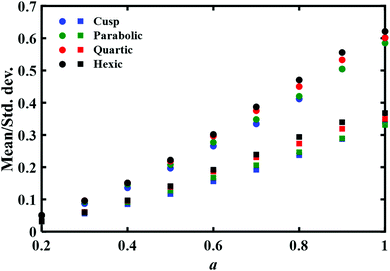
Multidimensional effects were also studied in depth. Satija, Berezhkovskii and Makarov32 introduced a coefficient of variation which is the ratio of standard deviation of the time distribution to its mean as a criterion for multidimensionality. They showed that for a one-dimensional diffusive model the coefficient of variation is always lower than unity. Values which are greater than unity indicate not only a broadening of the distribution, but that this results from multidimensional effects. Interestingly, as we also show below, for the available experimental results for the folding transition of DNA hairpins and Prp proteins, the observed coefficient of variation is lower than one. Multidimensional effects on protein folding have been studied rather intensively in recent years.33–35 However, these too have not led to firm conclusions, based on the experimentally determined distributions.
It is with this background in mind that one may ask, if so, what can one learn from the measured transition path time distributions. Is it only two parameters, a barrier and friction time scale, or can one elucidate more information from the experimentally measured distributions or suggest further experiments which could provide more insight into the actual transition dynamics and what governs them? Is the transition path barrier really of the order of 1kBT? The purpose of this paper is to provide at least partial answers to these questions.
The transition path time is in principle, sensitive to the shape of the barrier. In Section 2, using the Smoluchowski equation (with absorbing boundary conditions) we investigate the transition path dynamics for different barrier shapes: cusped, parabolic, quartic and hexic. We try to understand what can be gleaned from the experimental data, if one changes the extent of the transition region. As already noted in ref. 17, the larger the distance between the end-points used to measure the transition path time distribution from the barrier top, the higher is the transition path barrier, so that one should, at least in principle, by measuring this width dependence, obtain information on the barrier shape. Solving the diffusion equation numerically for parabolic, quartic, hexic and cusped potential models we find that although such experiments would provide information on the overall distance dependence of the barrier, the experimental noise prevents one from distinguishing between different functional forms.
Inspection of Fig. 3 of ref. 11 shows excellent agreement of the measured transition path time distribution with an analytic expression based on diffusive dynamics on a parabolic barrier with open boundary conditions. Alas, the experimental conditions used to measure the transition path time distribution are absorbing boundary conditions. This implies that the theoretical transition time would be shorter than that obtained from a theory based on open boundary conditions, since with absorbing boundaries there are no recrossings of the endpoints defining the transition region. We find in Section 2, that indeed, using absorbing boundary conditions reveals a long time tail in the experimental distribution, which thus far has not been accounted for.
In Section 3 we study the long time tails and their cause. Although anharmonicity affects the long time tails, the assumption of a bell shaped barrier whether symmetric or not, is not sufficient to explain the measured results. Since the transition path is in principle characterized by many microstates, there is no reason to assume a-priori, that the free energy surface is a simple single barrier separating the folded and unfolded states. A few previous experiments have indicated the possibility of “traps” mediating between the unfolded and folded states.36,37 The experimentally measured long time tails suggest that perhaps there exists a trap in the transition region which prevents a rapid crossing. With this in mind, we consider the effect of introducing a well along the free energy surface separated by barriers from the folded and unfolded states. We find that such a model not only accounts for the long time tails, it also suggests that the transition path free energy barrier measured in the experiments is of the order of ∼3kBT, while the transition path well depth is similar. Considering that the barrier separating the folded and unfolded states is of the order of ∼10kBT, this also removes the puzzling more than order of magnitude difference between the transition path barrier height and the true barrier height as reported in ref. 11. Furthermore, we find that the measured data is sufficient for extracting the well depth of this intermediate state, though one cannot distinguish the functional form of the free energy, both cusped and piece-wise quadratic forms give a good fit to the experimental data.
We conclude with a discussion of the results, suggesting that this present work indicates how experimental data may be further used to elucidate more information on the transition path dynamics, while at the same time, noting the limitations and some remaining open theoretical questions.
2 Transition path distributions for anharmonic barriers
The experimental data reported thus far is based on measuring a distance between two ends of a protein. This distance is readily measured between the local minima of the folded and unfolded proteins. The distance in the folded state is shorter than in the unfolded state. In the experiments one chooses two points whose distance lies half way between the distance of the minima. The transition path time is then defined as the time required to reach one of the boundaries starting from the other. It cannot be over-stressed that the experimental data is obtained by stopping the trajectory as soon as it reaches the end point. In other words the experimental distribution is obtained with absorbing boundary conditions. The distribution of times is then called the transition path time distribution.Here, we simulate this process by considering diffusive dynamics along a one dimensional reaction coordinate x. The diffusive (Smoluchowski) equation we use is
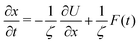 | (1) |
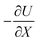 represents the force acting on the particle via the free energy surface U,
represents the force acting on the particle via the free energy surface U, 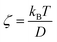 is a friction coefficient, kB denotes Boltzmann's constant, D is the diffusion coefficient and F(t) is a Gaussian random force with zero mean and (Dirac) delta function correlation
is a friction coefficient, kB denotes Boltzmann's constant, D is the diffusion coefficient and F(t) is a Gaussian random force with zero mean and (Dirac) delta function correlation| 〈F(t)〉 = 0 〈F(t)F(t′)〉 = 2ζkBTδ(t − t′) | (2) |
Numerical results are obtained by iterating eqn (1) with a discretized reduced time step. This is done on an equal footing for both experimental systems considered in this paper by scaling the time with the frequency factor 6 × 104 s−1 for the DNA hairpin and 3 × 103 s−1 for the Prp proteins. The (reduced) time step used in both cases was chosen to be 10−3. Distances are rescaled with L = 2.5 nm for both proteins.11,38 The Euler–Maruyama method is used to solve the stochastic differential equation.39 The transition path time for a single trajectory is obtained by imposing an absorbing boundary at the initial and final positions. The transition path sample size was 106 trajectories in each case studied.
The model barrier potentials we used are: cusped, parabolic, quartic and hexic potentials as shown in Fig. 1. We use dimensionless variables throughout so as to put the discussion of the various potentials on the same footing. The dimensionless symmetric cusped potential barrier is written as
βU(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = −βFL| ) = −βFL|![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) |; | |; |![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) | ≤ a; F > 0 | ≤ a; F > 0 | (3) |
 and L is the distance between the folded and unfolded minima, F is the absolute value of the force acting on the particle. βFL represents the reduced transition path barrier height. 2a denotes the chosen extent or width of the transition path. The symmetric parabolic, quartic and hexic (reduced) barrier potentials are
and L is the distance between the folded and unfolded minima, F is the absolute value of the force acting on the particle. βFL represents the reduced transition path barrier height. 2a denotes the chosen extent or width of the transition path. The symmetric parabolic, quartic and hexic (reduced) barrier potentials areβU(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = −βk1L2 ) = −βk1L2![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 2; −a ≤ 2; −a ≤ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≤ a; k1 > 0 ≤ a; k1 > 0 | (4) |
βU(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = −βk2L4 ) = −βk2L4![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 4; −a ≤ 4; −a ≤ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≤ a; k2 > 0 ≤ a; k2 > 0 | (5) |
βU(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) = −βk3L6 ) = −βk3L6![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) 6; −a ≤ 6; −a ≤ ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ≤ a; k3 > 0 ≤ a; k3 > 0 | (6) |
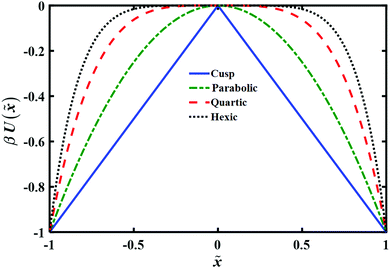 | ||
Fig. 1 Plot of model potentials used to study the transition path time distribution. The potential energy U(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) is given in units of kBT and the distance ) is given in units of kBT and the distance ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) is in units of L, as explained in the text. is in units of L, as explained in the text. | ||
In order to obtain the transition path time distribution, one needs to consider that the trajectories enter the transition region by crossing the left boundary located at −a and arrive at the right boundary a without returning to the initial position. The transition path time pTP is then defined as
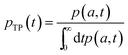 | (7) |
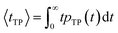 | (8) |
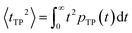 | (9) |
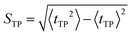 | (10) |
There are two striking results in this figure. On the one hand as expected, the mean time increases as the distance a between the endpoints increases. This implies that it would be worthwhile to repeat such a computation with the experimental data. The dependence of the mean time on the distance may be inverted to give the general shape of the free energy barrier. On the negative side, the second important result is that this mean time and its standard deviation are only weakly dependent on the functional form of the barrier. Given the uncertainty in any experimental measurement of the mean time it would not be possible to associate experimentally measured results with a specific barrier shape. We also note that the difference between the mean times and standard deviations for different barriers becomes more prominent as the distance a increases, which amounts also to an increase in the physical barrier height between the endpoints. Yet the differences would not be discernible at the present accuracy of the experimental data. The experimental error bars reported in the measured transition path times are ≈7% for the DNA hairpin and 20% for the Prp protein,11 which would mask the mean time differences shown in Fig. 2. Similar error bars were also reported (Fig. 5 of ref. 12) in sequence dependent transition path times for a DNA hairpin.12
A comparison between the theoretical transition path time distributions for the different barrier shapes with the experimentally measured time distribution for a DNA hairpin molecule is shown in Fig. 3. The experimental distribution is adapted from ref. 11 and normalized to unit area, as are the theoretical distributions shown in the Figure. The time scale is reduced using the experimentally fitted frequency factor 6 × 104 s−1. In other words the barrier height and time scales are identical to the ones used in the experimental fit of the data as reported in ref. 11. The differences are in the barrier shapes. The results presented in the Figure reveal a long time tail in the experimental distribution which is not there in the numerical results obtained from the diffusion equation. Inspection of Fig. 3 of ref. 11 shows excellent agreement between theory and experiment. What happened? Underlying this discrepancy is the difference between free and absorbing boundary conditions. The excellent agreement found in ref. 11 was obtained with an analytic expression based on free boundary conditions. Such conditions allow for trajectories to cross the endpoints and come back to them, leading to an increase in the transition path time. This is absent when the boundary conditions are absorbing. Thus, one should expect the free boundary condition theory to overestimate long time contributions, and this is striking when considering the results shown in Fig. 3. The free energy parabolic barrier obtained in ref. 11 does not account for the long time tail. Neither do the other functional forms investigated here. The anharmonicity of the potential at a fixed transition path barrier height does not account for the long time tail observed in the experimentally measured distribution. It has been suggested that a flattening of the barrier top would increase the time to cross the barrier4 and thus account for the long time tail. However, as may be inferred from the distributions shown in Fig. 3, flattening of the barrier, as one goes from a parabolic to a hexic barrier, fails to significantly increase the mean time and does not account for the long time tail measured experimentally.
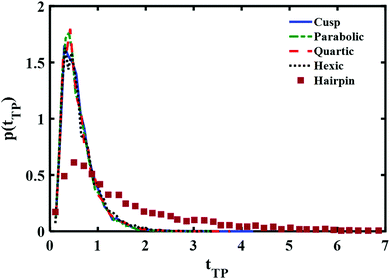 | ||
| Fig. 3 Comparison of the normalized (to unity) transition path time distributions at reduced transition path barrier height βUtp = 1. Distributions obtained with three different symmetric barrier functional forms are compared with the experimentally measured distribution of a DNA hairpin.11 | ||
Perhaps though the long time tail is just an artifact of the fitting of theory to experiment? Instead of fitting a free boundary condition theory, one might get a good fit by using the (nonanalytical) results of the simulation with absorbing boundary conditions. This is studied in Fig. 4 using a parabolic barrier. The measured distributions are functions of two parameters, a barrier height and frequency which are intertwined when the distance between the end points is fixed (see eqn (4)) and the diffusion coefficient D. Reducing the barrier frequency would lead to a longer time but would also reduce the barrier height, moving the maximum of the distribution to lower times. It is also apparent from Fig. 4 that although a reduction of barrier height may affect the long time tail of the distribution to some extent, it is not sufficient to explain the experimental result. Similarly, reduction of the diffusion coefficient from D = 1 (6 × 104L2 nm2 s−1) to D = 0.5 (3 × 104L2 nm2 s−1) leads to a longer time tail. However, the maximum of the distribution also shifts to longer times in disagreement with the experimental results. Hence, the observed long time tail challenges us to find an explanation for it.
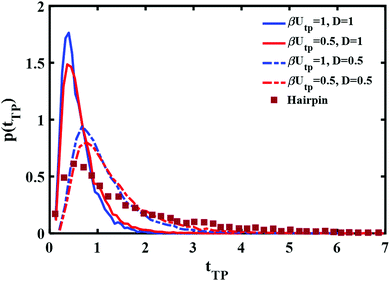 | ||
| Fig. 4 Parabolic barrier based transition path time distributions with absorbing boundary conditions and different barrier heights and diffusion coefficients are compared with the experimentally measured distribution of a DNA hairpin.11 | ||
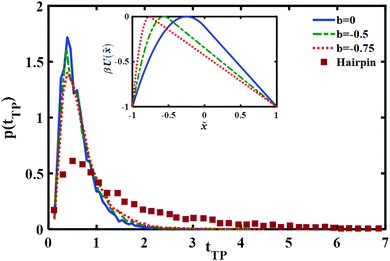
In a recent study, transition path times were investigated in presence of an asymmetric barrier.28 To follow up on this suggestion, we varied the degree of asymmetry in the barrier shape to observe its effect on producing the long time tail in the transition path time distribution. The asymmetric barrier potential form we used is defined (using the same reduced parameters as before) as
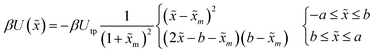 | (11) |
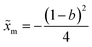 . The potential consists of parabolic and linear regimes. The asymmetry parameter b, indicates the decrease of the extent of the parabolic regime and the concomitant increase in the asymmetry of the barrier. As before, we kept the transition path barrier height fixed at βUtp = 1.
. The potential consists of parabolic and linear regimes. The asymmetry parameter b, indicates the decrease of the extent of the parabolic regime and the concomitant increase in the asymmetry of the barrier. As before, we kept the transition path barrier height fixed at βUtp = 1.
The results are shown in Fig. 5. It is quite evident that although the asymmetry may change somewhat the long time part of the distribution it is not sufficient to account for the experimentally measured long time tail.
3 Possible origin of the experimentally measured long time tails
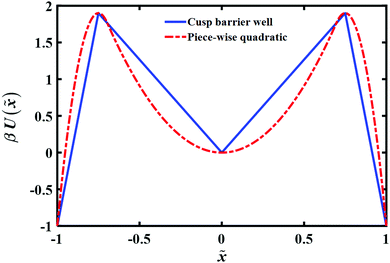
To account for the long time tail of the distribution it would seem from the results of the previous section that a simple bell shaped barrier is insufficient. Intuitively, inserting a well around the barrier top should lead to some trapping and thus could lead to a long time tail. To explore this, we consider in this section the transition path time distributions for two such model potential barriers as shown in (Fig. 6): (a) a cusped well inside a cusped barrier (b) a piece-wise quadratic potential. The potentials are constructed so as to give the same well depths, barrier heights and endpoint locations.The long time tail is mainly affected by two parameters – the extent of the well region and its depth. Increasing each of them will increase the time needed to cross the transition region. To fit the theoretical transition path time distribution one must vary both parameters as they also affect the short time dynamics. Fig. 7 shows the (quadratic) dependence of the mean transition path time on the well depth at a fixed transition path barrier height. One notes that the mean time for the piece-wise quadratic potential grows faster with the well depth as compared to the cusped potential and that the differences may be sufficiently large to be discernible experimentally by varying the location of the endpoints of the transition paths.
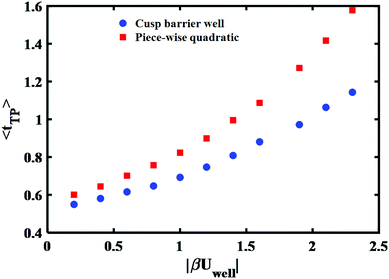 | ||
| Fig. 7 Well depth dependence of the mean transition path time for cusped and piece-wise quadratic barriers. The reduced barrier height is fixed and same as Fig. 6 that is βUtp = 2.9. | ||
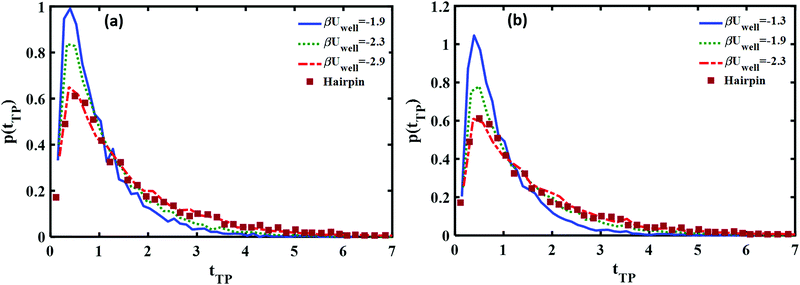
In Fig. 8 we show how the transition path time distributions vary with the well depth and compare them with the experimental distribution for the DNA hairpin. The left panel shows cusped potential results, the right panel is obtained with the piece-wise parabolic potential. The best fits with the experimentally measured distribution for the DNA hairpin are found for βUwell = −2.9 for the cusped potential and βUwell = −2.3 for the piece-wise parabolic potential. The transition path barrier heights for both potentials are βUtp = 2.9. The best fit to the experimental data is obtained by locating the well edges at the (reduced) distances of −0.75 and 0.75. The respective mean (reduced) times are 1.5 and 1.58 in agreement with the experimentally measured mean time of 1.62 ± 0.12.11
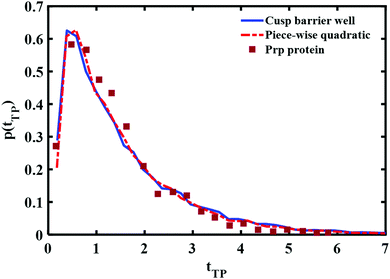
A comparison of the best fit of the theoretical transition time path distributions with the experimentally measured distribution for the Prp protein is given in Fig. 9. In this case, the end points of the wells are ±0.85 and the well depth is βUwell = −2.6 for the cusped potential and βUwell = −1.9 for the piece-wise parabolic potential. The transition path barrier height is βUtp = 2.6 for both potentials. The corresponding (reduced) mean times of 1.54 and 1.5 are in agreement with the experimentally measured values of 1.5 ± 0.3.11
From Fig. 8 and 9, one notes that the fit with the experimental distribution occurs at a smaller well depth for the piece-wise quadratic barrier as compared to the cusped potential. At present, the experimental data which is available only for one distance between the end points of the transition path does not suffice for distinguishing between the two potentials. There is an advantage to considering the cusped potential since analytical expressions have been derived for the mean transition path times.40,41 On the other hand, a smooth potential is more “physical”. In any case, the experimental long time tails seem to indicate the existence of at least one well between the two end points of the experimentally measured transition path times.
We also note that the transition path barrier height we need to fit the experimental data is ∼3kBT, much larger than previously fitted values based on a bell shaped barrier of ∼1kBT. Given that the overall free energy barrier for the unfolded to folded transition is ∼10kBT and that the experimental points of the transition path covered half the distance between the minima of the folded and unfolded structures, one would tend to conclude that the present estimate of the transition path barrier height is more realistic.
4 Discussion
The central goal of the present study was to understand what practical information one can obtain from measured transition path time distributions. The measurement of the transition path time distribution is an impressive achievement, however the study presented here shows that the amount of information that one may glean from such measurements at the present time is limited. The mean transition path time is, as might have been expected, an increasing function of the distance between the endpoints of transition paths. Measurement of the mean transition path time as a function of the distance between the endpoints should then reveal something about the free energy surface between the endpoints. However, as found in the simulations presented here, it is rather difficult to distinguish between different functional bell shaped forms. The present experimental uncertainty in the data does not allow for a unique identification.The study presented in this paper is based on numerical solution of the diffusion equation. This readily allows for obtaining the transition path time distribution using absorbing boundary conditions. The differences between the two boundary conditions are small when considering high transition path barriers (βUtp ≫ 1). However, initially, the experimental data indicated that the barriers are of the order unity, so that differences between the time dependence of the two boundary conditions become significant. Free boundary conditions allow for longer time trajectories. The experimental data are obtained using absorbing boundaries and so should be analysed accordingly. We showed that such an analysis reveals a long time contribution to the transition path time distribution which cannot be accounted for on basis of a theory that assumes only a single bell shaped free energy curve between the two end-points.
This long time tail of the experimental distribution turns out to be most informative. We suggested that it may indicate the existence of a “trap” along the reaction coordinate, which keeps the molecules for a longer time in the transition path region. We have modeled this trap in the form of a single well in the transition region and this suffices for obtaining good agreement between theory and experiment. Moreover, the theoretical results suggest that experimental determination of the mean transition path time as a function of the location of the end points could lead to distinguishing between functional forms for the free energy surface as well as pinpointing the well depth.
One may suggest that such a “trap” need not be a well in the free energy surface but could result from multidimensional effects. As noted in ref. 32 the coefficient of variation (C) of the distribution, defined as
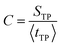 | (12) |
One may consider other explanations for the long time tails such as memory effects. However, thus far, there has been no comparison with experimental data which accounts for the long time tails to justify the claim that the origin is memory. Indeed, we note that including memory in a generalized Langevin equation tends to make the dynamics more conservative (rather than diffusive) and so would shorten the transition time. Using a power law spectral density with coefficient less than unity would increase the transition time.18,20,22 However, this is artificial, one needs to justify the usage of such a power law. In contrast, description of the “trap” as a potential well is “physical” in origin, there is no real reason to postulate that the free energy surface is structure-less.
Recent studies28 show that barrier asymmetry may lead to an increase in the transition path time. We have tested this assumption using asymmetric barriers with different combinations of parabolic and linear potentials and found that even an extreme asymmetric barrier shape, does not account quantitatively for the long time tail. A recent study of transition times with rugged barriers has also not accounted for the long time tails.29
Finally, we note that our suggestion that the long time tail indicates the existence of a trap in the intermediate region, in the form of a well is not “revolutionary”. Previous experiments have indicated the existence of one or multiple wells along the reaction coordinate.36,37,42 What is the physics and chemistry of such wells? This is difficult to answer and calls for much more extensive modelling of the unfolded to folded transition free energy surface.
In summary, based on the diffusion equation study presented here, we conclude that at present the experimental results may be interpreted as indicating the existence of a “trap” in the transition path region. This trap may be modeled successfully using a single well whose depth and range controls the long time tail. From the experimental data we concluded that the well depth is ∼2.5kBT. Adding the well leads to an increase in the estimate of the transition path barrier height to ∼3kBT, which is larger than the original estimate of only a ∼1kBT barrier height and more “reasonable” considering that the transition path length is half of the distance between the folded and unfolded molecules.
The present work also indicates the limitations of the experimental data measured thus far. It provides insight into the free energy surface and its structure, but not very detailed. Experimental uncertainties are too large for determination of the precise shape of the potential. We believe that these results should spur further experimental and numerical studies which could help in uncovering what should be the generic model and free energy surface for protein folding and unfolding and their associated transition path time distributions.
5 Author contributions
R. Dutta contributed to the relevant theory, implemented the computational work and was an equal contributor to the writing up of the manuscript. E. Pollak, suggested the topic, contributed to the theoretical developments and was an equal contributor to the writing up of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by a grant of the Israel Science Foundation and a joint grant of the Israel Science Foundation and the Natural Science Foundation of China.References
- G. Hummer, J. Chem. Phys., 2004, 120, 516–523 CrossRef CAS PubMed.
- A. Berezhkovskii and A. Szabo, J. Chem. Phys., 2005, 122, 014503 CrossRef PubMed.
- B. W. Zhang, D. Jasnow and D. M. Zuckerman, J. Chem. Phys., 2010, 132, 054107 CrossRef PubMed.
- S. Chaudhury and D. E. Makarov, J. Chem. Phys., 2010, 133, 034118 CrossRef PubMed.
- W. K. Kim and R. R. Netz, J. Chem. Phys., 2015, 143, 224108 CrossRef PubMed.
- E. Rhoades, M. Cohen, B. Schuler and G. Haran, J. Am. Chem. Soc., 2004, 126, 14686–14687 CrossRef CAS PubMed.
- H. S. Chung, J. M. Louis and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11837–11844 CrossRef CAS PubMed.
- H. S. Chung, K. McHale, J. M. Louis and W. A. Eaton, Science, 2012, 335, 981–984 CrossRef CAS PubMed.
- K. Neupane, D. B. Ritchie, H. Yu, D. A. Foster, F. Wang and M. T. Woodside, Phys. Rev. Lett., 2012, 109, 068102 CrossRef PubMed.
- H. S. Chung, S. Piana-Agostinetti, D. E. Shaw and W. A. Eaton, Science, 2015, 349, 1504–1510 CrossRef CAS PubMed.
- K. Neupane, D. A. Foster, D. R. Dee, H. Yu, F. Wang and M. T. Woodside, Science, 2016, 352, 239–242 CrossRef CAS PubMed.
- K. Neupane, F. Wang and M. T. Woodside, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1329–1334 CrossRef CAS PubMed.
- K. Neupane, N. Q. Hoffer and M. Woodside, Phys. Rev. Lett., 2018, 121, 018102 CrossRef CAS PubMed.
- H. S. Chung and W. A. Eaton, Curr. Opin. Struct. Biol., 2018, 48, 30–39 CrossRef CAS PubMed.
- N. Q. Hoffer, K. Neupane, A. G. Pyo and M. T. Woodside, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8125–8130 CrossRef CAS PubMed.
- N. G. Van Kampen, Stochastic processes in physics and chemistry, Elsevier, 1992, vol. 1 Search PubMed.
- E. Pollak, Phys. Chem. Chem. Phys., 2016, 18, 28872–28882 RSC.
- R. Satija, A. Das and D. E. Makarov, J. Chem. Phys., 2017, 147, 152707 CrossRef PubMed.
- E. Medina, R. Satija and D. E. Makarov, J. Phys. Chem. B, 2018, 122, 11400–11413 CrossRef CAS PubMed.
- E. Carlon, H. Orland, T. Sakaue and C. Vanderzande, J. Phys. Chem. B, 2018, 122, 11186–11194 CrossRef CAS PubMed.
- R. Satija and D. E. Makarov, J. Phys. Chem. B, 2019, 123, 802–810 CrossRef CAS PubMed.
- D. Singh, K. Mondal and S. Chaudhury, J. Phys. Chem. B, 2021, 125, 4536–4545 CrossRef CAS PubMed.
- E. Pollak, J. Chem. Phys., 1986, 85, 865–867 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- E. Pollak and P. Talkner, Chaos, 2005, 15, 026116 CrossRef PubMed.
- J.-L. Liao and E. Pollak, Chem. Phys., 2001, 268, 295–313 CrossRef CAS.
- M. Laleman, E. Carlon and H. Orland, J. Chem. Phys., 2017, 147, 214103 CrossRef CAS PubMed.
- M. Caraglio, T. Sakaue and E. Carlon, Phys. Chem. Chem. Phys., 2020, 22, 3512–3519 RSC.
- H. Li, Y. Xu, Y. Li and R. Metzler, Eur. Phys. J. Plus, 2020, 135, 1–22 CrossRef.
- R. Zwanzig, Proc. Natl. Acad. Sci. U. S. A., 1988, 85, 2029–2030 CrossRef CAS PubMed.
- R. Covino, M. T. Woodside, G. Hummer, A. Szabo and P. Cossio, J. Chem. Phys., 2019, 151, 154115 CrossRef PubMed.
- R. Satija, A. M. Berezhkovskii and D. E. Makarov, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27116–27123 CrossRef CAS PubMed.
- K. Itoh and M. Sasai, J. Chem. Phys., 2009, 130, 04B611 Search PubMed.
- G. Žoldák and M. Rief, Curr. Opin. Struct. Biol., 2013, 23, 48–57 CrossRef PubMed.
- T. Mori and S. Saito, J. Phys. Chem. B, 2016, 120, 11683–11691 CrossRef CAS PubMed.
- H. Yu, D. R. Dee, X. Liu, A. M. Brigley, I. Sosova and M. T. Woodside, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8308–8313 CrossRef CAS PubMed.
- F. Sturzenegger, F. Zosel, E. D. Holmstrom, K. J. Buholzer, D. E. Makarov, D. Nettels and B. Schuler, Nat. Commun., 2018, 9, 1–11 CrossRef CAS PubMed.
- H. Yu, A. N. Gupta, X. Liu, K. Neupane, A. M. Brigley, I. Sosova and M. T. Woodside, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14452–14457 CrossRef CAS PubMed.
- D. J. Higham, SIAM Rev., 2001, 43, 525–546 CrossRef.
- A. M. Berezhkovskii, L. Dagdug and S. M. Bezrukov, J. Phys. Chem. B, 2017, 121, 5455–5460 CrossRef CAS PubMed.
- A. M. Berezhkovskii, L. Dagdug and S. M. Bezrukov, J. Phys. Chem. B, 2019, 123, 3786–3796 CrossRef CAS PubMed.
- A. Mehlich, J. Fang, B. Pelz, H. Li and J. Stigler, Front. Chem, 2020, 8, 587824 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |