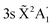Photodissociation of the methyl radical: the role of nonadiabatic couplings in enhancing the variety of dissociation mechanisms

Abstract

The nonadiabatic photodissociation dynamics of the CH₃ (and CD₃) radical from the 3p_z and 3s Rydberg states is investigated by applying a one-dimensional (1D) wave packet model that uses recently calculated ab initio 1D electronic potential-energy curves and nonadiabatic couplings. Calculated predissociation lifetimes are found to be too long as compared to the experimental ones. The 1D dynamical model, however, is able to predict qualitatively and explain the fragmentation mechanisms that produce the hydrogen-fragment translational energy distributions (TED) measured experimentally for the ground vibrational resonance of the 3p_z and 3s Rydberg states (CH₃(v = 0, 3p_z) and CH₃(v = 0, 3s)). The CH₃(v = 0, 3p_z) TED found experimentally displays a rather large energy spreading, while the experimental CH₃(v = 0, 3s) TED is remarkably more localized in energy. The present model also predicts a widely spread CH₃(v = 0, 3p_z) TED, produced by a complex dissociation mechanism which involves predissociation to one dissociative valence state through a nonadiabatic coupling, as well as transfer of population to a second valence state through three conical intersections. Also in agreement with experiment, the model predicts a rather localized CH₃(v = 0, 3s) TED because the conical intersections no longer operate in this photodissociation process, and predissociation occurs only into a single valence state. Another complex dissociation mechanism is predicted by the model for initial CH₃(v > 0, 3s) and CD₃(v > 0, 3s) resonances. In this case the mechanism is gradually activated, as vibrational excitation increases, by the interplay between the two nonadiabatic couplings connecting the 3s and 3p_x,y Rydberg states with the dissociative ²A₁ valence state, and produces complex TEDs with signals from several resonances of both 3s and 3p_x,y. Thus the present 1D quantum model reveals a rich photodissociation dynamics of methyl, where a variety of complex fragmentation mechanisms is favored by the presence of different nonadiabatic couplings between the electronic states involved.

---

1 Introduction

The methyl radical is a metastable species which is the simplest and smallest alkyl radical, being a precursor to other hydrocarbons. The relevance of this species extends to several areas of Chemistry and Physics. Among them, the methyl radical is of great importance in processes of atmospheric chemistry,¹ of formation of complex hydrocarbons in the interstellar medium,² and of hydrocarbon combustion.³

The first ultraviolet absorption spectrum of methyl was reported by Herzberg and Shoosmith,⁴ consisting of a strong transition observed at 216 nm, due to excitation to the 3s Rydberg state. A planar geometry of the CH₃ radical was further identified,⁵ which causes one-photon transitions from the ground state to several excited states to be forbidden. After these seminal spectroscopic works, many other experimental studies on the methyl radical were reported. Among them are two-photon transitions to the 3p_z and 4p_z Rydberg states,⁶ which were used to detect spectroscopically methyl radicals in the gas phase.^7,8 Different studies on the photodissociation dynamics of methyl after excitation of the first electronically excited 3s Rydberg state have also been reported.^9–12 The predissociation dynamics of CH₃ and CD₃ in the 4p_z¹³ and 3s^14,15 states was also investigated.

Despite the relevance of methyl, rather few theoretical studies on the spectroscopy and photodissociation dynamics of this radical species have been reported.^15–18 Restricted Hartree–Fock calculations with a small basis set followed by configuration interaction considering single and double substitutions (RHF-CISD) were carried out¹⁶ to obtain excitation energies to various excited electronic states, and to identify the possible fragmentation pathways CH₃ → CH₂ + H and CH₃ → CH + H₂, for the 3s and 3p Rydberg states. The dominant reaction pathway for the 3p_z state was predicted to be CH₂(¹B₁) + H.

More recently, a joint experimental and theoretical effort to deepen the understanding of the methyl photodissociation dynamics was carried out.^19,20 Experimentally, the real time predissociation dynamics of CH₃ and CD₃ from several vibrational levels of the 3p_z Rydberg state was first investigated.¹⁹ Then, the photodissociation dynamics of CH₃ in both the 3s and 3p_z Rydberg states was further studied by measuring the corresponding H-fragment translational energy and angular distributions.²⁰ On the theoretical side, one-dimensional (1D) multireference configuration interaction (MRCI) ab initio calculations of the potential-energy curves (PEC) of the ground and several excited electronic states were reported along the dissociation coordinate of the fragmentation pathway CH₃ → CH₂ + H.^19,20 In addition to the potential curves of the electronic states, nonadiabatic couplings leading to electronic predissociation from the 3s, 3p_x,y, and 3p_z Rydberg states were calculated, as well as three conical intersections (CI) between the above three Rydberg states and the dissociative ²B₁ and ²A₁ (in C_2v symmetry) valence states were identified, and their corresponding couplings were obtained.²⁰ The calculated electronic PECs and the corresponding couplings between them made possible to provide a qualitative interpretation of the data measured and of the possible methyl fragmentation mechanisms involved.^19,20 Later on, by adding to the C–H dissociative coordinate the HCH bending angle, the first two-dimensional ab initio representation of the potential surfaces of the above ground and excited Rydberg and valence states of CH₃ was generated, along with the couplings between them leading to predissociation of the radical.²¹

The interpretation of the experimental results based on the ab initio calculations relied essentially on the position of the PECs of the different electronic states and of the conical intersections between them.^19,20 Thus, such interpretation is necessarily qualitative and limited in order to propose dynamical mechanisms for the fragmentation of the methyl radical. A dynamics simulation is required to predict possible fragmentation mechanisms. A first attemp in this direction was carried out by simulating the CH₃ fragmentation from several vibrational levels of the 3s and 3p_z states, by applying a one-dimensional quasiclassical trajectory surface hopping method.²² The limitation of the model to a single coordinate describing the C–H fragmentation was imposed by the fact that the couplings associated with the three CI identified are calculated only in that single dimension,²⁰ despite that two-dimensional (2D) ab initio calculations were carried out later on.²¹ The reason was that the ab initio calculations of those very narrow couplings in 2D were very demanding computationally. Predissociation lifetimes and final populations for the different fragmentation channels were computed for all the vibrational levels studied. No H-fragment translational energy distributions were calculated. Possible fragmentation mechanisms were suggested on the basis of the simulation results. Agreement between the classical and the experimental results was also qualitative and rather limited, due to both the restriction of dimensionality and the classical nature of the model used to describe a nonadiabatic fragmentation process involving resonances.

Unfortunately, at present the best ab initio representation available for the methyl electronic states and the couplings between them, including the corresponding conical intersections (which are essential in the fragmentation process, as we shall see below), is still one-dimensional.²⁰ Thus, this limitation cannot be removed in a simulation. However, the classical nature of the previous model can be significantly improved by applying a quantum mechanical one. This has been done in the present work, where the one-dimensional nonadiabatic fragmentation dynamics of both CH₃ and CD₃ has been simulated starting from several vibrational levels of the 3s and 3p_z Rydberg states, by means of a wave packet method. The results obtained show that, despite its very much restricted dimensionality and its qualitative nature, this model is able to explain the most relevant experimental findings, and to predict and propose the likely fragmentation mechanisms involved.

The article is organized as follows. In Section 2 the theoretical methodology applied is described. In Section 3 the results are presented and discussed. Conclusions are given in Section 4.

2 Methodology

Wave paket dynamical simulations

Photodissociation of the methyl radical is described by representing the system in the dissociative coordinate along the fragmentation pathway CH₃ → CH₂ + H. The nonadiabatic frgamentation dynamics of methyl is simulated by means of a 1D wave packet treatment applied in the diabatic representation of the different electronic states involved in the photodissociation process. Such a treatment includes the first five excited electronic states of methyl, namely the three 3s, 3p_x,y, and 3p_z Rydberg states and the two dissociative ²A₁ and ²B₁ valence states, as well as all the nonadiabatic couplings between them. Photodissociation of CH₃ and CD₃ starts from different vibrational levels of the radical in the 3p_z and 3s electronic states (those investigated experimentally^19,20). The nonadiabatic photodissociation dynamics of methyl is simulated by solving the time-dependent Schrödinger equation,where the wave packet Φ is expressed aswhere Q denotes the electronic coordinates, |n〉 denote the five electronic states 3p_z (n = 1), ²B₁ (n = 2), 3p_x,y (n = 3), 3s (n = 4), and ²A₁ (n = 5), r is the dissociative CH₂–H coordinate, and ψ_n(r, t) are the nuclear wave packets generated in the different electronic states during the photodissociation dynamics.

The time evolution of Φ(r, Q, t) is determined by the evolution of the nuclear packets ψ_n(r, t), which is governed by eqn (1) and can be written in matrix form as

In eqn (3)T̂ is the kinetic energy operator of Ĥ, T̂ = −(ħ²/2μ_CH2–H)(∂²/∂r²), with μ_CH2–H being the reduced mass associated with r; the potential terms in the diagonal of the Hamiltonian matrix (V̂_3pz, V̂_²B1,…) are the potential-energy operators associated with the different electronic states; the nonzero off-diagonal terms correspond to the nonadiabatic couplings between the electronic states, with V̂_3pz–²B1, V̂_3px,y–²A1, and V̂_3s–²A1 being the couplings leading to electronic predissociation from the three Rydberg states, and , , and being the couplings associated with the three conical intersections identified previously.²⁰ The time evolution of the ψ_n(r, t) packets of eqn (2) is obtained by solving eqn (3) using the Chebychev polynomial expansion method.²³ In the simulations involving both CH₃ and CD₃ the r coordinate was represented in a uniform grid of 500 equally-spaced points ranging from 1.23 to 15.0 a₀. A time step Δt = 0.3 fs was applied in all the simulations. The total time of the simulations varied depending on the decay lifetime associated with the specific initial vibrational resonance state of CH₃ and CD₃ in the 3p_z and 3s Rydberg electronic states, and it ranged from 0.6 to 9000 ps. Absorbing boundary conditions were applied to the wave packet in the region of the largest CH₂–H distances of the grid, in order to avoid artificial appearance of wave packet amplitude in the short distance region of the grid. The absorbing function applied is f(r) = 1 for r < r_abs and f(r) = e^{−α(r−r_abs)2} for r ≥ r_abs, with r_abs = 12a₀ and α = 0.5a₀².

At t = 0 the initial conditions of eqn (3) are such that ψ_m(r, t = 0) = φ_v(r), with m = 1(4) for simulations starting from the 3p_z(3s) state, while ψ_k(r, t = 0) = 0 for k ≠ 1(4). The φ_v(r) wave function is the vibrational eigenfunction of the resonance state of CH₃ or CD₃ initially populated in either the 3p_z or 3s Rydberg states, and that will decay into the continuum of the CH₂ + H fragments. These wave functions and their associated energies E_v are obtained by solving the time-independent Schrödinger equation,

Ĥ_kφ_v(r) = E_vφ_v(r) (4)

by using a Truhlar–Numerov–Cooley algorithm.^24–30 In eqn (4)k = 3p_z, 3s, and Ĥ_k holds either for Ĥ_3pz = T̂ + V̂_3pz or for Ĥ_3s = T̂ + V̂_3s (i.e., two of the diagonal terms of the Hamiltonian matrix of eqn (3)). A grid of 20 000 equally-spaced points in the range between 1.89 and 6.61 a₀ in the r coordinate was used to solve eqn (4).

3 Results and discussion

Resonance energies and decay lifetimes of CH₃ and CD₃

Fig. 1 displays the potential-energy curves corresponding to the ground electronic state X̃, the three bound 3s , 3p_x,y²E′, and 3p_z Rydberg states, and the two dissociative ²A₁ and ²B₁ valence states along the r coordinate of the H(²S) + CH₂ fragmentation pathway. The locations of the three conical intersections between the Rydberg and the valence states are marked in the figure by arrows, and labelled as CI1 (the CI between 3p_z and the ²A₁ valence state), CI2 (the CI between 3p_x,y and the ²B₁ valence state), and CI3 (the CI between 3s and the ²B₁ valence state). The nonadiabatic couplings leading to electronic predissociation from the Rydberg states, as well as the couplings associated with the conical intersections are depicted in Fig. 6 of ref. 20. The locations of the maximum intensity of the couplings leading to predissociation from the 3p_z and 3s Rydberg states are indicated by vertical arrows pointing upwards in the figure and labelled as NAC. The position of the vibrational energy levels of CH₃(v, 3p_z) and CH₃(v, 3s) are shown in the figure for v = 0–4.

Fig. 1 Potential-energy curves of the ground state , the three bound , 3p_x,y²E′, and Rydberg states, and the two dissociative ²A₁ and ²B₁ valence states as a function of the r coordinate representing the H(²S) + CH₂ fragmentation pathway. The positions of the three conical intersections between the three Rydberg states and the two valence states are indicated by vertical arrows pointing downwards in the figure and labelled as CI1, CI2, and CI3. The regions of maximum intensity of the nanadiabatic couplings leading to predissociation from the 3p_z and 3s Rydberg states are indicated by vertical arrows pointing upwards in the figure and labelled as NAC. Two arrows tilted to the right indicate the passage from 3p_z to ²B₁ and from 3s to ²A₁ through predissociation. The vibrational energy levels of CH₃(v, 3p_z) and CH₃(v, 3s) for v = 0–4 are shown in the corresponding potential-energy curves.

By solving eqn (4) the resonance energies E_v are obtained for the 3p_z, 3p_x,y, and 3s Rydberg states of CH₃ and CD₃, and are collected in Table 1 for the first six vibrational states. The position of the resonance energy levels of CH₃(v, 3p_z) and CH₃(v, 3s) are shown in Fig. 1 for v = 0–4. As expected, the CD₃ resonance energies are remarkably lower than the corresponding ones of CH₃ due to the isotopic mass effect. The lower energies (below v = 4) of both 3p_z and 3s are found to be very similar.

Table 1 Energies E_v of the first six vibrational resonance states of the 3p_z, 3p_x,y, and 3s Rydberg electronic states of CH₃ and CD₃, obtained by solving eqn (4). The energies are referred to the minimum of the potential-energy curve of the corresponding Rydberg state

v	3pz	3pxy	3s
CH3 energy Ev (cm^−1)
0	1556.3	1392.4	1551.6
1	4579.3	3962.2	4604.8
2	7493.7	6313.5	7423.5
3	10325.8	8596.0	9888.2
4	13076.2	10855.5	11908.7
5	15715.0	13069.9	13457.4
CD3 energy Ev (cm^−1)
0	1130.8	1017.2	1124.3
1	3345.4	2934.8	3366.4
2	5498.0	4711.1	5524.4
3	7599.2	6394.0	7526.9
4	9659.4	8052.6	9344.4
5	11680.1	9701.6	10932.7

---

Dynamical simulations of the resonance decay by electronic predissociation leading to H + CH₂ (D + CD₂) fragments were carried out for the 3p_z and 3s Rydberg states for vibrational states in the range v = 0–4. The exponential decay of the initial resonance population was fitted to the exponential function e^−t/τ in order to obtain the decay lifetime τ. The calculated lifetimes are presented in Table 2 along with those measured experimentally in ref. 19.

Table 2 Decay lifetimes calculated for the first five vibrational resonances of 3p_z and 3s for the CH₃ and CD₃ radicals. The experimental lifetimes measured for CH₃ and CD₃ in the 3p_z state¹⁹ are also given for comparison

v	3pz			3s
	τ CH3 (ps)		τ CD3 (ps)		τ CH3 (ps)	τ CD3 (ps)
0	300 000	720	245 000		220	30 000
1	274	410	150 000	1200	0.01	0.11
2	1.75		479	520	0.01	0.11
3	0.063		4.3		0.01	0.11
4	0.016		0.142		0.017	0.11

---

The calculated lifetimes for 3p_z are found to be far larger compared to the experimental ones for v ≤ 3, both for CH₃ and CD₃. While the measured lifetimes are in the range of hundreds of fs, the calculated ones can reach hundreds or even hundreds of thousands of ps. For 3s the CH₃ and CD₃ lifetime is also very large for v = 0. The same trend of very large lifetimes for the lowest vibrational resonances was found in the previous trajectory surface hopping simulations.²² The only qualitative agreement between the present calculated lifetimes and the experimental ones is that they decrease remarkably with increasing energy of the resonance state.

It is interesting to note from Table 2 that the lifetimes associated with the 3s Rydberg state are in general remarkably shorter than those of the 3p_z state, for both CH₃ and CD₃. The likely explanation is the location of the regions of maximum intensity of the couplings leading to predissociation for the two Rydberg states. Indeed, this region is located at shorter distances for 3s than for 3p_z, as shown in Fig. 1. Thus, the 3s resonance wave functions have a larger overlap with the nonadiabatic coupling than those of the 3p_z state, which leads to much shorter lifetimes. Actually, the lowest v = 0 and 1 resonance wave functions of 3p_z (for both CH₃ and CD₃) overlap very little with the nonadiabatic coupling, which explains their long lifetimes shown in Table 2.

Clearly, the calculated lifetimes of Table 2 are completely unrealistic, being largely affected by the limitations of the 1D model. Indeed, the 1D model applied leads to much lower resonance energies and to associated resonance wave functions that take far longer to decay than the corresponding resonances computed with a larger dimensionality. The fast decrease of both the theoretical lifetimes of Table 2 and of the experimental ones of ref 19 with increasing vibrational excitation, seems to indicate that the coupling leading to predissociation becomes more intense with increasing vibrational energy (at least for a range of vibrational excitations). Thus, adding just a few more degrees of freedom (one or two) to the model will lead to higher vibrational resonance energies, that now contain the frequencies of the additional modes. Such energies will be closer to the energy region where the coupling is more intense, which is expected to improve the description of the decay lifetimes, by reducing them, and the agreement with experiment.

Fragmentation dynamics of CH₃(v = 0) and CD₃(v = 0) in the 3p_z and 3s states

The fragmentation dynamics of CH₃ was investigated experimentally in the 3p_z and 3s Rydberg states after excitation of the radical through the corresponding 0⁰₀ transitions.²⁰ In these transitions the system is excited to the ground resonance state (i.e., the equivalent to the present v = 0 state) in both 3p_z and 3s. Translational energy distributions of the H atom produced after photodissociation of the methyl radical into CH₂ + H were measured.

The experimental H-fragment translational energy distribution (TED) measured for photodissociation of the 3p_z Rydberg state was a widely spread distribution across the energy range 0–3.5 eV, peaked around 0.5 eV (see Fig. 3 of ref. 20). Such energy range covers the possible dissociation of CH₃ into the fragments H(²S) + CH₂(1 ¹B₁) (along the ²B₁ valence state), H(²S) + CH₂(1 ¹A₁) (along the ²A₁ valence state), and H(²S) + CH₂(X̃³B₁) (along the ground electronic state). Based on the ab initio potential-energy curves of Fig. 1, a complex dissociation mechanism was postulated involving transfer of population from the dissociative ²B₁ valence state where fragmentation occurs initially, to other electronic states through the conical intersections and nonadiabatic couplings, that would finally produce the CH₂(1 ¹A₁) and CH₂(X̃ ³B₁) fragments in addition to CH₂(1 ¹B₁).

The corresponding H-fragment TED has been calculated by projecting out the wave packet in the dissociative valence states ²B₁ and ²A₁ (i.e., by projecting out the ψ₂ and ψ₅ packets of eqn (2)) in the asymptotic region onto the plane waves representing the H + CH₂ fragments across the relevant range of translational energies. The calculated TED associated with the CH₃(v = 0, 3p_z) initial state is displayed in Fig. 2a. This distribution shows the intensity accumulated after 9000 ps of dynamical simulation.

Fig. 2 (a) H(²S)-fragment translational energy distribution obtained when photodissociation starts from the CH₃(v = 0, 3p_z) resonance. The distribution shows the intensity accumulated after 9000 ps of simulation. The two peaks displayed in the distribution correspond to the dissociation pathways H(²S) + CH₂(1 ¹B₁) and H(²S) + CH₂(1 ¹A₁). (b) The same distribution as in (a), obtained from photodissociation starting from CH₃(v = 0, 3p_z), but when the conical intersection between the 3p_z and the ²A₁ valence state is suppressed. See the text for details.

The TED of Fig. 2a consists of two narrow peaks located at ∼1.3 and ∼1.95 eV, which are the H fragment translational energies corresponding to dissociation of the CH₃(v = 0, 3p_z) initial resonance following the pathways of the two valence states that produce CH₂(1 ¹B₁) and CH₂(1 ¹A₁) fragments, respectively. The peaks are energetically very narrow because the CH₃(v = 0, 3p_z) resonance is correspondingly very narrow with a very long associated lifetime (see Table 2). It is noted that since the dynamical 1D model applied only considers the H + CH₂ dissociative mode, transfer of part of the energy available to other modes is not possible, which prevents the appearance of distribution intensity at translational energies lower than those of the above two peaks. Such energy transfer would of course be expected by applying larger dimensionality models. This absence of energy transfer to other modes also prevents internal relaxation of the initially excited state to the ground electronic state, which therefore is not included in the model.

The CH₃(v = 0, 3p_z) TED displays two interesting findings. The first one is related to the appearance of the peak at ∼1.95 eV associated with CH₂(1 ¹A₁) fragments. The 3p_z state is coupled to the ²B₁ valence state by a nonadiabatic coupling leading to predissociation. The only coupling between 3p_z and the ²A₁ valence state that may produce CH₂(1 ¹A₁) fragments is the conical intersection labelled as CI1 in Fig. 1, which appears to be the one responsible for the peak at ∼1.95 eV. In order to check this possibility a simulation was performed by suppressing the coupling associated with CI1, and the TED obtained is shown in Fig. 2b. Indeed it is found that the peak at ∼1.95 eV disappears in this case, confirming that this CI is the responsible for the formation of H(²S) + CH₂(1 ¹A₁) fragments.

The second interesting finding of the distribution of Fig. 2a is that, as a consequence of the appearance of the two peaks associated with the dissociation pathways through the two valence states, the calculated TED covers a rather large translational energy range, in good qualitative agreement with the experimental TED. It is correct that the intensity at higher energies in Fig. 2a is higher than at lower energies, in contrast to the experimental result. But again, such intensities depend on the intensities of the corresponding calculated 1D couplings between 3p_z and the two valence states, which can only be considered of a qualitative accuracy. The important result is that the present model predicts an energy broadening of the TED as a consequence of the existance of CI1, consistently with the distribution found experimentally.

The two peaks of the TED of Fig. 2a are very intense. However, by carrying out a closer inspection of the TED associated with dissociation through the ²A₁ valence state in the range of very low intensity, another interesting result is found. As shown in Fig. 3a, a structure of peaks associated with different resonances appears. Based on the resonance energies E_v calculated with eqn (4) such resonances can be identified. The most prominent of the peaks corresponds to the CH₃(v = 3, 3p_x,y) resonance. By reducing now the energy scale of the figure to the range 1.2–2.3 eV, this most intense peak is left out of the figure, and an expanded view of the remaining structure of resonance peaks is obtained and displayed in Fig. 3b. Several resonances are identified in the H-fragment translational energy range from 1.2 eV to 2.3 eV, that include the v = 0–3 vibrational states of the 3p_x,y Rydberg state, and the v = 3–11 resonances of the 3s state.

Fig. 3 (a) Low-intensity range of the H(²S)-fragment translational energy distribution of Fig. 2a obtained when photodissociation starts from CH₃(v = 0, 3p_z) and produces H(²S) + CH₂(1 ¹A₁) product fragments. A clear structure of peaks associated with resonances is displayed by the distribution. (b) An expanded view of panel (a) where the structure of resonaces is more clearly appreciated. Different resonances corresponding to the 3p_x,y and 3s states are indicated and labelled in the figure.

The mechanism of population of all the above resonances would be the following. The CH₃(v = 0, 3p_z) initial resonance predissociates into the ²B₁ valence state, and the dissociating wave packet amplitude travels across this state towards the asymptotic region. In its way to dissociation the ²B₁ wave packet finds the conical intersections CI2 and CI3, and a small portion of the amplitude is transferred through them to the 3p_x,y and 3s Rydberg states, respectively, populating several of the resonances of these two electronic states. The broad range of resonance energies populated is due to the uncertainty principle, which allows population of several resonances in 3p_x,y and 3s at energies much below and much above the energy of the CH₃(v = 0, 3p_z) initial state. The resonances populated in 3p_x,y and 3s will in turn predissociate with their characteristic lifetimes (reflected in the widths associated with the TED peaks) into the ²A₁ valence state, which is the only one coupled to 3p_x,y and 3s, giving rise to the peaks of the TED of Fig. 3 corresponding to the H(²S) + CH₂(1 ¹A₁) fragments.

The TED of Fig. 3 confirms the possible existence of a complex dissociation mechanism mediated by the conical intersections CI2 and CI3, and probably involving a rather long timescale, as previously postulated.²⁰ The intensity of the TED of Fig. 3 is much smaller than that of Fig. 2a, but as stated above, such relative intensities obtained with the 1D model should be taken with caution. This complex mechanism contributes to populate a large energy range of the H-fragment TED, and thus could also contribute to explain the large spreading of the experimental CH₃(v = 0, 3p_z) TED.

Dynamical simulations starting from the CH₃(v = 0, 3s) initial resonance were also carried out. Same as for 3p_z, the corresponding H-fragment TED was calculated by projecting out the wave packet in the asymptotic region of the ²B₁ and ²A₁ valence states, and the result is shown in Fig. 4. The distribution shows the intensity accumulated after 1800 ps of dynamical simulation. It is noted that due to the shorter lifetime of the CH₃(v = 0, 3s) resonance as compared to the CH₃(v = 0, 3p_z) one (see Table 2), a simulation of 1800 ps is more than enough for the resonance state to decay completely, and thus the distribution of Fig. 4 is a true asymptotic, final distribution. The TED only exhibits a single peak at ∼0.24 eV consistent with dissociation along the ²A₁ valence state producing H(²S) + CH₂(1 ¹A₁) fragments. No appreciable intensity associated with the ²B₁ valence state is found, because 3s is not coupled to it. Similarly as in Fig. 2a, the peak of Fig. 4 is very narrow, due to the long lifetime associated with the CH₃(v = 0, 3s) resonance (see Table 2).

Fig. 4 H(²S)-fragment translational energy distribution obtained when photodissociation starts from CH₃(v = 0, 3s). The distribution shows the intensity accumulated after 1800 ps of simulation. The peak displayed in the distribution corresponds to the dissociation pathway producing H(²S) + CH₂(1 ¹A₁) fragments.

The calculated TED of Fig. 4 agrees qualitatively with the relatively narrow experimental TED (see Fig. 2a of ref. 20) in that it is limited to a rather small range of hydrogen translational energies, in contrast to the behavior of the spread CH₃(v = 0, 3p_z) TED. The present simulations show that the absence of spreading in the CH₃(v = 0, 3s) TED is due to predissociation only into the ²A₁ valence state, while the remarkable spreading of the CH₃(v = 0, 3p_z) TED is caused by a more complex dissociation mechanism involving both ²B₁ and ²A₁ valence states that includes predissociation and transitions through the conical intersections (mainly the CI1 one). Thus the present 1D dynamical model is able to reproduce at least qualitatively the main features of the experimental CH₃(v = 0, 3p_z) and CH₃(v = 0, 3s) H-fragment TED, and also to propose dissociation mechanisms consistent with them.

The D-fragment TED calculated for CD₃(v = 0, 3p_z) after 9000 ps of simulation (not shown) displays an intense peak at ∼1.82 eV associated with dissociation along the ²A₁ valence state, and a much smaller peak at ∼1.19 eV, about 800 times less intense than the main peak, associated with predissociation into the ²B₁ valence state. Thus, in practice the CD₃(v = 0, 3p_z) TED consists of a single peak originated by population transfer from 3p_z to the ²A₁ state through the CI1 conical intersection. The implication is that at the CD₃(v = 0, 3p_z) resonance energy, which is the lowest one of the 3p_z state (see Table 1), the effect of CI1 is to make the mechanism of methyl dissociation along ²A₁ completely dominant over the mechanism of predissociation into ²B₁, which becomes negligible in practice. The D fragment TED obtained for CD₃(v = 0, 3s) consists of a single peak associated with predissociation into the ²A₁ valence state, very similar to that found for CH₃(v = 0, 3s) in Fig. 4, indicating that the dissociation mechanism is very similar in both cases.

Fragmentation dynamics of CH₃(v > 0) and CD₃(v > 0) in the 3p_z state

Dynamical simulations for initial resonances CH₃(v > 0, 3p_z) and CD₃(v > 0, 3p_z) up to v = 4 were carried out, and the corresponding H- (or D-) fragment TED was calculated. The TEDs associated with CH₃(v > 0, 3p_z) are shown in Fig. 5. In contrast to the CH₃(v = 0, 3p_z) TED of Fig. 2a, the TEDs of Fig. 5 display a single peak associated with predissociation into the ²B₁ valence state, producing H(²S) + CH₂(1 ¹B₁) fragments. No appreciable intensity in the ²A₁ valence state is found in the TEDs. This result indicates that as the initial vibrational excitation increases above the CH₃(v = 0, 3p_z) resonance, the CI1 conical intersection connecting with the ²A₁ state becomes uneffective, and methyl dissociation takes place essentially only through the predissociation pathway into the ²B₁ state. However, a closer inspection of the very low intensity region of the TEDs reveals a structure of resonances produced in the ²A₁ state similar to that of Fig. 3 (with similarly weak intensity), which indicates that the CI2 and CI3 conical intersections still operate. It is noted that the width of the TED main peaks increases remarkably with increasing v (and a Lorentzian shape is clearly apparent for v = 3 and 4), consistently with the associated sharp decrease of the corresponding lifetimes (see Table 2).

Fig. 5 H(²S)-fragment translational energy distributions obtained when photodissociation starts from CH₃(v, 3p_z), when v = 1–4. In all cases the initial resonance population has decayed completely to the continuum, so the distributions shown are final, asymptotic ones. Each of the four distributions displays a single peak associated with predissociation into the ²B₁ valence state, producing H(²S) + CH₂(1 ¹B₁) fragments. All the distributions have been normalized to unity at the maximum to facilitate the comparison.

Regarding the dissociation dynamics of CD₃(v > 0, 3p_z), the calculated D-fragment TEDs are presented in Fig. 6. Interestingly, the CD₃(v = 1, 3p_z) TED of Fig. 6a displays two peaks associated with dissociation along the two ²B₁ and ²A₁ valence states, with a relative intensity similar to that found for CH₃(v = 0, 3p_z) in Fig. 2a. Thus, the effect of the CI1 conical intersection still persists in the CD₃(v = 1, 3p_z) dissociation dynamics, due to the lower resonance energy associated (because of the mass effect), as compared to CH₃(v = 1, 3p_z).

Fig. 6 (a) D(²S)-fragment translational energy distribution obtained when photodissociation starts from CD₃(v = 1, 3p_z). The distribution shows the intensity accumulated after 1500 ps of simulation. The two peaks displayed in the distribution correspond to the dissociation pathways D(²S) + CD₂(1 ¹B₁) and D(²S) + CD₂(1 ¹A₁). (b) D(²S) fragment translational energy distribution obtained when photodissociation starts from CD₃(v, 3p_z) when v = 2–4. In all cases the initial resonance population has decayed completely to the continuum, so the distributions shown are final, asymptotic ones. Each of the three distributions displays a single peak associated with predissociation into the ²B₁ valence state, producing D(²S) + CD₂(1 ¹B₁) fragments. All the distributions have been normalized to unity at the maximum to facilitate the comparison.

For CD₃(v > 1, 3p_z) the corresponding TEDs become a single peak, as for CH₃(v > 0, 3p_z), associated with dissociation only along the ²B₁ valence state through predissociation, and the CI1 conical intersection is no longer effective in transferring population to the ²A₁ state. Actually a small intensity associated with the ²A₁ state is found in the TEDs (albeit negligible compared to the main peak intensity), which decreases rapidly with increasing v. This indicates that the effectiveness of population transfer of CI1 is limited to a small range of methyl vibrational energies (v = 0 and 1), and it vanishes quickly with increasing vibrational excitation.

A comment on the role played by the CI1 conical intersection in the methyl dissociation dynamics is now due. It was stated in ref. 20 that CI1 was not relevant to explain the experimental TED measured for CH₃(v = 0, 3p_z), due to its location at a relatively high energy that was not expected to be accessed by the experimental work. The present results show, however, that such statement appears not to be correct. Indeed, CI1 seems to be located low enough in energy as to largely affect the dissociation dynamics of both CH₃(v = 0, 3p_z) and CD₃(v < 2, 3p_z). In this sense, as discussed above, CI1 would be the main responsible of the large spreading at high energies of the CH₃(v = 0, 3p_z) TED obtained experimentally.²⁰

Fragmentation dynamics of CH₃(v > 0) and CD₃(v > 0) in the 3s state

Similarly as for v = 0, dynamical simulations for initial resonances CH₃(v > 0, 3s) and CD₃(v > 0, 3s) up to v = 4 were carried out, and the corresponding H- (or D-) fragment TED was calculated. The TEDs associated with CH₃(v > 0, 3s) are shown in Fig. 7. Since the lifetimes associated with the CH₃(v > 0, 3s) resonances are quite short (see Table 2), the simulations were performed for a total time of 3 ps (v = 1–3) and 11 ps (v = 4), which lead to complete decay of the initial resonance.

Fig. 7 H(²S)-fragment translational energy distributions obtained when photodissociation starts from CH₃(v, 3s), when v = 1–4. In all cases the initial resonance population has decayed completely to the continuum, so the distributions shown are final, asymptotic ones. All the distributions are associated with predissociation into the ²A₁ valence state, producing H(²S) + CH₂(1 ¹A₁) fragments.

The H-fragment TEDs associated with CH₃(v > 0, 3s) are very different from that obtained for CH₃(v = 0, 3s) (Fig. 4). Indeed, while in the CH₃(v = 0, 3s) TED a single and very narrow peak was found, the TEDs of Fig. 7 display several peaks, some of them with a remarkable width. Thus, contrary to the localization of the CH₃(v = 0, 3s) TED in a rather small energy region, the CH₃(v > 0, 3s) TEDs spread over a relatively large region of about 1.5 eV (from ∼0.5 to ∼2 eV). Each TED of Fig. 7 displays a main peak at an energy that corresponds to the initial v resonance, and several other peaks with a smaller intensity that decreases as energy increases. Some of the additional peaks to the main one appear at energies that correspond to the energies of the different CH₃(v, 3s) resonances.

The reason why the TEDs of Fig. 7 present several peaks is because the CH₃(v > 0, 3s) resonances have a substantial width and overlap, in contrast to the case of the very narrow CH₃(v = 0, 3s) resonance. Such an overlap is not surprising taking into account the short lifetimes of about 10–20 fs associated with the v > 0 resonances, as shown in Table 2. In a regime of overlapping resonances, when one of the resonances is populated the other overlapping resonances are also populated to a given extent. This is what explains the appearance of several peaks in addition to the main one in the TED, and the remarkable spreading of the distribution. In addition, the shape of the peaks of the TED, and particularly of the main peak, is no longer Lorentzian (as it is in Fig. 5 and 6 where the resonances are isolated ones), as expected for overlapping resonances.

The results of Fig. 7 reflect two interesting predictions of the present 1D model. The first prediction is that as vibrational excitation increases above v = 0, a regime of overlapping resonances is found due to the short lifetimes and the large widths associated with the resonances. This prediction might be very realistic, since it has been found experimentally in the 3s Rydberg state that the lifetime associated with the vibrationless ground state CH₃(v = 0, 3s) is between 60 and 82 fs (depending on the excitation of the overall rotation),¹⁴ while the CH₃(v = 1, 3s) lifetime was found to decrease to about 13 fs.¹⁵ Thus, the onset of overlapping resonances predicted here for the 3s state might well be the real behavior found in methyl as vibrational excitation increases. The second prediction is related to the fact that, due to the presence of overlapping resonances, the spreading of the TEDs associated with the CH₃(v > 0, 3s) initial states is remarkably larger than that of the CH₃(v = 0, 3s) TED. Experimental confirmation of these two predictions should be very interesting.

Now, the CH₃(v = 4, 3s) TED of Fig. 7d displays an interesting feature. This TED consists of a peak at ∼1.5 eV with a certain width along with some other very small peaks, similarly as in the TEDs corresponding to v = 1–3. However, an additional very narrow and intense peak appears also near 1.5 eV, superimposed on the previous main broad peak. In order to elucidate the origin of this narrow and intense peak, the time-dependent populations in the different electronic states involved in the photodissociation process are calculated. Such populations are displayed in Fig. 8 for the 3s, ²A₁, and 3p_x,y electronic states. The populations associated with the 3p_z and ²B₁ states are negligible, indicating that they do not play any role in the CH₃(v, 3s) predissociation.

Fig. 8 Time-dependent populations of the 3s and 3p_x,y Rydberg states and of the ²A₁ valence state obtained for the different CH₃(v > 0, 3s) initial resonances. Although the simulations are carried out for much longer times, only a limited time range is presented in the four panels in order to show more clearly the details of the different populations.

As expected for a resonance predissociation process, the general behavior found is a decay of the initial 3s population along with a corresponding increase of the ²A₁ population, that typically mirrors the 3s population decay. Superimposed on both the 3s and ²A₁ populations a structure of undulations is found. These undulations have opposite phase in the two populations, that is, the maxima (minima) of the 3s population coincide with the minima (maxima) of the ²A₁ population. The structure of undulations is originated by the fact that more than one overlapping resonance is initially populated (as reflected in the different peaks of the TEDs of Fig. 7), and the different resonances decay with different lifetimes. These different lifetimes are reflected in the result that there are more than one constant time separation between the undulations, each constant time separation corresponding to a specific decay lifetime. As the initial population of the additional overlapping resonances decreases, as in the cases of v = 3 and 4 (see Fig. 7c and d), the intensity of the undulations decreases as well, as found in Fig. 8c and d.

The most interesting feature of Fig. 8 is the gradual appearance of an oscillating population in the 3p_x,y Rydberg state. Such population is practically negligible for v = 1, but becomes appreciable already for v = 2 and 3, and accounts for 10% of the population for v = 4. It is expected that the 3p_x,y population will increase further for higher v > 4 initial states. The origin of the 3p_x,y population is that the nonadiabatic coupling between the 3p_x,y Rydberg state and the ²A₁ valence state begins to operate as vibrational excitation increases. Indeed, as Fig. 1 shows, the 3p_x,y and ²A₁ states cross at a relatively high energy above the minimum of the 3s state. Thus, for low 3s vibrational states (like v < 3), the nonadiabatic coupling between 3p_x,y and ²A₁ is still far in energy, and does not affect the photodissociation from the 3s state. But when enough vibrational excitation is reached, the coupling begins to operate transferring part of the population that is dissociating in ²A₁ to the 3p_x,y state, where some of the 3p_x,y resonances are populated. The resonances populated in 3p_x,y in this way will in turn decay through predissociation into the ²A₁ valence state, producing the oscillations found in the 3p_x,y population. The behavior expected is that as vibrational excitation (and therefore energy) increases in 3s, population transfer from ²A₁ to 3p_x,y will increase and reach a maximum. Then, as energy keeps increasing for higher v states, the nonadiabatic coupling becomes far in energy and its effect will gradually decrease and disapear.

When the effect of the nonadiabatic coupling is intense enough, as in the case of CH₃(v = 4, 3s), an interesting behavior is found. In this case a remarkable amount of population (∼20%) is initially transferred from ²A₁ to 3p_x,y at short times. One or more resonances of 3p_x,y (those closer to the energy of the CH₃(v = 4, 3s) resonance) are expected to be populated. Such resonance or resonances will then decay by predissociation, and part of the population will come back to ²A₁. In its way to dissociation, this population will find the nonadiabatic coupling between ²A₁ and the 3s state, and part of the population will be transferred from ²A₁ to 3s through this coupling, in a similar way as it occurred from ²A₁ to 3p_x,y. Again, the resonances populated now in 3s will predissociate into ²A₁, giving rise to another transfer of population to 3p_x,y. The alternating population transfers from ²A₁ to 3p_x,y and 3s produce the oscillations with opposite phase between the populations of the 3p_x,y and 3s states found in Fig. 8d at short times.

Another interesting feature of Fig. 8d is that both the populations of 3p_x,y and 3s take a long time to decay finally. Actually, after a simulation of the CH₃(v = 4, 3s) photodissociation of 11 ps, these two populations were not completely decayed. The likely explanation of this long decay is that after the different population transfers from ²A₁ to both 3p_x,y and 3s, the ground v = 0 resonance of the two Rydberg states is populated, and this resonance has associated a very long lifetime that delays remarkably the decay of the population. This would also explain the appearance of the very narrow and intense peak near 1.5 eV in the TED of Fig. 7d. For the same reason, one would expect that some of the small additional peaks appearing in the TEDs of Fig. 7 do not correspond to 3s overlapping resonances, but also to 3p_x,y resonances populated from ²A₁ that finally end up decaying to this valence state.

The results of Fig. 7 and 8 show a complex and rich dynamical behavior in the photodissociation from the 3s Rydberg state as vibrational excitation increases. In this case the origin of the complex behavior is not the presence of conical intersections, as discussed previously for the 3p_z state, but the presence of the nonadiabatic couplings responsible for predissociation from the 3p_x,y and 3s Rydberg states. However, the final effect is similar in the sense that the dynamical behavior is enriched, and new fragmentation channels and mechanisms are open. The characteristic feature that makes possible this result is that the two nonadiabatic couplings connect the same ²A₁ valence state with two different Rydberg states, which implies that actually the three electronic states are effectively coupled, at least in a range of vibrational excitations of the Rydberg states. Thus, a similar complex dynamical behavior is also expected to occur for a range of initial resonances of the 3p_x,y state. Such a complex dynamics opens the venue for control of the branching ration between the different dissociation mechanisms involved.^31,32

Simulations of the CD₃(v > 0, 3s) photodissociation up to v = 4 were carried out for a total time of 9 ps. The corresponding D fragment TEDs are collected in Fig. 9. The TEDs of Fig. 9 display a behavior essentially similar to that of Fig. 7, showing one or two dominant peaks and several additional peaks with much smaller intensity where there are both narrow and broad peaks. The main difference with the CH₃(v > 0, 3s) TEDs of Fig. 7 is that in the CD₃(v > 0, 3s) distributions the main peaks are much narrower. In any case, the CD₃(v > 0, 3s) TEDs seem to reflect also a regime of overlapping resonances, although apparently less intense than in CH₃(v > 0, 3s).

Fig. 9 D(²S)-fragment translational energy distributions obtained when photodissociation starts from CD₃(v, 3s), when v = 1–4. In all cases the initial resonance population has decayed completely to the continuum, so the distributions shown are final, asymptotic ones. All the distributions are associated with predissociation into the ²A₁ valence state, producing D(²S) + CH₂(1 ¹A₁) fragments.

The time-dependent populations associated with the 3s, ²A₁, and 3p_x,y electronic states are shown in Fig. 10 for photodissociation of the different CD₃(v > 0, 3s) initial states. Same as in the case of CH₃(v > 0, 3s), the 3s and ²A₁ populations display a structure of rapid oscillations superimposed on their general decay or increase behavior, respectively. Again these oscillations are due to the simultaneous decay of different 3s overlapping resonances with different lifetimes. A rapidly oscillating population also appears gradually in the 3p_x,y state, as in the CH₃(v > 0, 3s) photodissociation. The difference now is that the 3p_x,y population is much less intense for the same v initial resonance than in CH₃(v > 0, 3s). The explanation of this lower intensity is that the vibrational energy of a CD₃(v, 3s) initial state is remarkably lower than the corresponding energy of the same CH₃(v, 3s) vibrational state (see Table 1), and thus it takes more vibrational (or energy) excitation in CD₃(v, 3s) to reach a similar degree of effectiveness of the nonadiabatic coupling than in CH₃(v, 3s). Thus, the results of both Fig. 9 and 10 indicate that in CD₃(v > 0, 3s) operates the same complex dynamical mechanism as in CH₃(v > 0, 3s), consisting of alternating population transfers between ²A₁, 3s, and 3p_x,y, mediated by the two nonadiabatic couplings between these three states, with the difference that in CD₃(v > 0, 3s) it requires more vibrational excitation to become effective.

Fig. 10 Same as Fig. 8 but for CD₃(v > 0, 3s).

4 Conclusions

The nonadiabatic photodissociation dynamics of methyl and its deuterated isotopologue have been investigated by applying a one-dimensional (1D) wave packet treatment. The model is restricted to one dimension because only 1D potential-energy curves and the nonadiabatic couplings between them for the different electronic states involved, are available in the literature. The electronic predissociation dynamics of methyl is simulated starting from different vibrational resonances of the 3p_z and 3s Rydberg states, and the corresponding decay lifetimes are calculated. The theoretical lifetimes for the lowest resonances are found to be too long as compared to the experimental ones. Only a qualitative agreement is found with the experimental lifetimes, namely, that the lifetimes decrease rapidly with increasing vibrational excitation. Actually, it would be rather unrealistic to expect from the 1D model a quantitative or nearly quantitative description of the experimental lifetimes of a tetraatomic radical like methyl, with six internal degrees of freedom.

The 1D model, however, behaves remarkably better in the prediction and explanation of the fragmentation mechanisms consistent with the experimental measurements. In this context, the model is able to predict a hydrogen-fragment translational energy distribution (TED) produced from the CH₃(v = 0, 3p_z) initial state that is remarkably spread over a large energy range, in qualitative agreement with the experimental result. A similar behavior is found for the TEDs of the v = 1 and 2 initial states of CD₃(v, 3p_z) (not investigated experimentally). The energy spreading of the H(D) translational distribution is found to be caused by the fragmentation of methyl along two different dissociative valence states: On the one hand, along the ²B₁ state, coupled to 3p_z by the nonadiabatic coupling leading to predissociation, and on the other hand, along the ²A₁ state, coupled to 3p_z by a conical intersection. The energy separation between ²B₁ and ²A₁ is the cause of the spreading of the TED. Two additional conical intersections between the ²B₁ valence state and the 3p_x,y and 3s Rydberg states lead to transfer of part of the dissociating population in ²B₁ to the two Rydberg states, also contributing to the energy spreading of the TED, although to a much smaller extent. Thus, a complex fragmentation mechanism mediated by both the nonadiabatic coupling leading to predissociation and several conical intersections appears to determine the photodissociation dynamics of CH₃(v = 0, 3p_z) and CD₃(v = 0,1, 3p_z). The TED produced from the initial state CH₃(v = 0, 3s) (and from CD₃(v = 0, 3s)) is associated only with dissocition along the ²A₁ valence state, and thus is rather localized in energy, also in agreement with the experimental result. For initial vibrational excitations CH₃(v > 0, 3p_z) (and CD₃(v > 1, 3p_z)) the conical intersection coupling 3p_z with ²A₁ becomes uneffective, and dissociation along ²A₁ is not appreciably reflected in the corresponding TEDs.

The predissociation dynamics of CH₃(v > 0, 3s) and CD₃(v > 0, 3s) (with v = 1–4) was also simulated with the 1D model. Analysis of the corresponding calculated TEDs and of the populations associated with the different electronic states involved shows that a regime of overlapping resonances is present here, and that another complex dissociation mechanism operates in this case. Indeed, the ²A₁ dissociative valence state is nonadiabatically coupled to both the 3p_x,y and the 3s Rydberg states, and when the initial vibrational excitation in 3s increases, the nonadiabatic coupling between ²A₁ and 3p_x,y begins to operate, making possible transfer of dissociating population from ²A₁ to 3p_x,y. The consequence is that the initial population in a given v > 0 resonance of 3s is redistributed from ²A₁ to several 3p_x,y resonances; this population then decays back to ²A₁ which again redistributes it to different resonances of 3s, and so on and so forth until total decay of all the population. The TEDs produced by this mechanism are complex ones with signals from different resonances from both 3s and 3p_x,y. Experimental investigation of this possible mechanism for vibrational excitations of CH₃(3s) and CD₃(3s) should be very interesting. Finally, despite the clear limitations of the 1D quantum model applied to the methyl photodissociation, it appears to have enough (qualitative) predictive power as to explain some of the experimental findings, as well as to reveal a variety of interesting complex fragmentation mechanisms mediated by different nonadiabatic couplings.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was funded by the Ministerio de Ciencia e Innovación (MICINN, Spain), Grant No. PGC2018-096444-B-100. The Centro de Supercomputación de Galicia (CESGA, Spain) is acknowledged for the use of its resources.

References

1. R. F. Wayne, Chemistry of Atmospheres, Oxford University Press, Oxford, 2000.
2. H. Feuchtgruber, F. P. Helmich, E. F. van Dishoeck and C. M. Wright, Astrophys. J., Lett., 2000, 535, L111.
3. K. C. Smyth and P. H. Taylor, Chem. Phys. Lett., 1985, 122, 518–522.
4. G. Herzberg and J. Shoosmith, Can. J. Phys., 1956, 34, 523.
5. G. Herzberg, Proc. R. Soc. Lond., Ser. A, 1961, 262, 291.
6. J. W. Hudgens, T. G. DiGiuseppe and M. C. Lin, J. Chem. Phys., 1983, 79, 571–582.
7. J. M. Jasinski, B. S. Meyerson and B. A. Scott, Annu. Rev. Phys. Chem., 1987, 38, 109–140.
8. W. Zhang, H. Kawamata, A. J. Merer and K. Liu, J. Phys. Chem. A, 2009, 113, 13133–13138.
9. S. H. S. Wilson, J. D. Howe, K. N. Rosser, M. N. R. Ashfold and R. N. Dixon, Chem. Phys. Lett., 1994, 227, 456–460.
10. S. W. North, D. A. Blank, P. M. Chu and Y. T. Lee, J. Chem. Phys., 1995, 102, 792–798.
11. G. Wu, B. Jiang, Q. Ran, J. Zhang, S. A. Harich and X. Yang, J. Chem. Phys., 2004, 120, 2193–2198.
12. G. Wu, J. Zhang, S. A. Harich and X. Yang, Chin. J. Chem. Phys., 2006, 19, 109–116.
13. J. F. Black and I. Powis, J. Chem. Phys., 1988, 89, 3986.
14. S. G. Westre, P. B. Kelly, Y. P. Zhang and L. D. Ziegler, J. Chem. Phys., 1991, 94, 270.
15. S. G. Westre, T. E. Gansberg, P. B. Kelly and L. D. Ziegler, J. Phys. Chem., 1992, 96, 3610.
16. H. T. Yu, A. Sevin, E. Kassab and E. M. Evleth, J. Chem. Phys., 1984, 80, 2049–2059.
17. P. Botschwina, E. Schick and M. Horn, J. Chem. Phys., 1993, 98, 9215–9217.
18. A. M. Mebel and S.-H. Lin, Chem. Phys., 1997, 215, 329–341.
19. G. Balerdi, J. Woodhouse, A. Zanchet, R. de Nalda, M. L. Senent, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2016, 18, 110–118.
20. S. Marggi Poullain, D. V. Chicharro, A. Zanchet, M. G. González, L. Rubio-Lago, M. L. Senent, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2016, 18, 17054–17061.
21. A. Zanchet, L. Bañares, M. L. Senent and A. García-Vela, Phys. Chem. Chem. Phys., 2016, 18, 33195–33203.
22. A. Rodríguez-Fernández, M. Márquez-Mijares, J. Rubayo-Soneira, A. Zanchet, A. García-Vela and L. Bañares, Chem. Phys. Lett., 2018, 712, 171–176.
23. H. tal-Ezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967–3971.
24. J. C. Juanes-Marcos and A. García-Vela, J. Chem. Phys., 2000, 112, 4983.
25. G. Delgado-Barrio, A. M. Cortina, A. Varadé, P. Mareca, P. Villarreal and S. Miret-Artés, J. Comput. Chem., 1986, 7, 208.
26. D. G. Truhlar, J. Comput. Phys., 1972, 10, 123.
27. R. G. Gordon, J. Chem. Phys., 1969, 51, 14.
28. D. W. Norcross and M. S. Seaton, J. Phys. B: At. Mol. Phys., 1973, 6, 614.
29. J. W. Cooley, Math. Commun., 1961, 15, 363.
30. J. K. Cashion, J. Chem. Phys., 1963, 39, 1872.
31. A. García-Vela and N. E. Henriksen, J. Phys. Chem. Lett., 2015, 6, 824.
32. A. García-Vela, Phys. Rev. Lett., 2018, 121, 153204.

---