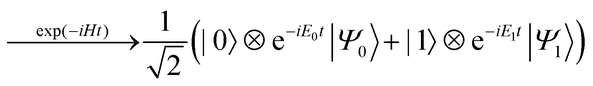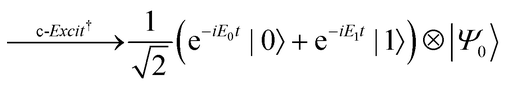Bayesian phase difference estimation: a general quantum algorithm for the direct calculation of energy gaps†
Received
12th July 2021
, Accepted 9th August 2021
First published on 2nd September 2021
Abstract
Quantum computers can perform full configuration interaction (full-CI) calculations by utilising the quantum phase estimation (QPE) algorithms including Bayesian phase estimation (BPE) and iterative quantum phase estimation (IQPE). In these quantum algorithms, the time evolution of wave functions for atoms and molecules is simulated conditionally with an ancillary qubit as the control, which make implementation to real quantum devices difficult. Also, most of the problems in chemistry discuss energy differences between two electronic states rather than total energies themselves, and thus direct calculations of energy gaps are promising for future applications of quantum computers to real chemistry problems. In the race of finding efficient quantum algorithms to solve quantum chemistry problems, we test a Bayesian phase difference estimation (BPDE) algorithm, which is a general algorithm to calculate the difference of two eigenphases of unitary operators in the several cases of the direct calculations of energy gaps between two electronic states on quantum computers, including vertical ionisation energies, singlet–triplet energy gaps, and vertical excitation energies. In the BPDE algorithm, state preparation is carried out conditionally on the ancillary qubit, and the time evolution of the wave functions in superposition of two electronic states are executed unconditionally. Based on our test, we conclude that BPDE is capable of computing the energy gap with an accuracy similar to BPE without controlled-time evolution simulations and with the smaller number of iterations in Bayesian optimisations.
1. Introduction
Quantum computers are believed to have the potential to revolutionise our lives in many ways. Anticipated applications of quantum computers range from secure communications,1 financial problems,2 machine learning,3 combinatorial optimisations,4 and material and drug designs.5 Among the diverse topics in quantum computing and quantum information processing, sophisticated quantum chemical calculations of atoms and molecules are one of the most intensively studied realms as the near future applications of quantum computers. In 1929, Dirac pointed out that “The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble”.6 The computational cost for full configuration interaction (full-CI) calculations that can give variationally best possible wave functions within the space spanned by the basis set being used increases exponentially against the system size. However, as Feynman pointed out, quantum mechanical systems can be efficiently simulated by using a computer built of quantum mechanical elements which obey quantum mechanical laws, namely a quantum computer.7 We note that if quantum computers are capable of performing sophisticated quantum chemical calculations of large and complex systems such as the Mn4CaO5 cluster of photosystem II8 and FeMo cofactor of nitrogenase,9 it will help us deeply understand chemical processes in nature and design novel compounds and materials with valuable functionalities. In fact, quantum computers allow us to calculate full-CI energy in polynomial time, by utilising a quantum phase estimation (QPE) algorithm.10 The first theoretical study of the QPE-based full-CI was reported in 2005,11 and proof-of-principle experiments of the full-CI/STO-3G calculations of H2 molecules were reported by using photonic and NMR quantum computers in 2010.12,13 Since then, many theoretical studies including quantum gate complexity improvement,14–19 spatial and spin symmetry adaptation,20–25 qubits and quantum gate resource estimations17,26,27 as well as experimental demonstrations of quantum chemical calculations28,29 have been reported. QPE needs N qubits to readout the eigenphase in N-digits in binary, while iterative QPE (IQPE)30,31 and Bayesian phase estimation (BPE),32,33 which are the family of QPE algorithms, use only one ancillary qubit. In 2014, a quantum–classical hybrid algorithm known as a variational quantum eigensolver (VQE) was proposed,34,35 which is capable of computing the energy expectation values of approximated wave functions using currently available noisy intermediate-scale quantum (NISQ) devices.36 Recent reviews in this field can be found elsewhere.37–41 Although it has been thought that advent of fault-tolerant quantum computers (FTQC) which have an ability to perform massive computations with quantum computational advantages is in the distant future, remarkable progress in quantum hardware is constantly being made. For example, two-dimensional quantum walks on a 62-qubit system have been reported recently,42 and Google Inc. announced that they aim for commercial-grade quantum computers by 2029.43 In this context, development of efficient quantum algorithms targeted at utilising FTQC is an important issue.
Importantly, the computational cost of quantum chemical calculations on quantum computers increases when we evaluate the energy in finer digits. This is because QPE calculates the energy range where the full-CI solution locates, rather than the full-CI energy itself. Length of the time evolution should be doubled to half the energy range. Thus, the computational cost is inversely proportional to the energy precision. In VQE, the energy expectation value is computed in a statistical manner by iteratively executing the state preparation and measurements, and therefore the statistical error is unavoidable. To half the statistical error of the energy expectation value, one should quadruple the number of measurements.35,40 From these reasons, it is quite difficult to precisely calculate the total energy of large molecules and molecules containing heavy atoms. Noticeably, we need several theoretical breakthroughs to open the door to solve real-world chemistry problems, as well as developments of quantum computing hardware. From the viewpoint of computational chemistry, almost all the problems in chemistry focus on the energy differences between two electronic states or structures of the molecular systems under study, rather than the total energies themselves relevant to the systems. Furthermore, the magnitude of the energy gap to be discussed is not greatly dependent on the molecular size. We have to discuss the similar magnitude of energy differences regardless of the size of molecules. The direct calculation of energy gaps between two electronic states on quantum computers is one of the plausible and promising solutions.44–47 Note that several approaches to calculate excitation energies have been proposed in VQE, such as subspace expansion,48 subspace search VQE,49 using orthogonality of wave functions,50 and so on. In these methods energy gaps are calculated by the subtraction of total energies of individual electronic states.
Recently, we proposed a quantum algorithm “Bayesian exchange coupling parameter calculator with broken-symmetry wave functions (BxB)”,45 that is capable of directly computing the energy difference between two electronic states belonging to different spin quantum numbers. From the numerical quantum circuit simulations, we demonstrated that the BxB quantum algorithm is able to predict the exchange coupling parameter J, which is half of the singlet–triplet energy gap, of small molecules within 1 kcal mol−1 of precision, with much lower computational costs than the conventional QPE-based approach.45 We also carried out numerical simulations for the direct calculations of vertical ionisation energies using the BxB algorithm, achieving 0.1 eV of energy precision.46 The BxB algorithm is powerful and applicable to larger systems, and exponential speedup against classical counterpart is guaranteed. Unfortunately, as discussed in detail in the next section, the BxB algorithm has drawbacks. It needs more ancillary qubits to execute quantum computation, compared with IQPE and BPE, and it cannot generally be applicable to calculations for any energy gaps. For example, singlet–singlet excitation energies, which are important in chemistry, cannot be calculated using the BxB algorithm.
In this work, we propose a new quantum algorithm, “Bayesian phase difference estimation (BPDE)”, whose capability is general in calculating the difference of two eigenphases of unitary operators, and apply the BPDE algorithm to direct calculations of various energy gaps. We emphasise that the number of qubits needed for implementing the BPDE equals that of IQPE and BPE, and unlike IQPE and BPE, the BPDE algorithm does not require any controlled-time evolution operation that is one of the most difficult parts of quantum algorithms to be implemented to real devices. Numerical quantum circuit simulations for the direct calculations of vertical ionisation energies of He, Li, Be, B, C, N, HF, BF, CF, CO, O2, NO, CN, F2, H2O, NH3, CH4, HCN, and HNC, singlet–triplet energy gaps of H2, C, O, NH, OH+, NF, NCN, and CNN, and vertical excitation energies of dihalocarbenes (CX2, X = F, Cl, and Br), dihalosilylenes (SiX2, X = F and Cl), and formaldehyde (HCHO) are given.
2. Theory
2.1 A Bayesian phase estimation (BPE) algorithm for full-CI calculations on quantum computers
Here we briefly review the theory of quantum chemical calculations on quantum computers and full-CI calculations using the BPE algorithm.32
The QPE algorithms including IQPE and BPE are based on the quantum simulation of the time evolution of wave functions conditionally on the ancillary qubit and following measurement of the ancillary qubit to project the wave function to the eigenfunction of Hamiltonian. The quantum circuit for BPE is illustrated in Fig. 1. Here, horizontal lines specify a qubit or NSO of qubits, and squares, circles, and vertical lines represent relevant quantum gates. NSO is the number of spin orbitals in the active space. Definitions of the quantum gates and quantum circuits are given in the ESI.†Tz is the phase shift gate defined in eqn (1).
| |  | (1) |
 |
| | Fig. 1 A quantum circuit for the BPE algorithm. NSO is the number of spin orbitals in the active space. | |
In the BPE, an approximate wave function |Ψ〉 having sufficiently large overlap with the full-CI wave function of the target electronic state is needed as the input. The Hartree–Fock wave function |ΨHF〉 is often used as |Ψ〉 for the ground state calculations of closed shell singlet molecules. By using a Jordan–Wigner transformation discussed below, |ΨHF〉 can be generated by Nelec of Pauli-X (NOT) gates from the qubits initialised to the |00⋯0〉 state. For open shell low-spin states or molecules with intermediate open shell characters, a symmetry-adapted configuration state function |ΨCSF〉 or a multiconfigurational wave function |ΨMC〉 are suitable for |Ψ〉. |ΨCSF〉 and |ΨMC〉 can be prepared using quantum circuits proposed by us.21,22,51 BPE starts by applying an Hadamard gate (Hd) to the ancillary qubit in the top of Fig. 1 (eqn (2)). The next step is for the controlled-time evolution of |Ψ〉. The time evolution operator exp(−iHt) is applied to |Ψ〉 if and only if the ancillary qubit is in the |1〉 state (eqn (3)). After that the Tz gate is applied to the ancillary qubit to cause the phase shift to the |1〉 state (eqn (4)). The following Hadamard gate on the ancillary qubit generates the quantum state in eqn (5).
| |  | (2) |
| |  | (3) |
| |  | (4) |
| |  | (5) |
The probability to obtain the |0〉 state in the measurement of the ancillary qubit, P(0), is calculated as in eqn (6).
| | 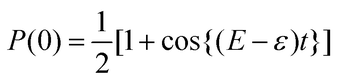 | (6) |
From
eqn (6), the measurement of the ancillary qubit always gives the |0〉 state if
E =
ε. In BPE, the rotational angle
θ =
εt of the
Tz(
θ) gate is optimised using Bayesian inference to maximise
P(0). The BPE returns a posterior distribution over the phase, rather than a point estimate. BPE is robust against experimental imperfections and noises, and it outperforms IQPE.
32
To adopt BPE for full-CI calculations of atoms and molecules, the wave functions should be mapped onto qubits. Several wave function mapping techniques were proposed,52–54 and here we use the mapping based on the Jordan–Wigner transformation (JWT).11,52 In the JWT, each qubit stores the occupancy of a particular spin orbital: the qubit is in the |1〉 state if the spin orbital is occupied by an electron, otherwise |0〉. A Hamiltonian for the systems under study is written in the second quantised formula as in eqn (7), where a†p and ap are creation and annihilation operators, respectively, acting on the p-th spin orbital. hpq and hpqrs are one- and two-electron integrals and they are computed on classical computers prior to quantum simulations. In the JWT, a†p and ap are transformed to the products of Pauli operators (Pauli strings) using eqn (8) and (9), respectively. As a result, the molecular Hamiltonian in eqn (7) is transformed to the qubit Hamiltonian consisting of a linear combination of Pauli strings, as in eqn (10) and (11).
| | 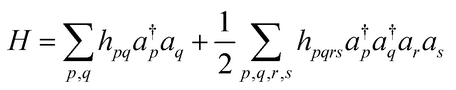 | (7) |
| |  | (8) |
| |  | (9) |
| |  | (10) |
| | | Pm = σNSO ⊗ σNSO−1 ⊗…⊗σ1, σk ∈ {I,X,Y,Z} | (11) |
By applying Trotter–Suzuki decomposition,55,56 the time evolution operator exp(−iHt) becomes products of the exponential of Pauli strings (eqn (12)).
| |  | (12) |
The quantum circuit that corresponds to the exponential of a Pauli string appearing in the time evolution operator can be constructed by following the literature.
57 The quantum circuit for exp(−
iwX
1Z
2Y
3t) is illustrated in
Fig. 2 as an example, where X
p, Y
p, and Z
p denote Pauli operators acting on the
p-th qubit. Note that in BPE the time evolution operation is executed conditional on the ancillary qubit. The controlled-exp(−
iwX
1Z
2Y
3t) is realised by substituting the
Rz(2
wt) gate in
Fig. 2 to the controlled-
Rz(2
wt) gate, where the control qubit is the ancillary qubit.
 |
| | Fig. 2 A quantum circuit for the time evolution operator exp(−iwX1Z2Y3t). | |
2.2 A BxB quantum algorithm for the direct calculation of spin state energy gaps
Because quantum computers can utilise quantum superposition states as their computational resources, it is possible to calculate the energy difference between two electronic states directly on quantum computers, by using the wave function approximated by a superposition of the two electronic states. The BxB quantum algorithm uses a broken-symmetry wave function |ΨBS〉 that is a mixture of wave functions belonging to different spin quantum numbers and is used for the calculations of an exchange coupling parameter J in terms of DFT58–60 as the input. For the two-spin systems |ΨBS〉 is described as in eqn (13).| | 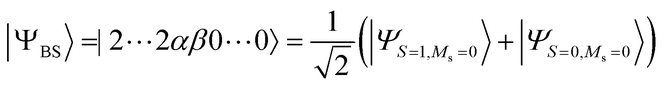 | (13) |
In the BxB algorithm, the calculation of the spin state energy gap is achieved by finding the j parameter in the shifted Hamiltonian defined in eqn (14), for which |ΨBS〉 given in eqn (15) becomes an eigenfunction of the shifted Hamiltonian H′.
| | 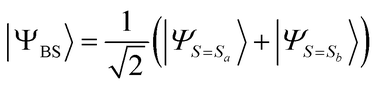 | (15) |
Here,
S2 is the spin squared operator giving an eigenvalue
S(
S + 1), where
S denotes a spin quantum number. The eigenvalues of |
ΨS=Sa〉 and |
ΨS=Sb〉 under the shifted Hamiltonian
H′ are given in eqn (16) and (17), respectively.
| | | ES=Sa′ = ES=Sa + jSa(Sa + 1) | (16) |
| | | ES=Sb′ = ES=Sb + jSb(Sb + 1) | (17) |
By writing the j parameter giving ES=Sa′ = ES=Sb′ as jopt, the spin state energy gap ΔE is calculated as follows.
| |  | (18) |
The quantum circuit for the BxB algorithm is given in Fig. 3. In the BxB algorithm, the deviation of |ΨBS〉 from the eigenfunction of H′ is evaluated by the quantum simulation of the time evolution of |ΨBS〉 under the shifted Hamiltonian H′ and following a SWAP test.61 The SWAP test consists of the controlled-SWAP operation that interchanges two quantum states |ϕ〉 and |φ〉 if the ancillary qubit is in the |1〉 state, flanked by two Hadamard gates on the ancillary qubit, and ancillary qubit measurement. The probability of obtaining the |0〉 state in the measurement is given in eqn (19), and therefore the square overlap |〈ϕ|φ〉|2 can be efficiently evaluated by the SWAP test.
| | | P(0) = (1 + |〈ϕ|φ〉|2)/2 | (19) |
In the BxB quantum algorithm, |
ϕ〉 is exp(−
iHt)|
ΨBS〉 and |
φ〉 is exp{−
i(−
jS2)
t}|
ΨBS〉. The probability
P(0) becomes a cosine function whose period is given by Δ
E′
t, where Δ
E′ is the energy gap between the two spin states under the shifted Hamiltonian
H′. By adopting the Bayesian inference to optimise the
j parameter giving a maximum
P(0), we can calculate the spin state energy gap directly, without inspecting the total energies of individual spin states.
 |
| | Fig. 3 A quantum circuit for the BxB algorithm. | |
As demonstrated in the preceding papers, the BxB algorithm can calculate the exchange coupling parameter J defined in Heisenberg spin Hamiltonian H = −2JijSi·Sj within 1 kcal mol−1 of errors,45 and vertical ionisation energies within 0.1 eV of precision.46 Also, the BxB algorithm can be extended to other problems, by replacing the penalty term introduced to the shifted Hamiltonian from jS2 to other operators such as a number operator of electrons  . However, any operators cannot be used as the penalty term in the BxB algorithm. It should commute with the original Hamiltonian H, otherwise the introduction of the penalty term changes the shape of eigenfunctions. Also, the eigenvalues of the penalty operator must be known. The two electronic states to calculate the energy gap should have different eigenvalues of the penalty operator. Operators satisfying these conditions are very rare, and thus the application of the BxB algorithm is limited. For example, the BxB algorithm can calculate the singlet–triplet energy gaps but it cannot compute singlet–singlet excitation energies. Furthermore, because the BxB algorithm uses the SWAP test, the number of qubits required for implementation is approximately doubled from the conventional QPE-based full-CI. It is highly desirable to overcome these shortcomings and to develop a new quantum algorithm enabling us to generally calculate any energy gaps. In the next section, we will introduce a new quantum algorithm, Bayesian phase difference estimation (BPDE), as a general algorithm capable of computing the differences of two eigenphases of unitary operators.
. However, any operators cannot be used as the penalty term in the BxB algorithm. It should commute with the original Hamiltonian H, otherwise the introduction of the penalty term changes the shape of eigenfunctions. Also, the eigenvalues of the penalty operator must be known. The two electronic states to calculate the energy gap should have different eigenvalues of the penalty operator. Operators satisfying these conditions are very rare, and thus the application of the BxB algorithm is limited. For example, the BxB algorithm can calculate the singlet–triplet energy gaps but it cannot compute singlet–singlet excitation energies. Furthermore, because the BxB algorithm uses the SWAP test, the number of qubits required for implementation is approximately doubled from the conventional QPE-based full-CI. It is highly desirable to overcome these shortcomings and to develop a new quantum algorithm enabling us to generally calculate any energy gaps. In the next section, we will introduce a new quantum algorithm, Bayesian phase difference estimation (BPDE), as a general algorithm capable of computing the differences of two eigenphases of unitary operators.
2.3 A Bayesian phase difference estimation (BPDE) algorithm
Let us rethink the reason why QPE algorithms including IQPE and BPE are difficult to implement on real quantum devices. Obviously, the biggest reason is that the quantum circuit for the time evolution is so deep that quantum error corrections are necessary to obtain meaningful computational results. Another reason is that QPE needs the controlled-time evolution operation. As discussed above, the controlled-time evolution requires many controlled-Rz gates with the same control qubit but different target qubits. Some quantum devices like those based on superconducting circuits can execute two qubit gates between physically connected qubits only. In order to implement the controlled-Rz gate to two qubits which are not physically connected, one has to construct a SWAP network to exchange the quantum states of the neighbouring qubits, so that the two qubits that the controlled-Rz gate acts on are placed next to each other. The SWAP network requires O(NSO) of additional gates, where we used a big-Oh notation to represent quantum gate complexity. Even if all qubits are fully connected, one has to minimise the crosstalk errors of the controlled-Rz gates. It is useful if QPE can be implemented without controlled-time evolution operations.
Again, let us rethink the mechanism of QPE algorithms. It calculates the phase shift caused by the time evolution of wave functions and readout the eigenphase by means of inverse quantum Fourier transformation (QPE) or Bayesian inference (BPE). The controlled-time evolution is introduced to calculate the phase difference of wave functions before and after the time evolution. However, it is possible to calculate the energy difference of two electronic states by simulating the time evolution of the wave function in the quantum superposition of the two electronic states without controlled operations, if we can prepare the quantum superposition of the two electronic states conditional to the quantum state of the ancillary qubit. This is the key idea in the quantum algorithms for direct calculations of energy gaps.44–47
The quantum circuit for the BPDE algorithm is given in Fig. 4. The quantum circuit consists of one ancillary qubit and NSO of qubits storing the wave function. Here, |Ψ0〉 can be any (approximated) eigenfunction of Hamiltonian H. Unless otherwise specified, we assume that |Ψ0〉 is the approximated wave function of the electronic ground state. The quantum circuit starts with an Hadamard gate on the ancillary qubit to generate the superposition of the |0〉 and |1〉 states. The following controlled-Excit gate (denoted by c-Excit in eqn (20)) applies an excitation operator to the wave function |Ψ0〉 if and only if the ancillary qubit is in the |1〉 state. This operation generates the superposition of the ground and excited states as given in the right hand side of eqn (20), and subsequent time evolution operation and inverse-controlled-Excit operation transform the quantum state as in eqn (21) and (22), respectively. The next step is application of the phase shift gate Tz to the ancillary qubit, giving the quantum state in eqn (23). By applying another Hadamard gate on the ancillary qubit, the quantum state before the measurement in Fig. 4 is given as eqn (24).
| |  | (20) |
| | 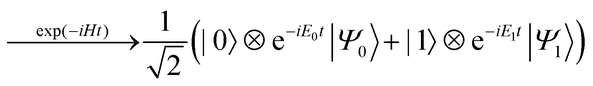 | (21) |
| | 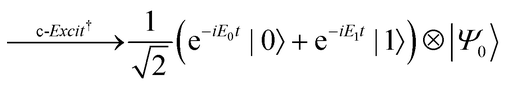 | (22) |
| |  | (23) |
| |  | (24) |
 |
| | Fig. 4 A quantum circuit for the BPDE algorithm. | |
The probability to obtain the |0〉 state in the measurement of the ancillary qubit can be calculated as in eqn (25).
| |  | (25) |
From eqn (25), it is clear that the measurement of the ancillary qubit always gives the |0〉 state if E1 − E0 = Δε. Thus, the energy gap between the two electronic states can be calculated by optimising the phase shift angle Δεt by means of Bayesian inference. The BPDE algorithm does not need a penalty operator and is capable of computing the difference of two eigenphases of unitary operators, if one can conditionally generate the superposition of two eigenfunctions. It should be emphasised that application of the BPDE algorithm is not limited to quantum chemical calculations, but to a wide variety of eigenvalue problems. Another merit of the BPDE algorithm against BxB is that the P(0) given in eqn (25) varies between 0 and 1, although P(0) in the BxB algorithm is given as P(0) = [3 + cos{(E1 − E0 − Δε)t}]/4,45 and thus it takes a value between 0.5 and 1. Thus, the range of the possible value for P(0) is wider in BPDE than in BxB, and the variation of P(0) by changing Δε becomes more apparent.
Note that the BPDE algorithm needs only one ancillary qubit, which is the same in IQPE and BPE. Importantly, both IQPE and BPE require controlled-time evolution operations but BPDE is free from them. In BPDE, the controlled operations appear in the state preparation (controlled-Excit) and inverse state preparation (controlled-Excit†). The controlled-Excit generates the excited state wave function conditionally, and therefore the quantum circuit for the controlled-Excit has the depth similar to that used for the state preparation in conventional QPE-based approaches. Importantly, we do not have to prepare the exact eigenfunction of a target electronic state in QPE, and preparation of the approximate wave function having sufficiently large overlap with the target electronic state is enough. The situation is the same in the BPDE algorithm, and we can calculate the energy gap correctly if the controlled-Excit can conditionally generate the wave function having large overlap with the target excited state. Thus, the quantum circuit for the controlled-Excit is usually very shallow and implementation of BPDE is much easier than IQPE and BPE those need controlled-time evolution operations. It should be also noted that the phase difference estimation algorithm described here can be easily extended to the IQPE scheme.
3. Results and discussion
To demonstrate the usefulness of the BPDE algorithm, we developed numerical quantum circuit simulation programs using Python with OpenFermion62 and Cirq63 libraries, and carried out numerical simulations for the direct calculations of vertical ionisation energies, singlet–triplet energy gaps, and vertical excitation energies. We also calculated the energy gaps using a naïve approach to compute total energies of individual electronic states by two separate BPE simulations and subtract them. The simulations were performed five times for each system. Details of computational procedures and conditions for the numerical simulations of BPDE and BPE are given in the ESI.†
3.1 Vertical ionisation energies
Accurate calculations of ionisation energies are important to understand electron transfer and oxidation processes in chemical reactions and nature of chemical bonding. As we demonstrated in the preceding paper, direct calculations of vertical ionisation energies are possible by using the BxB algorithm.45 Here, we adopt the BPDE algorithm to calculate the vertical ionisation energies of CH4, HCN, and HNC molecules as well as 16 chemical species (He, Li, Be, B, C, N, HF, BF, CF, CO, O2, NO, CN, F2, H2O, and NH3) studied previously by using the BxB algorithm.46 In order to calculate the vertical ionisation energies with the BPDE algorithm, we set the starting wave function |Ψ0〉 to be RHF/6-311G(d,p) or the ROHF/6-311G(d,p) wave function for closed shell and open shell species, respectively, of the neutral state. The largest systems under study are HCN and HNC with (10e, 9o) active spaces, those corresponding to 19 qubit quantum circuit simulations (18 qubits for the wave function storage and one ancillary qubit). Under the JWT, the controlled-Excit gate is realised by a CNOT gate with the ancillary qubit as the control and the qubit storing the occupation number of spin orbitals of which electron ionisation occurs as the target. We used the ionisation energy at the ΔSCF level, IE(ΔSCF) = EHF(cation) − EHF(neutral), as the initial estimate of the vertical ionisation energies.
The difference of the vertical ionisation energies from the quantum circuit simulations and that from the CAS-CI calculations are plotted in Fig. 5, and the values of the BPDE, BPE, and CAS-CI ionisation energies in conjunction with experimental ones are summarised in Table S2 in the ESI.† For all chemical species under study, both the BPDE and BPE algorithms reproduced the CAS-CI ionisation energy within 0.1 eV of errors. The ionisation energies computed by using BPDE and BPE are very close to each other, revealing that the accuracy of the vertical ionisation energy is almost the same between the direct calculation and naïve approach. In the HF molecule, both BPE and BPDE exhibit large deviations from the CAS-CI values. The deviation can be rationally explained by the errors arising from Trotter decomposition. In fact, the deviation from the CAS-CI value systematically improves by increasing the number of Trotter slices, and it becomes 0.004 eV if we use five times larger the number of Trotter slices in the calculation of HF molecule (see the ESI† for details).
 |
| | Fig. 5 Differences between the vertical ionisation energies from the quantum circuit simulations and those from the CAS-CI calculations for chemical species under study. | |
The BPDE simulation converges after eight optimisation cycles in all atoms and molecules under study, and thus the number of iterations does not depend on the system size. This is because BPDE optimises the energy difference directly. By contrast, in BPE the number of Bayesian optimisation cycles increases as the system size. For example, BPE optimisation of the neutral and cationic states of F2 takes 11 iterations. System size independence in the Bayesian optimisation in the BPDE algorithm cannot be overemphasised. This feature becomes more important in the calculations of larger molecules and molecules containing heavier atoms, as discussed in the excitation energy calculations of CBr2 (see Section 3.3).
3.2 Singlet–triplet energy gaps
Next we applied the BPDE algorithm to the direct calculations of singlet–triplet energy gap ΔES–T. The singlet–triplet energy gap is the most important physical quantity in biradicals. The ΔES–T of biradicals are usually in the order of a few kcal mol−1 or less, and accurate calculations of ΔES–T using quantum computers are very cost demanding. In this study, we focused on the covalent bond dissociation of the H2 molecule at the full-CI/STO-3G level, and atoms and small molecules including C, O, NH, OH+, NF, NCN, and CNN at the CAS-CI/6-311G(d,p) level. CAS-CI active spaces are summarised in the ESI.† For the calculation of the singlet–triplet energy gap, we used the |ΨCSF〉 of the MS = 0 of the spin-triplet state given in eqn (26) as |Ψ0〉, and the spin-singlet state given in eqn (27) is assigned to the excited state |Ψ1〉. In this formulation, ΔES–T becomes negative if the spin-singlet state has lower energy than the spin-triplet state.| |  | (26) |
| |  | (27) |
By setting |Ψ0〉 and |Ψ1〉 as described above, the controlled-Excit operation becomes a controlled-Z gate with the ancillary qubit as the control and one of the qubits storing the occupation number of singly occupied molecular orbitals (SOMOs) as the target. See the ESI† for details of the state preparations.
The results of the numerical quantum circuit simulations and the CAS-CI calculations are summarised in Fig. 6, and the ΔES–T values calculated at the BPDE, BPE, and CAS-CI methods are given in Tables S4 and S6 in the ESI.† From Fig. 6, both the BPE and BPDE succeed in predicting ΔES–T within 2 kcal mol−1 of errors in all systems under study. This corresponds to 1 kcal mol−1 of energy precision in the exchange coupling parameter J used in our preceding paper.45 Departures of the ΔES–T(BPE) and ΔES–T(BPDE) from the CAS-CI value are large for the H2 molecule with the interatomic distance R(H⋯H) ≤ 1.5 Å, but again this large deviation is mainly caused by the Trotter decomposition (see the ESI†). Another reason is that the spin-singlet wave function is not well approximated by |Ψ1〉. For shorter H⋯H distances contribution of the closed shell singlet electronic configuration to the full-CI wave function becomes significant, and therefore contributions from other electronic states to |Ψ1〉 are not negligible. As a result, the likelihood function becomes a linear combination of many cosine functions and P(0) becomes flattened. Adopting multiconfigurational wave functions constructed by using diradical character y for |Ψ1〉 using the quantum circuit proposed by us51 is a promising approach to improve the ΔES–T values, which is out of focus of this paper.
 |
| | Fig. 6 Differences between the singlet–triplet energy gaps from the quantum circuit simulations and those from the CAS-CI calculations. (a) H2 molecule with different atom–atom distances. (b) Atoms and other molecules under study. | |
3.3 Vertical excitation energies
Finally, we applied the BPDE algorithm to calculations of vertical excitation energies. These calculations were impossible by using the BxB algorithm, although it is essential to theoretically assign electronic transitions of the UV-vis spectra. In this study, we calculated the S0 → S1 and S0 → T1 excitation energies of dihalocarbenes (CX2, X = F, Cl, and Br) and dihalosilylenes (SiX2, X = F and Cl), and vertical excitation energies of the valence excited states of formaldehyde (HCHO). Active spaces for the CAS-CI calculations of dihalocarbenes and dihalosilylenes are provided as Fig. S9–S13 in the ESI,† and that of formaldehyde is given in Fig. 7.
 |
| | Fig. 7 CAS-CI active space of formaldehyde. | |
To calculate the excitation energies from the closed shell singlet ground state, we have to apply the symmetry-adapted excitation operators as the controlled-Excit gate. Spin-singlet and triplet states can be obtained by using the excitation operators Tja given in eqn (28) and (29), respectively, where j and a represent occupied and unoccupied molecular orbitals in the ground state, respectively.
| |  | (28) |
| |  | (29) |
The quantum circuits for the controlled-
Excit gates are illustrated in Fig. S16 in the ESI.
†
The calculated vertical excitation energies are summarised in Table 1. In Table 1, the BPE and BPDE excitation energies are given as the average of five numerical simulations. The 1 1B1 and 1 3B1 excited states of dihalocarbenes and dihalosilylenes are attributed to spin-allowed and spin-forbidden (spin–flip) HOMO → LUMO one electron transitions, respectively. In formaldehyde, the 1 1A2, 1 1B1, and 2 1A1 excited states are described mainly by the (2b2 → 2b1), (5a1 → 2b1), and (1b1 → 2b1) electron excitations, respectively. The calculated excitation energies are overestimated from the experimental values due to lack of dynamical electron correlation effects. The excitation energies obtained from the BPE and BPDE quantum circuit simulations agree to the CAS-CI value within ca. 0.1 eV of errors, exemplifying the accuracy of the BPE and BPDE algorithms.
Table 1 Vertical excitation energies of dihalocarbenes, dihalosilylenes, and formaldehyde
| Molecule |
Excited state |
Excitation energy/eV |
| BPE |
BPDE |
CAS-CI |
Exptl. |
|
Ref. 64.
Ref. 65.
Not available.
Ref. 66.
Ref. 67.
|
| CF2 |
1 1B1 |
6.200 |
6.199 |
6.143 |
4.615a |
| 1 3B1 |
3.060 |
3.062 |
2.999 |
2.458a |
| CCl2 |
1 1B1 |
3.188 |
3.186 |
3.191 |
2.139a |
| 1 3B1 |
1.354 |
1.362 |
1.360 |
0.9(2)b |
| CBr2 |
1 1B1 |
2.745 |
2.747 |
2.755 |
1.871a |
| 1 3B1 |
1.205 |
1.208 |
1.219 |
N.A.c |
| SiF2 |
1 1B1 |
6.622 |
6.622 |
6.643 |
5.469a |
| 1 3B1 |
3.639 |
3.651 |
3.663 |
3.262a |
| SiCl2 |
1 1B1 |
4.689 |
4.686 |
4.689 |
3.721a |
| 1 3B1 |
2.640 |
2.638 |
2.639 |
2.349a |
| HCHO |
1 1A2 |
5.292 |
5.297 |
5.359 |
4.1d |
| 1 1B1 |
10.467 |
10.466 |
10.525 |
8.6–9.0e |
| 2 1A1 |
11.586 |
11.603 |
11.692 |
10.7d |
As discussed above, the number of the iterations in the Bayesian optimisation does not depend on the system size in BPDE, although it strongly depends on the magnitude of total energy in BPE. This behaviour can be clearly seen in the calculation of CBr2. The CAS-CI(10e,6o)/6-31G* energy of the electronic ground state of CBr2 is −5181.9601544990 Hartree. BPE gives the ground state energy to be −5181.9600265599 Hartree (the average value of five runs). Error of the total energy is about 0.0035 eV and thus very small, but BPE simulations need 16 iterations to achieve the convergence. Note that in this study we used the 0.05 of Hartree–Fock energy as the initial variance of the Gaussian function (a prior distribution). Using tighter initial variance can accelerate the Bayesian optimisation. By contrast, the BPDE simulation converges after 8 iterations. Direct calculations of the energy gap are beneficial to reduce the computational costs related to Bayesian optimisations.
4. Conclusions
In this work, we examined the Bayesian phase difference estimation (BPDE) algorithm, which is a general quantum algorithm capable of computing the difference of two eigenphases of unitary operators, in several cases of direct calculations of energy gaps including vertical ionisation energies, singlet–triplet energy gaps, and vertical excitation energies. The BPDE algorithm is free from the controlled-time evolution operation that is necessary for putative QPE algorithms, and the number of qubits required for the implementation equals those in the IQPE and BPE algorithms. The BPDE algorithm is easier to be implemented on quantum devices than the BPE, and the accuracy of the energy gaps is comparable to the naïve approach based on two separate BPE quantum simulations. One of the most important features of the BPDE algorithm against the conventional BPE is that the number of iterations in the Bayesian optimisation to achieve the convergence does not depend on the system size, although it increases in BPE when the magnitude of the total energy becomes large. Direct calculations of energy gaps are also promising in terms of reducing the computational cost of Bayesian optimisation.
We emphasise that the usage of the BPDE algorithm is not limited to quantum chemical calculations. It is applicable to other unitary operators and therefore various applications can be anticipated. Even if we restrict ourselves to the topics of quantum chemical calculations, we can expect a variety of possible applications such as core ionisations, core excitations, Rydberg excitations, and charge-transfer excitations. Connection of the BPDE algorithm to the sophisticated methods for the wave function preparation such as multiconfigurational wave function preparations using diradical characters51 and adiabatic state preparation68,69 is another important extension of the algorithm. These applications potentially open the door to apply quantum computers to real-world chemistry problems.
Author contributions
K. Sugisaki, K. Sato, and T. Takui planned and conducted the project. K. Sugisaki proposed the theory. K. Sugisaki and C. Sakai performed quantum chemical calculations and numerical simulations. All the other authors discussed the results. K. Sugisaki and T. Takui wrote the paper.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by JST PRESTO “Quantum Software” project (Grant No. JPMJPR1914), Japan, and KAKENHI Scientific Research C (Grant No. 18K03465) from JSPS, Japan. This work was also supported by AOARD Scientific Project on “Molecular Spins for Quantum Technologies” (Grant FA2386-17-1-4040, 4041), USA, and JSPS KAKENHI Scientific Research C (21K03407), Japan.
Notes and references
-
F. Grasselli, Quantum Cryptography. From Key Distribution to Conference Key Agreement, Springer, Switzerland, 2021 Search PubMed.
- R. Orús, S. Mugel and E. Lizaso, Quantum computing for finance: Overview and prospects, Rev. Phys., 2019, 4, 100028 CrossRef.
-
M. Schuld and F. Petruccione, Supervised Learning with Quantum Computers, Springer, Switzerland, 2018 Search PubMed.
- Y. R. Sanders, D. W. Berry, P. C. S. Costa, L. W. Tessler, N. Wiebe, C. Gidney, H. Neven and R. Babbush, Compilation of fault-tolerant quantum heuristics for combinatorial optimization, PRX Quantum, 2020, 1, 020312 CrossRef.
- Y. Cao, J. Romero and A. Aspuru-Guzik, Potential of quantum computing for drug discovery, IBM J. Res. Develop., 2018, 62, 6 Search PubMed.
- P. A. M. Dirac, Quantum mechanics of many-electron systems, Proc. R. Soc. London, Ser. A, 1929, 123, 714–733 CAS.
- R. P. Feynman, Simulating physics with computers, Int. J. Theor. Phys., 1982, 21, 467–488 CrossRef.
- Y. Umena, K. Kawakami, J.-R. Shen and N. Kamiya, Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å, Nature, 2011, 473, 55–60 CrossRef CAS PubMed.
- T. Spatzal, J. Schlesier, E.-M. Burger, D. Sippel, L. Zhang, S. L. A. Andrade, D. C. Rees and O. Einsle, Nitrogenase FeMoco investigated by spatially resolved anomalous dispersion refinement, Nat. Commun., 2016, 7, 10902 CrossRef CAS PubMed.
- D. S. Abrams and S. Lloyd, Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors, Phys. Rev. Lett., 1999, 83, 5162–5165 CrossRef CAS.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Simulated quantum computation of molecular energies, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- B. P. Lanyon, J. D. Whitfield, G. G. Gillett, M. E. Goggin, M. P. Almeida, I. Kassal, J. D. Biamonte, M. Mohseni, B. J. Powell, M. Barbieri, A. Aspuru-Guzik and A. G. White, Towards quantum chemistry on a quantum computer, Nat. Chem., 2010, 2, 106–111 CrossRef CAS PubMed.
- J. Du, N. Xu, X. Peng, P. Wang, S. Wu and D. Lu, NMR implementation of a molecular hydrogen quantum simulation with adiabatic state preparation, Phys. Rev. Lett., 2010, 104, 030502 CrossRef PubMed.
- M. B. Hastings, D. Wecker, B. Bauer and M. Troyer, Improving quantum algorithms for quantum chemistry, Quantum Inf. Comput., 2015, 15, 1–21 CAS.
- R. Babbush, D. W. Berry, I. D. Kivlichan, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, Exponentially more precise quantum simulation of fermions in second quantization, New J. Phys., 2016, 18, 033032 CrossRef.
- R. Babbush, N. Wiebe, J. McClean, J. McClain, H. Neven and G. K.-L. Chan, Low-depth quantum simulation of materials, Phys. Rev. X, 2018, 8, 011044 CAS.
- R. Babbush, C. Gidney, D. W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler and H. Neven, Encoding electronic spectra in quantum circuits with linear T complexity, Phys. Rev. X, 2018, 8, 041015 CAS.
- I. D. Kivlichan, J. McClean, N. Wiebe, C. Gidney, A. Aspuru-Guzik, G. K.-L. Chan and R. Babbush, Quantum simulation of electronic structure with linear depth and connectivity, Phys. Rev. Lett., 2018, 120, 110501 CrossRef CAS.
- R. Babbush, D. W. Berry, J. R. McClean and H. Neven, Quantum simulation of chemistry with sublinear scaling in basis size, npj Quantum Info., 2019, 5, 92 CrossRef.
- J. D. Whitfield, Spin-free quantum computational simulations and symmetry adapted states, J. Chem. Phys., 2013, 139, 021105 CrossRef PubMed.
- K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum chemistry on quantum computers: A polynomial-time quantum algorithm for constructing the wave functions of open-shell molecules, J. Phys. Chem. A, 2016, 120, 6459–6466 CrossRef CAS PubMed.
- K. Sugisaki, S. Yamamoto, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Open shell electronic state calculations on quantum computers: A quantum circuit for the preparation of configuration state functions based on Serber construction, Chem. Phys. Lett.: X, 2019, 1, 100002 CAS.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum chemistry on quantum computers: Quantum simulations of the time evolution of wave functions under the S2 operator and determination of the spin quantum number S, Phys. Chem. Chem. Phys., 2019, 21, 15356–15361 RSC.
- K. Sugisaki, K. Toyota, K. Sato, D. Shiomi and T. Takui, A probabilistic spin annihilation method for quantum chemical calculations on quantum computers, Phys. Chem. Chem. Phys., 2020, 22, 20990–20994 RSC.
- K. Setia, R. Chen, J. E. Rice, A. Mezzacapo, M. Pistoia and J. D. Whitfield, Reducing qubit requirements for quantum simulations using molecular point group symmetries, J. Chem. Theory Comput., 2020, 16, 6091–6097 CrossRef CAS PubMed.
- D. Wecker, B. Bauer, B. K. Clark, M. B. Hastings and M. Troyer, Gate-count estimates for performing quantum chemistry on small quantum computers, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 022305 CrossRef.
- M. Reiher, N. Wiebe, K. M. Svore, D. Wecker and M. Troyer, Elucidating reaction mechanisms on quantum computers, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7555–7560 CrossRef CAS PubMed.
- P. J. J. O’Malley, R. Babbush, I. D. Kivlichan, J. Romero, J. R. McClean, R. Barends, J. Kelly, P. Roushan, A. Tranter, N. Ding, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. G. Fowler, E. Jeffrey, E. Lucero, A. Megrant, J. Y. Mutus, M. Neeley, C. Neill, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. C. White, P. V. Coveney, P. J. Love, H. Neven, A. Aspuru-Guzik and J. M. Martinis, Scalable quantum simulation of molecular energies, Phys. Rev. X, 2016, 6, 031007 Search PubMed.
- Y. Wang, F. Dolde, J. Biamonte, R. Babbush, V. Bergholm, S. Yang, I. Jakobi, P. Neumann, A. Aspuru-Guzik, J. D. Whitfield and J. Wrachtrup, Quantum simulation of helium hydride cation in a solid-state spin register, ACS Nano, 2015, 9, 7769–7774 CrossRef CAS PubMed.
- M. Dobšíček, G. Johansson, V. Shumeiko and G. Wendin, Arbitrary accuracy iterative quantum phase estimation algorithm using a single ancillary qubit: A two-qubit benchmark, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 030306 CrossRef.
- K. M. Svore, M. B. Hastings and M. H. Freedman, Faster phase estimation, Quantum Inf. Comput., 2014, 14, 306–328 Search PubMed.
- N. Wiebe and C. Granade, Efficient Bayesian phase estimation, Phys. Rev. Lett., 2016, 117, 010503 CrossRef PubMed.
- S. Paesani, A. A. Gentile, R. Santagati, J. Wang, N. Wiebe, D. P. Tew, J. L. O’Brien and M. G. Thompson, Experimental Bayesian quantum phase estimation on a silicon photonic chip, Phys. Rev. Lett., 2017, 118, 100503 CrossRef CAS PubMed.
- M.-H. Yung, J. Casanova, A. Mezzacapo, J. McClean, L. Lamata, A. Aspuru-Guzik and E. Solano, From transistor to trapped-ion computers for quantum chemistry, Sci. Rep., 2014, 4, 3589 CrossRef PubMed.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O’Brien, A variational eigenvalue solver on a photonic quantum processor, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- J. Preskill, Quantum computing in the NISQ era and beyond, Quantum, 2018, 2, 79 CrossRef.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Quantum chemistry in the age of quantum computing, Chem. Rev., 2019, 119, 10856–10915 CrossRef CAS PubMed.
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2020, 92, 015003 CrossRef CAS.
- B. Bauer, S. Bravyi, M. Motta and G. K.-L. Chan, Quantum algorithms for quantum chemistry and quantum materials science, Chem. Rev., 2020, 120, 12685–12717 CrossRef CAS PubMed.
- Y. Li, J. Hu, X.-M. Zhang, Z. Song and M.-H. Yung, Variational quantum simulation for quantum chemistry, Adv. Theory Simul., 2019, 2, 1800182 CrossRef CAS.
-
K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea, A. Anand, M. Degroote, H. Heimonen, J. S. Kottmann, T. Menke, W.-K. Mok, S. Sim, L.-C. Kwek and A. Aspuru-Guzik, Noisy intermediate-scale quantum (NISQ) algorithms, arXiv, 2021, preprint, arXiv:2101.08448, https://arxiv.org/abs/2101.08448.
- M. Gong, S. Wang, C. Zha, M.-C. Chen, H.-L. Huang, Y. Wu, Q. Zhu, Y. Zhao, S. Li, S. Guo, H. Qian, Y. Ye, F. Chen, C. Ying, J. Yu, D. Fan, N. Li, F. Liang, V. M. Bastidas, K. Nemoto, W. J. Munro, Y.-H. Huo, C.-Y. Lu, C.-Z. Peng, X. Zhu and J.-W. Pan, Quantum walks on a programmable two-dimensional 62-qubit superconducting processor, Science, 2021, 372, 948–952 CrossRef CAS PubMed.
-
S. Castellanos, Google plans quantum computer, The Wall Street Journal, appeared in the May 19, 2021.
- A. E. Russo, K. M. Rudinger, B. C. A. Morrison and A. D. Baczewski, Evaluating energy differences on a quantum computer with robust phase estimation, Phys. Rev. Lett., 2021, 126, 210501 CrossRef CAS PubMed.
- K. Sugisaki, K. Toyota, K. Sato, D. Shiomi and T. Takui, A quantum algorithm for spin chemistry: a Bayesian exchange coupling parameter calculator with broken-symmetry wave functions, Chem. Sci., 2021, 12, 2121–2132 RSC.
- K. Sugisaki, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum algorithm for the direct calculations of vertical ionization energies, J. Phys. Chem.
Lett., 2021, 12, 2880–2885 CrossRef CAS PubMed.
- Y. Matsuzaki, H. Hakoshima, K. Sugisaki, Y. Seki and S. Kawabata, Direct estimation of the energy gap between the ground state and excited state with quantum annealing, Jpn. J. Appl. Phys., 2021, 60, SBBI02 CrossRef CAS.
- J. R. McClean, M. E. Kimchi-Schwartz, J. Carter and W. A. de Jong, Hybrid quantum-classical hierarchy for mitigation of decoherence and determination of excited states, Phys. Rev. A, 2017, 95, 042308 CrossRef.
- K. M. Nakanishi, K. Mitarai and K. Fujii, Subspace-search variational quantum eigensolver for excited states, Phys. Rev. Res., 2019, 1, 033062 CrossRef CAS.
- O. Higgott, D. Wang and S. Brierley, Variational quantum computation of excited states, Quantum, 2019, 3, 156 CrossRef.
- K. Sugisaki, S. Nakazawa, K. Toyota, K. Sato, D. Shiomi and T. Takui, Quantum chemistry on quantum computers: a method for preparation of multiconfigurational wave functions on quantum computers without performing post-Hartree–Fock calculations, ACS Cent. Sci., 2019, 5, 167–175 CrossRef CAS PubMed.
- P. Jordan and E. Wigner, Über das Paulische äquivalenzverbot, Z. Phys., 1928, 47, 631–651 CrossRef CAS.
- J. T. Seeley, M. J. Richard and P. J. Love, The Bravyi–Kitaev transformation for quantum computation of electronic structure, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
- K. Setia and J. D. Whitfield, Bravyi–Kitaev superfast simulation of electronic structure on a quantum computer, J. Chem. Phys., 2018, 148, 164104 CrossRef PubMed.
- H. F. Trotter, On the product of semi-groups of operators, Proc. Am. Math. Soc., 1959, 10, 545–551 CrossRef.
- M. Suzuki, Relationship between d-dimensional quantal spin systems and (d + 1)-dimensional Ising systems: Equivalence, critical exponents and systematic approximants of the partition function and spin correlations, Prog. Theor. Phys., 1976, 56, 1454–1469 CrossRef.
- J. D. Whitfield, J. Biamonte and A. Aspuru-Guzik, Simulation of electronic structure Hamiltonians using quantum computers, Mol. Phys., 2011, 109, 735–750 CrossRef CAS.
- K. Yamaguchi, The electronic structures of biradicals in the unrestricted Hartree–Fock approximation, Chem. Phys. Lett., 1975, 33, 330–335 CrossRef CAS.
-
K. Yamaguchi, Y. Takahara and T. Fueno, Ab-initio molecular orbital studies of structure and reactivity of transition metal-OXO compounds, in Applied Quantum Chemistry, ed. V. H. Smith, H. F. Schaefer and K. Morokuma, Springer, 1986, pp. 155–184 Search PubMed.
- M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, A general algorithm for calculation of Heisenberg exchange integrals J in multi-spin systems, Chem. Phys. Lett., 2006, 432, 343–347 CrossRef CAS.
- H. Buhrman, R. Cleve, J. Watrous and R. de Wolf, Quantum fingerprinting, Phys. Rev. Lett., 2001, 87, 167902 CrossRef CAS PubMed.
- J. R. McClean, N. C. Rubin, K. J. Sung, I. D. Kivlichan, X. Bonet-Monroig, Y. Cao, C. Dai, E. Schuyler Fried, C. Gidney, B. Gimby, P. Gokhale, T. Häner, T. Hadikar, V. Havlíček, O. Higgott, C. Huang, J. Izaac, Z. Jiang, X. Liu, S. McArdle, M. Neeley, T. O’Brien, B. O’Gorman, I. Ozfidan, M. D. Radin, J. Romero, N. P. D. Sawaya, B. Senjean, K. Setia, S. Sim, D. S. Steiger, M. Steudtner, Q. Sun, W. Sun, D. Wang, F. Zhang and R. Babbush, OpenFermion: the electronic structure package for quantum computers, Quantum Sci. Technol., 2020, 5, 034014 CrossRef.
- Quantum AI team and collaborators. (March 5, 2021). quantumlib/Cirq: Cirq, Version v0.10.0. Zenodo DOI:10.5281/zenodo.4586899.
-
M. E. Jacox, Vibrational and electronic energy levels of polyatomic transient molecules, J. Phys. Chem. Ref. Data, 1994, Monograph No. 3 Search PubMed.
- S. W. Wren, K. M. Vogelhuber, K. M. Ervin and W. C. Lineberger, The photoelectron spectrum of CCl2−: the convergence of theory and experiment after a decade of debate, Phys. Chem. Chem. Phys., 2009, 11, 4745–4753 RSC.
- L. B. Harding and W. A. Goddard, Ab initio theoretical studies of the Rydberg states of formaldehyde, J. Am. Chem. Soc., 1977, 99, 677–683 CrossRef CAS.
- D. C. Moule and A. D. Walsh, Ultraviolet spectra and excited states of formaldehyde, Chem. Rev., 1975, 75, 67–84 CrossRef CAS.
- L. Veis and J. Pittner, Adiabatic state preparation study of methylene, J. Chem. Phys., 2014, 140, 214111 CrossRef PubMed.
- H. Yu and T.-C. Wei, Quantum Zeno approach for molecular energies with maximum commuting initial Hamiltonians, Phys. Rev. Res., 2021, 3, 013104 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Definitions of quantum gates, computational conditions for quantum chemical calculations, quantum circuits for the state preparations and controlled-Excit operations, numerical quantum circuit simulations for the BPDE and BPE algorithms, and Trotter decomposition error analysis. See DOI: 10.1039/d1cp03156b |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc,
Chikako
Sakai
a,
Kazuo
Toyota
a,
Kazunobu
Sato
*abc,
Chikako
Sakai
a,
Kazuo
Toyota
a,
Kazunobu
Sato
 *a,
Daisuke
Shiomi
*a,
Daisuke
Shiomi
 a and
Takeji
Takui
a and
Takeji
Takui
 *ad
*ad






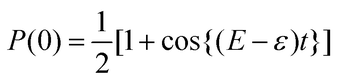
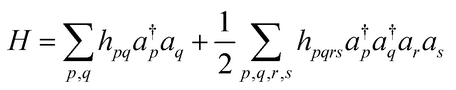




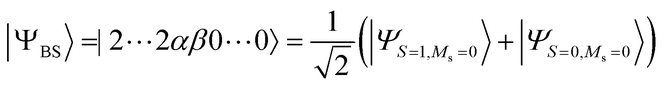
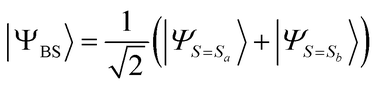

 . However, any operators cannot be used as the penalty term in the BxB algorithm. It should commute with the original Hamiltonian H, otherwise the introduction of the penalty term changes the shape of eigenfunctions. Also, the eigenvalues of the penalty operator must be known. The two electronic states to calculate the energy gap should have different eigenvalues of the penalty operator. Operators satisfying these conditions are very rare, and thus the application of the BxB algorithm is limited. For example, the BxB algorithm can calculate the singlet–triplet energy gaps but it cannot compute singlet–singlet excitation energies. Furthermore, because the BxB algorithm uses the SWAP test, the number of qubits required for implementation is approximately doubled from the conventional QPE-based full-CI. It is highly desirable to overcome these shortcomings and to develop a new quantum algorithm enabling us to generally calculate any energy gaps. In the next section, we will introduce a new quantum algorithm, Bayesian phase difference estimation (BPDE), as a general algorithm capable of computing the differences of two eigenphases of unitary operators.
. However, any operators cannot be used as the penalty term in the BxB algorithm. It should commute with the original Hamiltonian H, otherwise the introduction of the penalty term changes the shape of eigenfunctions. Also, the eigenvalues of the penalty operator must be known. The two electronic states to calculate the energy gap should have different eigenvalues of the penalty operator. Operators satisfying these conditions are very rare, and thus the application of the BxB algorithm is limited. For example, the BxB algorithm can calculate the singlet–triplet energy gaps but it cannot compute singlet–singlet excitation energies. Furthermore, because the BxB algorithm uses the SWAP test, the number of qubits required for implementation is approximately doubled from the conventional QPE-based full-CI. It is highly desirable to overcome these shortcomings and to develop a new quantum algorithm enabling us to generally calculate any energy gaps. In the next section, we will introduce a new quantum algorithm, Bayesian phase difference estimation (BPDE), as a general algorithm capable of computing the differences of two eigenphases of unitary operators.