Biliverdin chiral derivatives as chiroptical switches for pH and metal cation sensing

Abstract

A series of six optically active derivatives of the bile pigment biliverdin, namely (βS,β′S)-dimethylmesobiliverdin-XIIIα, cyclic esters of linear diols [HO(CH₂)_nOH] where n = 1–6, have been investigated by vibrational circular dichroism (VCD) and density functional theory (DFT) calculations. The results were correlated with the length (n) of the diester belt, the verdin helicity and an M ⇄ P conformational equilibrium – as previously shown by electronic circular dichroism (ECD). Furthermore, ECD spectra have been found to be quite sensitive to solvent nature and pH. TD-DFT calculations of the protonated/deprotonated verdins with n = 1 and 2 diester belts respectively have allowed one, moreover, to explain the spectroscopic data in terms of a change in the M ⇄ P equilibrium. Finally, the set of investigated compounds, together with other chirally functionalized “non-belted” biliverdin analogs, has also been found to be sensitive to the presence of metal ions, with which the verdins chelate. On the basis of ECD and VCD data, we propose that the spectroscopic changes observed are consistent with self-association (dimerization) of the verdin molecules promoted by the metal cations, as bolstered by DFT calculations, and for which a dimerization constant of 73 000 M⁻¹ is evaluated. We envision the use of current chiroptical spectroscopies in connection with chiral biliverdin derivatives as natural sensors or probes of the micro-environmental conditions, such as pH or the presence of metal ions.

---

Introduction

The blue-green tetrapyrrole bile pigment, biliverdin, is the primary catabolic product in heme metabolism and the precursor to bilirubin, the yellow pigment of mammalian bile.^1,2 Structure investigations of biliverdin and its analogs revealed a conjugated system of four pyrroles in a lock washer configuration.² Biliverdin is optically inactive but consists of two interconverting helical conformations (M and P); yet, there have been only a few studies of its chiropticity.³ Falk^2,4 showed the M ⇄ P helical inversion by linking the end ring nitrogens of a synthetic verdin, etiobiliverdin-IVγ, separating enantiomeric helices and observing circular dichroism (CD). Lehner^5,6 produced helically constrained verdins by linking the two exo vinyl groups of biliverdin-XIIIα; he separated enantiomers and again observed their intense CD. After preparing amides of the propionic acids groups of natural biliverdin with amino acids and peptides,^7–9 Lehner observed their CD. The few chiroptical studies of biliverdin itself focused on optical activity induced by chiral complexing agents such as liposomes and micelles as well as proteins.^2,3,10 Some years ago, a few of us conceived of modulating the helicity of an optically active biliverdin, (βS,β′S)-dimethylmesobiliverdin-XIIIα^11,12 by linking its two propionic acid groups as diesters with diols of varying length to produce “strapped” biliverdins.¹² In the following, we analyze those verdins and their metal complexes by vibrational and electronic CD (VCD and ECD, respectively) spectroscopy and DFT calculations. The zinc, nickel and silver complexes exhibit unexpected CD behavior.

It is well known that organic molecules in solution are rather sensitive to the solvent (type and concentration), to physical and chemical conditions (temperature, pH, ionic strength, etc.), and to interaction with other solutes, such as metal ions. Certain organic molecules are unique in that the changes induced by physico-chemical agents and by the local environment may translate into changes of handedness for specially designed chiral systems: such changes can then be easily and reliably monitored by chiroptical methods, which date from the times of Biot & Frésnel to more recent methods from the last half-century or so.^13–22

As recent examples of such sensitive molecules, which of course are not at all exhaustive of the very many ones present in the literature, we recall those in which a change of helicity is occurring in molecules employed in material science, due to changes in the status of the environment.^23–27 Such changes depend on the structural characteristics of the designed molecular systems and are critically dependent on the presence of metal ions. Another example is a quite strong excitonic system, where acidic conditions do not alter the configuration of the cyclohexane-based systems, but rather enhance all associated chiroptical properties, namely specific optical rotation, ECD spectra, VCD spectra and CPL (circularly polarized luminescence) spectra.²⁸

Herein we describe compounds 1–6 presented in Scheme 1, which had been previously synthesized and studied by NMR, ECD and Molecular Mechanics/Molecular Dynamics methods.¹² These cyclic diester analogs of biliverdin have their component dipyrrinones constrained to adopt a cisoid conformation and consequently to exhibit ECD spectra, which are quite sensitive to the number n of methylene units of the diester chain. Chiral biliverdin derivatives have been amply studied, not only for investigating aspects of the 3D structure of that medically important compound, but also to test its interaction with drugs, metals etcetera. In this regard it is useful to recall references^1,2 in which seminal studies were presented for the sensitivity to pH and metal ions respectively. The chiroptical technique employed to monitor such interaction was mainly ECD. More recently Urbanová and collaborators showed that VCD also provides similar and sometimes additional information for the interaction of biliverdin with metal ions and with chiral systems, e.g., lipids or proteins.^29,30 In the following we investigate molecules 1–6 by VCD, and perform DFT studies reproducing the VCD data with the aim of providing a solid ground to the picture of the helical conformation. This will allow us to confirm earlier conclusions¹² and to provide a quantitative estimate of the unbalance between P and M helicity imparted to the verdin skeleton by the chiral ester substituents, depending on the number of methylene units in the diester chain. In the second part of this work, we will study by ECD and by TD-DFT the dependence of spectroscopic response of some of the systems 1–6 on pH, as suggested by McDonagh for natural biliverdin by UV spectroscopy¹ and by Haidl et al. through ECD.⁷ In the third and final part we investigate by ECD and VCD, in conjunction with DFT calculations, the sensitivity of some of the 1–6 molecules to some metal ions, as done for zinc octaethyl formylbiliverdinate by Struckmeier et al.³¹

Scheme 1 Biliverdin-IXα, mesobiliverdin XIIIα, mesobiliverdin cyclic diesters 1–6, and two “non-bridged” mesobiliverdins investigated in this work.

Experimental methods

The verdins used here are cyclic diesters of (βS,β′S)-dimethylmesobiliverdin-XIIIα, which for simplicity we refer as simply “cyclic verdin”. In the following text, the compound called 1 in Scheme 1 refers to the cyclic verdin with n = 1 CH₂-units; compound 2 refers to the cyclic verdin with n = 2 CH₂-units, and so on. Cyclic verdin 1–6 were synthesized and first characterized by NMR and ECD.¹² The “non-bridged” dimethylmesobiliverdin-XIIIα (bottom row of Scheme 1) were synthesized as reported in ref. 32.

IR and VCD spectra were measured with a Jasco FVS6000 instrument on 2 × 10⁻³ M CDCl₃ solutions in 200 μm BaF₂ cells. 6000 scans were acquired with 4 cm⁻¹ resolution. IR and VCD spectra of verdin–metal complexes were measured in 500 μm BaF₂ cells at 1 × 10⁻³ M concentration.

The UV and ECD spectra were measured with a Jasco 815SE instrument using 200 nm min⁻¹ scan speed; on CHCl₃ or methanol solutions 1 × 10⁻⁵ M in 2 mm quartz cuvettes, with 5 scans. Solvent spectra were subtracted, both for absorption and CD. The UV and ECD spectra at different pH were carried out by adding small volume of concentrated hydrochloric acid (HCl 38%) or concentrated sodium hydroxide (10 M NaOH) in the methanol or DMSO solution of cyclic verdin. The UV-Vis and ECD spectra as a function of concentration were measured using cuvettes with different pathways, from 0.1 mm to 2 cm.

Metal complexes of 1–6 for ECD and VCD measurements were prepared by adding the metal salt (zinc triflate, nickel triflate or silver triflate), dissolved in chloroform, to the cyclic verdin,^31,33 keeping the ratio between biliverdin and the metal ion at 1 : 1. The resulting verdin–metal solutions were kept in the dark at room temperature, and the spectroscopic measurements were conducted six hours after sample preparation. Instead, when zinc chloride was used, the verdin–metal solutions were heated at 40 °C in the dark to increase the solubility of the chloride salt.

Computational methods

Prior to calculating the spectra of compounds 1 and 2, conformational analyses were carried out. Preliminary conformational searches were carried out using the CREST package.³⁴ The obtained conformers were successively optimized by Gaussian16 software³⁵ with B3LYP functional and TZVP basis set. IR and VCD spectra were calculated with B3LYP/TZVP. UV and ECD spectra were calculated with CAM-B3LYP functional and TZVP basis set. All calculations were performed in the IEF-PCM approximation, as embedded in the Gaussian16 software.

Results and discussion

As outlined in the introductory section, we first present and discuss the experimental VCD and IR spectra (in parallel to the ECD and UV-Vis absorption data) for all compounds 1 through 6. Then we study the pH dependence of the biliverdin first assayed by McDonagh¹ by UV-Vis spectroscopy herein, considering chiral derivatives, we employ ECD spectroscopy and TD-DFT calculations. Finally, we study how certain metal ions coordinate to the cyclic verdins 1–6, through the use of ECD and for some of them through VCD spectroscopy. Possible structures, some of them proposed in the literature, are tested by DFT calculations.

(I) The M ⇄ P equilibria in 1–6 studied by VCD

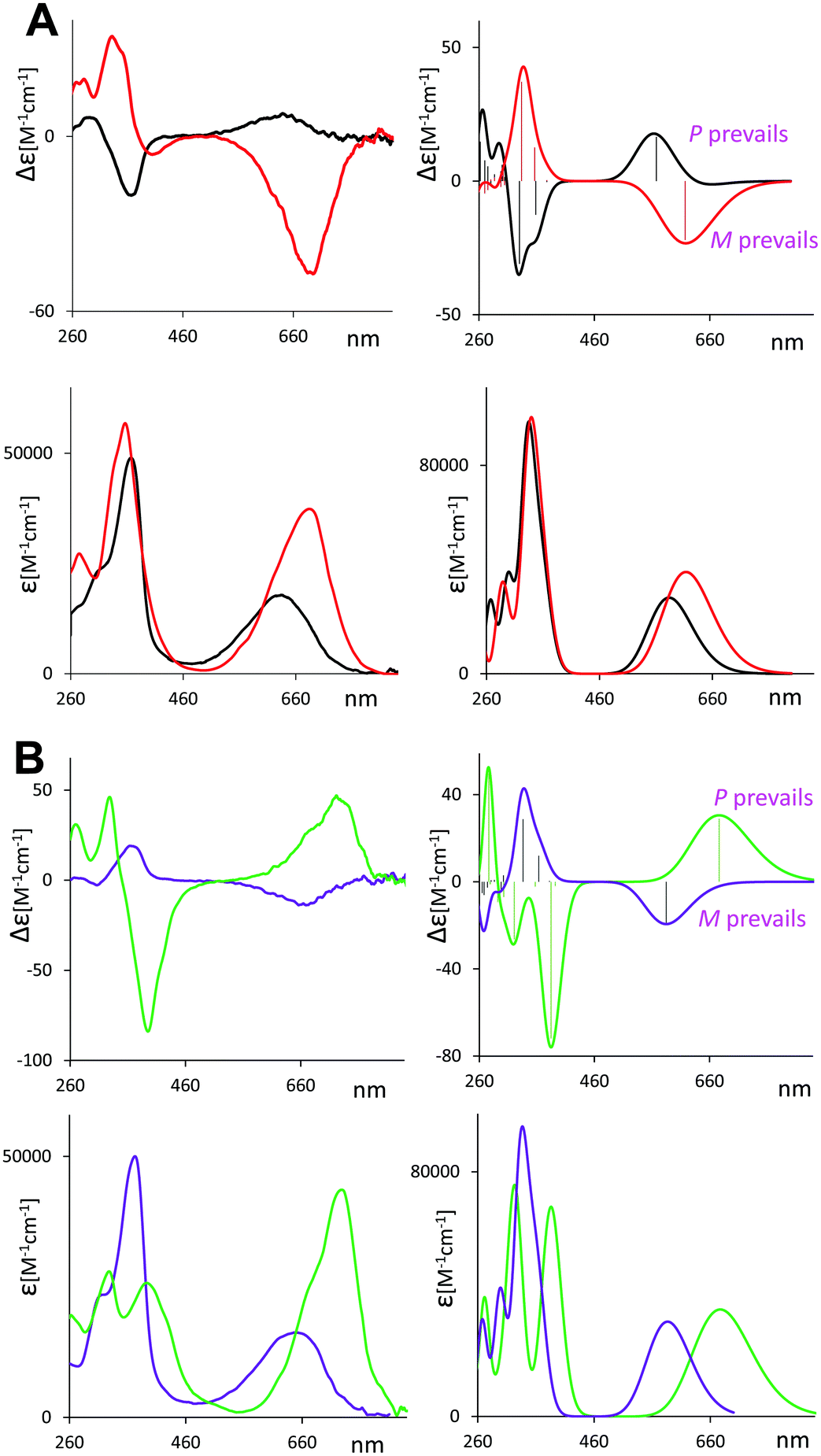
As mentioned above, induced VCD had been observed from optically inactive biliverdins in the presence of chiral inducing agents.^29,30 Our group has also employed VCD to study the closely related and equally relevant tetrapyrrole systems, i.e. some synthetic chiral bilirubin derivatives and the natural compounds L-stercobilin and D-urobilin.^36–38

In Fig. 1, we report the VCD and IR spectra of 1–6 in CDCl₃ solution (panels A and B, respectively) and display them beside their ECD and UV-Vis spectra in CHCl₃ (panels C and D, respectively), which had been recorded previusly¹² but were not shown there, since only the maximum/minimum value of molar ellipticity was tabulated.

Fig. 1 Cyclic verdin 1–6: VCD (A) and IR (B) spectra in deuterated chloroform at ca. 10⁻³ M concentration; ECD (C) and UV (D) spectra in chloroform at 1 × 10⁻⁵ M concentration (see Experimental section).

In Fig. 1A, the main VCD signals are found in the carbonyl-stretching region, with the main feature centered at 1695–1700 cm⁻¹ changing sign among the compounds. The same spectroscopic region of VCD spectra was demonstrated to be quite informative also by Goncharova and Urbanová³⁰ for biliverdin complexes with metals in the presence of β-cyclodextrin.

The mid-IR region below 1600 cm⁻¹ contains weaker signals. Although they are beyond experimental error, they appear to be less informative about the changes taking place from 1 to 6, especially if compared to the 1800–1600 cm⁻¹.

The IR spectra (Fig. 1B) show that increasing the number of the CH₂ units (n) of the diester belt results in a shift of the position of the peak at higher wavenumber (about 1750 cm⁻¹ for n = 1) toward the most intense adjacent peak (1700 cm⁻¹). Also, the next two peaks (1620 cm⁻¹ and 1585 cm⁻¹) move closer to each other when the number of methylene groups increases in the cyclic ester belt.

The ECD spectra of compounds 1–6 in Fig. 1C exhibit a broad and weak monosignate signal at 650 nm and an intense band at 360 nm of opposite sign and a weaker feature at ca. 300 nm, the latter having the same sign as the one at 650 nm. It is interesting to note (and we believe quite relevant) that the sign of VCD major band near 1700 cm⁻¹ always corresponds to the sign of the ECD band around 650 nm and is opposite to the ECD band at 360 nm.

In contrast, no appreciable changes in wavelength and intensity with n (n = 1–6) were observed in the UV spectra (Fig. 1D).

The ECD spectra confirm earlier reported data.¹² The changes with n were interpreted in terms of shifting M ⇄ P helical equilibrium, where predominant P helicity is associated with a positive long wavelength ECD. We have also tested the temperature dependence of ECD spectra of 1 and 2 (see Fig. S1, ESI†). As expected, the CD signal increases while lowering the temperature, indicating that the most stable conformers increase their population. The same sensitivity towards n is exhibited by the VCD spectra. Since the data in Fig. 1 suggest that in some cases the population of M-conformers prevails, while in other cases the conformer population is dominated by P-helicity we investigated the conformational space of compounds 1 and 2.

The relative population factors, conformational structures and calculated IR and VCD spectra of the most populated conformers of 1 and 2 are reported in Fig. S2 through Fig. S5 (ESI†). For compound 1, (Fig. S2 and S3, ESI†) the overall population of P-conformers prevails over that of M-conformers. In contrast, on compound 2 (Fig. S4 and S5, ESI†) calculations show that M-conformers prevail over P-conformers.

Fig. 2 compares the calculated Boltzmann averaged VCD and IR spectra of 1 and 2 with the corresponding experimental spectra. Overall, the calculated spectra are in good agreement with the experimental ones. Calculations allow one to make useful assignments of the bands.

Fig. 2 Comparison of experimental (black lines) and calculated weighted average VCD and IR spectra (blue lines) for 1 (A and B) and 2 (C and D).

In the carbonyl-stretching region, the weaker feature at 1750 cm⁻¹ corresponds to the C=O stretching for the carbonyl in the ester group, which, referring to each conformer, is dependent on the C=O orientation with respect to the tetrapyrrole skeleton. The latter peculiarity explains the broadness of the band. Correspondingly, VCD intensity is weak both in the experimental and calculated spectra, and its sign exhibits an erratic behavior with respect to n. The shape of this calculated feature may suggest a vibrational exciton coupling³⁹ but, examining the normal modes structure from calculations, we realized that it is associated to isolated vibrations.

The intense signal at 1700 cm⁻¹ is assigned to the C=O stretching of the carbonyl lactam rings. The sign of that band reflects the helicity of the tetrapyrrole (see also Fig. S3 and S5, ESI†), where the VCD for P conformers is calculated to be positive and for M conformers negative, independently of n. Between 1650 cm⁻¹ and 1550 cm⁻¹, the normal modes underneath the two observed IR bands and the three VCD bands contain contributions from NH in-plane bending, C=C stretching and CH in-plane bending. The two most intense VCD bands in that region are positive for 1 and negative for 2, and, as of Fig. S3 and S5 (ESI†), they show the same dependence on the overall helicity (P and M) as the 1700 cm⁻¹ band.

From calculations on the most populated structures (Fig. S3 and S5, ESI†), each M conformer gives an all negative VCD spectrum while each P conformer gives a positive one. This fact explains the diagnostic value of the most intense VCD bands which bear similar rotational strengths (in absolute value) for P and for M conformers, on the contrary the features at 1270 cm⁻¹ and 1150 cm⁻¹ beside being less intense show a variability in shape and intensity such that the corresponding average is not always correlated to the prevailing helicity. We end this section, by observing that the different ester bridge conformations (see Fig. S2 and S4 (ESI†) and ref. 12) have only a minor effect on the VCD signals, and the sign of the principal observed bands is determined almost totally by the helicity of the tetrapyrrole (Fig. S3 and S5, ESI†). This is true, as expected, also for the ECD spectra.

(II) ECD and corresponding TD-DFT calculations elucidate the pH-dependent chiroptical activity of cyclic verdin in solution.

McDonagh¹ reported the tendency of natural biliverdin to be easily protonated or deprotonated by strong acids or bases respectively, this change being accurately monitored by UV-Vis absorption spectroscopy. This is indeed a first hint that biliverdin may switch chiroptical properties by sensing pH, as observed in other cases, see for example.²⁸ We have thus repeated similar experiments by measuring not only UV-Vis but also ECD spectra on three compounds (1–3) in methanol and in DMSO solutions, by adding small volumes of acid (HCl) or base (NaOH), so as to have the acid/base concentration to reach ca. 0.01–0.02 M. The results are reported in Fig. 3. Further data, with step-by-step addition of acid for molecule 1 or base solution for molecule 2, are reported in Fig. S6 and S7 (ESI†) respectively.

Fig. 3 ECD (top and middle rows) and UV (bottom row) experimental spectra of 1, 2 and 3 in methanol solution (black curves) and DMSO solution (purple curves), in presence of 0.01 M of HCl (red curves) and in presence of NaOH 0.02 M (blue curves for basified methanol and green curves for basified DMSO solutions, respectively).

The three molecular systems exhibit ECD spectra dependence on pH in different ways. In the presence of acid, the ECD spectrum of 1 inverts sign and red shifts, as well as that of 3, whereas the ECD spectrum of 2 just decreases in intensity without changing sign. In presence of the acid a strong increase in the absorbance of the band at lower energy is observed, while a modest increase in the band at high energy is noticed.

Considering the basic condition, the chiroptical activity has been monitored both in methanol and DMSO solutions. The chosen solvent significantly impacts the aspect of the UV-Vis and ECD spectra. In basic methanol, the ECD spectra of 2 and 3 invert sign and slightly red shift, instead the ECD spectra of 1 does not invert. For all the three cases, the final ECD spectrum is weaker than the original one without base. In basic DMSO, the ECD pattern inverts for 2 and 3 but not for 1, as observed in methanol, however in this instance the final ECD spectra are much stronger and the red shift more consistent. A redshift of about 70 nm is also observed for the UV band at higher wavelength, which also increases in intensity. Instead the UV band at lower wavelength splits in two components.

Thus, the changes observed in DMSO are more significant than the changes observed in methanol, a proton donor. DMSO can act as proton acceptor, enhancing the rate of proton removal promoted by the base.

Our UV-Vis results in the DMSO-NaOH condition are similar to those reported by Falk^2,40,41 on verdins in DMSO with a base (tetramethylammonium hydroxide in that case). These spectra, together with the ¹H-NMR chemical shift data,^40,41 suggest the deprotonation of one nitrogen atom of the lactam rings,^2,40,41 resulting in an anionic species stabilized by resonance.

Concerning pH sensitivity, we note that the spectroscopic change observed in basified conditions is reversable upon addition of HCl (see Fig. S8, ESI†).

With the aim of elucidating the pH-dependent chiroptical activity of these cyclic verdins, we investigated the role of the diester bridge in the ECD chiroptical response. Is the cyclic diester bridge necessary for the observed spectral behavior? To answer this question, we have examined two enantiomerically pure “acyclic” analogs for pH dependent chiroptical switch behavior. Thus, we carried out ECD experiments on other “non-bridged” 8,12-bis[(1S)-methylpropyl]mesobiliverdin-XIIIα and 8,12-bis[3-acetoxy-(1S)-methylpropyl]mesobiliverdin-XIIIα. The spectra are shown in Fig. S9 (ESI†). In these “non-bridged” cases, in presence of the acid, all bands in the ECD spectra invert sign with respect to the neutral case, while the addition of a base in methanol introduces no significant changes. Whereas, in basic DMSO, the final ECD spectra are much stronger and red-shifted with respect to the neutral condition. The behavior of these chirally substituted mesobiliverdin-XIIIα are quite similar to that of 1 (and 6 as shown in Fig. S8, ESI†) while 2 and 3 are different. However, the intensity of the ECD signals is overall significantly lower than in compounds 1–6, thus less likely to use as pH sensors.

In conclusion, considering the cases presented here, the best sensitivity to the acid environment is shown by 1, 3 and 6 since in these molecules sign inversion with respect to the neutral condition occurs. For the basic condition in DMSO, the response is similar in all the molecules, presenting intensification and redshift of the longer wavelength CD band. In basic methanol, where the spectral changes are less evident, compounds 2 and 3 are the best choice since they both show inversion of the CD signal with respect to the neutral condition.

DFT calculations were applied to the “acidic” form of the smallest cyclic verdin (1). Indeed, one may easily assume that HCl addition induces protonation of the single free nitrogen. We considered all the conformers obtained from the previous conformational search of the neutral species, which has allowed us to interpret the VCD spectra in Fig. 2 for 1. The six main conformers have been protonated and then re-optimized. The resulting Boltzmann population factors are reported in Table S1 (ESI). We observed a change in the M ⇄ P equilibrium. While in the neutral cyclic verdin the P-conformers are predicted to prevail, in the protonated form the M-conformers dominate.

From the geometrical point of view, protonation appears to favor the increase of the central dihedral angle (N22–C9–C11–N23) value from ca. 14° to ca. 24° (see also Fig. S10, ESI†).

The optimized structures thus obtained are used for the TD-DFT calculation of UV and ECD spectra. In Fig. 4A, the experimental ECD and UV data for the neutral case and the protonated case (both recorded in methanol) are compared to the corresponding calculated ones. The calculated ECD spectra both for the neutral case and the protonated case correctly predict the sign of the bands.

Fig. 4 (A) Experimental (left) and calculated weighted average (right) ECD (top) and UV (bottom) spectra of 1 in methanol (black line) and acidic methanol solution (red line). (B) Experimental (left) and calculated weighted average (right) ECD (top) and UV (bottom) spectra of 2 in DMSO (purple line) and basic DMSO solution (green line).

The calculated spectra allow us to reproduce the above described changes occurring in the presence of acid. The redshift of the absorption band at longer wavelength in the acidic condition is reproduced by the calculations, as well as the intensity increase, though not by exactly the right amount. Of course, the most important feature simulated by the DFT calculation is the observed change of sign of the ECD band from neutral to acidic, due to the change in M ⇄ P equilibrium (see Table S1, ESI†). The electronic transition corresponding to the band at longer wavelength is a pure HOMO to LUMO one, while the next ones with largest oscillator strength involve the nearest and next-nearest MOs in energy (see Fig. S11 and S12, ESI†). In the protonated condition, the energy gap for a π–π* transition becomes narrower, with respect to the neutral species gap (0.150 eV versus 0.162 eV, respectively), consequently, the low-energy absorption band is red-shifted. This suggests a larger conjugated π-system, which is also the cause of the increased absorption intensity.

In Fig. 4B, we investigate the effect of the base on cyclic verdin: we chose to focus on molecule 2 in DMSO–NaOH, where the most significant changes are experimentally observed, also considering that the conformational space of the neutral compound had been already explored in Section I of this work. On the theoretical side, we employed the same approach used for studying the protonation of molecule 1. Thus, the conformers obtained from the previous conformational search of the neutral species of 2 have been deprotonated, removing a hydrogen from NH in a lactam ring (see Fig. S10, ESI†), and then re-optimized. The resulting Boltzmann population factors are reported in Table S2 (ESI†). The optimized structures were used for the TD-DFT calculation of UV and ECD spectra. We observe a change in the M ⇄ P equilibrium (Table S2, ESI†). While in the neutral 2 the M-conformers are predicted to prevail, in the deprotonated form the P-conformers dominate. Comparison of the geometrical structures (Fig. S10, ESI†) of the neutral 2 with the deprotonated 2, shows that in the latter case the dihedral angles N22–C6–C4–N21 and N23–C14–C16–N24 change from ca. 16° for the neutral geometry to ca. 7° for the deprotonated geometry.

The results of TD-DFT calculation for UV and ECD are shown in Fig. 4B and compared with the experimental spectra recorded in DMSO.

Most of the changes between neutral and basic conditions are well reproduced by calculations, such as the red shift of the UV and CD band at longer wavelength and the inversion of the CD trend, as well as the splitting of the UV features at shorter wavelengths, even though the increase of intensity for the UV band at longer wavelengths is underestimated by our calculations.

(III) Complexation of cyclic verdins with metal ion studied by VCD and ECD

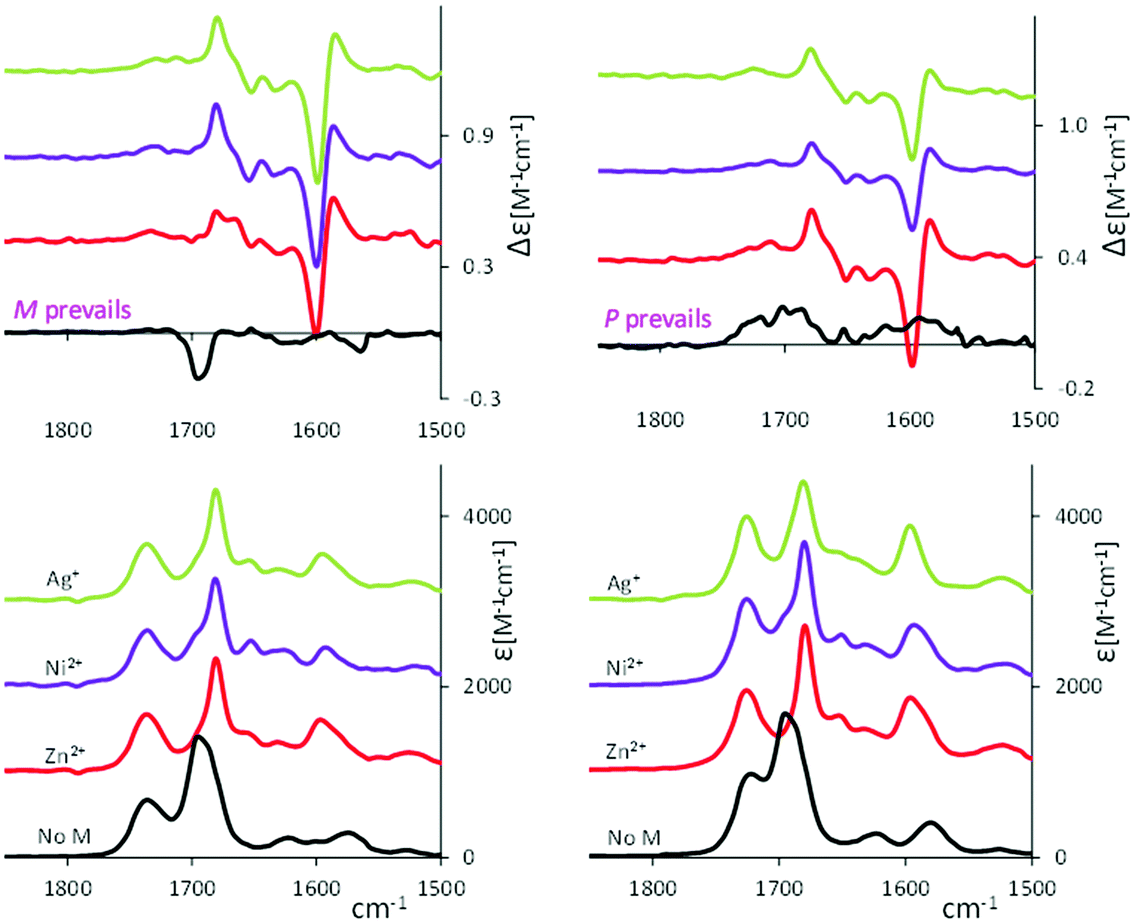
In this section we test whether the studied compounds may “sense” the presence of metal ions. Indeed, the behavior of verdins complexed with transition metal ions was studied for some years.^2,42 Biliverdin analogs complexed with various metal cations were crystallized and subjected to X-ray crystallographic analyses. They revealed a nonplanar helical conformation adopted by the tetrapyrrole.^43,44

Below we present our spectroscopic studies of the cyclic verdins with metal ions (Zn²⁺, Ni²⁺ and Ag⁺) reporting in Fig. 5 the VCD and IR spectra of 2 (left) and 6 (right) in presence of metal ions. See also Fig. S13 (ESI†) for the VCD spectra at different times after zinc addition.

Fig. 5 VCD (top) and IR (bottom) of 2 (left) and 6 (right) in 1 × 10⁻³ M CDCl₃ solution (black) denoted as “no M” in the figure, and with added triflates of zinc (red line), nickel (purple line) and silver (green line).

At first glance, with the addition of metal ions, the VCD spectra of 2 and 6 are more similar to each other than without coordination to metals. Let us comment spectra in detail. In comparison to the cyclic verdin without metal, the IR absorption band at ca. 1690 cm⁻¹ shifts to lower wavenumbers and gets narrower thus decreasing in intensity. Compared to the case without metal, the VCD features in this region invert sign in 2, becoming positive, and more intense. The same behavior is observed in 6, which in absence of metal exhibits very low and broad VCD features. In presence of metal ions, the major changes in the VCD spectra are noticed at lower wavenumbers, i.e. strong bisignate doublets appear at 1580 cm⁻¹, with the same sign-order for all metal ions, while in the IR spectra some intensity increase of the band at 1580 cm⁻¹ is observed.

Strong bisignate doublets (centered at 680 nm) are also observed in all verdin–metal complexes’ ECD spectra, reported in Fig. 6, while the UV spectra show a red shift of the absorption band at long wavelength. Similarly to what is observed by VCD, the ECD spectra of 2 and 6 in the presence of all metals have the same trend, irrespective of the fact that without the metal the cyclic verdins exhibit opposite and much weaker ECD signals (see Fig. S14 (ESI†) for the ECD spectra of 1-6 with zinc ion).

Fig. 6 ECD (top) and UV (bottom) of 2 (left) and 6 (right) in 5 × 10⁻⁵ M CHCl₃ solution (black line) denoted as “no M” in the figure, and with added triflates of zinc (red line), nickel (purple line) and silver (green line).

Similar behavior is observed after addition of zinc chloride to cyclic ester 6 (see Fig. S15, ESI†). The ECD of this complex excludes the possibility that the doublet observed at longer wavelength arises from an effect of the counter ion.

Further, a similar, even though not exactly the same, chiroptical behavior in presence of metal ions was found for “non-bridged” mesobiliverdin-XIIIα, as reported in Fig. S16 (ESI†) for 8,12-bis[(1S)-methylpropyl]mesobiliverdin-XIIIα, reiterating the independence of these phenomena on the fact that the added chiral inducing group forms a closed loop or not.

Considering Fig. 5 and 6, with addition of the metal ion in chloroform something special and new with respect to that discussed so far seems likely to have happened; in other words, in addition to possibly altered P ⇄ M equilibria, other phenomena appear. These phenomena look common to all verdin–metal complexes herein tested, independent of chiral substitutions. It is worth recalling the data on zinc-octaethyl-formylbiliverdinate.³¹ The crystal structures for monomeric penta-coordinated zinc-verdin complex (with four N and one axial H₂O molecule coordinating to zinc cation), and for a dimer involving two zinc ions shared by two verdin moieties were taken by Fuhrhop et al.³¹ (in passing we note that the interest in Zn²⁺ derives also from the biological importance of this ion in the biliverdin reductase enzyme).

To conduct a first test as to whether the presence of dimeric structures (or higher supramolecular assemblies) could be significant, we measured the UV and ECD spectra of cyclic verdin with Zn²⁺ at largely different concentrations (always maintaining a 1 : 1 ratio verdin : Zn²⁺). The spectra are reported in Fig. 7.

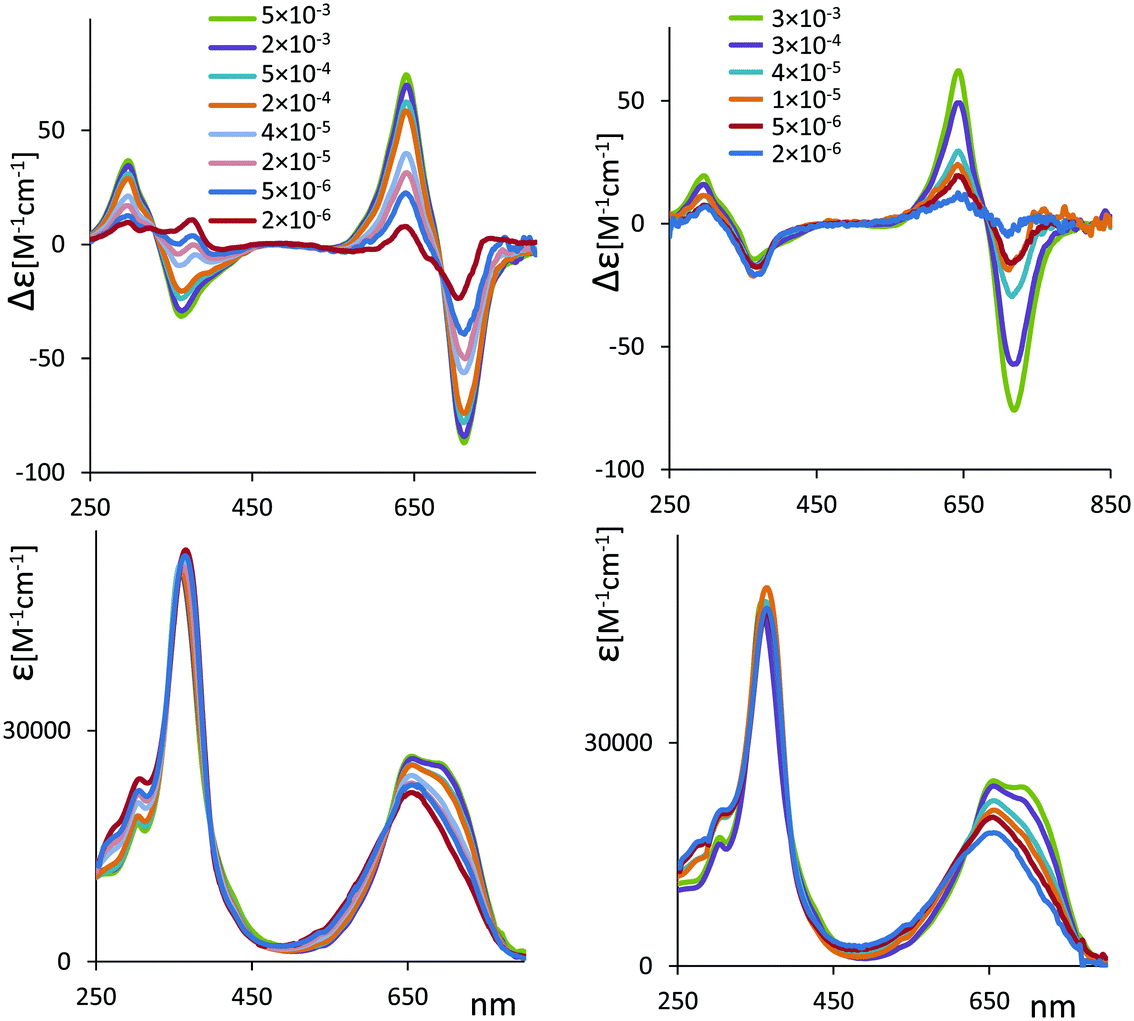Fig. 7 ECD (top) and UV absorption spectra (bottom) for chiral 2 (left) and 6 (right) complexed with Zn²⁺ at several concentrations. Molar concentration values indicated in the legend.

Recalling that the spectra of Fig. 7 are in ε and Δε, i.e. are in units per mole, that is number of cyclic verdin units, we notice that the maximum intensity of the CD couplet is observed in the case of the most concentrated solution (a concentration similar to the one used for VCD measurements) and decreases with subsequent dilutions, whereas one could expect a constant intensity value, in the case that just one species were present. At the more diluted condition, the couplet at longer wavelengths almost disappears leaving a predominant negative component for 2, and a predominant positive component for 6, similar to what observed in the case without metal (see Fig. 6). In case of 2, strong dilution leads to the inversion of the CD band at 340 nm, from negative to positive, while for 6 the CD band at 340 nm keeps the negative sign, more or less in agreement with the case without metal.

Employing a comparative analysis of the chiroptical data of the cyclic verdins complexed with metal ions, we find that:

(1) All chiroptical experiments (ECD and VCD) are suggestive of a common situation for all metal complexes, independent on the metal and independent on n; for the latter aspect, they are also independent on whether the chiral “inducer” is bridged or non-bridged.

(2) While the UV spectra at increasing concentration do not change in molar intensity, but only in the band-shape at longer wavelengths, the ECD spectra change a lot, especially (but not only) at longer wavelengths.

In particular, considering the difference of the maxima and minima of the excitonic couplet (ΔΔε_obs = Δε_max − Δε_min) as function of concentration C_tot, (see Fig. S17A, ESI†), it is clear that, with increasing C_tot, ΔΔε_obs tends toward a limiting value that we may assume to be the molar intensity of the excitonic couplet of the dimeric form ΔΔε_D (see also comments presented in ESI†). For simplicity we assume zero ΔΔε_M for the monomer. Following the treatment adopted by Nogales et al.⁴⁵ for the NH chemical shifts of methyl xanthobilirubinate and for methyl neoxanthobilirubinate as function of concentration and adapting it to our CD data, we have deduced that the dimer association constant has the value K_A = 72 930 M⁻¹ (see ESI† for details and discussion). The plot reported in Fig. S17B (ESI) is a strong backup to the hypothesis of monomer–dimer equilibrium.

(3) VCD, which was measured at ca. 10⁻³ M, seems to confirm what suggested by high concentration ECD measurement, namely that dimers are already formed.

(4) Fuhrhop et al.²⁸ proposed that special dimers are formed, as previously discussed herein.

Another problem which arises when considering the coordination with metal is the existence of a lactim form.² To test whether this hypothesis is true, it may be useful to examine the IR spectra. We observe that the band at 1690 cm⁻¹ decreases in integrated intensity by a factor of 2, when the metal complex is fully formed. Since that band hosts the C=O stretching modes of the two lactam end rings, this may mean that the number of C=O double bonds decreases and thus the lactam ⇄ lactim equilibrium, which in most instances favors the lactam form, is here unbalanced towards (possibly) a 50 : 50 equilibrium. This hypothesis has been, more or less explicitly, predicted earlier by others.^44,46,47 Beside this simple hypothesis, however, we may observe that the intensity area between 1800 and 1500 cm⁻¹ is conserved from uncomplexed to metal complex.

The above considerations led us to build a dimer for 2 following the published structure by Fuhrhop et al.³¹ who verified the existence of 2Zn²⁺ : 2verdin complex by X-ray crystallography. We allowed that both units of the 2Zn²⁺ : 2verdin dimer have one terminal ring in the lactim form, from here defined for short as “lactam/lactim form”. The dimer considered below is made of two P winded (or coiled) cyclic verdin units (ECD and VCD calculations on the analogous dimer based on two M units does not match experimental findings as can be seen in Fig. S18, ESI†). We optimized the dimers through Gaussian16 at the B3LYP/TZVP (CPCM/CHCl₃). The results are given in Fig. 8 (panel D). We also considered (panel C) the analogous dianionic dimer, with only lactam rings. Comparing geometries for the monomer Zn²⁺–verdin and for one of the units composing the dimer, we noticed that the latter has a larger angle between the mean planes of the dipyrrinones (62.7° in panel C and D, 33.5° in panel A and B).

Fig. 8 3D structure of the Zn²⁺–2 complexes. (A) Anionic monomer. (B) Monomer lactam/lactim. (C) Dianionic dimer. (D) Dimer lactam/lactim (see text).

In Fig. 9 we present the calculations of VCD and IR spectra for the two dimers; moreover, for completeness, we report the calculated spectra for the monomeric Zn²⁺–verdin complex in the lactam and lactam/lactim forms, after weighted average on the most populated conformers identified in molecule 2. We give in Fig. 8A and B the structures of the most populated conformers.

Fig. 9 Comparison of experimental (black line) and calculated VCD (top) and IR (bottom) spectra of zinc complexes of 2. Calculated IR and VCD spectra are shown for dianionic dimer (blue line), dimer lactam/lactim (red line), weighted average of anionic monomer (green line) and weighted average of lactam/lactim monomer (orange line).

Considering the region 1850–1450 cm⁻¹, we distinguish four main IR bands (1–4), common to all the calculations presented. The band 1 corresponds to the C=O stretching for the carbonyl in the ester group, while the band 2 corresponds to the C=O stretching of the carbonyl lactam rings, thus this band is weaker for the Zn²⁺-verdin complex bearing the lactim ring. Bands 3 and 4 contain contributions from NH in-plane bending, C=C stretching and CH in-plane bending. The IR band labelled as X, is present only in the lactam/lactim model and corresponds to NH in-plane bending and C=C stretching localized in the lactim moiety. Even if, in presence of metal the experimental intensity of the IR band at 1580 cm⁻¹ is increased, calculations overestimate it with bands 3 and 4. The IR for the spectra region 1850–1000 cm⁻¹ is reported in Fig. S19 (ESI†).

Regarding VCD, the calculation on dimeric Zn²⁺–verdin complexes shows some of the features present in the experimental data, in particular, the negative pattern at 1650–1620 cm⁻¹ and the +, − couplet at 1580 cm⁻¹. Instead, the calculated weighted average VCD spectra on the monomeric Zn²⁺–verdin complexes do not show common features with the experimental data. From the results reported in Fig. 9, we are not able to choose if the correct/prevalent species is the dianionic complex or the lactam/lactim complex.

We are aware that the matching between experiment and calculation is not perfect, but we based our calculations on the picture proposed by X-ray data.³¹ A test of all possible aggregate geometries has not been undertaken systematically; however, a few calculations have been carried out, and we found that, for example, the structures proposed for fecal pigments,⁴⁸ are not adequate for this metal complex. Despite the naïve picture adopted, a rationale for the observations is at least partially given.

In Fig. 10, we present the comparison of experimental and computed ECD and UV-Vis spectra of zinc complexes of 2. On the left side on the Fig. 10, we show the experimental data at 10⁻³ M compared with the calculated spectra on dimer complexes, while on the right side on the figure, we show the experimental data at 10⁻⁶ M compared with the calculated spectra on monomers. The TD-DFT calculations for the dimers, predict two electronic transitions in correspondence of longer wavelength absorption band, which result in the −, + doublet in the ECD spectra. The distance between these two transitions is calculated smaller with respect to the one experimentally observed in absorption (29 nm versus ca. 40 nm, respectively). The longer wavelength absorption band is much more intense in the dimer complex with respect to the monomeric form. We recall that the dimer obtained with opposite helicity (MM) presents a spectrum with opposite signals (Fig. S18, ESI†). The UV-Vis/ECD calculations on the monomeric Zn²⁺–verdin complexes predict a single transition for the longer wavelength absorption band, which corresponds to a monosignate band in the ECD spectrum. At shorter wavelength, the two positive calculated CD signals resemble to what observed at low concentration. At 10⁻⁶ M concentration, a small amount of dimers persists in the solution. Indeed, looking closer at the experimental ECD spectrum in Fig. 10 top-right, a small positive band is observed at 650 nm, somewhat recalling the feature observed at higher concentration. Similar observations can be made for the signal around 400 nm. Using the value K_A = 73 000 M⁻¹ in eqn (5) in the ESI,† at 10⁻⁶ M total concentration, one predicts 5% dimer concentration in solution.

Fig. 10 Left: Comparison of the experimental (black line) ECD (top) and UV-Vis (bottom) spectra of 10⁻³ M chloroform solution of zinc complexes of 2 with the corresponding calculated spectra of dianionic dimer (blue line), dimer lactam/lactim (red line). Right: Comparison of the experimental (black line) ECD (top) and UV-Vis (bottom) spectra of 10⁻⁶ M chloroform solution of zinc complexes of 2 with the corresponding calculated weighted of anionic monomer (green line) and weighted average of lactam/lactim monomer (orange line).

Thus, the comparison of ECD experiments and calculations appears to confirm the presence of dimerization phenomena: at high concentration dimer prevails and the observed spectrum matches the one calculated on an optimized “Fuhrhop” geometry based on two P-units.

Conclusions

In this work we have studied the set of six enantiomerically pure cyclic diesters of linear diols [HO(CH₂)_nOH] with the two propionic acids of (βS,β′S)-dimethylmesobliverdin XIIIα, where (n = 1–6). The esters had been synthesized some time ago and first characterized through ECD in chloroform solution.¹² Differences from one molecule to the other observed there had been rationalized in terms of different chiral conformational equilibria, mainly the P vs. M conformers of the verdin skeleton. Here, we examined the very same molecules by VCD spectroscopy and found further support to the proposed conformational equilibria.¹² Besides that, we recorded ECD spectra at acidic and basic pH and found significant changes of spectral response, which we were able to explain, with the support of DFT calculations, in terms of shifted P ⇄ M equilibria. The advantage of the studied compounds in comparison to natural biliverdin is that one does not need an additional CD inducer, since molecules 1–6 are already chiral, the disadvantage being that a non-trivial synthetic work is required. The ideal situation to obtain these biliverdin-based sensing systems should be to isolate some P (or M) helices with somewhat easier chemistry. We hope that this work may stimulate some interest towards that goal.

Finally, we were able to run both ECD spectra and VCD spectra, upon addition of metal cations, as obtained by dissolving metal salts in solution of the cyclic verdin. ECD spectra were examined over a wide range of verdin–metal complex concentration values, whereas VCD spectra were taken for fairly highly concentrated verdin–metal complex solutions, as possible with the current VCD technology. In the presence of metal ions, the spectral/chiroptical VCD-ECD changes are due to the self-assembling of verdin–metal aggregates, in particular to the formation of verdin–metal dimers. Analysis of the CD data leads to a dimerization constant of approx. 73 000 M⁻¹. Further characterization of the zinc–verdin complex could be assessed by other techniques, e.g. DOSY-NMR could be very useful to provide information about the hydrodynamic radius and the diffusion coefficient of the metal complex. In any case, further support to our conclusion come from the calculated spectra on the dimeric structure which correspond quite nicely to the experimental data. We thus conclude that the cyclic verdin may be used as sensitive probes of pH or of the presence of metal ions, thus justifying the hope of molecular chiroptical switches as used in the title of this work. Indeed, several examples of ad hoc synthesized chiral organic compounds have been presented in the literature, making the use of chiroptical techniques pivotal;^20–28 a possible advantage coming from this work is that we have focused on a compound of natural origin. As last observation, we notice that VCD shows great sensitivity to dimerization and metal complexation, on the contrary, it deals with acidic and basic conditions with some difficulty due to the presence of water. ECD is more versatile, allowing one to perform measurements in basic and acidic conditions more easily and allowing one to study a wide concentration range in the verdin–metal complex.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We acknowledge the use of CINECA facilities at Bologna, Italy: ISCRA Grants “IsC76_Bv-Me3” and “IsC63_SELFASS” and support from the Big & Open Data Innovation Laboratory (BODaI-Lab), University of Brescia, granted by Fondazione Cariplo and Regione Lombardia. Support from the Italian MIUR (PRIN 2017, Project “Physicochemical Heuristic Approaches: Nanoscale Theory of Molecular Spectroscopy” (PHANTOMS), prot. 2017A4XRCA) is acknowledged.

References

1. A. F. McDonagh, Bile Pigments: Bilatrienes and 5,15-Biladienes, in The Porphyrins, ed. D. Dolphin, Academic Press, New York, 1979, vol. VI, pp. 294–491.
2. H. Falk, The Chemistry of Linear Oligopyrroles and Bile Pigments, Springer, Wien, 1989.
3. S. E. Boiadjiev and D. A. Lightner, Tetrahedron: Asymmetry, 1999, 10, 607–655.
4. H. Falk and K. Thirring, Tetrahedron, 1981, 37, 761–766.
5. D. Krois and H. Lehner, Mon. Chem., 1995, 126, 349–354.
6. D. Krois and H. Lehner, J. Chem. Soc., Perkin Trans. II, 1989, 2085–2090.
7. E. Haidl, D. Krois and H. Lehner, Mon. Chem., 1985, 116, 119–131.
8. D. Krois and H. Lehner, J. Chem. Soc., Perkin Trans. II, 1987, 219–225.
9. D. Krois and H. Lehner, J. Chem. Soc., Perkin Trans. II, 1987, 1523–1526.
10. F. Zsila, Mol. Pharmaceutics, 2013, 10, 1668–1682.
11. S. E. Boiadjiev, R. V. Person, G. Puzicha, C. Knobler, E. Maverick, K. N. Trueblood and D. A. Lightner, J. Am. Chem. Soc., 1992, 114, 10123–10133.
12. S. E. Boiadjiev, D. T. Anstine and D. A. Lightner, Tetrahedron: Asymmetry, 1995, 6, 901–912.
13. C. Djerassi. Optical Rotatory Dispersion: Applications in Organic Chemistry, McGraw Hill, New York, 1960.
14. D. A. Lightner and J. E. Gurst. Organic Conformational Analysis and Stereochemistry from Circular Dichroism Spectroscopy, Wiley, New York, 2000.
15. L. A. Nafie. Vibrational Optical Activity: Principles and Applications, John Wiley & Sons, New York, 2011.
16. P. L. Polavarapu, Chiral Analysis—Advances in Spectroscopy, Chromatography and Emerging Methods, 2nd edn, Elsevier Science, Atlanta, GA, USA, 2018.
17. G. Longhi, E. Castiglioni, J. Koshoubu, G. Mazzeo and S. Abbate, Chirality, 2016, 28, 696–707.
18. H. Rhee, Y.-G. June, J.-S. Lee, K.-K. Lee, J.-H. Ha, Z. H. Kim, S.-J. Jeon and M. Cho, Nature, 2009, 458, 310–313.
19. S. Lüdeke, M. Pfeifer and P. Fischer, J. Am. Chem. Soc., 2011, 133, 5704–5707.
20. G. Yang and Y. Xu, Curr Chem, 2011, 298, 189–236.
21. T. Taniguchi, D. Manai, M. Shibata, Y. Itabashi and K. Monde, J. Am. Chem. Soc., 2015, 137, 12191–12194.
22. C. H. Pollok, T. Riesebeck and C. Merten, Angew. Chem., Int. Ed., 2017, 56, 1925–1928.
23. P. Reiné, A. M. Ortuño, S. Resa, L. Álvarez de Cienfuegos, V. Blanco, M. J. Ruedas-Rama, G. Mazzeo, S. Abbate, A. Lucotti, M. Tommasini, S. Guisán-Ceinos, M. Ribagorda, A. G. Campaña, A. Mota, G. Longhi, D. Miguel and J. M. Cuerva, Chem. Commun., 2018, 54, 13985–13988.
24. P. Reiné, J. Justicia, S. P. Morcillo, S. Abbate, B. Vaz, M. Ribagorda, A. Orte, L. Álvarez de Cienfuegos, G. Longhi, A. G. Campaña, D. Miguel and J. M. Cuerva, J. Org. Chem., 2018, 83, 4455–4463.
25. H. Isla, M. Srebro-Hooper, M. J. N. Vanthuyne, T. Roisnel, J. L. Lunkley, G. Muller, J. A. G. Williams, J. Autschbach and J. Crassous, Chem. Commun., 2016, 52, 5932–5935.
26. H. Maeda, Y. Bando, K. Shimomura, I. Yamada, M. Naito, K. Nobusawa, H. Tsumatori and T. Kawai, J. Am. Chem. Soc., 2011, 133, 9266–9269.
27. N. Saleh, B. Moore, M. Srebro, N. Vanthuyne, L. Toupet, J. A. G. Williams, C. Roussel, K. K. Deol, G. Muller, J. Autschbach and J. Crassous, Chem. – Eur. J., 2015, 21, 1673–1681.
28. G. Mazzeo, S. Abbate, G. Longhi, E. Castiglioni, S. E. Boiadjiev and D. A. Lightner, J. Phys. Chem. B, 2016, 120, 2380–2387.
29. P. Novotná, F. Králík and M. Urbanová, Biophys. Chem., 2015, 205, 41–50.
30. I. Goncharova and M. Urbanová, Anal. Biochem., 2009, 392, 28–36.
31. G. Struckmeier, U. Thewalt and J. H. Fuhrhop, J. Am. Chem. Soc., 1976, 98, 278–279.
32. S. E. Boiadjiev, W. P. Pfeiffer and D. A. Lightner, Synthesis and stereochemistry of bilirubin analogs lacking carboxylic acids, Tetrahedron, 1997, 53, 14547–14564.
33. A. L. Balch, F. L. Bowles, K. M. Kadish, K. M. Smith and R. Guilard, Handb. Porphyrin Sci., 2010, 8, 293–342.
34. S. Grimme, J. Chem. Theory Comput., 2019, 155, 2847–2862.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
36. S. Abbate, F. Lebon, G. Longhi, S. E. Boiadjiev and D. A. Lightner, J. Phys. Chem. B, 2012, 116, 5628–5636.
37. S. Ghidinelli, G. Longhi, M. Mazzeo, S. Abbate, S. E. Boiadjiev and D. A. Lightner, Chirality, 2018, 30, 19–28.
38. S. Ghidinelli, S. Abbate, S. E. Boiadjiev, D. A. Lightner and G. Longhi, J. Phys. Chem. B, 2018, 122, 12351–12362.
39. T. Taniguchi and K. Monde, Exciton chirality method in vibrational circular dichroism, J. Am. Chem. Soc., 2012, 134(8), 3695–3698.
40. H. Falk and U. Zrunek, Mon. Chem., 1983, 114, 1107–1123.
41. H. Falk, P. Wolschann and U. Zrunek, Mon. Chem., 1984, 115, 243–249.
42. C. Li and B. Kräutler, Dalton Trans., 2015, 44, 10116–10127.
43. J. V. Bonfiglio, R. Bonnett, D. G. Buckley, D. Hamzetash, M. B. Hursthouse, K. M. A. Malik, A. F. McDonagh and J. Trotter, Tetrahedron, 1983, 39, 1865–1874.
44. T. Mizutani and S. Yagi, J. Porphyrins Phthalocyanines, 2004, 8, 226–237.
45. D. F. Nogales, J.-S. Ma and D. A. Lightner, Tetrahedron, 1993, 49, 2361–2372.
46. H. Falk and T. Schlederer, Liebigs Ann. Chem., 1979, 10, 1560–1570.
47. J.-H. Fuhrhop, P. K. W. Wasser, J. Subramiam and U. Schrader, Liebigs Ann. Chem., 1974, 9, 1450–1466.
48. S. Prakash, S. Banu and A. K. Mishra, J. Mol. Struct., 2021, 1238, 130440.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 shows the ECD spectra of 1 and 2 as a function of temperature, Fig. S2–S5 provide 3D-structures of the most populated conformers of mesobiliverdin cyclic diesters 1 and 2, and their IR and VCD calculated spectra, Fig. S6 and S7 provide UV and ECD spectra during the titration with acid and base respectively, Fig. S8 shows the neutralization of basified methanol solution of 2, Table S1 reports the Boltzmann population factors for the main conformers in the neutral and protonated condition for compound 1, Table S2 reports the Boltzmann population factors for the main conformers in the neutral and deprotonated condition for compound 2. Fig. S9 shows the UV and ECD spectra of “non-bridged” biliverdins and 6. Superimposed calculated structures of the neutral, protonated and deprotonated species are shown in Fig. S10–S12 provide the molecular orbitals involved in the electronic transitions of neutral and protonated form of 1, Fig. S13 shows VCD and IR of 2 with added zinc triflate as function of time, Fig. S14 provides the ECD and UV of verdins 1–6 with added zinc triflate, Fig. S15 provides the ECD and UV of verdin 6 with added zinc chloride. Fig. S16 provides the VCD, IR, ECD and UV spectra of 8,12-bis[(1S)-methylpropyl]mesobiliverdin-XIIIα with added zinc triflate, Fig. S17 shows the analysis of CD spectra of verdin 2 at different concentration and ancillary text for theory, Fig. S18 shows the calculated UV/ECD and IR/VCD spectra for the dimeric zinc complexes of 2 based on two M units, Fig. S19 shows IR spectra of zinc complexes of 2 in the 1850–1000 cm⁻¹ region. See DOI: 10.1039/d1cp02571f

---