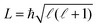Open Access Article
Open Access ArticleMultipole-moment effects in ion–molecule reactions at low temperatures: part I – ion-dipole enhancement of the rate coefficients of the He+ + NH3 and He+ + ND3 reactions at collisional energies Ecoll/kB near 0 K
Valentina
Zhelyazkova
 ,
Fernanda B. V.
Martins
,
Fernanda B. V.
Martins
 ,
Josef A.
Agner
,
Hansjürg
Schmutz
and
Frédéric
Merkt
,
Josef A.
Agner
,
Hansjürg
Schmutz
and
Frédéric
Merkt
 *
*
ETH Zurich, Zurich, Switzerland
First published on 27th September 2021
Abstract
The energy dependence of the rates of the reactions between He+ and ammonia (NY3, Y = {H,D}), forming NY2+, Y and He as well as NY+, Y2 and He, and the corresponding product branching ratios have been measured at low collision energies Ecoll between 0 and kB·40 K using a recently developed merged-beam technique [Allmendinger et al., ChemPhysChem, 2016, 17, 3596]. To avoid heating of the ions by stray electric fields, the reactions are observed within the large orbit of a highly excited Rydberg electron. A beam of He Rydberg atoms was merged with a supersonic beam of ammonia using a curved surface-electrode Rydberg–Stark deflector, which is also used for adjusting the final velocity of the He Rydberg atoms, and thus the collision energy. A collision-energy resolution of about 200 mK was reached at the lowest Ecoll values. The reaction rate coefficients exhibit a sharp increase at collision energies below ∼kB·5 K and pronounced deviations from Langevin-capture behaviour. The experimental results are interpreted in terms of an adiabatic capture model describing the rotational-state-dependent orientation of the ammonia molecules by the electric field of the He+ atom. The model faithfully describes the experimental observations and enables the identification of three classes of |JKMp〉 rotational states of the ammonia molecules showing different low-energy capture behaviour: (A) high-field-seeking states with |KM| ≥ 1 correlating to the lower component of the umbrella-motion tunnelling doublet at low fields. These states undergo a negative linear Stark shift, which leads to strongly enhanced rate coefficients; (B) high-field-seeking states subject to a quadratic Stark shift at low fields and which exhibit only weak rate enhancements; and (C) low-field-seeking states with |KM| ≥ 1. These states exhibit a positive Stark shift at low fields, which completely suppresses the reactions at low collision energies. Marked differences in the low-energy reactivity of NH3 and ND3—the rate enhancements in ND3 are more pronounced than in NH3—are quantitatively explained by the model. They result from the reduced magnitudes of the tunnelling splitting and rotational intervals in ND3 and the different occupations of the rotational levels in the supersonic beam caused by the different nuclear-spin statistical weights. Thermal capture rate constants are derived from the model for the temperature range between 0 and 10 K relevant for astrochemistry. Comparison of the calculated thermal capture rate coefficients with the absolute reaction rates measured above 27 K by Marquette et al. (Chem. Phys. Lett., 1985, 122, 431) suggests that only 40% of the close collisions are reactive.
1 Overview of the article series
This article is the first of a three-article series devoted to experimental studies of barrier-free ion–molecule reactions at low collision energies. The article series addresses fundamental aspects of chemical reactivity in low-energy ion–molecule collisions which play a crucial role in the understanding and modelling of ion–molecule reactions at low temperatures.1–10 The focus is placed on the measurement and theoretical analysis of the deviations of the collision-energy-dependent reaction rates k(Ecoll) from the Langevin rate kL at very low collision energies resulting from the electrostatic interaction between the charge of the ion and the electric dipole, quadrupole and octupole moments of the neutral molecule.For these studies, we have chosen He+ as a reactant ion because the high ionisation energy of He guarantees strongly exothermic barrier-free reactions with a broad range of neutral molecules. The neutral molecules we have selected are (i) ammonia (NH3 and ND3), which is a polar molecule with a dipole moment of 4.91 × 10−30 C m,11 (ii) N2, which does not have a permanent dipole moment but has a quadrupole moment of −4.65 × 10−40 C m2,12 and (iii) methane (CH4 and CD4), which has neither a permanent dipole moment nor a quadrupole moment, but an octupole moment of 7.41 × 10−50 C m3.13 The reactions of all three molecules are known from previous work to proceed with high rates.14,15 With these three molecules, we can examine the convergence of the capture rate coefficients at low energies towards the Langevin rate as the lowest non-vanishing member of the multipole expansion series of the neutral molecule gradually increases in the sequence dipole (nmp = 2), quadrupole (nmp = 4), and octupole (nmp = 8). This sequence also corresponds to the order of this three-article series, which presents our results on the nmp = 2 case in article I, and those on the nmp = 4 and nmp = 8 cases in articles II and III, respectively.
The experimental observations are analysed in the realm of an adiabatic capture model inspired by the earlier theoretical work of Clary and co-workers3,5,16 and Troe and co-workers.4,6,17–20 Because the existence or non-existence of a given nmp-pole moment is dictated by the molecular symmetry, the interpretation of the experimental observations requires consideration of the corresponding molecular-symmetry groups, in particular when determining the nuclear-spin symmetries and occupations of the rotational quantum states of the neutral molecules. We follow here earlier treatments, in particular those presented in ref. 21–24 and compare reactions of undeuterated and fully deuterated ammonia and methane to highlight specific aspects. The overall analysis gives insights into the dependence of the rate coefficients on the rotational quantum states of the neutral molecules and provides access to the thermal rate coefficients k(T) through statistical averaging.
The overall structure of this three-article series is as follows: in this first article, we present a general introduction to fast ion–molecule reactions and detail the experimental approach and set-up we have used, which are the same for all three studies. We also summarise the main aspects of the capture model we have implemented to interpret the experimental results in a general form, adequate to treat the effects of an arbitrary nmp moment. We then describe the experimental results we have obtained in our study of the He+ + NH3 and He+ + ND3 reactions and their analysis using the capture model for the nmp = 2 case. In the second article, we focus on the results obtained on the nmp = 4 case and present our studies of the He+ + N2 reaction. To clarify the role of the sign of the quadrupole, we also compare the results obtained for N2, which has a negative quadrupole moment, with those obtained for the reactions of D2+ with H2, which has a positive quadrupole moment. The last article is devoted to the study of the nmp = 8 case with the example of the He+ + CH4 and He+ + CD4 reactions. It also presents our main conclusions concerning the convergence of the low-energy capture rate coefficients towards Langevin rates. This structure offers the advantage that the introductory, experimental and theoretical-modelling sections of articles II and III could be reduced to a minimum, and that the general conclusions could be condensed in the last section of article III.
2 Introduction
Ion–molecule reactions play a key role in the chemistry of dilute environments, such as low-density plasmas, interstellar clouds and the upper layers of planetary atmospheres. Their rate coefficients and the branching ratios for different product channels are required as input in global kinetics models designed to describe and predict the chemical compositions of these environments.25–32 In particular, barrierless, exothermic ion–molecule reactions proceed with high rate coefficients even at very low temperatures and several of these reactions represent essential steps in the synthesis of molecules in the interstellar medium, enabling the formation of polyatomic molecules through reaction chains in cold (3–50 K) dark molecular clouds.Measurements of the rates of ion–molecule reactions at temperatures below 50 K are challenging because ions are easily heated up by stray electric fields and space-charge effects. An electric-potential difference of only 1 mV is indeed sufficient to accelerate ions to kinetic energies corresponding to about 12 K. Studies of ion–molecule reactions in ion guides and traps8,33,34 and in supersonic flows35,36 enable measurements of reaction rates down to ≈10 K, but the range below 10 K remains largely unexplored experimentally.
Advances in the experimental studies of ion–molecule reactions near 0 K have been recently made that rely on the use of laser-cooled and sympathetically cooled ions in ion traps and Coulomb crystals.9,37–39 Our own approach to study ion–molecule reactions at low energies consists of suppressing the stray-electric-field-induced heating of the ions by replacing the ion by an atom or molecule in a Rydberg state of high principal quantum number n.40–43 In such states, the Rydberg electron moves on an orbit of large radius (∝n2, e.g., ≈50 nm for n = 30), without significantly affecting the reactions involving the ion core.44–46 The distant Rydberg electron, however, effectively shields the reaction from stray electric fields. In addition, one can exploit the large induced dipole moments of Rydberg atoms and molecules (μmax ≈ 3400 D for n = 30) to manipulate their translational motion with inhomogeneous electric fields of modest magnitude. We have used this property to deflect, accelerate and decelerate beams of Rydberg atoms and molecules using on-chip Rydberg–Stark decelerators and deflectors.47–50 With such devices, supersonic beams of Rydberg atoms and molecules can be merged with supersonic beams of ground-state neutral molecules, allowing the study of ion–molecule reactions at very low collisional energies.
This merged Rydberg-packet—ground-state-beam approach exploits the large velocity dispersion of supersonic beams produced with short-pulse valves, as in recent elegant work on Penning-ionisation and associative-ionisation reactions at low collision energies by Narevicius and co-workers51–53 and Osterwalder and co-workers,54–56 and the well-defined spatial extent and mean velocity of the deflected Rydberg-atom cloud. This combination makes it possible to achieve a collision-energy resolution as low as ∼100 mK.43 In the last years, we have observed deviations from Langevin capture rates at low collisional energies, in particular: (a) a small enhancement (∼15%) of the H2+ + H2 reaction rate constant compared to kL at Ecoll/kB < 1 K,41 and (b) a strong enhancement by more than an order of magnitude of the He+ + CH3F capture rate constant at the lowest collisional energies.42 These enhancements were attributed to ion-quadrupole interactions for the reaction between H2+ and ortho-H2 molecules in the J = 1 rotational state, and to rotational-state-dependent Stark shifts of the polar CH3F molecules in the Coulomb field of the helium ion for the He+ + CH3F reaction. Despite these advances, experimental data on the rates of ion–molecule reactions in the range below 10 K remain extremely scarce.
In contrast, theoretical models describing ion–molecule reactions are advanced and represent the main source of rate constants for these reactions at low temperatures. At low temperatures, the dominant ion–molecule reactions are barrier-free reactions and their rates can be modelled by ion-neutral capture models. In the simplest such model, introduced by Langevin,57 the rates are determined by considering the charge-induced dipole interaction between the ion and the polarisable molecule and it is assumed that the reaction takes place with unit probability provided that the collision energy is larger than the centrifugal barrier in the effective intermolecular potential. In this regime, the rate constants are independent of the temperature or the collision energy Ecoll and are given by the Langevin rate constant (in SI units)
 | (1) |
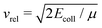 is the asymptotic relative velocity, α′ is the polarisability volume of the neutral molecule, Ze is the charge of the ion, μ is the reduced mass of the reactants and ε0 is the permittivity of vacuum. Whereas this treatment is often adequate above 100 K, it fails at low temperatures because long-range forces between the charge of the ion and the dipole, quadrupole, octupole, etc. moments of the neutral molecules affect their rotational motion.1,2,7 Specifically, the orientation of the molecular axes and the alignment of the rotational angular-momentum vector tend to be locked to the collision axis, leading to strong quantum-state (index i)- and collision-energy-dependent rate coefficients ki(Ecoll).3–6 In this range, thermal capture rate constants are determined from the ki(Ecoll) values by averaging over the populated translational and rovibrational states i of the reactants.
is the asymptotic relative velocity, α′ is the polarisability volume of the neutral molecule, Ze is the charge of the ion, μ is the reduced mass of the reactants and ε0 is the permittivity of vacuum. Whereas this treatment is often adequate above 100 K, it fails at low temperatures because long-range forces between the charge of the ion and the dipole, quadrupole, octupole, etc. moments of the neutral molecules affect their rotational motion.1,2,7 Specifically, the orientation of the molecular axes and the alignment of the rotational angular-momentum vector tend to be locked to the collision axis, leading to strong quantum-state (index i)- and collision-energy-dependent rate coefficients ki(Ecoll).3–6 In this range, thermal capture rate constants are determined from the ki(Ecoll) values by averaging over the populated translational and rovibrational states i of the reactants.
This article summarises the results of our studies of the reaction of He+ with NH3 and ND3. These reactions are of astrophysical importance. Ammonia was the first polyatomic molecule to be detected in the interstellar medium.58 NH3 and several of its isotopologues (NH2D, ND2H and ND3 and 15NH3) were later found in external galaxies, interstellar ices, proto-planetary disks, and in the atmosphere of Jupiter.59–63 Ammonia can be detected through transitions in the radio-frequency (transitions between the tunnelling components of the umbrella-inversion mode), microwave (rotational transitions), IR (vibrational transitions) and the visible/UV (electronic transitions) ranges of the electromagnetic spectrum. The ease of its detection makes it one of the most important molecules for the study of molecular clouds (ammonia is dubbed “the interstellar thermometer”).64 Helium is the second most abundant element in the universe (∼25% by mass)65 and can be ionised by cosmic rays in the interstellar medium to form He+.
The reaction between He+ and NH3 has been studied in the 1970s at temperatures at and above ∼300 K in flowing-afterglow,66 flow-drift tube67 and ion-cyclotron resonance68 experiments. The thermal reaction rate constant at 300 K in these studies was found to be in the range between 1.15(±20%) × 10−15 m3 s−1 and 2.20(±10%) × 10−15 m3 s−1 (kLHe++NH3 = 1.887 × 10−15 m3 s−1). An increase of the reaction rate constant with decreasing temperature in the 300–2900 K range was observed in ref. 67. Marquette et al.35 have measured the thermal rate coefficient in uniform supersonic flows and reported values of 4.5 × 10−15 m3 s−1 at 27 K, 3.0 × 10−15 m3 s−1 68 K, and 1.65 × 10−15 m3 s−1 at 300 K. Several reaction channels were identified with the following branching ratios:68
| He+ + NH3 → NH3+ + He (∼12%) | (R1) |
| →NH2+ + H + He (∼80%) | (R2) |
| →NH+ + H2 + He (∼8%). | (R3) |
Low-temperature and low-collisional-energy studies of the reaction between He+ and ammonia are, however, lacking, although this energy regime is particularly relevant for astrochemistry. The current work presents experimental and theoretical studies of the He+ + NH3 and He+ + ND3 reactions in the range of collisional energies Ecoll between 0 and kB·40 K with a resolution of kB·200 mK at Ecoll = 0.
3 The effect of molecular multipole moments on capture rate coefficients
3.1 The modified Langevin interaction potential
In the Langevin model, the interaction potential VL(R) between an ion and a molecule is described only through the centrifugal potential and the ion–induced-dipole interaction as: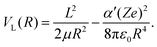 | (2) |
| Vint,i(R) = VL(R) + ΔEi(R), | (3) |
The electrostatic potential at a point R in space resulting from the molecular charge distribution, ρ(r′), can be expressed as:70
 | (4) |
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) is a Legendre polynomial:
θ) is a Legendre polynomial: | (6) |
 | (7) |
 | (8) |
In the symmetric-top wavefunction basis, |JKM〉, the matrix elements of the multipole operator are given by:70
 | (9) |
 | (10) |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) on the molecular symmetry axis and a space-fixed axis, respectively, and
on the molecular symmetry axis and a space-fixed axis, respectively, and 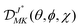 is a Wigner rotation matrix.
is a Wigner rotation matrix.
The R-dependent Stark-shifts, ΔEi=JKM(R), which describe the interaction between the ion charge and the multipole moments of the molecule, are obtained by diagonalising the Hamiltonian:
| Ĥ(R) = Ĥrot + ĤStark(R), | (11) |
 | (12) |
3.2 Determination of the rotational-state-dependent capture rate coefficients
From the total interaction potential Vint,i(R) associated with a given molecular i = |JKM〉 state, one can determine for each collision energy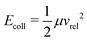 the classically allowed maximal value of the angular momentum, Lmax,i = μvrelbmax,i, for which the reaction can take place.
the classically allowed maximal value of the angular momentum, Lmax,i = μvrelbmax,i, for which the reaction can take place.
The reaction rate coefficient for state i is determined through the reaction cross-section σi = πbmax,i2 as:
 | (13) |
Adiabatic capture models3–6 such the one described in this section and used to interpret our experimental results include the effects of long-range interactions in the entrance channel but cannot predict the branching ratios between competing reaction channels, nor the product state distributions, nor angular distributions, nor vector correlations. Moreover, they predict the total cross section, whereas our experiments only measure the part of the capture cross section that leads to reactions products, which we estimate to be about 40% for the He+ + NH3 reaction, see Section 7. Calculations of the (nonadiabatic) dynamics on the relevant multidimensional potential energy surfaces would be needed for a full interpretation of the experimental results and a full description of the reaction dynamics.
4 Experimental approach
4.1 The merged-beam set-up
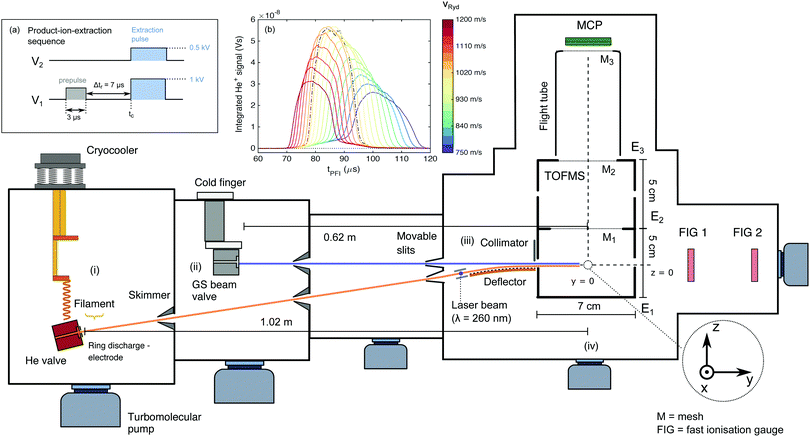
The experimental set-up has been briefly described in ref. 42 and is outlined schematically in Fig. 1. The merged-beam apparatus consists of two supersonic beams produced by home-built valves (nozzle-opening duration ∼20 μs, repetition rate of 25 Hz) – one for the He atoms subsequently excited to a Rydberg state, and the other for the ground-state (GS) beam consisting of either pure NH3 or ND3. The two beams propagate along axes initially separated by a 5° angle. The helium atoms are photoexcited to a Rydberg–Stark state (referred to as He(n) from here on) between two planar electrodes used to generate an electric field. They are then deflected by a 50-electrode Rydberg-Stark surface deflector and merged with the ground-state beam. The merged beams then enter a time-of-flight mass spectrometer (TOFMS), where the reaction takes place and the product ions are extracted toward a microchannel plate (MCP) detector in a direction perpendicular to the merged-beam propagation axis. The TOFMS consists of three cylindrical electrodes (labelled E1–3 in Fig. 1, with inner radius of 35.5 mm).The central point of the TOFMS along the beam-propagation axis defines the origin of the space-fixed coordinate system. The helium valve is positioned at (0, −102.5, −8.2) cm (see Fig. 1). Its copper body is tilted by a 5° angle with respect to the vertical (z) axis and is thermally connected by copper braids to the cold heads of a two-stage pulse-tube cryo-cooler. The He valve is temperature-stabilised to 100.0 ± 0.1 K and operated at a stagnation pressure of 2.5 bar. At the valve opening, a pulsed potential (∼+300 V, pulse duration 70 μs) applied to a ring electrode attracts a beam of electrons emitted by a tungsten filament, creating an electric discharge at the valve orifice. In this discharge, the metastable (1s)(2s) 3S1 state of helium (lifetime of 7.859 × 103 s)72 is populated, amongst other states.73 The metastable helium beam (referred to as He*) travels at a velocity of ∼1040 m s−1. After passing two skimmers, the He* beam intersects a pulsed laser beam (λexc ≅ 260 nm, pulse duration ∼10 ns, pulse energy ∼800 μJ, beam diameter ∼0.2 cm), produced by frequency tripling the output of a Nd:YAG-pumped commercial dye laser using two β-barium-borate crystals. The excitation takes place between two parallel metallic plates separated by 0.25 cm used to generate a dc electric field, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) exc. The laser is polarised parallel to
exc. The laser is polarised parallel to ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) exc; its frequency and the value of |
exc; its frequency and the value of |![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) exc| are tuned such that a one-photon excitation is driven to a low-field-seeking Rydberg–Stark state (n, k, m
exc| are tuned such that a one-photon excitation is driven to a low-field-seeking Rydberg–Stark state (n, k, m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) = (30, 21, 0) just below the Inglis–Teller limit [n and m
) = (30, 21, 0) just below the Inglis–Teller limit [n and m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) are the principal and magnetic quantum numbers, respectively, and k = −(n − m
are the principal and magnetic quantum numbers, respectively, and k = −(n − m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − 1)
− 1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (n − m
(n − m![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − 1)].74
− 1)].74
After excitation, the He(n) atoms are loaded into an electric quadrupole trap formed by applying time-dependent potentials to several sets of electrodes located at the surface of a ∼5 cm-long, 50-electrode surface Rydberg–Stark deflector (electrode dimensions dy = 0.5 mm, dx = 30 mm, separated by Δdy = 0.5 mm in the y direction). The deflector electrodes are patterned onto the surface of a printed circuit board, which is attached to a curved substrate (see Fig. 1 of ref. 42). By applying a sinusoidally-varying potential to each set of electrodes (see ref. 48 and 50), the trapped cloud of Rydberg atoms can be guided in a direction parallel to the surface of the chip. By setting a frequency chirp to these sinusoidally-varying potentials, one can also accelerate or decelerate the Rydberg atoms and precisely adjust their final velocity, vRyd, after release from the trap at the end of the decelerator. When it leaves the quadrupole trap, the Rydberg-atom cloud has a cigar shape of radius ∼0.5 mm42 and length ∼3 mm in the x direction (estimated from Monte Carlo simulations), and travels in a direction parallel to the y-axis, which is also the axis of propagation of the GS beam. We estimate the temperature of the Rydberg cloud from Monte Carlo simulations and from experiments to be in the 0.1–0.3 K range.42 A baffle at the end of the deflector blocks the He* beam and all Rydberg atoms which have not been captured by the quadrupole trap but have travelled over the deflector in a straight line. We estimate that approximately 100 Rydberg atoms exit the surface deflector and enter the TOFMS at every experimental cycle (repetition rate 25 Hz). The He(n) atom cloud has a width of ≈1 mm in the y direction in the centre of the reaction zone.
The orifice of the GS-beam valve is positioned at (0, −62, 0) cm and has an orifice diameter of ∼0.5 mm. It is operated with pure ammonia (either 14NH3 or 14ND3) kept at a stagnation pressure of about 1 bar. The valve is connected to an ice-filled reservoir and temperature-stabilised to 274.0 ± 0.5 K. Two fast ionisation gauges (FIGs) positioned after the TOFMS are used to determine the velocity distribution of the GS beam. The selected velocity of the NH3 (ND3) beam, vGS, was measured to be 1190 m s−1 (1170 m s−1). The GS beam valve is triggered such that the molecules travelling at vGS arrive at the centre of the TOFMS at the same time, designated as tc, as the Rydberg atoms.
The background pressures in the regions of the apparatus labelled (i)–(iv) in Fig. 1 rise from about 2 × 10−7 mbar in all regions to about 2 × 10−5 mbar in regions (i) and (ii), 7 × 10−7 mbar in region (iii) and 4 × 10−7 mbar in region (iv) when the pulsed valves are operated.
We use the TOFMS in two modes: (i) a product-ion-extraction mode with mass resolution and (ii) a He(n) pulsed-field ionisation mode. In mode (i), the product ions are extracted by applying potentials of 1 kV and 0.5 kV to electrodes E1 and E2, respectively (see Fig. 1), through high-potential switches, with a rise time of ∼30 ns. These potentials correspond to an electric field of 110 V cm−1 at the centre of the TOFMS. The ions are extracted toward an MCP detector with a phosphor screen (Photonis, diameter 4 cm), with its centre positioned at (0, 0, 14.5) cm. The front face of the MCP is biased at a potential of −1.96 kV to allow for maximal sensitivity while avoiding saturation effects caused by the strong He+ signal. The potentials E1 and E2 are optimised to achieve maximal ion-collection efficiency and mass resolution. To generate a homogeneous extraction electric field and a field-free flight tube, three meshes (M1–3 in Fig. 1) were installed in the ion-extraction stack. The time interval Δtr during which the ion–molecule reaction is observed (Δtr = 7 μs in the experiments presented here) was defined by applying a prepulse of V1 = 125 V to electrode E1 (corresponding to ∼25 V cm−1 at the TOFMS centre) to sweep out all ions located in the extraction region. The value of V1 was chosen to be high enough to sweep the ions formed prior to time tc − Δtr out of the ion-extraction zone, but not high enough to field-ionise the reactant He(n) atoms.
When the TOFMS is operated in He(n)-detection mode [mode (ii)], a high-electric-field pulse is applied to field-ionise the Rydberg helium atoms and extract the He+ ions towards the MCP detector. The ionisation electric field [∼1100 V cm−1 at point (0, 0, 0)] is generated by applying 5 kV to E1 while keeping electrodes E2 and E3 grounded. This field is sufficient to ionise Rydberg atoms of principal quantum number n ≥ 29.
4.2 Varying the velocity of the He(n) beam
We measure the dependence of the product-ion yields on the collision energy Ecoll by varying the central velocity of the Rydberg atoms, vRyd, and keeping the velocity vGS of the GS beam constant. The short gas-pulse duration leads to a large spatial dispersion of the GS beam over the 62 cm distance between the valve orifice and the reaction zone. The particles in the GS beam thus have a well-defined velocity (with a velocity spread ΔvGS = ±15 m s−1) in the region where it overlaps with the He(n) packet emerging from the chip. vRyd is set by applying the appropriate potentials to the surface deflector. The He(n) atoms have an estimated velocity spread of full width at half maximum (FWHM) around vRyd of ΔvFWHMRyd ≈ ±20 m s−1.To ensure that the same velocity class of the ammonia GS molecules interacts with the He(n) atoms regardless of the selected vRyd value, we perform a set of measurements in which we determine the arrival time of the Rydberg-atom cloud at the centre of the reaction zone,  , for every value of vRyd. The He(n) atoms can be detected if (i) the applied ionisation field is sufficiently high for pulsed field ionisation (PFI), and (ii) PFI takes place in a region inside the TOFMS such that the produced ions can reach the MCP and do not collide with the walls of the extraction stack. To obtain the data presented in inset (b) of Fig. 1, we operate the TOFMS in a He(n)-ionisation (single-pulse) mode and record the integrated He+ signal as a function of the time, tPFI, of application of the PFI pulse relative to the laser excitation time for each set value of vRyd. The dashed-dotted black curve represents the He+ signal measured when operating the surface deflector in guiding mode, i.e., with the He(n) atoms propagating at constant velocity over the deflector surface (vguideRyd = 1040 m s−1). This curve has an approximately Gaussian shape with a centre at
, for every value of vRyd. The He(n) atoms can be detected if (i) the applied ionisation field is sufficiently high for pulsed field ionisation (PFI), and (ii) PFI takes place in a region inside the TOFMS such that the produced ions can reach the MCP and do not collide with the walls of the extraction stack. To obtain the data presented in inset (b) of Fig. 1, we operate the TOFMS in a He(n)-ionisation (single-pulse) mode and record the integrated He+ signal as a function of the time, tPFI, of application of the PFI pulse relative to the laser excitation time for each set value of vRyd. The dashed-dotted black curve represents the He+ signal measured when operating the surface deflector in guiding mode, i.e., with the He(n) atoms propagating at constant velocity over the deflector surface (vguideRyd = 1040 m s−1). This curve has an approximately Gaussian shape with a centre at  = 85.5 μs and a FWHM of ∼17 μs.
= 85.5 μs and a FWHM of ∼17 μs.
By applying the appropriate frequency chirp to the time-dependent electrode potentials, we can accelerate or decelerate the He(n) atoms from an initial velocity of 1040 m s−1 to a final velocity in the 1200–750 m s−1 range during deflection. The maximum (minimum) velocity in this range corresponds to an increase (decrease) of the initial He(n) kinetic energy of ∼33% (∼48%). The value of  is obtained for each of the selected values of vRyd by determining the centres of the corresponding distributions depicted in Fig. 1(b). In addition, the spread of the measured He(n) profile increases for lower values of vRyd because the He(n) packet expands over a longer flight time. The GS-valve opening time is then adapted so that the centre of the GS beam overlaps with the deflected Rydberg cloud at tc.
is obtained for each of the selected values of vRyd by determining the centres of the corresponding distributions depicted in Fig. 1(b). In addition, the spread of the measured He(n) profile increases for lower values of vRyd because the He(n) packet expands over a longer flight time. The GS-valve opening time is then adapted so that the centre of the GS beam overlaps with the deflected Rydberg cloud at tc.
4.3 Normalising the measured product ion signal
In the experiment, we do not measure absolute values of the reaction rates because we do not accurately know the particle densities in the reaction zone. We measure relative values of the collision-energy-dependent rates, which we scale by a global factor for comparison with the calculated capture-rate coefficients.The total amount of He(n) that reaches the centre of the TOFMS decreases with increasing deceleration and acceleration. This decrease is illustrated by the decrease of the maximum measured height of the He(n) PFI profiles at time tc in Fig. 1(b). For example, only 56% and 47% of the atoms reach the centre of the stack for vRyd = 1200 m s−1 and 750 m s−1, respectively, compared to vRyd = 1040 m s−1. This decrease is attributed to the opening of the quadrupole trap in the reference frame of the moving atoms,48 which leads to a larger fraction of the atoms escaping the trap at the highest acceleration/deceleration. For the lower values of vRyd, additional losses result from the finite lifetimes of the Rydberg atoms. In order to correct for these effects, the integrated reaction-product signals are divided by the detected He+ signal, integrated over the [tc − Δtr/2, tc + Δtr/2] time interval, accounting for the times of flight of the ions to the MCP.
The different times of flight of the Rydberg cloud from the end of the deflector to the TOFMS centre correspond to different expansions in the plane perpendicular to the direction of propagation (the xz-plane). The ground-state-beam spatial extent is limited to 1.6 mm in the z-direction by the position of the baffle above the surface of the chip. The He(n)-cloud expansion can thus affect the geometric overlap with the GS beam, creating a detection bias in favour of product ions generated at higher values of vRyd. Monte-Carlo particle-trajectory simulations indicate that for the lowest values of vRyd (vRyd ≲ 700 m s−1), the cloud has expanded so much by the time it arrives at the stack centre that the Rydberg atoms located at its outer edge do not interact with the GS-beam molecules. This detection bias is corrected for when determining the collision-energy-dependent product yields.
5 Experimental results
Ammonia is an oblate symmetric-top molecule. It has C3v point-group symmetry in its two equivalent “umbrella” equilibrium structures located at values of ∼±22° of the umbrella inversion angle. These structures are separated by a relatively low energy barrier (∼2023 cm−1)75 for inversion through the D3h planar structure. Tunnelling through the potential-energy barrier thus leads to a splitting of ∼0.79 cm−1 (∼0.053 cm−1) of the ground vibrational state rotational levels in NH3 (ND3),23,76 the vibrational eigenfunctions being the symmetric (s) and antisymmetric (a) superpositions of the ground-state wavefunctions in each of the potential wells.The ammonia molecule has a dipole moment of 1.468 D at the C3v equilibrium geometry11 corresponding to a partial negative charge on the nitrogen side of the molecule, and a partial positive charge on the hydrogen side. The ammonia molecule can be described in the D3h point group, or the isomorphic permutation-inversion group  , with rovibrational energy states labelled by the irreducible representations:
, with rovibrational energy states labelled by the irreducible representations: 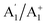 ,
, 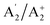 ,
,  ,
,  , E′/E+ and E′′/E− in
, E′/E+ and E′′/E− in  .22–24,76 According to the Pauli principle, the total internal wavefunction in NH3 (ND3) must have symmetry of either A+2 or A−2 (A+1 or A−1), i.e., it must be antisymmetric (symmetric) with respect to pairwise exchange of the identical fermions (bosons). The nuclear-spin states of 14NH3 and 14ND3 span the representations:
.22–24,76 According to the Pauli principle, the total internal wavefunction in NH3 (ND3) must have symmetry of either A+2 or A−2 (A+1 or A−1), i.e., it must be antisymmetric (symmetric) with respect to pairwise exchange of the identical fermions (bosons). The nuclear-spin states of 14NH3 and 14ND3 span the representations:
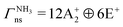 | (14) |
 | (15) |
 | (16) |
 | (17) |
 permutation inversion group. Adapted from ref. 23 and 24
permutation inversion group. Adapted from ref. 23 and 24
| Symmetry (rve) | J | K | g ns,i | |
|---|---|---|---|---|
| NH3 | s; A+1 | Even | 0 | 0 |
| a; A−1 | Odd | 0 | 0 | |
| s; A+2 | Odd | 0 | 12 | |
| a; A−2 | Even | 0 | 12 | |
| s, a; E± | All | 1, 2, 4, 5,… | 6 | |
| s, a; A1± | All | 3, 6, 9, 12,… | 0 | |
| s, a; A2± | All | 3, 6, 9, 12,… | 12 | |
| ND3 | s; A+1 | Even | 0 | 30 |
| a; A−1 | Odd | 0 | 30 | |
| s; A+2 | Odd | 0 | 3 | |
| a; A−2 | Even | 0 | 3 | |
| s, a; E± | All | 1, 2, 4, 5,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) … … |
24 | |
| s, a; A1± | All | 3, 6, 9, 12,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) … … |
30 | |
| s, a; A2± | All | 3, 6, 9, 12,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) … … |
3 | |
 | ||
Fig. 2 Rotational energy levels and symmetry labels in the lowest vibrational level of the ground electronic state of NH3 and ND3 in the  permutation inversion group, for |K| ≤ 2. The numbers in parentheses indicate the spin-statistical weights gns, the l and u letters indicate the lower and upper components of the inversion doublets.24 The rotational constants are taken from ref. 76 (NH3) and ref. 77 (ND3). permutation inversion group, for |K| ≤ 2. The numbers in parentheses indicate the spin-statistical weights gns, the l and u letters indicate the lower and upper components of the inversion doublets.24 The rotational constants are taken from ref. 76 (NH3) and ref. 77 (ND3). | ||
Because of the missing A1 levels, the inversion splitting is not observed in NH3 states with K = 0. Instead, this manifold consists of an alternating series of negative–positive parity J states (even/odd J states are of A−2/A+2 symmetry). At the typical rotational temperature of the molecules produced in our supersonic-beam source (Trot ≃ 6 K) and for the rotational constants of NH3 and ND3 (ANH3 = BNH3 = 9.444 cm−1, CNH3 = 6.196 cm−1; AND3 = BND3 = 5.143 cm−1, CND3 = 3.125 cm−1),76,77 only states with K = 0 and |K| = 1 are significantly populated. Taking into account the nuclear-spin symmetry, the ratio of states with K = 0 to states with |K| = 1 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 11
1 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 in NH3 and ND3, respectively. The occupation probabilities of the different ground-state rotational levels at a rotational temperature of Trot= 6 K are listed in Table 2.
16 in NH3 and ND3, respectively. The occupation probabilities of the different ground-state rotational levels at a rotational temperature of Trot= 6 K are listed in Table 2.
| NH3 | ND3 | ||
|---|---|---|---|
| K = 0 | J = 0 (l) | 0 | 0.295 |
| J = 0 (u) | 0.484 | 2.94 × 10−2 | |
| J = 1 (l) | 1.57 × 10−2 | 7.58 × 10−3 | |
| J = 1 (u) | 0 | 7.42 × 10−2 | |
| |K| = 1 | J = 1 (l) | 0.274 | 0.295 |
| J = 1 (u) | 0.226 | 0.291 | |
| J = 2 (l) | 5.29 × 10−5 | 3.49 × 10−3 | |
| J = 2 (u) | 4.39 × 10−5 | 3.54 × 10−3 | |
Displayed in Fig. 3 are reaction-product time-of-flight (TOF) spectra measured following reactions between He(n) atoms and NH3(a) and ND3(b) molecules, after a reaction time of Δtr = 7 μs. These spectra were recorded with the He(n) atoms accelerated to a final velocity of vRyd = 1050 m s−1, corresponding to collisional energies Ecoll ≈ kB·3.8 K (a) and kB·2.8 K (b). When the laser used to photoexcite He* to He(n) is on (black traces in Fig. 3), a prominent peak is visible at 1.6 μs, corresponding to the He+ ions generated by field ionisation of the He(n) atoms. The extraction electric field of 110 V cm−1 is not sufficient to ionise the initially prepared Rydberg helium atoms with n = 30 (this field can only ionise states with n ≳ 50). However, n-changing blackbody-radiation-induced transitions during the ∼85 μs flight time of the He(n) atoms from the photoexcitation region to the centre of the TOFMS populate a few higher-lying Rydberg states, which can then be field ionised with the extraction field. A constant background signal of ∼0.7 mV is also visible in the TOF traces in Fig. 3 beyond 1.6 μs. This background signal originates from a constant stream of He+ produced either through blackbody-radiation-induced ionisation or slow tunnelling ionisation of the He(n) Rydberg states in the extraction field.
In addition to the He+ peak, several other peaks are visible in the mass spectra and can be assigned to (a) NH+, NH2+, NH3+/OH+, H2O+ and N2+, and (b) ND+, OH+, ND2+/H2O+, ND3+ and N2+, as indicated in Fig. 3. The main product ions observed following the He(n) + NH3 (ND3) reaction are NH2+ and NH+ (ND2+ and ND+). The H2O+, OH+ and N2+ ions originate from Penning-ionisation processes involving metastable He* atoms produced in the discharge and background water and nitrogen present in the GS beam. The corresponding mass peaks in the TOF spectra are indeed observed even when the excitation laser is turned off (orange traces in Fig. 3). We have verified that the NH+, NH2+, ND+ and ND2+ product ions detected are generated by autoionisation of the corresponding Rydberg-molecule products.
The comparison of the TOF mass spectra recorded with the excitation laser turned on and off illustrates that the peaks corresponding to the OH+, NH3+, ND3+, H2O+ and N2+ ions originate mostly from Penning ionisation and that the NH+, ND+, NH2+ and ND2+ ions are only detected in significant quantities from reactions with He(n).
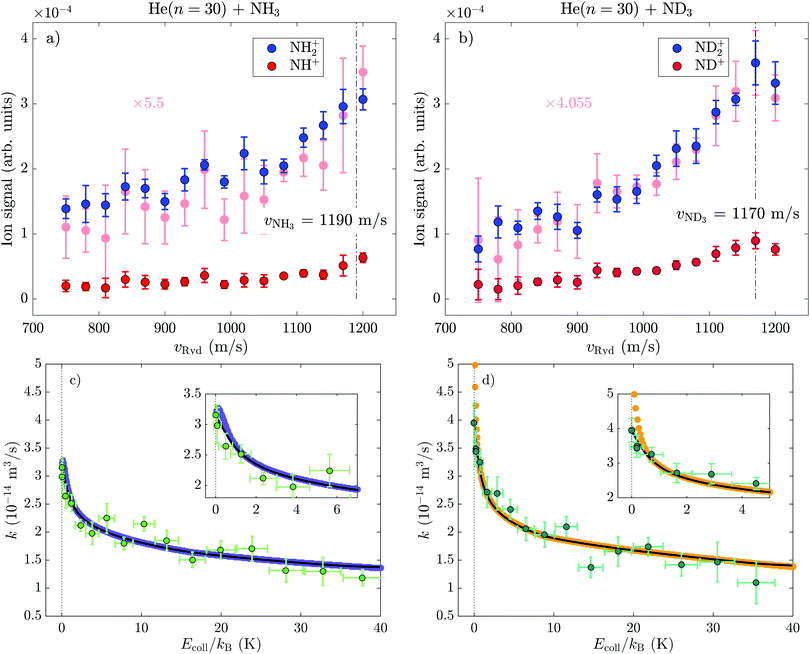
To measure the collision-energy dependence of the product yields, we record the integrated NH+, ND+, NH2+ and ND2+ product signals for several values of the He(n) velocity, vRyd, in the 750–1200 m s−1 range, keeping the GS-beam velocity constant. The results of these measurements are presented in Fig. 4(a and b). The range of He(n) velocities corresponds to collisional energies of Ecoll/kB ≲ 40 K. In order to subtract contributions from Penning-ionisation products from the He(n) + NH3/ND3 reaction products, mass spectra were recorded without the Rydberg-excitation laser and then subtracted prior to integration (see insets of Fig. 3). The integration of the light (NH+ and ND+) and heavy (NH2+ and ND2+) reaction product ions, respectively, was performed in temporal windows indicated by the red and blue shaded areas in the insets in Fig. 3. The measured integrated product-ion signals for each value of vRyd were further normalised following the procedure described in Section 4.3. The error bars are obtained from five sets of consecutive measurements, each corresponding to an average over 1000 experimental cycles.
The integrated normalised product-ion signals INH2+ and IND2+ are depicted as a function of the He(n) velocity using blue dots in Fig. 4(a and b). They show a pronounced increase as the He(n) velocity, vRyd, approaches the GS-beam velocity, which is designated by the dashed vertical lines. This increase is more pronounced for the He(n) + ND3 reaction than for the He(n) + NH3 reaction: for example, INH2+(1200 m s−1)/INH2+(750 m s−1) ≈ 2.21, while IND2+ (1170 m s−1)/IND2+(750 m s−1) ≈ 4.72. The measured values of INH+ and IND+ [red circles in Fig. 4(a and b)] are smaller than the measured values of INH2+ and IND2+ by a factor of fNH+ = 6 ± 1 and fND+ = 4.0 ± 0.6, respectively. The measured NH2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH+ branching ratio is slightly lower than the one reported in ref. 68. While in previous measurements the NH3+ product ions constituted approximately 12% of the total reaction yield,68 in our experiments all NH3+/ND3+ ions are primarily generated by Penning-ionisation processes and the NH3+ and ND3+ signals obtained after subtraction of the Penning-ionisation contributions are too weak and noisy for reliable estimates of the branching ratios to be carried out.
NH+ branching ratio is slightly lower than the one reported in ref. 68. While in previous measurements the NH3+ product ions constituted approximately 12% of the total reaction yield,68 in our experiments all NH3+/ND3+ ions are primarily generated by Penning-ionisation processes and the NH3+ and ND3+ signals obtained after subtraction of the Penning-ionisation contributions are too weak and noisy for reliable estimates of the branching ratios to be carried out.
6 Calculation of the capture-rate coefficients and comparison with experimental data
6.1 The Stark effect in NH3 and ND3 and the He+ + NH3/ND3 interaction potentials
The interaction between the molecular dipole moment and an electric field mixes states |JKM〉 ↔ |J′K′M′〉 with J′ = J, J ± 1 (eqn (9) with λ = 1). The electric-dipole selection rules are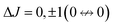 , ΔK = 0 and ΔM = 0.
, ΔK = 0 and ΔM = 0.
To describe the Stark effect in ammonia under the consideration of the inversion splitting, we expand the |JKM〉 basis set to include the inversion doublet sublevels, which have positive or negative parity. Since the rotational Hamiltonian is invariant under the parity operation, it is conventional to use the symmetrised rotational wavefunctions of well-defined parity |J,K,M,(+/−)〉. The Stark interaction mixes states of opposite parity and the non-vanishing Stark matrix elements in the symmetrised basis are:78
 | (18) |
The Stark effect in NH3 and ND3 was calculated by determining the eigenvalues of the Hamiltonian in eqn (11) for values of the ion–molecule separation R from 0.1 nm to 50 nm in steps of 0.1 nm (corresponding to electric fields ranging from ∼1.4 × 106 kV cm−1 to ∼5.7 kV cm−1, respectively). We use the rotational constants presented in Fig. 2.76,77 Because only J = 0 and 1 levels are significantly populated in our experiments, we neglect centrifugal-distortion effects. Convergence of the eigenvalues of the J = 0, 1 levels was reached with a basis set with a maximum value of Jmax = 6. The states are labelled according to their adiabatic limit for R → ∞ corresponding to field-free conditions. The results of the calculation for the states with J ≤ 1, |K| ≤ 1 for electric fields in the 5–5000 kV cm−1 range are presented in Fig. 5. Because of the smaller value of the tunnelling splitting and the smaller (by a factor of ∼2) values of the rotational constants, the Stark shifts are more pronounced in ND3 at low fields. In addition, the Stark effect of the J = 1, |K| = 1 levels becomes linear earlier in ND3.
We classify the Stark states of interest in ammonia in three types according to the energy shift they experience with increasing electric field: type A – strongly high-field-seeking states with a linear Stark shift, i.e., the lower-energy components of the inversion doublets with J = 1 and |KM| = 1; type B – high-field-seeking states with a quadratic Stark shift at low fields, e.g., the |J = 0, K = 0, M = 0, − 〉 and |J = 1, K = 0, M = 1, +〉 states; and type C – low-field-seeking states at relatively low fields which exhibit an energy maximum at intermediate values of the electric field before turning into high-field-seeking states at high fields, e.g., selected components of the inversion doublets with J = 1 and |KM| = 1.
States of type A comprise the lower components of the J = 1, |KM| = 1 inversion doublets in NH3 and ND3 (see Fig. 5). These states experience the strongest Stark shifts, ΔEi, in both NH3 and ND3: ΔE(A) ∼ −88 cm−1 in NH3 and ∼−95 cm−1 in ND3 at 5000 kV cm−1. States of type B with J = 0 (i.e., the |0,0,0,−〉 state in NH3 and the |0,0,0,+〉 and |0,0,0,−〉 states in ND3) do not have a dipole moment at low fields, but acquire one through mixing with the |1,0,0,±〉 states in an electric field. In states of type C, the potential energy barriers occur at lower values of the electric field and have lower heights in ND3 than in NH3 (see Table 3). At the lowest electric fields (≲80 kV cm−1), the inversion splitting of ∼0.79 cm−1 in NH3 causes the J = 1, |KM| = 1 states to undergo a quadratic Stark shift [inset of Fig. 5(a)]. In contrast, because of the much smaller inversion splitting of ∼0.053 cm−1 in ND3, the corresponding states experience a linear Stark shift, even at the lowest fields [insets of Fig. 5(b)]. The bottom panels in Fig. 5 show the electric-field-dependent dipole moments of the states depicted in the top panels.
| Height (cm−1) | Position (kV cm−1) | ||
|---|---|---|---|
| NH3 | J = 1, |KM| = 1 (+) | 11.4 | 1836 (R = 2.80 nm) |
| J = 1, K = M = 0 (+) | 6.03 | 1837 (R = 2.79 nm) | |
| ND3 | J = 1, |KM| = 1 (+) | 6.37 | 997.2 (R = 3.80 nm) |
| J = 1, K = M = 0 (+) | 3.32 | 1052 (R = 3.70 nm) | |
| J = 1, K = M = 0 (−) | 3.25 | 997.2 (R = 3.80 nm) | |
Because of the R−2 dependence of the ion–dipole interaction, the ΔEi(R) terms in eqn (3) dominate over the R−4-dependent charge–induced-dipole interaction term for all states, as illustrated in Fig. 6. This figure compares the total interaction potentials, Vint,i(R), for the states presented in Fig. 5 for an s-wave collision (L = 0, solid lines) and a collision with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 20 (L2 = ħ2
= 20 (L2 = ħ2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) + 1), dash-dotted lines), with VL (black solid and dash-dotted lines, respectively).
+ 1), dash-dotted lines), with VL (black solid and dash-dotted lines, respectively).
The Stark shifts significantly modify the potential barriers, and thus affect the value of Lmax,i for each collisional energy (see eqn (13)). In states of type A and B, the centrifugal barrier is substantially lowered compared to the centrifugal barrier in VL, the effect being significantly more pronounced in states of type A. For example, the ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 20 term creates a centrifugal barrier of ∼kB·14 K in the Langevin interaction potential [dash-dotted black line in Fig. 6(a)], whereas the total interaction potentials for the same value of
= 20 term creates a centrifugal barrier of ∼kB·14 K in the Langevin interaction potential [dash-dotted black line in Fig. 6(a)], whereas the total interaction potentials for the same value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) in the A states are strongly attractive. The Stark effect in states of type A and B thus effectively suppresses the centrifugal barriers, which leads to significantly larger value of L(A,B)max,i and to much higher capture rate coefficients k(A,B)i. As the collisional energy increases, the Ecoll−1/2 dependence of ki(Ecoll) [see eqn (13)] leads to a decrease of the rate coefficients. States of type C, in contrast, are characterised by a non-zero potential-energy barrier even for
in the A states are strongly attractive. The Stark effect in states of type A and B thus effectively suppresses the centrifugal barriers, which leads to significantly larger value of L(A,B)max,i and to much higher capture rate coefficients k(A,B)i. As the collisional energy increases, the Ecoll−1/2 dependence of ki(Ecoll) [see eqn (13)] leads to a decrease of the rate coefficients. States of type C, in contrast, are characterised by a non-zero potential-energy barrier even for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0. This
= 0. This ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0 potential-energy barrier is designated as V(C),maxint in Fig. 6(a and b). For molecules in states of type C, the ion–molecule pair experiences a repulsive potential and the capture rate coefficients vanish for Ecoll < V(C),maxint.
= 0 potential-energy barrier is designated as V(C),maxint in Fig. 6(a and b). For molecules in states of type C, the ion–molecule pair experiences a repulsive potential and the capture rate coefficients vanish for Ecoll < V(C),maxint.
6.2 The rotational-state-dependent capture rate coefficients
The calculated state-dependent capture rate coefficients, ki(Ecoll), for the He+ + NH3(J, K, M, ±) and He+ + ND3(J, K, M, ±) reactions with J = 0, 1 and |K| = 0, 1 are displayed in Fig. 6(c and d). The calculations were performed for collisional energies Ecoll/kB in the 0.05–40 K range, with a step size of 50 mK. For states of type A and B, the rate coefficients are significantly higher than the Langevin rate constant kL (black horizontal lines in the lower insets) and increase with decreasing collisional energy. The differences resulting from the quadratic Stark shift of B-type states and the linear Stark shift of the A-type states become apparent at collisional energies Ecoll/kB ≲ 20 K. Both A- and B-type states experience a gradual increase of k in the Ecoll/kB = 20–40 K range. However, below Ecoll/kB ≈ 20 K the k(A) rate coefficients exhibit a much faster increase than the k(B) rate coefficients. At the lowest collisional energies of Ecoll/kB = 50 mK, the rate coefficients of A-type states reach values of k(A),He++ND3 = 93.7 kL and k(A),He++NH3 = 50.9 kL. The enhancement of the capture rate coefficients at Ecoll/kB = 50 mK compared to 20 K is ∼1.1–1.3 (∼1.2–1.6) for type B states and ∼4.5 (∼6.8) for type A states in NH3 (ND3).The k(C) coefficients are zero for Ecoll < V(C),maxint. For Ecoll ≥ V(C),maxint, the rate coefficients rapidly increase with Ecoll, and typically already exceed the value of kL at Ecoll/kB ≈ 10–20 K [see the insets in Fig. 6(c and d)].
The behaviour of the capture rate coefficients in the high-collision-energy regime up to Ecoll/kB = 2.4 × 104 K is presented in Fig. 6(e and f). States of type A and B have rate coefficients which decrease monotonously with Ecoll, and approach the values of kL for Ecoll/kB ≳ 104 K. In the case of states of type C, in contrast, the rates reach a maximum at Ecoll/kB ≈ 100 K and 60 K in the He+ + NH3 and He+ + ND3 reactions, respectively. Then they decrease again, eventually converging to the value of kL at similar collision energies as the type-A and type-B states. Apparent in Fig. 6(e and f) is that the k(B) rate coefficients increase with decreasing Ecoll, but eventually stabilise below Ecoll/kB ≲ 5 K at a value of ∼7.5 kL (for the J = 1, KM = 0 states) and ∼13.5 kL (for the J = 0 states) in NH3 and ∼10 kL and ∼18 kL in ND3, respectively. The greater increase of the k(B) rates relative to kL in ND3 is a consequence of the larger quadratic Stark-shifts of the B-type states at low fields.
In the experiments, we measure the relative collision-energy-dependent product yields, which reflect the initial molecular population distribution over the J = 0, 1 |K| = 0, 1 rotational states of NH3 and ND3. However, because the A-type states experience a linear Stark shift and a large increase over kL even at relatively high collisional energies (e.g., below Ecoll/kB < 40 K), the overall rate coefficient is dominated by the contribution from these states, even though they are occupied only by a small fraction of the molecular population at Trot = 6 K (∼0.182 in NH3 and ∼0.196 in ND3, see Fig. 7 below).
 | ||
| Fig. 7 Occupation probabilities of the A-, B- and C-type of states in NH3 and ND3, at a rotational temperature of Trot = 6 K. See text for details. | ||
6.3 Modelling of the measured rate coefficients
To model the experimentally measured relative product-ion signals as a function of the collision energy for the two reactions, INH++NH2+ and IND++ND2+, we proceed in the following way: in a first step, we calculate the weighted sum of the rotational-state-dependent capture rate constants, ki(Ecoll), for a given rotational temperature, Trot, with weights determined by the corresponding state population. In a second step, we perform a convolution with a Gaussian distribution accounting for the collisional-energy-dependent energy-resolution, as described in ref. 42, using the equation: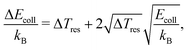 | (19) |
The comparison between the experimental data and the calculated data using the ion–molecule capture-rate model is presented in Fig. 4(c and d). The best agreement was achieved for Trot = 6 K and ΔTres = 200 mK for both reactions. The coloured (orange and purple) dots and the black curves are the rates obtained in the second and third steps of the procedure described above, respectively. The insets display the behaviour at low collisional energies (Ecoll/kB ≲ 6 K) on an enlarged scale. The agreement between the data and the model taking into account the finite resolution [black lines in Fig. 4(c and d)] is excellent for both reactions. The model thus quantitatively describes the experimentally observed increase of the product-ion signals with decreasing collisional energy. The overall behaviour exhibits a gradual, slow increase over the Ecoll/kB ≈ 5–40 K range and a much steeper increase for Ecoll/kB ≲ 5 K. The latter effect is significantly more pronounced for the He+ + ND3 reaction than for the He+ + NH3 reaction.
The calculated rate coefficients averaged over the rotational population of the molecules [purple and orange dots in Fig. 4(c and d)] and taking the finite experimental collision-energy resolution into account [black lines in Fig. 4(c and d)] are enhanced by factors of ∼2.29 (∼2.81) at a collision energy of kB·200 mK compared to the value at Ecoll = kB·40 K and of ∼1.71 (∼2.09) compared to the value at Ecoll = kB·10 K for the He+ + NH3 (He+ + ND3) reaction. The observed larger increase with decreasing collision energy of the rates of the He+ + ND3 reaction is perfectly reproduced by the calculations and originates from (i) the larger rotational-state-dependent rate constants compared to the He+ + NH3 reaction, as discussed in Section 6.2, and (ii) the higher contribution to the rate coefficients from type-A states in ND3 resulting from the nuclear-spin statistical factors, as is now explained.
The occupation probabilities p of the A-, B- and C-type states in NH3 and ND3 at a rotational temperature of Trot = 6 K are presented in Fig. 7 and are p(A),NH3 = 0.182, p(B),NH3 = 0.662 and p(C),NH3 = 0.156 for NH3 and p(A),ND3 = 0.196, p(B),ND3 = 0.580 and p(C),ND3 = 0.224 for ND3. The experimentally measured increase of product-ion signals with decreasing collisional energy can thus be almost entirely attributed to states of type A and B. The observed steeper increase below Ecoll/kB ≲ 5 K of the rate of the He+ + ND3 reaction compared to the rate of the He+ + NH3 reaction results from: (i) the more pronounced Stark effect in ND3 and (ii) the larger fraction of molecules in high-field-seeking states of type A: p(A),ND3/(p(A),ND3 + p(B),ND3) = 0.255 in ND3 compared to p(A),NH3/(p(A),NH3 + p(B),NH3) = 0.216 in NH3.
6.4 Thermal rate constants
The good agreement between the experimental and calculated collision-energy-dependent rates (see Fig. 4) validates the model used to calculate the rotational-state-specific rate coefficients ki(Ecoll) with i = |JKM ±〉. These coefficients can in turn be used to determine the thermal rate constants k(T) with the relations79 | (20) |
 | (21) |
In an environment where conversion between the two nuclear-spin isomers is possible, E0 is taken as the energy of the J = 0, K = 0 rotational ground state. If the nuclear-spin-symmetry is conserved, E0 represents the rotational energy of the ground state of the respective nuclear-spin isomer, i.e., E0 is the energy of the (J = 0, K = 0)u ground state for ortho NH3 and ND3, the energy of the lower tunnelling component of the (J = 1, K = 1) rotational level for para NH3 and ND3, and the energy of the (J = 0, K = 0)l for meta ND3 (see Fig. 2). The rate constants calculated assuming that the relative populations of the ortho, para and meta nuclear-spin isomers correspond to the nuclear-spin-statistical factors are presented in panels (a) and (b) of Fig. 8 for NH3 and ND3, respectively. In this figure, the full lines correspond to the case where the nuclear spin is assumed to be conserved and the dashed lines to the case where ortho–para conversion is assumed to be possible.
Whereas the nuclear-spin symmetry is known to be conserved to an excellent approximation in low-density gases and supersonic expansions,24,80 conversion between the different nuclear-spin isomers may take place if the ammonia molecules are adsorbed at the surface of certain materials and dust grains. The insets in Fig. 8 give the relative population of the different rotational levels for these two cases, labelled nuclear-spin-conservation (NSC) and nuclear-spin-relaxation (NSR), respectively. In both cases, the thermal capture rate is enhanced as the temperature decreases. However, the enhancement is more pronounced if the nuclear-spin symmetry is conserved because, in this case, there is always a significant population of the high-field-seeking tunnelling component of the J = 1, K = 1 state, even at 0 K.
Eqn (20) and (21) can be used to calculate the thermal capture rate coefficients at the temperatures of 27, 68, and 300 K for which the rate of the He+ + NH3 reaction was measured in uniform supersonic flows.35 The results are presented in Table 4, where the first and second rows of the body of the table list the rates calculated assuming that the nuclear-spin symmetry is conserved (NSC) or relaxed (NSR), respectively. Beyond 10 K, the state populations do not strongly depend any more on whether NSR or NSC is assumed, so that the thermal rate constant with both assumption are almost identical. The third row gives the experimental values reported by Marquette et al.35 The calculated rates are larger than the experimental ones, which is expected given that the calculated capture rates correspond to 100% reaction probability upon close encounter of the reactants whereas the experiments only monitor the reactive collisions. The comparison of experimental and calculated values of the thermal rate coefficient suggests that about 40 to 50% of the Langevin collisions are reactive. The last two columns of Table 4 present the ratios r1 and r2 of the thermal rate coefficient obtained at 27 K to those obtained at 68 and 300 K. The calculated r1 value is in perfect agreement with the experimental result, whereas the experimental and calculated values of r2 differ by about 30%.
| k(27 K) (m3 s−1) | k(68 K) (m3 s−1) | k(300 K) (m3 s−1) | r 1 | r 2 | |
|---|---|---|---|---|---|
| NSC | 1.13 × 10−14 | 7.39 × 10−15 | 3.18 × 10−15 | 1.5 | 3.6 |
| NSR | 1.14 × 10−14 | 7.48 × 10−15 | 3.11 × 10−15 | 1.52 | 3.7 |
| Exp.35 | 4.5 × 10−15 | 3.0 × 10−15 | 1.65 × 10−15 | 1.5 | 2.7 |
7 Conclusions
In this article, which is the first in a series of three articles dedicated to the role of long-range electrostatic interactions in ion–molecule reactions at low temperatures, we have presented the results of measurements of the collision-energy-dependent rates of the reactions between He+ and ammonia (NH3 and ND3) in the range of collision energies between kB·0.2 K and kB·40 K. To reach such low collision energies, we used a merged-beam approach and observed the reactions within the orbit of a highly excited Rydberg electron. In this range, we observed that the rates increase strongly with decreasing collision energy, the increase being particularly pronounced below kB·5 K. We have also observed that the rates of reactions involving ND3 increase more strongly than the rates of the reactions involving NH3 at low collision energies. To interpret the experimental results, we have calculated the rates using an adiabatic capture model3–6 based on the calculation of the Stark shifts of the rotational levels of NH3 and ND3 in the field of the He+ ion.The calculations provided a quantitatively accurate description of the experimental observations and could be used to rationalise the observed collision-energy-dependent reaction yields in terms of capture rate coefficient for rotationally state-selected (|JKM±〉) ammonia molecules. These states could be classified into three categories: (A) states with |KM| ≥ 1 correlating at low fields with the lower components of the inversion-tunnelling doublets. These states undergo linear negative Stark shifts in the field of the colliding ion, which suppresses the centrifugal barriers in the effective intermolecular potential and greatly enhances the capture rates at low collision energies; (B) states with KM = 0 which only become sensitive to the fields at high fields through the quadratic and higher-order Stark shifts. The corresponding capture rates are only weakly enhanced at low collision energies. (C) States with positive Stark shifts at low fields which generate large potential energy barriers and completely suppress the reactions at low collision energies (below ∼kB·15 K). At high collision energies, beyond kB·300 K, the capture rates for all three categories gradually converge to the Langevin capture rates. These observations are a direct consequence of the dipolar nature of ammonia.
The model also provided an explanation for the different behaviour of the reactions involving NH3 and ND3 at low collision energies. The stronger enhancements of the rates observed below kB·5 K in the reactions of ND3 was interpreted as arising from the smaller rotational energy intervals, the smaller tunnelling splittings of the inversion mode and from the larger population of the rotational states belonging to category A at the 6 K rotational temperature of the supersonic beams. From the calculated rotational-state-specific collision-energy-dependent captures rates, thermal capture rate coefficients were determined in the temperature range between 0.2 and 10 K of relevance for modelling reactions in the interstellar medium. Assuming that the relative populations of the ortho, para and meta nuclear-spin isomers reflect the nuclear-spin-statistical factors, as can be expected for dilute gases and supersonic expansions, leads to a large nonlinear increase of the thermal capture rates below 5 K. In NH3, the thermal capture rate constant reaches the value of 4.4 × 10−14 m3 s−1 at 0.2 K, which is more than 20 times larger than the Langevin rate constant. Assuming that ortho–para–meta conversion processes can take place, as might be the case if the molecules have thermalised at the surface of certain materials and dust grains, leads to slightly larger rate enhancements above ∼2 K, but to smaller rate enhancements at the lowest temperatures (see Fig. 8).
In future work, it will be important to obtain data at even lower temperatures and improved energy resolution. Moreover, the preparation of rotationally state-selected samples would enable more extensive tests of the model predictions. The generation of pure samples of molecules in high-field-seeking states of the category A seems particularly attractive in this regard, and recent experiments have demonstrated ways of generating such samples.81 Calculations of the (nonadiabatic) dynamics on the multidimensional potential-energy surfaces involved would be needed to interpret the observed branching ratios and the fact that only ∼40% of the close collisions appear to be reactive.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank M. Žeško for his contributions to the initial phase of this project and K. Höveler and J. Deiglmayr for fruitful discussions. This work is supported financially by the Swiss National Science Foundation (Grant No. 200020B-200478) and by the European Research Council through the ERC advanced grant (Grant No. 743121) under the European Union's Horizon 2020 Research and Innovation Programme.References
- Gas Phase Ion Chemistry: Vol. 1 and 2, ed. M. T. Bowers, Academic Press, New York, 1979 Search PubMed.
- Kinetics of Ion-Molecule Reactions, ed. P. Ausloos, Plenum Press, New York, 1978 Search PubMed.
- D. C. Clary, Mol. Phys., 1985, 54, 605–618 CrossRef CAS.
- J. Troe, Chem. Phys., 1987, 87, 2773–2780 CAS.
- D. C. Clary, Annu. Rev. Phys. Chem., 1990, 41, 61–90 CrossRef CAS.
- J. Troe, J. Chem. Phys., 1996, 105, 6249–6262 CrossRef CAS.
- State-selected and state-to-state ion-molecule reaction dynamics: Part 1. Experiment and Part 2. Theory, ed. C.-Y. Ng and M. Baer, John Wiley & Sons, Inc., New York, 1992 Search PubMed.
- D. Gerlich, The study of cold collisions using ion guides and traps, in Low Temperatures and Cold Molecules, ed. I. M. W. Smith, Imperial College Press, London, 2008, ch. 3, pp. 121-174 Search PubMed.
- S. Willitsch, M. T. Bell, A. D. Gingell and T. P. Softley, Phys. Chem. Chem. Phys., 2008, 10, 7200–7210 RSC.
- B. R. Heazlewood and T. P. Softley, Nat. Rev. Chem., 2021, 5, 125–140 CrossRef CAS.
- M. D. Marshall, K. C. Izgi and J. S. Muenter, J. Chem. Phys., 1997, 107, 1037–1044 CrossRef CAS.
- C. Graham, D. A. Imrie and R. E. Raab, Mol. Phys., 1998, 93, 49–56 CrossRef CAS.
- G. Birnbaum and E. R. Cohen, J. Chem. Phys., 1975, 62, 3807–3812 CrossRef CAS.
- D. Albritton, At. Data Nucl. Data Tables, 1978, 22, 1–89 CrossRef CAS.
- V. G. Anicich and W. T. Huntress, Astrophys. J., Suppl. Ser., 1986, 62, 553–672 CrossRef CAS.
- T. Stoecklin, D. C. Clary and A. Palma, J. Chem. Soc., Faraday Trans., 1992, 88, 901–908 RSC.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2005, 122, 184311 CrossRef CAS PubMed.
- M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 084311 CrossRef CAS PubMed.
- M. Auzinsh, E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2013, 139, 144315 CrossRef CAS PubMed.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, J. Chem. Phys., 2016, 145, 244315 CrossRef CAS PubMed.
- J. T. Hougen, Methane symmetry operations, in Spectroscopy, ed. D. A. Ramsay, Butterworths, London, 1976, vol. 3, pp. 75–125 Search PubMed.
- P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, Canada, 2006 Search PubMed.
- M. Snels, L. Fusina, H. Hollenstein and M. Quack, Mol. Phys., 2000, 98, 837–854 CrossRef CAS.
- G. Wichmann, E. Miloglyadov, G. Seyfang and M. Quack, Mol. Phys., 2020, 118, e1752946 CrossRef.
- E. Herbst and W. Klemperer, Astrophys. J., 1973, 185, 505 CrossRef CAS.
- E. Roueff, Phys. Scr., 1987, 36, 319–322 CrossRef CAS.
- D. Smith, Chem. Rev., 1992, 92, 1473–1485 CrossRef CAS.
- E. Herbst, Spectroscopy from space, in NATO science series, Series II, Mathematics, physics, and chemistry, ed. J. Demaisonet al., Kluwer Academic Publishers, Dordrecht, 2001, vol. 20 Search PubMed.
- T. P. Snow and V. M. Bierbaum, Annu. Rev. Anal. Chem., 2008, 1, 229–259 CrossRef CAS PubMed.
- I. W. M. Smith, Annu. Rev. Astron. Astrophys., 2011, 49, 29–66 CrossRef CAS.
- V. Wakelam, I. W. M. Smith, E. Herbst, J. Troe, W. Geppert, H. Linnartz, K. Öberg, E. Roueff, M. Agúndez, P. Pernot, H. M. Cuppen, J. C. Loison and D. Talbi, Space Sci. Rev., 2010, 156, 13–72 CrossRef CAS.
- E. F. van Dishoeck, Proc. Int. Astron. Union, 2017, 13, 3–22 CrossRef.
- R. Wester, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 154001 CrossRef.
- C. Markus, O. Asvany, T. Salomon, P. Schmid, S. Brünken, F. Lipparini, J. Gauss and S. Schlemmer, Phys. Rev. Lett., 2020, 124, 233401 CrossRef CAS PubMed.
- J. B. Marquette, B. R. Rowe, G. Dupeyrat, G. Poissant and C. Rebrion, Chem. Phys. Lett., 1985, 122, 431–435 CrossRef CAS.
- B. Rowe, A. Canosa and V. L. Page, Int. J. Mass Spectrom. Ion Processes, 1995, 149, 573–596 CrossRef.
- S. Willitsch, Chemistry with Controlled Ions, in Adv. Chem. Phys., ed. S. A. Rice and A. R. Dinner, 2017, vol. 162, pp. 307–340 Search PubMed.
- L. S. Petralia, A. Tsikritea, J. Loreau, T. P. Softley and B. R. Heazlewood, Nat. Commun., 2020, 11, 173 CrossRef CAS PubMed.
- J. Toscano, H. J. Lewandowski and B. R. Heazlewood, Phys. Chem. Chem. Phys., 2020, 22, 9180–9194 RSC.
- P. Allmendinger, J. Deiglmayr, O. Schullian, K. Höveler, J. A. Agner, H. Schmutz and F. Merkt, ChemPhysChem, 2016, 17, 3596–3608 CrossRef CAS PubMed.
- P. Allmendinger, J. Deiglmayr, K. Höveler, O. Schullian and F. Merkt, J. Chem. Phys., 2016, 145, 244316 CrossRef PubMed.
- V. Zhelyazkova, F. B. V. Martins, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 125, 263401 CrossRef CAS PubMed.
- K. Höveler, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Chem. Chem. Phys., 2021, 23, 2676–2683 RSC.
- S. T. Pratt, J. L. Dehmer, P. M. Dehmer and W. A. Chupka, J. Chem. Phys., 1994, 101, 882–890 CrossRef CAS.
- E. Wrede, L. Schnieder, K. Seekamp-Schnieder, B. Niederjohann and K. H. Welge, Phys. Chem. Chem. Phys., 2005, 7, 1577–1582 RSC.
- M. Matsuzawa, Phys. Rev. A, 2010, 82, 054701 CrossRef.
- S. D. Hogan, P. Allmendinger, H. Sassmannshausen, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2012, 108, 063008 CrossRef CAS PubMed.
- P. Allmendinger, J. Deiglmayr, J. A. Agner, H. Schmutz and F. Merkt, Phys. Rev. A, 2014, 90, 043403 CrossRef.
- S. D. Hogan, EPJ Techn. Instrum., 2016, 3, 2 CrossRef PubMed.
- V. Zhelyazkova, M. Žeško, H. Schmutz, J. A. Agner and F. Merkt, Mol. Phys., 2019, 117, 2980–2989 CrossRef CAS.
- Y. Shagam and E. Narevicius, J. Phys. Chem. C, 2013, 117, 22454–22461 CrossRef CAS.
- Y. Shagam, A. Klein, W. Skomorowski, R. Yun, V. Averbukh, Ch. P. Koch and E. Narevicius, Nat. Chem., 2015, 7, 921–926 CrossRef CAS PubMed.
- N. Bibelnik, S. Gersten, A. B. Henson, E. Lavert-Ofir, Y. Shagam, W. Skomorowski, Ch. P. Koch and E. Narevicius, Mol. Phys., 2019, 117, 2128–2137 CrossRef CAS.
- J. Jankunas, B. Bertsche, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2014, 140, 244302 CrossRef PubMed.
- J. Jankunas and A. Osterwalder, Ann. Rev. Phys. Chem., 2015, 66, 241–262 CrossRef CAS PubMed.
- S. D. S. Gordon and A. Osterwalder, Int. Rev. Phys. Chem., 2020, 39, 109–134 Search PubMed.
- P. Langevin, Ann. Chim. Phys., 1905, T5, 245–288 Search PubMed.
- A. C. Cheung, D. M. Rank, C. H. Townes, D. D. Thornton and W. J. Welch, Phys. Rev. Lett., 1968, 21, 1701–1705 CrossRef CAS.
- E. Roueff, D. C. Lis, F. F. S. van der Tak, M. Gérin and P. F. Goldsmith, Astron. Astrophys., 2005, 438, 585–598 CrossRef CAS.
- W. Hermsen, T. L. Wilson, C. M. Walmsley and W. Batrla, Astron. Astrophys., 1985, 146, 134–138 CAS.
- R. N. Martin and P. T. P. Ho, Astron. Astrophys., 1979, 74, L7–L9 CAS.
- V. N. Salinas, M. R. Hogerheijde, E. A. Bergin, L. I. Cleeves, C. Brinch, G. A. Blake, D. C. Lis, G. J. Melnick, O. Panić, J. C. Pearson, L. Kristensen, U. A. Yildiz and E. F. van Dishoeck, Astron. Astrophys., 2016, 591, A122 CrossRef.
- P. G. J. Irwin, N. Bowles, A. S. Braude, R. Garland and S. Calcutt, Icarus, 2018, 302, 426–436 CrossRef CAS.
- G. Danby, D. R. Flower, P. Valiron, P. Schilke and M. C. Walmsley, Mon. Not. R. Astr. Soc., 1988, 235, 229–238 CrossRef CAS.
- Y. I. Izotov and T. X. Thuan, Astrophys. J., 2010, 710, L67–L71 CrossRef CAS.
- R. C. Bolden, R. S. Hemsworth, M. J. Shaw and N. D. Twiddy, J. Phys. B: At., Mol. Opt. Phys., 1970, 3, 45–60 CrossRef CAS.
- W. Lindinger, D. L. Albritton and F. C. Fehsenfeld, J. Chem. Phys., 1975, 62, 4957–4958 CrossRef CAS.
- J. K. Kim and W. T. Huntress, Int. J. Mass Spectrom. Ion Phys., 1975, 16, 451–454 CrossRef CAS.
- B. Ruscic, R. E. Pinzon, G. von Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoy and A. F. Wagner, J. Phys. Conf. Ser., 2005, 16, 561–570 CrossRef CAS.
- S. S. M. Wong, Introductory Nuclear Physics, John Wiley & Sons, 1998 Search PubMed.
- R. N. Zare, Angular Momentum, John Wiley & Sons, New York, 1988 Search PubMed.
- G. Łach and K. Pachucki, Phys. Rev. A, 2001, 64, 042510 CrossRef.
- T. Halfmann, J. Koensgen and K. Bergmann, Meas. Sci. Technol., 2000, 11, 1510–1514 CrossRef CAS.
- T. F. Gallagher, Rydberg Atoms, Cambridge University Press, Cambridge, 1994 Search PubMed.
- G. Herzberg, Molecular Spectra and Molecular Structure, Volume II, Infrared and Raman Spectra of Polyatomic Molecules, Krieger Publishing Company, Malabar, 1991 Search PubMed.
- Š. Urban, R. D'Cunha, K. Narahari Rao and D. Papoušek, Can. J. Phys., 1984, 62, 1775–1791 CrossRef.
- F. Daniel, C. Rist, A. Faure, E. Roueff, M. Gérin, D. C. Lis, P. Hily-Blant, A. Bacmann and L. Wiesenfeld, Mon. Not. R. Astron. Soc., 2016, 457, 1535–1549 CrossRef CAS.
- S. Y. T. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828–4878 CrossRef CAS PubMed.
- R. D. Levine, Molecular Reaction Dynamics, Cambridge University Press, 2005 Search PubMed.
- C. Manca Tanner and M. Quack, Mol. Phys., 2012, 110, 2111–2135 CrossRef.
- L. Ploenes, P. Straňák, H. Gao, J. Küpper and S. Willitsch, Mol. Phys., 2021, 119, e1965234 CrossRef.
| This journal is © the Owner Societies 2021 |