The effect of particle size on the optical and electronic properties of magnesium oxide nanoparticles

Abstract

The quasiparticle states, fundamental gaps, optical gaps, exciton binding energies and UV-vis spectra for a series of cuboidal nanoparticles of the prototypical oxide magnesium oxide (MgO), the largest of which has 216 atoms and edges of 1 nm, were predicted using many-body perturbation theory (evGW-BSE). The evolution of the properties with the particle size was explicitly studied. It was found that, while the highest occupied and lowest unoccupied quasiparticle states and fundamental gap change with the particle size, the optical gap remains essentially fixed for all but the smallest nanoparticles, in line with what was previously observed experimentally. The explanation for these observations is demonstrated to be that, while the optical gap is associated with an exciton that is highly localised around the particle's corner atoms, the highest occupied and lowest unoccupied quasiparticle states, while primarily localised on the oxygen corner atoms (hole) and magnesium corner atoms (electron), show significant delocalisation along the edges. The strong localisation of the exciton associated with the optical gap on the corner atoms is argued to also explain why the nanoparticles have much smaller optical gaps and red-shifted spectra compared to bulk MgO. Finally, it is discussed how this non-quantum confinement behaviour, where the properties of the nanoparticles arise from surface defects rather than differences in localisation of quasiparticle or exciton states, appears typical of alkaline earth oxide nanoparticles, and that the true optical gap of bulk crystals of such materials is also probably the result of surface defects, even if unobservable experimentally.

---

Introduction

The effect of going from the bulk to nanosize particles on the optical and electronic properties of materials is interesting from both a fundamental and applied perspective.¹ Practically it offers an alternative way of tuning material properties besides changing the composition, while conceptually it raises questions about what exactly causes the properties of nanoparticles to differ from those of the bulk. Quantum confinement,^2,3 where the size of the particle constrains the size of the exciton – the excited-electron hole pair formed by the absorption of light – to a size smaller than in the bulk, is often invoked, but requires the states involved to be delocalised over the particle, which is unlikely to be the case for more ionic materials. Quantum confinement also only explains blue-shifts with respect to the bulk, as e.g. observed for CdS,⁴ CdSe,^5,6 PbS^7,8 and PBSe⁹ nanoparticles, but not red-shifts, as e.g. observed for MgO,^10,11 CaO¹¹ and SrO¹² particles. An alternative mechanism by which the properties of nanoparticles may differ from the bulk involves the localisation of relevant states on low-coordinated surface atoms, which are ubiquitous on (small) nanoparticles. While experimental spectroscopy can clearly demonstrate the effect of nanostructuring on the electronic and optical properties, elucidating the atomic scale origin of these changes requires the combination of experiment with theory.

Magnesium oxide (MgO) nanoparticles are an ideal system to study differences in the optical and electronic properties between nanoparticles and the bulk and to synthesize the results of experiment and theory. Well-defined MgO nanoparticles as small as 3 nm have been prepared experimentally by means of chemical vapour deposition without the need for capping agents and found to display UV-vis diffuse reflection and photoluminescence spectra that are significantly red-shifted relative to bulk magnesium oxide.^10,11 The lowest-energy most red-shifted exciton peak in the reflection spectrum of bulk MgO,^13,14 the bulk optical gap, is located at 7.7 eV (161 nm), while the lowest peak in the reflection spectrum of the 3 nm particles lies at ∼4.6 eV (270 nm).¹⁰ These 3 nm nanoparticles are confirmed to have the same rocksalt structure as bulk magnesium oxide, ruling out the observed red shift being the result of major structural changes. Indeed, computational global optimisation studies show that, in contrast to materials that in the bulk crystallise with the zinc blende or wurtzite structure, e.g. zinc or cadmium sulfide,^15–19 the lowest energy nanoparticles of materials that crystallise with the rocksalt structure, such as MgO,^20–22 are, even in the absence of capping agents, generally cut from that crystal structure. The fact that magnesium and oxygen are relatively light elements also means that relativistic effects including spin–orbit coupling will be small in MgO nanoparticles in contrast to other rocksalt nanoparticles, such as those made from PbS or PbSe. Finally, while the MgO nanoparticles’ UV-vis spectra are significantly red-shifted with respect to the bulk, the largest change in the diffuse reflectance spectra when changing the average particle size from 3 to 10 nm is not a shift in the peak positions but their relative intensities.¹⁰ This lack of a shift but a change in intensities has been proposed based on quantum chemistry calculations on computational models of corners, edges and faces of MgO nanoparticles,^23–26 see below, to result from the fact that the lowest energy excited states in such particles localise on the corners and edges rather than being delocalised over the volume of the particle. This is a proposal that we here will re-investigate by calculations on whole nanoparticles.

In contrast to the case of the optical properties, there appear to be no experimental reports on the electronic structure of MgO nanoparticles: i.e. the fundamental gap, the energy required to generate a non-interacting excited electron and hole pair rather than an interacting exciton and/or the energies of the highest occupied (the negative of the ionisation potential, –IP) and the lowest unoccupied (the negative of the electron affinity, –EA) quasiparticle states (see Fig. 1). The latter concepts in the case of periodic crystals, where it is appropriate to speak of bands, map on to the bandgap, valence band maximum and conduction band minimum, respectively. There are some reports in the literature of the fundamental gap narrowing for thin films of MgO.^27,28 However, as this is generally observed by means of electron energy loss spectroscopy (EELS) and as one of the loss mechanisms in EELS involves the generation of excitons, the feature at ∼6 eV in the EELS spectrum of thin magnesium oxide films linked to the apparent narrowing of the fundamental gap in reality might be due to surface exciton formation^29,30 and thus be evidence of the narrowing of the thin films’ optical gap instead.

Fig. 1 Cartoon illustrating the definition of the highest occupied and lowest unoccupied quasiparticle states (–IP and –EA), the fundamental gap (Δ_F), the optical gap (Δ_O), and the exciton binding energy (EBE).

The optical properties of MgO nanoparticles were previously studied^23–26,31 using time-dependent density functional theory (TD-DFT). The results of these TD-DFT calculations for whole nanoparticles were found to be rather sensitive to the exact density functional used³¹ because of the well-known issue^32,33 of TD-DFT where charge-transfer excitations are spuriously stabilised with respect to local, i.e. non-charge-transfer, excitations. Well-chosen density functionals with the optimal amount of exact exchange can reproduce the key features of the experimental spectra of magnesium oxide nanoparticles: the red shift with respect to the bulk and the intensity change for the diffuse reflection peaks when changing particle size,³¹ but the strong dependency on the amount of exact exchange makes these calculations more empirical than desirable. TD-DFT calculations using embedded cluster calculations^23–26 where only a region, e.g. a corner, of the nanoparticle is described explicitly using TD-DFT and the effect of the rest of the particle on this region is described in terms of classical point charges appear to be less sensitive to the functional choice, perhaps because many potential charge-transfer excitations, e.g. from oxygen corner atoms to magnesium corner atoms, are by definition absent in embedded cluster models.³¹ It is however difficult to explicitly study the effect of particle size in embedded cluster calculations. An additional complication when using TD-DFT is that the optical gap and the UV-vis spectra in general are not treated on the same footing as the particle's electronic properties. The highest occupied and lowest unoccupied quasiparticle states of a particle and its fundamental gap can in principle be calculated within the framework of ground state density functional theory (DFT) in two different ways, from the Kohn–Sham (KS) orbital energies or by using ΔDFT. In the former case, the highest occupied and lowest unoccupied quasiparticle states map on to the highest occupied and lowest unoccupied KS orbitals and the fundamental gap on to the energy gap between these two orbitals, the KS gap. In the latter case the energy of the highest occupied quasiparticle state is calculated from the difference in total energy between the neutral particle and the particle with one electron less, that of the lowest unoccupied quasiparticle state from the total energy difference between the neutral particle and the particle with an extra electron, and the fundamental gap from the difference in energy between the lowest unoccupied and highest occupied quasiparticle states. The ΔDFT approach is preferred as it can be shown that the KS gap, at least for pure density functionals, behaves more like the optical than the fundamental gap because the KS unoccupied orbitals feel the same field of N–1 electrons as the KS occupied orbitals instead of the correct N electrons.³⁴ However, regardless, it is not a given that the optimal density functional for calculating the spectra and optical gap values of particles is also optimal for calculating the particles’ electronic properties. This is especially critical for properties such as the exciton binding energy, the difference between the fundamental and optical gap and a measure of how strongly excitons are bound (see Fig. 1), which span both worlds. ΔDFT predictions of the highest occupied and lowest unoccupied quasiparticle energies of MgO particles, including particles with defects or in the presence of grain boundaries, have previously been reported by Shluger and co-workers based on embedded cluster calculations.^35–37

Here many-body perturbation theory, in the form of solving Hedin's GW equations^38–40 followed by the Bethe–Salpeter equation,^41–43 is used to calculate the optical and electronic properties of cuboidal MgO rocksalt nanoparticles, see Fig. 2, rather than (TD-)DFT. While computationally considerably more expensive than (TD-)DFT, GW-BSE has the advantage that it treats the optical and electronic properties on a similar footing and that application of partial self-consistency in the GW part of the calculation, evGW, removes most of the dependency on the specific density functional used in the underlying DFT calculation. Using GW-BSE the effect of particle size on the optical and fundamental gap of MgO nanoparticles, the localisation of the quasiparticle and excited state, and the excitonic character of the latter is explored in order to obtain an atomistic scale explanation of the differences between the nanoparticle properties and those of the bulk. By performing calculations on whole nanoparticles rather than embedded cluster calculations it is possible to explore the effect of the particle-size directly, as well as the interplay between different sites on which the excited state or quasiparticles can localise. The results of these calculations are not only relevant to understanding the properties of MgO nanoparticles but also lay the groundwork for future work on (rocksalt) nanoparticles of other materials.

Fig. 2 Structures of some of the cuboidal particles studied. The cubes (MgO)₄ (A), (MgO)₃₂ (B) and (MgO)₁₀₈ (C), as well as the cuboids (MgO)₁₈ (D), (MgO)₂₄ (E), (MgO)₆₄ (F) and (MgO)₉₀ (G).

Methodology

The geometry of the nanoparticles was optimised in DFT calculations, using the B3LYP^44–47 density functional in combination with the D3(BJ)^48,49 dispersion correction by Grimme and co-workers and either the def2-SVP or def2-TZVPP basis-set.⁵⁰ During the geometry optimisation the symmetry of the nanoparticles was fixed and, for the smaller particles, up to and including (MgO)₃₂, frequency calculations were performed to verify that the optimised structures correspond to minima.

Single-shot G₀W₀, eigenvalue-only self-consistent GW (evGW) and quasiparticle self-consistent (qsGW) calculations, as implemented by Holzer, van Setten, Klopper and co-workers in Turbomole,^51–53 were performed on the DFT optimised structures, starting from B3LYP orbitals and in selected cases PBE⁵⁴ orbitals. These calculations used either the def2-SVP or def2-TZVPP basis-set (and in selected cases the def2-QZVPP and aug-cc-pVTZ basis-sets) and one of two GW implementations that differ in how the self-energy is obtained; in terms of a spectral representation (SR) or by analytical continuation (AC). The GW calculations using the spectral representation are the most computationally expensive, scaling as N⁶, while the analytical continuation calculations are more computationally tractable, scaling as N⁴. In the case of analytical continuation only the highest occupied and lowest unoccupied quasiparticle states are explicitly calculated with GW and the rest of the orbitals simply shifted. The results of the different GW calculations are used as input for solving the BSE, again as implemented in Turbomole,⁵⁵ to obtain excitation energies and oscillator strength values. The character of the BSE excited-states is finally analysed in terms of the most prominent natural transition orbitals.⁵⁶ The same basis-sets are generally used for the geometry optimisation and the BSE-GW calculations, except where stated to the contrary.

For selected particles the lowest excitation energies are also calculated with LR-CCSD coupled-cluster theory on top of a Hartree–Fock ground-state. These correlated wavefunction calculations use either the def2-TZVPP or def2-QZVPP basis-set and are performed as single-point calculations on the DFT optimised geometry.

All calculations were performed using version 7.5 of the Turbomole code⁵⁷ and used a tight integration grid (m5) and tight SCF convergence criteria (scftol and denconv 1 × 10⁻⁷). All GW and BSE calculations additionally used the RI-K approximation and use of symmetry was limited to Abelian point groups. The GW and BSE calculations for (MgO)₄, (MgO)₃₂ and (MgO)₁₀₈, as well as (CaO)₃₂ and (SrO)₃₂, all of which have T_d symmetry, were hence performed in the D₂ point group instead.

Results

(MgO)₄ and (MgO)₃₂

First, the effect of the different GW approximations and implementations is studied by performing calculations on the smallest two perfect cubes, (MgO)₄ and (MgO)₃₂. Table 1 and 2 give the highest occupied and lowest unoccupied quasiparticle energies, fundamental gap, optical gap and exciton binding energy values predicted by the different method combinations for the two particles. Concentrating first on the effect of the basis-set, with increasing basis-set size the highest occupied and lowest unoccupied quasiparticle states both move to deeper, more negative, values, while the fundamental and optical gap increase and the exciton binding energy more or less remains the same. Generally, as would be expected, the shift when going from the triple-zeta def2-TZVPP to the quadruple-zeta def2-QZVPP basis-set is smaller than when going from def2-SVP to def2-TZVPP, except for the lowest unoccupied quasiparticle state, for which the shift is similar. A calculation using the augmented Dunning aug-cc-pVTZ basis-set suggests that the effect of adding additional diffuse basis functions is minor.

Table 1 Highest occupied (–IP) and lowest unoccupied (–EA) quasiparticle states, fundamental gap (Δ_F), optical gap (Δ_O) and exciton binding energy (EBE) values of (MgO)₄ as calculated by the different method combinations (TZVPP = def2-TZVPP, accTZ = aug-cc-pVTZ, QZVPP = def2-QZVPP, SVP = def2-SVP). All calculations using the def2-TZVPP optimised geometry

	G 0 W 0					evGW
	–IP	–EA	Δ F	Δ O	EBE	–IP	–EA	Δ F	Δ O	EBE
SR/TZVPP	−7.807	−0.518	7.29	2.731	4.56	−8.534	−0.287	8.25	3.675	4.57
AC/TZVPP	−7.823	−0.513	7.31	2.770	4.54	−8.556	−0.291	8.27	3.706	4.56
SR/accTZ	−7.868	−0.645	7.22	2.658	4.56	−8.594	−0.439	8.16	3.565	4.59
SR/QZVPP	−8.028	−0.645	7.38	2.831	4.55	−8.790	−0.430	8.36	3.784	4.58
SR/SVP	−7.452	−0.385	7.07	2.491	4.58	−8.137	−0.145	7.99	3.405	4.59
AC/SVP	−7.465	−0.378	7.09	2.530	4.56	−8.142	−0.146	8.00	3.422	4.57

---

Table 2 Highest occupied (–IP) and lowest unoccupied (–EA) quasiparticle states, fundamental gap (Δ_F), optical gap (Δ_O) and exciton binding energy (EBE) values of (MgO)₃₂ as calculated by the different method combinations (TZVPP = def2-TZVPP, SVP = def2-SVP). See Table S1 in the ESI for BSE/G₀W₀(AC)/def2-TZVPP data starting from PBE rather than B3LYP orbitals. All calculations using the def2-TZVPP optimised geometry

	G 0 W 0					evGW
	–IP	–EA	Δ F	Δ O	EBE	–IP	–EA	Δ F	Δ O	EBE
SR/TZVPP	−7.320	−0.365	6.96	3.710	3.24	−7.975	−0.145	7.83	4.538	3.29
AC/TZVPP	−7.333	−0.361	6.97	3.810	3.14	−8.009	−0.152	7.86	4.680	3.18
SR/SVP	−6.989	−0.172	6.82	3.531	3.29	−7.602	0.057	7.66	4.320	3.34
AC/SVP	−7.001	−0.167	6.83	3.691	3.14	−7.618	0.051	7.67	4.494	3.18

---

Second, the effect of the different GW approximations and implementations is considered. Going from G₀W₀ to evGW the highest occupied quasiparticle state moves to considerably deeper, more negative, values, the lowest unoccupied quasiparticle state to noticeably more shallow, less negative, values, and the fundamental and optical gaps increase significantly, while the exciton binding energy stays essentially the same. In contrast, as expected based on the literature, the variation of the results calculated between the different GW implementations is small. Similarly, the effect of going from evGW to full quasiparticle self-consistent qsGW is small other than for the optical gap, which increases by ∼0.3 eV, and the exciton binding energy values, which decrease by a similar amount.

The optical gap of the (MgO)₄ particles was also calculated using coupled-cluster theory by LR-CCSD calculations. LR-CCSD predicts optical gap values of 3.90 eV and 3.98 eV when using the def2-TZVPP and def2-QZVPP basis-sets, respectively. Comparing these values to the results in Table 1 shows that BSE/G₀W₀ calculations irrespective of the basis-set used significantly underestimate the optical gap relative to LR-CCSD. In contrast, the BSE/evGW optical gap values lie much closer to their LR-CCSD counterparts while BSE/qsGW essentially predicts the same values as LR-CCSD. It should be noted here that both the GW and LR-CCSD calculations ignore vibronic and zero-point motion effects and that as such this is a fair comparison but that the true experimental gap likely will be smaller as a result of such effects.

Based on the comparison with LR-CCSD, BSE/qsGW/def2-QZVPP would be the preferred method to study the electronic and optical properties of the MgO nanoparticles. However, that is in practice not tractable if one wants to study a large number of relatively large particles as the cost of the calculations scales strongly with the basis-set size and qsGW is only implemented in Turbomole in combination with the most computationally expensive spectral representation of GW. Therefore, in the remainder mostly G₀W₀ and evGW calculations will be presented, including calculations with the def2-SVP basis-set. The effect of the basis-set while significant is smaller than that of the GW approximation used; the optical gap values predicted by BSE/evGW/def2-SVP lie much closer to those predicted by LR-CCSD than for BSE/G₀W₀/def2-QZVPP. More importantly perhaps, all method combinations show the same changes when going from (MgO)₄ to (MgO)₃₂ and for each of the particles all method combinations predict very similar exciton binding energy values and hence a consistent balance between the fundamental and optical gaps.

Change in the quasiparticle state energies and optical gap with the particle size

Table 3 gives the highest occupied and lowest unoccupied quasiparticle energies, fundamental gap, optical gap and exciton binding energy values predicted by BSE/G₀W₀(AC)/def2-SVP and BSE/evGW(AC)/def2-SVP for a series of cubic and cuboid MgO nanoparticles. Data is shown for (MgO)₄, the n × 4 × 4 family, including (MgO)₃₂, and the n × 5 × 5 family, which includes (MgO)₁₀₈. Please note that in contrast to the data in Tables 1 and 2 the geometries of the nanoparticles in this case have been optimised using the same def2-SVP basis-set as used for the BSE/GW calculations.

Table 3 Highest occupied (–IP) and lowest unoccupied (–EA) quasiparticle states, fundamental gap (Δ_F), optical gap (Δ_O) and exciton binding energy (EBE) values of the different cuboidal nanoparticles as predicted using BSE/G₀W₀(AC)/def2-SVP and BSE/evGW(AC)/def2-SVP

MgO	G 0 W 0					evGW
	–IP	–EA	Δ F	Δ O	EBE	–IP	–EA	Δ F	Δ O	EBE
4 (2 × 2 × 2)	−7.311	−0.416	6.90	2.362	4.53	−7.984	−0.181	7.80	3.253	4.55
24 (3 × 4 × 4)	−6.802	−0.363	6.44	3.574	2.86	−7.429	−0.139	7.29	4.395	2.90
32 (4 × 4 × 4)	−6.904	−0.209	6.70	3.599	3.10	−7.524	0.015	7.54	4.409	3.13
40 (5 × 4 × 4)	−6.860	−0.229	6.63	3.601	3.03	−7.476	−0.008	7.47	4.403	3.06
48 (6 × 4 × 4)	−6.863	−0.200	6.66	3.604	3.06	−7.479	0.023	7.50	4.407	3.09
54 (4 × 6 × 6)	−6.535	−0.532	6.00	3.626	2.38	−7.160	−0.306	6.85	4.441	2.41
56 (7 × 4 × 4)	−6.853	−0.198	6.66	3.606	3.05	−7.468	0.025	7.49	4.407	3.09
64 (8 × 4 × 4)	−6.854	−0.189	6.67	3.609	3.06	−7.469	0.035	7.50	4.412	3.09
72 (4 × 6 × 6)	−6.823	−0.206	6.62	3.618	3.00	−7.434	0.017	7.45	4.415	3.04
90 (5 × 6 × 6)	−6.650	−0.340	6.31	3.607	2.70	−7.262	−0.119	7.14	4.402	2.74
108 (6 × 6 × 6)	−6.703	−0.246	6.46	3.597	2.86	−7.313	−0.022	7.29	4.392	2.90

---

Firstly, concentrating on the optical gap values, it can be observed that all particles studied, bar (MgO)₄, have essentially the same optical gap value of 3.6 eV (G₀W₀) or 4.1 eV (evGW). Analysis of the responsible excitation in terms of the most significant natural transition orbitals shows that for all these particles this involves an excitation where an electron gets excited from the 3-coordinated oxygen corner atoms to the immediately adjacent 4-coordinated magnesium edge atoms (see Fig. 3A). The localised nature of the excitation and the fact that the surface motif responsible is present in all cuboid particles where all edges are at least two unit-cell lengths probably explains the absence of variation in the optical gap with the particle size.

Fig. 3 Leading occupied (A, left) and unoccupied (A, right) natural transition orbitals for the lowest excitation of (MgO)₃₂ and the highest occupied (B, left) and lowest unoccupied (B, right) Kohn–Sham orbitals for the same particle. As the calculation was performed using the D₂ instead of the T_d point group, the triply degenerate T₂ excited state is described as a triplet of excited states of B₁, B₂ and B₃ symmetry, the natural transition orbitals of only one are shown in (A). Similarly (B, left) is one of three degenerate orbitals.

In contrast to the optical gap, the quasiparticle state energies and by extension also the fundamental gap do change with the particle size, even if the picture is confusing. Focussing first on the cubes: (MgO)₄, (MgO)₃₂ and (MgO)₁₀₈, it can be observed that the highest occupied quasiparticle state consistently moves to less negative, shallower, values. The lowest unoccupied quasiparticle state also moves to less negative, shallower, values when going from (MgO)₄ to (MgO)₃₂ but then moves to slightly more negative, deeper, values when going to (MgO)₁₀₈. The fundamental gap, finally, consistently gets smaller with increasing edge length and particle size.

For the cuboid n × 4 × 4 and n × 5 × 5 families, where n is even, increasing the length of one of the edges, e.g. going from (MgO)₃₂ to (MgO)₄₈, shifts the highest occupied quasiparticle state to less negative values, and decreasing the length of one of the edges, e.g. going from (MgO)₁₀₈ to (MgO)₇₂, shifts the highest occupied quasiparticle state to more negative values. The lowest unoccupied quasiparticle state shifts to less negative values with increasing edge length for the n × 3 × 3 family but, just like for the cubes, shifts to more negative values for the n × 5 × 5 family. For the n is odd cuboids, which differ from the cubes and the n is even cuboids in the fact that the corner atoms of the edge are the same (e.g. both oxygen atoms) rather than different, similar trends can be observed but the absolute values appear shifted. Just as for the cubes the fundamental gap for the different cuboid families appears to decrease with the particle size and edge length. For the highest occupied and lowest unoccupied quasiparticle states and the fundamental gap, finally, the effect of increasing the edge length appears to decrease in magnitude when one edge becomes much longer than the other two.

While the lowest excitation corresponding to the optical gap for all particles involves, as discussed above, the 3-coordinated oxygen corner atoms and the immediately adjacent 4-coordinated magnesium edge atoms, the ground-state Kohn–Sham orbitals from DFT corresponding to the highest occupied and lowest unoccupied quasiparticle states for all cubic and cuboid particles considered are localised on the 3-coordinated oxygen atoms, with minor contributions of the oxygen atoms on the edge or diagonal between these 3-coordinated oxygen atoms, and 3-coordinated magnesium atoms, respectively (see Fig. 3B). The fact that in the lowest excitation the electron gets excited from 4-coordinated magnesium edge atoms adjacent to the 3-coordinated oxygen corner atoms rather than from the 3-coordinated magnesium corner atoms combined with the fact that the optical gap is much smaller than the fundamental gap for all particles suggests that this excitation is excitonic in character.

Cuboid MgO particles with odd-numbered faces

Table 4 gives the highest occupied and lowest unoccupied quasiparticle energies, fundamental gap, optical gap and exciton binding energy values predicted by BSE/G₀W₀(AC)/def2-SVP and BSE/evGW(AC)/def2-SVP for a series of cuboid MgO nanoparticles of which two of the faces have an odd number of atoms. The same results calculated with def2-TZVPP for the smallest one ((MgO)₁₈) can be found in Table S2 in the ESI.† In the previous (TD-)DFT study of MgO nanoparticles it was noted that these odd-numbered faces behaved as if polar, even if infinitely extended (100) surfaces are not polar in the conventional sense.³¹ This polarity is the direct result of the particles exhibiting odd-membered faces. These particles can be thought of as stacking sequences of charged layers with an odd number of atoms, where the odd-menbered faces of the particle are the outer most layers of the stack. The layers contain alternatingly either one more oxygen atom or one more magnesium atom, alternating [Mg₅O₄]²⁺ and [Mg₄O₅]²⁻ layers in the case of the specific particles studied here. This alternation of charged layers gives rise to a very large dipole moment along the stacking axis, normal to the odd-membered faces (17.3 Debye and 32.6 Debye for (MgO)₁₈ and (MgO)₂₇, respectively), with the magnitude of the dipole increasing with the particle dimension along that axis. There is an analogy to so-called Tasker type 3 surfaces⁵⁸ other than in that case the infinitely extended surfaces are inherently polar and here they are not. This polarisation in the ground state goes together with a reduction in the optical and fundamental gap of these particles relative to cubes and cuboidal particles lacking these odd-membered faces, where the size of both gaps decreases with the particle dimension along the axis of the particle perpendicular to the odd-membered faces. Analysis of the ground state orbitals from DFT and the most significant natural transition orbitals from BSE for (MgO)₂₇ clearly shows the polarisation. The ground state orbital corresponding to the highest occupied quasiparticle state is localised on the central oxygen atom and the four oxygen corner atoms of the oxygen-rich odd-membered face and the orbital for the lowest unoccupied quasiparticle state is localised over the four magnesium corner atoms and the central magnesium atom of the magnesium-rich odd-membered face, while the most significant natural transition orbitals for the optical gap correspond to excitation of an electron from the oxygen atoms of the oxygen-rich odd membered face to the magnesium atoms of the magnesium rich face.

Table 4 Highest occupied (–IP) and lowest unoccupied (–EA) quasiparticle states, fundamental gap (Δ_F), optical gap (Δ_O) and exciton binding energy (EBE) values of the different cuboidal nanoparticles with odd-membered faces as predicted using BSE/G₀W₀(AC)/def2-SVP and BSE/evGW(AC)/def2-SVP

MgO	G 0 W 0					evGW
	–IP	–EA	Δ F	Δ O	EBE	–IP	–EA	Δ F	Δ O	EBE
18 (3 × 3 × 3)	−6.362	−0.772	5.59	3.278	2.31	−6.998	−0.548	6.45	4.127	2.32
27 (4 × 3 × 3)	−5.817	−1.225	4.59	3.082	1.51	−6.451	−0.997	5.45	3.950	1.50

---

While particles with odd-membered faces larger than (MgO)₂₇ were not considered here, the data suggests that for very large particle dimensions the fundamental and optical gaps of such particles might go to zero with the particles becoming metallic. However, as discussed below this situation is unlikely to be ever encountered in experiment.

Optical spectra of cubic MgO particles

Fig. 4 shows the vertical excitation spectrum of (MgO)₃₂ as predicted using BSE/evGW(SR)/def2-TZVPP, as well as the experimental UV-vis spectrum of 3 nm MgO particles¹⁰ measured by Stankic and co-workers. Despite the roughly four times difference in size there is a good match between the predicted and experimental spectrum, in line with the observation above that the energy of the lowest exciton is the same for all cuboid particles with even faces and all edges corresponding to at least two unit-cell lengths. All excitations shown in Fig. 4 are 4.6–1.9 eV smaller than the evGW(SR)/def2-TZVPP predicted fundamental gap, suggesting that not only the lowest energy/longest wavelength excitation but all excitations to at least 200 nm are excitonic in character.

Fig. 4 The vertical excitation spectrum of (MgO)₃₂ as predicted using BSE/evGW(SR)/def2-TZVPP (red line) and the experimental measured reflection spectrum of 3 nm MgO particles (blue line). Experimental data taken from ref. 10.

The bright excitations were analysed in terms of the most important natural transition orbitals. The lowest bright excitation at 4.54 eV or 273 nm, responsible for the most red-shifted broad peak, is, as discussed above, due to excitation of an electron from the 3-coordinated oxygen corner atoms to the immediately adjacent 4-coordinated magnesium edge atoms (see Fig. 3A). The shoulder at 240 nm is the sum of two bright excitations. The bright excitation at 5.12 eV or 242 nm corresponds to excitation of an electron from the 4-coordinated oxygen edge atoms to 3-coordinated corner magnesium atoms (see Fig. 5A), while the bright excitation at 5.17 or 240 nm corresponds just like the lowest bright excitation to excitation of an electron from the 3-coordinated oxygen corner atoms to the adjacent 4-coordinated magnesium edge atoms (see Fig. 5B). The two main contributions to the strongest peak at 220 nm are an excitation at 5.52 eV or 224 nm, corresponding just like the 5.12 eV or 242 nm excitation to excitation of an electron from the 4-coordinated oxygen edge atoms to 3-coordinated corner magnesium atoms (see Fig. 5C), and an excitation at 5.59 eV or 222 nm, which involves similar excitation of an electron from now both the 4-coordinated edge and 6-coordinated bulk oxygen atoms to the 3-coordinated corner magnesium atoms (see Fig. 5D). Higher-energy shorter-wavelength bright excitations up to 200 nm display increased contributions of 5- and 6-coordinated oxygen atoms and 4-coordinated magnesium atoms but the 3-/4-coordinated oxygen atoms and 3-coordinated magnesium atoms remain the most significant contributors.

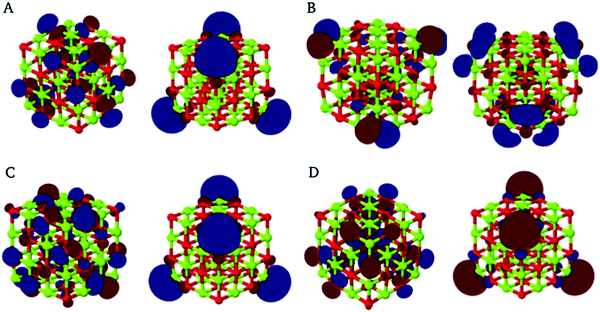Fig. 5 Leading natural transition orbitals for the 5.12 (A), 5.17 (B), 5.52 (C) and 5.59 (D) eV bright excitations of (MgO)₃₂. Similar to Fig. 3 only one of the three degenerate leading natural transition orbitals for each of the excitations is shown.

Compared to the previous TD-DFT calculations³¹ using the range-separated CAM-B3LYP functional, the main difference is the predicted character of the excitations responsible for the 240 nm shoulder. TD-CAM-BLYP predicts that one of the excitations contributing to that shoulder corresponds to excitation of an electron from a 3-coordinated corner oxygen atom to a 3-coordinated corner magnesium atom, something that is not observed in the BSE/evGW predicted spectra to much higher excitation energies/shorter wavelengths.

Beyond MgO

As discussed in the introduction, nanoparticles of CaO and SrO grown through chemical vapour deposition show experimentally the same red-shift relative to the bulk in the UV-vis reflection spectra as MgO nanoparticles. To probe if nanoparticles of such other rocksalt materials display the same physics as that discussed above for MgO nanoparticles, the optical and electronic properties of 4 × 4 × 4 (CaO)₃₂ and (SrO)₃₂ cubes were calculated using BSE/G₀W₀ and BSE/evGW, see Table 5.

Table 5 Highest occupied (–IP) and lowest unoccupied (–EA) quasiparticle states, fundamental gap (Δ_F), optical gap (Δ_O) and exciton binding energy (EBE) values of (CaO)₃₂ and (SrO)₃₂ cubes predicted using BSE/G₀W₀(AC)/def2-TZVPP and BSE/evGW(AC)/def2-TZVPP

	G 0 W 0					evGW
	–IP	–EA	Δ F	Δ O	EBE	–IP	–EA	Δ F	Δ O	EBE
a The lowest excited-state for (CaO)32 as calculated using BSE/evGW(AC)/def2-TZVPP is symmetry forbidden. The 3.736 eV excitation is the lowest optically allowed excitation, second lowest overall. The lowest BSE/evGW(AC)/def2-TZVPP excitation belongs to the A irrep for Td and has an excitation energy of 3.634 eV and an EBE value of 2.85 eV.
CaO (4 × 4 × 4)	−5.810	−0.015	5.80	3.079	2.72	−6.363	0.120	6.48	3.736^a	2.75
SrO (4 × 4 × 4)	−5.270	−0.042	5.23	2.640	2.59	−5.805	0.086	5.89	3.278	2.61

---

As can be seen from Table 5, the lowest excitations of these CaO and SrO particles are just as for their MgO counterparts excitonic in character with predicted exciton binding energies of more than 2 eV. Visualisation of the natural transition orbitals for these particles also shows that, just as in the case of MgO particles, the lowest energy excitons are strongly localised around the corner atoms, see Fig. S1 in the ESI.† Finally, the predicted optical gap values are comparable to experimentally measured lowest excitation energies of CaO (3.5 eV)¹¹ and SrO (3.7 eV)¹² nanoparticles.

Discussion

The BSE/evGW calculations show in line with the experimental work by Stankic and others that the optical gap of MgO nanoparticles is much smaller than that of the bulk and that such particles absorb light in the middle ultraviolet, 200–300 nm, where the bulk does not. The excitations responsible for the light absorption in that wavelength range are all predicted to be excitonic in character as the predicted fundamental gap of all particles considered, excluding those with odd-membered faces, is larger than 200 nm. The lowest exited-state in all cases bar the smallest nanoparticles corresponds to a well-localised exciton involving the 3-coordinated oxygen corner atoms and their immediate 4-coordinated magnesium atoms, where the optical gap does not change with the particle size. These MgO nanoparticles hence, as suggested by previous embedded cluster calculations discussed above, behave as defective insulators, where light absorption at longer wavelengths/lower energies than the bulk is due to excitations of electrons between what are essentially surface defects, rather than quantum dots.

As discussed above the quasiparticle states and the fundamental gap in contrast to the optical gap do change with the particle size. The relevant orbitals are again relatively localised but more delocalised than the excited state associated with the optical gap. The origin of the variation of these electronic properties with the particle size is unknown. Perhaps more interesting is the fact that the nature of the variation is unexpected. The highest occupied quasiparticle state is found to move to shallower values and the lowest unoccupied quasiparticle state to deeper values and hence the fundamental gap decreases with the particle size. The bulk fundamental gap cannot be calculated with the same exact set-up as used here for the particles. However, literature predictions of the fundamental gap of bulk MgO using G₀W₀ range from 7.5–8 eV^59–63 and for qsGW a value of 8.69 eV has been reported by Lambrecht and co-workers⁶⁴ (in all cases, like the GW calculations here, ignoring vibronic and zero point motion effects, the inclusion of the former brings the qsGW values for the bulk closer to the experimental value of 7.8 eV^65,66). Comparing these bulk values from the literature to the G₀W₀ and evGW ones reported here for the nanoparticles, than (i) the nanoparticles have smaller fundamental gaps than bulk MgO, (ii) the nanoparticle highest occupied and lowest unoccupied quasiparticle states likely lie within the fundamental gap of bulk MgO, and (iii) upon increasing the particle size the fundamental gap appears to diverge away from the bulk value rather than converge towards it. While these observations are by definition based on a limited range of particle sizes, e.g. the next cube has 232 MgO formula units and is hence for the moment beyond the horizon of what can be achieved with the GW implementation, it suggests that even for (macroscopically) large particles the corner atoms fix the highest occupied and lowest unoccupied quasiparticle states and the fundamental gap. That is even if this is experimentally unobservable by photoelectron spectroscopy due the relatively very small number of such corner atoms in large particles.

It turns out to be impossible to predict the (MgO)₁₀₈ spectrum using BSE/evGW, even when using the def2-SVP basis-set, due to the very large memory and disk-space requirements to calculate more than just the lowest excited states for this particle. However, it stands to reason that the observed trend in the intensities of the peaks in the experimental reflection spectra, where going from 3 to 10 nm particles the relative intensity of the 270 and 240 nm shoulders/peaks decreases and that of the 220 nm peak increases, finds its origin in the fact that the most red-shifted peaks involve excitations localised on exclusively 3-coordinated corner and 4-coordinated edge atoms while the 220 nm peak also involves 5-coordinated terrace and 6-coordinated bulk atoms and that when increasing the particle size the number of corner and edge atoms relative to surface and bulk atoms decreases. For the same reason and in analogy to the discussion above for the fundamental gap, even for macroscopically large MgO particles the true optical gap would likely be the same as that predicted here for nanoparticles but the optical gap observed in experiment would probably be the bulk value.

The exciton binding energy decreases with the particle size, driven by the reduction in the fundamental gap with the particle size. In the case of pure cubes, extrapolation to the infinite particle limit by plotting the BSE/evGW/def2-SVP exciton binding energy of the lowest energy exciton of the three cubes against the inverse of their edge lengths yields a value of 2.4 eV. This value is more than an order of magnitude larger than the binding energy of the n = 1 bulk exciton, 80 meV,^65,66 which is in line with the former probably⁶⁷ being a Wannier–Mott exciton while the lowest exciton in the nanoparticles, as discussed, is much more localised and hence more like a Frenkel exciton.

The nanoparticles with odd-membered faces have rather different optical and electronic properties relative to their counterparts that only have even-membered faces. However, particles displaying such odd-membered surfaces are unlikely to be observed in experiment as the same ground-state dipole moment that gives rise to these different optical and electronic properties also destabilises them energetically. Previous global optimisation studies find that while for (MgO)₁₈ the cuboidal rocksalt structure is still the predicted global minimum, as it is for particles with only even-membered faces (i.e. (MgO)₂₄, (MgO)₃₂ and (MgO)₄₀), for (MgO)₂₇ a reconstructed cuboidal structure with a much reduce ground-state dipole moment (0.3 instead of 32.6 Debye) is found to be more stable²¹ (see Fig. 6). As expected this reconstructed (MgO)₂₇ particle also has a larger optical gap (4.48 eV instead of 3.95 eV when calculated with BSE/evGW(AC)/def2-SVP, see Table S3 in the ESI†), which is similar to that of the cubic particles with even-membered faces. In analogy to classically polar surfaces, these particles with odd-membered surfaces can thus be thought to reconstruct to eliminate the large dipole moment and in the process also eliminate their more out of kilter optical properties.

Fig. 6 Structure of the alternative structure considered for (MgO)₂₇, the global minimum as proposed by Dixon and co-workers.²¹

Finally, while this paper studies primarily MgO nanoparticles, the same physics is likely in play in nanoparticles of other oxides. Indeed, as mentioned in the introduction, nanoparticles of CaO and SrO have experimentally been observed to display the same red-shift relative to the bulk as MgO nanoparticles and the BSE/GW calculations discussed above confirm that for these materials the lowest energy excitations are excitonic in nature and strongly localised around the corner atoms of the nanoparticles. Comparing the BSE/evGW predicted optical gap for the nanoparticles with the experimental excitation energy of the lowest exciton peak in bulk CaO (7 eV)⁶⁸ and SrO (5.7 eV)^69–71 confirms the bulk to nanoparticle red-shift for these materials. As noted above for MgO, an exact one-to-one comparison to properties predicted for the bulk is difficult, but the BSE/G₀W₀/PBE optical gap values predicted for the CaO and SrO nanoparticles (see Table S4, ESI†) are also indeed significantly smaller than those extracted from the results of periodic BSE/G₀W₀/PBE calculations from the literature.^62,72 Interestingly, a comparison of the fundamental gap predicted for bulk CaO^62,73 and SrO,^72,73 using G₀W₀/PBE, and the equivalent fundamental gap of the nanoparticles shows that they are more similar than for MgO, especially in the case of SrO, for which the G₀W₀/PBE fundamental gap (4.85 eV) is virtually identical to that predicted for the bulk. While the lowest energy excitons for nanoparticles of these materials remain clearly localised around the particles’ corner atoms and the optical properties are thus governed by the presence of these low-coordinated atoms, the highest occupied and lowest unoccupied quasiparticle states appear less tied down.

Conclusions

evGW-BSE calculations on realistic oxide nanoparticles such as those made from MgO are found to be computationally tractable and using such calculations it is demonstrated that the optical and electronic properties of MgO nanoparticles are governed by the presence of low-coordinated atoms on their surfaces, in other words surface defect states. States localised on these corner and edge atoms are responsible for the highest occupied and lowest unoccupied quasiparticle states, i.e. the ionisation potential and the electron affinity, of the particle, and thus the magnitude of the fundamental gap, as well as the lowest excited states and thus the size of the optical gap. As a result the optical gap of all cuboidal rocksalt MgO nanoparticles bar the absolute smallest and particles with odd membered faces is predicted to be essentially the same and to not vary with the particle size. By extrapolation it can be assumed that the same holds true for macroscopic MgO particles, even if this might be hard to observe experimentally due to the much smaller surface to volume ratio for such particles. The BSE/evGW spectrum predicted for (MgO)₃₂ agrees well with the experimental spectra for MgO nanoparticles reported in the literature.

Nanoparticles with odd membered faces are predicted to have reduced optical gaps and display large ground state dipole moments perpendicular to the odd membered faces. The presence of such large dipole moments destabilises these particles relative to particles that lack odd membered faces and hence they can be argued to reconstruct to reduce the dipole moments, akin to what happens in the case of polar surfaces.

Finally, calculations on CaO and SrO nanoparticles show that they display the same physics as MgO nanoparticles with the lowest energy excitations corresponding to excitons localised on the particles’ corners. Nanoparticles of MgO are thus not unique in having electronic and optical properties governed by surface states instead of quantum confinement effects. In fact, the behaviour observed for MgO appears typical of nanoparticles of all alkaline earth oxides and perhaps many other oxides.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Drs Uwe Hunlar, Christof Holzer, Johannes Lischner and Slavica Stankic are kindly acknowledged for discussion. The UK Engineering and Physical Sciences Research Council (EPSRC) is thanked for funding part of this work through grants EP/I004424/1 and EP/N004884/1.

References

1. A. L. Efros and L. E. Brus, Nanocrystal Quantum Dots: From Discovery to Modern Development, ACS Nano, 2021, 15, 6192–6210.
2. L. Brus, Electronic Wave Functions in Semiconductor Clusters: Experiment and Theory, J. Phys. Chem., 1986, 90, 2555–2560.
3. L. E. Brus, Electron–Electron and Electron-Hole Interactions in Small Semiconductor Crystallites: The Size Dependence of the Lowest Excited Electronic State, J. Chem. Phys., 1984, 80, 4403–4409.
4. W. W. Yu and X. Peng, Formation of High-Quality CdS and Other II–VI Semiconductor Nanocrystals in Noncoordinating Solvents: Tunable Reactivity of Monomers, Angew. Chem., Int. Ed., 2002, 41, 2368–2371.
5. C. B. Murray, D. J. Norris and M. G. Bawendi, Synthesis and Characterization of Nearly Monodisperse CdE (E = Sulfur, Selenium, Tellurium) Semiconductor Nanocrystallites, J. Am. Chem. Soc., 1993, 115, 8706–8715.
6. X. Peng, J. Wickham and A. P. Alivisatos, Kinetics of II-VI and III-V Colloidal Semiconductor Nanocrystal Growth:  “Focusing” of Size Distributions, J. Am. Chem. Soc., 1998, 120, 5343–5344.
7. L. Cademartiri, E. Montanari, G. Calestani, A. Migliori, A. Guagliardi and G. A. Ozin, Size-Dependent Extinction Coefficients of PbS Quantum Dots, J. Am. Chem. Soc., 2006, 128, 10337–10346.
8. M. A. Hines and G. D. Scholes, Colloidal PbS Nanocrystals with Size-Tunable near-Infrared Emission: Observation of Post-Synthesis Self-Narrowing of the Particle Size Distribution, Adv. Mater., 2003, 15, 1844–1849.
9. C. B. Murray, S. Sun, W. Gaschler, H. Doyle, T. A. Betley and C. R. Kagan, Colloidal Synthesis of Nanocrystals and Nanocrystal Superlattices, IBM J. Res. Dev., 2001, 45, 47–56.
10. S. Stankic, M. Müller, O. Diwald, M. Sterrer, E. Knözinger and J. Bernardi, Size-Dependent Optical Properties of MgO Nanocubes, Angew. Chem., Int. Ed., 2005, 44, 4917–4920.
11. S. Stankic, J. Bernardi, O. Diwald and E. Knözinger, Optical Surface Properties and Morphology of MgO and CaO Nanocrystals, J. Phys. Chem. B, 2006, 110, 13866–13871.
12. S. Stankic, J. Bernardi, O. Diwald and E. Knözinger, Photoexcitation of Local Surface Structures on Strontium Oxide Grains, J. Phys. Chem. C, 2007, 111, 8069–8074.
13. M. L. Cohen, P. J. Lin, D. M. Roessler and W. C. Walker, Ultraviolet Optical Properties and Electronic Band Structure of Magnesium Oxide, Phys. Rev., 1967, 155, 992–996.
14. D. M. Roessler and W. C. Walker, Spin-Orbit Splitting of the Gamma Exciton in MgO, Phys. Rev. Lett., 1966, 17, 319–320.
15. E. Spanó, S. Hamad and C. R. A. Catlow, Computational Evidence of Bubble ZnS Clusters, J. Phys. Chem. B, 2003, 107, 10337–10340.
16. E. Spanó, S. Hamad and C. R. A. Catlow, ZnS Bubble Clusters with Onion-Like Structures, Chem. Commun., 2004, 864–865.
17. S. Hamad, C. R. A. Catlow, E. Spanó, J. M. Matxain and J. M. Ugalde, Structure and Properties of ZnS Nanoclusters, J. Phys. Chem. B, 2005, 109, 2703–2709.
18. E. Sanville, A. Burnin and J. J. BelBruno, Experimental and Computational Study of Small (N = 1–16) Stoichiometric Zinc and Cadmium Chalcogenide Clusters, J. Phys. Chem. A, 2006, 110, 2378–2386.
19. M. A. Zwijnenburg, Optical Excitations in Stoichiometric Uncapped ZnS Nanostructures, Nanoscale, 2011, 3, 3780–3787.
20. C. Roberts and R. L. Johnston, Investigation of the Structures of MgO Clusters Using a Genetic Algorithm, Phys. Chem. Chem. Phys., 2001, 3, 5024–5034.
21. M. Chen, A. R. Felmy and D. A. Dixon, Structures and Stabilities of (MgO)_N Nanoclusters, J. Phys. Chem. A, 2014, 118, 3136–3146.
22. S. G. E. T. Escher, T. Lazauskas, M. A. Zwijnenburg and S. M. Woodley, Synthesis Target Structures for Alkaline Earth Oxide Clusters, Inorganics, 2018, 6, 29.
23. P. E. Trevisanutto, P. V. Sushko, A. L. Shluger, K. M. Beck, M. Henyk, A. G. Joly and W. P. Hess, A Mechanism of Photo-Induced Desorption of Oxygen Atoms from MgO Nano-Crystals, Surf. Sci., 2005, 593, 210–220.
24. M. Müller, S. Stankic, O. Diwald, E. Knözinger, P. V. Sushko, P. E. Trevisanutto and A. L. Shluger, Effect of Protons on the Optical Properties of Oxide Nanostructures, J. Am. Chem. Soc., 2007, 129, 12491–12496.
25. K. P. McKenna, D. Koller, A. Sternig, N. Siedl, N. Govind, P. V. Sushko and O. Diwald, Optical Properties of Nanocrystal Interfaces in Compressed MgO Nanopowders, ACS Nano, 2011, 5, 3003–3009.
26. A. Sternig, D. Koller, N. Siedl, O. Diwald and K. McKenna, Exciton Formation at Solid–Solid Interfaces: A Systematic Experimental and Ab Initio Study on Compressed MgO Nanopowders, J. Phys. Chem. C, 2012, 116, 10103–10112.
27. M.-C. Wu, C. M. Truong and D. W. Goodman, Electron-Energy-Loss-Spectroscopy Studies of Thermally Generated Defects in Pure and Lithium-Doped MgO(100) Films on Mo(100), Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 12688–12694.
28. A. Kolmakov, J. Stultz and D. W. Goodman, Characterization of Surface Defects on MgO Thin Films by Ultraviolet Photoelectron and Metastable Impact Electron Spectroscopies, J. Chem. Phys., 2000, 113, 7564–7570.
29. P. A. Cox and A. A. Williams, Surface Excitons on Ionic Crystals, Surf. Sci. Lett., 1986, 175, L782–L786.
30. M. Rohlfing, N.-P. Wang, P. Krüger and J. Pollmann, Image States and Excitons at Insulator Surfaces with Negative Electron Affinity, Phys. Rev. Lett., 2003, 91, 256802.
31. M. C. C. Wobbe, A. Kerridge and M. A. Zwijnenburg, Optical Excitation of MgO Nanoparticles; a Computational Perspective, Phys. Chem. Chem. Phys., 2014, 16, 22052–22061.
32. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation Energies in Density Functional Theory: An Evaluation and a Diagnostic Test, J. Chem. Phys., 2008, 128, 044118.
33. D. J. Tozer, R. D. Amos, N. C. Handy, B. O. Roos and L. Serrano-Andres, Does Density Functional Theory Contribute to the Understanding of Excited States of Unsaturated Organic Compounds?, Mol. Phys., 1999, 97, 859–868.
34. E. J. Baerends, O. V. Gritsenko and R. van Meer, The Kohn–Sham Gap, the Fundamental Gap and the Optical Gap: The Physical Meaning of Occupied and Virtual Kohn–Sham Orbital Energies, Phys. Chem. Chem. Phys., 2013, 15, 16408–16425.
35. P. V. Sushko, J. L. Gavartin and A. L. Shluger, Electronic Properties of Structural Defects at the MgO (001) Surface, J. Phys. Chem. B, 2002, 106, 2269–2276.
36. K. P. McKenna and A. L. Shluger, First-Principles Calculations of Defects near a Grain Boundary in MgO, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224116.
37. K. P. McKenna and A. L. Shluger, Electron and Hole Trapping in Polycrystalline Metal Oxide Materials, Proc. R. Soc. A, 2011, 467, 2043–2053.
38. L. Hedin, New Method for Calculating the One-Particle Green's Function with Application to the Electron-Gas Problem, Phys. Rev., 1965, 139, A796–A823.
39. F. Aryasetiawan and O. Gunnarsson, The GW method, Rep. Prog. Phys., 1998, 61, 237–312.
40. D. Golze, M. Dvorak and P. Rinke, The GW Compendium: A Practical Guide to Theoretical Photoemission Spectroscopy, Front. Chem., 2019, 7, 377.
41. E. E. Salpeter and H. A. Bethe, A Relativistic Equation for Bound-State Problems, Phys. Rev., 1951, 84, 1232–1242.
42. G. Strinati, Application of the Green's Functions Method to the Study of the Optical Properties of Semiconductors, La Rivista del Nuovo Cimento (1978-1999), 1988, 11, 1–86.
43. X. Blase, I. Duchemin, D. Jacquemin and P.-F. Loos, The Bethe–Salpeter Equation Formalism: From Physics to Chemistry, J. Phys. Chem. Lett., 2020, 11, 7371–7382.
44. S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58, 1200–1211.
45. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
46. A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652.
47. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627.
48. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
49. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
50. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
51. M. J. van Setten, F. Weigend and F. Evers, The GW-Method for Quantum Chemistry Applications: Theory and Implementation, J. Chem. Theory Comput., 2013, 9, 232–246.
52. X. Gui, C. Holzer and W. Klopper, Accuracy Assessment of GW Starting Points for Calculating Molecular Excitation Energies Using the Bethe–Salpeter Formalism, J. Chem. Theory Comput., 2018, 14, 2127–2136.
53. C. Holzer and W. Klopper, Ionized, Electron-Attached, and Excited States of Molecular Systems with Spin–Orbit Coupling: Two-Component GW and Bethe–Salpeter Implementations, J. Chem. Phys., 2019, 150, 204116.
54. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
55. K. Krause and W. Klopper, Implementation of the Bethe−Salpeter Equation in the Turbomole Program, J. Comput. Chem., 2017, 38, 383–388.
56. R. L. Martin, Natural Transition Orbitals, J. Chem. Phys., 2003, 118, 4775–4777.
57. S. G. Balasubramani, et al., Turbomole: Modular Program Suite for Ab Initio Quantum-Chemical and Condensed-Matter Simulations, J. Chem. Phys., 2020, 152, 184107.
58. P. W. Tasker, The Stability of Ionic Crystal Surfaces, J. Phys. C: Solid State Phys., 1979, 12, 4977–4984.
59. G. Cappellini, S. Bouette-Russo, B. Amadon, C. Noguera and F. Finocchi, Structural Properties and Quasiparticle Energies of Cubic SrO, MgO and SrTiO₃, J. Phys.: Condens. Matter, 2000, 12, 3671–3688.
60. A. Schleife, F. Fuchs, J. Furthmüller and F. Bechstedt, First-Principles Study of Ground- and Excited-State Properties of MgO, ZnO, and CdO Polymorphs, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245212.
61. P. Rinke, A. Schleife, E. Kioupakis, A. Janotti, C. Rödl, F. Bechstedt, M. Scheffler and C. G. Van de Walle, First-Principles Optical Spectra for F Centers in MgO, Phys. Rev. Lett., 2012, 108, 126404.
62. H. Nejatipour and M. Dadsetani, Excitonic Effects in the Optical Properties of Alkaline Earth Chalcogenides from First-Principles Calculations, Phys. Scr., 2015, 90, 085802.
63. W. Gao, W. Xia, X. Gao and P. Zhang, Speeding up GW Calculations to Meet the Challenge of Large Scale Quasiparticle Predictions, Sci. Rep., 2016, 6, 36849.
64. W. R. L. Lambrecht, C. Bhandari and M. van Schilfgaarde, Lattice Polarization Effects on the Screened Coulomb Interaction W of the GW Approximation, Phys. Rev. Mater., 2017, 1, 043802.
65. D. M. Roessler and W. C. Walker, Electronic Spectrum and Ultraviolet Optical Properties of Crystalline MgO, Phys. Rev., 1967, 159, 733–738.
66. R. Schmidt-Grund, A. Carstens, B. Rheinländer, D. Spemann, H. Hochmut, G. Zimmermann, M. Lorenz, M. Grundmann, C. M. Herzinger and M. Schubert, Refractive Indices and Band-Gap Properties of Rocksalt Mg_xZn₁−_XO (0.68 ≤ X ≤ 1), J. Appl. Phys., 2006, 99, 123701.
67. V. Begum; M. E. Gruner; C. Vorwerk; C. Draxl and R. Pentcheva, Theoretical Description of Optical and X-Ray Absorption Spectra of MgO Including Many-Body Effects, Phys. Rev. B, 2021, 103, 195128.
68. R. C. Whited and W. C. Walker, Exciton Spectra of CaO and MgO, Phys. Rev. Lett., 1969, 22, 1428–1430.
69. A. S. Rao and R. J. Kearney, Logarithmic Derivative Reflectance Spectra of BaO and SrO, Phys. Status Solidi B, 1979, 95, 243–250.
70. G. P. Summers, Optical Absorption and Emission near the Band Edge of SrO, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 5275–5279.
71. E. Feldbach, R. Kink, M. Kirm, A. Lushchik, C. Lushchik, A. Lôhmus, A. Maaroos and I. Martinson, Electronic Excitations and Uv Luminescence in SrO Crystals at 8 K, Chem. Phys. Lett., 1995, 241, 597–602.
72. C. Ma, T. Liu and Q. Chang, Study on the Electronic Structures and Optical Absorption of F Center in the SrO Crystal with G₀W₀–BSE, Comput. Theor. Chem., 2016, 1080, 79–83.
73. A. Riefer, F. Fuchs, C. Rödl, A. Schleife, F. Bechstedt and R. Goldhahn, Interplay of Excitonic Effects and Van Hove Singularities in Optical Spectra: Cao and AlN Polymorphs, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075218.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02683f

---