Open Access Article
Open Access ArticleCrucial impact of exchange between layers on temperature programmed desorption†
Tobias
Dickbreder
 *,
Ralf
Bechstein
and
Angelika
Kühnle
*,
Ralf
Bechstein
and
Angelika
Kühnle
Physical Chemistry I, Bielefeld University, Universitätsstraße 25, 33615 Bielefeld, Germany. E-mail: dickbreder@uni-bielefeld.de
First published on 6th August 2021
Abstract
Desorption of molecules from surfaces constitutes an elementary process that is fundamental in both natural and application-oriented fields, including dewetting, weathering and catalysis. A powerful method to investigate desorption processes is temperature-programmed desorption (TPD), which offers the potential to provide mechanistic insights into the desorption kinetics. Using TPD, the desorption order, the energy barrier as well as the entropy change upon desorption can be accessed. In the past, several analysis methods have been developed for TPD data. These methods have in common that they rely on the Polanyi–Wigner equation, which requires proposing a desorption mechanism with a single (or at least dominating) desorption path. For real systems, however, several coupled desorption paths can be easily envisioned, which cannot be disentangled. Here, we analyse the influence of exchange between the first and the second adsorbate layer on the desorption process. We present a kinetic model, in which molecules can desorb directly from the first layer or change into the second layer and desorb from there. Interestingly, considering this additional desorption pathway alters the desorption spectrum considerably, even if the transient second-layer occupation remains as small as 4 × 10−6 monolayers. We show that the impact of this layer exchange can be described by a modified Polanyi–Wigner equation. Our study demonstrates that layer exchange can crucially impact the TPD data.
1 Introduction
Desorption processes are omnipresent both in nature and technology. For example, desorption of molecules from solid surfaces governs dewetting and weathering in the environment.1 Likewise, desorption processes are fundamental in many industrial processes, including, e.g., catalysis.2 Consequently, the desorption of molecules from solid surfaces has been studied intensively to gain a detailed understanding of the involved elementary steps.3–15 A powerful technique for investigating desorption is temperature-programmed desorption (TPD).16,17 To perform a TPD experiment, molecules are deposited onto a cold sample kept in ultrahigh vacuum. Subsequently, the sample is heated with a given heating rate and the desorbing molecules are detected using a mass spectrometer. Despite being conceptually rather simple, the resulting desorption spectra are often challenging to analyse.18 Several analysis methods have been developed in the past. Starting from the simple relationship published by Redhead in 1962,19 the analysis procedures became increasingly elaborate when considering the leading edge analysis (also referred to as Habenschaden–Küppers method)20 and the complete analysis (also referred to as King's method or Taylor–Weinberg method).16,21 While these methods differ in the way the data are treated, they all rely on the Polanyi–Wigner equation (see eqn (1)), in which the rate of desorbing atoms or molecules rd per number of adsorption sites Nad is given by a pre-exponential factor ν, the coverage θ, the desorption order n, and an exponential term that includes the desorption energy barrier ΔEd, the temperature T, and Boltzmann's constant kB. A simple expression for the pre-exponential factor is given by the transition state theory as shown in eqn (2), where ΔSd is the entropy difference between the transition state and the adsorbed state, and h is Planck's constant.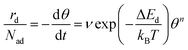 | (1) |
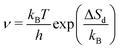 | (2) |
Based on the Polanyi–Wigner equation, the kinetic parameters of the desorption process, namely ΔEd, ΔSd and n, can be obtained. At this point, it is important to note that the Polanyi–Wigner equation only considers a single desorption path. Applying the above-mentioned analysis methods to a TPD measurement, thus, assumes that the investigated desorption process is a single process or – in case of several steps – that one step is dominating over the others. Whether this assumption is justified or not will surely require to consider the properties of the specific system of interest. However, in real systems desorption often involves coupled desorption pathways. For example, even if single-crystal surfaces are considered, an exchange between various adsorption positions like step edges, kink sites, and defects is possible. Moreover, molecules can jump from the first to the second layer and adopt adsorption positions in the second layer. Since adsorbates can typically form more than one layer, layer exchange is a rather common phenomenon. This leads to coupled desorption pathways if the barrier for molecules to jump into the second layer is comparable to (or smaller than) the desorption barrier. Such coupled desorption pathways can be addressed by a kinetic model as has been shown in various other cases in literature.12–15,22–31 Here, we evaluate the impact of this layer exchange on TPD data analysis using a generic kinetic model. To this end, we model the desorbing molecules (or atoms) on a support surface. The elementary processes such as desorption from the first (second) layer as well as layer exchange from the first (second) to the second (first) layer are described by their respective rate constants. Depending on the balance between the desorption barriers and the barriers for layer exchange, three different cases can be identified. If the barriers for layer exchange are (a) significantly higher than the barriers for desorption, the layer exchange is kinetically hindered. In this case, two independent desorption processes occur, manifesting in two desorption peaks that can be treated separately with the Polanyi–Wigner equation. Note, however, that in this case the common method to determine the coverage by observing the appearance of the second-layer peak fails. If the barriers for layer exchange are (b) similar to the barriers for desorption, the analysis of the kinetics becomes difficult as layer exchange sets in at the same temperature as desorption occurs. If the barriers for layer exchange are (c) small compared to the barriers for desorption, layer occupation is in quasi-equilibrium throughout the desorption process. In this case, second-layer occupation becomes important even for coverages as small as 4 × 10−6 monolayers (ML). The resulting TPD spectra differ significantly from a TPD curve as expected based on the Polanyi–Wigner equation. We show that this situation cannot be described correctly based on the Polanyi–Wigner equation. Instead, a correction is required that can be expressed by a simple modification of the Polanyi–Wigner equation.
The paper is organized as follows. In the next section, we describe the concept of the kinetic model. In Section 3 we present the results of the model and discuss consequences of the layer exchange and second-layer occupation on the TPD data analysis. We show that a modified Polanyi–Wigner equation can be derived that accounts for the effect of the layer exchange. We will conclude with the finding that exchange between layers can crucially impact TPD data.
2 Kinetic layer model for desorption
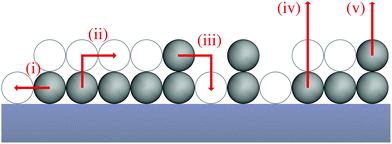
To shed light on how the exchange of molecules (or atoms) between the first and second layer influences the desorption process we develop a kinetic rate model based on a model geometry and the relevant elementary processes. In our model, adsorbed molecules (or atoms) referred to as particles can occupy a regular array of adsorption sites. This array consists of two layers of adsorption sites on the surface, whereas adsorption sites in the second layer can be occupied only if all adjacent adsorption sites in the layer underneath are occupied. We do not consider particles on top of unoccupied adsorption sites as these are assumed to be in an transition state rather than at a stable adsorption site. The number of occupied adsorption sites underneath a stable second layer adsorption site is determined by the lattice geometry – e.g., three for hexagonal layers – so the results of our model depend on the particles layer geometry. Here, we focus on the general influence of layer exchange on desorption and, therefore, we present our model for a rather simple particle-layer geometry, where the particles in the first layer create one-dimensional chains and the particles in the second layer reside directly on top of a particle in the first layer as shown in Fig. 1. Despite its simplicity, this geometry yields the same qualitative results as a more complex particle-layer geometry shown in the ESI.† Moreover, we assume that particles are not interacting with other particles within their layer, i.e., we exclude lateral interactions. In terms of processes, our model accounts for three different types of processes, which are diffusion of particles within their layer (i), exchange of particles between layers – from first to second (ii) and from second to first layer (iii) – as well as desorption from the first (iv) and from the second layer (v). The modelled geometry and processes are presented schematically in Fig. 1.Diffusion
Concerning diffusion (i), we assume the diffusion of particles within their layer to be in equilibrium in the temperature range relevant for desorption. This is motivated by the consideration that for layer exchange or desorption it is necessary that most or all bonds between adsorbate and surface are broken as the adsorption geometry and surface–particle distance drastically change during these processes. For in-layer diffusion, in contrast, some bonds might stay intact or gradually change, because the particle remains in a similar adsorption state during the whole process. Consequently, we expect in-layer diffusion to have a smaller energy barrier and be significantly faster than layer exchange or desorption for a wide range of adsorbate/substrate systems. In case of diffusion equilibrium, particles are placed randomly on the surface in systems without lateral interactions. This random particle placement enables us to use simple stochastic methods to describe the particle distribution. As an example, the occupation probability for an adsorption site in the first layer is equal to the first layer coverage θ1 independent of the adsorption environment.Layer exchange
As part of this model, particles can change from the first to the second layer and vice versa if there is a vacant adsorption site in the other layer as shown in Fig. 1. To derive the corresponding net layer exchange rate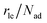 as required for kinetic modelling, it is necessary to consider all possible configurations suitable for a layer exchange and calculate the corresponding probabilities. For the here discussed simple chain geometry the precursor state of layer exchange from the first to the second layer (ii) are two adjacent particles in the first layer with no particles on top as shown in Fig. 1(ii). As every particle in the second layer is placed directly on top of a molecule in the first layer, the fraction of free molecules in the first layer is equivalent to the difference of the first and second layer coverages θ1 − θ2. If we also pay attention to the fact that every particle has two neighbouring adsorption sites, the reaction rate of layer exchange from the first to the second layer reads as 2kle,1→2(θ1 − θ2)2, where kle,1→2 is the corresponding rate constant. The layer exchange from the second to the first layer is shown in Fig. 1(iii). A particle in the second layer (probability θ2) can jump into the first layer if an adjacent adsorption site in the first layer is empty (probability (1 − θ1)). As every particle has two adjacent adsorption sites, the exchange rate from the second to the first layer is given by 2kle,2→1(1 − θ1)θ2, where kle,2→1 is the rate constant for layer exchange from the second to the first layer. When both layer exchange rates are combined, the net layer exchange rate for the first layer reads as eqn (3).
as required for kinetic modelling, it is necessary to consider all possible configurations suitable for a layer exchange and calculate the corresponding probabilities. For the here discussed simple chain geometry the precursor state of layer exchange from the first to the second layer (ii) are two adjacent particles in the first layer with no particles on top as shown in Fig. 1(ii). As every particle in the second layer is placed directly on top of a molecule in the first layer, the fraction of free molecules in the first layer is equivalent to the difference of the first and second layer coverages θ1 − θ2. If we also pay attention to the fact that every particle has two neighbouring adsorption sites, the reaction rate of layer exchange from the first to the second layer reads as 2kle,1→2(θ1 − θ2)2, where kle,1→2 is the corresponding rate constant. The layer exchange from the second to the first layer is shown in Fig. 1(iii). A particle in the second layer (probability θ2) can jump into the first layer if an adjacent adsorption site in the first layer is empty (probability (1 − θ1)). As every particle has two adjacent adsorption sites, the exchange rate from the second to the first layer is given by 2kle,2→1(1 − θ1)θ2, where kle,2→1 is the rate constant for layer exchange from the second to the first layer. When both layer exchange rates are combined, the net layer exchange rate for the first layer reads as eqn (3).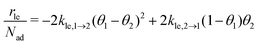 | (3) |
Desorption
The kinetics of desorption is modelled with a first-order approach for the first and second layer, respectively, which is consistent with our model not including any dissociation or recombination processes. However, the particles in the first layer can only desorb if they are not hindered by particles on top of them. Therefore the first layer desorption rate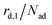 is not proportional to θ1, but to the fraction of free particles in the first layer. As discussed before, the fraction of free particles in the first layer is equivalent to the difference of the first and second layer coverages θ1 − θ2. Consequently, the desorption rate from the first layer
is not proportional to θ1, but to the fraction of free particles in the first layer. As discussed before, the fraction of free particles in the first layer is equivalent to the difference of the first and second layer coverages θ1 − θ2. Consequently, the desorption rate from the first layer 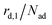 is given by eqn (4), where kd,1 is the corresponding rate constant. In contrast, particles in the second layer can always desorb freely and the second layer desorption rate
is given by eqn (4), where kd,1 is the corresponding rate constant. In contrast, particles in the second layer can always desorb freely and the second layer desorption rate 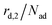 can be written with the second layer desorption rate constant kd,2 as eqn (5).
can be written with the second layer desorption rate constant kd,2 as eqn (5).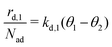 | (4) |
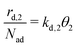 | (5) |
The total desorption rate 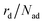 is the sum of the individual layers' desorption rates and reads as eqn (6).
is the sum of the individual layers' desorption rates and reads as eqn (6).
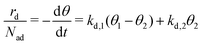 | (6) |
Now, we can combine the expressions for the net layer exchange rate (eqn (3)) and the desorption rates (eqn (4) and (5)) to obtain differential equations for the first- and second-layer coverage, respectively (eqn (7) and (8)).‡
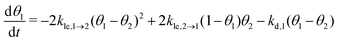 | (7) |
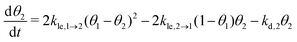 | (8) |
This set of two coupled differential equations describes how the model system evolves with time in terms of layer exchange and desorption in case of diffusion equilibrium. Hence, we can use these equations to calculate the coverages of the first and second layer during a simulated TPD experiment numerically. The desorption rate can be calculated with eqn (6).
Additionally, our model requires the knowledge of the elementary steps' kinetic rate constants as well as their temperature dependence to calculate desorption spectra (see eqn (7) and (8)). Here, we assume that the rate constants kx (x denotes the process, e.g., x = d for desorption) are given by transition state theory according to eqn (9). The quantities ΔEx and ΔSx are the corresponding potential energy barriers and entropy changes between the initial and transition states.
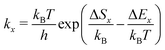 | (9) |
The Gibbs free energy barrier ΔGx of a process in relation to the kinetic parameters ΔEx and ΔSx is given by the Gibbs–Helmholtz-eqn (10). Here, it is important to note that eqn (10) assumes that energy and enthalpy are identical for condensed phases.33
| ΔGx = ΔEx − TΔSx | (10) |
Our model includes one kinetic rate constant for every elementary step considered explicitly, i.e., for every process discussed here except for diffusion, because diffusion is considered to be in equilibrium. As we describe each of these rate constants with two parameters ΔEx and ΔSx in terms of transition state theory, this makes a total of eight independent model parameters. For applications of our model, however, it can be desirable to minimize the number of model parameters, because it simplifies both the fit of our model to experimental data and the interpretation of our model. Hence, we consider the following strictly optional assumptions, which can be used in order to reduce the number of independent model parameters. The layer exchange can be interpreted as one process, but in two directions, so we assume that the layer exchange takes place over the same transition state independent from the initial state of the molecule. For desorption, it is reported in literature that the desorption process is reversible with a negligible energy barrier for many cases of molecular adsorption.34 In this case the interaction between adsorbate and surface is negligible in the transition state,34 so we assume that desorption from the first and second layer share one transition state. Considering these assumptions and the energy balance between the involved processes, the kinetic rate constants of layer exchange and desorption are related by eqn (11). This reduces the number of independent model parameters from eight to six.
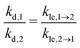 | (11) |
3 Results and discussion
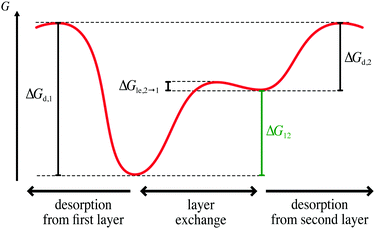
In the following, we use our model to elucidate the influence of layer exchange between the first and second layer on the desorption process. To this end, we consider a case where the rates of layer exchange are significantly higher than the rates of the competing desorption processes, i.e., layer exchange from the first (second) to the second (first) layer is significantly faster than desorption from the first (second) layer. This high difference in rates between layer exchange and desorption leads to a state, where layer exchange is at quasi-equilibrium on the timescale of desorption. Hence, we refer to this case as quasi-equilibrium layer exchange.In terms of Gibbs free energy, the case of quasi-equilibrium layer exchange corresponds to a significantly smaller barrier of layer exchange from the first to the second layer ΔGle,1→2 than desorption from the first layer ΔGd,1. Moreover, the barrier of layer exchange from the second to the first layer ΔGle,2→1 needs to be significantly smaller than the barrier of desorption from the second layer ΔGd,2. This situation is shown schematically in Fig. 2. However, under the already-made assumptions it is sufficient to consider either ΔGle,2→1 ≪ ΔGd,2 or ΔGle,1→2 ≪ ΔGd,1.§
Here, we focus on systems, where ΔGle,2→1 ≪ ΔGd,2, because we expect this to be relevant for a wide variety of real adsorbate–substrate systems. For desorption it is necessary to break all existing bonds of a particle as the particle is removed from the surface. In contrast, for layer exchange the moving particle can still interact with adjacent particles and the surface, e.g., via hydrogen bonds or dispersion interactions. These interactions can stabilize the particle in the transition state of layer exchange compared to desorption, which is why we expect that the activation barrier for layer exchange is often significantly smaller than for desorption. Consequently, the case of quasi-equilibrium layer exchange is especially relevant for the analysis of TPD experiments. Additionally, this is the case where layer exchange is the most relevant for the kinetics of desorption, because the rate of layer exchange is high compared to the rate of desorption. Thus, the case of quasi-equilibrium layer exchange can reveal the maximum impact of layer exchange on the kinetics of desorption.
In general, however, there are three cases for the relations between the rates of layer exchange and desorption: (a) desorption is significantly faster than layer exchange, (b) the rates of layer exchange and desorption are of the same order as well as (c) layer exchange is significantly faster than desorption. Thus, our model also yields the two other cases of (a) kinetically-hindered layer exchange and (b) balance between layer exchange and desorption in addition to the case of (c) quasi-equilibrium layer exchange. In the following, we first describe the characteristics of desorption spectra in cases (a) and (b). After that, we discuss case (c) and provide a strategy for the analysis of TPD data in case of quasi-equilibrium layer exchange. Guided by the situation found in many real systems,4,11,35–40 we consider a model system in which the first layer binds more strongly to the substrate than the second layer to the first for all three cases. Moreover, we consider well separated peaks for desorption from the first layer and second layer as this enables us to differentiate between the effects of layer exchange on desorption from the first layer and desorption from the second layer, respectively. An interactive visualisation of simulated desorption spectra can be found online (https://doi.org/10.4119/unibi/2955951). Additional simulations for the two cases of kinetically-hindered layer exchange and balance between layer exchange can be found in the ESI.†
(a) Kinetically-hindered layer exchange
Layer exchange is significantly slower than desorption if the Gibbs free energy barrier for layer exchange is significantly higher than for the competing desorption processes (ΔGle,2→1 ≫ ΔGd,2). Hence, layer exchange is negligible on the timescale of desorption and the desorption spectrum is solely governed by desorption. As a consequence, the desorption spectrum can be described with a separate Polanyi–Wigner term for each peak. However, in this case the desorption spectrum depends on the initial coverages in the first and second layer as particles cannot change their layer after dosing. This can lead to problems with the determination of the desorption spectrum corresponding to an initial coverage of 1.0 ML as the second layer desorption peak appears before the first layer is completely filled.Only in this case, the integral over the first (second) layer desorption signal corresponds to the respective initial coverage in the first (second) layer. The individual desorption signals can be analysed with standard Polanyi–Wigner based analysis methods each.16,20,21
(b) Balance between layer exchange and desorption
In this case the rates of layer exchange and desorption are of the same order, which corresponds to similar energy barriers for both processes (ΔGle,2→1 ≈ ΔGd,2). Therefore, neither layer exchange nor desorption alone govern the desorption spectrum but the balance between both processes is crucial for the kinetics of desorption.Especially, desorption from the first layer can take place via two different desorption paths: particles can either desorb directly from the first layer or hop on top of other particles prior to desorption. The presence of these two desorption paths causes a larger peak width and flatter leading edge than observed for a comparable first-order desorption peak. Consequently, a Polanyi–Wigner approach according to eqn (1) cannot describe the kinetics of desorption in this case. Instead, we need to consider the full kinetics of layer exchange and desorption as given by eqn (6)–(8). In the analysis of TPD data, this could, e.g., be realised by optimisation of the model parameters and initial layer coverages to match the experimental data.
Moreover, the similar barriers for layer exchange and desorption cause that layer exchange from the second to the first layer and desorption from the second layer to be activated in a similar temperature range. Hence, the appearance of the desorption spectrum depends on the initial coverages in the first and second layer like in case (a). However, in this case the initial coverage distribution also influences the observed kinetics of the second-layer desorption peak. For a partial first-layer and second-layer occupation as obtained by dosing the shape of the second-layer desorption peak is determined by layer exchange from the second to the first layer and desorption from the second layer. This causes a shift in the desorption maxima to higher temperatures with increasing coverage. In contrast, the second-layer desorption signal is solely determined by desorption for a layer-by-layer initial coverage distribution as obtained by annealing. This simpler desorption kinetics is caused by the fact that layer exchange from the second to the first layer cannot take place if the first layer is completely occupied. Additionally, this simpler desorption kinetics is advantageous for the analysis of experimental TPD data as it enables the use of standard Polanyi–Wigner based analysis methods for second-layer desorption.
(c) Quasi-equilibrium layer exchange
In case of quasi-equilibrium layer exchange, layer exchange is much faster than the competing desorption processes in both layers, because the energy barriers for layer exchange are significantly smaller than for desorption (see Fig. 2). Hence, layer exchange is in a state of quasi-equilibrium on the timescale of desorption, i.e., the net layer exchange rate (eqn (3)) is approximately zero.Next, we discuss the case of quasi-equilibrium layer exchange on the example of simulated TPD data shown in Fig. 3. To ensure that the simulated TPD data presented here are relevant for real systems as well, we based our simulation on kinetic parameters of desorption similar as those reported for TPD experiments in literature.3–9,38–49 Specifically, we chose kinetic parameters of ΔEd,1 = 1.0 eV and ΔSd,1 = 10kB for desorption from the first layer, which are in the typical range for the desorption of molecularly adsorbed molecules from metals or metal oxides.3,4,8,40 Concerning desorption from the second layer, we consider a system where the particles in the second layer bind much weaker to the first layer than the first layer to the substrate. Hence, we chose an energy barrier of ΔEd,2 = 0.5 eV for desorption from the second layer, which corresponds to a significant binding energy difference of ΔE1,2 = 0.5 eV between the first and second layer within the already-made assumptions. As the particles in the second layer are bound significantly weaker than in the first layer, we assume that they are more mobile as well. Thus, we consider a significantly smaller entropy difference between the adsorbed and transition state than for desorption from the first layer. We chose an entropy change of ΔSd,2 = 2kB.
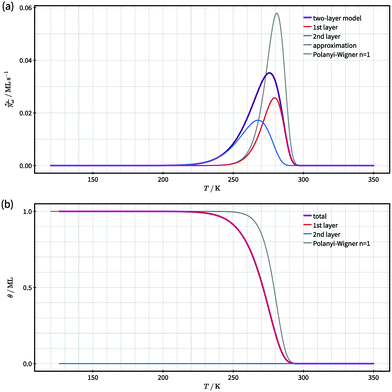 | ||
| Fig. 3 Comparison of simulated desorption spectra (a) and total coverage as a function temperature (b) for a two-layer system with quasi-equilibrium layer exchange according to our model (violet) and a first order Polanyi–Wigner process with the same kinetic parameters as used for desorption from the first layer (grey). For the two-layer model the contributions of desorption from the first (red) and second (blue) layer are shown in (a) and the corresponding coverages in (b). An approximate desorption spectrum according to eqn (13) is displayed in black. It coincides with the model desorption spectrum in violet within the accuracy of this figure. The TPD data was calculated with the kinetic parameters for desorption given in the text. | ||
Concerning the numerical simulation, we also need to consider the different timescales of layer exchange and desorption in case of quasi-equilibrium layer exchange. Due to the high difference in rates of layer exchange and desorption, the accurate numerical treatment of layer exchange requires a very small time step on the timescale of desorption. Therefore, the simulation of desorption spectra based on the model differential equations (eqn (7) and (8)) is inefficient. Instead, we integrated eqn (6) as a differential equation of the total coverage with a fourth order Runge–Kutta algorithm. For this treatment it is necessary to know the first-layer and second-layer coverages as functions of the total coverage. We calculated these layer coverages from the total coverage and the equilibrium condition for layer exchange (rle ≈ 0) numerically with a Newton–Raphson algorithm. This strategy yields excellent results for sufficiently small energy barriers of layer exchange, while still being numerically efficient. Details of the numerical simulation procedure are described in the ESI.†
In Fig. 3 we present the desorption spectrum and corresponding coverages gained from our kinetic two-layer model for an initial coverage of 1.0 ML. The modelled desorption spectrum (violet curve) in Fig. 3(a) shows a single asymmetric peak with a larger peak width, lower maximum desorption rate and more pronounced low-temperature rise than the first-order process displayed for comparison (grey curve). It is evident that a first-order Polanyi–Wigner approach according to eqn (1) cannot describe the modelled desorption spectrum and, thus the modelled kinetics of desorption.
To understand the origin of the larger peak width and flatter low-temperature rise of the modelled desorption spectrum, we analyse the contributions of first and second layer desorption to the total desorption signal (red and blue curves in Fig. 3(a)). This analysis reveals a significant contribution of second-layer desorption to the spectrum, even though only a very small fraction of particles (≈4 × 10−6 ML) resides in the second layer over the full temperature range (see Fig. 3(b)). We conclude that this contribution originates from a two-step desorption path where particles hop on top of other particles prior to desorption. As this desorption path depends on both, desorption and layer exchange, layer exchange is pivotal for understanding the kinetics of desorption. Consequently, it is necessary to identify whether or not layer exchange needs to be considered in the analysis of TPD data. Otherwise it is impossible to ensure correct results.
Next, we present a simple strategy whereby desorption via hop on top can be included in the Polanyi–Wigner based analysis of TPD data. Fig. 3 reveals, that only a very small fraction of particles resides in the second layer (θ2 ≪ θ1) when desorption from the first layer takes place. The reason for this is that we investigate a system with a high free energy difference between the first and second layer ΔG12 (see Fig. 2), so the second layer is thermodynamically highly unfavourable. Indeed, the second-layer coverage is generally much smaller than the coverage in the first layer during desorption from the first layer if the free energy difference between the layers is sufficiently high. Hence, we can approximate θ1 − θ2 ≈ θ1 and θ ≈ θ1. Using these assumption in eqn (3), we derive for the quasi-equilibrium case (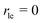 ) eqn (12) for the approximate coverage in the second layer.
) eqn (12) for the approximate coverage in the second layer.
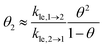 | (12) |
Insertion of the approximate second-layer coverage (eqn (12)) and the relation between the rate constants (eqn (11)) in the total desorption rate (eqn (6)) yields eqn (13) as an the approximate total desorption rate. The given approximation reveals that in the limit of small second layer coverage (and quasi-equilibrium layer exchange) the desorption rate depends on two contributions. The first term (kd,1θ) corresponds to the expected first-order Polanyi–Wigner description of desorption from the first layer. The second term (kd,1θ2/(1 − θ)) describes second-layer desorption via the hop on top desorption mechanism.
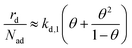 | (13) |
Interestingly, the ratio between these two contributions to the submonolayer desorption rate does not depend on the free energy difference between the layers, as long as this energy difference is sufficiently high (i.e., a small fraction of particles resides in the second layer). However, the relative contribution of desorption via hop on top increases with coverage. For small coverages nearly all particles desorb directly from the first layer (θ > θ2/(1 −θ)) as there are only very little adsorption sites in the second layer. With increasing coverage the number of adsorption sites in the second layer increases and more particles desorb via hop on top. For coverages greater than 0.5 ML more particles desorb via hop on top than directly from the first layer (θ < θ2/(1 −θ)). Consequently, the total contribution of desorption via hop on top increases with increasing initial coverage.¶
A further comparison of eqn (13) with the Polanyi–Wigner eqn (1) shows that both equations only differ in the coverage function, which is θn for the Polanyi–Wigner-equation and 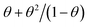 for our model. Therefore we expect that most standard analysis procedures for TPD data like leading edge20 or complete analysis16,21 work with eqn (13) as well.
for our model. Therefore we expect that most standard analysis procedures for TPD data like leading edge20 or complete analysis16,21 work with eqn (13) as well.
For other geometries we find similar expressions for the desorption rate, where the second contribution in eqn (13) varies with the expected number of adsorption positions in the second layer. We describe this in detail in the ESI.†
Concerning the accuracy of eqn (13), Fig. 3(a) shows that the desorption spectrum calculated with eqn (13) (black) is identical with the not-approximated model desorption spectrum (violet) within the figure's accuracy. We conclude that eqn (13) is an excellent approximation for the rather complex model equations (eqn (7) and (8)) within the temperature range, where desorption from the first layer takes place. It requires, however, that the system is in a quasi-equilibrium state for layer exchange and the energy difference between the layers is sufficiently high (i.e. only a small fraction of molecules resides in the second layer).
So far, we discussed the three different cases for our model and outlined possible analysis strategies for each case. For real systems, however, the applicable case is generally not known before the analysis. Within the framework of our model, one strategy to overcome this problem is to classify the investigated system based on characteristic features of the desorption spectrum. We discussed before that the appearance of the second-layer desorption signal before the first-layer desorption signal is saturated is an indicator for a kinetic-hindrance of layer exchange. In contrast, a significantly broader first-layer desorption peak with a flatter low temperature rise indicates that layer exchange influences the desorption spectrum. Based on these information we conclude that a systems which shows the former (latter) but not the latter (former) most likely belongs to case (a) (case (c)) and can be analysed as such. Experimental desorption spectra showing indications for both, a (partly) hindered layer exchange and the influence of layer exchange on the desorption signals, can be classified and analysed as case (b). Here, it is important to note that systems with, e.g., lateral interactions or additional adsorption sites might show desorption spectra with similar features. These alternative origins need to be considered as well.
4 Conclusions
A kinetic model is presented to analyse the influence of layer exchange on the desorption process as studied using TPD. We show that layer exchange can significantly alter the shape of the TPD curve, even if the second-layer occupation remains as small as 4 × 10−6 ML. For a critical analysis, the balance between the desorption barriers from the two layers and the barriers of layer exchange between the first (second) and the second (first) layer needs to be considered. For the experimentally relevant case of small barriers for layer exchange as compared to desorption, the TPD spectrum shows a single peak that cannot be correctly described by the Polanyi–Wigner equation. Instead, a modified equation can be derived that accounts for desorption via a hop on top mechanism.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Antonia Köhler for help with literature research. Stimulating discussions with Lev Kantorovich and Michael Reichling are gratefully acknowledged. We gratefully acknowledge financial support from the DFG through grant INST 215/552-1 FUGG.References
- G. E. Brown and G. Calas, Geochem. Perspect., 2012, 1, 483–742 CrossRef.
- H. J. Freund, M. Baumer, J. Libuda, T. Risse, G. Rupprechter and S. Shaikhutdinov, J. Catal., 2003, 216, 223–235 CrossRef CAS.
- C. T. Campbell and J. R. V. Sellers, Chem. Rev., 2013, 113, 4106–4135 CrossRef CAS PubMed.
- S. R. Kachel, B. P. Klein, J. M. Morbec, M. Schoniger, M. Hutter, M. Schmid, P. Kratzer, B. Meyer, R. Tonner and J. M. Gottfried, J. Phys. Chem. C, 2020, 124, 8257–8268 CrossRef CAS.
- G. Mercurio, E. R. McNellis, I. Martin, S. Hagen, F. Leyssner, S. Soubatch, J. Meyer, M. Wolf, P. Tegeder, F. S. Tautz and K. Reuter, Phys. Rev. Lett., 2010, 104, 4 CrossRef PubMed.
- S. M. Bashir and H. Idriss, J. Chem. Phys., 2020, 152, 044712 CrossRef CAS PubMed.
- M. Roos, A. Breitruck, H. E. Hoster and R. J. Behm, Phys. Chem. Chem. Phys., 2010, 12, 818–822 RSC.
- M. Meier, J. Hulva, Z. Jakub, J. Pavelec, M. Setvin, R. Bliem, M. Schmid, U. Diebold, C. Franchini and G. S. Parkinson, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E5642–E5650 CrossRef CAS PubMed.
- R. Ramsier, K.-W. Lee and J. Yates, Surf. Sci., 1995, 322, 243–255 CrossRef CAS.
- F. Maass, Y. D. Jiang, W. Liu, A. Tkatchenko and P. Tegeder, J. Chem. Phys., 2018, 148, 7 CrossRef PubMed.
- R. S. Smith, J. Matthiesen and B. D. Kay, J. Phys. Chem. A, 2014, 118, 8242–8250 CrossRef CAS.
- J. Gottfried, K. Schmidt, S. Schroeder and K. Christmann, Surf. Sci., 2003, 525, 184–196 CrossRef CAS.
- M. J. P. Hopstaken and J. W. Niemantsverdriet, J. Phys. Chem. B, 2000, 104, 3058–3066 CrossRef CAS.
- S. Gudmundsdottir, E. Skulason, K.-J. Weststrate, L. Juurlink and H. Jonsson, Phys. Chem. Chem. Phys., 2013, 15, 6323–6332 RSC.
- A. Makeev and M. Slinko, Surf. Sci., 1996, 359, L467–L472 CrossRef CAS.
- D. A. King, Surf. Sci., 1975, 47, 384–402 CrossRef CAS.
- J. L. Falconer and J. A. Schwarz, Catal. Rev., 1983, 25, 141–227 CrossRef CAS.
- D. L. S. Nieskens, A. P. van Bavel and J. W. Niemantsverdriet, Surf. Sci., 2003, 546, 159–169 CrossRef CAS.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- E. Habenschaden and J. Kuppers, Surf. Sci., 1984, 138, L147–L150 CrossRef CAS.
- J. L. Taylor and W. H. Weinberg, Surf. Sci., 1978, 78, 259–273 CrossRef CAS.
- H. Asada and M. Masuda, Surf. Sci., 1989, 207, 517–524 CrossRef CAS.
- H. Conrad, G. Ertl, J. Küppers and E. Latta, Surf. Sci., 1977, 65, 245–260 CrossRef CAS.
- T. G. Gambu, R. K. Abrahams and E. van Steen, Catalysts, 2019, 9, 310 CrossRef.
- H. J. Kreuzer, Langmuir, 1992, 8, 774–781 CrossRef CAS.
- A. Paul, C. J. Jenks and B. E. Bent, Surf. Sci., 1992, 261, 233–242 CrossRef CAS.
- S. Payne, J. Zhang and H. Kreuzer, Surf. Sci., 1998, 396, 369–387 CrossRef CAS.
- M. Pineda and M. Stamatakis, J. Chem. Phys., 2017, 147, 024105 CrossRef CAS PubMed.
- R. S. Smith, J. Matthiesen, J. Knox and B. D. Kay, J. Phys. Chem. A, 2011, 115, 5908–5917 CrossRef CAS.
- T. Wagner, H. Karacuban and R. Möller, Surf. Sci., 2009, 603, 482–490 CrossRef CAS.
- X. Xia, J. Strunk, S. Litvinov and M. Muhler, J. Phys. Chem. C, 2007, 111, 6000–6008 CrossRef CAS.
- J. I. Seeman, Chem. Rev., 1983, 83, 83–134 CrossRef CAS.
- K. Christman, Introduction to Surface Physical Chemistry, Springer Verlag, Berlin Heidelberg, 1991, p. 32 Search PubMed.
- C. T. Campbell and J. R. V. Sellers, J. Am. Chem. Soc., 2012, 134, 18109–18115 CrossRef CAS PubMed.
- A. R. Bishop, G. S. Girolami and R. G. Nuzzo, J. Phys. Chem. B, 2000, 104, 754–763 CrossRef CAS.
- A. Lobo and H. Conrad, Surf. Sci., 2003, 523, 279–286 CrossRef CAS.
- M. B. Hugenschmidt, L. Gamble and C. T. Campbell, Surf. Sci., 1994, 302, 329–340 CrossRef CAS.
- M. A. Henderson, Surf. Sci., 1994, 319, 315–328 CrossRef CAS.
- S. L. Tait, Z. Dohnálek, C. T. Campbell and B. D. Kay, J. Chem. Phys., 2005, 122, 164708 CrossRef PubMed.
- F. Maass, M. Ajdari, F. C. Kabeer, M. Vogtland, A. Tkatchenko and P. Tegeder, J. Phys. Chem. Lett., 2019, 10, 1000–1004 CrossRef CAS PubMed.
- M. A. Henderson and S. A. Chambers, Surf. Sci., 2000, 449, 135–150 CrossRef CAS.
- A. S. Bolina, A. J. Wolff and W. A. Brown, J. Phys. Chem. B, 2005, 109, 16836–16845 CrossRef CAS.
- G. Ertl, M. Neumann and K. Streit, Surf. Sci., 1977, 64, 393–410 CrossRef CAS.
- Z. Jakub, F. Kraushofer, M. Bichler, J. Balajka, J. Hulva, J. Pavelec, I. Sokolović, M. Müllner, M. Setvin, M. Schmid, U. Diebold, P. Blaha and G. S. Parkinson, ACS Energy Lett., 2019, 4, 390–396 CrossRef CAS.
- D. J. Lavrich, S. M. Wetterer, S. L. Bernasek and G. Scoles, J. Phys. Chem. B, 1998, 102, 3456–3465 CrossRef CAS.
- H. H. Kan, R. J. Colmyer, A. Asthagiri and J. F. Weaver, J. Phys. Chem. C, 2009, 113, 1495–1506 CrossRef CAS.
- M. J. T. C. van der Niet, A. den Dunnen, L. B. F. Juurlink and M. T. M. Koper, J. Chem. Phys., 2010, 132, 174705 CrossRef PubMed.
- M. A. van Spronsen, K.-J. Weststrate, A. den Dunnen, M. E. van Reijzen, C. Hahn and L. B. F. Juurlink, J. Phys. Chem. C, 2016, 120, 8693–8703 CrossRef CAS.
- P. Lackner, J. Hulva, E.-M. Koeck, W. Mayr-Schmoelzer, J. I. J. Choi, S. Penner, U. Diebold, F. Mittendorfer, J. Redinger, B. Kloetzer, G. S. Parkinson and M. Schmid, J. Mater. Chem. A, 2018, 6, 17587–17601 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Quantitative discussion on case stability, additional desorption spectra for cases (a) and (b), additional information on simple chain geometry, two-layer model for a shifted-chain geometry, coverage and geometry dependence of desorption via hop on top, details of the numerical calculations. See DOI: 10.1039/d1cp01924d |
| ‡ From these two equations it can be seen that the Curtin–Hammett principle does not apply here as these equations deviate from first-order kinetics required in the Curtin–Hammett principle.32 |
| § We already assume that eqn (11) holds true and, thus, ΔGle,1→2 − ΔGd,1 = ΔGle,2→1 − ΔGd,2. As both differences between the barriers of layer exchange and desorption are equivalent either both or neither are sufficiently high. |
| ¶ We provide additional information on the coverage and geometry dependence of desorption via hop on top in the ESI.† |
| This journal is © the Owner Societies 2021 |