Systematic assessment of DFT methods for geometry optimization of mononuclear platinum-containing complexes

Abstract

Platinum is used extensively as a catalyst for a wide variety of chemical reactions, though its scarcity and price present limitations to expansions of its use. To understand the origin of platinum's versatility—with the goals of both improving the efficiency of existing catalysts and mimicking its reactivity with more abundant metals—the mechanisms of platinum-catalyzed chemical reactions must be understood via structural and spectroscopic characterization of these catalysts under operando conditions. Such data, typically consisting of complex mixtures of species, often prove challenging to interpret, inviting the aid of chemical theory. DFT calculations in particular have proven successful at predicting structural and spectroscopic parameters of transition metal species, though a thorough investigation of how these methods perform for platinum-based complexes has yet to be undertaken. Herein, we evaluated the performance of geometry optimization for five commonly used functionals (BP86, PBE, B3LYP, PBE0, and TPSSh) in combination with various ligand basis sets, relativistic approximations, and solvation and dispersion models. We applied these DFT methods to a training set of 14 platinum-containing complexes with varying sizes, oxidation states, and number and type of ligands and determined that the best-performing method was the PBE0 functional together with the def2-TZVP basis set for the ligand atoms, the ZORA relativistic approximation, and solvation and dispersion corrections. The ability of this DFT methodology to accurately predict metrical parameters was confirmed using two case studies, most notably by comparing the DFT optimized geometry of a previously uncharacterized complex to newly collected EXAFS data, which showed excellent agreement.

---

Introduction

Platinum-based catalysts have found wide use in both laboratory and industrial processes—e.g. catalytic converters¹ and fuel cells in automobiles,² the refining of gasoline,³ sustainable production of lactic acid for bioplastics,⁴ and the oxidation of furfural during the refining of biomass⁵—due in large part to their efficiency and stability. Unfortunately, despite these desirable properties, platinum is a rare and expensive metal and the large and increasing demand is further increasing its price.⁶

Due to this cost and scarcity, numerous efforts are underway to increase the efficiency of platinum use. A cornerstone of these efforts is the drive to understand the mechanisms of platinum-catalyzed reactions by probing the geometric and electronic structures of the chemical species involved in catalysis. Critical information includes the metal and ligand oxidation states, the number of ligands and their chemical identities, and the overall geometries of the active catalyst and reaction intermediates. By understanding how these catalysts operate and, indeed, how they become inactive, we will have a foundation for rational catalyst improvement and de novo design. Unfortunately, while this information is oftentimes straightforward to obtain for static compounds, it is typically much more challenging to elucidate for catalytic intermediates, which often only exist for a short time, generally cannot be crystallized, and typically are present as part of a mixture of chemically-related species.

A strategy for overcoming some of the challenges associated with studying bulk material catalysts that also greatly improves the efficiency of platinum use is to employ platinum as single site catalysts, whereby individually-bound platinum atoms are employed as catalytic species.⁷ These site-isolated catalysts are typically composed of platinum centers dispersed on inorganic supports such as zeolites or metal oxides. Because these catalysts are in the limit of very small clusters, they differ from bulk metal catalysts in that all platinum atoms are available for catalysis, making them significantly more efficient than bulk materials and even nanoclusters.^8,9 Moreover, in the limit of mono- to oligonuclear species, the properties and behavior of the metal centers approach those of homogeneous catalysts, thereby enabling their study by the battery of structural and spectroscopic characterization methods available to small molecules.

To this end, a sizable toolbox of characterization methods is available that can be applied even to the demanding conditions of operando catalytic reactions of an at times “spectroscopically quiet” metal like platinum. Vibrational techniques like IR and Raman spectroscopy provide information about the identity of the ligands¹⁰ and the nuclearity and uniformity of the catalytic centers.^8,11 NMR, both of light atoms and of platinum itself, can offer detailed insight into the structure of the catalytic center and its ligands; e.g.¹³C NMR can distinguish between different small ligands (e.g. CO vs. carbonates) and their location (e.g. bridging vs. terminal),¹² while ¹⁹⁵Pt NMR can offer insight into the geometric features of the metal centers, even distinguishing between isomers.^13,14 X-ray absorption and emission spectra, on the other hand, contain information on the metal oxidation state, coordination environment, and metal–ligand bond distances.^7,15,16 These techniques, often combined with mass spectrometric and kinetic analyses, have provided detailed insight into the mechanisms of many catalytic reactions.

Even with this battery of methods available, however, significant challenges still remain. Critically, the interpretation of the resulting data can prove difficult since, by definition, catalytic reactions involve multiple, closely related species—resting catalyst, various intermediate and inactivated states, and product—that all exist simultaneously and can contribute to any collected data. It is here that aid from chemical theory can provide guidance, allowing theoretical properties and spectra to be computed and compared to experiment, thus enabling hypotheses about contributing species to be ruled out. In order to be successful, computational methods must be able to reliably predict the geometric structure of candidate species, since calculation of properties and spectroscopic parameters depends critically on accurate molecular geometries.

Density functional theory (DFT) has proven to be a useful computational tool for predicting the geometries of transition metal complexes, with the ability to accurately reproduce the structures of a wide range of compounds.^17–20 Despite platinum's catalytic importance, however, few of these studies have focused on this metal, and nearly all those that have narrowly focused on a single compound or small subset of compounds (e.g. cisplatin).^21–23 Such a narrow scope makes such studies susceptible to bias in favor of the investigated species and thus in danger of lacking wide generalizability. A superior approach is to investigate a broad array of complexes comprising various oxidation states, geometries, and ligand identities to establish how well a given methodology holds up generally. To our knowledge, there has been no such systematic study evaluating the performance of commonly used DFT methods for platinum compounds.

In this paper, we investigate how well various DFT methods reproduce the crystallographically-determined structures of a set of 14 platinum-containing complexes (Fig. 1). These complexes range in size, geometry, ligand identity, and oxidation state of the platinum center. We evaluated the performance of five commonly used functionals, as well as the effect of ligand basis set, relativistics, solvation, and dispersion. Once top-performing methods were identified for this training set, we then applied them to two “case studies” to evaluate their performance. First, the methods were used to reproduce the structure of a complex with quite different chemical functionality from what was present in the training set to assess their generalizability. Second, we used the DFT methods to predict the metrical parameters of a complex lacking a crystallographically-determined structure and compared the results to EXAFS-determined metrics reported herein. Both of these tests confirmed the excellent performance of the DFT optimization methodology determined herein.

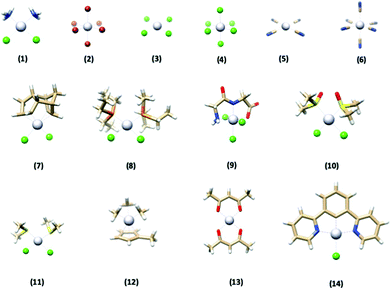Fig. 1 The structures of the 14 platinum-based complexes that comprised the training set used in this study. Gray = Pt, blue = N, red = O, tan = C, white = H, green = Cl, orange = P, yellow = S.

Methods

Computational details

All calculations were performed using the ORCA program versions 4.1 and 4.2.²⁴

Geometry optimizations were initiated from structures available from the Cambridge Structural Database or the Crystallography Open Database (Table 1) and employed the BP86,^25,26 PBE,²⁷ B3LYP,^25,28,29 PBE0,³⁰ and TPSSh³¹ functionals. All calculations used a dense DFT integration grid (Grid7) while calculations with hybrid and meta-hybrid functionals used the RIJCOSX³² approximation and also a dense COSX integration grid (GridX7 to GridX9). For all calculations, the all-electron relativistically contracted TZVP basis set (SARC-ZORA-TZVP or SARC-DKH-TZVP in ORCA notation) was used on platinum together with an integration accuracy of 7. The basis set used for the ligand atoms was either def2-SVP or def2-TZVP³³ (with the corresponding SARC/J auxiliary basis set).^34–38 Relativistics were accounted for using either ZORA^39–41 or DKH2^42–44 while dispersion effects, when used, were included via the Becke–Johnson damping scheme (D3BJ).^45,46 Lastly, when solvation effects were modeled, they were accounted for using the CPCM model⁴⁷ in an infinite dielectric and with a Gaussian charge scheme (only available in ORCA 4.2). In the end, 80 different methods were employed for each complex studied (five functionals, two ligand basis sets, two relativistic methods, presence or absence of dispersion, and presence or absence of solvation). For all calculations, the geometry optimized structures were confirmed to be energetic minima by vibrational frequency analysis. Sample input files can be found in the ESI.† ‡

Table 1 List of the complexes studied

Number	Complex name	Ref.
(1)	Cisplatin	56
(2)	Hexabromoplatinate(IV)	57
(3)	Tetrachloroplatinate(II)	58
(4)	Hexachloroplatinate(IV)	59
(5)	Tetracyanoplatinate(II)	60
(6)	Hexacyanoplatinate(IV)	61
(7)	Dichloro(dicyclopentadienyl)platinum(II)	62
(8)	cis-Dichlorobis(triethylphosphine)platinum(II)	63
(9)	(Glycylglycine)-trichloro-platinum(IV)	64
(10)	cis-Dichlorobis(dimethylsulfoxide)platinum(II)	65
(11)	cis-Dichlorobis(dimethyl sulfide)platinum(II)	66
(12)	Trimethyl(methylcyclopentadienyl)platinum(IV)	67
(13)	Platinum(II) bis(acetylacetonate)	68
(14)	[2,6-Bis(2-pyridyl)phenyl-C,N,N′]chloroplatinum(II)	69

---

Comparison of optimized structures

To evaluate the performance of each method, we compared the optimized geometry of each complex to its reported X-ray crystallographic structure using three different measures, each of which captures a different component of the optimization's performance. First, we assessed the RMSD of only atoms bonded directly to the Pt center (RMSD_Pt), which reports on how well a method reproduces the geometry of the metal center and the first shell bonding of its ligating atoms. Next, the overall RMSD of all non-hydrogen atoms (RMSD_all) was assessed, giving a sense for how well a method is able to reproduce the entire 3D structure of a complex (for complexes containing solely monoatomic ligands, this is identical to RMSD_Pt). Lastly, we also computed the mean percent deviation of the Pt–L bond lengths for all atoms bonded to the platinum center (Δ), a measure that is similar to RMSD_Pt but that focuses solely on the metal–ligand bond distances and not changes to the 3D arrangement of atoms, making it comparable to the data collected during, e.g., an EXAFS measurement. The RMSD values were calculated using UCSF Chimera⁴⁸ while Δ was computed as in ref. 49. Vibrational corrections were not made to the computed bond lengths as these corrections are expected to be appreciably smaller^50,51 than even the best Δ values obtained. The equations used for these determinations are provided in the ESI.†

Statistical methods

Because the results from the training set are not expected to have a normal distribution, averages and standard deviations were calculated using a bootstrapping procedure.⁵² Namely, for each structural metric, the data was sampled with replacement as many times as there were data points and the average was computed. This process was repeated 1000 times, and the averages and standard deviations of the bootstrapped values are reported.

EXAFS data collection and processing

X-ray absorption spectra were collected in transmission mode at the PIPOXS beamline (ID2A) at the Cornell High Energy Synchrotron Source, operated at 6 GeV and 100 mA. The incident energy was selected using a cryogenically-cooled Si(111) monochromator and harmonic rejection was achieved with a pair of rhodium-coated mirrors upstream of the sample. The incident beam energy was calibrated using a Pt foil (11564 eV). Scans were carried out at the Pt L₃-edge over the energy range 11 340–12 600 eV and lasted 21 minutes; the intensity was measured using nitrogen-filled ion chambers. To prevent beam damage, the sample was cooled to 100 K using a nitrogen cryostream and the beam intensity was attenuated by detuning and the use of Al foil attenuation upstream of the sample.

Data processing was carried out using the Demeter⁵³ suite. 11 scans were averaged in Athena. Background and spline removal were handled by the AUTOBK function over a k range of 1 to 12, with an Rbkg parameter of 1.0 and a k weight of 3. Fitting was performed using Artemis. The scattering paths for EXAFS fitting were calculated using FEFF 9.0⁵⁴ using a model structure built in ChemCraft⁵⁵ and including all atoms of the complex. Fitting was performed from k = 3–12 and, during fitting, the coordination numbers were systematically varied (see ESI†) while the distances (R), Debye–Waller factors (σ²), and zero-energy shift (ΔE₀) were allowed to float. The S₀² value was fixed at 1.0.

Results

The goals of this work were twofold: (1) to identify the DFT method(s) that best reproduces the crystallographically-determined geometry of platinum-based compounds, and (2) to assess the robustness of this method(s) by challenging it with more complex structures than those found in the training set. To begin, we evaluated the performance of five commonly used functionals along with two ligand basis sets, two relativisitic approximations, and evaluated the effect of solvation and dispersion. By combining these factors, we optimized the geometry of each complex using 80 different methods (full list of methods included in Table S1, ESI†). The effect of functional, relativistics, basis set, solvation, and dispersion are explored in the following sections. Once the top-performing methods were identified, they were (1) challenged to reproduce the geometry of a large crystallographically-characterized complex containing chemical functionality not found in the training set, and (2) used to predict the structure of a Pt complex lacking previous structural characterization and the results compared to newly-obtained EXAFS data.

Overall assessment

To obtain an overall assessment of how well each method could reproduce crystallographic geometries, a bootstrapping algorithm was used to sample the sets of RMSD_all, RMSD_Pt, and Δ values for all 14 complexes in the training set, thus returning an overall average and standard deviation for each of these three metrics. The results (Table S2, ESI†) indicate that the agreement between experimental and calculated geometries varied considerably between the tested computational methods, with the apparent agreement also varying depending on the metric used for evaluation; in general, the more holistic a metric was (RMSD_all > RMSD_Pt > Δ) the greater the uncertainty in its average performance.

The 15 methods with the best agreement as assessed by RMSD_all (RMSD = 0.066–0.082 Å) are reported in Table 2 (complete results can be found in Table S2, ESI†), and already several conclusions can be drawn from just these topline results. While method performance varied according to the metric used, there was considerable overlap between the three metrics—indeed, the top three methods were the same, and in the same order, for all three of the metrics. On the other hand, the significant uncertainties of the averages (often ∼20%) resulted in no single method standing above all others; for RMSD_all there were 12 methods with averages within one standard deviation of the best, while there were seven and three methods within one standard deviation for RMSD_Pt and Δ, respectively. The Δ result is noteworthy as it reveals a relatively steep drop in agreement as compared to the two RMSD values; the 15th best method as recorded by Δ has an average that is 80% larger than the best method, while the 15th best as recorded by RMSD_all and RMSD_Pt are only 25% and 35% larger than their respective best. As such, it is apparent that the more holistic RMSD metrics potentially mask real and chemically meaningful deviations in Pt-ligand bond lengths.

Table 2 Comparison of the top 15 methods as assessed by RMSD_all

Method	RMSDall (Å)	RMSDPt (Å)	Δ (%)	Rank by RMSDall	Rank by RMSDPt	Rank by Δ
a Indicates the method is within one standard deviation of the best method for that metric.
PBE0/ZORA/TZVP/D3BJ/CPCM	0.066 ± 0.014	0.034 ± 0.009	0.60 ± 0.13	1^a	1^a	1^a
PBE0/ZORA/TZVP/CPCM	0.067 ± 0.013	0.034 ± 0.007	0.64 ± 0.13	2^a	1^a	2^a
PBE0/ZORA/SVP/D3BJ/CPCM	0.069 ± 0.014	0.038 ± 0.009	0.69 ± 0.13	3^a	3^a	3^a
TPSSh/ZORA/TZVP/D3BJ/CPCM	0.071 ± 0.013	0.039 ± 0.010	0.85 ± 0.14	4^a	4^a	5
TPSSh/ZORA/TZVP/CPCM	0.071 ± 0.012	0.039 ± 0.009	0.96 ± 0.14	5^a	5^a	8
TPSSh/ZORA/SVP/CPCM	0.074 ± 0.012	0.044 ± 0.009	1.09 ± 0.15	6^a	11	15
TPSSh/ZORA/SVP/D3BJ/CPCM	0.075 ± 0.013	0.043 ± 0.011	0.96 ± 0.15	7^a	7^a	7
PBE/ZORA/TZVP/D3BJ/CPCM	0.077 ± 0.013	0.042 ± 0.009	1.08 ± 0.15	8^a	6^a	14
PBE/ZORA/SVP/CPCM	0.078 ± 0.012	0.047 ± 0.009	1.28 ± 0.17	9^a	16	27
PBE/ZORA/TZVP/CPCM	0.079 ± 0.013	0.044 ± 0.008	1.20 ± 0.16	10^a	9	22
PBE/ZORA/SVP/D3BJ/CPCM	0.079 ± 0.012	0.045 ± 0.009	1.14 ± 0.16	11^a	13	17
B3LYP/ZORA/SVP/D3BJ/CPCM	0.080 ± 0.012	0.051 ± 0.008	1.49 ± 0.17	12^a	22	35
B3LYP/ZORA/TZVP/D3BJ/CPCM	0.081 ± 0.012	0.040 ± 0.008	1.50 ± 0.16	13	19	36
BP86/ZORA/TZVP/CPCM	0.082 ± 0.013	0.046 ± 0.009	1.39 ± 0.18	14	15	29
BP86/ZORA/SVP/D3BJ/CPCM	0.082 ± 0.012	0.047 ± 0.009	1.21 ± 0.17	14	17	23

---

Looking at the methods themselves, all of the 15 methods present in Table 2 employed the ZORA relativistic approximation and modeled solvation using CPCM, indicating the importance of including these parameters. The effect of the other computational inputs, however, was more variable, and will be explored in more detail individually in the following section (vide infra). Briefly, the PBE0 and TPSSh functionals tended to perform best, though PBE, BP86, and B3LYP also appeared among the top 15 methods present in Table 2. The impact of ligand basis set and dispersion corrections was even more varied, with no clear conclusions apparent from the subset of data in Table 2.

Effects of computational parameters

The results in Table 2 and Table S2 (ESI†) enable several broad conclusions to be made about the effects of the various computational parameters employed. Perhaps most noteworthy, all of the 15 methods present in Table 2 make use of solvation modeling via CPCM and account for relativistics using ZORA. That the inclusion of solvation is required for good agreement between theory and experimental data on solid state structures is likely unsurprising, though the complete absence of any methods using DKH2 is notable. Closer investigation of this result reveals that, for every functional tested, structures optimized using DKH2 have on average >3× greater deviation from experiment as measured by RMSD_all (Fig. 2) than do those optimized using ZORA. The large deviation from experiment generally derived from DKH2 calculations underestimating metal–ligand distances by large margins (>0.2 Å), often to values outside physical plausibility; indeed, the agreement as measured by Δ was even worse than RMSD_all, with DKH2 performing ≥5× worse than ZORA (Fig. S2, ESI†). While unexpected, this behavior has been documented previously and can be attributed to numerical instabilities in the DKH2 implementation in ORCA.§ The errors introduced by the DKH2 method were so large that they overwhelmed the effects from the other computational parameters and, as such, all further analysis was performed solely taking account of the ZORA calculations (the performance of all methods, including DKH2, can be found in Table S2 in the ESI†).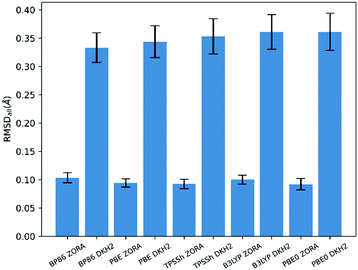

Fig. 2 RMSD_all-measured performance of the five functionals coupled with two ways of accounting for relativstics.

Other than relativistics and solvation, the other computational parameters investigated—functional, ligand basis set, and dispersion—had more nuanced influences on the results. Taking all of the ZORA calculations in aggregate, the PBE0 functional tended to produce the best agreement with experiment (Fig. S3–S5, ESI†), though only when assessed using Δ was this agreement statistically better than all other functionals tested. Conversely, B3LYP and BP86 consistently had the lowest agreement with experiment, again being most notable when measured by Δ.

The impact of ligand basis set on the agreement to experiment was more difficult to discern; seven of the 15 methods present in Table 2 employ SVP while the other eight use TZVP. To more carefully assess the influence of ligand basis set, pairwise comparisons were made between calculations that were identical except that one used SVP and the other used TZVP; e.g. PBE0/ZORA/SVP/CPCM vs. PBE0/ZORA/TZVP/CPCM. By comparing the difference in agreement to experiment between the two, the effect of choosing TZVP over SVP could be assessed; for (SVP minus TZVP), a positive result indicates better agreement using TZVP. We found significant spread in these differences—for some methods with some complexes, TZVP produced better agreement, while the reverse was true for other methods/complexes. In aggregate though, TZVP produced better results (Fig. S6–S8, ESI†), improving on the results using SVP in 73%, 75%, and 57% of the comparisons as measured by RMSD_all, RMSD_Pt, and Δ, respectively, corresponding to median improvements of 0.004 Å, 0.003 Å, and 0.036%. Thus, while a subtle effect, it appears choosing TZVP over SVP can generally be expected to slightly improve optimized geometries.

Lastly, the effect of dispersion was investigated. Analogously to ligand basis set, for this comparison the difference in agreement (as measured by each of the three metrics) between pairs of calculations—identical except one included dispersion and one did not—were calculated and are plotted in Fig. S9–S11 (ESI†) (improved agreement upon inclusion of dispersion appears as positive values). Despite clear spread in the results, on average including dispersion in the geometry optimization resulted in better agreement with experiment, a result that holds true across all of the functionals tested. Across all 280 pairs of calculations that were assessed, including dispersion increased agreement with experiment in 64%, 71%, and 84% of cases as measured by RMSD_all, RMSD_Pt, and Δ, respectively, median improvements of 0.002 Å, 0.002 Å, and 0.14%. These results were nearly identical when only calculations that also included solvation were compared though, interestingly, this improvement in agreement did not correlate with the size of the complex. Much as with the TZVP basis set on the ligands, including dispersion corrections appeared to, on average, yield a small improvement in the calculated geometries.

Taking the individual assessments of each computational parameter together then, the combination that would be expected to produce the best agreement with experiment would be PBE0/ZORA/TZVP/D3BJ/CPCM, a result which matches precisely the topline result in Table 2.

Chemical effects on performance

Since significant variation was found in the ability of the various computational methods to reproduce experimental structures, we next looked at whether this performance varied based on chemical attributes of the complex being optimized. Specifically, we looked at the method performance as a function of platinum oxidation state (+2 or +4), overall complex charge (charged or uncharged), and the identity of the atoms bonded to the Pt center (only by light atoms or only not by light atoms); complete results can be found in Tables S3–S8 (ESI†).

While the smaller sizes of the chemistry-based subgroups often resulted in larger uncertainties in how well the methods produced structures that agreed with experiment—and, thus, more methods with statistically equivalent performance—overall the chemistry of the complex was found to have little impact on method performance. Indeed, the general ordering of results found in Table 2, where PBE0/ZORA/TZVP/D3BJ/CPCM, PBE0/ZORA/TZVP/CPCM, and PBE0/ZORA/SVP/D3BJ/CPCM were the statistically best methods, was largely unchanged regardless of the subgroup analyzed.

The largest deviations from the results in Table 2 were observed for the only light atom ligands (Table S7, ESI†) and no light atom ligands (Table S8, ESI†) subgroups. For the subgroup with no light atom ligands, the RMSD_Pt and Δ for the method with best agreement (PBE0/ZORA/TZVP/D3BJ/CPCM) had quite small uncertainties of 0.002 Å and 0.05%, respectively, rendering this the single statistically best method. The subgroup with only light atom ligands, on the other hand, had much larger uncertainties and, indeed, a different ordering of the methods, with solvation appearing much less important for good agreement than most of the other subgroups. Closer inspection of this small subgroup—containing only four complexes—revealed that the aggregate ordering of the methods was driven by anomalously poor agreement of complex (12), wherein the methylcyclopentadienyl group rotated relative to the methyl ligands to yield large RMSD values (>3× the average for PBE0/ZORA/TZVP/CPCM and >4× the average for PBE0/ZORA/TZVP/D3BJ/CPCM). Given the expected low barrier for this rotation, the poor agreement for (12) should likely be interpreted as a spurious result rather than an accurate indication of method performance. The effect of (12) also appears in the Pt(IV) subgroup, where again solvation appears less important for good agreement with experiment.

Discussion

The approach of this study was to determine which DFT computational method is best able to reproduce the crystallographically-determined structures of Pt-containing complexes. The strategy of comparing calculated geometries to crystallographic structures was chosen instead of, say, comparisons of calculated total energies, because geometry is a readily accessible observable and because methods best able to reproduce geometries are not necessarily also the best at computing accurate total energies. Accurate structures are critical for correct descriptions of the potential energy surface and, indeed, more exact energies (and spectral parameters) can be obtained by performing higher level single point calculations on reliable optimized structures. Using crystal structures as reference data does invite complications due to crystal packing effects, which for some species may exert an influence on the experimental geometries that would not be reproduced by these infinite dielectric calculations. This is the case for cisplatin, for example, where calculations employing a dimer resulted in better agreement with experiment over those using only a monomer.⁵¹ As shown in ref. 51, this caveat can often be mitigated by building higher order assemblies before geometry optimization in cases where crystal packing is known or suspected to be important.

To determine which computational methodology is best able to reproduce the experimental geometries of the 14 Pt-based complexes in our training set, as assessed by three different structural metrics, Table 2 reveals that only three methods stand above the others in terms of performance: PBE0/ZORA/TZVP/D3BJ/CPCM, PBE0/ZORA/TZVP/CPCM, and PBE0/ZORA/SVP/D3BJ/CPCM. Analysis of each of the computational parameters individually—functional, relativistics, solvation, ligand basis set, and dispersion—supported these topline results. Modelling solvation using CPCM and relativistics using ZORA were found to be essential for good agreement, while the PBE0 functional performed somewhat better than the other functionals tested. The ligand basis set and inclusion of dispersion corrections had much smaller influences on the agreement with experiment, though on average use of TZVP and dispersion corrections was found to improve agreement.

These results are consistent with previous studies that have shown hybrid functionals tending to perform better for third-row transition metals than pure GGAs.^18,21–23 Notably, while there are examples in recent literature of the popular B3LYP functional being used to predict the structures of complexes containing these heavy transition metals,^70–73 this study indicates that, for the case of platinum-containing complexes, B3LYP is a relatively poor choice and is outperformed by PBE0 and TPSSh; the potential that this observation is also true for other third row transition metals merits exploration.

Relatedly, it has been noted before but bears repeating here: Achieving accurate results for third row transition metals often requires more than simply applying a method that has been shown to work well for first row transition metals. The calculations reported here all required very dense integration grids (Grid7 and GridX7–X9 in ORCA notation), increased integration accuracy for the platinum center, and stringent convergence criteria in order to converge to stationary point structures (see ESI†). These criteria are much more stringent than those generally needed for first row metals, so it should not be assumed that a method successful for first row metals will have equally good performance for heavy metals such as platinum.

Given that the training set was necessarily limited, we sought to evaluate the robustness and generality of our conclusions by subjecting the two top-performing methods—PBE0/ZORA/TZVP/D3BJ/CPCM and PBE0/ZORA/TZVP/CPCM—to two “case studies”. First, the methods were used to optimize a large complex with chemical functionality not found in the training set, and second by optimizing a complex without previous structural characterization and comparing the results to newly obtained EXAFS data.

Case study 1: Application beyond the training set

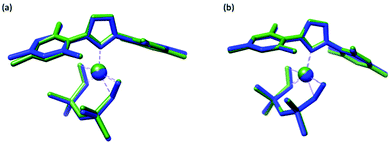
Our first case study involved optimizing the structure of (1,3-dimesitylimidazol-2-ylidene)-(η²,η²-1,3-divinyl-1,1,3,3-tetramethyldisiloxane)-platinum(0)⁷⁴ (15), a platinum complex that is both larger than any used in the training set (77 atoms) and also with a platinum oxidation state (Pt⁰) and ligands (an N-heterocyclic carbene and divinylsiloxane) not found in that set.

Overlays between the crystallographic and optimized structures can be found in (Fig. 3) and indicate that both methods reproduce the crystallographic geometry with good fidelity. Numerical data are reported in Table 3, along with the data from complex (8), the largest complex from the training set (47 atoms). These data indicate that PBE0/ZORA/TZVP/D3BJ/CPCM had better agreement to experiment when measured by RMSD_all (the use of dispersion reduced RMSD_all by 30%), while PBE0/ZORA/TZVP/CPCM performed slightly (4%) better when assessed using Δ. The RMSD values for both methods were comparable to those obtained for complex (8), indicating that these methods can work well for large complexes as well. The Δ values, while higher than those found for (8) by >2×, were still within the range found for other complexes in the training set and were smaller than Δ obtained for (1) (∼1.1%), (7) (∼1.1%), and (12) (∼2.2%).

Table 3 comparison of DFT results for complexes (15) and (8)

Complex	Number of atoms	Method	RMSDall (Å)	RMSDPt (Å)	Δ (%)
(15)	77	PBE0/ZORA/TZVP/CPCM	0.176	0.023	0.89
		PBE0/ZORA/TZVP/D3BJ/CPCM	0.118	0.023	0.93
(8)	47	PBE0/ZORA/TZVP/CPCM	0.153	0.024	0.41
		PBE0/ZORA/TZVP/D3BJ/CPCM	0.153	0.020	0.38

---

Fig. 3 Visual comparison of (a) the reported crystallographic structure (green) and the optimized structure (blue) of (15) using PBE0/ZORA/TZVP/CPCM and (b) the same comparison using PBE0/ZORA/TZVP/D3BJ/CPCM.

Case study 2: Prediction of bond metrics for a large complex

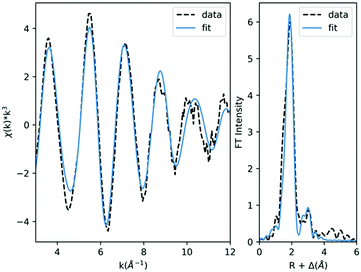
Lastly, to further test the performance of the two top DFT methods and get a better idea of how they will perform under “real world” conditions of predicting the metrics for an unknown structure, we applied them to tetrakis(triphenylphosphine)platinum(0) (16). This complex is considerably larger than any other in this investigation (137 atoms) and does not have a reported crystallographic structure, making it an ideal test case. As such, metrical data were obtained via newly-collected EXAFS which can be found in Table 4 and Fig. 4. The best fit to the data was obtained with three shells of scatterers: a shell of P scatterers at 2.32 Å and two shells of C scatterers at 3.61 Å and 3.80 Å; additional fits can be found in Table S11 (ESI†). The metrical results all match expectations except for the coordination numbers of the second and third shells, which are lower than would be expected for this complex; this discrepancy is likely the result of static disorder within the structure due to the large number of atoms at these distances.^75,76 Computationally, the starting structure was constructed in ChemCraft and then geometry optimized using both PBE0/ZORA/TZVP/CPCM and PBE0/ZORA/TZVP/D3BJ/CPCM; the calculated metrics were then compared with those determined experimentally (Table 5).

Table 4 EXAFS best fit parameters for (16)

Scatterer	N	R (Å)	σ ^2 × 10^−3 (Å^2)
ΔE0 = 1.42 eV. R-Factor = 0.041.
Pt–P	4	2.32	10.01
Pt–Cshort	5	3.61	7.60
Pt–Clong	5	3.80	9.50

---

Fig. 4 EXAFS and corresponding Fourier transform of (16) at the platinum L₃-edge.

Table 5 DFT results for (16)

Method	Pt–Paverage	Pt–Cshort	Pt–Clong
PBE0/ZORA/TZVP/CPCM	2.39	3.68	4.04
PBE0/ZORA/TZVP/D3BJ/CPCM	2.34	3.59	3.85
Experimental	2.32	3.61	3.80

---

While both DFT methods generally performed well in reproducing the experimental metrics, it is notable that PBE0/ZORA/TZVP/D3BJ/CPCM calculated a structure for (16) that matches the experimental data to within the precision of the EXAFS (±0.02 Å) for both the first and second shells of scatterers; even the weak third shell is reproduced to within 0.05 Å. On the other hand, PBE0/ZORA/TZVP/CPCM universally overestimated the metal–ligand distances, predicting first and second shell distances that are 0.07 Å too long and a third shell that is >0.2 Å too long.

These results convincingly demonstrate that the PBE0/ZORA/TZVP/D3BJ/CPCM method can reliably predict the geometric structure of large Pt-based complexes, even under the “real world” conditions where an experimentally-determined starting geometry is not available. This case study also highlights that, especially for large complexes, PBE0/ZORA/TZVP/D3BJ/CPCM has superior performance as compared to that of PBE0/ZORA/TZVP/CPCM and thus is the preferred method for the optimization of Pt-based complexes.

Conclusions

Herein we investigated the performance of DFT methods for their ability to reproduce the crystallographically-determined structures of platinum-containing complexes. Of the 80 methods tested, PBE0/ZORA/SVP/CPCM, PBE0/ZORA/TZVP/D3BJ/CPCM and PBE0/ZORA/TZVP/D3BJ/CPCM performed the best on our test set of 14 complexes. When the latter two of these methods were applied to a large platinum complex with a platinum oxidation state and ligand identities not found in the test set, they both produced good agreement with experiment, indicating the generally applicability of these methods. When challenged to predict the metrics of a complex without a reported crystallographic structure, the PBE0/ZORA/TZVP/D3BJ/CPCM method stood out as providing superior agreement to the metrics obtained from EXAFS. Taken together, we conclude that PBE0/ZORA/TZVP/D3BJ/CPCM is the preferred method to employ for the geometry optimization of platinum-containing complexes.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors thank the members of the ORCA forum for helpful discussions on solvation modeling and relativistic approximations. This work is based upon research conducted at the Center for High Energy X-ray Sciences (CHEXS) which is supported by the National Science Foundation under award DMR-1829070. This work was also supported by NSF-PREM: Center for Interfacial Electrochemistry of Energy Materials (CiE2M) under award DMR-1827622.

Notes and references

1. J. M. A. Harmsen, J. H. B. J. Hoebink and J. C. Schouten, Catal. Lett., 2001, 71, 81–90.
2. Y. Bing, H. Liu, L. Zhang, D. Ghosh and J. Zhang, Chem. Soc. Rev., 2010, 39, 2184–2202.
3. M. L. Kastens and R. Sutherland, Ind. Eng. Chem., 1950, 42, 582–593.
4. W. Oberhauser, C. Evangelisti, C. Tiozzo, F. Vizza and R. Psaro, ACS Catal., 2016, 6, 1671–1674.
5. A. M. Román, J. C. Hasse, J. W. Medlin and A. Holewinski, ACS Catal., 2019, 9, 10305–10316.
6. Y. Sun, M. Delucchi and J. Ogden, Int. J. Hydrogen Energy, 2011, 36, 11116–11127.
7. J. D. Kistler, N. Chotigkrai, P. Xu, B. Enderle, P. Praserthdam, C. Y. Chen, N. D. Browning and B. C. Gates, Angew. Chem., Int. Ed., 2014, 53, 8904–8907.
8. L. DeRita, S. Dai, K. Lopez-Zepeda, N. Pham, G. W. Graham, X. Pan and P. Christopher, J. Am. Chem. Soc., 2017, 139, 14150–14165.
9. X. P. Yin, H. J. Wang, S. F. Tang, X. L. Lu, M. Shu, R. Si and T. B. Lu, Angew. Chem., Int. Ed., 2018, 57, 9382–9386.
10. M. Torres, S. Khan, M. Duplanty, H. C. Lozano, T. J. Morris, T. Nguyen, Y. V. Rostovtsev, N. J. Deyonker and N. Mirsaleh-Kohan, J. Phys. Chem. A, 2018, 122, 6934–6952.
11. A. S. Hoffman, C. Y. Fang and B. C. Gates, J. Phys. Chem. Lett., 2016, 7, 3854–3860.
12. V. Klimavicius, S. Neumann, S. Kunz, T. Gutmann and G. Buntkowsky, Catal. Sci. Technol., 2019, 9, 3743–3752.
13. S. Todisco, G. Saielli, V. Gallo, M. Latronico, A. Rizzuti and P. Mastrorilli, Dalton Trans., 2018, 47, 8884–8891.
14. K. R. Koch and L. Engelbrecht, Dalton Trans., 2017, 46, 9303–9315.
15. I. S. Kim, Z. Li, J. Zheng, A. E. Platero-Prats, A. Mavrandonakis, S. Pellizzeri, M. Ferrandon, A. Vjunov, L. C. Gallington, T. E. Webber, N. A. Vermeulen, R. L. Penn, R. B. Getman, C. J. Cramer, K. W. Chapman, D. M. Camaioni, J. L. Fulton, J. A. Lercher, O. K. Farha, J. T. Hupp and A. B. F. Martinson, Angew. Chem., Int. Ed., 2018, 57, 909–913.
16. K. A. Lomachenko, E. Borfecchia, C. Negri, G. Berlier, C. Lamberti, P. Beato, H. Falsig and S. Bordiga, J. Am. Chem. Soc., 2016, 138, 12025–12028.
17. T. Strassner and M. A. Taige, J. Chem. Theory Comput., 2005, 1, 848–855.
18. M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. Neese, J. Chem. Theory Comput., 2008, 4, 1449–1459.
19. F. A. Cotton and X. Feng, J. Am. Chem. Soc., 1997, 119, 7514–7520.
20. Y. Minenkov, Å. Singstad, G. Occhipinti and V. R. Jensen, Dalton Trans., 2012, 41, 5526–5541.
21. M. Malik and D. Michalska, Spectrochim. Acta, Part A, 2014, 125, 431–439.
22. J. Vícha, M. Patzschke and R. Marek, Phys. Chem. Chem. Phys., 2013, 15, 7740–7754.
23. H. Gao, F. Xia, C. Huang and K. Lin, Spectrochim. Acta, Part A, 2011, 78, 1234–1239.
24. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
25. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
26. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
30. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
31. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137.
32. F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. F. Weigend, Phys. Chem. Chem. Phys., 2006, 22, 1057–1065.
35. D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229–2238.
36. D. A. Pantazis, X. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919.
37. D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684.
38. D. A. Pantazis and F. Neese, Theor. Chem. Acc., 2012, 131, 1292.
39. C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399.
40. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
41. E. van Lenthe, A. van der Avoird and P. E. S. Wormer, J. Chem. Phys., 1998, 108, 4783–4796.
42. A. Wolf, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 9215–9226.
43. M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956.
44. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
45. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
46. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
47. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
48. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
49. A. M. Amado, S. M. Fiuza, M. P. M. Marques and L. A. E. B. de Carvalho, J. Chem. Phys., 2007, 127, 185104.
50. S. M. Cybulski, Int. J. Quantum Chem., 2011, 111, 873–879.
51. N. Tasinato, C. Puzzarini and V. Barone, Angew. Chem., Int. Ed., 2017, 56, 13838–13841.
52. B. Efron, Ann. Stat., 1979, 7, 1–26.
53. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
54. J. J. Rehr, J. J. Kas, F. D. Vila, M. P. Prange and K. Jorissen, Phys. Chem. Chem. Phys., 2010, 12, 5503–5513.
55. Chemcraft - graphical software for visualization of quantum chemistry computations, https://www.chemcraftprog.com, accessed April 30, 2019.
56. G. Raudaschl, B. Lippert, J. D. Hoeschele, H. E. Howard-Lock, C. J. L. Lock and P. Pilon, Inorg. Chim. Acta, 1985, 106, 141–149.
57. K. Ha, Z. Kristallogr. - New Cryst. Struct., 2013, 228, 255–256.
58. S. Ohba, S. Sato, S. Yoshihiko, K.-I. Ohshima and J. Harada, Acta Crystallogr., 1983, B39, 49–53.
59. K. Ha, Z. Kristallogr. - New Cryst. Struct., 2012, 227, 31–32.
60. C. Mühle, J. Nuss, R. E. Dinnebier and M. Jansen, Z. Anorg. Allg. Chem., 2004, 630, 1462–1468.
61. J. A. Schlueter, R. J. Funk and U. Geiser, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2005, C61, m304–m306.
62. G. Avitabile, P. Ganis, U. Lepore and A. Panunzi, Inorg. Chim. Acta, 1973, 7, 329–330.
63. S. Otto and A. J. Muller, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, C57, 1405–1407.
64. M. Watabe, M. Kai, S. Asanuma, M. Yoshikane, A. Horiuchi, A. Ogasawara, T. Watanabe, T. Mikami and T. Matsumoto, Inorg. Chem., 2001, 40, 1496–1500.
65. K. v Luzyanin, P. v Gushchin, A. J. L. Pombeiro, M. Haukka, V. I. Ovcharenko and V. Y. Kukushkin, Inorg. Chem., 2008, 47, 6919–6930.
66. G. W. Horn, R. Kumar, A. W. Maverick, F. R. Fronczek and S. F. Watkins, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, C46, 10135–10137.
67. Z. Xue, M. J. Strouse, D. K. Shuh, C. B. Knobler, H. D. Kaesz, R. F. Hicks and R. S. Williams, J. Am. Chem. Soc., 1989, 111, 8779–8784.
68. K. Ha, Z. Kristallogr. - New Cryst. Struct., 2011, 226, 329–330.
69. D. J. Cardenas and A. M. Echavarren, Organometallics, 1999, 18, 3337–3341.
70. X. Zhou, J. Yang and C. Li, J. Phys. Chem. A, 2012, 116, 9985–9995.
71. T. Kinnunen and K. Laasonen, THEOCHEM, 2001, 540, 91–100.
72. H. Q. Wang, X. Y. Kuang and H. F. Li, J. Phys. Chem. A, 2009, 113, 14022–14028.
73. Z. J. Wu, Chem. Phys. Lett., 2005, 406, 24–28.
74. G. Berthon-Gelloz, O. Buisine, J.-F. Briere, G. Michaud, S. Sterin, G. Mignani, B. Tinant, J.-P. Declercq, D. Chapon and I. E. Marko, J. Organomet. Chem., 2005, 690, 6156–6168.
75. M. A. Beckwith, W. Ames, F. D. Vila, V. Krewald, D. A. Pantazis, C. Mantel, J. Pécaut, M. Gennari, C. Duboc, M. N. Collomb, J. Yano, J. J. Rehr, F. Neese and S. Debeer, J. Am. Chem. Soc., 2015, 137, 12815–12834.
76. M. J. Baldwin, T. L. Stemmler, P. J. Riggs-Gelasco, M. L. Kirk, E. P. H. James and V. L. Pecoraro, J. Am. Chem. Soc., 1994, 116, 11349–11356.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01851e

‡ These input files are representative of the majority of the calculations that were run. In a few isolated cases, it was necessary to increase the SCF/geometry convergence thresholds, gridx size, and the integration accuracy in order to obtain positive frequencies. An example of this is included in the ESI.†

§ Discussion of these effects can be found on the ORCA support forum, e.g. in the thread located here: https://orcaforum.kofo.mpg.de/viewtopic.php?f=11&t=1392.

---