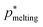Fcc vs. hcp competition in colloidal hard-sphere nucleation: on their relative stability, interfacial free energy and nucleation rate

Abstract

Hard-sphere crystallization has been widely investigated over the last six decades by means of colloidal suspensions and numerical methods. However, some aspects of its nucleation behaviour are still under debate. Here, we provide a detailed computational characterisation of the polymorphic nucleation competition between the face-centered cubic (fcc) and the hexagonal-close packed (hcp) hard-sphere crystal phases. By means of several state-of-the-art simulation techniques, we evaluate the melting pressure, chemical potential difference, interfacial free energy and nucleation rate of these two polymorphs, as well as of a random stacking mixture of both crystals. Our results highlight that, despite the fact that both polymorphs have very similar stability, the interfacial free energy of the hcp phase could be marginally higher than that of the fcc solid, which in consequence, mildly decreases its propensity to nucleate from the liquid compared to the fcc phase. Moreover, we analyse the abundance of each polymorph in grown crystals from different types of inserted nuclei: fcc, hcp and stacking disordered fcc/hcp seeds, as well as from those spontaneously emerged from brute force simulations. We find that post-critical crystals fundamentally grow maintaining the polymorphic structure of the critical nucleus, at least until moderately large sizes, since the only crystallographic orientation that allows stacking close-packed disorder is the fcc (111) plane, or equivalently the hcp (0001) one. Taken together, our results contribute with one more piece to the intricate puzzle of colloidal hard-sphere crystallization.

---

I. Introduction

The formation of a crystalline embryo within a metastable fluid is an activated process that requires the surmounting of a free energy barrier.^1,2 A subtle interplay between the nucleus interfacial free energy, its size, and the chemical potential difference between the emerging crystal and the surrounding metastable liquid, critically controls the appearance, and consecutive growth or dissolution of the rising nuclei.³ However, most of these magnitudes, that regulate the ephemeral stability of the nuclei, are hardly accessible through standard experimental setups.⁴ Moreover, the sizes of the critical nuclei, those capable to drive the phase transition, are usually rather small and exhibit fast growth after their emergence, which on top of their stochastic nature, make extremely challenging their direct observation.^5–8 Nonetheless, impressive efforts to detect the in situ formation of crystalline embryos with atomistic resolution, as recently performed for NaCl nanocrystals⁹ or prenucleating clusters of metal–organics frameworks¹⁰ are continuously ramping up.

On the other hand, colloidal science is enormously contributing in advancing our understanding on the governing principles in liquid-crystal nucleation.^4,11–15 Colloids, besides displaying a wide range of fascinating and technological applications,^16,17 and behaving as tunable building blocks in self-assembly materials,^18,19 represent one of the few systems in which the evolution of the nuclei can be directly monitored from the surrounding fluid.^5,8 Because of their slow motion and large particle size, typically of the order of a few hundreds of nanometers, colloidal suspensions are well suited systems to unveil the mechanisms by which crystalline clusters induce the liquid-to-solid transition.^8,20–22 Moreover, real imaging of colloidal particles can provide useful insights on the cluster critical sizes, incubation times, or size and shape evolution of the different emerging nuclei.^5,23 However, different experimental challenges such as avoiding heterogeneous nucleation from the sample container²⁴, accurately controlling the colloidal packing fraction of the systems²⁵, or obtaining density matched suspensions,^26,27 hamper the execution of these experiments.

A very appealing alternative strategy to complement our molecular and thermodynamic understanding on nucleation and crystallization phenomena are computer simulations.^28–32 Pioneering landmark studies such as those of Alder and Wainwright³³, Hoover and Ree³⁴ or Barker and Henderson³⁵ were crucial in our understanding of hard-spheres and its fluid–solid transition. Molecular simulations, besides being highly suitable to fit the typical sizes and timescales of the rising nuclei, can provide invaluable information on the shape, composition, structure, and subsequent growth of the clusters.^36–40 Moreover, crucial thermodynamic aspects that are not experimentally accessible, such as nucleation free energy barriers, kinetic pre-factors, chemical potential differences, or cluster interfacial free energies, can be conveniently estimated from molecular simulations.^28,30,41,42 Outstanding information about these key magnitudes on the homogeneous crystallization of colloidal hard-spheres,^{28–30,37,43} water,^44–52 alloys,^53,54 Argon^42,55,56 or even electrolytic aqueous solutions^39,40,57 have been provided through molecular simulations. Remarkably, more recently a huge effort on expanding our knowledge on heterogeneous nucleation of colloidal particles,^{24,38,58–61} but also of water,^50,62–64 as well as on crystal growth prevention through antifreeze surfaces^65–68 is being devoted.

However, despite the fact that multiple approaches and successful numerical methods^69–73 proposed over the last six decades have led to important advances on the field, yet some significant discrepancies on specific system magnitudes respect to the experimental predictions (e.g., the homogeneous nucleation rate of hard-spheres at moderate supersaturation^{4,11–13,74,75}) or the limitations of certain theoretical frameworks, persist unresolved.⁷⁶ For instance, the validity of the Classical Nucleation Theory (CNT)^77,78 to successfully describe nucleation in widely diverse scenarios is still a matter of debate.^76,79–81 While a considerable body of literature supports its applicability to provide fair predictions on the nucleation behaviour of many substances,^82–85 as for the case of hard-spheres,^29,55,86 other substantial studies have pointed out its limitations when describing certain specific systems^87–90 (even for hard-spheres⁸¹), or when assuming different approximations (i.e., the capillary approximation: the fact that the surface tension of a planar interface is roughly the same as that of the clusters).⁹¹ In that respect, the nucleation mechanisms of certain ‘so-called’ simple fluids such as hard-sphere colloidal particles,^36,74,81,92 water,^44,93–95 or Lennard-Jones fluids^96,97 remain yet hotly debated.

On top of the aforementioned considerations to reach a consensus on crystal nucleation, certain substances also present an additional challenge: different crystal polymorphs that tightly compete for nucleating from the same metastable fluid. The most common liquid-to-crystal phase transition on Earth, ice nucleation, presents two competing ice polymorphs, ice I_c and I_h, which evenly compete for driving crystallization at normal pressure.^98–101 Even though both polymorphs present highly similar stability¹⁰², and despite ice I_h is the thermodynamically most stable phase below 0 Celsius degrees at ambient pressure¹⁰³, the formation of the critical nuclei and their growth, is mediated by a stacking disordered mixture of ice I_c and I_h (I_sd).^95,99,102 In a similar way, at about 2000 bar, ice I and III equally compete in stability and propensity to nucleate,^104,105 although between these two polymorphs ice stacking mixtures cannot be attained. But polymorphic competition is not at all an exclusive feature of water, also in colloidal suspensions of oppositely charged colloids¹⁰⁶, different crystal polymorphs with positionally-charge order and disorder tightly play to nucleate from the same metastable fluid at moderate temperature and high pressure.^89,107 Additionally, in Lennard-Jones supercooled fluids, it has been shown how polymorphic selection can be finely tuned in order to promote either body-centered cubic (bcc) or face-centered-cubic (fcc) crystallization.⁹⁷ Moreover, it has been found that fcc crystallites also present a notable abundance of hexagonal-closed packed (hcp) clusters.¹⁰⁸

In hard-sphere colloids, it has been extensively studied the relative stability of fcc vs. hcp crystals, concluding that the difference in their free energy is almost negligible, being the fcc phase marginally more stable than the hcp one.^109–115 This consensus has entailed a considerable volume of free energy calculations^109,113,116 over more than two decades. Nonetheless, little is known about their relative interfacial free energies, or their ability to nucleate from the same metastable fluid (i.e., nucleation rate). The scarce available data suggests that nucleation at high packing fraction might be mediated by both polymorphs, since both were found present in small critical nuclei^36,74 and post-critical crystallites.¹¹⁷ In this work, we aim to narrow down this gap by characterizing in detail the most relevant thermodynamic and kinetic magnitudes controlling their polymorphic competition, such as their chemical potential difference (i.e., relative stability), the interfacial free energy of their different crystal faces, and the nucleation rate of the two different competing polymorphs as well as that of stacking disordered nuclei of both phases. Moreover, we investigate the abundance of each polymorph in grown crystallites over a wide range of supersaturation conditions. Overall, our work contributes to clarify the intricate relation between these two highly similar close-packed phases on colloidal hard-sphere crystallization.

II. Results

A. Fcc and hcp melting pressure and relative stability

To model hard-sphere (HS) colloids, we employ the Pseudo-hard-sphere (PHS) continuous potential proposed by Jover et al.¹¹⁸ which quantitatively reproduces many properties of the HS phase behaviour such as the melting pressure,¹¹⁹ equation of state,¹¹⁸ diffusion coefficient,¹²⁰ surface tension¹²¹ and nucleation rate among many others.⁸⁶ The expression for the PHS potential is given by:where the diameter of the hard-sphere particles is represented by σ, λ_a =49 and λ_r = 50 are the exponents of the attractive and repulsive terms respectively, ε_R accounts for the energy shift of the pseudo hard-sphere interaction and r is the distance between two PHS particles. The main advantage of the PHS potential is that it conveniently enables the use of efficient and parallel standard Molecular Dynamics (MD) simulation packages, such as LAMMPS¹²² or GROMACS¹²³, to perform hard-sphere simulations. However, to correctly describe the phase behaviour of standard HS, temperature needs to be fixed at T* = 1.5.¹¹⁸ Here, we employ reduced units as follows: reduced temperature is defined as T* = k_BT/ε_R, reduced pressure as p* = pσ³/k_BT, reduced density as ρ* = (N/V)σ³, and the unit of time as τ = σ²/6D_L, where D_L is the liquid diffusion coefficient at each corresponding state, σ our unit of distance (and the molecular diameter of the hard-spheres), and k_BT our unit of energy. For PHS simulations, in the practice, one can also use the parameters for the Lennard-Jones potential for Argon (i.e., σ = 3.405 Å, ε_R/k_B = 119.87 K, m = 6.63 × 10⁻²⁶ kg and T = 179.81 K) and then convert the output of the MD simulation package from real to reduced units.

We evaluate the melting pressure (in reduced units) of the fcc and hcp crystal phases with the fluid by means of Direct Coexistence (DC) simulations.^124,125 To accurately compute the melting pressure, we perform DC simulations of different system sizes to account for possible finite-size effects (see Fig. 1(a)). We find that for moderately small system sizes (<6000 HS particles including both phases), the melting pressure of the hcp phase is slightly lower than that of fcc crystals (see Table 1). However, when we extrapolate our results to infinitely large system sizes (1/N_tot → 0), the melting pressure of both phases is the same within the uncertainty of our calculations (see Fig. 1(b) and Table 1). We also compare our estimations of (using LAMMPS¹²² and the Np_zT anisotropic ensemble with the barostat only applied in the z direction) with those computed by some of us¹¹⁹ for the fcc phase using GROMACS¹²³ and both the anisotropic NpT ensemble in all directions (up triangles) and only in the z direction (i.e., the perpendicular direction to the fluid–solid interface, down triangles). In all cases, the same is predicted in the thermodynamic limit (independently of the chosen ensemble or MD package). Given that a finite-size scaling study of the fcc phase was already reported in ref. 119, here we only perform the finite-size study for the hcp phase. For both crystal phases we find that smaller system sizes tend to stabilize the solid respect to the fluid, and thus, underestimate the melting pressure.

Fig. 1 (a) Snapshots of direct coexistence (DC) simulations of a fcc crystal (top), hcp crystal (middle), and a stacking disordered hcp/fcc mixture (bottom) with a liquid at p* = 11.65. Fcc-like particles are coloured in black, hcp-like in orange, and liquid-like in grey. To discriminate between different particle environments, we employ the q̄₄–q̄₆ local order parameter proposed by Lechner and Dellago¹²⁶ as it will be further explained in Sections IIB and D. (b) Melting pressure of the different crystal phases as a function of the inverse of the total number of particles in our DC simulations. Note that in the initial configuration of our DC simulations half of the HS particles correspond to the crystal phase and the other half to the fluid one. Filled orange circles represent the obtained values with hcp crystal slabs for different system sizes, black squares those using fcc-like slabs, and the green triangle for a stacking disordered crystal slab of randomly alternated fcc and hcp layers along the fcc (111) crystallographic orientation as shown in (a) bottom. Empty symbols account for the linearly extrapolated melting pressure at infinitely large system size of the pure fcc (black) and hcp (orange) crystals. The fcc melting pressures with the fluid reported by Espinosa et al.¹¹⁹ for the PHS potential evaluated for different system sizes and simulation ensembles are also included.

Table 1 Melting pressure and system size details of our direct coexistence simulations for the fcc, hcp and for a stacking disordered crystal slab of randomly alternated hcp and fcc layers (Fig. 1(a), bottom). The extrapolated pressure of our DC simulations to infinitely large system size is also included. Please note that while the section of our DC simulation box remains constant over time, the long side z (for which we provide its initial value after quick equilibration) varies over time to accommodate the desired pressure (Np_zT barostat). The z axis is perpendicular to the fluid–solid interface which is parallel to the x, y plane. Moreover, for the hcp DC simulations, please note that the angles between x and y box sides correspond to 60 and 120 degrees

Crystal phase	N total	Box dimensions (x, y, z)/σ
fcc	8000	15.7 × 15.7 × 33.2	11.666(20)
fcc	39 304	26.7 × 26.7 × 56.9	11.666(10)
fcc	N → ∞	—	11.666(10)
hcp	2916	9.6 × 9.6 × 34.1	11.602(20)
hcp	5808	12.1 × 12.1 × 46	11.625(10)
hcp	23 328	19.8 × 19.8 × 69.3	11.645(10)
hcp	42 592	24.5 × 24.5 × 84.6	11.650(10)
hcp	N → ∞	—	11.653(10)
Stacking mixture	5324	12.2 × 9.9 × 45	11.650(10)

---

Furthermore, we compute the melting pressure for a close-packed crystal with stacking fcc/hcp disorder in which AB or ABC stacking is randomly alternated along the fcc (111) crystal orientation (see Fig. 1(a), bottom). In this solid, hybrid stacking is reached by periodically and randomly alternating after an initial given hexagonal close-packed 2-dimensional layer (say A), a consecutive layer of one of the two other possible stacking planes (randomly selected, say B or C), along the (111) orientation. This process is repeated successively until we get a large enough crystal. In this way, the obtained stacking disordered solid will approximately contain half fcc-like and half hcp-like particles. Before placing the stacking disordered crystal in contact with the fluid, we verify by means of the q̄₄ local order parameter¹²⁶, (which will be further explained later in Section IIB), that the amount of fcc-like vs. hcp-like particles in the hybrid crystal are commensurate. Then, we perform DC simulations for a moderately large solid of ∼2750 crystal particles in coexistence with ∼2750 fluid particles. We recover the same (green triangle) within the uncertainty as those obtained for the pure fcc and hcp crystals, being this result in agreement with free energy calculations of Woodcock for hybrid structures of the unit stacking type –ABCAB–.¹¹⁴ Since the difference in the melting pressure between pure fcc and hcp crystals in the thermodynamic limit is below our uncertainty (<1/1000), and we have already recovered the same 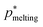(within the error) for a moderately large stacking hcp/fcc crystal, we assume that for arbitrarily large randomly stacked crystals the same rule will hold. Nevertheless, we note that it would be interesting, if possible (due to the extremely small differences in stability), to elucidate whether the melting pressure of the stacking mixture is in between both pure crystals, or even slightly more stable than them due to further entropic stabilization caused by the randomly stacking layering. However, resolving those minor differences in stability are out of the scope of our work due their negligible role in determining the nucleation and crystallization scenario in hard-sphere colloids.

Even though DC simulations cannot achieve the required level of accuracy to unequivocally discriminate whether fcc crystals are marginally more stable than hcp ones, we can fairly argue that the continuous PHS potential for colloidal hard-spheres also recovers the very similar stability of both polymorphs widely investigated in pure HS by means of free energy calculations.^109–115 The reported free energy difference for pure HS between both polymorphs is so small (<1/1000)¹¹², that even considering that this would be also the case for the PHS model¹¹⁸, its implications on the polymorphic nucleation competition of these two crystals would be still much smaller than the current uncertainty of the rare-event methods ordinarily used to predict nucleation barriers and nucleation rates.^55,69–73 Therefore, for our purpose, the ∼0.1% uncertainty in DC simulations is acceptable. We also note that the most accepted melting pressure for pure HS is p* = 11.567.¹²⁷ Therefore, even small, there is a slight difference in the predicted melting pressure through the PHS potential (p* = 11.66) compared to that of pure HS.

To compute the relative stability of the different solids with the fluid, and also among them, as a function of pressure (the magnitude which controls the degree of metastability in the HS fluid), we evaluate the equation of state (EOS) of the fluid and of the different crystal polymorphs (see Fig. 2). We find that both fcc and hcp crystals, as well as the stacking mixture of both of them, show a remarkably similar EOS. Given that the melting pressure of the three crystal solids and their equation of state is the same within the uncertainty of our calculations (∼0.1%), when performing thermodynamic integration¹²⁷ to compute the chemical potential difference between each solid and the fluid, Δμ, we obtain a single curve where the three solids overlap within their uncertainty (Fig. 2 inset). To carry out the thermodynamic integration of the three polymorphs we consider the following melting pressures: 11.666 for the fcc crystal, 11.653 for the hcp phase, and 11.65 for the stacking disordered fcc/hcp mixture (being the uncertainty in the determination of all of them ∼0.01 p* as indicated in Fig. 1(b) and Table 1. Our results of Δμ clearly demonstrate the negligible stability difference along pressure between hcp and fcc phases (Fig. 2 inset), as previously highlighted by multiple free energy calculations for conventional hard-spheres.^109–115

Fig. 2 Equation of state (in packing fraction ϕ = ρ*(π/6) for the fluid (blue), fcc phase (black), hcp (orange) and for a stacking disordered crystal of randomly alternated fcc and hcp layers along the fcc (111) crystallographic orientation (green). Inset: Chemical potential difference (Δμ) between the different crystal phases and the fluid as a function of pressure (in reduced units). The same colour code of the main figure is applied in the inset. Please note that, within the uncertainty, the three Δμ curves overlap into a single one despite considering the slightly different melting pressure of each solid phase (<0.1%) along the thermodynamic integration.

B. Interfacial free energy of fcc and hcp crystal phases

Since the chemical potential difference to drive crystallization in fcc and hcp crystals is remarkably alike, we now focus on the interfacial free energy (γ) of both phases. To that end, we employ the mold integration (MI) method^121,128 to evaluate γ for several different crystallographic orientations of both solids. This technique allows the direct calculation of γ between the solid and its melt by reversibly computing the free energy work needed to induce the formation of a thin crystal slab at coexistence conditions (in our case at the melting pressure). The Gibbs free energy work, ΔG, to reversibly form the slab from the fluid can be directly related to the interfacial free energy as:

ΔG = 2Aγ; (2)

where 2A refers to the area of the two interfaces that the crystal slab exposes to the fluid. The formation of the crystal slab is induced by switching on an attractive interaction between the mold of potential energy wells and the fluid particles. The wells are placed at the equilibrium particle positions of the crystal (fcc or hcp) plane of interest at coexistence conditions. By gradually switching on the interaction between the potential wells and the fluid particles, we directly compute the required free energy work ΔG to induce the slab. Within this method, γ is computed as follows:where N_w is the total number of wells in the mold, and 〈N_fw(ε)〉 is the average number of filled wells through a Np_xT simulation for potential wells of ε depth (the barostat in the simulation is only applied in the perpendicular direction to the crystal–fluid interface). The method consists on performing a thermodynamic integration along the path in which the depth of the potential mold wells is gradually increased to a maximum value of ε_m. The integral of eqn (3) must be reversible, and to ensure its reversibility, the crystal structure induced by the mold must quickly melt when the interaction between the potential wells and the fluid is switched off. To that end, the thermodynamic integration has to be performed at well radii (r_w) that are wider than the optimal one, r^o_w, at which the crystal slab is fully formed, and thus, its stability does no longer depend on the mold–fluid interactions. In practice, γ(r_w) can be estimated for several values of r_w > r^o_w, and then, be extrapolated to r^o_w, which is the well radius that provides the correct value of γ. In that respect, the uncertainty in γ fundamentally comes from the statistical error to determine the optimal r^o_w. For a detailed explanation of how to identify r^o_w and the associated uncertainty in γ for a given system, please see ref. 121.

We evaluate the interfacial free energy for the (100), (110) and (111) fcc crystal faces, and for the (0001), (112̄0) and (101̄0) hcp planes. Note that the fcc (111) and hcp (0001) crystal orientations are equivalent. In Fig. 3(a), we plot the value of γ for different crystal orientations of both polymorphs (fcc in black and hcp in orange) as a function of r_w. Filled symbols represent our γ(r_w) estimations using eqn (3) at r_w values in which the thermodynamic integration is reversible, and empty symbols depict the value of γ linearly extrapolated to the optimal r^o_w in which the free energy work of creating the crystal slab is fully recovered. In Table 2, we report the obtained values of γ at r^o_w for the different studied crystal orientations as well as the employed system sizes. To ensure that our estimations of γ were not affected by significant finite-size effects, we perform calculations for the fcc (111) plane with a system size approximately two times larger (orange squares with black borders) than those typically used for the rest of the planes, obtaining within the uncertainty, the same value of γ that we found when using a regular system size (Fig. 3(a) and Table 2). As it can be noticed, our results for the fcc (100), (110) and (111) (or hcp (0001)) are in reasonable agreement with previous estimations.^129–133 However, to the best of our knowledge, for the (112̄0) and (101̄0) hcp planes there is no available data. We note that the anisotropy of the different crystal faces of both polymorphs is rather modest. Nonetheless, the (112̄0) plane of the hcp crystal shows a slightly higher γ than any of those found for the fcc polymorph. This marginally higher surface tension of the hcp crystal could slightly lower its propensity to nucleate from the fluid compared to that of the fcc phase as it will be shown in the following section.

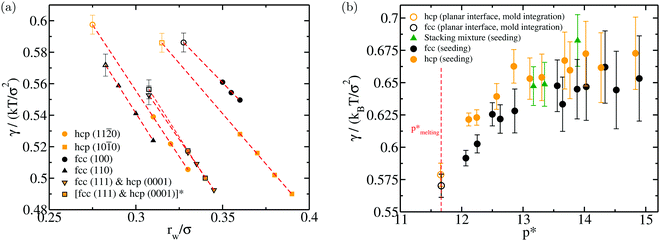Fig. 3 (a) Interfacial free energy for a planar fluid–solid interface as a function of r_w for different fcc (black) and hcp (orange) crystal orientations computed through the Mold Integration method.¹²¹ Filled symbols indicate the values of γ obtained at r_w values where the thermodynamic integration was performed (i.e., the formation of the slab is reversible), while empty ones account for the linearly extrapolated values of γ to r^o_w, where the crystal slab is fully formed, and thus, the exact required free energy work to create the slab is reached. Please note that since the (111) fcc and (0001) hcp planes are equivalent, a single calculation for both crystal orientations has been performed. Additionally, for this crystal orientation we perform calculations for two system sizes: 5880 HS particles (down orange triangles with black borders) and 11 760 HS (orange squares with black borders). (b) Averaged γ (for planar fluid–solid interfaces) of the different crystal orientations computed in (a) for each polymorph at coexistence conditions (empty circles). For the fcc crystal (black), we plot the mean of the (100), (110) and (111) γ values, while for the hcp (orange) the γ average of the (112̄0), (101̄0) and (0001) planes. Filled circles depict the interfacial free energy of the inserted fcc (black), hcp (orange) and stacking disordered (green) spherical clusters of our Seeding simulations.

Table 2 Interfacial free energy (in k_BT/σ²) of several different crystal orientations of each polymorph evaluated by means of the Mold Integration technique¹²¹ at the liquid-crystal coexistence pressure. The system sizes of the different crystal orientation calculations were the following: fcc (100): 3136 HS particles, 98 potential wells and 10.968 × 10.968 σ⁻² box cross-section area; fcc (110): 5120 HS particles, 98 potential wells and 15.515 × 11.044 σ⁻² box cross-section area; fcc (111) and hcp (0001): medium size; 5880 HS particles, 168 potential wells and 15.509 × 11.512 σ⁻² box cross-section area, and large size: 11 760 HS particles, 336 potential wells, and 15.509 × 23.025 σ⁻² box cross-section area (since γ is the same within the uncertainty for both system sizes – 0.553(6) for the medium system size and 0.555(6) for the large one – the provided value in the table is an average of both system sizes); hcp (112̄0): 4860 HS particles, 108 potential wells and 17.269 × 10.855 σ⁻² box cross-section area; hcp (101̄0): 2430 HS particles, 120 potential wells (arranged in two layers) and 11.078 × 10.855 σ⁻² box cross-section area. Notice that previous estimations were obtained for the standard HS potential, whereas the results of this work have been obtained for the pseudo-hard-sphere continuous potential (PHS). However, we do not expect significant differences between these two potential models

	fcc (100)	fcc (110)	fcc (111) and hcp (0001)	hcp (112̄0)	hcp (101̄0)
This work	0.586(6)	0.572(7)	0.554(6)	0.597(6)	0.586(6)
Davidchack (2010)^129	0.582(2)	0.559(2)	0.542(3)	—	—
Benjamin et al. (2015)^130	0.596(6)	0.577(4)	0.556(3)	—	—
Schmitz et al. (2015)^131	0.581(3)	0.559(1)	0.544(8)	—	—
Bültman et al. (2020)^132	0.591(11)	—	—	—	—

---

Next, we apply the Seeding technique^85,134,135 to explore what Classical Nucleation Theory^77,78 in combination with computer simulations can teach us about the polymorphic fcc vs. hcp competition in hard-spheres, as well as on the interfacial free energy of both solids. To that aim, we embed spherical crystal seeds of both polymorphs, ranging from ∼200 to ∼95 000 particles into metastable HS fluids of about 15–25 times larger than the size of the inserted clusters. Clusters with spherical shape are inserted since that geometry is the one that better optimises the surface/volume ratio of a cluster, and hence, minimises the interfacial free energy penalty that can destabilise it. Moreover, in ref. 102 and 136 it has been shown how when performing Seeding simulations with cubic crystal seeds, they rapidly equilibrate into spherical shapes before even growing or melting, thus, supporting our choice of spherical shapes. We quantify the number of particles in the critical clusters (N_c) by means of the q̄₄–q̄₆ local order parameter proposed by Lechner and Dellago¹²⁶ using the mislabelling criterion.^55,137 We determine the optimal q̄₄ and q̄₆ thresholds as a function of pressure with the mislabelling criterion as shown in ref. 107 to distinguish among fluid-like and solid-like particles (q̄₆), and to discriminate between fcc-like and hcp-like solid particles (q̄₄). The optimal q̄₆ and q̄₄ thresholds as a function of pressure are described by the following linear equations: q̄_6t,fcc = 0.133 + 0.01819p* for distinguishing between fcc-like and fluid-like particles, q̄_6t,hcp = 0.14883 + 0.014595p* for hcp-like and fluid-like particles and q̄_6t,sm = 0.1667 + 0.01392p* for distinguishing between stacking disordered fcc/hcp-like and fluid-like particles, where larger q̄_6,t values than those given in the fits account for solid-like particles and lower ones for liquid-like particles. The q̄₄ threshold for discriminating between fcc-like and hcp-like particles is: q̄_4t = 0.09019 + 0.002906p*, where q̄_4t values greater than those given in the fit indicate fcc-like environment and lower values than q̄_4t hcp-like one. These thresholds have been optimized for a pressure range between p* = 11.65 and p* = 17. The cut-off distance for computing both q̄₄ and q̄₆ parameters and identifying the biggest solid cluster has been 1.35σ. We note that for distinguishing fcc-like and hcp-like particles, the w̄₄ parameter can be also employed, however, this parameter cannot be successfully used to discriminate between hcp-like and liquid-like particles¹²⁶, therefore, we choose a combination of the q̄₄–q̄₆ parameters to identify the number and type of solid-like particles in our Seeding simulations and to distinguish fcc from hcp solids.

In Table 3, we report the number of particles of the critical cluster (N_c) of each polymorph, as well as those obtained for the stacking disordered fcc/hcp nuclei. For the different inserted clusters, we determine the pressure at which they become critical , that is when the probability (out of ten independent trajectories) of growing or shrinking is roughly the same. By means of the CNT expression for the interfacial free energy of a spherical cluster, we estimate γ as:

where is the number solid density at the pressure at which the cluster becomes critical, and Δμ the chemical potential difference between the crystal and the fluid at the same conditions. Given that the dependence of and Δμ as a function of pressure for the three solids has been already evaluated in Fig. 2, we can now conveniently estimate γ for all the different clusters.

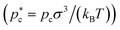Table 3 Value of the number of particles of the critical cluster (N_c), liquid packing fraction (ϕ_l) and pressure at which clusters were found critical, reduced liquid and solid densities at such pressure (where ρ* = (N/V)σ³), chemical potential difference between the solid and the fluid (Δμ* = Δμ/(k_BT)) at those conditions, interfacial free energy of the cluster (γ* = γ/(k_BT/σ²)), nucleation free energy barrier , attachment rate (f⁺* = f⁺/(6D_L/σ²), being D_L the diffusion coefficient of the fluid particles in bulk at the given conditions, and 6D_L/σ² the required time for a particle to diffuse its molecular diameter), and decimal logarithm of the nucleation rate (log₁₀[J/(6D_L/σ⁵)]) for fcc, hcp and stacking disordered fcc/hcp crystalline clusters of our Seeding simulations

N c	ϕ l				Δμ*	γ*		f ^+*	log10 J
fcc
232	0.5213	14.895	0.996	1.104	−0.321	0.653	37.21	2277	−14.87
322	0.5184	14.52	0.990	1.098	−0.285	0.644	45.85	1472	−18.91
426	0.5169	14.337	0.987	1.094	−0.267	0.662	56.89	2704.6	−23.52
573	0.5145	14.03	0.983	1.089	−0.237	0.647	67.97	3548	−28.31
690	0.5133	13.882	0.980	1.086	−0.223	0.645	76.85	5494	−32.03
918	0.5113	13.645	0.976	1.081	−0.199	0.633	91.54	6842.5	−38.40
1124	0.5105	13.558	0.975	1.079	−0.191	0.648	107.25	3089	−45.62
4070	0.5045	12.865	0.963	1.065	−0.122	0.628	247.53	4299	−106.79
7700	0.5023	12.628	0.959	1.060	−0.098	0.622	376.07	7550	−162.55
12 092	0.5012	12.50	0.957	1.057	−0.085	0.625	511.98	9501	−221.61
31 595	0.4988	12.253	0.953	1.051	−0.059	0.603	939.02	21 085	−407.01
95 520	0.4971	12.068	0.949	1.047	−0.040	0.5916	1932.58	79 700	−838.25
hcp
266	0.5208	14.834	0.995	1.103	−0.316	0.673	42.00	2687	−16.92
453	0.5164	14.272	0.986	1.093	−0.262	0.662	59.28	3813	−24.43
642	0.5144	14.023	0.982	1.088	−0.237	0.672	76.23	4054	−31.86
857	0.5123	13.765	0.978	1.083	−0.212	0.660	90.94	5480	−38.20
1005	0.5116	13.679	0.977	1.082	−0.204	0.667	102.39	5439	−43.23
1750	0.5084	13.306	0.971	1.074	−0.167	0.654	145.98	8935	−62.11
2546	0.5067	13.111	0.968	1.070	−0.147	0.653	187.63	7715	−80.37
4830	0.5043	12.85	0.963	1.065	−0.121	0.663	292.73	9553	−126.11
9739	0.5018	12.57	0.958	1.058	−0.093	0.639	452.55	12 985	−195.59
34 194	0.4988	12.245	0.953	1.051	−0.060	0.623	1023.40	33 886	−443.47
72 578	0.4975	12.115	0.950	1.048	−0.047	0.621	1689.32	50 675	−732.71
Stacking disordered mixture
799	0.5133	13.89	0.980	1.086	−0.224	0.683	89.68	3253	−37.86
1577	0.5088	13.35	0.972	1.075	−0.171	0.649	135.00	6941	−57.42
2199	0.5072	13.17	0.969	1.071	−0.153	0.647	168.54	6324	−72.12

---

In Fig. 3b, we show the obtained γ values for the different cluster sizes of each polymorph and those of stacking disordered fcc/hcp clusters. For both polymorphs (and the stacking mixture), the interfacial free energy moderately increases with pressure. However, the estimated γ from our Seeding simulations cannot be ascribed to any specific crystal orientation rather than to a curved interface which contains different contributions of distinct crystal orientations. This behaviour of γ with pressure was already known for the fcc crystal phase,^29,55,86,138 and it has also been recently reported for oppositely charged colloidal hard-spheres.¹⁰⁷ We find that at high pressure (i.e., p* > 14), the interfacial free energy of both polymorphs is rather similar (within the uncertainty of our calculations), however, at low pressure (i.e., p* < 13), γ is slightly lower for fcc clusters. Even though these results might be biased by the employed local order parameter, the qualitative prediction that fcc clusters might show lower γ than hcp ones, is in agreement with our observations at coexistence conditions for different crystal planes with the Mold Integration method.¹²¹ In fact, a linear extrapolation to coexistence of the predicted γ by the largest clusters of both polymorphs reasonably agrees with the averaged estimation of the different crystal planes of each polymorph by Mold Integration (Fig. 3(b)), evidencing the reliability of the chosen local order parameter and the mislabelling criterion.^55,137 On the other hand, when the inserted clusters present stacking disordered fcc/hcp layering (green triangles), the interfacial free energy is roughly in between those of pure fcc and hcp clusters. Given that Δμ is highly similar in both polymorphs, the slightly lower γ of fcc clusters reduces the required size, or number of particles in the critical cluster, needed to overcome the nucleation free energy barrier as shown in Table 3. Interestingly, it can be also noticed how the slope of γ vs. pressure moderately decreases in the high pressure regime for both polymorphs, although the large uncertainty in those estimations on top of the impossibility of performing Seeding simulations at higher pressures, avoids the accurate determination of γ in this regime. Nevertheless, we note that when linearly fitting and extrapolating our γ values as a function of pressure, we recover the brute force nucleation rates computed at very high pressure (p* > 17), therefore, suggesting that γ is likely to monotonically augment with pressure (rather than having a maximum) at least up to p* < 18.5. That would indicate that the free energy barrier for nucleation is different from zero even when nucleation is found in brute force simulations, suggesting that the free energy barrier is finite and small, so that it is accessible via thermal fluctuations.

C. Nucleation competition of hcp and fcc crystal polymorphs

In the previous sections, we have analysed the different factors that critically control the propensity of a system to nucleate: Δμ and γ. Now, by means of the Classical Nucleation framework,^77,78 we evaluate the nucleation rate J, the number of critical nuclei per unit of time and volume, of the different crystal phases. The CNT expression for J is:where ΔG_c/(k_BT) is the nucleation free energy barrier and f⁺ is the frequency of particle attachment/detachment to the critical cluster, which can be computed as²⁸:being N(t) the number of particles of a cluster around the top of the free energy barrier at a given time t. To determine f⁺, we perform 10 independent short trajectories at the pressure at which each cluster was found critical avoiding substantial growth or shrinkage to ensure that the cluster remains critical along the whole trajectory, and then we apply eqn (6). In Table 3, we provide the obtained values for the different magnitudes needed to compute J by means of eqn (5), as well as the decimal logarithm of the nucleation rate. Moreover, in Fig. 4, we plot our Seeding estimations of J for both polymorphs as a function of the liquid packing fraction (ϕ_l). The fcc nucleation rates (black squares) are marginally higher than those from hcp clusters (orange ones), and widely similar to those of stacking disordered clusters (green squares). In fact, the uncertainties of all of them partially overlap, although it consistently seems that J is slightly higher for fcc clusters than for hcp ones along the studied supersaturation conditions. We also find a remarkable agreement between our Seeding estimations (slightly better for fcc rates) and brute force simulations (cyan diamonds) at high liquid packing fraction, which highlights once again, the validity of the Classical Nucleation Theory to describe hard-sphere nucleation.^29,55,86 Moreover, a very good agreement with previous Umbrella Sampling^28,30 and Forward Flux Sampling calculations³⁰ of pure HS is achieved, exhibiting again the reliability of the chosen local order parameter¹²⁶ and the mislabelling criterion^55,137 within the Seeding framework. Nucleation rates considering hydrodynamic effects for the Weeks–Chandler–Andersen (WCA) model¹³⁹ at moderate¹⁴⁰ and very high¹⁴¹ pressure are also depicted in Fig. 4, the former obtained by means of Seeding (of fcc clusters) simulations, and the later through Brute force simulations. Both calculations are in reasonable agreement with our predictions and the rest of previous J estimations, therefore, evidencing the minor effect of hydrodynamics in HS crystal nucleation. Nonetheless, the significant discrepancy with experimental nucleation rates at moderate liquid packing fractions (blue symbols)^11–13 still persists (although in ref. 24 a possible justification which could explain the discrepancy has been proposed).

Fig. 4 Decimal logarithm of the nucleation rate for different crystal polymorphs (fcc, hcp and for a stacking disordered mixture of fcc and hcp) as a function of the liquid packing fraction. Our Seeding results and brute force nucleation rates for the PHS model¹¹⁸ are depicted by filled squares and cyan diamonds respectively. Continuous lines indicate CNT-like fits for our Seeding results, as explained in ref. 137, and dashed lines account for the uncertainty (statistical + systematic) of our Seeding calculations. Umbrella, Forward Flux Sampling and brute force nucleation rates (maroon empty symbols) for standard HS are also included.^28,30 Moreover, computational nucleation rates considering hydrodynamic effects are also plotted (purple empty symbols).^140,141 Blue symbols indicate experimental nucleation rates from different authors.^11–13

D. Polymorphic characterisation of the emerged crystals

Nucleation is a key step in the crystallization process, however, when several polymorphs are possible, different complex scenarios may arise.¹⁴² A well-known example is the Ostwald step rule¹⁴³ proposed in 1897 (and later reexamined by Stranski and Totomanow¹⁴⁴), where it was postulated that the crystal phase that nucleates from the fluid needs not be the one that is thermodynamically most stable, but the one with the lowest free energy barrier. An opposite behaviour recently reported by us, is parasitic crystallization¹⁰⁷, in which the nucleating phase is the thermodynamically most stable one, but the post-critical crystal growth occurs through an out-of-equilibrium process by which a different (metastable) parasitic phase from the nucleating one and/or the most stable one, grows from the critical nucleus. These different possible intricate crystallization scenarios highlight how polymorphic competition can also take place beyond the nucleus formation. In this section, we elucidate the structure of the grown crystals from our simulations (under different supersaturation conditions) to characterise the interplay between fcc and hcp polymorphs in post-critical crystallization.

First, we analyse the structure of the emerged crystals from the different orientations studied by means of the Mold Integration method in Section IIB. From MI simulations at r_w < r^o_w, where stable crystal slabs were already formed, we set a marginally higher pressure than the melting one, and we simulate until the full system crystallizes. To discriminate between fcc-like and hcp-like particles, we employ the q̄₄ order parameter¹²⁶ within the mislabelling scheme (as detailed in Section IIB).^55,107,137 We find that among all the studied crystal faces, the fcc (111) (or equivalently hcp (0001)) plane is the only crystal face that enables stacking disordered growth of both polymorphs (see Fig. 5(a)) as suggested in ref. 145 and 146. In contrast, the rest of the crystal orientations only grow as the phase that they belong to. Moreover, when increasing supersaturation (i.e., p* ∼ 15), the abundance of crystal defects slightly increases, but still the predominant polymorph is that of the crystal from which it grows except for the fcc (111) plane.

Fig. 5 (a) Snapshots of Mold Integration simulations at r_w = 0.25σ and p* = 11.7 for different fcc and hcp crystal orientations (as indicated above of each system) right after emerging the crystal slab (left), and after crystallizing the whole system (right). Liquid-like particles are coloured in grey, fcc-like ones in black, and hcp-like ones in orange. The particle labelling is performed through the q̄₄ and q̄₆ local order parameter¹²⁶ as shown in Fig. 6. (b) Average composition (in percentage) of fcc-like and hcp-like particles in post-critical crystallites grown from fcc, hcp, stacking disordered hcp/fcc crystal seeds and brute force simulations. The analysis of the Seeding simulations has been performed to all post-critical crystals grown from critical clusters found from p* = 12.5 to p* = 15. Note that the analysis has been completed discounting the initial composition of the inserted clusters, and only considering maximum post-critical crystal sizes that have not percolated yet through the periodic boundary conditions of the simulation box. The brute force analysis was performed for 30 independent trajectories at p* = 16.75. Green error bars indicate the typical uncertainty of the local order parameter when identifying particles near the crystal–fluid interface. Note that the average composition refers to the mean polymorphic composition of the crystals rather than the probability of growing one pure crystal phase or the other from the critical nuclei. (c) Probability distribution function of the fcc abundance (in %) of the grown post-critical crystals (described in (b)) of hcp (orange), fcc (black) and stacking disordered fcc/hcp (green) from Seeding simulations, as well as from brute force simulations at p* = 16.75 (blue). Note that crystals %hcp abundance is just (1-%fcc abundance).

We also evaluate the composition of the post-critical crystals from our Seeding and Brute force simulations. The average composition (in percentage) of fcc-like (black) vs. hcp-like (orange) particles of the grown crystals is shown in Fig. 5(b). When fcc clusters are inserted, the predominant polymorph of the post-critical crystals, almost independently of the chosen pressure, is the fcc phase. Similarly, when hcp clusters are introduced, the prevailing phase is also that of the inserted seed. These results clearly support our observations of growth from a planar interface, in which we find that only common fcc and hcp planes, as the (111) or the (0001) respectively, can promote indistinctly growth of fcc or hcp crystals (Fig. 5(a)). Furthermore, stacking disordered fcc/hcp clusters (with approximately a 50 : 50 abundance of each polymorph) post-critically expand with an equivalent composition of both phases, supporting also our previous observations of growth from a planar interface. Please note that this analysis has been performed discounting the initial composition of the inserted clusters, and only considering maximum crystal sizes that have not percolated yet through the periodic boundary conditions of the simulation box.

Additionally, we elucidate the crystal composition of 30 independent unbiased brute force trajectories at p* = 16.75 starting from an homogeneous fluid. Given that the critical nuclei at these conditions are rather small (N_c < 40 particles), and both polymorph structures are very similar, we cannot unequivocally identify the critical nucleus structure (it is not even clear if the attempt to label a solid cluster with less than 40 particles as fcc or hcp makes any physical sense). However, when analysing the post-critical crystals (of about 16 000 HS particles), we observe a similar abundance in average of both polymorphs, although with slightly higher abundance of the fcc phase (Fig. 5b). These observations are in agreement with light-scattering measurements of hard-sphere colloidal crystals in which stacking close-packed planes with a high degree of randomness were found.^146,147 Nonetheless, the composition distribution of these (spontaneously emerged) crystals is much wider than those developed from our Seeding simulations (Fig. 5c). Even though the average composition of the 30 independent trajectories points to a similar abundance of both phases, the polymorphic distribution analysis shows crystallites with highly predominant fcc composition (higher than 75%), as well as with very low (<25%), or intermediate fcc abundance. From the 30 brute force simulations, 10 crystallites exhibited more than 75% fcc composition, 6 crystals had more than >75% hcp composition (or <25% fcc), and 14 showed intermediate abundance ranged from 25 to 75%. These results (which are also reflected through a mild maximum in probability at high fcc composition (Fig. 5c) on top of our observations that crystals predominantly grow as they nucleate (Fig. 5a and b), qualitatively agree with the fact that the obtained fcc nucleation rate is slightly higher than that of the hcp phase (Fig. 4), due to the fcc marginally lower liquid-crystal interfacial free energy (Fig. 3).

Interestingly, when identifying the polymorphic composition of the crystals by means of the q̄₄ order parameter, we find that the inserted fcc clusters of our Seeding simulations, just after very short equilibration and before even growing, already display a thin hcp-like layer along their surface (Fig. 6(a)). This is a very striking result, since according to Mold Integration and Seeding simulations, the interfacial free energy of hcp crystals could be slightly higher (or at least similar) than that of fcc ones. Therefore, there is no free energy gain for the cluster when arranging their interfacial particles into a hcp-like organization. On the contrary, when performing the same analysis for inserted hcp clusters, we find that, before growing, all their particles are correctly labelled as hcp-like ones (Fig. 6(b)). To better understand this behaviour, in Fig. 6 we plot the q̄₄–q̄₆ maps for two Seeding simulations (with an initial fcc cluster in (a) and with a hcp cluster in (b)) along the maps of a bulk liquid phase (blue), a bulk fcc phase (black) and a bulk hcp crystal (orange) at the same conditions of each Seeding simulation. Moreover, an horizontal dotted line depicts the q̄₆ threshold between bulk fluid and bulk solid-like particles and a vertical dotted line accounts for the q̄₄ threshold between the two crystal polymorphs. The threshold values were tuned according to the mislabeling criterion^55,137 at the corresponding thermodynamic conditions of each system: p* = 13.88 in (a) and p* = 14.02 in (b).

Fig. 6 (a) Left: q̄₄–q̄₆ plot of the initial configuration (after very short equilibration) of a Seeding trajectory with a fcc cluster of 690 particles embedded in fluid of 18 824 HS particles (brown), for a bulk hcp crystal (orange), a bulk fcc crystal (black) and a bulk liquid phase (blue) at p* = 13.88. The horizontal and vertical dotted lines depict the optimal q̄₆ and q̄₄ thresholds, respectively, according to the mislabelling criterion^55,137 at that pressure. The q̄₆ threshold distinguishes between bulk fluid and bulk solid-like particles, while the q̄₄ threshold between particles of the two crystal polymorphs. Right: Snapshot of the initial Seeding configuration described before. Fcc-like particles are depicted in black, hcp-like ones in orange, and liquid-like ones in grey (and with a reduced size to improve the visualization of the cluster) according to the q̄₄–q̄₆ plot on the left. (b) Left: q̄₄–q̄₆ plot for the initial configuration (after very short equilibration) of a Seeding trajectory with a hcp cluster of 642 particles embedded in fluid of 30 857 HS particles (cyan), for a bulk hcp crystal (orange), a bulk fcc crystal (black) and a bulk liquid phase (blue) at p* = 14.02. The horizontal and vertical dotted lines depict the optimal q̄₆ and q̄₄ thresholds, respectively, according to the mislabelling criterion at that pressure. Right: Snapshot of the initial Seeding configuration described in (b) left. The same colour code employed in (a) right applies here, although following the q̄₄–q̄₆ mislabelling criterion shown in (b) left.

It can be clearly noted that while for the hcp Seeding simulation the q̄₄–q̄₆ cloud mainly lies over the bulk liquid cloud and partially over the hcp one, in the fcc Seeding simulation, a great fraction of the interfacial points of the cloud connecting the fcc-like particles and the liquid-like ones lies over the hcp region (Fig. 6(a)). This incorrect labelling of the interfacial particles as hcp-like ones, that independently occurs of the chosen q̄₆ threshold and system pressure (since the relative position of the three bulk phases q̄₆−q̄₄ clouds is always similar), may lead to wrong conclusions on the structure of the outermost layer of the critical nuclei.^54,108,148 However, as we demonstrate here (and previously for the emergence of ice 0 from ice I nuclei in supercooled water, see Electronic Supplementary Information (ESI) of ref. 149), the hcp-like coating of the clusters is an artifact of the order parameter when dealing with fluid–fcc interfaces. The spurious labeling of interfacial particles as ‘hcp’ is likely contributing to moderately increase the number of hcp-like particles identified in the polymorphic analysis composition of the post-critical crystals shown in Fig. 5. Nonetheless, that proportion of possibly mislabelled particles is reasonably small, as indicated by the green error bars, since the considered crystals were large, and therefore, their volume/surface ratio as well. We also note that the drawback of ascribing interfacial particles to either a liquid phase or different crystal phases is a general feature of any local order parameter (i.e., q̄₄, q̄₆, w̄₄ or w̄₆,), however, different cut-off choices, spherical harmonic orders, or normalization factors may lead to distinct positioning of the point clouds leading to more sensitive (or more spurious) identification of the interfacial particles (see ESI of ref. 149).

III. Conclusions

In this work we investigate the differences and similarities between the fcc and hcp crystal structures in colloidal hard-spheres. To that end, we perform MD simulations of the PHS model¹¹⁸, a continuous potential for hard-spheres that accurately reproduces their phase behaviour,^86,118–121 while conveniently enabling the use of standard and parallel MD simulation packages.^122,123 We evaluate the melting pressure and the chemical potential difference between both polymorphs and a stacking disordered mixture of both of them with the liquid, finding that within the uncertainty of our simulations, the three solids present highly similar stability with respect to the liquid. Moreover, the equation of state of the three crystals is remarkably alike. We also compute the liquid–solid interfacial free energy for different crystal orientations of both polymorphs at coexistence conditions by means of the Mold Integration method.¹²¹ Even though the crystal anisotropy of γ for the different studied orientations is modest (lower than 10%), the hcp (112̄0) plane shows a moderately higher interfacial free energy than any other fcc crystal face, leading to a slightly higher γ average of the different hcp crystal planes studied over those of the fcc phase.

Alternatively, by means of the Seeding technique,^85,134,135 we evaluate the interfacial free energy for spherical nuclei of both polymorphs. Despite being γ almost identical for both crystals, as found at coexistence, we consistently obtain marginally higher values of γ for hcp clusters than for fcc ones, being such difference more evident for huge cluster sizes (i.e., >30 000 particles). Furthermore, a linear extrapolation of the γ values obtained from our Seeding simulations of large clusters (>1000 particles), fairly agrees with our predictions at coexistence conditions using the Mold Integration method. This fact directly demonstrates that CNT^77,78 can successfully describe the nucleation behaviour of colloidal hard-spheres when a reasonable order parameter (in our case the q̄₄–q̄₆ parameter within the mislabelling scheme) is employed to determine the size of the critical nuclei. In addition to our pure crystal Seeding simulations, we also compute the interfacial free energy for clusters with a stacking disordered fcc/hcp structure, finding that their γ values are roughly in between and very similar to those of fcc and hcp nuclei.

This very modest higher γ of hcp clusters leads to slightly lower nucleation rates for hcp nuclei compared to those of fcc. Similarly as in γ, stacking disordered fcc/hcp clusters present roughly intermediate nucleation rates between both pure polymorphs. Importantly, we find a remarkable agreement between the predicted Seeding nucleation rates with those obtained from brute force simulations at high pressure, being the fcc nucleation rates in marginally better agreement with those from brute force. This is a second robust confirmation that Classical Nucleation Theory can provide a fair description of hard-spheres nucleation, on top of the fact that we also recover the independently predicted interfacial free energies of the two polymorphs at coexistence conditions with our Seeding simulations. Also, we can conclude that hcp nucleation rates cannot either explain the discrepancy between computational and experimental homogeneous nucleation rates in colloidal hard-spheres.^{4,24,26,27,74,75,140,150–152}

Furthermore, we elucidate the polymorphic composition of post-critical grown crystals within a wide range of conditions. The only crystal orientation that indistinctly enables fcc or hcp growth is the (111) fcc plane or the (0001) hcp one, which are equivalent, and permit stacking layering of both phases. The impossibility of growing one phase from the other, except through this crystal orientation, possibly explains our observation of the growth of the same polymorph that initially nucleates. We quantify the relative composition of post-critical crystallites emerged from fcc, hcp and stacking disordered nuclei, finding that grown crystals mainly maintain the initial structure of the critical nuclei. Also, for crystallized systems from brute force simulations at high supersaturation, we perform the same analysis concluding that a huge distribution of different polymorphic compositions can be achieved. Nonetheless a higher number of crystallites with governing fcc composition (>75% fcc) are found compared to crystals with predominant hcp composition (>75% hcp). These results indicate, according to our crystal growth analysis from different types of nuclei, that the propensity of fcc crystals to nucleate could be slightly higher than those of hcp clusters, as our Seeding simulations indicate, and was previously suggested³⁰, being this fact a consequence of the very modest lower γ average that fcc crystals show respect to those of hcp.

Finally, we perform an analysis of the structure of the interface of the Seeding clusters. We find that local order parameters tuned to label particles in a bulk-like environment can lead to incorrect conclusions regarding the structure of the interface. More specifically, the order parameters used in this work tend to spuriously label interfacial particles as hcp-like. This observation serves as a warning to studies where conclusions are drawn from the liquid–solid interfacial structure, or from very small crystal clusters, using the same kind of order parameters employed in this work. On the whole, our study contributes to elucidate the polymorphic competition between two almost twin crystal phases in hard-sphere nucleation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to dedicate this paper to the memory of three scientists that passed away recently, and played a key role in our understanding of hard-spheres, including the fluid–solid transition. Berni Alder who invented MD and showed the first evidence of the fluid–solid transition of HS by using computer simulations, Francis H. Ree who performed free energy calculations to show that there was a pressure at which the chemical potential of both phases was identical (in collaboration with Bill Hoover) and to Douglas Henderson who developed a perturbation theory for simple liquids as Ar, using the structure and thermodynamic properties of hard spheres. This project has received funding from the Oppenheimer Research Fellowship of the University of Cambridge. J. R. E. also acknowledges funding from the Roger Ekins Research Fellowship of Emmanuel College. I. S.-B. acknowledges funding from the Oppenheimer Fellowship, Derek Brewer scholarship of Emmanuel College and EPSRC Doctoral Training Programme studentship, number EP/T517847/1. This work has been performed using resources provided by the Cambridge Tier-2 system operated by the University of Cambridge Research Computing Service (http://www.hpc.cam.ac.uk) funded by EPSRC Tier-2 capital grant EP/P020259/1. C. V and E. S acknowledge funding from Grant PID2019-105898GB-C21 of the MEC and by project FI-2020-2-0031 of the RES.

References

1. K. F. Kelton, Crystal Nucleation in Liquids and Glasses, Academic, Boston, 1991.
2. G. Debenedetti, Metastable liquids: Concepts and Principles, Princeton University Press, 1996.
3. G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla and A. Zen, et al., Crystal nucleation in liquids: Open questions and future challenges in molecular dynamics simulations, Chem. Rev., 2016, 116(12), 7078–7116.
4. T. Palberg, Crystallization kinetics of colloidal model suspensions: Recent achievements and new perspectives, J. Phys.: Condens. Matter, 2014, 26(33), 333101.
5. U. Gasser, E. R. Weeks, A. Schofield, N. Pusey and D. A. Weitz, Real-space imaging of nucleation and growth in colloidal crystallization, Science, 2001, 292, 258.
6. A. J. Amaya and B. E. Wyslouzil, Ice nucleation rates near ∼225 K, J. Chem. Phys., 2018, 148(8), 084501.
7. A. Manka, H. Pathak, S. Tanimura, J. Wolk, R. Strey and B. E. Wyslouzil, Freezing water in no man's land, Phys. Chem. Chem. Phys., 2012, 14, 4505–4516.
8. F. Ziese, G. Maret and U. Gasser, Heterogeneous nucleation and crystal growth on curved surfaces observed by real-space imaging, J. Phys.: Condens. Matter, 2013, 25(37), 375105.
9. T. Nakamuro, M. Sakakibara, H. Nada, K. Harano and E. Nakamura, Capturing the moment of emergence of crystal nucleus from disorder, J. Am. Chem. Soc., 2021, 143(4), 1763–1767.
10. J. Xing, L. Schweighauser, S. Okada, K. Harano and E. Nakamura, Atomistic structures and dynamics of prenucleation clusters in mof-2 and mof-5 syntheses, Nat. Commun., 2019, 10(1), 1–9.
11. J. L. Harland and W. van Megen, Crystallization kinetics of suspensions of hard colloidal spheres, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 3054.
12. C. Sinn, A. Heymann, A. Stipp and T. Palberg, Solidification kinetics of hard-sphere colloidal suspensions, in Trends in Colloid and Interface Science XV, Springer, 2001, pp. 266–275.
13. K. Schätzel and B. J. Ackerson, Density fluctuations during crystallization of colloids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48(5), 3766.
14. P. N. Pusey and W. van Megen, Phase behaviour of concentrated suspensions of nearly hard colloidal spheres, Nature, 1986, 320(27), 340.
15. C. P. Royall, W. C. K. Poon and E. R. Weeks, In search of colloidal hard spheres, Soft Matter, 2013, 9(1), 17–27.
16. R. Blaak, M. A. Miller and J. P. Hansen, Reversible gelation and dynamical arrest of dipolar colloids, Europhys. Lett., 2007, 78, 26002.
17. M. E. Leunissen, C. G. Christova, A. P. Hynninen, C. Royall, A. I. Campbell and A. Imhof, et al., Ionic colloidal crystals of oppositely charged particles, Nature, 2005, 437, 235.
18. Z. Zhang and S. C. Glotzer, Self-assembly of patchy particles, Nano Lett., 2004, 4(8), 1407–1413.
19. I. C. Pons-Siepermann and S. C. Glotzer, Design of patchy particles using quaternary self-assembled monolayers, ACS Nano, 2012, 6(5), 3919–3924.
20. R. Besseling, E. R. Weeks, A. B. Schofield and W. C. K. Poon, Three-dimensional imaging of colloidal glasses under shear, Phys. Rev. Lett., 2007, 99, 028301.
21. E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Three-dimensional direct imaging of structural relaxation near the colloidal glass transition, Science, 2000, 287, 627.
22. J. Savage and A. Dinsmore, Experimental evidence for two-step nucleation in colloidal crystallization, Phys. Rev. Lett., 2009, 102(19), 198302.
23. Z. Wang, F. Wang, Y. Peng, Z. Zheng and Y. Han, Imaging the homogeneous nucleation during the melting of superheated colloidal crystals, Science, 2012, 338(6103), 87–90.
24. J. R. Espinosa, C. Vega, C. Valeriani, D. Frenkel and E. Sanz, Heterogeneous versus homogeneous crystal nucleation of hard spheres, Soft Matter, 2019, 15(47), 9625–9631.
25. P. N. Pusey and W. van Megen, Phase behaviour of concentrated suspensions of nearly hard colloidal spheres, Nature, 1986, 320, 340.
26. N. Wood, J. Russo, F. Turci and C. P. Royall, Coupling of sedimentation and liquid structure: Influence on hard sphere nucleation, J. Chem. Phys., 2018, 149(20), 204506.
27. J. Russo, A. C. Maggs, D. Bonn and H. Tanaka, The interplay of sedimentation and crystallization in hard-sphere suspensions, Soft Matter, 2013, 9(30), 7369–7383.
28. S. Auer and D. Frenkel, Prediction of absolute crystal-nucleation rate in hard-sphere colloids, Nature, 2001, 409, 1020.
29. D. Richard and T. Speck, Crystallization of hard spheres revisited. II. Thermodynamic modeling, nucleation work, and the surface of tension, J. Chem. Phys., 2018, 148(22), 224102.
30. L. Filion, M. Hermes, R. Ni and M. Dijkstra, Crystal nucleation of hard spheres using molecular dynamics, umbrella sampling, and forward flux sampling: A comparison of simulation techniques, J. Chem. Phys., 2010, 133(24), 244115.
31. C. Valeriani, E. Sanz and D. Frenkel, Rate of homogeneous crystal nucleation in molten NaCl, J. Chem. Phys., 2005, 122, 194501.
32. W. G. Hoover and C. G. Hoover, From hard spheres and cubes to nonequilibrium maps with thirty-some years of thermostatted molecular dynamics, J. Chem. Phys., 2020, 153(7), 070901.
33. B. J. Alder and T. E. Wainwright, Phase transition for a hard sphere system, J. Chem. Phys., 1957, 27(5), 1208–1209.
34. W. G. Hoover and F. H. Ree, Melting transition and communal entropy for hard spheres, J. Chem. Phys., 1968, 49(8), 3609–3617.
35. J. A. Barker and D. Henderson, What is “liquid”? understanding the states of matter, Rev. Mod. Phys., 1976, 48(4), 587.
36. J. Russo and H. Tanaka, The microscopic pathway to crystallization in supercooled liquids, Sci. Rep., 2012, 2, 505.
37. T. Schilling, S. Dorosz, H. J. Schöpe and G. Opletal, Crystallization in suspensions of hard spheres: A monte carlo and molecular dynamics simulation study, J. Phys.: Condens. Matter, 2011, 23(19), 194120.
38. S. Dorosz and T. Schilling, On the influence of a patterned substrate on crystallization in suspensions of hard spheres, J. Chem. Phys., 2012, 136(4), 044702.
39. H. Jiang, A. Haji-Akbari, P. G. Debenedetti and A. Z. Panagiotopoulos, Forward flux sampling calculation of homogeneous nucleation rates from aqueous NaCl solutions, J. Chem. Phys., 2018, 148(4), 044505.
40. G. D. Soria, J. R. Espinosa, J. Ramirez, C. Valeriani, C. Vega and E. Sanz, A simulation study of homogeneous ice nucleation in supercooled salty water, J. Chem. Phys., 2018, 148(22), 222811.
41. J. R. Espinosa, G. D. Soria, J. Ramirez, C. Valeriani, C. Vega and E. Sanz, Role of salt, pressure, and water activity on homogeneous ice nucleation, J. Phys. Chem. Lett., 2017, 8, 4486.
42. A. O. Tipeev, E. D. Zanotto and J. P. Rino, Diffusivity, interfacial free energy, and crystal nucleation in a supercooled Lennard-Jones liquid, J. Phys. Chem. C, 2018, 122(50), 28884–28894.
43. S. Punnathanam and P. Monson, Crystal nucleation in binary hard sphere mixtures: A Monte Carlo simulation study, J. Chem. Phys., 2006, 125(2), 024508.
44. A. Haji-Akbari and P. G. Debenedetti, Direct calculation of ice homogeneous nucleation rate for a molecular model of water, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(34), 10582–10588.
45. A. V. Brukhno, J. Anwar, R. Davidchack and R. Handel, Challenges in molecular simulation of homogeneous ice nucleation, J. Phys.: Condens. Matter, 2008, 20(49), 494243.
46. T. Li, D. Donadio, G. Russo and G. Galli, Homogeneous ice nucleation from supercooled water, Phys. Chem. Chem. Phys., 2011, 13, 19807–19819.
47. A. Haji-Akbari, R. S. DeFever, S. Sarupria and P. G. Debenedetti, Suppression of sub-surface freezing in free-standing thin films of a coarse-grained model of water, Phys. Chem. Chem. Phys., 2014, 16, 25916–25925.
48. A. Hudait and V. Molinero, Ice crystallization in ultrafine water-salt aerosols: Nucleation, ice-solution equilibrium, and internal structure, J. Am. Chem. Soc., 2014, 136(22), 8081–8093.
49. E. B. Moore and V. Molinero, Structural transformation in supercooled water controls the crystallization rate of ice, Nature, 2011, 479(7374), 506–508.
50. S. J. Cox, S. M. Kathmann, B. Slater and A. Michaelides, Molecular simulations of heterogeneous ice nucleation. I. controlling ice nucleation through surface hydrophilicity, J. Chem. Phys., 2015, 142(18), 184704.
51. M. Fitzner, G. C. Sosso, S. J. Cox and A. Michaelides, Ice is born in low-mobility regions of supercooled liquid water, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(6), 2009–2014.
52. A. Zaragoza, J. R. Espinosa, R. Ramos, J. A. Cobos, J. L. Aragones and C. Vega, et al., Phase boundaries, nucleation rates and speed of crystal growth of the water-to-ice transition under an electric field: A simulation study, J. Phys.: Condens. Matter, 2018, 30(17), 174002.
53. A. Mahata, M. A. Zaeem and M. I. Baskes, Understanding homogeneous nucleation in solidification of aluminum by molecular dynamics simulations, Modell. Simul. Mater. Sci. Eng., 2018, 26(2), 025007.
54. C. Desgranges and J. Delhommelle, Molecular simulation of the crystallization of aluminum from the supercooled liquid, J. Chem. Phys., 2007, 127(14), 144509.
55. J. R. Espinosa, C. Vega, C. Valeriani and E. Sanz, Seeding approach to crystal nucleation, J. Chem. Phys., 2016, 144, 034501.
56. V. G. Baidakov, A. O. Tipeev, K. S. Bobrov and G. V. Ionov, Crystal nucleation rate isotherms in Lennard-Jones liquids, J. Chem. Phys., 2010, 132(23), 234505.
57. N. E. Zimmermann, B. Vorselaars, J. R. Espinosa, D. Quigley, W. R. Smith and E. Sanz, et al., NaCl nucleation from brine in seeded simulations: Sources of uncertainty in rate estimates, J. Chem. Phys., 2018, 148(22), 222838.
58. A. Cacciuto, S. Auer and D. Frenkel, Onset of heterogeneous crystal nucleation in colloidal suspensions, Nature, 2004, 428(6981), 404–406.
59. S. Auer and D. Frenkel, Line tension controls wall-induced crystal nucleation in hard-sphere colloids, Phys. Rev. Lett., 2003, 91(1), 015703.
60. B. B. Laird and R. L. Davidchack, Wall-induced prefreezing in hard spheres: A thermodynamic perspective, J. Phys. Chem. C, 2007, 111(43), 15952–15956.
61. M. Dijkstra, Capillary freezing or complete wetting of hard spheres in a planar hard slit?, Phys. Rev. Lett., 2004, 93(10), 108303.
62. M. Fitzner, P. Pedevilla and A. Michaelides, Predicting heterogeneous ice nucleation with a data-driven approach, Nat. Commun., 2020, 11(1), 1–9.
63. B. Glatz and S. Sarupria, Heterogeneous ice nucleation: Interplay of surface properties and their impact on water orientations, Langmuir, 2018, 34(3), 1190–1198.
64. L. Lupi, A. Hudait and V. Molinero, Heterogeneous nucleation of ice on carbon surfaces, J. Am. Chem. Soc., 2014, 136(8), 3156–3164.
65. Z. Zhang and X.-Y. Liu, Control of ice nucleation: freezing and antifreeze strategies, Chem. Soc. Rev., 2018, 47(18), 7116–7139.
66. A. Hudait, N. Odendahl, Y. Qiu, F. Paesani and V. Molinero, Ice-nucleating and antifreeze proteins recognize ice through a diversity of anchored clathrate and ice-like motifs, J. Am. Chem. Soc., 2018, 140(14), 4905–4912.
67. M. Naullage, L. Lupi and V. Molinero, Molecular recognition of ice by fully flexible molecules, J. Phys. Chem. C, 2017, 121(48), 26949–26957.
68. V. Bianco, J. R. Espinosa and C. Vega, Antifreeze proteins and homogeneous nucleation: On the physical determinants impeding ice crystal growth, J. Chem. Phys., 2020, 153(9), 091102.
69. G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling, J. Comput. Phys., 1977, 23(2), 187–199.
70. R. J. Allen, D. Frenkel and P. R. ten Wolde, Forward flux sampling-type schemes for simulating rare events: Efficiency analysis, J. Chem. Phys., 2006, 124(19), 194111.
71. P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Transition path sampling: Throwing ropes over rough mountain passes, in the dark, Annu. Rev. Phys. Chem., 2002, 53, 291.
72. X.-M. Bai and M. Li, Calculation of solid–liquid interfacial free energy: A classical nucleation theory based approach, J. Chem. Phys., 2006, 124(12), 124707.
73. P. Koss, A. Statt, P. Virnau and K. Binder, Free energy barriers for crystal nucleation from fluid phases, 2017, arXiv 1705.08216.
74. L. Filion, R. Ni, D. Frenkel and M. Dijkstra, Simulation of nucleation in almost hard-sphere colloids: The discrepancy between experiment and simulation persists, J. Chem. Phys., 2011, 134(13), 134901.
75. U. Gasser, Crystallization in three-and two-dimensional colloidal suspensions, J. Phys.: Condens. Matter, 2009, 21(20), 203101.
76. R. P. Sear, The non-classical nucleation of crystals: Microscopic mechanisms and applications to molecular crystals, ice and calcium carbonate, Int. Mater. Rev., 2012, 57(6), 328–356.
77. M. Volmer and A. Weber, Keimbildung in ubersattigten gebilden, Z. Phys. Chem., 1926, 119, 277.
78. R. Becker and W. Doring, Kinetische behandlung der keimbildung in ubersattigten dampfen, Ann. Phys., 1935, 416, 719–752.
79. J. Merikanto, E. Zapadinsky, A. Lauri and H. Vehkamäki, Origin of the failure of classical nucleation theory: Incorrect description of the smallest clusters, Phys. Rev. Lett., 2007, 98(14), 145702.
80. A. Cacciuto, S. Auer and D. Frenkel, Breakdown of classical nucleation theory near isostructural phase transitions, Phys. Rev. Lett., 2004, 93(16), 166105.
81. T. Schilling, H. J. Schöpe, M. Oettel, G. Opletal and I. Snook, Precursor-mediated crystallization process in suspensions of hard spheres, Phys. Rev. Lett., 2010, 105(2), 025701.
82. S. Wonczak, R. Strey and D. Stauffer, Confirmation of classical nucleation theory by monte carlo simulations in the 3-dimensional ising model at low temperature, J. Chem. Phys., 2000, 113(5), 1976–1980.
83. I. Saika-Voivod, P. H. Poole and R. K. Bowles, Test of classical nucleation theory on deeply supercooled high-pressure simulated silica, J. Chem. Phys., 2006, 124(22), 224709.
84. H. Niu, Y. I. Yang and M. Parrinello, Temperature dependence of homogeneous nucleation in ice, Phys. Rev. Lett., 2019, 122(24), 245501.
85. B. C. Knott, V. Molinero, M. F. Doherty and B. Peters, Homogeneous nucleation of methane hydrates: Unrealistic under realistic conditions, J. Am. Chem. Soc., 2012, 134, 19544–19547.
86. P. Montero de Hijes, J. R. Espinosa, V. Bianco, E. Sanz and C. Vega, Interfacial free energy and Tolman length of curved liquid–solid interfaces from equilibrium studies, J. Phys. Chem. C, 2020, 124(16), 8795–8805.
87. A. Kuhnhold, H. Meyer, G. Amati, P. Pelagejcev and T. Schilling, Derivation of an exact, nonequilibrium framework for nucleation: Nucleation is a priori neither diffusive nor Markovian, Phys. Rev. E, 2019, 100(5), 052140.
88. M. Sorokin, V. Dubinko and V. Borodin, Applicability of the Fokker–Planck equation to the description of diffusion effects on nucleation, Phys. Rev. E, 2017, 95(1), 012801.
89. E. Sanz, C. Valeriani, D. Frenkel and M. Dijkstra, Evidence for out-of-equilibrium crystal nucleation in suspensions of oppositely charged colloids, Phys. Rev. Lett., 2007, 99, 055501.
90. M. Horsch, J. Vrabec and H. Hasse, Modification of the classical nucleation theory based on molecular simulation data for surface tension, critical nucleus size, and nucleation rate, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78(1), 011603.
91. M. Schrader, P. Virnau and K. Binder, Simulation of vapor-liquid coexistence in finite volumes: A method to compute the surface free energy of droplets, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79(6), 061104.
92. T. Kawasaki and H. Tanaka, Formation of a crystal nucleus from liquid, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(32), 14036–14041.
93. J. Russo, F. Romano and H. Tanaka, New metastable form of ice and its role in the homogeneous crystallization of water, Nat. Mater., 2014, 13(7), 733–739.
94. E. B. Moore and V. Molinero, Is it cubic? Ice crystallization from deeply supercooled water, Phys. Chem. Chem. Phys., 2011, 13, 20008.
95. L. Lupi, A. Hudait, B. Peters, M. Grünwald, R. G. Mullen and A. H. Nguyen, et al., Role of stacking disorder in ice nucleation, Nature, 2017, 551(7679), 218–222.
96. S. Jungblut and C. Dellago, Crystallization of a binary Lennard-Jones mixture, J. Chem. Phys., 2011, 134(10), 104501.
97. C. Desgranges and J. Delhommelle, Controlling polymorphism during the crystallization of an atomic fluid, Phys. Rev. Lett., 2007, 98(23), 235502.
98. T. L. Malkin, B. J. Murray, C. G. Salzmann, V. Molinero, S. J. Pickering and T. F. Whale, Stacking disorder in ice i, Phys. Chem. Chem. Phys., 2015, 17(1), 60–76.
99. E. B. Moore and V. Molinero, Is it cubic? ice crystallization from deeply supercooled water, Phys. Chem. Chem. Phys., 2011, 13(44), 20008–20016.
100. T. Li, D. Donadio, G. Russo and G. Galli, Homogeneous ice nucleation from supercooled water, Phys. Chem. Chem. Phys., 2011, 13(44), 19807–19813.
101. A. Hudait, S. Qiu, L. Lupi and V. Molinero, Free energy contributions and structural characterization of stacking disordered ices, Phys. Chem. Chem. Phys., 2016, 18(14), 9544–9553.
102. A. Zaragoza, M. M. Conde, J. R. Espinosa, C. Valeriani, C. Vega and E. Sanz, Competition between ices ih and ic in homogeneous water freezing, J. Chem. Phys., 2015, 143(13), 134504.
103. M. Celli, L. Ulivi and L. del Rosso, Raman investigation of the ice ic-ice ih transformation, J. Phys. Chem. C, 2020, 124(31), 17135–17140.
104. H. Kanno, R. Speedy and C. Angell, Supercooling of water to-92 c under pressure, Science, 1975, 189(4206), 880–881.
105. J. R. Espinosa, A. L. Diez, C. Vega, C. Valeriani, J. Ramirez and E. Sanz, Ice ih vs. ice iii along the homogeneous nucleation line, Phys. Chem. Chem. Phys., 2019, 21(10), 5655–5660.
106. M. E. Leunissen, C. G. Christova, A. P. Hynninen, C. P. Royall, A. I. Campbell and A. Imhof, et al., Ionic colloidal crystals of oppositely charged particles, Nature, 2005, 437(7056), 235–240.
107. I. Sanchez-Burgos, A. Garaizar, C. Vega, E. Sanz and J. R. Espinosa, Parasitic crystallization of colloidal electrolytes: Growing a metastable crystal from the nucleus of a stable phase, Soft Matter, 2021, 17(3), 489–505.
108. C. Desgranges and J. Delhommelle, Molecular mechanism for the cross-nucleation between polymorphs, J. Am. Chem. Soc., 2006, 128(32), 10368–10369.
109. D. Frenkel and A. J. Ladd, New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres, J. Chem. Phys., 1984, 81(7), 3188–3193.
110. H. Koch, C. Radin and L. Sadun, Most stable structure for hard spheres, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72(1), 016708.
111. K. W. Kratky, Stability of fcc and hcp hard-sphere crystals, Chem. Phys., 1981, 57(1–2), 167–174.
112. P. G. Bolhuis, D. Frenkel, S.-C. Mau and D. A. Huse, Entropy difference between crystal phases, Nature, 1997, 388(6639), 235–236.
113. S.-C. Mau and D. A. Huse, Stacking entropy of hard-sphere crystals, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59(4), 4396.
114. L. Woodcock, Computation of the free energy for alternative crystal structures of hard spheres, Faraday Discuss., 1997, 106, 325–338.
115. E. G. Noya and N. G. Almarza, Entropy of hard spheres in the close-packing limit, Mol. Phys., 2015, 113(9–10), 1061–1068.
116. C. Vega and E. G. Noya, Revisiting the Frenkel–Ladd method to compute the free energy of solids: The Einstein molecule approach, J. Chem. Phys., 2007, 127(15), 154113.
117. V. Luchnikov, A. Gervois, P. Richard, L. Oger and J. Troadec, Crystallization of dense hard sphere packings: Competition of hcp and fcc close order, J. Mol. Liq., 2002, 96, 185–194.
118. J. Jover, A. J. Haslam, A. Galindo, G. Jackson and E. A. Muller, Pseudo hard-sphere potential for use in continuous molecular-dynamics simulation of spherical and chain molecules, J. Chem. Phys., 2012, 137(14), 144505.
119. J. R. Espinosa, E. Sanz, C. Valeriani and C. Vega, On fluid–solid direct coexistence simulations: The pseudo-hard sphere model, J. Chem. Phys., 2013, 139(14), 144502.
120. P. Rosales-Pelaez, P. M. de Hijes, E. Sanz and C. Valeriani, Avalanche mediated devitrification in a glass of pseudo hard-spheres, J. Stat. Mech.: Theor. Exp., 2016,(9), 094005.
121. J. R. Espinosa, C. Vega and E. Sanz, The mold integration method for the calculation of the crystal–fluid interfacial free energy from simulations, J. Chem. Phys., 2014, 141(13), 134709.
122. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117(1), 1–19.
123. H. J. Berendsen, D. van der Spoel and R. van Drunen, Gromacs: A message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91(1–3), 43–56.
124. A. J. Ladd and L. V. Woodcock, Triple-point coexistence properties of the Lennard-Jones system, Chem. Phys. Lett., 1977, 51(1), 155–159.
125. R. Garcia-Fernandez, J. L. F. Abascal and C. Vega, The melting point of ice ih for common water models calculated from direct coexistence of the solid–liquid interface, J. Chem. Phys., 2006, 124(14), 144506.
126. W. Lechner and C. Dellago, Accurate determination of crystal structures based on averaged local bond order parameters, J. Chem. Phys., 2008, 129(11), 114707.
127. D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, London, 1996.
128. J. R. Espinosa, C. Vega and E. Sanz, Ice-water interfacial free energy for the tip4p, tip4p/2005, tip4p/ice and mw models as obtained from the mold integration technique, J. Phys. Chem. C, 2016, 120, 8068–8075.
129. R. L. Davidchack, Hard spheres revisited: Accurate calculation of the solid–liquid interfacial free energy, J. Chem. Phys., 2010, 133(23), 234701.
130. R. Benjamin and J. Horbach, Crystal–liquid interfacial free energy of hard spheres via a thermodynamic integration scheme, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91(3), 032410.
131. F. Schmitz and P. Virnau, The ensemble switch method for computing interfacial tensions, J. Chem. Phys., 2015, 142(14), 144108.
132. M. Bültmann and T. Schilling, Computation of the solid–liquid interfacial free energy in hard spheres by means of thermodynamic integration, Phys. Rev. E, 2020, 102(4), 042123.
133. B. B. Laird, The solid–liquid interfacial free energy of close-packed metals: Hard-spheres and the Turnbull coefficient, J. Chem. Phys., 2001, 115(7), 2887–2888.
134. X. M. Bai and M. Li, Differences between solid superheating and liquid supercooling, J. Chem. Phys., 2005, 123, 151102.
135. E. Sanz, C. Vega, J. R. Espinosa, R. Caballero-Bernal, J. L. F. Abascal and C. Valeriani, Homogeneous ice nucleation at moderate supercooling from molecular simulation, J. Am. Chem. Soc., 2013, 135(40), 15008–15017.
136. J. R. Espinosa, C. Vega, C. Valeriani and E. Sanz, The crystal–fluid interfacial free energy and nucleation rate of NaCl from different simulation methods, J. Chem. Phys., 2015, 142(19), 194709.
137. J. R. Espinosa, E. Sanz, C. Valeriani and C. Vega, Homogeneous ice nucleation evaluated for several water models, J. Chem. Phys., 2014, 141, 18C529.
138. S. Auer and D. Frenkel, Numerical prediction of absolute crystallization rates in hard-sphere colloids, J. Chem. Phys., 2004, 120(6), 3015–3029.
139. J. D. Weeks, D. Chandler and H. C. Andersen, Role of repulsive forces in determining the equilibrium structure of simple liquids, J. Chem. Phys., 1971, 54(12), 5237–5247.
140. G. Fiorucci, G. M. Coli, J. T. Padding and M. Dijkstra, The effect of hydrodynamics on the crystal nucleation of nearly hard spheres, J. Chem. Phys., 2020, 152(6), 064903.
141. M. Tateno, T. Yanagishima, J. Russo and H. Tanaka, Influence of hydrodynamic interactions on colloidal crystallization, Phys. Rev. Lett., 2019, 123(25), 258002.
142. P. R. ten Wolde and D. Frenkel, Homogeneous nucleation and the Ostwald step rule, Phys. Chem. Chem. Phys., 1999, 1(9), 2191–2196.
143. W. Ostwald, File: Wilhelm Ostwald-Studien über die bildung und umwandlung fester körper.pdf, Z. Phys. Chem., 1897, 22, 289–330.
144. I. Stranski and D. Totomanow, Rate of formation of (crystal) nuclei and the Ostwald step rule, Z. Phys. Chem., 1933, 163, 399–408.
145. A. Mori, Computer simulations of crystal growth using a hard-sphere model, Crystals, 2017, 7(4), 102.
146. J. Zhu, M. Li, R. Rogers, W. Meyer, R. Ottewill and W. Russel, et al., Crystallization of hard-sphere colloids in microgravity, Nature, 1997, 387(6636), 883–885.
147. P. Pusey, W. Van Megen, P. Bartlett, B. Ackerson, J. Rarity and S. Underwood, Structure of crystals of hard colloidal spheres, Phys. Rev. Lett., 1989, 63(25), 2753.
148. T. Kawasaki and H. Tanaka, Structural origin of dynamic heterogeneity in three-dimensional colloidal glass formers and its link to crystal nucleation, J. Phys.: Condens. Matter, 2010, 22(23), 232102.
149. J. R. Espinosa, A. Zaragoza, P. Rosales-Pelaez, C. Navarro, C. Valeriani and C. Vega, et al., Interfacial free energy as the key to the pressure-induced deceleration of ice nucleation, Phys. Rev. Lett., 2016, 117, 135702.
150. D. Roehm, S. Kesselheim and A. Arnold, Hydrodynamic interactions slow down crystallization of soft colloids, Soft Matter, 2014, 10(30), 5503–5509.
151. S. Ketzetzi, J. Russo and D. Bonn, Crystal nucleation in sedimenting colloidal suspensions, J. Chem. Phys., 2018, 148(6), 064901.
152. M. Radu and T. Schilling, Solvent hydrodynamics speed up crystal nucleation in suspensions of hard spheres, EPL, 2014, 105(2), 26001.

---