 Open Access Article
Open Access ArticleOxygen chemistry of halogen-doped CeO2(111)†
Matthew J. Wolf
 *a,
Ernst D. Larsson
*a,
Ernst D. Larsson b and
Kersti Hermansson
b and
Kersti Hermansson
 *c
*c
aDepartment of Physics, University of Bath, Claverton Down, Bath, BA2 7AY, UK. E-mail: m.j.wolf@bath.ac.uk
bDivision of Theoretical Chemistry, Lund University, Chemical Centre, P. O. Box 124, SE-221
00 Lund, Sweden
cDepartment of Chemistry – Ångström
Laboratory, Uppsala University, Box 538, SE-751 21 Uppsala, Sweden. E-mail: kersti@kemi.uu.se
First published on 2nd September 2021
Abstract
We study substitutional fluorine, chlorine and bromine impurities at CeO2(111), and their effects on the oxygen chemistry of the surface, using density functional theory. We find that impurity formation results in a halide ion and one Ce3+ ion for all three halogens, although the formation energy depends strongly on the identity of the halogen; however, once formed, all three halogens exhibit a similar propensity to form impurity–impurity pairs. Furthermore, while the effects of halogen impurities on oxygen vacancy formation are marginal, they are more significant for oxygen molecule adsorption, due to electron transfer from the Ce3+ ion which results in an adsorbed superoxide molecule. We also consider the displacement of a halide ion on to the surface by half of an oxygen molecule, and find that the energy required to do so depends strongly not only on the identity of the halogen, but also on whether or not a second halogen impurity, with its associated Ce3+ ion, is present; if it is, then the process is greatly facilitated. Overall, our results demonstrate the existence of a rich variety of ways in which the oxygen chemistry of CeO2(111) may be modified by the presence of halogen dopants.
1 Introduction
One of the ways in which the catalytic activity or selectivity of a metal oxide can be modified is by the introduction of foreign atoms, or dopants, into the material. Typically, doping is performed with metal cations,1–3 while much less attention has been paid to the possibilities offered by anion doping. Although the situation has begun to change in recent years (see, for example, the review presented in ref. 4), understanding of the effects of anion doping in the context of heterogeneous catalysis remains limited.Herein, we aim to contribute to that understanding by studying—by means of density functional theory (DFT) calculations—a series of halogen impurities at the surface of CeO2. CeO2, known commonly as ceria, is a widely studied reducible metal oxide with numerous applications in the field of heterogeneous catalysis, where it acts both as a support for noble metal particles, and as an oxygen buffer.5–7 More specifically, our study focuses on fluorine, chlorine and bromine impurities at the most prevalent surface facet of ceria, namely that corresponding to the (111) lattice plane.
The relevance of fluorine impurities stems originally from a number of reports of the unintentional fluorination of ceria.8–11 Subsequent studies on deliberately fluorinated ceria thin films grown on Rh(111) demonstrated that fluorine incorporation can be used to increase the concentration of Ce3+ ions and to modify the valence band electronic structure.12,13 Furthermore, fluorinated ceria nanoparticles have been shown to exhibit enhanced catalytic activity14,15 with respect to pure ceria. Similarly, research on chlorinated ceria was initially motivated by the observation of unintentional chlorine incorporation when noble metal precursor compounds containing chlorine were used in the production of ceria based catalysts.16,17 Most studies on chlorinated ceria based catalysts have reported poorer performance with respect to unchlorinated samples, which has been ascribed both to the suppression of hydrogen spill-over,18,19 and to the suppression of the oxidative capability of the host material20,21 due to the formation of a bulk oxychloride phase. On the other hand, there is evidence that the catalytic activity of ceria in the oxidative dehydrogenation of ethane is enhanced by the formation of an oxychloride surface phase in the presence of chlorine containing molecules.22 Furthermore, more recent research on the possible usage of ceria as a catalyst for the oxidation of hydrogen chloride, also known as the Deacon reaction,23,24 has indicated that a chlorinated surface phase, which forms during the course of the reaction, is the active catalytic phase, and that the pure ceria surface is inactive.25 Ceria has also been studied as a possible catalyst for the analogous Deacon-like reaction involving bromine,26,27 although in that case CeO2 was found to be highly susceptible to bulk bromination, which deactivates the catalyst.26 A comparative study has also been performed of the effects of fluorine, chlorine and bromine doping on the performance of ceria based catalysts for the preferential methanation of carbon monoxide, which demonstrated significant differences between the three halogens.28
Although motivated by them, the aim of the present study is not to address directly the complicated systems and reactions described above; instead, we will focus on elementary reactions that characterise more fundamentally the properties of halogen impurities at the (111) surface facet of ceria, and their effects on the surface oxygen chemistry. More specifically, our study is constructed around the comparison of fluorine, chlorine and bromine impurities in the context of the following seven elementary reactions.
The first of the reactions is the formation of a halogen impurity (‘X-imp’) at the stoichiometric surface (‘Sto surf’):
| Sto surf + 1/2X2(g) → Surf with X-imp + 1/2O2(g), | (R1) |
| Surf with 2 isolated X-imps → Surf with 2 adjacent X-imps, | (R2) |
We then examine the effects of halogen impurities on the interaction of ceria with oxygen in terms of five reactions, the first of which is the formation of an oxygen vacancy (‘O-vac’):
| Surf with X-imp → Surf with X-imp and O-vac + 1/2O2(g). | (R3) |
| Surf with X-imp + O2(g) → Surf with X-imp and O2(ads), | (R4) |
| Surf with X-imp + 1/2O2(g) → Sto surf with X(ads), | (R5a) |
| Surf with 2 X-imp + 1/2O2(g) → Surf with X-imp and X(ads), | (R5b) |
| Surf with X-imp and X(ads) + 1/2O2(g) → Sto surf with 2 X(ads). | (R5c) |
2 Computational details
The DFT calculations reported herein were performed using the projector augmented wave method (PAW),29 as implemented in the Vienna ab initio simulation package (VASP),30–33 version 5.3.5. The Perdew–Burke–Ernzerhof (PBE) exhange–correlation functional34,35 was used with the associated ‘standard’ PAW potentials that are distributed with VASP, and a plane-wave basis set for the Kohn–Sham states corresponding to a cut-off energy of 400 eV.It is well known that semi-local density functionals such as PBE artificially favour delocalised electronic states over localised ones such as those associated with Ce3+ ions, due to the so-called self-interaction error.36 In order to mitigate those effects, the DFT+U method was employed in the widely used, simplified form developed by Dudarev and co-workers,37 using the f-state projectors of the Ce PAW potentials. An (effective) U value of 3 eV was used, which has been demonstrated to provide more accurate reduction energies of pure ceria than the more commonly used values of 4–6 eV, while retaining the correct localised description of the Ce3+ states.38–41 In addition, we used the occupation matrix control (OMC) method42,43 initially to localise the excess electrons on particular cerium sites in the vicinity of halogen impurities and oxygen vacancies. Following structural optimisation using OMC, the resulting structures and wave functions were used as the starting points for fully unconstrained optimisations, and it is the final results of that two-step procedure that are reported herein. In all calculations, the positions of all atoms were optimised until the net force on each was less than 0.01 eV Å−1.
Optimisation of the bulk lattice parameter was performed using a conventional cubic unit cell and a 5 × 5 × 5, Γ-point centred k-point mesh, generated automatically according to the Monkhorst–Pack scheme.44 With this computational set-up, a value of 5.488 Å was obtained for the length of the cubic unit-cell vector. The same cell and k-point mesh were used in the calculation of the high-frequency relative permittivity (dielectric constant), ε∞, via density-functional perturbation theory. A value for ε∞ of 7.05 was obtained, which is similar to the values of 6.5545 and 6.6746 obtained in previous theoretical studies using similar methods. We note that all three computed values are substantially greater than the experimentally measured value of 5.31.47
All of the structural models for systems involving CeO2(111) were constructed from a periodic (super)cell containing a slab
three O–Ce–O triple layers thick, and a vacuum region equivalent to
five O–Ce–O triple layers' thickness, normal to the surface plane.
The periodicity within the surface plane was that of a p(5
× 5) (111) surface supercell, except for the models that were used
in the calculation of the ionisation energy of a surface oxygen vacancy
(see Section 3.1). In those cases, corresponding to a neutral and
singly ionised vacancy, a  surface supercell was used,
due to the necessity of applying a charge correction to the total
energy of the slab containing the ionised vacancy, and the restricted
applicability to orthorhombic cells of the code that was used to calculate
the correction, SLABCC.48 Due to the
relatively large sizes of the periodic cells used in the slab calculations, k-point sampling was restricted to the Γ point.
surface supercell was used,
due to the necessity of applying a charge correction to the total
energy of the slab containing the ionised vacancy, and the restricted
applicability to orthorhombic cells of the code that was used to calculate
the correction, SLABCC.48 Due to the
relatively large sizes of the periodic cells used in the slab calculations, k-point sampling was restricted to the Γ point.
Calculations of the total energies of neutral halogen and oxygen molecules, and neutral and negatively charged halogen atoms, were performed in a periodic cubic cell with a side length of 20 Å, and at the Γ point only. Corrections to the total energies of the negatively charged atoms were also calculated using SLABCC.48
3 Results and discussion
In Sections 3.1–3.5, the seven reactions discussed in Section 1, (R1)–(R5c), are addressed in turn. Fig. 2–9 contain schematic drawings of the reactions, and the reaction energies are collected in Table 2.When discussing structures in the remainder of the paper, frequent reference will be made to a site being a first, second or third nearest neighbour (1-NN, 2-NN or 3-NN, respectively) of a surface halogen. The site referred to could be that of an oxygen in the first or third (surface or sub-surface, respectively) atomic layers, or a cerium in the second atomic layer. Schematic depictions of the different possibilities are presented in Fig. 1.
Ball-model figures of all of the relaxed, low energy configurations discussed in the remainder of the paper are provided in the ESI.†
3.1 Formation of isolated halogen impurities (reaction (R1))
We begin by examining isolated halogen impurities in the surface (i.e. first atomic) layer of CeO2(111), which, when fully stoichiometric, consists solely of oxide ions.The substitution of a fluorine, chlorine or bromine atom for a surface oxide ion results in the formation of the corresponding halide ion (X−) and one Ce3+ ion. As has been observed for other anionic defects, such as oxygen vacancies and hydroxyl groups,49–51 the energy of a halogen impurity depends on the separation between the halide and Ce3+ ions. Calculations of the total energy of each of the halogen impurities with the Ce3+ ion located at lattice sites that are first, second, and third nearest neighbours to the halide ion (1-NN, 2-NN and 3-NN, respectively; see Fig. 1b) indicate that the Ce3+ ion is located preferentially at a 1-NN site to a fluoride ion, while it is located at a 2-NN site to a chloride or bromide ion (see Fig. S3 of the ESI†).
The formation energy of a halogen impurity, Eform[X-imp], corresponding to reaction (R1) (see Section 1), is calculated here as follows:
 | (1a) |
Eqn (1a) is general in the sense that it is applicable to the substitution of any oxygen in the slab with a halogen, but it is applied here to the substitution of a surface oxygen. This process is depicted schematically in Fig. 2, along with the values of Eform[X-imp] for each of the surface halogen impurities, with the Ce3+ located at the most energetically favourable site in each case. From those values, it is clear that fluorine impurity formation is highly exothermic, while chlorine impurity formation is significantly less so, and bromine impurity formation is endothermic.
 | ||
| Fig. 2 Formation of a surface halogen impurity. Top row: Schematic depictions of the initial and final states considered in the calculation of Eform[X-imp], as defined in eqn (1a). An asterisk indicates the presence of a Ce3+ ion. See Fig. S1a and Fig. S3 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of Eform[X-imp] for the three halogens. | ||
It is not immediately obvious to what extent the differences in the formation energies are due to differences in the elementary properties of the halogens, or due to differences in their interaction with the ceria surface. To attempt to answer this question, we assume approximate equality between the energy and the enthalpy, and invoke Hess' law—which states that the change in enthalpy of a reaction is equal to the sum of the changes in enthalpy of an (arbitrary) series of sub-reactions with the same initial and final states—to decompose Eform[X-imp] as follows:
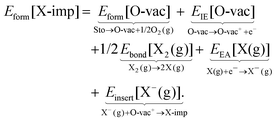 | (1b) |
The decomposition scheme defined in eqn (1b), as applied to the formation of a surface halogen impurity, is shown schematically in Fig. 3. It consists of the energies of two sub-reactions involving ceria alone (Eform[O-vac] and EIE[O-vac]), two involving the halogens alone (Ebond[X2(g)] and EEA[X(g)]), and a final sub-reaction which quantifies the interaction between the two (Einsert[X−(g)]). We note the similarity of the decomposition scheme to the well known Born–Haber cycle, and in particular, the analogy between the lattice energy in the Born–Haber cycle and Einsert[X−(g)].
 | ||
| Fig. 3 Schematic depictions of the elementary reaction steps comprising the decomposition scheme defined in eqn (1b). An asterisk indicates the presence of a Ce3+ ion. See text surrounding eqn (1a) and 1(b) for further details and definitions, and Table 1 for values of the various energies for each halogen species. | ||
The first term on the right-hand side of eqn (1b), Eform[O-vac], is the oxygen vacancy formation energy. For an oxygen vacancy in the surface layer of the otherwise stoichiometric slab, with two Ce3+ ions at 2-NN sites (see Fig. S2a of the ESI†), the value of Eform[O-vac] is 2.38 eV, using our computational set up. This is slightly higher than the energy required to form a vacancy in the sub-surface layer (2.27 eV; see Section 3.3) but the formation energy of the surface vacancy is used for consistency with the location of the halogen impurity.
The second term, EIE[O-vac], is the oxygen vacancy ionisation energy. This was calculated by first removing one electron from the relaxed structure of the (overall) neutral surface oxygen vacancy, computing the total energy with the structure held fixed and applying a charge correction according to the scheme of Komsa and Pasquarello.48,52 Following that procedure, we obtain a vertical ionisation energy of 1.04 eV. Relaxation of the ionised structure led to a reduction in the total energy of 0.44 eV, resulting in a final value for EIE[O-vac] of 0.61 eV.
Table 1 contains the values of the terms in eqn (1b) that directly involve the halogens. Comparing fluorine and bromine, the values of the electron attachment energy and the bond dissociation energy of the two elements differ only slightly, yet it costs 2.02 eV more to create a bromine impurity than a fluorine impurity in the surface layer of CeO2(111), indicating that the major contribution to the large difference in formation energy is the difference in insertion energy. We ascribe this large difference primarily to the difference in the radii of the fluoride and bromide ions; according to the data presented in the work of Shannon,53 the (6 co-ordinated) crystal ionic radius of a bromide ion is 182 pm, which is much larger than the corresponding value of 119 pm for a fluoride ion, which itself is only slightly smaller than the value of 126 pm of the oxide ion that it replaces in the lattice. The large difference between the ionic radii (almost 50% of the radius of the oxide ion) is also reflected in the fact that, while the small fluoride ion is well embedded into the surface, the bromide ion protrudes from it quite significantly (see Fig. S3 of the ESI†); quantitatively, the fluoride protrudes from the oxygen sub-lattice by only 26 pm while the bromide protrudes by 124 pm.
| Reaction energy (eV) | Fluorine | Chlorine | Bromine |
|---|---|---|---|
| E form[X-imp] | −1.86 | −0.15 | +0.16 |
| 1/2Ebond[X2(g)] | +1.14 | +1.43 | +1.24 |
| E EA[X(g)] | −3.70 | −3.59 | −3.42 |
| E insert[X−(g)] | −2.29 | −0.98 | −0.65 |
The formation energy of a surface chlorine impurity is 0.31 eV smaller than that of a surface bromine impurity. In this case, the chlorine molecule's larger bond dissociation energy is counterbalanced by the more negative electron attachment energy of the chlorine atom, so that the difference in formation energy is almost exactly equal to the difference in insertion energy, consistent with the chloride's smaller ionic radius of 167 pm. Like the bromide ion, the chloride ion protrudes significantly from the surface (by 102 pm), albeit less so than the bromide ion, consistent with the smaller radius of the chloride ion (see Fig. S3 of the ESI†).
We conclude this section by comparing the energies calculated for this work using DFT with their experimentally measured counterparts where available; namely, the halogen atomic electron attachment energies and the halogen and oxygen molecular dissociation energies. For the atomic electron attachment energies, the calculated values agree quite well with their experimental counterparts: to within 2% for chlorine and bromine and within 10% for fluorine.54 The error in the calculated molecular dissociation energies is larger, such that in all cases (F, Cl, Br, O) the experimental binding energy is only 70–80% of the corresponding calculated value.55 However, these systematic errors in the calculated values with respect to the experimental references do not alter our main conclusion regarding the major role of the insertion energy in determining the halogen impurity formation energy.
3.2 Pairing of halogen impurities (reaction (R2))
We next consider the interaction between two halogen impurities of the same species, in terms of the formation of an impurity pair (reaction (R2); see Section 1) from two isolated impurities. The corresponding ‘pairing energy’, Epair[X-imp], is defined as:
 | (2) |
The initial and final states of the pairing process for surface halogen impurities are illustrated schematically in Fig. 4. The dependence of Epair[X-imp] on the proximity of the two constituent surface halide ions was investigated by considering the cases in which the halide ions are at first, second and third nearest neighbour anionic lattice sites (1-NN, 2-NN and 3-NN; see Fig. 1a) to each other. Furthermore, for each separation of the halide ions, we also explored the dependence of Epair[X-imp] on the locations of the charge compensating Ce3+ ions in the second atomic layer, since such effects have been found to be significant for aggregates of other commonly considered anionic defects, namely oxygen vacancies and hydroxyl groups.50,56 Given the large number of possible locations for the Ce3+ ions in the vicinity of the two halide ions for each separation of the latter, the configurations that we considered were restricted to those in which the Ce3+ ions were at most 2-NN from at least one of the two halide ions. Moreover, we first considered charged systems of 1-NN, 2-NN and 3-NN halide pairs with a single Ce3+ ion, adding the second Ce3+ ion only after locating the lowest energy position for the first, and fixing its location at that site.
 | ||
| Fig. 4 Pairing of two surface halogen impurities. Top two rows: Schematic depictions of the initial and final states considered in the calculation of Epair[X-imp], as defined in eqn (2). An asterisk indicates the presence of a Ce3+ ion. See Fig. S1a, S3 and S4 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of Epair[X-imp] for the three halogens. | ||
In the case of fluorine, the lowest energy arrangement is one in which the two F− ions occupy 1-NN surface anionic sites, with one Ce3+ between them and the other next to one of the F− ions (see Fig. S4 of the ESI†). Associated with this structure is a relatively small, but non-negligible, value of Epair[X-imp] of −0.09 eV. We note that the lowest energy arrangement found here confirms the result reported in previous publications,57–59 which was based on a less extensive search for the lowest energy locations of the halide pair and the Ce3+ ions.
In contrast, in the lowest energy arrangements for chlorine and bromine impurity pairs, the two halide ions occupy 2-NN sites with respect to one another, with one Ce3+ between the two halides and the other at a 2-NN site with respect to one of the halides (see Fig. S4 of the ESI†). Interestingly, the pairing energies for chlorine and bromine impurities are very similar to that for fluorine impurities, namely −0.09 eV for chlorine and −0.08 eV for bromine, despite the lowest energy arrangement being different.
3.3 Formation of an oxygen vacancy in the vicinity of a halogen impurity (reaction (R3))
Oxygen vacancies play a central role in most applications of ceria, and hence we begin our consideration of the effects of halogen impurities on the oxygen chemistry of CeO2(111) by computing the formation energy of an oxygen vacancy in the vicinity of a halogen impurity (reaction (R3); see Section 1), Eform[O-vac near X-imp], which is defined as follows:
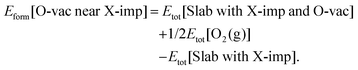 | (3) |
As has been well established in numerous theoretical studies (see e.g. ref. 60 and 61 and further references therein), the lowest energy configuration for an oxygen vacancy in the near surface region of otherwise stoichiometric CeO2(111) is that in which the missing oxide ion resides in the sub-surface oxygen layer, with the two charge compensating Ce3+ ions at 2-NN sites (see Fig. S1b of the ESI†). Therefore, we compute Eform[O-vac near X-imp] for a surface halogen impurity with the oxygen vacancy in the sub-surface layer, as depicted schematically in Fig. 5, and compare it with the energy required to form a sub-surface oxygen vacancy at the stoichiometric surface.
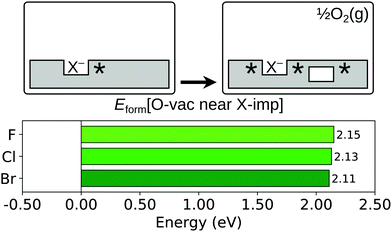 | ||
| Fig. 5 Oxygen vacancy formation in the vicinity of a halogen impurity. Top row: Schematic depictions of the initial and final states considered in the calculation of Eform[O-vac near X-imp], as defined in eqn (3). An asterisk indicates the presence of a Ce3+ ion. See Fig. S3 and S5 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of Eform[O-vac near X-imp] for the three halogens. | ||
The value of Eform[O-vac near X-imp] was computed with the missing sub-surface oxide ion at first, second and third nearest neighbour (1-NN, 2-NN and 3-NN respectively) lattice sites to the surface halide ion (see Fig. 1c). Similarly to the halogen impurity pairing energy, Epair[X-imp], discussed in Section 3.2, the value of Eform[O-vac at X-imp] depends not only on the separation between the halide ion and the missing oxide ion, but also on the locations of the three charge compensating Ce3+ ions. In order to determine the lowest energy distribution of the Ce3+ ions for each separation of the halide ion and missing oxide ion, we followed an approach analogous to that used in Section 3.2. However, since three Ce3+ ions are associated with the impurity–vacancy defect pair (i.e., one more than the two Ce3+ ions associated with the impurity–impurity pair), the calculations were performed in three stages: first, the lowest energy location of a single Ce3+ for each separation of the surface halide ion and missing sub-surface oxide ion was determined, subject to the restriction that the sites considered were at most 2-NN to either the halide or the missing oxide. A second Ce3+ ion was then introduced, and the same procedure was followed with the location of the first Ce3+ fixed in the lowest energy position determined in the preceding stage. Finally, the third Ce3+ ion was introduced, and the lowest energy location was determined with the first and second Ce3+ ion fixed at the locations determined in the earlier stages.
We compare the values of Eform[O-vac near X-imp] with the formation energy of a sub-surface oxygen vacancy at the otherwise stoichiometric surface, which is calculated to be 2.27 eV with the computational set-up used here. For all three halogen impurities, the formation energy of an oxygen vacancy at a 1-NN site to the halide is greater than at the stoichiometric surface, with the values of Eform[O-vac near X-imp] being 2.41 eV, 2.58 eV and 2.64 eV for fluorine, chlorine and bromine respectively, which follow the order of the ionic radii. However, we find that the lowest energy structures, in which the missing oxide ion is at a 3-NN site with respect to the halide ion (see Fig. S5 of the ESI†), lead to values of Eform[O-vac near X-imp] that are slightly reduced with respect to the stoichiometric surface. We note that the formation energies of 2.15 eV, 2.13 eV and 2.11 eV for fluorine, chlorine and bromine follow the inverse ordering of the ionic radii at this separation, although the differences are arguably negligible.
3.4 Adsorption of an oxygen molecule in the vicinity of a halogen impurity (reaction (R4))
We next consider the effects of surface halogen impurities on the adsorption of an oxygen molecule (reaction (R4); see Section 1). The adsorption energy of an oxygen molecule in the vicinity of a halogen impurity, Eads[O2 near X-imp], is calculated as follows:
 | (4) |
When considering oxygen adsorption in the vicinity of a halogen impurity, the pure ceria system to which we should compare is not entirely obvious. An oxygen molecule adsorbed on the stoichiometric CeO2(111) surface is one natural choice. On the other hand, a halogen impurity has one Ce3+ ion associated with it, and therefore comparison with an oxygen molecule adsorbed in the vicinity of an oxygen vacancy (which has two Ce3+ ions associated with it) is also relevant.
As has been observed in previous studies,38,62 an oxygen molecule physisorbs very weakly on the stoichiometric CeO2(111) surface, ‘hovering’ above a Ce4+ ion in a tilted configuration (see Fig. S1c of the ESI†), with an adsorption energy of just −0.03 eV. The O–O bond length of the adsorbed molecule is 1.23 Å, and the value of the spin density integrated over the two oxygen atoms is 1.6; both values are identical to those calculated in this work of a neutral O2 molecule in the gas phase. In contrast, as is depicted schematically in Fig. 6, we find that the molecule is chemisorbed as a superoxide (O2−) in the vicinity of a surface halogen impurity, due to charge transfer from the Ce3+ ion to the oxygen molecule. The O2− molecule also lies closer to the Ce ion on which it is adsorbed, and in a characteristically flatter configuration (see Fig. S5 of the ESI†), than does the neutral O2 molecule above a Ce ion on the stoichiometric surface. Indeed, the adsorption configuration is similar to that reported in a number of theoretical studies on oxygen molecule adsorption in the vicinity of an oxygen vacancy at CeO2(111),62,63 and in our own calculations (see Fig. S2b of the ESI†); note that we are not (yet) considering the possibility of the molecule entering the vacancy, a scenario that is addressed in Section 3.5. Having considered adsorption above a 1-NN, 2-NN and 3-NN cerium site of the surface halide ion (see Fig. 1b), we find that the energetically most favourable adsorption site for an O2− in the vicinity of each halide corresponds to the energetically most favourable location of the Ce3+ ion before adsorption of the molecule (i.e. the molecule is adsorbed on a 1-NN Ce of the fluoride ion, but on a 2-NN Ce of the chloride and bromide ions, as shown in Fig. S6 of the ESI†). The values of Eads[O2 near X-imp] of −0.28 eV, −0.25 eV and −0.24 eV for the fluorine, chlorine and bromine impurities respectively, are also similar to the adsorption energy of a molecule in the vicinity of a vacancy, which is −0.34 eV using our computational set up.
 | ||
| Fig. 6 O2 molecule adsorption in the vicinity of a halogen impurity. Top row: Schematic depictions of the initial and final states considered in the calculation of Eads[O2 near X-imp], as defined in eqn (4). An asterisk indicates the presence of a Ce3+ ion. See Fig. S3 and S6 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of Eads[O2 near X-imp] for the three halogens. | ||
Although the configuration of the adsorbed O2− molecule is very similar for all three halogen impurities, and the surface oxygen vacancy, there are some small quantitative differences. Firstly, while the O–O bond length is 1.31 Å for an O2− adsorbed in the vicinity of a fluorine impurity or a vacancy, it is slightly smaller for an O2− adsorbed in the vicinity of a chlorine or bromine impurity, at 1.30 Å. Secondly, the (integrated) spin density distribution is slightly different, with 1.0 on the molecule in the vicinity of a fluorine impurity or a vacancy, and 1.1 in the vicinity of a chlorine or bromine impurity; furthermore the value on the Ce ion on which the molecule is adsorbed is −0.29 in the vicinity of a fluorine impurity or a vacancy, but −0.37 in the vicinity of a chlorine or bromine impurity. Although the differences described above are small, and possibly the result of numerical inaccuracy in the calculations, they are consistent with the results of electron paramagnetic resonance (EPR) experiments that have been carried out on pure and chlorinated ceria samples exposed to molecular oxygen at 77 K.64 In those experiments, it was found that (i) exposing both types of sample to molecular oxygen resulted in the formation of O2− species, but features were observed in the spectra of the chlorinated samples that were not observed in the spectra of the pure samples, and (ii) the spectral features that were unique to the chlorinated samples were less stable with respect to temperature. Those findings are consistent with our observations that (i) the spin density distribution associated with an O2− adsorbed in the vicinity of a chlorine impurity is different from that associated with an O2− adsorbed in the vicinity of a vacancy, and (ii) the adsorption energy of an O2 in the vicinity of a chlorine impurity is lower than that of an O2 adsorbed in the vicinity of an oxygen vacancy.
To conclude this section, we note that a second halogen impurity located in close proximity to the first (in one of the impurity pairs described above, for example) could, in principle, provide a second electron to the adsorbed superoxide molecule (via transfer from the Ce3+ ion associated with the second impurity), reducing it further to a peroxide (O22−) molecule. However, it was found previously to be energetically unfavourable for an adsorbed peroxide to form in the vicinity of a fluorine impurity pair.58 Given the similar effects of isolated fluorine, chlorine and bromine impurities on O2 adsorption, we expect that an adsorbed peroxide would also be unstable in the presence of chlorine and bromine impurity pairs, and do not consider the possibility further.
3.5 Reoxidation of halogen impurities (reactions (R5a)–(R5c))
The similarities between oxygen adsorption in the vicinity of a surface halogen impurity, and oxygen adsorption in the vicinity of a surface oxygen vacancy, discussed in Section 3.4, suggest an additional, alternative mode of interaction between halogen impurities and molecular oxygen. It is well established that it is energetically favourable for an O2 molecule to enter a surface vacancy—that is, to be absorbed into the surface, as opposed to being adsorbed on to it—and for electron transfer to take place from the two Ce3+ ions to the O2 to produce a peroxide molecule (O22−) embedded in the surface (see Fig. S2c of the ESI†).38,63,65–67 Furthermore, it is then energetically favourable for the peroxide molecule to dissociate and one half to return to the gas phase as half of an oxygen molecule.58 The end result of this sequence is that the vacancy is healed by half of a gas phase oxygen molecule, with a change in energy equal to the negative of the oxygen vacancy formation energy, i.e. −Eform[O-vac].The analogous healing process for a halogen impurity is the reverse of the formation process discussed in detail in Section 3.1, and depicted schematically in Fig. 2. Here, we consider an additional possibility, namely the process shown in Fig. 7, which results in an intermediate state in which the surface halide ion has been replaced with half of an oxygen molecule, but the halogen remains on the surface instead of desorbing in the form of half of a halogen molecule (i.e.reaction (R5a); see Section 1). We refer to this process as ‘reoxidation’ of the impurity, with an associated change in energy Ereox[X-imp] that is calculated as follows:
 | (5a) |
 | ||
| Fig. 7 Reoxidation of an isolated surface halogen impurity. Top row: Schematic depictions of the initial and final states considered in the calculation of Ereox[X-imp], as defined in eqn (5a). An asterisk indicates the presence of a Ce3+ ion, and δ illustrates the partial charge transfer between the ceria slab and the adsorbed halogen, the magnitude of which depends on the halogen species. See Fig. S3 and S7 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of Ereox[X-imp] for the three halogens. | ||
The resulting state—that is, the stoichiometric ceria surface with an adsorbed halogen—has been considered previously in the literature for fluorine58 and for chlorine and bromine68 (we note that the state was considered as resulting from the direct adsorption of a chlorine or bromine atom on the stoichiometric surface in ref. 68, rather than the reoxidation process considered here and in ref. 58). As was done in ref. 68, we considered two possible adsorption modes, one in which the halogen is adsorbed on a Ce ion (‘X–Ce’), and the other in which it is adsorbed on top of an oxide ion (‘X–O’) with which it forms a covalent bond. In line with the results of ref. 68 for chlorine and bromine, we find that the X–Ce structure (see Fig. S7 of the ESI†) is more stable than the X–O one, for all three of the halogens under consideration; however, the values of Ereox[X-imp] of 0.65 eV, 0.38 eV and 0.12 eV for fluorine, chlorine and bromine respectively, indicate that such a structure is less stable than the initial one in which the halide ion is embedded in the surface.
Comparing the reoxidation process with the healing of an oxygen vacancy at the otherwise stoichiometric surface, there is an important difference between an oxygen vacancy and a halogen impurity, namely that the former defect has two Ce3+ associated with it, while the latter has only one. This impedes the full reduction of the oxygen atom that displaces the halide ion on to the surface. However, it has been shown for the case of fluorine that the competition can be alleviated by the presence of a second halogen impurity, and its associated Ce3+,58 to the extent that the reaction is exothermic. Thus, we consider here the energy change, E1streox[X-imp pair], associated with the process depicted schematically in Fig. 8, i.e. the displacement on to the surface of one halide ion which is initially part of a halogen impurity pair (i.e.reaction (R5b); see Section 1):
 | (5b) |
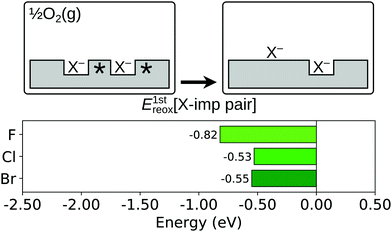 | ||
| Fig. 8 First reoxidation of a surface halogen impurity pair. Top row: Schematic depictions of the initial and final states considered in the calculation of E1streox[X-imp pair], as defined in eqn (5b). An asterisk indicates the presence of a Ce3+ ion. See Fig. S4 and S8 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of E1streox[X-imp pair] for the three halogens. | ||
We calculated values of E1streox[X-imp pair] for the resulting X–Ce species discussed above at 1-NN, 2-NN and 3-NN sites of the impurity remaining in the surface (see Fig. 1b), and as expected, a fully reduced surface oxide ion was formed in all cases. It was found that the lowest energy arrangement for fluorine was that in which the X–Ce is located at a 1-NN site, but for chlorine and bromine it was energetically favourable for the X–Ce to be located at a 2-NN site (see Fig. S8 of the ESI†). The values of E1streox[X-imp pair] corresponding to those structures are −0.82 eV for fluorine, −0.53 eV for chlorine and −0.55 eV for bromine.
Finally, we consider the process shown schematically in Fig. 9, in which the second halogen impurity is also displaced on to the surface (i.e.reaction (R5c); see Section 1), with an associated energy change, E2ndreox[X-imp pair], defined as follows:
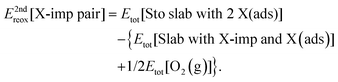 | (5c) |
 | ||
| Fig. 9 Second reoxidation of a surface halogen impurity pair. Top row: Schematic depictions of the initial and final states considered in the calculation of E2ndreox[X-imp pair], as defined in eqn (5c). An asterisk indicates the presence of a Ce3+ ion, and δ1 and δ2 illustrate the partial charge transfer between the ceria slab and the adsorbed halogens, the magnitudes of which depend on the halogen species. See Fig. S8 and S9 of the ESI† for ball models of the optimised structures of the initial and final states. Bottom row: Bar chart of the values of E2ndreox[X-imp pair] for the three halogens. | ||
For the possible structures resulting from this process, we considered those studied in detail for two adsorbed chlorine and bromine atoms in ref. 68, which are combinations of the X–O and X–Ce species described above. In ref. 68, only the structures in which the X–O and X–Ce are 1-NN to each other was considered, but here we also consider 2-NN and 3-NN separations (see Fig. 1b, understanding the location of the halogen as being on top of a surface oxygen, instead of substituting for it). For chlorine and bromine, we find that X–O and X–Ce being 2-NNs to each other is the lowest energy arrangement. Interestingly, we also find that, starting from the structure in which the F–O and F–Ce are 2-NNs, the F–O species dissociates spontaneously during the structural relaxation. The optimised structure comprises two F–Ce's that are 2-NNs to each other, with a peroxide molecule, formed of a surface and sub-surface oxygen ion, in between them (see Fig. S9 of the ESI†). We also calculated the energies of the equivalent structures for chlorine and bromine, and a structure with two F–Ce's as 1-NNs with a peroxide molecule between them, but found that the energy was greater than for the structures described above in all cases. In any case, we find that the structures in which both halide ions are displaced on to the surface are higher in energy than those in which one of the halogens remains in the surface (i.e. as an impurity) for all three halogens, with values of E2ndreox[X-imp pair] of 0.89 eV, 0.54 eV and 0.26 eV for fluorine, chlorine and bromine respectively.
4 Conclusion
We have presented the results of an investigation into the properties of substitutional fluorine, chlorine and bromine impurities, and some elementary reactions which indicate their effects on the oxygen chemistry of CeO2(111). Particular care was taken to determine the lowest energy structure in each reaction, with respect to the separations of the constituent chemical species. The resulting lowest energies associated with the elementary reactions (R1)–(R5c) listed in Section 1 are collected in Table 2. In summary, our main results are as follows:| Reaction energy (eV) | Eqn | Fig. | Fluorine | Chlorine | Bromine |
|---|---|---|---|---|---|
| a Cf. the formation energy of a sub-surface oxygen vacancy at the otherwise stoichiometric surface, +2.27 eV. b Cf. the adsorption energy of an oxygen molecule on the stoichiometric surface, −0.03 eV, and in the vicinity of a surface oxygen vacancy, −0.34 eV. | |||||
| E form[X-imp] | (1a) | 2 | −1.86 | −0.15 | +0.16 |
| E pair[X-imp] | (2) | 4 | −0.09 | −0.09 | −0.08 |
| E form[O-vac near X-imp]a | (3) | 5 | +2.15 | +2.13 | +2.11 |
| E ads[O2 near X-imp]b | (4) | 6 | −0.28 | −0.25 | −0.24 |
| E reox[X-imp] | (5a) | 7 | +0.65 | +0.38 | +0.12 |
| E 1streox[X-imp pair] | (5b) | 8 | −0.82 | −0.53 | −0.55 |
| E 2ndreox[X-imp pair] | (5c) | 9 | +0.89 | +0.54 | +0.26 |
(1) The substitution of a halogen for a lattice oxygen in the surface layer results in the formation of a halide ion and the reduction of one Ce4+ ion to Ce3+, but the formation energy depends strongly on the identity of the halogen. In order to rationalise the differences in formation energies, a simple decomposition scheme was devised and applied, inspired by the well known Born–Haber cycle for ionic crystals. The decomposition scheme enabled the identification of the largest contribution to the differences between the halogens, namely the energy required to insert a halide ion from the gas phase into an ionised surface vacancy (Table 1), which we ascribe in turn to the differences in the radii of the three halide ions.
(2) The formation of pairs of surface halogen impurities from isolated impurities is slightly energetically favourable for all three halogens.
(3) The formation energy of a (sub-surface) oxygen vacancy in the vicinity of a halogen impurity is slightly reduced with respect to the formation energy of an oxygen vacancy at the stoichiometric surface. In particular, the effect is significantly smaller than for e.g. transition metal cation dopants, where low-lying empty d orbitals are available to accept the excess electrons that are produced upon oxygen vacancy formation.
(4) The adsorption of an oxygen molecule from the gas phase in the vicinity of a surface halogen impurity involves electron transfer from the Ce3+ ion of the impurity defect to the molecule, thereby forming an adsorbed superoxide molecule. The adsorption energy is significantly larger than that associated with the adsorption of a neutral oxygen molecule on stoichiometric CeO2(111), for all three halogens, but it is similar to the adsorption energy in the vicinity of a (surface) oxygen vacancy.
(5) The displacement on to the surface of a substitutional halide ion, and the filling of the resulting vacancy by half an oxygen molecule—a process to which we refer here as reoxidation—depends strongly on whether or not there is a second halogen impurity present in the vicinity of the displaced ion. In short, if there is a second halogen impurity present, then the process is energetically favourable, otherwise it is not. This is due to the requirement of a second Ce3+ to reduce fully the oxygen atom that replaces the halide ion in the lattice. The magnitude of the change in energy also depends significantly on the identity of the halogen.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the Swedish Research Council (Vetenskapsrådet) and from the Swedish strategic collaborative research programme in e-science, eSSENCE. The calculations described in this paper were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC. We thank Dr J. Kullgren for commenting on a draft of the paper.References
- E. W. McFarland and H. Metiu, Chem. Rev., 2013, 113, 4391–4427 CrossRef CAS PubMed.
- H. J. Kim, M. G. Jang, D. Shin and J. W. Han, ChemCatChem, 2020, 12, 11–26 CrossRef CAS.
- R. Schmitt, A. Nenning, O. Kraynis, R. Korobko, A. I. Frenkel, I. Lubomirsky, S. M. Haile and J. L. Rupp, Chem. Soc. Rev., 2020, 49, 554–592 RSC.
- Y. Liu, W. Wang, X. Xu, J.-P. M. Veder and Z. Shao, J. Mater. Chem. A, 2019, 7, 7280–7300 RSC.
- R. J. Gorte, AIChE J., 2010, 56, 1126–1135 CAS.
- Catalysis by ceria and related materials, 2nd edn, ed. A. Trovarelli and P. Fornasiero, Imperial College Press, London, 2013 Search PubMed.
- T. Montini, M. Melchionna, M. Monai and P. Fornasiero, Chem. Rev., 2016, 116, 5987–6041 CrossRef CAS PubMed.
- S. R. Gilliss, J. Bentley and C. B. Carter, Appl. Surf. Sci., 2005, 241, 61–67 CrossRef CAS.
- J. Zarraga-Colina, R. M. Nix and H. Weiss, J. Phys. Chem. B, 2005, 109, 10978–10985 CrossRef CAS PubMed.
- D. Barreca, A. Gasparotto, C. Maccato, C. Maragno and E. Tondello, Langmuir, 2006, 22, 8639–8641 CrossRef CAS PubMed.
- H. Pieper, C. Derks, M. Zoellner, R. Olbrich, L. Tröger, T. Schroeder, M. Neumann and M. Reichling, Phys. Chem. Chem. Phys., 2012, 14, 15361–15368 RSC.
- M. Kettner, K. Ševčková, T. Duchoň, P. Kúš, Z. Rafaj and V. Nehasil, J. Phys. Chem. C, 2016, 120, 26782–26792 Search PubMed.
- M. Kettner, T. Duchoň, M. J. Wolf, J. Kullgren, S. D. Senanayake, K. Hermansson, K. Veltruská and V. Nehasil, J. Chem. Phys., 2019, 151, 044701 CrossRef PubMed.
- S. Ahmad, K. Gopalaiah, S. N. Chandrudu and R. Nagarajan, Inorg. Chem., 2014, 53, 2030–2039 CrossRef CAS PubMed.
- B. Liu, Z. Huang and J. Liu, Nanoscale, 2016, 8, 13562–13567 RSC.
- F. Le Normand, L. Hilaire, K. Kili, G. Krill and G. Maire, J. Phys. Chem., 1988, 92, 2561–2568 CrossRef CAS.
- F. Fajardie, J.-M. Manoli, G. Djega-Mariadassou and G. Blanchard, J. Chem. Soc., Faraday Trans., 1998, 94, 3727–3735 RSC.
- S. Bernal, F. Botana, J. Calvino, M. Cauqui, G. Cifredo, A. Jobacho, J. Pintado and J. Rodriguez-Izquierdo, J. Phys. Chem., 1993, 97, 4118 CrossRef CAS.
- D. I. Kondarides and X. E. Verykios, J. Catal., 1998, 174, 52–64 CrossRef CAS.
- L. Kepiński, M. Wołcyrz and J. Okal, J. Chem. Soc., Faraday Trans., 1995, 91, 507–515 RSC.
- R. Taha, D. Martin, S. Kacimi and D. Duprez, Catal. Today, 1996, 29, 89–92 CrossRef CAS.
- S. Sugiyama, K. Sogabe, T. Miyamoto, H. Hayashi and J. B. Moffat, Catal. Lett., 1996, 42, 127–133 CrossRef CAS.
- A. P. Amrute, C. Mondelli, M. Moser, G. Novell-Leruth, N. López, D. Rosenthal, R. Farra, M. E. Schuster, D. Teschner, T. Schmidt and J. Pérez-Ramírez, J. Catal., 2012, 286, 287–297 CrossRef CAS.
- R. Farra, S. Wrabetz, M. E. Schuster, E. Stotz, N. G. Hamilton, A. P. Amrute, J. Pérez-Ramrez, N. López and D. Teschner, Phys. Chem. Chem. Phys., 2013, 15, 3454–3465 RSC.
- C. Sack, P. Lustemberg, V. Koller, M. V. Ganduglia-Pirovano and H. Over, J. Phys. Chem. C, 2018, 122, 19584–19592 CrossRef CAS.
- M. Moser, G. Vilé, S. Colussi, F. Krumeich, D. Teschner, L. Szentmiklósi, A. Trovarelli and J. Perez-Ramirez, J. Catal., 2015, 331, 128–137 CrossRef CAS.
- G. Zichittella, V. Paunović, A. P. Amrute and J. Perez-Ramirez, ACS Catal., 2017, 7, 1805–1817 CrossRef CAS.
- M. V. Konishcheva, D. I. Potemkin, P. V. Snytnikov, V. P. Pakharukova and V. A. Sobyanin, Energy Technol., 2017, 5, 1522–1525 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- J. L. Bao, L. Gagliardi and D. G. Truhlar, J. Phys. Chem. Lett., 2018, 9, 2353–2358 CrossRef CAS PubMed.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B, 1998, 57, 1505 CrossRef CAS.
- M. Huang and S. Fabris, Phys. Rev. B, 2007, 75, 081404 CrossRef.
- C. Loschen, J. Carrasco, K. M. Neyman and F. Illas, Phys. Rev. B, 2007, 75, 035115 CrossRef.
- G. Pacchioni, Catal. Lett., 2015, 145, 80–94 CrossRef CAS.
- D. Du, M. J. Wolf, K. Hermansson and P. Broqvist, Phys. Rev. B, 2018, 97, 235203 CrossRef CAS.
- B. Dorado, B. Amadon, M. Freyss and M. Bertolus, Phys. Rev. B, 2009, 79, 235125 CrossRef.
- J. P. Allen and G. W. Watson, Phys. Chem. Chem. Phys., 2014, 16, 21016–21031 RSC.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188 CrossRef.
- J. Buckeridge, D. Scanlon, A. Walsh, C. Catlow and A. Sokol, Phys. Rev. B, 2013, 87, 214304 CrossRef.
- C. Schilling, A. Hofmann, C. Hess and M. V. Ganduglia-Pirovano, J. Phys. Chem. C, 2017, 121, 20834–20849 CrossRef CAS.
- S. Mochizuki, Phys. Status Solidi B, 1982, 114, 189–199 CrossRef CAS.
- M. F. Tabriz, B. Aradi, T. Frauenheim and P. Deák, Comput. Phys. Commun., 2019, 240, 101–105 CrossRef.
- J. J. Plata, A. M. Márquez and J. F. Sanz, J. Phys. Chem. C, 2013, 117, 25497–25503 CrossRef CAS.
- D. Fernández-Torre, J. Carrasco, M. V. Ganduglia-Pirovano and R. Pérez, J. Chem. Phys., 2014, 141, 014703 CrossRef PubMed.
- M. J. Wolf, C. W. Castleton, K. Hermansson and J. Kullgren, Front. Chem, 2019, 7, 212 CrossRef CAS PubMed.
- H.-P. Komsa and A. Pasquarello, Phys. Rev. Lett., 2013, 110, 095505 CrossRef PubMed.
- R. D. Shannon, Acta Crystallogr. A, 1976, 32, 751–767 CrossRef.
- S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. Linstrom and W. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 2018 Search PubMed.
- K.-P. Huber and G. Herzberg, Molecular spectra and molecular structure: IV. Constants of diatomic molecules, Springer Science & Business Media, 1979 Search PubMed.
- G. E. Murgida and M. V. Ganduglia-Pirovano, Phys. Rev. Lett., 2013, 110, 246101 CrossRef PubMed.
- J. Kullgren, M. J. Wolf, C. Castleton, P. Mitev, W. Briels and K. Hermansson, Phys. Rev. Lett., 2014, 112, 156102 CrossRef CAS PubMed.
- M. J. Wolf, J. Kullgren, P. Broqvist and K. Hermansson, J. Chem. Phys., 2017, 146, 044703 CrossRef PubMed.
- J. Kullgren, M. J. Wolf, P. D. Mitev, K. Hermansson and W. J. Briels, J. Phys. Chem. C, 2017, 121, 15127–15134 CrossRef CAS.
- J. Paier, C. Penschke and J. Sauer, Chem. Rev., 2013, 113, 3949–3985 CrossRef CAS PubMed.
- M. Nolan, in Catalysis by Materials with Well-Defined Structures, Elsevier, 2015, pp. 159–192 Search PubMed.
- H.-T. Chen, J.-G. Chang, H.-L. Chen and S.-P. Ju, J. Comput. Chem., 2009, 30, 2433–2442 CrossRef CAS PubMed.
- Y. Zhao, B.-T. Teng, X.-D. Wen, Y. Zhao, Q.-P. Chen, L.-H. Zhao and M.-F. Luo, J. Phys. Chem. C, 2012, 116, 15986–15991 CrossRef CAS.
- A. Martínez-Arias, J. C. Conesa and J. Soria, Res. Chem. Intermed., 2007, 33, 775–791 CrossRef.
- H.-Y. Li, H.-F. Wang, X.-Q. Gong, Y.-L. Guo, Y. Guo, G. Lu and P. Hu, Phys. Rev. B, 2009, 79, 193401 CrossRef.
- J. C. Conesa, Catal. Today, 2009, 143, 315–325 CrossRef CAS.
- J. Fan, C. Li, J. Zhao, Y. Shan and H. Xu, J. Phys. Chem. C, 2016, 120, 27917–27924 CrossRef CAS.
- Z. Hu and H. Metiu, J. Phys. Chem. C, 2012, 116, 6664–6671 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Ball-model figures of the low energy relaxed structures discussed in the text. See DOI: 10.1039/d1cp01320c |
| This journal is © the Owner Societies 2021 |

