Open Access Article
Open Access ArticleInfrequent metadynamics study of rare-event electrostatic channeling†
Yan
Xie
 and
Scott
Calabrese Barton
and
Scott
Calabrese Barton
 *
*
Department of Chemical Engineering and Materials Science, Michigan State University, East Lansing, MI 48824, USA. E-mail: scb@msu.edu
First published on 31st May 2021
Abstract
The efficiency of cascade reactions, which consist of multiple chemical transformations that occur in a single pot without purification steps, is limited by the transport efficiency of intermediates between adjacent steps. Electrostatic channeling is a proven strategy for intermediate transfer in natural chemical cascades, but implementation into artificial cascades remains a challenge. Here, we combine infrequent metadynamics (InMetaD), umbrella sampling (US), and kinetic Monte Carlo (KMC) models to computationally study the transfer mechanism of glucose-6-phosphate (G6P) on a poly-arginine peptide bridging hexokinase (HK) and glucose-6-dehydrogenase (G6PDH). Transport of G6P by hopping in the presence of poly-arginine peptides is shown to be a rare event, and InMetaD is used to compute the hopping activation energy. US simulations capture the configurational change in the desorption process and enable the determination of the desorption energy. Parameterized by these results, a KMC model is used to estimate transport efficiency for the bridged enzyme complex. Results are compared to a similar complex using a poly-lysine bridge, using kinetic lag time as a metric. Even at a high ionic strength of 120 mM, poly-arginine peptides may be capable of more efficient transport as compared to poly-lysine, with a predicted lag time of 6 seconds for poly-arginine, compared to a previously reported lag time of 59 seconds for poly-lysine. This work indicates that poly-arginine peptides may be an improved bridge structure for electrostatic channeling of anionic intermediates.
Introduction
Cascade reactions that combine multiple chemical transformations into a single step, without purification steps, have attracted attention recently due to benefits such as minimal complexity, reduced labor requirements, and decreased waste.1 Design and control of cascade reactions requires a deep understanding of the mechanism and a substantial toolbox with which to build cascade architectures.Many examples are found in nature where substrate channeling improves the efficiency of cascade reactions, by enabling intermediate transport between adjacent reaction active sites without equilibrating with a bulk concentration.2 Intermediates can be thereby protected from unfavorable binding or reaction in the bulk, enhancing overall cascade reaction efficiency. Some strategies of substrate channeling observed in nature are intramolecular tunneling,3 chemical swing arms,4,5 spatial organization,4,6,7 and electrostatic channeling.7–9 Electrostatic channeling controls the transport of charged intermediates via electrostatic interaction with the oppositely charged surface between active sites. It is a promising way to channel artificial cascades because it is not limited by structural aspects, and most metabolic intermediates are charged.10
The transport efficiency of electrostatic channeling can be measured by the determination of the transient lag time—the time the system takes to reach steady-state flux. For a perfect channeling mechanism, the lag time is near zero; for an electrostatically channeled system, a lower lag time reflects increased channeling efficiency.11
In recent decades, considerable efforts have focused on two well-studied examples of electrostatic channeling in nature. The first example is the bifunctional enzyme dihydrofolate reductase-thymidylate synthase (DHFR-TS), where bounded diffusion guides negatively charged dihydrofolate intermediates on the positively charged protein structure between two active sites.10 The other often studied example is the super enzyme complex of malate dehydrogenase (MDH) and citrate synthase (CS) within the tricarboxylic acid (TCA) cycle, where oxaloacetate, carrying two negative charges, crosses the positively charged surface between MDH and CS via electrostatic interaction.12 Structural characterization of each of these systems has revealed a charged surface present between active sites, and lag time analyses have demonstrated the influence of this surface on kinetics.10,13 However, experimental approaches provide a limited view of how intermediates interact with these electrostatic surfaces. Thus, advanced computational simulations provide a view into the interaction mechanisms underlying electrostatic channeling.
 | ||
| Scheme 1 Dual site conversion of glucose to gluconolactone via hexokinase (HK) and glucose-6-phosphate dehydrogenase (G6PDH). Glucose-6-phosphate (G6P) is a stable intermediate. | ||
Computational studies have addressed substrate channeling mechanisms, including DNA-scaffolded bienzyme systems,7,14,15 co-immobilization,16 and encapsulation,17–20 in artificial cascades. Our group and collaborators have recently reported studies of electrostatic channeling in an artificial cascade comprising hexokinase (HK) and glucose-6-phosphate dehydrogenase (G6PDH) where the reactions take place according to Scheme 1.21–23
In those works, an enzyme complex of HK and G6PDH was covalently conjugated by a positively charged poly-lysine peptide, and the negatively charged intermediate glucose-6-phosphate (G6P) was channeled through electrostatic interactions. A hopping transport mode was considered, and diffusion and desorption energy barriers were computed for intermediate transport along the poly-lysine bridge. Computational results along with experimental data were used to parameterize a kinetic Monte Carlo (KMC) model to compute the transport efficiency of G6P in terms of lag time. Computational results matched well with the experiment, and both results demonstrated the effectiveness of the poly-lysine bridge in decreasing lag time by the increasing transport efficiency of the intermediate. Electrostatic channeling efficiency was shown to decrease with increasing ionic strength, and loss of intermediate was found to be significant at each terminal enzyme, particularly for HK, which has a significant net negative charge.
As an alternative cationic amino acid to lysine, arginine residues are more polarized and can form multidentate hydrogen bonds with phosphate groups,24 enabling stronger interaction with charged intermediates. Because of the strong interaction, poly-arginine peptides are more electrostatically “sticky” than poly-lysine, increasing both the desorption energy and hopping activation energy of G6P on poly-arginine peptides. High desorption energy lowers desorption probability and prevents G6P's leakage at high ionic strength.
However, such high hopping activation energy traps G6P in energy wells on the poly-arginine peptide, increasing the time scale between observed hopping events to hundreds of nanoseconds. Hopping of G6P in the presence of arginine is thus a rare event in MD simulations. In contrast, the hopping process of G6P remains orders of magnitude faster than the HK enzyme's turnover frequency of 0.7 s−1.22
Based on these considerations, poly-arginine peptides represent a promising electrostatic bridge candidate, and the study of rare hopping events using poly-arginine bridges would benefit from advanced sampling techniques. Among the methods of advanced sampling of MD simulation, infrequent metadynamics (InMetaD)25 is efficient in calculating kinetic rates and has been successfully applied to ligand binding and unbinding studies of various systems.26–28 For example, InMetaD has successfully estimated the unbinding rate of an inhibitor from the p38 mitogen-activated protein (MAP) kinase to be 0.02 s−1, comparable to the experimental result 0.14 s−1,28 and reveals the unbinding mechanism of a ligand from α7 nicotinic acetylcholine receptor with the unbinding rate to be 0.0033 s−1, comparable with the experimental value of 0.0003 s−1.26
InMetaD enhances the sampling of a system by adding bias on predefined collective variables (CVs) to release the system from energy minima, enabling observation of system dynamics and kinetics. A key aspect of implementing InMetaD is the selection of CVs. Good CVs properly describe a system in terms of both thermodynamics and kinetics, and common CVs include separation distances between atoms and molecules, bond angles, and combinations of these. Here we use infrequent metadynamics to study the rate and energy barrier of hopping of G6P on a poly-arginine peptide. The desorption pathway and energy barrier were studied using umbrella sampling.29 Rate constants obtained by infrequent metadynamics and umbrella sampling were used as parameters for KMC studies to estimate lag time due to transport over the polypeptide surface. These studies provide an improved understanding of the influence of scaffolding architecture in electrostatic channeling.
Methods
Molecular dynamics
Model poly-arginine peptide structures were built using Avogadro software.30 Two alanine residues on each end and eight arginine residues in the middle were used to form a peptide chain (Fig. 1a). The structure of glucose-6-phosphate (G6P) was obtained from the Zinc database.31 Molecular dynamics (MD) simulations were conducted using GROMACS 2020.132 with the CHARMM36 force field.33 G6P was parameterized using CgenFF (CHARMM General Force Field).34 The TIP3P model was used to solvate the peptide–ligand complex in a dodecahedral box, and six Cl− ions were added to neutralize the system. Energy minimization was conducted with the steepest descent minimization algorithm. Afterward, the system was equilibrated with an NVT ensemble for 0.1 ns and an NPT ensemble for 1.0 ns. MD simulations were conducted under an NPT ensemble with temperature governed by the velocity-rescale thermostat and pressure governed by the Parrinello–Rahman barostat. Periodic boundary conditions were applied in all directions for all simulations. Simulations were conducted at five discrete temperatures between 280 K and 320 K with the first and last alpha carbons of the peptide restrained to mimic the situation when the bridge is incorporated into the HK-G6PDH cascade. At each temperature, 32 parallel simulations were run with random initial velocities generated according to the Maxwell–Boltzmann distribution at the designated temperature.Infrequent metadynamics
Metadynamics simulation was conducted using GROMACS with the PLUMED 2.2 plugin.35 In a metadynamics simulation, the external history-dependent bias potential V(s,t′) was applied over selected collective variables (CV) at time t′, with the following equation:36 | (1) |
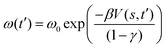 | (2) |
 | (3) |
We adopted three CVs based on distances between the phosphate group of G6P and arginine residues. The first, labeled d246, represents the sum of the distances, di, between the center of mass of the G6P phosphate group and the center of mass of the guanidinium group of the ith arginine residue, for three arginine residues numbered 2, 4, and 6 in Fig. 1a. Initially, the phosphate group was closely associated with these residues, where a close association is defined as di ≤ 0.5 nm, and d246 = d2 + d4 + d6 = d246 ≈ 1.5 nm, which was considered to be a minimum value. Besides d246, 19 other possible triple association basins were defined; the details are in ESI.†
The second collective variable, nA, represents the number of arginine residues with which the phosphate group is closely associated at each time step. The following function defines nA continuously:
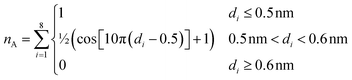 | (4) |
The third and final CV is nS, representing the ligand's solvation number (i.e., the number of water oxygens near the ligand). The value nS can be defined continuously as:28
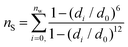 | (5) |
A committer analysis was implemented in all simulations. Specifically, 32 simulations were initiated with d246 ≈ 1.5 nm and terminated once any of the 19 predefined triple association energy basins has been reached within a wall time of 48 hours (simulation time ∼24 ns). A committer basin is defined based on the sum of three associated distances, dijk where i, j, and k indicate an arginine residue as labeled in Fig. 1a. When the sum dijk is less than 1.5 nm for a specific basin, while dijk for all other basins is greater than 2.0 nm, that basin is considered to be occupied.
Once any of the predefined basins is occupied, the simulation was terminated, and the simulated time was converted to unbiased transition times using eqn (3). Assuming that the transitions are stochastically independent, they may be treated as Poisson processes, and the reaction times should follow an exponential distribution.38 Thus, the empirical cumulative distribution function (ECDF) was computed from the unbiased transition times, t, and compared with the theoretical cumulative distribution function (TCDF) of a homogeneous Poisson process:28
 | (6) |
To validate the precision of the recovered transition times, the two-sample Kolmogorov–Smirnov (KS) test was conducted, following the procedure of Salvalaglio et al.,38 to determine whether they were exponentially distributed. When the p-value of the KS test exceeds the threshold of 0.05, the dataset is deemed to conform to an exponential distribution. This is an important step in InMetaD analysis as it ensures that recovered times are uncorrelated and reliable.
Umbrella sampling
In the US simulations, the d246 triple association configuration represented in Fig. 1b was used as the initial association state, and a steered MD simulation was conducted by pulling G6P perpendicular to the peptide axis while restraining the entire poly-arginine backbone. The pull rate was 2 nm ns−1, and the simulation was conducted for 0.8 ns, yielding a maximum pull distance of 1.6 nm, defined as the distance between the center of mass of the alpha carbons of arginine residues 2, 4, and 6, and that of the phosphate group on G6P.From this data, over 20 US windows were chosen, with a higher window density below 1 nm, where the energy gradient was greatest. All US simulations were conducted at 300 K with a spring constant, k = 2000 kJ mol−1 nm−2 applied over two coordinates. The first US coordinate was the pull distance x1 as defined above. The second, x2, represents the pull vector, defined as the magnitude of (CA2 + CA4 + CA6)/3 − P where CAi is the position of the alpha carbon of the associated arginine residue i, and P is the position of the phosphorus atom of G6P.
MD sampling of each US window was conducted for 20 ns. Grossfield-WHAM39 code was used to calculate the 2D potential of mean force. The average of the area defined by |x1 − x2| = 0.05 nm was used as the projection of the PMF on the pull distance, x1 (Fig. S4, ESI†).
Kinetic Monte Carlo
The ratio of hopping rate to desorption rate for varying ionic strengths was used to parameterize the kinetic Monte Carlo model described by Liu et al.21 Six hopping sites on the peptide bridge and two active sites on HK and G6PDH were considered in the KMC model. The rate ratios for hopping from enzyme to bridge and from the bridge to enzyme were assumed to be the same as those on the bridge. At each site, all possible events were considered (hopping, desorption, adsorption, and reaction) and rate constants were assigned accordingly (Fig. S1, ESI†). Reaction events were only considered at the enzyme active sites, labeled as HK and G6PDH in Fig. S1 (ESI†). The timescale of reactions at these sites was given by the rate constants k1cat and k2cat, respectively. According to the KMC algorithm, a random number ρ1 between 0 and 1 was generated to choose an event:21,40 | (7) |
| Δt = −ln(ρ2)/Γtotal | (8) |
Results and discussion
Electrostatic channeling dynamics
Previously, a poly-lysine bridge was found to electrostatically channel glucose 6-phosphate (G6P) between the consecutive enzymes hexokinase (HK) and glucose-6-phosphate dehydrogenase (G6PDH).21 Here, we studied the molecular dynamics of G6P's motion in electrolytes of varying ionic strengths in the presence of either a poly-lysine bridge or a poly-arginine bridge. On the poly-lysine bridge, the association distribution, Fig. S2 (ESI†), indicates that G6P mainly associates with one or two lysine residues, a mode that we describe as a single association and a double association, respectively. A hop is made when transferring from a double association to the next double association with a single association as the intermediate state.21 The hopping rate was estimated to be 0.6 ± 0.04 ns−1 at 310 K.21 In comparable simulations for G6P channeling on poly-arginine peptides, three dominant interaction energy were observed from the electrostatic interaction energy plot as shown in Fig. S3 (ESI†). After visualizing the trajectories, we observed that these three energy states correspond to the three association states of single, double, and triple. In certain time periods, rapid fluctuations in association state are observed, for example near 40 ns and 80 ns in Fig. S3 (ESI†). Triple association with electrostatic interaction energy of 750 kJ mol−1 on poly-arginine peptides is much stronger than the double association of 400 kJ mol−1 on poly-lysine peptides.22 In addition, association with three arginine residues, or triple association, was primarily observed, as shown structurally in Fig. 1b for the poly-arginine bridge. This is possible because of the longer side chain of arginine, making it more amenable to triple associations.Due to this strong electrostatic interaction, escaping from the energy well of triple associations is rarely observed within the time scale of MD. Fig. 2a shows residues with which G6P associates (di < 0.5 nm) and the number of associated residues over time at 293 K. After an initial period of the double association with residues 6 and 7, and then with residues 3 and 5, G6P was trapped in the triple association with residues 1, 3, and 5 starting at ∼26 ns. As temperature increases (Fig. 2b), the occurrence of a single association remains relatively rare, while that of a double association decreases, and that of a triple association increases. In our observations, triple association dominates over the entire simulated temperature range from 293 K to 318 K. Thus, we define a full hop on the poly-arginine bridge as a transition between different triple association states. To increase the frequency of transitions, we seek advanced sampling techniques.
 | ||
| Fig. 2 (a) Associated arginine residue indices (top) and evolution of association number (nA, bottom) over 100 ns. (b) Association state probability dependence on temperature. | ||
Hopping activation
Among the enhanced sampling methods of molecular dynamics, metadynamics is efficient in forcing MD systems out of local energy minima, enabling the sampling of otherwise inaccessible regions by applying a history-dependent bias.36 The key step of applying metadynamics is the selection of collective variables (CVs). Here we biased three CVs with the following motivations: (1) biasing d246 to force the system out of its initial triple association state; (2) biasing nA to destabilize other triple-association energy basins and enable the system to move to any other association states such as double or single; (3) biasing nS to accelerate water molecule dynamics around G6P without affecting interaction with arginine residues.However, metadynamics is mainly used to quantify thermodynamic properties and is not generally applied to recover kinetic information. To calculate the rate of hopping between triple association states, we adopted infrequent metadynamics (InMetaD).25 The essential difference between metadynamics and InMetaD is that in InMetaD, the rate of bias deposition is much slower than in metadynamics, and is intended to move the system out low-energy basins without disturbing the kinetics in high-energy transition regions.25,38
The theoretical and empirical cumulative distributions of the transition times at IS = 0 mM, 310 K are shown in Fig. 3a, where the characteristic time, τ, was 126 ± 3 ns. The p-value was 0.95 as calculated by the Kolmogorov–Smirnov (KS) test.41 This value is much greater than the threshold of 0.05, indicating that the transition time conformed to an exponential distribution. This approach was subsequently applied to calculate values of τ for temperatures from 280 K to 320 K, for which all the p-values were above 0.05.
The hopping rate, khop, can be defined simply as khop = τ−1. At 310 K, khop is 7 ± 0.6 μs−1. Compared to the poly-lysine bridge, the hopping rate on the poly-arginine bridge is 85-fold slower at 310 K. Similarly, the hopping rates and their errors were estimated from the characteristic times and their errors across all the studied temperatures and ionic strengths. Overall, khop displays Arrhenius behavior, and the hopping activation energy was computed for a range of ionic strengths from 0 mM to 120 mM (Fig. 3b). No trend was observed for the dependence of either hopping rate or activation energy with respect to ionic strength. This observation that ionic strength had little impact on hopping kinetics of G6P on poly-arginine peptides is consistent with previous calculations using the poly-lysine peptide.21 In both cases, transport is influenced locally by short-range interactions within the Stern layer, where counterions have relatively little influence. Hopping activation energy of 25 ± 3.6 kJ mol−1 was obtained by simultaneous fitting of rate data at all ionic strengths and is used in the KMC model. Notably, this hopping activation energy value of poly-arginine is about double that observed for poly-lysine (13 ± 0.5 kJ mol−1).21
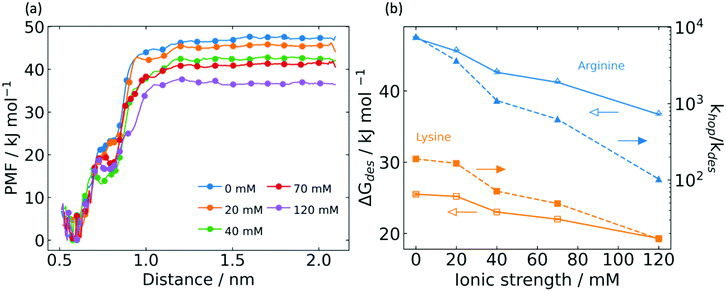
Desorption energy
Mobile G6P traversing the electrostatic surface of a charged peptide may desorb into the bulk, which represents the major loss mechanism in electrostatic channeling of cascade reactions. To quantify the desorption energy and the ratio of hopping rate to desorption rate, umbrella sampling (US) simulations were conducted. This desorption energy is a free energy difference that considers changes in entropy. It is therefore not directly comparable to the electrostatic interaction energy, which is a potential energy difference that does not include entropic effects. We computed the desorption energy from the triple association state by considering the center of mass distance between G6P and associated arginine residues as a CV. The desorption energy dependence on ionic strength was studied, as shown in the potential of mean force (PMF) plot in Fig. 4a. Here, the PMF is referenced to the triply associated state, and we observed the desorption energy at zero IS to be 47 ± 0.2 kJ mol−1. This value is double the desorption energy from the poly-lysine peptide,21 consistent with the argument that the triple association of G6P with poly-arginine peptides was much stronger than the double association with poly-lysine peptides.It is worth noting the feature that appears in the PMF traces of Fig. 4a near 0.72 nm, which varies with ionic strength. By inspection of trajectories, we observed that 0.72 nm is a position beyond which the system transitions from triple to double and single association. Generally speaking, this transition feature becomes less smooth and shifts to lower distances at higher ionic strength, reflecting the effect of counterions to weaken electrostatic interactions with the arginine bridge. As shown in Fig. 4b, the desorption energy declines significantly with increasing ionic strength. This is explained by the counterion shielding of long-range electrostatic forces between G6P and the arginine bridge.
Based on the above InMetaD and US results, we can calculate the rate ratio of hopping to desorption by:
 | (9) |
Transfer efficiency
We conducted Kinetic Monte Carlo (KMC) simulations to study the transfer efficiency and quantify the reaction lag time of the two-step cascade. The KMC model was parameterized by using the rate ratio of hopping and desorption (Fig. 4b) and experimental turnover frequencies of HK and G6PDH.22 In the KMC model, we set the hopping rate to be 100 times the turnover frequency. This is because the enzyme turnover frequencies (0.7 s−1 for HK, 6.2 s−1 for G6PDH) are much lower than the hopping rate, and we are only interested in the magnitude difference between hopping and reaction. We also neglected the desorption of intermediate from HK and assumed that the hopping to desorption ratio from the bridge to G6PDH is the same as that on the bridge. These assumptions simplify the model to focus on a comparison between poly-arginine bridges and poly-lysine bridges. Using these assumptions, the KMC model can predict and compare lag time results for both the HK-G6PDH couple bridged with poly-lysine or poly-arginine and freely standing HK-G6PDH without any bridges.Stop-flow lag time analysis was employed to evaluate the channeling efficiency from all the KMC data. As shown in Fig. 5, the lag time for the poly-arginine bridge was 1.9 s at zero IS and increases slightly to 6.5 s at 120 mM. In comparison, the lag time for the poly-lysine bridge increases three-fold over the same range of ionic strength. Comparison to calculated results for the free enzyme,21 poly-lysine bridge,21 and poly-arginine bridge provides a clear indication that electrostatic channeling can significantly improve transfer efficiency as compared to a free enzyme system, and that poly-arginine represents a better bridge candidate compared to poly-lysine for this molecular motif.
 | ||
| Fig. 5 Comparison of calculated lag time at varying ionic strength between the free enzyme system, the poly-lysine bridge channeled system, and the poly-arginine bridge channeling system. | ||
As the reaction system achieves steady state, desorption from the bridge approaches equilibrium, creating the possibility of multiple intermediates adsorbed there. To understand this, we used KMC model results to obtain the probability distribution for the number of the adsorbed intermediates on the poly-lysine and the poly-arginine bridges, each with six hopping sites (Fig. S6, ESI†). Our results show that the bridge was empty for about 80% of the time, the bridge adsorbed one intermediate for about 20% of the time, and the occurrence of more than two adsorbed intermediates was rare for both poly-lysine and poly-arginine bridges. This can be explained by the fact that the turnover frequency of G6PDH is much faster than that of HK and the transit time of the intermediate on either the poly-lysine bridge or the poly-arginine bridge is even faster, so there is relatively little accumulation of G6P intermediates on the bridge. Owing to its higher adsorption energy, the poly-arginine bridge does demonstrate a consistently higher probability for multiple adsorbed intermediates as compared to poly-lysine.
This work only accounts for the movement of G6P on the bridge and did not consider the desorption from HK active site to bridge and bridge to G6PDH active site. These phenomena lead to additional loss of intermediate transport efficiency and therefore higher lag times.23 Additionally, the model assumes that the hopping rate between the bridge and enzyme is the same as that on the bridge, which is only a rough approximation. A more realistic prediction of transfer efficiency and lag time would be obtained by studying the transport of intermediate over the enzyme surfaces in the presence of the poly-arginine bridge, as has been demonstrated for the poly-lysine bridge. We are also pursuing experimental validation of these results by synthesis of the HK-polyArg-G6PDH system followed by stop-flow experiments to determine lag time.
Conclusions
The transport of G6P in the presence of poly-arginine peptides was investigated using the combination of infrequent metadynamics (InMetaD) and umbrella sampling (US) in MD simulations. Although arginine and lysine both carry one positive charge, the interaction of G6P with arginine is much stronger than that with lysine. The strong local interaction reduces hopping rates 85-fold at 310 K as determined by InMetaD. The desorption of G6P from the triple association on poly-arginine peptides displays large fluctuation due to the transition from triple association to double and single association. The hopping activation energy is less sensitive to ionic strength change compared to the desorption energy, leading to large hopping![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) desorption rate ratio that persists at high ionic strength.
desorption rate ratio that persists at high ionic strength.
Kinetic Monte Carlo studies based on this rate ratio predict significantly lower lag times for systems built with the poly-arginine bridge as compared to the poly-lysine bridge, and lag time is more resistant to changes in ionic strength. These results will be ameliorated somewhat by including transport losses in the vicinity of the enzymes, an effect that can be studied computationally and validated experimentally.
This demonstrates the use of InMetaD to study transport phenomena at longer time scales, which may be applied to channeling phenomena in other multi-enzyme fusions including TS-DHFR and MDH-CS. This work also aids the design of efficient artificial cascade reactions using electrostatic bridges.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge support from Army Research Office MURI (#W911NF1410263) via The University of Utah.References
- E. Ricca, B. Brucher and J. H. Schrittwieser, Adv. Synth. Catal., 2011, 353, 2239–2262 CrossRef CAS.
- I. Wheeldon, S. D. Minteer, S. Banta, S. C. Barton, P. Atanassov and M. Sigman, Nat. Chem., 2016, 8, 299–309 CrossRef CAS PubMed.
- T. R. Schneider, E. Gerhardt, M. Lee, P.-H. Liang, K. S. Anderson and I. Schlichting, Biochemistry, 1998, 37, 5394–5406 CrossRef CAS PubMed.
- J. Fu, Y. R. Yang, A. Johnson-Buck, M. Liu, Y. Liu, N. G. Walter, N. W. Woodbury and H. Yan, Nat. Nanotechnol., 2014, 9, 531–536 CrossRef CAS PubMed.
- S. Vijayakrishnan, S. M. Kelly, R. J. C. Gilbert, P. Callow, D. Bhella, T. Forsyth, J. G. Lindsay and O. Byron, J. Mol. Biol., 2010, 399, 71–93 CrossRef CAS PubMed.
- O. Idan and H. Hess, ACS Nano, 2013, 7, 8658–8665 CrossRef CAS PubMed.
- J. Fu, M. Liu, Y. Liu, N. W. Woodbury and H. Yan, J. Am. Chem. Soc., 2012, 134, 5516–5519 CrossRef CAS PubMed.
- A. H. Elcock, M. J. Potter, D. A. Matthews, D. R. Knighton and J. A. McCammon, J. Mol. Biol., 1996, 262, 370–374 CrossRef CAS PubMed.
- C. Eun, P. M. Kekenes-Huskey, V. T. Metzger and J. A. McCammon, J. Chem. Phys., 2014, 140, 105101 CrossRef PubMed.
- D. R. Knighton, C.-C. Kan, E. Howland, C. A. Janson, Z. Hostomska, K. M. Welsh and D. A. Matthews, Nat. Struct. Biol., 1994, 1, 186–194 CrossRef CAS PubMed.
- A. H. Elcock, G. A. Huber, J. Andrew McCammon and J. A. McCammon, Biochemistry, 1997, 36, 16049–16058 CrossRef CAS PubMed.
- F. Wu and S. Minteer, Angew. Chem., Int. Ed., 2015, 54, 1851–1854 CrossRef CAS PubMed.
- B. Bulutoglu, K. E. Garcia, F. Wu, S. D. Minteer and S. Banta, ACS Chem. Biol., 2016, 11, 2847–2853 CrossRef CAS PubMed.
- O. I. Wilner, Y. Weizmann, R. Gill, O. Lioubashevski, R. Freeman and I. Willner, Nat. Nanotechnol., 2009, 4, 249–254 CrossRef CAS PubMed.
- V. Linko, M. Eerikäinen and M. A. Kostiainen, Chem. Commun., 2015, 51, 5351–5354 RSC.
- F. Jia, B. Narasimhan and S. K. Mallapragada, AIChE J., 2013, 59, 355–360 CrossRef CAS.
- J. L. Lin, J. Zhu and I. Wheeldon, ACS Synth. Biol., 2017, 6, 1534–1544 CrossRef CAS PubMed.
- Y. Elani, R. V. Law and O. Ces, Nat. Commun., 2014, 5, 1–5 Search PubMed.
- H. Yuan, H. Bai, L. Liu, F. Lv and S. Wang, Chem. Commun., 2015, 51, 722–724 RSC.
- C. G. Palivan, R. Goers, A. Najer, X. Zhang, A. Car and W. Meier, Chem. Soc. Rev., 2016, 45, 377–411 RSC.
- Y. Liu, I. Matanovic, D. P. Hickey, S. D. Minteer, P. Atanassov and S. C. Barton, ACS Catal., 2018, 8, 7719–7726 CrossRef CAS.
- Y. Liu, D. P. Hickey, J.-Y. Guo, E. Earl, S. Abdellaoui, R. D. Milton, M. S. Sigman, S. D. Minteer and S. Calabrese Barton, ACS Catal., 2017, 7, 2486–2493 CrossRef CAS.
- Y. Liu, D. P. Hickey, S. D. Minteer, A. Dickson and S. Calabrese Barton, J. Phys. Chem. C, 2019, 123, 15284–15292 CrossRef CAS PubMed.
- D. Frigyes, F. Alber, S. Pongor and P. Carloni, THEOCHEM, 2001, 574, 39–45 CrossRef CAS.
- P. Tiwary and M. Parrinello, Phys. Rev. Lett., 2013, 111, 1–5 CrossRef PubMed.
- Y. Zhou, R. Zou, G. Kuang, B. Långström, C. Halldin, H. Ågren and Y. Tu, J. Chem. Inf. Model., 2019, 59, 3910–3918 CrossRef CAS PubMed.
- Z. F. Brotzakis, V. Limongelli and M. Parrinello, J. Chem. Theory Comput., 2019, 15, 743–750 CrossRef CAS PubMed.
- R. Casasnovas, V. Limongelli, P. Tiwary, P. Carloni and M. Parrinello, J. Am. Chem. Soc., 2017, 139, 4780–4788 CrossRef CAS PubMed.
- J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652–1660 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- J. J. Irwin and B. K. Shoichet, J. Chem. Inf. Model., 2005, 45, 177–182 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindah, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- J. Huang and A. D. MacKerell Jr, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690 CAS.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 20603 CrossRef PubMed.
- M. Salvalaglio, P. Tiwary and M. Parrinello, J. Chem. Theory Comput., 2014, 10, 47 CrossRef PubMed.
- A. Grossfield, WHAM: the weighted histogram analysis method. Version 2.0.9. http://membrane.urmc.rochester.edu/content/wham.
- M. Andersen, C. Panosetti and K. Reuter, Front. Chem., 2019, 7, 202 CrossRef CAS PubMed.
- F. J. Massey, J. Am. Stat. Assoc., 1951, 46, 68–78 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp01304a |
| This journal is © the Owner Societies 2021 |