Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibrational circular dichroism studies of exceptionally strong chirality inducers in liquid crystals†
Mark A. J.
Koenis
 a,
Valentin P.
Nicu
a,
Valentin P.
Nicu
 b,
Lucas
Visscher
b,
Lucas
Visscher
 c,
Christian
Kuehn
d,
Matthias
Bremer
c,
Christian
Kuehn
d,
Matthias
Bremer
 d,
Mireille
Krier
e,
Harald
Untenecker
e,
Ulmas
Zhumaev
e,
Bernd
Küstner
e and
Wybren Jan
Buma
d,
Mireille
Krier
e,
Harald
Untenecker
e,
Ulmas
Zhumaev
e,
Bernd
Küstner
e and
Wybren Jan
Buma
 *af
*af
aVan 't Hoff Institute for Molecular Sciences, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: w.j.buma@uva.com
bFaculty of Agricultural Sciences, Food Industry and Environmental Protection, Lucian Blaga University of Sibiu, Ioan Ratiu Street, 550012 Sibiu, Romania
cAmsterdam Center for Multiscale Modeling, Section Theoretical Chemistry, Faculty of Sciences, Vrije Universiteit Amsterdam, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands
dElectronics, Liquid Crystals R&D, Merck KGaA, Frankfurter Str. 250, 64293 Darmstadt, Germany
eSite Management, Central Analytics Department, Merck KGaA, Frankfurter Str. 250, 64293 Darmstadt, Germany
fRadboud University, Institute for Molecules and Materials, FELIX Laboratory, Toernooiveld 7c, 6525 ED Nijmegen, The Netherlands
First published on 9th April 2021
Abstract
7,7′-Disubstituted 2,2′-methylenedioxy-1,1′-binaphthyls are highly efficient chirality inducers in nematic liquid crystals. The absolute configuration of these compounds is, however, hard to determine as they only crystallize as racemic mixtures. In this work a Vibrational Circular Dichroism (VCD) study is reported that provides an unambiguous determination of the absolute configuration of these compounds. An in-depth General Coupled Oscillator (GCO) analysis of the source of the VCD signal reveals that the unusual structure of these binaphthyl compounds inherently leads to strong and robust VCD bands. Combined with linear transit calculations, our VCD studies allow for the determination of key structural parameters.
1 Introduction
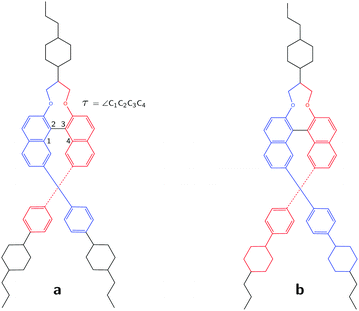
Liquid Crystals (LCs) are unique mesophase materials that have properties of both liquids and solids.1 Although they are best known for their applications in liquid crystal displays, their use ranges from polarisers, reflectors and lasers to artificial muscles, bio-sensors and drug delivery agents.2–12 Beyond this wide range of applications, liquid crystal science had also contributed significantly to our understanding of how symmetry breaking can modify the physical behaviour of materials. A well-known phenomenon is the doping of a non-chiral LC with chiral molecules, which even at seemingly insignificantly low concentrations of the chiral compound can induce helical structuring of the LC.13,14 The extent to which a chiral dopant is able to induce helical structure is expressed as its helical twisting power (HTP).15 This HTP is highly dependent on the molecular structure of the dopant and the strength of the dopant/solvent interactions.16 As yet, the rational design of such molecules is still a formidable challenge since structure–property relations are not trivial17,18 and because it is extremely difficult to apply HTP theory to this purpose.19–25Recently, a study was published on 7,7′-disubstituted 2,2′-methylenedioxy-1,1′-binaphthyls which showed that these compounds have extremely high helical twisting powers.26 These molecules have axial chirality due to the configuration of the binaphthyl group which is kept in place by steric interactions. A priori one would assume that the two long branches of the molecule (see Fig. 1) form helical grooves for the LC to follow, and thus be a dominating factor in determining its HTP. Such a reasoning could indeed very well explain the large HTP values found for this type of molecules. At the same time, it would imply that the handedness of the dopant induces a similar handedness of the LC phase. In order to elucidate why these molecules have such high HTP values -and potentially develop in a rational manner novel compounds with even higher HTPs-it is important to compare the twist in these compounds with the helical twisting they induce in LCs.
The standard method to determine the absolute configuration of a chiral molecule is X-ray diffraction (XRD).27 This technique requires, however, the formation of crystals of a single handedness. Upon crystallizing the binaphthyl compound it was quickly discovered that only crystals consisting of racemic mixtures were formed, causing this technique to be unable to determine the absolute configuration of the molecule. Electronic Circular Dichroism (ECD) – which measures the difference in absorption of left- and right-circularly polarized light (circular dichroism) for electronic transitions is used extensively to determine the axial chirality of compounds with a 1,1′-binaphthyl (BINAP) or 1,1′-bi-2-naphthol (BINOL) chromophore. The disadvantage of the technique is that it is primarily sensitive to the electronic properties of these chromophores and does not provide further information on the spatial structure of the chromophores nor on the parts that are not involved in the electronic transition. In particular for extended systems and for compounds that can adopt several conformations such as the ones of interest here this is a significant drawback.
A less known technique capable of determining the absolute configuration of chiral systems is Vibrational Circular Dichroism (VCD).28–31 This technique measures the circulair dichroism for vibrational transitions and as such is intrinsically sensitive to the detailed molecular structure. However, in order to come to a reliable assignment of the absolute configuration and retrieve structural information, a careful comparison between the experimentally recorded VCD spectrum and theoretically predicted spectra is required since it is almost never possible to come to an assignment merely on the basis of the experimental spectrum.28–31 Such a theoretical modelling can be challenging as the VCD spectrum is extremely sensitive to the finer details of the molecular conformation.32,33 This structural sensitivity arises from the fact that intense VCD signals often arise from the coupling between vibrational motions in different parts of the molecule via the General Coupled Oscillator (GCO) mechanism32 – which is the vibrational counterpart of the well-known exciton–exciton interactions in ECD28,34 – and this coupling depends strongly on the relative orientation of the two interacting molecular fragments. Moreover, under the employed experimental conditions several conformations might be thermally accessible. As a result, extensive conformational searches are needed to ensure that all relevant conformations are taken into account when simulating the VCD spectra.
In this work we report a VCD study on one of the prototypical 7,7′-disubstituted 2,2′-methylenedioxy-1,1′-binaphthyl compounds (Fig. 1) referred to in the following as compound 1 whose synthesis has been reported before, but for which the determination of its absolute configuration using XRD was not possible.26 We show that application of VCD leads quite straightforwardly to the determination of the absolute configuration of these binaphthyls compounds. Based on an extensive GCO analysis we elucidate the structural features that are at the basis of the signs and signal intensities of the bands in the VCD spectrum.
2 Theory: general coupled oscillator analysis
The VCD signal is computed as the rotational strength, R01, which is defined as the product of the electric and magnetic dipole transition moments (EDTM and MDTM):35R01(j) = −Im[![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 01(j)· 01(j)·![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) 10(j)] 10(j)] | (1) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 01(j) and
01(j) and ![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) 10(j) are the EDTM and MDTM of vibrational mode j from its ground state (0) to its first excited state (1). Important to notice is that the MDTM is about four to five orders of magnitude smaller than its electric equivalent. VCD signals are therefore typically much smaller than vibrational absorption signals whose intensity is determined by the square of the EDTMs. Because the MDTM are origin dependent and imaginary by definition, eqn (1) does not allow a simple and intuitive interpretation of the sign and magnitude of the VCD signals.
10(j) are the EDTM and MDTM of vibrational mode j from its ground state (0) to its first excited state (1). Important to notice is that the MDTM is about four to five orders of magnitude smaller than its electric equivalent. VCD signals are therefore typically much smaller than vibrational absorption signals whose intensity is determined by the square of the EDTMs. Because the MDTM are origin dependent and imaginary by definition, eqn (1) does not allow a simple and intuitive interpretation of the sign and magnitude of the VCD signals.
We therefore employ here the recently introduced General Coupled Oscillator (GCO) mechanism32 VCD analysis. This is a post-calculation analysis method that decomposes the rotational strengths computed with DFT into contributions from three molecular fragments and the interaction between these parts. Typically, there are two important fragments referred to as the GCO fragments, and an ancillary fragment. These fragments can quite often be defined in an intuitive manner as is done in the present work. Alternatively, a simple optimizing algorithm can be used to find the best coupling molecular fragments.36 The GCO analysis decomposes R01 into three contributions:
| R01(j) = RGCO01(j) + RIF01(j) + RR01(j) | (2) |
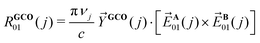 | (3) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) A01 and
A01 and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) B01 are the EDTMs associated with the GCO fragments A and B, νj the frequency of vibration j, c the speed of light in vacuum and
B01 are the EDTMs associated with the GCO fragments A and B, νj the frequency of vibration j, c the speed of light in vacuum and ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) GCO the GCO vector.32 To have the
GCO the GCO vector.32 To have the ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) GCO(j) vector fully defined by the choice of molecular fragments, we have chosen it along the
GCO(j) vector fully defined by the choice of molecular fragments, we have chosen it along the ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) A01(j) ×
A01(j) × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) B01(j) vector.
B01(j) vector.
Eqn (2) and (3) allow for a very simple and intuitive interpretation of the VCD signals: the bulk of the VCD intensity of a mode is determined by the interaction of the ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) A01 and
A01 and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) B01 currents separated by a distance |
B01 currents separated by a distance |![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) GCO|. Eqn (3) resembles the coupled-oscillator equation40 that in recent years has found renewed interest as a quick alternative to DFT calculations for determining the absolute configurations of chiral compound.41–44 Unlike this equation, eqn (3) is exact and can be applied to the majority of the normal modes of a chiral molecule. As will be shown here, the GCO analysis is a very useful tool, which allows one to understand the exact origin of the measured VCD signals and to asses the reliability of an assignment made with VCD.
GCO|. Eqn (3) resembles the coupled-oscillator equation40 that in recent years has found renewed interest as a quick alternative to DFT calculations for determining the absolute configurations of chiral compound.41–44 Unlike this equation, eqn (3) is exact and can be applied to the majority of the normal modes of a chiral molecule. As will be shown here, the GCO analysis is a very useful tool, which allows one to understand the exact origin of the measured VCD signals and to asses the reliability of an assignment made with VCD.
3 Methods
Vibrational Absorption (VA) and Vibrational Circular Dichroism (VCD) spectra have been recorded using a Biotools Chiral-2X spectrometer and a 75 μm BaF2 sample cell. Compound 1 was measured at a concentration of 0.272 M in CDCl3. To correct for the baseline, spectra of CDCl3 were subtracted from the VA and VCD spectra of the compound. Samples were measured for 48 hours.Calculations have been performed using the SCM software suite (2017, r58813).45–47 A conformational search was performed using the program RDKIT embedded in the software.48 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations were generated, optimized using the universal force field (UFF)49 and then filtered using an RMS-filter of 0.1 Å and an energy window of 10 kcal mol−1. The resulting 27 conformations were further optimized using Density Functional Theory (DFT) at a BP86/TZP level of theory50–52 and afterwards checked for duplicates using an in-house script employing structural equality criteria, taking two conformations to be identical if the difference in interatomic distances was less than 0.1 Å and the difference in dihedral angle less than 30°. This led to 9 unique structures with a binding energy within 2 kcal mol−1 of the lowest energy conformation for which analytic frequency calculations including the computation of the VCD parameters were performed.53 The resulting spectra were convoluted using a Lorentzian function with a full-width-at-half-maximum of 8 cm−1. Computed frequencies were shifted to optimize the overlap between the calculated and experimental VA spectrum using the method proposed by Shen et al.54 This resulted in shifting factors of 1.011, 1.019, 1.006 and 1.011 for the 900–1195, 1195–1275, 1275–1500 and 1500–1800 cm−1 frequency intervals, respectively.
000 conformations were generated, optimized using the universal force field (UFF)49 and then filtered using an RMS-filter of 0.1 Å and an energy window of 10 kcal mol−1. The resulting 27 conformations were further optimized using Density Functional Theory (DFT) at a BP86/TZP level of theory50–52 and afterwards checked for duplicates using an in-house script employing structural equality criteria, taking two conformations to be identical if the difference in interatomic distances was less than 0.1 Å and the difference in dihedral angle less than 30°. This led to 9 unique structures with a binding energy within 2 kcal mol−1 of the lowest energy conformation for which analytic frequency calculations including the computation of the VCD parameters were performed.53 The resulting spectra were convoluted using a Lorentzian function with a full-width-at-half-maximum of 8 cm−1. Computed frequencies were shifted to optimize the overlap between the calculated and experimental VA spectrum using the method proposed by Shen et al.54 This resulted in shifting factors of 1.011, 1.019, 1.006 and 1.011 for the 900–1195, 1195–1275, 1275–1500 and 1500–1800 cm−1 frequency intervals, respectively.
4 Results and discussion
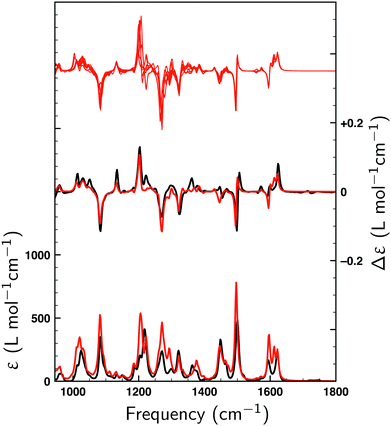
Fig. 2 displays the VA and VCD spectra measured for the dissolved compound and for the solvent only. Since the intensities of the VCD bands are significantly larger than the baseline artifacts, the observed small offset can be ignored. Thus, even though ideally a racemic mixture should have been used for the baseline, it is clear that the measured spectrum can be trusted for the entire spectral region between 950 and 1800 cm−1. In Fig. 3 the Boltzmann-weighted VA and VCD spectra obtained for the (S) low-energy conformers are plotted on top of the experimental spectrum. Comparison of measured and predicted spectra shows an excellent agreement as quantified by the SimVCD value54 of 0.628. We can therefore safely conclude that the measured compound has the (S) axial configuration. VCD spectroscopy, unlike XRD, thus allows one to easily differentiate between the enantiomers of these compounds and determine their absolute configuration.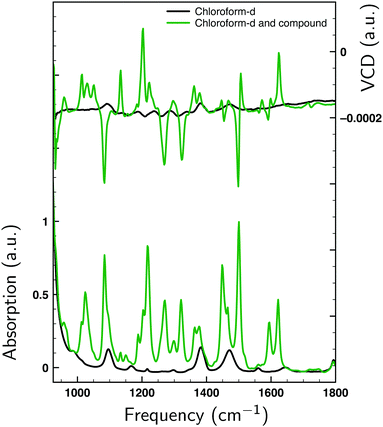 | ||
| Fig. 2 VA (bottom) and VCD (top) spectra measured for 1 at 0.272 M in CDCl3 (green) and for neat CDCl3 (black). | ||
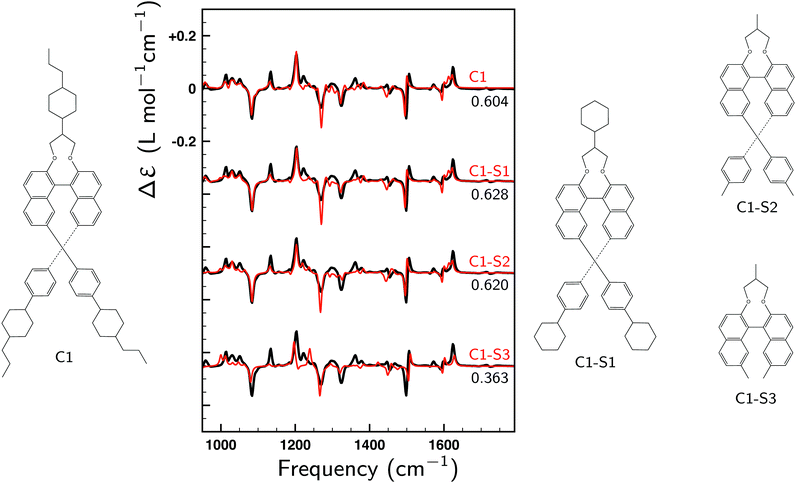
To understand the high SimVCD value (0.628), which is significantly larger than what one would normally expect for such a large and flexible molecule, a series of GCO analyses have been performed. First, we note that molecule 1 has two long branches, which form together a helical structure. Since the molecule is not symmetric, these two branches most often have different conformations. However, because their chemical structure is identical, many normal modes have contributions from both branches. As a result, the EDTMs associated with the two branches couple through space. This triggers the GCO VCD mechanism,32 which in turn induces very intense VCD signals. A careful analysis of the atomic contributions to the EDTMs of each branch shows that for most fingerprint normal modes the contributions of the propyl-cyclohexane group located at the end of each branch are negligible. Although the majority of the conformations of 1 are determined by the relative orientation and conformation of the propyl-cyclohexane groups, the VCD spectrum measured for the fingerprint spectral region is therefore almost entirely determined by the inner core of the helical structure, which is rigid and does not change very much among the low-energy conformations. This explains why the VCD spectra computed for the low-energy conformers of 1 are so similar as can be seen in the top trace of Fig. 3. For compounds with several low-energy conformers we have found in the past that taking the uncertainty in the calculated energy into account can lead to a significant improvement of the agreement between the experimental and the computed VCD spectrum.55 The high similarity of the VCD spectra of the low-energy conformers of 1 explains why in the present case such an approach hardly improves the SimVCD value.
To illustrate the key role of the GCO mechanism for this molecule, we consider the lowest-energy conformer of 1 designated as C1 and perform a GCO analysis using the molecular fragments defined in Fig. 1a. In Fig. 4 the experimental VCD spectrum is compared to simulated spectra obtained by convoluting R01 and its RGCO01, RIF01 and RR01 contributions in the same manner as the spectrum reported in Fig. 3. As can be seen, the RGCO01 spectrum is almost identical to the full spectrum (R01) which reproduces the experiment very well. The spectra associated with the RIF01 and RR01 contributions, on the other hand, are significantly less intense than RGCO01 and exhibit only minor, unimportant features. The same picture emerges from Table 1 where the quantitative result of the GCO analysis are reported for all dominant VCD modes and which shows that for these modes RGCO01 is typically 3–5 times larger than the other two contributions to R01. It is therefore clear that the interaction of the GCO fragments highlighted in Fig. 1a is the primary source of VCD intensity.
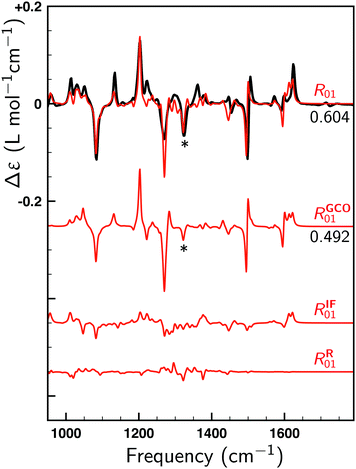 | ||
| Fig. 4 Comparison between the experimental VCD spectrum (black) and simulated spectra (red). R01 is the spectrum computed for the lowest-energy conformer (C1). RGCO01, RIF01 and RR01 spectra have been constructed using the contributions to the rotational strength from the GCO analysis performed for C1 using the GCO fragments defined in Fig. 1a. For the R01 and RGCO01 spectra SimVCD values are given, the SimVCD value for the RGCO01 + RIF01 spectrum (not shown) being 0.597. The VCD band highlighted by a star is associated with mode 260, which is the only intense mode in the fingerprint region that requires larger GCO fragments (see Table 1). | ||
| NM | Freq. | R 01 | R GCO 01 | R IF 01 | R R 01 | |YGCO| |
|---|---|---|---|---|---|---|
| 195 | 1070.5 | 280.7 | 192.1 | 88.6 | 0.0 | 7.2 |
| 203 | 1119.2 | −65.7 | −61.6 | −5.2 | 1.1 | 6.4 |
| 217 | 1189.9 | −383.7 | −331.6 | −40.9 | −11.2 | 4.4 |
| 235 | 1246.5 | 324.4 | 266.7 | 68.7 | −10.9 | 9.0 |
| 260 | 1314.2 | 129.6 | 63.3 | 22.9 | 43.4 | 7.2 |
| *260 | 1314.2 | 129.6 | 93.4 | 37.5 | −1.4 | 10.9 |
| 321 | 1487.5 | 538.9 | 529.2 | 16.3 | −6.7 | 8.1 |
| 322 | 1489.3 | −456.8 | −478.2 | 12.8 | 8.6 | 8.1 |
| 329 | 1578.3 | 133.7 | 130.7 | 3.9 | −0.9 | 4.8 |
| 330 | 1582.0 | −90.6 | −108.7 | 17.1 | 1.1 | 5.4 |
| 331 | 1594.2 | 62.4 | 80.5 | −15.8 | −2.4 | 3.9 |
| 332 | 1594.5 | −128.3 | −116.5 | −15.5 | 3.8 | 4.4 |
| 334 | 1604.5 | −95.2 | −79.7 | −14.6 | −0.8 | 4.6 |
Table 1 shows that a GCO analysis using the fragments defined in Fig. 1a leads for almost all dominant modes to negligible RR01 contributions. Interestingly, this is not the case for mode 260, which is associated with the band highlighted with a star in Fig. 4. Although the large VCD intensity of this mode arises from the GCO interaction of the two branches as well, we find that in this case the GCO fragments need to include the cyclohexane moiety (see Fig. 1b) in order to obtain only a minor contribution from RR01 (see *260 row in Table 1).
Above it has been concluded that the VCD spectrum of the fingerprint region is predominantly determined by the inner core of the helical structure. To determine more precisely to which parts of the branches the VCD spectrum is sensitive and thus to determine to what extent VCD can elucidate the conformational structure of these branches three smaller structures (C1–S1, C1–S2 and C1–S3) have been considered that were obtained by removing to an increasing extent the outer parts of the two branches of the relaxed structure of the lowest-energy conformer (C1) and adding H atoms to obtain neutral systems (Fig. 5). For these three new structures VCD spectra have been calculated without relaxing their structure. These spectra are compared in Fig. 5 with the experimental VCD spectrum of 1. As can be seen, C1–S1 and C1–S2 yield SimVCD values that are slightly larger than that of C1, while the C1–S3 spectrum still manages to reproduce the experiment surprisingly well (SimVCD = 0.36). This shows clearly that the experimental VCD spectrum measured for 1 contains limited structural information on the outer parts of the two branches. As such, it can be considered as a signature of the middle part of the helical structure, of which the specific details are, however, determined by the two branches.
Table 1 shows significant variations in the magnitude of the |YGCO| vector for the various modes. This magnitude can be interpreted as the distance between the interacting currents, and we therefore expect it to reflect the localised/delocalised character of a given GCO mode. Indeed, we find that modes involving more localised movements (e.g. on the naphthalene moieties) have smaller |YGCO| values as the distance between the interacting EDTMs is smaller, while the modes involving movements that are delocalised over the entire GCO fragments have large |YGCO| values. Exemplary in this respect is mode *260 for which larger GCO fragments were needed, and which in fact has the largest |YGCO| value.
The axial chirality of 1 is described by a single dihedral angle τ (see Fig. 1a). Interestingly, we find that our DFT calculations on the isolated molecule predict a Boltzmann-weighted angle of 68.2° (all angles τ lying between 67.1° and 69.2°) while in the XRD studies an angle of 57.0° was found. This difference clearly shows that the intermolecular interactions present in the crystal can have a significant effect. As a result, it is important to investigate the dependence of the computed VCD spectra on τ. On the one hand, the sign of the GCO VCD signals can be affected by τ.37 On the other hand, τ affects directly the properties of materials based on these compounds and as such it is important to assess how accurately the calculations can determine this angle. We have therefore performed linear transit (LT) calculations in which the geometry of the molecule was optimized for a fixed value of τ and the associated VCD spectrum was calculated. Fig. 6a and b show the corresponding spectra and energies.
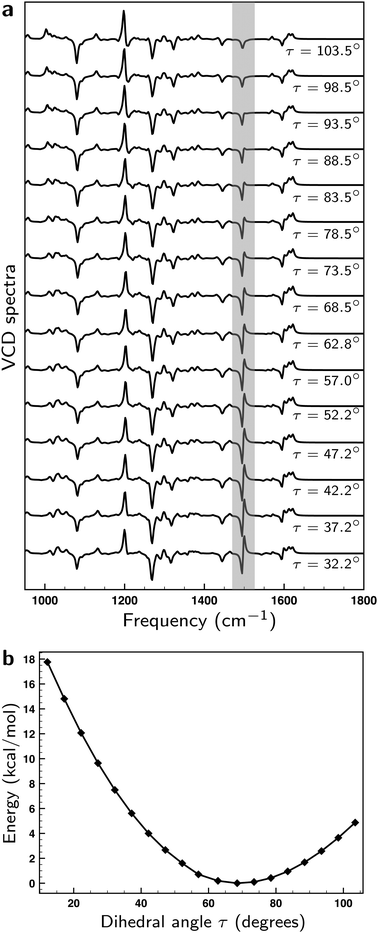 | ||
| Fig. 6 (a) Linear transit VCD spectra computed for the lowest-energy conformer for different values of angle τ (see Fig. 1a). (b) Energies computed for the lowest-energy conformer for different values of angle τ. | ||
Remarkably, we find that the VCD spectra do not show as large changes upon variation of τ as a priori might have been expected. In fact, the bisignate band at ∼1500 cm−1 is the only one that exhibits a significant change. To explain this behaviour, we list in Table S1 (see ESI†) the values of |![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) A01|, |
A01|, |![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) B01|, |
B01|, |![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) A01 ×
A01 × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) B01|, and ξ (the angle made by
B01|, and ξ (the angle made by ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) A01 and
A01 and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) B01) for the GCO modes of the linear transit structures within an energetic window of ∼2 kcal mol−1 corresponding to Δτ = ±20°. The overall variations observed for the magnitude and relative orientation of the interacting EDTMs are small, typically around 10%. While this leads to some variations in the magnitude of the signals, there are no sign changes and the overall pattern of the VCD spectrum remains unchanged. Consequently, it is clear that the prediction made with VCD for the absolute configuration of 1 is a very reliable one.
B01) for the GCO modes of the linear transit structures within an energetic window of ∼2 kcal mol−1 corresponding to Δτ = ±20°. The overall variations observed for the magnitude and relative orientation of the interacting EDTMs are small, typically around 10%. While this leads to some variations in the magnitude of the signals, there are no sign changes and the overall pattern of the VCD spectrum remains unchanged. Consequently, it is clear that the prediction made with VCD for the absolute configuration of 1 is a very reliable one.
The bisignate band at ∼1500 cm−1 is associated with modes 327 and 328, which can be assigned as an in- and out-of-phase pair of modes. They exhibit the largest VCD intensities of all fingerprint modes but because their frequencies are very similar (1487.5 vs. 1489.3 cm−1) a significant amount of their GCO contributions cancels out. As can be seen in Table S1 (ESI†), the EDTMs of these two modes and the associated R01 and RGCO01 values exhibit variations of less than 10% during the LT scan. We thus conclude that the variation of the total intensity and the distribution over the negative and positive part of the band is not caused by changes in the relative orientation of the interacting EDTMs but by a very small change (∼0.9 cm−1) in their separation.
Our LT calculations show that the energy profile for variations of τ is rather flat, and that in solution one may expect large-amplitude motions inducing variations in τ up to ±15°. Boltzmann-weighting over the associated VCD spectra will, however, lead effectively to bands with signs and intensities as calculated for the equilibrium structure. The only outstanding exception is the bisignate band at ∼1500 cm−1 which appears to be an excellent ‘sensor’ for this angle. With the knowledge of the origin of its sensitivity to τ, we conclude that ∼10° would be a conservative estimate of the accuracy with which τ can be determined from a comparison between experimental and calculated VCD spectra.
5 Conclusions
We have presented an in-depth VCD study on an axial chiral 7,7′-disubstituted 2,2′-methylenedioxy-1,1′-binaphthyls compound. Our studies have demonstrated that VCD spectroscopy is an effective and powerful tool to determine the absolute configuration of these compounds, which is even more relevant given that with standard techniques such as XRD the absolute configuration of the compound could not be determined. We have shown that the extremely strong and robust VCD bands in the fingerprint region can be well understood on the basis of a General Coupled Oscillator (GCO) analysis. Such an analysis reveals that these bands all originate from the coupling of vibrational motions of the two arms of the molecule. The fact that these arms have the same chemical structure and are spatially ‘locked’ by steric hindrance is the direct cause for the strong and stable coupled oscillator VCD signals. Comparison of the structure of the lower-energy conformations with the structure determined from XRD on racemic crystals has led to the conclusion that crystal packing significantly influences the dihedral angle τ between the two halves of the compound. Linear transit calculations indicate that VCD spectroscopy allows for a relatively accurate determination of this angle. On a more general level, our studies are a perfect example showing that VCD spectroscopy is a mature and powerful means to perform research and analysis in a large range of fundamental and applied areas.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. A. J. K., L. V. and W. J. B. acknowledge financial support from NWO in the framework of the Fund New Chemical Innovations (NWO Project No. 731.014.209). V. P. N. acknowledges funding from UEFISCDI (PN-III-P4-ID-PCE-2020-2783, contract no. PCE 190/2021).Notes and references
- P.-G. De Gennes and J. Prost, The physics of liquid crystals, Oxford University Press, 1993, vol. 83 Search PubMed.
- S. Furumi and N. Tamaoki, Adv. Mater., 2010, 22, 886–891 CrossRef CAS PubMed.
- D. Broer, J. Lub and G. Mol, Nature, 1995, 378, 467–469 CrossRef CAS.
- N. Y. Ha, Y. Ohtsuka, S. M. Jeong, S. Nishimura, G. Suzaki, Y. Takanishi, K. Ishikawa and H. Takezoe, Nat. Mater., 2008, 7, 43–47 CrossRef CAS PubMed.
- M. Mitov, Adv. Mater., 2012, 24, 6260–6276 CrossRef CAS PubMed.
- P. van der Asdonk, P. J. Collings and P. H. Kouwer, Adv. Funct. Mater., 2017, 27, 1701209 CrossRef.
- R. S. Kularatne, H. Kim, M. Ammanamanchi, H. N. Hayenga and T. H. Ware, Chem. Mater., 2016, 28, 8489–8492 CrossRef CAS.
- P. Im, D.-G. Kang, D.-Y. Kim, Y.-J. Choi, W.-J. Yoon, M.-H. Lee, I.-H. Lee, C.-R. Lee and K.-U. Jeong, ACS Appl. Mater. Interfaces, 2016, 8, 762–771 CrossRef CAS PubMed.
- T. Seki, S. Nagano and M. Hara, Polymer, 2013, 54, 6053–6072 CrossRef CAS.
- K. Kristinaityte, A. Marsalka, L. Dagys, K. Aidas, I. Doroshenko, Y. Vaskivskyi, Y. Chernolevska, V. Pogorelov, N. R. Valeviciene and V. Balevicius, J. Phys. Chem. B, 2018, 122, 3047–3055 CrossRef CAS PubMed.
- I. Tadwee, S. Shahi, V. Ramteke and I. Syed, Int. J. Pharm. Res. Allied Sci., 2012, 1, 6–11 CAS.
- R. Bosire, D. Ndaya and R. M. Kasi, Polym. Int., 2020 DOI:10.1002/pi.6113.
- P. M. Chaikin and T. C. Lubensky, Principles of condensed matter physics, Cambridge University Press, 1995 Search PubMed.
- C. Tschierske, Liq. Cryst., 2018, 45, 2221–2252 CrossRef CAS.
- G. Solladié and R. G. Zimmermann, Angew. Chem., Int. Ed. Engl., 1984, 23, 348–362 CrossRef.
- A. di Matteo, S. M. Todd, G. Gottarelli, G. Solladié, V. E. Williams, R. P. Lemieux, A. Ferrarini and G. P. Spada, J. Am. Chem. Soc., 2001, 123, 7842–7851 CrossRef CAS PubMed.
- K. Kishikawa, Y. Furukawa, T. Watanabe, M. Kohri, T. Taniguchi and S. Kohmoto, Liq. Cryst., 2017, 44, 956–968 CrossRef CAS.
- R. J. Mandle and J. W. Goodby, Liq. Cryst., 2018, 45, 1567–1573 CrossRef CAS.
- A. Ferrarini, G. Moro and P. Nordio, Mol. Phys., 1996, 87, 485–499 CrossRef CAS.
- A. Ferrarini, G. J. Moro and P. L. Nordio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 53, 681–688 CrossRef CAS PubMed.
- A. Ferrarini and P. Nordio, J. Chem. Soc., Perkin Trans. 2, 1998, 455–460 RSC.
- A. Ferrarini, G. Gottarelli, P. Luigi Nordio and G. Piero Spada, J. Chem. Soc., Perkin Trans. 2, 1999, 411–418 RSC.
- H. G. Kuball, T. Müller, H. Brüning and A. Schonhöfer, Mol. Cryst. Liq. Cryst., 1995, 261, 205–216 CrossRef CAS.
- H. G. Kuball, H. Brüning, T. Müller, O. Türk and A. Schonhöfer, J. Mater. Chem., 1995, 5, 2167–2174 RSC.
- H. G. Kuball and H. Brüning, Chirality, 1997, 9, 407–423 CrossRef CAS.
- C. Kühn, M. Bremer and P. R. Schreiner, Liq. Cryst., 2019, 46, 1763–1768 CrossRef.
- H. D. Flack and G. Bernardinelli, Chirality, 2008, 20, 681–690 CrossRef CAS PubMed.
- N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, Comprehensive Chiroptical Spectroscopy, John Wiley & Sons, New York, NY, 2 edn, 2012, vol. 1 Search PubMed.
- L. A. Nafie, Vibrational Optical Activity, John Wiley & Sons, 1st edn, 2011 Search PubMed.
- P. J. Stephens, F. J. Devlin and J. R. Cheeseman, VCD Spectroscopy for Organic Chemists, CRC Press, 2012 Search PubMed.
- P. L. Polavarapu, Chiroptical Spectroscopy: Fundamentals and Applications, CRC Press, Boca Raton, 1st edn, 2016 Search PubMed.
- V. P. Nicu, Phys. Chem. Chem. Phys., 2016, 18, 21202–21212 RSC.
- Y. Xia, M. A. J. Koenis, J. F. Collados, P. Ortiz, S. R. Harutyunyan, L. Visscher, W. J. Buma and V. P. Nicu, ChemPhysChem, 2018, 19, 561–565 CrossRef CAS PubMed.
- H. Harada and K. Nakanishi, Circular Dichroic Spectroscopy: Exciton Coupling in Organic Stereochemistry, University Science Books, Mill Valley, CA, 1st edn, 1983 Search PubMed.
- L. Rosenfeld, Z. Phys., 1929, 52, 161–174 CrossRef.
- M. A. J. Koenis, O. Visser, L. Visscher, W. J. Buma and V. P. Nicu, J. Chem. Inf. Model., 2020, 60, 259–267 CrossRef CAS PubMed.
- V. P. Nicu, Phys. Chem. Chem. Phys., 2016, 18, 21213–21225 RSC.
- M. A. J. Koenis, L. Visscher, W. J. Buma and V. P. Nicu, J. Phys. Chem. B, 2020, 124, 1665–1677 CAS.
- M. A. J. Koenis, C. S. Chibueze, M. A. Jinks, V. P. Nicu, L. Visscher, S. M. Goldup and W. J. Buma, Chem. Sci., 2020, 11, 8469–8475 RSC.
- G. Holzwarth and I. Chabay, J. Chem. Phys., 1972, 57, 1632–1635 CrossRef CAS.
- T. Taniguchi and K. Monde, J. Am. Chem. Soc., 2012, 134, 3695–3698 CrossRef CAS PubMed.
- S. Abbate, G. Mazzeo, S. Meneghini, G. Longhi, S. E. Boiadjiev and D. A. Lightner, J. Phys. Chem. A, 2015, 119, 4261–4267 CrossRef CAS PubMed.
- C. L. Covington, V. P. Nicu and P. L. Polavarapu, J. Phys. Chem. A, 2015, 119, 10589–10601 CrossRef CAS PubMed.
- G. Mazzeo, E. Santoro, S. Abbate, C. Zonta, F. Fabris and G. Longhi, Chirality, 2020, 32, 907–921 CrossRef CAS PubMed.
- Amsterdam Density Functional program, http://www.scm.com, accessed November 8, 2017.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- RDKIT: Open-source cheminformatics, http://www.rdkit.org accessed March 6, 2017.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. Goddard III and W. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- V. P. Nicu, J. Neugebauer, S. K. Wolff and E. J. Baerends, Theor. Chem. Acc., 2008, 119, 245–263 Search PubMed.
- J. Shen, C. Zhu, S. Reiling and R. Vaz, Spectrochim. Acta, Part A, 2010, 76, 418–422 CrossRef PubMed.
- M. A. J. Koenis, Y. X. Xia, S. R. Domingos, L. Visscher, V. P. Nicu and W. J. Buma, Chem. Sci., 2019, 10, 7680–7689 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00854d |
| This journal is © the Owner Societies 2021 |