Gas-phase aluminium acetylacetonate decomposition: revision of the current mechanism by VUV synchrotron radiation†
Received
16th February 2021
, Accepted 17th June 2021
First published on 18th June 2021
Abstract
Although aluminium acetylacetonate, Al(C5H7O2)3, is a common precursor for chemical vapor deposition (CVD) of aluminium oxide, its gas-phase decomposition is not well-known. Here, we studied its thermal decomposition in a microreactor by double imaging photoelectron photoion coincidence spectroscopy (i2PEPICO) between 325 and 1273 K. The reactor flow field was characterized by CFD. Quantum chemical calculations were used for the assignment of certain species. The dissociative ionization of the room temperature precursor molecule starts at a photon energy of 8.5 eV by the rupture of the bond to an acetylacetonate ligand leading to the formation of the Al(C5H7O2)2+ ion. In pyrolysis experiments, up to 49 species were detected and identified in the gas-phase, including reactive intermediates and isomeric/isobaric hydrocarbons, oxygenated species as well as aluminium containing molecules. We detected aluminium bis(diketo)acetylacetonate-H, Al(C5H7O2)C5H6O2, at m/z 224 together with acetylacetone (C5H8O2) as the major initial products formed at temperatures above 600 K. A second decomposition channel affords Al(OH)2(C5H7O2) along with the formation of a substituted pentalene ring species (C10H12O2) as assigned by Franck–Condon simulations and quantum chemical calculations. Acetylallene (C5H6O), acetone (C3H6O) and ketene (C2H2O) were major secondary decomposition products, formed upon decomposition of the primary products. Three gas-phase aromatic hydrocarbons were also detected and partially assigned for the first time: m/z 210, m/z 186 (C14H18 or C12H10O2) and m/z 146 (C11H14 or C9H6O2) and their formation mechanism is discussed. Finally, Arrhenius parameters are presented on the gas-phase decomposition kinetics of Al(C5H7O2)3, aided by numerical simulation of the flow field.
1. Introduction
Due to its wear and corrosion resistance, high band gap and beneficial refractive index, aluminium oxide (Al2O3) is a popular coating, widely used in a variety of applications in, for instance, protective coatings, microelectronics, and optical devices. In particular, Al2O3 can act as a passivating layer, as an alternative gate dielectric oxide,1,2 anti-corrosion and permeation barrier coating,3–6 as well as surface enhancement coating in the cutting tool industry.7,8 Thanks to high growth rates and comprehensive surface coverage, Al2O3 layers are frequently synthesized by metal–organic chemical vapor deposition (MOCVD), a widely used technique for the preparation of functional coatings.9 In MOCVD processes, a volatile, metal-containing precursor is used for the deposition of thin films. Metal β-diketonates are advantageous, due to their relatively high vapor pressure at moderate temperatures and their thermal stability,10 which explains the increased use of the non-toxic and inexpensive aluminium tris(acetylacetonate) Al(C5H7O2)3 as a precursor in MOCVD.11–19 It is well-known that gas-phase reactions play an important role in the determination of the film composition, purity, and growth rate.9 Due to the high activation energy of the unimolecular dissociation of metal β-diketonates, the homogeneous decomposition of the gaseous precursor is considered as the rate-limiting step for film growth.10 Unwanted particle formation and nucleation processes may also occur in the gas-phase, which reduce the growth rate significantly.9 Consequently, the characterization of the gas-phase chemistry is of particular interest. This explains efforts to study the reaction kinetics20,21 and attempts to characterize21–23 primary gaseous reaction products of the thermal decomposition of Al(C5H7O2)3, although the definitive reaction mechanism has remained elusive so far.
In an early work, Hoene and coworkers22 used ex situ mass spectrometry to identify the primary decomposition products of the thermal degradation of Al(C5H7O2)3 in vacuum at temperatures of 423–673 K. They identified carbon dioxide (CO2) and acetone (C3H6O) as the major decomposition products and found traces of acetylacetone (C5H8O2), too.22 A drawback of this study was the possible interaction between the condensed and the gas-phase, which may lead to side reactions. Tackling this, Minkina20 investigated the gas-phase pyrolysis at a low pressure of 1 kPa under static conditions by the manometric method between 653 and 723 K. Besides methane (CH4) and ketene (C2H2O), acetone, carbon dioxide, butene (C4H8), and carbon monoxide (CO) were the most abundant species detected. Because of the large excess of acetone and carbon dioxide, she concluded that these products originated from the sequential decomposition of acetylacetone. Therefore, only secondary decomposition products of Al(C5H7O2)3 were identified. Covering a wider temperature range from 423 to 923 K, Bykov and colleagues21 determined the onset of the thermal decomposition of Al(C5H7O2)3 in a heated reactor to be around 563 K by electron ionization mass spectrometry. Additionally, they recorded temperature-dependent species profiles, which showed three distinct temperature regimes, and proposed reaction schemes for each. According to their findings, the first decomposition step proceeds via the loss of acetylacetone and the subsequent formation of acetone and ketene. A second decomposition pathway involves the cleavage of the enolic C–O bond combined with an intramolecular rearrangement of the central H-atom, followed by loss of an uncharacterized C5H6O isomer at m/z 82. The formation of a cyclic diketone at m/z 164, which further decomposes upon ketene loss to yield 3,5-dimethylphenol at m/z 122, represents the third proposed decomposition pathway. It has been stated that this mechanism can be explained by an Al–O bond breakage and a transformation of bidentate C5H7O2 ligand into a monodentate one.23 However, standard 70 eV electron ionization mass spectra suffer from fragmentation, which complicates the assignment of the detected m/z peaks to their neutral parent species. To address this, Rhoten and DeVore24 conducted an in situ study of the thermal decomposition of Al(C5H7O2)3 in a low-pressure stationary flow reactor in the 500–900 K temperature range by Fourier-transform infrared spectroscopy (FTIR) and subsequent gas chromatography-mass spectrometry (GC-MS) analysis of the sample residue. They identified at least ten volatile organic products. In addition to a confirmation of the findings by Bykov et al.,21 they could assign C5H6O to 3-pentyn-2-one and emphasized the role of H-atom migration with intramolecular rearrangement in the reaction mechanism. However, they did not detect aluminium-containing intermediates or products besides the precursor itself and indicated that the species characterization using GC-MS can be biased by the reaction of Al(C5H7O2)3 in the column. Previous studies probing the gas-phase of CVD processes using Al(C5H7O2)3 show that the experimental results under CVD process conditions are often too complex to be exploitable, because mostly secondary decomposition products were detected and the real nature of the mechanism remained elusive so far. As the deposition temperature increases, gas-phase chemistry may initiate complex sequential reactions leading to the production of surface-active reaction products that facilitate or even allow the desired film growth. This means that relying exclusively on such methods may result in major reaction pathways being overlooked. This motivated us to identify aluminium containing decomposition products of Al(C5H7O2)3 definitely and isomer-selectively to provide comprehensive insight into the reaction mechanism.
Recently, tuneable vacuum ultraviolet (VUV) synchrotron radiation has been used as a soft ionization technique to probe harsh environments, such as flames,25–27 flow reactors,28–30 and MOCVD31,32 processes, to characterize reactive intermediates and products unambiguously. Combining the tunability of the photon energy and velocity map imaging (VMI) kinetic energy analysis of the photoelectrons, double imaging photoelectron photoion coincidence spectroscopy (i2PEPICO),33 has been shown to be a promising tool for the isomer-selective identification and characterization of reactive intermediates upon pyrolysis.34 These sophisticated techniques to detect short-lived gas-phase species have proven to be useful not only to determine and characterize elusive reactive intermediates but also to delimit surface-bound and gas-phase chemistry. An accurate description of the gas-phase kinetics is of great importance to model and understand film growth processes. This holds especially true for modelling the whole deposition process, where a complete set of reactions in necessary. The present work reports on the photolysis and thermal decomposition of highly diluted Al(C5H7O2)3 in inert carrier gas in a SiC flow tube microreactor at reduced pressure and temperatures between 325 and 1273 K. To model the flow field inside the SiC reactor, we applied computational fluid dynamics (CFD). Products leaving the reactor expand into high vacuum and form a molecular beam, in which reactive molecules are preserved. The intermediates and products are subsequently ionized by tuneable VUV synchrotron radiation and detected by imaging photoelectron photoion coincidence spectroscopy (i2PEPICO). Temperature-dependent photoionization mass spectra offer insights into the decomposition steps. Photoionization spectra (PIS) and photoion mass-selected threshold photoelectron spectra (ms-TPES) were recorded in the 7.0–11.5 eV photon energy range to assign the reactive intermediates and the products formed. In contrast to previous studies, we are able to detect metal-containing intermediates when their lifetime is at least a few microseconds.
2. Methods
2.1 Experimental setup
The experiments were performed at the vacuum ultraviolet (VUV) beamline35 at the Swiss Light Source of the Paul Scherrer Institute in Switzerland. A detailed description of the experimental apparatus,36,37 as well as the reactor setup pioneered by Chen et al.,38 can be found elsewhere.39 A schematic sketch of the experimental setup is shown in Fig. 1. Aluminium tris(acetylacetonate) (>99%, Sigma-Aldrich Inc.) is sublimed in a stainless steel tube, heated within a copper block (reddish brown in Fig. 1), to ensure isothermal sublimation conditions. The temperature and pressure of the sublimation chamber are monitored and kept constant during each measurement. Unimolecular reaction conditions are achieved by a relatively low pressure and a highly diluted sample stream to minimize the likelihood of reactive collisions. Argon (99.9999%), was delivered by calibrated mass flow controllers (MKS Instruments) at a constant flow rate of 22 sccm. To reveal potential bimolecular chemistry in the reactor, we conducted six separate experimental sets operating at evaporator pressures of 550 and 1600 mbar and sublimation temperatures of 395/405/420 K. Assuming thermal equilibrium, the precursor mole fractions at the reactor inlet ranged between 6.8 × 10−5 < xAl(acac)3 < 4.8 × 10−4. After sublimation, the mixture is expanded through a 100 μm pinhole into a resistively heated silicon carbide (SiC)40 flow microreactor with an inner diameter (I.D.) of 1.0 mm and a heated length of 10 mm. To measure the decomposition temperature, a type C thermocouple, with an estimated uncertainty in the examined temperature range of 1%, was attached centrally to the outer surface of the pyrolysis reactor in the middle of the heated range. Earlier studies quote the overall uncertainty of the centreline temperature to be ±100 K.41,42 The temperature readings were used as boundary condition in the numerical simulation of the flow field and will be given in the results part. This procedure has been already established in previous studies.43,44 After passing the reaction zone, the reactive mixture is rapidly expanded to high vacuum at 6 × 10−5 mbar and forms an effusive molecular beam. The rapid drop in collision frequency preserves the gas composition, including highly reactive species. After expansion from the reactor, a nickel skimmer with a 2 mm orifice cuts out the central part of the gas mixture, letting a fraction of the pyrolyzed gas sample proceed towards the ionization chamber, which is kept at a background pressure of less than 10−6 mbar. In the ionization region, the sample beam is crossed by the monochromatized VUV radiation at an energy resolution of 6 meV. The resulting cations and photoelectrons are separated by a constant extraction field of 243 V cm−1, which accelerates them in opposite directions. After passing the respective flight tubes, electrons and ions are detected by two Roentdek DLD40 fast position-sensitive delay-line anode detectors in delayed coincidence in velocity map imaging (VMI) conditions. This means that the impact radius is proportional to the species’ initial kinetic energy corresponding to its momentum perpendicular to the extraction axis.45 VMI allows us to spatially separate the parent ions from the room temperature background in the chamber and also from ions formed in dissociative ionization, which is often accompanied by large kinetic energy release perpendicular to the beam propagation direction (see region of interest (ROI) highlighted in Fig. 1).37 In all experiments, the photon energy was either kept constant at near-threshold photoionization energies of the decomposition species of interest or was scanned with a step size of 0.025 eV in the 7.0–11.5 eV range. To minimize fragmentation and to be above the ionization threshold for various molecules, we recorded mass spectra of the reaction mixtures at 7.8, 8.0, 8.5, 9.0, 9.5, 10.0, 10.5, and 11.5 eV within a temperature range of 325 K to 938 K. Single measurements were carried out at higher temperatures up to 1273 K to investigate secondary and tertiary decomposition products. The spectra were corrected by the known photon flux at the respective photon energies and were used to derive temperature-dependent species profiles. In order to account for the higher internal energies of the pyrolyzed species and the corresponding red shift of the ionization onset, we shifted the literature spectra for better comparison by less than 0.1 eV. Species were assigned based on their molecular mass, photoionization spectrum (PIS) or their mass-selected threshold photoelectron spectrum (ms-TPES). The latter are based on the centre signal of the electron detector, where threshold electrons are detected, from which the hot electron contribution has been subtracted according to the procedure by Sztáray and Baer.46 The photoelectron spectra allow for an unambiguous identification of most of the primary decomposition products by comparing them to reference spectra.33 Additionally, quantum chemistry can help in species identification, as shown below.
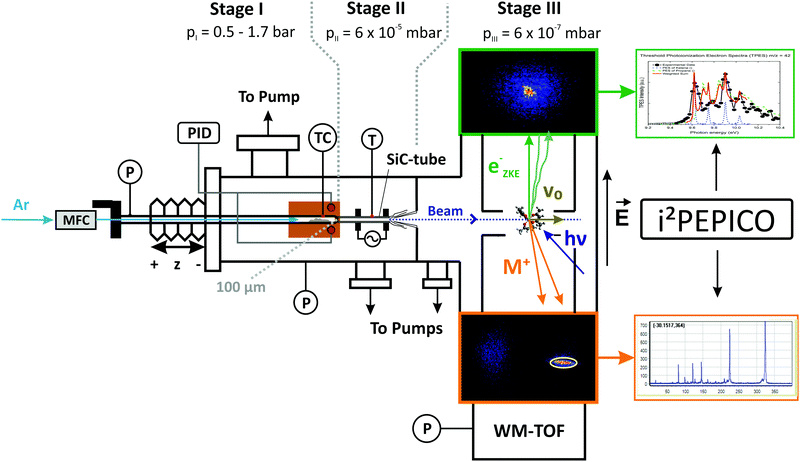 |
| | Fig. 1 Schematic drawing of the pyrolysis reactor coupled to the i2PEPICO experimental apparatus. The working principle of velocity map imaging (VMI) and the raw data are shown on the right hand side; the yellow circle in the ion (bottom) image displays the region of interest chosen to sample the translationally cold molecular beam directly, suppressing the background and the dissociative photoionization signal. | |
2.2 Quantum chemical calculations
The Gaussian 16 A0347 suite of programs has been utilized to calculate the adiabatic ionization energies of some of the detected species. Geometries were optimized on the B3LYP/6-311++G(d,p) level of theory and the vibrational frequencies of both neutral and ionic species have been calculated. Adiabatic ionization energies were calculated using composite methods, such as CBS-QB348 or G4.49 The hydrogen transfer reaction of the initial decomposition reaction of aluminium tris(acetylacetonate) was explored using constrained geometry scans applying B3LYP/6-311++G(d,p) and further refined by utilizing the synchronous transit-guided quasi-Newton method50 to locate the transition state. We have refined the energetics of this reaction applying CBS-QB3 computations.51 Franck–Condon (FC) simulations have been carried out in the double harmonic approximation, based on frequency analysis at the optimized geometries of the neutral and cation utilizing eZspectrum.52 The stick spectra were convoluted with a 20–40 meV full width at half maximum Gaussian function to account for the rotational envelope and the energy resolution and the adiabatic ionization energy was shifted to fit the experimental TPE spectrum. Time-dependent density functional theory (TD-DFT) calculations were carried out to identify excited-state bands in the photoelectron spectrum, at the B3LYP/6-311++G(d,p) level of theory.53
2.3 CFD simulation of the microreactor
Reactive intermediates are not detectable at long residence times, because they are converted to more stable products. Thus, the reactor is designed such that secondary reactions are minimized by ensuring short residence times (<100 μs).43 This requires small reactor geometries, whose characterization is not straightforward. For instance, the microreactor surface temperature is measured at one point on the outer surface, while the whole temperature profile is of interest. To interpret and quantify the experimental observations, the flow field in the microreactor must be known, as well as residence times, pressure, and temperature fields. As the conditions in the microreactor are hardly measurable directly,54 modelling was used to estimate them. The Boltzmann equation provides a general description of the evolution of a gas and represents the motion of gas molecules at each location in the gas and the change with time due to collisions between molecules.55 When the fluid's molecules have a short mean free path, the fluid can be treated by continuum mechanics, for instance with the Navier–Stokes equations (see ESI:† eqn (E1) and (E2)). The Knudsen number (Kn) represents the ratio of the mean free path to the characteristic length of the flow region (see ESI:† eqn (E3) and (E4)), and determines whether the continuum mechanics formulation can be used. Depending on Kn, the flow region can be divided into a continuous flow region (Kn < 0.01), a slip flow region (0.01 ≤ Kn < 0.1), a transition flow region (0.1 ≤ Kn < 10), and a free-molecular flow region (Kn ≥ 10). The flow in the slip region can be predicted by considering a slip (boundary) condition with the Navier–Stokes equations when Kn deviates from the continuum regime just slightly (0.01 ≤ Kn < 0.1). Since Kn is between 0.005 and 0.02 in the microreactor, it is in the slip condition range as shown in ESI:† Fig. S3. Thus, to investigate the flow field, the Navier–Stokes equations with a slip (boundary) condition (see ESI:† eqn (E5) and (E6)) are solved using ANSYS Fluent 19.1.56 Furthermore, gaseous flows should be considered as compressible when the pressure changes are more than approximately 20% of the mean pressure.57 The microreactor flow must be considered compressible, since its outlet is connected to high vacuum at 6 × 10−5 mbar. Compressibility is accounted for using the second-order upwind Roe-flux difference splitting scheme (Roe-FDS).58
The simulation was performed with pure argon flow, because the concentration of the precursor is negligible. The viscosity and thermal conductivity of argon were determined by Bich et al.59 To obtain simulation results for different operating conditions efficiently, the computational domain was set up as axisymmetric two-dimensional geometry (see ESI,† Fig. S1). A single simulation took approximately 300 core hours with 1.09 M nodes and 1.08 M cells with 10 μm grid size. This grid size is small enough to resolve the flow field (see ESI:† Fig. S2 and S3). Due to the lack of experimental data for such systems, as for instance pressure and temperature readings inside the reactor, we validated our approach on a similar numerical microreactor study utilizing the boundary-layer model by Weddle et al.60 The flow field of our approach correlated fairly well with the reference data (see ESI:† Fig. S4), which shows its feasibility under the present experimental conditions. Results of our CFD calculations are taken into account, when the effective pyrolysis temperature as well as the kinetics are determined based on the measured surface temperature and the modelled flow field temperatures. The findings (see Section 3.7) show that the reactor geometry and experimental conditions should allow radicals to survive up to the reactor outlet, so that they can be probed after expansion into high vacuum.
2.4 Kinetics
Studies that use microreactors to investigate the thermal decomposition processes rarely quantify the reaction kinetics because the conditions inside the reactor are poorly known. We overcame this by modelling the flow field inside the SiC reactor, which includes detailed temperature fields and residence times for various reaction conditions (see Section 3.7). This information, combined with the measured species profiles, enabled us to carry out a kinetic analysis of the primary decomposition step. The steps to determine the temperature dependence of the Al(C5H7O2)3 mole fraction proceed according to Zhang et al.61 In our case, argon is used as reference species for the determination of the gas expansion coefficient λ(T), which summarizes temperature-dependent signal variations of argon (m/z 40), representing the variation in sampling efficiency due to changing expansion behaviour as a function of temperature. The mass-dependency is not further investigated in our case, because it only affects light species, such as H2, significantly.61 The gas expansion coefficient has been determined by recording temperature-dependent mass spectra at a fixed photon energy of 15.8 eV in the 346–909 K range and is shown as ESI:† Fig. S6. For an incident photon energy of 8 eV and fixed photon flux, the mole fraction of Al(C5H7O2)3 at temperature T can be calculated by eqn (1),| | 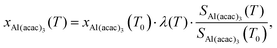 | (1) |
where Si(T) represents the ion signal intensity measured at temperature T and xAl(acac)3 is defined as the precursor mole fraction measured at temperature T. The inlet mole fraction was calculated assuming saturated conditions inside the evaporator; for an evaporation temperature of 405 K this results in xAl(acac)3(T0) = 4.15 × 10−4 from vapour pressure data.62 Arrhenius plots were derived using the integral method for the unimolecular dissociation reaction| | 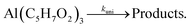 | (2) |
Unimolecular gas-phase dissociation reactions of organometallic precursors often follow first order kinetics as shown in eqn (3):| | | kuni(T) = A0·exp(Ea/RT), | (3) |
with the respective Arrhenius behaviour, representing A0 as the pre-exponential factor and Ea as the molar activation energy in kJ mol−1. Previous experiments demonstrated that this is also the case for surface reactions following the Langmuir–Hinshelwood mechanism, which is first order at low partial pressures of Al(C5H7O2)3.23 Surface and gas-phase reactions may take place concurrently in our microreactor, thus the total rate constant is the sum of both contributions. Both were derived simultaneously and the kinetic constants for each follows the Arrhenius expression given in (3), where:| | | ktot(T) = kgas(T) + ksurf(T). | (4) |
The time dependent concentration change for a unimolecular reaction is given by:| | 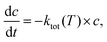 | (5) |
leading tocombined with (3) and (4) the following expression results:| | | c = c0e−[A0,g·exp(Ea,g/RT)+A0,s·exp(Ea,s/RT)]×t | (7) |
This expression was used to fit the four unknowns A0,g, A0,s, Ea,g and Ea,s to the experimental data c(c0,T,t).
3. Results and discussion
In the following, first the photoionization of room temperature Al(C5H7O2)3 is shown in order to properly distinguish pyrolysis from dissociative ionization leading to the same m/z species. Next, the identification of the pyrolysis products is described, which is rationalised by photoionization and ms-TPE spectra, compared with reference spectra or Franck–Condon simulations. These results are subsequently used to obtain temperature-dependent species profiles, from which a reaction scheme is derived. By invoking the known reactor conditions given by the CFD simulations, we finally investigate the reaction kinetics of the primary Al(C5H7O2)3 decomposition step.
3.1 Dissociative photoionization of Al(C5H7O2)3
Since the incident photon beam can, depending on the energy, dissociatively photoionize the sample, it is often difficult to distinguish directly ionized thermal decomposition products from those stemming from dissociative photoionization (DPI) of the neutral precursor surviving the pyrolysis reactor. To address this, we analysed the room temperature dissociative ionization of Al(C5H7O2)3 in the 7.5–11.5 eV energy range. Mass-selected threshold photoelectron spectra (Fig. 2(a)) were recorded to shed light on the dissociative ionization mechanism of Al(C5H7O2)3. The first band of the parent m/z 324 ms-TPES (red curve) is centred at 8.14 eV and its maximum agrees with the literature value of IEvert = 8.17 eV,63 as well as with the calculated adiabatic ionization energy IEad = 7.81 eV. Trivalent cations produce even-electron fragment ions upon dissociation by losing a C5H7O2 radical and consecutive dissociation have rarely been observed, because of the energetically favoured 3+ valence state of the fragment ion.64 This explains the main dissociation channel, the loss of a C5H7O2 ligand, leading to the formation of Al(C5H7O2)2+ at m/z 225 (blue curve, Fig. 2(b)). The daughter ion signal starts to rise at around 8.5 eV. However, with increasing photon energy, m/z 100 also appears in the spectra. It can clearly be stated that m/z 100 and its fragment m/z 85 is due to enolone- and diketo-acetylacetone, since Antonov et al.65 ascertained that the ionization energy of enolone-acetylacetone is 8.9 eV, which fits the onset of our m/z 100 ms-TPE spectrum (see ESI:† S5: 300 K). Given the narrow lateral kinetic energy distribution of the m/z 100 ions, traces of acetylacetone are indeed in the sample at room temperature. Consequently, the room temperature m/z 100 signal is due to sample impurities. We can rely on these insights to derive the temperature-dependent species profiles.
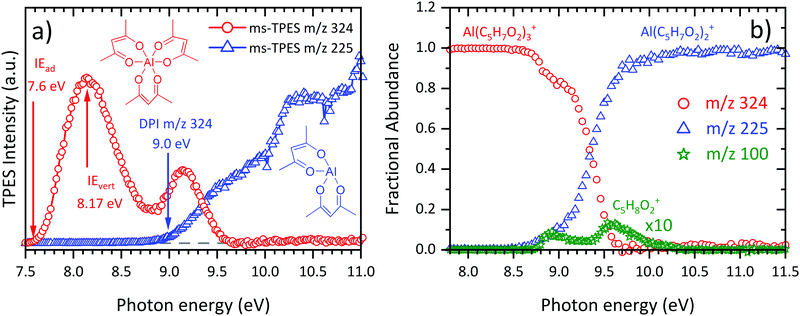 |
| | Fig. 2 (a) Mass-selected threshold photoelectron spectra (ms-TPES) recorded at room temperature in the 7.5–11.0 eV photon energy range. The main dissociative ionization product at m/z 225 is denoted in blue, whereas the parent molecule Al(C5H7O2)3 is displayed in red along with literature ionization energies.63 (b) Breakdown diagram of Al(C5H7O2)3 at room temperature without considering the m/z 100 signal (see text for discussion). | |
3.2 Photoionization mass spectra of the pyrolysis products
After insights in the dissociative ionization of the precursor have been gained, Al(C5H7O2)3 was pyrolyzed in the temperature range of 325–973 K. Photoionization mass spectra were recorded and evaluated at fixed photon energies. Representative photoionization mass spectra at fixed photon energies of 8.0 and 9.5 eV are shown in Fig. 3. When the SiC reactor is heated above 525 K, we clearly see a depletion of the precursor signal and product peaks at m/z 122, 164, and 224–225 are observed (Fig. 3, left). This threshold value agrees well with the 523 K pyrolysis onset observed by Rhoten and coworkers.24 Since we only evaluate the ion signal intensities that emerge from the molecular beam at low ionization energies, these ions are almost exclusively assigned to the primary decomposition products of Al(C5H7O2)3 with small contributions of dissociative ionization. Increasing the reactor temperature to 655 K, the intensity of the m/z 224–225 peak increases by a factor of 10, while the precursor molecule signal decreases. Additionally, new product peaks arise in the spectrum at m/z 82 and 146. To assess product species with lower masses, mass spectra at higher photon energies were recorded (Fig. 3, right). At temperatures above 700 K, several peaks appear below m/z 100, while the primary decomposition product signal at m/z 224–225, is reduced markedly. In addition to the previously reported species in the literature, our mass spectra show species with m/z 146, 186, and 210 rising in concert with the depletion of the primary gas-phase decomposition product m/z 224.
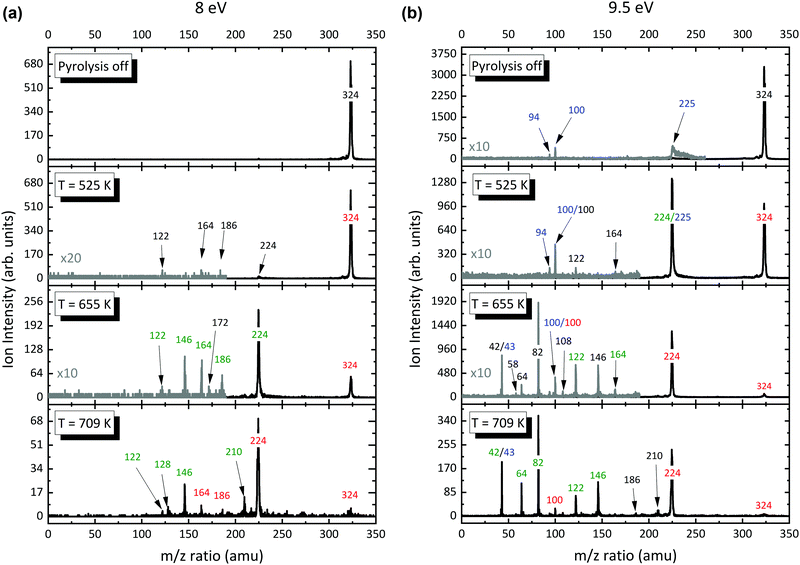 |
| | Fig. 3 Temperature-dependent mass spectra of Al(C5H7O2)3 pyrolysis recorded at a photon energy of 8 (a) and 9.5 eV (b) and an inlet mole fraction of 4.15 × 10−4 (0.05%). The major peaks are labelled by their m/z ratio and with respect to their absolute decay (red) or increase (green) in comparison to the previous spectrum at lower decomposition temperature. Species that emerge for the first time are marked in black, whereas the blue numbers indicate that the species are due to dissociative ionization or impurities. For better comparison, the grey spectra are multiplied by a factor of 10 or 20. | |
3.3 Identification of the primary decomposition product
Regarding the temperature-dependent mass-spectra in Fig. 3, the question arises whether and to which extent the peak at m/z 224/225 is a pyrolysis product or formed by DPI of the parent molecule. Fig. 4(a) shows temperature-dependent mass-selected threshold photoelectron spectra (ms-TPES) of the precursor molecule as well as its primary decomposition and DPI product convoluted in the m/z 224 and 225 range. The ionization energy of the Al(C5H7O2)2 radical to form the singlet and triplet cation state at m/z 225 are calculated to be 4.76 and 7.81 eV at the CBS-QB3 level of theory, respectively. Therefore, we conclude that m/z 225 is formed exclusively by DPI. This is also substantiated by the broad kinetic energy distribution of the beam component of m/z 225 in the VMI images displayed in Fig. 4(b–d) at 9.5 eV. In contrast, at 633 K, the m/z 224/225 channel follows the shape of the parent molecule m/z 324 and further increases above 9 eV, when dissociative ionization is observed at RT, leading to the assumption that at higher temperatures, a convolution of DPI and pyrolysis species is present. For an unambiguous verification of the temperature onset and nature of the primary decomposition product observed, representative VMIs of m/z 224 ion channel at 8.0 eV photon energy are displayed in Fig. 4(b–d). We can clearly differentiate between the room temperature velocity distribution (denoted as “BG”) and those ions that have a large velocity perpendicular to the incident photon beam (denoted as “Beam”). Unlike in the lower part of Fig. 4(c), where the beam component exhibits a broad kinetic energy distribution, typical for kinetic energy release in dissociative ionization, the former VMI shows a narrow distribution inside the molecular beam region. The ratio of m/z 224 to m/z 225 increases at higher temperatures, as seen in the increasing contribution of the cold molecular beam component of the band, which is substantiated by the m/z 224 kinetic energy distribution at 723 K (Fig. 4(d)). At this point, the parent molecule m/z 324 is almost fully pyrolyzed, and only the first ms-TPES band is seen for the fragment channel, centred at around 8.2 eV. This indicates that the primary decomposition product m/z 224 contributes almost exclusively to this signal, as opposed to DPI delivering ions at m/z 225. Our assignment of Al(C5H7O2)C5H6O2 is corroborated by adiabatic ionization energy calculations, which find a value of 6.64 eV at the CBS-QB3 level of theory. The FC simulation of the ground state (see S3 in the ESI†) predicts a broad band centred at 6.8 eV. At 7 eV, the lowest photon energy studied herein, the ms-TPES shows signal, which overlaps with the simulation but drops quickly. TD-DFT excited ion state calculations revealed vertical IEs to the Ã+, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) +, and
+, and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) + states of Al(C5H7O2)C5H6O2+ at 8.2, 8.8 and 9.2 eV using B3LYP/6-311++G(d,p), which agrees with the observed features in the 723 K ms-TPE spectrum. Thus, we tentatively assign the m/z 224 peak to the Al(C5H7O2)C5H6O2 aluminium species. Following this argumentation, near-threshold photon energies of 8 eV will be used for the detection of Al(C5H7O2)3 and the primary decomposition product Al(C5H7O2)C5H6O2, respectively. This allows us to suppress the DPI interference with the pyrolysis products at higher temperatures.
+ states of Al(C5H7O2)C5H6O2+ at 8.2, 8.8 and 9.2 eV using B3LYP/6-311++G(d,p), which agrees with the observed features in the 723 K ms-TPE spectrum. Thus, we tentatively assign the m/z 224 peak to the Al(C5H7O2)C5H6O2 aluminium species. Following this argumentation, near-threshold photon energies of 8 eV will be used for the detection of Al(C5H7O2)3 and the primary decomposition product Al(C5H7O2)C5H6O2, respectively. This allows us to suppress the DPI interference with the pyrolysis products at higher temperatures.
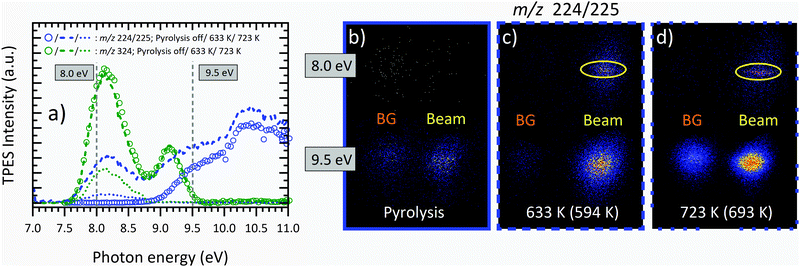 |
| | Fig. 4 (a) Temperature-dependent ms-TPES of m/z 224/225 (blue) and m/z 324 (green) at photon energies from 7.0 to 11.0 eV at the pyrolysis temperatures of 303 K (circle), 633 K (dashed), and 723 K (dotted). The decay of the intensity signal for m/z 324 due to thermal decomposition can clearly be observed. Representative VMI images of m/z 224/225 at photon energies of 8.0 and 9.5 eV are shown at temperatures of (b) 303 K, (c) 633 K, and (d) 723 K. The CFD estimated centreline temperature is given in brackets. The ROI for the molecular beam signal is marked in yellow. The kinetic energy distributions enable us to identify pyrolysis and dissociative ionization products. | |
3.4 Assignment of further pyrolysis products
Besides the mass-selective identification of the ions from the photoionization mass spectra (Fig. 3), we rely on photoionization spectra (PIS) and mass-selected photoelectron spectra (ms-TPES) to assign further pyrolysis products. Following the approach of Hemberger et al.,66 we analysed the threshold photoionization matrix (TPM), i.e., the threshold photoionization signal as a function of ion m/z and photon energy, of Al(C5H7O2)3 under pyrolysis at reactor temperatures of 633 K, 738 K and 824 K, at which we observe ca. 25, 50 and 100% depletion of the precursor signal and progressively larger product signals. In total, we observed 31 temperature-resolved ion peaks (see Table 1), which we assigned to 49 unique pyrolysis and dissociative ionization products of the precursor molecule. It is generally known that the dissociative ionization onset is shifted to lower ionization energies if the sample temperature is increased, as the initial thermal energy is also available for the dissociation of the parent ion.67 As discussed above, these DPI contributions could be established with the help of ion VMI. The experimental spectra generally correlated well with the reference data for the assigned species. Experimental ionization energies are listed for better comparison in Table 1. The peaks at m/z 18 and 32 were assigned to H2O+ and O2+, identified by a single photon energy measurement at 12.8 eV, close to their ionization energies. In similar manner, we recorded spectra at 14.2 eV and assigned the signal at m/z 28 exclusively to CO+, as the peak was absent at lower photon energies. A series of C1–14 hydrocarbons was identified in the pyrolyzed sample. Representative examples of the species identification for the most relevant pyrolysis products are shown in Fig. 5 and 6, which are addressed in this paragraph. Additional PIS and ms-TPE spectra with the corresponding assignments can be found in paragraph S4 of the ESI.†
Table 1 Species assignment in Al(C5H7O2)3 pyrolysis by VUV-i2PEPICO using adiabatic and vertical ionization energies. Reference spectra and energies have been taken from the literature and are denoted at the respective value
|
m/z |
Formula |
Name |
IE (eV) |
| Ref. |
This work |
| *Species marked with an asterisk correspond to tentative assignments. |
| 15 |
CH3 |
Methyl radical |
9.8468 |
9.82 |
| 18 |
H2O |
Water |
12.6269 |
— |
| 26 |
C2H2 |
Acetylene |
11.470 |
11.42 |
| 28 |
CO |
Carbon monoxide |
14.0171 |
— |
| 30 |
CH2O |
Formaldehyde |
10.8972 |
10.90 |
| 32 |
O2 |
Oxygen |
12.3373 |
— |
| 39 |
C3H3 |
Propargyl radical |
8.7174 |
8.72 |
| 40 |
C3H4 |
Allene |
9.6975 |
9.70 |
| Propyne |
10.3876 |
10.38 |
| 42 |
C2H2O |
Ketene |
9.6277 |
9.60 |
| C3H6 |
Propene |
9.7378 |
9.72 |
| 43 |
C2H3O |
DI-acetone |
10.3079 |
— |
| DI-diketo AcAc |
10.4265 |
— |
| 44 |
C2H4O |
Vinyl alcohol |
anti-: 9.1780 |
— |
|
syn-: 9.3080 |
| Acetaldehyde |
10.2381 |
— |
| 52 |
C4H4 |
1-Buten-3-yne (vinylacetylene) |
9.5878 |
9.59 |
| 54 |
C4H6 |
1,3-Butadiene |
9.0782 |
— |
| 1,2-Butadiene |
9.3369 |
|
| 2-Butyne |
9.5978 |
— |
| 1-Butyne |
10.1869 |
— |
| 58 |
C3H6O |
Acetone |
9.7179 |
9.68 |
| 64 |
C5H4 |
Pentatetraene |
Vert.: 8.9983 |
8.98 |
| Ethynylallene |
9.2284 |
9.20 |
| Methyldiacetylene |
9.5085,86 |
9.48 |
| 65 |
C5H5 |
Cyclopentadienyl radical |
8.4187 |
8.42 |
| 66 |
C5H6 |
1,3-Cyclopentadiene |
8.5888 |
8.56 |
| 1,2,4-Pentatriene |
8.8889 |
8.86 |
| 1-Penten-3-yne |
9.178 |
8.96 |
| 82 |
C5H6O |
2-Methylfuran |
8.3890 |
8.40 |
| Acetylallene |
9.4465 |
9.42 |
| 86 |
C5H10O |
2-Pentanone |
9.3869 |
9.39 |
| 94 |
C6H6O |
Phenol |
8.4969 |
— |
| 100 |
C5H8O2 |
Acetylacetone (enol) |
8.965 |
8.9 |
| Acetylacetone (diketo) |
9.565 |
9.51 |
| 108 |
C7H8O |
Phenol, 2-methyl/anisole |
8.3991 |
8.4 |
| 122 |
C8H10O |
2,6-Dimethylphenol |
8.0592 |
— |
| 128 |
C10H8 |
Azulene |
7.4293 |
— |
| 146 |
C11H14 |
2,4,6-Trimethylstyrene |
8.3394 |
|
| Bezocycloheptene |
8.4495 |
| C9H6O2 |
1,2-Indenedione |
8.896 |
| 164 |
C10H12O2 |
Dimethyl-dihydroxo-dihydropentalene |
7.29 (this work) |
— |
| Dimethyl-hydroxo-keto-tetrahydropentalene |
7.55 (this work) |
| 186 |
C14H18 |
Octahydroanthracene |
7.8697 |
— |
| C12H10O2 |
Naphthaleneacetic acid |
8.0591 |
| 210 |
C16H18*/C14H10O2* |
Aromatic hydrocarbon* |
— |
— |
| 224 |
Al(C5H7O2)(C5H6O) |
Aluminium bis(acetylacetonate)-H* |
6.64 (this work) |
|
| 225 |
DI of Al(C5H7O2)3 |
Al(C5H7O2)2+ |
EI: 9.163 |
Ad.: 8.6 eV |
| 324 |
Al(C5H7O2)3 |
Aluminum tris(acetylacetonate) |
Ad.: 7.663 |
Ad.: 7.81 eV |
| Vert.: 8.1763 |
 |
| | Fig. 5 Representative examples of product species identification and assignment for C2–3 hydrocarbons and oxygenated species generated by pyrolysis of Al(C5H7O2)3 using TPE spectra (a, c and d) and PIS (b) (black lines with circles); literature reference spectra (red) and cross sections (blue, red) are as follows: (a) m/z 39 (C3H3)74 and (b) m/z 40 (C3H4),75,76 (c) m/z 42 (C2H2O)77 (C3H6)78 and (d) m/z 58 (C3H6O).79 | |
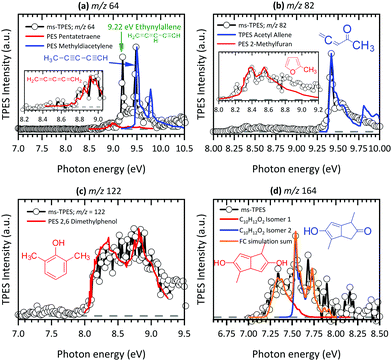 |
| | Fig. 6 Product species identification and assignment for C5–10 hydrocarbons and oxygenated hydrocarbons formed by pyrolysis of Al(C5H7O2)3 using TPE-spectra (black lines with circles); literature reference spectra (red and blue) as well as our FC simulations are as follows: (a) m/z 64 (C5H4)83–85 and (b) m/z 82 (C5H6O),65,90 (c) m/z 122 (C8H10O)92 and (d) m/z 164 (C10H12O2) (this work). | |
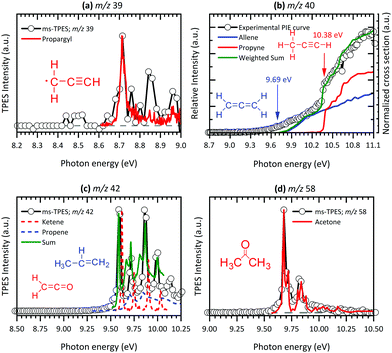
At 8.70 eV, a clear peak emerges in the TPES of m/z 39, which corresponds to the published ionization potential of the propargyl radical (IE = 8.70 eV,74 see Fig. 5(a)). The analysis of the m/z 42 ms-TPE spectrum in Fig. 5(c) shows a clear onset at 9.60 eV and confirmed that ketene (C2H2O) is the most abundant product that contributes to the m/z 42 channel (IE = 9.62 eV).21,24,77 Interestingly, propane (C3H6)78 was also observed in the spectrum. Strong evidence of a mixture of allene and propyne was found for the m/z 40 channel by comparing their photoionization spectra to reference cross sections,75 revealing a relative ratio of 1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 (Fig. 5(b)). As will be seen a number of times later, hot and sequence bands are responsible for the red shift of the ionization onset of allene to below 9.69 eV,76 due to the inefficient cooling in the molecular beam. Acetone (C3H6O) has been identified as a major pyrolysis product by its ionization energy threshold in the TPE spectrum shown in Fig. 5(d) with an onset at 9.69 eV.79 The most interesting result was observed for the m/z 64 channel in Fig. 6(a), where pentatetraene (IE = 8.99 eV)83 is unambiguously confirmed using a reference PES,83 in addition with the formation of its isomers ethynylallene (IE = 9.22 eV)84 and methyldiacetylene (IE = 9.50 eV).85 These pyrolysis products were not observed in previous studies,20,21,24 although their formation plays a significant role in the gas-phase decomposition of Al(C5H7O2)3. The existence of C5H6O among the pyrolysis products has been reported by others,21,24 whereas no unambiguous assignment has been proposed yet. Clear onsets in the ms-TPE spectra in Fig. 6(b) revealed that this channel can indeed be assigned to 2-methylfuran90 and acetylallene.65 Rhoten and DeVore24 proposed the formation of CH3C(O)CCCH3 based on FTIR data, which differs from our conclusion that acetyl allene is the dominant product in this mass channel. In contrast to earlier studies,21,24,98 we were able to detect hydrocarbon intermediates in the gas-phase, as well as the aluminium containing intermediate at m/z 224, thanks to the low residence time, the soft ionization method and molecular beam sampling preserving these intermediates. We found clear evidence for aromatic compounds among the pyrolysis products in the ms-TPE spectra. The most abundant was 2,6-dimethylphenol (C10H8O), identified by its clear onset at IE = 8.26 eV that fits the literature value92 well (see Fig. 6(c)). The second most abundant species has been detected in the m/z 164 channel and attributed to C10H12O2, which was proposed to be a 8-membered ring cyclic diketone in previous studies.21,23 By using FC simulations and G4 ionization energy calculations of possible isomers, we identified dimethyl-dihydroxo-dihydropentalene IEad(calc.) = 7.29 eV and its tautomer dimethyl-hydroxo-keto-tetrahydropentalene IEad(calc.) = 7.55 eV to be the major carrier of the ms-TPES in Fig. 6(d). Additionally, we newly found compounds at m/z 146, 186 and 210 as important pyrolysis products (see ESI:† Fig. S11). Since they have not been reported by others, the question arises whether these heavy species are gas-phase aluminium-containing intermediates or can be assigned to the group of aromatic compounds. To review the question, we first calculated ionization energies for possible aluminium-intermediates, namely Al(C4H5O2)(OH)2 (m/z 146), Al(C5H7O2)(C2H3O2) (m/z 186) and Al(C5H7O2)Al(C5H7O2)(C4H4O2) (m/z 210) with IE's of 9.15 eV, 5.25 eV and 5.25 eV, respectively. These do not match the recorded ms-TPE spectra in Fig. S11 (ESI†). Although the spectra for m/z 186 and 210 are rather weak, we can still identify a broad band in the 7–9 eV range, representative of a large molecular geometry change upon ionization. This in turn leads to unfavourable FC factors at the adiabatic ionization energy and a broad band in the threshold photoelectron spectrum. This is often the case for larger aromatic compounds studied in the literature.69 Possible matches were found for m/z 146, where at least three possible species, 2,4,6-trimethylstyrene, IE = 8.33 eV,94 benzocycloheptene, IE = 8.44 eV95 (C11H14), and 1,2-indanedione, IE = 8.8 eV96 (C9H6O2), may contribute to the spectrum (Fig. S11 (top), ESI†). Additionally, octahydroanthracene, IE = 7.86 eV97 (C14H18), and naphthaleneacetic acid, IE = 8.05 eV91 (C12H10O2), were identified in the m/z 186 channel, whereas other contributions remain unclear (see Fig. S11 (middle), ESI†). Thus, it is most likely that m/z 186 and 210 (Fig. S11 (bottom), ESI†) can also be assigned to aromatic hydrocarbons rather than to aluminium-containing intermediates.
1.0 (Fig. 5(b)). As will be seen a number of times later, hot and sequence bands are responsible for the red shift of the ionization onset of allene to below 9.69 eV,76 due to the inefficient cooling in the molecular beam. Acetone (C3H6O) has been identified as a major pyrolysis product by its ionization energy threshold in the TPE spectrum shown in Fig. 5(d) with an onset at 9.69 eV.79 The most interesting result was observed for the m/z 64 channel in Fig. 6(a), where pentatetraene (IE = 8.99 eV)83 is unambiguously confirmed using a reference PES,83 in addition with the formation of its isomers ethynylallene (IE = 9.22 eV)84 and methyldiacetylene (IE = 9.50 eV).85 These pyrolysis products were not observed in previous studies,20,21,24 although their formation plays a significant role in the gas-phase decomposition of Al(C5H7O2)3. The existence of C5H6O among the pyrolysis products has been reported by others,21,24 whereas no unambiguous assignment has been proposed yet. Clear onsets in the ms-TPE spectra in Fig. 6(b) revealed that this channel can indeed be assigned to 2-methylfuran90 and acetylallene.65 Rhoten and DeVore24 proposed the formation of CH3C(O)CCCH3 based on FTIR data, which differs from our conclusion that acetyl allene is the dominant product in this mass channel. In contrast to earlier studies,21,24,98 we were able to detect hydrocarbon intermediates in the gas-phase, as well as the aluminium containing intermediate at m/z 224, thanks to the low residence time, the soft ionization method and molecular beam sampling preserving these intermediates. We found clear evidence for aromatic compounds among the pyrolysis products in the ms-TPE spectra. The most abundant was 2,6-dimethylphenol (C10H8O), identified by its clear onset at IE = 8.26 eV that fits the literature value92 well (see Fig. 6(c)). The second most abundant species has been detected in the m/z 164 channel and attributed to C10H12O2, which was proposed to be a 8-membered ring cyclic diketone in previous studies.21,23 By using FC simulations and G4 ionization energy calculations of possible isomers, we identified dimethyl-dihydroxo-dihydropentalene IEad(calc.) = 7.29 eV and its tautomer dimethyl-hydroxo-keto-tetrahydropentalene IEad(calc.) = 7.55 eV to be the major carrier of the ms-TPES in Fig. 6(d). Additionally, we newly found compounds at m/z 146, 186 and 210 as important pyrolysis products (see ESI:† Fig. S11). Since they have not been reported by others, the question arises whether these heavy species are gas-phase aluminium-containing intermediates or can be assigned to the group of aromatic compounds. To review the question, we first calculated ionization energies for possible aluminium-intermediates, namely Al(C4H5O2)(OH)2 (m/z 146), Al(C5H7O2)(C2H3O2) (m/z 186) and Al(C5H7O2)Al(C5H7O2)(C4H4O2) (m/z 210) with IE's of 9.15 eV, 5.25 eV and 5.25 eV, respectively. These do not match the recorded ms-TPE spectra in Fig. S11 (ESI†). Although the spectra for m/z 186 and 210 are rather weak, we can still identify a broad band in the 7–9 eV range, representative of a large molecular geometry change upon ionization. This in turn leads to unfavourable FC factors at the adiabatic ionization energy and a broad band in the threshold photoelectron spectrum. This is often the case for larger aromatic compounds studied in the literature.69 Possible matches were found for m/z 146, where at least three possible species, 2,4,6-trimethylstyrene, IE = 8.33 eV,94 benzocycloheptene, IE = 8.44 eV95 (C11H14), and 1,2-indanedione, IE = 8.8 eV96 (C9H6O2), may contribute to the spectrum (Fig. S11 (top), ESI†). Additionally, octahydroanthracene, IE = 7.86 eV97 (C14H18), and naphthaleneacetic acid, IE = 8.05 eV91 (C12H10O2), were identified in the m/z 186 channel, whereas other contributions remain unclear (see Fig. S11 (middle), ESI†). Thus, it is most likely that m/z 186 and 210 (Fig. S11 (bottom), ESI†) can also be assigned to aromatic hydrocarbons rather than to aluminium-containing intermediates.
3.5 DPI of pyrolysis products
Earlier studies21,24 reported m/z 100 to be a primary decomposition product upon thermal decomposition of Al(C5H7O2)3. In contrast, we observe just small quantities of acetylacetone in the gas-phase. As we already pointed out, most of the signal attributed to m/z 100 at room temperature (300 K) is due to impurities in the sample. At higher temperatures, acetylacetone tends to shift its equilibrium to the diketo side, with having m/z 43 as major fragment upon photoionization (see S5 in the ESI†).65 Nevertheless this does not explain the majority of the large ion signal at m/z 43 upon pyrolysis that we observe in this study, since the abundance of C5H8O2 is relatively low at pyrolysis temperatures. As can be seen in Fig. S12 of the ESI† (right), most of this channel indeed corresponds to a DPI product according to its broad velocity distribution perpendicular to the molecular beam propagation axis in the VMI at 738 K. The major dissociative photoionization product of acetone, another expected pyrolysis product,21 at energies higher than 10.3 eV is m/z 43 by the loss of a methyl radical to form C2H3O+.79,99 Because of the hot pyrolysis products, a significant red shift in the appearance of the m/z 43 fragment ion is to be expected.67 These findings are considered in the temperature-dependent species profiles, discussed later in this study.
3.6 Primary decomposition pathways
We now compare relative product signal intensities upon pyrolysis as a function of temperature, to understand the reaction mechanism. Now, the ionization photon energy for each temperature scan is selected to rule out or minimize possible DPI contributions and capture pyrolysis products close to their ionization thresholds. We calculated the centreline temperature by CFD calculations of the flow field (see Section 3.7). Temperature-dependent species profiles form the pyrolysis of Al(C5H7O2)3 between 325 and 923 K are shown in Fig. 7 and 8. The precursor signal, as well as its primary gas-phase decomposition product m/z 224, Al(C5H7O2)C5H6O2, are shown on the top, to better understand the decomposition steps. Note that the fractional abundances may not reflect the absolute mole fractions, as the underlying intensities are not scaled by the absolute ionization cross sections, which are unknown for most of the detected species. This especially holds true for reactive intermediates in the gas-phase, as for instance Al-containing species. Nevertheless, the apparent trends provide hints regarding the decomposition mechanism, summarized in Scheme 1. Considering the temperature dependence of the dissociative ionization, no signals, other than the ones belonging to the precursor were observed up to ca. 450 K, indicating thermal stability of the sample. In the view of the isomer-resolved species characterization and the temperature-dependent mass spectra, three major thermal dissociation channels can be established for Al(C5H7O2)3 at temperatures >450 K (see Scheme 1):
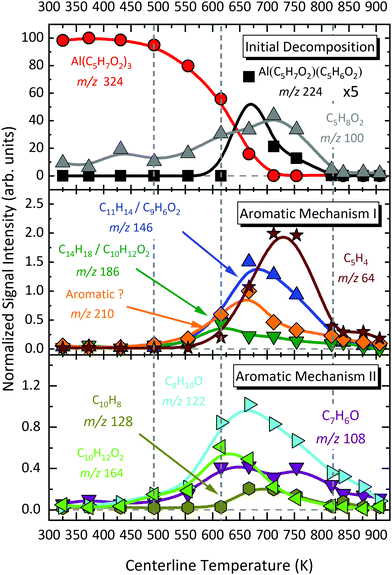 |
| | Fig. 7 Temperature-dependent species profile of aromatic hydrocarbons and oxygenated species detected as products of Al(C5H7O2)3 pyrolysis, which are labelled by their assignment based on ms-TPE spectra. | |
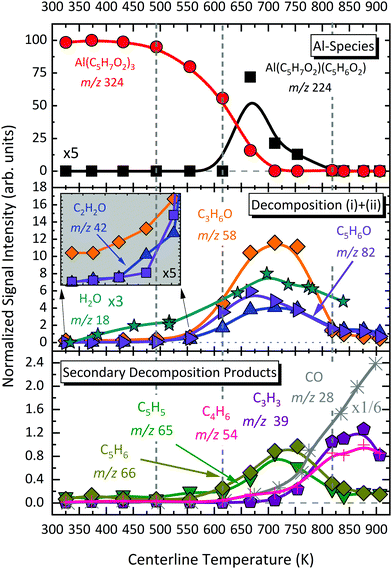 |
| | Fig. 8 Temperature-dependent species profiles of primary and secondary decomposition products, labelled by their assigned species based on ms-TPES and mechanistic analysis. | |
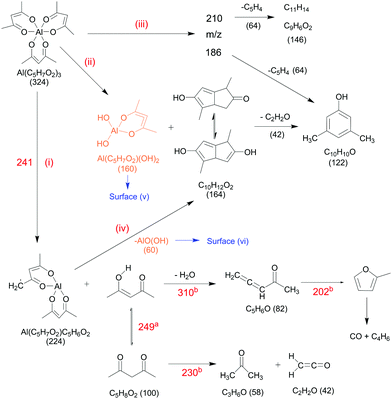 |
| | Scheme 1 Proposed primary thermal dissociation mechanism of Al(C5H7O2)3 in the gas-phase on the basis of the i2PEPICO analysis. Calculated values for the activation energies are denoted in red and are partially taken form aAntonov et al.48 and bRussel et al.77 | |
(i) Direct decomposition.
Unimolecular decomposition to yield aluminium bis(diketo)acetylacetonate-H, Al(C5H7O2)C5H6O2 and acetylacetone (C5H8O2), according to:| | | Al(C5H7O2)3 → Al(C5H7O2)(C5H6O2) + C5H8O2. | (i) |
The temperature-dependent species profiles in Fig. 7 and 8 confirm this to be the major decomposition pathway in the gas-phase, at least for temperatures above 600 K, where m/z 224 is detectable. Due to its major contribution to the mass spectra (see Fig. 3), DFT calculations were carried out to rationalize the reaction pathway (see Fig. 9). A hydrogen transfer (TS1 at 2.50 eV) from the CH3 group of the axial/equatorial acetylacetonate ligand to the second axial/equatorial one initiates the reaction, while a metal–oxygen bond is cleaved. This leads to a bound intermediate at 2.08 eV relative to the precursor with five Al–O bonds (INT1). INT1 is only shallowly bound and breaking the second Al–O bond leads to m/z 224 aluminium bis(diketo)acetylacetonate-H, Al(C5H7O2)C5H6O2 and acetylacetone (m/z 100). Our calculations show that the unimolecular decomposition is endothermic with a computed energy of 2.28 eV (FS). In contrast, the direct loss of an acetylacetonate (C5H7O2) radical would require an activation energy of 4.82 eV and is thus deemed unlikely to occur. The H-transfer mechanism is further supported by the steady rise in the acetylacetone signal, which was obtained by summing the ion signals at m/z 100, 72, and 85, the latter two being the dissociative photoionization signals belonging to its diketo and enol tautomers. Thus, channel (i) is the dominant primary decomposition step. Two pathways may produce m/z 82 (acetyl allene, CH2CCHC(O)CH3). First, a dehydration of Al(C5H7O2)3 with C–O bond cleavage in one ligand yielding aluminium bis(diketo)acetylacetonate-H and acetyl allene (CH2CCHC(O)CH3). Second, water elimination from the enol-tautomer of acetylacetone produces acetyl allene, which may also contribute to the m/z 82 signal. This was computed by Antonov et al. to require a barrier of 3.82 or 4.05 eV.65 According to an infrared laser pyrolysis study of acetylacetone by Russel et al.,100 acetylallene may react further at 202 kJ mol−1 by a 1,2-hydrogen shift and simultaneous cyclization to produce 2-methylfuran. This leads to the assumption that both products are due to sequential reactions of acetylacetone at higher temperatures, as also observed in our study, rather than being primary decomposition products of aluminium acetylacetonate. This observation most likely also applies to the formation of ketene (C2H2O) and acetone (C3H6O) at higher temperatures, which may be formed in an intramolecular process by further unimolecular decomposition of the liberated ligand through C–C bond cleavage and H-atom transfer with a calculated activation barrier of 230 kJ mol−1.100 Both products are also observed at relatively low temperatures starting from a centreline temperature of 450 K, where we observe a decrease in precursor signal intensity. In this temperature regime, they may be formed by surface rather than gas-phase reactions. Therefore, we conclude that this channel corresponds to a sequential decomposition step at high temperatures above 600 K, since we observe acetylacetone represented by its fragments m/z 72 and m/z 85 at those temperatures in the gas-phase.
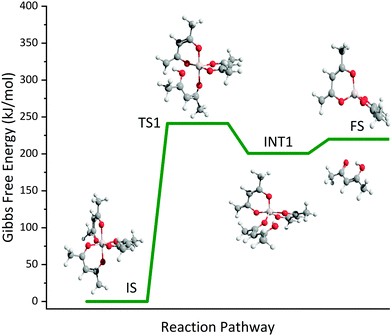 |
| | Fig. 9 Potential energy surface of the unimolecular decomposition of Al(C5H7O2)3 at CBS-QB3 level of theory. | |
(ii) Aromatic pathway I.
The species profile of m/z 164 shows that the signal intensity of the cyclic diketone C10H12O2 is non-zero even when the precursor exhibits full conversion. Indeed, we found evidence that, in contrast to previous findings by Bykov et al.,21 the formation of a cyclic diketone cannot be solely attributed to the decomposition of the trivalent Al precursor to form m/z 164 (C10H12O2)21 and possible surface reactions of the precursor.98 Additionally, Bykov and colleagues proposed a second channel for the formation of m/z 164 by a dimerization reaction of m/z 82 (C5H6O).21 Since the precursor is heavily diluted (<0.1%) in our experiment, we consider it as rather unlikely that bimolecular chemistry plays a major role in the decomposition mechanism under the prevailing conditions. Furthermore, we did not find a connection between the gas-phase concentration of the precursor and the peak intensity at m/z 164. We also tested the influence of possible surface reactions of two adjacent Al(C5H7O2)3 molecules as proposed by Igumenov98 that may also lead to a formation of m/z 164 (see S6 of the ESI†). Since surface reactions may play a role in the investigated system, we evaluated the diffusion length, i.e., the root mean square (rms) displacement along the radial direction of an arbitrary Al(C5H7O2)3 molecule inside the reactor to be below 0.04 mm in the whole temperature range. Considering that the reactor diameter is 1 mm, thus, much larger, we assume that wall reactions will play at most a minor role, but they cannot be completely ruled out (see also Fig. S5, ESI†). We estimate that ca. 8–20% of the gas-phase molecules will get in contact with the surface, and larger conversions must be due to gas-phase reactions, as observed starting at ca. 550–600 K. For temperatures below this threshold, our findings substantiate the proposed mechanism by Bykov et al.,21 shown as channel (ii) in Scheme 1:| | | Al(C5H7O2)3 → Al(C5H7O2)(OH)2 + C10H12O2. | (ii) |
Only traces of the gas-phase intermediate m/z 160 were detected in our study, likely corresponding to Al(C5H7O2)(OH)2.21 This supports the proposition of Igumenov et al.98 that this species is almost completely adsorbed on the surface (i.e., in our microreactor) and subsequently reacts at higher temperatures according to:| | | 2Al(C5H7O2)(OH)2 → Al2O3 + C5H6O + 3H2O + CO, | (v) |
leading to various organic products and radicals, as also observed here. Since CO is only detected at temperatures above 700 K in significant amounts, the activation barrier for surface reaction (v) appears to be higher than that of the decomposition reaction to form m/z 164. Our data reveal that this species may additionally be formed during the thermally activated decomposition of Al(C5H7O2)C5H6O2, m/z 224, at temperatures higher than 675 K according to channel (iv). This is supported by the increasing H2O signal correlating with depleting m/z 224 signal, because water is a product of the surface reaction (vi):| | | 2AlO(OH) → Al2O3 + H2O | (vi) |
(iii) Aromatic pathway II.
At temperatures above 500 K, where the decomposition of the parent molecule becomes evident, the signal at m/z 210 exhibits a small increase (see Fig. 8). By further heating the reactor to temperatures above 550 K, the signal intensity increases further, while the precursor m/z 324 has its steepest descent. This may identify m/z 324 as possible source of m/z 210. For further clarification, we tracked the ion intensity as a function of temperature and saw that, in a secondary decomposition step, m/z 210 may lose m/z 64 (C5H4) to form C11H14 or C9H6O2 (m/z 146), assigned in Fig. S11 of the ESI.† This correlates with the simultaneous increase of m/z 15, 64, and 146 signal intensities while m/z 210 attenuates. We therefore assume that m/z 210 is likely a C16H18 or C14H10O2 isomer.
In contrast to the aforementioned species, the convoluted signal of at least two species in the m/z 186 channel, C12H10O2 and C14H18 (see Fig. S8, ESI†) exhibits an earlier maximum at approximately 650 K. This supports the idea that this gas-phase product may predominantly be formed from the parent molecule. Nevertheless, its intensity is non-zero at complete conversion of Al(C5H7O2)3. At temperatures higher than 650 K, C14H18 may further decompose and contribute to the m/z 146 channel by the loss of C3H4 to form C11H14 (m/z 146). The species profiles in Fig. 7 also show evidence for an alternative reaction pathway upon the loss of ketene (C2H2O) to form m/z 144, C10H8O. This pathway seems to have a higher activation barrier, since it is mainly observed at temperatures higher than 600 K. In addition, an oxygenated hydrocarbon at m/z 146 (C10H10O) may additionally be formed by the dehydration of m/z 164, C10H12O2. This is supported by the increase of the H2O signal intensity at temperatures around 650 K, whereas the amount of m/z 164 decreases simultaneously.
3.7 Flow conditions in the microreactor
Since the flow inside the microreactor is accelerated by the large pressure difference, the temperature profile differs from the ideal “plug-flow” characteristics. The upper part of Fig. 10 shows three contour plots of the temperature profile along the reactor centreline, as modelled by CFD. Starting at low temperatures of 423 K, where heat transfer is fast enough, we observe a relatively small temperature difference across the reactor length. Nevertheless, even at such low surface temperatures, the centreline temperature at x = 8.5 mm differs by ca. 43 K (10.3%) from the recorded surface temperature. This effect becomes more apparent, when the surface temperature is increased to 553 K (54 K, 9.8%) and 673 K (65 K, 9.7%) (see bottom of Fig. 10). The temperature gradient becomes smaller closer to the exit of the reactor starting at a reactor length of above ca. 5 mm. This spot, where most of the chemical reactions occur, has also been reported by Guan et al.43 The temperature deviation within this area is only about 6–10% depending on the applied surface temperature. Since this area is relatively small and, as seen in Fig. 11, the temperature dependent axial velocity is relatively high at 225–400 m s−1, a small residence time of 25–46 μs is achieved in the heated section of the reactor. This is beneficial for the suppression of bimolecular reactions and helps to isolate reactive intermediates.
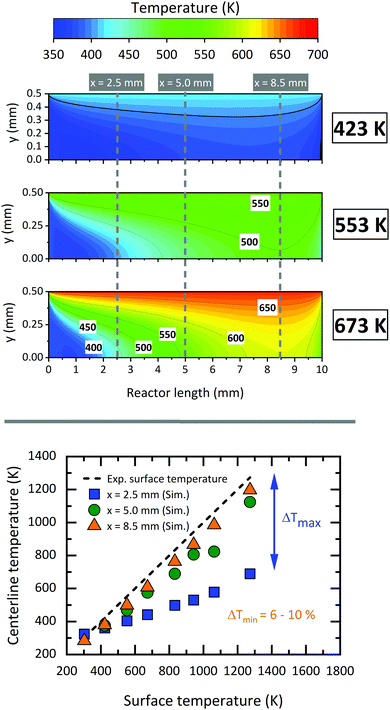 |
| | Fig. 10 Top: Contour plots of the reactor temperature obtained from the numerical calculations; bottom: centreline temperature as a function of the measured surface temperature 2.5 mm (blue squares), 5.0 mm (green dots) and 8.5 mm (orange triangles) from the beginning of the heated part. The maximum deviation between the centreline and the surface temperature is >500 K at the inlet of the reactor. | |
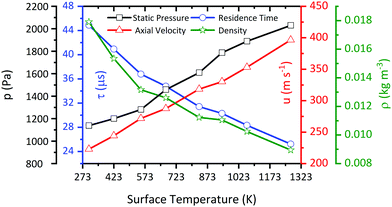 |
| | Fig. 11 Calculated pressure, velocity, and density at the midpoint (x = 5 mm) of the reactor as a function of pyrolysis temperature, along with the residence time in the pyrolysis zone from x = 5 to 10 mm at an inlet nozzle pressure of 1.6 bar. | |
3.8 Kinetics of the primary dissociation step
Supported by the modelling of the flow field, we were able to determine the residence times, temperatures, and pressure more accurately inside the microreactor (see Fig. 11). This enabled us to relate the mole fraction profile (see Fig. 12; left) for m/z 324, Al(C5H7O2)3 to the centreline temperature. Invoking the information from CFD, a reasonable Arrhenius plot was derived for the pyrolysis of Al(C5H7O2)3 as presented in Fig. 12 (right). The data evaluation was described above, the measured mole fractions at different temperatures and reaction times were used to fit the parameters of eqn (7), in order to derive both activation energies and pre-exponential factors. We also included the scaled signals at mass 224 as primary product from the gas-phase (grey dots, Fig. 12). At temperatures below 650 K, the signal stems, as discussed above, from contributions at m/z = 224 and 225, which could not be deconvoluted. Thus, for the lower temperatures only an upper limit can be given; they are marked as grey error bars. The Arrhenius plot can be understood as a sum of two reaction rates with different activation energies; both have an equivalent rate at 492 K. The fit to the data for the whole temperature range (green curve), with an activation energy of Ea,s = 14 ± 9 kJ mol−1 and a pre-exponential factor of A0,s = 3.7 × 103 s−1 is obtained for the low temperature region (red curve). One should note that the variance of the kinetic constants is quite high, because of the limited number of points that could be measured at the low temperature range, where the reaction rate is low. At higher conversion and higher temperature, a larger activation energy is observed with Ea,g = 57 ± 4 kJ mol−1 and a pre-exponential factor of A0,g = 2.4 × 108 s−1 (blue curve), respectively. This is also the temperature regime where aluminium containing intermediates are detected. At these high temperatures, the depletion of Al(C5H7O2)3 is dominated by gas-phase reactions, because they get faster, and dominate ktot as seen on the right side of Fig. 12. It is further very unlikely that alumina, formed at the surface, evaporates again, thus, aluminium products detected at higher temperatures are expected to be formed directly in the gas-phase rather than in surface reactions. Earlier experimental determinations of the kinetic rate constants range between 68.6–100 kJ mol−1 from EI-TOF23 as well as FTIR24 and static very low pressure pyrolysis studies.20 The high temperature regime activation energy is near to the value of ca. 68.1 kJ mol−1, as obtained by Tsyganova et al.23 They quoted the existence of a surface reaction regime and reported Langmuir-surface catalysed kinetics for Al(C5H7O2)3 which is, per se, first order at low partial pressures of the precursor.23 This is additionally indicating that surface reactions may have been of some importance here. Our interpretation is that surface reactions dominate the low temperature regime up to 492 K, where the conversion is low, as is the activation energy with 14 ± 9 kJ mol−1. The value by Tsyganova et al. agrees well with our higher temperature result of 57 ± 4 kJ mol−1, which we attribute to gas-phase kinetics. In contrast, earlier works by DeVore24 and Minkina20 quote values of ca. 100 kJ mol−1 using a static system and mass spectrometry. Bykov et al. also reported a lower value, 83.8 kJ mol−1,21 utilizing EI-mass spectrometry. However, those previous studies only consider the global reaction pathway because none of them detected all of the intermediates observed herein, including the major gas-phase intermediate at m/z 224. Additionally, they suffered from a high degree of fragmentation due to hard ionization, precursor loss in the analysis column, or product loss in the reactor. This may have led to a convolution of fragment and product ion signals or signal loss and therefore a possible bias in the determination of the kinetic constants. Notwithstanding the limitations of the kinetic analyses reported previously as well as in our approach herein, the good agreement with literature results, albeit contingent on a few reasonable assumptions, illustrates that the process of CFD flow field modelling of microreactors to derive reaction kinetics data, is reasonable.
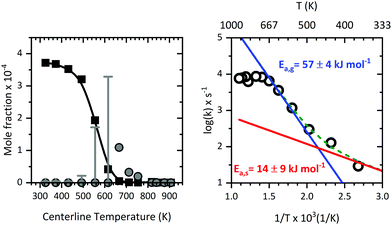 |
| | Fig. 12 Left: Mole fraction profile (b-spline: black curve, data: squares) of Al(C5H7O2)3 and a scaled relative profile of m/z 224 (grey dots) together with a convoluted profile of m/z 224/225 at temperatures below 650 K (grey error bars), obtained with aid of CFD modelling at a computed average pressure of 1600 Pa and residence times from 25 to 45 μs. Right: Arrhenius plot (fit: coloured curves, data: circles) derived for the decomposition of Al(C5H7O2)3. The apparent activation energy for each temperature region is given next to the plot. | |
4. Conclusion
We have investigated the pyrolysis of Al(C5H7O2)3 in the temperature range of 325–1278 K by flash vacuum pyrolysis using tuneable VUV photoionization and double imaging photoelectron photoion coincidence (i2PEPICO) spectroscopy, to detect and unambiguously identify pyrolysis intermediates and products. Studying the decomposition mechanism with a combined experimental and numerical approach provided unique insights into the decomposition mechanism of Al(C5H7O2)3. Temperature-dependent photoionization and ms-TPE spectra of the precursor enabled us to distinguish between soft, fragmentation free ionization of neutrals and dissociative ionization of heavier species yielding fragments at the same m/z in the temperature-dependent species profiles. Our investigations of the photoion mass-selected threshold photoelectron spectra provided new mechanistic insights, while confirming some conclusions of previous studies. First, considerable progress has been made in the detection and characterization of aluminium-containing gas-phase intermediates. The primary decomposition pathway is revised, because the loss of H2O and C5H6O is energetically unfavourable. Indeed, we found that the formation of a major aluminium-containing intermediate, Al(C5H7O2)C5H6O2 and acetylacetone is the primary decomposition step in the gas-phase. Possible pathways (i) for its initial formation and further secondary decomposition were proposed, based on the temperature-dependent species profiles. Especially the proposed surface reaction pathways (v–vi) characterize the inherited intermediate species as the true precursors, directly responsible for the desired film growth in thin film applications. Second, we confirmed the first aromatic decomposition step (ii), already proposed in the literature.21 Additionally, besides the formation of already detected aromatic hydrocarbons, e.g., dimethylphenol and m/z 164, we point out that a third pathway (iii) may lead to the formation of additional aromatic hydrocarbons, notably at m/z 146, 186 and 210. At low temperatures, these may be formed in surface reactions, but we could also identify a homogeneous gas-phase reaction as a likely source of m/z 164 (C10H12O2) at higher temperatures.
In contrast to previous studies, we were able to identify various species and isomers for the first time, such as C5H4, C3H3 and C3H4, which are considered secondary reaction products. We were also able to assign acetylallene (m/z 82), facilitating the development of a complete reaction mechanism. Additionally, this mechanism may help understand possible nucleation and particle formation temperature thresholds and pathways, leading to unwanted particle contamination and, consequently, a decrease in film growth rate.9
By utilizing the gas expansion factor, it was possible to calculate mole fraction profiles, based on the vapor pressure derived inlet concentration of the precursor molecule. With the aid of a numerical simulation of the microreactor, we obtained residence times and temperature profiles, opening the way to estimate kinetic parameters, such as the activation energy. For the unimolecular decomposition, our experimental data predicts the overall rate constant in quite good agreement with the literature values. This shows the feasibility of numerical flow field modelling to aid the interpretation of experimental results in complex environments. Nevertheless, there is still some discrepancy between the experimental and calculated values for the newly proposed aluminium intermediate pathway (i). A major source of uncertainty is the inlet mole fraction, which was only calculated based on literature vapor pressure data and not measured directly. Second, we were not able to record smaller temperature increments to better resolve the linear regions, especially the one at low temperature in Fig. 12. Third, although the loss of precursor through wall reactions is expected to be small, it still contributes at lower temperatures, below 492 K, to the conversion of Al(C5H7O2)3. The importance of surface reactions at these temperatures is mainly concluded from the absence of Al-containing intermediates and from the low activation energy. At higher temperatures, gas-phase reactions clearly dominate and an Al-containing intermediate is detected, together with an increase of the observed activation energy to 57 ± 4 kJ mol−1. The contribution of surface reactions may explain some of the difference between the experimental and calculated values. The combination of state-of-the-art mass spectrometric detection methods with mild photoionization as well as quantum chemical and CFD calculations represents a promising way to tackle the kinetics of organometallic compounds in the gas-phase, as demonstrated here for one archetypical aluminium precursor.
Author contributions
S. Grimm: investigation, formal analysis, visualization, writing – original draft; S.-J. Baik: methodology, investigation, software, writing – review & editing; P. Hemberger: investigation, resources, writing – review & editing; A. Bodi: investigation, resources, writing – review & editing; A. Kempf: methodology, supervision, writing – review & editing, project administration, funding acquisition. T. Kasper: conceptualization, methodology, supervision, project administration, funding acquisition; B. Atakan: conceptualization, methodology, supervision, writing – review & editing, project administration, funding acquisition.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors BA, TK and SG gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft DFG under contract 399583933. We thank Sascha Lau Dennis Kaczmarek and Thomas Bierkandt for their help during the measurement campaign. The measurements have been performed at the VUV beamline of the Swiss Light Source, at the Paul Scherrer Institute in Villigen (Switzerland).
References
- Z. Li, Y. Xin, Y. Liu, H. Liu, D. Yu and J. Xiu, Coatings, 2021, 11(4), 389 CrossRef CAS
 .
.
- J. Cui, M. G. Kast, B. A. Hammann, Y. Afriyie, K. N. Woods, P. N. Plassmeyer, C. K. Perkins, Z. L. Ma, D. A. Keszler, C. J. Page, S. W. Boettcher and S. E. Hayes, Chem. Mater., 2018, 30(21), 7456 CrossRef CAS
 .
.
- J. S. Pérez, F. J. López and E. S. Pérez, JART, 2020, 18(3), 95–100 Search PubMed
 .
.
- S. Zhang, L. Zheng, G. Wei, L. Guo, J. Li, R. Tu, L. Zhang, T. Goto and H. Ohmori, Int. J. Appl. Ceram. Technol., 2019, 16(4), 1356 CrossRef CAS
 .
.
- A. Michau, Y. Gazal, F. Addou, F. Maury, T. Duguet, R. Boichot, M. Pons, E. Monsifrot, H. Maskrot and F. Schuster, Surf. Coat. Technol., 2019, 375, 894 CrossRef CAS
 .
.
- D. Samelor, L. Baggetto, R. Laloo, V. Turq, T. Duguet, D. Monceau and C. Vahlas, Mater. Sci. Forum, 2018, 941, 1846 Search PubMed
 .
.
- R. Tu, Y. Yuan, L. Guo, J. Li, S. Zhang, M. Yang, Q. Li, L. Zhang, T. Goto, H. Ohmori, J. Shi and H. Li, Int. J. Appl. Ceram. Technol., 2019, 16(6), 2265 CrossRef CAS
 .
.
- S. Zhang, L. Zheng, G. Wei, L. Guo, J. Li, R. Tu, L. Zhang, T. Goto and H. Ohmori, Int. J. Appl. Ceram. Technol., 2019, 16(4), 1356 CrossRef CAS
 .
.
-
A. C. Jones and M. L. Hitchman, Chemical vapour deposition: Precursors, processes and applications, RSC Publishing, Cambridge, 2009 Search PubMed
 .
.
- L. G. Hubert-Pfalzgraf, Appl. Organomet. Chem., 1992, 6(8), 627 CrossRef CAS
 .
.
- M. Danzinger, R. Haubner and B. Lux, Int. J. Refract. Met. Hard Mater., 1996, 14(1–3), 59 CrossRef CAS
 .
.
- A. Devi, S. A. Shivashankar and A. G. Samuelson, J. Phys. IV, 2002, 12(4), 139 Search PubMed
 .
.
- C. Pflitsch, A. Muhsin, U. Bergmann and B. Atakan, Surf. Coat. Technol., 2006, 201(1–2), 73 CrossRef CAS
 .
.
- S. Li, D. He, X. Liu, S. Wang and L. Jiang, J. Nucl. Mater., 2012, 420(1–3), 405 CrossRef CAS
 .
.
- A. Ito, R. Tu and T. Goto, Surf. Coat. Technol., 2010, 204(14), 2170 CrossRef CAS
 .
.
- A. Nebatti, C. Pflitsch, B. Curdts and B. Atakan, Mater. Sci. Semicond. Process., 2015, 39, 467 CrossRef CAS
 .
.
- P. Rodriguez, B. Caussat, C. Ablitzer, X. Iltis and M. Brothier, Chem. Eng. Res. Des., 2013, 91(12), 2477 CrossRef CAS
 .
.
- T. Goto, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2016, 31(1), 1 CrossRef CAS
 .
.
- F. A. D. Battaglin, E. S. Prado, L. Caseli, T.F.d. Silva, M. H. Tabacniks, N. C. D. Cruz and E. C. Rangel, Mater. Res., 2017, 20(4), 926 CrossRef CAS
 .
.
- V. G. Minkina, Inorg. Mater., 1993, 29(11), 1400 Search PubMed
 .
.
- A. F. Bykov, A. E. Turgambaeva, I. K. Igumenov and P. P. Semyannikov, J. Phys. IV, 1995, 5(C5), C5-191 CrossRef
 .
.
- J. V. Hoene, R. G. Charles and W. M. Hickam, J. Phys. Chem., 1958, 62(9), 1098 CrossRef
 .
.
- E. I. Tsyganova and L. M. Dyagileva, Russ. Chem. Rev., 1996, 65(4), 315 CrossRef
 .
.
- M. C. Rhoten and T. C. DeVore, Chem. Mater., 1997, 9(8), 1757 CrossRef CAS
 .
.
- N. Hansen, W. Li, M. E. Law, T. Kasper, P. R. Westmoreland, B. Yang, T. A. Cool and A. Lucassen, Phys. Chem. Chem. Phys., 2010, 12(38), 12112 RSC
 .
.
- D. Felsmann, K. Moshammer, J. Krüger, A. Lackner, A. Brockhinke, T. Kasper, T. Bierkandt, E. Akyildiz, N. Hansen, A. Lucassen, P. Oßwald, M. Köhler, G. A. Garcia, L. Nahon, P. Hemberger, A. Bodi, T. Gerber and K. Kohse-Höinghaus, Proc. Combust. Inst., 2015, 35(1), 779 CrossRef CAS
 .
.
- J. Pieper, S. Schmitt, C. Hemken, E. Davies, J. Wullenkord, A. Brockhinke, J. Krüger, G. A. Garcia, L. Nahon, A. Lucassen, W. Eisfeld and K. Kohse-Höinghaus, Z. Phys. Chem., 2018, 232(2), 153 CrossRef CAS
 .
.
- T. Wang, S. Li, B. Yang, C. Huang and Y. Li, J. Phys. Chem. B, 2007, 111(10), 2449 CrossRef CAS PubMed
 .
.
- T. Zhang, L. Zhang, X. Hong, K. Zhang, F. Qi, C. K. Law, T. Ye, P. Zhao and Y. Chen, Combust. Flame, 2009, 156(11), 2071 CrossRef CAS
 .
.
- P. Hemberger, J. A. van Bokhoven, J. Pérez-Ramírez and A. Bodi, Catal. Sci. Technol., 2020, 8, 110 Search PubMed
 .
.
- N. Bahlawane, P. A. Premkumar, Z. Tian, X. Hong, F. Qi and K. Kohse-Höinghaus, Chem. Mater., 2010, 22(1), 92 CrossRef CAS
 .
.
- Z. Zhang, Y. Pan, J. Yang, Z. Jiang and H. Fang, J. Cryst. Growth, 2017, 473, 6 CrossRef CAS
 .
.
- A. Bodi, P. Hemberger, D. L. Osborn and B. Sztáray, J. Phys. Chem. Lett., 2013, 4(17), 2948 CrossRef CAS
 .
.
- J. Bourgalais, Z. Gouid, O. Herbinet, G. A. Garcia, P. Arnoux, Z. Wang, L.-S. Tran, G. Vanhove, M. Hochlaf, L. Nahon and F. Battin-Leclerc, Phys. Chem. Chem. Phys., 2020, 22(3), 1222 RSC
 .
.
- M. Johnson, A. Bodi, L. Schulz and T. Gerber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 610(2), 597 CrossRef CAS
 .
.
- B. Sztáray, K. Voronova, K. G. Torma, K. J. Covert, A. Bodi, P. Hemberger, T. Gerber and D. L. Osborn, J. Chem. Phys., 2017, 147(1), 13944 CrossRef PubMed
 .
.
- A. Bodi, P. Hemberger, T. Gerber and B. Sztáray, Rev. Sci. Instrum., 2012, 83(8), 83105 CrossRef PubMed
 .
.
- P. Chen, S. D. Colson, W. A. Chupka and J. A. Berson, J. Phys. Chem., 1986, 90(11), 2319 CrossRef CAS
 .
.
- D. W. Kohn, H. Clauberg and P. Chen, Rev. Sci. Instrum., 1992, 63(8), 4003 CrossRef CAS
 .
.
- D. W. Kohn, H. Clauberg and P. Chen, Rev. Sci. Instrum., 1992, 63(8), 4003 CrossRef CAS
 .
.
- J. Bouwman, H. R. Hrodmarsson, G. B. Ellison, A. Bodi and P. Hemberger, J. Phys. Chem. A, 2021, 125(8), 1738 CrossRef CAS PubMed
 .
.
- T. K. Ormond, A. M. Scheer, M. R. Nimlos, D. J. Robichaud, T. P. Troy, M. Ahmed, J. W. Daily, T. L. Nguyen, J. F. Stanton and G. B. Ellison, J. Phys. Chem. A, 2015, 119(28), 7222 CrossRef CAS PubMed
 .
.
- Q. Guan, K. N. Urness, T. K. Ormond, D. E. David, G. Barney Ellison and J. W. Daily, Int. Rev. Phys. Chem., 2014, 33(4), 447 Search PubMed
 .
.
- M. V. Zagidullin, R. I. Kaiser, D. P. Porfiriev, I. P. Zavershinskiy, M. Ahmed, V. N. Azyazov and A. M. Mebel, J. Phys. Chem. A, 2018, 122(45), 8819 CrossRef CAS PubMed
 .
.
- T. Baer and R. P. Tuckett, Phys. Chem. Chem. Phys., 2017, 19(15), 9698 RSC
 .
.
- B. Sztáray and T. Baer, Rev. Sci. Instrum., 2003, 74(8), 3763 CrossRef
 .
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, 2016 Search PubMed
 .
.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112(15), 6532 CrossRef CAS
 .
.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126(8), 84108 CrossRef PubMed
 .
.
- C. Peng and H. Bernhard Schlegel, Isr. J. Chem., 1993, 33(4), 449 CrossRef CAS
 .
.
- T. Yu, X. Wu, X. Zhou, A. Bodi and P. Hemberger, Combust. Flame, 2020, 222, 123 CrossRef CAS
 .
.
-
V. A. Mozhayskiy and A. I. Krylov, ezSpectrum.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256(4–5), 454 CrossRef CAS
 .
.
- J. H. Baraban, D. E. David, G. B. Ellison and J. W. Daily, Rev. Sci. Instrum., 2016, 87(1), 14101 CrossRef CAS PubMed
 .
.
-
K. Huang, Statistical mechanics, New York, Wiley, 2nd edn, 1987 Search PubMed
 .
.
- Ansys® Academic Multiphysics, Release 19.1.
-
C. J. Geankoplis, Transport processes and unit operations, PTR Prentice Hall, Engelwood Cliffs, NJ, 3rd edn, 1993 Search PubMed
 .
.
- P. L. Roe, Annu. Rev. Fluid Mech., 1986, 18(1), 337 CrossRef
 .
.
- E. Bich, J. Millat and E. Vogel, J. Phys. Chem. Ref. Data, 1990, 19(6), 1289 CrossRef CAS
 .
.
- P. J. Weddle, C. Karakaya, H. Zhu, R. Sivaramakrishnan, K. Prozument and R. J. Kee, Int. J. Chem. Kinet., 2018, 50(7), 473 CrossRef CAS
 .
.
- T. Zhang, J. Wang, T. Yuan, X. Hong, L. Zhang and F. Qi, J. Phys. Chem. A, 2008, 112(42), 10487 CrossRef CAS PubMed
 .
.
- M. A. Siddiqi, R. A. Siddiqui and B. Atakan, Surf. Coat. Technol., 2007, 201(22–23), 9055 CrossRef CAS
 .
.
- A. Y. Ustinov, V. I. Vovna and O. M. Ustinova, J. Electron Spectrosc. Relat. Phenom., 1998, 88–91, 103 CrossRef CAS
 .
.
- M. J. Lacey and J. S. Shannon, Org. Mass Spectrom., 1972, 6(8), 931 CrossRef CAS
 .
.
- I. Antonov, K. Voronova, M.-W. Chen, B. Sztáray, P. Hemberger, A. Bodi, D. L. Osborn and L. Sheps, J. Phys. Chem. A, 2019, 123(26), 5472 CrossRef CAS PubMed
 .
.
- P. Hemberger, V. B. F. Custodis, A. Bodi, T. Gerber and J. A. van Bokhoven, Nat. Commun., 2017, 8, 15946 CrossRef PubMed
 .
.
- S. Liang, P. Hemberger, N. M. Neisius, A. Bodi, H. Grützmacher, J. Levalois-Grützmacher and S. Gaan, Chemistry, 2015, 21(3), 1073 CrossRef CAS PubMed
 .
.
- B. K. Cunha de Miranda, C. Alcaraz, M. Elhanine, B. Noller, P. Hemberger, I. Fischer, G. A. Garcia, H. Soldi-Lose, B. Gans, L. A. V. Mendes, S. Boyé-Péronne, S. Douin, J. Zabka and P. Botschwina, J. Phys. Chem. A, 2010, 114(14), 4818 CrossRef CAS PubMed
 .
.
-
NIST Chemistry WebBook, ed. P. J. Linstrom and W. G. Mallard, NIST Standard, Reference Database Number 69, National Institute of Standards and Technology, Gaithersburg MD, 20899, DOI:10.18434/T4D303, (retrieved June 29, 2021)
 .
.
- T. A. Cool, J. Wang, K. Nakajima, C. A. Taatjes and A. Mcllroy, Int. J. Mass Spectrom., 2005, 247(1–3), 18 CrossRef CAS
 .
.
- A. W. Potts and T. A. Williams, J. Electron Spectrosc. Relat. Phenom., 1974, 3(1), 3 CrossRef CAS
 .
.
- B. Niu, D. A. Shirley and Y. Bai, J. Chem. Phys., 1993, 98(6), 4377 CrossRef CAS
 .
.
- M. S. Banna and D. A. Shirley, J. Electron Spectrosc. Relat. Phenom., 1976, 8(4), 255 CrossRef CAS
 .
.
- P. Hemberger, M. Lang, B. Noller, I. Fischer, C. Alcaraz, B. K. Cunha de Miranda, G. A. Garcia and H. Soldi-Lose, J. Phys. Chem. A, 2011, 115(11), 2225 CrossRef CAS PubMed
 .
.
- Z. Z. Yang, L. S. Wang, Y. T. Lee, D. A. Shirley, S. Y. Huang and W. A. Lester, Chem. Phys. Lett., 1990, 171(1–2), 9 CrossRef CAS
 .
.
- J. Krüger, G. A. Garcia, D. Felsmann, K. Moshammer, A. Lackner, A. Brockhinke, L. Nahon and K. Kohse-Höinghaus, Phys. Chem. Chem. Phys., 2014, 16(41), 22791 RSC
 .
.
- B. Niu, Y. Bai and D. A. Shirley, J. Chem. Phys., 1993, 99(4), 2520 CrossRef CAS
 .
.
- G. Bieri, F. Burger, E. Heilbronner and J. P. Maier, Helv. Chim. Acta, 1977, 60(7), 2213 CrossRef CAS
 .
.
- E. E. Rennie, A.-M. Boulanger, P. M. Mayer, D. M. P. Holland, D. A. Shaw, L. Cooper and L. G. Shpinkova, J. Phys. Chem. A, 2006, 110(28), 8663 CrossRef CAS PubMed
 .
.
- G. Y. Matti, O. I. Osman, J. E. Upham, R. J. Suffolk and H. W. Kroto, J. Electron Spectrosc. Relat. Phenom., 1989, 49(2), 195 CrossRef CAS
 .
.
- A. J. Yencha, M. R. F. Siggel-King, G. C. King, A. E. R. Malins and M. Eypper, J. Electron Spectrosc. Relat. Phenom., 2013, 187, 65 CrossRef CAS
 .
.
- P. Masclet, G. Mouvier and J. F. Bocquet, J. Chim. Phys., 1981, 78, 99 CrossRef CAS
 .
.
- G. Bieri, J. D. Dill, E. Heilbronner, J. P. Maier and J. L. Ripoll, Helv. Chim. Acta, 1977, 60(2), 629 CrossRef CAS
 .
.
- N. Hansen, S. J. Klippenstein, J. A. Miller, J. Wang, T. A. Cool, M. E. Law, P. R. Westmoreland, T. Kasper and K. Kohse-Höinghaus, J. Phys. Chem. A, 2006, 110(13), 4376 CrossRef CAS PubMed
 .
.
- F. Brogli, E. Heilbronner, V. Hornung and E. Kloster-Jensen, Helv. Chim. Acta, 1973, 56(7), 2171 CrossRef
 .
.
- S. Soorkia, A. J. Trevitt, T. M. Selby, D. L. Osborn, C. A. Taatjes, K. R. Wilson and S. R. Leone, J. Phys. Chem. A, 2010, 114(9), 3340 CrossRef CAS PubMed
 .
.
- J. Bouwman, A. Bodi, J. Oomens and P. Hemberger, Phys. Chem. Chem. Phys., 2015, 17(32), 20508 RSC
 .
.
- M. Gerlach, A. Bodi and P. Hemberger, Phys. Chem. Chem. Phys., 2019, 21(35), 19480 RSC
 .
.
- P. Bischof, R. Gleiter, H. Hopf and F. T. Lenich, J. Am. Chem. Soc., 1975, 97(19), 5467 CrossRef CAS
 .
.
- T. Veszprémi, L. Nyulászi and J. Nagy, J. Organomet. Chem., 1987, 331(2), 175 CrossRef
 .
.
- L. Klasinc, B. Kovac and H. Gusten, Pure Appl. Chem., 1983, 55(2), 289 CAS
 .
.
- T. Kobayashi and S. Nagakura, Bull. Chem. Soc. Jpn., 1974, 47(10), 2563 CrossRef CAS
 .
.
- H. W. Jochims, H. Rasekh, E. Rühl, H. Baumgärtel and S. Leach, Chem. Phys., 1992, 168(1), 159 CrossRef CAS
 .
.
- T. Kobayashi, K. Yokota and S. Nagakura, J. Electron Spectrosc. Relat. Phenom., 1973, 2(5), 449 CrossRef CAS
 .
.
- J. P. Maier and D. W. Turner, J. Chem. Soc., Faraday Trans. 2, 1973, 69, 196 RSC
 .
.
- V. Galasso, F. P. Colonna and G. Distefano, J. Electron Spectrosc. Relat. Phenom., 1977, 10(3), 227 CrossRef CAS
 .
.
- M. Meot-Ner, J. Phys. Chem., 1980, 84(21), 2716 CrossRef CAS
 .
.
- I. K. Igumenov, A. E. Turgambaeva and P. P. Semyannikov, J. Phys. IV, 2001, 11(PR3), Pr3-505 Search PubMed
 .
.
- A. Bodi, T. Baer, N. K. Wells, D. Fakhoury, D. Klecyngier and J. P. Kercher, Phys. Chem. Chem. Phys., 2015, 17(43), 28505 RSC
 .
.
- D. K. Russell and A. Yee, New J. Chem., 2005, 29(3), 485 RSC
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00720c |
|
| This journal is © the Owner Societies 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Seung-Jin
Baik
*ab,
Seung-Jin
Baik
 bc,
Patrick
Hemberger
bc,
Patrick
Hemberger
 d,
Andras
Bodi
d,
Andras
Bodi
 d,
Andreas M.
Kempf
bc,
Tina
Kasper
be and
Burak
Atakan
d,
Andreas M.
Kempf
bc,
Tina
Kasper
be and
Burak
Atakan
 ab
ab
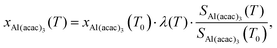
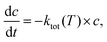

![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) +, and
+, and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) + states of Al(C5H7O2)C5H6O2+ at 8.2, 8.8 and 9.2 eV using B3LYP/6-311++G(d,p), which agrees with the observed features in the 723 K ms-TPE spectrum. Thus, we tentatively assign the m/z 224 peak to the Al(C5H7O2)C5H6O2 aluminium species. Following this argumentation, near-threshold photon energies of 8 eV will be used for the detection of Al(C5H7O2)3 and the primary decomposition product Al(C5H7O2)C5H6O2, respectively. This allows us to suppress the DPI interference with the pyrolysis products at higher temperatures.
+ states of Al(C5H7O2)C5H6O2+ at 8.2, 8.8 and 9.2 eV using B3LYP/6-311++G(d,p), which agrees with the observed features in the 723 K ms-TPE spectrum. Thus, we tentatively assign the m/z 224 peak to the Al(C5H7O2)C5H6O2 aluminium species. Following this argumentation, near-threshold photon energies of 8 eV will be used for the detection of Al(C5H7O2)3 and the primary decomposition product Al(C5H7O2)C5H6O2, respectively. This allows us to suppress the DPI interference with the pyrolysis products at higher temperatures.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.0 (Fig. 5(b)). As will be seen a number of times later, hot and sequence bands are responsible for the red shift of the ionization onset of allene to below 9.69 eV,76 due to the inefficient cooling in the molecular beam. Acetone (C3H6O) has been identified as a major pyrolysis product by its ionization energy threshold in the TPE spectrum shown in Fig. 5(d) with an onset at 9.69 eV.79 The most interesting result was observed for the m/z 64 channel in Fig. 6(a), where pentatetraene (IE = 8.99 eV)83 is unambiguously confirmed using a reference PES,83 in addition with the formation of its isomers ethynylallene (IE = 9.22 eV)84 and methyldiacetylene (IE = 9.50 eV).85 These pyrolysis products were not observed in previous studies,20,21,24 although their formation plays a significant role in the gas-phase decomposition of Al(C5H7O2)3. The existence of C5H6O among the pyrolysis products has been reported by others,21,24 whereas no unambiguous assignment has been proposed yet. Clear onsets in the ms-TPE spectra in Fig. 6(b) revealed that this channel can indeed be assigned to 2-methylfuran90 and acetylallene.65 Rhoten and DeVore24 proposed the formation of CH3C(O)CCCH3 based on FTIR data, which differs from our conclusion that acetyl allene is the dominant product in this mass channel. In contrast to earlier studies,21,24,98 we were able to detect hydrocarbon intermediates in the gas-phase, as well as the aluminium containing intermediate at m/z 224, thanks to the low residence time, the soft ionization method and molecular beam sampling preserving these intermediates. We found clear evidence for aromatic compounds among the pyrolysis products in the ms-TPE spectra. The most abundant was 2,6-dimethylphenol (C10H8O), identified by its clear onset at IE = 8.26 eV that fits the literature value92 well (see Fig. 6(c)). The second most abundant species has been detected in the m/z 164 channel and attributed to C10H12O2, which was proposed to be a 8-membered ring cyclic diketone in previous studies.21,23 By using FC simulations and G4 ionization energy calculations of possible isomers, we identified dimethyl-dihydroxo-dihydropentalene IEad(calc.) = 7.29 eV and its tautomer dimethyl-hydroxo-keto-tetrahydropentalene IEad(calc.) = 7.55 eV to be the major carrier of the ms-TPES in Fig. 6(d). Additionally, we newly found compounds at m/z 146, 186 and 210 as important pyrolysis products (see ESI:† Fig. S11). Since they have not been reported by others, the question arises whether these heavy species are gas-phase aluminium-containing intermediates or can be assigned to the group of aromatic compounds. To review the question, we first calculated ionization energies for possible aluminium-intermediates, namely Al(C4H5O2)(OH)2 (m/z 146), Al(C5H7O2)(C2H3O2) (m/z 186) and Al(C5H7O2)Al(C5H7O2)(C4H4O2) (m/z 210) with IE's of 9.15 eV, 5.25 eV and 5.25 eV, respectively. These do not match the recorded ms-TPE spectra in Fig. S11 (ESI†). Although the spectra for m/z 186 and 210 are rather weak, we can still identify a broad band in the 7–9 eV range, representative of a large molecular geometry change upon ionization. This in turn leads to unfavourable FC factors at the adiabatic ionization energy and a broad band in the threshold photoelectron spectrum. This is often the case for larger aromatic compounds studied in the literature.69 Possible matches were found for m/z 146, where at least three possible species, 2,4,6-trimethylstyrene, IE = 8.33 eV,94 benzocycloheptene, IE = 8.44 eV95 (C11H14), and 1,2-indanedione, IE = 8.8 eV96 (C9H6O2), may contribute to the spectrum (Fig. S11 (top), ESI†). Additionally, octahydroanthracene, IE = 7.86 eV97 (C14H18), and naphthaleneacetic acid, IE = 8.05 eV91 (C12H10O2), were identified in the m/z 186 channel, whereas other contributions remain unclear (see Fig. S11 (middle), ESI†). Thus, it is most likely that m/z 186 and 210 (Fig. S11 (bottom), ESI†) can also be assigned to aromatic hydrocarbons rather than to aluminium-containing intermediates.
1.0 (Fig. 5(b)). As will be seen a number of times later, hot and sequence bands are responsible for the red shift of the ionization onset of allene to below 9.69 eV,76 due to the inefficient cooling in the molecular beam. Acetone (C3H6O) has been identified as a major pyrolysis product by its ionization energy threshold in the TPE spectrum shown in Fig. 5(d) with an onset at 9.69 eV.79 The most interesting result was observed for the m/z 64 channel in Fig. 6(a), where pentatetraene (IE = 8.99 eV)83 is unambiguously confirmed using a reference PES,83 in addition with the formation of its isomers ethynylallene (IE = 9.22 eV)84 and methyldiacetylene (IE = 9.50 eV).85 These pyrolysis products were not observed in previous studies,20,21,24 although their formation plays a significant role in the gas-phase decomposition of Al(C5H7O2)3. The existence of C5H6O among the pyrolysis products has been reported by others,21,24 whereas no unambiguous assignment has been proposed yet. Clear onsets in the ms-TPE spectra in Fig. 6(b) revealed that this channel can indeed be assigned to 2-methylfuran90 and acetylallene.65 Rhoten and DeVore24 proposed the formation of CH3C(O)CCCH3 based on FTIR data, which differs from our conclusion that acetyl allene is the dominant product in this mass channel. In contrast to earlier studies,21,24,98 we were able to detect hydrocarbon intermediates in the gas-phase, as well as the aluminium containing intermediate at m/z 224, thanks to the low residence time, the soft ionization method and molecular beam sampling preserving these intermediates. We found clear evidence for aromatic compounds among the pyrolysis products in the ms-TPE spectra. The most abundant was 2,6-dimethylphenol (C10H8O), identified by its clear onset at IE = 8.26 eV that fits the literature value92 well (see Fig. 6(c)). The second most abundant species has been detected in the m/z 164 channel and attributed to C10H12O2, which was proposed to be a 8-membered ring cyclic diketone in previous studies.21,23 By using FC simulations and G4 ionization energy calculations of possible isomers, we identified dimethyl-dihydroxo-dihydropentalene IEad(calc.) = 7.29 eV and its tautomer dimethyl-hydroxo-keto-tetrahydropentalene IEad(calc.) = 7.55 eV to be the major carrier of the ms-TPES in Fig. 6(d). Additionally, we newly found compounds at m/z 146, 186 and 210 as important pyrolysis products (see ESI:† Fig. S11). Since they have not been reported by others, the question arises whether these heavy species are gas-phase aluminium-containing intermediates or can be assigned to the group of aromatic compounds. To review the question, we first calculated ionization energies for possible aluminium-intermediates, namely Al(C4H5O2)(OH)2 (m/z 146), Al(C5H7O2)(C2H3O2) (m/z 186) and Al(C5H7O2)Al(C5H7O2)(C4H4O2) (m/z 210) with IE's of 9.15 eV, 5.25 eV and 5.25 eV, respectively. These do not match the recorded ms-TPE spectra in Fig. S11 (ESI†). Although the spectra for m/z 186 and 210 are rather weak, we can still identify a broad band in the 7–9 eV range, representative of a large molecular geometry change upon ionization. This in turn leads to unfavourable FC factors at the adiabatic ionization energy and a broad band in the threshold photoelectron spectrum. This is often the case for larger aromatic compounds studied in the literature.69 Possible matches were found for m/z 146, where at least three possible species, 2,4,6-trimethylstyrene, IE = 8.33 eV,94 benzocycloheptene, IE = 8.44 eV95 (C11H14), and 1,2-indanedione, IE = 8.8 eV96 (C9H6O2), may contribute to the spectrum (Fig. S11 (top), ESI†). Additionally, octahydroanthracene, IE = 7.86 eV97 (C14H18), and naphthaleneacetic acid, IE = 8.05 eV91 (C12H10O2), were identified in the m/z 186 channel, whereas other contributions remain unclear (see Fig. S11 (middle), ESI†). Thus, it is most likely that m/z 186 and 210 (Fig. S11 (bottom), ESI†) can also be assigned to aromatic hydrocarbons rather than to aluminium-containing intermediates.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.








