Open Access Article
Open Access ArticleNon-uniform sampling in pulse dipolar spectroscopy by EPR: the redistribution of noise and the optimization of data acquisition†
Anna G.
Matveeva
 ab,
Victoria N.
Syryamina
ab,
Victoria N.
Syryamina
 c,
Vyacheslav M.
Nekrasov
c,
Vyacheslav M.
Nekrasov
 bc and
Michael K.
Bowman
bc and
Michael K.
Bowman
 *de
*de
aInstitute of Solid State Chemistry and Mechanochemistry of the Siberian Branch of the Russian Academy of Sciences, 630090 Novosibirsk, Russia
bNovosibirsk State University, 630090 Novosibirsk, Russia
cVoevodsky Institute of Chemical Kinetics and Combustion of the Siberian Branch of the Russian Academy of Sciences, 630090 Novosibirsk, Russia
dN. N. Vorozhtsov Novosibirsk Institute of Organic Chemistry of the Siberian Branch of the Russian Academy of Sciences, 630090 Novosibirsk, Russia
eDepartment of Chemistry & Biochemistry, The University of Alabama, Tuscaloosa, AL 35487, USA. E-mail: mkbowman@ua.edu
First published on 21st April 2021
Abstract
Pulse dipolar spectroscopy (PDS) in Electron Paramagnetic Resonance (EPR) is the method of choice for determining the distance distribution function for mono-, bi- or multi- spin-labeled macromolecules and nanostructures. PDS acquisition schemes conventionally use uniform sampling of the dipolar trace, but non-uniform sampling (NUS) schemes can decrease the total measurement time or increase the accuracy of the resulting distance distributions. NUS requires optimization of the data acquisition scheme, as well as changes in data processing algorithms to accommodate the non-uniformly sampled data. We investigate in silico the applicability of the NUS approach in PDS, considering its effect on random, truncation and sampling noise in the experimental data. Each type of noise in the time-domain data propagates differently and non-uniformly into the distance spectrum as errors in the distance distribution. NUS schemes seem to be a valid approach for increasing sensitivity and/or throughput in PDS by decreasing and redistributing noise in the distance spectrum so that it has less impact on the distance spectrum.
Introduction
Pulse dipolar spectroscopy (PDS) by Electron Paramagnetic Resonance (EPR) is a set of pulse EPR techniques with applications in a wide range of fields, e.g., polymers, biomacromolecules, biology and nanomaterials.1,2 A noteworthy feature of PDS is its ability to extract the distance distribution function between pairs of paramagnetic centers (PCs) with separations in the range of 1.5–16 nm. Many approaches have been described to extract the distance distribution.3–14 But no implementation is recognized as clearly superior; although the Tikhonov regularization method in DeerAnalysis5 is a convenient benchmark for comparisons.The PDS signal, denoted here as V(T), is also known as the dipolar trace or dipolar decay. In principle, it is the time domain lineshape of the dipolar interaction within pairs of PCs. The dipolar trace is measured by several PDS methods: PELDOR/DEER, DQC, SIFTER or RIDME. For isolated PC pairs having a distance distribution function P(r), the dipolar trace is usually written as a Fredholm integral of the first kind:2,15,16
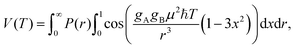 | (1) |
V(T) is easily calculated from the distance distribution P(r) viaeqn (1). However, the analysis of a PDS measurement requires the inverse: calculation of the distance distribution from an experimental measurement of the dipolar trace, and that presents a major difficulty. The inverse solution of the Fredholm integral in eqn (1) is well-known in mathematics as an ill-posed problem. According to the Hadamard criterion, this means that even a slight perturbation of the dipolar trace can produce a very different distance distribution.
Every experimental PDS measurement contains many perturbations, collectively known as noise s(T), arising for several reasons. For instance, there is the ‘random’ noise inherent in every physical measurement. Random noise can be reduced by signal averaging but can’t be eliminated. Also, every PDS measurement takes samples of the continuous dipolar trace only at discrete points, and only within a limited range of times T. This results in some loss of information. We will call this lost information ‘sampling’ and ‘truncation’ noise, respectively. There is also systematic ‘noise’ resulting from violations of assumptions underlying eqn (1) due to limitations of the sample or the spectrometer. Systematic noise will not be considered here. Unfortunately, ‘noise’ is used to refer to errors and defects in both the measured dipolar trace and in the distance distribution spectrum, which sometimes can be confusing.
In summary, PDS measurements do not yield V(T), but V(T) + s(T). Only part of s(T) is reproducible noise that can be measured independently and removed. So, instead of needing to invert eqn (1) to obtain P(r), PDS is faced with inverting
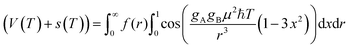 | (2) |
Even when the magnitude of s(T) is small compared to V(T), f(r) can be quite different from P(r). Frequently f(r) is not even physically reasonable. Consequently, most approaches for analyzing PDS data involve a step known as ‘regularization’ that encourages f(r) to have characteristics expected for P(r) and to give a dipolar trace ‘consistent’ with the experimental V(T) + s(T) data. Such strategy is very successful and widely used for experimental PDS data analysis. When successful, regularization results in a distance distribution consistent with some set of a priori expectations about P(r) while partially rejecting noise.
But the regularization is almost always based on f(r), which means the errors, i.e., noise, that propagate into the resulting distance spectrum depends on P(r).17 The noise and the distance distribution function become quite entangled. This regularization approach makes it difficult to understand how random noise affects experimental results because identical noise in the dipolar trace affects the distance spectrum differently for every different P(r). In effect, every sample becomes a special case that should be considered individually, making it difficult to make a generalization about the propagation of random noise into the distance spectrum without extensive arrays of simulations.
However, there is a Mellin Transform-based approach11 to PDS data analysis that implements the regularization somewhat differently. It tries to make the experimental dipolar trace ‘reasonable’ according to eqn (1) in a way that affects only the noise s(r), independent of P(r) of V(T). This uncouples the noise and the distance distribution function in data analysis, making it much easier to study the propagation of noise. Each individual realization of noise in the experimental dipolar trace propagates into its own individual set of noise in the distance distribution for all P(r) or V(T), requiring only a single calculation to show how that set of noise propagates into every P(r).
There are at least two important reasons for understanding how the different types of noise in experimental PDS data propagate into the distance spectrum. (1) It becomes possible to recognize and exclude the noise from further analysis and interpretation once it is understood where and how the noise appears in the distance spectrum. (2) Data collection protocols can be optimized to reduce or redistribute noise in the distance spectrum to improve the accuracy, reliability, and throughput of measurements.
Here we examine in silico the propagation of random, truncation and sampling noise into the distance spectrum and compare data acquisition protocols for reducing the impact of random noise. We find that in the conventional data acquisition approach, random measurement noise has its greatest impact on f(r) at shorter distances. But other sampling schemes will reduce that impact, giving improved accuracy and/or more rapid measurements.
We start with a brief description of the Mellin Transform analysis and the properties that are important in this examination of noise propagation. The Mellin Transform is benchmarked against the familiar Tikhonov regularization to provide a point of reference, revealing that random noise causes larger errors in the distance spectrum at shorter distances. The propagation of truncation and sampling noise is considered so that those types of noise can be kept insignificant. Finally, the optimization of measurements with respect to random noise is considered.
Methods
Calculation of f(r)
An analytical inverse solution of eqn (1) and (2) has been found that uses the Mellin Transform.11,18,19 Using this solution, f(r) is calculated from the experimentally measured dipolar trace. For convenience, we will refer to this Mellin Transform analysis as MeTA. Most regularization methods used for PDS analysis seem to lack the property of linearity. But MeTA, like the ubiquitous Fourier Transform, has this very useful property; meaning that the noise s(T) after transformation is the same regardless of the P(r) or V(T):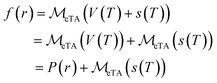 | (3) |
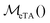 denotes the operator performing the MeTA. Thus, the error caused by any noise is simply
denotes the operator performing the MeTA. Thus, the error caused by any noise is simply 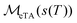 .
.
The linearity property makes it simple to study how measurement noise s(T) propagates into f(r). The noise in the distance distribution is simply 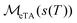 and is unaffected by either P(r) or V(T). Although noise propagates into the distance spectrum independent of the P(r) or V(T), the noise itself sometimes depends on P(r) or V(T). For instance, truncation noise and sampling noise depend on P(r) or V(T) and must be considered in the context of a particular P(r) or V(T). It is often useful to view them as distorting P(r), while random noise is an independent contribution to the f(r).
and is unaffected by either P(r) or V(T). Although noise propagates into the distance spectrum independent of the P(r) or V(T), the noise itself sometimes depends on P(r) or V(T). For instance, truncation noise and sampling noise depend on P(r) or V(T) and must be considered in the context of a particular P(r) or V(T). It is often useful to view them as distorting P(r), while random noise is an independent contribution to the f(r).
Mellin Transform methods are quite new in PDS and in magnetic resonance, so the MeTA approach as implemented11 is benchmarked against the widely used Tikhonov regularization, as implemented in DeerAnalysis.5 The Mellin Transform can be written in terms of the Fourier Transform and shares several properties18,19 that make the Fourier Transform so useful in magnetic resonance spectroscopy. MeTA11 uses the fact that the Mellin Transform is loss-less and has an inverse. No information is lost when the Mellin Transform converts the time-domain dipolar trace into a distance-domain spectrum of separations within pairs of PCs. Just as the Fourier Transform loses no information in converting an FID into a frequency-domain NMR spectrum. The Mellin Transformation and MeTA simply present all the information in the dipolar trace in a form that is easier for us to perceive.
The linearity property means that to see how noise s(T) in the dipolar trace propagates into noise in the distance spectrum, only the single calculation of 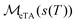 is needed. On the other hand, with regularization methods lacking linearity, the noise in the distance spectrum depends not only on s(T), but also on P(r).17 The linearity of MeTA provides a simple, convenient tool to study how random noise propagates into the distance spectrum regardless of the distance distribution function. Without that linearity, every P(r) can be a special case, requiring its own individual set of calculations.
is needed. On the other hand, with regularization methods lacking linearity, the noise in the distance spectrum depends not only on s(T), but also on P(r).17 The linearity of MeTA provides a simple, convenient tool to study how random noise propagates into the distance spectrum regardless of the distance distribution function. Without that linearity, every P(r) can be a special case, requiring its own individual set of calculations.
For the benchmarking and the initial study of random noise propagation, the trimodal P(r), Table 1, was used with eqn (1) to calculate V(T) for a sampling step dT = 64 ns and Tmax = 6.64 μs. This time window provides at least two cycles of the dipolar frequency at the peak of each of the three modes, which is regarded as adequate recovery an accurate f(r).2,21 As seen later, truncation and sampling noise are negligible for these parameters. This distribution has three peaks with different intensities but similar widths, providing a reasonable, but not problematic, model of PELDOR/DEER data.
Mean Distance ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , nm , nm |
ω
D at ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , MHz , MHz |
Width δr, nm | Relative width, δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) |
Normalized Weight |
|---|---|---|---|---|
| a This distribution was used by Kuznetsova et al.20 | ||||
| Trimodal P(r)a | ||||
| 3.2 | 1.592 | 0.3 | 0.094 | 0.323 |
| 4 | 0.815 | 0.2 | 0.050 | 0.071 |
| 5 | 0.417 | 0.4 | 0.080 | 0.606 |
| Bimodal P(r) for testing non-uniform acquisition schemes. | ||||
| 3.0 | 1.932 | 0.3 | 0.1 | 0.5 |
| 5.0 | 0.417 | 0.75 | 0.15 | 0.5 |
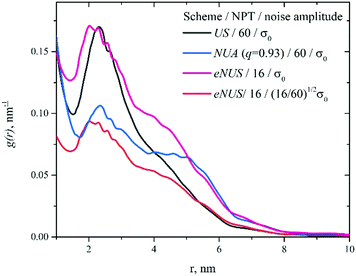
Gaussian random noise with σ = 0.017 and a mean of zero was added to V(T). Nine datasets were created with the same P(r) but different realizations of the noise. The f(r) was calculated from each dataset by MeTA and by the Tikhonov regularization in DeerAnalysis2013 with the regularization parameter chosen by DeerAnalysis. The families of fi(r) obtained by the two analysis methods were compared with each other and to the known P(r). In later studies of non-uniform sampling, a more challenging bimodal P(r) was used with two components having slight overlap and different widths.
The freely available version of MeTA was used for all MeTA calculations. It was created by NI LabView2016 and is shared at https://sites.google.com/view/anna-matveeva/ as a simple exe-file with short instructions for users. One internal parameter of MeTA can be optimized for each f(r). For the trimodal distribution from Table 1 (Fig. 1 and Fig. 1S, ESI†), the parameter Nτ = 1500 was used. All other calculations use Nτ = 1250; because it was optimal for the bimodal distribution in Table 1.
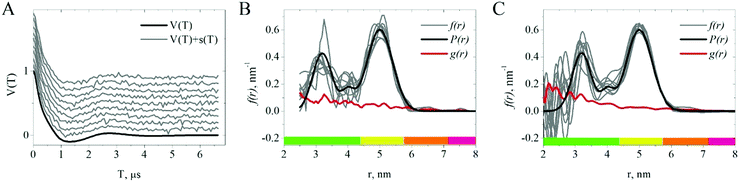 | ||
| Fig. 1 (A) Dipolar traces for the model distance distribution function in Table 1, Black: with no noise, Grey: with nine realizations of random noise with s = 0.017, successive traces are shifted upward for clarity; (B and C) Black: distance distribution, the color bars are discussed in relation to truncation noise, Grey: distance spectra for each trace, Red: the error propagation function g(r); (B) processed by DeerAnalysis, (C) processed by MeTA. With the default parameters, DeerAnalysis gave no result for r < 2.5 nm. The MeTA calculations are plotted to r = 2.0 nm to show that the trends persist beyond the ‘open window’. | ||
Error propagation function g(r)
To make it easier to follow the distribution of noise in the distance spectrum, an error propagation function was calculated as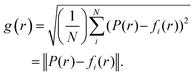 | (4) |
This g(r) reveals how the errors in f(r) are distributed as a function of distance.
The ‘open window’
Comparisons of different sampling schemes are made with respect to what we refer to as the ‘open window’ in the distance spectrum. If the P(r) lies within the ‘open window’, there is no truncation or sampling noise and we only need to consider random noise and P(r) in the distance spectrum. Any component of P(r) lying outside that ‘open window’ will produce truncation and sampling noise that overlaps P(r) in the distance spectrum and generally extends to shorter distances.The edges of this ‘open window’ are set operationally with very conservative limits to simplify study of random noise propagation. Improvements in random noise in this ‘open window’ translate directly to improvements in f(r) because truncation and sampling noise are insignificant for this ‘open window’. However, valid useful information about P(r) can be obtained outside the window.
Results and discussion
MeTA benchmark
Both analysis methods – MeTA and DeerAnalysis – gave similar, but not identical, results when applied to the same datasets. The families of distance spectra produced by DeerAnalysis, Fig. 1B, and MeTA, Fig. 1C, are consistent with each other and with the original P(r). The curves produced by each method from the datasets with nine realizations of random noise encompass the original P(r). The two components with large weights, Table 1, are readily apparent, while the weakest component is lost in the noise. As r increases, the error propagation function g(r), as well as the scatter of the underlying fi(r) decreases. Significantly, the g(r) from DeerAnalysis and MeTA overlap each other, Fig. S1 (ESI†), showing that the random noise in the dipolar traces propagates in similar fashion into the distance spectrum.DeerAnalysis provides a color-coded indication of the reliability of the distance spectrum, which are replicated at the bottom of the plots, Fig. 1B and C. The colors are anticorrelated with the errors from random noise random noise, being green where the errors from random noise are greatest. They do correlate well with truncation noise and will be discussed later in that context.
These two analysis methods produce comparable distributions of noise on datasets with distances and distributions that are not atypical of many experimental studies. One important difference is that the error propagation function from MeTA would be obtained for this noise with every P(r), while the one from DeerAnalysis would change if this noise was present with any other P(r). The general agreement between the error propagation functions suggests that whatever is learned from MeTA about noise propagation does have relevance to the analysis of PDS data by Tikhonov and other regularization methods. A detailed comparison of all known methods for PDS analysis is beyond the scope of this work but is being attempted by others.10,14,22–28
Propagation of random noise
The benchmark calculations show how random noise propagates into the f(r) and g(r). The errors in the distance spectrum caused by random noise diminish as the distance increases. Random noise has its greatest impact at short distances, so that the distance spectrum is more accurate for PC pairs with larger separations. This puzzling trend does have a simple explanation. The dipolar trace from pairs at long distances is represented by more datapoints before it decays to zero and therefore is known more accurately relative to the random noise. Consequently, the signal to noise ratio and g(r) are better for pairs with longer distances than ones with shorter distances, Fig. 1.Decreasing the sampling step dT and the length of the measured dipolar trace (Ttrace) would provide more samples of the dipolar trace at the short times that are most important for short distances. This tactic could be expected to increase the signal to noise ratio and hence the accuracy of f(r) at small r. Unfortunately, it would also severely truncate the dipolar trace at the long times needed for longer distances with their small ωD.
The competing demands made by pairs with short versus long distances provided the impetus to explore non-uniform data schemes in which the signal is measured more at short times than at long times in order to improve the accuracy of the distance spectrum at smaller values of r with minimal penalties at large r. However, before exploring such schemes, the response the distance distribution to truncation noise and sampling noise must be understood. It would be counterproductive if those types of noise simply replaced random errors as sampling schemes were altered.
Propagation of truncation noise
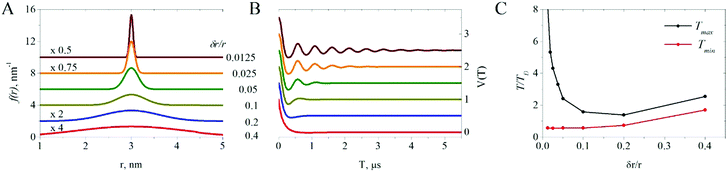
The length Ttrace of the dipolar trace needed to recover a reasonably accurate f(r) has been estimated to be two periods of the dipolar frequency ωD at the mean spin–spin distance![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , i.e., Ttrace = 4π/ωD, and this value should be increased for a narrow distance distribution function.2,29 However, many published PDS studies successfully use much longer or shorter values of Ttrace. The linearity property of MeTA makes it easy to study how truncation noise from a component or mode propagates into f(r) independent of truncation noise from all other modes and independent of other types of noise. This allows us to consider a simple monomodal Gaussian distribution with mean distance
, i.e., Ttrace = 4π/ωD, and this value should be increased for a narrow distance distribution function.2,29 However, many published PDS studies successfully use much longer or shorter values of Ttrace. The linearity property of MeTA makes it easy to study how truncation noise from a component or mode propagates into f(r) independent of truncation noise from all other modes and independent of other types of noise. This allows us to consider a simple monomodal Gaussian distribution with mean distance ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) and width (standard deviation) δr
and width (standard deviation) δr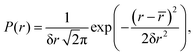 | (5) |
In the limiting case of a delta-function δr = 0, the long-time asymptotic behavior of the dipolar trace is given by the inner integral in eqn (1):16
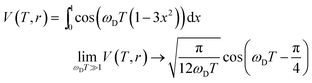 | (6) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) < 0.025 more than four modulation periods are distinguishable, while at δr/
< 0.025 more than four modulation periods are distinguishable, while at δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) > 0.1 the oscillations have almost vanished, which should decrease the required Ttrace. However, for very broad P(r) with δr/
> 0.1 the oscillations have almost vanished, which should decrease the required Ttrace. However, for very broad P(r) with δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) > 0.1, the dipolar trace lasts even longer because the first minimum for some pairs shifts to longer times.
> 0.1, the dipolar trace lasts even longer because the first minimum for some pairs shifts to longer times.
Let us examine the time Tmax at which the dipolar trace decays to an arbitrary 1% of its initial value, i.e., V(T > Tmax) < 0.01, and the time Tmin of its first minimum. The Tmin increases slowly with δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , Fig. 2C, but Tmax initially decreases rapidly as the oscillations in the dipolar trace are increasingly damped, and then increases slowly, in parallel with Tmin, at large δr/
, Fig. 2C, but Tmax initially decreases rapidly as the oscillations in the dipolar trace are increasingly damped, and then increases slowly, in parallel with Tmin, at large δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) . Thus, Ttrace should depend on the shape of P(r), but Ttrace = 2TD seems reasonable for δr/
. Thus, Ttrace should depend on the shape of P(r), but Ttrace = 2TD seems reasonable for δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) between 0.05 and 0.3.
between 0.05 and 0.3.
In a multimodal distribution, each component has its own Tmax. The kernel in eqn (1) scales with r−3, so that increasing r → nr but keeping δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) constant would increase Tmax by a factor of n3. Thus, for a multimodal distribution whose components have similar δr/
constant would increase Tmax by a factor of n3. Thus, for a multimodal distribution whose components have similar δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , the mode with the largest
, the mode with the largest ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) determines Tmax.
determines Tmax.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0.05) and a “broad” (δr/
= 0.05) and a “broad” (δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0.1) distribution with the same mean
= 0.1) distribution with the same mean ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 3 nm, Fig. 3B and C. Truncation is easier to understand in terms of a distortion of the distance spectrum, so we look at f(r) rather than the transformed noise
= 3 nm, Fig. 3B and C. Truncation is easier to understand in terms of a distortion of the distance spectrum, so we look at f(r) rather than the transformed noise 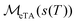 . As Tmax decreases and the dipolar trace is increasingly truncated, the position of the maximum rmax shifts to shorter distances, Fig. 3D; the peak amplitude changes, Fig. 3E; the peak width increases; and the peak shape becomes asymmetric, Fig. 3F. The shift of rmax is minimal when truncation occurs beyond 2TD and does not depend strongly on δr/
. As Tmax decreases and the dipolar trace is increasingly truncated, the position of the maximum rmax shifts to shorter distances, Fig. 3D; the peak amplitude changes, Fig. 3E; the peak width increases; and the peak shape becomes asymmetric, Fig. 3F. The shift of rmax is minimal when truncation occurs beyond 2TD and does not depend strongly on δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) . But, the errors in the peak width do depend on δr/
. But, the errors in the peak width do depend on δr/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) : the “narrow” peak broadens if the dipolar trace is truncated before its 2TD, whereas the “broad” peak narrows. The narrow peak is distorted and asymmetric if it is measured well beyond 2TD, but the broad peak still retains its overall shape even when truncated at TD, Fig. 3C. For both distributions, it appears safe to truncate the data after the dipolar oscillation decays to ∼10% of the initial value.
: the “narrow” peak broadens if the dipolar trace is truncated before its 2TD, whereas the “broad” peak narrows. The narrow peak is distorted and asymmetric if it is measured well beyond 2TD, but the broad peak still retains its overall shape even when truncated at TD, Fig. 3C. For both distributions, it appears safe to truncate the data after the dipolar oscillation decays to ∼10% of the initial value.
For a multimodal distribution, the distortions in f(r) occur independently for each component, so that components with shorter distances and shorter TD can usually be expected to have more accurate f(r) than components at larger distances. Unfortunately, truncation errors from each component extend out to shorter distances, so that a peak at a short distance can be overlapped by truncation noise from more distant components. However, truncation noise can be kept minimal in the distance spectrum by using an acquisition window with Ttrace ≥ 2TD for the most distant component. We take this simple relationship as a very conservative limit for a distance spectrum free of truncation noise for our study of random noise and sampling schemes. This limit can certainly be relaxed when greater levels of noise can be tolerated or when truncation noise is specifically included in the interpreting the distance spectrum.
DeerAnalysis provides colored bars as an indication of the reliability of f(r), Fig. 1B and C. Those bars mirror the trends in the propagation of truncation noise seen in Fig. 3. Within an acquisition window, a component with small r is least distorted by truncation noise in the distance spectrum, although it is subject to truncation noise from components at larger distances, Fig. 3.
Propagation of sampling rate noise
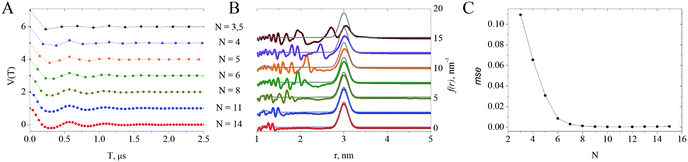
The rate at which the dipolar signal is sampled can introduce errors into f(r). The higher frequency components in the dipolar trace might not be sampled often enough to uniquely determine their frequency. This resembles the violation of the Nyquist limit in the discrete Fourier Transform: sampling with too large a step causes fold-over, wrap-around, or aliasing of high frequencies in the spectrum. The highest frequency for a delta-function distance distribution is 2ωD at the furthest edge of the dipolar Pake pattern. However, for distributions like those in Fig. 2A, the shortest distance and the largest ωD are not clearly defined because the distribution asymptotically approaches zero. For non-uniform sampling where the step size changes between samples, it is not clear a priori how the sampling noise might behave.It is convenient to consider sampling noise in terms of a distortion of P(r), as done with truncation noise. The conventional scheme of uniform sampling US uses a constant step size. Dipolar traces without random noise were calculated for a monomodal Gaussian P(r), eqn (5), with ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 3 nm and δr = 0.1 nm with the same Ttrace but different step sizes, Fig. 4A. Their f(r) were calculated by MeTA, Fig. 4B. There was always some noise at very short distances, even when the position shape and intensity of P(r) were completely reproduced. How closely f(r) reproduces the P(r) peak depends on the sampling rate: N ∼ 11 points per period TD of the dipolar frequency are sufficient for accurate recovery of f(r); at 6 points per period, f(r) has slight distortions in width and symmetry; and by 3.5 points per period, f(r) has major distortions. In Fig. 4C, the mean square deviation between f(r) and P(r) integrated for r > 2.7 nm shows that the minimum number of points for a nearly unperturbed f(r) peak is about 8. Based on the scaling properties of the dipolar trace, we set the maximum US step for a distance
= 3 nm and δr = 0.1 nm with the same Ttrace but different step sizes, Fig. 4A. Their f(r) were calculated by MeTA, Fig. 4B. There was always some noise at very short distances, even when the position shape and intensity of P(r) were completely reproduced. How closely f(r) reproduces the P(r) peak depends on the sampling rate: N ∼ 11 points per period TD of the dipolar frequency are sufficient for accurate recovery of f(r); at 6 points per period, f(r) has slight distortions in width and symmetry; and by 3.5 points per period, f(r) has major distortions. In Fig. 4C, the mean square deviation between f(r) and P(r) integrated for r > 2.7 nm shows that the minimum number of points for a nearly unperturbed f(r) peak is about 8. Based on the scaling properties of the dipolar trace, we set the maximum US step for a distance ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) very conservatively at
very conservatively at
dT ≤ π![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 3ns/nm3 3ns/nm3 | (7) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) increases rapidly for N < 6 and the peak in the distance spectrum becomes increasingly distorted.
increases rapidly for N < 6 and the peak in the distance spectrum becomes increasingly distorted.
Because of the linearity property of MeTA, the shortest ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) , in a multimodal P(r) sets the sampling rate needed with US for accurate recovery of the full multimodal distance distribution. The sampling noise is confined to shorter distances, so that components of f(r) at large distances can be measured without sampling noise even if other components are undersampled and seriously distorted by sampling noise. The amplitude of the sampling noise in the distance spectrum does not increase at short distances as it does for random noise.
, in a multimodal P(r) sets the sampling rate needed with US for accurate recovery of the full multimodal distance distribution. The sampling noise is confined to shorter distances, so that components of f(r) at large distances can be measured without sampling noise even if other components are undersampled and seriously distorted by sampling noise. The amplitude of the sampling noise in the distance spectrum does not increase at short distances as it does for random noise.
Non-uniform sampling
The three types of noise considered here have somewhat different properties. Random noise makes a disproportionate contribution to errors in f(r) at short r but can be reduced by increasing the quality, i.e., signal to noise ratio, of the data. Truncation noise is basically determined by the P(r) component with the longest distance and can be kept minimal by using a large Tmax. Sampling noise is largely determined by the P(r) component with the shortest distance but can be kept minimal by using a small dT.The different characteristics of these types of noise leave little scope for optimization of PELDOR/DEER measurements using US without increasing the experimental measurement time. However, non-uniform measurement might significantly reduce noise in f(r) by making fewer measurements at long times but more at short times if sampling and truncation noise does not significantly increase.
Random noise can be reduced in principle by sampling each point more times; by sampling more points, but the same number of times; or by a combination of these two. We consider two approaches: non-uniform sampling (NUS) where some regions of the dipolar trace are sampled more densely in time and non-uniform data accumulation (NUA) where some points in the dipolar trace are signal averaged more thoroughly than others.
NUS is actively used in NMR with several reviews,17,30–34 and NUA has been tried.35,36 Compressed sensing can be considered a form of NUS,37,38 and is used in many forms of spectroscopy and imaging, including NMR, but uses a rather different approach to convert raw data into a spectrum than we are considering here. NUS was demonstrated in EPR pulse hyperfine spectroscopy and relaxation measurements.39–42 NUS generally keeps the number of samples per point constant, focusing more on enhancing resolution while measuring fewer points than on increasing the signal to noise ratio of each point.
Two variations of PELDOR/DEER depart from a strictly US scheme. One is GloPel (Global analysis of PELDOR data)43 which simultaneously analyzes a short dipolar trace with a high sampling rate and a long trace with a low sampling rate. GloPel can be regarded as a segmented NUS scheme. The second method is RELOAD (Relaxation-Optimized Acquisition Length Distribution), where the dipolar trace is measured segmentally, and the segments are stitched into a full trace.44 RELOAD can be implemented as a NUA scheme. Both schemes gave enhanced accuracy and reduced measuring time for a complicated P(r). But the propagation of random noise into f(r) was not characterized for either scheme, so there is little basis for optimizing these schemes.
Sampling schemes
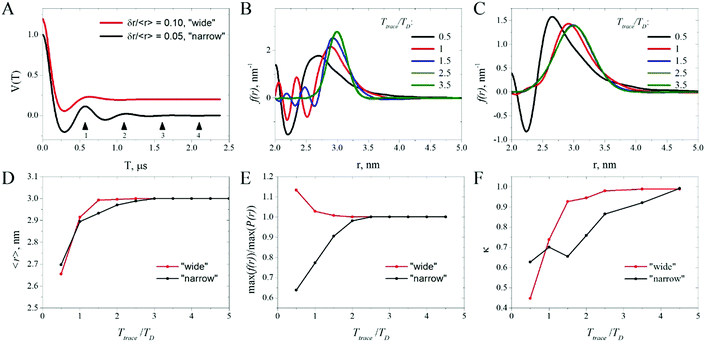
MeTA readily accommodates NUA or NUS schemes, providing a simple approach to examine noise propagation and optimization of those schemes. We consider two non-uniform measurement schemes. But while trying to reduce random noise in the f(r), it is important not to introduce sampling and truncation noise into what we call the ‘open window’ in the distance spectrum that is free of truncation and sampling noise. We try not to significantly narrow or even close the ‘open window’. For this phase of in silico experiments, we use a window suited to the bimodal P(r), Table 1, with resolved peaks at 3.0 and 5.0 nm; but the results are easily applied to other P(r).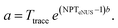 | (8) |
Truncation noise in eNUS and NUA
Truncation noise, as defined earlier, is simply the signal V(T > Ttrace) at times beyond the (time) measurement window. It does not depend on how the signal is measured within the window; only on what lies outside the window. As a result, the truncation noise for 4-pulse PELDOR/DEER, RIDME or DQC is determined by Ttrace and propagates identically into the distance spectrum for identical Ttrace. Consequently, we use the same Ttrace = 5.04 μs to compare the performance of the different sampling schemes.Sampling noise in eNUS and NUA
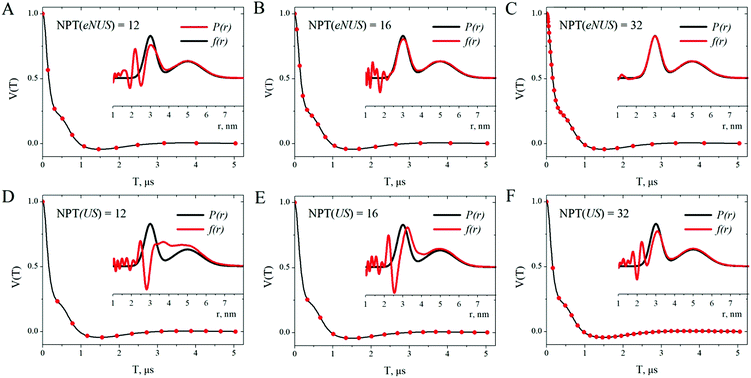
Sampling noise is the result of knowing the signal only at certain discrete delays within the measurement window. Any errors in the measurements at those points are considered here as random noise. US and NUA schemes have identical sampling noise because the signal is sampled at identical delays and have identical values after normalization. However, eNUS measurements are made with a different set of delays which results in different sampling noise that we have not yet examined.The initial part of the dipolar trace can be sampled more densely with eNUS. This should produce less sampling noise at the short distances than US and NUA for the same NPT because the initial values of dTeNUS are much smaller than dTUS. This expectation is easily verified with MeTA. The V(T) for the bimodal distribution, Table 1, with no random noise, was sampled at 12, 16 and 32 points according to the US and eNUS schemes in Table 2.
| NPT | US/NUA | eNUS | |||
|---|---|---|---|---|---|
| dTUS nsa | r min nm | a, ns | dT1, nsb | r min nmc | |
| a Time step dTUS rounded to an even number of ns. b Initial time step dT1 for eNUS rounded to a whole number of ns. c r min for eNUS with b = 0.2 based on eqn (7) and (9). d PELDOR/DEER is typically not applicable at distances less than 1.5 nm. | |||||
| 32 | 162 | 3.67 | 10.249 | 2 | <1.5d |
| 30 | 174 | 3.76 | 15.305 | 3 | <1.5d |
| 24 | 220 | 4.06 | 51.176 | 11 | 1.51 |
| 20 | 264 | 4.32 | 115.327 | 25 | 1.98 |
| 16 | 336 | 4.67 | 264.074 | 58 | 2.62 |
| 12 | 458 | 5.26 | 628.036 | 139 | 3.49 |
The V(T) and the points at which it was sampled are shown in Fig. 5, together with the P(r) and f(r) in the insets. At the same NPT, eNUS has much less sampling noise, Fig. 5A–C, than does US, Fig. 5D–F. The eNUS with 12 sampled points, Fig. 5A, performs about as well as US with 32, Fig. 5F, giving a similar f(r). It is noteworthy that the first three or four samples in Fig. 5A and F have very similar delays and deliver similar rmin. With eNUS, the component at 3.0 nm is reproduced well with NPT ≥ 15. For the 5.0 nm component even NPT = 12 is adequate, Fig. 5A.
In contrast, US accurately recovers only the 5.0 nm component with NPT = 16, Fig. 5E, while the peak at 3.0 nm is distorted and major errors appear at smaller distances. The relative amounts of short- and long-distance components are distorted by US for NPT ≤ 32, Fig. 5D–F. That was expected because the points per dipolar cycle ranges between 1.2–3.3 for the 3 nm peak. Eqn (7) predicts distortions from sampling noise until NPT ≥ 60.
These results are supported by experiments with a monomodal distance distribution where NPT was systematically varied, see section S.5. The mse between P(r) and f(r), Fig. S7 (ESI†), drops rapidly as NPT increases reaching zero roughly when the first eNUS step is
dT1 = T1 − T0 = a × (eb − 1) ≤ π![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 3ns/nm3. 3ns/nm3. | (9) |
This is the same criterion (at least with b = 0.2) as for US. But with eNUS, the steps proceed to grow so that many fewer delays need to be measured before reaching Ttrace. It is important to note that mse does go to zero, confirming negligible truncation noise with eNUS when Ttrace ≥ 2TD.
It is now possible to select and manipulate the ‘open window’ for US, eNUS, and NUA sampling schemes. Any reasonable distance distribution P(r) whose ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) lie within that window will produce distance spectra substantially free of truncation and sampling noise.
lie within that window will produce distance spectra substantially free of truncation and sampling noise.
Random noise in eNUS and NUA
We are now able to compare the random noise performance of different sampling schemes on a consistent basis. MeTA allows us to take random noise and convert it into the random noise component of f(r) and g(r) in the whole distance spectrum. If the P(r) lies within the ‘open window’, only random noise and P(r) appear in the distance spectrum. Changes in random noise in this ‘open window’ translates directly to changes in the quality of f(r) because truncation and sampling noise are insignificant.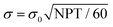 to reflect the signal averaging changes. For NUA, the noise at each point i is given by eqn (S1) (ESI†).
to reflect the signal averaging changes. For NUA, the noise at each point i is given by eqn (S1) (ESI†).
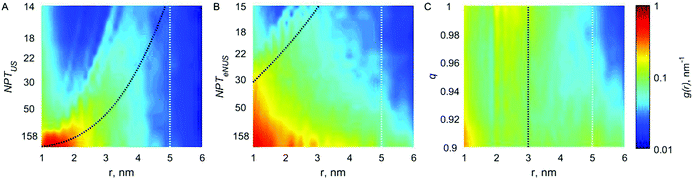 | ||
| Fig. 6 Comparison of error propagation functions g(r) for random noise in different sampling schemes. (A) US and (B) eNUS for different NPT stacked vertically, and (C) NUA for different values of q with NPT = 60, NUA at q = 1.0 is the same as US. The color scheme for the magnitude of g(r) has logarithmic scaling. The black dashed lines show rmin for each sampling scheme, so that f(r) to the right of that line is undistorted by sampling noise. Ttrace = 5.04 μs, so truncation noise becomes significant for r > 5.0 nm (indicated by the gray vertical line). Also see Fig. S8 (ESI†). | ||
Fig. 6A shows how random noise propagates in US as NPT changes. A PDS measurement delivers a horizontal slice (at some value of NPT from this plot). Decreasing NPT increases dT to keep Ttrace constant. Consequently, rmin (black curve) increases, narrowing the ‘open window’ between rmin and 5.0 nm. The two-dimensional plot of Fig. 6A shows that in the ‘open window’, NPT has little effect on the random noise at a given distance, but virtually closes the ‘open window’ as NPT gets small. Thus, there is no room to optimize the US measurement if Tall is fixed. To the left of the ‘open window’, the noise does change, but sampling noise becomes significant for any portion of P(r) lying in that region.
Random noise produces the largest errors in the ‘open window’ at small r. Decreasing NPT does not alter that, it simply narrows the window and the short distances fall outside the window, making their g(r) and f(r) less relevant. Vertical slices in this plot show that for random noise, the error at a fixed value of r is independent of NPT while r remains within the ‘open window’ defined by the black and white lines.
In short, noise and sensitivity with US depends only on Tall and the total number of shots while NPT only controls rmin. This behavior is expected because the dipolar trace changes slowly and smoothly for distances within the window, so that it does not matter if the signal is measured a few times at many different delays or many times at a few delays. There are large blue areas, nearly free of random noise, on the right and upper left portions of Fig. 6A, and to some extent in the other subplots. Unfortunately, they lie far outside the ‘open window’ and are useless; any portion of P(r) in those areas would be overwhelmed by truncation and sampling noise, respectively.
The eNUS scheme, Fig. 6B, has a more complex g(r) from the random noise. Within the ‘open window’, g(r) is larger at shorter distances, but it also grows as NPT increases, in contrast to US. The ‘open window’ is much broader than with US at the same NPT, because the initial dT are very much smaller with eNUS. Inside the ‘open window’, the random noise contribution to g(r) decreases as NPT decreases. Thus, using fewer points but measuring each one more accurately decreases the impact of random noise in the distance spectrum. Further improvement may be possible by optimizing the value of b.
The ‘open window’ does not change for the NUA scheme, Fig. 6C. The acquisition parameter q has some effect on g(r) from random noise, but the improvements relative to US are modest. There is a region of q from 0.93 to 0.96 where g(r) is flatter than for US: smaller at short r, but greater at long r.
Comparisons of sampling schemes should be made for similar ‘open windows’, which is tricky with Fig. 6 because the ‘open windows’ vary so much. Slices of g(r) for the three schemes are compared, Fig. 7. For US and NUA (q = 0.93), NPT = 60 was used, and for eNUS, 16. The ‘open windows’ are similar: 3.0–5.0 nm for US and NUA, and 2.62–5.0 nm for eNUS. The g(r) for US falls steadily as r increases in the window, consistent with Fig. 2 and Fig. S1 (ESI†).
With Tall constant, g(r) from random noise for eNUS (red curve) is nearly two-fold lower near rmin than for US (black), but they are nearly the same at the end of the ‘open window’. This is a redistribution (flattening) and net decrease of the errors from random noise. For NUA (blue), g(r) starts lower but ends higher compared to US, crossing near r = 4 nm. This is mostly a redistribution of errors within the ‘open window’ without a net decrease, giving a flatter error curve for random noise than for either US or eNUS. However, eNUS consistently delivers the lowest g(r) from random noise at any r within the ‘open window’.
Practical aspects of non-uniform schemes
The non-uniform schemes show potential for significantly improving PDS methods, such as PELDOR/DEER and DQC, by decreasing the impact of random noise on the distance spectra. This would result in increased quality of the distance spectra and/or increased throughput and efficiency. However, the in silico experiments here use idealized signals and idealized noise to examine how three different types of noise affect the distance spectra and how changes in the sampling scheme can improve the noise propagation function.Real experimental data contain other noise that were not considered but could be studied by analogous in silico experiments. Experimental dipolar traces typically have a baseline offset, delay time offsets, and decays of the signal and baseline. Such noise types are shared with US schemes and several strategies for dealing with it are in use and more are in development.27,45 Signal decay can cause the magnitude of the random noise to change as the delay time increases. This will affect the optimization of NUS and NUA schemes, so that, e.g., different q may be needed for different signal decays. But there appear to be no difficulties unique to non-uniform schemes.
A second practical problem concerns the method for solving the inverse problem. The prototypical Tikhonov-based approach, like other time-domain approaches, assumes uniformly spaced delay times. They require modifications to the algorithm to accommodate NUS data. Fourier-based techniques (for example, the Monte-Carlo approach)9,12 require either abandoning the classic fast Fourier transform, or some interpolation of the dipolar trace onto a uniform time grid. Some additional effort will be needed to adapt the popular analytical approaches to use non-uniformly sampled data, but the results here suggest significant rewards. Although the different approaches used by spectroscopists to regularize the inverse PDS problem do vary in their characteristics and performance, we expect that they will produce better distance spectra when given better dipolar trace data based on the results obtained here.
The final concern is how to set up a measurement to use a non-uniform scheme. To avoid truncation and sampling rate noise, it is necessary to estimate the smallest and largest distances, rmin and rmax, between PC pairs in the sample, to set the desired distance window. This can be based on knowledge or expectations about the sample, or on preliminary measurements. If P(r) has features outside the ‘open window’, those at shorter distances can appear with sampling noise extending to short distances, while those at larger distances can produce truncation noise extending into the ‘open window’ set by the values chosen for Ttrace ≈ 2TD (from rmax) and dT = πrmin3 from eqn (7).
For NUA, Ttrace and dT dictate NPT = Ttrace/dT and only q remains to be chosen. Some adjustment of parameters is usually necessary to accommodate the spectrometer capabilities. It is almost never possible for q to prescribe an integral number of shots for each point in an NUA. Some rounding is required, but the actual number of shots must be used to normalize the data at each point.
For eNUS, Ttrace is determined by the desired rmax. Then two more values must be selected from among dT1 (subject to eqn (9) and the desired rmin), NPT, a, and b. These parameters are not entirely independent. Some adjustment is needed to accommodate the spectrometer, particularly its resolution in generating delays. The actual delays used in the measurement must be used in the analysis to produce the distance spectrum.
Conclusions
This work has two important, immediate results. (1) The noise propagation function g(r) reveals that random noise in the PDS measurement propagates non-uniformly into errors in the distance spectrum. (2) Changing the traditional US scheme to a non-uniform scheme alters the distribution of random noise in the distance spectrum and can even decrease the net amount. Both results give a new impetus for exploring both the experimental design and the solution of the inverse problem in PDS.The paradigm of the noise propagation function g(r) enables a more detailed and precise consideration of experimental design and analysis in PDS. Together with the linearity property of MeTA, it allows a detailed investigation of how, and where, the different types of noise propagate into errors in the distance spectrum. Its use here demonstrated that the errors from random measurement noise can be redistributed and even decreased by changing the experimental measurement protocol. Explicitly considering g(r) may produce even better algorithms for solving the inverse PDS problem to improve recovery of the distance distribution.
This work demonstrates the validity and potential of non-uniform data acquisition, but additional work is required to understand the extent of the benefits and how robust the approach can be made. But NUS should increase the quality of experimental results from current spectrometers without increasing measurement time. All properly designed US, NUA, or NUS schemes will all recover the exact P(r). They differ, though, in how and where random noise appears in each distance spectrum. This means that measurements can be designed to distribute the random noise toward those parts of the distance spectrum where it has the least impact on the desired regions of P(r).
Finally, we now see the way that truncation and sampling noise propagate into the distance spectrum. This knowledge impacts how PDS measurements should be set up. Truncation noise should always be avoided when selecting Ttrace. The PC pairs with the largest separation distance are the first to give truncation noise which overlaps peaks from all other pairs. Sampling noise appears first from pairs with shorter separation distances, but their sampling noise overlaps only pairs with even smaller separations. Consequently, some sampling noise can be tolerated and will not interfere if the measurement is only concerned with pairs having even larger separations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful to Prof. Sergei A. Dzuba and Dr. Nikolay Isaev for helpful discussions and advice. This study was supported by the Ministry of Science and Higher Education of the Russian Federation (grant 14.W03.31.0034); AGM worked within the State Assignment to ISSCM SB RAS (project no. FWUS-2021-0005) by the Ministry of Science and Higher Education, VMN and VNS worked within the State Assignment to ICKC SB RAS (VMN – project no. AAAA-A21-121011390039-8, VNS – project no. AAAA-A21-121011390038-1) by the Ministry of Science and Higher Education.References
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
- Y. D. Tsvetkov, M. K. Bowman and Y. A. Grishin, Pulsed Electron–Electron Double Resonance: Nanoscale Distance Measurement in the Biological, Materials and Chemical Sciences, Springer International Publishing, 2019 Search PubMed.
- G. Jeschke, A. Koch, U. Jonas and A. Godt, J. Magn. Reson., 2002, 155, 72–82 CrossRef CAS PubMed.
- Y. W. Chiang, P. P. Borbat and J. H. Freed, J. Magn. Reson., 2005, 177, 184–196 CrossRef CAS PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- K. I. Sen, T. M. Logan and P. G. Fajer, Biochemistry, 2007, 46, 11639–11649 CrossRef PubMed.
- S. Brandon, A. H. Beth and E. J. Hustedt, J. Magn. Reson., 2012, 218, 93–104 CrossRef CAS PubMed.
- E. A. Lukina, A. A. Popov, M. N. Uvarov and L. V. Kulik, J. Phys. Chem. B, 2015, 119, 13543–13548 CrossRef CAS.
- S. A. Dzuba, J. Magn. Reson., 2016, 269, 113–119 CrossRef CAS PubMed.
- T. H. Edwards and S. Stoll, J. Magn. Reson., 2016, 270, 87–97 CrossRef CAS PubMed.
- A. G. Matveeva, V. M. Nekrasov and A. G. Maryasov, Phys. Chem. Chem. Phys., 2017, 19, 32381–32388 RSC.
- A. G. Matveeva, Y. V. Yushkova, S. V. Morozov, I. A. Grygor'ev and S. A. Dzuba, Z. Phys. Chem., 2017, 231, 671–688 CrossRef CAS.
- M. Srivastava and J. H. Freed, J. Phys. Chem. Lett., 2017, 8, 5648–5655 CrossRef CAS PubMed.
- S. G. Worswick, J. A. Spencer, G. Jeschke and I. Kuprov, Sci. Adv., 2018, 4, eaat5218 CrossRef CAS PubMed.
- A. D. Milov, K. M. Salikhov and M. D. Shirov, Sov. Phys. Solid State, 1981, 23, 565–569 Search PubMed.
- K. M. Salikhov, I. T. Khairuzhdinov and R. B. Zaripov, Appl. Magn. Reson., 2014, 45, 573–619 CrossRef CAS.
- M. Kaur, C. M. Lewis, A. Chronister, G. S. Phun and L. J. Mueller, J. Phys. Chem. A, 2020, 124, 5474–5486 CrossRef CAS PubMed.
- J. Bertrand, P. Bertrand and J. Ovarlez, in The Transforms and Applications Handbook, ed. A. D. Poularikas, CRC Press, LLC, Boca Raton, 2nd edn, 2000 DOI:10.1201/9781315218915.
- F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Biosvert, C. W. Clark, B. R. Miller, B. V. Saunders, H. S. Cohl and M. A. McClain, NIST Digital Library of Mathematical Functions, http://dlmf.nist.gov/, Release 1.1.0 of 2020-12-15 edn, 2020.
- A. A. Kuznetsova, A. G. Matveeva, A. D. Milov, Y. N. Vorobjev, S. A. Dzuba, O. S. Fedorova and N. A. Kuznetsov, Nucleic Acids Res., 2018, 46, 11454–11465 CrossRef CAS PubMed.
- A. D. Milov, A. G. Maryasov and Y. D. Tsvetkov, Appl. Magn. Reson., 1998, 15, 107–143 CrossRef CAS.
- T. H. Edwards and S. Stoll, Biophys. J., 2016, 110, 153a CrossRef.
- P. Kumar, T. H. Edwards, S. Stoll and M. Huber, Biophys. J., 2018, 114, 559a–560a CrossRef.
- T. H. Edwards and S. Stoll, J. Magn. Reson., 2018, 288, 58–68 CrossRef CAS PubMed.
- T. H. Edwards and S. Stoll, Biophys. J., 2018, 114, 158a–159a CrossRef.
- L. Fábregas Ibáñez and G. Jeschke, J. Magn. Reson., 2019, 300, 28–40 CrossRef PubMed.
- L. Fábregas Ibáñez and G. Jeschke, Phys. Chem. Chem. Phys., 2020, 22, 1855–1868 RSC.
- S. R. Sweger, S. Pribitzer and S. Stoll, J. Phys. Chem. A, 2020, 124, 6193–6202 CrossRef CAS PubMed.
- G. Jeschke and Y. Polyhach, Phys. Chem. Chem. Phys., 2007, 9, 1895–1910 RSC.
- M. Mobli and J. C. Hoch, Concepts Magn. Reson., Part A: Bridging Educ. Res., 2008, 32A, 436–448 CrossRef CAS PubMed.
- M. Mobli and J. C. Hoch, Prog. Nucl. Magn. Reson. Spectrosc., 2014, 83, 21–41 CrossRef CAS PubMed.
- F. Delaglio, G. S. Walker, K. Farley, R. Sharma, J. Hoch, L. Arbogast, R. Brinson and J. P. Marina, Am. Pharm. Rev., 2017, 20, 339681 Search PubMed.
- M. A. Zambrello, A. D. Schuyler, M. W. Maciejewski, F. Delaglio, I. Bezsonova and J. C. Hoch, Methods, 2018, 138–139, 62–68 CrossRef CAS PubMed.
- M. Mobli and T. M. Miljenovic, J. Magn. Reson., 2019, 300, 103–113 CrossRef CAS PubMed.
- M. R. Palmer, C. L. Suiter, G. E. Henry, J. Rovnyak, J. C. Hoch, T. Polenova and D. Rovnyak, J. Phys. Chem. B, 2015, 119, 6502–6515 CrossRef CAS PubMed.
- B. Simon and H. Kostler, J. Biomol. NMR, 2019, 73, 155–165 CrossRef CAS PubMed.
- K. Kazimierczuk and V. Orekhov, Magn. Reson. Chem., 2015, 53, 921–926 CrossRef CAS PubMed.
- K. Kazimierczuk, in Emagres, ed. R. K. Harris and R. L. Wasylishen, 2018, pp. 1–8 DOI:10.1002/9780470034590.emrstm1583.
- M. Mayzel, J. Rosenlow, L. Isaksson and V. Y. Orekhov, J. Biomol. NMR, 2014, 58, 129–139 CrossRef CAS PubMed.
- K. K. Nakka, Y. A. Tesiram, I. M. Brereton, M. Mobli and J. R. Harmer, Phys. Chem. Chem. Phys., 2014, 16, 16378–16382 RSC.
- H. Chen, A. G. Maryasov, O. Y. Rogozhnikova, D. V. Trukhin, V. M. Tormyshev and M. K. Bowman, Phys. Chem. Chem. Phys., 2016, 18, 24954–24965 RSC.
- L. Fábregas Ibáñez, J. Soetbeer, D. Klose, M. Tinzl, D. Hilvert and G. Jeschke, J. Magn. Reson., 2019, 307, 106576 CrossRef PubMed.
- S. Rein, P. Lewe, S. L. Andrade, S. Kacprzak and S. Weber, J. Magn. Reson., 2018, 295, 17–26 CrossRef CAS PubMed.
- S. Milikisiyants, M. A. Voinov, A. Marek, M. Jafarabadi, J. Liu, R. Han, S. Wang and A. I. Smirnov, J. Magn. Reson., 2019, 298, 115–126 CrossRef CAS PubMed.
- D. R. Kattnig, J. Reichenwallner and D. Hinderberger, J. Phys. Chem. B, 2013, 117, 16542–16557 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional plots concerning the distribution of noise and errors; scaling of interactions; and the redistribution of noise with different sampling schemes. See DOI: 10.1039/d1cp00705j |
| This journal is © the Owner Societies 2021 |