Benchmark ab initio stationary-point characterization of the complex potential energy surface of the multi-channel Cl + CH₃NH₂ reaction

Abstract

We characterize the exothermic low/submerged-barrier hydrogen-abstraction (HCl + CH₂NH₂/CH₃NH) as well as, for the first time, the endothermic high-barrier amino-substitution (CH₃Cl + NH₂), methyl-substitution (NH₂Cl + CH₃), and hydrogen-substitution (CH₂ClNH₂/CH₃NHCl + H) pathways of the Cl + CH₃NH₂ reaction using an accurate composite ab initio approach. The computations reveal a CH₃NH₂⋯Cl complex in the entrance channel, nine transition states corresponding to different abstractions, Walden-inversion substitution, and configuration-retaining front-side attack substitution pathways, as well as nine post-reaction complexes. The global minima of the electronic and vibrationally adiabatic potential energy surfaces correspond to the pre-reaction CH₃NH₂⋯Cl and post-reaction CH₂NH₂⋯HCl complexes, respectively. The benchmark composite energies of the stationary points are obtained by considering basis-set effects up to the correlation-consistent polarized valence quadruple-zeta basis augmented with diffuse functions (aug-cc-pVQZ) using the explicitly-correlated coupled-cluster singles, doubles, and perturbative triples CCSD(T)-F12b method, post-(T) correlation up to CCSDT(Q) including full triples and perturbative quadruples, core correlation, and scalar relativistic and spin–orbit effects, as well as harmonic zero-point energy corrections.

---

I. Introduction

Reactions of atoms such as H, F, and Cl with molecules from H₂via H₂O, NH₃, and CH₄ to C₂H₆ have attracted significant scientific attention from the 1970s to the present day.^1–18 Moving beyond these systems that have only equivalent H atoms, one may consider molecules with two different functional groups, thereby opening multiple hydrogen-abstraction reaction pathways. One possibility is to study the reactions of methanol (CH₃OH), which combines the functional groups of H₂O and CH₄. The F/Cl + CH₃OH reactions have been investigated recently by several experimental and theoretical groups.^19–23 The present study aims to combine the functional groups of NH₃ and CH₄ and investigates the reaction pathways of the Cl + CH₃NH₂ multi-channel reaction. The H-abstraction channels of this reaction forming HCl and CH₂NH₂ or CH₃NH were investigated in a joint experimental−theoretical study in 2003.²⁴ Experimentally, the HCl rotational distributions were measured, while theoretically the stationary points of the H-abstraction channels were characterized by the G2//MP2/6-311G(d,p) level of theory.²⁴ In 2009 a theoretical study applied W1’ theory, which utilizes UQCISD/6-31+G(d,p) geometries, HF, CCSD, and (T) extrapolations as well as core and scalar relativistic corrections, to map the reaction pathway of the HCl + CH₂NH₂ channel.²⁵ In 2013 the F + CH₃NH₂ reaction was investigated with the CCSD(T) method using the aug-cc-pVnZ [n = D, T, Q] basis sets.²⁶ Going back to Cl + CH₃NH₂, in 2015 the rate coefficients were measured and computed with a master equation model.²⁷ This latest study used the MP2/cc-pVTZ level of theory to determine the stationary-point geometries for the H-abstraction pathways, which was followed by single-point energy computations at the CCSD(T)-F12a/aug-cc-pVTZ level.

In this work we plan to provide additional insights into the mechanisms of the Cl + CH₃NH₂ reaction by searching for new reaction pathways besides the previously studied H-abstraction channels. One may consider substitution of the CH₃ and NH₂ groups by the Cl atom or one of the H atoms of either the CH₃ or NH₂ group. Previous work on atom/OH + CH₄/C₂H₆ reactions^16,28,29 showed that the substitution may occur via Walden-inversion and/or front-side attack pathways; thus, we aim to seek these mechanisms in the case of the title reaction as well. Furthermore, we plan to improve the accuracy of the previous studies^24,25,27 on the title reaction by using the explicitly-correlated CCSD(T)-F12b method for geometry optimizations and frequency computations as well as considering basis set effects up to aug-cc-pVQZ, post-(T) electron correlation effects up to CCSDT(Q), core correlation corrections, scalar relativistic effects, and geometry-dependent spin–orbit corrections. This complete and accurate characterization of the stationary points of the title reaction may provide guidance for future global potential energy surface developments and reaction dynamics studies.

II. Computational details

To determine the important stationary points of the reaction channels we start the search with the restricted open-shell second-order Møller–Plesset perturbation theory (RMP2)³⁰ with the correlation-consistent aug-cc-pVDZ basis set³¹ using initial structures based on chemical intuition and previous studies.^{16,24–27,29} Utilizing the minima and saddle-point geometries obtained at the RMP2/aug-cc-pVDZ level, we optimize with the restricted open-shell Hartree–Fock (ROHF)-based unrestricted explicitly-correlated coupled-cluster singles, doubles and perturbative triples (CCSD(T)-F12b) method,³² and apply two different basis sets: aug-cc-pVDZ and aug-cc-pVTZ.³¹ With the above-mentioned methods and basis sets, the harmonic vibrational frequencies are computed as well. Gradients and Hessians are obtained numerically usually using the default settings of Molpro.³³ For optimizations this means a gradient threshold of 3 × 10⁻⁴ a.u., which is tightened to be 10⁻⁵ a.u. in a few cases where low-lying frequencies occur. It is computationally too expensive (and also unnecessary, see later) to perform geometry optimization at the CCSD(T)-F12b level with the aug-cc-pVQZ basis set; therefore we compute CCSD(T)-F12b/aug-cc-pVQZ single-point energies at the geometries obtained with the aug-cc-pVTZ basis set.

To reach sub-chemical accuracy, the following energy contributions should be taken into account with single-point-energy computations, using the most accurate CCSD(T)-F12b/aug-cc-pVTZ geometries: post-CCSD(T) correlation, core-core and core-valence electron correlation (in short, core correlation), scalar relativistic effect, and spin–orbit coupling correction. For the correction of post-CCSD(T) correlation, unrestricted CCSD(T),³⁴ CCSDT³⁵ and CCSDT(Q)³⁶ methods are used with unrestricted Hartree–Fock (UHF) reference and the cc-pVDZ basis set. The corrections are defined as:

δ[CCSDT] = ΔE(CCSDT/cc-pVDZ) − ΔE(CCSD(T)/cc-pVDZ) (1)

δ[CCSDT(Q)] = ΔE(CCSDT(Q)/cc-pVDZ) − ΔE(CCSDT/cc-pVDZ) (2)

The frozen-core (FC) approach, which is used as a default unless otherwise noted, correlates valence electrons only, while all-electron (AE) computations correlate valence electrons and 1s² (C and N) and 2s²2p⁶ (Cl) electrons as well. The core electron correlation is obtained as the difference between FC and AE energies computed at the ROHF-based unrestricted CCSD(T)-F12b level of theory, with the cc-pCVTZ-F12 basis set:³⁷

Δ_core = ΔE(AE-CCSD(T)-F12b/cc-pCVTZ-F12) − ΔE(FC-CCSD(T)-F12b/cc-pCVTZ-F12) (3)

To determine the scalar relativistic effect, second-order Douglas–Kroll (DK)³⁸ relativistic energies are computed at the AE-CCSD(T)/aug-cc-pwCVTZ-DK^34,39 level of theory and the following formula is used:

Δ_rel = ΔE(DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK) − ΔE(AE-CCSD(T)/aug-cc-pwCVTZ) (4)

Spin–orbit (SO) coupling effect computations are performed utilizing the interacting-states approach⁴⁰ with the Davidson-corrected⁴¹ all-electron multi-reference configuration interaction⁴² (MRCI+Q) method in combination with the aug-cc-pwCVTZ basis set⁴³ and with active space of 5 electrons in 3 spatial 3p-like orbitals corresponding to Cl. The Davidson correction (+Q) estimates the effect of higher-order excitations and the corrected MRCI energies replace the diagonal elements of the 6 × 6 SO matrix, which provides the SO eigenstates by diagonalization. The correction is the difference between the SO ground-state (SO₁) and the non-SO ground-state (non-SO₁) energies:

Δ_SO = SO₁(MRCI+Q/aug-cc-pwCVTZ) − non-SO₁(MRCI+Q/aug-cc-pwCVTZ) (5)

The following expression is used for the calculation of benchmark classical relative energies:

ΔE_classical = CCSD(T)-F12b/aug-cc-pVQZ + δ[CCSDT] + δ[CCSDT(Q)] + Δ_core + Δ_rel + Δ_SO (6)

where classical refers to static nuclei without vibrational zero-point energy. With zero-point energy correction (Δ_ZPE), which is obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory, the vibrationally adiabatic, i.e., vibrational zero-point energy-corrected, relative energies are calculated as:

ΔE_adiabatic = CCSD(T)-F12b/aug-cc-pVQZ + δ[CCSDT] + δ[CCSDT(Q)] + Δ_core + Δ_rel + Δ_SO + Δ_ZPE (7)

Computations of the MP2, CCSD(T)-F12b, AE, DK, MRCI, and SO results are carried out with the Molpro³³ program package. For CCSD(T)-F12b the default auxiliary basis sets and accuracy thresholds are used as implemented in Molpro. The frozen-core CCSD(T), CCSDT, and CCSDT(Q) energies are obtained with MRCC⁴⁴ interfaced to Molpro.

III. Results and discussion

1. Reaction pathways

Six different channels of the Cl + CH₃NH₂ reaction are investigated:

(1) Methyl hydrogen-abstraction leading to HCl + CH₂NH₂ (CH₃ HA)

(2) Amino hydrogen-abstraction leading to HCl + CH₃NH (NH₂ HA)

(3) Methyl hydrogen-substitution leading to H + CH₂ClNH₂ (CH₃ HS)

(4) Amino hydrogen-substitution leading to H + CH₃NHCl (NH₂ HS)

(5) Methyl-substitution leading to NH₂Cl + CH₃ (MS)

(6) Amino-substitution leading to CH₃Cl + NH₂ (AS)Furthermore, the hydrogen-substitution in the methyl group and the amino-substitution can proceed via a Walden inversion (W) transition state (TS) or a front-side-attack (FS) TS.

The eight reaction pathways are shown in Fig. 1, with the computed benchmark classical(vibrationally adiabatic) energies relative to the reactants. Some characteristic structural parameters of the geometries displayed on this diagram are detailed at three different levels of theory in Fig. 2. In the entrance channel we have found a deep minimum stabilizing a CH₃NH₂⋯Cl complex with substantial D_e(D₀) dissociation energies of 15.30(14.22) kcal mol⁻¹. This pre-reaction minimum (PREMIN) may play an important steering role in the entrance channel and may make the reaction indirect, especially at low collision energies. The two hydrogen-abstraction reactions occur with small (CH₃ HA) and negative (NH₂ HA) barriers. The thermodynamically favored HA from the methyl-group is exothermic with −6.29(−10.79) kcal mol⁻¹, while from the amino-group the reaction is slightly endothermic (with 1.36 kcal mol⁻¹) classically and exothermic (−3.88 kcal mol⁻¹) adiabatically.

Fig. 1 Energy diagram of the Cl + CH₃NH₂ reaction pathways showing benchmark classical(vibrationally adiabatic) relative energies, acquired from eqn (6) (eqn (7)). See Table 1. * denotes the use of MP2/aug-cc-pVDZ geometry and ** denotes MP2/cc-pVDZ relative energy. Intrinsic reaction coordinate (IRC) computations show that PREMIN is along the amino hydrogen-substitution pathway, but it is not connected, because PREMIN may play significant roles in the other pathways as well.

Fig. 2 Structures of reactants, stationary points, and products with the most important distances (Å) and angles (degree) at the MP2/aug-cc-pVDZ (blue), CCSD(T)-F12b/aug-cc-pVDZ (green), and CCSD(T)-F12b/aug-cc-pVTZ (red) levels of theory. * denotes distances at MP2/cc-pVDZ. PREMIN is shown at amino hydrogen-substitution based on IRC computations, but PREMIN may also play significant roles in the other pathways.

In the case of methyl hydrogen-abstraction, two transition-state geometries (CH₃ HA TS′ and CH₃ HA TS′′) are found. We report both, because we experience severe electronic structure problems in this region and the computational procedure described in Section II could not be executed for these stationary points. To guide future work, we provide some details about these ab initio issues. The represented structures are obtained with the MP2 method using the cc-pVDZ and aug-cc-pVDZ basis sets for CH₃ HA TS′ (TS′) and CH₃ HA TS′′ (TS′′), respectively. The geometry optimizations at CCSD(T)-F12b with the aug-cc-pVDZ and aug-cc-pVTZ basis sets are not converged due to Hartree–Fock (TS′) and CCSD (TS′′) convergence issues. The elongation of the breaking C–H bond is significant (0.154 Å) in the TS′′ geometry, whereas modest in TS′ (0.028 Å). The single-point energy computations can be performed only in the former case (TS′′), because Hartree–Fock does not converge for the latter (TS′). The reason why we do not report only TS′′ is that visualization of the normal mode corresponding to the imaginary frequency shows that this mode does not exactly belong to the C–H bond stretching. Furthermore, Nicovich et al.²⁷ reported a geometry of this transition state obtained at the MP2/cc-pVTZ level of theory, where this C–H bond is 1.134 Å long, like in TS′. Moreover, TS′ provides a lower barrier for HA than TS′′ as seen in Fig. 1. The problems with this CH₃ HA TS were also reported by Taylor et al., who found that a TS′-like structure can be obtained at the CCSD(T)/6-31G(d) level, whereas the same method with larger 6-31+G(d,p) and 6-311+G(2df,p) basis sets fails to locate a TS′-like saddle point.²⁵

After the hydrogen-abstractions, the amino-substitution (AS) via the Walden TS has the lowest barrier, 31.74(29.72) kcal mol⁻¹; moreover this channel is only slightly endothermic (ΔE(ΔH₀) = 4.76(0.25) kcal mol⁻¹). In spite of this, the AS front-side attack TS (AS TS FS) has the largest barrier height, 52.00(49.55) kcal mol⁻¹, which is higher by 20.26(19.83) kcal mol⁻¹ than that of the corresponding Walden inversion TS (AS TS W). The relative energies of the post-reaction minima are very similar, for example 2.93(−0.97) kcal mol⁻¹ for AS MIN W and 2.43(−1.34) kcal mol⁻¹ for AS MIN FS, in accordance with the similar C–Cl (1.786 Å) and comparably large C–N (3.260/3.254 Å) distances. The barrier of the FS transition state is higher than that of the Walden inversion TS at the methyl hydrogen-substitution (CH₃ HS TS) as well. The difference is 6.22(6.08) kcal mol⁻¹ and the relative energy of the CH₂ClNH₂ + H products is 15.47(10.53) kcal mol⁻¹. The endothermicity of the MS channel, ΔE(ΔH₀) = 27.47(22.45) kcal mol⁻¹, is higher than that of the amino-substitution, with 22.71(22.20) kcal mol⁻¹. The most endothermic pathway is the hydrogen-substitution from the amino-group, with ΔE(ΔH₀) = 45.56(39.87) kcal mol⁻¹, whose TS (NH₂ HS TS) is just slightly above the product level, as seen in Fig. 1.

In the case of the substitution pathways the relative-energy differences between the products and product-like minimum (MIN) complexes are only 0.28−2.32(0.01−1.58) kcal mol⁻¹. In the case of CH₃ HA MIN′, CH₃ HA MIN′′, and NH₂ HA MIN, the product complexes are more stable with D_e(D₀) dissociation energies of 6.09(4.39), 6.57(4.77), and 8.00(6.07) kcal mol⁻¹, respectively. This finding is expected, because the HA MINs are stabilized by dipole–dipole interactions, whereas only dipole-atom and dipole–quadrupole forces occur in the HS and MS complexes, respectively. As seen above, for CH₃ HA we have found two minima in the exit channel. CH₃ HA MIN′ is along the CH₃ HA pathway where the departing HCl fragment hydrogen bonds to the C atom, whereas at the slightly deeper CH₃ HA MIN′′ the HCl unit connects to the amino group as shown in Fig. 1 and 2. Adiabatically the CH₃ HA MIN′′ complex is the global minimum of the system, whereas classically PREMIN is deeper by 2.44 kcal mol⁻¹.

One may consider an additional product channel of the Cl + CH₃NH₂ reaction leading to NH₃ + CH₂Cl. This thermodynamically favorable channel, with ΔE(ΔH₀) = −3.70(−8.20) kcal mol⁻¹, must be kinetically hidden, because, unlike the above-discussed six channels, NH₃ + CH₂Cl requires breaking and forming two bonds instead of one. In the exit channel we have found a CH₂Cl⋯NH₃ complex with C_s symmetry, where CH₂Cl connects to NH₃ with a single CH⋯N hydrogen bond. The D_e(D₀) values of the CH₂Cl⋯NH₃ complex are 3.05(1.91) kcal mol⁻¹ obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory and the corresponding classical(vibrationally adiabatic) energies relative to the reactants are −7.40(−10.76) kcal mol⁻¹; thus, PREMIN(CH₃ HA MIN′′) remains the global minimum of the system.

Besides the NH₃ + CH₂Cl channel, the kinetically also hindered NHCl + CH₄ formation may be considered, but it turns out to be endothermic with ΔE(ΔH₀) = 14.24(9.82) kcal mol⁻¹ (Table 1); thus, this channel is not competitive for the lowest-energy configuration of the title reaction.

Table 1 Benchmark classical and vibrationally adiabatic energies (eqn (6) and (7)) with auxiliary energy contributions (eqn (1)−(5)) relative to reactants (kcal mol⁻¹)

Stationary points	MP2	CCSD(T)-F12b			δ[T]^e	δ[(Q)]^f	Δ core	Δ rel	Δ SO	Classical^j	Δ ZPE	Adiabatic^l
	aVDZ^a	aVDZ^b	aVTZ^c	aVQZ^d
a MP2/aug-cc-pVDZ relative energies obtained at MP2/aug-cc-pVDZ geometries. b CCSD(T)-F12b/aug-cc-pVDZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVDZ geometries. c CCSD(T)-F12b/aug-cc-pVTZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries. d CCSD(T)-F12b/aug-cc-pVQZ relative energies obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries. e CCSDT–CCSD(T) obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries with cc-pVDZ basis set. f CCSDT(Q)–CCSDT obtained at CCSD(T)-F12b/aug-cc-pVTZ geometries with cc-pVDZ basis set. g Core correlation corrections obtained as the differences between all-electron and frozen-core CCSD(T)-F12b/cc-pCVTZ-F12 relative energies at CCSD(T)-F12b/aug-cc-pVTZ geometries. h Scalar relativistic effects obtained as the differences between DK-AE-CCSD(T)/aug-cc-pwCVTZ-DK and AE-CCSD(T)/aug-cc-pwCVTZ relative energies at CCSD(T)-F12b/aug-cc-pVTZ geometries. i Spin–orbit (SO) corrections obtained as the differences between the SO and non-SO ground-state MRCI+Q/aug-cc-pwCVTZ relative energies at CCSD(T)-F12b/aug-cc-pVTZ geometries. j Benchmark classical relative energies obtained as CCSD(T)-F12b/aug-cc-pVQZ relative energies + δ[T] (e) + δ[(Q)] (f) + Δcore (g) + Δrel (h) + ΔSO (i). k Zero-point energy (ZPE) corrections obtained at CCSD(T)-F12b/aug-cc-pVTZ. l Benchmark vibrationally adiabatic relative energies obtained as classical relative energies (j) + ΔZPE (k). m CH3 HA TS′′ relative energies and corrections obtained at MP2/aug-cc-pVDZ geometry. n Obtained with UMP2.
PREMIN	−16.35	−16.39	−15.76	−15.92	−0.02	−0.13	−0.11	+0.06	+0.81	−15.30	+1.08	−14.22
CH3 HA TS′′^m	2.33	3.49	3.99	3.92	−0.13	−0.14	+0.00	+0.07	+0.82	4.55	−0.65	3.90
NH2 HA TS	−0.31^n	−4.14	−3.43	−3.55	−0.28	−0.15	−0.04	+0.14	+0.83	−3.05	−4.45	−7.50
AS TS W	41.25	31.72	31.50	31.51	−0.66	−0.37	+0.47	−0.02	+0.81	31.74	−2.02	29.72
AS TS FS	60.57	52.12	52.42	52.44	−1.22	−0.48	+0.49	−0.05	+0.81	52.00	−2.44	49.55
MS TS	40.00	33.91	34.42	34.41	−0.59	−0.38	+0.39	−0.02	+0.83	34.64	−2.94	31.70
CH3 HS TS W	38.59	35.96	36.36	36.22	−0.35	−0.34	+0.09	+0.11	+0.81	36.55	−4.15	32.40
CH3 HS TS FS	45.30	42.70	43.13	42.85	−0.56	−0.40	−0.03	+0.09	+0.83	42.77	−4.29	38.48
NH2 HS TS	50.64	46.33	47.48	47.51	−0.15	−0.37	+0.20	+0.05	+0.83	48.06	−4.60	43.46
CH3 HA MIN′	−11.73	−13.91	−12.97	−13.06	−0.07	−0.11	−0.22	+0.25	+0.83	−12.38	−2.80	−15.18
CH3 HA MIN′′	−12.53	−14.50	−13.52	−13.60	−0.07	−0.10	−0.20	+0.27	+0.84	−12.86	−2.70	−15.56
NH2 HA MIN	−4.88	−8.58	−7.45	−7.50	−0.15	−0.02	+0.00	+0.19	+0.84	−6.64	−3.31	−9.94
AS MIN W	5.65	1.19	1.90	1.87	−0.10	−0.01	+0.21	+0.13	+0.84	2.93	−3.90	−0.97
AS MIN FS	5.30	0.53	1.40	1.39	−0.10	−0.02	+0.20	+0.13	+0.84	2.43	−3.77	−1.34
MS MIN	29.05	23.60	24.44	24.41	−0.09	−0.14	+0.17	+0.11	+0.84	25.30	−4.00	21.29
CH3 HS MIN W	11.61	13.13	14.41	14.30	+0.06	−0.18	−0.02	+0.18	+0.84	15.19	−4.69	10.50
CH3 HS MIN FS	11.51	12.91	14.26	14.15	+0.06	−0.18	−0.02	+0.18	+0.84	15.03	−4.51	10.52
NH2 HS MIN	43.83	42.73	44.23	44.24	+0.07	−0.25	+0.10	+0.12	+0.84	45.11	−4.99	40.12
CH3NHCl + H	44.14	43.30	44.69	44.68	+0.07	−0.25	+0.11	+0.12	+0.84	45.56	−5.70	39.87
NH2Cl + CH3	31.60	25.94	26.65	26.55	−0.07	−0.13	+0.17	+0.11	+0.84	27.47	−5.02	22.45
CH2ClNH2 + H	11.82	13.45	14.71	14.58	+0.06	−0.17	−0.02	+0.18	+0.84	15.47	−4.94	10.53
CH3Cl + NH2	7.89	3.08	3.76	3.69	−0.09	−0.01	+0.21	+0.12	+0.84	4.76	−4.51	0.25
HCl + CH3NH	4.16	−0.39	0.40	0.38	−0.13	+0.01	+0.11	+0.15	+0.84	1.36	−5.23	−3.88
HCl + CH2NH2	−4.42	−7.64	−6.99	−7.09	−0.07	−0.06	−0.15	+0.25	+0.84	−6.29	−4.50	−10.79
CH4 + NHCl	22.56	12.59	13.57	13.53	−0.32	−0.09	+0.26	+0.02	+0.83	14.24	−4.42	9.82
NH3 + CH2Cl	−0.05	−5.18	−4.35	−4.53	−0.14	−0.06	−0.02	+0.22	+0.84	−3.70	−4.50	−8.20

---

1.1. Benchmark structures and relative energies. First, the stationary points of the reactions are searched with the MP2 method, and based on these geometries, the coupled-cluster computations are performed, as described in Section II. In eleven cases, the geometries were very close to C_s point-group symmetry; therefore in these cases the differences between relative and zero-point energies of the stationary points with C_s and C₁ symmetry have been examined at MP2/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVDZ levels of theory. As can be seen in Fig. 3, the differences of the C_s and C₁ classical relative energies are practically negligible, even with the CCSD(T)-F12b method the largest absolute difference is only 0.0014 kcal mol⁻¹ (2 × 10⁻⁶E_h), well below the desired chemical accuracy (uncertainty less than 1 kcal mol⁻¹) or the 0.01 kcal mol⁻¹ precision of the data given in the present study. The deviations of ZPEs are slightly larger in certain instances at MP2, where the average absolute deviation is 0.286 kcal mol⁻¹. Nevertheless, with the CCSD(T)-F12b method, which is utilized for higher-level computations, this average ZPE uncertainty decreases to 0.0545 kcal mol⁻¹. Taking these findings into account, the high-level computations are carried out using C_s point-group symmetry for the stationary points shown in Fig. 3. This choice does not compromise the accuracy of the benchmark classical relative energies and gives about 0.1 kcal mol⁻¹ (CH₃ HA MIN′, AS W TS, and AS FS TS) and 0.3 kcal mol⁻¹ (AS FS MIN) uncertainty for some of the vibrationally adiabatic energies (see Fig. 3).

Fig. 3 Relative energy and zero-point energy comparisons of stationary points obtained with C₁ and C_s point-group symmetry at the MP2/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVDZ levels of theory.

The geometry optimizations are performed at MP2/aug-cc-pVDZ, CCSD(T)-F12b/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVTZ levels of theory. The most important structural parameters of each pathway are collected (Fig. 2). In most cases, the difference between the MP2 and coupled-cluster results occurs in the hundredths of angstrom, while between the aug-cc-pVDZ and aug-cc-pVTZ CCSD(T)-F12b distances the deviations appear in the thousandths of angstrom, showing the excellent basis set convergence of the explicit-correlated CCSD(T)-F12b method.

The benchmark relative energies are obtained using the most accurate CCSD(T)-F12b/aug-cc-pVTZ geometries. To check the geometry effect on the relative energies, we have performed optimizations for the reactant and products at the CCSD(T)-F12b/aug-cc-pVQZ level of theory. We have found that the CCSD(T)-F12b/aug-cc-pVQZ relative energies at the CCSD(T)-F12b/aug-cc-pVQZ and CCSD(T)-F12b/aug-cc-pVTZ geometries agree well within 0.001 kcal mol⁻¹, showing that the geometry effects on the energies are clearly negligible, around the numerical noise level.

The convergence of the relative energies and corresponding auxiliary corrections are shown in Table 1 and presented graphically in Fig. 4 and 5. The CCSD(T)-F12b method is needed to reach the sub-chemical accuracy, because the MP2/aug-cc-pVDZ energies differ from the corresponding CCSD(T)-F12b data by 2.70 kcal mol⁻¹ on average and the maximum deviation is as large as almost 10 kcal mol⁻¹ (AS TS W). The basis convergence of the explicitly-correlated CCSD(T)-F12b method is outstanding, as seen in Fig. 4, which is also confirmed by the fact that the root-mean-square deviation (RMSD) is 0.84 kcal mol⁻¹ for DZ vs. QZ, which decreases to 0.10 kcal mol⁻¹ for the TZ-QZ differences. Furthermore, our previous study showed that the CCSD(T)-F12b method with a QZ basis provides relative energies approaching the standard CCSD(T) QZ/5Z-extrapolation-based complete-basis-set limits within 0.1 kcal mol⁻¹.⁴⁵ However, the most accurate relative energies, reported in this work, are obtained by considering the energy contributions mentioned below.

Fig. 4 Convergence of the relative energies of the stationary points and products, obtained with MP2/aug-cc-pVDZ and CCSD(T)-F12b with the aug-cc-pVDZ, aug-cc-pVTZ, and aug-cc-pVQZ basis sets.

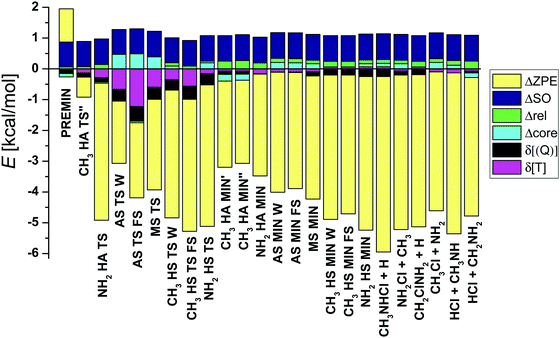Fig. 5 Auxiliary energy contributions (eqn (1)–(5)) and zero-point energy corrections for the stationary points and products.

1.1.1. Energy contributions. Based on the values shown in Table 1 and the graphical representation of the corrections (Fig. 5), it is obvious that the harmonic ZPE correction is the most significant. The effects on the relative energies are negative (except for PREMIN) and the mean of the absolute magnitude is 3.89 kcal mol⁻¹ (not considering the CH₃ HA TS′′, since the ZPE was computed at MP2 level of theory in this case). The products have always larger zero-point corrections than the corresponding TSs and post-reaction complexes have (the RMSD is 1.37 kcal mol⁻¹).

The post-CCSD(T) correlation corrections are essential to reach “exact” energies, mainly for the transition states, because these structures differ the most from the equilibrium, and hence these geometries have the greatest relevance of the electron correlation. The fact that sub-chemical accuracy cannot be achieved without these corrections is also shown by the finding that in most cases the sum of δ[CCSDT] and δ[CCSDT(Q)] in absolute value is around 1 kcal mol⁻¹ and, for example, nearly 2 kcal mol⁻¹ in the case of AS TS FS.

The core correlation corrections (Δ_core) and the scalar relativistic effects (Δ_rel) are small and usually positive corrections around 0.1–0.2 kcal mol⁻¹ (see Table 1). The largest Δ_core values are found for the AS W/FS and MS TSs, i.e., +0.47/0.49 and +0.39 kcal mol⁻¹, respectively, whereas the corresponding Δ_rel values are small, –(0.02–0.05) kcal mol⁻¹. The largest Δ_rel effect of +0.27 kcal mol⁻¹ is obtained for CH₃ HA MIN′′. In general, the absolute Δ_core contributions are larger for saddle points than minima, whereas an opposite trend is seen for Δ_rel.

It is needed to reckon the increase of the relative energies due to the relativistic spin–orbit interaction in the Cl atom. The ²P non-relativistic ground state (non-SO) of the Cl atom splits into two energy levels, ²P_1/2 and ²P_3/2. The former level has higher energy by 2ε/3 than non-SO and the latter has lower energy by ε/3. The measured SO splitting of Cl is ε = 2.52 kcal mol⁻¹, and therefore the SO interaction lowers the reactant asymptote by ε/3 = 0.84 kcal mol⁻¹, which is exactly reproduced by our computations. SO corrections for the stationary points are positive in all cases: 0.84 kcal mol⁻¹ for the products and MIN complexes (for CH₃ HA MIN′ 0.83 kcal mol⁻¹), while slightly less (0.81–0.83 kcal mol⁻¹) for transition states and PREMIN. These results show that even at PREMIN the SO interaction is almost fully quenched; thus, the SO shift of the reactant level effectively increases the relative energies. In addition, the cases, when the methylamine is approached by the chlorine atom from seven different directions are investigated and the potential curves, relative to the ground non-SO asymptotic limit, are shown in Fig. 6. As seen, due to the interaction with methylamine, six different states are present. The twofold degenerate SO₁ and twofold degenerate excited SO₂ result from the splitting of the ²P_3/2 state and SO₃ correlates to ²P_1/2. The non-SO ground state (non-SO₁) and two non-SO excited states (non-SO₂, non-SO₃) are the non-relativistic split ²P states. As shown in Fig. 6, the deepest van der Waals wells of SO₁ with depths of 9.04, 2.66, and 2.22 kcal mol⁻¹ appear when the methylamine is approached by the chlorine atom with C–N–Cl angle of 108.5° as in PREMIN, perpendicularly to the C–N bond on the side opposite to the hydrogens of the amino-group, and in the case of the attack of the amino-group in line with the C–N bond, respectively. This implies that approach from the methyl-group has a shallower well than from the NH₂ as expected, because the latter is a more polar group than the former. Interestingly, as Fig. 6 also shows, the difference between the energy of SO and non-SO ground states does not drop to zero rapidly, the decrease occurs from about 4 to 2 Å inter-fragment distances. In the case of OH + C₂H₆ and OH + CH₄ this effect moves within sharper boundaries.²⁹ At the TS and product regions the SO vs. non-SO energy differences are close to zero, which means that the SO effects on the relative energies are close to ε/3 as mentioned above.

Fig. 6 Potential energy curves of the Cl⋯CH₃NH₂ system obtained at the MRCI+Q/aug-cc-pwCVTZ level of theory for seven different separation directions, while methylamine is kept frozen at its equilibrium geometry. The seven orientations are: the Cl atom approaching CH₃NH₂ in the same orientation as in the PREMIN complex (first row), approaching the methyl-group (second row), approaching one H atom of the methyl-group (third row), perpendicularly the C–C bond from two directions (fourth and fifth rows), from the amino-group (sixth row) and approaching one H atom of the amino-group (seventh row). The curves in the right panels show the distance-dependence of E(SO₁)–E(non-SO₁).

1.2. Comparison with experimental data. To compare the computed benchmark vibrationally adiabatic relative energies (eqn (7)) with experimental data, the Active Thermochemical Tables (ATcT)⁴⁶ are used. ATcT is a freely available database, where the best experimental and computed thermochemical data are stored. Note that we call the ATcT data “experimental” even if they are derived from a network of different measured and computed quantities. The 0 K enthalpies of formation of chemical species involved in the two hydrogen-abstraction (HA), the amino-substitution (AS), and NH₃ + CH₂Cl formation reactions can be retrieved from this database and the corresponding reaction enthalpies are shown in Table 2. The absolute deviation of the present computed and experimental values in the case of CH₃ HA, NH₂ HA, AS, and NH₃ + CH₂Cl are 0.15, 0.30, 0.07, and 0.28 kcal mol⁻¹, respectively, which are mostly within or around the experimental uncertainty. This good agreement is the proof of the fact that in addition to the CCSD(T)-F12b/aug-cc-pVQZ energies, the auxiliary corrections are also required to reach this accuracy. Furthermore, the present comparison confirms the accuracy of the theoretical predictions for the experimentally not available quantities as well.

Table 2 Comparison of the 0 K reaction enthalpies (kcal mol⁻¹) of four reactions, showing the benchmark vibrationally adiabatic relative energies obtained in this work or retrieved from the ATcT database

Reaction	This work^a	Experiment^b
a Obtained in this work from eqn (7). b Determined from Active Thermochemical Tables (version 1.122p).^46 Gaussian error propagation law is applied to determine the uncertainties, based on the uncertainties (corresponding to 95% confidence limits) of the enthalpy of formation data given in ATcT.
Cl + CH3NH2 → HCl + CH2NH2	−10.79	−10.93 ± 0.12
Cl + CH3NH2 → HCl + CH3NH	−3.88	−4.18 ± 0.13
Cl + CH3NH2 → NH2 + CH3Cl	0.25	0.32 ± 0.08
Cl + CH3NH2 → NH3 + CH2Cl	−8.20	−7.92 ± 0.22

---

IV. Summary and conclusions

The pathways of the Cl + CH₃NH₂ multi-channel reaction have been investigated using a high-level composite ab initio method. Besides the previously known exothermic H-abstraction channels leading to HCl + CH₂NH₂ (−10.79) and HCl + CH₃NH (−3.88), amino-, methyl-, and H-substitution pathways, resulting in CH₃Cl + NH₂ (0.25), NH₂Cl + CH₃ (22.45), and CH₂ClNH₂/CH₃NHCl + H (10.53/39.87), respectively, are also revealed, showing the benchmark vibrationally adiabatic reaction enthalpies (kcal mol⁻¹) in parentheses. In the four cases, where experimental data are available for comparison, good agreement has been observed between theory and experiment. In the entrance channel there is a CH₃NH₂⋯Cl complex with substantial D_e(D₀) value of 15.30(14.22) kcal mol⁻¹. The presence of this deep minimum in the entrance channel of the title reaction is in sharp contrast to the Cl + CH₄/C₂H₆ reactions, where the depth of the entrance-channel well is only 0.6–1.0 kcal mol⁻¹.^12,16 H-abstraction is clearly/nearly barrierless from the amino/methyl group, whereas the substitution processes have high barriers in the 30–50 kcal mol⁻¹ range and in the amino-, methyl-, and H-substitution increasing energy order. H-substitution is both kinetically and thermodynamically favored from the methyl group. For the methyl-H-substitution and the amino-substitution we have found front-side attack TSs besides the Walden-inversion ones, and the front-side attack pathways have always higher barriers by about 6 and 20 kcal mol⁻¹, respectively. In the exit channels product-like complexes are found, which are the most stable in the case of the H-abstraction channels with about twice as large binding energies than those of the corresponding product complexes of the Cl + CH₄/C₂H₆ reactions. On the basis of the present computations, the Guinness (lowest-energy) structure⁴⁷ of the Cl + CH₃NH₂ system corresponds to the CH₃NH₂⋯Cl and CH₂NH₂⋯HCl complexes without and with zero-point energies, respectively.

Our benchmark energy computations show that the CCSD(T)-F12b/aug-cc-pVQZ results are basis-set converged within 0.1 kcal mol⁻¹, the post-(T) correlation effects are substantial for the TSs where their mean absolute value is 0.41 kcal mol⁻¹, the core and scalar relativistic corrections have small usually positive values around 0.1–0.2 kcal mol⁻¹, and the spin–orbit coupling is almost fully quenched at the TSs, product channels, and even at the CH₃NH₂⋯Cl pre-reaction complex, and therefore, the SO shift of the Cl atom effectively increases the relative energies by 0.81–0.84 kcal mol⁻¹, and the ZPE effects are the most substantial, often decreasing the relative energies by 3–6 kcal mol⁻¹. Considering the uncertainties of the post-(T) correlation (0.1 kcal mol⁻¹), core correlation (0.1 kcal mol⁻¹), relativistic effects (0.1 kcal mol⁻¹), and harmonic ZPE corrections (0.1 kcal mol⁻¹) as well as basis-set errors (0.1 kcal mol⁻¹), neglected non-Born–Oppenheimer effects (<0.1 kcal mol⁻¹ based on ref. 48) and anharmonicity (∼5% of the ZPE corrections, i.e., 0.1–0.3 kcal mol⁻¹), we estimate 0.2–0.3 and 0.3–0.4 kcal mol⁻¹ uncertainty for the present benchmark classical and vibrationally adiabatic relative energies, respectively.

As a future research direction, one may develop a global analytical potential energy surface for the title reaction, which would allow dynamics investigations and further comparisons with experiments. The present benchmark stationary-point data provide guidance for such dynamics studies and help to assess the accuracy of the potential energy surface. Dynamics simulations can reveal the atomic-level mechanisms of the title reaction and the collision-energy-dependent branching ratios of the different product channels as well as HCl rotational distributions allowing critical comparison with experiment. Furthermore, the new findings of the present study may motivate the research community to consider fundamental reactions as complex, and multi-channel processes.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the National Research, Development and Innovation Office–NKFIH, K-125317, the Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT, and the Momentum (Lendület) Program of the Hungarian Academy of Sciences for financial support.

References

1. G. C. Schatz and A. Kuppermann, J. Chem. Phys., 1975, 62, 2502.
2. G. C. Schatz, M. C. Colton and J. L. Grant, J. Phys. Chem., 1984, 88, 2971.
3. H. W. Song, M. H. Yang and H. Guo, J. Chem. Phys., 2016, 145, 131101.
4. Z. H. Kim, A. J. Alexander, H. A. Bechtel and R. N. Zare, J. Chem. Phys., 2001, 115, 179.
5. S. Yoon, S. Henton, A. N. Zivkovic and F. F. Crim, J. Chem. Phys., 2002, 116, 10744.
6. R. Welsch and U. Manthe, J. Chem. Phys., 2013, 138, 164118.
7. F. Meng, W. Yan and D. Wang, Phys. Chem. Chem. Phys., 2012, 14, 13656.
8. C. Murray, J. K. Pearce, S. Rudić, B. Retail and A. J. Orr-Ewing, J. Phys. Chem. A, 2005, 109, 11093.
9. W. W. Harper, S. A. Nizkorodov and D. J. Nesbitt, J. Chem. Phys., 2000, 113, 3670.
10. J. P. Layfield, A. F. Sweeney and D. Troya, J. Phys. Chem. A, 2009, 113, 4294.
11. C. Murray and A. J. Orr-Ewing, Int. Rev. Phys. Chem., 2004, 23, 435.
12. G. Czakó and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 2839.
13. K. Liu, J. Chem. Phys., 2015, 142, 080901.
14. B. Fu, X. Shan, D. H. Zhang and D. C. Clary, Chem. Soc. Rev., 2017, 46, 7625.
15. J. Espinosa-Garcia, J. C. Corchado, M. Garcia-Chamorro and C. Rangel, Phys. Chem. Chem. Phys., 2018, 20, 19860.
16. D. Papp, B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 396.
17. D. Papp, V. Tajti, T. Győri and G. Czakó, J. Phys. Chem. Lett., 2020, 11, 4762.
18. D. Papp and G. Czakó, J. Chem. Phys., 2020, 153, 064305.
19. A. W. Ray, J. Agarwal, B. B. Shen, H. F. Schaefer III and R. E. Continetti, Phys. Chem. Chem. Phys., 2016, 18, 30612.
20. M. L. Weichman, J. A. DeVine, M. C. Babin, J. Li, L. Guo, J. Ma, H. Guo and D. M. Neumark, Nat. Chem., 2017, 9, 950.
21. D. Lu, J. Li and H. Guo, Chem. Sci., 2019, 10, 7994.
22. D. Lu, J. Li and H. Guo, CCS Chem., 2020, 2, 882.
23. D. Lu and J. Li, Theor. Chem. Acc., 2020, 139, 157.
24. S. Rudić, C. Murray, J. N. Harvey and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2003, 5, 1205.
25. M. S. Taylor, S. A. Ivanic, G. P. F. Wood, C. J. Easton, G. B. Bacskay and L. Radom, J. Phys. Chem. A, 2009, 113, 11817.
26. H. Feng, W. Sun, Y. Xie and H. F. Schaefer III, ChemPhysChem, 2013, 14, 896.
27. J. M. Nicovich, S. Mazumder, P. L. Laine, P. H. Wine, Y. Tang, A. J. C. Bunkan and C. J. Nielsen, Phys. Chem. Chem. Phys., 2015, 17, 911.
28. L. Krotos and G. Czakó, J. Phys. Chem. A, 2017, 121, 9415.
29. B. Gruber and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 14560.
30. R. D. Amos, J. S. Andrews, N. C. Handy and P. J. Knowles, Chem. Phys. Lett., 1991, 185, 256.
31. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007.
32. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
33. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz and others, Molpro, version 2015.1, a package of ab initio programs, see http://www.molpro.net.
34. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
35. J. Noga and R. J. Bartlett, J. Chem. Phys., 1987, 86, 7041.
36. M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105.
37. J. G. Hill, S. Mazumder and K. A. Peterson, J. Chem. Phys., 2010, 132, 054108.
38. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89.
39. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48.
40. A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823.
41. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61.
42. K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101.
43. K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 2002, 117, 10548.
44. MRCC, a quantum chemical program suite written by M. Kállay, Z. Rolik, I. Ladjánszki, L. Szegedy, B. Ladóczki, J. Csontos and B. Kornis, See also Z. Rolik and M. Kállay, J. Chem. Phys., 2011, 135, 104111 , as well as: http://www.mrcc.hu.
45. G. Czakó, I. Szabó and H. Telekes, J. Phys. Chem. A, 2014, 118, 646.
46. B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122p of the Thermochemical Network (2020); available at http://ATcT.anl.gov.
47. M. A. Suhm, Angew. Chem., Int. Ed., 2014, 53, 1714.
48. G. Czakó, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 130, 084301.

---