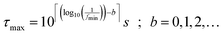Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Insights into the sodiation mechanism of hard carbon-like materials from electrochemical impedance spectroscopy†
Konstantin
Schutjajew‡
 *a,
Tim
Tichter
*a,
Tim
Tichter
 b,
Jonathan
Schneider
b,
Markus
Antonietti
b,
Jonathan
Schneider
b,
Markus
Antonietti
 a,
Christina
Roth
a,
Christina
Roth
 c and
Martin
Oschatz‡
c and
Martin
Oschatz‡
 *a
*a
aDepartment of Colloid Chemistry, Max Planck Institute of Colloids and Interfaces, Am Mühlenberg 1, 14476 Potsdam, Germany. E-mail: Martin.Oschatz@mpikg.mpg.de; Konstantin.Schutjajew@mpikg.mpg.de
bInstitute of Physical and Theoretical Chemistry, Freie Universität Berlin, Arnimallee 22, 14195 Berlin, Germany
cElectrochemical Process Engineering, Universität Bayreuth, Bayerisches Zentrum für Batterietechnik, Universitätsstraße 30, 95447 Bayreuth, Germany
First published on 29th April 2021
Abstract
To render the sodium ion battery (SIB) competitive among other technologies, the processes behind sodium storage in hard carbon anodes must be understood. For this purpose, electrochemical impedance spectroscopy (EIS) is usually undervalued, since fitting the spectra with equivalent circuit models requires an a priori knowledge about the system at hand. The analysis of the distribution of relaxation times (DRT) is an alternative, which refrains from fitting arbitrarily nested equivalent circuits. In this paper, the sodiation and desodiation of a hard carbon anode is studied by EIS at different states of charge (SOC). By reconstructing the DRT function, highly resolved information on the number and relative contribution of individual electrochemical processes is derived. During the sloping part of the sodiation curve, mass transport is found to be the most dominant source of resistance but rapidly diminishes when the plateau phase is reached. An equivalent circuit model qualitatively reproducing the experimental data of the sloping region was built upon the DRT results, which is particularly useful for future EIS studies on hard carbon SIB anodes. More importantly, this work contributes to establish EIS as a practical tool to directly study electrode processes without the bias of a previously assumed model.
Introduction
Lithium-ion batteries (LIBs) are indispensable for the small-scale storage of electrical energy, e.g. in portable electronic devices or electromotive applications. However, due to the scarcity and the uneven geographical distribution of many key components required in LIBs (e.g. cobalt ores and lithium salts) alternative solutions based on more abundant materials moved into the focus of current research. Among them, the sodium ion battery (SIB) is probably the most attractive system, as it offers an operational voltage and an energy density similar to LIBs. Furthermore, it shares many aspects of cell chemistry with its lithium-analogue. The similarity between lithium and sodium provides the opportunity that many components such as the electrolyte and the range of cathode materials can be almost directly adopted from LIBs to SIBs.1,2Yet, in contrast to LIBs, an anode material with high sodium storage capacity at a potential close to Na/Na+ and at the same time with a high operational safety, is much more complicated to find. While the implementation of metal oxides and alloys in conversion anodes promises high theoretical capacities, this approach is impaired by the significant volume expansion during operation, causing severe limitations. Hence, such materials are still mainly relevant from an academic point of view.3
In case of LIB, the most widely used anode material is graphite. Graphite can form a series of binary Li–C intercalation compounds during the lithiation process which contributes to an excellent capacity which is theoretically limited to 372 mA h g−1 for the final stoichiometry of LiC6. Unfortunately, graphite does not show any considerable sodium storage capacity as no binary intercalation compounds of graphite and sodium are known.4 Contrarily, the use of carbonaceous materials as anode is a practically promising approach owing to the considerable alkali metal storage capability of most carbon types and a virtually unlimited amount of possible carbon structures and modifications.5
Particularly the so-called hard carbons (HCs) are considered as an alternative to graphite and have been subject of extensive research activities for many years.3,6 Hard carbons are carbon materials without a long-range order, usually considered non-graphitizable. They can be best described as turbostratically contorted, curved graphene layers that are—to some extent—aligned in parallel to each other, forming a material with partially graphitic domains as well as small internal cavities.7,8
Hard carbons are usually obtained from precursors, which develop a high degree of cross-linking during pyrolysis. However, their particular structure is not only dependent on the type of precursor but can also be significantly influenced by the synthesis conditions.9 Hence, structural features like porosity, carbon binding motifs, or even heteroatom content must be considered when employing a hard carbon for sodium storage. All of these properties influence the sodium storage mechanism and thus the operating potential of the anode at the respective state of charge, represented by the voltage profile.7 Profound understanding of their individual and combined influence on sodium storage is a crucial requirement for future targeted improvement of the capacity and stability of HC anodes.
The voltage profile during the sodiation of hard carbons can be generally divided into three regions: (1) a sloping region at potentials higher than 1.5 V vs. Na/Na+ extending over a low capacity range, (2) a sloping region with a slower potential decay at approx. 1.5–0.2 V vs. Na/Na+, and (3) a voltage plateau at 0.2–0.0 V vs. Na/Na+.
While it is agreed upon that ion adsorption to defect sites is responsible for the first, high potential stage, the assignment of distinct chemical processes corresponding to the latter two stages is still under debate.10–13 Multiple characterization tools have been applied in combination with suitable model materials to elucidate the corresponding mechanisms.
Stevens and Dahn were the first who studied the sodium insertion into hard carbon electrodes, using in situ X-ray scattering techniques. They reported an extension of the (002) interlayer spacing during the sloping and a change in electron density in the ultramicropores during the plateau phase.6,14,15 Therefore, they assigned the intercalation of sodium between the graphene layers to the sloping, and the pore filling to the plateau regions, respectively. Their results were corroborated by X-ray diffraction and NMR-data of other groups.16–18 Liu et al.19 suggested that intercalation between graphene layers with larger interlayer spacing contributes to the charge storage in the plateau as well. This was confirmed later on by Ji et al.20 employing the galvanostatic intermittent titration technique (GITT). More recently, Bai et al. selectively adjusted the defect- and micropore-content of a HC-material, and found out that the former is closely related to the sloping and the latter to the plateau region.21 In a series of small-angle and wide-angle X-ray scattering (SAXS and WAXS) experiments, Morikawa et al.22 observed the appearance of characteristic scattering peaks related to quasimetallic sodium confined in narrow micropores only at later stages of the plateau region, very close to 0 V vs. Na/Na+. Those findings indicate not a single phenomenon, but a fluent passage from intercalation processes into graphene interlayers to micropore deposition of sodium to be responsible for the voltage plateau. While we agree with the common view on the role of micropores in sodium storage, we consider the explanation of intercalation into the graphitic interlayer space during the sloping phase as somewhat incomplete. This is justified by the typically linear decrease in potential which hints towards an adsorptive mechanism occurring, where sodium is present as a cation and the electron remains mostly at the electrode.23,24 Alternatively, a phase similar to a solid-solution could be imagined at this stage of sodiation.25 NMR studies generally support this view, since the chemical shift of elemental sodium remains similar to that of positively charged sodium ions during the sloping region and, on the other hand, the well-studied process of intercalating lithium into graphite results in a strong and distinct chemical shift, which is not the case during the sloping region in a sodium anode.17,18,26,27
So far, the common view on the sodiation mechanism of HCs is mainly based on the results of charge/discharge and cyclic voltammetry measurements combined with (ex situ) structural analysis.9,20,28,29 Another characterization tool that is widely applied for the investigation of practically all kinds of electrochemical processes is electrochemical impedance spectroscopy (EIS).30 Though, more detailed insights into the sodiation process of hard carbons might be gained from EIS, the possibilities of this method have not been exploited to their full extent yet. This is potentially caused by the fact that the most commonly applied method for EIS-analysis—equivalent circuit fitting (ECF)—requires for a relatively precise knowledge of all the possible mechanistic aspects of the system under study. Since due to the multiplicity of processes involved such an information is a mere guess for HC based sodium-ion anodes, ECF might provide rather ambiguous results instead of physicochemically relevant parameters.
In order to overcome these drawbacks, the EIS-spectra can be evaluated alternatively in terms of the distribution of relaxation times (DRT) analysis. This approach does not require any a priori knowledge on the system under investigation. In contrast, it offers direct information on the number of individual processes occurring during the reaction as well as their relative contribution to the total impedance. Furthermore, it provides a significantly enhanced resolution, when compared to the Nyquist or Bode representation of EIS data which can unravel up to three processes per frequency decade. This method has already been successfully applied successfully to solid oxide fuel cells and was proven viable for a LiFePO4 cathode31 as well as for lithium ion full cells.32 Porous carbon anodes in LIBs as well as metallic sodium anodes were investigated by DRT, recently.33,34 However, to the best of our knowledge a DRT-study of a hard carbon sodium ion battery anode has not been performed yet.31,32,35–37
Therefore, the scope of the present work is to apply the DRT-method for the investigation of the Na storage in sodium-ion anodes on a fundamental level and to gain primary insights on the sodiation mechanism. For this purpose, impedance spectra of a hard carbon-like anode material are recorded at a broad range of different states of sodiation/desodiation and subsequently analyzed with the DRT approach. Following the method of Schmidt et al.,31 data from symmetrical cell measurements is compared to hard carbon/sodium half-cell experiments and the processes are assigned to the respective cell components and processes. Most importantly, the nature of the sodium species formed during the low-voltage plateau phase of the sodiation is elucidated and the kinetics of their formation is found to be strikingly similar to that of sodium plated in the bulk of the electrode. This finding supports previous models of quasi-metallic phases forming in carbon nanopores and provides profound insights about alkali-ion storage in hard carbon-like materials.
Results and discussion
Data processing
Experimental data of electrochemical impedance spectroscopy is usually evaluated by exploiting equivalent circuit models from which the electrokinetic parameters are obtained by complex non-linear least-square (CNLS) fitting routines. However, in many electrochemical systems, especially in electrodes made of complex materials with a rough or porous structure, equivalent circuit models, constructed from the three basic circuit elements resistor R, capacitor C and inductor L, are inherently ambiguous in describing the measured impedance spectra. This is caused by the fact that real systems are mostly characterized by parameters with a certain distribution.30,38 In such cases distributed elements, like the constant phase element (CPE), provide a mathematically better fit but are not necessarily more realistic in describing an electrochemical system.Another way of approximating the measured EIS data is the analysis of their distribution of relaxation times (DRT). By considering a continuous series connection of RC-elements (time constants) any electrochemical system might be expressed by the following (DRT) integral equation:
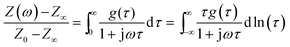 | (1) |
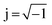 the imaginary unit, τ is the time constant with τ = 2πω−1 = RC and g(τ) stands for the normalized distribution of relaxation times function which has to be determined. Obtaining the function, g(τ), according to eqn (1) requires for solving a Fredholm integral equation of the first kind.30 This is a mathematically ill-posed problem in the definition of Hadamard. In case of experimental, i.e. non-ideal data, this enforces that the solution (if it exists) might not be unique and/or suffer from strong oscillations. Therefore, a variety of approaches for approximating g(τ) employ regularization methods to stabilize the solution. Among them, e.g. Fourier transformation,35,39 Tikhonov regularization,37,40–43 maximum entropy,44,45 or evolutionary programming46,47 have been proposed. At this stage, it is exceptionally worth to note that choosing a suitable regularization is crucial for obtaining a reliable DRT. Herein, we are using Tikhonov regularization to reconstruct the underlying DRT function from our experimental data. We chose this approach owing to its ease of implementation and its capability to faithfully reproduce a DRT even in rather complex cases.48,49 Our methodology is similar to the one outlined by Hahn et al.37 and can be briefly summarized as follows.
the imaginary unit, τ is the time constant with τ = 2πω−1 = RC and g(τ) stands for the normalized distribution of relaxation times function which has to be determined. Obtaining the function, g(τ), according to eqn (1) requires for solving a Fredholm integral equation of the first kind.30 This is a mathematically ill-posed problem in the definition of Hadamard. In case of experimental, i.e. non-ideal data, this enforces that the solution (if it exists) might not be unique and/or suffer from strong oscillations. Therefore, a variety of approaches for approximating g(τ) employ regularization methods to stabilize the solution. Among them, e.g. Fourier transformation,35,39 Tikhonov regularization,37,40–43 maximum entropy,44,45 or evolutionary programming46,47 have been proposed. At this stage, it is exceptionally worth to note that choosing a suitable regularization is crucial for obtaining a reliable DRT. Herein, we are using Tikhonov regularization to reconstruct the underlying DRT function from our experimental data. We chose this approach owing to its ease of implementation and its capability to faithfully reproduce a DRT even in rather complex cases.48,49 Our methodology is similar to the one outlined by Hahn et al.37 and can be briefly summarized as follows.
Since the DRT is computed numerically, eqn (1) is first discretized.
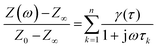 | (2) |
| z = Kγ. | (3) |
In eqn (2), γ(τ) = τg(τ)Δln(τ) where Δln(τ) is the spacing of τ-increments spanning a logarithmic grid. In eqn (3), the vector z contains all m measured data points and K is the m × n kernel matrix, whose entries are given by eqn (4).
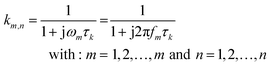 | (4) |
The vector γ contains the sought-after distribution function. The number of time constants n is chosen as an integer multiple of the number of measured data points.
| n = a × m; a = 1,2,3,… | (5) |
For the calculations related to this paper we set a = 10, as a suitable balance between resolution of the obtained DRT and the time required for computation. The pre-defined time constants are chosen to span an equally spaced logarithmic grid between τmin and τmax, obtained as eqn (6), where floor and ceiling functions of x are denoted as ⌊x⌋ and ⌈x⌉, respectively.
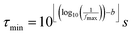 | (6) |
Herein, parameter b allows for an expansion of the time domain beyond the range of experimental frequencies. This enhances the quality of the fit at the boundaries of the measured spectrum. By our experience it is sufficient to use b = 3.
Having set up the time constants and having constructed the kernel matrix K, the DRT is obtained by solving eqn (3) with respect to γ. This is achieved by least-squares minimization and finding:
| min{‖Kγ − z2‖} | (7) |
| min{‖Kγ − z‖2 + λ‖Mγ‖2} | (8) |
Since negative contributions to the impedance are not reasonable according to eqn (1), we used a non-negative least-squares (NNLS) solver.50 This, however, causes three important implications.
Any possible inductive contribution to the impedance will be neglected during the fitting routine.
The NNLS solver cannot handle complex valued inputs and it is only able to deal with problems in the form of eqn (7), but not in the form of eqn (8).
Implication (I) will not be a problem, since our data does not show any sign of inductive contribution. Consequently, utilizing the somewhat restricted NNLS approach is well justified. Fortunately, implication (II) can be circumvented as follows. Implementing complex valued inputs is avoided if only the real or imaginary part of the impedance is considered. It might be defined that:
| min{‖K*γ − z*‖2} |
| with K* = ℜe(K) and z* = ℜe(z) |
| or K* = ℑm(K) and z* = ℑm(z) | (9) |
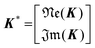 | (10) |
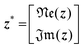 | (11) |
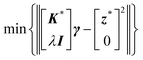 | (12) |
| min{||K*γ − z*||2 + λ||Iγ||2} | (13) |
Structural and electrochemical characterization
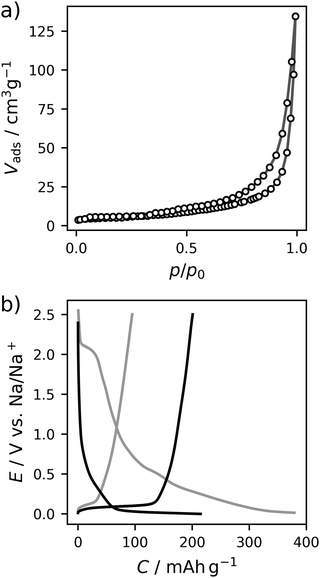
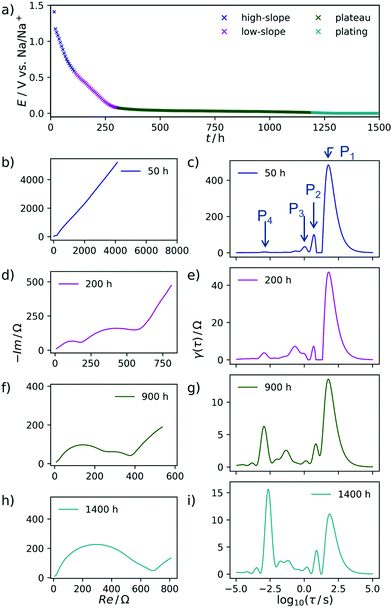
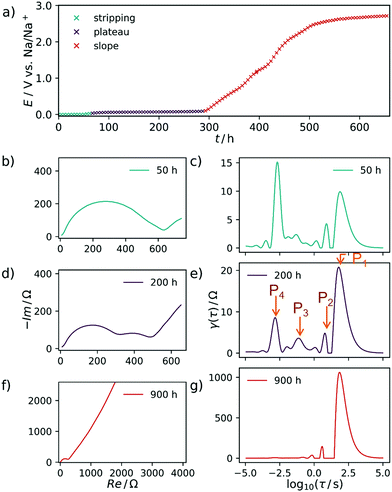
The carbon material denoted as C-HAT-1600 used in this study is obtained from the direct thermal condensation of the nitrogen-rich precursor hexaazatriphenylene-hexacarbonitrile (HAT-CN). During the heat treatment the precursor molecules undergo condensation and cross-linking, resulting in a highly microporous, hard carbon-like network with significant nitrogen content, as was already reported by Walczak et al.53 The fundamental structural and electrochemical characterization of HAT-CN-derived materials was subject to previous work in our group and will therefore be treated only briefly in the following.54The present sample of C-HAT-1600 is a hard carbon that is non-porous when analyzed by Ar physisorption at 87 K with a BET surface area of 20 m2 g−1 as shown in Fig. 1a. It contains 0.5 wt% of nitrogen according to elemental analysis. Despite the low surface area, a high irreversible capacity of 379 mA h g−1 can be seen in the first sodiation cycle in Fig. 1b and the material reaches a stable reversible capacity of 216 mA h g−1 in subsequent, capacity limited cycles. Despite the modest capacity values the material delivers, it is an interesting model substance to study the hard carbon sodiation mechanism for several reasons. It exhibits both sloping and plateau regions to reasonable extents and furthermore contains a sufficient amount of high-energy ion-adsorption sites due to the presence of heteroatoms. Therefore, sampling EIS-spectra along the sodiation curve of this material provides the opportunity to study the kinetics of each individual step of the sodiation process. Fig. 2a depicts the points in the sodiation curves at which EIS were recorded. Note that the elapsed time is plotted on the x-axis, in order to account for the relaxation steps, as the current pulse in each step only lasts 10 min. The curve shows four significantly distinct regions. These are (I) a sloping region with a higher slope (0–100 h, highlighted in blue), (II) a sloping region with a lower slope (100–300 h, highlighted in purple), (III) a prolonged plateau (300–1200 h, highlighted in green) and (IV), a region where the cell equilibrated around 0 V (t > 1200 h, highlighted in cyan).
In Fig. 2b the respective Nyquist impedance is shown for each of the four aforementioned regions. All spectra, which have been acquired at equilibrium potentials above 0 V, share the same qualitative feature—one semicircle of around 200 Ω on the real axis in diameter.
A second arc, decreasing in diameter with an increasing degree of sodiation can be perceived after 50 h. It clearly manifests in the impedance data after 200 h.
The DRT of the cell at each of the SOCs is shown in Fig. 2ci. Each peak corresponds to an RC-element with a characteristic time constant τ at the center of the peak. Therefore, it can be assigned to a certain electrochemical process which might (or might not) be coupled to mass transfer. The height of γ(τ) can be interpreted as the impedance with which the respective process contributes to the total impedance of the cell at a given SOC.
Interpretation of the EIS/DRT data
The ascending branch in the low-frequency region of the Nyquist-plots in Fig. 2 suggests the presence of a slow electrochemical process, i.e. diffusion, which plays an essential role in the sodiation of the hard carbons. This quantity will usually render a decent interpretation of the pure electrode kinetics exceptionally arduous. Schmidt et al.55 approached a similar problem, yet related to LIB, by modelling the low-frequency part of the EIS of a LiFePO4 cathode with a finite-length Warburg- in series with a capacitive element. By subtracting this portion from the experimental impedance data and finally performing DRT on the resulting spectrum, the authors were able to isolate the electrode kinetics. This procedure appears suitable for a system with relatively distinct and well understood processes underlying the EIS. However, the analysis of complex and less defined mechanisms—such as ones related to the sodium storage in hard carbons—should be kept as free from models and assumptions as possible. Therefore, we decided to use the raw impedance data for the calculation of the DRT in a first instance. Subsequently, we interpret the respective DRT results by assigning certain processes to the distinct signals of the DRT, and propose a mechanism which combines our own findings with insights known from the literature. Finally, we support our results by formulating a model which captures the experimentally observed trend.As expected already from the evaluation of the Nyquist plots, the main contribution to the impedance during the first, steeper sloping region arises from a process with a slow time constant of approximately τ = 19 s, called P1 henceforth. Due to the large time constant and the non-closing shape of the Nyquist plot, this process is interpreted as diffusive mass transfer of an ion, presumably sodium ions reaching their binding sites in the SEI layer. Two additional processes, P2 and P3, can be identified at τ = 2 s and τ = 0.6 s, respectively and one distinct and invariant peak P4 is found at τ = 10−3 s. It stands to reason to assume that these are related again to diffusive Na+ transport, here however already in the carbon material, after passing the SEI.
In the EIS, obtained during the less steep slope region, exemplarily shown at 200 h, the signals P1, P2, and P3 are decreasing in height and area. Therefore, their contribution to the overall impedance (relative to the P4 peak) decreases, either. All spectra after 900 h are characterized by only two essential processes, one at τ = 20 s and one at τ = 10−3 s, respectively. Due to the consistent nature of the process P4 within time and its relatively fast time constant, we propose that this particular process is related to electron transfer processes at metallic interfaces. After 1250 h the DRT-peak P4 is approximately doubled in height, which we explain by the formation of extended patches of metallic sodium starting to deposit on the working electrode from this point in time. Once sodium plating has occurred, there should be no (or at most a negligible) difference between the working electrode kinetics and the sodium-metal counter electrode.
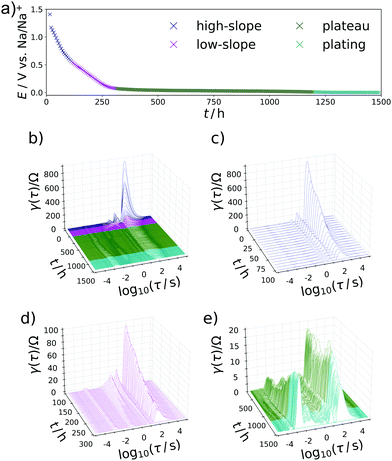
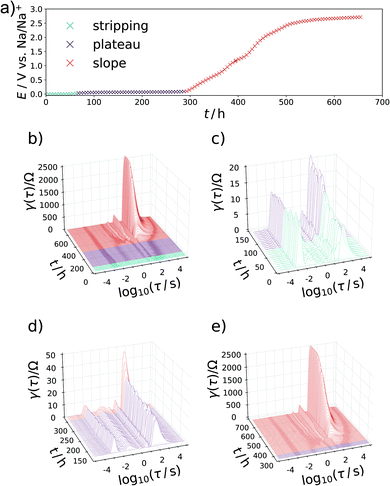
In a two-electrode setup the total impedance of both the working and counter electrode is measured. Therefore, to corroborate this assignment, the EIS of a symmetrical Na/Na cell was measured. The corresponding Nyquist plot and DRT are depicted in Fig. 3. Essentially, one semicircle is obtained in the Nyquist plot with a width being at least in the same range as the EIS of a charged Na/C cell after 900 h. The corresponding DRT shows the major peak at approximately τ = 10−3 s. Meanwhile, an additional peak centered at τ = 1 s is obtained in the DRT of the hard carbon/sodium cell, which is related to the small tail on the imaginary axis at low frequencies in the Nyquist representation. This signal can be assigned to the diffusion of Na+ ions through the separator. The difference between the two DRTs therefore has to be related to the carbon/SEI system. This experiment additionally hints at the stability of the electrolyte as well as the formed SEI within the time scale relevant for this study. To obtain a decent understanding of the remaining two peaks of the sloping region, the evolution of the DRT over several SOCs has to be monitored. For this purpose, 3D waterfall plots are presented in Fig. 4, where the DRTs are plotted versus time.
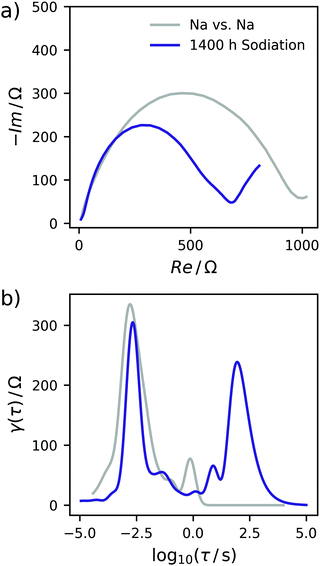 | ||
| Fig. 3 (a) Nyquist plot of the symmetrical Na/Na cell. (b) DRT of the symmetrical cell. Data of the C-HAT-1600 anode is shown for comparison. | ||
The specific characteristics of the DRTs over the course of sodiation are therein closely related to the potential/charge where it is taken. Therefore, the data were subdivided into the previously defined regions with (I) high slope, (II) lower slope, (III) plateau, and (IV) electroplating region. In the high-slope region the DRT is dominated by two strong and slow processes centered at τ = 19 s and 5 s. With further loading, these peaks are shrinking and shifting to slightly faster time constants (τ = 16 s and 2 s) towards the end of this loading stage.
Another important feature occurs throughout the second, low-slope phase in Fig. 4d which was formally attributed to the Na+ transport in the carbon phase. Besides further diminution of the τ = 16 s peak an additional splitting of the τ = 2 s peak into a signal which is constant and a process with a gradually decreasing relaxation time can be observed. This behaviour can be translated in a representative equivalent circuit model for the sodiation process, which is described and compared to the experimental results in the following section. The interplay between the processes P1 and P2 can be illustrated as follows: If P1 is due to the diffusion of Na-ions into the formed SEI and through it, it will stay relevant throughout the whole battery cycling process, where conductivity of this layer will of course improve with both increasing Na+ content and increasing driving potentials (for jump charge transport), thus explaining the slight shift and lowering relaxation strength with time. Exceeding a certain potential, the SEI ensured a steady sodium ion supply to the carbon, but P1 never disappears from the DRT, because the flux of sodium has to be ensured during the entire sodiation process. The carbon phase then can be loaded with increasing amounts of Na+ with increasing potential, as we also know from carbon supercapacitors. As P2 occurs mainly during the low-slope phase and becomes irrelevant as soon as P3 sets in, we assign it to the diffusive transport sodium ions into the carbon host to high adsorption energy binding sites. The faster process P3 is loading invariant and speculatively attributed to the faster electron transport in the defective carbon. The plateau phase sets in when the potential is close enough to the standard Na reduction potential so that Na(0) can be formed and deposited, i.e. the system moves from Na+/e− pair storage to sodium atom storage and deposition/intercalation. This region is split into an underpotential deposition region (where the materials environment adds stabilization energy which helps the sodium to be reduced), and an overpotential region where metallic sodium can form even without extra energy contributions. During the plateau phase between 300 h and 1150 h in Fig. 4e, the DRT does not change substantially as soon as the P3 mode is established. This indicates not only a kinetically homogenous process occurring in this voltage range, but also suggests that P3 is closely related to the sodium reduction, that is potentially the electron transfer through the carbon to reduce the preadsorbed sodium ions. This is in agreement with the common view on the sodiation of hard carbon anodes. Towards the transition of the plateau region into sodium electroplating a diminishing of the previously emerged DRT-peak at τ = 10−1 s in favor of the P4-peak can be observed, implying the end of carbon controlled processes and “free” overpotential electroplating.
The desodiation process
This established procedure is now also applied to the desodiation process. However, when we compare equilibrium sodiation and desodiation curves in Fig. 2a and 5a, the desodiation plateau is much shorter in time than the sodiation plateau, at constant current. This leaking of energy is related to the chosen special experimental conditions. Unlike usually directly recorded charge–discharge curves, the presented recording of dielectric spectra in every point under load takes several weeks (1000 hours correspond to about 42 days). We found that the sodium structures formed in the sodiation plateau cannot be maintained in our experimental cell over such a prolonged time. This is mostly self-discharge, but on top the fact that metallic sodium species with a formal oxidation state close to zero in nanodimensions rearrange over time (e.g., by coalescence or Ostwald ripening), leading to the formation of metallic sodium species not contacted by the anode. For this process to occur sodium must be neutral, as otherwise a rearrangement would not be possible.The sloping region however is unchanged and extends over 200 h in both forward and reverse process. The impedance spectra and DRTs for the release of sodium (shown in Fig. 5b–f) are similar to the ones measured during respective stages of the sodiation process. It follows that processes occurring during the voltage slope are highly reversible in nature. This is of special relevance for the sloping region, where ion adsorption or the formation of a solid solution of Na+ in a negatively charged carbon host is now plausible.25 Any intercalation process in between of two graphitic layers would change the structure and cause an expansion of the material, which of course would cause a hysteresis of the charge and discharge curve but could not proceed in such a reversible manner.
The development of the impedance spectra and DRTs during desodiation is presented as waterfall plots in Fig. 6. Upon changing from the electrostripping region at 0 V to the plateau region, the DRTs are comprised of the same four signals as in the sodiation. As soon as the sloping mechanism begins after about 300 h, the high-frequency peak at τ = 10−3 s again reduces, and low-frequency peaks begin to dominate the DRT, where the one at τ = 2 s develops first and reaches a steady state. After that, the signal at τ = 16 s gradually increases in significance. Remarkably, a shift in frequency of the peaks with SOC is not observed during the desodiation.
These data again show that diffusion of Na-ions is the main rate determining factor during the sodiation and desodiation of a hard carbon anode and by far outweighs processes such as charge transfer from support to carbon and from carbon to electrolyte. Improvement of the anode's performance can be achieved by adjusting its characteristics relevant for mass transport, such as particle size, porosity, and density, but the rate limiting step is related to the structure of the SEI, which is formed in the present case by an essentially uncontrolled random process in the first loading cycle. Further, the analysis of the cell by combined use of EIS and DRT can be employed to identify when the sodiation capacity of the carbon is reached and metallic sodium plating commences, by observing the size/area of the respective peak. This is particularly interesting in a full cell setup, where in a “healthy” cell no bulk sodium is present and therefore the appearance of an electroplating signal in the DRT should be seen immediately. This method could hence facilitate online monitoring of a cell.
Generally, the kinetics of the sodiation and desodiation are similar to each other where the desodiation proceeds in reverse order to the sodiation.
Lastly, it should be noted that the long-term stability of the structures formed during the plateau phase of the sodiation is questionable and probably less affected by frequent cycling than by long storage times at high states of charge. Temperature and material dependence of the stability should be considered, as the underlying processes such as Ostwald-ripening are highly temperature dependent.
Modelling upon the DRT results
To explain and illustrate the DRT results of the sodiation process by parameters with a physical meaning, the development of a suitable equivalent circuit model is inevitable. This model has to capture both, mass transport and electrode kinetics, for the sodium and the hard carbon electrode simultaneously.Furthermore, it has to be constructed from a reasonable amount of circuit elements in order to retain the physical relevance and to avoid overfitting.
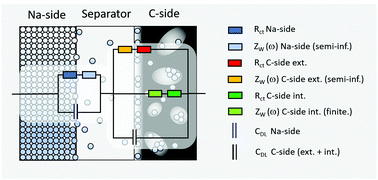
One possible equivalent circuit model, which we propose herewith, is depicted in Fig. 7. The sodium side of a full cell is therein described by a single charge transfer resistance which is connected in series with a planar finite transmissive Warburg element to account for the diffusion of sodium ions through the separator. This serial connection of resistances is in turn connected in parallel to a capacitor which accounts for the electrochemical double-layer capacity (Fig. 7, left hand side). The C-side (right hand side of Fig. 7) is in turn modelled by parallel connection of (a) a serial connection of a charge transfer resistance and a planar finite transmissive Warburg element at the boundary electrode/separator, (b) a charge transfer resistance in combination with a planar finite reflective Warburg element which accounts for the diffusion inside of the carbon and (c) a capacitor to account for the double layer capacity of the carbon. In case of (c), the double layer capacity cannot be subdivided into one part belonging to the finite and one belonging to the semi-infinite diffusion branch, since capacities connected in parallel unify to one capacity.
Though, the assumption of a planar finite reflective Warburg element (analogue to a thin layer cell) is certainly not ideal for quantitatively describing a porous hard-carbon electrode which consists of almost any kind of pore shapes, sizes and geometries, a qualitative approximation will still be possible. This is justified by the fact that any kind of finite-length diffusion will share the feature of an interrupted mass transfer in a reflective diffusion domain. At this stage it is therefore exceptionally worth to note that all of the following derivations and remarks do particularly not intend to provide a quantitative interpretation of the actual electrode kinetics. Instead, they should serve as a physical and mathematical supplement to the experimental results and a support for the proposed model. If one wished to quantitatively characterize the electrode kinetics, another—yet much more decent—model which captures the actual electrode porosity will be mandatory. However, developing such a model is certainly beyond the scope of this paper.
Setting up the model
The overall impedance of the equivalent circuit depicted in Fig. 6 is given by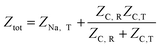 | (14) |
Defining the faradaic impedance as the combination of Warburg impedance and charge transfer resistance, one can rewrite the individual impedances (Zk,l with k,l = C,R,;C,T;Na,T) as
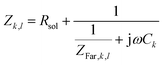 | (15) |
 and ZFar,k,l is the faradaic impedance of component k. For the transmissive elements it is defined as
and ZFar,k,l is the faradaic impedance of component k. For the transmissive elements it is defined as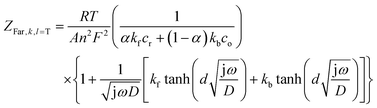 | (16) |
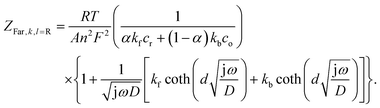 | (17) |
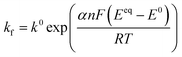 | (18) |
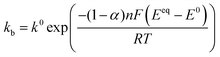 | (19) |
Generating impedance data of the base of eqn (14) can be performed readily by invoking eqn (15)–(19). The most crucial point is then the careful and reasonable choice of the parameters utilized for the simulations. Following this strategy, we have generated a set of EIS data which reproduces the experimentally observed peak drift in the DRT representation of the sloping region during the sodiation process. The respective experimental and simulated data is depicted in Fig. 8. The set of parameters used for the simulation is given in Table S1 (ESI†). Based on the qualitative model, the experimentally obtained features in the DRT might be explained as follows.
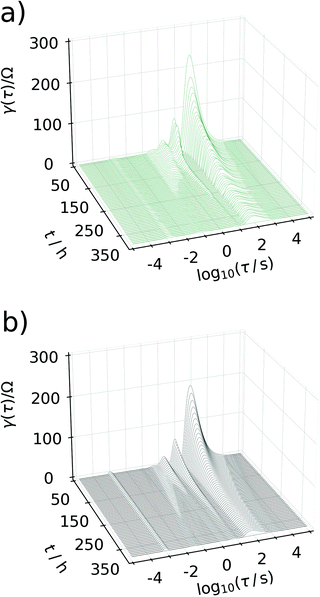 | ||
| Fig. 8 Waterfall plot comparing the DRTs calculated between 50 h and 350 h. In (a) experimental data are depicted, (b) shows DRTs calculated from simulated data assuming the model described in Fig. 7. | ||
At the beginning of the sodiation process, only a very low amount of sodium from former charge/discharge cycles is left inside of the carbon electrode. Consequently, the faradaic impedance (diffusion and charge transfer) of the carbon side will dominate the overall impedance owing to a low concentration of electrochemically active species. With an increasing degree of sodiation this particular resistance will decrease since (a) the amount of sodium inside of the electrode most likely located in the SEI increases progressively and, particularly, (b) the electrode potential will get closer to the E0. Since the electrode potential is related to the resistances in an exponential manner, only small changes in the difference of equilibrium potential and E0 will enforce a significant change in the resistance. Therefore, adjusting the equilibrium potential more towards E0 results in a significant decay of the peak related to the faradaic impedance at the beginning of the sodiation and previous to the sloping region. As the sodiation process continues, the carbon electrode will get progressively filled with sodium. However, the non-exponential potential drift in the sodiation curve which emerges in the sloping region cannot be explained in terms of a standard Nernstian system. It might be described accurately, by considering that the E0 of the carbon electrode can also adjust with an increasing degree of sodiation. This assumption appears to be reasonable, since an increasing degree of sodiation might be interpreted alternatively as a non-equilibrium phase transition and the resulting Na/C phase will possess its own and distinct E0 value. In this manner, an almost linear potential drift results, which was utilized in turn for the simulations. It shall not be left unnoticed that the frequency shift of the peak can only be reproduced, if the concentration of sodium in the carbon phase is assumed about three orders of magnitude smaller than it is estimated from Faraday's second law. It indicates that not all of the reversibly bound sodium is forming a Na/C phase, but electrodeposition of metallic sodium in carbon pores and other suitable sites of the material is more likely to start towards the end of the sloping phase.
The major, experimentally observed, feature which was reproduced by the simulation is the peak splitting and the peak drift in the DRT. This particular observation can be explained as follows. As the degree of sodiation in the carbon side increases, the individual resistances belonging to the reflective and the transmissive faradaic impedance will behave inherently different in the diffusive, but similar in the charge transfer part. As an increasing degree of sodiation decreases both resistances, the relative peak height in the DRT will decay. However, as soon as reflective diffusion path starts to block the current from flowing, the resistance will be governed more and more by the transmissive branch (since the carbon side is considered as a parallel connection of a transmissive and a reflective branch). At exactly this point, the peak splitting in the DRT will start. Since the equilibrium potential will adjust progressively towards the E0 of sodium with an increasing degree of sodiation, the remaining transmissive branch of the carbon side will also tend towards the peak associated with the sodium side which finally explains the drifting peak and concludes our remarks on the sloping region.
Conclusion
Electrochemical impedance spectra measured during the sodiation and desodiation of a hard carbon anode were investigated by means of DRT analysis. Generally, sodiation and desodiation were found to proceed via analogous pathways in a reverse order, therefore the following statements apply to both procedures. Spectra obtained during the sloping region of the sodiation curve were found to be largely dominated by diffusion processes, which became less relevant or simpler the more sodium was accommodated in the hard carbon. A constant DRT profile was observed during the plateau region. Upon exceeding the sodiation limit of the anode, the onset of electroplating could be followed in the DRT, rendering the method potentially useful to identify the formation of bulk sodium dendrites in full cells in equilibrium under practically relevant conditions.Finally, an equivalent circuit model based on the results gained from the DRT analysis could be set up and was used to simulate impedance data during the sloping region between 50 and 350 h.
Although the model is inherently qualitative, the processes, as well as their trends over time could be reproduced with sufficient precision. By choice of appropriate fit parameters, it was concluded that the deposition of sodium in appropriate sites of the carbon is the main process occurring during the plateau phase. In the next steps, it would be promising to validate the assignment of processes to DRT-features, which can only be realized by the combination with in situ methods. By acquisition of impedance data of anodes sodiated to several SOCs and in situ or even better operando measurement of NMR spectra it should be possible to follow the change of chemical shift and therefore the oxidation state of sodium.18,27 Small-angle X-ray scattering performed on such samples could furthermore provide valuable information on the region, where sodium is deposited within the electrode.22,57,58 With such a study, an entire view on the sodiation process of hard carbons can be proposed and afterwards EIS/DRT could be used to characterize the sodium storage mechanism of a hard carbon on a laboratory but also industrially more relevant scale. The calculation of a DRT from impedance data not only provides valuable insights into the sodiation mechanism of hard carbon anodes, but also provides guidelines for the tailored design of high-capacity sodium storage materials, as well as their electrochemical characterization.
Experimental section
Hexaazatriphenylenehexacarbonitrile (HAT-CN) was synthesized following the procedure of Rademacher et al.,56 in order to serve as the precursor for the preparation of the carbon material under study. HAT-CN was directly carbonized in a horizontal tube furnace under argon atmosphere according to the method of Walczak et al.53 In particular, HAT-CN was first heated to 60 °C at a heating rate of 4 °C min−1 and held for 30 min. In the second heating step, the material was at the same rate heated to the target temperature 1000 °C. Subsequently, the material was transferred to a high-temperature horizontal tube furnace and subjected to another heat treatment in an Ar atmosphere at 1600 °C for 60 min with a heating ramp of 3 °C min−1. It was denoted C-HAT-1600, 1600 indicating its final carbonization temperature.Gas physisorption measurements were conducted on a Vapor200C analyzer by 3P Instruments with Ar at −186 °C, and CO2 at 0 °C as probe gases. The samples were degassed under vacuum at 150 °C for at least 20 h before each measurement.
Specific surface areas were calculated from the adsorption branch by the multipoint BET-method in a p/p0-range of 0.01–0.15. Pore size distributions were calculated by quenched solid density functional theory (QSDFT) from the adsorption branch for slit/cylindrical shaped carbon pores, provided in the ASiQWin software package by Quantachrome Instruments. The nitrogen content was determined from combustive elemental analysis (EA) on a MICRO CHNS analyzer by elementar.
For the electrochemical characterization, the carbon material was fabricated into an ink by grinding it together with carbon black (SuperP, Alfa Aesar) as the conductive additive and adding an aqueous solution of carboxymethylcellulose (Sigma) as the binder in the ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of the respective components. The ink was dispersed in an ultrasonic bath for 1 h and stirred overnight, before it was coated on copper foils of 10 mm in diameter to achieve an area loading of approx. 1 mg cm−1. Electrochemical parameters obtained with such electrodes typically vary within 5% error.54 The impact of SuperP accounts to less than 5% of the capacity and therefore was neglected during the study in favour of the advantages it provides for the electrode conductivity.59 A 1 M solution of NaPF6 in a 6
1 of the respective components. The ink was dispersed in an ultrasonic bath for 1 h and stirred overnight, before it was coated on copper foils of 10 mm in diameter to achieve an area loading of approx. 1 mg cm−1. Electrochemical parameters obtained with such electrodes typically vary within 5% error.54 The impact of SuperP accounts to less than 5% of the capacity and therefore was neglected during the study in favour of the advantages it provides for the electrode conductivity.59 A 1 M solution of NaPF6 in a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 v/v mixture of ethylene carbonate and diethyl carbonate was used as the electrolyte. Potentials are always referred to as against Na/Na+, unless otherwise stated.
4 v/v mixture of ethylene carbonate and diethyl carbonate was used as the electrolyte. Potentials are always referred to as against Na/Na+, unless otherwise stated.
The electrochemical measurements were performed in 2-electrode Swagelok-type cells on a BioLogic MPG-2 potentiostat. Cells were assembled in asymmetrical setup of active material vs. sodium, and symmetrical cells with sodium vs. sodium in order to assign the processes to the respective half-cell reaction.
Charge discharge curves were recorded in different modes using (a) voltage limitation between 2.5 V and 0.002 V and (b) a lower capacitance limit of 85% of the previously determined plating capacity. The latter enables capacities at voltages below 0 V to be considered as well and hence losses due to overpotentials are overcome.
The measurement routine to obtain EIS data for DRT analysis consisted of 5 initial charge discharge cycles, after which the cell was fully desodiated to 2.5 V and left to rest for 30 min. Next, a current pulse of 18.6 mA g−1 was applied to the cell for 10 min, followed by a resting period of 5 h, to obtain a steady potential for the subsequent EIS at 10 mV amplitude in a frequency range from 20 kHz to 10 mHz with 11 frequencies per decade. The three steps of current pulse, rest, and EIS were repeated until and beyond the maximum sodiation of the working electrode, characterized by a crystallization overpotential due to the nucleation of bulk sodium.
Author contributions
KS: Conceptualization, Methodology, Validation, Formal analysis Investigation, Writing – Original Draft, Writing – Review and Editing, Visualization. TT: Conceptualization, Methodology, Software, Formal analysis, Writing – Original Draft, Writing – Review and Editing; JS: Methodology, Software, Formal analysis, Writing – Original Draft, Writing – Review and Editing; MA: Resources, Writing – Review and Editing; Supervision; CR: Writing – Review and Editing; Supervision; MO: Resources, Writing – Review and Editing; Supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support within the Max Planck-Fraunhofer Cooperation programme (CLUSTERBATT) is gratefully acknowledged by KS, MA and MO. TT and CR acknowledge funding by the Freie Universität Berlin as well as University of Bayreuth. JS gratefully acknowledges financial support by BMWi project 03 ET6129C (DegraBat). The authors thank Antje Völkel for the careful conduction of elemental analyses. Special thanks go to Dr. Jonas Pampel for ideas and fruitful discussions. Open Access funding provided by the Max Planck Society.Notes and references
- Y. You and A. Manthiram, Progress in High-Voltage Cathode Materials for Rechargeable Sodium-Ion Batteries, Adv. Energy Mater., 2018, 8, 1–11 CrossRef.
- X. Xiang, K. Zhang and J. Chen, Recent advances and prospects of cathode materials for sodium-ion batteries, Adv. Mater., 2015, 27, 5343–5364 CrossRef CAS PubMed.
- P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, From Lithium-Ion to Sodium-Ion Batteries: Advantages, Challenges, and Surprises, Angew. Chem., Int. Ed., 2018, 57, 102–120 CrossRef CAS PubMed.
- B. Jache and P. Adelhelm, Use of graphite as a highly reversible electrode with superior cycle life for sodium-ion batteries by making use of co-intercalation phenomena, Angew. Chem., Int. Ed., 2014, 53, 10169–10173 CrossRef CAS PubMed.
- E. Irisarri, A. Ponrouch and M. R. Palacin, Review—Hard Carbon Negative Electrode Materials for Sodium-Ion Batteries, J. Electrochem. Soc., 2015, 162, A2476–A2482 CrossRef CAS.
- D. A. Stevens and J. R. Dahn, The Mechanisms of Lithium and Sodium Insertion in Carbon Materials, J. Electrochem. Soc., 2001, 148, A803 CrossRef CAS.
- D. Saurel, J. Segalini, M. Jauregui, A. Pendashteh, B. Daffos, P. Simon and M. Casas-Cabanas, A SAXS outlook on disordered carbonaceous materials for electrochemical energy storage, Energy Storage Mater., 2019, 21, 162–173 CrossRef.
- A. Gibaud, J. S. Xue and J. R. Dahn, A small angle X-ray scattering study of carbons made from pyrolyzed sugar, Carbon, 1996, 34, 499–503 CrossRef CAS.
- D. Saurel, B. Orayech, B. Xiao, D. Carriazo, X. Li and T. Rojo, From Charge Storage Mechanism to Performance: A Roadmap toward High Specific Energy Sodium-Ion Batteries through Carbon Anode Optimization, Adv. Energy Mater., 2018, 8, 1–33 Search PubMed.
- P. C. Tsai, S. C. Chung, S. K. Lin and A. Yamada, Ab initio study of sodium intercalation into disordered carbon, J. Mater. Chem. A, 2015, 3, 9763–9768 RSC.
- C. Bommier, X. Ji and P. A. Greaney, Electrochemical Properties and Theoretical Capacity for Sodium Storage in Hard Carbon: Insights from First Principles Calculations, Chem. Mater., 2019, 31, 658–677 CrossRef CAS.
- J. Jiao, R. Xiao, M. Tian, Z. Wang and L. Chen, First-principles calculations on lithium and sodium adsorption on graphene edges, Electrochim. Acta, 2018, 282, 205–212 CrossRef CAS.
- E. Olsson, G. Chai, M. Dove and Q. Cai, Adsorption and migration of alkali metals (Li, Na, and K) on pristine and defective graphene surfaces, Nanoscale, 2019, 11, 5274–5284 RSC.
- D. A. Stevens and J. R. Dahn, High Capacity Anode Materials for Rechargeable Sodium-Ion Batteries, J. Electrochem. Soc., 2000, 147, 1271 CrossRef CAS.
- D. A. Stevens and J. R. Dahn, An In Situ Small-Angle X-Ray Scattering Study of Sodium Insertion into a Nanoporous Carbon Anode Material within an Operating Electrochemical Cell, J. Electrochem. Soc., 2000, 147, 4428 CrossRef CAS.
- S. Komaba, W. Murata, T. Ishikawa, N. Yabuuchi, T. Ozeki, T. Nakayama, A. Ogata, K. Gotoh and K. Fujiwara, Electrochemical Na insertion and solid electrolyte interphase for hard-carbon electrodes and application to Na-ion batteries, Adv. Funct. Mater., 2011, 21, 3859–3867 CrossRef CAS.
- K. Gotoh, T. Ishikawa, S. Shimadzu, N. Yabuuchi, S. Komaba, K. Takeda, A. Goto, K. Deguchi, S. Ohki, K. Hashi, T. Shimizu and H. Ishida, NMR study for electrochemically inserted Na in hard carbon electrode of sodium ion battery, J. Power Sources, 2013, 225, 137–140 CrossRef CAS.
- J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Mechanistic insights into sodium storage in hard carbon anodes using local structure probes, Chem. Commun., 2016, 52, 12430–12433 RSC.
- Y. Cao, L. Xiao, M. L. Sushko, W. Wang, B. Schwenzer, J. Xiao, Z. Nie, L. V. Saraf, Z. Yang and J. Liu, Sodium ion insertion in hollow carbon nanowires for battery applications, Nano Lett., 2012, 12, 3783–3787 CrossRef CAS PubMed.
- C. Bommier, T. W. Surta, M. Dolgos and X. Ji, New Mechanistic Insights on Na-Ion Storage in Nongraphitizable Carbon, Nano Lett., 2015, 15, 5888–5892 CrossRef CAS PubMed.
- P. Bai, Y. He, X. Zou, X. Zhao, P. Xiong and Y. Xu, Elucidation of the Sodium-Storage Mechanism in Hard Carbons, Adv. Energy Mater., 2018, 8, 1–9 Search PubMed.
- Y. Morikawa, S. ichi Nishimura, R. ichi Hashimoto, M. Ohnuma and A. Yamada, Mechanism of Sodium Storage in Hard Carbon: An X-Ray Scattering Analysis, Adv. Energy Mater., 2020, 10, 1–9 Search PubMed.
- B. E. Conway, Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications, Springer Science + Business Media New York, New York, NY, 1st edn, 1999 Search PubMed.
- C. Costentin and J. M. Savéant, Energy storage: Pseudocapacitance in prospect, Chem. Sci., 2019, 10, 5656–5666 RSC.
- M. B. Armand, in Materials for Advanced Batteries, ed. D. W. Murphy, J. Broadhead and B. C. H. Steele, Plenum Press, New York, NY, 1st edn, 1980, pp. 145–162 Search PubMed.
- R. Morita, K. Gotoh, M. Fukunishi, K. Kubota, S. Komaba, N. Nishimura, T. Yumura, K. Deguchi, S. Ohki, T. Shimizu and H. Ishida, Combination of solid state NMR and DFT calculation to elucidate the state of sodium in hard carbon electrodes, J. Mater. Chem. A, 2016, 4, 13183–13193 RSC.
- K. Gotoh, T. Yamakami, I. Nishimura, H. Kometani, H. Ando, K. Hashi, T. Shimizu and H. Ishida, Mechanisms for overcharging of carbon electrodes in lithium-ion/sodium-ion batteries analysed by operando solid-state NMR, J. Mater. Chem. A, 2020, 8, 14472–14481 RSC.
- K. Kubota, S. Shimadzu, N. Yabuuchi, S. Tominaka, S. Shiraishi, M. Abreu-Sepulveda, A. Manivannan, K. Gotoh, M. Fukunishi, M. Dahbi and S. Komaba, Structural Analysis of Sucrose-Derived Hard Carbon and Correlation with the Electrochemical Properties for Lithium, Sodium, and Potassium Insertion, Chem. Mater., 2020, 32, 2961–2977 CrossRef CAS.
- F. Xie, Z. Xu, Z. Guo and M.-M. Titirici, Hard carbons for sodium-ion batteries and beyond, Prog. Energy, 2020, 2, 042002 CrossRef.
- A. Lasia, Electrochemical Impedance Spectroscopy and its Applications, Springer New York, New York, NY, NY, 2014, vol. 9781461489 Search PubMed.
- J. P. Schmidt, T. Chrobak, M. Ender, J. Illig, D. Klotz and E. Ivers-Tiffée, Studies on LiFePO4 as cathode material using impedance spectroscopy, J. Power Sources, 2011, 196, 5342–5348 CrossRef CAS.
- J. P. Schmidt, P. Berg, M. Schönleber, A. Weber and E. Ivers-Tiffée, The distribution of relaxation times as basis for generalized time-domain models for Li-ion batteries, J. Power Sources, 2013, 221, 70–77 CrossRef CAS.
- M. Hahn, A. Schiela, P. Mößle, F. Katzer and M. A. Danzer, Revealing inhomogeneities in electrode lithiation using a real-time discrete electro-chemical model, J. Power Sources, 2020, 477, 228672 CrossRef CAS.
- M. Mandl, J. Becherer, D. Kramer, R. Mönig, T. Diemant, R. J. Behm, M. Hahn, O. Böse and M. A. Danzer, Sodium metal anodes: Deposition and dissolution behaviour and SEI formation, Electrochim. Acta, 2020, 354, 136698 CrossRef CAS.
- H. Schichlein, A. C. Müller, M. Voigts, A. Krügel and E. Ivers-Tiffée, Deconvolution of electrochemical impedance spectra for the identification of electrode reaction mechanisms in solid oxide fuel cells, J. Appl. Electrochem., 2002, 32, 875–882 CrossRef CAS.
- A. Leonide, V. Sonn, A. Weber and E. Ivers-Tiffée, Evaluation and Modeling of the Cell Resistance in Anode-Supported Solid Oxide Fuel Cells, J. Electrochem. Soc., 2008, 155, B36 CrossRef CAS.
- M. Hahn, S. Schindler, L.-C. Triebs and M. A. Danzer, Optimized process parameters for a reproducible distribution of relaxation times analysis of electrochemical systems, Batteries, 2019, 5, 43 CrossRef CAS.
- Impedance spectroscopy, ed. E. Barsoukov and J. R. Macdonald, Wiley & Sons, Hoboken, NJ, 2nd edn, 2005 Search PubMed.
- A. D. Franklin and H. J. Bruin, The Fourier analysis of impedance spectra for electroded solid electrolytes, Phys. Status Solidi, 1983, 75, 647–656 CrossRef CAS.
- M. Saccoccio, T. H. Wan, C. Chen and F. Ciucci, Optimal Regularization in Distribution of Relaxation Times applied to Electrochemical Impedance Spectroscopy, Electrochim. Acta, 2014, 147, 470–482 CrossRef CAS.
- Y. Zhang, Y. Chen, M. Yan and F. Chen, Reconstruction of relaxation time distribution from linear electrochemical impedance spectroscopy, J. Power Sources, 2015, 283, 464–477 CrossRef CAS.
- Y. Zhang, Y. Chen, M. Li, M. Yan, M. Ni and C. Xia, A high-precision approach to reconstruct distribution of relaxation times from electrochemical impedance spectroscopy, J. Power Sources, 2016, 308, 1–6 CrossRef CAS.
- A. Weiß, S. Schindler, S. Galbiati, M. A. Danzer and R. Zeis, Distribution of Relaxation Times Analysis of High-Temperature PEM Fuel Cell Impedance Spectra, Electrochim. Acta, 2017, 230, 391–398 CrossRef.
- T. Hörlin, Maximum entropy in impedance spectroscopy of non-inductive systems, Solid State Ionics, 1993, 67, 85–96 CrossRef.
- T. Hörlin, Deconvolution and maximum entropy in impedance spectroscopy of noninductive systems, Solid State Ionics, 1998, 107, 241–253 CrossRef.
- A. B. Tesler, D. R. Lewin, S. Baltianski and Y. Tsur, Analyzing results of impedance spectroscopy using novel evolutionary programming techniques, J. Electroceram., 2010, 24, 245–260 CrossRef.
- S. Hershkovitz, S. Baltianski and Y. Tsur, Harnessing evolutionary programming for impedance spectroscopy analysis: A case study of mixed ionic-electronic conductors, Solid State Ionics, 2011, 188, 104–109 CrossRef CAS.
- B. A. Boukamp, Derivation of a Distribution Function of Relaxation Times for the (fractal) Finite Length Warburg, Electrochim. Acta, 2017, 252, 154–163 CrossRef CAS.
- B. A. Boukamp and A. Rolle, Use of a distribution function of relaxation times (DFRT) in impedance analysis of SOFC electrodes, Solid State Ionics, 2018, 314, 103–111 CrossRef CAS.
- C. L. Lawson and R. J. Hanson, Solving Least Squares Problems, Society for Industrial and Applied Mathematics, Philadelphia, 1995 Search PubMed.
- M. Schönleber, D. Klotz and E. Ivers-Tiffée, A Method for Improving the Robustness of linear Kramers-Kronig Validity Tests, Electrochim. Acta, 2014, 131, 20–27 CrossRef.
- L. Wu, A parameter choice method for Tikhonov regularization, Electron. Trans. Numer. Anal., 2003, 16, 107–128 Search PubMed.
- R. Walczak, B. Kurpil, A. Savateev, T. Heil, J. Schmidt, Q. Qin, M. Antonietti and M. Oschatz, Template- and Metal-Free Synthesis of Nitrogen-Rich Nanoporous “Noble” Carbon Materials by Direct Pyrolysis of a Preorganized Hexaazatriphenylene Precursor, Angew. Chem., Int. Ed., 2018, 57, 10765–10770 CrossRef CAS PubMed.
- K. Schutjajew, J. Pampel, W. Zhang, M. Antonietti and M. Oschatz, Small, 2021, 2006767 CrossRef PubMed.
- J. Illig, T. Chrobak, M. Ender, J. P. Schmidt, D. Klotz and E. Ivers-Tiffée, Studies on LiFePO 4 as cathode material in Li-ion batteries, ECS Trans., 2010, 28, 3–17 CrossRef CAS.
- J. T. Rademacher, K. Kanakarajan and A. W. Czarnik, Improved Synthesis of 1,4,5,8,9,12-Hexaazatriphenylenehexacarboxylic Acid, Synthesis, 1994, 378–380 CrossRef CAS.
- C. Prehal, S. Grätz, B. Krüner, M. Thommes, L. Borchardt, V. Presser and O. Paris, Carbon, 2019, 152, 416–423 CrossRef CAS.
- C. Prehal, C. Koczwara, N. Jäckel, H. Amenitsch, V. Presser and O. Paris, Phys. Chem. Chem. Phys., 2017, 19, 15549–15561 RSC.
- C. M. Wu, P. I. Pan, Y. W. Cheng, C. P. Liu, C. C. Chang, M. Avdeev and S. Kang Lin, J. Power Sources, 2017, 340, 14–21 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00610j |
| ‡ Current address: Friedrich-Schiller-University Jena, Institute for Technical Chemistry and Environmental Chemistry, Center for Energy and Environmental Chemistry Jena (CEEC Jena), Philosophenweg 7a, 07743, Jena, Germany. |
| This journal is © the Owner Societies 2021 |