Dynamical decoupling in water–glycerol glasses: a comparison of nitroxides, trityl radicals and gadolinium complexes

Abstract

Our previous study on nitroxides in o-terphenyl (OTP) revealed two separable decoherence processes at low temperatures, best captured by the sum of two stretched exponentials (SSE) model. Dynamical decoupling (DD) extends both associated dephasing times linearly for 1 to 5 refocusing pulses [Soetbeer et al., Phys. Chem. Chem. Phys., 2018, 20, 1615]. Here we demonstrate an analogous DD behavior of water-soluble nitroxides in water–glycerol glass by using nitroxide and/or solvent deuteration for component assignment. Compared to the conventional Hahn experiment, we show that Carr–Purcell and Uhrig DD schemes are superior in resolving and identifying active dephasing mechanisms. Thereby, we observe a partial coherence loss to intramolecular nitroxide and trityl nuclei that can be alleviated, while the zero field splitting-induced losses for gadolinium labels cannot be refocused and contribute even at the central transition of this spin-7/2 system. Independent of the studied spin system, Uhrig DD leads to a characteristic convex dephasing envelope in both protonated water–glycerol and OTP glass, thus outperforming the Carr–Purcell scheme.

---

1 Introduction

Dynamical decoupling refers to the application of control pulses in an effort to extend the coherence time of the observed spin system.¹ For pulsed electron paramagnetic resonance (EPR), the application of nπ refocusing pulses therefore provides a spectroscopic handle on the electronic phase memory time. This quantity generally determines the available time window to manipulate the transverse magnetization, which in turn limits the distance range attainable by DEER experiments.² The 5-pulse^3,58 and 7-pulse DEER sequences⁴ utilize dynamical decoupling (DD) to push this distance frontier by adhering to the Carr–Purcell⁵ (CP) scheme for n = 2 and 3 refocusing pulses, respectively, at the expense of additional signal processing.^6,59 Similarly, CP set-ups with n = 2 and 4 have been integrated in the nDEER experiment that relies on non-selective excitation by chirp pulses.⁷ It is therefore of central importance to identify experimental conditions for which multiple refocusing provides an effective building block for pulsed EPR experiments, with dipolar spectroscopy being of particular interest. We consequently focus our attention on glassy matrices as the most commonly used spin environment. Our previous DD study addressed nitroxides in glassy o-terphenyl (OTP) and examined the influence of temperature, deuteration and concentration on the refocusing effect of n = 1 to 5 pulses.⁸ Temperature-dependent Hahn relaxation (n = 1) revealed two separable relaxation contributions between 10 and 60 K, which required the introduction of a sum of two stretched exponentials (SSE) model. This expression includes an individual dephasing time T_mi, and a stretch parameter ξ_i for the fast (i = 1) and slow (i = 2) relaxation component, weighted by their respective amplitudes c_i. Variation of sample composition by nitroxide and/or OTP deuteration enabled the assignment of the fast contribution to a mainly nitroxide-driven and the slow contribution to a matrix-induced process. Temperatures above 60 K render the two mechanisms indistinguishable due to the thermal activation of the relaxation-inducing rotation of the geminal methyl groups present in the nitroxide. Generally, (intra)molecular motion hampers the refocusing effect with no and little DD gain for n > 1 at 80 K and room temperature (RT), respectively. Freezing out these classical motions by operating in the low temperature regime, e.g. at 40 K, results instead in a linear increase of T_m2 with n, and a solvent-specific ξ₂ value range. The SSE model therefore provides a convenient framework to characterize DD performance, and facilitates a detailed comparison regarding the specific arrangement of the control pulses. While the equidistant CP sequence achieves longer T_m2 values in deuterated OTP (dOTP), the optimized interpulse delays according to Uhrig⁹ proofed superior in OTP, yielding larger ξ₂ and somewhat larger T_m2 values. Independent of all experimental conditions described so far, a low radical concentration suppresses spin–spin interactions that cannot be refocused in case of magnetically equivalent spin populations.^8,10,11

Here we go beyond the model character of OTP, as a homogeneous solvent that does not induce specific solute–solvent interactions, and study water–glycerol glasses, bringing DD closer to EPR applications of chemical and biological interest. This heterogeneous solvent is potentially more complex due to its ability to form hydrogen bonds^12,13 and the effect of preferential solvation,^14–16 while its glass-transition temperature (T_g) of 165 K¹⁷ (for 50 : 50 v : v water : glycerol ≈ 20 mol% glycerol) limits the temperature range of the glassy state relative to OTP (T_g = 243 K). For large solutes in small-molecule solvents, such as spin-labeled proteins in water–glycerol, solute dynamics can be slaved by solvent dynamics.¹⁸Vice versa it has been found by simulations that collective modes of the protein influence water dynamics.¹⁹ Mode-coupling theory of binary mixtures suggests that at the ergodic–non-ergodic transition, which corresponds to the glass transition, dynamical correlations of very dilute solutes decay to zero in spite of such slaving.²⁰ While these phenomena are important for understanding electron spin relaxation in the vicinity of the glass transition temperature²¹ and above, we here focus on the non-ergodic regime well below the glass transition temperature where fast collective motion might still be expected to influence longitudinal relaxation, but proceeds on a time scale well separated from the one that influences transverse relaxation.

Moreover, we explore a wider range of paramagnetic species to match the considerable progress in spin-label development in the last ∼15 years,^22,23 that addressed limitations faced when working with gem-dimethyl-nitroxide-labeled bio-molecules under physiological conditions. These being nitroxide reduction in the cellular environment to an EPR-inactive species²⁴ and T_m values in the nanosecond range at room temperature under immobilization.²⁵ Triarylmethyl(trityl) radicals and gadolinium(III) complexes are chemically more inert, so that the introduction of corresponding spin labels enabled in-cell measurements.^26–28 Secondly, their diverse spectroscopic properties with respect to nitroxide radicals allow for orthogonal labeling schemes.^29–31 The carbon-based trityl radical is by design unique in its narrow lineshape stemming from limited hyperfine (HF) couplings to intra-molecular magnetic nuclei and a small g-anisotropy due to the high symmetry of the molecular structure. In contrast to these two organic S = 1/2 systems, gadolinium(III) is an EPR active high-spin species with S = 7/2 and thus seven allowed EPR transitions that are affected by zero-field splitting (ZFS). Its characteristic powder spectrum consists of a narrow −1/2 ↔ +1/2 transition in the center, and a broad feature arising from |m_S| > 1/2 transitions at Q- and W-band frequencies.

We compare the DD performance of these three different paramagnetic species in water–glycerol glass at low temperature and concentration. Under the chosen conditions, the excited electron spins (A with resonance frequency ω_A) are sufficiently diluted to avoid dephasing via other pulse-flipped spins, a process called instantaneous diffusion (ID).³² Also, electron spin diffusion (SD) due to dipole–dipole interactions with the non-excited electron spin population (B with resonance frequency ω_B) becomes negligible, as T₁ flips are too slow and dilution scales the dipolar term required to overcome the energy difference ω_A–ω_B. Instead, nuclear spin diffusion (NSD) is the driving dephasing mechanism,³³ leading to spectral diffusion of the electronic magnetization into the dipolar-coupled nuclear spin bath. Some nuclei close to the paramagnetic center are excluded from this mechanism as they experience a paramagnetic shift and therefore lie within the radius of the so called diffusion barrier,³⁴ which depends on the system's spin density distribution. Beside this effect, NSD requires a difference in HF coupling to two decoherence-inducing I₁ = I₂ = 1/2 nuclei, such as protons, that is comparable to the dipole–dipole coupling of this nuclei pair to enable diffusion-driving nuclear flip-flop transitions. Naturally, this matching condition depends on the molecular structure of the spin system and the characteristics of the chosen solvent. We assess dephasing contributions from intra-molecular interactions for three different paramagnetic species shown in Fig. 1 and couplings to solvent nuclei by CP and Uhrig DD experiments for up to five π pulses. To this end, we introduce H-mNOPEG and D-mNOPEG as presented in Fig. 1(c), which are analogues of the stiff nitroxides H-mNOHex and D-mNOHex used in the OTP study⁸ and shown in Fig. 1(b), to compare matrix effects induced by OTP to those of water–glycerol mixtures.

Fig. 1 Chemical structures of nitroxides (a) H-NO and D-NO that correspond to the paramagnetic moeity of H-mNOPEG and D-mNOPEG, respectively, (b) H-mNOHex and D-mNOHex soluble in OTP, and their water-soluble analogues (c) H-mNOPEG and D-mNOPEG. Chemical structures of the studied (d) trityl radicals and (e) gadolinium(III) complexes together with the names used for these compounds within the manuscript.

The trityl radical OX063 and its partially deuterated version OX071, see Fig. 1(d), feature reduced inter-molecular HF couplings compared to nitroxides, and a comparison to gadolinium(III) complexes addresses contributions from ZFS. The magnitude of this strong spin–spin interaction can be tuned by ligand choice³⁵ and/or selective excitation of the |m_S| = 1/2 or |m_S| > 1/2 transitions.³⁶ As ZFS affects the former transition only to second order,³⁷ we evaluate to what extent DD results for pure S = 1/2 system translate to the −1/2 ↔ +1/2 transition of gadolinium complexes with increasing static ZFS, using the complexes Gd-NO₃Pic, Gd-DOTA-M and Gd-PCTA presented in Fig. 1(e).

Overall, this study of protonated/partially deuterated nitroxides and trityl radicals, as well as gadolinium(III) complexes in protonated/deuterated water–glycerol glass demonstrates that the presence of two distinguishable dephasing pathways is not limited to nitroxides in o-terphenyl. Under favorable conditions, these dephasing contributions can already be identified by traditional Hahn relaxation measurements, while DD experiments with n > 1 are superior in resolving them. In addition, we demonstrate that DD schemes are more than just a building block for pulsed EPR experiments, as the scaling of the stretched exponential parameters with n provides sample information beyond the conventional Hahn relaxation analysis.

2 Materials and methods

2.1 Choice of glass former and paramagnetic species

The equivolume mixture of water and glycerol was chosen as a glass former for its relevance to chemical and biological EPR applications. Moreover, this mixture approximates the most widely used matrix for dynamic nuclear polarization (DNP) experiments of biological systems, known as “DNP juice” (60 : 30 : 10 vol% glycerol-d₈ : D₂O : H₂O).³⁸

Fig. 1 displays all paramagnetic species relevant for this work, including the nitroxides H-mNOHex and D-mNOHex that have been used in our previous OTP study.⁸ They resemble the popular spin label MTSSL and combine them with a long stiff tail. Note, that the different tail lengths of H-mNOHex and D-mNOHex do not translate into a different decoherence behavior of these nitroxides, in particular in the low temperature regime investigated here.⁸ The analogous water-soluble nitroxides H- and D-mNOPEG feature three poly(ethylene oxide) (PEG) chains to make the otherwise hydrophobic tail compatible with the aqueous matrix.³⁹ This long stiff tail avoids complications from local motions in the glass voids, which may induce dephasing in case of smaller nitroxides such as H- and D-NO. This effect would make our DD results potentially less transferable to spin-labeled biomolecules. Moreover, we rely on deuteration of the geminal methyl groups attached to the pyrroline ring to assign relaxation contributions stemming from intra-molecular and solvent nuclei. The trityl radical OX063 and its partially deuterated analog OX071 were chosen for their hydrophilic properties. The recent development and characterization of OX063- and OX071-based spin labels⁴⁰ showcase the advantageous properties of the OX063 core, such as a small tendency to aggregate and long T_m values at 50 K.

Our choice of gadolinium(III) complexes was determined by the relative size of their axial ZFS parameter D: Gd-NO₃Pic exhibits the smallest value of 485 ± 20 MHz, Gd-DOTA/Gd-DOTA-M an intermediate value of 714 ± 43 MHz and Gd-PCTA the largest value with 1861 ± 135 MHz.³⁵ Many used gadolinium(III) spin labels rely on the DOTA-ligand or variations thereof, though the benefits of Gd-NO₃Pic-based labels for DEER experiments have also been demonstrated.⁴¹

2.2 EPR spectroscopy and sample preparation

EPR samples were prepared from stock solutions of the paramagnetic molecule of interest in H₂O or D₂O. A serial dilution of H-mNOPEG in H₂O characterized this nitroxide by its concentration-dependent continuous-wave (CW) EPR spectrum at RT. Samples for pulsed EPR experiments were prepared by diluting the stock solutions to final spin concentrations of 10 to 25 μM in equal volumes of H₂O:glycerol or D₂O:glycerol-d₈. Deuterated water and glycerol-d₈ were purchased from Sigma-Aldrich, and glycerol from Acros Organics. Approximately 40 μL of the resulting mixture were filled into 3 mm o.d. quartz capillaries, flash frozen under ambient conditions and stored in liquid nitrogen to form and maintain a glassy frozen state. The influence of oxygen dissolved in the solvent on the low-temperature relaxation behavior of trityl radicals was specifically tested, as they serve as oxygen probes at room temperature.⁴² To this end, a solution of OX071 in D₂O:glycerol-d₈ was degassed with ten freeze–pump–thaw cycles by drawing vacuum for 1 minute and flushing for 10 seconds with nitrogen gas. Additionally, an oxygen-saturated sample was prepared by bubbling the solution for 30 minutes with oxygen gas.

2.2.1 Continuous-wave EPR. RT CW EPR spectra of nitroxide H-mNOPEG were recorded with a Bruker Elexsys E500 spectrometer at an X-band frequency of 9.5 GHz, using the Bruker super-high-Q resonator ER4122SHQ. Glass capillaries of 1.5 mm o.d. were filled with a volume of 10 μL. All spectra were acquired with common settings of 0.6362 mW microwave power (25 dB attentuation), 100 kHz field modulation, and 0.1 mT amplitude modulation. The spin concentration was determined by double-integration of the nitroxide spectrum with respect to a reference sample of known concentration.

2.2.2 Pulsed EPR. All pulsed EPR experiments were performed at Q-band frequencies, while some additional W-band DD measurements were carried out for Gd-NO₃Pic in H₂O:glycerol. We selected these bands, as pulsed dipolar spectroscopy (PDS) experiments with the here investigated paramagnetic molecules are most commonly performed at these frequencies. This choice also avoids strong nuclear modulation from deuterium present in the sample. A commercial Q-band spectrometer, Bruker ElexSysII E580, was used in combination with a 200 W traveling wave tube (TWT) amplifier and a home-built resonator designed for 3 mm o.d. capillaries.⁴³ The W-band measurements were conducted with an ElexSys E680 spectrometer using an EN 680-1021H resonator. Q-band Hahn echo experiments with t_π = 2·t_π/2 = 12 ns or t_π = 2·t_π/2 = 96 ns established the influence of temperature, spin concentration and the presence of oxygen on the decoherence behavior of specific samples. In this way, favorable experimental conditions for DD series of n = 1 to 5 refocusing pulses were identified. All decoherence experiments were performed using rectangular, monochromatic pulses at the maximum of the respective powder spectrum (B_max), while for the three gadolinium(III) complexes in H₂O:glycerol the field position corresponding to the lower kink of their spectrum was additionally probed (B_kink). Temperature and sample composition determine the experimental shot repetition time (SRT). Its optimal value was chosen by monitoring the Hahn echo intensity as a function of SRT to avoid T₁ saturation effects.

DD experiments were run with constant-bandwidth pulses (Q band: t_π = t_π/2 = 12 ns, W band: t_π = t_π/2 = 16 ns) and full phase cycles to isolate the correct coherence pathway.⁸ Specifically, a two-step phase cycle on the π/2 pulse with [(+x) − (−x)] suffices for the Hahn experiment (n = 1) to cancel the receiver offset, instead sequences with n > 1 require 4ⁿ⁻¹ steps. These phase cycles consist of the same phase variation for the π/2 pulse, while all n π pulses apart from the last two are cycled in phase by [(+x) − (−y) + (+x) − (−y)], ensuring inversion of coherence order. The last π pulse has a constant phase, while the pulse with index n − 1 is subject to a [(+x) − (−x)] cycle. The n π pulses were arranged according to DD schemes of CP and Uhrig that determine the n + 1 interpulse delays Δ_j with 1 ≤ j ≤ n + 1. For a total sequence length T, the CP experiment relies on equidistant interpulse delays Δ₁ = Δ_n+1 = T/(2n) and Δ_j = T/n for 2 ≤ j ≤ n, while the optimized interpulse delays derived by Uhrig⁹ are defined by

For n = 2 the CP and Uhrig pulse sequence are identical and for n = 1 they both reduce to the Hahn experiment. The decoherence under a given DD experiment was measured by incrementing the total sequence length, and integrating symmetrically around the maximum of the last refocused echo formed at time T. The resulting electron spin coherence decay is reported as a function of t, referring to the elapsed time after the first π/2 pulse. Note that the time resolution of the spectrometer (in our case Q band: 2 ns, W band: 4 ns) induces round-off errors to the initial interpulse delays as well as increments of the Uhrig DD experiment. We found that deviations by a few percentages with respect to the optimal delays according to eqn (1) did not affect the experimental outcome. For some slowly relaxing species, required trace length exceeded the maximum length of the TWT gate. In these cases, we assembled the total relaxation trace from two separate acquisitions, placing all pulses first in a single TWT window, and second in individual windows.

Dipolar oscillations were recorded with the 4-pulse DEER sequence⁶⁰ π/2_obs–τ₁–π_obs–(τ₁ + t_dip)–π_pump–(τ₂ − t_dip)–π_obs–τ₂ by placing the pump pulse (π_pump = 12 ns) at B_max of the nitroxide powder spectrum and the observation pulses (π/2_obs = π_obs = 16 ns) at an offset of 100 MHz. The interpulse delays τ₁ and τ₂ were set to 200 ns and 3 μs, respectively, and the dipolar evolution time t_dip was incremented by 8 ns in combination with an 8-step nuclear modulation phase cycle.

2.3 Data treatment

The stretched exponential (SE) expression c·exp[−(t/T_m)^ξ] originates from a semi-classical electron spin decoherence description⁴⁴ that models the driving nuclei flip-flop transitions as a stochastic process. After its first introduction,⁴⁵ the SE model has found wide application in capturing the shape of electron spin relaxation V(t) in glassy matrices. Our previous DD study of nitroxides H-mNOHex and D-mNOHex in OTP and dOTP required the introduction of the sum of two stretched exponentials (SSE) model defined byfeaturing a fast (i = 1) and slow (i = 2) relaxation contribution. The relative weight of the two pathways can be expressed by the respective normalized amplitude factor . After phase-correction, each experimental decoherence trace was subject to a non-linear least-square fitting routine to both the SE and SSE model. The ESI† describes the procedure in more detail. To quantify the uncertainty associated with the resulting, optimal parameter values for T_m1 and ξ_i, the 95% confidence intervals were computed. The corresponding A₁ confidence intervals result from error propagation with respect to c₁ and c₂. In cases where electron spin echo envelope modulation (ESEEM) affect the beginning of the decay trace, the fit was only based on the maxima of these oscillations to correctly parameterize the underlying envelope of the relaxation.⁴⁵ Finally, the choice for the appropriate dephasing model was based on the fit quality of the SE in comparison to the SSE expression. Whenever the fit residuals were comparable, the simpler SE model was selected based on the principle of parsimony.

3 Results and discussions

3.1 Synthesis of H-mNOPEG and D-mNOPEG

The water soluble nitroxides H-mNOPEG (H-1) and D-mNOPEG (D-1) were synthesized as shown in Fig. 2.

Fig. 2 Synthesis of the water soluble nitroxides H-mNOPEG and D-mNOPEG. The syntheses of iodide 2 and alkyne 3 are described in the ESI,† Part A. Nitroxide D-12 was not isolated. DMAP = 4-(dimethylamino)pyridine, phen = phenanthroline, THF = tetrahydrofuran, TolH = toluene, TMS = trimethylsilyl, TIPS = triisopropylsilyl, rt = room temperature.

We adhered to the established strategy^39,46,47 to attach the PEG substituents rather late in the reaction sequence in order to minimize the cases in which a highly polar and water soluble compound needs to be isolated. Both nitroxides were constructed using iodide 2. Their syntheses differ in the sequence of attaching the nitroxide moiety and installing the PEG substituents and in the reaction type used for combining the nitroxide moiety with the overall tail. The overall yield was much better for H-mNOPEG (41%; calculation included synthesis of alkyne 3 from 4-ethynylaniline and H-11) than for D-mNOPEG (17%). However, please note that none of the transformations was optimized. The route used to obtain D-mNOPEG is of advantage as the most precious part, the perdeuterated nitroxide moiety, is introduced in the very last step. In addition, it circumvents the risk of CuI-induced reduction of the nitroxide to a hydroxylamine, a side reaction that occurs occassionally during an alkynyl-aryl coupling⁴⁶ which is used here to link together iodide 2 and alkyne 3. On the other hand, the route used to assemble H-mNOPEG is attractive when the rod-like moiety is very precious or is to be varied because the consecutive steps in this route are smaller in number. Furthermore, other experiments suggest that iodide 2 can be furnished with PEG substituents first and then alkyne 3 can be coupled, a sequence that would reduce the number of steps performed with molecules carrying the nitroxide moiety, to only two: synthesis of alkyne 3 and its CC cross coupling to obtain H- and D-mNOPEG. The syntheses of H- and D-mNOPEG provide blueprints for the synthesis of water soluble analogs of the dinitroxides with rod-like spacers and hexyl side chains⁴⁸ soluble in o-terphenyl.

3.1.1 EPR characterization. Initial EPR characterization of H-mNOPEG in H₂O by CW spectroscopy at RT resulted in a spectrum dominated by the characteristic triplet line that arises from HF coupling to ¹⁴N present in the nitroxide structure as shown in Fig. 3(a).

Fig. 3 Characterization of H-mNOPEG by EPR spectroscopy. (a) Concentration-dependent X-band CW spectra of H-mNOPEG in H₂O recorded at RT and at a microwave frequency of 9.5 GHz (blue to yellow). The dashed, red line corresponds to an EasySpin simulation using the chili function with g = [2.0150 2.0057 2.0037], one HF coupled ¹⁴N nucleus with [16 16 98] MHz, four HF coupled ¹³C nuclei with [7 7 37] MHz, a Gaussian peak-to-peak linewidth of 0.1005 mT and a rotational correlation time tensor of t_corr = [0.3136 122] ns. (b) Concentration-dependent dipolar oscillations of H-mNOPEG in H₂O:glycerol measured using the 4-pulse DEER experiment at 60 K.

The isotropic tumbling of a small nitroxide, such as H-NO, in the viscous solvent H₂O leads to equal peak-to-peak amplitudes of these three signals. The reorientation of H-mNOPEG follows an anisotropic motion instead and the tumbling is slower as evident from the relative intensities as well as width of the lines. In addition, ¹³C satellites are visible for the two low-field transitions, yet these are significantly broadened at a spin concentration of 200 μM. By a dilution series down to 25 μM we studied concentration dependence of the CW EPR spectrum. The results point to aggregation of H-mNOPEG as the source of the broadening. Aggregate formation can be avoided by operating below the critical concentration. The corresponding CW spectrum can be simulated using EasySpin⁴⁹ in the slow-motional regime (chili) by including HF couplings to one ¹⁴N and four ¹³C nuclei and an axial rotational correlation time tensor in line with the linear and rigid structure of H-mNOPEG. Fig. 3(a) suggests a critical concentration somewhat above 25–45 μM in H₂O and at RT, as the low concentration spectrum agrees well with the simulation.

For low-temperature EPR experiments it was crucial to understand whether addition of the cryo-protectant glycerol and/or subsequent shock-freezing affects the aggregation equilibrium. Attempts to isolate the effect of glycerol by CW spectra of H-mNOPEG in H₂O:glycerol at RT failed, as glycerol addition slowed the tumbling motion, so that the additionally broadened lines masked any concentration effects. We turned to the 4-pulse DEER experiment to monitor the aggregation behavior in water–glycerol glass at low temperature. Fig. 3(b) displays the distinct dipolar oscillations observed at spin concentrations of 80 and 45 μM that reveal structurally well-defined aggregates. Fig. Sa3, ESI† show distance distributions obtained from the 80 μM sample by Tikhonov regularization. The flat background of the DEER traces implies relatively small sizes of the formed aggregates and thus a small number of molecules that form these aggregates. Decreasing the concentration leads to a reduced modulation depth corresponding to a smaller number of dipolar-coupled spins. Contributions of non-refocusable spin–spin interactions to the decoherence measurements were therefore excluded by working with nitroxide concentrations of ≤30 μM. Our combined CW and DEER results suggest that glycerol addition and rapid freezing do not shift the aggregation equilibrium significantly. However, we noted an appearance of dipolar oscillations of a 30 μM sample after EPR experiments close to the T_g of H₂O:glycerol upon re-cooling to 60 K. Clearly, local re-organization takes place as soon as the glass starts to soften. We avoided complications from the thermal history¹² of samples by storing the capillaries in liquid nitrogen between measurements. We have obtained analogous results as described in this Section 3.1.1 by CW and pulsed EPR measurements of D-mNOPEG.

3.2 Comparing OTP to water–glycerol glass: nitroxides

3.2.1 Temperature-dependent Hahn echo decay. The Hahn echo decay of H-NO and D-NO in both H₂O:glycerol and D₂O:glycerol-d₈ were measured as a function of temperature to characterize the transverse relaxation behavior of these water-soluble nitroxides before the compounds H-mNOPEG and D-mNOPEG became available. The chosen temperature range of 10 to 140 K ensures the glassy state of the solvent mixture. Previous temperature-dependent decoherence results for H-mNOHex and D-mNOHex in OTP and dOTP were obtained at spin concentrations of 100 μM. For reasons of comparison, the same concentration as well as pulse lengths of t_π = 2·t_π/2 = 12 ns were used for the study of H- and D-NO.‡ Both the SE and SSE model were fit to the experimental relaxation traces. The ESI† reports the individual fitting results for the four samples in Fig. Sa5–Sa8 and compares the SE/SSE parameter values as a function of temperature in Fig. Sa4. In most cases the SE fit clearly deviate from the experimental Hahn data by much more than the noise level. Additionally, Hahn echo decays were recorded with softer pulses (t_π = 2·t_π/2 = 96 ns) to identify contributions from ID.

In summary, we obtain analogous temperature-dependent transverse relaxation results in water–glycerol and OTP for temperatures between 10 and 140 K, where both solvents are in the glassy state. Three central similarities are found:

1. Distinct temperature regimes:

• A low-temperature regime between 10 and 60 K that is characterized by the prevailing SSE model.

• A borderline regime between 70 and 140 K, where the relaxation can be either described by the SE or SSE model.

2. Two separable relaxation contributions in the low-temperature regime, as can be demonstrated either by SSE parameterization or experimental pulse-length variation in combination with nitroxide and/or solvent deuteration.

3. Effect of solvent deuteration on the fit parameter values of T_m2 and ξ₂ in the low-temperature regime.

Note, that the SSE model was applicable to all combinations of H-mNOHex and D-mNOHex with OTP and dOTP in the previously defined low-temperature regime. In water–glycerol glass, D-NO in protonated solvent H₂O:glycerol between 10 and 40 K poses an exception, as fits to its Hahn echo decay cannot reliably separate the fast from the slow contribution. We tested whether pulse length variation could reveal the two components instead. This approach varies the pulse-length dependent ID mechanism with respect to NSD that dominates the fast and/or slow relaxation pathway if the sample features a protonated nitroxide and/or solvent.⁸ Only a minor pulse-length effect results for D-NO in H₂O:glycerol as visible in Fig. Sa9, ESI.† In contrast to the Hahn experiment, DD schemes with n > 1 can resolve the two underlying processes as discussed in Section 3.2.2.

Upon comparing the SSE parameter values in the low-temperature regime for both solvents, it is evident that the matrix-related ξ₂ is generally larger than the nitroxide-related ξ₁, while ξ₂ values associated with proton-driven processes are reduced upon deuteration. Overall, the stretch parameters are somewhat smaller for water–glycerol systems with ξ₁ ≤ 1 and ξ₂ ≥ 1.5, relative to the ones in o-terphenyl with ξ₁ ≈ 1 and ξ₂ ≥ 2. Specifically in H₂O:glycerol the difference in dephasing time and stretch parameter between the nitroxide-related fast and the matrix-related slow process is considerably smaller relative to OTP, rendering the separation challenging, as illustrated for D-NO in H₂O:glycerol. Solvent deuteration significantly prolongs T_m2, while the precise factor depends on the chosen matrix. Exchanging OTP by dOTP doubles the T_m2 value, while the corresponding substitution by D₂O:glycerol-d₈ causes a larger increase in the temperature range of 10 to 40 K. This observation shows that the effect of deuteration does not simply scale with the gyromagnetic ratio of ²H relative to ¹H, as often argued. Instead, other factors contribute, such as the quadrupole coupling of the I = 1 nuclei in a deuterated matrix. As discussed below, different closest hydrogen–hydrogen distances in the two matrices may also play a role. Interestingly, both deuterated solvents display a strong temperature dependence of the SSE parameters T_m2 and ξ₂ at 50 and 60 K, while in OTP and H₂O:glycerol these parameters only decrease slightly in this temperature window.

3.2.2 DD at 40 K. DD data sets of H-mNOPEG and D-mNOPEG in H₂O:glycerol and D₂O:glycerol-d₈ were acquired at 40 K to compare the refocusing effects to results from the corresponding experiments in OTP and dOTP, while operating in the temperature window with constant stretched exponential parameters for both the protonated as well as deuterated matrices. Fig. Sa10, ESI† shows the resulting data for all four samples at a spin concentration of 10 μM. Thereby, the described aggregation effects are avoided and the chosen experimental conditions match the OTP study (20 μM), as these low concentrations suppress contributions from ID that cannot be refocused. Fig. Sa12–Sa15, ESI† demonstrate that the SSE framework has to be utilized to model the DD results for all four samples. The Hahn decay of D-mNOPEG in H₂O:glycerol poses an exception (analogue to D-NO in Section 3.2.1), whereas DD experiments with n > 1 can resolve the two relaxation contributions as shown in Fig. Sa11(c), ESI† with relatively large ξ_i 95% confidence intervals.

The DD characteristics of H- and D-mNOHex in o-terphenyl and H- and D-mNOPEG in water–glycerol glass are compared by the SSE parameter value dependence on n as summarized in Table 1 and shown in Fig. Sa11, ESI† for the four samples in water–glycerol. Fig. 4(a and b) highlight the comparison for the fully protonated case, i.e. H-mNOHex in OTP and H-mNOPEG in H₂O:glycerol, while Fig. 5(a and b) present their deuterated analogues D-mNOHex in dOTP and D-mNOPEG in D₂O:glycerol-d₈.

Table 1 DD characteristics for studied nitroxides (20 μM in o-terphenyl, 10 μM in water–glycerol), trityl radicals (10 μM) and gadolinium complexes (25 μM) based on CP and Uhrig experiments with n = 1 to 5, obtained from corresponding SSE fits. Linear regression determines the reported T_m1/n slopes

Paramagnetic molecule	Matrix	Temperature [K]	[μs]	[μs]	ξ 2 range	T m1/n [μs]	ξ 1 range
a Excluding ξ1 value of Hahn.
H-mNOHex	OTP	40	9.2	11.1	2.7–5.1	2.4	0.7–1.0
D-mNOHex	OTP	40	11.3	11.1	2.7–5.1	5.0	0.7–2.4
H-mNOPEG	H2O:glycerol	40	6.3	6.5	2.7–5.7	2.4	0.4–1.3
D-mNOPEG	H2O:glycerol	40	6.2	6.6	2.6–6.3	4.0	0.5–2.9
OX063	H2O:glycerol	110	6.3	6.3	2.7–5.4	4.2	1.7–2.1
OX071	H2O:glycerol	110	6.3	6.4	2.8–5.3	4.0	1.6–2.0
Gd-NO3Pic	H2O:glycerol	10	6.0	6.0	2.6–5.2	4.0	1.5–2.2^a
Gd-DOTA-M	H2O:glycerol	10	5.6	5.9	2.6–5.0	3.4	1.3–1.8^a
Gd-PCTA	H2O:glycerol	10	4.7	4.9	2.3–3.9	2.7	1.3–1.7^a
H-mNOHex	dOTP	40	17.5	15.4	2.2–2.8	4.1	0.4–1.4
D-mNOHex	dOTP	40	17.2	15.2	2.0–2.7	4.0	1.2–2.1
H-mNOPEG	D2O:glycerol-d8	40	14.2	13.6	1.9–3.0	1.9	0.4–1.1
D-mNOPEG	D2O:glycerol-d8	40	14.9	13.9	1.6–2.8	3.4	1.6–2.5

---

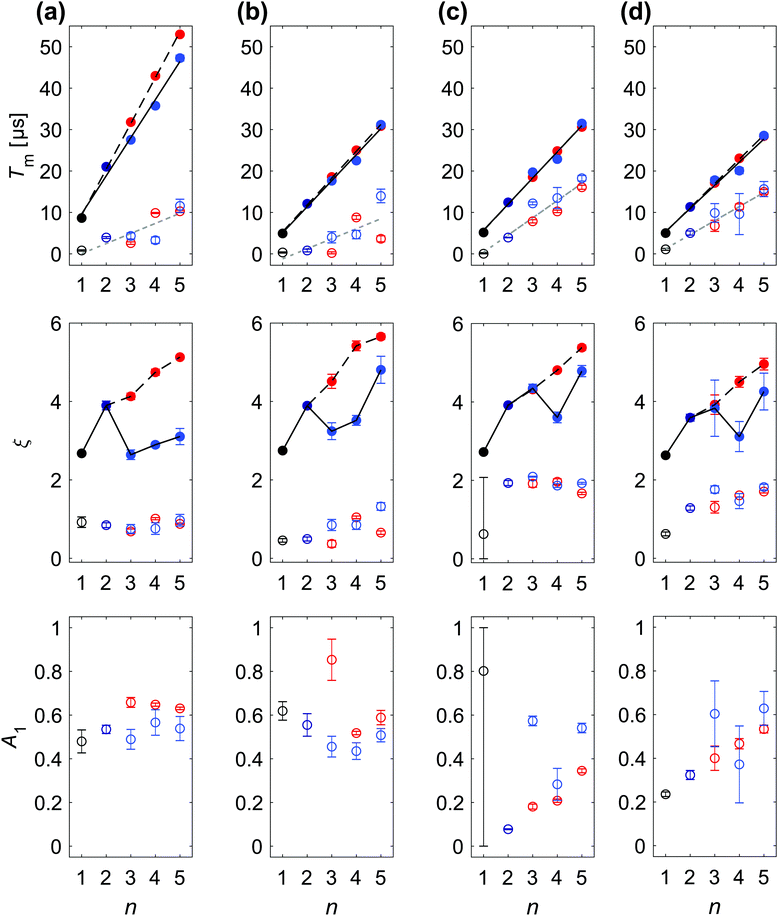Fig. 4 SSE parameterization of DD data recorded at B_max for protonated paramagnetic molecules in protonated solvent: (a) H-mNOHex in OTP (20 μM) at 40 K, (b) H-mNOPEG in H₂O:glycerol (10 μM) at 40 K, (c) OX063 in H₂O:glycerol (10 μM) at 110 K, (d) Gd-DOTA-M in H₂O:glycerol (25 μM) at 10 K. Each column displays the fitting parameters T_m1, ξ_i, A₁ (top to bottom) with the associated 95% confidence intervals for a particular sample as a function of n. The color encodes the DD experiment with Hahn (●), CP/Uhrig n = 2 (), CP n > 2 () and Uhrig n > 2 (), while empty circles correspond to the fast (i = 1), and filled to the slow (i = 2) relaxation contribution. Lines in the T_m1 subplots report linear regression results for experiment-specific T_m2 increase with n for CP (black, solid) and Uhrig (black, dashed), whereas a common T_m1 gain with n (grey, dashed) was determined. All resulting slopes are summarized in Table 1. Black lines shown in the ξ_i subplot serve as a guide for the eye to indicate ξ₂ dependence on n for CP (solid) and Uhrig (dashed) experiments.

Fig. 5 SSE and SE parameterization of DD data recorded at B_max for partially deuterated nitroxide and trityl radicals and for protonated Gd-DOTA-M in deuterated solvent: (a) D-mNOHex in dOTP (20 μM) at 40 K, (b) D-mNOPEG in D₂O:glycerol-d₈ (10 μM) at 40 K, (c) OX071 in D₂O:glycerol-d₈ (10 μM) at 110 K, (d) Gd-DOTA-M in D₂O:glycerol-d₈ (25 μM) at 10 K. Each column displays the fitting parameters T_mi, ξ_i, A₁ (top to bottom) with the associated 95% confidence intervals for a particular sample as a function of n. The color encodes the DD experiment with Hahn (●), CP/Uhrig n = 2 (), CP n > 2 () and Uhrig n > 2 (), while the fast (i = 1) and slow (i = 2) relaxation contributions in case of the SSE model are distinguished by empty and filled circles, respectively. Lines in the corresponding T_mi subplots report linear regression results for experiment-specific T_m2 increase with n for CP (black, solid) and Uhrig (black, dashed), whereas a common T_m1 gain with n (grey, dashed) was determined. All resulting slopes are summarized in Table 1. The SE fit for (c) and (d) resulted in a non-linear increase of T_m with n, modeled by a power law ∝ n^γ. Black lines shown in the ξ_i subplot serve as a guide for the eye to indicate ξ₂ dependence on n for CP (solid) and Uhrig (dashed) experiments.

DD experiments in both o-terphenyl and water–glycerol result in a linear increase of T_mi with n along with a characteristic ξ_i dependence. However, the DD effect of each π pulse is generally smaller in water–glycerol than in o-terphenyl as evident from the reduced T_m2/n slopes summarized in Table 1. Specifically in protonated solvents, the slow relaxation contribution yields a T_m2 value range of 5–30 μs in H₂O:glycerol relative to 9–55 μs in OTP for n = 1 to 5. The same decrease in dephasing time was reported for the X-band Hahn decay of TEMPONE at 40 K with a T_m value of 8.5 μs in OTP and 4.6 μs in H₂O:glycerol.³³ The study attributes this effect to the roughly two-fold higher proton concentration in H₂O:glycerol, and a thus doubled flip-flop frequency relative to OTP. In fact, the (shortest) intramolecular ¹H–¹H distance in the respective solvent molecule may rather be the decisive structural parameter.§ You et al.⁵⁰ performed cluster correlation expansion (CCE) calculations to demonstrate that distinct orientations of all closest proton pairs in single crystal malonic acid determine T_m and ξ of CPMG traces with n = 1–6. Experiments confirmed these decoherence predictions as a function of single crystal orientations and suggested that the same proton pair control persists in polycrystalline malonic acid. A CCE implementation was also used to compute the spin dynamics of TEMPO and TEMPO-d₁₈ in H₂O from their solvated structures under the Hahn experiments and allowed to deal with the large Hilbert space arising from ∼1500 nuclei required for a converged decoherence description.⁵¹ Sorting these nuclei by their individual T_m contributions, mapped the most effective NSD-driving protons at a distance of 4–8 Å from the central electron spin.⁵¹ The two protons of a water molecule show a similar contribution to the electron dephasing, forming a flip-flopped proton pair with a larger dipolar coupling than any two intramolecular OTP protons.

Also in the deuterated solvents, n = 1 to 5 achieve smaller T_m2 of 20–80 μs in D₂O:glycerol-d₈ relative to 25–100 μs in dOTP. It is evident that solvent deuteration suppresses the dephasing more strongly in H₂O:glycerol than in OTP glass, as already observed for Hahn relaxation. Specifically, the T_m2 value on average doubles for all DD experiments in dOTP as compared to the experiments in OTP, while refocusing in D₂O:glycerol-d₈ leads on average to a 2.8-fold increase in T_m2 with respect to refocusing in H₂O:glycerol. Additionally, the performance difference between CP and Uhrig refocusing is reduced in water–glycerol compared to o-terphenyl with Uhrig decoupling still attaining somewhat larger T_m2 and ξ₂ values in H₂O:glycerol relative to CP, and vice versa in D₂O:glycerol-d₈. Whereas, the absolute T_m2 values differ for water–glycerol and o-terphenyl, the associated ξ₂ parameters are similar. In particular, protonated solvents lead to convex Uhrig DD traces, associated with large ξ₂ values. Considering the fast relaxation component, the parameters T_m1 and ξ₁ of H- and D-mNOPEG match the results for H- and D-mNOHex in T_m1/n increase and ξ₁ range as summarized in Table 1. Nitroxide deuteration increases the dephasing time of the fast pathway in combination with somewhat larger ξ₁ values. Overall, these results firstly imply that the separation of the fast from the slow relaxation contribution is more challenging for water–glycerol matrices than for the o-terphenyl matrix. Secondly, the nitroxide nuclei clearly contribute to the overall coherence loss in both matrices. The origin of the distinct time scales T_m1 < T_m2 may arise from either of the two following mechanisms: the methyl nuclei reside within the diffusion barrier,⁵¹ which does not entirely suppress NSD but instead renders the associated decoherence pathway independent from the solvent nuclei-driven process. Alternatively, the methyl nuclei have to be viewed as a rigid but hindered C₃ rotor, whose rotational ground state is sufficiently populated at low temperatures. The effect of rotational tunneling can then either enhance or suppress decoherence depending on the system's tunneling splitting.⁵² Importantly, in both cases the methyl nuclei distinguish themselves from o-terphenyl, water or glycerol protons by this additional tunneling term that alters the effective NSD-based mechanism.⁵²

Finally, we briefly discuss the parameter A₁, which is difficult to interpret as for three out of four sample compositions its values do not exhibit a clear trend with n. Only for the two fully deuterated cases, i.e. D-mNOHex in dOTP and D-mNOPEG in D₂O:glycerol-d₈, the corresponding Fig. 5(a and b) show a clear increase of A₁ with n. Interestingly, these A₁ values are generally larger for protonated nitroxides. Each DD experiment probes an ensemble of nitroxides in a given matrix, therefore the A₁ parameter indicates which radical fraction relaxes through close-by nitroxide-nuclei rather than solvent-nuclei, and therefore reports on the heterogeneity of the direct spin environment.

3.2.3 DD at 60 K. Upon increasing the temperature from 40 to 60 K, the achievable DD gain defined by(where T_10% refers to the time point T at which 10% of the initial Hahn intensity is reached, serving as a reference level) generally decreases for nitroxides with geminal methyl groups as the decoherence-inducing classical methyl group rotation starts to set in.⁸ However, there is an interest to explore temperatures slightly above 40 K, as the optimal signal-to-noise ratio of an echo experiment is determined not only by T_m, but also by the polarization of the probed spin transition and the longitudinal relaxation time T₁. For example, 4-, 5-, and 7-pulse DEER experiments are generally performed at 50 K, as this temperature has been identified to lead to an optimal signal-to-noise ratio for 4-pulse DEER experiments.² If the DEER observer sequence is, however, arranged according to a DD scheme, this optimum may shift depending on g_DD. Fig. Sa16, ESI† presents the DD results for H-mNOPEG in H₂O:glycerol and D₂O:glycerol-d₈ at 60 K. Upon increasing the temperature from 40 to 60 K, the decoupling effect is more strongly reduced in the deuterated solvent. Namely, the maximal g_DD is achieved by Uhrig n = 5 for H-mNOPEG in H₂O:glycerol with g_DD = 4.8 at 40 K that reduces to 4.0 at 60 K. In D₂O:glycerol-d₈ CP n = 5 leads to the largest observed g_DD factor of 2.4 at 40 K that decreases to 1.3 at 60 K. Under the latter experimental conditions, the refocusing effect saturates for n = 2–3, as the magnetization loss due to pulse imperfection dominates the decoupling efforts. The observed difference in DD behavior between the prontonated and deuterated solvent confirms the Hahn decoherence results between 50 and 60 K as discussed in Section 3.2.1. Upon thermal activation of the methyl rotation this dephasing pathway becomes more efficient, in particular if solvent-induced NSD is suppressed by deuteration. For this reason a larger g_DD results for H₂O:glycerol with refocusable proton-driven NSD, while the absolute T_m values in D₂O:glycerol-d₈ are larger in combination with a reduced DD effect. This suggests that already for the conventional 4-pulse DEER experiments an optimal signal-to-noise ratio is achieved at temperatures below 50 K, if the spin environment can be sufficiently deuterated.

For biological applications, the refocused magnetization does not arise from isolated nitroxide radicals but instead from spin labels attached to a biomolecule. To mimic this effect to some extent, we compare the DD performance of the small H-NO with the elongated H-mNOPEG, which imitates an attached spin-label, in H₂O:glycerol at 40 and 60 K as shown in Fig. Sa17, ESI.† At 40 K, the respective DD traces nearly overlap with a slight increase in decoherence observed for H-mNOPEG. This difference is significantly larger at 60 K, resulting in less convex shapes for H-mNOPEG particularly visible for Uhrig experiments. Therefore, local motion of H-NO in the glass voids does not induce serious dephasing at 40 K, while already at 60 K H-mNOPEG is subject to small anisotropic reorientation that modulate the hyperfine field induced by the surrounding solvent protons. This finding can be utilized twofold. First, our DD results at 40 K are expected to translate to solvent-exposed spin-labeled biomolecules in the low temperature limit. Second, local dynamics impact the refocusing effect, so DD experiments may serve as a spectroscopic tool in itself to identify the motional fingerprint.

3.3 Trityl radicals

Trityl radicals are characterized by a narrow and symmetric spectrum, arising from limited intramolecular hyperfine couplings and a small g-anisotropy. Consequently, the Q-band field-swept echo-detected EPR spectrum of OX063 is by a factor of ∼5 narrower than that of H-mNOPEG in H₂O:glycerol as shown in Fig. 6(a). Placing a π pulse of 12 ns length at B_max covers the entire trityl radical line, while inverting only a fraction of the nitroxide spins.

Fig. 6 Normalized field-swept echo-detected Q-band EPR spectra presented on a relative frequency axis for comparison. The shaded area in yellow indicates the excitation bandwidth of a pulse of length t_p = 12 ns, placed at the maximum of the respective EPR line. (a) H-mNOPEG at 40 K (blue) and OX063 at 110 K (orange) in H₂O:glycerol at a spin concentration of 10 μM and (b) 25 μM Gd-NO₃Pic (black), Gd-DOTA-M (dark-grey) and Gd-PCTA (grey) in H₂O:glycerol at 10 K. The lighter the color, the larger is the ZFS of the shown gadolinium complex, as evident from the increasing width of the spectrum. The field positions B_max (blue arrow) and B_kink (orange stars) are indicated.

Therefore, OX063 and its partially deuterated analog OX071 provide ideal spin systems to assess contributions from off-resonance excitation effects on DD. Furthermore, the center of spin density is shielded from both intramolecular and solvent protons unlike in nitroxide radicals. Before comparing the decoupling performance on these two organic S = 1/2 species, we discuss the effect of temperature, concentration and oxygen on the Hahn relaxation of OX063 and OX071.

3.3.1 Relaxation characterization by Hahn experiment. The trityl sample with the highest deuterium content, namely OX071 in D₂O:glycerol-d₈, was chosen as the most sensitive probe to determine at which spin concentration ID contributions can be neglected. Fig. Sa19(a), ESI† presents the pulse-length dependent Hahn relaxation data at 50 K and at spin concentrations of 10 and 20 μM. An eight-fold decrease in excitation bandwidth suppresses the dephasing substantially at 20 μM, while a small appears to remain at 10 μM. For identical pulse lengths, ID therefore contributes to trityl decoherence at a relatively low spin concentration as compared to nitroxide radicals. While the Q-band nitroxide line is spectrally diluted, the higher density of states in the trityl case results in a larger fraction of excited spins at a given excitation bandwidth and thus a higher probability for ID.

We tested the effect of solvated oxygen on the trityl Hahn relaxation at 50 K by saturating a 20 μM OX071 D₂O:glycerol-d₈ solution with oxygen gas prior to flash freezing the sample. In solution, trityl radicals serve as agents for oximetric imaging as their linewidth depends on the oxygen concentration.⁴² Under these conditions, the Heisenberg exchange mechanism dominates, so that collisions with molecular oxygen lead to broadened lines and faster relaxation rates. At low temperatures, the required translational dynamics is frozen out, yet Fig. Sa19(b), ESI† demonstrates that other oxygen-induced processes become relevant at 50 K. Saturating the solution with oxygen thereby accelerates T_m relative to the flash frozen sample under atmospheric conditions, while ID contributes equally in both cases. In addition, we observed a decrease in T₁ as the permissible SRT value is reduced from 18 to 14 ms. The driving mechanism relies either on local field fluctuations induced by modulated dipole–dipole interactions between the trityl radical and the triplet state of the molecular oxygen, or T₁ flips of the oxygen electrons.⁵³ However, the effect is subtle and degassing a 10 μM solution and subsequent freezing had little to no effect on the Hahn relaxation at 110 K as shown in Fig. Sa19(c), ESI.† For this reason, all other experiments were performed without degassing the sample.

Finally, the temperature range between 50 to 120 K was screened to optimize the temperature for a reasonable SRT, rendering DD experiments feasible, while staying below T_g of water–glycerol. According to temperature-dependent X-band relaxation measurements of 200 μM OX063 in H₂O:glycerol,⁵⁴T₁ and therefore the required SRT is continuously reduced with increasing temperature, while T_m remains nearly constant between 80 and 140 K. Fig. Sa18(a), ESI† displays temperature-dependent Hahn relaxation of 10 μM OX063 in D₂O:glycerol-d₈ along with the determined SRT values in brackets. We chose a temperature of 110 K, where a convenient SRT of 2 ms can be used, while accepting a loss ΔT_10% ≈ −6 μs relative to the longest T_10% value of 28.6 μs in our temperature series at 50 K.

3.3.2 DD at 110 K. The relaxation behavior under DD was determined for OX063 and OX071 in H₂O:glycerol and D₂O:glycerol-d₈ under optimized experimental conditions as described in Section 3.3.1, namely by preparing all four possible sample compositions at a spin concentration of 10 μM and flash freezing the mixture under normal atmosphere before measuring the DD data sets at 110 K as presented in Fig. Sa20, ESI.† Evidently, the nature of the solvent determines both the achievable decoherence time as well as shape of the electron spin relaxation. In particular, in protonated solvent Uhrig decoupling leads to a characteristic convex dephasing envelope, while the CP experiments yield less convex envelopes. Fig. Sa22–S25, ESI† show to what extent the SE or SSE model is able to capture the experimental DD results. Interestingly, the optimal model switches depending on the solvent and n. For H₂O:glycerol, the SSE model is necessary to fit data acquired with n > 1, while the SE model is sufficient for the Hahn relaxation, i.e. n = 1. The contrary is observed for D₂O:glycerol-d₈, where the SE model applies for n > 1 and n = 1 requires the parameter-richer SSE model. For the following discussion, we somewhat simplify the situation and rely on the SSE model for the protonated, and on the SE model for the deuterated matrix. Thus, the Hahn relaxation in H₂O:glycerol is overfitted by the SSE model (as visible by the large 95% confidence intervals associated with the ξ₁ and A₁ parameter for n = 1 in Fig. 4(c)), while the SE model underfits the Hahn relaxation in D₂O:glycerol-d₈ (as indicated by the oscillating residuals visible in Fig. Sa23 and S25, ESI†). The dependence of the stretched exponential(s) parameters on n for all four samples is summarized in Fig. Sa21, ESI,† while the fully protonated and deuterated case, i.e. OX063 in H₂O:glycerol and OX071 D₂O:glycerol-d₈, are presented in Fig. 4(c) and 5(c), respectively. A comparison of these two subplots demonstrates the striking difference in DD performance between protonated and deuterated water–glycerol: each additional refocusing pulse applied to OX063 in H₂O:glycerol results in an analogous gain of T_m2 with n as observed for H-mNOPEG in the same solvent. The ξ₂ parameter increases in both cases with n, while Uhrig induces larger ξ₂ values, i.e. more convex decay shapes, compared to CP decoupling. In contrast, all DD traces of OX071 in D₂O:glycerol-d₈ follow a mostly exponential decay with ξ = 1.0–1.2, showing little difference between the CP and Uhrig refocusing scheme. The T_m gain with n is sub-linear, indicating a saturation behavior and can be modeled by a power-law expression ∝ n^γ with γ = 0.02–0.03.

3.3.3 Comparing DD results of trityl radicals and nitroxides. We have found similarities and differences in the DD effect between nitroxides and trityl radicals in water–glycerol glass. Now, we deepen this comparison by noting that both types of paramagnetic species face the same dephasing mechanisms despite the difference in temperature at which the nitroxide (40 K) and the trityl DD data were acquired (110 K). All samples were prepared with the same solvent mixture and fall into the low-concentration regime so that ID/SD effects are negligible as established before. Similarly, we demonstrated that 40 and 110 K is close to the low temperature limit for H/D-mNOPEG and OX063/OX071, respectively. Field fluctuations that are induced by classical motion are therefore frozen out, and the large difference in temperature directly results from the absence of methyl groups in the OX063 or OX071 structure. Modified nitroxides that feature spirocyclohexyl groups instead of geminal methyl groups⁵⁵ are thus expected to eliminate this temperature difference. Consequently, NSD drives the dephasing as evident from the strong isotope effect observed upon deuteration. Assuming that the dipole–dipole couplings of nuclear pairs in the H₂O:glycerol and D₂O:glycerol-d₈ matrix are temperature independent between 40 and 110 K, the change of DD behavior should directly reflect the difference in HF coupling between the electron spin and the coupled nuclei.

In H₂O:glycerol the SSE parameter values associated with the slow relaxation pathway agree well between H-mNOPEG and the trityl radical OX061 as visible from Fig. 4(b and c). Independent of the radical, decoupling the water–glycerol protons achieves an increase in T_m2 by 6.2–6.6 μs per n increment as summarized in Table 1. Secondly, the T_m2/n slope is the same for CP and Uhrig refocusing with ξ^Uhrig₂ > ξ^CP₂. In contrast to OTP, the water–glycerol ξ₂ values are somewhat larger, in combination with a visible difference in T_m2/n increase for CP and Uhrig. Therefore, the slow relaxation contribution for trityl radicals in H₂O:glycerol can be certainly assigned to the solvent protons, even though solvent deuteration did not enable this identification due to the described model switching. Focusing on the fast relaxation process, T_m1/n values range from 4.0–4.2 μs for OX063 and OX071, matching D-mNOPEG with 4.0 μs. H-mNOPEG differs by a smaller T_m1 increase of 2.4 μs per n increment along with smaller ξ₁ and somewhat larger A₁ values. For both types of radicals, the intramolecular protons/deuterons are not strictly inside the diffusion barrier and participate in NSD.^16,51 Practically, the deuteration of the nitroxide methyl groups appears equivalent to keeping all hydrogen atoms at a distance from the unpaired electron, as it was the design idea for the trityl radicals. In both cases the intramolecular HF coupling is scaled (neglecting possible effects from the quadrupole coupling of the C–²H bond) and the potential contribution from rotational tunneling is suppressed, affecting the fast relaxation pathway in a comparable way. Experimentally, this reduction in HF coupling is also evident from the diminished ESEEM for OX071 in H₂O:glycerol in Fig. Sa20(c) (ESI†) compared to D-mNOPEG in H₂O:glycerol in Fig. Sa10(c), ESI.†

As discussed, trityl radicals in D₂O:glycerol-d₈ show a distinctive DD behavior apparent from applicability of the simpler SE model with ξ values independent of n and a sub-linear T_m/n increase. Solvent deuteration combined with weak intramolecular HF couplings of OX063 and OX071, renders the intramolecular and solvent nuclei indistinguishable so that a single relaxation process is observed. In H₂O:glycerol, solvent-induced NSD is the same for nitroxide and trityl radicals, implying comparable HF couplings to the matrix protons. The deuterated water–glycerol mixture strongly alters the HF field experienced by the electron spin of the trityl radicals, as apparent from the reduced linewidth (suppression of unresolved HF couplings to solvent protons) of the trityl Q-band spectrum in Fig. Sa18(b), ESI.† Further, the ²H ESEEM modulation depth of the trityl radicals (Fig. Sa20(b), ESI†) is smaller than for H-mNOPEG in the same solvent (Fig. Sa10(b), ESI†), confirming the expectation that the electron spin in trityl radicals is shielded from nearby solvent nuclei by the bulk of the molecule. OX063 differs from OX071 by 24 ¹H versus 24 ²H atoms present in the hydroxyethyl substituents as shown in Fig. 1(d). According to Fig. Sa21, ESI† these protons induce ξ^OX063 > ξ^OX071 in D₂O:glycerol-d₈ along with a reduced T_m saturation behavior of OX063 (γ^OX071 = 0.02–0.03 compared to γ^OX063 = 0.4–0.5). While the Hahn relaxation of OX071 is generally slowed compared to OX063, their relaxation traces cross for n > 1, as decoupling of the additional intermolecular protons in OX063 is more efficient for the first half of the DD decays, whereas deuteration proofs superior for longer total sequence lengths T. This observation teaches an important lesson for future assessment of potential spin labels: characterizing the decoherence decay by the Hahn experiment does not necessarily transfer linearly to the spin label's behavior in a multi-pulse experiment. Firstly, DD experiments can reveal relaxation contributions that are not resolved by a single refocusing pulse. Secondly, spin label characterization by decoupling sequences allows for an educated trade-off between a spectroscopic effort, e.g. pulsed dipolar spectroscopy by 5-pulse, 7-pulse or n-DEER, and a synthetic effort. Of course, the optimal choice depends on the required signal-to-noise ratio for a given spectrometer sensitivity and available measurement time.

Finally, the characteristic trityl line reveals a systematic limitation that multi-pulse EPR experiments generally appear to face: all DD data sets recorded so far feature a progressive decrease in initial echo intensity with increasing number of refocusing pulses independent of the CP or Uhrig scheme. In case of nitroxides, we hypothesized that effects from off-resonance excitation accumulate with increasing n. However, experiments with frequency-modulated hyperbolic secant pulses (testing pulse bandwidths of 50–500 MHz) applied to H-mNOHex in OTP and dOTP could not suppress these losses. Neither do errors in the pulse amplitude account for the decrease in absolute echo intensity, as the Meiboom-Gill⁵⁶ variation of the CP sequence did not suppress the observed cumulative error. Relative to the nitroxide Q-band powder spectrum, the trityl linewidth is dramatically reduced and can be entirely inverted by the π pulses employed for the DD experiments, as illustrated in Fig. 6(a). Since the same echo intensity losses are observed for nitroxide and trityl radicals, off-resonance effects can be safely disregarded. Excitation of formally forbidden electron–nuclear transitions may contribute to the observed losses. But given the ESEEM modulation depths that we detect, additional sources of currently unknown origin are likely to contribute.

3.4 Gadolinium

Gadolinium(III) complexes used for pulsed dipolar spectroscopy feature ZFS parameter D values that are much smaller than their electron Zeeman term at Q- and W-band fields.³⁷ This high-field limit results in spectra with a narrow central transition associated with |m_S| = 1/2 and a broad envelope stemming from a superposition of the remaining |m_S| > 1/2 transitions. The D values of Gd-NO₃Pic, Gd-DOTA-M and Gd-PCTA increase in this order, as visible from the progressively broadened Q-band field-sweept echo-detected EPR spectra in Fig. 6(b). We study the influence of ZFS on DD in two ways: first by comparing Gd-NO₃Pic (D = 485 ± 20 MHz), Gd-DOTA-M (D = 714 ± 43 MHz) to Gd-PCTA (D = 1861 ± 135 MHz),³⁵ and second by placing the refocusing pulses at B_max or B_kink (as indicated in Fig. 6(b)) to probe the transition dependence. These experiments assess whether the transverse relaxation behavior of the central transition can be approximated by an effective spin S′ = 1/2 and match the DD results of the here studied organic S = 1/2 radicals.

3.4.1 Relaxation characterization by Hahn experiment. The Hahn experiment was used to identify an appropriate concentration and temperature that render the DD data comparable to the presented nitroxide and trityl results. Between 10 and 30 K, the transverse relaxation rate of Gd-NO₃Pic in H₂O:glycerol recorded at B_max increases with temperature as shown in Fig. Sa26(b), ESI.† For all further experiments, we chose a temperature of 10 K to avoid non-refocusable contributions from T₁ flips that were previously reported to limit the W-band transverse relaxation of Gd-DOTA in D₂O:glycerol-d₈ at temperatures of 18 K and above.³⁶ Our data set for a different ligand points to a somewhat higher temperature, as a non-linear decrease of T_10% sets in only between 20 and 30 K. We ensured that our concentration choice of 25 μM sufficiently suppresses ID based on pulse-length dependent Hahn relaxation measurements of Gd-DOTA-M in D₂O:glycerol-d₈ at 10 K. Fig. Sa26(a) (ESI†) demonstrates the absence of ID both at B_max as well as B_kink. Note, that the observed decoherence is most sensitive to ID in a deuterated solvent (as NSD is suppressed) and in particular for the central gadolinium transition as the narrow line leads to a high density of states.

3.4.2 DD at 10 K. All DD experiments were performed at 10 K and at a spin concentration of 25 μM.
Unbound Gd-complexes. Q-band DD data sets were acquired at B_max in both protonated and deuterated water–glycerol glass. Fig. 7(a) compares the results for Gd-NO₃Pic, Gd-DOTA-M, Gd-PCTA in H₂O:glycerol (Fig. Sa27, ESI† shows the individual data sets), and subplot (c) illustrates the DD behavior in D₂O:glycerol-d₈ for Gd-DOTA-M.

Fig. 7 DD data sets of gadolinium complexes acquired at 10 K and a spin concentration of 25 μM. (a) A comparison of Gd-NO₃Pic (thick line), Gd-DOTA-M (medium line) and Gd-PCTA (thin line) in H₂O:glycerol at B_max along with a legend that defines the color code for the DD experiments. (b) A comparison of Gd-NO₃Pic (thick line), Gd-DOTA-M (medium line) and Gd-PCTA (thin line) in H₂O:glycerol at B_kink. This field position is 95, 140 and 616 MHz below B_max of the respective Q-band gadolinium line. (c) Gd-DOTA-M in D₂O:glycerol-d₈ at B_max and (d) Gd-DOTA-M-labeled protein (single mutant Q388C of the cysteine-free RNA recognition motifs 3/4 of the polypyrimidine tract binding protein) in D₂O:glycerol-d₈ at B_max.

The decoupling effect clearly differs between the protonated and deuterated solvent, as the refocusing pulses prolong the dephasing time in H₂O:glycerol with g_DD > 1 from T^Hahn_10% = 6.8 μs. Instead, in D₂O:glycerol-d₈ no gain (g_DD ≈ 1) is achieved beyond T^Hahn_10% = 64 μs so that losses of unknown origin (as discussed in Section 3.3.3) counteract the decoupling efforts. Consequently, the T_m parameter of the well fitting SE model (Fig. Sa32, ESI† compares the fit quality of the SE and SSE model) saturate with n, yielding a power law dependence with γ = 0.01–0.02 as shown in Fig. 5(d). Raitsimring et al.³⁶ demonstrated that the W-band Hahn relaxation rate for Gd-DOTA in D₂O:glycerol-d₈ at 10 K increases from B_max to the outer field positions. Assuming that the dephasing of the central transition is driven by NSD, the study assigns the increase in relaxation rate for |m_S| > 1/2 to a transition-dependent transient ZFS (tZFS) effect that arises from small ligand dynamics (displacements by ≈0.01 Å or librations by ≈0.1°), if all other mechanisms, i.e. NSD, ID, SD and T₁ flips, are suppressed. We therefore did not investigate the DD effect in D₂O:glycerol-d₈ for other field positions B₀ ≠ B_max as the gain for each refocusing pulse will deteriorate even further for |m_S| > 1/2 transitions. Instead we focus on H₂O:glycerol that results in the typical DD fingerprint of proton-driven NSD for all three gadolinium complexes with a more convex relaxation trace for Uhrig relative to CP decoupling. However, an additional ZFS-based relaxation pathway contributes, as is visible from the DD traces for n > 1 in Fig. 7(a).

The SSE expression models the DD data well (as demonstrated in Fig. Sa29–Sa31, ESI,† except for the Hahn relaxation of Gd-NO₃Pic) and the stretched exponential parameters quantify the ZFS effect on the fast and slow dephasing pathway as summarized in Table 1 and illustrated for Gd-DOTA-M in H₂O:glycerol in Fig. 4(d) (Fig. Sa28, ESI† displays the corresponding plot for all three gadolinium complexes in H₂O:glycerol). Independent of the refocusing scheme, the T_m2/n values of the gadolinium complexes are systematically smaller compared to nitroxide and trityl radicals, with similar slopes for Gd-NO₃Pic and Gd-DOTA-M, while Gd-PCTA leads to a reduced T_m2 gain with n. The same observation applies for ξ₂, while ξ^Uhrig₂ > ξ^CP₂ holds. ZFS also diminishes the decoupling effect on the fast process as seen from the progressively smaller T_m1/n slope from Gd-NO₃Pic to Gd-PCTA. Although ESEEM is observed for all three gadolinium complexes and likely arises from ¹⁴N nuclei present in the ligands, we cannot assign the two relaxation pathways to intramolecular and solvent nuclei, as both processes display a ZFS dependence. Overall, NSD controls the dephasing of the central transition as evident from the strong solvent deuteration effect and the characteristic decoupling behavior in H₂O:glycerol. In addition, our DD results demonstrate that ZFS effects clearly contribute to the transverse relaxation probed at B_max – independent of the solvent. In H₂O:glycerol both T_m1 and T_m2 are affected, implying that the proton flip-flop transitions and the ZFS-induced fluctuations occur at a similar time scale. As a spin A-spin A interaction,¹⁰ the ZFS-driven mechanism cannot be refocused by the same DD scheme and consequently dominates the dephasing in D₂O:glycerol-d₈.¶

Placing the refocusing pulses at B_kink reduces the decoupling effect with respect to placing the pulses at B_max. Fig. 7(b) compares the nearly overlapping relaxation traces of Gd-NO₃Pic and Gd-DOTA-M in H₂O:glycerol to the somewhat accelerated transverse relaxation of Gd-PCTA (Fig. Sa34, ESI† shows the DD data sets individually), analogous to the observations at B_max. For all three complexes, CP n = 2 achieves a g_DD of 1.4, while the effect of n > 2 pulses saturates independent of the refocusing scheme. The SE model describes the DD data at B_kink by a sub-linear increase of T_m with n as shown in Fig. Sa35, ESI† along with a stretch parameter value ξ ≈ 1.5 that is roughly constant with n. Consequently, the superposition of various |m_S| > 1/2 dephases mostly via the tZFS pathway, while contributions from proton-driven NSD at lower frequencies allow for a limited refocusing effect. Note that all DD traces lack visible ESEEM as the nuclear frequencies interfere destructively at B_kink.

We also performed W-band DD experiments of Gd-NO₃Pic in H₂O:glycerol to evaluate whether the refocusing effect becomes more efficient at W-relative to Q-band magnetic fields, as the central transition is narrowed by D²/gB₀,³⁷i.e. by a factor of three. Due to the limited time resolution of our W-band spectrometer (4 ns), pulses with t_π = t_π/2 = 16 ns had to be used. Fig. Sa39, ESI† compares the resulting traces to Q-band data. While the Q- and W-band Hahn relaxation traces overlap, refocusing schemes with n > 1 achieve a somewhat slower dephasing in W-band, both, for Uhrig or CP decoupling, preserving ξ^Uhrig > ξ^CP. This effect can be attributed to a more selective excitation of the central |m_S| = 1/2 transition at W-band relative to Q-band frequencies. Instead, the contribution from NSD remains unchanged as all required interactions are field-independent. Namely, the hyperfine coupling to the protons as well as the proton–proton dipolar coupling that dominates the width of the proton NMR line both at Q- and W-band. Only the suppressed ESEEM indicate a local field change experienced by the nuclei due to the increased nuclear Zeeman term at W-band, reducing the probability for forbidden transitions. Moving away from B_max to the W-band B_kink field position results in a saturated DD behavior as previously described for Q-band. Before discussing the implications of these DD results for both spin label characterization and DD-based PSD experiments featuring gadolinium(III) labels, we illustrate the effect of attaching a spin label to a bio-molecule of interest.

Biomolecule-attached Gd-complex. So far we have considered nitroxides, trityl radicals and gadolinium complexes dissolved in water–glycerol. In D₂O:glycerol-d₈ a sub-linear increase of T_m with n for trityl radicals was observed relative to T^Hahn_10% = 43 μs (OX071), while for Gd-DOTA-M in the same solvent ZFS-driven dephasing renders DD ineffective beyond T^Hahn_10% = 64 μs. In both cases deuteration achieves a rather long transverse relaxation time already under the Hahn experiment, leaving little to no refocusable dephasing contributions. However, if a spin label is attached to a biomolecule, it is likely to experience an additional HF field in particular from the protons of the biomolecule's backbone. We illustrate this effect on the DD performance in both protonated and deuterated water–glycerol glass using a Gd-DOTA-M-labeled single mutant (Q388C) of the cysteine-free pair of RNA recognition motifs 3/4 of the polypyrimidine tract binding protein.⁵⁷ In H₂O:glycerol the DD traces of unbound and attached Gd-DOTA-M are identical, which proofs the general transferability of our low temperature DD results in protonated solvent. In contrast, the presence of the protein strongly reduces T^Hahn_10% from 64 μs to 21 μs in D₂O:glycerol-d₈ as demonstrated in Fig. 7(d). This three-fold reduction in the Hahn dephasing time relative to the unbound spin label can be counter-acted by refocusing with n = 2 (2.3 × reduction) or n > 2 (1.6 × reduction) pulses, achieving overall longer coherence survival compared to any DD trace of the fully protonated sample. This anecdotal observation does not only provide practical advise on optimal sample preparation for DD-based experiments, but also suggests DD as an analytical tool to study the spin label environment in deuterated solvent or buffer e.g. to determine solvent versus protein induced hyperfine fields.
Considerations for spin-label characterization and DD-based PSD. The Q- and W-band DD results have demonstrated that the relaxation behavior of the central gadolinium transition (for complexes studied here with D ranging from 485 to 1861 MHz) cannot be fully described by an effective spin S′ = 1/2 because a ZFS-driven mechanism contributes or even dominates the decoherence in protonated or deuterated water–glycerol glass, respectively. Modeling the W-band dephasing of Gd-DOTA in D₂O:glycerol-d₈ at B_max as an effective spin S′ = 1/2 is the underlying assumption used to extract the m_S-dependent tZFS relaxation rates for B₀ ≠ B_max.³⁶ A previous study¹⁵ already suggested that this estimation oversimplifies the driving decoherence mechanisms at the central transition in deuterated solvent. The argument of this study relies on Q-band Hahn echo-detected field sweeps acquired as a function of interpulse delays (increasing Δ₁ = Δ₂ from 0.4 μs to 3 μs and 5 μs). While the contribution from the central transition increases for Gd-DOTA-M in D₂O:glycerol-d₈ when scaled to the echo intensity at B_kink, the opposite trend is observed for Gd-DOTA-M in H₂O:glycerol.¹⁵ In fact, a comparison of the Hahn decay probed at B_max and B_kink matches this experimental demonstration as shown in Fig. Sa33(a and b), ESI.† In H₂O:glycerol the Hahn decays at B_max and B_kink cross, while the decoherence in D₂O:glycerol-d₈ is systematically faster for transitions involving an |m_S| > 1/2 state compared to the central transition. Importantly, for any DD experiment with n > 1 the latter behavior is also observed in H₂O:glycerol as illustrated by CP n = 2 in Fig. Sa33(c), ESI.† Hence, we can re-emphasize the claim made in context of our trityl DD results in Section 3.3.3: relative to the mentioned studies that are based on Hahn relaxation measurements, a series of DD experiments is superior in detecting the origin of local field fluctuations that induce decoherence. Implicitly, the dephasing behavior of (future) spin labels should be evaluated under multi-pulse experiments not only to generate a better understanding of the spin dynamics, but to optimize the relevant target function for PDS and not a rough approximation thereof. This may be in particular relevant for the 4-pulse DEER experiment, as its observer sequence violates the DD condition.

The optimal set-up and experimental conditions for Gd–Gd 4-pulse DEER experiments have been determined theoretically as well as empirically,³⁷ while decoherence limitations have been exclusively addressed via spin label design.⁴¹ Based on our experimental DD results, gadolinium-based distance measurements are expected to benefit from application of the 5-pulse DEER sequence, in particular if the observer pulses are placed at B_max of the gadolinium line. This set-up trades modulation depth for sensitivity relative to pumping on B_max in an Gd–Gd experiment, while an orthogonal spin-labelling approach that pumps on a nitroxide or trityl radical may off-set this sacrifice.

4 Conclusions

We have demonstrated that the SSE model, previously introduced for describing the low-temperature electronic dephasing of nitroxides in o-terphenyl, is not restricted to this matrix or paramagnetic species. First, we found that the same two associated decoherence pathways are also active for nitroxides in water–glycerol glass. Second, other paramagnetic systems, such as trityl radicals and gadolinium(III) complexes in H₂O:glycerol, were found to require an SSE description as well. While the Hahn echo experiment cannot always resolve the two time scales of the fast and slow dephasing process, DD schemes reveal these contributions by refocusing the magnetization to a larger extent during a given total sequence length T. Besides variation in temperature, concentration and deuteration, the number of refocusing pulses n and their arrangement in time therefore provides an additional experimental handle to identify contributing relaxation mechanisms. Thereby, we showed that the intramolecular nuclei of the here studied nitroxide and trityl radicals lead to a partial coherence loss. Further, we determined that a ZFS-driven mechanism contributes to the decoherence of the central gadolinium transition.

Generally, multiple refocusing is most effective in decoupling NSD arising from strongly HF coupled solvent nuclei, as evident from the linear increase of phase memory time T_m2 with number n of refocusing pulses. This slope is steeper in o-terphenyl compared to water–glycerol glass, and we tentatively attribute this difference to the larger intramolecular proton–proton or deuteron-deuteron distance present in the OTP and dOTP molecule, respectively. Independent of the solvent nature and spin system, the optimized Uhrig scheme is superior in decoupling field fluctuations that arise from the solvent protons, as reflected in ξ^Uhrig₂ > ξ^CP₂. Especially in deuterated solvents, spin A-spin A interactions reduce or even override the DD effect, since ID and/or, in case of spin systems with S > 1/2, ZFS-driven dephasing dominates decoherence and is not amenable to DD. Aside from using DD as a spectroscopic tool that characterizes the spin environment, it provides a building block for dipolar spectroscopy. So far 5-pulse, 7-pulse and n-DEER experiments have been exclusively applied to nitroxide–nitroxide distance measurements. Our results suggest comparable gains in the attainable dipolar evolution time for other spin labels, specifically if the immediate spin environment cannot be sufficiently deuterated. Apart from gadolinium(III) complexes, copper(II) or manganese(II)-based spin labels are expected to display comparable relaxation behavior under multiple refocusing if the temperature is low enough to ensure sufficiently long T₁ times. With respect to chemical and biological EPR applications, the here presented DD behavior of nitroxides, trityl radicals and gadolinium(III) complexes in water–glycerol glass is representative for water-soluble spin-labeled (bio-)molecules. For solvent-exposed labeling sites our low temperature and low concentration results will be directly transferable to EPR application work under comparable experimental conditions. If the spin label is subject to additional field fluctuations, e.g. arising from a biomolecule's backbone, DD traces are likely to exhibit a fingerprint of this dynamics. In upcoming work, we plan to address the effect of repeated refocusing in a lipid environment. This milieu is highly relevant for studies of spin-labeled membrane proteins and increases the complexity of the coupled nuclear spin bath with respect to o-terphenyl or water–glycerol glass.

Author contributions

M. H. synthesized the nitroxides H-/D-mNOHex and H/D-mNOPEG under the supervision of A. G. J. S. performed all nitroxide experiments and associated data analysis. J. S. designed the DD studies of trityl radicals and gadolinium complexes with input from Y. P. and G. J. J. S. supervised M. M. and K. Z., who carried out the EPR measurements and data analysis for the trityl radicals and gadolinium complexes, respectively. Y. P. and G. J. contributed to the interpretation of the EPR results. M. H. and A. G. wrote the synthesis part and J. S. the EPR part of the manuscript. All authors reviewed the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank H. Zimmermann for the synthesis of D-NO, J. Wegner for synthesizing Gd-NO₃Pic and Gd-PCTA, and C. Gmeiner for the Gd-DOTA-M-labeled protein sample. J. H. Ardankjær-Larsen is gratefully acknowledged for providing OX063 and OX071. M. H. und A. G. thank M. Qi for support in writing the manuscript. Financial support by Deutsche Forschungsgemeinschaft (DFG) within SPP1601 (GO555/6-2) is gratefully acknowledged. J. S. is grateful to the Günthard Foundation for a PhD scholarship.

Notes and references

1. L. Viola, E. Knill and S. Lloyd, Phys. Rev. Lett., 1999, 82, 2417–2421.
2. G. Jeschke and Y. Polyhach, Phys. Chem. Chem. Phys., 2007, 9, 1895.
3. P. P. Borbat, E. R. Georgieva and J. H. Freed, J. Phys. Chem. Lett., 2013, 4, 170–175.
4. P. E. Spindler, I. Waclawska, B. Endeward, J. Plackmeyer, C. Ziegler and T. F. Prisner, J. Phys. Chem. Lett., 2015, 6, 4331–4335.
5. H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630–638.
6. L. Fábregas Ibáñez, G. Jeschke and S. Stoll, Magn. Reson., 2020, 1, 209–224.
7. A. Doll and G. Jeschke, Phys. Chem. Chem. Phys., 2017, 19, 1039–1053.
8. J. Soetbeer, M. Hülsmann, A. Godt, Y. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2018, 20, 1615–1628.
9. G. S. Uhrig, Phys. Rev. Lett., 2007, 98, 100504.
10. J. S. Waugh, C. H. Wang, L. M. Huber and R. L. Vold, J. Chem. Phys., 1968, 48, 662.
11. J. R. Harbridge, S. S. Eaton and G. R. Eaton, J. Magn. Reson., 2003, 164, 44–53.
12. E. Bordignon, A. I. Nalepa, A. Savitsky, L. Braun and G. Jeschke, J. Phys. Chem. B, 2015, 119, 13797–13806.
13. A. Nalepa, K. Möbius, M. Plato, W. Lubitz and A. Savitsky, Appl. Magn. Reson., 2019, 50, 1–16.
14. B. M. Baynes and B. L. Trout, J. Phys. Chem. B, 2003, 107, 14058–14067.
15. L. Garbuio, K. Zimmermann, D. Häussinger and M. Yulikov, J. Magn. Reson., 2015, 259, 163–173.
16. K. O. Tan, M. Mardini, C. Yang, J. H. Ardenkjær-Larsen and R. G. Griffin, Sci. Adv., 2019, 5, eaax2743.
17. D. Banerjee and S. Bhat, J. Non-Cryst. Solids, 2009, 355, 2433–2438.
18. P. W. Fenimore, H. Frauenfelder, B. H. McMahon and F. G. Parak, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 16047–16051.
19. V. C. Nibali, G. D'Angelo, A. Paciaroni, D. J. Tobias and M. Tarek, J. Phys. Chem. Lett., 2014, 5, 1181–1186.
20. M. Priya, N. Bidhoodi and S. P. Das, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 062308.
21. Y. H. Kuo and Y. W. Chiang, ACS Cent. Sci., 2018, 4, 645–655.
22. A. M. Raitsimring, C. Gunanathan, A. Potapov, I. Efremenko, J. M. Martin, D. Milstein and D. Goldfarb, J. Am. Chem. Soc., 2007, 129, 14138–14139.
23. G. W. Reginsson, N. C. Kunjir, S. T. Sigurdsson and O. Schiemann, Chem. – Eur. J., 2012, 18, 13580–13584.
24. W. Couet, R. Brasch, C. Sosnovsky, J. Lukszo, I. Prakash, C. Gnewech and T. Tozer, Tetrahedron, 1985, 41, 1165–1172.
25. A. A. Kuzhelev, R. K. Strizhakov, O. A. Krumkacheva, Y. F. Polienko, D. A. Morozov, G. Y. Shevelev, D. V. Pyshnyi, I. A. Kirilyuk, M. V. Fedin and E. G. Bagryanskaya, J. Magn. Reson., 2016, 266, 1–7.
26. A. Martorana, G. Bellapadrona, A. Feintuch, E. D. Gregorio, S. Aime and D. Goldfarb, J. Am. Chem. Soc., 2014, 136, 13458–13465.
27. M. Qi, A. Groß, G. Jeschke, A. Godt and M. Drescher, J. Am. Chem. Soc., 2014, 136, 15366–15378.
28. J. J. Jassoy, A. Berndhäuser, F. Duthie, S. P. Kühn, G. Hagelueken and O. Schiemann, Angew. Chem., 2017, 129, 183–187.
29. I. Kaminker, H. Yagi, T. Huber, A. Feintuch, G. Otting and D. Goldfarb, Phys. Chem. Chem. Phys., 2012, 14, 4355.
30. L. Garbuio, E. Bordignon, E. K. Brooks, W. L. Hubbell, G. Jeschke and M. Yulikov, J. Phys. Chem. B, 2013, 117, 3145–3153.
31. B. Joseph, V. M. Tormyshev, O. Y. Rogozhnikova, D. Akhmetzyanov, E. G. Bagryanskaya and T. F. Prisner, Angew. Chem., Int. Ed., 2016, 55, 11538–11542.
32. J. Klauder and P. Anderson, Phys. Rev., 1962, 125, 912–932.
33. A. Zecevic, G. R. Eaton, S. S. Eaton and M. Lindgren, Mol. Phys., 1998, 95, 1255–1263.
34. W. E. Blumberg, Phys. Rev., 1960, 119, 79–84.
35. J. A. Clayton, K. Keller, M. Qi, J. Wegner, V. Koch, H. Hintz, A. Godt, S. Han, G. Jeschke, M. S. Sherwin and M. Yulikov, Phys. Chem. Chem. Phys., 2018, 20, 10470–10492.
36. A. Raitsimring, A. Dalaloyan, A. Collauto, A. Feintuch, T. Meade and D. Goldfarb, J. Magn. Reson., 2014, 248, 71–80.
37. D. Goldfarb, Phys. Chem. Chem. Phys., 2014, 16, 9685.
38. M. Rosey, PhD thesis, Massachusetts Institute of Technology, 2001.
39. M. Qi, M. Hülsmann and A. Godt, J. Org. Chem., 2016, 81, 2549–2571.
40. V. M. Tormyshev, A. S. Chubarov, O. A. Krumkacheva, D. V. Trukhin, O. Y. Rogozhnikova, A. S. Spitsyna, A. A. Kuzhelev, V. V. Koval, M. V. Fedin, T. S. Godovikova, M. K. Bowman and E. G. Bagryanskaya, Chem. – Eur. J., 2020, 26, 2705–2712.
41. A. Shah, A. Roux, M. Starck, J. A. Mosely, M. Stevens, D. G. Norman, R. I. Hunter, H. El Mkami, G. M. Smith, D. Parker and J. E. Lovett, Inorg. Chem., 2019, 58, 3015–3025.
42. J. H. Ardenkjaer-Larsen, I. Laursen, I. Leunbach, G. Ehnholm, L.-G. Wistrand, J. S. Petersson and K. Golman, J. Magn. Reson., 1998, 133, 1–12.
43. Y. Polyhach, E. Bordignon, R. Tschaggelar, S. Gandra, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2012, 14, 10762.
44. W. Yang, W.-L. Ma and R.-B. Liu, Rep. Prog. Phys., 2017, 80, 016001.
45. M. Lindgren, G. R. Eaton, S. S. Eaton, B.-H. Jonsson, P. Hammarström, M. Svensson and U. Carlsson, J. Chem. Soc., Perkin Trans. 2, 1997, 2549–2554.
46. I. Ritsch, H. Hintz, G. Jeschke, A. Godt and M. Yulikov, Phys. Chem. Chem. Phys., 2019, 21, 9810–9830.
47. K. Keller, I. Ritsch, H. Hintz, M. Hülsmann, M. Qi, F. D. Breitgoff, D. Klose, Y. Polyhach, M. Yulikov, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2020, 22, 21707–21730.
48. G. Jeschke, M. Sajid, M. Schulte, N. Ramezanian, A. Volkov, H. Zimmermann and A. Godt, J. Am. Chem. Soc., 2010, 132, 10107–10117.
49. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
50. J. You, D. Carić, B. Rakvin, Z. Štefanić, K. Užarević and M. Kveder, J. Chem. Phys., 2019, 150, 164124.
51. E. R. Canarie, S. M. Jahn and S. Stoll, J. Phys. Chem. Lett., 2020, 11, 3396–3400.
52. M. Kveder, B. Rakvin and J. You, J. Chem. Phys., 2019, 151, 164124.
53. I. M. Brown, J. Chem. Phys., 1976, 65, 630–638.
54. A. J. Fielding, P. J. Carl, G. R. Eaton and S. S. Eaton, Appl. Magn. Reson., 2005, 28, 231–238.
55. V. Meyer, M. A. Swanson, L. J. Clouston, P. J. Boratyński, H. S. Mchaourab, A. Rajca, S. S. Eaton and G. R. Eaton, Biophys. J., 2015, 108, 1213–1219.
56. S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691.
57. C. Gmeiner, G. Dorn, F. H. Allain, G. Jeschke and M. Yulikov, Phys. Chem. Chem. Phys., 2017, 19, 28360–28380.
58. F. D. Breitgoff, J. Soetbeer, A. Doll, G. Jeschke and Y. O. Polyhach, Phys. Chem. Chem. Phys., 2017 10.1039/C7CP01488K.
59. F. D. Breitgoff, Y. O. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2017 10.1039/c7cp01487b.
60. M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000 DOI:10.1006/jmre.1999.1944.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp00055a

‡ Note that relaxation data acquired for H-mNOPEG and D-mNOPEG at spin concentrations of 100 μM would include contributions from increased spin–spin interaction due to the described aggregate formation.

§ Zecevic et al.³³ take this parameter in their decoherence simulations into account (¹H–¹H of 2.5 Å for OTP and 1.8 Å for H₂O:glycerol) but do not interpret this difference.

¶ In analogy to the nuclear quadrupole term that remains unaffected under the NMR CP n = 2 experiment,¹⁰ the ZFS interaction remains unaffected, as it is characterized by an equivalent Hamiltonian.

---