 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conformation-changing enzymes and macromolecular crowding†
Tomasz
Skóra
 a,
Mihail N.
Popescu
a,
Mihail N.
Popescu
 b and
Svyatoslav
Kondrat
b and
Svyatoslav
Kondrat
 *abc
*abc
aInstitute of Physical Chemistry, Polish Academy of Sciences, 01-224 Warsaw, Poland. E-mail: svyatoslav.kondrat@gmail.com; skondrat@ichf.edu.pl
bMax-Planck-Institut für Intelligente Systeme, Heisenbergstraße 3, 70569 Stuttgart, Germany
cIV. Institut für Theoretische Physik, Universität Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany
First published on 25th March 2021
Abstract
We study how crowding affects the activity and catalysis-enhanced diffusion of enzymes and passive tracers by employing a fluctuating-dumbbell model of conformation-changing enzymes. Our Brownian dynamics simulations reveal that the diffusion of enzymes depends qualitatively on the type of crowding. If only enzymes are present in the system, the catalysis-induced enhancement of the enzyme diffusion – somewhat counter-intuitively – increases with crowding, while it decreases if crowding is due to inert particles. For the tracers, the diffusion enhancement increases with increasing the enzyme concentration. We also show how the enzyme activity is reduced by crowding and propose a simple expression to describe this reduction. Our results highlight subtle effects at play concerning enzymatic activity and macromolecular transport in crowded systems, such as, e.g., the interior of living cells.
Macromolecular crowding plays the key role in the cellular life;1–3 it affects protein stability,4 chemical equilibria,5 gene regulation,6 enzymatic reactions7–9 and diffusion of metabolites and macromolecules.10–17 In particular, the macromolecular diffusion in vivo is an order of magnitude slower than in “infinite” dilution,10–17 while enzymatic reactions can be either sped up or decelerated by crowding.7,8
Recently, a number of experimental studies reported that – somewhat surprisingly – the diffusion of enzymes may be significantly enhanced by the chemical reactions they catalyze.18–21 Although there are ongoing debates about possible artefacts affecting some of those experiments,22–26 it is intuitively clear that the enzyme diffusion indeed can be enhanced if the catalytic step is associated with a reduction of the size of the enzyme due to conformational changes when binding a substrate. For example, the size of F1ATPase reduces by about 15% when adenosine triphosphate binds to its active site;27 experimental studies confirm that, correspondingly, the F1ATPase diffusion is enhanced by approximately the same amount, at sufficiently high concentrations of adenosine triphosphate.28
Such a catalysis-induced enhancement of the diffusion could provide simple explanations for the observation of a dramatic slow-down of tracer diffusion in cells with reduced metabolic activity.29 However, since the interior of a cell is crowded with macromolecules, questions naturally arise as to whether catalysis-enhanced diffusion remains a relevant feature also in crowding conditions and, vice versa, how the enhanced diffusion of catalytically active enzymes influences the transport of other macromolecular components constituting the crowded environment. Herein, we address such issues via Brownian dynamics (BD) simulations of mixtures of model shape-fluctuating enzymes (see below and Fig. 1) and spherical beads acting as crowders or tracers.
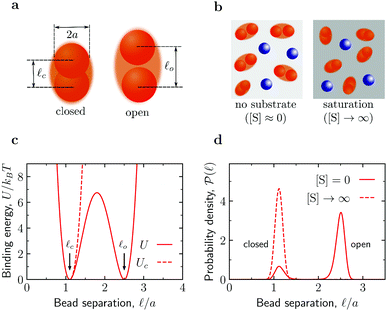 | ||
Fig. 1 Fluctuating dumbbell model of conformation-changing enzymes and simulation systems. (a) The model enzyme consists of two identical spherical beads of hydrodynamic radius a and can be found in a closed or an open state as characterized by different average separations ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c and c and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) o between the beads, respectively. (b) A typical simulation system consists of enzymes (red dumbbells) and inert particles (blue spheres) of hydrodynamic radius a. In the absence of substrates ([S] = 0), the enzymes can be in the open or closed states according to the probability given by the binding potential U( o between the beads, respectively. (b) A typical simulation system consists of enzymes (red dumbbells) and inert particles (blue spheres) of hydrodynamic radius a. In the absence of substrates ([S] = 0), the enzymes can be in the open or closed states according to the probability given by the binding potential U(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) (see panels (c) and (d)). At saturation ([S] → ∞), the enzymes can only be in the closed state due to substrate-enzyme binding. In the simulations, the substrate is accounted for implicitly via the effect it has on the state of the enzyme. (c) Binding potentials between the enzyme's beads. A double-well potential U models an enzyme in the absence of substrate (eqn (S4) in the ESI†), while a single-well potential Uc models the enzyme's closed state and mimics a system with [S] = ∞ (eqn (S5) in the ESI†). (d) Probability density function of the separation between the enzyme's beads in the closed state (potential Uc, corresponding to [S] → ∞) and for the double-well potential U corresponding to [S] = 0. ) (see panels (c) and (d)). At saturation ([S] → ∞), the enzymes can only be in the closed state due to substrate-enzyme binding. In the simulations, the substrate is accounted for implicitly via the effect it has on the state of the enzyme. (c) Binding potentials between the enzyme's beads. A double-well potential U models an enzyme in the absence of substrate (eqn (S4) in the ESI†), while a single-well potential Uc models the enzyme's closed state and mimics a system with [S] = ∞ (eqn (S5) in the ESI†). (d) Probability density function of the separation between the enzyme's beads in the closed state (potential Uc, corresponding to [S] → ∞) and for the double-well potential U corresponding to [S] = 0. | ||
The fluctuating-dumbbell enzyme model30–32 employed in our BD simulations consists of two identical spherical beads (subunits) subject to a certain binding potential (Fig. 1c). In the absence of substrates ([S] = 0), the enzyme can be either in the closed (c) or open (o) state, which are characterized by different average separations between the beads (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c and
c and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) o, respectively, see Fig. 1a) with probability defined by a double-well binding potential U(
o, respectively, see Fig. 1a) with probability defined by a double-well binding potential U(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) (eqn (S4) in the ESI,†Fig. 1). We consider conformation-changing enzymes that close when binding a substrate;27 accordingly, for a system with substrate in abundance ([S] → ∞), we model our dumbbell enzymes by a single-well binding potential Uc possessing a minimum at
) (eqn (S4) in the ESI,†Fig. 1). We consider conformation-changing enzymes that close when binding a substrate;27 accordingly, for a system with substrate in abundance ([S] → ∞), we model our dumbbell enzymes by a single-well binding potential Uc possessing a minimum at ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c (eqn (S5) in the ESI;† see also Fig. 1). The BD simulations use a customized version of the package BD_BOX33 and, for simplicity, account only for soft-core repulsive and hydrodynamic interactions (approximated via the generalized Rotne–Prager–Yamakawa tensor,34–37 see Section S1 in the ESI†) between the various components. From the BD trajectories, we calculated mean-square displacements MSD(t) = 〈|r(t) − r(0)|2〉 of the center of mass r of the various components (enzymes and crowders) and extracted the corresponding long-time diffusion coefficients Dl (for details see Section S1 E in the ESI†).
c (eqn (S5) in the ESI;† see also Fig. 1). The BD simulations use a customized version of the package BD_BOX33 and, for simplicity, account only for soft-core repulsive and hydrodynamic interactions (approximated via the generalized Rotne–Prager–Yamakawa tensor,34–37 see Section S1 in the ESI†) between the various components. From the BD trajectories, we calculated mean-square displacements MSD(t) = 〈|r(t) − r(0)|2〉 of the center of mass r of the various components (enzymes and crowders) and extracted the corresponding long-time diffusion coefficients Dl (for details see Section S1 E in the ESI†).
Reduced enzyme activity due to crowding. We first considered the enzymes in the absence of substrates ([S] = 0) and investigated how crowding affects enzyme's conformations. To gather enough statistics, we simulated systems containing 100 enzymes mixed with crowders at various concentrations (Fig. 2a). At [S] = 0, these enzymes contribute about 5.2% to the total occupied volume fraction ϕocc. Fig. 2b shows that the probability of an enzyme to be in the open state decreases with adding crowders, and correspondingly the probability of the closed state increases. To quantify these changes, we computed the free energy of enzyme opening
ΔF = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, K, | (1) |
 | ||
Fig. 2 Effect of crowding on the enzyme's conformation and activity. (a) Snapshots from Brownian dynamics (BD) simulations of the system at various levels of crowding. (b) Probability density function ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) ( (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) of finding the enzyme subunits separated by a distance ) of finding the enzyme subunits separated by a distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for the occupied volume fractions ϕocc from panel (a). (c) Free energy of opening ΔF as a function of ϕocc. Symbols: ΔF from eqn (1) with po from BD simulations; line: prediction of the scaled particle theory, eqn (2), with the shape of an enzyme approximated as a spherocylinder (Section S5 in the ESI†). (d) Reduction of the enzyme's catalytic activity, k/k0, as a function of ϕocc. Symbols: eqn (3) with po from BD simulations; line: eqn (4) using the scaled-particle theory for ΔΔF. for the occupied volume fractions ϕocc from panel (a). (c) Free energy of opening ΔF as a function of ϕocc. Symbols: ΔF from eqn (1) with po from BD simulations; line: prediction of the scaled particle theory, eqn (2), with the shape of an enzyme approximated as a spherocylinder (Section S5 in the ESI†). (d) Reduction of the enzyme's catalytic activity, k/k0, as a function of ϕocc. Symbols: eqn (3) with po from BD simulations; line: eqn (4) using the scaled-particle theory for ΔΔF. | ||
By counting an enzyme with the bead-bead separation ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) <
< ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m = (
m = (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) c +
c + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) o)/2 as being in the closed state and with
o)/2 as being in the closed state and with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) >
> ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m as being in the open state, one finds that for a single enzyme (“infinite” dilution) at room temperature po ≈ 0.83 and pc ≈ 0.17 (Section S2 in the ESI†); this renders ΔF ≈ −1.57kBT. By using the
m as being in the open state, one finds that for a single enzyme (“infinite” dilution) at room temperature po ≈ 0.83 and pc ≈ 0.17 (Section S2 in the ESI†); this renders ΔF ≈ −1.57kBT. By using the ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) obtained from BD simulations (Fig. 2b), we find that ΔF increases significantly as ϕocc (i.e., crowding) increases (Fig. 2c). As shown in Fig. 2c (the solid line), the BD data are consistent with the scaled particle theory38,39 for the free-energy change due to macromolecular crowding (Section S5 in the ESI†)
) obtained from BD simulations (Fig. 2b), we find that ΔF increases significantly as ϕocc (i.e., crowding) increases (Fig. 2c). As shown in Fig. 2c (the solid line), the BD data are consistent with the scaled particle theory38,39 for the free-energy change due to macromolecular crowding (Section S5 in the ESI†)
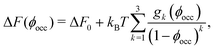 | (2) |
Since an enzyme in the closed state cannot bind a substrate, the results in Fig. 2b and c imply that crowding reduces the enzyme's catalytic activity. Noting that the rate constant is proportional to the probability of an enzyme to be in the open state, k ∼ po, the reduction of the enzyme activity (at saturation) due to crowding can be written as
| k(ϕocc)/k0 = po(ϕocc)/po(0), | (3) |
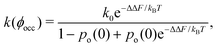 | (4) |
Eqn (4) may help analyse experiments on activity reduction with crowding. Frequently, such experiments use identical spherical crowders,7,8,42 in which case gk = hkϕkocc, where hk (k = 1, 2, 3) depend on the crowder radius and the change in the enzyme's geometric characteristics in the open and closed state (eqn (S20) in the ESI†). Treating these parameters and po(0) as fitting variables to analyse experimental data will allow one to obtain information on the enzymes properties in the open and closed states.
Since the reasoning leading to eqn (4) can apply to other similar processes, e.g. opening and closing a flap covering the active site of an enzyme,43,44 this equation may describe a broader class of enzymes. We stress, however, that eqn (4) is limited to two-state enzymes and assumes hard-core interactions between an enzyme and crowders. The latter assumption is reasonable only when there are no long-range electrostatic interactions involved.38
Enhanced enzyme diffusion in crowded environments. Since our fluctuating-dumbbell enzyme model mimics the change of the enzyme size upon binding a substrate (closed state in Fig. 1), it exhibits an enhanced diffusion Dl([S]) due to catalytic activity.30–32 This enhancement is quantified via the dimensionless factor
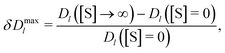 | (5) |
In the absence of crowders (the infinite dilution limit), BD simulations of the dynamics of a single enzyme give δDmaxl ≈ 17.5% (Fig. S2 in the ESI†). This value is comparable to that observed experimentally for F1-ATPase, where the diffusion enhancement was attributed to the size change upon binding a substrate.28
To reveal the effects of crowding on the enhanced enzyme diffusion, we calculated the long-time diffusion constant of enzymes for the three crowded systems shown in Fig. 2a. We recall that, in order to gather sufficient statistics, we had 100 enzymes in the simulation box; this contributes about 5.2% to the total occupied volume fraction. The addition of spherical crowders reduces the enzyme diffusion coefficient, both in the absence of substrates ([S] = 0) as well as at saturation ([S] → ∞), as intuitively expected. Note that Dl/D0 > 1 for [S] → ∞, where D0 is the enzyme diffusion coefficient in the absence of both substrates and crowders. In this regime, the enzymes are always in the smaller-sized closed state and diffuse faster even in a crowded system. Irrespective of the level of crowding, the diffusion is indeed enhanced, but the enhancement δDmaxl is less pronounced as the crowding increases (filled symbols in Fig. 3). This is due to the slower decrease of Dl([S] = 0) with crowding. The crowding promotes the closed state for [S] = 0 (Fig. 2b) and thus part of the reduction in diffusion, due to the less available volume, is compensated by an increase in diffusion due to a decrease in the average size of the enzyme.
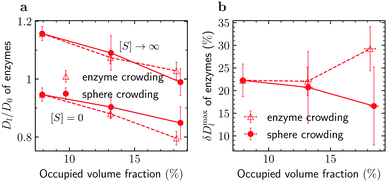 | ||
| Fig. 3 Macromolecular crowding and enhanced enzyme diffusion. (a) Reduced diffusion coefficient of enzymes, Dl/D0, in the absence of substrates ([S] = 0) and with substrates in abundance ([S] → ∞) versus occupied volume fraction. (b) Maximal enhancement of enzyme diffusion δDmaxl, eqn (5), as a function of the occupied volume fraction. Error bars show uncertainties due to sampling errors. Filled and open symbols denote the results for crowding being due to spherical crowders and enzymes, respectively (see also Fig. 2a and 4a). | ||
For comparison, we studied enzyme diffusion when crowding was created by increasing the number of enzymes. The catalysis ([S] → ∞) enhances the enzyme diffusion in this case too, but the behaviour of δDmaxl is strikingly different: δDmaxl grows with increasing crowding (Fig. 3b). The growth is obviously due to a steeper decrease of Dl([S] = 0) with increasing ϕocc in the systems with enzyme crowding. This result is surprising, as the enzymes average size decreases with increasing ϕocc (Fig. 2a), which reduces the excluded volume (compare Tables S2 and S3 in the ESI†). While we cannot precisely pinpoint the cause of this behaviour, a plausible explanation is that the additional flows induced by the fluctuations of the beads lead to stronger hydrodynamic interactions between the enzymes and a hindering of the diffusion.
Enhanced diffusion of passive tracers. We also investigated diffusion of crowders in a solution of active enzymes (Fig. 4). To this end, we first simulated a system of such tracers in the absence of enzymes to obtain the long-time diffusion coefficient D0,t of the tracers at [E] = 0 (occupied volume fraction ϕocc ≈ 0.025). As shown in Fig. 4b, the reduced tracer diffusion coefficient, Dl/D0,t, decreases with increasing [E], but the magnitude of the decrease depends on [S]. The decrease is more significant for [S] = 0. This is because this system excludes more volume to the tracers than the system with [S] → ∞, owing to the larger size of the enzyme in the open state (Fig. 1a).
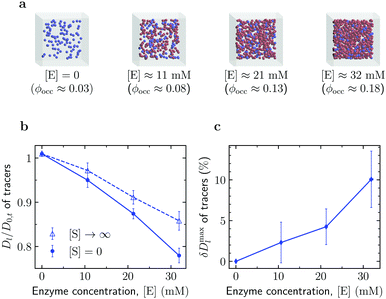 | ||
| Fig. 4 Diffusion of passive tracers in a solution of active enzymes. (a) Snapshots of Brownian dynamics simulations at various enzyme concentrations [E]. The corresponding total occupied volume fractions were computed via Monte Carlo simulations (Section S3 in the ESI†). (b) Effect of enzyme concentration [E] on the diffusion of passive tracers in the absence of substrates ([S] = 0) and with substrates in abundance ([S] → ∞). (c) Maximal diffusion enhancement of passive tracers (eqn (5)) as a function of enzyme concentration. Error bars show uncertainties due to sampling errors. | ||
Thus, similarly to the enhanced enzyme diffusion (Fig. 3), also the diffusion of passive tracers is accelerated by the catalytic activity of size-changing enzymes. To quantify this enhancement, we calculated a similarly defined factor δDmaxl, eqn (5), for the tracers; the result is shown in Fig. 4c. The enhancement reaches about 10% in the most crowded system studied (ϕocc = 18.2%), a value that is in principle measurable with FCS or other techniques. For example, for nanosized tracers in solutions of aldolase and urease an enhancement of this order has been reported by the FCS study in ref. 45. However, it should be noted that while the experiment used nanomolar concentration of enzymes, in our case the number densities of enzymes at which the 10% enhancement of the tracer diffusion was observed correspond to ≈30 mM.
In conclusion, we have performed Brownian dynamics simulations of mixtures of spherical crowders and shape-changing, fluctuating-dumbbell enzymes—a simple, qualitative model for the interior of a cell (which is densely populated with enzymes and other macromolecules). We revealed that the diffusion constant of either component is enhanced when the enzymes become catalytically active (Fig. 3 and 4). The magnitude of the relative enhancement depends on the level of crowding and can be significant (15 to 30%). Surprisingly, for enzymes, the maximum diffusion enhancement depends sensitively on whether the crowding is due to passive crowders or enzymes (Fig. 3b). This suggests that the hydrodynamic flow induced by the enzymes fluctuations plays a significant role in the observed phenomena.
We also showed that crowding promotes the smaller-sized closed state of an enzyme and thereby reduces its activity (Fig. 2); this behaviour agrees qualitatively with experimental observations,42 and it can be rationalised and quantitatively captured by an approximate scaled particle theory. The simple expression, eqn (4), can yield information about changes in the enzyme conformation during catalysis by fitting experimental data on the activity reduction as a function of crowding, provided that sufficiently many data points are available. While such data are currently scarce, we hope that this perspective will stimulate new, comprehensive experimental studies in this direction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by NCN grant No. 2017/25/B/ST3/02456 to S. K and T. S. We thank PLGrid for providing computational resources.References
- S. B. Zimmerman and A. P. Minton, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65 CrossRef CAS PubMed
.
- J. Herzfeld, J. Mol. Recognit., 2004, 17, 376–381 CrossRef CAS PubMed
.
-
M. Weiss, Crowding, diffusion, and biochemical reactions, Elsevier Inc., 1st edn, 2014, vol. 307, pp. 383–417 Search PubMed
.
- D. Gomez, K. Huber and S. Klumpp, J. Phys. Chem. Lett., 2019, 10, 7650–7656 CrossRef CAS PubMed
.
- R. J. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef CAS PubMed
.
- M. Tabaka, T. Kalwarczyk and R. Hołyst, Nucleic Acids Res., 2014, 42, 727–738 CrossRef CAS PubMed
.
- M. G. Norris and N. Malys, Biochem. Biophys. Res. Commun., 2011, 405, 388–392 CrossRef CAS PubMed
.
- I. Pastor, L. Pitulice, C. Balcells, E. Vilaseca, S. Madurga, A. Isvoran, M. Cascante and F. Mas, Biophys. Chem., 2014, 185, 8–13 CrossRef CAS PubMed
.
- A. Kuzmak, S. Carmali, E. von Lieres, A. J. Russell and S. Kondrat, Sci. Rep., 2019, 9, 1–7 CAS
.
- E. Dauty and A. S. Verkman, J. Mol. Recognit., 2004, 17, 441–447 CrossRef CAS PubMed
.
- J. A. Dix and A. Verkman, Annu. Rev. Biophys., 2008, 37, 247–263 CrossRef CAS PubMed
.
- S. R. McGuffee and A. H. Elcock, PLoS Comput. Biol., 2010, 6, e1000694 CrossRef PubMed
.
- T. Ando and J. Skolnick, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18457–18462 CrossRef CAS PubMed
.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed
.
- S. Kondrat, O. Zimmermann, W. Wiechert and E. V. Lieres, Phys. Biol., 2015, 12, 046003 CrossRef PubMed
.
- M. Feig, I. Yu, P. H. Wang, G. Nawrocki and Y. Sugita, J. Phys. Chem. B, 2017, 121, 8009–8025 CrossRef CAS PubMed
.
- T. Skóra, F. Vaghefikia, J. Fitter and S. Kondrat, J. Phys. Chem. B, 2020, 124, 7537–7543 CrossRef PubMed
.
- C. Riedel, R. Gabizon, C. A. M. Wilson, K. Hamadani, K. Tsekouras, S. Marqusee, S. Pressé and C. Bustamante, Nature, 2015, 517, 227–230 CrossRef CAS PubMed
.
- X. Zhao, H. Palacci, V. Yadav, M. M. Spiering, M. K. Gilson, P. J. Butler, H. Hess, S. J. Benkovic and A. Sen, Nat. Chem., 2018, 10, 311–317 CrossRef CAS PubMed
.
- M. Feng and M. K. Gilson, Annu. Rev. Biophys., 2020, 49, 87–105 CrossRef CAS PubMed
.
- S. Ghosh, A. Somasundar and A. Sen, Annu. Rev. Condens. Matter Phys., 2020, 12, 177 CrossRef
.
- J.-P. Günther, M. Börsch and P. Fischer, Acc. Chem. Res., 2018, 51, 1911–1920 CrossRef PubMed
.
- Y. Zhang, M. J. Armstrong, N. M. B. Kazeruni and H. Hess, Nano Lett., 2018, 18, 8025–8029 CrossRef CAS PubMed
.
- A.-Y. Jee, K. Chen, T. Tlusty, J. Zhao and S. Granick, J. Am. Chem. Soc., 2019, 141, 20062–20068 CrossRef CAS PubMed
.
- Z. Chen, A. Shaw, H. Wilson, M. Woringer, X. Darzacq, S. Marqusee, Q. Wang and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21328–21335 CrossRef CAS PubMed
.
- S. Pressé, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 32189–32191 CrossRef PubMed
.
- B. Böttcher, I. Bertsche, R. Reuter and P. Gräber, J. Mol. Biol., 2000, 296, 449–457 CrossRef PubMed
.
- M. Börsch, P. Turina, C. Eggeling, J. R. Fries, C. A. Seidel, A. Labahn and P. Gräber, FEBS Lett., 1998, 437, 251–254 CrossRef
.
- B. R. Parry, I. V. Surovtsev, M. T. Cabeen, C. S. O'Hern, E. R. Dufresne and C. Jacobs-Wagner, Cell, 2014, 156, 183–194 CrossRef CAS PubMed
.
- P. Illien, X. Zhao, K. K. Dey, P. J. Butler, A. Sen and R. Golestanian, Nano Lett., 2017, 17, 4415–4420 CrossRef CAS PubMed
.
- P. Illien, T. Adeleke-Larodo and R. Golestanian, EPL, 2017, 119, 40002 CrossRef
.
- S. Kondrat and M. N. Popescu, Phys. Chem. Chem. Phys., 2019, 21, 18811–18815 RSC
.
- M. Długosz, P. Zieliński and J. Trylska, J. Comput. Chem., 2011, 32, 2734–2744 CrossRef PubMed
.
- J. Rotne and S. Prager, J. Chem. Phys., 1969, 50, 4831–4837 CrossRef CAS
.
- H. Yamakawa, J. Chem. Phys., 1970, 53, 436–443 CrossRef CAS
.
- P. J. Zuk, E. Wajnryb, K. A. Mizerski and P. Szymczak, J. Fluid Mech., 2014, 741, R5 CrossRef CAS
.
- E. R. Smith, I. K. Snook and W. Van Megen, Phys. A, 1987, 143, 441–467 CrossRef
.
- A. P. Minton, Methods Enzymol., 1998, 295, 127–149 CAS
.
- A. G. Gasic, M. M. Boob, M. B. Prigozhin, D. Homouz, C. M. Daugherty, M. Gruebele and M. S. Cheung, Phys. Rev. X, 2019, 9, 041035 CAS
.
- A. B. Fulton, Cell, 1982, 30, 345–347 CrossRef CAS PubMed
.
- S. B. Zimmerman and S. O. Trach, J. Mol. Biol., 1991, 222, 599–620 CrossRef CAS PubMed
.
- K. Maximova, J. Wojtczak and J. Trylska, Eur. Biophys. J., 2019, 48, 685–689 CrossRef CAS PubMed
.
- D. D. L. Minh, C. en Chang, J. Trylska, V. Tozzini and J. A. McCammon, J. Am. Chem. Soc., 2006, 128, 6006–6007 CrossRef CAS PubMed
.
- S. Qin, D. D. L. Minh, J. A. McCammon and H.-X. Zhou, J. Phys. Chem. Lett., 2009, 1, 107–110 CrossRef PubMed
.
- X. Zhao, K. K. Dey, S. Jeganathan, P. J. Butler, U. M. Córdova-Figueroa and A. Sen, Nano Lett., 2017, 17, 4807–4812 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06631a |
| This journal is © the Owner Societies 2021 |
