 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dielectric response of light, heavy and heavy-oxygen water: isotope effects on the hydrogen-bonding network's collective relaxation dynamics†
Bence
Kutus
 a,
Andrey
Shalit
b,
Peter
Hamm
b and
Johannes
Hunger
a,
Andrey
Shalit
b,
Peter
Hamm
b and
Johannes
Hunger
 *a
*a
aDepartment of Molecular Spectroscopy, Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: hunger@mpip-mainz.mpg.de
bDepartment of Chemistry, University of Zurich, Winterthurerstrasse 190, 8057 Zurich, Switzerland
First published on 23rd February 2021
Abstract
Isotopic substitutions largely affect the dielectric relaxation dynamics of hydrogen-bonded liquid water; yet, the role of the altered molecular masses and nuclear quantum effects has not been fully established. To disentangle these two effects we study the dielectric relaxation of light (H216O), heavy (D216O) and heavy-oxygen (H218O) water at temperatures ranging from 278 to 338 K. Upon 16O/18O exchange, we find that the relaxation time of the collective orientational relaxation mode of water increases by 4–5%, in quantitative agreement with the enhancement of viscosity. Despite the rotational character of dielectric relaxation, the increase is consistent with a translational mass factor. For H/D substitution, the slow-down of the relaxation time is more pronounced and also shows a strong temperature dependence. In addition to the classical mass factor, the enhancement of the relaxation time for D216O can be described by an apparent temperature shift of 7.2 K relative to H216O, which is higher than the 6.5 K shift reported for viscosity. As this shift accounts for altered zero-point energies, the comparison suggests that the underlying thermally populated states relevant to the activation of viscous flow and dielectric relaxation differ.
Introduction
The substitution of hydrogen for deuterium in water has strong impact on its dynamic properties, such as viscosity,1–5 translational and rotational self-diffusion,5,6 resonance frequency of molecular vibrations,5,7 echo decay time for hydrogen-bond vibrations obtained from Raman-terahertz (THz) spectroscopy,8 as well as dipole–dipole correlation times measured by dielectric relaxation9–15 and THz time-domain spectroscopies.16–18 Relative to light water (H216O), the different dynamics of heavy water (D216O) can be largely explained by the altered strength of its hydrogen-bonding network, which arises from nuclear quantum effects,5,8,19–25e.g. different zero-point energy and reduced delocalization of deuterium due to its higher nuclear mass.5 Despite these differences, numerous dynamic properties of H216O and D216O collapse onto a single curve when nuclear quantum effects are accounted for by an apparent temperature shift, ΔT.2–4,8,16 That is, the properties of D216O at T + ΔT equal those of H216O at T, reflecting that increased thermal fluctuations of D216O mimic enhanced quantum fluctuations of H216O.8,19,20,23,26,27Besides these nuclear quantum effects, classical mechanics already predict a change in the properties of water for different isotopes due to their different nuclear masses.5 To assess these classical mass effects, it is instructive to compare the properties of H216O to those of D216O and heavy-oxygen water, H218O.1,5,8,28,29 Both, 16O/18O and H/D substitutions, result in a nearly identical increase in the molecular mass of water. For instance, these increased masses give rise to a trivial increase in the volumetric densities.28 For molecular vibrations, for which resonance frequencies scale with the inverse square root of the oscillators’ reduced mass, isotope shifts due to classical mass effects are most pronounced for H/D exchange: the center frequency of the OD stretching band is 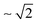 times lower than the OH stretching frequency, whereas heavy oxygen – which increases the reduced mass only by ∼0.6% – hardly affects these local dynamics.5,7
times lower than the OH stretching frequency, whereas heavy oxygen – which increases the reduced mass only by ∼0.6% – hardly affects these local dynamics.5,7
In case of collective dynamics involving more than one water molecule, classical mass effects are arguably less straightforward to predict. The macroscopic viscosity is one example for properties that reflect such non-local dynamics.30–33 For non-associated liquids, Eyring proposed as early as in 1936 that the thermally activated translation of a single molecule provides a good description for viscous flow, which in turn predicts viscosity to scale with the square root of the molecular mass.34 For hydrogen-bonded liquids, however, correlated molecular motions, i.e. the restructuring of the hydrogen-bonding network alters viscosity.30–33 This structural rearrangement also involves rotational motions of water molecules,33,35,36 for which the rate scales with the inverse square root of the moments of inertia.6 Viscometric experiments using isotopic 16O/18O substitution, which alters the moments of inertia of a water molecule by ∼0.6% but increases its molecular mass by ∼13%, have however shown that the ∼5% increase in viscosity is consistent with a translational mass factor, 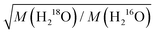 .1 Conversely, the substantial increase in viscosity (15–30%) upon H/D exchange is largely attributed to nuclear quantum effects.2,8 Empirically, this enhancement has been modelled using the same translational mass factor (5%) as found for 16O/18O substitution and an apparent temperature shift of 6.5 K to account for (temperature-dependent) nuclear quantum effects.2–4,8 Yet, for translational diffusion – which is intimately related to viscosity – the ratio of diffusivities of H216O and D216O seems to be even lower than the translational mass factor at elevated temperatures.5 Based on MD simulations,36 such deviations have been attributed to coupling to rotational motions. Furthermore, Raman-THz echoes have been shown to be rather insensitive to classical mass effects,8 despite their correlation with structural aspects related to viscosity of aqueous solutions.37 As such, the role of isotope effects in the collective dynamics of water has remained elusive.
.1 Conversely, the substantial increase in viscosity (15–30%) upon H/D exchange is largely attributed to nuclear quantum effects.2,8 Empirically, this enhancement has been modelled using the same translational mass factor (5%) as found for 16O/18O substitution and an apparent temperature shift of 6.5 K to account for (temperature-dependent) nuclear quantum effects.2–4,8 Yet, for translational diffusion – which is intimately related to viscosity – the ratio of diffusivities of H216O and D216O seems to be even lower than the translational mass factor at elevated temperatures.5 Based on MD simulations,36 such deviations have been attributed to coupling to rotational motions. Furthermore, Raman-THz echoes have been shown to be rather insensitive to classical mass effects,8 despite their correlation with structural aspects related to viscosity of aqueous solutions.37 As such, the role of isotope effects in the collective dynamics of water has remained elusive.
Such collective dynamics are also reflected in the dynamics probed with dielectric relaxation spectroscopy (DRS), which is sensitive to dipolar reorientation of an ensemble of water molecules. At 298 K, the dielectric spectrum of water is dominated by an intense relaxation mode centered at ∼20 GHz, which is attributed to dipole fluctuations upon rearrangement of the hydrogen-bonding network.38–42 To quantitatively reproduce the static permittivity of water using ab initio molecular dynamics simulations, correlated motion of water molecules across a few hydration shells has to be taken into account, which has led to the notion that dielectric relaxation reports on the collective relaxation dynamics of water.43 Despite the collectivity of the detected dynamics, the corresponding relaxation time of 8.3 ps at 298 K is consistent with what one would expect for uncorrelated, diffusive motion of dipolar water molecules in the liquid phase and the variation of the relaxation time with temperature is correctly predicted by the Stokes–Einstein–Debye equation over a remarkably wide temperature range.44–46 Hence, viscous friction appears to dominate the dielectric relaxation dynamics. Consistent with this notion, the relaxation time of water increases upon H/D exchange.9–16 Yet, the increase in viscosity and the increase in relaxation time upon H/D exchange do not agree quantitatively6,9 and are certainly different for H216O/D216O mixtures.12 Therefore, in addition to altered viscosity, librational and vibrational motions have been invoked to explain the slow-down of the dipolar reorientation dynamics.12 Overall, besides water in the gas-phase, where the variation of rotational transitions are accurately predicted by the altered moments of inertia,47 the origin of isotope effects in dielectric relaxation dynamics is not yet fully understood. In particular, the role of classical mass and nuclear quantum effects has not been disentangled.
In this work, we separate such classical mass effects from nuclear quantum effects by studying the broadband dielectric response of H216O, H218O, and D216O at temperatures ranging from 278 to 338 K to provide a unifying view on isotope effects on the dielectric response of water. In line with previous findings, we observe that, relative to H216O, D216O exhibits a significantly reduced orientational relaxation rate, whereas the relaxation of H218O slows down to a lesser extent. We find that the corresponding increase in the relaxation time and the increase in viscosity are strongly correlated for both D216O and H218O. The longer relaxation time of H218O can be fully accounted for by the increased viscosity, suggesting that the isotope enhancement for both observables are determined by the same classical mass effect. On the other hand, nuclear quantum effects upon H/D substitution result in a temperature dependent retardation of the relaxation dynamics of D216O (as compared to H216O) and the relative enhancement of the relaxation time slightly exceeds the relative increase in the viscosity.
Experimental
Materials
For dielectric measurements, de-ionized H216O was obtained from a Milli-Q purification system (18.2 MΩ cm, Merck Millipore). D216O (99.90 atom% D, Eurisotop) and H218O (97 atom% 18O, Sigma-Aldrich) were used as received. Prior to each measurement, fresh aliquots of H216O were obtained. D216O and H218O were stored in tight-lid glass vials.Dielectric relaxation spectroscopic measurements (DRS)
DRS probes the frequency-dependent macroscopic polarization of a sample induced by a low-amplitude, oscillating electric field with field frequency ν,48 commonly expressed in terms of the complex permittivity, ε′(ν):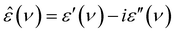 | (1) |
In the present study, 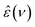 spectra were recorded using an Anritsu Vector Network Analyzer (model MS4647A). The range 0.05 ≤ ν/GHz ≤ 50 was covered using a frequency-domain reflectometer, equipped with a coaxial open-ended probe based on 1.85 mm connectors. Measurements at 50 ≤ ν/GHz ≤ 125 were performed using an open-ended probe, connected with 1 mm connectors to an external frequency converter module (Anritsu 3744A mmW).15 To calibrate the setup, air, conductive silver paint, and H216O were used as calibration standards using the dielectric spectra of H216O reported in literature.15
spectra were recorded using an Anritsu Vector Network Analyzer (model MS4647A). The range 0.05 ≤ ν/GHz ≤ 50 was covered using a frequency-domain reflectometer, equipped with a coaxial open-ended probe based on 1.85 mm connectors. Measurements at 50 ≤ ν/GHz ≤ 125 were performed using an open-ended probe, connected with 1 mm connectors to an external frequency converter module (Anritsu 3744A mmW).15 To calibrate the setup, air, conductive silver paint, and H216O were used as calibration standards using the dielectric spectra of H216O reported in literature.15
The temperature was varied from 278 to 338 K at increments of 10 K. To maintain constant temperature, the samples were placed into a double-walled sample holder connected to a Julabo F12-ED thermostat. The temperature stability in the center of the sample was estimated to be ±0.5 K. The spectra were recorded 6–8 times for each water isotope and this set of experiments was repeated at least once.
Results and discussion
Spectral analysis and qualitative trends
In Fig. 1a we show the dielectric spectrum of H218O at 298 K, which exhibits a dominant relaxation at ∼20 GHz. This relaxation is characterized by a dispersion in ε′ and a peak in ε′′. For H216O, this relaxation mode has been attributed to the collective rearrangement of its three-dimensional hydrogen-bonding network38–42 and can be excellently described by a Debye-type relaxation with its center position characterized by the collective relaxation time, τc. At higher frequencies (>50 GHz), the spectra of water deviate from a single Debye relaxation,13,15–17,39–41,45,49–53 which is often accounted for by an additional Debye relaxation – the so-called fast relaxation – with relaxation time τf.13,15–17,39,45,49,50,53 In line with these earlier studies, we model the experimental spectra of all three isotopic species of water with a combination of two Debye-type relaxations: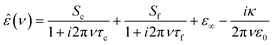 | (2) |
 | ||
| Fig. 1 (a) Relative permittivity (ε′, left axis) and dielectric loss (ε′′, right axis) spectra of H218O at 298 K. Squares and circles represent the experimental ε′ and ε′′ data, respectively; the black solid lines show the fits using eqn (2). Red and purple shaded areas depict the contribution of the cooperative and fast relaxation modes to ε′′, as obtained from the fit. For visual clarity, the last term of eqn (2) was subtracted from ε′′. (b) Comparison of the ε′′ spectra of H216O (solid lines), H218O (dashed lines) and D216O (dotted lines), respectively, at selected temperatures as obtained from the fits using eqn (2). | ||
To reduce the parameter space when fitting eqn (2) to the data, we constrain ε∞ for H216O and H218O to the values reported for H216O in ref. 15 (based on the similarity of their other physical properties1,28,29) and for D216O to the values reported in the same reference. We perform the fits for each spectrum individually by minimizing the sum of the squared deviations between simulated and experimental data on a logarithmic scale. For all three water isotopes, the averages of the thus obtained parameters and the corresponding error bars (estimated as three times the standard deviation) are listed in Tables S1–S3 in the ESI.†
Similar to previous findings for H216O13,15–17,39,45,49,50,53 (see also Fig. S1a, ESI†), we find that eqn (2) provides an excellent fit for the experimental 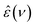 spectra for H218O (Fig. 1a) and D216O (Fig. S1b, ESI†). The experimental frequency range of this work fully covers the collective relaxation, reflected by low relative errors of the corresponding relaxation parameters for εs, Sc and τc (Tables S1–S3, ESI†). For Sf and τf, the experimental uncertainties are higher, since the center of the fast relaxation (H216O: ∼650 GHz, D216O: ∼550 GHz at 298 K15,17) is beyond the detected frequency range, in particular at elevated temperatures. Thus, we restrict the quantitative analysis to the collective relaxation.
spectra for H218O (Fig. 1a) and D216O (Fig. S1b, ESI†). The experimental frequency range of this work fully covers the collective relaxation, reflected by low relative errors of the corresponding relaxation parameters for εs, Sc and τc (Tables S1–S3, ESI†). For Sf and τf, the experimental uncertainties are higher, since the center of the fast relaxation (H216O: ∼650 GHz, D216O: ∼550 GHz at 298 K15,17) is beyond the detected frequency range, in particular at elevated temperatures. Thus, we restrict the quantitative analysis to the collective relaxation.
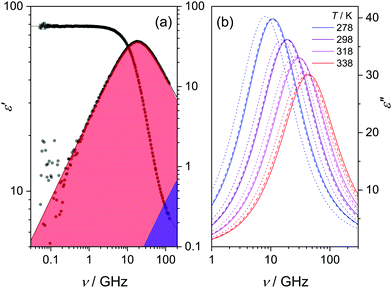
In Fig. 1b, the fitted dielectric losses for all studied isotopic species at four temperatures are displayed. For each species, we observe a shift of the dominant relaxation to higher frequencies upon increasing temperature, which demonstrates that the relaxation is thermally activated. Simultaneously, the relaxation strength (i.e. Sc + Sf, the area of the loss peaks; see Fig. S2, ESI†) markedly decreases, as enhanced thermal fluctuations counter dipolar alignment.54,55
Upon isotopic substitution, we find the loss peak for D216O to shift to lower frequencies at all temperatures as compared to H216O, consistent with previous studies.9–15 This red-shift is also reflected by the longer τc relaxation times of D216O (Fig. 2). For H218O, we detect a weaker, yet significant, shift to lower frequencies, which is again accompanied by the higher values of τc (Fig. 2). As such, we find that not only H/D exchange, but also 16O/18O substitution slows down the (dipolar) rotational relaxation of water. For the relaxation time of the fast mode, τf (inset in Fig. 2), the scatter of the data does not allow to discern a clear trend, as the values are the same within experimental error for the three species below 308 K. The increase in τf(D216O) above 308 K parallels the decrease in Sf(D216O), indicative of strong correlation of these two fitted parameters (see the inset in Fig. S2, ESI†). As such, the higher values of τf(D216O), relative to τf(H218O) and τf(H216O), above 308 K presumably reflect the shift of the fast relaxation to frequencies significantly higher than those covered by our experiments.
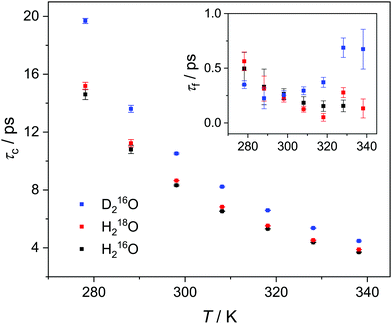 | ||
| Fig. 2 Relaxation time of the collective relaxation (τc) for H216O, H218O as well as D216O as a function of temperature, as obtained by fitting eqn (2) to the experimental complex permittivity spectra. Inset: Relaxation time of the fast relaxation (τf). The corresponding error bars represent the triple standard deviation. | ||
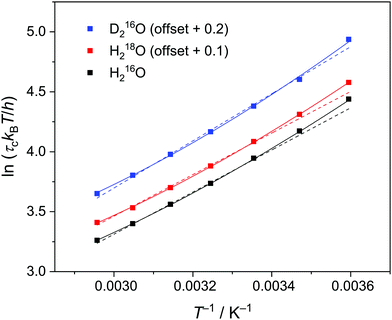 | ||
| Fig. 3 Eyring plot for the relaxation time of the collective relaxation (τc) for H216O, H218O, and D216O. Symbols represent the experimental data, while dashed and solid lines are the results of the fits using eqn (3) and (3)–(5), respectively. The corresponding error bars are smaller than the size of the symbols. For visual clarity, the data of H218O and D216O are offset by 0.1 and 0.2, respectively, along the vertical axis. | ||
The effect of temperature on the relaxation time of the cooperative mode
To quantify the thermal activation of τc, we use the Eyring theory,39,56 which assumes that the relaxation pathway passes through a thermally activated transition state: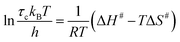 | (3) |
 values versus 1/T deviate from linearity (see eqn (3), dashed lines in Fig. 3), in agreement with previous findings.39,42,45,57 This deviation indicates that ΔH# and ΔS# are temperature-dependent, which can be accounted for by the isobaric heat capacity of activation, Δcp#:39,57
values versus 1/T deviate from linearity (see eqn (3), dashed lines in Fig. 3), in agreement with previous findings.39,42,45,57 This deviation indicates that ΔH# and ΔS# are temperature-dependent, which can be accounted for by the isobaric heat capacity of activation, Δcp#:39,57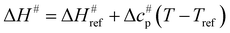 | (4) |
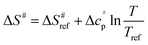 | (5) |
Comparison of the activation parameters shows that thermal activation for the dipolar relaxation of H218O and H216O are the same, within the experimental uncertainty. Conversely, we find ΔH#(D216O) > ΔH#(H216O). Given that the reorientation of water molecules is associated with hydrogen-bond breaking,39,58 ΔH# is intimately related to the hydrogen bond strength.34 As such, the observation of ΔH#(D216O) > ΔH#(H216O) is consistent with D216O forming stronger hydrogen bonds than H216O.5,59 Furthermore, the ∼12% higher activation entropy of D216O relative to H216O supports the notion that D216O is more structured than H216O.5,19,20,23,24 Overall, our results indicate that an increase in τc upon H/D substitution arises predominantly from the higher ΔH#(D216O) relative to ΔH#(H216O). Conversely, we detect no significant difference between the activation parameters of H216O and H218O, indicating close structural similarity and similar interaction strengths of their hydrogen-bonding networks, in line with the findings of a previous X-ray diffraction study.22
The effect of viscosity on the relaxation dynamics
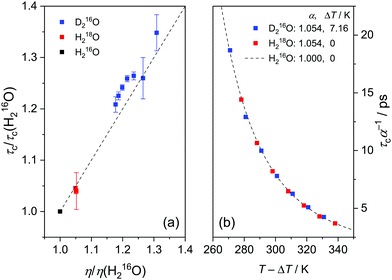
As the Stokes–Einstein–Debye equation45 predicts τc to be proportional to the macroscopic viscosity η, we first investigate the relationship between τc and η. For both H216O and D216O, our data for τc indeed scale linearly with η (viscosity data were taken from ref. 2), but this variation is not identical for the two isotopic species (see Fig. S3, ESI†). For H218O, although literature data for its viscosity are scarce and limited to 288–308 K,1 we find that the plots of τcvs. η for H216O and H218O collapse onto a single line (Fig. S3, ESI†), indicating that the relaxation times are affected by viscosity in the same manner.To gain further information about the isotope effects, it is instructive to compare the enhancements of the viscosities and relaxation times. In Fig. 4a, we show the plots of τc(D216O)/τc(H216O) vs. η(D216O)/η(H216O) together with τc(H218O)/τc(H216O) vs. η(H218O)/η(H216O). In the case of 16O/18O substitution, we find that both τc and η increase by a factor of ∼1.04–1.05, independent of temperature. As such, viscosity and relaxation times are equally affected by the replacement of oxygen with heavy oxygen. Hence, similar to viscosity,1,5,8 the difference between τc(H218O) and τc(H216O) can be described by the square root of their masses:
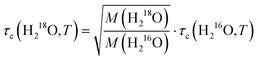 | (6) |
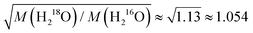 as found for viscosity.1,5,8 Rotational motions, which would scale with the square root of the ratio of the moments of inertia (
as found for viscosity.1,5,8 Rotational motions, which would scale with the square root of the ratio of the moments of inertia (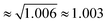 ), seem to play a minor role.
), seem to play a minor role.
 | ||
| Fig. 4 (a) Enhancement of the relaxation time of the collective relaxation (τc) as a function of viscosity enhancement for H216O, H218O as well as D216O relative to H216O. Symbols represent experimental data together with the dashed line through the origin with unity slope. (b) Scaled τc for H216O, H218O, and D216O as a function of temperature. Symbols represent experimental data divided by the mass factor, α = (M(isotope)/M(H216O))1/2 = 1.054 and shifted on the temperature scale by ΔT. The dashed line is the fitted curve of τc(H216O), based on eqn (3)–(5) and the parameters listed in Table 1. | ||
Fig. 4a shows that the relative increase in the relaxation time and viscosity upon H/D exchange is more pronounced (∼15–35%) than for 16O/18O substitution (∼4–5%), which therefore cannot be explained solely by translational mass effects. Rather, the temperature dependence of both ratios is a strongly indicative of nuclear quantum effects.8 For viscosity, such differences between D216O and H216O have been accounted for by an apparent temperature shift (ΔT = 6.5 K) in addition to the translational mass factor.2–4 Based on the strong correlation between the ratios of τc(D216O)/τc(H216O) and η(D216O)/η(H216O), we test an analogous empirical relationship for τc(D216O) and τc(H216O):
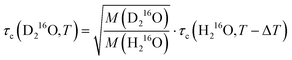 | (7) |
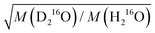 in eqn (7)) as an adjustable parameter, we obtain this factor to be 1.054, in quantitative agreement with
in eqn (7)) as an adjustable parameter, we obtain this factor to be 1.054, in quantitative agreement with 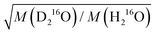 (Fig. S5, ESI†). As such, our data strongly suggest that classical mass effects on the dielectric relaxation time scale with the square root of water's molecular mass.
(Fig. S5, ESI†). As such, our data strongly suggest that classical mass effects on the dielectric relaxation time scale with the square root of water's molecular mass.
The determined value for ΔT = 7.16 K is in close agreement with ΔT = 7.2 K obtained earlier from THz spectroscopic measurements (performed at ν > 100 GHz),16 although in ref. 16 the mass factor has not been included. Interestingly, the enhancement for τc upon H/D exchange is consistently higher than for η (Fig. 4a), in line with previous findings.6,9,12 Given the mass factor is the same for both quantities, this difference is reflected by the higher ΔT for τc, as compared to the temperature shift reported for η (ΔT = 6.5 K).2–4 Hence, the slightly different isotope effect for viscosity and relaxation time upon H/D exchange suggests that the role of the relevant molecular motions involved in the thermal activation of viscous flow and dipolar reorientation are somewhat different.
Conclusions
We study the effect of isotopic substitution on the dielectric relaxation of water at temperatures ranging from 278 to 338 K. In line with earlier reports on H216O, the spectra of D216O and H218O at frequencies ranging from 0.05 to 125 GHz can be excellently described with two Debye relaxations. The dominant relaxation is centered at 8–40 GHz – depending on temperature and isotopic composition – and has been ascribed to the cooperative dipolar rearrangement of water's three-dimensional hydrogen-bonded network. Upon H/D exchange, we find a 20–35% increase in the corresponding relaxation time, whereas 16O/18O substitution results in a markedly weaker (∼4–5%) slow-down of the dynamics. Analysis of the thermal activation of the relaxation using the extended Eyring theory shows that the activation parameters for H216O and for H218O are virtually the same. For D216O, the enthalpy of activation is higher than for H216O, in line with stronger hydrogen-bonding of D216O.We find that the increase in the relaxation time of H218O relative to H216O is invariant of temperature suggesting that the isotope effect is dominated by (temperature independent) classical mass effects. The enhancement upon 16O/18O substitution can be well described by the translational mass factor 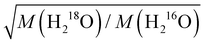 , despite the dipolar relaxation of water having rotational character, for which one would expect the moments of inertia to determine the relaxation time. The increase in the relaxation time is in quantitative agreement with the increase in the viscosity, indicating that the slow-down of the relaxation dynamics of H218O is governed by higher viscous friction.
, despite the dipolar relaxation of water having rotational character, for which one would expect the moments of inertia to determine the relaxation time. The increase in the relaxation time is in quantitative agreement with the increase in the viscosity, indicating that the slow-down of the relaxation dynamics of H218O is governed by higher viscous friction.
Conversely, upon H/D exchange, the increase in relaxation time is markedly higher and exhibits strong temperature dependence. Nevertheless, the relaxation times of D216O coincide with those of H216O when scaling with the translational mass factor and accounting for nuclear quantum effects with an apparent temperature shift. We find this temperature shift for the dielectric relaxation time to be larger (7.16 K) than that for viscosity (6.5 K![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2–4). Hence, despite the dielectric relaxation of water being intimately related to viscosity, the different temperature shifts point towards subtly different molecular motions involved in the thermal activation of the corresponding dynamics.
2–4). Hence, despite the dielectric relaxation of water being intimately related to viscosity, the different temperature shifts point towards subtly different molecular motions involved in the thermal activation of the corresponding dynamics.
Conflicts of interest
There are not conflicts of interest to declare.Acknowledgements
B. K. gratefully acknowledges financial support from the Alexander von Humboldt Foundation. We acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 714691) and the German Research Foundation (DFG, HU 1860/8). This work has been supported by the MaxWater program of the Max Planck Society. Open Access funding provided by the Max Planck Society.References
- A. I. Kudish, D. Wolf and F. Steckel, J. Chem. Soc., Faraday Trans., 1972, 68, 2041–2046 RSC.
- C. H. Cho, J. Urquidi, S. Singh and G. W. Robinson, J. Phys. Chem. B, 1999, 103, 1991–1994 CrossRef CAS.
- K. L. Harris, Phys. Chem. Chem. Phys., 2002, 4, 5841–5845 RSC.
- K. L. Harris and L. A. Woolf, J. Chem. Eng. Data, 2004, 49, 1064–1069 CrossRef CAS.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS.
- E. H. Hardy, A. Zygar, M. D. Zeidler, M. Holz and F. D. Sacher, J. Chem. Phys., 2001, 114, 3174–3181 CrossRef CAS.
- S. E. Lappi, B. Smith and S. Franzen, Spectrochim. Acta, Part A, 2004, 60, 2611–2619 CrossRef.
- A. Berger, G. Ciardi, D. Sidler, P. Hamm and A. Shalit, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2458–2463 CrossRef CAS.
- C. H. Collie, J. B. Hasted and D. M. Ritson, Proc. Phys. Soc., London, 1948, 6, 145–160 CrossRef.
- P. S. Yastremskii, J. Struct. Chem., 1971, 12, 483–484 CrossRef.
- A. A. Zharkikh, A. K. Lyashchenko, V. S. Kharkin, V. V. Goncharov and A. S. Lileev, Russ. J. Phys. Chem., 1991, 65, 553–557 CAS.
- U. Kaatze, Chem. Phys. Lett., 1993, 203, 1–44 CrossRef CAS.
- C. Hölzl, PhD thesis, University of Regensburg, 1998.
- K. Okada, M. Yao, Y. Hiejima, H. Kohno and Y. Kajihara, J. Chem. Phys., 1999, 110, 3026–3036 CrossRef CAS.
- S. Schrödle, PhD thesis, University of Regensburg, 2005.
- C. Rønne and S. R. Keiding, J. Mol. Liq., 2002, 101, 199–218 CrossRef.
- H. Yada, M. Nagai and K. Tanaka, Chem. Phys. Lett., 2009, 464, 166–170 CrossRef.
- P. Zalden, L. Song, X. Wu, H. Huang, F. Ahr, O. D. Mücke, J. Reichert, M. Thorwart, P. K. Mishra, R. Welsch, R. Santra, F. X. Kärtner and C. Bressler, Nat. Commun., 2018, 9, 1–7 CrossRef CAS.
- S. A. Kuharski and P. J. Rossky, J. Chem. Phys., 1985, 82, 5164–5177 CrossRef.
- J. S. Badyal, D. L. Price, M.-L. Saboungi, D. R. Haeffner and S. R. Shastri, J. Chem. Phys., 2002, 116, 10833–10837 CrossRef.
- L. Hernández de la Peña and P. G. Kusalik, J. Chem. Phys., 2004, 121, 5992–6002 CrossRef.
- R. T. Hart, C. J. Benmore, J. Neuefeind, S. Kohara, B. Tomberli and P. A. Egelstaff, Phys. Rev. Lett., 2005, 94, 047801 CrossRef CAS.
- U. Bergmann, D. Nordlund, P. Wernet, M. Odelius, L. G. M. Pettersson and A. Nilsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024202 CrossRef.
- A. K. Soper and C. J. Benmore, Phys. Rev. Lett., 2008, 108, 065502 CrossRef.
- T. Clark, J. Heske and T. D. Kühne, ChemPhysChem, 2019, 20, 2461–2465 CrossRef CAS.
- F. Paesani, S. Iuchi and G. A. Voth, J. Chem. Phys., 2007, 127, 074506 CrossRef.
- P. Hamm, G. S. Fanourgakis and S. S. A. Xantheas, J. Chem. Phys., 2017, 147, 064506 CrossRef.
- F. Steckel and S. Szapiro, Trans. Faraday Soc., 1963, 59, 331–343 RSC.
- K. R. Harris and L. A. Woolf, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 377–385 RSC.
- S. Perticaroli, B. Mostofian, G. Ehlers, J. C. Neuefeind, S. O. Diallo, C. B. Stanley, L. Daemen, T. Egami, J. Katsaras, X. Cheng and J. D. Nickels, Phys. Chem. Chem. Phys., 2017, 19, 25859–25869 RSC.
- T. Iwashita, B. Wu, W.-R. Chen, S. Tsutsui, A. Q. R. Baron and T. Egami, Sci. Adv., 2017, 3, e1603079 CrossRef.
- T. Yamaguchi, J. Phys. Chem. B, 2018, 122, 1255–1260 CrossRef CAS.
- A. Yahya, L. Tan, S. Perticaroli, E. Mamontov, D. Pajerowski, J. Neuefeind, G. Ehlers and J. D. Nickels, Phys. Chem. Chem. Phys., 2020, 22, 9494–9502 RSC.
- H. Eyring, J. Chem. Phys., 1936, 4, 283–291 CrossRef CAS.
- J. Teixeira, M.-C. Bellissent-Funel, S. H. Chen and A. J. Dianoux, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1913–1917 CrossRef CAS.
- D. Manogaran and Y. Subramanian, J. Phys. Chem. B, 2017, 121, 11344–11355 CrossRef CAS.
- A. Shalit, S. Ahmed, S. Savolainen and P. Hamm, Nat. Chem., 2017, 9, 273–278 CrossRef CAS.
- N. Agmon, J. Phys. Chem., 1996, 100, 1072–1080 CrossRef CAS.
- R. Buchner, J. Barthel and J. Stauber, Chem. Phys. Lett., 1999, 306, 57–63 CrossRef CAS.
- I. Popov, P. B. Ishai, A. Khamzin and Y. Feldman, Phys. Chem. Chem. Phys., 2016, 18, 13941–13953 RSC.
- D. C. Elton, Phys. Chem. Chem. Phys., 2017, 19, 18739–18749 RSC.
- U. Kaatze, J. Mol. Liq., 2018, 259, 304–318 CrossRef CAS.
- M. Sharma, R. Resta and R. Car, Phys. Rev. Lett., 2007, 98, 247401 CrossRef.
- E. H. Grant, J. Chem. Phys., 1957, 26, 1575–1577 CrossRef CAS.
- C. Rønne, L. Thrane, P.-O. Åstrand, A. Wallqvist, K. V. Mikkelsen and S. R. Keiding, J. Chem. Phys., 1997, 107, 5319–5331 CrossRef.
- P. Kumar, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12955–12956 CrossRef CAS.
- J. W. C. Johns, J. Opt. Soc. Am. B, 1985, 2, 1340–1354 CrossRef CAS.
- F. Kremer and A. Schönhals, in Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer, Berlin-Heidelberg, 2003, ch. 1, pp. 1–33 Search PubMed.
- J. T. Kindt and C. A. Schuttenmaer, J. Phys. Chem., 1996, 100, 10373–10379 CrossRef CAS.
- T. Fukasawa, T. Sato, J. Watanabe, Y. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802 CrossRef.
- A. Y. Zasetsky, Phys. Rev. Lett., 2011, 107, 117601 CrossRef.
- N. Q. Vinh, M. S. Sherwin, S. J. Allen, D. K. George, A. J. Rahmani and K. W. Plaxco, J. Chem. Phys., 2015, 152, 164502 CrossRef.
- V. Balos, S. Imoto, R. R. Netz, M. Bonn, D. J. Bonthuis, Y. Nagata and J. Hunger, Nat. Commun., 2020, 11, 1611 CrossRef.
- J. G. Kirkwood, J. Chem. Phys., 1939, 7, 911–919 CrossRef CAS.
- H. Fröhlich, Theory of Dielectrics, Clarendon Press, Oxford, 1958 Search PubMed.
- S. Glasstone, K. J. Laidler and H. Eyring, The Theory of Rate Processes, McGraw-Hill, New York, 1941 Search PubMed.
- B. E. Conway, Can. J. Chem., 1959, 37, 613–628 CrossRef CAS.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS.
- Q. Hu, S. Ouyang, J. Li and Z. Cao, J. Raman Spectrosc., 2017, 48, 610–617 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06460b |
| This journal is © the Owner Societies 2021 |
