Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient and low-scaling linear-response time-dependent density functional theory implementation for core-level spectroscopy of large and periodic systems†
Augustin
Bussy
 * and
Jürg
Hutter
*
* and
Jürg
Hutter
*
Department of Chemistry, University of Zurich, Winterthurerstrasse 190, CH-8057 Zurich, Switzerland. E-mail: augustin.bussy@chem.uzh.ch; hutter@chem.uzh.ch
First published on 8th February 2021
Abstract
We discuss our implementation of linear-response time-dependent density functional theory (LR-TDDFT) for core level near-edge absorption spectroscopy. The method is based on established LR-TDDFT approaches to X-ray absorption spectroscopy (XAS) with additional accurate approximations for increased efficiency. We validate our implementation by reproducing benchmark results at the K-edge and showing that spin–orbit coupling effects at the L2,3-edge are well described. We also demonstrate that the method is suitable for extended systems in periodic boundary conditions and measure a favorable sub-cubic scaling of the calculation cost with system size. We finally show that GPUs can be efficiently exploited and report speedups of up to a factor 2.
X-ray absorption spectroscopy (XAS) is a very useful tool to investigate the structure of matter. It is a local and element specific probe, providing insights into both geometric and electronic properties of molecules and solids. Advances in experimental techniques and increased availability of high quality X-ray sources have turned XAS into a central characterization technique in many fields, from surface sciences to biochemistry. The high energy of X-rays allow excitations of electrons from core states, yielding information otherwise inaccessible.
The XAS spectrum can be split into two regions, first of which is the X-ray absorption near edge structure (XANES), situated close to the ionization edge and mostly yielding insights about the electronic structure. At higher energies, the extended X-ray absorption fine structure (EXAFS) is found, providing more geometrical information. Since XAS is element specific, multiple spectra can be resolved for a given sample, one for each atomic kind and core state combination. The nomenclature depends on the donor core state, namely K-edge for 1s excitations, L1-edge for 2s, L2,3-edge for 2p, etc.
In order to help interpret XANES experiments, significant theoretical efforts were made leading to the development and adaptation of a variety of simulation methods. Well known density functional theory (DFT) based methods such as ΔSCF1 and transition-potential DFT2,3 deliver insights at an afforable computational cost. The former is however only well defined for the first excited state, making the simulation of a full spectrum challenging (but possible4). Transition-potential DFT methods do not suffer from this, although the spectra they produce are typically of lower quality than the next level of theory: time-dependent DFT. There are two approaches to it, real-time TDDFT5 and linear-response TDDFT6–8 (LR-TDDFT), both commonly used for core electronic spectroscopy. However, the improved results come at the expense of more complex implementations and increased computational costs. Much more involved are wave function based approaches such as those from the coupled-cluster family.9,10 Spectra produced by such methods are usually in excellent agreement with experiments, but their high computational cost make them prohibitively expensive for everything but small molecules.11
We believe that LR-TDDFT with hybrid functionals offers a good compromise between cost and accuracy for XANES simulations. Throughout this work, we report our implementation of it in the CP2K12 software package. Building on common approaches to XAS LR-TDDFT, we include additional core-specific cost-reduction measures and prove their validity. We also show that our method can accurately describe the L2,3-edge where spin–orbit effects are important and demonstrate its applicability in periodic boundary conditions. We finally discuss the favorable scaling of our method and how GPUs can be exploited for additional speed.
1 Theory
1.1 Linear-response TDDFT
For a system of N interacting electrons in the ground state, the time-independent Kohn–Sham (KS) equations| Fσ|ϕ0iσ〉 = εiσ|ϕ0iσ〉 | (1) |
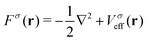 | (2) |
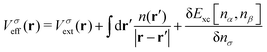 | (3) |
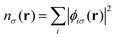 . The exchange–correlation potential above is defined as the functional derivative of the approximate exchange–correlation energy functional, expressed in hybrid DFT as
. The exchange–correlation potential above is defined as the functional derivative of the approximate exchange–correlation energy functional, expressed in hybrid DFT as| Exc[n] = EDFTc[n] + (1 − cHF)EDFTx[n] + cHFEHFx[n] | (4) |
with a fraction cHF of Hartree–Fock exchange.
In practice, the ground state KS orbitals are expanded in a finite basis set {φp(r)}, which is here taken to be made of non-orthogonal atom-centered Gaussian type orbitals (GTOs), such that
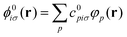 | (5) |
| Spq = 〈φp|φq〉. | (6) |
The KS equations can then be cast into matrix form as an Hermitian generalized eigenvalue problem, to be solved for the coefficients {c0piσ}:
| Fσc0 = Sc0ε | (7) |
For the simulation of electronic absorption spectroscopy in the Sternheimer approach to LR-TDDFT,13,14 the absorbed photon is modelled as a harmonic perturbation to the external ground state potential:
| Vext(t,r) =V0ext(r) + V−(r)e−iωt + V+(r)eiωt | (8) |
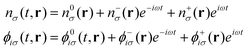 | (9) |
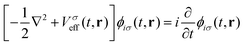 | (10) |
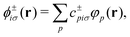 | (11) |
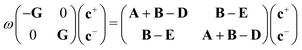 | (12) |
| Gpiσ,qjτ = Spqδijδστ, | (13) |
| Apiσ,qjτ = (Fσpq − εiSpq)δijδστ, | (14) |
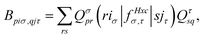 | (15) |
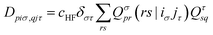 | (16) |
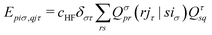 | (17) |
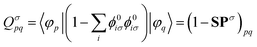 | (18) |
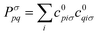 . The Hartree exchange–correlation kernel in eqn (15) is, within the adiabatic approximation,17 expressed as
. The Hartree exchange–correlation kernel in eqn (15) is, within the adiabatic approximation,17 expressed as | (19) |
Non-Hermitian eigenvalue problems such as eqn (12) are harder and more expensive to solve than their Hermitian counterparts. Casida18 showed that, assuming real orbitals, the LR-TDDFT eigenvalue problem can be cast into Hermitian form at the cost of a matrix square root. Another way of simplifying the problem is the so-called Tamm–Dancoff approximation (TDA),19 which yields excitation energies of similar quality with respect to full TDDFT.20 The TDA is obtained by setting c+ = 0 in eqn (12), resulting in
| ωGc− = (A + B − D)c−, | (20) |
1.2 Core specific approximations
Obtaining core excitation energies from standard LR-TDDFT is impractical at best since the corresponding eigenvalues, which are much larger than those of valence excitations, are not efficiently computed by conventional iterative solvers. Therefore, extra steps need to be taken to model excitation of core electrons in an affordable manner.In 1980, in the context of many-body theory of core holes, Cederbaum et al.22 argued that core and valence states are only weakly coupled due to their large energy difference and localization in space. This was later adapted to LR-TDDFT by Stener et al.,6 which allows for ignoring valence excitations when building the eigenvalue problem. In practice, this reduces the span of the MO indices i, j in matrices (13-17) to only a handful of core states, drastically reducing their size. This also brings core to low lying unoccupied bound states excitation to the smallest eigenvalues, making iterative solvers relevant again. This approach is commonly used in the community,5,7,23 although other methods based on core specific iterative solvers are also available.24,25
DeBeer George et al.8 went one step further by invoking the sudden approximation,26 which neglects electronic relaxation of the system beyond the core region after a core electron is excited. Combined with the localized nature of core states, this allows further decoupling of core excitations. The XANES spectrum can then be built as a sum of independent one donor core orbital contributions. This approach boosts the efficiency even further as diagonalizing a series of small matrices scales better than solving one large eigenvalue problem. This however requires donor core MOs to be local in space, which is not necessarily the case for canonical KS orbitals that are equivalent under symmetry. In such instances, the core orbitals need to be actively localized using schemes such as Foster and Boys,27 Pipek and Mezey28 or maximally localized Wannier functions.29 Note that in the case of L2,3 spectroscopy, the three degenerate 2p states must be treated simultaneously.
With the matrix sizes and diagonalization costs brought down, the bottleneck of such TDDFT calculations may become the evaluation of 4-center 2-electron integrals needed for the kernel matrices (15), (16) and (17). The cost of these integrals formally scales with the fourth power of the system size, although symmetries and resolution of the identity (RI) schemes30 are usually used for efficiency. In the context of XANES, all electron repulsion integrals involve a core orbital, which locality can be exploited for additional screening.31 We further utilize the local nature of core states by introducing a reduced RI scheme for increased efficiency. For the Hartree kernel:
 | (21) |
 | (22) |
 | (23) |
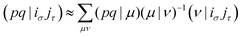 | (24) |
After solving eqn (12), the XANES spectrum is obtained by calculating oscillator strengths in the dipole approximation. LR-TDDFT is known to produce correct spectra, with accurate feature spacing and relative intensities, but in the wrong place on the energy axis. This is mainly due to the lack of relaxation upon the core hole creation and self interaction error. Different solutions have been proposed to tackle the latter,34–36 including new core excitation specific range-separated hybrid functionals.37,38 However, when standard XAS LR-TDDFT is employed, the calculated spectra usually have to be shifted to match experiments, either empirically or using a ΔSCF calculation.11,39,40
We implemented our method in the open source CP2K12 software package, based on the GAPW method41 for ground state calculations. By default, the RI basis sets are automatically generated using the method of Stoychev and co-workers.42 The 2- and 3-center Coulomb and exchange integrals are computed analytically using the Libint library43 and the exchange–correlation kernel is evaluated using the LIBXC44 library. Most basis sets come from Basis Set Exchange.45
1.3 Spin–orbit coupling
Relativistic effects play a role when dealing with core electrons as they attain very high speeds, typically reaching considerable fractions of the speed of light. The simplest and most well known way of treating such effects is the scalar relativistic approximation, in which only the mass-velocity and Darwin terms of Dirac's equations are kept. This however leads to the complete neglect of the spin–orbit coupling (SOC), which is at the origin of many important effects in chemistry and physics, such as L2,3-edge peak splitting in XANES.Within LR-TDDFT, scalar relativistic effects are added at the ground state level as a modification to the KS Hamiltonian, lowering the orbital energies of core states. Thus, resulting spectra are blue-shifted with respect to non-relativistic calculations, but the overall shape remain essentially unchanged. Since XAS LR-TDDFT spectra need to be rigidly shifted anyways, scalar relativistic effects can usually be assumed to be accounted for that way.11 Adding SOC to TDDFT is less trivial and generally involves more computationally intensive methods such as two-56,57 or even four-component58 relativistic TDDFT. A simpler approach consists of adding SOC as a perturbation to a non-relativistic calculation by coupling excited state wave functions of different spin multiplicities.59,60 This can be rigorously done within LR-TDDFT using the auxiliary set of many-electron wave functions (AMEW) framework proposed by de Carvalho and co-workers.61
In the general case of the LR-TDDFT Sternheimer based formalism, the AMEW expansion for an excited state I with excitation energy ωI is:
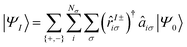 | (25) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) I±iσ)† is the creation operator for the LR orbitals. Note that this expression simplifies for core excitation within the sudden approximation as the sum over occupied states reduces to one core state only (three for degenerate 2p states). In case of TDA, the sum over {+, −} vanishes as the c+piσ LR coefficients are set to zero.
I±iσ)† is the creation operator for the LR orbitals. Note that this expression simplifies for core excitation within the sudden approximation as the sum over occupied states reduces to one core state only (three for degenerate 2p states). In case of TDA, the sum over {+, −} vanishes as the c+piσ LR coefficients are set to zero.
Following quasi-degenerate perturbation theory (QDPT),59 the Born–Oppenheimer Hamiltonian is perturbed with the addition of SOC matrix elements
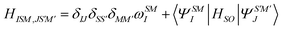 | (26) |
In restricted closed-shell systems, four kinds of excited states can cohabit; singlets with quantum numbers s = 0, ms = 0, spin-conserving triplets with s = 1, ms = 0 and spin–flip triplets with s = 1, ms = ±1. All of them can be described within the AMEW formalism and standard LR-TDDFT. Diagonalizing the complex Hermitian matrix yields new excited states as linear combination of singlets and triplets AMEWs with excitation energies that are corrected for SOC. The above formalism can easily be extended to open-shell systems by adding AMEWs built on spin–flip TDDFT65–67 to the standard spin-conserving excitations. Note that systems with a strong multi-reference character would still be out of reach, as LR-TDDFT is inherently a single reference method.
Adding SOC effects for L-edge spectroscopy does not come without cost. Indeed, the TDDFT eigenvalue problem needs to be solved twice (once for singlets and once for triplets) and the QDPT matrix can potentially reach very large sizes, leading to expensive diagonalizations. That latter point can easily be addressed by only considering excited states lying in the near-edge region of the spectra, which are limited in number.
1.4 ADMM acceleration
With the efficient core specific approximations described above, the bottleneck of XAS LR-TDDFT calculation may actually become the ground state KS SCF procedure, especially at the hybrid DFT level. Indeed, the addition of non-local Hartree–Fock exchange (HFX) to local generalized gradient approximation (GGA) adds a heavy computational burden that technically scales with the fourth power of the system size, as 4-electron 2-center electron repulsion integrals (ERIs) need to be evaluated. Although integral screening68 and the use of short range exchange operators32,69 have done much to bring that cost down, scaling with respect to basis set quality remains poor. To tackle this issue, the auxiliary density matrix method (ADMM) was developed70 and implemented in the CP2K software package. The HFX energy is a functional of the density matrix P and can be written as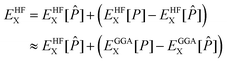 | (27) |
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) ≈ P was introduced. The assumption is that the difference in Hartree–Fock exchange energy between the primary and the auxiliary density matrices is well captured by GGA, which allows for the costly evaluation of ERIs in a smaller and/or less diffuse auxiliary basis set.
≈ P was introduced. The assumption is that the difference in Hartree–Fock exchange energy between the primary and the auxiliary density matrices is well captured by GGA, which allows for the costly evaluation of ERIs in a smaller and/or less diffuse auxiliary basis set.
There are two main flavors of ADMM, known as purified wave function fitting or ADMM1 and nonpurified wave function fitting or ADMM2. In the latter approach, the auxiliary MO coefficients are obtained by minimizing
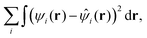 | (28) |
![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i(r) be orthogonal. This ensures that the auxiliary density matrix fulfills the properties of a pure density matrix, i.e. symmetry, idempotency and particle conservation. Note that, in purified wave function fitting, the ADMM Kohn–Sham matrix resulting from the SCF procedure cannot directly serve as a base for LR-TDDFT, as its eigenvalue do not correspond to orbital energies. As described in the original ADMM paper, an additional step for eigenvalue correction needs to be taken. Nonpurified wave function fitting, ADMM2, does not require any post SCF treatment. The exact speedup in HFX energy evaluation due to the ADMM method depends on the choice of primary and auxiliary basis sets and can typically reach orders of magnitude. Further studies have confirmed that the assumption expressed in eqn (27) is sound71 and that ADMM is usually faster, although less accurate, than other RI based acceleration schemes.72
i(r) be orthogonal. This ensures that the auxiliary density matrix fulfills the properties of a pure density matrix, i.e. symmetry, idempotency and particle conservation. Note that, in purified wave function fitting, the ADMM Kohn–Sham matrix resulting from the SCF procedure cannot directly serve as a base for LR-TDDFT, as its eigenvalue do not correspond to orbital energies. As described in the original ADMM paper, an additional step for eigenvalue correction needs to be taken. Nonpurified wave function fitting, ADMM2, does not require any post SCF treatment. The exact speedup in HFX energy evaluation due to the ADMM method depends on the choice of primary and auxiliary basis sets and can typically reach orders of magnitude. Further studies have confirmed that the assumption expressed in eqn (27) is sound71 and that ADMM is usually faster, although less accurate, than other RI based acceleration schemes.72
2 Validation
2.1 K-edge
To asses the quality of the method, the first excitation energy at the K-edge was computed for a series of small molecules for a variety of functionals and basis sets (without TDA). The structures were optimized at the B3LYP/cc-pVTZ level. Our results, displayed in Table 1, are in very good agreements with other similar publications (ref. 78 and 79). In particular, the mean absolute deviation (MAD) of the energies obtained with the cc-pCVTZ basis set is only 0.02 eV compared to those of Inanura, Otsuka and Nakai.78 This is significant since they solved the full LR-TDDFT equations, without any further approximation. The MAD compared to the work of Lestrange, Nguyen and Li,79 who use a energy specific iterative eigensolver for core excitations and the 6-311+G** basis set, is 0.05 eV. The small amplitude of the MADs indicates that the introduction of the sudden approximation and our local RI scheme have a negligible impact on accuracy. Note that the calculations of these averages do not involve all entries of Table 1, since the overlap with the other works is not complete. Experimental excitation energies are not reported here as the focus is on the consistency of our method with respect to other TDDFT implementations only.| cc-pCVTZ | 6-311+G** | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BLYP | PBE | B3LYP | PBE0 | BHHLYP | BLYP | PBE | B3LYP | PBE0 | BHHLYP | |
| C 2H2 | 269.97 | 269.26 | 275.36 | 276.29 | 283.68 | 269.74 | 268.95 | 275.83 | 276.16 | 283.62 |
| C 2H4 | 269.05 | 268.29 | 274.36 | 275.24 | 282.58 | 268.82 | 268.07 | 274.24 | 275.13 | 282.53 |
| C O | 271.32 | 270.56 | 276.17 | 276.90 | 283.58 | 271.27 | 270.41 | 276.10 | 276.84 | 283.57 |
| C H2O | 270.23 | 269.40 | 275.26 | 275.98 | 283.01 | 270.09 | 269.24 | 275.17 | 275.90 | 282.96 |
| C HFO | 272.69 | 271.83 | 277.67 | 278.35 | 285.28 | 272.57 | 271.70 | 277.61 | 278.29 | 285.25 |
| C F2O | 275.43 | 274.53 | 280.31 | 280.93 | 287.76 | 275.29 | 274.40 | 280.19 | 280.84 | 287.71 |
| N 2 | 382.49 | 381.77 | 388.55 | 389.70 | 397.97 | 382.37 | 381.61 | 389.32 | 389.64 | 397.98 |
| N H3 | 380.97 | 380.47 | 388.09 | 389.74 | 399.08 | 380.67 | 380.04 | 388.02 | 389.45 | 398.96 |
| N TNO | 382.59 | 381.89 | 388.89 | 390.14 | 398.68 | 382.40 | 381.68 | 388.81 | 390.05 | 398.66 |
| NNCO | 386.16 | 385.46 | 392.33 | 393.53 | 401.86 | 385.96 | 385.24 | 392.16 | 393.36 | 401.73 |
| CO | 512.33 | 511.63 | 519.82 | 521.45 | 531.65 | 512.12 | 511.43 | 519.71 | 521.35 | 531.63 |
| N2O | 512.49 | 511.83 | 520.46 | 522.25 | 533.14 | 512.29 | 511.61 | 520.34 | 522.14 | 533.09 |
| CH2O | 509.41 | 508.70 | 516.68 | 518.23 | 528.13 | 509.24 | 508.53 | 516.60 | 518.16 | 528.13 |
| CHFO | 510.24 | 509.53 | 517.64 | 519.23 | 529.28 | 510.08 | 509.37 | 517.54 | 519.15 | 529.24 |
| CF2O | 510.96 | 510.26 | 518.44 | 520.07 | 530.21 | 510.79 | 510.06 | 518.31 | 519.94 | 530.12 |
| CHFO | 659.95 | 659.17 | 669.59 | 671.76 | 684.99 | 659.79 | 659.00 | 669.47 | 671.65 | 684.92 |
| CF2O | 661.36 | 660.59 | 671.02 | 673.21 | 686.43 | 661.12 | 660.35 | 670.83 | 673.04 | 686.29 |
Additionally, basis set convergence studies were conducted at the K-edge. The difference between the first and second excitation energies (ω2 − ω1) was computed for the H2O, CO, NH3 and C2H4 molecules across the members of the pcseg80 and the core-specific pcX81 basis families. Note that the converging quantity was chosen such that self-interaction errors and related shifts do not play a role. The energy difference was generally found to converge quickly. For H2O, NH3 and C2H4, triple zeta quality basis sets were already sufficient. It was also observed that using the core uncontracted pcX basis sets did not drastically change the convergence rate nor the converged values. The detailed results can be found in the ESI.†
2.2 L-edge
At the L-edge, spin–orbit coupling is responsible for the splitting of the L2,3 peaks. To demonstrate the validity of our method together with the AMEW formalism and QDPT, we simulated the L2,3-edge XANES spectra for three closed-shell molecules and transition metal complexes, namely TiCl4, SiCl4 and CrO2Cl2 (without TDA). The results are displayed together with experimental data on Fig. 1. The computed spin–orbit splitting is remarkably consistent with experimental results and the spectral features are generally well reproduced, both in relative intensities and relative energies. Note that the choice of basis set and functional is such that our results can be directly compared to those of Kasper and co-workers,56 who use a more advance two-component relativistic TDDFT scheme. Despite the comparative simplicity of our method, the spectra we obtain are very similar. To illustrate the importance of SOC in L2,3-edge calculations, the scond row in Fig. 1 shows LR-TDDFT results without the AMEW and QDPT treatment. Except for arguably SiCl4 where spin–orbit splitting is small, leading to overlapping L2 and L3 features, the simulated spectra have neither descriptive nor predictive power.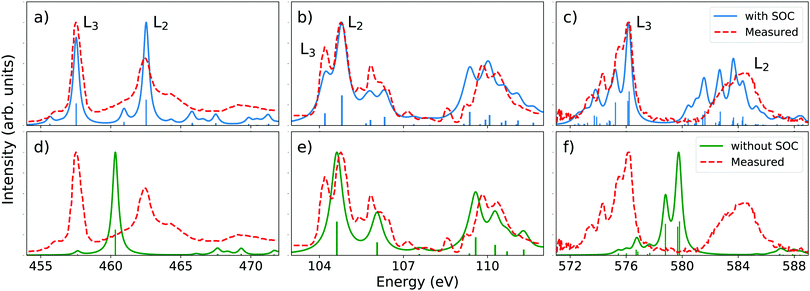 | ||
| Fig. 1 Top row: Simulated XANES L2,3-edge spectra for (a) TiCl4, (b) SiCl4 and (c) CrO2Cl2. Calculations are done at the B3LYP/def2-TZVPD73,74 level with SOC added on top of XAS LR-TDDFT, combining the AMEW and QDPT formalisms. The calculated spectra were rigidly shifted by 10.44, 5.42 and 7.30 eV, respectively, and a constant Lorenztian broadening with fwhm of 0.5 eV was applied. Bottom row: LR-TDDFT spectra of (d) TiCl4, (e) SiCl4 and (f) CrO2Cl2 without SOC corrections. Shifts and broadening are the same as for SOC calculations. Experimental data come from ref. 75–77. | ||
2.3 ADMM acceleration
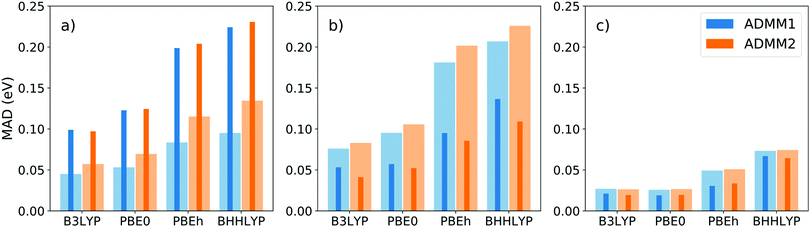
The performance of the ADMM1 and ADMM2 schemes have been assessed using the CORE65 benchmark set82 structures, which contains 32 small first and second row molecules. The set is initially meant for core ionization benchmarks, covering 30 C1s, 21 O1s, 11 N1s and 3 F1s core levels, although we use it here for core excitations. Reference full HFX calculations were done over the whole set using hybrid functionals with increasing fractions of exact exchange, namely B3LYP (20%), PBE0 (25%), PBEh83 with α = 0.45 (45%) and BHHLYP (50%). The basis sets of choice were the pcseg (double-, triple- and quadruple-zeta quality) and corresponding admm84 families, which are, to the best of our knowledge, the only available all-electron ADMM compatible basis sets. Results, computed within the TDA, are displayed on Fig. 2.The mean absolute deviation of the first excitation energies, shown as clear wide bars, varies significantly depending on the basis set and functional combination, from 0.03 eV for pcseg-3/PBE0 up to 0.23 eV for pcseg-2/BHHLYP. Logically, the error systematically increases with the Hartree–Fock fraction of the functional. Basis set quality, however, does not seem to correlate with the error.
Arguably more important than the absolute first excitation energy is the energy spacing between spectral features, since the LR-TDDFT spectrum needs shifting anyways. The thin dark bars represent the MAD of the first and third excited energies difference, i.e. ω3 − ω1, over the different basis sets and functionals. The error systematically decreases with basis set quality and, from triple-zeta on, is better than the absolute ω1 error. Note that the somewhat arbitrary ω3 − ω1 difference was chosen as to avoid ω2, which is often degenerate with the first excitation energy.
There is neither significant nor systematic difference between the two ADMM schemes. Since the nonpurified flavor (ADMM2) is simpler and requires less operations, this makes it the go to choice, especially for larger calculations. Note that finally, all errors reported here are quite small compared to the span of the near-edge region of the XAS spectrum which typically stretches over 15 to 20 eV. Therefore, inaccuracies due to the introduction of ADMM for the ground state should be barely noticeable. The speedups measured for HFX 4-center integral evaluations were 10.1, 8.6 and 3.8 for pcseg-1, pcseg-2 and pcseg-3, respectively.
2.4 Extended systems
Two systems were considered to evaluate the validity of the method in periodic boundary conditions; liquid water and tetrahedral sodium aluminate (NaAlO2). The former is a relatively sparse and disordered molecular system whereas the second is a much denser well ordered crystal. This difference motivated our choice, as we want to show the applicability of our method in those different regimes.
Fig. 3 shows the LR-TDDFT spectra of a 64 molecules liquid water periodic cell. To take the dynamical nature of the system into account, 50 frames were randomly selected from a 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, 20 ps long molecular dynamics simulation at the BLYP+D391 level at a temperature of 300 K. A XAS LR-TDDFT calculation was done for each snapshot and the results averaged. Both the MD simulation and the XANES calculations were conducted in periodic boundary conditions. Note that the 1s core electron of all 64 oxygen atoms were excited every time since their individual contributions to the overall spectrum, which are influenced by their local surroundings, may slightly vary. The features of the experimental spectrum are well identifiable in the simulated one, although not perfectly reproduced. Note that the divergence is likely at least partially due to the approximate structure of DFT water.
000 steps, 20 ps long molecular dynamics simulation at the BLYP+D391 level at a temperature of 300 K. A XAS LR-TDDFT calculation was done for each snapshot and the results averaged. Both the MD simulation and the XANES calculations were conducted in periodic boundary conditions. Note that the 1s core electron of all 64 oxygen atoms were excited every time since their individual contributions to the overall spectrum, which are influenced by their local surroundings, may slightly vary. The features of the experimental spectrum are well identifiable in the simulated one, although not perfectly reproduced. Note that the divergence is likely at least partially due to the approximate structure of DFT water.
 | ||
| Fig. 3 Oxygen K-edge XANES spectrum of liquid water at 300 K. The ADMM-PBEh (α = 0.45) functional and all-electron triple-zeta pcseg-2 and admm-2 basis sets were used on all atoms. The calculated LR-TDDFT spectrum was broadened with Lorentzians of fwhm of 0.6 eV and shifted by 5.50 eV to match measurements.85 | ||
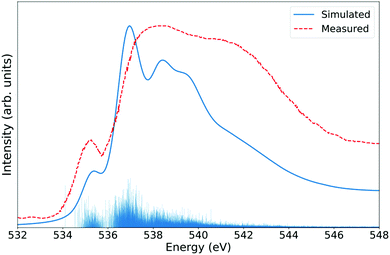
The simulated spectra of sodium aluminate can be seen on Fig. 4. The 128 atom model was first geometry optimized at the PBE+D3 level before a XAS LR-TDDFT calculation was performed. Because of symmetry, all aluminium atoms in the system are equivalent, and thus, the excitation from a single Al 1s core state can be considered. For the same reason, only one aluminium was described at the all-electron level whereas pseudopotentials were used for all remaining atoms. The experimental and simulated spectra are in remarkable agreement.
 | ||
| Fig. 4 Aluminium K-edge XANES spectrum of periodic crystalline sodium aluminate. The LR-TDDFT simulation was carried at the ADMM-PBEh (α = 0.45) level of theory. The calculated spectrum was rigidly shifted by 23.55 eV and Lorentzian broadened with a constant fwhm of 1.5 eV to match experimental data.86 The all-electron triple-zeta pcseg-2 basis set and its admm-2 auxiliary counterpart were used for the single excited Al atom. All other atoms were described with the DZVP-MOLOPT-SR-GTH87 and ADMM-FIT370 basis sets and corresponding GTH pseudopotentials.88–90 | ||
Both calculations were made using the PBEh (α = 0.45) hybrid functional, since it is well established that a high percentage of Hartree–Fock exchange is preferable for the description of core excitations.5,7,79 Because of the periodic nature of the systems, the truncated Coulomb operator was used for the ground state HFX energy and the exact exchange kernel. As physically sound,33 the truncation radius was taken to be less than half the simulation cell, namely 6 Å for water and 5 Å for sodium aluminate. All the approximations discussed in the theory part of this paper were used: the sudden approximation, allowing to solve for one core state at a time, the Tamm–Dancoff approximation, which makes the eigenvalue problem Hermitian, the ADMM method, reducing the cost of the ground state hybrid DFT calculation and our XAS specific local RI scheme, which makes the evaluation of the kernel integrals particularly efficient. Fig. 3 and 4 show that the combination of these shortcuts does not undermine the quality of the results.
3 Scaling and performance
Within the Tamm–Dancoff approximation and in periodic boundary conditions, three stages of the XAS LR-TDDFT calculations dominate in terms of cost. First of which is the evaluation of the ADMM four-center electron repulsion integrals. Because of integral screening and the use of short range exchange potentials, this is expected to scale linearly with the size of the system, albeit with a large prefactor. The second stage involves all the exchange correlation kernel integrals of eqn (21), (22) and (24). Thanks to the local RI scheme used there, all these quantities are purely local and expected to require a constant amount of work for each excited atom, for an overall linear scaling with system size. Finally, setting up and diagonalizing the eigenvalue problem of eqn (20) suffers from the worst scaling, as both matrix multiplications (by the projector matrix Qσ) and diagonlization technically scale as![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n3). However, the use of atom-centered Gaussian basis sets in large systems tends to bring sparsity into the matrices, reducing the cost of multiplication. Moreover, iterative solvers bring the cost of diagonalization down to
(n3). However, the use of atom-centered Gaussian basis sets in large systems tends to bring sparsity into the matrices, reducing the cost of multiplication. Moreover, iterative solvers bring the cost of diagonalization down to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (mn2), where m is the number of lowest eigenvalues to solve for. Since the focus is the near edge region of the spectrum, m tends to be small. Note that because the matrix operations take place for each excited atom in the system, the overall scaling is further increased by a power of one.
(mn2), where m is the number of lowest eigenvalues to solve for. Since the focus is the near edge region of the spectrum, m tends to be small. Note that because the matrix operations take place for each excited atom in the system, the overall scaling is further increased by a power of one.
To actually measure the scaling of the method, calculations were performed on systems of increasing sizes with constant computational power. Because of their different features, both liquid water and crystalline sodium aluminate are considered. The PBEh (α = 0.45) functional with truncation radii of 6 and 5 Å was used. All calculations were performed on 12 nodes of a Cray XC50 machine with 12 cores per nodes and a total of 384 GB of RAM. Note that depending on the amount of available memory, all ADMM integrals cannot necessarily be stored and a fraction needs to be recomputed at each SCF cycle. For a fair comparison between the different systems, only the cost of the initial integral evaluation is reported.
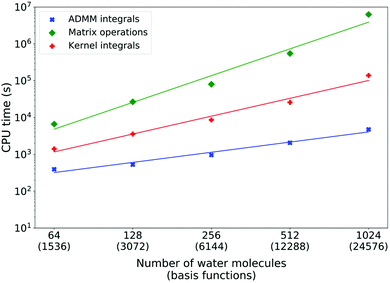
Fig. 5 shows the measured costs of XAS LR-TDDFT calculations for water systems of increasing sizes (cubic cells) with the double-zeta pcesg-1 and admm-1 basis sets. Matrix operations are systematically dominating the overall timings and are typically one to two orders of magnitude more expensive than kernel integrals and up to three orders of magnitude costlier than ADMM ERIs. As expected from the discussion above, ADMM integrals scaling was fitted to be linear (power of 0.9). On the other hand, matrix operations scaling was measured as the power of 2.4, which is much more favorable than the worst case scenario of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n4). This is due to matrix sparsity, which is exploited by DBCSR,92 CP2K's matrix–matrix multiplication library. Finally, the kernel integrals scaling was measured as the power of 1.6. This is worse than the theoretical linear scaling and the cause of this will be discussed later. However, since the cost is anyway at least ten times less with respect to matrix operations and still with a more favorable scaling, this is not much of a problem.
(n4). This is due to matrix sparsity, which is exploited by DBCSR,92 CP2K's matrix–matrix multiplication library. Finally, the kernel integrals scaling was measured as the power of 1.6. This is worse than the theoretical linear scaling and the cause of this will be discussed later. However, since the cost is anyway at least ten times less with respect to matrix operations and still with a more favorable scaling, this is not much of a problem.
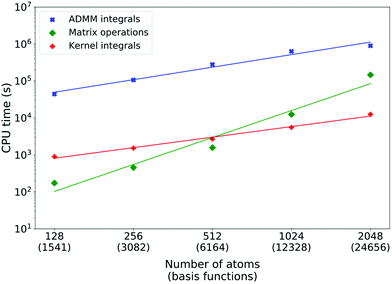
On Fig. 6, timings for sodium aluminium XAS LR-TDDFT calculations are reported. Note that the starting 128 atoms system has a cubic cell, but larger models are obtained by doubling one or more dimensions of the initial simulation box, leading to non-cubic cells. Similarly, the initial system has only one aluminium atom from which the excitation takes place, but this number doubles every time. The double-zeta pcseg-1 and admm-1 all-electron basis sets were used for excited aluminium atoms and DZVP-MOLOPT-SR-GTH/ADMM-FIT3 bases as well as GTH pseudopotentials were employed for all other atoms. Here, the ADMM ERIs evaluation systematically dominates and its scaling is also measured to be linear (fitted power of 1.1). Matrix operations are almost negligible for smaller systems, but their measured scaling of power 2.4 indicates that they would eventually take over as the main bottleneck. The cost of computing kernel integrals scales linearly as theoretically predicted (fitted power of 0.9) and is systematically two orders of magnitude less than ADMM ERIs evaluation.
The reason why the kernel integrals scaling differs between liquid water and crystalline sodium aluminate is due to both the implementation and the systems differences. While the actual evaluation of the 3-center RI integrals in the AO basis (pq|ν) scales linearly in both cases, it is the dominant operation for NaAlO2 but not for H2O. For efficient evaluation of the latter and favorable load balance, multiple optimization steps (integral screening, distribution over the processors, etc.) take place and they typically involve loops over the overlap matrix elements (or a fraction of those). Sparsity is such that when the system size doubles, the number of overlap matrix elements increases linearly and so does the cost of optimization, for each excited atom. In the case of water, the combination of high sparsity and small basis sets lead to a special case where the optimization overhead dominates. For sodium aluminate, lower sparsity and larger basis sets (especially the all-electron basis for excited aluminium atoms) lead to negligible optimization costs compared to the actual integral evaluation. A detailed scaling analysis of optimization and integral evaluation costs is available in the supplementary information.
The DBCSR matrix–matrix multiplication library has GPU support implemented. Since matrix operations are so dominant in the water calculations, we investigate whether they can be GPU accelerated. Fig. 7 shows execution times with and without GPU support, for the total calculation and the XAS LR-TDDFT matrix operations only. For the 256 molecules system, the GPU runs are actually slightly slower. This is probably due to the overhead of transferring data to and from the device for relatively few operations. As the systems grow, the GPUs start accelerating the calculations, up to a factor 2.0 in the case of matrix operations for the 1024 molecules system (factor 1.9 for the total execution time).
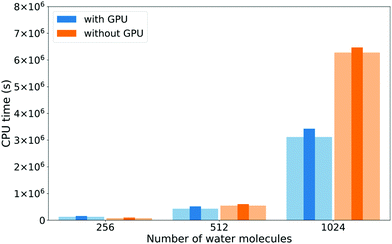 | ||
| Fig. 7 Comparison of total execution times (thin dark bars) and XAS LR-TDDFT matrix operations timings (wide clear bars) with and without GPU support for the DBCSR matrix–matrix multiplication library. Functional and basis set choices are the same as for Fig. 5. Calculations were done on 144 cores of a Cray XC50 machine (12 nodes). | ||
4 Conclusions
We have given the details of our LR-TDDFT implementation for core-level spectrocopy in the Sternheimer formalism13,14 and using Gaussian type orbital basis sets. Building on existing approaches to XAS LR-TDDFT that decouple core and valence excitations6,7 and exploit the sudden approximation,8 we further increase the efficiency by introducing new and accurate approximations. Namely, we exploit the localized nature of core orbitals and atom-centered Gaussian basis sets for a tailored resolution of the identity scheme to reduce the effort of calculating the many 2-electron 4-center integrals required. Additionally, we build the LR-TDDFT eigenvalue problem on top of a hybrid DFT ground state calculation that is greatly accelerated by the auxiliary density matrix method70 (ADMM) scheme.We have shown that our local RI scheme does not impact accuracy by reproducing benchmark results at the K-edge.78,79 Moreover, we have demonstrated that our treatment of spin–orbit coupling at the L-edge, combining the auxiliary many electron wave function formalism61 and the quasi-degenerate perturbation approach59 can reproduce experimental results. We have also quantified the error introduced by ADMM on excitation energies and concluded that they are negligible on the scale of a full XANES spectrum. Finally, we have shown the applicability of our method for extended systems in periodic boundary conditions by simulating liquid water and tetrahedral sodium aluminate. We measured a favorable sub-cubic scaling of the cost with system size and reported up to factor 2 speedups when using GPUs in calculations where matrix operations dominate.
Although our method is accurate, efficient and able to tackle large systems, it is still necessary to rigidly shift the simulated spectra to match experiments. This makes it more descriptive rather than predictive, although a ΔSCF1 calculation could be used to calculate the shift ab-initio. Such calculations can however be tedious and hard to converge. Therefore, our next efforts will go into the development of a first principles correction scheme for XAS LR-TDDFT that can be included in the current approach.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the MARVEL National Centre for Competency in Research funded by the Swiss National Science Foundation (grant agreement ID 51NF40-182892). Computer time was generously provided by he Swiss National Super-computing Center (CSCS) under project IDs d110 and s965.References
- N. A. Besley, A. T. Gilbert and P. M. Gill, J. Chem. Phys., 2009, 130, 124308 CrossRef.
- D. Jayawardane, C. J. Pickard, L. Brown and M. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115107 CrossRef.
- B. Hetényi, F. De Angelis, P. Giannozzi and R. Car, J. Chem. Phys., 2004, 120, 8632–8637 CrossRef.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2020, 11, 775–786 CrossRef CAS.
- K. Lopata, B. E. van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS.
- M. Stener, G. Fronzoni and M. de Simone, Chem. Phys. Lett., 2003, 373, 115–123 CrossRef CAS.
- N. A. Besley and A. Noble, J. Phys. Chem. C, 2007, 111, 3333–3340 CrossRef CAS.
- S. DeBeer George, T. Petrenko and F. Neese, Inorg. Chim. Acta, 2008, 361, 965–972 CrossRef CAS.
- S. Coriani and H. Koch, J. Chem. Phys., 2015, 143, 181103 CrossRef.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS.
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al. , J. Chem. Phys., 2020, 152, 194103 CrossRef.
- J. Hutter, J. Chem. Phys., 2003, 118, 3928–3934 CrossRef CAS.
- R. Sternheimer, Phys. Rev., 1951, 84, 244 CrossRef CAS.
- E. Runge and E. K. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- R. van Leeuwen, Phys. Rev. Lett., 1999, 82, 3863 CrossRef CAS.
- E. Gross and W. Kohn, Adv. Quantum Chem., 1990, 21, 287–323 CrossRef.
- M. E. Casida, Recent Advances In Density Functional Methods: (Part I), World Scientific, 1995, pp. 155–192 Search PubMed.
- A. L. Fetter and J. D. Walecka, Quantum theory of many-particle systems, Courier Corporation, 2012 Search PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206 CrossRef CAS.
- Y. Zhang, J. D. Biggs, D. Healion, N. Govind and S. Mukamel, J. Chem. Phys., 2012, 137, 194306 CrossRef.
- W. Liang, S. A. Fischer, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2011, 7, 3540–3547 CrossRef CAS.
- N. Schmidt, R. Fink and W. Hieringer, J. Chem. Phys., 2010, 133, 054703 CrossRef.
- J. Rehr, E. Stern, R. Martin and E. Davidson, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 560 CrossRef CAS.
- J. Foster and S. Boys, Rev. Mod. Phys., 1960, 32, 300 CrossRef CAS.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
- N. Marzari and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 12847 CrossRef CAS.
- O. Vahtras, J. Almlöf and M. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- N. A. Besley, J. Chem. Theory Comput., 2016, 12, 5018–5025 CrossRef CAS.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2009, 5, 3010–3021 CrossRef CAS.
- A. Nakata, Y. Imamura and H. Nakai, J. Chem. Phys., 2006, 125, 064109 CrossRef.
- G. Tu, Z. Rinkevicius, O. Vahtras, H. Ågren, U. Ekström, P. Norman and V. Carravetta, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 76, 022506 CrossRef.
- Y. Imamura and H. Nakai, Int. J. Quantum Chem., 2007, 107, 23–29 CrossRef CAS.
- J.-W. Song, M. A. Watson, A. Nakata and K. Hirao, J. Chem. Phys., 2008, 129, 184113 CrossRef.
- N. A. Besley, M. J. Peach and D. J. Tozer, Phys. Chem. Chem. Phys., 2009, 11, 10350–10358 RSC.
- S. DeBeer George and F. Neese, Inorg. Chem., 2010, 49, 1849–1853 CrossRef CAS.
- F. A. Asmuruf and N. A. Besley, Chem. Phys. Lett., 2008, 463, 267–271 CrossRef CAS.
- G. Lippert, J. Hutter and M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140 Search PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS.
- E. F. Valeev, Libint: A library for the evaluation of molecular integrals of many-body operators over Gaussian functions, http://libint.valeyev.net/, 2020, version 2.7.0-beta.6.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- J. M. Kasper, P. J. Lestrange, T. F. Stetina and X. Li, J. Chem. Theory Comput., 2018, 14, 1998–2006 CrossRef CAS.
- G. Fronzoni, M. Stener, P. Decleva, F. Wang, T. Ziegler, E. Van Lenthe and E. Baerends, Chem. Phys. Lett., 2005, 416, 56–63 CrossRef CAS.
- M. Kadek, L. Konecny, B. Gao, M. Repisky and K. Ruud, Phys. Chem. Chem. Phys., 2015, 17, 22566–22570 RSC.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, J. Chem. Phys., 2013, 138, 204101 CrossRef.
- D. Maganas, S. DeBeer and F. Neese, J. Phys. Chem. A, 2018, 122, 1215–1227 CrossRef CAS.
- F. Franco de Carvalho, B. F. Curchod, T. J. Penfold and I. Tavernelli, J. Chem. Phys., 2014, 140, 144103 CrossRef.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- P.-O. Löwdin, Phys. Rev., 1955, 97, 1474 CrossRef.
- Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818 CrossRef CAS.
- F. Wang and T. Ziegler, J. Chem. Phys., 2004, 121, 12191–12196 CrossRef CAS.
- Z. Li and W. Liu, J. Chem. Phys., 2012, 136, 024107 CrossRef.
- D. L. Strout and G. E. Scuseria, J. Chem. Phys., 1995, 102, 8448–8452 CrossRef CAS.
- J. Spencer and A. Alavi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 193110 CrossRef.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS.
- P. Merlot, R. Izsák, A. Borgoo, T. Kjærgaard, T. Helgaker and S. Reine, J. Chem. Phys., 2014, 141, 094104 CrossRef.
- E. Rebolini, R. Izsák, S. S. Reine, T. Helgaker and T. B. Pedersen, J. Chem. Theory Comput., 2016, 12, 3514–3522 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- A. Wen and A. Hitchcock, Can. J. Chem., 1993, 71, 1632–1644 CrossRef CAS.
- J. Bozek, K. Tan, G. Bancroft and J. Tse, Chem. Phys. Lett., 1987, 138, 33–42 CrossRef CAS.
- G. Fronzoni, M. Stener, P. Decleva, M. d. Simone, M. Coreno, P. Franceschi, C. Furlani and K. Prince, J. Phys. Chem. A, 2009, 113, 2914–2925 CrossRef CAS.
- Y. Imamura, T. Otsuka and H. Nakai, J. Comput. Chem., 2007, 28, 2067–2074 CrossRef CAS.
- P. J. Lestrange, P. D. Nguyen and X. Li, J. Chem. Theory Comput., 2015, 11, 2994–2999 CrossRef CAS.
- F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085 CrossRef CAS.
- M. A. Ambroise and F. Jensen, J. Chem. Theory Comput., 2018, 15, 325–337 CrossRef.
- D. Golze, L. Keller and P. Rinke, J. Phys. Chem. Lett., 2020, 11, 1840–1847 CrossRef CAS.
- V. Atalla, M. Yoon, F. Caruso, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165122 CrossRef.
- C. Kumar, H. Fliegl, F. Jensen, A. M. Teale, S. Reine and T. Kjærgaard, Int. J. Quantum Chem., 2018, 118, e25639 CrossRef.
- I. Waluyo, D. Nordlund, U. Bergmann, D. Schlesinger, L. G. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 140, 244506 CrossRef.
- J. L. Fulton, N. Govind, T. Huthwelker, E. J. Bylaska, A. Vjunov, S. Pin and T. D. Smurthwaite, J. Phys. Chem. B, 2015, 119, 8380–8388 CrossRef CAS.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703 CrossRef CAS.
- C. Hartwigsen, S. Gœdecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641 CrossRef CAS.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- U. Borštnik, J. VandeVondele, V. Weber and J. Hutter, Parallel Computing, 2014, 40, 47–58 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp06164f |
| This journal is © the Owner Societies 2021 |