Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental test of Babinet's principle in matter-wave diffraction†
Lee Yeong
Kim‡
 a,
Ju Hyeon
Lee‡
b,
Yun-Tae
Kim
c,
Sanghwan
Park
c,
Chang Young
Lee
a,
Ju Hyeon
Lee‡
b,
Yun-Tae
Kim
c,
Sanghwan
Park
c,
Chang Young
Lee
 c,
Wieland
Schöllkopf
c,
Wieland
Schöllkopf
 *b and
Bum Suk
Zhao
*b and
Bum Suk
Zhao
 *ad
*ad
aDepartment of Physics, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea. E-mail: zhao@unist.ac.kr
bFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, 14195 Berlin, Germany. E-mail: wschoell@fhi-berlin.mpg.de
cSchool of Energy and Chemical Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea
dDepartment of Chemistry, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea
First published on 15th February 2021
Abstract
We report on an experimental test of Babinet's principle in quantum reflection of an atom beam from diffraction gratings. The He beam is reflected and diffracted from a square-wave grating at near grazing-incidence conditions. According to Babinet's principle the diffraction peak intensities (except for the specular-reflected beam) are expected to be identical for any pair of gratings of complementary geometry. We observe conditions where Babinet's principle holds and also where it fails. Our data indicate breakdown conditions when either the incident or a diffracted beam propagates close to the grating surface. At these conditions, the incident or the diffracted He beam is strongly affected by the dispersive interaction between the atoms and the grating surface. Babinet's principle is also found to break down, when the complementary grating pair shows a large asymmetry in the strip widths. For very small strip widths, edge diffraction from half planes becomes dominant, whereas for the complementary wide strips the atom–surface interactions leads to a strong reduction of all non-specular diffraction peak intensities.
Introduction
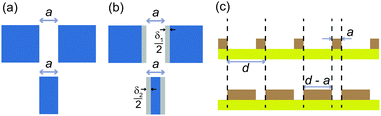
Babinet's principle is a basic theorem of classical optics, first formulated by the French scientist Jacques Babinet in 1837. It states that two complementary geometric objects, such as, for instance, a slit and a strip of the same size and shape (see Fig. 1a), produce identical diffraction intensities, except for the part of direct geometrical illumination.1 In the example of a slit in an opaque membrane and an opaque strip suspended in free space, it is obvious that the forward intensity must be far larger in the case of the strip than it is for the slit, because the slit limits the total transmitted flux. The intensities diffracted away from the geometrical ray direction are, however, identical according to Babinet's principle. As a result, Babinet's principle often allows for simplification of diffraction models. It has been applied to designing broadband antennas2 and forming frequency-selective surfaces in the far infrared.3 It also holds in acoustics.4 In sub-wavelength optics where Wood anomalies and related surface waves play important roles, Babinet's principle holds between light transmission through hole arrays and reflection from complementary disk arrays.5–7 Furthermore, it has found recent applications in the design of metasurfaces and metamaterials.8,9Because of its generality in wave optics, Babinet's principle was as well used in understanding matter-wave optical phenomena. This includes the scattering of diffraction beams of He atoms at a grazing exit angle from surface defects10 and Poisson's spot in matter-wave optics.11–14 In addition, Babinet's principle was used together with Fraunhofer–Kirchhoff diffraction theory to explain collisions between rare-gas atoms and molecules.15–17 Here, the collision is described in terms of diffraction of an incident matter-wave by a target molecule assumed to be a sharp-edged object.
Furthermore, Babinet's principle was also used for studying deviations between classical optics and matter-wave optics. The breakdown of Babinet's principle can occur for weakly bound diatomic system such as He2 because of breakup and finite-size effects when diffracted from strips, slits or a transmission grating.18 Even for point particles, the dispersive interaction between the particle and a geometric object, such as a slit or a strip, can change the conditions for Babinet's principle. For instance, it was reported that the dispersive particle–surface interaction narrows an effective slit width from a to a − δ1,19,20 from which we can deduce that the interaction can widen a strip width from its geometrical width a to a + δ2. In Fig. 1b, the effect of the interaction potential is illustrated by gray areas. The widths δ1,2 depend on the polarizability and the velocity of the particle,19,20 and the thickness of the object.21,22 Therefore, a complementary pair of slit and strip, fulfilling Babinet's principle with matter waves, would need to have their effective widths rather than their geometrical widths to be identical, as depicted in Fig. 1b.
In this work, we present results from an experimental study of Babinet's principle in diffraction of He atoms from plane square-wave gratings at grazing incidence conditions. The gratings used in the experiments all have a period d = 400 μm, but different strip widths. Diffraction patterns obtained from 4 pairs of gratings of complementary geometries (strip widths are a and d − a, e.g. 10 and 390 μm, as shown in Fig. 1c) are compared to test Babinet's principle. The strip widths of the complementary grating pairs are listed in Table 1. For a wide range of conditions we find Babinet's principle to hold. However, for the smallest incidence angles around 0.5 mrad we find that all diffraction peak intensities (except the specular peak) are larger for the grating with the narrow strips as compared to its complementary counterpart with wide strips. In addition, we observe that those outgoing diffraction beams, which propagate at very small angle with respect to the grating surface, are also more intense for the narrower strips than for the complementary wider strip widths. Furthermore, the data indicate that deviations from Babinet's principle are the more pronounced the more “asymmetric” a pair of complementary gratings is. These observations indicate that deviations from Babinet's principle occur when the atoms spend sufficient time close to the grating surface. Therefore, we attribute the breakdown of Babinet's principle to the effect of the atom–surface interaction potential, which, for each pair of complementary gratings, is more effective for the grating with wide strips.
| Pair no. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Grating | 10 μm | 30 μm | 70 μm | 100 μm |
| Complementary grating | 390 μm | 370 μm | 330 μm | 300 μm |
| Asymmetry ratio ra | 39.0 | 12.3 | 4.7 | 3.0 |
The particle–surface interaction plays a crucial role in these experiments, because quantum reflection of the incident He atoms from the diffraction grating has been identified as the coherent reflection mechanism.23 In contrast to the classical picture of a point particle reflected from a repulsive potential at a classical turning point, where the potential energy equals the incident kinetic energy, quantum reflection is based on the quantum-mechanical wave picture. For large de Broglie wavelengths of the incident particle, the wave is partly reflected by the long-range attractive particle–surface potential (van der Waals or Casimir–Polder potential). In the limit of vanishing incident kinetic energy, the quantum reflection probability approaches unity.24–30
For typical (thermal) conditions quantum reflection probabilities are negligible. Only for a sufficiently large de Broglie wavelengths (corresponding to excessively small incident velocities) one can expect detectable quantum-reflection probabilities. Accordingly, the first observation of quantum reflection of atoms from a solid was reported with ultracold metastable atoms31 and, later, also with a Bose–Einstein condensate.32,33 Alternatively, sufficiently small velocities can be achieved when an atomic or molecular beam scatters from a solid at grazing incidence.23,34,35 Due to the grazing incidence geometry the relevant velocity z-component, perpendicular to the surface, can approach extremely small values resulting in appreciable quantum-reflection probabilities. The comparatively large parallel velocity component does not restrict the quantum reflection process. Quantum reflection of He beams from plane surfaces34,35 as well as laminar23 and blazed ruled36 gratings has been reported.
Recently, quantum reflection of weakly bound ground-state helium dimers (He2 binding energy ≈ 0.1 μeV) and trimers (He3 binding energy ≈ 10 μeV)37,38 was also reported. Following the above description of classical scattering, the forces in the molecule-surface potential well region will inevitably lead to bond breakup, because the well depth (order of magnitude 10 meV) is ≈105 times and ≈103 times larger than the binding energy of helium dimers and trimers, respectively. Therefore, the observation of non-destructive reflection of He2 and He3 provides direct evidence for quantum reflection. Furthermore, the fact that diffraction patterns are found indicates that quantum reflection leads to coherent reflection of matter waves.
Experimental
The diffraction apparatus used in this work is shown schematically in Fig. 2.39 The He atom beam is formed by free-jet expansion of pure 4He gas from a source cell (kept at stagnation temperature T0 = 52 K and pressure P0 = 26 bar) through a 5 μm-diameter orifice into high vacuum. As indicated in Fig. 2, the beam is collimated by two narrow slits, each 20 μm wide, located 15 cm and 115 cm downstream from the source. The 25 μm-wide detector-entrance slit, located 38 cm downstream from the grating, limits the angular width of the atomic beam to a full width at half maximum of ≈120 μrad. The electron-impact ionization mass spectrometer used to detect the diffraction patterns is rotated precisely around the angle θ indicated in Fig. 2.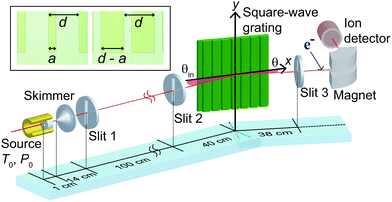 | ||
| Fig. 2 Schematic of the experimental set-up. The inset shows microscope images of a pair of complementary 400 μm-period gratings with strip widths of 100 μm (left) and 300 μm (right). | ||
The reflection grating is positioned at the intersection of the horizontal atom beam axis and the vertical detector pivot axis such that the incident beam approaches under grazing incidence (incident grazing angle θin), with the grating strips aligned parallel to the pivot axis. Diffraction patterns at a fixed incidence angle are measured by rotating the detector around θ and measuring the signal at each angular position. In addition, the grating can be removed from the beam path all together making it possible to measure the direct beam profile, i.e. the undisturbed incident beam, as a function of θ.
Each reflection grating consists of a 50 mm-wide microstructured array of 1.1 μm-thick and 4 mm-long parallel strips of a photoresist on a commercial gold mirror. Details of the gratings and the photolithographic fabrication techniques are provided in the ESI.† The nominal strip widths of the four pairs of complementary gratings are summarized in Table 1. For each pair the ratio of larger-to-smaller strip width ra indicates the degree of asymmetry of the complementary gratings. The inset of Fig. 2 shows microscope images of one of the complementary grating pairs. As the period is d = 400 μm, the gold surface between the strips is completely shadowed by the strips for all incidence angles used. Due to the small grazing incidence angles on the order of 1 mrad, diffraction patterns are observable despite the fact that the grating period is about 107 times larger than the de Broglie wavelength.
Results
In Fig. 3 we compare two contour plots presenting the full sets of diffraction data for the complementary gratings with 30 and 370 μm wide strips. Each plot shows the helium signal on a logarithmic scale as a function of incidence angle θin (horizontal axis) and detection angle θ (vertical axis). The range of θin and θ are from 0.5 to 2 mrad and from 0 to 2.5 mrad, respectively. Gray continuous curves depict the nth-order-diffraction angles θn calculated by using the grating equation, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θin − cos
θin − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θn = nλ/d. As θin increases, the first five negative-order diffraction beams appear successively at θin = θR,m and θ = 0 mrad. The Rayleigh incidence angle θR,m where the mth-order diffraction beam emerges is indicated by vertical dashed white lines.36
θn = nλ/d. As θin increases, the first five negative-order diffraction beams appear successively at θin = θR,m and θ = 0 mrad. The Rayleigh incidence angle θR,m where the mth-order diffraction beam emerges is indicated by vertical dashed white lines.36
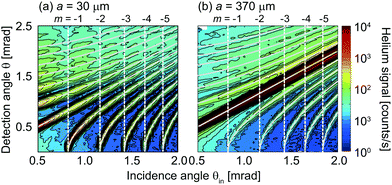 | ||
| Fig. 3 Contour plots composed of diffraction patterns measured at various incidence angles with two complementary gratings of (a) a = 30 μm and (b) 370 μm. The vertical dashed white lines indicate the Rayleigh incidence angle θR,m where the mth-order diffraction beam emerges from the grating.36 The continuous grey lines present the calculated diffraction angles. | ||
The two contour plots in Fig. 3 are clearly not identical. Most prominently, the specular intensity along the θ = θin line is much larger for the 370 μm strip-width grating than for the complementary grating with 30 μm strip width. This is as expected, because the specular intensity is the direct geometrical illumination (or 0th-diffraction order), which must be larger given the fact that the ra ratio of the strip widths is about 12. In addition, with increasing incidence angle one finds the weak specular intensity of the 30 μm strip-width grating to decrease with small oscillations, while for 370 μm strip width the decrease appears to be monotonous.
Further comparison of the two contour plots reveals that also parts of the non-specular diffraction peaks are different, which should not be so according to Babinet's principle. The diffraction peak intensities at very small incidence angle (close to the left edge of the plots, where θin < θR,−1) and at very small detection angle (close to the lower edge of the plots, where θn gets very small) are larger for the 30 μm strip-width grating than for the complementary grating. Furthermore, just like the specular intensity, the nth-order diffraction intensity shows a small oscillation along the continuous gray curves in Fig. 3a. The oscillations are absent in Fig. 3b. They are linked to the emerging beam resonances in the sense that the minima of the intensity appear close to the Rayleigh angles θR,m. The deviations in the non-specular parts of the contour plots indicate a breakdown of Babinet's principle.
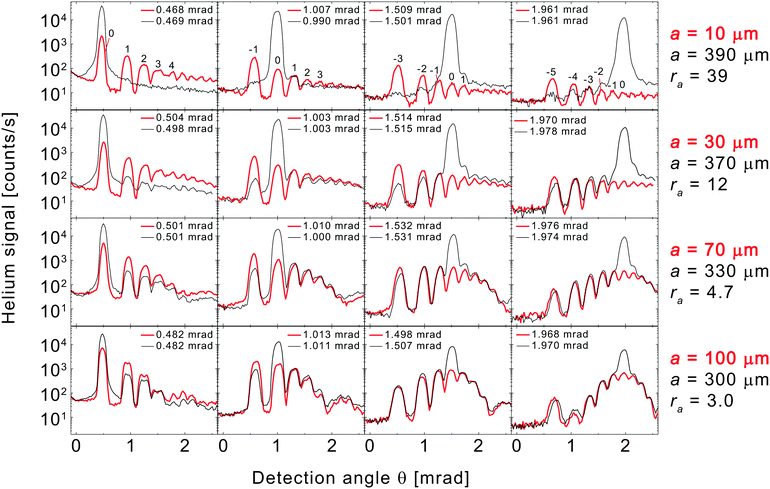
To investigate the deviations from Babinet's principle in more detail, we compare pairs of individual diffraction patterns from complementary gratings. Fig. 4 shows 16 such pairs of angular spectra at four incidence angles near 0.5, 1.0, 1.5, and 2.0 mrad for our 4 pairs of complementary gratings. In each diffraction pattern the helium signal is plotted on a logarithmic intensity scale as a function of the detection angle θ. It, hence, presents a vertical cross section of a contour plot like the ones shown in Fig. 3. In each plot, the red thick and the black thin spectra are from the grating with narrow strips and from its complementary counterpart, respectively. The numbers in the first-row plots indicate the diffraction orders assigned to the peaks in each column of plots. The 16 plots are arranged such that the incidence angle increases from left to right and the asymmetry of the complementary gratings, quantified by ra, increases from bottom to top. Thus, for the plots in the lower right corner of the graph the incidence angles are comparatively large and the asymmetry of the complementary gratings is small.
The systematic comparison of diffraction patterns from complementary gratings shown in Fig. 4 exhibits the following aspects regarding Babinet's principle's validity.
(I) Babinet's principle is found to hold in the lower right corner of the graph. For instance, at θin ≃ 2.0 mrad for ra = 4.7 (fourth column, third row) and at θin ≃ 1.5 mrad for ra = 3.0 (third column, fourth row) the red thick and the black thin spectrum overlap nicely, except for the specular peaks, as predicted by Babinet's principle.
(II) As the grazing incidence angle decreases (from right to left), the two diffraction patterns in each plot generally deviate more and more. For example, at θin ≃ 0.5 mrad (left most column), all non-specular diffraction peaks of the gratings with narrow strips (red thick patterns) are more intense than the corresponding ones of the complementary gratings with wide strips (black thin patterns). This disagrees with Babinet's principle.
(III) The difference between the two diffraction patterns becomes more distinct as the asymmetry ratio ra increases (from bottom to top). This again is most obvious at small incidence angle (left most column, θin ≃ 0.5 mrad), where the difference in diffraction peak intensity (n ≠ 0) between the two patterns is most pronounced for the most asymmetric grating pair (top left corner). But even for larger incidence angles diffraction peaks are hardly visible for the 390 μm strip-width grating (top row) in contrast to its 10 μm strip-width complementary counterpart.
(IV) For any plot, if deviations between the two diffraction patterns occur, they are most likely to show up at small detection angle. Apparently, diffraction beams close to the grating surface (small θ) are most likely to exhibit deviations from Babinet's principle. This is well visible in e.g. the four central plots of the graph.
(V) For ra = 12.3 and 39, at larger incidence angle (upper right of the graph), some intensities in the black thin spectrum are larger than the ones in the red thick spectrum. This can be attributed to the larger diffusive background occurring for wider strip widths. This effect is stronger for the diffraction peaks closer to the specular peak, since the diffusive signal is concentrated near the specular peak.35 The effect gets weaker as ra decreases.
Discussion
Our observations confirm the applicability of Babinet's principle to matter-wave grating diffraction for the experimental conditions corresponding to the lower right plots of Fig. 4, i.e. for comparatively large incident and outbound angles of more than ≈1 mrad and for relatively symmetric geometries of the complementary gratings. A break-down of Babinet's principle is observed, if one or more of these conditions do not apply. If the incident atom beam propagates under a very small angle to the grating surface, deviations from Babinet's principle are observed for all outbound diffraction peaks. If an outbound diffraction beam propagates under a very small angle to the grating surface, this beam's intensities deviate from Babinet's principle. The deviations get more pronounced, if the strip-width ratio of the complementary gratings is large.To explain the observations, we attribute the break-down of Babinet's principle to the effects of the atom-surface interaction between the He atoms and the strips of the grating on the diffraction intensities. The interaction affects an outbound diffraction beam appreciably, if the beam passes sufficiently close to the surface over an extended region in space, as is the case for a very small angle θn. The same holds true for the incident beam at sufficiently small θin, with the difference that any effect on the incident beam will as well affect each of the outbound diffraction beams. Furthermore, the wider the strip width the longer the lengths of interaction, and, hence, the more asymmetric complementary grating pairs can be expected to exhibit more pronounced deviations from Babinet's principle. Thus, the atom-surface interaction can well explain the trends of the observations in a qualitative manner.
The effect of the atom-surface interaction between He atoms and the bars of a transmission grating was investigated in detail by Grisenti et al.19 It was shown that the effect can be modelled by an effective width of the grating bars which is larger than the geometrical bar width. The difference between effective and geometrical bar width was found to increase with increasing interaction strength. Application of the effective-width model to the experiments of this work allows for a qualitative explanation of why Babinet's principle fails. As depicted schematically in Fig. 1(b), the effective strip width is the sum of the geometrical strip width a plus an interaction-induced term δi. As δi is added to both the narrow and wide strip width of the complementary gratings, the effective strip widths are no longer complementary in the sense that their sum will now be larger than the period d by δ1 + δ2. This implies that the geometrical strip widths would need to be smaller by δi, as indicated by the sketch in Fig. 1(b), such that the sum of the geometrical slit widths plus δ1 + δ2 adds up to d.
In particular, the effective slit-width model can explain the trend of vanishing diffraction peak heights observed for the widest strip width of 390 μm (black thin spectra in the top row of Fig. 4). Any increase of the 390 μm strip width by an additional δ will push the effective slit width towards the period d = 400 μm or beyond, at which point the periodicity of the structure is effectively lost. In this case the grating acts like a non (or hardly) structured flat surface with no (or very weak) non-specular diffraction peaks; exactly what the black thin data in the top row of Fig. 4 show.
However, the effective slit-width model cannot explain the observed diffraction patterns for the narrowest strip width of 10 μm (red spectra in the top row of Fig. 4). In contrast to their complementary counterparts, these patterns reveal intense diffraction peaks with a striking asymmetry between negative and positive diffraction orders. The peak intensities decrease with increasing order, a trend that includes the specular (0th-order) beam. This behavior is still present, albeit less pronounced, for 30 μm wide strips (2nd row of Fig. 4).
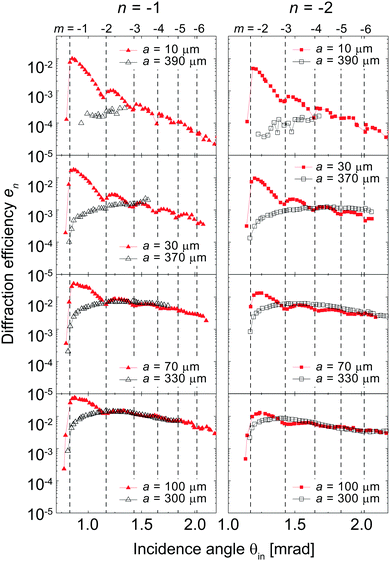
The diffraction peak intensities of selected diffraction orders (n = −1 and n = −2) as a function of incidence angle θin are plotted in Fig. 5. The n-th order diffraction efficiency en is defined as the n-th order diffraction intensity (given by the area of a measured diffraction peak) divided by the intensity of the direct beam profile (the undisturbed incident beam which is measured with the grating removed from the beam path). As expected from the above observations, when the −1st and −2nd-order diffraction beams emerge at their Rayleigh incidence angles, a substantial disagreement is found between the efficiencies for the two complementary gratings. For narrow strip widths of 10 and 30 μm we find a characteristic shape that combines a steep decay with saw-tooth shaped minima at the Rayleigh angles. In recent work we have shown that this behavior results from edge diffraction of the matter waves from half planes.40 Edge diffraction becomes the dominant reflection mechanism for very narrow strips that act like half-planes diffracting the incident de Broglie wave.
Fig. 5 also illustrates the emerging beam resonance effect, which is not well visible from the individual diffraction patterns at selected incidence angles shown in Fig. 4. Emerging beam resonances occur at every Rayleigh incidence angle θR,m (dashed vertical lines in Fig. 5) and affect, in principle, every diffraction beam.36 The saw-tooth shaped minima at incidence angle near θR,m in the red curves of Fig. 5 are well visible emerging beam resonances. By contrast emerging beam resonances are absent for the complementary grating of the wider strip width (black curves in Fig. 5). We presume that the strong reduction of the diffraction efficiencies e−1 and e−2 at θR,−1 and θR,−2, respectively, where the black curves begin, is caused by the atom-surface interaction along the long interaction length above the wide strips. The strong reduction of the emerging beam's intensity results, in turn, in a suppression of the emerging beam resonances at the corresponding Rayleigh angles. (Resonances are only detectable when the emerging beam is relatively intense.36)
Conclusions
We attribute the breakdown of Babinet's principle to the effect of the atom-surface interaction between the He atoms and the grating strips in combination with edge diffraction from half planes.40 The influence of atom-surface interaction on matter-wave diffraction phenomena has been studied before for diffraction from a nanoscale transmission grating19,21,22,41 and, most recently, for indium atoms diffracted by sub-micron silicon oxide spheres.14 In the latter experiment it was found that the van der Waals interaction between the indium atoms and a silica sphere can significantly enhance the intensity of the Poisson spot observed behind the spheres. In either experiment the particle–surface interaction causes an interaction-induced shift of the matter-wave phase.42 For diffraction from a transmission-grating the resulting changes in diffraction intensities can be accounted for by an effective width of the grating strips.19 The effective strip width model can, qualitatively, explain our observation of the non-specular diffraction intensities fading for the largest strip widths used in this work.For very small strip widths, on the other hand, edge diffraction from half planes40 becomes dominant and leads to asymmetric diffraction patterns with intense diffraction beams at small outbound angles with respect to the grating surface. This also implies that an emerging diffraction beam at Rayleigh conditions36 is intense for small strip widths, while it is weak for complementary large strip widths. As a consequence from this, emerging beam resonances (dips in the curves of Fig. 5) appear pronounced for small strip widths and absent for the complementary large strip widths. Therefore, we conclude that the combination of the two effects; enhancement of diffraction intensities for narrow strips due to edge diffraction and reduction of diffraction intensities for complementary wide strips due to atom-surface interactions, explains the observed conditions of breakdown of Babinet's principle.
Babinet's principle and the explanation of its breakdown given here make it possible to qualitatively predict matter-wave diffraction phenomena when a full calculation accounting for atom-surface interactions, as recently demonstrated,29 is not available or not needed. Diffraction efficiency ratios en/e0, for instance, can be calculated using Fraunhofer–Kirchhoff theory at conditions where Babinet's principle holds. On the other hand, at conditions where Babinet's principle breaks down, experimental results can provide a sensitive test of theoretical models for quantum reflection, which accurately account for the atom-surface interaction. Consequently, the comparison of these data with a fully confirmed model can serve as a new method for studying particle–surface interaction.
In summary, we did an experimental test of the applicability of Babinet's principle to matter-wave diffraction. Diffraction of a He atom beam at grazing incidence conditions from four different pairs of complementary square-wave gratings of 400 μm period up to the 5th diffraction order was observed. The data indicate that Babinet's principle is indeed valid for conditions when the incidence angle and the angles of the outbound beams are sufficiently large and the asymmetry ratio of the strip widths of complementary gratings is small. However, Babinet's principle fails when either the incident or a diffracted beam propagates close to the grating surface and/or when the complementary grating pair shows a large strip width asymmetry. We explain the observed breakdown of Babinet's principle qualitatively in terms of atom-surface interactions in combination with the effect of edge diffraction from half planes.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (Grant No. NRF-2015R1A2A2A01005458, NRF-2017H1A2A1042369, NRF-2019R1A2C1084928, and NRF-2020R1A2C3003701) and the Basic Science Institute Research Fund (1.200075.01) of UNIST (Ulsan National Institute of Science and Technology). Open Access funding provided by the Max Planck Society.References
- M. Born and E. Wolf, Principles of Optics, Pergamon Press, London, 1959 Search PubMed.
- T. H. Lee, Planar microwave engineering: a practical guide to theory, measurement, and circuits, Cambridge University Press, 2004, vol. 1 Search PubMed.
- R. Ulrich, Infrared Phys., 1967, 7, 37–55 CrossRef CAS.
- H. Feshbach and P. M. Morse, Methods of theoretical physics, McGraw-Hill Interamericana, 1953 Search PubMed.
- H. J. Lezec and T. Thio, Opt. Express, 2004, 12, 3629–3651 CrossRef.
- F. G. De Abajo, R. Gómez-Medina and J. Sáenz, Phys. Rev. E, 2005, 72, 016608 CrossRef.
- F. J. García de Abajo, Rev. Mod. Phys., 2007, 79, 1267 CrossRef.
- F. Falcone, T. Lopetegi, M. A. G. Laso, J. D. Baena, J. Bonache, M. Beruete, R. Marqués, F. Martín and M. Sorolla, Phys. Rev. Lett., 2004, 93, 197401 CrossRef CAS.
- M. Hentschel, T. Weiss, S. Bagheri and H. Giessen, Nano Lett., 2013, 13, 4428–4433 CrossRef CAS.
- D. Farías, M. Patting, K.-H. Rieder and J. R. Manson, Phys. Rev. B, 2002, 65, 165435 CrossRef.
- T. Reisinger, A. A. Patel, H. Reingruber, K. Fladischer, W. E. Ernst, G. Bracco, H. I. Smith and B. Holst, Phys. Rev. A, 2009, 79, 053823 CrossRef.
- T. Reisinger, G. Bracco and B. Holst, New J. Phys., 2011, 13, 065016 CrossRef.
- I. G. da Paz, R. Soldati, L. A. Cabral, J. G. G. de Oliveira Jr and M. Sampaio, Phys. Rev. A, 2016, 94, 063609 CrossRef.
- N. Gack, C. Reitz, J. L. Hemmerich, M. Könne, R. Bennett, J. Fiedler, H. Gleiter, S. Y. Buhmann, H. Hahn and T. Reisinger, Phys. Rev. Lett., 2020, 125, 050401 CrossRef CAS.
- M. Faubel, J. Chem. Phys., 1984, 81, 5559–5569 CrossRef CAS.
- M. Lemeshko and B. Friedrich, J. Chem. Phys., 2008, 129, 024301 CrossRef.
- J. Onvlee, S. D. S. Gordon, S. N. Vogels, T. Auth, T. Karman, B. Nichols, A. van der Avoird, G. C. Groenenboom, M. Brouard and S. Y. T. van de Meerakker, Nat. Chem., 2017, 9, 226–233 CrossRef CAS.
- G. C. Hegerfeldt and T. Köhler, Phys. Rev. A, 2000, 61, 023606 CrossRef.
- R. E. Grisenti, W. Schöllkopf, J. P. Toennies, G. C. Hegerfeldt and T. Köhler, Phys. Rev. Lett., 1999, 83, 1755–1758 CrossRef CAS.
- A. D. Cronin, J. Schmiedmayer and D. E. Pritchard, Rev. Mod. Phys., 2009, 81, 1051–1129 CrossRef CAS.
- T. Juffmann, A. Milic, M. Müllneritsch, P. Asenbaum, A. Tsukernik, J. Tüxen, M. Mayor, O. Cheshnovsky and M. Arndt, Nat. Nanotechnol., 2012, 7, 297–300 CrossRef CAS.
- C. Brand, M. Sclafani, C. Knobloch, Y. Lilach, T. Juffmann, J. Kotakoski, C. Mangler, A. Winter, A. Turchanin and J. Meyer, et al. , Nat. Nanotechnol., 2015, 10, 845–848 CrossRef CAS.
- B. S. Zhao, S. A. Schulz, S. A. Meek, G. Meijer and W. Schöllkopf, Phys. Rev. A, 2008, 78, 010902(R) CrossRef.
- R. B. Doak and A. V. G. Chizmeshya, Europhys. Lett., 2000, 51, 381–387 CrossRef CAS.
- H. Friedrich, G. Jacoby and C. G. Meister, Phys. Rev. A, 2002, 65, 032902 CrossRef.
- A. Mody, M. Haggerty, J. M. Doyle and E. J. Heller, Phys. Rev. B, 2001, 64, 085418 CrossRef.
- S. Miret-Artés and E. Pollak, J. Phys. Chem. Lett., 2017, 8, 1009–1013 CrossRef.
- J. Petersen, E. Pollak and S. Miret-Artés, Phys. Rev. A, 2018, 97, 042102 CrossRef CAS.
- G. Rojas-Lorenzo, J. Rubayo-Soneira, S. Miret-Artés and E. Pollak, Phys. Rev. A, 2018, 98, 063604 CrossRef CAS.
- G. Rojas-Lorenzo, J. Rubayo-Soneira, S. Miret-Artés and E. Pollak, Phys. Rev. A, 2020, 101, 022506 CrossRef CAS.
- F. Shimizu, Phys. Rev. Lett., 2001, 86, 987–990 CrossRef CAS.
- T. A. Pasquini, et al. , Phys. Rev. Lett., 2004, 93, 223201 CrossRef CAS.
- T. A. Pasquini, et al. , Phys. Rev. Lett., 2006, 97, 093201 CrossRef CAS.
- V. Druzhinina and M. DeKieviet, Phys. Rev. Lett., 2003, 91, 193202 CrossRef CAS.
- B. S. Zhao, H. C. Schewe, G. Meijer and W. Schöllkopf, Phys. Rev. Lett., 2010, 105, 133203 CrossRef.
- B. S. Zhao, G. Meijer and W. Schöllkopf, Phys. Rev. Lett., 2010, 104, 240404 CrossRef.
- B. S. Zhao, G. Meijer and W. Schöllkopf, Science, 2011, 331, 892–894 CrossRef CAS.
- B. S. Zhao, W. Zhang and W. Schöllkopf, Mol. Phys., 2013, 111, 1772–1780 CrossRef CAS.
- This apparatus was built in the 1990's in Prof. J. P. Toennies's Dept. of Molecular Interactions at the Max-Planck-Institut für Strömungsforschung in Göttingen, Germany, and was relocated to the Fritz-Haber-Institut der Max-Planck-Gesellschaft in Berlin, Germany in 2005 where it has been in use ever since.
- J. H. Lee, L. Y. Kim, Y.-T. Kim, C. Y. Lee, W. Schöllkopf and B. S. Zhao, Phys. Rev. Lett., 2019, 122, 040401 CrossRef CAS.
- J. D. Perreault, A. D. Cronin and T. A. Savas, Phys. Rev. A, 2005, 71, 053612 CrossRef.
- J. D. Perreault and A. D. Cronin, Phys. Rev. Lett., 2005, 95, 133201 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05694d |
| ‡ L. Y. K. and J. H. L. contributed equally to this work. |
| This journal is © the Owner Societies 2021 |