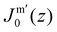Open Access Article
Open Access ArticleStructural and mechanical parameters of lipid bilayer membranes using a lattice refined self-consistent field theory†
N.
de Lange
 ,
J. M.
Kleijn
,
J. M.
Kleijn
 and
F. A. M.
Leermakers
and
F. A. M.
Leermakers

Physical Chemistry and Soft Matter, Wageningen University & Research Center, Stippeneng 4, 6708 WE Wageningen, The Netherlands. E-mail: frans.leermakers@wur.nl
First published on 8th February 2021
Abstract
The self-consistent field theory of Scheutjens and Fleer is implemented on a grid with (lattice) sites that are smaller than the segment size. In this quasi lattice-free implementation we consider united atom-like molecular models and study bilayer self-assembly of phospholipids in a selective solvent (water). We find structural as well as mechanical parameters for these bilayers. The mean (κ) and Gaussian (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) bending moduli, as well as the spontaneous curvature of the monolayer (Jm0), are computed for the first time following a grand canonical ensemble route. Results are in line with previous estimates for mechanical parameters that at the time could not be made following this correct route. This proves that the mean bending modulus is only a very weak function of the membrane tension. We performed a systematic study on the effects of model parameter variations. The mean bending modulus generally grows with increasing bilayer thickness. As expected Jm0 and
) bending moduli, as well as the spontaneous curvature of the monolayer (Jm0), are computed for the first time following a grand canonical ensemble route. Results are in line with previous estimates for mechanical parameters that at the time could not be made following this correct route. This proves that the mean bending modulus is only a very weak function of the membrane tension. We performed a systematic study on the effects of model parameter variations. The mean bending modulus generally grows with increasing bilayer thickness. As expected Jm0 and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) behave oppositely with respect to each other and for classical phospholipids assumes values near zero. As an example, an increase in the lipophilic to hydrophilic ratio in the lipids, may cause the Gaussian bending rigidity to switch sign from negative to positive, while – not necessarily at the same point – the spontaneous curvature of the monolayer may switch sign from positive to negative. Together with other investigated trends, these results point to mechanisms of how topological phase transitions of the lipid bilayer membranes may be regulated in the biological context, which correlates with known lipid phase behaviour.
behave oppositely with respect to each other and for classical phospholipids assumes values near zero. As an example, an increase in the lipophilic to hydrophilic ratio in the lipids, may cause the Gaussian bending rigidity to switch sign from negative to positive, while – not necessarily at the same point – the spontaneous curvature of the monolayer may switch sign from positive to negative. Together with other investigated trends, these results point to mechanisms of how topological phase transitions of the lipid bilayer membranes may be regulated in the biological context, which correlates with known lipid phase behaviour.
1 Introduction
A spontaneous assembly of lipids and proteins into bilayer membranes is the scene of fascinatingly complex phenomena fundamental to life. The fluid mosaic model of Singer and Nicolson,1 the cornerstone of membrane understanding, still leaves many important questions, e.g., regarding the (in)stability against topological changes, unanswered.The complexity of the biological membrane is manifest in the many different functions membranes have even inside a single cell. Membranes such as those occurring in mitochondria and chloroplasts, or the membranes of the endoplasmatic reticulum (ER) and nucleus have fascinatingly complex structures and often non-lamellar topologies. Non-lamellar topologies are often associated with proteins or protein complexes, but the role of the lipid composition of the membrane is arguably undervalued. A good example is the double membrane which forms the nuclear envelope. Topologically this double-membrane is in fact a single membrane due to the presence of so-called nucleopores: you may ‘walk’ along the inner membrane, via the nucleopore to the outer membrane without the need to leave the bilayer. While a large protein complex facilitates this double-membrane pore-like structure,2 the physical nature of the lipid assembly needs to allow for such non-trivial curvatures. In other words: curving the lipid-bilayer itself into a continuous structure connecting both membranes should not cost excessive amounts of energy. To date, the question what lipid mix is needed for such bending properties remains unanswered.
In the field of interfacial structures, bilayer assemblies of lipids are truly exotic. While the vast majority of interfaces have a finite interfacial tension (grand potential per unit area, γ) and thus a tendency to minimize their areas, large freely dispersed lipid bilayer sheets are in first-order free of tension (γ = 0) and maintain a huge interfacial area essentially proportional to the number of lipids in them. Fundamental to this exotic feature is the solvent symmetry, i.e., the same solvent (mainly water) exists on either side of the bilayer. A finite positive value of the interfacial tension of the membrane, to which we also refer as ‘membrane tension’ for short, would lead to a decrease of its area (and a concomitant increase of the membrane thickness) and a negative tension would do the reverse. By virtue of the mentioned symmetry, fully equilibrated bilayers will also show no interest in curving in a preferred direction. We say that its spontaneous curvature vanishes, that is, J0 = 0. In other words, the planar tensionless bilayer is the so-called ground state.
We haste to mention that in living cells, membranes are typically constrained in some way and subjected to concentration gradients, i.e. they are kept away from equilibrium. This implies that the symmetry is broken and membranes do become asymmetric, resulting in a spontaneous curvature, and may develop a non-zero tension. As usual in modeling situations, we however consider bilayers in the equilibrium state. Only after the equilibrium properties are established we can have hopes to understand the more general cases.
Ignoring end-effects, that is considering very large freely dispersed lipids assemblies, membranes are thus free of tension, have a well-defined thickness and no spontaneous curvature. Moreover, the chemical potential of its lipids, as well as the solvent in the system, are also well defined. They furthermore do not depend on the number of lipids in the membrane, or equivalently the membrane area.
Similar to a polymer chain, which assumes a coil shape if the ends are not constrained, bilayer membranes will not remain in a perfectly flat configuration either. For entropic reasons freely dispersed membranes must wander (more or less) around through space. For a linear polymer chain, the tendency to form a coil is controlled by its persistence length. Similarly, in the case of the lipid bilayer, there is a membrane persistence length lm, which in turn depends on the mean bending rigidity κ of the bilayer.3 The membrane persistence length grows exponentially with the membrane rigidity lm ∝ l![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ακ/kBT), with a coefficient α that does not deviate much from unity and l is a length comparable to the size of a water molecule. This means that when κ ≫ kBT, which tends to be the typical case for lipid bilayer systems, the membrane is essentially flat on the length scale of, e.g., its thickness. For this reason, it is not too exciting to have a strong focus on the mean bending modulus of phospholipid membranes. Much more interesting is to know how the Gaussian bending modulus (
exp(ακ/kBT), with a coefficient α that does not deviate much from unity and l is a length comparable to the size of a water molecule. This means that when κ ≫ kBT, which tends to be the typical case for lipid bilayer systems, the membrane is essentially flat on the length scale of, e.g., its thickness. For this reason, it is not too exciting to have a strong focus on the mean bending modulus of phospholipid membranes. Much more interesting is to know how the Gaussian bending modulus (![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) and the spontaneous curvature of the monolayer Jm0 are controlled because these parameters determine the topological (in)stability of lipid bilayer membranes.
) and the spontaneous curvature of the monolayer Jm0 are controlled because these parameters determine the topological (in)stability of lipid bilayer membranes.
Relatively few strong predictions exist for the Gaussian bending rigidity. It is generally accepted that a positive value of this quantity would promote non-lamellar, saddle-like topologies as these exist in bicontinuous triple periodic cubic phases. A negative value of this quantity is needed for the lamellar stability, which is especially important for membranes with a barrier function.
A large non-zero value for the spontaneous curvature of the monolayer may be the second cause of loss of the topological stability of bilayers. An individual monolayer may either curve preferentially towards the tails (as in micelles) and this gives Jm0 > 0 or towards the headgroup (as in reversed micelles), that is, Jm0 < 0. One expects that the planar bilayer is most stable when the monolayer spontaneous curvature is close to zero, i.e., Jm0 ≈ 0. It was shown earlier that when Jm0 is strongly positive, the bilayer can perforate and then gives way to cylindrical or spherical micelles.4 A similar bilayer stability catastrophe may happen when Jm0 ≪ 0.
The mechanical parameters of the bilayer feature in the Helfrich equation. This is an expansion of the interfacial tension γ (grand potential per unit area) of a membrane in terms of the mean curvature 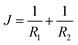 and Gaussian curvature
and Gaussian curvature 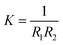 in a grand canonical ensemble. Here, R1 and R2 are the two principal curvatures that characterize the shape of the membrane.
in a grand canonical ensemble. Here, R1 and R2 are the two principal curvatures that characterize the shape of the membrane.
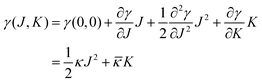 | (1) |
Since Helfrich published his membrane elasticity theory in 19735 many researchers have focused on estimating and measuring the membrane bending rigidities. A review published by Dimova et al.6 provides a good account of existing reports. Because the Gaussian bending rigidity cannot directly be measured experimentally and should be inferred from the phase behavior, experiments were aimed primarily on determining the mean bending rigidity. There are various methods that basically give comparable results. One can, for example, study shape fluctuations of giant vesicles,7–10 pull a tether by a pipette suction11–14 or study fluctuations of membranes in a lamellar phase by suitable scattering techniques.15,16 For lipid bilayer membranes that can form giant vesicles, one typically finds values for the mean bending modulus of order 10kBT. However, we know that not all lipid mixtures are suitable to create giants and the effective mean bending modulus of the bilayer is then not determinable with the same certainty. It may well be that a too low value for the bending modulus is the reason why they fail to form giants.
The situation concerning the value for the Gaussian bending rigidity is less clear. While topology changes of lipid systems can be observed and recorded in phase diagrams, direct correlations between such changes and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , in particular following the expected sign switch of
, in particular following the expected sign switch of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , remain to some degree in the realm of speculations. Early flawed modeling predictions for the Gaussian bending rigidity (see next section) may have had a negative impact on the trust that such a sign-switch of
, remain to some degree in the realm of speculations. Early flawed modeling predictions for the Gaussian bending rigidity (see next section) may have had a negative impact on the trust that such a sign-switch of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) correlates with a topological transition of the bilayer. The more recent, and also the current more realistic predictions for
correlates with a topological transition of the bilayer. The more recent, and also the current more realistic predictions for ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , should restore this trust. This recovery of confidence may materialize when a deeper understanding is generated in the relation between the molecular constituents of lipid bilayer membranes and the value of the Gaussian bending rigidity.
, should restore this trust. This recovery of confidence may materialize when a deeper understanding is generated in the relation between the molecular constituents of lipid bilayer membranes and the value of the Gaussian bending rigidity.
This paper aims to introduce and apply an improved protocol to predict the mechanical parameters κ, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0 of lipid bilayers using Scheutjens–Fleer self-consistent field (SF-SCF) theory, and to test the trends found as a function of lipid molecular properties against experimentally known phase behavior of lipids. Therefore, in the next sections, we will first review earlier attempts to find bilayer mechanical properties using classical SF-SCF theory, providing the context for moving to a quasi lattice-free model. This is followed by a discussion on the implementation of lattice refinements. After defining our lipid models and a brief introduction of the default parameter set, we will show that lattice refinements not only simplify the protocol to predict the mechanical parameters κ,
and Jm0 of lipid bilayers using Scheutjens–Fleer self-consistent field (SF-SCF) theory, and to test the trends found as a function of lipid molecular properties against experimentally known phase behavior of lipids. Therefore, in the next sections, we will first review earlier attempts to find bilayer mechanical properties using classical SF-SCF theory, providing the context for moving to a quasi lattice-free model. This is followed by a discussion on the implementation of lattice refinements. After defining our lipid models and a brief introduction of the default parameter set, we will show that lattice refinements not only simplify the protocol to predict the mechanical parameters κ, ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0, but also give access to accurate mean-field values of these parameters. It is this simplified approach that allows us to subsequently implement a systematic survey into the effects of changing the hydrophobic/hydrophilic balance in the lipid molecule and the architecture of the lipid tails on the structural and mechanical properties of the lipid bilayer. This in turn is important in the understanding of how a lipid bilayer membrane can be positioned in the vicinity of a topological transition.
and Jm0, but also give access to accurate mean-field values of these parameters. It is this simplified approach that allows us to subsequently implement a systematic survey into the effects of changing the hydrophobic/hydrophilic balance in the lipid molecule and the architecture of the lipid tails on the structural and mechanical properties of the lipid bilayer. This in turn is important in the understanding of how a lipid bilayer membrane can be positioned in the vicinity of a topological transition.
2 Finding the lipid bilayer bending moduli using self-consistent field theory
Theoretical approaches to find the bilayer rigidities from molecular models have many intricacies. It is often unclear what exactly is the status of the existing theoretical predictions because the strict rules to compute these quantities, as outlined below, are in many cases not obeyed. A general survey of the literature is beyond the scope of the current paper. Instead, we will review our own track record in Scheutjens–Fleer self-consistent field (SF-SCF) modeling, which unfortunately has also been one with ups and downs. Early predictions were definitely flawed (cf. ref. before 2013).17,18 The protocols used at that time were based on combining curvature energies of cylindrically and spherically curved bilayers. It was not yet realized that cylindrically curved bilayers are under tension and erroneously the full grand potential of cylindrically curved bilayers was interpreted as curvature energy. This resulted in too large values for κ and too negative values for![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , implying a too high predicted stability of lamellar phases. This was definitely not consistent with experimental phase diagrams.
, implying a too high predicted stability of lamellar phases. This was definitely not consistent with experimental phase diagrams.
In a more recent, revised protocol we still made use of the cylindrical geometry.19,20 As it turns out the grand potential of the cylindrically curved bilayer consists of two exactly equal contributions. One part is taken up by the stretching energy of the bilayer and the other part is invested in bending. Therefore, the revised protocol assigned only half of the grand potential to the bending energy resulting in a prediction for the mean bending modulus which is twice lower than the early protocols. The spherical vesicle was then used to find the combination of the mean and the Gaussian bending moduli. In this revised protocol definitely more trustworthy results were reported for typical phospholipid membranes: the Gaussian bending rigidity is rather close to zero and the trends that were found correlated well with the known phase behavior of lipid systems. The fact that this revised protocol gave reasonable results must to some extent be seen as a surprise as it violates the important requirement for determining the bending moduli that upon curving the chemical potentials should remain unchanged. More specifically, the cylindrically curved membrane has a finite tension and thus its constituents have a chemical potential that must differ (usually only slightly) from that of the planar bilayer.
As advertised more recently,21,22 in the ideal route to evaluate the mechanical parameters of bilayer membranes one should consider membrane assemblies in different curvature states with the strong constraint that the chemical potentials of its constituents are identical to the ones found in the planar bilayer (ground state) case: the correct route to evaluate the mechanical parameters must involve the grand canonical ensemble! In physical terms, keeping the chemical potentials of the constituents constant implies allowing flip-flop of the lipids from the inner to the outer monolayer as well as exchange of lipids with the bulk, where high curvatures require (relatively) more exchanges during bending than weak curvatures.
The grand canonical ensemble route combines the planar bilayer membrane system with spherically curved vesicles. In more detail, it is well known that one can compute the Gaussian bending rigidity from the planar bilayer already. For this the grand potential density profile ω(z) is used. This profile represents (minus) the local lateral pressure in the membrane and we will come back later in this paper on how this quantity is computed in the SCF formalism. In several publications it has been shown and discussed that the Gaussian bending modulus is found from the second moment of the grand potential density profile,23,24
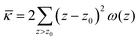 | (2) |
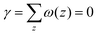 . In eqn (2) the symmetry plane of the planar bilayer is at z = z0. By the same token we mention that the corresponding first moment is related to the product of the mean bending modulus and the spontaneous curvature of the monolayer:23,24
. In eqn (2) the symmetry plane of the planar bilayer is at z = z0. By the same token we mention that the corresponding first moment is related to the product of the mean bending modulus and the spontaneous curvature of the monolayer:23,24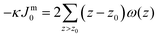 | (3) |
Ω = 4π(2κ + ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ) ) | (4) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) known from the planar bilayer, one can extract the mean bending modulus indirectly. Next, using eqn (3) the spontaneous curvature of the monolayer can be calculated. This route is implemented in the current work.
known from the planar bilayer, one can extract the mean bending modulus indirectly. Next, using eqn (3) the spontaneous curvature of the monolayer can be calculated. This route is implemented in the current work.
In the work of Pera and coworkers19 this correct route has been explored, but was rejected at that time for accuracy reasons. In that study the molecules were represented as strings of discrete segments (coarse grained atoms). Additionally, the space was discretized in a grid of cells (lattice), where each cell had a characteristic size equal to the segment size. The problem was that lattice discretization errors made the value of the thickness of the planar bilayer flawed up to perhaps 0.5 lattice layer. Of course similar lattice artifacts appeared in the cylindrical and spherical geometry calculations, but these could more or less be averaged out by using results from a (laborious) systematic variation of the radii of the vesicles, as will be explained in more detail below. As a result, Pera et al. could only use the formally incorrect route of combining cylindrically curved and spherically curved bilayers to obtain the bending rigidities. They also used an approximate route to estimate the spontaneous curvature of the monolayer. To date, we do not know how reliable the route followed by Pera et al. is in practice. In support of the revised protocol, we can say that when the cylindrical vesicles have a sufficiently large radius R, the deviations of the chemical potentials from the ground state are not very large, and one can always attempt to take the limit of R → ∞. Unfortunately, Pera et al. were restricted to use vesicles with a rather small radius, so the reliability issue is not resolved.
To use successfully the advertised correct (grand canonical) route one should find ways to reduce the lattice artifacts in SF-SCF predictions. It proved necessary to implement the self-consistent field equations on a finer grit. This is exactly what the technical task presented in the current paper is We discuss in depth a quasi lattice-free implementation of the SF-SCF model, developed along similar lines as the approach pioneered by Romeis et al. in the context of polymer brushes.25 Within the lattice-refined SF-SCF model, the lattice site is smaller by a factor 2, 3 or more than the segment size and the lattice artifacts are reduced correspondingly. The smaller the lattice site in comparison to the segment size, the more accurate we can estimate the membrane structure and the more accurate solutions for, e.g., the Gaussian bending rigidity are obtained. This also improves the accuracy of the indirectly obtained mean bending rigidity and finally allows the evaluation of the preferred curvature of the monolayer with eqn (3).
3 Lattice refined SF-SCF
From the above, it is clear that theoretical models for lipid bilayer membranes should, on top of structural information, give access to thermodynamical data so that the mechanical parameters of the bilayers can be computed. The self-consistent field theory can deliver these albeit within a framework that makes use of a mean-field approximation. The mean-field approach has intrinsic limitations and we will point these out below while elaborating the theory. We zoom in on the way the segment potentials (quantities that feature in Boltzmann weights) are computed from the segment densities (volume fractions) and vice versa. After obtaining the so-called self-consistent field solution as explained below, we can evaluate the then optimized free energy and corresponding thermodynamical parameters for the system.At the basis of the SF-SCF theory is a mean-field free energy functional which needs to be optimized. To put this functional in action, one needs to (i) make choices for the chain model, so that one can compute the single-chain partition functions for each type of molecule from (known) potentials, (ii) decide on which interactions are taken into account and how these are evaluated so that one can compute the interaction part of the free energy from (known) segment distributions. With these elements in place, one can evaluate the mean-field free energy functional, which is then expressed in terms of the segment volume fraction profiles φ(r) and segment potential profiles u(r), frequently complemented with Lagrange parameters to implement constraint relations.
The extremization of the mean-field free energy functional encompasses three steps. (i) The maximization of this mean-field free energy with respect to the potentials gives the rule on how to evaluate the volume fractions. (ii) The minimization of this free energy with respect to the volume fractions gives an equation for the segment potentials. (iii) Invariably, there is a compressibility relation to which the above results must obey and when necessary other constraints may be imposed. Each of these constraints will introduce a Lagrange parameter as an extra variable in the free-energy functional. Optimization of the mean-field free energy with respect to these Lagrange parameters effectively imposes these constraints. The extremization of the free energy in these three steps typically involves a numerical scheme with successive guesses. When the saddle point of the free energy functional is found, the segment potentials and volume fractions are mutually consistent with each other and in line with all imposed constraints, and this ‘fixed point’ is known as the self-consistent field solution.
The SF-SCF method combines a freely-jointed chain (FJC) model, with short-range contact interactions accounted for using the Bragg–Williams mean-field approximation, and an incompressibility constraint with lattice approximations, similarly as in the Flory–Huggins model. The latter is applied in spatially homogeneous systems (typically bulk phases); the SF-SCF method on the other hand focuses on concentration gradients, which are important at interfaces, e.g., for (polymer) adsorption, and for self-assembly, to name a few. Below we will highlight several elements in this protocol and focus on those elements that depend on the discretization scheme. More specifically, we will elaborate on ways to implement the SF-SCF equations on a lattice grit that is finer than the bond length. Such grits are needed to prevent lattice artifacts to dominate the results. For a more systematic discussion of the SF-SCF theory, we refer to the literature.19,26
The single-chain partition functions follow from solving the Edwards equation.27 Edwards realized that the analogy between a diffusing particle and the path followed by a flexible polymer chain suggests a diffusion-like (or Schrödinger-like) equation for polymer problems, wherein the time t is replaced by a contour length parameter s, and the (dimensionless) diffusion constant has a proposed value of 1/6. On top of this Edwards realized that real chains have a finite volume and he proposed to use a segment potential u to self-consistently account, on a mean-field level, for these ‘volume’ effects. The Edwards equation implements the Gaussian chain model:
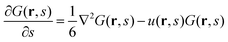 | (5) |
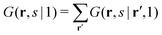 . The physical meaning of the end-point distribution G(r,s|1) is the statistical weight of all possible walks that start with a chain fragment near s = 1 and end at the chain fragment near s at position r. The fragment near s = 1 in this case can be near any coordinate in the system, which is compatible with the possible walks of a chain-fragment with length s.
. The physical meaning of the end-point distribution G(r,s|1) is the statistical weight of all possible walks that start with a chain fragment near s = 1 and end at the chain fragment near s at position r. The fragment near s = 1 in this case can be near any coordinate in the system, which is compatible with the possible walks of a chain-fragment with length s.
Typically, the SF-SCF formalism is applied to systems with a given ‘symmetry’. For example, for adsorption onto a planar surface, the density gradients normal to the surface are of main interest. Then the coordinate r is typically replaced by z and a mean-field approximation is applied in the x–y direction parallel to the surface. The Laplace operator in eqn (5) for this case reduces to ∇2 = ∂2/∂z2. Two- and three-gradient extensions (systems with less symmetry) are straightforwardly implemented. One-gradient spherical and cylindrical geometries are also frequently used, e.g. when spherical or cylindrically shaped vesicles are considered, respectively. In this case the coordinate r is replaced by r and the Laplace operator 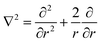 for spherical and
for spherical and 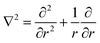 for cylindrical geometry, respectively.
for cylindrical geometry, respectively.
There are many strategies to numerically evaluate the Edwards equation. In the SF-SCF protocol, a finite element approach is used. We split the (polymer) chain into so-called statistical segments with ranking numbers s = 1,2,…,N. The size of such a segment does not necessarily need to coincide with the chemical notion of a segment, e.g., a polymeric monomer. It is assumed that on the length scale of the segment the chain is flexible. Segments are connected with bonds and the center-to-center distance between connected segments is b, also referred to as ‘bond length’. In addition, a discrete set of coordinates is used, which in a one-gradient version has lattice layer number z = 1,2,…,M. Without mentioning otherwise we will consider the one-gradient planar symmetry. The volume of a lattice site is given by v = l3, where l is the characteristic length of a lattice site. In the classical SF-SCF implementations, it is taken that b = l, or in other words, neighboring segments along the chain can only occupy neighboring lattice sites on the lattice. Scheutjens and Fleer used the propagator equation as the discrete variant of the Edward equation. The propagator also features the statistical weight G(z,s) (here the initial conditions are not specified yet and we use the generalized notation) and can be expressed as:
| G(z,s ± 1) = G(z)〈G(z,s)〉 | (6) |
| 〈G(z,s)〉 = λG(z − 1,s) + (1 − 2λ)G(z,s) + λG(z + 1,s) | (7) |
It is instructive to briefly show the link between the propagator and the Edwards equation. We will follow quite heuristic steps. We first rewrite eqn (7) as
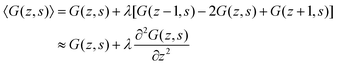 | (8) |
Let us next assume that the segment potential felt by the fragment from s to s + 1 is small, we may write the Taylor series expansion G(z) ≈ 1 − u(z). Combining this expansion and eqn (8) with the propagator (eqn (6)) leads to
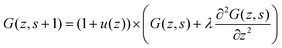 | (9) |
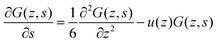 | (10) |
In the above, we illustrated that the classical lattice approximations lead to a simple propagator formalism. In many cases, the accuracy of this discretization scheme is sufficient to find reasonable results. However when gradients in G are not small, one can run into problems. These problems are known under the common denominator of ‘lattice artifacts’. Lattice artifacts for example occur for lipid membrane modeling when the core–corona or core–water interface is sharp compared to the segment size. The results then depend on, e.g., how exactly the membrane is positioned with respect to the lattice sites. A natural solution to fix this problem is to move to a more refined discretization scheme. In this paper, we implement a quasi lattice-free implementation of the self-consistent field equations inspired by Romeis et al.25,28 who used a similar implementation for polymer brushes and generalise the refinement strategy to non-planar geometries. The key idea is to keep the discretization for the segments the same, that is use the same ranking numbers s = 1,2,…,N, but to reduce the spatial coordinate, for example, by setting l = b/2. To cover the same volume, in case of a planar geometry the number of lattice sites in the z direction has to double with respect to the classical choice l = b; in this case, z = 1,2,…,2M. Here and below, the bond length b is chosen to normalize all lengths in the system.
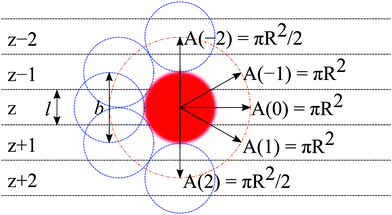
In the following, we will focus on the case l = b/2 and take it that the generalization to even more refined lattices is straightforward. One of the consequences of a refined lattice with respect to the segment size is that neighboring segments along the chain, no longer need to be placed at neighboring coordinates in the lattice. When segment s is in layer z = zs, segment s − 1 can be positioned in either zs − 2, zs − 1, zs, zs + 1, or zs + 2 as demonstrated in Fig. 1. Hence the FJC model implemented on this refined lattice implies a five-choice propagator and we will refer to this case as the five-choice FJC model:
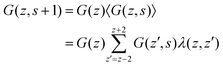 | (11) |
A legitimate task is to show how this 5-point stencil relates to the Edwards equation. We can rewrite the site fraction as
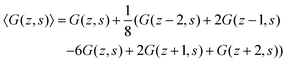 | (12) |
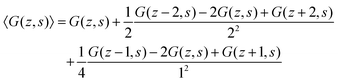 | (13) |
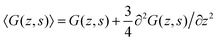 . One should realize that spacing for z is half that for s. The ‘effective’ diffusion coefficient, which was 1/4 for the three-choice SCF in a hexagonal lattice, is therefore slightly reduced to 3/16 (expressed in units b). This is in line with the expected increase in flexibility of the chain when the lattice sites are reduced in size.
. One should realize that spacing for z is half that for s. The ‘effective’ diffusion coefficient, which was 1/4 for the three-choice SCF in a hexagonal lattice, is therefore slightly reduced to 3/16 (expressed in units b). This is in line with the expected increase in flexibility of the chain when the lattice sites are reduced in size.
Typically, the propagators need to be supplemented with initial conditions. In the SF-SCF protocol, we start these recurrence relations at the chain ends. Linear polymers have two ends, one at s = 1 and the other at s = N and we therefore develop two sets of end-point distribution functions G(z,s|1) and G(z,s|N) (now the extended notation is used). These end-point distributions are generated by the one upward (increase in s) and one downward (decrease in s) running propagator:
| G(z,s + 1|1) = G(z)〈G(z,s|1)〉 | (14) |
| G(z,s − 1|N) = G(z)〈G(z,s|N)〉 | (15) |
| G(z,1|1) = G(z) | (16) |
| G(z,N|N) = G(z) | (17) |
The volume fraction profiles φ(z,s), that is, the fraction of sites in coordinate z occupied by segments with ranking number s, are found by the so-called composition law, which combines complementary end-point distribution functions:
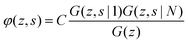 | (18) |
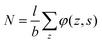 . Summing the densities over all segments gives the overall distribution for the polymer
. Summing the densities over all segments gives the overall distribution for the polymer 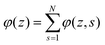 . The integral over the overall density is the amount
. The integral over the overall density is the amount 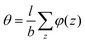 . The number of molecules as well as θ is specified on the bond length level. As a result, in the canonical ensemble
. The number of molecules as well as θ is specified on the bond length level. As a result, in the canonical ensemble 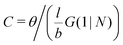 . We define the chain partition function
. We define the chain partition function 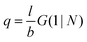 .
.
The Edwards equation must be supplemented with proper boundary conditions and the propagators require these as well. It is easily seen that evaluation of G(z,s|1) or G(z,s|N) in the region z = 1,…,2M requires values for end-point distribution functions specified for z < 0 and z > 2M. We distinguish different boundary conditions, which we will illustrate for G(z,s|1). (i) Neumann boundary conditions or, in SF-SCF language, adsorbing boundary conditions, typically used to model a solid phase at the system boundary. In this case, the chains cannot pass the boundary and we take G(z,s|1) = 0 for all z < 1 when the Neumann boundary conditions apply near the lower boundary of the system and G(z,s|1) = 0 when z > 2M when these conditions apply to the upper boundary. (ii) Dirichlet boundary conditions or, in SF-SCF language, mirror-like boundary conditions. In this case, the target is to have vanishing gradients (gradients are zero) at the boundaries of any spatial distribution in the system. As a consequence, lipid chains are allowed to cross the symmetry plane and there are no entropic restrictions felt by the molecules at the system boundary. Therefore we set G(z,s|1) = G(1 − z,s|1) for all z < 0 and G(z,s|1) = G(4M + 1 − z,s|1) for all z > 2M. (iii) Periodic boundary conditions are implemented by G(z,s|1) = G(z + 2M,s|1) when z < 1 and G(z,s|1) = G(z − 2M,s|1) when z > 2M. It is understood that for G(z,s|N) and for all segment densities φ(z,s) and thus also for φ(z) similar boundary conditions may be implemented when necessary. In this work, we use the Dirichlet boundary conditions.
The generalization to multiple types of chains in the system is only an organizational issue: the notation in the above equations must be extended to include the chain type i = 1,2,…,I. For example, the volume fraction distribution of molecule i is typically referred to as φi(z). The polymer chains may be composed of different segments. Let the segment types be scanned by the variable X = A,B,…. When the chain architecture is known from the input, we can define chain-architecture operators δXi,s. These quantities take the value unity when segment s of chain i is of segment type X and are zero otherwise. Each unique segment type X has its unique potential profile, uX(z), and thus has its unique free segment distribution function GX(z) = exp(−uX(z)). We may generalize the free segment distribution function, GX(z), to one which depends on the molecule i and segment ranking number s, Gi(z,s), as follows
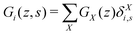 | (19) |
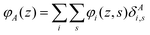 | (20) |
In SF-SCF modeling the Flory–Huggins equation of state is used. Segment interactions are parameterized by Flory–Huggins exchange interaction parameters χAB = Z/kBT(2UAB − UAA − UBB)/2, where Z is a lattice coordination number and U is the (potential) energy of the specified pairwise interaction, that is, the depth of the square-well potential for each specified contact. From this definition one can see that for ‘like’ contacts the FH parameter is zero by definition, i.e., χAA = 0. Such ‘Archimedes-like’ choice for the interaction parameter, is appropriate for systems that are incompressible because in such a system segments cannot ‘escape’ from interactions. In the Flory–Huggins theory (and also in SF-SCF) the Bragg–Williams approximation is implemented, which means that the probability (per unit area) of having an A–B ‘contact’ is given by the product of the respective volume fractions φA × φB. This is an approximation because segments that like each other will have a higher probability than the average value to be next to each other and vice versa. This correlation effect is thus ignored. Optimization of the mean-field free energy within the Flory–Huggins way of accounting for interactions leads to the following rule how to compute the segment potentials
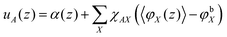 | (21) |
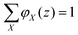 | (22) |
To evaluate the segment potentials (eqn (21)) we also need to evaluate the site fraction (cf.eqn (7)). This quantity depends on the discretization scheme in the same way as the end-point distributions do. The appropriate boundary conditions must be implemented to evaluate the site fraction near the system boundaries. The use of the site fraction to evaluate the potentials is a unique feature of the SF-SCF theory. In the field of polymer micro-phase segregation, the Edwards equation is typically solved using a finite element scheme that retains the Gaussian chain model, yet it loses the length of the chain as an independent variable. Instead, the product χN is retained. In such an approach it is not natural to account for the site fraction in the potential and typically the approximation is introduced that ϕ(z) = 〈ϕ(z)〉. One can say that only the local contribution is used and the non-local contributions, which in a lattice model come in to approximate the second derivative, are ignored. We have shown that such an approach is not without its consequences,22 especially when one is interested in results in the weak segregation limit.
When on top of the short-range contact interactions other interactions exist in the system, one has to extend the free energy functional with the corresponding terms, leading to additional terms in the segment potentials. A well-known example is electrostatic interactions when there are charged species in the system. In this case, we need to take into account the electrostatic potential and for this we need to solve the Poisson equation. Here we will not go into these details because the evaluation of the Poisson equation on a finer grit essentially takes place in the same way as for a less refined grit.19
The numerical methods to find the ‘fixed point’, or the self-consistent solution for the set of equations, do not depend on the discretization scheme and details of this can be found elsewhere.30 It suffices to mention that routinely the solutions are obtained with 8 to 10 significant digits. This is sufficient to accurately evaluate various thermodynamic potentials and the interfacial rigidities.
Non-planar geometries
Above we have elaborated on the main details of the SF-SCF theory and we have shown how one can use a grit with lattice sites that are twice smaller than the segment size (or equivalently the bond size). It is of significant interest to elaborate further on how one can implement the corresponding strategy in spherical or cylindrical one-gradient coordinate systems. From the above, it is clear that the main challenge is to implement the Laplacian in the five-choice FJC model. In the lattice we have spherical (or cylindrical) lattice layers which we number once again by z = 1,2,…,2M and understand that the r-coordinate (units b) takes values r = (z − 1/2)/2. In the planar lattice we arrived at transition probabilities λ(z − z′), where z − z′ obtained values −2, −1, 0, 1, 2. It is clear that for finite r we will need to modify these transition probabilities with an r-dependent function such that in the limit r → ∞ the planar quantities are recovered.| λ(r,r′) = Λ(r,r′)λ(z − z′) | (23) |
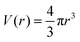 in spherical and πr2 in cylindrical geometry. Hence, in spherical coordinates L(r) ≈ 4πr2 and in cylindrical coordinates L(r) = 2πr. Next we need to make sure that the statistical weight to make steps from r to r′ is the same as the weight to make steps from r′ to r (so-called inversion symmetry), which requires that L(r)Λ(r,r′) = L(r′)Λ(r′,r). Similarly as in the classical approach we therefore take the transition probabilities proportional to the area A(r′′), where A(r) = 4πr2 in spherical and A(r) = 2πr in cylindrical geometry, of the plane at r′′ halfway between the coordinates r and r′:
in spherical and πr2 in cylindrical geometry. Hence, in spherical coordinates L(r) ≈ 4πr2 and in cylindrical coordinates L(r) = 2πr. Next we need to make sure that the statistical weight to make steps from r to r′ is the same as the weight to make steps from r′ to r (so-called inversion symmetry), which requires that L(r)Λ(r,r′) = L(r′)Λ(r′,r). Similarly as in the classical approach we therefore take the transition probabilities proportional to the area A(r′′), where A(r) = 4πr2 in spherical and A(r) = 2πr in cylindrical geometry, of the plane at r′′ halfway between the coordinates r and r′: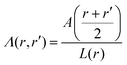 | (24) |
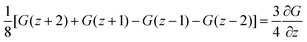 . The coefficient 3/4 is in line with the result from eqn (13) discussed above. Hence, the corresponding Edward equation reads
. The coefficient 3/4 is in line with the result from eqn (13) discussed above. Hence, the corresponding Edward equation reads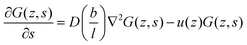 | (25) |
The continuous limit
It is possible to repeat this exercise for other lattice refinement factors b/l. Assuming b/l is an integer number we can follow the above strategy to find the transition probabilities. The resulting ‘diffusion coefficient’ D(b/l) takes the form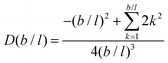 when the bond length units are used. As the nominator can be shown to be equal to
when the bond length units are used. As the nominator can be shown to be equal to 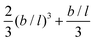 , we find the remarkable result
, we find the remarkable result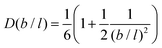 | (26) |
Importantly, in the classical SF-SCF method with b/l = 1 it is advised to use a hexagonal lattice rather than the simple cubic lattice. Interestingly, the latter choice has been the default and rarely SF-SCF results have been reported using the hexagonal lattice!
Thermodynamic relations
When the self-consistent field solution is found numerically, we know that we have optimized the mean-field free energy F. Using this quantity we can evaluate the grand potential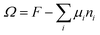 , where μi is the chemical potential of component i. The grand potential can be written as the sum over the grand potential density ω(z), i.e.
, where μi is the chemical potential of component i. The grand potential can be written as the sum over the grand potential density ω(z), i.e.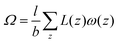 . Interestingly, there is a closed expression for the grand potential density:30
. Interestingly, there is a closed expression for the grand potential density:30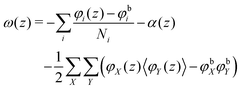 | (27) |
4 The molecular model, parameter set and approach
4.1 Molecular architectures
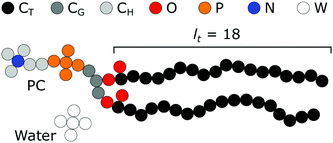
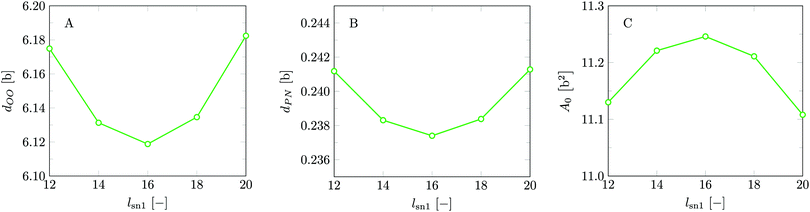
As mentioned in the introduction a rather long tradition exists in evaluating the structural, thermodynamic, and mechanical parameters of model lipid bilayers using the self-consistent field method.17,19,29,31–35 Calculations presented in this paper aim to elaborate on and extend the results of Pera et al.19 Our default system is therefore strongly linked to the one used by these authors. We will introduce this model and reiterate some arguments in support of this model.Our focus is basically on membranes that are composed of (model) phospholipids in a solvent that aims to represent water. Both of these components bring in modeling challenges by themselves. Water is an associative solvent which forms a hydrogen-bonded network effectively preventing that water units go to the membrane core: it is said that the membrane core is dry. At the same time, the chemical potential of the surfactant should not exceed the value that corresponds to the so-called critical micellization concentration (CMC), which can only be found from complementary calculations. Obtaining satisfying estimates for the experimental CMC with having a dry core is impossible in the Flory–Huggins equation of state when water is modeled as a monomer. We follow Pera et al., who argued that a reasonable way to achieve both aspects, is to represent water as small clusters of 5 W segments. In Fig. 2 we have schematically illustrated such a water component. In the same figure, we present the architecture of the standard lipid that is used. In these lipids, there is a glycerol backbone onto which two tails and one headgroup are connected. The challenge to accurately model the self-assembly of amphiphiles is to represent the size and shape of the molecules at least in first-order correctly. As is illustrated in this figure a united atom description is adopted to realize this. All the individual ‘united atoms’, here represented by a small filled circle, have a size b. Depending on the discretization scheme this size is a value b/l times larger than the lattice site. Classically b/l = 1, however in the present study most of the calculations were done for b/l = 3. Here and below we have used b = 0.35 nm as an estimate of the size of these segments. We have named the C-segments in the different parts of the molecule differently so that we can vary the ‘hydrophobicity’ in the three regions, i.e. the tail region, the glycerol region, and the headgroup region, independently. We hope that by doing so we will learn more about how the hydrophobic/hydrophilic balance is reflected correspondingly in the membrane properties. As illustrated in Fig. 2 the default lipid has two fatty acid ‘tails’ with a tail length (lt) of 18 carbons. They are attached to the sn1 and sn2 position of a glycerol backbone. A phosphatidylcholine (PC) ‘head’ is attached to the sn3 position. As double bonds are not implemented in our chain model, this structure could resemble the unsaturated dioleoyl phosphatidylcholine (DOPC) as well as the saturated distearyl phophatidylcholine (DSPC). However as our modeled lipid bilayers remain in the liquid state in all cases, we choose to use DOPC to name our default model lipid. The oxygens of the phosphate group are included in the P-units, the ones in the glycerol moiety (esters connecting the tails) are given by the O's. The quaternary nitrogen (in blue) is surrounded by three methyls and is connected to the phosphate by an ethyl unit. Note that in the SCF model no gel-to-liquid phase transition occurs and therefore we can probe the effects of changes in the tail length without the (experimental) complication that the liquid state of the membrane core is compromised above a certain tail length (e.g. lt > 18).
4.2 Interaction parameters
We have decided not to follow the model of Pera et al.19 in the way electrostatic interactions were accounted for. Pera et al. included these types of interactions by solving the Poisson equation in addition to the Edwards equation. This resulted in an extended Poisson Boltzmann-like model with a relatively large number of variables and quite a number of these were linked to the electrostatic effects. To reduce the number of parameters in the model we replaced all electrostatic interactions by effective short-range Flory–Huggins interactions. This is a not too strong simplification because in the biological context the ionic strength is relatively high and as a result, electrostatic interactions are short-ranged. We do not claim here that electrostatic interactions are irrelevant, but we argue that a full account of all possible electrostatic effects should account for many additional features such as the size and solubility of the ions, the hydration levels of the ions, the concentration, etcetera. We are of the opinion that only a dedicated study towards these effects will do justice to the real effects of electrostatics. The ‘idealized’ settings as used by Pera and coworkers simplify the matter too much (brushing complicating effects under the carpet so to say) and therefore we feel that at this stage it is better to remove electrostatics completely from our models and replace it with short-range interactions. The downside of our choice to drop the electrostatic interactions is that we cannot generate new insights in how for example the ionic strength modulates the mechanical parameters and phase behaviour of lipid systems.An overview of the default χ-parameter set used for this simplified model system can be found in Table 1. As the explicit charges are removed from the model, we have, with respect to the model of Pera et al., slightly modified the interaction parameters to mimic the effect of electrostatics at reasonably high ionic strengths. Since actual PC lipids are zwitterionic, we ‘compensated’ for this by choosing an attractive interaction parameter between nitrogen and the phosphate, χPN = −0.5. In addition, the carbon groups in the headgroup have been given a slightly lower interaction parameter (less water repellent) with water (χCHW = 0.6) to represent the somewhat hydrophilic nature of this region and to compensate for the positive charge of the nitrogen group. In combination with χCN, χCP and χCO all set to unity, this caused the choline group to be slightly further away from the core than the phosphate group, consistent with experimental results.36–38 Other interaction parameters have been kept the same compared to the previous model:19χW-N,P,O = −0.2 to represent a weak attraction of the headgroup monomers with water; importantly, χCTW = χCGW = 1.2, chosen as this leads to a dependence of the critical micelle concentration (CMC) on the tail length close to experimental results. Finally, χCT-N,P,O = χCG-N,P,O = 2 and χCH–CT,CG = 0.5 are chosen to ensure a strong segregation of the headgroup from the bilayer core.
| W | CH | N | P | O | |
|---|---|---|---|---|---|
| CT/CG | 1.2 | 0.5 | 2 | 2 | 2 |
| O | −0.2 | 1 | 0 | 0 | |
| P | −0.2 | 1 | −0.5 | ||
| N | −0.2 | 1 | |||
| CH | 0.6 |
4.3 Systematic variations of interaction parameters and lipid structure
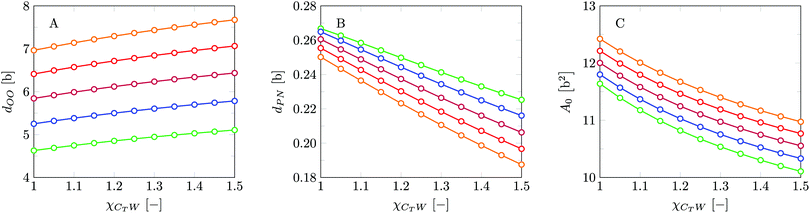
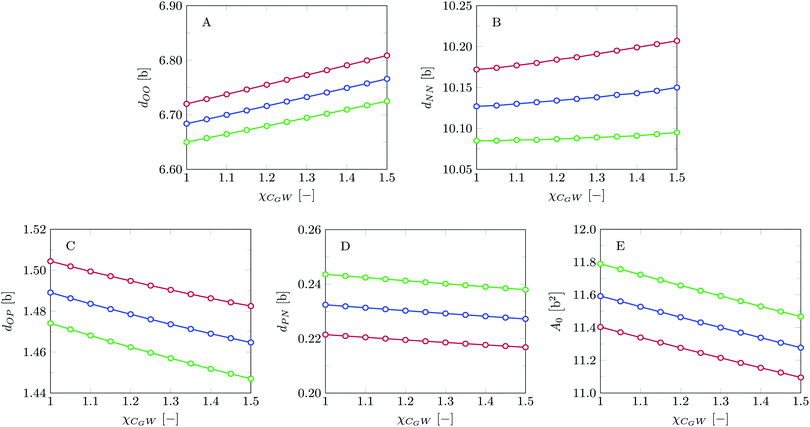
Invariably in a multi-parameter model system for the lipid bilayer membrane, it is relevant to know how sensitive the results are for changes in the parameter set. Unlike in MD simulations in which a particular force field has known pros and cons, the parameter set presented above has a far less established character. In this light, it is timely to find out how the structural and mechanical parameters are subject to change when the Flory–Huggins interaction parameters are varied within reasonable ranges. In the classical SF-SCF theory, the lattice artifacts were seriously limiting such an exercise. However, in a lattice-refined SF-SCF approach such project suddenly becomes of interest not only because it is relevant to know how sensitive parameters determine results, but also because it opens avenues to learn more about the membrane mechanics. For example, by interaction parameter (less water repellent χCTW, χCGW and χCHW we can determine how the hydrophobicity of various regions of the lipid influences structural and mechanical parameters of the bilayer. We can project such results on different classes of lipids. For example, previous studies have shown that varying χCTW effectively influences lipid tail stretching and bilayer thickness.19 Nature can do so by tuning the degree of unsaturation of the fatty acid tails.14,39 Changing the parameterization of the segments of the glycerol moiety of lipids arguable is not only relevant for the understanding of how glycerol-based lipids differ from e.g. sphingolipids, but it also gives generic insight in the role of the polarity gradient from head to tail that characterizes so many lipids. Headgroups of lipids are overall hydrophilic but typically contain not only polar but also apolar groups. Modifying the interaction parameters of (parts of) the headgroup with for example water may influence the readiness to hydrate the headgroup and this will affect the tension in the headgroup region (headgroup overlap) as a stopping force for the membrane formation. Insight into how much these changes can influence the overall membrane properties may lead to a deeper understanding of the relevance of headgroup variations in nature.Apart from a parametric study on the interaction parameters, we have varied relevant structural features of the lipid tails. These variations comprise lipid tail length (lt), including tails of different lengths in one lipid molecule, and variations in tail bulkiness by introducing a branching point in the tails.
To structure our results we have divided these into separate sections according to variations of the lipid tails, glycerol backbone, and the headgroups.
4.4 Data analysis
The structural features of the lipid bilayer predicted by the SF-SCF calculations can be extracted from the volume fraction distributions of all the segments per molecule. Typically these distributions are added together resulting in the overall lipid volume fraction profile, φlipid(z). Alternatively, one can group these per segment type, e.g. the P units are grouped in φP(z). When in a parameter study the interaction parameters are changed it is not productive to show all the changes in the corresponding volume fraction profiles. Instead, we have decided to follow and report on various measures that quantify the membrane structure in some way.One of these measures is the average z position of the monomers CG and CH and the O, P, and N segments in the bilayer configuration. Because of the symmetry, it suffices to determine the average z positions over just one leaflet of the bilayer. These averages follow from the so-called first-moment analysis
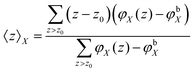 | (28) |
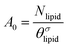 | (29) |
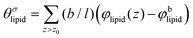 is the excess amount of segments of the lipid molecule per unit area (per leaflet) of the membrane, and N is the number of segments in the lipid molecule (measure for the molar volume). Multiplying A0 by b2 results in the area per molecule, a quantity that is known and tabulated for many types of lipids. Frequently this area is referred to as the headgroup area because in the planar geometry the bilayer tails occupy the same area as the heads. This should be distinguished from the headgroup area featuring in the so-called surfactant packing parameter P = v/(la0). This phenomenological parameter introduced by Israelachvili40,41 features an ‘experimental’ area that a surfactant occupies, e.g. on the air/liquid interface, a0. Together with theoretical values of the tail volume v and the (average) length of the tail(s), the value of P is indicative of the preferred association shape for self-assembly. If it is near 1/3 one should expect spherical micelles, near 1/2 cylindrical micelles, and for values near 1 bilayers. Often the packing parameter is used in a loose sense to rationalise various trends in phase behaviour for series of surfactants. An example is the prediction that for a given v and l an increase in the value of a0 will give a trend from lamellar to cylinder to spheres and vice versa. The value of Jm0 is the SCF counterpart of this packing parameter. We may argue that trends predicted from P-changes could also be predicted from Jm0-changes. Similar arguments practised in surfactant science to discuss trends in P can thus be used to rationalise trends in Jm0.
is the excess amount of segments of the lipid molecule per unit area (per leaflet) of the membrane, and N is the number of segments in the lipid molecule (measure for the molar volume). Multiplying A0 by b2 results in the area per molecule, a quantity that is known and tabulated for many types of lipids. Frequently this area is referred to as the headgroup area because in the planar geometry the bilayer tails occupy the same area as the heads. This should be distinguished from the headgroup area featuring in the so-called surfactant packing parameter P = v/(la0). This phenomenological parameter introduced by Israelachvili40,41 features an ‘experimental’ area that a surfactant occupies, e.g. on the air/liquid interface, a0. Together with theoretical values of the tail volume v and the (average) length of the tail(s), the value of P is indicative of the preferred association shape for self-assembly. If it is near 1/3 one should expect spherical micelles, near 1/2 cylindrical micelles, and for values near 1 bilayers. Often the packing parameter is used in a loose sense to rationalise various trends in phase behaviour for series of surfactants. An example is the prediction that for a given v and l an increase in the value of a0 will give a trend from lamellar to cylinder to spheres and vice versa. The value of Jm0 is the SCF counterpart of this packing parameter. We may argue that trends predicted from P-changes could also be predicted from Jm0-changes. Similar arguments practised in surfactant science to discuss trends in P can thus be used to rationalise trends in Jm0.
5 Results and discussion
This section is split into two parts. In the first one, we will discuss the structural and mechanical properties of the membrane using the default parameter set. The first task that is picked up is to establish the effectiveness of lattice refinement to find numerically accurate values for the bending rigidities. We will do this by focusing on the grand potential of spherically curved vesicles. In principle, the grand potential of spherical vesicles is scale-invariant. However, in the SCF computations this is not strictly the case in particular when lattice artifacts are manifest. The idea here is to show that the variations that are found for this value upon a change of the vesicle radius decreases rapidly when the ratio between segment and grit size, b/l, is increased. For a b/l ratio that gives sufficiently smooth results, we can derive the mechanical parameters of the bilayer from a single vesicle calculation: no laborious averaging is needed anymore. In the second part of this section, we will present results from systematic variations of structural and interaction parameters for the case that the discretization parameter b/l = 3. In order, we pay attention to variations in the lipid tails, we introduce changes in the glycerol backbone region and finally, we consider various ways to change the headgroup properties of the lipids. The overall goal of this section is to give insight in the sensitivity of the parameterization, but an important derived target is to learn how structural as well as mechanical parameters of lipid bilayer membranes can be regulated (at least in principle).5.1 The default system
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (cf.eqn (4)). Focusing on this spherical lattice we can thus find κs as well as smax = (Ωmax − Ωmin)/(4π) the difference between the maximum and minimum values for the effective bending rigidity along an oscillation (here taken when the radius of the vesicle R = 100). Pera et al. used the face-centered cubic (FCC) lattice with λ = 1/3, which was found to give the smallest value for smax. For obvious reasons, we here focus on the hexagonal lattice (λ = 1/4) for which smax is relatively large unless lattice refinement techniques are implemented. The results for the default lipid bilayer are collected in Table 2.
(cf.eqn (4)). Focusing on this spherical lattice we can thus find κs as well as smax = (Ωmax − Ωmin)/(4π) the difference between the maximum and minimum values for the effective bending rigidity along an oscillation (here taken when the radius of the vesicle R = 100). Pera et al. used the face-centered cubic (FCC) lattice with λ = 1/3, which was found to give the smallest value for smax. For obvious reasons, we here focus on the hexagonal lattice (λ = 1/4) for which smax is relatively large unless lattice refinement techniques are implemented. The results for the default lipid bilayer are collected in Table 2.
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) including the maximum deviation from the average (smax) for spherical vesicles of R ≈ 100b consisting of the standard lipids (see Fig. 2) at different lattice refinements (b/l)
including the maximum deviation from the average (smax) for spherical vesicles of R ≈ 100b consisting of the standard lipids (see Fig. 2) at different lattice refinements (b/l)
| b/l [—] | κ s ± smax [kBT] |
|---|---|
| 1 | −17 ± 345 |
| 2 | 6.03 ± 0.03 |
| 3 | 5.507 ± 0.001 |
| 4 | 5.3305 ± 0.0005 |
| 5 | 5.2495 ± 0.0005 |
Inspection of Table 2 reveals that the deviation smax is enormous for b/l = 1. Indeed smax is much larger than the average value κs. This was one of the challenges using the classical SCF theory to evaluate the mechanical parameters of lipid bilayers. It illustrates that the classical approach truly has a problem. Again, the workaround for this problem implemented by Pera et al. was to use the FCC lattice (λ = 1/3) which compared to the hexagonal (λ = 1/4) or simple cubic lattice (λ = 1/6) reduces smax to more or less acceptable values. In addition, Pera et al. used spherical vesicles that were as small as possible so that the oscillations around the mean were not yet overwhelming large. This explains why still reasonable predictions for the bending rigidity could be made. As seen in Table 2 for the hexagonal lattice smax is much larger than κs and it is clear that the estimates for the average are not very accurate. Already for b/l = 2 the value of smax is significantly smaller than κs and one can have confidence in the reported estimate for κs at least up to 0.1 unit of kBT. For b/l > 3 the error no longer is due to lattice artifacts but merely by the precision in which the SCF solution was generated. As the computational cost increases with increasing lattice refinement, we have chosen to use a lattice refinement of b/l = 3 for the remainder of our calculations.
Apart from the reduced deviations, it is found that the average effective modulus κs decreases with increasing b/l. This implies that the membranes become slightly easier to bend. This must be attributed to a systematic change in the chain model. In the freely-jointed chain (FJC) model subsequent segments may be placed onto 1 + 2b/l different lattice positions. This increase in the number of positions with increasing b/l is reflected in an increase in the conformational entropy in the chain. Apparently, the lipid molecules are intrinsically more flexible with increasing b/l. To prevent a too high internal flexibility of the chains is another reason for choosing b/l = 3 over higher lattice refinement calculations. In the FJC model, the excluded volume correlations along a chain further than one segment are ignored. One can implement, e.g. the rotational isomeric state (RIS) scheme29,31,42 wherein short-range correlations of (in this case) three segments are accounted for. In such a model the local stiffness of the chain can be incorporated to compensate for the increased flexibility of the chain when b/l is increased. To construct a RIS scheme in a lattice-refined model will be a task that is high on the agenda in the near future as this may restore the chain model to arguably more realistic ones. Until then, we have to accept the rather high flexibility of the chains as an SCF feature.
The small drift of the chain model with an increasing value of b/l has not only measurable effects on the mechanical parameters of the bilayer membranes but also has structural counterparts. Since the z-coordinate is based on the segment size b rather than on the size of the lattice site (we use b as the unit length), these structural differences are typically rather small and it is not too interesting to elaborate on these in detail. That is why we decided to show and discuss as an example the segment density profiles over the bilayer for the standard lipid and standard parameter set and discuss differences compared to the previous model using overall membrane measures. In Fig. 3A the full bilayer cross-section is shown and in panel B an enlarged part for the headgroup region is given. We have selected a planar geometry for which both leaflets are identical; z = 0 is set at the symmetry plane. In corresponding cross-sections of spherically and cylindrically curved bilayers the symmetry is broken and curvature effects may be seen on segment density profile level. We do not go here in detail and refer to the literature for an analysis of these effects.33
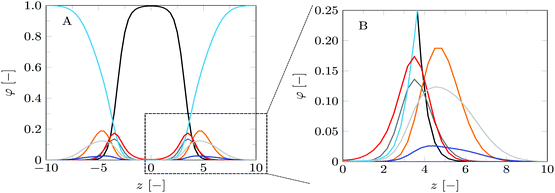 | ||
| Fig. 3 Volume fraction profiles of the default lipid bilayer membrane in a planar geometry. (A) Shows the volume fraction profiles for a full bilayer, whereas (B) shows a zoomed-in version, focusing on the headgroup and glycerol parts of a single leaflet of the bilayer. The profiles are presented in colors corresponding to the segment colors used in Fig. 2: C = black, O = red, P = orange, N = blue, CG = dark grey, CH = light grey. Water is depicted in light blue. The profiles correspond to SF-SCF calculations using a refined lattice (b/l = 3). | ||
The volume fraction profiles shown in Fig. 3 are fully consistent with the generally accepted view of the lipid bilayer membrane. The core of the bilayer is predominantly populated by the tails (C monomers, black curves) and in this region, the water density is less than 1%. This is in line with experimental data and with computer simulations at large. The glycerol moiety sits in between the core and the headgroups. Near the maximum of the O's of the glycerol backbone, the solvent (water) density starts to grow so that in the region of the headgroups water is already the main component. Fig. 3B gives a closer view of the distribution of the headgroup segments. It is of interest to notice that the width of the distribution of the headgroup region is comparable to the width of the hydrophobic core. This observation can only in part be attributed to the higher density and the flexible nature of the lipid tails in the core. Contributions to the broadening of the distribution of the headgroup segments are conformational fluctuations of the headgroup and protrusion-like fluctuations of lipids as a whole (that is fluctuations in the position of the molecules in the z-direction).
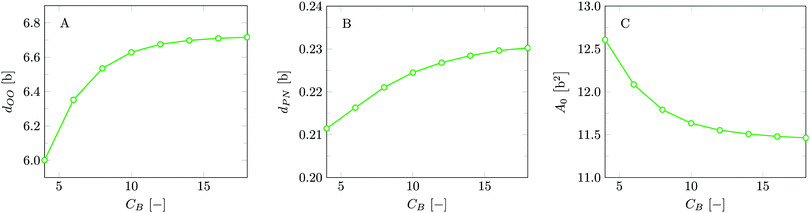
For this case study, the bilayer width as given by dNN amounts to approximately 10.1b, which translates to about 3.5 nm, and the equilibrium area per lipid molecule A0 = 11.5b2, corresponding to approximately 0.9 nm2. These values are comparable to numbers found before with SF-SCF modeling19 albeit that compared to previous estimates the area went up by a few percent and the thickness went down by some 10%. Also compared to experimental estimates14,15,43–47 the theoretical result underestimates the thickness and overestimates the area and the current model does this a bit more than the classical result of Pera et al. These differences are not unexpected. As mentioned above, compared to the real lipids we overestimate the chain flexibility. In addition, the mean-field model underestimates excluded volume effects. Both these facts can explain the observed shortcomings. We should also note that in SF-SCF the thickness of the bilayer is the so-called intrinsic thickness. Undulation fluctuations of the bilayer, which broaden the membrane thickness and typically influence experimentally reported membrane widths, are fully ignored. The underestimation of the membrane width and the small overestimation of the area per molecule have a corresponding impact on the mean bending modulus as will be discussed below.
The bilayer core thickness dOO = 6.72b represents about 2/3 of the total bilayer width, fairly consistent with literature.45 The headgroup orientation can be related to the relative position of the nitrogen with respect to the phosphate group. Our results give a result of dPN = 0.23b indicating that the headgroup lies relatively flat on the surface of the bilayer, with the choline group slightly further outward compared to the phosphate group, similar to previous results.19 The rather flat average orientation of the headgroups does not imply that all headgroups are parallel to the membrane plane. The rather broad distributions of N and P groups indicate that there are considerable fluctuations in the headgroup orientation. The width of these distributions may increase, and so will the conformational entropy, when the headgroup is on average parallel to the membrane surface compared to the perpendicular orientation. So there is also an entropic argument that disfavors large values for dPN. Strong excluded volume effects in the headgroup region (when the area per lipid is small) will push the choline group to the outside and then larger values are expected for dPN.
The values found for the structural properties of the lipid bilayer membrane are largely in line with all-atom computer simulations.35,42,48–51 There are many ways to coin this result but to us this is remarkable because the CPU-time needed to find the SF-SCF result is on the order of a few CPU-seconds on a single CPU, while for full-atom MD simulations the computational efforts, which obviously scale with the number of lipids in the membrane piece considered and the length of time over which the results have been averaged, are easily 104 times longer. As SF-SCF is computationally inexpensive it is doable to conduct a parameter study (see below). Moreover, because the mean-field free energy is available we can evaluate thermodynamic and mechanical parameters for the lipid bilayer membranes. Computing mechanical parameters by MD is even more CPU time consuming so that we are aware of only few attempts for this,52,53 let alone that trends in these quantities have been simulated for systematically modified bilayers.
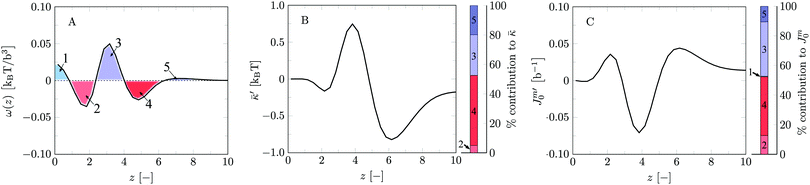
Let us next focus on the mechanical parameters of the default bilayer system as these follow from SCF. Here and below we have used the method of combining results from the planar geometry with a result for a spherical vesicle (the grand canonical route). Typically we used a vesicle with a radius R ≈ 100b. Alternatively the mean and Gaussian bending rigidities could be evaluated combining the cylindrical and spherical geometries (previously used approach). When for both cylindrical and spherical vesicles a radius of R ≈ 100b is used, the tension in the cylindrical vesicle remains sufficiently small so that on the level of the accuracy of the calculations the mean bending rigidity is not affected and both routes give closely the same results. On the one hand this internal consistency check is satisfying and raises confidence in our results. On the other hand, it means that a small membrane tension does not have an impact on the mean bending modulus. Otherwise the method of Pera et al. would have failed. In retrospect, it indicates that the results of Pera et al. are indeed trustworthy, albeit that the numerical noise on their data is considerable. The new approach of combining planar and spherical results is strictly executed in the grand canonical ensemble and is preferred because it is computationally the most efficient and formally the correct route.
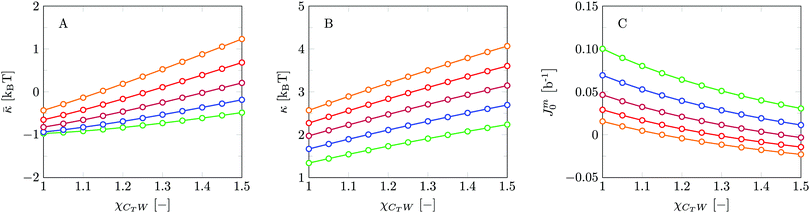
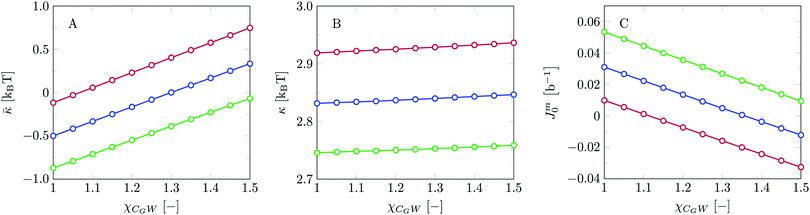
We find the bending modulus κ = 2.84kBT, the Gaussian bending modulus ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) = −0.17kBT and the spontaneous curvature of the monolayer Jm0 ≈ 0.014b−1, i.e. close to 0. The negative value for
= −0.17kBT and the spontaneous curvature of the monolayer Jm0 ≈ 0.014b−1, i.e. close to 0. The negative value for ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and the small value for Jm0 show that the default lipid indeed is rather ‘satisfied’ with the planar bilayer assembly. Of course, the default parameterization was tuned to give these results as it is expected for a phosphatidylcholine lipid with two tails with length lt = 18. The fact the numerical value of
and the small value for Jm0 show that the default lipid indeed is rather ‘satisfied’ with the planar bilayer assembly. Of course, the default parameterization was tuned to give these results as it is expected for a phosphatidylcholine lipid with two tails with length lt = 18. The fact the numerical value of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is rather close to zero indicates that the bilayer is not too far from a topological transition, which we consider realistic.
is rather close to zero indicates that the bilayer is not too far from a topological transition, which we consider realistic.
Experimental estimates are available only for the mean bending modulus. For most lipid bilayer membranes, reported values for this quantity are significantly higher, values as high as 10–50kBT.54 The largest numerical values may be linked to membranes in or extremely close to the gel-state. It is possible to upgrade the SCF approach to include the gel-to-liquid transition32 by more accurately accounting for excluded volume effects of densely packed tails. This route, however, was abandoned due to the huge lattice artifacts that presented themselves. In a lattice-refined SCF approach, the ideas to introduce cooperative chain alignment effects may become of interest again. For the time being, however, such an extension of the theory is not available. Within the current lattice-refined SCF theory, the model bilayers are significantly more flexible than their real counterparts. As explained this result must not be coined as a surprise. Above we have seen that the theory underpredicts the membrane thickness, basically because the molecules do not feel sufficient excluded volume correlations and the chains are intrinsically too flexible. On the other hand, it cannot be ruled out that experimental estimates of the mean bending modulus could be on the high side because it is difficult to measure such quantities in a full equilibrium setting. For example, when the bending modulus is measured on time scales for which lipid flip-flop is not possible one must find significantly higher values for the bending modulus than from measurements on larger time scales.
Even though the current mean-field theory underestimates the value of the mean bending modulus, it is not expected that the same systematic underestimations or possible systematic overestimations would occur for ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0. The relative preference for a bilayer to be in the planar state compared to some saddle-shaped configuration may depend more on how the hydrophobic/hydrophilic balance is spread throughout the lipid molecule rather than that it is influenced by the flexibility of the chain and/or the bilayer thickness per se. Furthermore, since similar (flexibility) errors are anticipated in the different geometries, we expect that the trends in
and Jm0. The relative preference for a bilayer to be in the planar state compared to some saddle-shaped configuration may depend more on how the hydrophobic/hydrophilic balance is spread throughout the lipid molecule rather than that it is influenced by the flexibility of the chain and/or the bilayer thickness per se. Furthermore, since similar (flexibility) errors are anticipated in the different geometries, we expect that the trends in ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0 that are discussed below are comparatively realistic. To substantiate this argument we continue the analysis of the default bilayer by focusing on the grand potential density profile.
and Jm0 that are discussed below are comparatively realistic. To substantiate this argument we continue the analysis of the default bilayer by focusing on the grand potential density profile.
As given by eqn (2) and (3), ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0 follow from the second and first moment of the grand potential density profile, respectively. It is of more than average interest to pay attention to the grand potential profile. In Fig. 4A such a profile is shown for the default membrane, which is free of tension. This means that
and Jm0 follow from the second and first moment of the grand potential density profile, respectively. It is of more than average interest to pay attention to the grand potential profile. In Fig. 4A such a profile is shown for the default membrane, which is free of tension. This means that 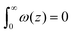 . In this profile, we have identified five regions. The regions 1, 3, and 5 give a positive contribution to the membrane tension and are given colors from light to dark blue. The regions 2 and 4, colored light, and dark red give a negative contribution to the membrane tension. The total area for the red regions equals that of the blue regions because the membrane tension is zero. The positive contributions imply a tendency of the membrane area to decrease while a negative contribution indicates a tendency to increase the membrane area. Positive excursions may be identified as ‘driving forces’ for membrane formation, while the negative ones contribute to the ‘stopping forces’. Typically the hydrophobic tails that are in contact with the solvent at the core–corona interface invoke a positive local tension (region 3), and this is seen as the important driving force for the assembly of the membrane. The negative tension of region 2 results from stretching of the tails in the normal direction. This is a known but not often mentioned stopping mechanism for self-assembly. The negative tension in region 4 is referred to as the headgroup pressure, which is related to headgroup overlap, a stopping force as well. The positive contribution near the center of the bilayer (region 1) is often found for lipid bilayer membranes. A physical implication of this local positive tension is that the tails of the two leaflets of the bilayer attract each other so that no density dip occurs in the membrane core. This also permits the interdigitation of the tails into opposite monolayers which are known to happen to some extent.32 Sometimes region 5 occurs at the periphery of the membrane surface. When this local positive tension is large we expect that membranes are mutually attractive. So a large positive contribution in region 5 is indicative of the loss of the colloidal stability of freely dispersed bilayers. In the default case, the colloidal stability is not compromised. When electrostatics are accounted for, one usually will find a small attraction due to dipole–dipole attraction of the PC headgroups.
. In this profile, we have identified five regions. The regions 1, 3, and 5 give a positive contribution to the membrane tension and are given colors from light to dark blue. The regions 2 and 4, colored light, and dark red give a negative contribution to the membrane tension. The total area for the red regions equals that of the blue regions because the membrane tension is zero. The positive contributions imply a tendency of the membrane area to decrease while a negative contribution indicates a tendency to increase the membrane area. Positive excursions may be identified as ‘driving forces’ for membrane formation, while the negative ones contribute to the ‘stopping forces’. Typically the hydrophobic tails that are in contact with the solvent at the core–corona interface invoke a positive local tension (region 3), and this is seen as the important driving force for the assembly of the membrane. The negative tension of region 2 results from stretching of the tails in the normal direction. This is a known but not often mentioned stopping mechanism for self-assembly. The negative tension in region 4 is referred to as the headgroup pressure, which is related to headgroup overlap, a stopping force as well. The positive contribution near the center of the bilayer (region 1) is often found for lipid bilayer membranes. A physical implication of this local positive tension is that the tails of the two leaflets of the bilayer attract each other so that no density dip occurs in the membrane core. This also permits the interdigitation of the tails into opposite monolayers which are known to happen to some extent.32 Sometimes region 5 occurs at the periphery of the membrane surface. When this local positive tension is large we expect that membranes are mutually attractive. So a large positive contribution in region 5 is indicative of the loss of the colloidal stability of freely dispersed bilayers. In the default case, the colloidal stability is not compromised. When electrostatics are accounted for, one usually will find a small attraction due to dipole–dipole attraction of the PC headgroups.
For the impact of the various contributions of regions 1–5 to the Gaussian bending rigidity and the spontaneous curvature of the monolayer, not only the absolute values are important but also the precise location is relevant. In this case the local maxima occur at z = 0, at z ≈ 3.2 and at z ≈ 7 (regions 1, 3 and 5). The minima occur around z ≈ 1.8 and z = 4.8 (region 2 and 4).
To further quantify how regions 1–5 contribute to the Gaussian bending rigidity and the spontaneous curvature of the monolayer, it is instructive to introduce cumulative functions that collect respective contributions up to layer z to ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0(z):
and Jm0(z):
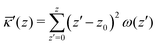 | (30) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and
and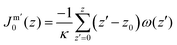 | (31) |
![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) ′(z) goes to the Gaussian bending rigidity
′(z) goes to the Gaussian bending rigidity ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , and the similar limit for Jm0(z) is identical to Jm0. The charts next to Fig. 4B and C give the fractional contributions of the integrated parts of regions 1–5.
, and the similar limit for Jm0(z) is identical to Jm0. The charts next to Fig. 4B and C give the fractional contributions of the integrated parts of regions 1–5.
As ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is associated with the second moment of the grand potential density profile, contributions at larger z, i.e. regions 3 and 4, are more relevant then regions 1 and 2. For the spontaneous curvature of the monolayer, which is linked to the first moment, all regions are more equally important. These features are recognized in Fig. 4B and C. The fact that
is associated with the second moment of the grand potential density profile, contributions at larger z, i.e. regions 3 and 4, are more relevant then regions 1 and 2. For the spontaneous curvature of the monolayer, which is linked to the first moment, all regions are more equally important. These features are recognized in Fig. 4B and C. The fact that ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) < 0 can be attributed to the dominance of region 4. The positive value for Jm0 is traced to the relatively large contribution of the tension generated in region 3.
< 0 can be attributed to the dominance of region 4. The positive value for Jm0 is traced to the relatively large contribution of the tension generated in region 3.
We anticipate that details in the glycerol backbone region may influence region 3, whereas an increment of the chain length will position all the regions 1–5 to somewhat larger z-values, with concomitant changes in ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0. Below we will not present all the details of the grand potential density profiles, but in order to rationalize why particular changes in the mechanical parameters are found, we have made use of this type of information. In the ESI,† more information can be found on how the grand potential density changes for a selected number of parameter variations. For example, the minimum in region 4 generally becomes less deep when it is found at larger values of z. Therefore it is likely that Jm0 will become less positive but the effect on
and Jm0. Below we will not present all the details of the grand potential density profiles, but in order to rationalize why particular changes in the mechanical parameters are found, we have made use of this type of information. In the ESI,† more information can be found on how the grand potential density changes for a selected number of parameter variations. For example, the minimum in region 4 generally becomes less deep when it is found at larger values of z. Therefore it is likely that Jm0 will become less positive but the effect on ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) is less clear because the weighting with z2 may compensate for the reduced amplitude.
is less clear because the weighting with z2 may compensate for the reduced amplitude.
5.2 Parameter variation for the lipid tails
Several parameters can be varied for the lipid tails. We will start with varying the tail length (lt) and the hydrophobicity of the tails by changing χCTW. In nature lipids with different tail lengths are frequently found in different types of biomembranes, and the hydrophobicity of the tails is altered by the degree of unsaturation of the fatty acids. It is expected that a higher degree of unsaturation decreases the hydrophobicity of the tails, as an increased solubility in water is observed.14,39 In addition, we will consider the effect of a difference in length between tails on sn1 and sn2 positions in the lipid molecule. Finally, we pay attention to the effect of branching of the lipid tails. For all these variations we will first present changes of structural parameters of the bilayers and then pay attention to the corresponding mechanical parameters.The larger χCTW, the stronger is the repulsion between the tails and water (the C's in the glycerol backbone and in the heads remain unaltered). We varied this parameter around the default value of 1.2. It relates to the amount of water in the hydrophobic core. When χCTW = 1 the water content is unacceptably high (above 1%). It also relates to the freely dispersed lipid concentration in the solvent (CMC). When χCW ≈ 1.5, the CMC is much lower than the experimental estimates. We should keep this in mind when we discuss the trends, which are to some extent non-trivial. One would expect that with increasing driving force for assembly (longer or more hydrophobic tails) the two stopping forces would become stronger, that is, the area per molecule should go down and the stretching in the tails should increase. We see these trends for the increase in the hydrophobicity of the tails, but not for the increase in the tail length. When the tails are repelled stronger by water, the tension at the core–corona interface increases somewhat and this triggers both a stronger stretching of the tails and a reduced area per molecule. When for a given strength of the repulsion between tails and water the tail length is increased the area per molecule goes up. This is only possible when the stretching of the tails is becoming a more dominant stopping mechanism. Experimentally the area per lipid in the membrane was found to depend on whether or not the tails were saturated or not.55 For lipids with unsaturated bonds the ordering of lipid tails in the core is expected to be less than for the saturated tails and for these less ordered bilayers, the increase in membrane area with increasing tail length is indeed reported.55
The core size dOO increases with both increasing tail hydrophobicity χCTW and tail length lt. The overall thickness of the bilayer dNN follows the trend of dOO as shown in the ESI.† This trend is consistent with experimental results.55 The headgroup orientation (as deduced from dNP) tends to become more parallel to the membrane surface when the tails become more hydrophobic as well as when the tails become longer. When χCTW is increased the tension between core and corona increases somewhat and this triggers the choline group to be closer to the core: it becomes stronger adsorbed at this interface at the expense of water. Such an adsorption effect goes against the natural response that a decrease in area per molecule leads to a larger tilt of the headgroup. This shows that the headgroup orientation is the result of a complex interplay of effects.
Referring to Fig. 6 we find increases in ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and κ and a decrease in Jm0 for both increasing lt and χCTW. These trends are in good agreement with previous work.19 Pera et al. argued that the mechanical parameters of the bilayers can be rationalized using structural arguments: both
and κ and a decrease in Jm0 for both increasing lt and χCTW. These trends are in good agreement with previous work.19 Pera et al. argued that the mechanical parameters of the bilayers can be rationalized using structural arguments: both ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and Jm0 can be correlated with the shape of the lipid, which for amphiphilic molecules is generally described by the critical packing (surfactant) parameter40,41 and κ could be correlated to the overall bilayer thickness. We will also use similar arguments and try to deepen the insight where possible.
and Jm0 can be correlated with the shape of the lipid, which for amphiphilic molecules is generally described by the critical packing (surfactant) parameter40,41 and κ could be correlated to the overall bilayer thickness. We will also use similar arguments and try to deepen the insight where possible.
As with respect to the mean bending modulus (panel B) we find a strong correlation between this parameter and the membrane thickness dNN (see also ESI,† Fig. S2B). A thicker bilayer is simply harder to bend. Interestingly, we find a rather weak dependence with lt. To a reasonable approximation κ grows linearly with lt. The increase in the area per molecule which also takes place with increasing lt must have contributed to this weak dependence.
The Gaussian bending modulus as well as the spontaneous curvature of the monolayer are expected to correlate to the topological stability of the bilayers. However, the corresponding effects on the topological stability of the self-assembled bilayers are subtle and hard to rationalize. More specifically, the sign-switch of ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) that is predicted both for relatively hydrophobic tails and in the limit of long tails, tells us that both these trends destabilize the lamellar topology in favor of phases with saddle shapes, e.g. a cubic phase of some sort. The spontaneous curvature of the monolayer tends to become negative for long tails and/or very hydrophobic tails. This means that ‘inverted’ assemblies gradually should become the more favorable aggregation state. Pera et al. reasoned using surfactant packing parameter arguments. A hurdle in this approach is that we do not know exactly how the surfactant packing parameter responds to the changes in the parameters and there is some arbitrariness in it. Alternatively, to explain these trends we could relate them to the changes of the grand potential density profiles. However, it goes too far to show all these profiles individually. In addition, a formal ‘explanation’ of trends in terms of how the grand potential density profile changes, should be accompanied with arguments why the particular grand potential density profile did change as a response to variation of some parameter. This in turn is a challenging task in itself. In the following, we will combine both approaches to understand and qualitatively explain the trends.
that is predicted both for relatively hydrophobic tails and in the limit of long tails, tells us that both these trends destabilize the lamellar topology in favor of phases with saddle shapes, e.g. a cubic phase of some sort. The spontaneous curvature of the monolayer tends to become negative for long tails and/or very hydrophobic tails. This means that ‘inverted’ assemblies gradually should become the more favorable aggregation state. Pera et al. reasoned using surfactant packing parameter arguments. A hurdle in this approach is that we do not know exactly how the surfactant packing parameter responds to the changes in the parameters and there is some arbitrariness in it. Alternatively, to explain these trends we could relate them to the changes of the grand potential density profiles. However, it goes too far to show all these profiles individually. In addition, a formal ‘explanation’ of trends in terms of how the grand potential density profile changes, should be accompanied with arguments why the particular grand potential density profile did change as a response to variation of some parameter. This in turn is a challenging task in itself. In the following, we will combine both approaches to understand and qualitatively explain the trends.
It is known that relatively small headgroup sizes promote Gaussian curvatures and/or inverted assemblies. Alternatively for fixed headgroup properties, increasing the size of the tails or the hydrophobicity of the tails should induce the same trend. Indeed these expectations, based on ‘geometric’ arguments, are supported by the analysis of the grand potential density profiles, shown in Fig. S1A (ESI†): the peaks for regions 2–5 shift to larger values of z both with increasing lt and increasing χCTW, consistent with an increase in bilayer thickness. Peaks at higher z tend to have a reduced amplitude and therefore it is hard to see how the first or second moment of these profiles is changing in a particular way. In this case, the relative contribution of region 3 (driving force) overshadows the other contributions, and ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) increases as well as Jm0 decreases. The relative increase in the importance of the tail stretching to the stopping force may have contributed to this trend. The negative grand potential in the headgroup region is less pronounced and the Gaussian bending rigidity is not receiving a concomitant negative contribution of the heads so that it can become positive. The same argument can be made for the trend of Jm0.
increases as well as Jm0 decreases. The relative increase in the importance of the tail stretching to the stopping force may have contributed to this trend. The negative grand potential in the headgroup region is less pronounced and the Gaussian bending rigidity is not receiving a concomitant negative contribution of the heads so that it can become positive. The same argument can be made for the trend of Jm0.
To investigate the effects of different tail lengths within one lipid, we have chosen to consider lipids with a fixed total of 32 carbons in their tails. Hence, when we choose a tail length of 14 carbons on the sn1 position (lsn1 = 14), the lipid tail on the sn2 position will thus have 18 carbons (lsn2 = 18), and so on. The structural membrane properties of the lipid bilayer are shown in Fig. 7 as a function of the length of the sn1 tail.
Inspection of this figure proves that there are noticeable differences in whether the lipids have equally long tails or not, yet the magnitude of these differences is much smaller compared to changing the length of both tails lt or χCTW. In general, the SCF theory predicts that tails of equal lengths, in this case with two C16 tails, have a smaller dOO and dPN and a higher A0 compared to a lipid with two unequal tails. When the lengths of the two tails are different, the lipid can position the long tail more to the membrane center, while the shorter one can remain closer to the head (the lipid tails can split tasks). This degree of freedom allows for further optimization of the free energy which subsequently leads to slightly more lipids per unit area (reduced headgroup size) compared to the case that both tails are equally long and behave similarly. We may also argue that the membrane core size scales with the longest tail, which obviously is the case in the limit that all tail segments are in a single tail. As the longest tail increases with increasing asymmetry between the tail lengths, it is natural to expect that the core size increases with increasing difference in lengths. The minimum in the area per molecule, when the two tails have equal length, reflects in a maximum in the headgroup area and the headgroup orientation is most parallel to the membrane surface (dPN goes through a minimum).
Close inspection of the curves proves that there is a slight asymmetry in the values whether or not the sn1 tail is the longest. The reason for this is that the headgroup is closer to the sn2 tail than to the sn1 tail. As a result, the sn1 tail is buried slightly deeper in the bilayer than the sn2 (when both tails are equally long). Increasing the tail length of sn2 has therefore less impact than increasing the sn1 tail because it has first to catch up with sn1 before it can be the tail that can go deepest in the bilayer.
Interestingly, while the changes in bilayer structure seem very subtle, the effect on ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , κ and Jm0 are surprisingly large: the relative increase in κ for lipids with tails of equal lengths over unequal tail lengths, is in the order of 10%, see Fig. 8.
, κ and Jm0 are surprisingly large: the relative increase in κ for lipids with tails of equal lengths over unequal tail lengths, is in the order of 10%, see Fig. 8.
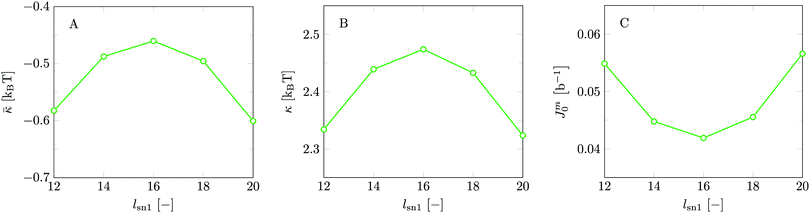 | ||
Fig. 8 Estimation of the bending rigidities ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (A) and κ (B), and Jm0 (C) as a function of the lipid tail length on the sn1 position (lsn1). The total amount of tail segments was chosen to be 32. Parameters similar as in Fig. 7. (A) and κ (B), and Jm0 (C) as a function of the lipid tail length on the sn1 position (lsn1). The total amount of tail segments was chosen to be 32. Parameters similar as in Fig. 7. | ||
One of the reasons why we present the effect of chain length variation within one lipid is that from a packing parameter point of view no differences are expected. Nevertheless, significant variations are found. The mean bending modulus in this case does not follow the trend that a thicker bilayer is harder to bend. Just the opposite is found! Clearly, when the tails are of unequal length, the lipid can target one tail to the center and the other tail more towards the corona. In this way, the bilayer can deal better with an imposed membrane curvature. This is reflected in a more flexible bilayer even with its thickness is slightly increased.
The Gaussian bending rigidity for the default lipid is close to zero and understandingly when the structure of the lipids is varied, small changes in the Gaussian bending rigidity can have large effects. The Gaussian bending rigidity deviates more from zero when the chains are more asymmetric in length. The stopping mechanism is distributed slightly less in the tail stretching and more in the headgroup overlap and therefore, region 4 becomes more important for the Gaussian bending rigidity. The trend for the spontaneous curvature of the monolayer can be rationalized in the same way.
To test these expectations we introduce a systematic change of the bulkiness of the tails by introducing a branching point in each lipid tail while keeping the total number of carbon monomers per tail the same, here 18 per tail. For example, by introducing a branching point on the fourth carbon from the glycerol (CB = 4), we subsequently have two smaller tail fragments each with a length of 7 carbon monomers. As such by varying the position of the branching point in the lipid tail, we can tune the effective bulkiness of the tails. The structural properties of the membrane as a function of the positions of the branching point are presented in Fig. 9. The core thickness is smallest for the lipids with the branching point closest to the backbone and it grows to the value of the unbranched chain when the branching point occurs at large values of CB. At the same time, the area per molecule is largest when the branching point is near the headgroup. The larger the headgroup area is, the smaller is the z distance between N and P (dPN), corresponding with the smallest angle between the headgroup and the plane of the bilayer. This trend is in line with the expectations sketched above. There is a strong nonlinear dependence on CB. As expected the effects of branching near the backbone have a stronger effect than branching near the tail ends.
The consequences for the mechanical parameters of the lipid bilayer membranes are presented in Fig. 10. As can be seen from Fig. 10B, the mean bending modulus follows the membrane thickness: the thicker the bilayer, the stiffer it is. In line with the trend of the surfactant packing parameter, the Gaussian bending rigidity is clearly positive for the lipid with tail branching near the glycerol backbone and approaches the value for the default lipid (a small but negative value) when the tail branching occurs far towards the tail ends. The spontaneous curvature of the monolayer also follows the surfactant packing parameter prediction. It is negative (meaning that inverted assemblies are promoted) when the branching is close to the heads and shifts to the value for the default lipid (which is slightly positive) for lipids with branching near the tail ends.
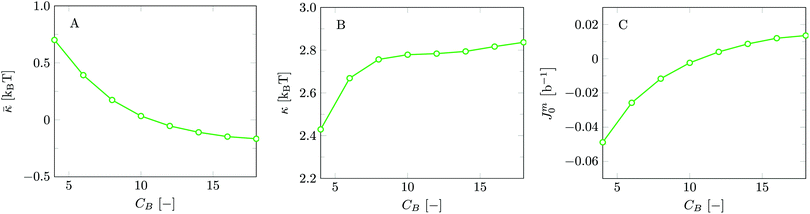 | ||
Fig. 10 SCF predictions of Gaussian bending rigidity ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (A), mean bending rigidity κ (B) and Jm0 (C) as a function of branching point (CB) for the same bilayers with branched lipids as in Fig. 9. (A), mean bending rigidity κ (B) and Jm0 (C) as a function of branching point (CB) for the same bilayers with branched lipids as in Fig. 9. | ||
It is clear that bilayers consisting of lipids with shorter and bulkier tails have a higher tendency to form cubic phases compared to lipids with fewer and longer tails. Depending on the goal, varying the bulkiness of the tails can be a systematic strategy to obtain self-assembled structures of a desired topology. We do not know of experimental counterparts to substantiate this prediction. For the way in which we varied the lipid branching, SCF theory predicts that the Gaussian bending rigidity changes sign almost simultaneously with the change of sign of the spontaneous curvature of the monolayer. For the desired change of phases, it may well be relevant which of the two quantities changes sign first.
5.3 Parameter variation for the glycerol backbone
The role of the polarity of the glycerol backbone is the next focus of our parameter variation study. In the study to understand lipid bilayer properties one typically considers the effects of tails and the effects of headgroups of the lipids, but the role of the transition between heads and tails, for phospholipids the glycerol backbone, is generally neglected. Nature, however, does consider lipids of various sorts which do differ in how the tails and the headgroups are linked to each other, cf. phospholipids versus sphingolipids. The difficulty in understanding the role of variations in the region between heads and tails is that when the structure is changed, also the gradients from polar to apolar are affected. Here we decided to keep the architecture of the lipids the same and only modify the interaction parameters in this region of the molecule. In this way, we hope to generate a more clear picture of what happens to structural as well as mechanical parameters of the membranes when the gradient from polar to apolar in the lipids occurs relatively abruptly or more gradually.We have varied the hydrophobicity of the glycerol backbone in two ways. The first one is by varying the repulsion between water and the hydrocarbons from the glycerol backbone, χCGW, and the second one is by changing the attraction of water to the O's, χOW. The results regarding the structural effects of the lipid bilayers are collected in Fig. 11. Besides reporting on the headgroup area A0, the orientation of the headgroup dPN and the core size dOO, we also show the effects on the overall membrane thickness dNN, and the distance between the phosphate group and the O in the glycerol backbone dOP. We note that increasing χCGW as well as making χOW less negative implements two complementary ways to make the glycerol backbone region overall more hydrophobic. Making χOW more negative implies a wider gradient in polarity from head to tail within the lipid molecule, but not necessarily implies a wider region of polarity in the lipid bilayer as the conformations of the molecules respond to the imposed interactions.
As there are only a few O's per lipid and also the number of hydrocarbon units in the glycerol backbone is small, we cannot expect huge effects on the overall membrane properties. The modest changes that do occur are as follows. The dOO thickness increases with increasing glycerol hydrophobicity, the headgroup orientation flattens, i.e. dPN goes down, and the area per lipid A0 decreases. This smaller headgroup area implies that the glycerol backbone contributes to some extent to the stopping force for self-assembly: reduction of the hydrophilicity of the glycerol backbone requires a stronger overlap of the headgroups to make the membranes free of tension. Just as with varying χCTW, the decrease in A0 is accompanied with a flatter headgroup orientation, probably due to water being pushed out of the headgroup region. In other words, the choline group is pulled towards the core at the expense of water molecules being in contact with tails (adsorption effect). Interestingly, although their general effects are comparable, small differences exist between varying χCGW and χOW, in particular in the strength of their effects. This is best seen in the bilayer thickness dNN, where almost no change is observed when varying χCGW, while a clear increase in dNN is observed increasing χOW. The distance between the phosphate and the O of the glycerol decreases when χCGW is increased at a fixed polarity of the O-groups. It is also decreased when at fixed χCGW the O's are made more polar. This means that the conformations of the glycerol backbone, especially of the part in contact with the headgroups, can be modified to bring hydrophilic O's near the polar groups of the head and close to water.
The corresponding effects on the bending rigidities and spontaneous curvature of the monolayer are collected in Fig. 12. Again one would have expected just modest changes, but surprisingly large effects are found for the Gaussian bending rigidity and the spontaneous curvature of the monolayer, proving that the region connecting the headgroup and the tails is not unimportant for the topological stability of lipid bilayer membranes.
In line with the reported changes in the membrane thickness dNN, it is found that the mean bending modulus slightly increases with the hydrophobicity of the hydrocarbons of the glycerol backbone and somewhat stronger with the polarity of the O's.
With respect to the Gaussian bending modulus and the spontaneous curvature of the monolayer, the trends follow the same patterns as for χCTW and lt. That is, the increase in ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) and decrease in Jm0 correlate with a decrease in A0.
and decrease in Jm0 correlate with a decrease in A0.
5.4 Parameter variation for the head groups
In nature, many different lipid headgroups have evolved. The headgroup is the water-loving part of the lipids. Frequently this water-solubility is enhanced by charged groups. Again, one can vary the headgroup architecture, and several parameters will vary simultaneously. For example, in a phosphatidylethanolamine (PE) headgroup the methyl groups on the nitrogen present in the PC headgroup are replaced by hydrogen atoms, making the headgroup significantly more hydrophilic and less bulky. With respect to charge, headgroups vary from zwitterionic to nonionic or completely ionic. Following the same pattern as for the lipid tails and glycerol backbone, we vary the hydrophilicity of the headgroups by changing the interaction parameter of the carbon monomers with water χCHW. Variations in headgroup polarity have been explored before19 albeit using a slightly different strategy, and as we found similar effects here, we will keep this part of the study short.In Fig. 13 we focus once again on the core thickness, the headgroup orientation, and the area per lipid. In short, with increasing hydrophobicity of the headgroup (increasing χCHW) tail stretching is enhanced, manifested as a slight increase in dOO. The distance between P and N in the headgroup, dPN, is a strong function of χCHW and it turns negative for χCHW > 0.8, meaning that the choline groups are oriented with respect of the phosphate group towards the core. Even though the core thickness increases, the overall thickness, dNN, decreases because of the changing orientation of the choline group. As also reported by Pera et al.,19 the area per molecule A0 decreases with increasing dOO, which occurs when the hydrophilicity of the headgroup decreases.
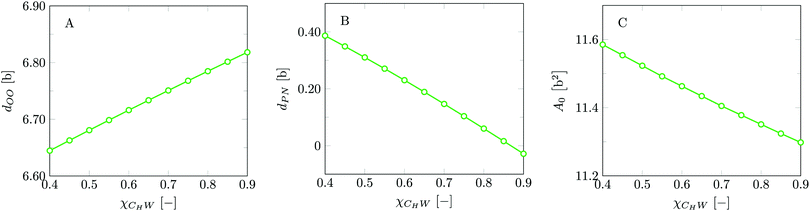 | ||
| Fig. 13 Structural analysis of lipid bilayers as a function of hydrophilicity of the headgroups, χCHW. (A) Bilayer core width dOO; (B) headgroup orientation dPN; (C) area per lipid A0. | ||
The effects on the mechanical parameters follow the generic rules: κ decreases as the bilayer thickness decreases; ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) increases and Jm0 decreases in line with smaller headgroup areas, see Fig. 14.
increases and Jm0 decreases in line with smaller headgroup areas, see Fig. 14.
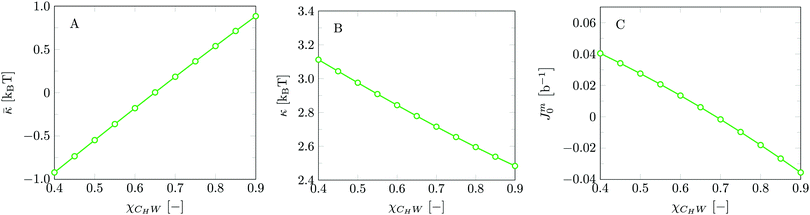 | ||
Fig. 14 Estimation of the bending rigidities ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) (A), κ (B) and Jm0 (C) as a function of hydrophilicity of the headgroups, χCHW. (A), κ (B) and Jm0 (C) as a function of hydrophilicity of the headgroups, χCHW. | ||
6 Outlook
The self-assembly of lipids in aqueous solution is of fundamental research interest. One-, two- and three-dimensional mesophases can be found depending on the spontaneous curvature of the monolayer and the values of the mean and Gaussian bending rigidity. Transitions between the lamellar phase and, for example, bicontinuous triple periodic phases, such as the primitive (P, Im3m), the diamond (D, Pn3m), and the gyroid (G, Ia3d) cubic phases, are thought to be driven by a transition from negative to positive Gaussian bending rigidity and are usually induced by adding amphiphilic additives. In our modeling study we have explored an unusual route in which the transition from lamellar to, e.g., a bicontinuous cubic phase is inferred by parameter changes in the model. This route not only helps us to identify for our model lipid the proper range of parameters consistent with the lamellar topology, but it also gives insight into the properties that provide other types of lipids, like monogalactosyl diacylglycerol (MGDG) lipids as a main component in the thylakoid membrane, the tendency to assemble in non-bilayer topologies. As it is progressively clear that in nature besides the lamellar topology, which is essential for the barrier function of biomembranes, also bicontinuous phases are relevant,57–59 there is an urgent need to know more about the phase behavior of lipids in the biological context.Self-assembly of lipid molecules in bilayer membranes is a complex phenomenon, which we have shown can be captured by SF-SCF models when molecularly detailed models are used. The complex interplay between the various types of interactions and the corresponding conformational changes of the lipids in the tensionless bilayers makes it hard to come up with simple arguments to support the predicted trends for the mechanics of lipid bilayer membranes. This is unfortunate because we are definitely in need of simple guidelines. However, we can count our blessings and be happy that a computationally inexpensive SCF machinery does provide us with interesting dependencies, which appear consistent with experimentally known phase behavior of lipids in general. We know that the current approach is still very approximate and therefore it is not yet the time to bring theory and experiments one-to-one together. For this, further improvements on the lattice-refined SCF theory is required, including an optimization (tuning) of the parameter set to correlate the mechanical parameters better to experimental data. Nevertheless, we consider the trends that we have investigated to be stepping stones for membrane understanding.
We have varied the polarity of the lipid molecules in various ways. We changed the hydrophobicity of the tails, we varied the polarity in the glycerol backbone, and made polarity changes in the headgroup region. The default lipid, resembling DOPC, and the default parameters were selected so that the lipid bilayer was stable (negative Gaussian bending rigidity and a spontaneous curvature of the monolayer close to zero). We found that when the lipid molecules are made somehow more hydrophobic than our default lipid it is possible to induce a sign switch of either ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) or Jm0 or both. These sign-switches do not necessarily take place at the same set of parameters, because the Gaussian bending rigidity follows from the second moment of the grand potential density profile, while the spontaneous curvature of the monolayer is proportional to the first moment. Experimentally, when the spontaneous curvature of the monolayer becomes sufficiently negative before the saddle splay modulus becomes positive, there is a window for which the inverted hexagonal phase is expected. However, when
or Jm0 or both. These sign-switches do not necessarily take place at the same set of parameters, because the Gaussian bending rigidity follows from the second moment of the grand potential density profile, while the spontaneous curvature of the monolayer is proportional to the first moment. Experimentally, when the spontaneous curvature of the monolayer becomes sufficiently negative before the saddle splay modulus becomes positive, there is a window for which the inverted hexagonal phase is expected. However, when ![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) turns positive while the preferred radius is still positive or close to zero, we expect a bicontinuous cubic topology in a concentrated lipid system.
turns positive while the preferred radius is still positive or close to zero, we expect a bicontinuous cubic topology in a concentrated lipid system.
For all membranes, we have seen that the mean bending modulus is positive and small changes in this parameter were expected to be of little consequence. However, the lower the mean bending modulus is, the more prominent membrane undulations will be. When in a bicontinuous phase the mean bending modulus is large, there will be a natural tendency that a minimal surface develops. For a minimal surface, the mean curvature is zero everywhere and there is no effect of the mean bending modulus. However, when the mean bending modulus is not very large, we can expect phases for which the mean curvature can locally deviate from zero. The smaller this value the larger are the undulations and eventually, a periodic bicontinuous cubic phase will melt in favor of a sponge phase in which long-range order is not present. Above we have seen that it is possible to reduce the mean bending modulus while the Gaussian bending rigidity becomes positive and the spontaneous curvature is close to zero. This happens for example when the lipid tails are branched in the limit that one phospholipid has effectively four short tails compared to the classical two long ones. Small molecular weight additives are expected to do the same.60
Above, we have considered model bilayer membranes composed of just one type of lipid. In the biological context however, membranes are composed of many different types of amphiphilic compounds. It is known that when there are two or more lipids the mean bending modulus can be lower than the computational average of the bending modulus of the two individual bilayers.19,61 This is because, in mixtures, the individual lipids can take different average positions in the curved bilayer so that the bending of the bilayer is facilitated. Similar effects may influence the Gaussian bending modulus as well as the spontaneous curvature of the monolayer. In the lattice-refined SCF model, the evaluation of mechanical parameters of mixed bilayer membranes becomes more feasible than in the classical approach and therefore such a study should be high on our scientific agenda.
The lattice-refined SF-SCF theory is far from completely developed. The chain model that is adopted is of the freely-jointed chain type. This implies that the chain is very flexible and the flexibility increases with increasing the lattice refinement b/l value. In the past, extensions of the SF-SCF route were considered in which the chain model was more realistic. For example, the rotational isomeric state (RIS) scheme has been used to model lipids with a higher rigidity along the chain.31 It is feasible to combine the lattice-refinement approach and the RIS scheme so that the semi-flexibility of the tails can be restored. This more elaborate approach will lead to thicker and more stiff bilayers. In addition, we reckon that a better account of the excluded volume effects is needed for a more realistic description of densely packed lipids. Again in combination with the lattice-refinement technique explored in this paper, we expect that improved excluded volume correlations can be introduced, similarly as in earlier work.32 Hence, the lattice-refinement approach reopens old and opens new avenues in the modeling of lipid bilayer membranes.
7 Conclusions
By implementing a lattice refinement in the SF-SCF approach, we were able to significantly reduce lattice artifacts which in turn enabled us to implement the grand canonical route to predict mechanical parameters such as![[small kappa, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cb.gif) , κ, and Jm0. An accurate estimation of these parameters can now be established from the evaluation of the tensionless planar bilayer and a corresponding bilayer curved in the spherical geometry (vesicle). This method replaces a previous, computationally more expensive route, which combined cylindrically curved bilayers and spherically curved ones, to estimate the mean bending κ and indirectly the Gaussian bending rigidity.19 This previous route is formally flawed because it used bilayers for which the lipids were not at the chemical potential equal to that of the planar ground state. We traced the problem to the cylindrical vesicles which invariably balance bending energy with stretching energy and therefore have a finite tension and cannot exist at the chemical potential equal to that of the planar one. Fortunately, we found that the mean bending modulus of bilayer membranes did not depend much on the membrane tension and this explains why the current predictions for the mechanical parameters of lipid bilayer membranes are in good agreement with the ones found by the previously used route.
, κ, and Jm0. An accurate estimation of these parameters can now be established from the evaluation of the tensionless planar bilayer and a corresponding bilayer curved in the spherical geometry (vesicle). This method replaces a previous, computationally more expensive route, which combined cylindrically curved bilayers and spherically curved ones, to estimate the mean bending κ and indirectly the Gaussian bending rigidity.19 This previous route is formally flawed because it used bilayers for which the lipids were not at the chemical potential equal to that of the planar ground state. We traced the problem to the cylindrical vesicles which invariably balance bending energy with stretching energy and therefore have a finite tension and cannot exist at the chemical potential equal to that of the planar one. Fortunately, we found that the mean bending modulus of bilayer membranes did not depend much on the membrane tension and this explains why the current predictions for the mechanical parameters of lipid bilayer membranes are in good agreement with the ones found by the previously used route.
In the lattice-refined SCF approach, we are able to numerically accurately predict mean-field values for the mechanical characteristics as well as structural parameters of tensionless bilayers. Unfortunately in this approach, the lipids have rather high chain flexibility which renders the bilayer to be relatively thin and correspondingly has a too low mean bending rigidity.14,54 Further extension of the SF-SCF scheme is envisioned to correct for this shortcoming. The rotational isometric state scheme as well as an improved account for the excluded volume effects, which cause densely packed tails to cooperatively align,32 are now high on the to-do list to be incorporated in lattice-refined self-consistent field theory.
The default parameter set used for model DOPC bilayers gives a membrane for which the Gaussian bending rigidity is slightly negative and a slightly positive spontaneous curvature of the monolayer. This is consistent with the observation that for such lipids the bilayer has a lamellar topology. When we deviate from the default parameter set, we can find bilayers for which the lamellar topology no longer is stable. More specifically, an increase in hydrophobicity, by increasing either the repulsion between the hydrocarbon segments of the tails with water, or the hydrophobicity of the glycerol backbone or that of the headgroup, leads to a sign-switch of both the Gaussian bending modulus and the spontaneous curvature of the monolayer. For such a system we may expect, for example, a bicontinuous cubic phase, or an inverted hexagonal phase. These types of computations help us to understand the relation between the composition, topology, and function of lipid membranes in the biological context and how lipid phase behavior may be modified, e.g. by using lipids with different hydrophobic/hydrophilic balances or by using additives.
Conflicts of interest
There are no conflicts to declare.References
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CrossRef CAS.
- S. K. Vasu and D. J. Forbes, Curr. Opin. Cell Biol., 2001, 13, 363–375 CrossRef CAS.
- P.-G. De Gennes and P.-G. Gennes, Scaling concepts in polymer physics, Cornell University Press, 1979 Search PubMed.
- H. Pera, J. M. Kleijn and F. A. M. Leermakers, J. Chem. Phys., 2015, 142, 01B614_1 CrossRef.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CAS.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS.
- J. Genova, V. Vitkova and I. Bivas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 022707 CrossRef.
- P. Méléard and T. Pott, Advances in planar lipid bilayers and liposomes, Elsevier, 2013, vol. 17, pp. 55–75 Search PubMed.
- A. F. Loftus, S. Noreng, V. L. Hsieh and R. Parthasarathy, Langmuir, 2013, 29, 14588–14594 CrossRef CAS.
- C. Monzel and K. Sengupta, J. Phys. D: Appl. Phys., 2016, 49, 243002 CrossRef.
- J. R. Henriksen and J. H. Ipsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 14, 149–167 CrossRef CAS.
- V. Heinrich and W. Rawicz, Langmuir, 2005, 21, 1962–1971 CrossRef CAS.
- T. Portet, S. E. Gordon and S. L. Keller, Biophys. J., 2012, 103, L35–L37 CrossRef CAS.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- J. Pan, S. Tristram-Nagle, N. Kučerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS.
- G. Pabst, N. Kučerka, M.-P. Nieh, M. Rheinstädter and J. Katsaras, Chem. Phys. Lipids, 2010, 163, 460–479 CrossRef CAS.
- M. M. A. E. Claessens, B. F. Van Oort, F. A. M. Leermakers, F. A. Hoekstra and M. A. C. Stuart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011903 CrossRef CAS.
- R. A. Kik, J. M. Kleijn and F. A. M. Leermakers, J. Phys. Chem. B, 2005, 109, 14251–14256 CrossRef CAS.
- H. Pera, J. M. Kleijn and F. A. M. Leermakers, J. Chem. Phys., 2014, 140, 02B606_1 CrossRef.
- F. A. M. Leermakers, J. Chem. Phys., 2013, 138, 04B610 Search PubMed.
- F. A. M. Leermakers, J. Chem. Phys., 2013, 138, 124103 CrossRef CAS.
- R. Varadharajan and F. A. M. Leermakers, Phys. Rev. Lett., 2018, 120, 028003 CrossRef CAS.
- S. M. Oversteegen and F. A. M. Leermakers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 8453 CrossRef CAS.
- A. Ben-Shaul and W. M. Gelbart, Micelles, Membranes, Microemulsions, and Monolayers, Springer, 1994, pp. 1–104 Search PubMed.
- D. Romeis, H. Merlitz and J.-U. Sommer, J. Chem. Phys., 2012, 136, 044903 CrossRef CAS.
- G. Fleer, M. A. C. Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at interfaces, Springer Science & Business Media, 1993 Search PubMed.
- S. F. Edwards, Proc. Phys. Soc., 1965, 85, 613 CrossRef CAS.
- A. Egorov, D. Romeis and J.-U. Sommer, J. Chem. Phys., 2012, 137, 064907 CrossRef.
- L. A. Meijer, F. A. M. Leermakers and J. Lyklema, J. Phys. Chem., 1995, 99, 17282–17293 CrossRef CAS.
- O. A. Evers, J. M. H. M. Scheutjens and G. J. Fleer, Macromolecules, 1990, 23, 5221–5233 CrossRef CAS.
- F. A. M. Leermakers and J. M. H. M. Scheutjens, J. Chem. Phys., 1988, 89, 3264–3274 CrossRef CAS.
- F. A. M. Leermakers and J. M. H. M. Scheutjens, J. Chem. Phys., 1988, 89, 6912–6924 CrossRef CAS.
- F. A. M. Leermakers and J. M. H. M. Scheutjens, J. Phys. Chem., 1989, 93, 7417–7426 CrossRef CAS.
- R. A. Kik, F. A. M. Leermakers and J. M. Kleijn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021915 CrossRef.
- F. A. M. Leermakers, A. L. Rabinovich and N. K. Balabaev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011910 CrossRef CAS.
- K. Gawrisch, D. Ruston, J. Zimmerberg, V. A. Parsegian, R. P. Rand and N. Fuller, Biophys. J., 1992, 61, 1213–1223 CrossRef CAS.
- J. Seelig, P. M. MacDonald and P. G. Scherer, Biochemistry, 1987, 26, 7535–7541 CrossRef CAS.
- L. Saiz and M. L. Klein, J. Chem. Phys., 2002, 116, 3052–3057 CrossRef CAS.
- P. S. Niemelä, M. T. Hyvönen and I. Vattulainen, Biophys. J., 2006, 90, 851–863 CrossRef.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- J. N. Israelachvili, S. Marčelja and R. G. Horn, Q. Rev. Biophys., 1980, 13, 121–200 CrossRef CAS.
- A. L. Rabinovich, P. O. Ripatti, N. K. Balabaev and F. A. M. Leermakers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011909 CrossRef CAS.
- L. J. Lis, D. M. McAlister, N. Fuller, R. P. Rand and V. A. Parsegian, Biophys. J., 1982, 37, 657 CAS.
- B. A. Lewis and D. M. Engelman, J. Mol. Biol., 1983, 166, 211–217 CrossRef CAS.
- J. F. Nagle and S. Tristram-Nagle, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469, 159–195 CrossRef CAS.
- N. Kučerka, S. Tristram-Nagle and J. F. Nagle, Biophys. J., 2006, 90, L83–L85 CrossRef.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Biophys. J., 2008, 95, 2356–2367 CrossRef.
- M. Saeedimasine, A. Montanino, S. Kleiven and A. Villa, Sci. Rep., 2019, 9, 1–12 CrossRef CAS.
- L. Saiz and M. L. Klein, Biophys. J., 2001, 81, 204–216 CrossRef CAS.
- S.-W. Chiu, E. Jakobsson, S. Subramaniam and H. L. Scott, Biophys. J., 1999, 77, 2462–2469 CrossRef CAS.
- R. S. Armen, O. D. Uitto and S. E. Feller, Biophys. J., 1998, 75, 734–744 CrossRef CAS.
- E. Boek, J. Padding, W. K. den Otter and W. J. Briels, J. Phys. Chem. B, 2005, 109, 19851–19858 CrossRef CAS.
- R. M. Venable, F. L. Brown and R. W. Pastor, Chem. Phys. Lipids, 2015, 192, 60–74 CrossRef CAS.
- J. F. Nagle, M. S. Jablin, S. Tristram-Nagle and K. Akabori, Chem. Phys. Lipids, 2015, 185, 3–10 CrossRef CAS.
- N. Kučerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, 2011, 1808, 2761–2771 CrossRef.
- S. Ali, J. M. Smaby, M. M. Momsen, H. L. Brockman and R. E. Brown, Biophys J., 1998, 74, 338–348 CrossRef CAS.
- M. Rappolt, in The biological relevant lipid mesophases as “seen” by X-rays, ed. A. Leitmannova-liu, Advances in planar lipid bilayers and liposomes, 2006 Search PubMed.
- A. T. Tenorio, E. De Jong, C. Nikiforidis, R. Boom and A. Van Der Goot, Soft Matter, 2017, 13, 608–618 RSC.
- I. Brentel, E. Selstam and G. Lindblom, Biochim. Biophys. Acta, Biomembr., 1985, 812, 816–826 CrossRef CAS.
- L. van’t Hag, S. L. Gras, C. E. Conn and C. J. Drummond, Chem. Soc. Rev., 2017, 46, 2705–2731 RSC.
- M. Claessens, B. Van Oort, F. Leermakers, F. Hoekstra and M. C. Stuart, Biophys. J., 2004, 87, 3882–3893 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp05597b |
| This journal is © the Owner Societies 2021 |