Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio Gibbs ensemble Monte Carlo simulations of the liquid–vapor equilibrium and the critical point of sodium
Zhi
Li
 *a,
Christophe
Winisdoerffer
b,
François
Soubiran
*a,
Christophe
Winisdoerffer
b,
François
Soubiran
 ac and
Razvan
Caracas
ad
ac and
Razvan
Caracas
ad
aCNRS, École Normale Supérieure de Lyon, Laboratoire de Géologie de Lyon LGLTPE UMR 5276, 46 allée d'Italie, Lyon 69364, France. E-mail: zhi.li@ens-lyon.fr
bUniversité de Lyon, École Normale Supérieure de Lyon, Centre de Recherche Astrophysique de Lyon UMR 5574, 46 allée d'Italie, Lyon 69364, France
cCEA, DAM, DIF, 91297 Arpajon, France
dThe Centre for Earth Evolution and Dynamics (CEED), University of Oslo, Postbox 1028 Blindern, N-0315 Oslo, Norway
First published on 21st December 2020
Abstract
The ab initio (ai) Gibbs ensemble (GE) Monte Carlo (MC) method coupled with Kohn–Sham density functional theory is successful in predicting the liquid–vapour equilibrium of insulating systems. Here we show that the aiGEMC method can be used to study also metallic systems, where the excited electronic states play an important role and cannot be neglected. For this we include the electronic free energy in the formulation of the effective energy of the system to be used in the acceptance criteria for the MC moves. The application of this aiGEMC method to sodium yields a good agreement with available experimental data on the liquid–vapour equilibrium densities. We predict a critical point for sodium at 2338 ± 108 K and 0.24 ± 0.03 g cm−3. The liquid structure stemming from aiGEMC simulations is very similar to the one from ab initio molecular dynamics. Since this method can determine phase transition without computing the Gibbs free energy, it may offer a new possibility to study other materials with a reasonable computational cost.
1 Introduction
Phase equilibria are fundamental processes in chemistry and physics and have dramatic consequences in every field of science and every aspect of our lives. For example, vaporization and condensation of water or freezing and melting of ice are crucial for the climate change and water circulation on Earth as well as for the emergence of life.1 The equilibria between liquids and solids are cornerstones of the whole evolution of rocky planets.2,3 Fluid–fluid mixing and unmixing are of utmost importance from soft matter science and the industry of emulsions all the way to planetary differentiation.4–6Given the available experimental apparatus, the equilibria between condensed phases and gases are much more difficult to investigate than the transitions in condensed matters. And difficulties are only increasing when addressing the critical points, i.e. the points where differences between two phases, like liquids and gases, vanish. Critical points have been extensively studied experimentally especially under near-ambient conditions.7 Under higher pressure, multi-anvil press and diamond anvil cell have been used for decades.8 Unfortunately, critical points lying above 1500 K and at low densities are extremely challenging to obtain experimentally. For these particular conditions, computational studies can be extremely useful, and sometimes are the only way forward for the time being.
The numerical study of phase equilibria is a relatively straightforward problem since it means equating the pressures, temperatures and chemical potentials of two different systems.9 If the first two are relatively easy to achieve numerically, the difficulty comes from the last equality: computing chemical potentials is extremely difficult since it requires the knowledge of the entropy of each phase, which can only be derived from the absolute partition function. Techniques such as molecular dynamics (MD) or Monte Carlo (MC) simulations only provide average quantities but not the absolute partition function.10 Numerous methods have been proposed to circumvent this issue. The most evident one consists in computing the free energy of the system using a reference point and the thermodynamic integration (TDI).11 This is however computationally expensive and a reference system is not always easy to find. A more direct approach consists in simulating layers of two different phases and observe the evolution of the interfaces to determine the most stable phase.12,13 This is more efficient than the TDI but is challenging to set up and highly prone to finite-size effects. Finally, in the Gibbs ensemble Monte Carlo (GEMC) method, one simulates two nearly independent phases at the same time through a MC simulation and ensures the equilibrium by performing specific Metropolis moves allowing to exchange volume and particles.14 This directly mimics the macroscopic equilibrium at a microscopic level, but avoids the interface issues allowing for a more reliable determination of the phase equilibrium.
The success of all the methods outlined in the previous paragraph rely on the quality of the description of the interatomic interaction. In classical simulations these interactions are reproduced by simplified functions that disregard the actual complexity of the electronic interactions. A viable alternative is to fully consider the quantum effects, which are especially important for molecular systems or for metals where the electronic states and occupations change with temperature and pressure. The state-of-the-art method to tackle this issue is the Kohn–Sham formulation (KS) of density functional theory (DFT),15,16 and its finite temperature extension (FT) by Mermin,17 which can account for the quantum behavior of the electrons in a computationally cost-effective manner. TDI18–22 and two-phase simulations23,24 have been linked to DFT calculations to significantly improve the accuracy of the predictions of phase transitions for condensed matter.
In the classical Gibbs ensemble scheme,25 the potential energy evaluated from a force field is used in the acceptance criterion for a trial move. This can be extended to include ab initio simulations, where the internal energy of the electron–ion system plays a similar role as the potential energy in the classical scheme. In the pioneering work of Siepmann et al.,26 the GEMC method has been combined with KS-DFT – often referred as ab initio (aiGEMC) – to improve its accuracy. Ever since different groups have applied the aiGEMC technique to calculate the liquid–vapor equilibrium line of water,27–29 methanol, methane30 and argon.31 All above materials are insulators and have a critical point that is below 700 K. Due to the relatively large band gaps, the thermal excitation of electrons in these systems is not significant, while it may play an important role in determining the phase equilibrium of metallic systems at high temperature.
In metals, in order to capture the thermal excitations of electrons, it is necessary to make full use of FT-KS-DFT which explicitly includes the contribution of excited electronic states. Because of the extra electronic entropy term in FT-KS-DFT framework, at finite temperature, a great care should be given to the electronic contribution as the excited states also play a role in the acceptance ratio. A first attempt of ab initio MC simulations on a metal was performed on liquid lithium in the isothermal–isobaric and canonical ensemble32 with encouraging success.
In the present paper, we present the formalism of the Gibbs ensemble coupled to FT-KS-DFT, followed by its practical implementation. We then apply the finite temperature aiGEMC method to compute the liquid–vapor equilibrium of sodium for which several experimental data sets are available.33–35 The critical densities and temperatures range from 0.175 to 0.3 g cm−3 in density and from 2485 to 2573 K in temperature. The sodium vapor is mainly an atomic gas without large clusters,36 which thus greatly simplifies the structural constraints. Moreover, as FT-KS-DFT has proven to be reliable in the study of the condensed phases of sodium,37,38 it may serve as an excellent testing ground to extend this application of FT-KS-DFT to cover the gaseous phase of a metal as well. We demonstrate that the aiGEMC offers a great way of computing a fully ab initio liquid–vapor phase diagram and of positioning the critical point.
2 Methodology
2.1 Statistical physics considerations
Statistical mechanics enables access to the thermodynamic properties of a system through the computation of its partition function. Although the expression of this partition function depends on the statistical ensemble, disregarding some very peculiar situations, the Gibbs theorem39–42 ensures that all the statistical ensembles are equivalent in the thermodynamic limit. Unfortunately, evaluating the partition function is a formidable task and cannot be performed analytically except for a few well-known cases, e.g. the ideal gas. It was soon realized that computational approaches offer a convenient way to circumvent these difficulties, as illustrated by the famous numerical experiment run by Metropolis and collaborators on the MANIAC computer.43 These methods have been extensively used in many scientific fields, with numerous refinements specific to each context. However, one major concern needs to be addressed before investigating the liquid–gas equilibrium of sodium within a GEMC approach. Unlike previous studies with aiGEMC on systems with a low critical temperature and large band gap, the studied temperature range here is high enough so that electronic excitations must be taken into account consistently within the framework of finite temperature DFT. This problem is of considerable conceptual importance, and thus warrants a brief outline of statistical mechanics derivations in order to find an appropriate energy term that can be used in the acceptance criterion for a MC trial move.![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) }N and momenta {
}N and momenta {![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) }N, and their corresponding Ne electrons {{
}N, and their corresponding Ne electrons {{![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) }Ne,{
}Ne,{![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) }Ne}, can be described by a Hamiltonian H associated to some boundary conditions. The canonical partition function reads:40,44
}Ne}, can be described by a Hamiltonian H associated to some boundary conditions. The canonical partition function reads:40,44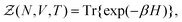 | (1) |
![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) }N,{
}N,{![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) }N,{
}N,{![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) }Ne,{
}Ne,{![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) }Ne), β = (kBT)−1, kB is the Boltzmann constant, and T is the temperature. The number of electrons Ne does not appear as a variable in
}Ne), β = (kBT)−1, kB is the Boltzmann constant, and T is the temperature. The number of electrons Ne does not appear as a variable in 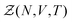 as the charge neutrality is assumed. The Hamiltonian can be split into three parts: a nuclear part Hn({
as the charge neutrality is assumed. The Hamiltonian can be split into three parts: a nuclear part Hn({![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) }N,{
}N,{![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) }N), an electronic part He({
}N), an electronic part He({![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) }Ne,{
}Ne,{![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) }Ne), and a third part, which takes into account the interaction between the electrons and the nuclei Hn–e({
}Ne), and a third part, which takes into account the interaction between the electrons and the nuclei Hn–e({![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) }N,{
}N,{![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) }Ne). It should be emphasized that, at this stage, the partition function is expressed in purely quantum mechanical terms, as H depends on both the nuclear operators {
}Ne). It should be emphasized that, at this stage, the partition function is expressed in purely quantum mechanical terms, as H depends on both the nuclear operators {![[R with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0052_0302.gif) }N,{
}N,{![[P with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0050_0302.gif) }N and the electronic operators {
}N and the electronic operators {![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) }Ne,{
}Ne,{![[p with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0070_0302.gif) }Ne. Because of the smallness of the mass ratio m/M, where m is the electronic mass and M the nuclear one, the quantum behaviour of the nuclei can be safely neglected for most of the thermodynamic conditions. Then the partition function takes the following form, up to some
}Ne. Because of the smallness of the mass ratio m/M, where m is the electronic mass and M the nuclear one, the quantum behaviour of the nuclei can be safely neglected for most of the thermodynamic conditions. Then the partition function takes the following form, up to some 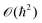 corrective terms:45
corrective terms:45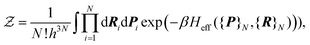 | (2) |
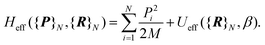 | (3) |
The first term is the kinetic nuclear term and the second is the effective nuclear potential term; the latter includes the free energy of the electrons of the system for a given nuclei configuration {R}N:
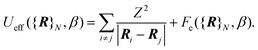 | (4) |
The first term is the Coulomb interaction of the nuclei of charge Z, and the second term is the electronic free energy at fixed nuclear configuration:
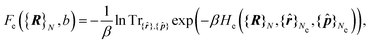 | (5) |
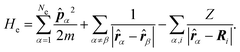 | (6) |
The electrons are thus treated for a specific nuclear configuration and then an average must be performed over the different configurations. Note that in eqn (6), the electronic positions and momenta are operators because the electrons must be treated in the quantum mechanical framework.
At this point, we need to stress that eqn (2) is the standard expression of the classical partition function for the canonical ensemble. It means that the nuclei are treated according to the classical mechanics in an effective potential Ueff [eqn (4)] which includes all electronic degrees of freedom [eqn (5)] plus the coulombic interaction between nuclei. This effective nuclear potential Ueff encompasses the quantum behaviour of the electrons in a consistent way through the computation of the corresponding free energy contribution.
In practice, we split the computation of the partition function eqn (2) in two distinct problems. The first deals with the evaluation of the multi-dimensional (6N) integral, which is sampled using the MC Gibbs ensemble approach. The second corresponds to the computation of the effective nuclear potential energy including the free energy of electrons, which is done using FT-KS-DFT.17 In the following sub-sections we detail the methodology that we have developed in order to perform such a computation.
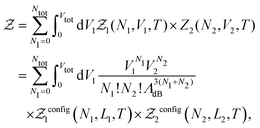 | (7) |
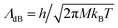 is the de Broglie wavelength,
is the de Broglie wavelength, 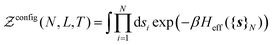 and si ∈ [0;1] ∀i. It should be emphasized that Heff({s}N) corresponds to the Hamiltonian of the N nuclei interacting through an effective potential associated to the electronic free energy within a box with volume V = L3. It is interesting to note that the partition function as written in eqn (7) includes the possibility for one box to be empty or to have zero volume. Although counter-intuitive, these states, if explored by the GEMC algorithm, must be taken into account. This was already pointed out by Smit in the 80s.46 However it means that we need to pay a peculiar attention to the definition of the statistical quantities since for instance the specific energy is then undefined. Nevertheless, extensive quantities are all properly defined.
and si ∈ [0;1] ∀i. It should be emphasized that Heff({s}N) corresponds to the Hamiltonian of the N nuclei interacting through an effective potential associated to the electronic free energy within a box with volume V = L3. It is interesting to note that the partition function as written in eqn (7) includes the possibility for one box to be empty or to have zero volume. Although counter-intuitive, these states, if explored by the GEMC algorithm, must be taken into account. This was already pointed out by Smit in the 80s.46 However it means that we need to pay a peculiar attention to the definition of the statistical quantities since for instance the specific energy is then undefined. Nevertheless, extensive quantities are all properly defined.
Ensemble averages can be estimated by the famous MC importance sampling algorithm introduced by Metropolis et al.43 which is at the core of the GEMC approach. For obvious reasons, full monographs were dedicated to the presentation and discussion of this method and its possible improvements.47–51 Three types of trial move o(ld) → n(ew) are considered in our GEMC simulations: (i) random displacement of a randomly chosen particle, (ii) random volume rearrangement, (iii) random transfer of a randomly chosen particle between the two sub-systems. The Metropolis scheme defines the following acceptance rules as:
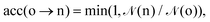 | (8) |
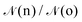 given by:10,25,52
given by:10,25,52
• (i) particle (belonging to box j) displacement:
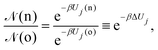 | (9) |
• (ii) volume exchange V1(o) → V1(n) and V2(o) → V2(n):
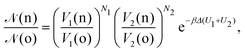 | (10) |
• (iii) particle transfer from box j = 1 to box j = 2:
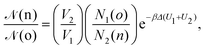 | (11) |
2.2 Setup of the GEMC calculations
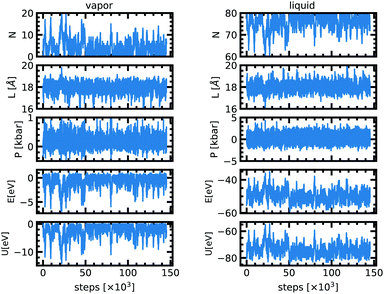
The implementation of the Markov chain described in the previous section is relatively straightforward. We define three probabilities ηDispl. = 0.5, ηVol. = 0.25, and ηPart. = 0.25 for the choice among the different moves for each cycle, such as ηDispl. + ηVol. + ηPart.= 1. We define δsmax as the maximal (normalized) particle displacement, which can be different for the two boxes, chosen such as to reach an acceptance ratio for moves of type (i) around 50% for each sub-system, and δVmax as the maximal volume exchange, similarly optimized for an acceptance rate of about 50%. The detailed values are compiled in Table 2.In particular for sodium we used as initial conditions a liquid box of 17 Å with 80 atoms and an empty vapor box of 25 Å for the simulations below 2000 K, and a liquid box of 18 Å with 80 atoms and an empty vapor box of 18 Å at 2000 K. One accepted configuration at 2000 K served as starting point for the simulations at 2100 K, 2200 K, 2300 K and 2400 K. At 2500 K, we start with two 40-atoms boxes of 17 Å. In addition, we have performed an extra simulation at 2000 K with 120 atoms to estimate the finite-size effect, which is found to be small at this condition (see Fig. 1). All the simulation boxes are cubic and the dimensions above define the edge of the box. The equilibrium values and their uncertainty were calculated using the autocorrelation technique.10 The error bars reported in the following sections are one-Sigma error bars.
When compared to single-box simulations, GEMC is rightfully considered to be affected by surface finite-size effects. It means that if a liquid–gas phase transition should happen, interface issues are avoided. However one should keep in mind that other finite-size effects exist, such as divergence of the correlation length and critical slowing down, and may play an important role, especially in the vicinity of a critical point. These effects are at the heart of the brilliant refinements of the “basic algorithm” that are implemented in codes designed to run GEMC simulations such as MCCCS Towhee,53 VMMC54 and CP2K.26 The limited number of atoms we have in our cells does not preclude such finite-size effects. However, as we will show in Section 3, the relatively good agreement with the experimental data is reassuring. We also chose on purpose to not include pre-biased moves or more complex moves to our algorithm in order to carefully check our implementation using VASP and the electron free energy. We thus limit the possible flaws in our sampling. It is clear that in order to have a faster algorithm one needs to consider such more intricate moves.
2.3 Setup of the DFT calculations
We compute the energy of the two sub-systems at each MC step using first-principles calculations in the projector augmented wave (PAW) method55,56 of the DFT in the VASP57,58 implementation. We employ the Generalized-Gradient Approximation in the Perdew–Burke–Ernzerhof formalism59 for the exchange correlation term. We treat the 3s1 as valence electron configurations for the PAW pseudopotentials. The partial occupancies for the electronic calculation are calculated using a Fermi–Dirac smearing scheme with a width corresponding to the nuclear temperature. The energy cut-off for the plane-wave basis set was set to 400 eV. The break condition for the electronic self-consistent loop was 10−4 eV. The number of electronic bands was adapted to the temperature conditions such as to cover the entire spectrum of the fully and partially occupied states and to include enough non-occupied bands. The Brillouin zone was sampled with the Baldereschi point.60 A test with a grid of 2 × 2 × 2 k-points yields results within 0.5% difference in energy. At each MC step, for each ionic configuration we compute the energy Ueff as defined in eqn (4) including the free energy of the electrons in a coulombic potential due to the ions and the ion–ion interaction. Our implementation is done outside of the VASP package,57 which is called only as an energy routine.To compare with the Gibbs ensemble method, we also performed molecular dynamics simulations of the liquid phase in the DFT framework at several densities along the 2000 K isotherm. In order to stay consistent with the MC calculations we used the same DFT parameters for the MD simulations. The temperature was kept constant thanks to a Nosé thermostat.61 We used a fixed volume cell containing 80 atoms. The time step was set to 2 fs for a total duration of 20 ps.
3 Results and discussion
3.1 Stationary state and equilibrium
At the very beginning of the simulation there is a net particle flux from the liquid box to the vapor box since the latter is initially empty (Fig. 1). The driving force is the difference in chemical potentials. Because of the random character of the acceptance of moves along the Markov chains, particles from the gas box may also be transferred to the liquid box. This is captured by fluctuations of the density in each of the two boxes. After about 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 attempted moves, both boxes have reached a stationary state and the equilibrium is achieved. At equilibrium, for a temperature of 2000 K the cell length of both boxes fluctuates around 18 Å. The pressure in the liquid phase is 0.0 ± 0.2 kbar and 0.08 ± 0.03 kbar for the vapor phase. The liquid phase has 76 atoms on average but the vapor phase only 4. The stationary state thus seems to correspond to a thermal, dynamical and chemical equilibrium.
000 attempted moves, both boxes have reached a stationary state and the equilibrium is achieved. At equilibrium, for a temperature of 2000 K the cell length of both boxes fluctuates around 18 Å. The pressure in the liquid phase is 0.0 ± 0.2 kbar and 0.08 ± 0.03 kbar for the vapor phase. The liquid phase has 76 atoms on average but the vapor phase only 4. The stationary state thus seems to correspond to a thermal, dynamical and chemical equilibrium.
The acceptance ratios reported in Table 2 are very satisfactory with typical values between 10 and 75% for each move. The 1200 K simulation shows a very low acceptance rate for the particle exchange because the temperature is very low compared to the energy barrier. Since the acceptance rate is non zero and since we ensured a long enough run we anticipate that the results are still reliable. Fig. 1 shows the evolution of different quantities as a function of the MC steps at 2000 K. Table 1 lists all the values of the thermodynamic quantities.
| Temperature (K) | N vap | N liq | ρ vap (g cm−3) | ρ liq (g cm−3) | P vap (kbar) | P liq (kbar) | U vap (eV) | U liq (eV) |
|---|---|---|---|---|---|---|---|---|
| a We perform an extra simulation at 2000 K with 120 atoms to estimate the finite-size effect on the liquid–vapour equilibrium density. b At 2400 and 2500 K, only one phase is present. The density, pressure, effective energy of gas and liquid phase indicate the average properties in each box. | ||||||||
| 1200 | 0.04 ± 0.02 | 79.96 ± 0.02 | 9 × 10−5 ± 4 × 10−5 | 0.60 ± 0.01 | 2 × 10−4 ± 1 × 10−4 | −0.36 ± 0.35 | −0.011 ± 0.008 | −83.47 ± 0.16 |
| 1500 | 0.52 ± 0.32 | 79.48 ± 2.35 | 0.001 ± 0.0008 | 0.58 ± 0.01 | 0.003 ± 0.001 | −0.37 ± 0.34 | −0.23 ± 0.04 | −81.55 ± 0.32 |
| 1800 | 2.26 ± 0.67 | 78.74 ± 1.52 | 0.014 ± 0.004 | 0.54 ± 0.01 | 0.06 ± 0.03 | −0.21 ± 0.28 | −1.01 ± 0.33 | −78.94 ± 0.45 |
| 2000 | 4.22 ± 1.86 | 75.78 ± 1.88 | 0.03 ± 0.01 | 0.50 ± 0.02 | 0.08 ± 0.03 | 0.0 ± 0.2 | −2.33 ± 0.37 | −74.19 ± 0.67 |
| 2000a | 7.48 ± 2.90 | 112.52 ± 3.22 | 0.04 ± 0.01 | 0.51 ± 0.02 | 0.10 ± 0.01 | 0.20 ± 0.34 | −4.34 ± 1.51 | −111.38 ± 1.03 |
| 2100 | 7.20 ± 1.59 | 72.80 ± 2.42 | 0.05 ± 0.01 | 0.46 ± 0.02 | 0.12 ± 0.05 | 0.20 ± 0.23 | −69.44 ± 1.45 | −5.11 ± 1.93 |
| 2200 | 12.27 ± 2.35 | 59.20 ± 6.29 | 0.074 ± 0.02 | 0.43 ± ± 0.05 | 0.15 ± 0.08 | 0.44 ± 0.50 | −8.06 ± 1.54 | −55.99 ± 6.52 |
| 2300 | 14.47 ± 3.84 | 57.07 ± 12.22 | 0.15 ± 0.04 | 0.42 ± 0.07 | 0.13 ± 0.52 | 0.36 ± 0.67 | −10.35 ± 3.28 | −52.97 ± 11.89 |
| 2400b | 38.37 ± 5.44 | 41.63 ± 5.32 | 0.28 ± 0.04 | 0.26 ± 0.03 | 0.33 ± 0.13 | 0.43 ± 0.11 | −32.25 ± 0.98 | −34.63 ± 0.74 |
| 2500b | 38.54 ± 6.60 | 41.46 ± 7.98 | 0.31 ± 0.03 | 0.32 ± 0.04 | 0.44 ± 0.24 | 0.46 ± 0.20 | −31.42 ± 1.71 | −38.27 ± 0.84 |
| Temperature [K] | Particle displacement in Box1 | Particle displacement in Box2 | Volume exchange | Atom swap acceptance ratio | |||
|---|---|---|---|---|---|---|---|
| Acceptance ratio | δsmax | Acceptance ratio | δsmax | Acceptance ratio | δVmax [Å3] | ||
| a We perform an extra simulation at 2000 K with 120 atoms to estimate the finite-size effect on the liquid–vapour equilibrium density. | |||||||
| 1200 | 0.50 | 0.035 | 0.78 | 0.23 | 0.55 | 300 | 0.006 |
| 1500 | 0.41 | 0.052 | 0.73 | 0.16 | 0.50 | 420 | 0.07 |
| 1800 | 0.58 | 0.05 | 0.41 | 0.10 | 0.45 | 700 | 0.13 |
| 2000 | 0.54 | 0.055 | 0.50 | 0.13 | 0.60 | 550 | 0.18 |
| 2000a | 0.48 | 0.04 | 0.39 | 0.1 | 0.46 | 700 | 0.14 |
| 2100 | 0.52 | 0.07 | 0.54 | 0.1 | 0.56 | 700 | 0.21 |
| 2200 | 0.49 | 0.072 | 0.58 | 0.08 | 0.57 | 710 | 0.26 |
| 2300 | 0.61 | 0.07 | 0.45 | 0.10 | 0.52 | 800 | 0.29 |
| 2400 | 0.53 | 0.078 | 0.55 | 0.08 | 0.59 | 650 | 0.39 |
| 2500 | 0.50 | 0.078 | 0.53 | 0.08 | 0.52 | 650 | 0.37 |
3.2 Liquid–vapor equilibrium
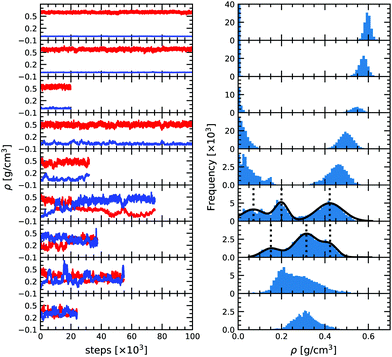
As can be seen from Fig. 2, at low temperature there is a clear distinction between the low density and the high density phases, with two distinct peaks corresponding to the two densities. It is then possible to determine the average thermodynamic quantities of both the vapor and the liquid phases by averaging over each distinct distribution.As temperature increases the distributions become less and less separated, eventually preventing for a clear difference between the two phases. As we approach the critical temperature, the simulations have a higher probability of switching identity or even having two phases at once in the same simulation box. The latter is due to a comparable magnitude of the surface tension effect and the entropy contribution as already observed by Smit et al. (1989).46 It results in the appearance of three peaks in the density distribution plot. In order to better quantify the density of the three phases (gas, liquid and the mixed phase), we fitted the three peaks by three Gaussian functions (solid black line in Fig. 2) as suggested by Smit et al. (1989).46 The center of the Gaussian is assumed to be the average density of each phase and its width is the standard deviation entering in the determination of the uncertainty. The low density peak corresponds to the gaseous phase and the high density peak to the liquid phase. The middle peak, close to the average density of the two boxes is the mixed phase, and is disregarded in the liquid–vapor equilibrium analysis. At 2300 K, the fluctuations become extremely large and we thus decided to only show the results in the density plot for reference but not to use them for the fit since they offer too loose a constraint on the critical point. For 2400 and 2500 K both boxes reach a very similar equilibrium and seem identical. This means that these conditions are above the critical point.
Based on the equilibrium densities, we can plot a vapor–liquid coexistence curve as shown in Fig. 3. In general we obtain a good agreement compared to experimental data available in the literature.33 At 1200 K, the saturated liquid density is 20% lower than that of experiments, which may be due to the choice of PBE as an exchange correlation functional as already noted in previous studies of argon.31 A precise direct determination of the critical point is made difficult by the finite size of our system since the correlation length is expected to tend to infinity at the critical point; this cannot be captured within our small simulation cells. The critical point may however be approximated using the law of rectilinear diameter:62
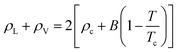 | (12) |
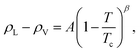 | (13) |
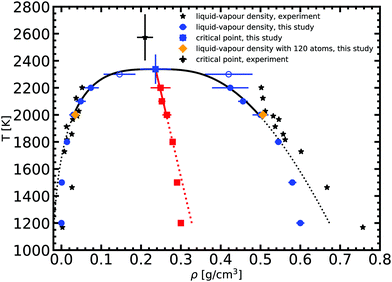 | ||
| Fig. 3 Liquid–vapor equilibrium of Na obtained from the ab initio Gibbs ensemble simulations (blue circles) and its comparison with the experiment33 (black stars). The black solid line is a fit for the scaling law to all data points above 2000 K, while the black dotted line denotes the extrapolation to lower temperature. The red solid and dotted line is the law of rectilinear diameter with A = 0.87 ± 0.1 and B = 0.19 ± 0.03 parameters (see text for more details). | ||
We obtained the critical point by applying the scaling law to all data points above 2000 K. Using our data we obtain our best fit with A = 0.87 ± 0.1 and B = 0.19 ± 0.03. The critical point lies at 2338 ± 108 K and 0.24 ± 0.03 g cm−3. We stress here that the density values at 1800 K are compatible with the extrapolation of the scaling law, providing confidence in our fit. Our theoretical critical temperature is slightly lower than the experimental value at 2573 ± 171 K,33 and the critical density is similar to the experimental value of 0.21 ± 0.02 g cm−3. We want to underline that both our values and the experimental ones are the result of extrapolations, as in both cases it is too challenging to obtain equilibrium data in the very vicinity of the critical point. With this in mind, the good agreement that we obtain between our calculations and experiments confirms the suitability of the ab initio Gibbs ensemble method for the determination of accurate coexistence curves. We also include the Clausius–Clapeyron plot of the saturated vapor pressure and density as a function of the inverse temperature in Fig. 5. We obtain a nice affine behavior for both the logarithm of the density and of the pressure on these plots. We also have a relatively good agreement with the experimental density data.
In order to check our Gibbs ensemble results, we also performed a set of ab initio molecular dynamics simulations in the canonical ensemble at 2000 K for different densities. This allows us to analyse the structure of the liquid and to determine the corresponding spinodal point.65Fig. 4 shows the variation of pressure as a function of the density along the 2000 K isotherm. This curve exhibits a clear minimum close to 0.48 g cm−3; this is the liquid spinodal point. This is the smallest density at which the liquid is metastable. Above this density the fluid is homogeneous, as shown for example in the insets of Fig. 4. At lower densities, in the unstable branch, bubbles form proving that the liquid becomes unstable. The density of the spinodal point is close yet lower than the equilibrium density of 0.50 ± 0.02 g cm−3 predicted by the Gibbs ensemble method. We thus have a full consistency between these two completely different methods ensuring the reliability of the Gibbs ensemble method.
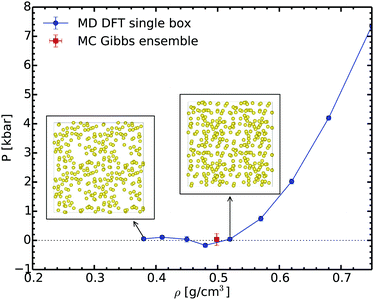 | ||
| Fig. 4 Pressure evolution during the isothermal volume expansion for sodium at 2000 K. The insets show the snapshots at 0.52 and 0.38 g cm−3, respectively. | ||
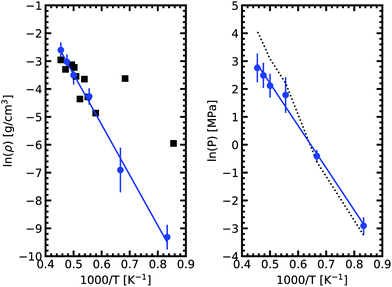 | ||
| Fig. 5 Clausius–Clapeyron plot of the logarithm of the saturated vapor pressure and density as a function of the inverse temperature. The solid black squares are experimental date.33 The dashed line on the right graph denotes the pressures from fitting vapor density to the ideal gas law. As expected, a good agreement with calculated pressure is achieved in the low density range. In the high density region, a deviation is observed. | ||
3.3 Structure of the liquid
We compare the structure of the liquid as we obtain it using the MC Gibbs ensemble and the MD approach. We analyse the radial distribution function (RDF), which is defined as,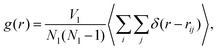 | (14) |
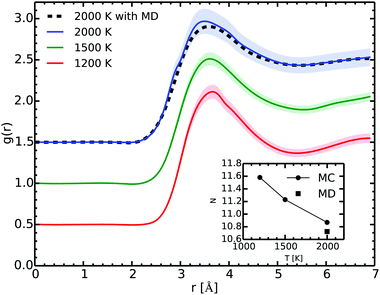
Fig. 6 shows the RDF at several temperatures as extracted from our Gibbs ensemble simulations. The main peak lies around 3.5 Å. Along the vapor–liquid equilibrium line, the position of the peak changes slightly and broadens due mostly to the temperature effects. The spherical integration of the RDF from 0 to its first minimum gives the coordination number.
At 2000 K and 0.52 g cm−3 the agreement of the RDF as obtained in the MC and in the MD simulations is excellent. As the two methods start from different initial configurations and use different paths, they give a remarkable consistent outcome as they explore the configurational space. While this is not an absolute proof that we achieved ergodicity, it strongly suggests that our simulations are satisfying it.
4 Conclusions
We implemented the ab initio Gibbs ensemble algorithm and performed a series of simulations to compute the liquid–vapor equilibrium line and the critical point of sodium. We emphasize the electronic contribution at finite temperature, which is essential for metallic systems, but not always clearly explained in the literature. The effective nuclear potential energy defined in eqn (4) should be used in the acceptance rule for a MC trial move in the Gibbs ensemble. We demonstrated that our simulations reached a mechanical and chemical equilibrium and the calculated phase coexistence curve and critical point are in a good agreement with the experimental results. The comparison of our results with molecular dynamics also showed very good consistency. Therefore, we confirm the reliability and validity of the ab initio Gibbs ensemble method.This method offers a new possibility to study phase transitions without computing the complete Gibbs free energy and therefore paves the way for the outstanding questions regarding phase equilibria. It is clear that the high computer cost of such an ab initio Gibbs ensemble method precludes the use of large simulation cells, at least for now. However, considering a good agreement between our results and experimental data, we can expect to obtain very satisfactory liquid–vapor equilibrium curves for other materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 681818 IMPACT to RC) and under the Marie Skłodowska-Curie program (grant agreement no. 750901 ABISSE to FS), and by the Research Council of Norway through its Centres of Excellence funding scheme, project number 223272. We acknowledge access to the GENCI supercomputers (Occigen at CINES, Ada and Jean-Zay at IDRIS, and Curie and Irene at TGCC) through the stl2816 series of eDARI computing grants, and the PRACE grant RA4947.Notes and references
- D. K. Cassel and B. B. Thapa, Water cycle, 2005 Search PubMed.
- D. L. Anderson, New Theory of the Earth, Cambridge University Press, 2010 Search PubMed.
- R. Caracas, K. Hirose, R. Nomura and M. D. Ballmer, Earth Planet. Sci. Lett., 2019, 516, 202–211 CrossRef CAS.
- D. J. Stevenson, Planet. Space Sci., 1982, 30, 755–764 CrossRef CAS.
- B. Militzer, F. Soubiran, S. M. Wahl and W. Hubbard, J. Geophys. Res.: Planets, 2016, 121, 1552 Search PubMed.
- F. Soubiran, S. Mazevet, C. Winisdoerffer and G. Chabrier, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165114 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, Florida, 85th edn, 2003 Search PubMed.
- T. Gasparik, Phase Diagrams for Geoscientists, Springer, 2nd edn, 2003 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon Press, 3rd edn, 1980 Search PubMed.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier Science, 2001 Search PubMed.
- M. Watanabe and W. P. Reinhardt, Phys. Rev. Lett., 1990, 65, 3301–3304 CrossRef CAS PubMed.
- K. E. Gubbins, Fluid Phase Equilib., 1993, 83, 1–14 CrossRef CAS.
- J. R. Morris, C. Z. Wang, K. M. Ho and C. T. Chan, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 3109–3115 CrossRef CAS PubMed.
- A. Z. Panagiotopoulos, Mol. Simul., 1992, 9, 1–23 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443 CrossRef.
- G. A. De Wijs, G. Kresse and M. J. Gillan, Phys Rev B, 1998, 57, 8223–8234 CrossRef CAS.
- D. Alfè, G. D. Price and M. J. Gillan, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165118 CrossRef.
- M. A. Morales, E. Schwegler, D. Ceperley, C. Pierleoni, S. Hamel and K. Caspersen, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1324–1329 CrossRef CAS PubMed.
- B. Militzer, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014202 CrossRef.
- F. Soubiran and B. Militzer, Astrophys. J., 2015, 806, 228 CrossRef.
- D. Alfè, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 060101 CrossRef.
- J. Bouchet, S. Mazevet, G. Morard, F. Guyot and R. Musella, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 094102 CrossRef.
- A. Z. Panagiotopoulos, Mol. Phys., 1987, 61, 813–826 CrossRef CAS.
- M. J. McGrath, J. I. Siepmann, I.-F. W. Kuo, C. J. Mundy, J. VandeVondele, M. Sprik, J. Hutter, F. Mohamed, M. Krack and M. Parrinello, Comput. Phys. Commun., 2005, 169, 289–294 CrossRef CAS.
- M. J. McGrath, J. I. Siepmann, I.-F. W. Kuo, C. J. Mundy, J. VandeVondele, J. Hutter, F. Mohamed and M. Krack, J. Phys. Chem. A, 2006, 110, 640–646 CrossRef CAS PubMed.
- P. Schienbein and D. Marx, J. Phys. Chem. B, 2018, 122, 3318–3329 CrossRef CAS PubMed.
- M. J. McGrath, J. I. Siepmann, I.-F. W. Kuo and C. J. Mundy, Mol. Phys., 2006, 104, 3619–3626 CrossRef CAS.
- M. J. McGrath, I.-F. W. Kuo, J. N. Ghogomu, C. J. Mundy and J. I. Siepmann, J. Phys. Chem. B, 2011, 115, 11688–11692 CrossRef CAS PubMed.
- H. Goel, S. Ling, B. N. Ellis, A. Taconi, B. Slater and N. Rai, J. Chem. Phys., 2018, 148, 224501 CrossRef PubMed.
- L. D. Gelb and T. N. Carnahan, Chem. Phys. Lett., 2006, 417, 283–287 CrossRef CAS.
- I. G. Dillon, P. A. Nelson and B. S. Swanson, J. Chem. Phys., 1966, 44, 4229 CrossRef CAS.
- B. F. Hensel, G. F. Hohl, D. Schaumlöffel and W. C. Pilgrim, Zeitschrift für Physikalische Chemie, 2000, 214, 823–831 Search PubMed.
- J. Fink and L. Leibowitz, Thermodynamic and transport properties of sodium liquid and vapor, Anl/re-95/2 technical report, 1995.
- V. V. Chaban and O. V. Prezhdo, J. Phys. Chem. A, 2016, 120, 4302–4306 CrossRef PubMed.
- M. S. Miao and R. Hoffmann, J. Am. Chem. Soc., 2015, 137, 3631–3637 CrossRef CAS PubMed.
- S. Zhang, K. P. Driver, F. Soubiran and B. Militzer, J. Chem. Phys., 2017, 146, 74505 CrossRef PubMed.
- J. Gibbs, Elementary Principles in Statistical Mechanics: Developed with Especial Reference to the Rational Foundations of Thermodynamics, C. Scribner's sons, 1902 Search PubMed.
- K. Huang, Statistical mechanics, Wiley, New York, 2nd edn, 1987 Search PubMed.
- D. Ruelle, Statistical Mechanics: Rigorous Results, World Scientific, 1999 Search PubMed.
- H. Touchette, J. Stat. Phys., 2015, 159, 987–1016 CrossRef.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- R. Balian, D. Haar and J. Gregg, From Microphysics to Macrophysics: Methods and Applications of Statistical Physics, Springer, Berlin Heidelberg, 2006 Search PubMed.
- R. W. Zwanzig, Phys. Rev., 1957, 106, 13–15 CrossRef CAS.
- B. Smit, P. D. Smedt and D. Frenkel, Mol. Phys., 1989, 68, 931–950 CrossRef CAS.
- M. E. J. Newman and G. T. Barkema, Monte Carlo Methods in Statistical Physics, Clarendon Press, 1999 Search PubMed.
- C. Robert and G. Casella, Monte Carlo Statistical Methods, Springer, New York, 2005 Search PubMed.
- D. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, 2005 Search PubMed.
- D. Kroese, T. Taimre and Z. Botev, Handbook of Monte Carlo Methods, Wiley, 2013 Search PubMed.
- R. Y. Rubinstein and D. P. Kroese, Simulation and the Monte Carlo Method: Third Edition, Wiley, 2016 Search PubMed.
- A. Z. Panagiotopoulos, N. Quirke, M. Stapleton and D. J. Tildesley, Mol. Phys., 1988, 63, 527–545 CrossRef CAS.
- M. G. Martin, Mol. Simul., 2013, 39, 1212–1222 CrossRef CAS.
- S. Whitelam and P. L. Geissler, J. Chem. Phys., 2007, 127, 154101 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Baldereschi, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 7, 5212–5215 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- J. S. Rowlinson and F. Swinton, Liquids and liquid Mixtures, Butterworth, London, Third edn, 1982 Search PubMed.
- J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Clarendon Press, Oxford, 1982 Search PubMed.
- N. B. Wilding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 52, 602–611 CrossRef CAS PubMed.
- R. J. Speedy, J. Phys. Chem., 1982, 86, 982–991 CrossRef CAS.
| This journal is © the Owner Societies 2021 |