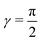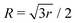Time-dependent quantum mechanical wave packet dynamics†‡
Narayanasami
Sathyamurthy
 *a and
Susanta
Mahapatra
*a and
Susanta
Mahapatra
 b
b
aIndian Institute of Science Education and Research Mohali, SAS Nagar, 140306, India. E-mail: nsathyamurthy@gmail.com
bSchool of Chemistry, University of Hyderabad, Hyderabad, 500 046, India. E-mail: susanta.mahapatra@uohyd.ac.in
First published on 19th October 2020
Abstract
Starting from a model study of the collinear (H, H2) exchange reaction in 1959, the time-dependent quantum mechanical wave packet (TDQMWP) method has come a long way in dealing with systems as large as Cl + CH4. The fast Fourier transform method for evaluating the second order spatial derivative of the wave function and split-operator method or Chebyshev polynomial expansion for determining the time evolution of the wave function for the system have made the approach highly accurate from a practical point of view. The TDQMWP methodology has been able to predict state-to-state differential and integral reaction cross sections accurately, in agreement with available experimental results for three dimensional (H, H2) collisions, and identify reactive scattering resonances too. It has become a practical computational tool in predicting the observables for many A + BC exchange reactions in three dimensions and a number of larger systems. It is equally amenable to determining the bound and quasi-bound states for a variety of molecular systems. Just as it is able to deal with dissociative processes (without involving basis set expansion), it is able to deal with multi-mode nonadiabatic dynamics in multiple electronic states with equal ease. We present an overview of the method and its strength and limitations, citing examples largely from our own research groups.
1 Introduction
Some time ago, when a friend of ours was looking at our results obtained from an investigation of time-dependent quantum mechanical wave packet (TDQMWP) dynamics by solving the time-dependent Schrödinger equation (TDSE) on a three dimensional (3D) grid, he questioned the wisdom of adding another dimension (time, t) to the difficult problem when one could get all the information (experimental observables) by solving the time-independent Schrödinger equation (TISE). What he did not say, but we guess he implied, was that Schrödinger himself solved the stationary state problems of the hydrogen atom,1 the harmonic oscillator, the rigid rotor and diatomic molecules2 before looking at scattering processes and the like in the 4th paper in the series.3 In some sense, the question of our friend was like asking what the need was to watch a football game when all one needed to know was the final score!Schrödinger seemed to have been interested in addressing only the conceptual difficulties in his papers as he believed that the mathematical aspects were easily solvable. Dirac,4 however, was more pragmatic. He declared, “The fundamental laws necessary for the mathematical treatment of a large part of physics and the whole of chemistry are thus completely known and the difficulty lies only in the fact that application of these laws leads to equations that are too complex to be solved.” Numerical solutions were far away in the future as computers were yet to be invented.
From a formal point of view, the TISE is an eigenvalue problem, while the TDSE is an initial value problem. The latter has an advantage in that it can include continuum states with equal ease and basis set convergence would not be an issue, which means that collision induced dissociation, photodissociation and similar processes on solid/liquid surfaces can be treated with ease using the time-dependent quantum mechanical (TDQM) approach. It took nearly three decades after the publication of Schrödinger's papers for the first numerical solutions to be obtained using computers Illiac and IBM-704 by Mazur and Rubin.5 The work was path breaking in that it computed the rate constant for a collinear (H, H2) exchange reaction using a model potential energy surface (PES) by solving the TDSE for the nuclear motion. It also laid the foundation for carrying out wave packet (WP) dynamics on one dimensional (1D) and two dimensional (2D) grids.
McCullough and Wyatt6 used the finite difference method for evaluating the second derivative of the wave function with respect to the spatial coordinates and finite difference and explicit methods for evaluating the first derivative of the wave function with respect to time for the collinear (H, H2) exchange reaction on a realistic PES. They were perhaps the best possible numerical approaches at that time, with the then available computational resources.
Glen E. Kellerhals,7 a senior PhD scholar in the research group of Professor Lionel M. Raff at Oklahoma State University, had estimated that he had spent US $40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 worth of computer time on an IBM system 360/65 machine in solving model collinear (A + BC) exchange reactions for completing his PhD thesis work in 1974. In contrast, Aditya Narayan Panda,8 a PhD student at the Indian Institute of Technology, Kanpur, in 2004 could compute the reaction probability values for the (He, H2+) exchange reaction in three dimensions (for total angular momentum J = 0) using the TDQMWP methodology on a Pentium IV machine with 256 MB RAM in about 4.5 h. In 2012, Sujitha Kolakkondy,9 another PhD student in the same lab, was able to carry out TDQMWP calculations for (He, H2+) reactive scattering in three dimensions for a number of J (= 0–70) (K = 0–10) states and compute reaction cross section values over a range of translational energy (Etrans = 0–4.7 eV) by using PCs and workstations in the lab. Such a development has been possible largely due to larger computer memory and increased computing speed becoming readily available in recent decades. Levitt has pointed out elsewhere10 how the price of computers and their physical size have come down (from a main frame computer occupying a large air conditioned hall to a laptop) by four orders of magnitude while the available computer memory and the CPU (central processing unit) speed have increased by four orders of magnitude, during the same period 1967–2013.
000 worth of computer time on an IBM system 360/65 machine in solving model collinear (A + BC) exchange reactions for completing his PhD thesis work in 1974. In contrast, Aditya Narayan Panda,8 a PhD student at the Indian Institute of Technology, Kanpur, in 2004 could compute the reaction probability values for the (He, H2+) exchange reaction in three dimensions (for total angular momentum J = 0) using the TDQMWP methodology on a Pentium IV machine with 256 MB RAM in about 4.5 h. In 2012, Sujitha Kolakkondy,9 another PhD student in the same lab, was able to carry out TDQMWP calculations for (He, H2+) reactive scattering in three dimensions for a number of J (= 0–70) (K = 0–10) states and compute reaction cross section values over a range of translational energy (Etrans = 0–4.7 eV) by using PCs and workstations in the lab. Such a development has been possible largely due to larger computer memory and increased computing speed becoming readily available in recent decades. Levitt has pointed out elsewhere10 how the price of computers and their physical size have come down (from a main frame computer occupying a large air conditioned hall to a laptop) by four orders of magnitude while the available computer memory and the CPU (central processing unit) speed have increased by four orders of magnitude, during the same period 1967–2013.
As decades went by and the time resolution of the experimental investigation of elementary chemical processes improved from milliseconds to micro-, nano-, pico- and femtoseconds, it made more sense to look at the time evolution of chemical dynamical systems.11,12 Although our thinking is “classical”, the dynamical processes at the atomic/molecular level are quantum mechanical in nature.13
Interestingly, quasi-classical trajectory (QCT) calculations were also initiated14 at about the same time as TDQM calculations and the former made much more rapid progress in modelling many elementary chemical reactions in the following years.15 Molecular dynamics (MD) simulations have become common and have been extended to large biomolecular systems in recent years.10
While QCT calculations accounted for much of the averaged observables in state-selected and state-to-state chemistry for a number of systems, quantal effects like resonances could only be accounted for through detailed time-independent quantum mechanical (TIQM) and TDQM calculations.16,17
Thanks to the sustained efforts of chemists in probing the transition state, “capturing” the transition state18,19 and identifying reactive scattering resonances experimentally20,21 became a reality. As more efforts went into “controlling” chemical reactions dynamically (rather than passively through initial state selection) in real time using laser pulses,22–25 it made more sense to follow a TDQM approach to investigate elementary chemical reactions.
Photo-excitation/dissociation processes also lent themselves to a dynamical description in real time.26 Increased experimentation in femtochemistry meant increased use of the time-dependent approach. These developments also warranted the inclusion of more than one electronic state and nonadiabatic coupling in dynamical investigations. Recent developments in the use of attosecond pulses in probing atomic and molecular processes27 require dealing with multi-electronic state dynamical processes in real time. Our earlier write ups28–32 and those of others33–37 on the TDQMWP approach outlined the motive behind the method and the developments in the methodology till then.
We present an overview of subsequent developments in the field and indicate the likely future directions for the area of research. Since this is not a review article, we do not review all the research papers published in the field. We restrict ourselves largely to what is called the grid method in this perspective, although we do point out the developments in combining it with other methods.
2 Theoretical background
Any problem in non-relativistic physics, chemistry and biology can, in principle, be solved by solving the TDSE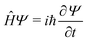 | (1) |
The TDQMWP approach is conceptually simple to adopt and straightforward to implement. It is easy to interpret the dynamical outcomes and to compare the results with (experimental) observables. It consists of (i) defining the initial state of the system in terms of the wave function, Ψ(0), for example, on a grid in suitable coordinates, (ii) evolving the wave function, Ψ(t), with time, given the Hamiltonian of the system and (iii) analysing the wave function at different time intervals to obtain insight into the dynamics and computing the observables for comparing with experimental results at the “end” of the time evolution. The size of the grid in the TDQMWP method depends on the choice of problem under investigation. For vibrational spectra of a diatomic molecule in its low vibrational states, for example, it is enough to concentrate on a set of grid points along the internuclear distance (r) in the vicinity of the potential energy minimum. For investigating associative/dissociative processes, one needs to consider grid points over an extended range of r. While the magnitude of dV/dr (force) varies gradually with a variation in r for large r, it varies dramatically for small r. Therefore, in principle, one can choose a coarse mesh for large r and a fine mesh for small r. In practice, this is not easily implementable. Some authors38 have used a floating grid. But this is not simple. Unless one is careful, the results may not be time reversible. Choi and Vaníček39 have come up with a strategy to include the spatial grid in the time evolution, to make sure that the evolution is time reversible.
While one can use a large number (64/128/256/512) of grid points in one dimension, it becomes difficult to keep the number of grid points large in higher dimensions. While an A + BC exchange reaction in three dimensions calls for the use of three variables, larger polyatomic systems require TDQM investigations in larger dimensions. That explains why it took time for the TDQMWP method to become a practical tool in the study of chemical reactions and why it was restricted initially to systems involving very few atoms. Before getting into the details of the above mentioned three steps in the grid method, it is important to discuss the difficulties involved in formulating the potential energy surface (PES) for the system under consideration and the choice of coordinates. For a diatomic molecule (or ionic species) in its ground electronic state, there is only one coordinate that the potential energy depends upon, that is, r. For polyatomic molecules, there are 3n − 5(6) vibrational degrees of freedom, depending upon whether the molecule is linear or nonlinear. For small amplitude motions, normal coordinates40 might suffice. But for large amplitude motions and for events involving bond breaking and bond forming, some other coordinates have to be used.
For a reactive A + BC (triatomic) system in collinear geometry, scaled and skewed coordinates (x, y) were developed long ago41 to describe the motion equivalently to that of a single particle of mass 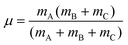 in (x, y) space, where
in (x, y) space, where
x = rAB + βrBC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
y = βr2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (3) |
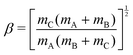 | (4) |
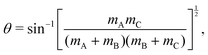 | (5) |
For noncollinear geometries, one could use the mass-scaled Jacobi coordinates (R, r, γ) illustrated in Fig. 1. It is evident that there is more than one possible set of Jacobi coordinates, depending upon the arrangement channel. The difficulty in choosing the right set of Jacobi coordinates at different stages of a collision event can be circumvented by working in Delves coordinates42 in two dimensions and in hyperspherical coordinates (ρ, θ, ϕ) in three dimensions. The latter coordinates are defined in many different ways in the literature.43–47 However, the most often used ones are due to Morse and Feshbach,43 who defined them in terms of the Jacobi vectors ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) and
and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) as
as
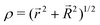 | (6) |
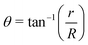 | (7) |
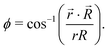 | (8) |
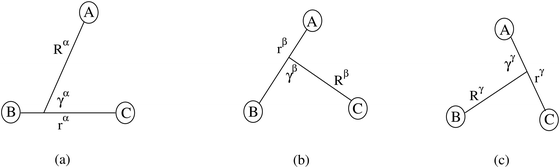 | ||
| Fig. 1 The Jacobi coordinates for the α, β and γ arrangement channels of the A + BC collisional system. | ||
The Hamiltonian can be written in any of the stated coordinates for a given molecular process. For example, the Hamiltonian of the A + BC collisional system in the reactant channel (α-channel in Fig. 1) mass-scaled body-fixed Jacobi coordinates (R, r, γ) is given by48–51
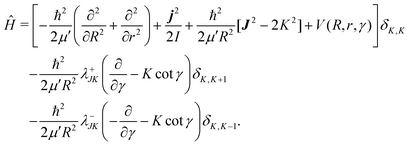 | (9) |
In the above equation, j is the rotational angular momentum operator of the BC diatom, J is the total (three-body) angular momentum operator, V(R,r,γ) is the interaction potential, 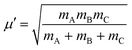 is the three-body scaled reduced mass and
is the three-body scaled reduced mass and 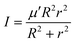 is the three-body moment of inertia. The quantity K = −J, …, 0, …, +J is the projection of J and also j on the body-fixed Z-axis and
is the three-body moment of inertia. The quantity K = −J, …, 0, …, +J is the projection of J and also j on the body-fixed Z-axis and 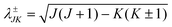 . The last two off-diagonal terms in eqn (9) couple the various K states in the body-fixed frame and are known as Coriolis coupling terms.52 When these terms are neglected, one arrives at the well-known coupled-states or centrifugal sudden (CS) approximation.53,54 Within this approximation K is a good quantum number and is conserved in the body-fixed Jacobi frame. This approximation simplifies the J ≠ 0 calculations by reducing the dimensionality of the problem from four to three.
. The last two off-diagonal terms in eqn (9) couple the various K states in the body-fixed frame and are known as Coriolis coupling terms.52 When these terms are neglected, one arrives at the well-known coupled-states or centrifugal sudden (CS) approximation.53,54 Within this approximation K is a good quantum number and is conserved in the body-fixed Jacobi frame. This approximation simplifies the J ≠ 0 calculations by reducing the dimensionality of the problem from four to three.
Generating PESs of chemical accuracy (±1 kcal mol−1) or of spectroscopic accuracy (±1 cm−1) by carrying out high level ab initio quantum chemical calculations for any polyatomic system is a challenging task. Some of the nuances involved in the process have been discussed recently by Dawes and Ndengué.55 Fitting an analytic function to the computed potential energy (PE) values or interpolating/extrapolating them numerically is an additional challenge.56–58 Briefly, the potential energy curve for a diatomic species near the potential minimum (rm) can be approximated as that of a harmonic oscillator,
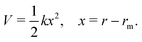 | (10) |
For larger displacements, suitable analytic functions can be fitted, the simplest being the Morse potential.59 Several other analytic functions have been proposed over the years. Some of them have been reviewed elsewhere.56–58 For triatomic reactive systems, the London–Eyring–Polanyi–Sato (LEPS) formalism60–62 served as the basis for analytic fitting of the PESs in the earlier years. A diatomics-in-molecules (DIM) approach63 was also used for some systems. As ab initio quantum chemical methods improved and the ease of computing ab initio PE values increased and the cost of generating them came down, one realized that the LEPS and DIM formalisms did not have enough flexibility in them to fit the ab initio PE values. Many body expansion methods were proposed for fitting ab initio PESs.64 That is, the PES for a triatomic system, for example, was broken into 1-, 2- and 3-body terms. While the 1-body (atomic) energy could be taken as zero (or constant), the 2-body term for each diatomic component could be reproduced by one of the analytic functions mentioned above. The 3-body term was invariably expanded in terms of a polynomial and a range function that died off at long range. Some of the earlier efforts have been described by Murrell et al.57 and Aguado and Paniagua.65 For a programme implementation of the many body approach for systems containing up to four atoms, the reader may see the recent paper by Rocha and Varandas.66 Considerable effort has been expended in recent years in fitting permutationally invariant polynomials (PIPs) to ab initio data for larger (up to 11 atoms) systems.67–69 Significant progress has been made in using artificial neural networks (ANN) methods and a hybrid of the PIP and ANN methods for fitting a large number of points on the PES.68–71 The method of Gaussian Process Regression (GPR) seems like an attractive alternative for fitting a PES with a limited number of data points.72,73 Some of the earlier efforts in numerical interpolation of ab initio PES points included 1D/2D/3D splines.74 The application of the spline-fitting approach to higher dimensions has been discussed by Patricio et al.75
In principle, if we know the coordinates and the spatial grid in which the time evolution of the wave function is to be carried out, it is a onetime effort to compute the PES on that grid of points in the coordinate space. In practice, however, one has to see which set of coordinates suits the system under investigation the best and alter the sampling of the grid as the work progresses. The concept of a potential energy curve/surface breaks down when the Born–Oppenheimer (BO) approximation breaks down.76–81 One has to deal with a number of electronic states and nonadiabatic couplings between them (see below). Double many body expansion methods have been proposed to deal with such systems.82
In what follows, we describe the three steps involved in a standard TDQMWP approach, first within the BO approximation (see Sections 2.1, 2.2 and 2.3), and then when we go beyond the BO approximation (see Section 2.4).
2.1 Step 1: choosing the initial wave function
For a particle moving in the presence of a potential well or a barrier, the initial state could be represented by a minimum uncertainty Gaussian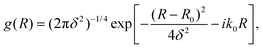 | (11) |
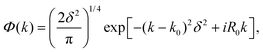 | (12) |
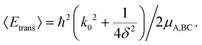 | (13) |
An optimal width parameter of δ = 0.25–1 a.u. of the WP is chosen in most studies. If the WP has a narrow width in momentum space, it would be spread out in position space, which would require a large spatial grid, which in turn would necessitate large computer memory and time for any dynamical study. On the other hand, if the WP is narrow in position space, it would be spread out in momentum space, compromising the energy resolution for the reaction attributes. The location of the WP is also critical in that it should be away from the interaction region and yet not too close to the outer edge of the grid to prevent reflection of the WP from the edge(s).
The initial condition (t = 0) for an A + BC reactive system
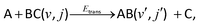 | (R1) |
| Ψ(r,R) = g(R)ϕv,j(r). | (14) |
The translational part, g(R), is usually taken as a (minimum uncertainty) Gaussian (see eqn (11) above) and ϕv,j(r) is the vib-rotational wave function of the diatomic molecule BC. To calculate reactive scattering cross sections over an energy range more accurately, the use of a sinc wave packet was proposed by Hankel et al.83 In contrast to the Gaussian wave packet, the amplitude of the wave packet remains nearly constant over an energy range in the sinc wave packet. For photoabsorption/dissociation processes, the wave function of the initial (v, j) state of the molecule in its ground electronic state is modified using the transition dipole moment and taken as the initial wave function for dynamics on the excited state(s). For molecule–surface systems, similar suitable initial wave functions are chosen for studying the time evolution of the system.
2.2 Step 2: time evolution of the wave function
The evolution of a dynamical system can be followed in real time by solving the TDSE. This simple looking first-order differential equation can be solved readily if the application of the Hamiltonian operator on Ψ can be computed readily. Formally,| Ψ(t) = U(t,t0)Ψ(t0), | (15) |
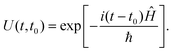 | (16) |
In the absence of an external field, Ĥ can be written as
Ĥ = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) + + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) | (17) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the kinetic energy operator and
is the kinetic energy operator and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the potential energy operator. Unfortunately,
is the potential energy operator. Unfortunately, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and
and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) do not commute with each other as the former is “local” in momentum space and the latter is “local” in position space. In the second-order split-operator method,84 the evolution operator can be applied repeatedly over several slices (Δt) through
do not commute with each other as the former is “local” in momentum space and the latter is “local” in position space. In the second-order split-operator method,84 the evolution operator can be applied repeatedly over several slices (Δt) through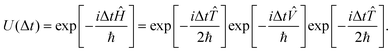 | (18) |
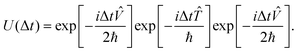 | (19) |
The split-operator method is norm, ||Ψ(t)||, conserving. Therefore, one can easily check the robustness of the algorithm by checking the norm of the wave function. Robustness here refers to numerical stability. It also raises the question of how “long” the time evolution can be carried out numerically accurately. This is often checked by evolving the final wave function back in time and ensuring that it coincides with the wave function we started with. Tal-Ezer and Kosloff85 showed that “exact” results could be obtained using the Chebyshev polynomial method. There have been several refinements made to the split-operator approach over the years. A detailed discussion of the increased accuracy of higher order split-operator methods for a one dimensional (Morse) potential and (A + BC) reactive scattering has been given by Sun et al.86 They also compared the efficacy of the split-operator methods with the Chebyshev polynomial method. To obtain a spectral resolution of (±1 cm−1), for example, in the dynamical attributes, the uncertainty principle requires that the time evolution be carried out for at least 5300 fs (5.3 ps). The second order split operator method and the Chebyshev polynomial method are numerically stable and robust enough for such long time evolution. Braun et al. have shown87 that the second order split operator method was stable enough for time evolution of the order of nanoseconds and yielded eigenfunctions and eigenvalues to acceptable accuracy. Sun et al.86 have shown that for systems involving deep potential wells and/or a large number of narrow resonances, one may (have to) resort to higher order split operator methods.
When Ĥ is explicitly time-dependent, time ordering is important in arriving at Ψ(t). Pfeifer and Levine88 and Peskin and Moiseyev89 used the (t, t′) method for this purpose. Very recently, Balanarayan and coworkers90 have proposed a (t, t′, t′′) method to obtain exact results for molecules interacting with short pulse lasers. One of the bottlenecks in solving the TDSE has been in determining the operation of the kinetic energy operator on Ψ for the reasons mentioned earlier. By switching to the momentum representation, the kinetic energy part can be evaluated to machine accuracy through the fast Fourier transform (FFT) route84,91,92
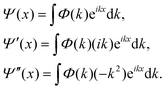 | (20) |
The second order spatial derivative of the wave function is thus obtained by Fourier transforming the wave function Ψ(x), multiplying the Fourier transform Φ(k) by (−k2) and taking an inverse Fourier transform of the resultant product. Although this approach works well in Cartesian coordinates for a localised wave function in an extended grid, the FFT algorithm transforms a large number of zeroes into zeroes at every step of time evolution.93 A simple way to alleviate this problem is to choose a floating grid so that the FFT operation is carried out in limited space. This would save substantial computing time and memory. The difficulty with this approach is that we need to know in advance how the spread in the wave packet in (r, R)-space would be. Mowrey and Kouri94,95 suggested the use of an L-shaped grid to alleviate the problem. Values of the initial state selected (but summed over the final states) probability and cross section are obtained by computing the flux (![[Doublestruck F]](https://www.rsc.org/images/entities/char_e169.gif) ) across a dividing line in the product channel.96
) across a dividing line in the product channel.96
Unfortunately, because of the finite size of the grid, part of the wave packet would get reflected from the edges. This is prevented by extending the range of the grid, which has its limitations. An alternative is to use an absorbing potential in the form of a negative imaginary potential (NIP) added to the Hamiltonian near the grid edges and this was proposed by various practitioners in the field.48,97–105 Despite the widespread use of NIPs, they were found to cause instability of various time-evolution schemes.106,107 The problem arises because the Hamiltonian becomes non-Hermitian in their presence. Mahapatra and Sathyamurthy carried out a detailed analysis and came up with a real damping function of a sine type as an alternative105
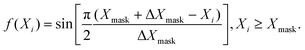 | (21) |
The discrete variable representation (DVR) method, originally introduced in the area of molecular reaction dynamics by Light and co-workers,108 involves expanding the wave function Ψ(x,t) in an orthonormal basis set {ϕi(x), i = 1,…,N}:
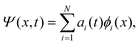 | (22) |
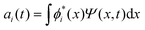 .
.
It uses a quadrature rule, consisting of a set of quadrature points {xi, i = 1,…,N} and the corresponding weights {wi, i = 1,…,N} such that
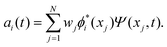 | (23) |
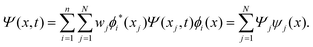 | (24) |
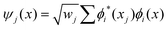 | (25) |
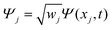 | (26) |
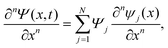 | (27) |
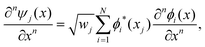 | (28) |
Although the DVR method scales as N2 when compared to the FFT method, which scales as N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) N, the former has the distinct advantage in that there is no need to transform the wave function to momentum space and back at every timestep. It is also possible to keep the number of basis functions required in the expansion to a minimum if an appropriate basis set is chosen keeping in mind the nature of the potential.
N, the former has the distinct advantage in that there is no need to transform the wave function to momentum space and back at every timestep. It is also possible to keep the number of basis functions required in the expansion to a minimum if an appropriate basis set is chosen keeping in mind the nature of the potential.
2.3 Step 3: analysing the time evolved wave function
| C(t) = 〈Ψ(0)|Ψ(t)〉, | (29) |
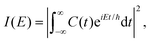 | (30) |
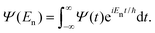 | (31) |
The Fourier transform involves time in the range [−∞, ∞]. In reality, the time evolution is carried out for a finite time T. Using time reversal symmetry, the integral can be written as if the time evolution were carried out for 2T.110 This helps in improving the energy resolution of the eigenstates as the length of the time evolution is related to the energy resolution through the uncertainty principle. Often one uses a window function w(t) to account for the finite value of T and to ensure that spurious eigenvalues are not obtained.
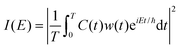 | (32) |
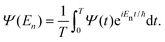 | (33) |
It is common to use a (Hanning) window function:111
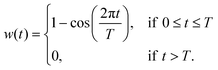 | (34) |
This approach reveals the quasi-bound states and hence the transition state resonances as well. The size and the range of the grid are often extended and the time evolution repeated to ensure that the results obtained are converged with respect to the (finite) range of the grid used.
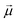 ·
·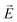 :
: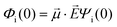 | (35) |
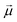 is the transition dipole vector and E the electric field of the photon. The time evolution of the promoted state is governed by the Hamiltonian (Ĥex) of the excited state(s) and
is the transition dipole vector and E the electric field of the photon. The time evolution of the promoted state is governed by the Hamiltonian (Ĥex) of the excited state(s) and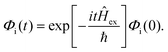 | (36) |
The autocorrelation function Cii(t) would then be
| Cii(t) = 〈Φi(0)|Φi(t)〉. | (37) |
The absorption spectrum σA(ω) would be:
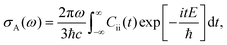 | (38) |
| Cfi(t) = 〈Φf|Φi(t)〉, | (39) |
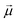 ·
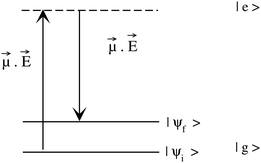
·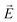 Ψf is the wave function corresponding to the (final) vibrational state f in the ground electronic state (see Fig. 2 for an illustration). Raman amplitude αfi(ω) is obtained from
Ψf is the wave function corresponding to the (final) vibrational state f in the ground electronic state (see Fig. 2 for an illustration). Raman amplitude αfi(ω) is obtained from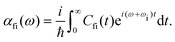 | (40) |
The quantity ωi in eqn (40) is the frequency of the incident radiation. The “observable” Raman scattering intensity or the Raman excitation profile Ifi(ω) follows:
| Ifi(ω) ∝ ωωs3|αfi(ω)|2, | (41) |
The utility of the above mentioned methodology in studying photo-excitation processes involving one or more excited states in one dimension has been demonstrated by Mahapatra et al.31 For a standard treatment of the subject, the reader may refer to ref. 24 and 113.
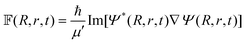 | (42) |
| qJK′(R′, r′, γ′, t + τ) = −qJK′(R′, r′, γ′, t − τ) + 2H′qJK′(R′, r′, γ′, t). | (43) |
In the above equation qJK′ is the real part of the initial WP that is defined in the reagent Jacobi frame (as above) and transformed to the product Jacobi frame (the primed quantities) prior to propagation. The quantity K′ is analogous to K, defined in the product Jacobi frame. The scaled Hamiltonian in the product Jacobi coordinate is denoted by Ĥ′.121 To start the iteration eqn (43) requires qJK′ at the first time step τ. The imaginary part of the WP is utilized once for this purpose and is evaluated by
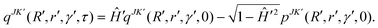 | (44) |
The action of the operator 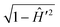 on pJK′ in eqn (44) is carried out by expanding it in terms of Chebyshev polynomials of the first kind.37 In contrast to the flux operator method in the reagent Jacobi coordinates, the analysis of the product states is done by projecting the time evolved WP on the vib-rotational wave function of the product on an analysis line in the product channel. The resulting time-dependent coefficients are Fourier transformed to the energy domain and finally the energy dependent scattering matrix elements are derived. This scheme was quite successful in calculating the reaction cross section for scattering systems of varying complexity.121,123,124 The salient features of the WP propagation within the TDQM framework on a grid in the reagent or product Jacobi coordinates have been reviewed by Balint-Kurti.37 Various approximate schemes introduced in the literature from time-to-time to deal with photodissociation and reactive scattering problems were also discussed by Balint-Kurti.37
on pJK′ in eqn (44) is carried out by expanding it in terms of Chebyshev polynomials of the first kind.37 In contrast to the flux operator method in the reagent Jacobi coordinates, the analysis of the product states is done by projecting the time evolved WP on the vib-rotational wave function of the product on an analysis line in the product channel. The resulting time-dependent coefficients are Fourier transformed to the energy domain and finally the energy dependent scattering matrix elements are derived. This scheme was quite successful in calculating the reaction cross section for scattering systems of varying complexity.121,123,124 The salient features of the WP propagation within the TDQM framework on a grid in the reagent or product Jacobi coordinates have been reviewed by Balint-Kurti.37 Various approximate schemes introduced in the literature from time-to-time to deal with photodissociation and reactive scattering problems were also discussed by Balint-Kurti.37
Yet another approach is to use a reactant coordinate based (RCB) scheme.125,126 As mentioned earlier, one way to avoid the channel-dependent Jacobi coordinates is to work in hyperspherical coordinates. The number of papers published using hyperspherical coordinates in the TDSE framework is rather limited127–131 because of the difficulty in the final state analysis. Another practical aspect of the TDQMWP approach (applicable to the TIQM approach as well) is the number of J values for which the calculations have to be repeated. It is also known that with an increase in the value of J, the initial wave packet has to be located farther out in the reactant channel because of the centrifugal barrier. This means that the grid has to be extended farther for calculations for large J. Understandably, some of the earlier 3D calculations were carried out for J = 0 only. With an increase in the computational resources becoming available, calculations were carried out for larger J until the results converged with respect to J, but using the centrifugal sudden approximation. Later calculations included Coriolis coupling, but were limited to small helicity (K) numbers.9,132–135 Parallel computing resources have enabled the inclusion of large J and K numbers.52,136–138 Goldfield and Gray52 devised an algorithm for efficient parallelization of K substates. Later it was employed to calculate the ICS for the H + O2 reactive system by Meijer and Goldfield.139 In recent years, the RWP method has been used to carry out large scale converged parallel calculations.123,124 However, there has been no report in the literature of results that are both J- and K-converged so far. The distinct advantage of the TDQMWP approach is that the reaction attributes over a range of Etrans can be computed in one go, in contrast to the TIQM approach, which requires the massive calculations to be repeated for each Etrans value that we are interested in. Unfortunately, the TDQMWP method is not suited for investigations at low energies as it would require a larger spread in the wave packet in the coordinate space and would be relatively time consuming. The TIQM method, on the other hand, has an advantage in that the number of vibrotational channels to be included in the dynamics would be limited at low Etrans.
2.4 Adiabatic to nonadiabatic via the diabatic route
The vast majority of early developments of the TDQMWP methodology were restricted to chemical processes occurring on a single adiabatic PES. Increased realization of the importance of vibronic coupling in electronic spectroscopy and photo-dissociation processes led to a treatment of reactive chemical processes on coupled multi-sheet PESs by the TDQMWP technique in subsequent years.Historically, the seminal paper of von Neumann and Wigner140 laid the foundation for the study of nonadiabatic interactions in 1929 and the importance of the crossing of PESs was recognized in the 1930s.141–143 Nearly two decades later, pioneering contributions by Herzberg and Longuet–Higgins144–146 led to the development of new concepts in the area. The field underwent monumental growth thereafter and a variety of molecular processes have been studied by several groups77,147–160 over the years. A review of all the developments on PES crossing is beyond the scope of the present perspective. Therefore, we focus on the essential aspects of treating the nuclear dynamics on coupled electronic states by the TDQMWP methodology here.
The immediate and the most fundamental consequence of crossing of PESs is a break-down of the Born–Oppenheimer (BO) approximation.161,162 The electronic and nuclear motions get entangled and they occur concurrently. In the framework of the Born–Oppenheimer–Huang formalism,161,162 the nuclear Schrödinger equation in its time-independent form reads
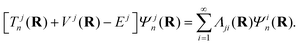 | (45) |
In the above eqn (45), n is the nuclear index. The quantity Tjn(R) is the nuclear kinetic energy operator of the jth electronic state depending on the set of nuclear coordinates R. The adiabatic potential energy of the jth electronic state resulting from the solution of the electronic Schrödinger equation,
| Hjel(r;R)ψjel(r;R) = Vj(R)ψjel(r;R), | (46) |
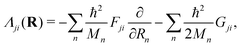 | (47) |
| Fji(R) = 〈ψjel(r;R)|∇n|ψiel(r;R)〉, | (48a) |
| Gji(R) = 〈ψjel(r;R)|∇n2|ψiel(r;R)〉, | (48b) |
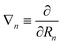 . It is obvious from eqn (48a) and (48b) that when Fji and Gji are non-zero, the electronic states i and j are coupled through nuclear motion. This dynamical coupling (Λji) is zero in the BO approximation. When the adiabatic potential energy, Vj(R), is corrected by retaining the diagonal elements of the scalar coupling (Gji), it is known as the Born–Huang (BH) correction.162 Using the Hellmann–Feynman theorem,163 the elements of the vector (derivative) coupling operator (cf., eqn (48a)) are given by148,151
. It is obvious from eqn (48a) and (48b) that when Fji and Gji are non-zero, the electronic states i and j are coupled through nuclear motion. This dynamical coupling (Λji) is zero in the BO approximation. When the adiabatic potential energy, Vj(R), is corrected by retaining the diagonal elements of the scalar coupling (Gji), it is known as the Born–Huang (BH) correction.162 Using the Hellmann–Feynman theorem,163 the elements of the vector (derivative) coupling operator (cf., eqn (48a)) are given by148,151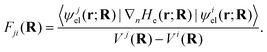 | (49) |
At the point of degeneracy of electronic states, Vj(R) = Vi(R), and Fji(R) becomes singular. Since the nonadiabatic coupling operator is inversely proportional to the nuclear mass (cf.eqn (47)), for widely separated electronic states the mass factor ensures that Λ is negligible and the BO approximation is justified. However, if the electronic states are closely spaced in energy, the denominator of eqn (49) outweighs the mass factor, leading to a break-down of the BO approximation.
The electronic representation discussed above is referred to as the adiabatic representation and the coupling between states is defined by the off-diagonal elements of the nuclear kinetic energy operator, known as nonadiabatic coupling terms (NACTs) or nonadiabatic coupling matrix elements (NACMEs). Furthermore, the participating electronic states in this representation lack analytic continuation owing to the diverging derivative of the electronic wave function.148 Therefore, the adiabatic representation is ill-suited for a numerical solution of the Schrödinger equation (cf.eqn (1)) when the nonadiabatic coupling becomes important.
To circumvent the limitations of the adiabatic representation, one resorts to a diabatic representation introduced by Litchen164 in the context of ion–atom collisions. Diabatic electronic states were defined by Smith165 in terms of differential equations of the adiabatic-to-diabatic transformation (ADT) matrix requiring the singular derivative coupling of the adiabatic basis to vanish in this representation. This work focused on atom–atom collisions and Baer and coworkers166,167 extended it to atom–diatom collisions. Mathematically, diabatic electronic states are obtained by an orthogonal transformation of a subset of the complete set of adiabatic states as
| Ψd = SΨad, | (50a) |
| Hd = SHadS† = Tn1 + U. | (50b) |
The superscripts d and ad refer to the diabatic and adiabatic representations, respectively, and S defines the ADT matrix.165 For a two state problem, the ADT matrix is given by
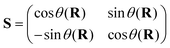 | (51) |
The ADT angle θ(R) depends on the set of nuclear coordinates R. Eqn (50b) above reiterates that the nuclear kinetic energy operator is diagonal (1 is a 2 × 2 diagonal unit matrix) and the electronic potential energy (U) contains off-diagonal elements in the diabatic representation. It is important to note that diabatic electronic states are not eigenstates of the electronic Hamiltonian (cf.eqn (46)) and are not “observables”. However, the analytic continuation of the electronic energy is restored in this representation (as the diverging derivative coupling is removed). As a result, the diabatic representation is amenable to numerical application. The requirement that Fji (j ≠ i) = 0 in eqn (48a) in this new basis leads to the following differential equation of the ADT angle166
| ∇θ(R) + Fji = 0. | (52) |
For a one dimensional problem (a diatomic system), the above equation can be solved trivially for θ(R) with the aid of ab initio computed NACTs, Fji.168 For a multi-dimensional problem, it was proposed to carry out the integration in a stepwise fashion along each coordinate. The fact that the final result is invariant to the order of such sequential operations requires that ∇ × F = 0 (F being the derivative coupling matrix), known as the curl condition.166 The summation on the right hand side of eqn (45) runs over the complete set of adiabatic electronic basis states. The curl condition is satisfied only when this set is complete. The situation is trivial in diatomic systems for which there is only one coordinate and there is no curl condition. However, for polyatomic systems, construction of diabatic electronic states by satisfying the curl condition is not possible when a small subset of interacting electronic states is considered for the convenience of numerical computation.169
The above mentioned difficulties led colleagues to develop several approximate schemes to construct diabatic electronic states. Readers are referred to several review articles that have appeared over the years170–172 for a comprehensive account of the subject. We mention here only one such scheme introduced by Thiel and Köppel173 for an (E ⊗ e)-Jahn–Teller (JT) system and later extended to a more general case introducing the concept of regularized diabatic states.174 In these schemes, the diabatic states are constructed from the adiabatic potential energies by circumventing the tedious calculations of NACTs. The important aspect of the removability of the leading derivative coupling terms in the neighborhood of the intersection seam is ensured in these schemes through numerical tests and practical applications.173,174 The results presented later for the H + H2 reactive system in this perspective were obtained by utilizing this scheme of diabatization. It is worth noting here that the cusp of the potential energy curves in one dimension as defined by the singular derivative coupling evolves into conical intersections (CIs) of PESs in higher dimensions. The surfaces remain degenerate along a hypersurface in n − 2 dimensional (n is the number of nuclear degrees of freedom) space and the locus of the degeneracy defines the seam of the CIs. CIs of PESs are known to be ubiquitous and they open up a variety of new mechanistic pathways in the dynamics of polyatomic molecular systems.77,145,149,151,157–160,175,176
The second major consequence of potential energy curve crossings due to CIs is that the adiabatic electronic wave function ceases to be single-valued. It was shown by Herzberg and Longuet-Higgins145 that a real adiabatic electronic wave function changes sign when it traverses around a CI in a closed loop an odd number of times. To restore the single-valued nature of the wave function, Longuet-Higgins and coworkers144,146 introduced an additional phase factor to the wave function with the requirement that it also changes sign when transported along the closed loop around a CI. Such a geometry dependent phase factor is known as a Longuet-Higgins phase or geometric phase146,177 or in a more general context a Berry phase178 in the literature. It is important to note here that prior to the work of Longuet-Higgins (and Berry) such a phase change was originally discovered by Pancharatnam in crystal optics.179
Subsequent to the work of Longuet-Higgins and coworkers,144,146 Mead and Truhlar150 considered two possibilities: (1) to impose a multi-valued boundary condition on the nuclear wave function and (2) to multiply the nuclear wave function by an extra phase factor, which changes sign upon an excursion around a CI in a closed loop. Both the possibilities have been examined rigorously by various practitioners in the field. Possibility (1) is well-studied in a TIQM framework and is cumbersome to implement as a basis set expansion of the nuclear wave function on a grid in a TDQMWP study. Possibility (2) is easily implementable in the TDQMWP framework. When possibility (2) is considered, the nuclear Schrödinger equation acquires a vector potential.150 This topological phase change has been discussed by many researchers in different contexts (see the review article in ref. 180). For a two-state system, Baer181 showed that the Longuet-Higgins phase144,146 is not arbitrary and is given by a first-order differential equation identical to the one satisfied by the ADT angle
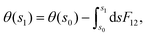 | (53) |
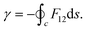 | (54) |
It is evident that the nonadiabatic coupling operator Λ contains contributions from the derivative coupling, BH correction and the geometric phase (GP). In a coupled electronic state dynamics study, it is necessary to include all three factors in the TDQMWP formalism discussed above for the single surface case. Since the adiabatic electronic representation is not suitable for numerical applications, the TDSE is numerically solved in a diabatic representation. However, it is more realistic to prepare the initial state in the adiabatic representation and to carry out the propagation in the diabatic representation. The final analysis can be done in either of the two representations. The time evolution schemes, viz., split-operator scheme, Chebyshev polynomial method, etc. are extended to the coupled state representation. For further numerical and technical details of the solution of the TDSE in a coupled diabatic representation, readers are referred to ref. 183. In a reaction dynamics study the quantum flux operator can be represented in a diabatic as well as in the adiabatic electronic representation.184,185 Since the kinetic energy operator is diagonal in a diabatic basis, the flux operator also has the same property. The total reactive flux in this representation is the sum of the reactive flux components calculated at the product asymptote of each diabatic state. The flux operator, on the other hand, contains off-diagonal elements as the kinetic energy operator is non-diagonal in the adiabatic representation. The off-diagonal elements of the flux operator can make contributions when the product channel in each coupled electronic state is open at a given energy. It is, however, found that the reaction probability values calculated in either way are identical in magnitude.184,185 The application of the above formalism to study the nuclear dynamics in triatomic hydrogen is discussed further below.
3 Applications
3.1 Bound states of molecular species
Although the bound and the quasi-bound states of molecular species could be determined by solving the TISE, one could solve the TDSE and obtain the same results with comparable accuracy. In addition, one could identify the nature of resonances, if any, and estimate their lifetimes too.Perhaps the first demonstration of the utility of the TDQMWP method in computing the bound states for a molecular system was for a 1D double well potential and 2D Henon–Heiles potential.84 That was followed by the computation of bound states for SO2, O3 and H2O.91
Maiti et al.186 found only one bound state for HeH2+ on the McLaughlin–Thompson–Joseph–Sathyamurthy (MTJS) PES, but one set of two peaks for HeHD+ and another set for HeDH+, in three dimensions, for J = 0 using the TDQMWP approach. Interestingly, TDQMWP calculations187 on the Palmieri et al. PES revealed several bound states for HeH2+ in three dimensions for J = 0. In addition, their studies revealed a number of quasibound states that could be identified as shape resonances or Feshbach resonances (see above). They could also determine the eigenfunctions of several quasibound states and investigate their characteristics in terms of hyperspherical modes and periodic orbits.188 Recently, Koner et al.189 have determined the bound states of HeH2+ for J = 0 as well as J > 0 using their newly constructed PES.
Panda and Sathyamurthy190 reported the bound states of He2H+ and He2D+ in three dimensions on a newly computed ab initio PES. They found a slightly larger number of bound states than what was reported by Lee and Secrest earlier.191 Very recently, Koner et al.192 have computed the bound states of N3+ in three dimensions, for J = 0, using the TDQMWP method on a newly computed ab initio PES and found that the resulting lowest 20 bound states were in excellent agreement with those obtained using the TIQM method and DVR3D code available.193
3.2 Reactive scattering on a single (adiabatic) PES
A detailed dynamical theory would predict the state-to-state differential cross section at the molecular level and rate coefficients at the macro level and other observables at an intermediate level for a chemical reaction. The first TDQMWP calculation5 in the year 1959 predicted the rate coefficient for a model collinear (H, H2) exchange reaction. Subsequent TDQMWP studies have been able to predict the reaction probabilities in two and three dimensions and differential and integral cross sections for the reaction| H + H2 → H2 + H | (R1) |
The reaction
| H− + H2 → H2 + H− | (R2) |
A new ab initio PES was generated for reaction (R2) in three dimensions and fitted to an analytic function by Panda and Sathyamurthy.198 TDQMWP studies using an L-shaped grid for J = 0 showed minor oscillations in the PR(Etrans) curve for v = 0 on the Panda–Sathyamurthy PES and were superimposable on the results obtained using the TIQM method and the ABC code published by Skouteris et al.199 The number and magnitude of oscillations in the PR(Etrans) curve increased with an increase in v from 0 to 1 and 2 and decreased in going from j = 0 to 1 to 2. Our results were comparable to the results of Jaquet and Heinen200 on the SM surface and differed significantly from the results of Mahapatra201 on the DIM surface. Understandably, the latter surface is semi-empirical whereas the SM surface is ab initio.
Panda et al.202 extended their studies by including J values up to 40 and 60 for (H−, H2) collisions and isotopic variants (H−, D2) and (D−, H2) and computed integral reaction cross section values. The results for (H−, D2) were comparable to the experimental results of Zimmer and Linder203 for Etrans ≤ 1.5 eV and those of Huq et al.204 at 3.0 eV. Our results for both (H−, D2) and (D−, H2) were significantly larger than the more recent experimental results of Haufler et al.205 Giri and Sathyamurthy206 examined the influence of j on the integral reaction cross section for both (H−, D2(v = 0)) and (D−, H2(v = 0)) collisions, within the centrifugal sudden approximation, and found that the j-weighted integral reaction cross section values were in good agreement with the experimental results of Zimmer and Linder for Etrans up to 1.5 eV and with the results reported by Haufler et al. for Etrans < 1.0 eV. It is worth pointing out that the experimental results of Haufler et al. showed a lower reaction threshold than what was predicted by theory.
Our group has investigated the dynamics of the exchange reaction
| He + H2+ → HeH+ + H | (R3) |
| He + HD+ → HeH+ + D; HeD+ + H | (R4) |
| He + H2+ → He + H + H+ | (R5) |
The very first TDQMWP study of reaction (R3) was modest in its approach and scope.207 It investigated the dynamics of the exchange reaction in collinear geometry on a limited grid using a spline-fitted ab initio PES and obtained average reaction probability values for the vibrational states v = 0, 1, 2. Subsequently, TDQM studies208 were carried out on the MTJS surface209,210 and it was shown that they could yield average reaction probability values in agreement with the averaged TIQM results on the same surface.
This study208 used the FFT method for evaluating the second derivative of the wave function with respect to the spatial coordinates and the second order finite difference method for evaluating the temporal derivatives. A special feature of this investigation was the use of different grid sizes (64 × 64, 128 × 64, 128 × 128, and 256 × 256) to ensure convergence of the results and minimization of errors due to reflection of the wave function from the edges of the grid. More refined studies were carried out on a 256 × 128 grid using the FFT route for the spatial derivatives and Chebyshev polynomial for the time propagation.211 Using the wave function splitting algorithm of Heather and Metiu117 and an absorbing boundary in the exit channel,99 energy resolved reaction probabilities were obtained for different vibrational states. In addition, the study mapped the quantal flux patterns during the course of the collision event. Subsequent studies by the same authors212 using a 192 × 128 spatial grid and a Lanczos procedure213,214 for time evolution of the wave function coupled with time–energy mapping of the flux demonstrated the power of the TDQMWP method in reproducing the highly energy resolved reaction probability results for different vibrational states of H2+ reported by Sakimoto and Onda215 using the TIQM approach. Many of the oscillations in the plots of PRversus Etrans for the exchange reaction were identified earlier as Feshbach resonances arising from quasibound states supported by vibrationally adiabatic potentials.216 Quasiclassical trajectory calculations for the collinear (He, H2+) reaction revealed bands of reactive and nonreactive trajectories and a number of chaotic trajectories with fractal characteristics.217
Time evolution of a chosen quantum mechanical wave packet on a 256 × 256 grid in mass-scaled Jacobi coordinates for the collinear geometry accompanied by computation of the autocorrelation function helped identify a number of transition state resonances.218 An analysis of the eigenvalue spectrum for the quasibound states of collinear HeH2+ revealed the signature of the underlying quantum chaos.219,220 Similar studies for collinear (He, HD+) and (He, DH+) revealed dramatically different behaviors. While the reaction probability for HeH+ formation plotted as a function of energy (Etrans) showed a ladder like structure, with each step corresponding to the opening up of a new product vibrational channel, PR(Etrans) for HeD+ formation showed a highly oscillatory structure. The transition state spectra for HeHD+ and HeDH+ revealed the characteristics of different dynamical behaviors in the two systems.219,221
Energy resolved reaction probabilities PRv,j(Etrans) for different (v, j) states of H2+ in collision with He in three dimensions were computed by solving the TDSE in mass scaled reactant channel Jacobi coordinates (R, r, γ) for total angular momentum J = 0 on a 128 × 64 × 32 grid by integrating the flux across a dividing line.222 The PRv,j(Etrans) results showed a number of oscillations indicative of the underlying reactive scattering resonances and also the vibrational enhancement that was observed in experiments.
While the FFT method was used for evaluating the second order spatial derivatives of the wave function with respect to R and r, the DVR–FBR route was used for the angular part. The time evolution of the wave function was followed using the second order split-operator method. Similar studies were carried out for He, HD+ collisions in three dimensions223 using an L-shaped grid in (R, r). In the interaction region, a 160 × 128 grid was used, while in the reactant channel an 80 × 64 grid was used. The angular grid consisted of 60 Gauss–Legendre quadrature points.
The computed PRv,j(Etrans) values showed fewer oscillations for HeD+ formation than for HeH+. The calculations also pointed out the need to compute PRv,j(Etrans) values for nonzero J and for J-averaging for the branching ratio between the HeD+ and HeH+ channels to compare with experimental results.
An investigation of the dynamical resonances in 3D HeH2+ and HeHD+ systems for J = 0 using the TDQMWP approach by Maiti et al.186 revealed one bound state for HeH2+ and two pairs of bound states for HeHD+ and a large number of quasibound states for both systems. While the quasibound states at low energies could be interpreted in terms of local modes, some of the higher energy state eigenfunctions were reminiscent of hyperspherical modes. Many higher energy states could not be assigned quantum numbers, indicating underlying unstable periodic orbits.
An elaborate TDQMWP study, within the CS approximation, by Maiti et al.224 yielded PRv,j(Etrans) values for v = 0–3, j = 0, and J = 0–35(45), and thence cross section (σRv0(Etrans)) values for the exchange reaction. Although the computed σRv0(Etrans) values showed oscillations, particularly for the higher v states, they were in reasonable agreement with the experimental results.225,226
While most of the dynamical studies of HeH2+ collisions were carried out on the MTJS PES till then, Panda and Sathyamurthy227 reported the results of TDQMWP studies on the newly reported PES by Palmieri et al.228 for v = 0–3 and j = 0 for a range of J values, within the CS approximation. They also showed a number of oscillations in the PRv0 (Etrans) curves, indicating the underlying dynamical resonances. There was noticeable dampening in the oscillations in the PRv0 (Etrans) curves with an increase in J. They also showed that the oscillations persisted in the σR(Etrans) curves, particularly for v = 3, suggesting that they might be amenable to experimental observation.
Tiwari et al.229 revisited the problem of (He, HD+) collisions and computed the reaction probabilities and integral reaction cross sections for HeH+ and HeD+ formation and their branching ratio for different vibrational states of HD+ with j = 0, averaged over J, within the CS approximation using the TDQMWP approach on the MTJS as well as the Palmieri et al. PES. Although HeD+ formation was generally preferred over HeH+ for different v states of HD+ over a range of Etrans on both the PESs, there were noticeable (quantitative) differences between the dynamical outcomes on the two different surfaces. Unfortunately, the available experimental results are not adequate enough to decide in favour of the results on one surface or the other. The effect of reagent rotation on the branching ratio between HeH+ and HeD+ was investigated230 on the MTJS PES using the TDQMWP approach within the CS approximation by including nonzero J values and the helicity quantum number (K). The PRv,j (Etrans) values were highly oscillatory for both the channels. Yet, it was clear that HeH+ formation was preferred over HeD+ for large J and HeD+ was the preferred channel for small J for all rotational states (j = 0, 1, 2, 3). It is important to point out that the PRv,j (Etrans) values and hence partial cross section values depended strongly on K, thus necessitating K-averaging, in addition to J-averaging, while arriving at the reaction cross section values and hence the branching ratio for different (v, j) states. In a more elaborate calculation135 including Coriolis coupling on the same PES, it was found that the results did not change with the inclusion of Coriolis coupling for the HeD+ channel, but they depended heavily on K for the HeH+ channel. Kolakkandy9 has extended the calculations on a refined version of the Palmieri et al. PES published by Ramachandran et al.231 Although the final results are not much different between the MTJS PES and that of Ramachandran et al.,231 the calculations reiterated the importance of Coriolis coupling.
Kolakkandy et al.116 carried out TDQMWP calculations within the CS approximation on the MTJS PES over an extended energy range (up to 4.7 eV) to investigate the competition between the exchange reaction (R3) and collision induced dissociation (R5) in (He, H2+) collisions for v = 0, 1, 2 and j = 0–3. Although the computed results were in reasonable agreement with the available experimental results,225,226,232,233 they were strongly dependent on K. More calculations including Coriolis coupling on the Ramachandran et al. PES are clearly needed.
The number of triatomic and larger systems studied using the TDQMWP method has increased over the years as is evident from the reviews by Althorpe and Clary16 and Zhang and Guo.17 We have performed a limited survey of the systems investigated till 2004.198 The power and utility of the method is evident from the variety of systems investigated thus far: (H, H2),5,6,32,100,101,104,114,118,119,121,184 (H, HD),130,234 (H,D2),120,123,134,235 (F, H2(HD,D2)),134,236 (O, H2(HD,D2)),83,237 (C, H2),238 (H, O2),125,132,139,239 (N, O2),240 (O, HCl),241 (F, HCl),242 (N, OH),243 (C, OH),244 (S, OH),245 (N, N2),246 (O, O2),247 (Li, FH),120,248 (Li, H2),249 (H, LiH),250 (H, LiH+),251 (N, H2),252 (H−, H2),134,197,198,200–202,206,253 (He, H2+),8,105,116,131,135,207,208,211,212,222–224,227,229,230 (He, HeH+),254 (He, NeH+),255 (Ne, HeH+),256 (Ne, NeH+),257 (H, HBr),258 (Br, HD),259 (H2(HD,D2), OH),260 (H, H2O),261 (OH, CO),262 (H2, CN),263 (H, HCN(DCN)),264 (H, CH4),265 (O, CH4),266 (Cl, CH4),267,268 and (F, CH4).269
The power of the TDQMWP method can be gauged further by a recent study of the reaction
| Cl + HCH3 → ClH + CH3 |
3.3 Nonadiabatic interactions
Unlike a spectroscopic study of bound molecular systems and reactive scattering on a single adiabatic PES, the study of scattering dynamics on coupled electronic states is much more complex and tedious. Much of the complexity arises due to the difficulty in representing the large amplitude molecular motion and asymptotic behaviour in a resonably acceptable diabatic electronic framework. It is only recently that some attempts have been made to investigate the effect of nonadiabatic coupling on photodissociation26,270–272 and bi-molecular reactive scattering273–287 dynamics. In the following we discuss the developments in the nonadiabatic dynamics study of (R1) in the recent past employing TDQMWP methods.The electronic ground state of H3 in its equilateral triangle geometry is orbitally degenerate and it belongs to the 12E′ electronic term of the D3h symmetry point group. This electronic degeneracy is lifted on distortion of H3 along its degenerate bending and asymmetric stretching vibrational modes and the two split components form CIs in the D3h symmetry configurations. This is the simplest and a classic example of an E ⊗ e-Jahn–Teller system.288 The lower adiabatic component (V−) of the split 12E′ surface is highly repulsive and the reaction dynamics occurs on it predominantly via a collinear reaction path. The upper adiabatic component (V+), on the other hand, is bound in nature in the absence of its coupling to the lower surface. The seam of the CIs of the two component PESs occurs in the D3h symmetry configuration of H3.
The repulsive lower adiabatic PES (V−) of H3 has been calculated by different groups289–292 with improved accuracy to study the dynamics of (R1). Among them, the double many body expansion (DMBE) PES of Varandas and coworkers290 represented both the adiabatic sheets of the 12E′ state of H3 for the first time. The DMBE PES is based on an analytic continuation technique that is found to be sufficiently accurate near the seam of the intersection of the two PESs. Recently, Yarkony carried out extensive ab initio calculations of the adiabatic energies V− and V+ and their nonadiabatic coupling terms. These ab initio points were utilized by Abrol and Kuppermann293,294 to develop new coupled diabatic PESs of the electronic ground state of H3. We have utilized the adiabatic energies of the DMBE PES along with the diabatization scheme of Thiel and Köppel173 to carry out the nuclear dynamics. In this scheme173 the diabatic potential energy matrix is given by
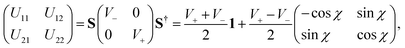 | (55) |
Early work on the electronic nonadiabatic effects in the nuclear dynamics of H3 considered the inclusion of the GP in the single surface calculations. The transition state resonances of the lower adiabatic sheet (V−)109,129 and the bound states of the upper adiabatic sheet (V+)129 were studied using the time autocorrelation function approach. While no noticeable effect of the GP was found on the transition state resonances, the bound vibrational levels of the upper adiabatic sheet were found to undergo a considerable energy shift when the GP was included. This energy shift was first reported by Kuppermann and coworkers295 in a TIQM study. In addition to the energy shift, these authors also reported a change in the symmetry properties of the vibrational eigenstates of V+ upon inclusion of the GP. The effect of nonadiabatic coupling on the transition state resonances in the H + H2 and H + D2 reactions was also studied by Varandas and coworkers296,297 with a coupled diabatic model in a TDQMWP framework and it was found that the GP had practically no effect on the measurables.
Mahapatra and Köppel298 investigated the effect of nonadiabatic coupling on the transition state resonances of V− and bound vibrational levels of V+ by devising a two-state diabatic model employing the adiabatic DMBE PESs. The calculations were carried out using the TDQMWP approach and the vibronic eigenvalue spectra and eigenfunctions were determined by the spectral quantization method. A detailed analysis revealed that resonances were not prominent in the neighborhood of the CIs and only a minor impact of nonadiabatic coupling on them showed up for energies below the minimum of the seam of the CIs occurring at ∼2.74 eV. This impact was attributed to the effect of the GP, which can be significant at energies below the intersection minimum.177 At an energy above this minimum some noticeable blurring of the eigenvalue spectrum was observed due to nonadiabatic coupling.
In contrast to the above, nonadiabatic coupling was found to have an extremely strong influence on the vibronic structure of V+.298 The discrete bound vibrational level spectrum of V+ in the absence of nonadiabatic coupling changes to a broad and structureless envelope with embedded resonances when the coupling is turned on. The bound states of V+ were classified into A1 and E vibronic symmetry based on the nodal pattern of the corresponding eigenfunctions.298 While the eigenfunctions of A1 symmetry exhibit heavy build-up of probability density along the D3h line (the intersection seam at 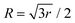 in Fig. 3), the latter falls in the nodal plane of the eigenfunctions of E symmetry. The A1 symmetry levels are therefore immediately affected by the strong nonadiabatic coupling as compared to the levels of E symmetry in their decay dynamics in the coupled electronic manifold. The relaxation times of both types of vibronic levels are quantitatively estimated from the short-time decay of the adiabatic electronic population as well as |C(t)|. It was found that the A1 levels decayed within ∼3 fs and the E levels within ∼6 fs, illustrating the mode specificity in the decay mechanism.298 Such an extremely fast decay time scale of molecular eigenstates was not known at that time and was in accordance with the phenomenological relaxation time of ∼2 fs used by Bruckmeier et al.299 to simulate the experimental Rydberg emission spectrum of D3. Furthermore, in addition to the very fast mode specific decay of the vibronic levels of V+, the location of each peak appearing as a resonance in the broad spectral envelope shifted to a higher energy, supporting the earlier results that included the GP.295,296
in Fig. 3), the latter falls in the nodal plane of the eigenfunctions of E symmetry. The A1 symmetry levels are therefore immediately affected by the strong nonadiabatic coupling as compared to the levels of E symmetry in their decay dynamics in the coupled electronic manifold. The relaxation times of both types of vibronic levels are quantitatively estimated from the short-time decay of the adiabatic electronic population as well as |C(t)|. It was found that the A1 levels decayed within ∼3 fs and the E levels within ∼6 fs, illustrating the mode specificity in the decay mechanism.298 Such an extremely fast decay time scale of molecular eigenstates was not known at that time and was in accordance with the phenomenological relaxation time of ∼2 fs used by Bruckmeier et al.299 to simulate the experimental Rydberg emission spectrum of D3. Furthermore, in addition to the very fast mode specific decay of the vibronic levels of V+, the location of each peak appearing as a resonance in the broad spectral envelope shifted to a higher energy, supporting the earlier results that included the GP.295,296
To this end we would like to point out that the above work laid the foundation for a theoretical demonstration and interpretation of the recorded Rydberg emission spectrum of H3 and its deuterated isotopomers.300 The experimentally observed bimodal emission profile for the system was shown to arise from the lower and upper adiabatic sheets of the 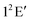 electronic ground state. Extremely strong nonadiabatic coupling and ultrafast internal conversion make the recorded spectrum completely structureless.300 It is clear that the effect of nonadiabatic coupling is strong on the vibronic structure of V+ and the theoretical results corroborate the experimental observations extremely well.
electronic ground state. Extremely strong nonadiabatic coupling and ultrafast internal conversion make the recorded spectrum completely structureless.300 It is clear that the effect of nonadiabatic coupling is strong on the vibronic structure of V+ and the theoretical results corroborate the experimental observations extremely well.
It was discussed above that the nonadiabatic coupling operator Λ consists of three components viz., the BH correction term, the diverging derivative coupling term and the GP. Rajagopala Rao et al.127 examined the effect of each of these three terms in the recorded Rydberg emission spectrum of D3.299 It turned out to be an appropriate (and perhaps the best) system to investigate as the emission experiment directly probes the dynamics of D3 at and in the immediate neighborhood of the CIs of the 12E′ electronic ground state. The study was based on a TDQMWP approach in the modified hyperspherical coordinates of Johnson.47 The GP effect was incorporated into the formalism through the vector potential approach of Mead and Truhlar.150 The diagonal BH correction term assumes a simple form within a linear coupling approach and was shown to be given in terms of the magnitude (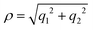 , with q1 and q2 representing the mass-weighted cartesian components of the degenerate vibration) of the degenerate vibration of D3 as184
, with q1 and q2 representing the mass-weighted cartesian components of the degenerate vibration) of the degenerate vibration of D3 as184
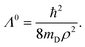 | (56) |
In eqn (56) mD is the mass of the deuterium atom and ρ represents the mass-weighted coordinate of the degenerate vibration in a polar representation. The complete nonadiabatic coupling was incorporated through the same diabatization ansatz of Thiel and Köppel173 as discussed above. It was shown that127 the pseudorotation angle χ is equal to the hyperangle ϕ (cf. Appendix A in ref. 127).
The emission profile to the lower adiabatic sheet (V−) was broad and diffuse already when the states were not coupled. Inclusion of the coupling between V− and V+ did not cause any significant change in the spectral profile. This is due to the repulsive nature of V−. Upon arrival in this state, the WP reaches various dissociation channels within ∼10 fs. The discrete bound vibrational spectrum of uncoupled V+, on the other hand, was found to be strongly affected by the surface coupling (vide supra). Inclusion of both the GP and BH corrections caused a shift of each of its peaks to a higher energy without affecting the structure of the spectrum. It was found that both the GP and BH corrections caused nearly the same energy shift in the spectral peaks. The GP correction introduces a node in the nuclear wave function and the corresponding vibrational level shifts to a higher energy. The appearance of the node implies that the wave function does not encircle the CI. The BH term (cf., eqn (56)) is like a centrifugal term and it becomes singular at the CIs. It shifts the electronic potential to a higher energy and hence the underlying vibrational levels. Despite an overall energy shift, the detailed fine structure of the spectrum remained unaltered in this situation as compared to the uncoupled surface results. Upon inclusion of the NACTs, the dynamics on V+ changed dramatically. The discrete vibrational level structure transformed to an extremely broad spectral envelope. While the inclusion of the GP and BH corrections shifted the envelope to a higher energy, the off-diagonal derivative coupling caused ultrafast internal conversion of the WP to the lower adiabatic sheet and a huge broadening of the spectral envelope. The minimum of the upper adiabatic sheet occurs at the minimum of the seam of the CIs. Therefore, upon arrival at this (V+) sheet, the WP is perturbed by the strong nonadiabatic coupling. The theoretical results discussed above were shown to be in accord with the experiment and therefore established that both the GP and BH corrections led to an energy correction. However, the most crucial effect of ultrafast relaxation of the molecular electronic state is caused by the off-diagonal elements of the nonadiabatic coupling operator. Complete surface coupling includes all the three effects on the dynamics in a coherent fashion. A summary of the results discussed above is given in Fig. 4. A movie containing the time evolution of the WP on the lower (V−) and upper (V+) adiabatic sheet of the electronic ground state of D3 under a strict BO approximation, including the BH and GP corrections and full surface coupling, can be downloaded from the URL http://chemistry.uohyd.ac.in/~sm/SMGID/animation.html.
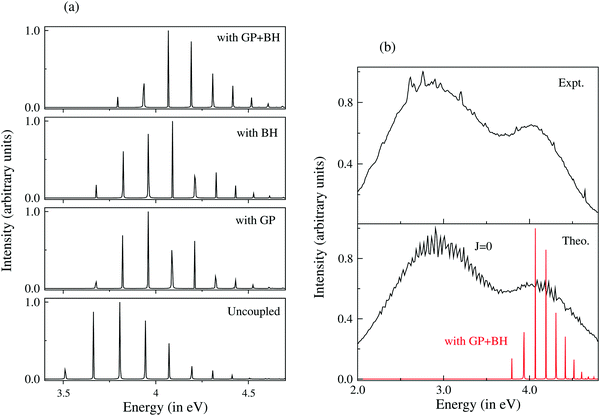 | ||
| Fig. 4 Optical emission spectrum of D3 from the 3p2E′ Rydberg electronic state to the upper adiabatic sheet of the JT split 12E′ electronic ground state. (a) The discrete vibrational energy level spectrum of uncoupled V+, with the GP, with the BH correction and with both the GP and BH corrections shown in the panels starting from the bottom, respectively. It is clear that both the GP and the BH correction cause an energy shift of each peak without affecting the spectral width. (b) Theoretical coupled-state results (the broad bimodal envelope in the bottom panel) compared to the experimental recording (top panel) are reproduced in ref. 127. The theoretical results of the top panel of (a) are included in the bottom panel of (b) to clearly indicate that both the GP and BH corrections are required to get the center-of-gravity of the spectrum at the right energy. The contribution of the nonadiabatic coupling to the spectral broadening of V+ is obvious from the plot. | ||
Early work on electronic nonadiabatic interactions in H + H2 scattering considered the inclusion of GP change in the adiabatic electronic wave function in the nuclear dynamics on V− only. Mead301 carried out the first study and proposed that inclusion of a phase factor of type e3iη/2 (η, describes the coordinate of the path around the CI) is necessary for the single surface dynamics treatment owing to the existence of conical intersections on the H + H2 PES and also to take care of the permutation symmetry of the identical nuclei. He301 pointed out that the GP changes the interference between the reactive and nonreactive scattering amplitudes of identical nuclei when compared to the non-GP case. More than a decade later, Kuppermann and coworkers302–306 carried out a series of more rigorous studies employing the multi-valued wave function basis approach of Mead and Truhlar150 and established that the GP significantly changed the differential reaction cross section (DCS). It was shown that the DCS of the H + D2 (v = 0) reaction at a collision energy of 1.26 eV agreed well with the experiment when the GP effect was included. Later, in a number of combined experimental and theoretical studies307–312 it was shown that theoretical calculations without the GP could also reproduce the experimental results satisfactorily. This issue remained a subject of debate for some time. Kendrick313 performed TIQM calculations using the vector potential approach of Mead and Truhlar150 and showed that the effects of the GP were small and showed up in the state-to-state reaction probability above a total energy of 1.8 eV. The surprising result at that time was that the GP effects that appeared in the reaction probability results cancelled each other on summing over the partial wave contributions while arriving at the integral reaction cross section (ICS) values.
Althorpe and coworkers314 performed TDQMWP calculations using the vector potential approach of Mead and Truhlar and reached unequivocal agreement with the results of Kendrick.313 Althorpe and coworkers extended the calculations to larger J values and found that small GP effects that showed up in the DCSs disappered in the ICS values. Subsequently, they315 extended their study to higher (total) energies up to 4.5 eV. In addition to the GP, the authors also considered the inclusion of the BH correction and rigorous surface coupling following the theoretical model of Mahapatra et al.184 It was found that the BH term contributed to the dynamics at energies above ∼2.5 eV as was found by Mahapatra et al.184 It was further demonstrated that the BH term, which is like a spike, protected the WP from the singularity of the vector potential and reduced the sideways scattering and the rotational temperature of the product H2.315 The GP was shown to have strong effects on the DCS at energies above ∼3.5 eV, which however cancelled upon summing over all partial wave contributions to arrive at the ICS. These authors have also provided an explanation for such a cancellation by separating the contribution to the DCS from two different paths going over one and two transition states, respectively, and subsequent interference at high energies.
A summary of the above discussion is in order here. The lower adiabatic surface V− of H3 is highly repulsive and the WP readily accesses the dissociation channels both in spectroscopy and scattering studies. Reactive scattering is dominated by the collinear reaction path and resonances are not prominent in the neighborhood of the D3h seam. The upper adiabatic sheet V+ has its minimum at the minimum of the intersection seam at ∼2.74 eV. The dynamics of this state is, therefore, dramatically affected by the nonadiabatic interactions with V−.
While quite intense research activity on the effect of the GP on H + H2 scattering dynamics still continues,316 Mahapatra et al.184 devised a theoretical model for the first time to include explicit surface coupling in a TDQMWP framework. In addition to computing reaction probabilities, the model was further extended to calculate ICSs and thermal rate constants.317,319,320 The state-selected PR results for (v = 0, j = 0) of H2, J = 0, were examined over the energy range starting from the onset of the exchange reaction at 0.55 eV to the three-body dissociation limit (∼4.74 eV). It was found that the coupled electronic state results remained almost identical to the uncoupled state results. Only very small differences between the two were found beyond the energetic minimum of the seam of the CIs at ∼2.74 eV. This difference disappered when the BH correction was included in the uncoupled state calculations. In the adiabatic picture, the reactive flux of the WP flows to the product asymptote of the lower adiabatic sheet (V−) only. An analysis of the electron population revealed that less than 1% of the WP traverses the upper adiabatic sheet during the entire course of the dynamics. It was also found that the sum of the reaction probabilities obtained on the two diabatic product asymptotes was identical to that obtained in the adiabatic picture. This additionally reveals that the upper adiabatic sheet makes little contribution to the reaction dynamics in this case.
While the above results were obtained within the CS approximation, Jayachander Rao et al. included the CC terms of the Hamiltonian in a later study.317 The reaction probability for H2 (v = 0, j = 0) was calculated up to a total energy of 3.0 eV. It was found that the location of the resonances shifted to higher energies as compared to the CS results. Such a shift was also reported by Padmanaban and Mahapatra318 in an earlier study. It was found that the difference between the uncoupled and coupled state results increased with an increase in K for lower J values. However, with an increase in J this difference decreased, implying that CC did not promote nonadiabaticity in the H + H2 dynamics. A similar observation of the CC effect on the uncoupled state dynamics with the GP was noted by Bouakline et al.315 Jayachander Rao et al.319 also studied the effect of reagent vibrational and rotational excitation on the nonadiabatic reactive dynamics of H + H2. It was found that reagent vibrational excitation did not promote nonadiabaticity, whereas reagent rotational excitation did. The difference between the uncoupled and coupled surface results showed up in the reaction probability values and also in the ICSs, particularly for H2 (j = 3). Interestingly, the difference was found to be quite substantial at energies below the minimum of the seam of the CIs for j = 3. This was due to the GP effect (as stated above) even if the upper surface is inaccessible to the WP at these energies. No effect of surface coupling was found on the thermal rate constants.
Rajagopala Rao et al.320 performed a detailed study of the dynamics of the H + D2, D + H2, H + HD and D + HD reactions. Reaction probabilities, ICSs and thermal rate constants were calculated with and without the NACTs for energies up to the three-body dissociation limit and also with vibrationally and rotationally excited reagents. No dramatic effect of nonadiabatic coupling was found on the dynamics of any of the four isotopic variants mentioned above. Both the ICSs and thermal rate constants were found to remain the same on the uncoupled and coupled surfaces and agreed well with the available experimental results.321 Lu et al.297 have reported ICSs of the H + D2 reaction using the original diabatic DMBE PES of H3290 that compared very well with ours (up to a collision energy of 2 eV), implying that the diabatic DMBE PES of H3 is as accurate as the diabatization scheme employed by us.
In summary, it can be stated that the nonadiabatic coupling has similar effects on the reaction dynamics of H + H2 and its isotopic variants. It was found by Althorpe and coworkers315 that the state-to-state DCSs calculated by including the GP and BH corrections were identical to the results obtained with the two state diabatic model over an extended energy range. It therefore emerges that the participation of the upper surface is minimal in the dynamics of the lower surface also for energies much above the minimum of the seam of the CIs and this still remains a mystery. More experimental and theoretical work are necessary to resolve this mystery.322
Some of the other systems that have been investigated using the TDQMWP method including non-adiabatic coupling are: (H+, H2),128,285,286 (F, H2),277,323 (Cl, H2),32,279,324 (Br, H2),325 (O, H2),274,326 and more recently (F, CH4).287
4 Large systems
Despite the overwhelming success of the traditional TDQMWP method with the development of powerful integrators and improved algorithms, computational bottlenecks prevented its application to systems involving a large number n of degrees of freedom (DOF). The number N of nodes needed increases as Nn. Efforts have been made in the past to overcome this problem by devising both approximate and numerically exact methods applicable to large systems, with affordable computational cost. To name a few, the methods in the approximate category include the Gaussian wave packet (GWP) method of Heller,327 semiclassical approaches,328 the time-dependent self consistent field method329 and mixed classical and quantal approaches.330 In the numerically exact category path integral approaches,331 the multi-configuration time-dependent Hartree (MCTDH) method332 and self-consistent hybrid methods333 are noteworthy. Each of the above methods has its own limitations for it to be applicable to a given problem with a given Hamiltonian. Considerable efforts have been made in recent years to ensure the generality of some of these methods.We mention selected methods from each of the two categories that use TDQMWP propagation. In the numerically exact category, the MCTDH method is the most promising one. It was originally formulated by Manthe, Meyer and Cederbaum and it emerged as a state-of-the-art technique to solve the TDSE numerically exactly on a grid for systems with large DOFs. It utilizes a DVR basis combined with the FFT algorithm and powerful integrators to propagate the WP. The crucial aspect of the method lies in the design of the initial WP, in contrast to the traditional grid method. The MCTDH method uses a product separable multi-configurational ansatz for the wave function in which each configuration is expressed as a Hartree product of time-dependent basis functions called single particle functions (SPFs). Several DOFs are combined to form the latter with a multi-set formulation and the WP is expanded in terms of them. This cuts down the computational cost heavily by effectively reducing the dimensionality of the problem. The MCTDH equations of motion are derived using the Dirac–Frenkel variational principle,334 ensuring an optimal description of the WP by the evolving SPFs. In that way the time-dependent basis moves with the WP, making the method efficient while keeping the basis size optimally small. For more technical details of the method and its applicability, the reader is referred to the URL: https://www.pci.uni-heidelberg.de/cms/mctdh.html. We note that the complex reactive scattering problem H + CH4 has been studied with the MCTDH method and the resulting reaction cross sections and rates were reported.335 The number of papers published (although the list is not exhaustive) utilizing the Heidelberg MCTDH program modules can be found in the given URL.
The MCTDH method mentioned above is further extended to a greater height by introducing variational flexibility in the initial trial wave function in a multilayer (ML) formulation called the ML-MCTDH method. This method was introduced by Wang and Thoss336 and the complex theoretical formulation was made implementable with the introduction of a recursive dynamically optimized layering scheme and layered correlation DVR by Manthe.337 In contrast to the original MCTDH method, which uses a static primitive basis to express the SPFs, the ML-MCTDH scheme uses a time-dependent expansion at different levels in the hierarchy. The ML-MCTDH scheme was shown to be quite efficient and successful to treat thousands of DOFs. The dynamics of the H + CH4 reaction was also studied with the ML-MCTDH method by Welsch and Manthe.338 To deal with systems of identical particles and to account for exchange symmetry, multi-configuration time-dependent Hartree–Fock339 and multi-configuration time-dependent Hartree–Bose340 methods were formulated for Fermionic and Bosonic systems, respectively.
In the mixed classical and quantal approach of the approximate category, a large scale dynamical system is divided into two parts in which the most crucial DOFs are treated quantum mechanically in a numerically exact way and the rest of the DOFs are treated classically. Adhikari and co-workers341 have developed the algorithm called time-dependent DVR (TDDVR) in which the quantum part of the problem is treated in DVR basis and the WP propagation is carried out in a way similar to that in the MCTDH method. The classical part of the problem is treated by solving Newton's equations of motion. These authors have applied the method to a variety of problems that have been treated with the MCTDH approach and showed that the dynamical results from the two methods complemented each other.
At this point we mention two other promising methods developed for large systems, based on the idea underlying Gaussian wave packet dynamics.327,342 The first one, called the G-MCTDH method, developed by Burghardt and co-workers,343,344 utilizes the separation of the DOFs of the system in the spirit of the mixed classical and quantal approach.330 The large number of DOFs is divided into primary (strong coupling) and secondary (weak coupling) modes. The primary modes are treated with the numerically exact MCTDH equations of motion on a grid and the secondary modes are treated with an approximate propagation scheme, avoiding the grid representation. The latter, therefore, allows combining a large number of secondary modes into a package which is subsequently represented in terms of parameterized correlated multidimensional Gaussians. The Dirac–Frenkel variational principle334 is utilized to derive the equations of motion of the time dependent parameters.342 Here the method differs from the classical evolution of the Gaussian basis set327 and conforms to a semiclassical evolution. The correlation between the primary and the secondary modes is ensured in the propagation scheme employed and it also accounts for the quatum mechanical phase coherence. The method is developed both in the wave function and density matrix representations and extended to account for dissipative effects. It is potentially applicable to a wide variety of dynamical processes occurring in the gas phase as well as in the condensed phase and also to ones involving a thermal initial state.
The second promising method falls under the umbrella of ab initio molecular dynamics. It is called the ab initio multiple spawning method (AIMS) and was developed by Martinez and collaborators.345,346 In this method both the electronic and nuclear Schrödinger equations are solved simultaneously without separating the electronic structure and dynamics. In contrast to the methods discussed thus far, which require the multidimensional PES as a prerequisite, the PES is calculated on-the-fly in the AIMS approach. It has a classical flavour in the sense that it connects the local quantum chemistry information to the global nature of the nuclear Schrödinger equation as the global PES is not available to the nuclei for their motion at any instance. The central feature of the method is to use an adaptive basis set, which is time-dependent and nonorthogonal. For a nonadiabatic problem, a new basis set is generated when the wave function approaches the neighbourhood of the coupling region of the PESs (spawning). The AIMS method attempts to solve the nuclear dynamics with a time-dependent basis evolved from the classical framework.327 The total wave function is expanded in terms of electronic wave functions dependent parametrically on the nuclear coordinates and the nuclear wave function dependent on the nuclear coordinates and time and time-dependent coefficents. While the set of electronic wave functions is obtained from the quantum chemistry solution on-the-fly, the nuclear wave function is represented in terms of a superposition of multidimensional travelling frozen parameterized Gaussians with time-dependent coefficients.327 The time-dependent position and momentum parameters of the Gaussians are propagated with the aid of the classical Hamilton's equations of motion327 and the nuclear phase is propagated semiclassicaly as an integral of the Lagrangian. The time-dependent coefficients of the total wave function are calculated variationally. The calculations are initiated by providing the basis set parameters (position, momentum and phase) drawn randomly from an appropriate Wigner distribution and in the beginning only one electronic state is populated. As the calculations progress new basis functions are spawned in a different electronic state while the parent basis passes through a region of nonadiabaticity. Complementary methods called variational multi-configurational Gaussian (vMCG)347 and coherent coupled states (CCS) are also developed within the framework of AIMS. The former is developed along the same lines as the G-MCTDH method of Burghardt and co-workers and is fully variational. The latter (the CCS method) developed by Shalashilin et al.348–350 falls in between the AIMS and vMCG methods. It has some additional quantum effects accounted for (as compared to AIMS) by averaging the trajectories over the Gaussians.
A summary and an outlook of the methods discussed for large systems are in order here. The MCTDH method is exactly quantum mechanical in nature globally and the rest of the methods are not. Approximations are made to alleviate the computational bottleneck. Heller's approach to the wave packet dynamics was a landmark in the field and it has led to significant advancements. A large number of complex systems have been treated by his method to bring in reasonable understanding of the dynamics on par with modern experiments. We believe that the developments noted above are still in their infancy and would evolve further with time.
5 Molecular dynamics on solid surfaces
The dynamics of molecules on solid surfaces is more complex than in the gas phase as one has to deal with not only the molecular (electronic and vib-rotational) degrees of freedom, but also the interaction with the surface and the characteristics of the solid surface. While some of the earlier TDQMWP studies351 on H2/Cu, for example, treated the solid surface as rigid and flat, subsequent studies introduced corrugation. Kroes and collaborators352 have investigated the dynamics of H2 dissociation on the Cu(111) surface using a chemically accurate potential. Gerrits et al.353 combined the power of the WP method with the utility of the neural network approach for potential determination for CHD3/Cu(111). Tiwari et al.354 have shown that the lattice motion influences the reactivity of the methane molecule on the nickel (111) surface. The same set of authors355 reiterated their findings for dissociative chemisorption of methane on nickel and platinum surfaces using the reaction path Hamiltonian method.356 Guo and collaborators357,358 examined the role of vibrational excitation in the dissociative chemisorption of water on copper and nickel surfaces using density functional theory based potentials and six dimensional TDQMWP studies. The application of the TDQMWP method to study the dissociation of water and methane molecules on Cu/Ni surfaces has been reviewed recently by Tiwari and coworkers.359 The 9-dimensional study of methane dissociation on metal surfaces by Zhang and Jiang360 is particularly worth mentioning.6 Software development
The TIQM method had matured to a level that the (A + BC) reactive scattering code was made available as early as the year 2000.199 Subsequently, public domain software under the name Dynasol361 was made available by J. Z. H. Zhang in 2004 for carrying out TDQMWP calculations. Software named DIFFREALWAVE137 of Hankel and Balint-Kurti was made available in 2008 to carry out RWP calculations.6.1 Machine learning and quantum dynamics
The TDQMWP approach relies on (i) generation of an ab initio PES for a given system, (ii) fitting an analytic function to or numerical interpolation/extrapolation of or a combination of both of the generated points on the PES and (iii) solving the TDSE on a spatial grid for a length of time and extracting the dynamical information and the observables. When we go beyond the BO approximation, a manifold of PESs needs to be generated and nonadiabatic coupling included before the multi-state quantum dynamics is carried out. Recent developments of machine learning (ML) tools in the form of neural networks, Gaussian processes and kernel methods could enable the generation of the PES for moderate size (3 ≤ N ≤ 6) systems, using a limited number of ab initio points in 3N − 6 dimensional space. Going beyond the BO approximation does not seem to be a serious bottleneck in this endeavour. The possibility of extending the ML tools to estimate observables like (l-averaged) reaction cross sections and (ensemble averaged) reaction rate coefficients along with error estimates based on Bayesian optimization opens up new horizons.362 When these tools become more practical, the entire area of ab initio quantum dynamics will undergo a sea change and more and more systems would be amenable to theoretical/computational investigations.7 Summary and conclusion
We have outlined in this article the evolution of the TDQMWP methodology from its first use in predicting the rate coefficients for a model collinear (H, H2) exchange reaction to predicting the state-to-state differential and integral reaction cross sections for reaction (R1) in three dimensions on an accurate ab initio PES. That the predicted observables are in agreement with the available experimental results bears testimony to the reliability of the method. That the method has been extended to a number of atom–diatom exchange reactions and collision induced processes points out its practical utility. That the method is extendable to larger polyatomic systems either on its own or in conjunction with other methods demonstrates its versatility. That the method can be extended readily to include nonadiabatic coupling terms to predict vibronic interactions indicates its power. That the method is amenable to the use of machine learning tools in its implementation assures its future in the hands of theoretical spectroscopists and reaction dynamicists.For some time, it appeared that the TDQMWP method had reached its limit and would not be applicable to systems involving more than three atoms or three dimensions because the number of grid points required along the approach coordinate in an exchange reaction or the retreat coordinate in photo-dissociation for obtaining reaction attributes with spectroscopic accuracy is large. One cannot afford to use the same number of grid points along all other degrees of freedom, in view of the increased demand on computer time and memory. The combination of the FFT route for evaluating the Laplacian of the wave function with Chebyshev polynomial expansion for the (time) evolution operator yielded results to machine accuracy. Although the FFT method scaled as N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) N, where N is the number of grid points, the DVR method came in as an attractive alternative, despite its scaling as N2, the reason being that the latter method could be more efficient if an appropriate basis set is chosen for expanding the wave function. The second order split operator method for time evolution was robust enough and it could provide insight into the dynamics during the entire course of time evolution for several dynamical systems. With the development of higher order SO methods, the accuracy and stability of the algorithm ceased to be an issue. As we have shown in the main body of the text, the time evolution required of many dynamical studies of reactive scattering, photodissociation, gas-surface scattering, etc. is at most of the order of a few picoseconds and seldom of the order of nanoseconds. In addition to the grid size, the bottleneck in the application of the grid method that remained was the lack of availability of multi-dimensional PESs for larger (more than three or four atoms) systems. Once that was overcome by using methods such as permutationally invariant polynomials and artificial neural networks or a combination of the two, the wave packet method got a new life. Parallelization of computer codes definitely helped in dealing with systems that required calculations for a large number of J states, even for triatomic systems.
N, where N is the number of grid points, the DVR method came in as an attractive alternative, despite its scaling as N2, the reason being that the latter method could be more efficient if an appropriate basis set is chosen for expanding the wave function. The second order split operator method for time evolution was robust enough and it could provide insight into the dynamics during the entire course of time evolution for several dynamical systems. With the development of higher order SO methods, the accuracy and stability of the algorithm ceased to be an issue. As we have shown in the main body of the text, the time evolution required of many dynamical studies of reactive scattering, photodissociation, gas-surface scattering, etc. is at most of the order of a few picoseconds and seldom of the order of nanoseconds. In addition to the grid size, the bottleneck in the application of the grid method that remained was the lack of availability of multi-dimensional PESs for larger (more than three or four atoms) systems. Once that was overcome by using methods such as permutationally invariant polynomials and artificial neural networks or a combination of the two, the wave packet method got a new life. Parallelization of computer codes definitely helped in dealing with systems that required calculations for a large number of J states, even for triatomic systems.
In the case of photo-excitation processes also, three atom systems remained the norm for some time. When it came to gas–surface scattering, two or three spatial dimensions were the norm until a few years ago. Practitioners in the field have come up with clever ways to include lattice vibrations in molecule-solid surface interactions. Here again, the neural network methods are beginning to facilitate the extension of the method to surfaces involving more than a few atoms.
Alternative methods such as MCTDH and its variants and other methods such as TDDVR, AIMS, vMCG, CCS etc. have made the time-dependent approach practical for a variety of multi-dimensional systems.
Going beyond the BO approximation, dealing with dynamics that involves several electronic states and nonadiabatic coupling between them in more than one or two dimensions is a challenge. To start with, multi-sheet potential energy surfaces with their crossings and/or avoided crossings have to be determined in a readily usable form. In principle, one could take the diabatic route and use the existing TDQMWP methodology for solving multi-electronic state problems. In practice, it is a demanding task and it has been accomplished for a handful of systems (only). Mercifully, the computational time required for following the nuclear dynamics in such systems scales approximately linearly with an increase in the number of electronic states. Like in any scientific enterprise, as the challenges come up, solutions emerge too!
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Aditya Narayan Panda of IIT Guwahati for the graphic illustration of the evolution of the wave packet for (He, H2+) dynamics in collinear and in 3D geometries. S. M. acknowledges the financial support from the Department of Science and Technology, New Delhi, through the grant no. EMR/2017/004592 and from the University Grants Commission (UGC-BSR mid career award grant No. F.19-231/2018(BSR)), New Delhi. Computational facilities availed in the CMSD, University of Hyderabad, are gratefully acknowledged. We thank Mr Jayakrushna Sahoo for help with the production of the manuscript.References
- E. Schrödinger, Ann. Phys., 1926, 4(79), 361–376 CrossRef.
- E. Schrödinger, Ann. Phys., 1926, 4(79), 489–527 CrossRef.
- E. Schrödinger, Ann. Phys., 1926, 4(81), 109–139 CrossRef.
- P. A. M. Dirac, Proc. R. Soc. A, 1929, 123, 714–733 CAS.
- J. Mazur and R. J. Rubin, J. Chem. Phys., 1959, 31, 1395–1412 CrossRef CAS.
- E. A. McCullough and R. E. Wyatt, J. Chem. Phys., 1969, 51, 1253–1254 CrossRef CAS; E. A. McCullough and R. E. Wyatt, J. Chem. Phys., 1971, 54, 3578–3591 CrossRef; E. A. McCullough and R. E. Wyatt, J. Chem. Phys., 1971, 54, 3592–3600 CrossRef.
- G. E. Kellerhals, N. Sathyamurthy and L. M. Raff, J. Chem. Phys., 1976, 64, 818–825 CrossRef CAS.
- A. N. Panda and N. Sathyamurthy, Proc. Indian Natl. Sci. Acad., Part A, 2004, 70, 635–648 CAS.
- S. Kolakkandy, PhD thesis, Indian Institute of Technology Kanpur, 2012.
- M. Levitt, Ernst Chain Lecture, Imperial College, London, 2014, https://www.youtube.com/watch?v=Wy0OGgmjzPM Search PubMed.
- L. R. Khundkar and A. H. Zewail, Annu. Rev. Phys. Chem., 1990, 41, 15–60 CrossRef CAS.
- A. H. Zewail and J. M. Thomas, 4D Electron Microscopy, Imperial College Press, London, 2010 Search PubMed.
- T. S. Rose, M. J. Roskar and A. H. Zewail, J. Chem. Phys., 1989, 91, 7415–7436 CrossRef CAS.
- F. T. Wall, L. A. Hiller Jr. and J. Mazur, J. Chem. Phys., 1958, 29, 255–263 CrossRef CAS.
- R. N. Porter and L. M. Raff, in Dynamics of Molecular Collisions Part B, ed. W. H. Miller, Plenum, New York, 1976, ch. 1 Search PubMed.
- S. C. Althorpe and D. C. Clary, Annu. Rev. Phys. Chem., 2003, 54, 493–529 CrossRef CAS.
- D. H. Zhang and H. Guo, Annu. Rev. Phys. Chem., 2016, 67, 135–58 CrossRef CAS.
- N. Sathyamurthy, in Reaction Dynamics: Recent Advances, ed. N. Sathyamurthy, Narosa, New Delhi, 1991, ch. 2 Search PubMed.
- A. H. Zewail, The Chemical Bond: Structure and Dynamics, Academic Press, San Diego, 1992 Search PubMed.
- Y. T. Lee, Angew. Chem., 1987, 26, 939–1058 CrossRef.
- F. Fernández-Alonso and R. N. Zare, Annu. Rev. Phys. Chem., 2002, 53, 67–99 CrossRef.
- M. Shapiro and P. Brumer, Principles of the Quantum Control of Molecular Processes, Wiley-VCH, 2003 Search PubMed.
- D. Neuhauser and H. Rabitz, Acc. Chem. Res., 1993, 26, 496–501 CrossRef CAS.
- D. J. Tannor, Introduction to Quantum Mechanics: A time-dependent perspective, University Science Books, Sausalito, CA, 2007 Search PubMed.
- G. G. Balint-Kurti, S. Zou and A. Brown, Adv. Chem. Phys., 2008, 138, 43–94 CrossRef CAS.
- R. Schinke, Photodissociation Dynamics, Cambrige Univ. Press, Cambridge, 1993 Search PubMed.
- K. Ramasesha, S. R. Leone and D. M. Neumark, Annu. Rev. Phys. Chem., 2016, 67, 41–63 CrossRef CAS.
- V. Mohan and N. Sathyamurthy, Curr. Sci., 1986, 55, 115–119 CAS.
- V. Mohan and N. Sathyamurthy, Comput. Phys. Rep., 1988, 7, 213–258 CrossRef CAS.
- N. Balakrishnan, C. Kalyanaraman and N. Sathyamurthy, Phys. Rep., 1997, 280, 79–144 CrossRef CAS.
- S. Mahapatra, N. Chakrabarti and N. Sathyamurthy, Int. Rev. Phys. Chem., 1999, 18, 235–262 Search PubMed.
- S. Mahapatra, Int. Rev. Phys. Chem., 2004, 23, 483–512 Search PubMed.
- R. B. Gerber, R. Kosloff and M. Berman, Comput. Phys. Rep., 1986, 5, 59–114 CrossRef.
- R. Kosloff, J. Phys. Chem., 1988, 92, 2087–2100 CrossRef CAS.
- Thematic issue on time-dependent methods for quantum dynamics, in Comput. Phys. Commun., ed. K. C. Kulander, 1991, vol. 63 Search PubMed.
- J. Z. H. Zhang, Theory and application of quantum molecular dynamics, World Scientific, Singapore, 1999 Search PubMed.
- G. G. Balint-Kurti, Adv. Chem. Phys., 2003, 128, 249–301 CAS; G. G. Balint-Kurti, Int. Rev. Phys. Chem., 2008, 27, 507–539 Search PubMed.
- C. Leforestier, Chem. Phys., 1984, 87, 241–261 CrossRef CAS.
- S. Choi and J. Vaníček, J. Chem. Phys., 2019, 151, 234102 CrossRef.
- E. B. Wilson, J. C. Decius and P. C. Cross, Molecular Vibrations, Dover, New York, NY, 1955 Search PubMed.
- S. Glasstone, K. J. Laidler and H. Eyring, The theory of rate processes, McGraw-Hill, New York, 1941, p. 101 Search PubMed.
- L. M. Delves, Nucl. Phys., 1959, 9, 391–399 CrossRef; L. M. Delves, Nucl. Phys., 1960, 20, 275–308 CrossRef.
- P. M. Morse and H. Feshbach, Methods of Theoretical Physics, McGraw-Hill, New York, 1953, p. 1728–1734 Search PubMed.
- F. T. Smith, J. Math. Phys., 1962, 3, 735–748 CrossRef.
- R. C. Whitten and F. T. Smith, J. Math. Phys., 1968, 9, 1103–1113 CrossRef.
- A. Kuppermann, Chem. Phys. Lett., 1975, 32, 374–375 CrossRef CAS.
- B. R. Johnson, J. Chem. Phys., 1980, 73, 5051–5058 CrossRef CAS.
- T. Seideman and W. H. Miller, J. Chem. Phys., 1992, 96, 4412–4422 CrossRef CAS; T. Seideman and W. H. Miller, J. Chem. Phys., 1992, 97, 2499–2514 CrossRef.
- U. Manthe and W. H. Miller, J. Chem. Phys., 1993, 99, 3411–3419 CrossRef CAS.
- J. Z. H. Zhang and D. H. Zhang, J. Chem. Phys., 1994, 101, 1146–1156 CrossRef.
- A. J. H. M. Meijer and E. M. Goldfield, J. Chem. Phys., 1998, 108, 5404–5413 CrossRef CAS.
- E. M. Goldfield and S. K. Gray, Comput. Phys. Commun., 1996, 98, 1–14 CrossRef CAS.
- R. T Pack, J. Chem. Phys., 1974, 60, 633–639 CrossRef.
- P. McGuire and D. J. Kouri, J. Chem. Phys., 1974, 60, 2488–2499 CrossRef CAS.
- R. Dawes and S. A. Ndengué, Int. Rev. Phys. Chem., 2016, 35, 441–478 Search PubMed.
- N. Sathyamurthy, Comput. Phys. Rep., 1985, 3, 1–70 CrossRef CAS.
- J. N. Murrell, S. Carter, S. C. Farantos, P. Huxley and A. J. C. Varandas, Molecular Potential Energy Functions, Wiley, Chichester, 1984 Search PubMed.
- G. C. Schatz, Rev. Mod. Phys., 1989, 61, 669–688 CrossRef CAS.
- P. M. Morse, Phys. Rev., 1929, 34, 57–64 CrossRef CAS.
- F. London, Probleme der Modernen Physik (SommerfeldFestschrift), S. Hirzel, Leipzig, 1928, p. 104; F. London, Z. Elektrochem., 1929, 35, 552–555 Search PubMed.
- H. Eyring and M. Polanyi, Z. Phys. Chem. B, 1931, 12, 279–311 CAS; H. Eyring and M. Polanyi, Z. Phys. Chem., 2013, 227, 1221–1245 Search PubMed.
- J. C. Polanyi and J. L. Schreiber, in Physical Chemistry, an Advanced Treatise, Kinetics of Gas Reactions, ed. H. Eyring, W. Jost and D. Henderson, Academic Press, New York, 1974, ch. 6, vol. VIA Search PubMed.
- P. J. Kuntz, Chem. Phys. Lett., 1972, 16, 581–583 CrossRef CAS.
- K. S. Sorbie and J. N. Murrell, Mol. Phys., 1975, 29, 1387–1407 CrossRef CAS.
- A. Aguado, C. Tablero and M. Paniagua, Comput. Phys. Commun., 1998, 108, 259–266 CrossRef CAS.
- C. M. R. Rocha and A. J. C. Varandas, Comput. Phys. Commun., 2020, 247, 106913 CrossRef CAS.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 151–175 CrossRef CAS.
- L. M. Raff, R. Komanduri, M. Hagan and S. T. S. Bukkapatnam, Neural Networks in Chemical Reaction Dynamics, Oxford Univ. Press, Oxford, 2012 Search PubMed.
- M. Majumder, S. A. Ndengué and R. Dawes, Mol. Phys., 2015, 114, 1–18 CrossRef.
- A. Kamath, R. A. Vargas-Hernández, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef.
- Y. Guan, S. Yang and D. H. Zhang, Mol. Phys., 2018, 116, 823–834 CrossRef CAS.
- N. Sathyamurthy and L. M. Raff, J. Chem. Phys., 1975, 63, 464–473 CrossRef CAS.
- M. Patrício, J. L. Santos, F. Patrício and A. J. C. Varandas, J. Math. Chem., 2013, 51, 1729–1746 CrossRef.
- H. Nakamura, Nonadiabatic transition, World Scientific, Singapore, 2002 Search PubMed.
- Conical Intersections: Electronic Structure, Dynamics and Spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientific, Singapore, 2004, vol. 15 Search PubMed.
- M. Baer, Beyond Born-Oppenheimer: Conical intersections and electronic nonadiabatic coupling terms, John Wiley & Sons, Hoboken, New Jersey, USA, 2006 Search PubMed.
- T. Yonehara, K. Hanasaki and K. Takatsuka, Chem. Rev., 2012, 112, 499–542 CrossRef CAS.
- M. S. Schuurman and A. Stolow, Annu. Rev. Phys. Chem., 2018, 69, 427–450 CrossRef CAS.
- B. Mukherjee, K. Naskar, S. Mukherjee, S. Ghosh, T. Sahoo and S. Adhikari, Int. Rev. Phys. Chem., 2019, 38, 287–341 Search PubMed.
- A. J. C. Varandas, in ref. 77, pp. 205–270.
- M. Hankel, G. G. Balint-Kurti and S. K. Gray, J. Phys. Chem. A, 2001, 105, 2330–2339 CrossRef CAS; M. Hankel, G. G. Balint-Kurti and S. K. Gray, Int. J. Quantum Chem., 2003, 92, 205–211 CrossRef.
- M. D. Feit, J. A. Fleck Jr. and A. Steiger, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS.
- H. Tal-Ezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967–3971 CrossRef CAS.
- Z. Sun, W. Yang and D. H. Zhang, Phys. Chem. Chem. Phys., 2012, 14, 1827–1845 RSC.
- M. Braun, C. Meier and V. Engel, Comput. Phys. Commun., 1996, 93, 152–158 CrossRef CAS.
- P. Pfeifer and R. D. Levine, J. Chem. Phys., 1983, 79, 5512–5519 CrossRef CAS.
- U. Peskin and N. Moiseyev, J. Chem. Phys., 1993, 99, 4590–4596 CrossRef CAS; U. Peskin, O. E. Alon and N. Moiseyev, J. Chem. Phys., 1994, 100, 7310–7318 CrossRef; U. Peskin, R. Kosloff and N. Moiseyev, J. Chem. Phys., 1994, 100, 8849–8855 CrossRef; N. Moiseyev, M. Chrysos and R. Lefebvre, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2599–2609 CrossRef.
- P. Raj, A. Gugalia and P. Balanarayan, J. Chem. Theory Comput., 2020, 16, 35–50 CrossRef CAS.
- M. D. Feit and J. A. Fleck Jr., J. Chem. Phys., 1982, 78, 301–308 CrossRef.
- D. Kosloff and R. Kosloff, J. Comput. Phys., 1983, 52, 35–53 CrossRef CAS.
- J. Manz, private communication.
- R. C. Mowrey and D. J. Kouri, J. Chem. Phys., 1986, 84, 6466–6473 CrossRef CAS.
- R. C. Mowrey, J. Chem. Phys., 1991, 94, 7098–7105 CrossRef CAS.
- D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1994, 101, 3671–3678 CrossRef CAS; D. Neuhauser, M. Baer, R. S. Judson and D. J. Kouri, J. Chem. Phys., 1990, 93, 312–322 CrossRef; D. Neuhauser, Chem. Phys. Lett., 1992, 200, 173–178 CrossRef.
- C. Leforestier and R. E. Wyatt, J. Chem. Phys., 1983, 78, 2334–2344 CrossRef CAS.
- R. Kosloff and D. Kosloff, J. Comput. Phys., 1986, 63, 363–376 CrossRef.
- D. Neuhauser and M. Baer, J. Chem. Phys., 1989, 90, 4351–4355 CrossRef.
- D. Neuhauser, M. Baer, R. S. Judson and D. J. Kouri, J. Chem. Phys., 1989, 90, 5882–5884 CrossRef CAS.
- D. Neuhauser, M. Baer and D. J. Kouri, J. Chem. Phys., 1990, 93, 2499–2505 CrossRef CAS.
- M. S. Child, Mol. Phys., 1991, 72, 89–93 CrossRef CAS.
- Á. Vibók and G. G. Balint-Kurti, J. Phys. Chem., 1992, 96, 8712–8719 CrossRef.
- M. Monnerville, P. Halvick and J. C. Rayez, Chem. Phys., 1992, 159, 227–234 CrossRef CAS.
- S. Mahapatra and N. Sathyamurthy, J. Chem. Soc., Faraday Trans., 1997, 93, 773–779 RSC.
- C. Leforestier, R. Bisseling, C. Cerjan, M. D. Feit, R. Friesner, A. Gulberg, A. Hammerich, G. Jolicard, W. Karrlein, H.-D. Meyer, N. Lipkin, O. Roncero and R. Kosloff, J. Comput. Phys., 1991, 94, 59–80 CrossRef.
- T. N. Truong, J. J. Tanner, P. Bala, J. A. McCammon, D. J. Kouri, B. Lesyng and D. K. Hofmann, J. Chem. Phys., 1992, 96, 2077–2084 CrossRef CAS.
- J. V. Lill, G. A. Parker and J. C. Light, Chem. Phys. Lett., 1982, 89, 483–489 CrossRef CAS; J. C. Light, I. P. Hamilton and J. V. Lill, J. Chem. Phys., 1985, 82, 1400–1409 CrossRef; Z. Bačić and J. C. Light, Annu. Rev. Phys. Chem., 1989, 40, 469–498 CrossRef.
- R. T. Skodje, R. Sadeghi, H. Köppel and J. L. Krause, J. Chem. Phys., 1994, 101, 1725–1729 CrossRef CAS.
- U. Manthe, PhD thesis, Universität Heidelberg, 1991 CrossRef CAS; V. Engel, Chem. Phys. Lett., 1992, 189, 76–78 CrossRef CAS; U. Manthe, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1992, 97, 9062–9071 CrossRef.
- W. H. Press, W. P. Flannery, S. A. Teukolksy and W. T. Vetterling, Numerical Recipes, Cambridge Univ. Press, 1986 Search PubMed.
- A. B. Myers, Acc. Chem. Res., 1996, 30, 519–527 CrossRef.
- S. Mukamel, Principles of nonlinear optics, Oxford Univ. Press, Oxford, 1995 Search PubMed.
- S. C. Althorpe, J. Chem. Phys., 2001, 114, 1601–1616 CrossRef CAS.
- J. J. Sakurai, in Modern Quantum Mechanics, ed. S. F. Tuan, Addison-Wesley publishing company, 1994, p. 101 Search PubMed.
- S. Kolakkandy, K. Giri and N. Sathyamurthy, J. Chem. Phys., 2012, 136, 244312 CrossRef.
- R. Heather and H. Metiu, J. Chem. Phys., 1987, 86, 5009–5017 CrossRef CAS.
- T. Peng and J. Z. H. Zhang, J. Chem. Phys., 1996, 105, 6072–6074 CrossRef CAS; W. Zhu, T. Peng and J. Z. H. Zhang, J. Chem. Phys., 1997, 106, 1742–1748 CrossRef.
- R. S. Judson, D. J. Kouri, D. Neuhauser and M. Baer, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 351–366 CrossRef CAS; S. Y. Lin and H. Guo, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 022703 CrossRef; S. Gómez-Carrasco and O. Roncero, J. Chem. Phys., 2006, 125, 054102 CrossRef.
- A. Zanchet, O. Roncero, T. González-Lezana, A. Rodríguez-López, A. Aguado, C. Sanz-Sanz and S. Gómez-Carrasco, J. Phys. Chem. A, 2009, 113, 14488–14501 CrossRef CAS.
- M. Hankel, S. C. Smith, R. J. Allan, S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 2006, 125, 164303 CrossRef.
- S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 1998, 108, 950–962 CrossRef CAS.
- T.-S. Chu, K.-L. Han, M. Hankel and G. G. Balint-Kurti, J. Chem. Phys., 2007, 126, 214303 CrossRef.
- M. Hankel, S. C. Smith and A. J. C. Varandas, Phys. Scr., 2011, 84, 028102 CrossRef CAS; H. Yang, K.-L. Han, G. C. Schatz, S.-H. Lee, K. Liu, S. C. Smith and M. Hankel, Phys. Chem. Chem. Phys., 2009, 11, 11587–11595 RSC; P. G. Jambrina, F. J. Aoiz, N. Bulut, S. C. Smith, G. G. Balint-Kurti and M. Hankel, Phys. Chem. Chem. Phys., 2010, 12, 1102–1115 RSC; R. Lü, T.-S. Chu, Z.-S. Chang and W.-Q. Zhang, Bull. Chem. Soc. Jpn., 2014, 87, 670–676 CrossRef; Z. Shen, H. Ma, C. Zhang, M. Fu, Y. Wu, W. Bian and J. Cao, Nat. Commun., 2017, 8, 14094 CrossRef.
- Z. Sun, X. Xu, S. Y. Lee and D. H. Zhang, J. Phys. Chem. A, 2009, 113, 4145–4154 CrossRef CAS.
- Z. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112 CrossRef.
- T. Rajagopala Rao and S. Mahapatra, J. Chem. Phys., 2011, 134, 204307 CrossRef.
- S. Ghosh, S. Mukherjee, B. Mukherjee, S. Mandal, R. Sharma, P. Chaudhury and S. Adhikari, J. Chem. Phys., 2017, 147, 074105 CrossRef.
- A. J. C. Varandas and H. G. Yu, J. Chem. Soc., Faraday Trans., 1997, 93, 819–824 RSC.
- H. Zhao, X. Hu, D. Xie and Z. Sun, J. Chem. Phys., 2018, 149, 174103 CrossRef.
- N. Balakrishnan and N. Sathyamurthy, Proc. Indiana Acad. Sci., 1994, 106, 531–538 CAS.
- A. J. H. M. Meijer and E. M. Goldfield, Phys. Chem. Chem. Phys., 2001, 3, 2811–2818 RSC.
- R. Padmanaban and S. Mahapatra, J. Phys. Chem. A, 2006, 110, 6039–6046 CrossRef CAS.
- T.-S. Chu and K.-L. Han, Phys. Chem. Chem. Phys., 2008, 10, 2431–2441 RSC.
- A. K. Tiwari, S. Kolakkandy and N. Sathyamurthy, J. Phys. Chem. A, 2009, 113, 9568–9574 CrossRef CAS.
- M. T. Cvitas and S. C. Althorpe, Comput. Phys. Commun., 2007, 177, 357–361 CrossRef CAS.
- M. Hankel, S. C. Smith, S. K. Gray and G. G. Balint-Kurti, Comput. Phys. Commun., 2008, 179, 569–578 CrossRef CAS.
- S. Adhikari and A. J. C. Varandas, Comput. Phys. Commun., 2013, 184, 270–283 CrossRef CAS.
- A. J. H. M. Meijer and E. M. Goldfield, J. Chem. Phys., 2000, 113, 11055–11062 CrossRef.
- J. von Neumann and E. Wigner, Phys. Z., 1929, 30, 465–467 Search PubMed.
- R. Renner, Z. Phys., 1934, 92, 172–193 CrossRef CAS.
- E. Teller, J. Phys. Chem., 1937, 41, 109–116 CrossRef CAS.
- H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220–235 CAS.
- H. C. Longuet-Higgins, U. Opik, M. H. L. Pryce and R. A. Sack, Proc. R. Soc. London, Ser. A, 1958, 244, 1–16 CAS.
- G. Herzberg and H. C. Longuet-Higgins, Discuss. Faraday Soc., 1963, 35, 77–82 RSC.
- H. C. Longuet-Higgins, in Advances in Spectroscopy, ed. H. W. Thompson, Interscience, New York, 1961, vol. II; H. C. Longuet-Higgins, Proc. Roy. Soc. London, Ser. A, 1975, 344, 147–156 Search PubMed.
- M. D. Sturge, Solid State Phys., 1967, 20, 91–211 Search PubMed.
- R. Englman, The Jahn-Teller Effect in Molecules and Crystals, Wiley, New York, 1972 Search PubMed.
- T. Carrington, Discuss. Faraday Soc., 1972, 53, 27–34 RSC; T. Carrington, Acc. Chem. Res., 1974, 7, 20–25 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef CAS.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 Search PubMed.
- I. B. Bersuker, The Jahn-Teller Effect and Vibronic interactions in Modern Chemistry, Plenum Press, New York, 1984 Search PubMed; I. B. Bersuker and V. Z. Polinger, Vibronic interactions in Molecules and Crystals, Springer-Verlag, Berlin, 1989 Search PubMed.
- G. Fischer, Vibronic coupling, Academic Press, New York, 1984 Search PubMed.
- R. L. Whetten, G. S. Ezra and E. R. Grant, Annu. Rev. Phys. Chem., 1985, 36, 277–320 CrossRef CAS.
- B. H. Lengsfield and D. R. Yarkony, Adv. Chem. Phys., 1992, 82, 1–71 CAS.
- W. Domcke and G. Stock, Adv. Chem. Phys., 1997, 100, 1–169 Search PubMed; F. Bernadi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321–328 RSC.
- Conical intersections in Photochemistry, Spectroscopy and Chemical Dynamics, in Chemical Physics, ed. Y. Hass, M. Klessinger and S. Zilberg, Elsevier, 2000, vol. 259 Search PubMed.
- G. A. Worth and M. A. Robb, Adv. Chem. Phys., 2002, 124, 355–431 CAS.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS.
- Conical Intersections: Theory, Computation and Experiment, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientific, Singapore, 2011, vol. 17 Search PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 84, 457–484 CrossRef CAS.
- M. Born and K. Huang, Dynamical theory of Crystal Lattices, Oxford University Press, New York, 1954 Search PubMed.
- W. Pauli Jr, Ann. Phys., 1922, 68, 177–240 CrossRef CAS; P. Güttinger, Z. Phys., 1932, 73, 169–184 CrossRef; H. G. A. Hellmann, Z. Phys., 1933, 85, 180–190 CrossRef; R. P. Feynman, Phys. Rev., 1939, 56, 340–343 CrossRef.
- W. Lichten, Phys. Rev., 1963, 131, 229–238 CrossRef CAS.
- F. T. Smith, Phys. Rev., 1969, 179, 111–123 CrossRef.
- M. Baer, Chem. Phys. Lett., 1975, 35, 112–118 CrossRef CAS; M. Baer, Mol. Phys., 1980, 40, 1011–1013 CrossRef.
- Z. H. Top and M. Baer, J. Chem. Phys., 1977, 66, 1363–1371 CrossRef CAS.
- E. F. van Dishoeck, M. C. van Hemert, A. C. Allison and A. Dalgarno, J. Chem. Phys., 1984, 81, 5709–5724 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1982, 77, 6090–6098 CrossRef CAS.
- T. F. O'Malley, Adv. At. Mol. Phys., 1971, 7, 223–249 Search PubMed; C. I. Ballhausen and A. E. Hansen, Annu. Rev. Phys. Chem., 1972, 23, 15–38 CrossRef CAS; V. Sidis, Adv. Chem. Phys., 1992, 82, 73–134 Search PubMed; M. Baer, Adv. Chem. Phys., 1992, 82, 187–241 Search PubMed.
- T. Pacher, L. S. Cederbaum and H. Köppel, Adv. Chem. Phys., 1993, 84, 293–391 CAS.
- H. Köppel, in ref. 77, pp. 175–204.
- A. Thiel and H. Köppel, J. Chem. Phys., 1999, 110, 9371–9383 CrossRef CAS.
- H. Köppel, J. Gronki and S. Mahapatra, J. Chem. Phys., 2001, 115, 2377–2388 CrossRef.
- D. R. Yarkony, Acc. Chem. Res., 1998, 31, 511–518 CrossRef CAS.
- S. Mahapatra, Acc. Chem. Res., 2009, 42, 1004–1015 CrossRef CAS.
- C. A. Mead, Rev. Mod. Phys., 1992, 64, 51–85 CrossRef CAS.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45–57 Search PubMed.
- S. Pancharatnam, Proc. - Indian Acad. Sci., Sect. A, 1956, 44, 247–262 CrossRef.
- B. K. Kendrick, in ref. 77, pp. 521–553.
- M. Baer, J. Chem. Phys., 1997, 107, 2694–2695 CrossRef CAS.
- M. Baer, J. Chem. Phys., 1997, 107, 10662–10666 CrossRef CAS.
- U. Manthe and H. Köppel, J. Chem. Phys., 1990, 93, 345–356 CrossRef CAS; U. Manthe and H. Köppel, J. Chem. Phys., 1990, 93, 1658–1669 CrossRef; U. Manthe, H. Köppel and L. S. Cederbaum, J. Chem. Phys., 1991, 95, 1708–1720 CrossRef.
- S. Mahapatra, H. Köppel and L. S. Cederbaum, J. Phys. Chem. A, 2001, 105, 2321–2329 CrossRef CAS.
- S. Mahapatra, in ref. 77, pp. 555–581.
- B. Maiti, S. Mahapatra and N. Sathyamurthy, J. Chem. Phys., 2000, 113, 59–66 CrossRef CAS.
- B. Maiti and N. Sathyamurthy, Chem. Phys. Lett., 2001, 345, 461–470 CrossRef CAS.
- P. Bhatia, B. Maiti, N. Sathyamurthy, S. Stamatiadis and S. C. Farantos, Phys. Chem. Chem. Phys., 1999, 1, 1105–1113 RSC; B. Maiti, N. Sathyamurthy, S. Stamatiadis and S. C. Farantos, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2000, 39, 338–344 Search PubMed.
- D. Koner, J. C. S. V. Veliz, A. van der Avoird and M. Meuwly, Phys. Chem. Chem. Phys., 2019, 21, 24976–24983 RSC.
- A. N. Panda and N. Sathyamurthy, J. Phys. Chem. A, 2003, 107, 7125–7131 CrossRef CAS.
- J. S. Lee and D. Secrest, J. Chem. Phys., 1986, 85, 6565–6575 CrossRef CAS.
- D. Koner, M. Schwilk, S. Patra, E. J. Bieske and M. Meuwly, 2020, arXiv:2004.12404v1.
- J. Tennyson, M. A. Kostin, P. Barletta, G. J. Harris, O. L. Polyansky, J. Ramanlal and N. F. Zobov, Comput. Phys. Commun., 2004, 163, 85–116 CrossRef.
- F. J. Aoiz, L. Bañares and V. J. Herrero, Int. Rev. Phys. Chem., 2005, 24, 119–190 Search PubMed.
- J. Stärck and W. Meyer, Chem. Phys., 1993, 176, 83–95 CrossRef.
- S. Mahapatra, N. Sathyamurthy, S. Kumar and F. A. Gianturco, Chem. Phys. Lett., 1995, 241, 223–228 CrossRef CAS.
- S. Mahapatra and N. Sathyamurthy, J. Phys. Chem., 1996, 100, 2759–2761 CrossRef CAS.
- A. N. Panda and N. Sathyamurthy, J. Chem. Phys., 2004, 121, 9343–9351 CrossRef CAS.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128–135 CrossRef CAS.
- R. Jaquet and M. Heinen, J. Phys. Chem., 2001, 105, 2738–2747 CrossRef CAS.
- S. Mahapatra, Phys. Chem. Chem. Phys., 2000, 2, 671–677 RSC.
- A. N. Panda, K. Giri and N. Sathyamurthy, J. Phys. Chem. A, 2005, 109, 2057–2061 CrossRef CAS.
- M. Zimmer and F. Linder, Chem. Phys. Lett., 1992, 195, 153–158 CrossRef CAS; M. Zimmer and F. Liner, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2671–2687 CrossRef.
- M. S. Huq, L. D. Doverspike and R. L. Champion, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 27, 2831–2839 CrossRef.
- E. Haufler, S. Schlemmer and D. Gerlich, J. Phys. Chem. A, 1997, 101, 6441–6447 CrossRef CAS.
- K. Giri and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 13843–13849 CrossRef CAS.
- C. Stroud, N. Sathyamurthy, R. Rangarajan and L. M. Raff, Chem. Phys. Lett., 1977, 48, 350–353 CrossRef CAS.
- N. Balakrishnan and N. Sathyamurthy, Comput. Phys. Commun., 1991, 63, 209–215 CrossRef CAS.
- D. R. McLaughlin and D. L. Thompson, J. Chem. Phys., 1979, 70, 2748–2769 CrossRef CAS.
- T. Joseph and N. Sathyamurthy, J. Chem. Phys., 1987, 86, 704–714 CrossRef CAS.
- N. Balakrishnan and N. Sathyamurthy, Chem. Phys. Lett., 1993, 201, 294–300 CrossRef CAS.
- N. Balakrishnan and N. Sathyamurthy, Chem. Phys. Lett., 1995, 240, 119–124 CrossRef CAS.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255–282 CrossRef.
- T. J. Park and J. C. Light, J. Chem. Phys., 1986, 85, 5870–5876 CrossRef CAS.
- K. Sakimoto and K. Onda, Chem. Phys. Lett., 1994, 226, 227–234 CrossRef CAS.
- N. Sathyamurthy, T. Joseph and M. Baer, Chem. Phys., 1987, 114, 73–83 CrossRef CAS.
- V. Balasubramanian, B. K. Mishra, A. Bahel, S. Kumar and N. Sathyamurthy, J. Chem. Phys., 1991, 95, 4160–4167 CrossRef CAS.
- S. Mahapatra and N. Sathyamurthy, J. Chem. Phys., 1995, 102, 6057–6066 CrossRef CAS.
- S. Mahapatra, N. Sathyamurthy and R. Ramaswamy, Pramana, 1997, 48, 411–424 CrossRef CAS.
- S. Mahapatra, R. Ramaswamy and N. Sathyamurthy, J. Chem. Phys., 1996, 104, 3989–3997 CrossRef CAS.
- S. Mahapatra and N. Sathyamurthy, J. Chem. Phys., 1996, 105, 10934–10943 CrossRef CAS.
- S. Mahapatra and N. Sathyamurthy, J. Chem. Phys., 1997, 107, 6621–6626 CrossRef CAS.
- C. Kalyanaraman, D. C. Clary and N. Sathyamurthy, J. Chem. Phys., 1999, 111, 10910–10918 CrossRef CAS.
- B. Maiti, C. Kalyanaraman, A. N. Panda and N. Sathyamurthy, J. Chem. Phys., 2002, 117, 9719–9726 CrossRef CAS.
- W. A. Chupka, M. E. Russell and K. Refaey, J. Chem. Phys., 1968, 48, 1518–1527 CrossRef CAS.
- W. A. Chupka and M. E. Russell, J. Chem. Phys., 1968, 49, 5426–5437 CrossRef CAS.
- A. N. Panda and N. Sathyamurthy, J. Chem. Phys., 2005, 122, 054304 CrossRef.
- P. Palmieri, C. Puzzarini, V. Aquilanti, G. Capecchi, S. Cavalli, D. De Fazio, A. Aguilar, X. Giménez and J. M. Lucas, Mol. Phys., 2000, 98, 1835–1849 CrossRef CAS.
- A. K. Tiwari, A. N. Panda and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 389–395 CrossRef CAS.
- A. K. Tiwari and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 11200–11207 CrossRef CAS.
- C. N. Ramachandran, D. De Fazio, S. Cavalli, F. Tarantelli and V. Aquilanti, Chem. Phys. Lett., 2009, 469, 26–30 CrossRef CAS.
- W. A. Chupka, J. Berkowitz and M. E. Russell, Sixth International Conference on the Physics of Electronic and Atomic Collisions, MIT, Cambridge, 1969, p. 71 Search PubMed.
- W. A. Chupka, in Ion-molecule reactions, ed. J. L. Franklin, Plenum, New York, 1972, ch. 3, vol. 1, p. 72 Search PubMed.
- D. Yuan, Y. Guan, W. Chen, H. Zhao, S. Yu, C. Luo, Y. Tan, T. Xie, X. Wang, Z. Sun and D. H. Zhang, Science, 2018, 362, 1289–1293 CrossRef CAS; S. Zhang, Z. Tan, H. Zhang, Y. Zhang and J. Z. H. Zhang, Chem. Phys., 2000, 255, 397–402 CrossRef; D. Yuan, S. Yu, W. Chen, J. Sang, C. Luo, T. Wang, X. Xu, P. Casavecchia, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Nat. Chem., 2018, 10, 653–658 CrossRef.
- D. Yuan, W. Chen, C. Luo, Y. Tan, S. Li, Y. Huang, Z. Sun, X. Yang and X. Wang, J. Phys. Chem. Lett., 2020, 11, 1222–1227 CrossRef CAS; N. C.-M. Bartlett, J. Jankunas, T. Goswami, R. N. Zare, F. Bouakline and S. C. Althorpe, Phys. Chem. Chem. Phys., 2011, 13, 8175–8179 RSC; H. Gao, M. Sneha, F. Bouakline, S. C. Althorpe and R. N. Zare, J. Phys. Chem. A, 2015, 119, 12036–12042 CrossRef; J. Jankunas, M. Sneha, R. N. Zare, F. Bouakline and S. C. Althorpe, J. Chem. Phys., 2013, 138, 094310 CrossRef; S. Sukiasyan and H.-D. Meyer, J. Chem. Phys., 2002, 116, 10641–10647 CrossRef.
- D. Neuhauser, R. S. Judson, R. L. Jaffe, M. Baer and D. J. Kouri, Chem. Phys. Lett., 1991, 176, 546–550 CrossRef CAS; D. H. Zhang, S.-Y. Lee and M. Baer, J. Chem. Phys., 2000, 112, 9802–9809 CrossRef.
- T. Peng, D. H. Zhang, J. Z. H. Zhang and R. Schinke, Chem. Phys. Lett., 1996, 248, 37–42 CrossRef CAS; J. Dai, J. Chem. Phys., 1997, 107, 4934–4942 CrossRef; G. G. Balint-Kurti, A. I. Gonzalez, E. M. Goldfield and S. K. Gray, Faraday Discuss., 1998, 110, 169–183 RSC; S. K. Gray, E. M. Goldfield, G. C. Schatz and G. G. Balint-Kurti, Phys. Chem. Chem. Phys., 1999, 1, 1141–1148 RSC; M. Hankel, G. G. Balint-Kurti and S. K. Gray, J. Chem. Phys., 2000, 113, 9658–9677 CrossRef; T. Carroll and E. Goldfield, J. Phys. Chem. A, 2001, 105, 2251–2256 CrossRef; S. Y. Lin and H. Guo, Chem. Phys. Lett., 2004, 385, 193–197 CrossRef; S. Y. Lin and H. Guo, J. Chem. Phys., 2008, 129, 124311 CrossRef.
- T. González-Lezana, P. Larrégaray, L. Bonnet, Y. Wu and W. Bian, J. Chem. Phys., 2018, 148, 234305 CrossRef CAS; Z. Shen, J. Cao and W. Bian, J. Chem. Phys., 2015, 142, 164309 CrossRef; Z.-P. Sun, W.-K. Zhao and C.-L. Yang, J. Chem. Phys., 2017, 117, e25431 Search PubMed; L. Mouret, J.-M. Launay, M. Terao-Dunseath and K. Dunseath, Phys. Chem. Chem. Phys., 2004, 6, 4105–4110 RSC; S. Y. Lin and H. Guo, J. Chem. Phys., 2003, 119, 11602–11608 CrossRef; S. Y. Lin and H. Guo, J. Phys. Chem. A, 2004, 108, 2141–2148 CrossRef; S. Y. Lin and H. Guo, J. Chem. Phys., 2004, 121, 1285–1292 CrossRef.
- S. Ghosh, R. Sharma, S. Adhikari and A. J. C. Varandas, Phys. Chem. Chem. Phys., 2019, 21, 20166–20176 RSC; S. Y. Lin, H. Guo, P. Honvault and D. Xie, J. Phys. Chem. A, 2006, 110, 23641–23643 CrossRef CAS; P. Bargueño, T. González-Lezana, P. Larrégaray, L. Bonnet and J. C. Rayez, Phys. Chem. Chem. Phys., 2007, 9, 1127–1137 RSC; S. Y. Lin, H. Guo, G. Lendvay and D. Xie, Phys. Chem. Chem. Phys., 2009, 11, 4715–4721 RSC; S. Y. Lin, E. J. Rackham and H. Guo, J. Phys. Chem. A, 2006, 110, 1534–1540 CrossRef; S. Y. Lin, Z. Sun, H. Guo, D. H. Zhang, P. Honvault, D. Xie and S.-Y. Lee, J. Phys. Chem. A, 2008, 112, 602–611 CrossRef; Z. Sun, D. H. Zhang, C. Xu, S. Zhou, D. Xie, G. Lendvay, S.-Y. Lee, S. Y. Lin and H. Guo, J. Am. Chem. Soc., 2008, 130, 14962–14963 CrossRef; M. Hankel, S. C. Smith and A. J. H. M. Meijer, J. Chem. Phys., 2007, 127, 064316 CrossRef.
- P. Defazio, S. K. Gray, C. Petrongolo and C. Oliva, J. Chem. Phys., 2001, 115, 3208–3214 CrossRef CAS; P. Defazio, C. Petrongolo, C. Oliva, M. González and R. Sayós, J. Chem. Phys., 2002, 117, 3647–3655 CrossRef.
- P. Bargueño, P. G. Jambrina, J. M. Alvariño, M. Menéndez, E. Verdasco, M. Hankel, S. C. Smith, F. J. Aoiz and T. González-Lezana, Phys. Chem. Chem. Phys., 2011, 13, 8502–8514 RSC; H. Yang, K.-L. Han, S. Nanbu, G. G. Balint-Kurti, H. Zhang, S. C. Smith and M. Hankel, J. Theor. Comput. Chem., 2009, 8, 1003–1024 CrossRef CAS; H. Yang, K.-L. Han, S. Nanbu, H. Nakamura, G. G. Balint-Kurti, H. Zhang, S. C. Smith and M. Hankel, J. Chem. Phys., 2008, 128, 014308 CrossRef; M. Bittererová, J. M. Bowman and K. Peterson, J. Chem. Phys., 2000, 113, 6186–6196 CrossRef; M. Bittererová and J. M. Bowman, J. Chem. Phys., 2000, 113, 1–3 CrossRef; S. Y. Lin, K.-L. Han and J. Z. H. Zhang, Chem. Phys. Lett., 2000, 324, 122–126 CrossRef.
- B.-Y. Tang, B.-H. Yang, K.-L. Han, R.-Q. Zhang and J. Z. H. Zhang, J. Chem. Phys., 2000, 113, 10105–10113 CrossRef CAS; P. Defazio and C. Petrongolo, J. Phys. Chem. A, 2009, 113, 4208–4212 CrossRef; A. Li, H. Guo, Z. Sun, J. Kłos and M. H. Alexander, Phys. Chem. Chem. Phys., 2013, 15, 15347–15355 RSC; N. Bulut, J. Kłos and M. H. Alexander, J. Chem. Phys., 2012, 136, 104304 CrossRef.
- M.-D. Chen, B.-Y. Tang, K.-L. Han, N.-Q. Lou and J. Z. H. Zhang, J. Chem. Phys., 2003, 118, 6852–6857 CrossRef CAS; C. Xie, A. Li, D. Xie and H. Guo, J. Chem. Phys., 2011, 135, 164312 CrossRef; N. Bulut, O. Roncero, M. Jorfi and P. Honvault, J. Chem. Phys., 2011, 135, 104307 CrossRef; A. Li, C. Xie, D. Xie and H. Guo, J. Chem. Phys., 2011, 134, 194309 CrossRef; M.-H. Ge, T.-S. Chu and K.-L. Han, J. Theor. Comput. Chem., 2008, 7, 607–613 CrossRef.
- S. Y. Lin, H. Guo and P. Honvault, Chem. Phys. Lett., 2008, 453, 140–144 CrossRef CAS; N. Bulut, A. Zanchet, P. Honvault, B. Bussery-Honvault and L. Bañares, J. Chem. Phys., 2009, 130, 194303 CrossRef; M. Jorfi, P. Honvault, B. Bussery-Honvault, L. Bañares and N. Bulut, Mol. Phys., 2011, 109, 543–550 CrossRef; A. Zanchet, T. González-Lezana, O. Roncero, M. Jorfi, P. Honvault and M. Hankel, J. Chem. Phys., 2012, 136, 164309 CrossRef; T. Rajagopala Rao, S. Goswami, S. Mahapatra, B. Bussery-Honvault and P. Honvault, J. Chem. Phys., 2012, 136, 094318 Search PubMed; S. Goswami, B. Bussery-Honvault, P. Honvault and S. Mahapatra, Mol. Phys., 2017, 115, 2658–2672 CrossRef; S. Goswami, J. Sahoo, T. Rajagopala Rao, B. Bussery-Honvault, P. Honvault and S. Mahapatra, Eur. Phys. J. D, 2018, 72, 225 CrossRef.
- S. Goswami, T. Rajagopala Rao, S. Mahapatra, B. Bussery-Honvault and P. Honvault, J. Phys. Chem. A, 2014, 118, 5915–5926 CrossRef CAS.
- D. Wang, J. R. Stallcop, W. M. Huo, C. E. Dateo, D. W. Schwenke and H. Partridge, J. Chem. Phys., 2003, 118, 2186–2189 CrossRef CAS; D. Wang, W. M. Huo, C. E. Dateo, D. W. Schwenke and J. R. Stallcop, J. Chem. Phys., 2004, 120, 6041–6050 CrossRef; Y. Wang, F. Meng, P. Yan and D. Wang, Chem. Phys. Lett., 2015, 633, 202–207 CrossRef; E. Garcia, A. Laganà and D. Skouteris, Phys. Chem. Chem. Phys., 2012, 14, 1589–1595 RSC; D. Skouteris, L. Pacifici and A. Laganà, Mol. Phys., 2004, 102, 2237–2248 CrossRef.
- K.-L. Yeh, D. Xie, D. H. Zhang, S.-Y. Lee and R. Schinke, J. Phys. Chem. A, 2003, 107, 7215–7219 CrossRef CAS; C. H. Yuen, D. Lapierre, F. Gatti, V. Kokoouline and V. G. Tyuterev, J. Phys. Chem. A, 2019, 123, 7733–7743 CrossRef; Y. Li, Z. Sun, B. Jiang, D. Xie, R. Dawes and H. Guo, J. Chem. Phys., 2014, 141, 081102 CrossRef; W. Xie, L. Liu, Z. Sun, H. Guo and R. Dawes, J. Chem. Phys., 2015, 142, 064308 CrossRef; Z. Sun, D. Yu, W. Xie, J. Hou, R. Dawes and H. Guo, J. Chem. Phys., 2015, 142, 174312 CrossRef; Z. Sun, L. Liu, S. Y. Lin, R. Schinke, H. Guo and D. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 555–558 CrossRef.
- F. Gogtas, G. G. Balint-Kurti and A. Offer, J. Chem. Phys., 1996, 104, 7927–7939 CrossRef CAS; A. Aguado, M. Paniagua, M. Lara and O. Roncero, J. Chem. Phys., 1997, 106, 1013–1025 CrossRef; W. Zhu, D. Wang and J. Z. H. Zhang, Theor. Chem. Acc., 1997, 96, 31–38 Search PubMed; M. Lara, A. Aguado, M. Paniagua and O. Roncero, J. Chem. Phys., 2000, 113, 1781–1794 CrossRef; W.-T. Lia, M.-D. Chen and Z. Sun, Chin. J. Chem. Phys., 2015, 28, 415–425 CrossRef; X. Liu, C. Xie and H. Guo, Chem. Phys., 2018, 509, 66–71 CrossRef.
- J. Song and Z. Zhu, Comput. Theor. Chem., 2020, 1173, 112703 CrossRef CAS; D. He, J. Yuan, H. Li and M. Chen, Sci. Rep., 2016, 6, 25083 CrossRef; D. He, J. Yuan and M. Chen, Sci. Rep., 2017, 7, 3084 CrossRef.
- R. Padmanaban and S. Mahapatra, J. Chem. Phys., 2002, 117, 6469–6477 CrossRef CAS; R. Padmanaban and S. Mahapatra, J. Chem. Phys., 2004, 121, 7681–7691 CrossRef; R. Padmanaban and S. Mahapatra, J. Phys. Chem. A, 2006, 110, 6039–6046 CrossRef; T. Roy and S. Mahapatra, J. Chem. Phys., 2012, 136, 174313 CrossRef.
- T. Roy, T. Rajagopala Rao and S. Mahapatra, Chem. Phys. Lett., 2011, 501, 252–256 CrossRef CAS.
- B. Jayachander Rao and S. Mahapatra, J. Chem. Phys., 2007, 127, 244307 CrossRef CAS.
- X. He, W. Li, H. Meng, C. Li, G. Guo, X. Qiu and J. Wei, Phys. Chem. Chem. Phys., 2019, 21, 7196–7207 RSC , and references therein.
- S. Bhattacharya and A. N. Panda, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 085201 CrossRef.
- D. Koner and A. N. Panda, J. Phys. Chem. A, 2013, 117, 13070–13078 CrossRef CAS; D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, J. Chem. Phys., 2014, 141, 114302 CrossRef.
- D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, J. Phys. Chem. A, 2015, 119, 12052–12061 CrossRef CAS.
- D. Koner, L. Barrios, T. González-Lezana and A. N. Panda, J. Chem. Phys., 2016, 144, 034303 CrossRef.
- A. N. Panda and S. C. Althorpe, Chem. Phys. Lett., 2007, 439, 50–54 CrossRef CAS.
- A. N. Panda, J. Phys. Chem. A, 2008, 112, 5327–5331 CrossRef CAS.
- B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2016, 145, 184106 CrossRef CAS; C. Xiao, X. Xu, S. Liu, T. Wang, W. Dong, T. Yang, Z. Sun, D. Dai, X. Xu, D. H. Zhang and X. Yang, Science, 2011, 333, 440–442 CrossRef; S. Liu, C. Xiao, T. Wang, J. Chen, T. Yang, X. Xu, D. H. Zhang and X. Yang, Faraday Discuss., 2012, 157, 101–111 RSC; S. Liu, X. Xu and D. H. Zhang, J. Chem. Phys., 2012, 136, 144302 CrossRef; B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2016, 145, 134308 CrossRef; Z. Zhao, S. Liu and D. H. Zhang, J. Chem. Phys., 2016, 145, 134301 CrossRef.
- S. Liu and D. H. Zhang, Chem. Sci., 2016, 7, 261–265 RSC; D. H. Zhang and J. C. Light, J. Chem. Soc., Faraday Trans., 1997, 93, 691–697 RSC; D. H. Zhang, M. A. Collins and S.-Y. Lee, Science, 2000, 290, 961–963 CrossRef CAS; B. Fu and D. H. Zhang, J. Chem. Phys., 2013, 138, 184308 CrossRef; B. Fu and D. H. Zhang, J. Chem. Phys., 2015, 142, 064314 CrossRef; Z.-q. Zhao, S. Liu and D. H. Zhang, Chin. J. Chem. Phys., 2017, 30, 16–24 CrossRef.
- D. M. Medvedev, S. K. Gray, E. M. Goldfield, M. J. Lakin, D. Troya and G. C. Schatz, J. Chem. Phys., 2004, 120, 1231–1238 CrossRef CAS; R. Valero, D. A. McCormack and G.-J. Kroes, J. Chem. Phys., 2004, 120, 4263–4272 CrossRef; R. Valero and G.-J. Kroes, J. Phys. Chem. A, 2004, 108, 8672–8681 CrossRef; S. Liu, X. Xu and D. H. Zhang, J. Chem. Phys., 2011, 135, 141108 CrossRef; S. Liu, X. Xu and D. H. Zhang, Theor. Chem. Acc., 2012, 131, 1068 Search PubMed; J. Ma, J. Li and H. Guo, J. Phys. Chem. Lett., 2012, 3, 2482–2486 Search PubMed; C. Wang, S. Liu and D. H. Zhang, Chem. Phys. Lett., 2012, 537, 16–20 CrossRef; S. Liu, J. Chen, B. Fu and D. H. Zhang, Theor. Chem. Acc., 2014, 133, 1558 Search PubMed; D. H. Zhang, J. Chem. Phys., 2006, 125, 133102 CrossRef.
- W. Zhu, J. Z. H. Zhang, Y. C. Zhang, Y. B. Zhang, L. X. Zhan, S. L. Zhang and D. H. Zhang, J. Chem. Phys., 1998, 108, 3509–3516 CrossRef CAS; S. Bhattacharya, A. Kirwai, A. N. Panda and H.-D. Meyer, J. Chem. Sci., 2012, 124, 65–73 CrossRef; J. Z. H. Zhang and S.-Y. Lee, J. Chem. Phys., 2000, 112, 203–211 CrossRef.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 224310 CrossRef CAS; W.-Y. Ma, K.-L. Han and J. Z. H. Zhang, J. Chem. Phys., 2002, 117, 5642–5646 CrossRef; W.-Y. Ma, K.-L. Han, M. L. Wang and J. Z. H. Zhang, J. Chem. Phys., 2002, 117, 172–176 CrossRef.
- R. Liu, H. Xiong and M. Yang, J. Chem. Phys., 2012, 137, 174113 CrossRef CAS; W. Zhang, Y. Zhou, G. Wu, Y. Lu, H. Pan, B. Fu, Q. Shuai, L. Liu, S. Liu, L. Zhang, B. Jiang, D. Dai, S.-Y. Lee, Z. Xie, B. J. Braams, J. M. Bowman, M. A. Collins, D. H. Zhang and X. Yang, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12782–12785 CrossRef; Z. Zhao, Z. Zhang, S. Liu and D. H. Zhang, Nat. Commun., 2017, 8, 14506 CrossRef; M. Yang, D. H. Zhang and S.-Y. Lee, J. Chem. Phys., 2002, 117, 9539–9542 CrossRef; Y. Zhou, C. Wang and D. H. Zhang, J. Chem. Phys., 2011, 135, 024313 CrossRef; S. Liu, J. Chen, Z. Zhang and D. H. Zhang, J. Chem. Phys., 2013, 138, 011101 CrossRef; Z. Zhang, J. Chen, S. Liu and D. H. Zhang, J. Chem. Phys., 2014, 140, 224304 CrossRef; Z. Zhang and D. H. Zhang, J. Chem. Phys., 2014, 141, 144309 CrossRef.
- M. Yang, S.-Y. Lee and D. H. Zhang, J. Chem. Phys., 2007, 126, 064303 CrossRef CAS; R. Liu, M. Yang, G. Czakó, J. M. Bowman, J. Li and H. Guo, J. Phys. Chem. Lett., 2012, 3, 3776–3780 CrossRef; M.-L. Wang, Y.-M. Li and J. Z. H. Zhang, J. Phys. Chem. A, 2001, 105, 2530–2534 CrossRef; W. Yan, F. Meng and D. Wang, J. Phys. Chem. A, 2013, 117, 12236–12242 CrossRef.
- Z. Zhang, Y. Zhou, D. H. Zhang, G. Czakó and J. M. Bowman, J. Phys. Chem. Lett., 2012, 3, 3416–3419 CrossRef CAS; R. Liu, F. Wang, B. Jiang, G. Czakó, M. Yang, K. Liu and H. Guo, J. Chem. Phys., 2014, 141, 074310 CrossRef; N. Liu and M. Yang, J. Chem. Phys., 2015, 143, 134305 CrossRef.
- Z. Chen, J. Chen, R. Chen, T. Xie, X. Wang, S. Liu, G. Wu, D. Dai, X. Yang and D. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9202–9207 CrossRef CAS.
- T.-S. Chu, K.-L. Han and J. Espinosa-Garcia, J. Chem. Phys., 2009, 131, 244303 CrossRef CAS; D. Wang and G. Czakó, J. Phys. Chem. A, 2013, 117, 7124–7130 CrossRef; J. Qi, H. Song, M. Yang, J. Palma, U. Manthe and H. Guo, J. Chem. Phys., 2016, 144, 171101 CrossRef.
- R. J. Butler, Annu. Rev. Phys. Chem., 1998, 49, 125–171 CrossRef.
- A. D. Hammerich, U. Manthe, R. Kosloff, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1994, 101, 5623–5646 CrossRef.
- C. Woywod, M. Stengle, W. Domcke, H. Flöthmann and R. Schinke, J. Chem. Phys., 1997, 107, 7282–7295 CrossRef CAS; H. Flöthmann, C. Beck, R. Schinke, C. Woywod and W. Domcke, J. Chem. Phys., 1997, 107, 7296–7313 CrossRef; D. Simah, B. Hartke and H.-J. Werner, J. Chem. Phys., 1999, 111, 4523–4534 CrossRef; D. Skouteris, B. Hartke and H.-J. Werner, J. Phys. Chem. A, 2001, 105, 2458–2467 CrossRef.
- K. Drukker and G. C. Schatz, J. Chem. Phys., 1999, 111, 2451–2463 CrossRef CAS; Y.-T. Hsu, K. Liu, L. A. Pederson and G. C. Schatz, J. Chem. Phys., 1999, 111, 7931–7944 CrossRef; M. R. Hoffmann and G. C. Schatz, J. Chem. Phys., 2000, 113, 9456–9465 CrossRef; X. Liu, J. J. Lin, S. Harich, G. C. Schatz and X. Yang, Science, 2000, 289, 1536–1538 CrossRef; F. J. Aoiz, L. Bañares, J. F. Castillo, V. J. Herrero, B. Martinez-Haya, P. Honvault, J. M. Launay, X. Liu, J. J. Lin, S. Harich, C. C. Wang and X. Yang, J. Chem. Phys., 2002, 116, 10692–10703 CrossRef.
- S. K. Gray, G. G. Balint-Kurti, G. C. Schatz, J. J. Lin, X. Liu, S. Harich and X. Yang, J. Chem. Phys., 2000, 113, 7330–7344 CrossRef CAS.
- T. W. Whiteley, A. J. Dobbyn, J. N. L. Connor and G. C. Schatz, Phys. Chem. Chem. Phys., 2000, 2, 549–556 RSC.
- S.-H. Lee and K. Liu, J. Phys. Chem. A, 1998, 102, 8637–8640 CrossRef CAS; A. S. Zyubin, A. M. Mebel, S. D. Chao and R. T. Skodje, J. Chem. Phys., 2001, 114, 320–330 CrossRef.
- Y. Zhang, T.-X. Xie, K.-L. Han and J. Z. H. Zhang, J. Chem. Phys., 2003, 119, 12921–12925 CrossRef CAS; Y. Zhang, T.-X. Xie and K.-L. Han, J. Phys. Chem. A, 2003, 107, 10893–10896 CrossRef.
- M. H. Alexander, G. Capecchi and H.-J. Werner, Faraday Discuss., 2004, 127, 59–72 RSC; D. Skouteris, Z. Laganà, G. Capecchi and H.-J. Werner, Phys. Chem. Chem. Phys., 2004, 6, 5000–5006 RSC.
- S. Ghosal and S. Mahapatra, J. Chem. Phys., 2004, 121, 5740–5753 CrossRef CAS; S. Ghosal and S. Mahapatra, J. Photochem. Photobiol., A, 2007, 190, 161–168 CrossRef.
- X. Wang, W. Dong, C. Xiao, L. Che, Z. Ren, D. Dai, X. Wang, P. Casavecchia, X. Yang, B. Jiang, D. Xie, Z. Sun, S.-Y. Lee, D. H. Zhang, H.-J. Werner and M. H. Alexander, Science, 2008, 322, 573–576 CrossRef CAS.
- H. Yang, M. Hankel, Y. Zheng and A. J. C. Varandas, J. Chem. Phys., 2011, 135, 024306 CrossRef.
- T.-S. Chu, T.-X. Xie and K.-L. Han, J. Chem. Phys., 2004, 121, 9352–9360 CrossRef CAS; P. Defazio, P. Gamallo and C. Pentrogolo, J. Chem. Phys., 2012, 136, 054308 CrossRef.
- S. Wang, Z. Yiang, J. Yuan and M. Chen, Sci. Rep., 2018, 8, 17960 CrossRef CAS.
- L. A. Pederson, G. C. Schatz, T. Hollebeek, T.-S. Ho, H. Rabitz and L. B. Harding, J. Phys. Chem. A, 2000, 104, 2301–2307 CrossRef CAS.
- N. Marković and G. D. Billing, Chem. Phys., 1995, 191, 247–260 CrossRef CAS; T.-S. Chu, A. J. C. Varandas and K.-L. Han, Chem. Phys. Lett., 2009, 471, 222–228 CrossRef; S. Ghosh, T. Sahoo, S. Adhikari, R. Sharma and A. J. C. Varandas, J. Phys. Chem. A, 2015, 119, 12392–12403 CrossRef.
- T. S. Chu and K.-L. Han, J. Phys. Chem. A, 2005, 109, 2050–2056 CrossRef CAS; R.-F. Lu, T. S. Chu and K.-L. Han, J. Phys. Chem. A, 2005, 109, 6683–6688 CrossRef.
- B. Zhao and U. Manthe, J. Chem. Phys., 2020, 152, 231102 CrossRef CAS.
- R. N. Porter, R. M. Stevens and M. Karplus, J. Chem. Phys., 1968, 49, 5163–5178 CrossRef CAS.
- P. Siegbahn and B. Liu, J. Chem. Phys., 1978, 68, 2457–2465 CrossRef CAS; D. G. Truhlar and C. J. Horowitz, J. Chem. Phys., 1978, 68, 2466–2476 CrossRef; D. G. Truhlar and C. J. Horowitz, J. Chem. Phys., 1979, 71, 1514(E) CrossRef.
- A. J. C. Varandas, F. B. Brown, C. A. Mead, D. G. Truhlar and N. C. Blais, J. Chem. Phys., 1987, 86, 6258–6269 CrossRef CAS.
- A. I. Boothroyd, W. J. Keogh, P. G. Martin and M. R. Peterson, J. Chem. Phys., 1991, 95, 4343–4359 CrossRef CAS.
- A. I. Boothroyd, W. J. Keogh, P. G. Martin and M. R. Peterson, J. Chem. Phys., 1996, 104, 7139–7152 CrossRef CAS.
- R. Abrol, A. Shaw, A. Kuppermann and D. R. Yarkony, J. Chem. Phys., 2001, 115, 4640–4659 CrossRef CAS.
- R. Abrol and A. Kuppermann, J. Chem. Phys., 2002, 116, 1035–1062 CrossRef CAS.
- B. Lepetit, Z. Peng and A. Kuppermann, Chem. Phys. Lett., 1990, 166, 572–580 CrossRef CAS.
- A. J. C. Varandas and H. G. Yu, Chem. Phys. Lett., 1996, 259, 336–341 CrossRef CAS.
- R.-F. Lu, T. S. Chu, Y. Zhang, K.-L. Han, A. J. C. Varandas and J. Z. H. Zhang, J. Chem. Phys., 2006, 125, 133108 CrossRef.
- S. Mahapatra and H. Köppel, J. Chem. Phys., 1998, 109, 1721–1733 CrossRef CAS.
- R. Bruckmeier, Ch. Wunderlich and H. Figger, Phys. Rev. Lett., 1994, 72, 2550–2553 CrossRef CAS.
- S. Mahapatra and H. Köppel, Phys. Rev. Lett., 1998, 81, 3116–3119 CrossRef CAS.
- C. A. Mead, J. Chem. Phys., 1980, 72, 3839–3840 CrossRef CAS.
- B. Lepetit and A. Kuppermann, Chem. Phys. Lett., 1990, 166, 581–588 CrossRef CAS.
- Y. M. Wu, A. Kuppermann and B. Lepetit, Chem. Phys. Lett., 1991, 186, 319–328 CrossRef CAS.
- A. Kuppermann and Y.-S. M. Wu, Chem. Phys. Lett., 1993, 205, 577–586 CrossRef CAS.
- A. Kuppermann and Y.-S. M. Wu, Chem. Phys. Lett., 1995, 241, 229–240 CrossRef CAS.
- A. Kuppermann and Y.-S. M. Wu, Chem. Phys. Lett., 2001, 349, 537–546 CrossRef CAS.
- L. Schnieder, K. Seekamp-Rahn, J. Borkowski, E. Wrede, K. Welge, F. J. Aoiz, L. Bañares, M. J. D’Mello, V. J. Herrero, V. Sáez Rábanos and R. E. Wyatt, Science, 1995, 269, 207–210 CrossRef CAS; E. Wrede, L. Schnieder, K. H. Welge, F. J. Aoiz, L. Bañares, J. F. Castillo, B. Martínez-Haya and V. J. Herrero, J. Chem. Phys., 1999, 110, 9971–9981 CrossRef.
- S. C. Althorpe, F. Fernández-Alonso, B. D. Bean, J. D. Ayres, A. E. Pomerantz, R. N. Zare and E. Wrede, Nature, 2002, 416, 67–70 CrossRef CAS.
- S. A. Harich, D. Dai, C. C. Wang, X. Yang, S. D. Chao and R. T. Skodje, Nature, 2002, 419, 281–284 CrossRef CAS.
- D. Dai, C. C. Wang, S. A. Harich, X. Wang, X. Yang, S. D. Chao and R. T. Skodje, Science, 2003, 300, 1730–1734 CrossRef CAS.
- K. Koszinowski, N. T. Goldberg, J. Zhang, R. N. Zare, F. Bouakline and S. C. Althorpe, J. Chem. Phys., 2007, 127, 124315 CrossRef.
- K. Koszinowski, N. T. Goldberg, A. E. Pomerantz, R. N. Zare, J. C. Juanes-Marcos and S. C. Althorpe, J. Chem. Phys., 2005, 123, 054306 CrossRef.
- B. K. Kendrick, J. Chem. Phys., 2000, 112, 5679–5704 CrossRef CAS; B. K. Kendrick, J. Phys. Chem. A, 2003, 107, 6739–6756 CrossRef; B. K. Kendrick, J. Chem. Phys., 2003, 118, 10502–10522 CrossRef.
- J. C. Juanes-Marcos and S. C. Althorpe, J. Chem. Phys., 2005, 122, 204324 CrossRef.
- F. Bouakline, S. C. Althorpe and D. Peláez Ruiz, J. Chem. Phys., 2008, 128, 124322 CrossRef.
- D. Yuan, Y. Guan, W. Chen, H. Zhao, S. Yu, C. Luo, Y. Tan, T. Xie, X. Wang, Z. Sun, D. H. Zhang and X. Yang, Science, 2018, 362, 1289–1293 CrossRef CAS; Y. Xie, H. Zhao, Y. Wang, Y. Huang, T. Wang, X. Xu, C. Xiao, Z. Sun, D. H. Zhang and X. Yang, Science, 2020, 368, 767–771 CrossRef.
- B. Jayachander Rao and S. Mahapatra, J. Chem. Sci., 2009, 121, 789–795 CrossRef.
- R. Padmanaban and S. Mahapatra, J. Theor. Comput. Chem., 2006, 5, 871–885 CrossRef CAS.
- B. Jayachander Rao, R. Padmanaban and S. Mahapatra, Chem. Phys., 2007, 333, 135–147 CrossRef.
- T. Rajagopala Rao, B. Jayachander Rao and S. Mahapatra, Chem. Phys., 2009, 365, 129–137 CrossRef CAS; S. Ghosal, B. Jayachander Rao and S. Mahapatra, J. Chem. Sci., 2007, 119, 401–407 CrossRef.
- G. W. Johnston, B. Katz, K. Tsukiyama and R. Bersohn, J. Phys. Chem., 1987, 91, 5445–5451 CrossRef CAS; A. A. Westenberg and N. De Haas, J. Chem. Phys., 1967, 47, 1393–1405 CrossRef.
- J. Jankunas, M. Sneha, R. N. Zare, F. Bouakline, S. C. Althorpe, D. Herráez-Aguilar and F. J. Aoiz, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15–20 CrossRef CAS.
- T.-X. Xie, Y. Zhang, M.-Y. Zhao and K.-L. Han, Phys. Chem. Chem. Phys., 2003, 5, 2034–2038 RSC; Y. Zhang, T.-X. Xie, K.-L. Han and J. Z. H. Zhang, J. Chem. Phys., 2004, 120, 6000–6004 CrossRef CAS; Y. Zhang, T.-X. Xie, K.-L. Han and J. Z. H. Zhang, J. Chem. Phys., 2006, 124, 134301 CrossRef.
- D. Skouteris, A. Laganà, G. Capecchi and H.-J. Werner, Phys. Chem. Chem. Phys., 2004, 6, 5000–5006 RSC; Z. Sun, D. H. Zhang and M. H. Alexander, J. Chem. Phys., 2010, 132, 034308 CrossRef CAS.
- B. Jiang, C. Xie and D. Xie, J. Chem. Phys., 2011, 135, 164311 CrossRef; C. Xie, B. Jiang, D. Xie and Z. Sun, J. Chem. Phys., 2012, 136, 114310 CrossRef.
- S. K. Gray, C. Pentrogolo, K. Drukker and G. C. Schatz, J. Phys. Chem. A, 1999, 103, 9448–9459 CrossRef CAS; Z. Sun, S. Y. Lin and Y. Zheng, J. Chem. Phys., 2011, 135, 234301 CrossRef; T.-S. Chu, X. Zhang and K.-L. Han, J. Chem. Phys., 2005, 122, 214301 CrossRef; S. Y. Lin and H. Guo, J. Phys. Chem. A, 2009, 113, 4285–4293 CrossRef; J. Zhao, J. Chem. Phys., 2013, 138, 134309 CrossRef; B. Han and Y. Zheng, J. Comput. Chem., 2011, 32, 3520–3525 CrossRef.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS; E. J. Heller, J. Chem. Phys., 1981, 75, 2923–2931 CrossRef.
- M. F. Herman and E. A. Kluk, Chem. Phys., 1984, 91, 27–34 CrossRef CAS; W. H. Miller, J. Phys. Chem. A, 2001, 105, 2942–2955 CrossRef; M. Thoss and H. Wang, Annu. Rev. Phys. Chem., 2004, 55, 299–332 CrossRef; E. Martin-Fierro and E. Pollak, J. Chem. Phys., 2007, 126, 164108 CrossRef.
- A. D. McLachlan, Mol. Phys., 1964, 8, 39–44 CrossRef.
- G. D. Billing, Chem. Phys. Lett., 1975, 30, 391–393 CrossRef CAS; G. D. Billing, Chem. Phys., 1978, 33, 227–247 CrossRef; N. Balakrishnan and G. D. Billing, J. Chem. Phys., 1996, 104, 4005–4011 CrossRef; S. Adhikari and G. D. Billing, Chem. Phys. Lett., 1999, 309, 249–256 CrossRef; S. Adhikari and G. D. Billing, J. Chem. Phys., 1999, 111, 48–53 CrossRef; R. B. Gerber, V. Buch and M. A. Ratner, J. Chem. Phys., 1982, 77, 3022–3030 CrossRef; J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef; G. Stock and M. Thoss, Adv. Chem. Phys., 2005, 131, 243–375 CrossRef.
- R. P. Feynman, Rev. Mod. Phys., 1948, 20, 367–387 CrossRef CAS; N. Makri, Chem. Phys. Lett., 1992, 193, 435–445 CrossRef; S. Krempl, M. Winterstetter, H. Plöhn and W. Domcke, J. Chem. Phys., 1994, 100, 926–937 CrossRef; S. Krempl, M. Winterstetter and W. Domcke, J. Chem. Phys., 1995, 102, 6499–6510 CrossRef; N. Makri and D. E. Makarov, J. Chem. Phys., 1995, 102, 4600–4610 CrossRef.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS; U. Manthe, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1992, 97, 3199–3213 CrossRef; M. H. Beck, A. Jaekle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef.
- H. Wang, M. Thoss and W. H. Miller, J. Chem. Phys., 2001, 115, 2979–2990 CrossRef CAS.
- J. Frenkel, Wave Mechanics, Clarendon Press, Oxford, UK, 1934 Search PubMed.
- G. Schiffel and U. Manthe, J. Chem. Phys., 2010, 132, 084103 CrossRef; G. Schiffel and U. Manthe, J. Chem. Phys., 2010, 132, 191101 CrossRef; G. Schiffel and U. Manthe, J. Chem. Phys., 2010, 133, 174124 CrossRef; R. Ellerbrock and U. Manthe, J. Chem. Phys., 2017, 147, 241104 CrossRef.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2008, 128, 164116 CrossRef.
- R. Welsch and U. Manthe, J. Chem. Phys., 2012, 137, 244106 CrossRef.
- T. Kato and H. Kono, Chem. Phys. Lett., 2004, 392, 533–540 CrossRef CAS; J. Calliat, J. Zanghellini, M. Kitzler, O. Koch, W. Kreuzer and A. Scrinzi, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 012712 CrossRef; M. Nest, T. Klamroth and P. Saalfrank, J. Chem. Phys., 2005, 122, 124102 CrossRef.
- O. E. Alon, A. I. Strelstov and L. S. Cederbaum, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 033613 CrossRef; O. E. Alon, A. I. Strelstov and L. S. Cederbaum, J. Chem. Phys., 2007, 127, 154103 CrossRef.
- S. Mandal, S. Ghosh, S. Sardar and S. Adhikari, Int. Rev. Phys. Chem., 2019, 37, 607–700 Search PubMed , and references therein.
- S.-I. Sawada, R. Heather, B. Jackson and H. Metiu, J. Chem. Phys., 1985, 83, 3009–3027 CrossRef CAS; S.-I. Sawada and H. Metiu, J. Chem. Phys., 1986, 84, 227–238 CrossRef.
- I. Burghardt, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 111, 2927–2939 CrossRef CAS.
- I. Burghardt, M. Nest and G. A. Worth, J. Chem. Phys., 2003, 119, 5364–5378 CrossRef CAS; I. Burghardt, K. Giri and G. A. Worth, J. Chem. Phys., 2008, 129, 174104 CrossRef; G. A. Worth, H.-D. Meyer, H. Köppel, L. S. Cederbaum and I. Burghardt, Int. Rev. Phys. Chem., 2008, 27, 569–606 Search PubMed; S. Römer, M. Ruckenbauer and I. Burghardt, J. Chem. Phys., 2013, 138, 064106 CrossRef.
- T. J. Martínez, M. Ben-Nun and R. D. Levine, J. Phys. Chem., 1996, 100, 7884–7895 CrossRef.
- M. Ben-Nun and T. J. Martínez, J. Chem. Phys., 2000, 112, 6113–6121 CrossRef CAS; M. Ben-Nun and T. J. Martínez, Adv. Chem. Phys., 2002, 121, 439–512 CrossRef; S. Yang, J. D. Coe, B. Kaduk and T. J. Martínez, J. Chem. Phys., 2009, 130, 134113 CrossRef; M. Ben-Nun and T. J. Martínez, Isr. J. Chem., 2007, 47, 75–88 CrossRef.
- G. A. Worth and I. Burghardt, Chem. Phys. Lett., 2003, 368, 502–508 CrossRef CAS.
- D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2000, 113, 10028–10036 CrossRef CAS; D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2001, 114, 9296–9304 CrossRef; D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2001, 115, 5367–5375 CrossRef.
- D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2004, 121, 3563–3568 CrossRef CAS; D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2008, 128, 054102 CrossRef.
- D. V. Shalashilin, J. Chem. Phys., 2010, 132, 244111 CrossRef.
- B. Jackson, Annu. Rev. Phys. Chem., 1995, 46, 251–274 CrossRef CAS.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G.-J. Kroes, Science, 2009, 326, 832–834 CrossRef.
- N. Gerrits, K. Shakouri, J. Behler and G.-J. Kroes, J. Phys. Chem. Lett., 2019, 10, 1763–1768 CrossRef CAS.
- A. K. Tiwari, S. Nave and B. Jackson, Phys. Rev. Lett., 2009, 103, 253201 CrossRef.
- S. Nave, A. K. Tiwari and B. Jackson, J. Phys. Chem. A, 2014, 118, 9615–9631 CrossRef CAS.
- W. H. Miller, J. Phys. Chem., 1983, 87, 3811–3819 CrossRef CAS.
- B. Jiang, X. Ren, D. Xie and H. Guo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10224–10227 CrossRef CAS.
- P. M. Hundt, B. Jiang, M. E. van Reijzen, H. Guo and R. D. Beck, Science, 2014, 344, 504–507 CrossRef CAS.
- S. Roy, K. J. Nayanthara, N. Tiwari and A. K. Tiwari, Int. Rev. Phys. Chem., 2020, 39, 267–318 Search PubMed.
- L. Zhang and B. Jiang, Phys. Rev. Lett., 2019, 123, 106001 CrossRef CAS.
- T. Peng, D. H. Zhang, D. Wang, Y. Li and J. Z. H. Zhang, Comput. Phys. Commun., 2000, 128, 492–495 CrossRef CAS.
- R. V. Krems, Phys. Chem. Chem. Phys., 2019, 21, 13392–13410 RSC.
Footnotes |
| † Dedicated to J. P. Toennies on his 90th birthday. |
| ‡ Electronic supplementary information (ESI) available: A graphic illustration of the time evolution of a wave packet in scaled and skewed coordinates for the collinear (He, H2+) exchange reaction and that in Jacobi coordinates for 3D (He, H2+) collisions. See DOI: 10.1039/d0cp03929b |
| This journal is © the Owner Societies 2021 |